Prediction of Three Pressures and Wellbore Stability Evaluation Based on Seismic Inversion for Well Huqian-1
Abstract
1. Introduction

2. Methods
2.1. Fundamentals of Layer Seismic Inversion
2.2. Pre-Processing of Logging Data
2.3. Synthetic Seismic Records
2.4. Establishment of Initial Wave Impedance Model
2.5. Inversion Calculation
2.6. Seismic Impedance Correlated with Wellbore Stability
2.7. Procedure of Seismic Impedance Inversion
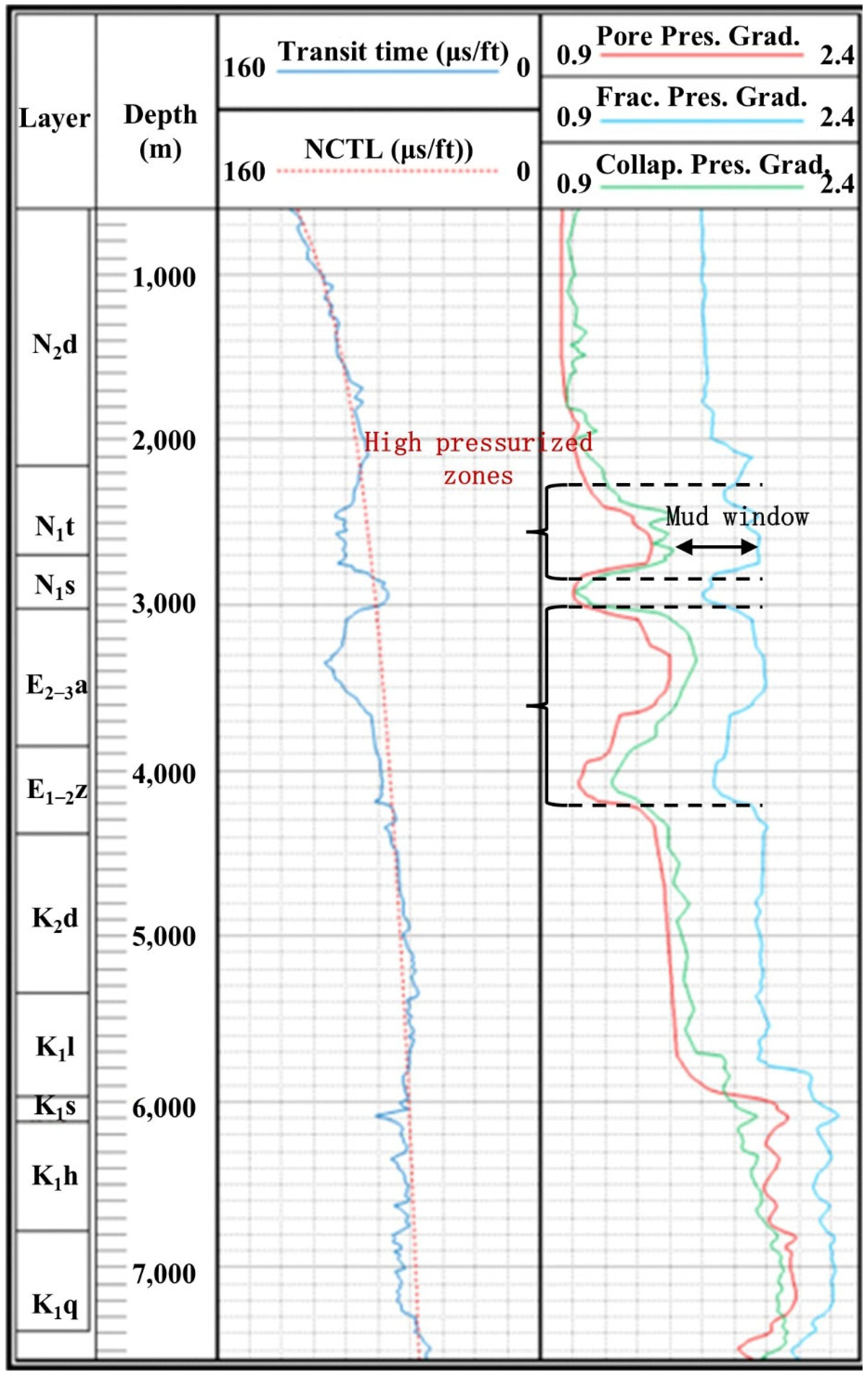
3. Field Application
4. Conclusions
- (1)
- Based on seismic inversion, borehole stability could be evaluated by constructing the relationship between three pressures and seismic velocity. The input data include seismic, logging, and geological information, which together could realize real-time prediction of acoustic and density log data of undrilled formations.
- (2)
- In the ultra-deep well Huqian−1, two abnormal highly pressurized sections are confirmed as Taxihe and Anjihaihe groups, which conforms to the practical drilling activities. The preliminary results demonstrate that the relationship between three pressures and seismic velocity is effective for the Hutubi area.
- (3)
- This model is applicable to P-wave real-time prediction of borehole stability within the scope of multiple wells in the same geological block. The precision of the prediction is satisfactory for the real-time operation requirements for local drilling.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hou, B.; Zeng, C.; Chen, D.; Fan, M.; Chen, M. Prediction of Wellbore Stability in Conglomerate Formation Using Discrete Element Method. Arab. J. Sci. Eng. 2017, 42, 1609–1619. [Google Scholar] [CrossRef]
- Hou, B.; Xie, S.; Chen, M.; Jiang, G.; Jin, Y.; Liang, C. New Method of Layered Drilling Fluid Design to Overcome Wellbore Instability of Piedmont Structures. Adv. Mater. Res. 2012, 524–527, 1480–1483. [Google Scholar] [CrossRef]
- Wu, C.; Liu, J.; Zhang, D.; Chen, X.; Zhao, W. A Prediction of Borehole Stability While Drilling Preliminary Prospecting Wells Based on Seismic Impedance. Pet. Explor. Dev. 2015, 42, 427–433. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, M.; Zhang, X. Study on Prediction for Borehole Stability before Drilling. Acta Pet. Sin. 2001, 22, 96–99. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, M.; Yang, X. Prediction of Safe Mud Density Window by Interval Velocity before Drilling. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2004, 23, 2430–2433. [Google Scholar] [CrossRef]
- Yang, J.; Yin, C.; Dai, R.; Yang, S.; Zhang, F. Seismic Impedance Inversion via L0 Gradient Minimisation. Explor. Geophys. 2019, 50, 575–582. [Google Scholar] [CrossRef]
- Wu, C.; Chen, M.; Jin, Y. Real-Time Prediction Method of Borehole Stability. Pet. Explor. Dev. 2008, 35, 80–84. [Google Scholar] [CrossRef]
- Wu, C.; Liu, J.H.; Zhang, D.Q.; Wang, L. Predicting Borehole Stability While Drilling Based on Nonlinear Inversion. Yantu Gongcheng Xuebao/Chin. J. Geotech. Eng. 2015, 37, 1810–1817. [Google Scholar] [CrossRef]
- Bloch, M.; Gupta, A. A New Strategy for near Real-Time Prediction of Borehole Stability. J. Can. Pet. Technol. 2001, 40. [Google Scholar] [CrossRef]
- Ji, D.; Xu, Y.; Pang, Z.; Yuan, B.; Zhao, K. Classification of Typical Tectonic Styles and Exploration of Hydrocarbon Accumulation Patterns in Southern Junggar Basin, China. Energies 2022, 15, 6715. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, M. Prediction of Borehole Stability by Seismic Records. Shiyou Xuebao/Acta Pet. Sin. 2004, 25, 89–92. [Google Scholar] [CrossRef]
- Xiao, Y.; Hurich, C.; Butt, S.D. Assessment of Rock-Bit Interaction and Drilling Performance Using Elastic Waves Propagated by the Drilling System. Int. J. Rock Mech. Min. Sci. 2018, 105, 11–21. [Google Scholar] [CrossRef]
- Xiao, Y.; Hurich, C.; Butt, S.D. Characterization of Rotary-Percussion Drilling as a Seismic-While-Drilling Source. J. Appl. Geophys. 2018, 151, 142–156. [Google Scholar] [CrossRef]
- Wu, C.; Chen, M.; Jin, Y. Pre-Drilling Prediction of Wellbore Stability Using Seismic Inversion Technology. Oil Drill. Prod. Technol 2006, 2, 18–20, 82. [Google Scholar] [CrossRef]
- Sun, X.K.; Feng, S.M. Wavelet Extraction Methods in Seismic Inversion System. Comput. Tech. Geophys. Geochem. Explor. 2010, 32, 120–125, 107. Available online: https://en.cnki.com.cn/Article_en/CJFDTOTAL-WTHT201002003.htm (accessed on 6 May 2010).
- Pranowo, W. Time-Varying Wavelet Estimation and Its Applications in Deconvolution and Seismic Inversion. J. Pet. Explor. Prod. Technol. 2019, 9, 2583–2590. [Google Scholar] [CrossRef]
- Hu, Y.; Yu, X.H.; Li, S.L.; Chen, G.Y.; Zhou, Y.L.; Gao, Z.P. Improving the Accuracy of Geological Model by Using Seismic Forward and Inversion Techniques. Pet. Explor. Dev. 2014, 41, 208–216. [Google Scholar] [CrossRef]
- Wu, C.; Chen, M.; Jin, Y. Predicting Borehole Stability before Drilling Using Seismic Attributes. Pet. Drill. Tech. 2006, 34, 35–37. Available online: https://en.cnki.com.cn/Article_en/CJFDTOTAL-SYZT200603018.htm (accessed on 25 May 2006).
- Luo, H.Z.; Ji, Y.X.; Wang, X.L.; Wang, X.M. Making P-SV Shear Wave Synthetic Seismic Record. Zhongguo Shiyou Daxue Xuebao (Ziran Kexue Ban)/J. China Univ. Pet. (Ed. Nat. Sci.) 2010, 34, 37–40, 45. Available online: https://zkjournal.upc.edu.cn/zgsydxxben/article/abstract/20100108 (accessed on 20 February 2010).
- Xiyuan, L.; Wangshui, H.; Nan, Z.; Heng, Z.; Xuan, L. Synthetic Seismic Recording Method by the Continuous Wavelet-Reflection Superposition. Pet. Geol. Oilfield Dev. Daqing 2020, 39, 133–138. [Google Scholar] [CrossRef]
- Li, Q.Z. On Strategy of Seismic Restricted Inversion. Pet. Geophys. Prospect. 1998, 4, 423–438, 572. [Google Scholar] [CrossRef]
- Treitel, S.; Lines, L. Past, Present, and Future of Geophysical Inversion: A New Millennium Analysis. Geophysics 2012, 66, 21–24. [Google Scholar] [CrossRef]
- Wen, X.; Yang, J.; Li, L.; He, J.; Li, B. Low-Frequency Sparse Double-Constrained Broadband Seismic Impedance Inversion. Nat. Gas Ind. B 2019, 6, 556–563. [Google Scholar] [CrossRef]
- Yang, Y.Q.; Guo, H.L.; Hui, C.; Li, W.D.; Jin, C.G.; Zhuo, X.U. Cross-Well Seismic Constrained Acoustic Impedance Inversion. J. Jilin Univ. (Earth Sci. Ed.) 2006, 36, 468–473. Available online: http://xuebao.jlu.edu.cn/dxb/EN/abstract/abstract8492.shtml (accessed on 6 May 2006).
- Fan, H.; Zhang, C. Determination and Regression of Overburden Pressure Gradient. Pet. Drill. Technol. 2002, 3, 6–8. [Google Scholar] [CrossRef]
- Li, Z.; Pan, Y. Stability Analysis of Wellbore with Permeation. Eng. Mech. 2002, 19, 105–108. Available online: https://en.cnki.com.cn/Article_en/CJFDTOTAL-GCLX200203020.htm (accessed on 1 June 2002).






| Formation | Bottom Vertical Depth (m) | Pore-Pressure Gradient (g/cm3) | Collapse Pressure Gradient (g/cm3) | Fracture Pressure Gradient (g/cm3) |
|---|---|---|---|---|
| Dushanzi Group-N2d | 0~2450 | 0.99~1.00 | 1.64~1.87 | 1.12~1.35 |
| Taxihe Group-N1t | 2450~2970 | 1.00~1.38 | 1.75~1.92 | 1.35~1.53 |
| Shawan Group-N1s | 2970~3240 | 1.00~1.37 | 1.65~1.91 | 1.53 |
| Anjihaihe Group-E2−3a | 3240~3985 | 1.02~1.50 | 1.76~1.95 | 1.30~1.85 |
| Ziniquanzi Group-E1−2z | 3985~4630 | 1.02~1.50 | 1.70~1.95 | 1.30~1.70 |
| Donggou Group-K2d | 4630~5700 | 1.49~1.50 | 1.90~1.94 | 1.70~1.75 |
| Lianmuqin Group-K1l | 5700~6255 | 1.50~1.92 | 1.90~2.16 | 1.73~2.15 |
| Shengjinkou Group-K1s | 6255~6470 | 1.87~2.00 | 2.17~2.28 | 2.13~2.14 |
| Hutubi Group-K1h | 6470~7150 | 1.90~2.01 | 2.16~2.25 | 2.14~2.18 |
| Qingshuihe Group-K1q | 7150~7770 | 1.93~2.07 | 2.16~2.27 | 2.08~2.18 |
| Formation | Bottom Vertical Depth (m) | Pore-Pressure Gradient (g/cm3) | Collapse Pressure Gradient (g/cm3) | Fracture Pressure Gradient (g/cm3) |
|---|---|---|---|---|
| Dushanzi Group-N2d | 0~2450 | 0.99~1.00 | 1.00~1.19 | 1.64~1.87 |
| Taxihe Group-N1t | 2450~2970 | 1.00~1.38 | 1.18~1.52 | 1.75~1.92 |
| Shawan Group-N1s | 2970~3240 | 1.00~1.37 | 1.06~1.48 | 1.65~1.91 |
| Anjihaihe Group-E2−3a | 3240~3985 | 1.02~1.50 | 1.31~1.71 | 1.76~1.95 |
| Ziniquanzi Group-E1−2z | 3985~4630 | 1.02~1.50 | 1.31~1.52 | 1.70~1.95 |
| Donggou Group-K2d | 4630~5700 | 1.49~1.50 | 1.48~1.75 | 1.90~1.94 |
| Lianmuqin Group-K1l | 5700~6255 | 1.50~1.92 | 1.62~1.78 | 1.90~2.16 |
| Shengjinkou Group-K1s | 6255~6470 | 1.87~2.05 | 1.78~1.92 | 2.17~2.25 |
| Hutubi Group-K1h | 6470~7150 | 1.90~2.05 | 1.81~1.98 | 2.16~2.30 |
| Qingshuihe Group-K1q | 7150~7770 | 1.93~2.03 | 1.97~2.00 | 2.16~2.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, X.; Gan, R.; Wang, X.; Cheng, Z.; Yu, P.; Zheng, W.; Song, X.; Xiao, Y. Prediction of Three Pressures and Wellbore Stability Evaluation Based on Seismic Inversion for Well Huqian-1. Processes 2025, 13, 2772. https://doi.org/10.3390/pr13092772
Mao X, Gan R, Wang X, Cheng Z, Yu P, Zheng W, Song X, Xiao Y. Prediction of Three Pressures and Wellbore Stability Evaluation Based on Seismic Inversion for Well Huqian-1. Processes. 2025; 13(9):2772. https://doi.org/10.3390/pr13092772
Chicago/Turabian StyleMao, Xinjun, Renzhong Gan, Xiaotao Wang, Zhiguo Cheng, Peirong Yu, Wei Zheng, Xiaoying Song, and Yingjian Xiao. 2025. "Prediction of Three Pressures and Wellbore Stability Evaluation Based on Seismic Inversion for Well Huqian-1" Processes 13, no. 9: 2772. https://doi.org/10.3390/pr13092772
APA StyleMao, X., Gan, R., Wang, X., Cheng, Z., Yu, P., Zheng, W., Song, X., & Xiao, Y. (2025). Prediction of Three Pressures and Wellbore Stability Evaluation Based on Seismic Inversion for Well Huqian-1. Processes, 13(9), 2772. https://doi.org/10.3390/pr13092772






