Real-Time Joint Fault Detection and Diagnosis of Hexapod Robot Based on Improved Random Forest
Abstract
1. Introduction
2. The Traditional Random Forest Framework for Fault Detection in Hexapod Robots
2.1. Random Forest Algorithm for Spatial Geometric Features (SGRF)
2.2. Random Forest Algorithm with Fusion of Physical Features (PFRF)
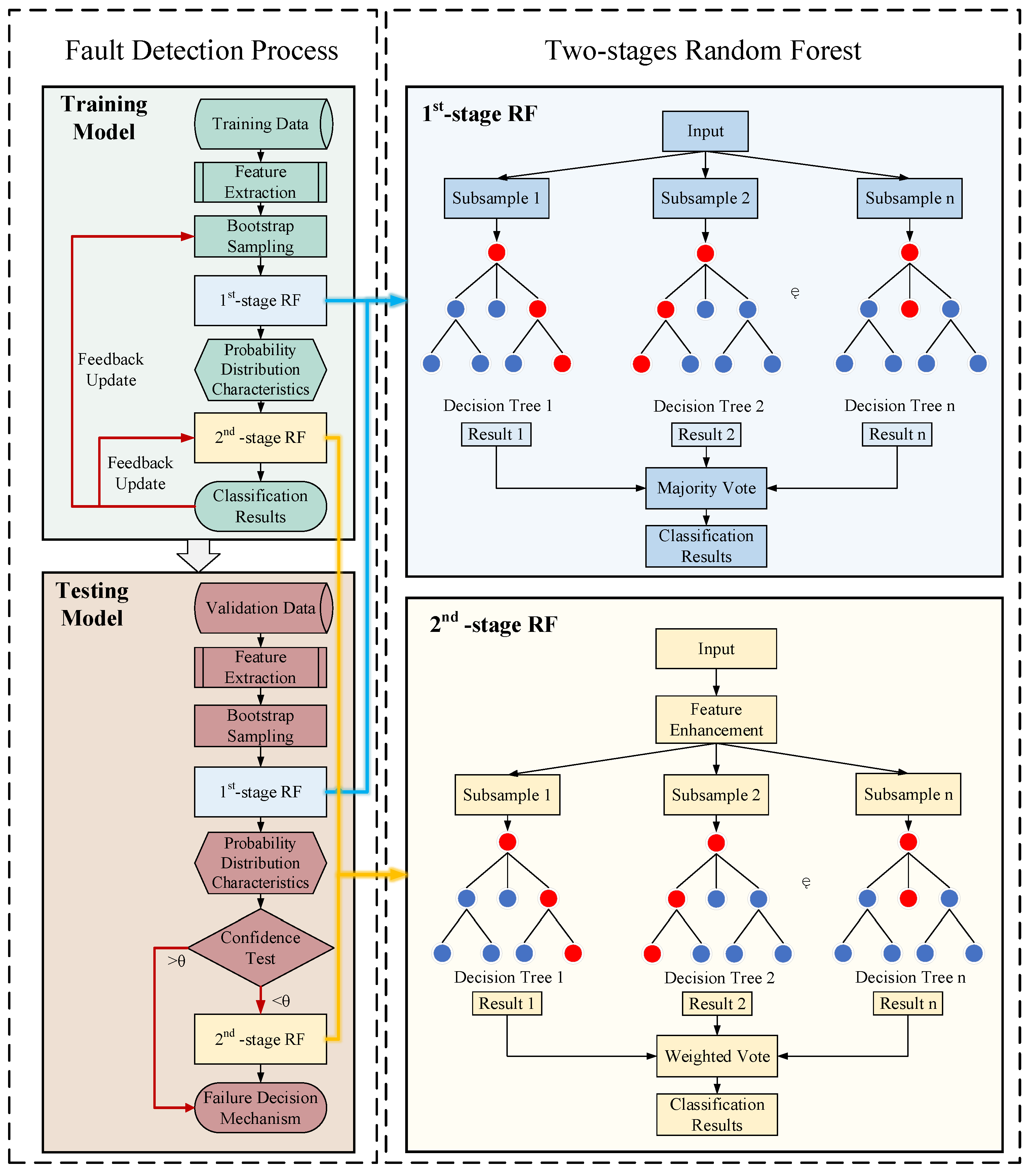
3. Two-Stages Random Forest (TSRF)
3.1. Training Process
3.2. Testing Process
4. Experiment
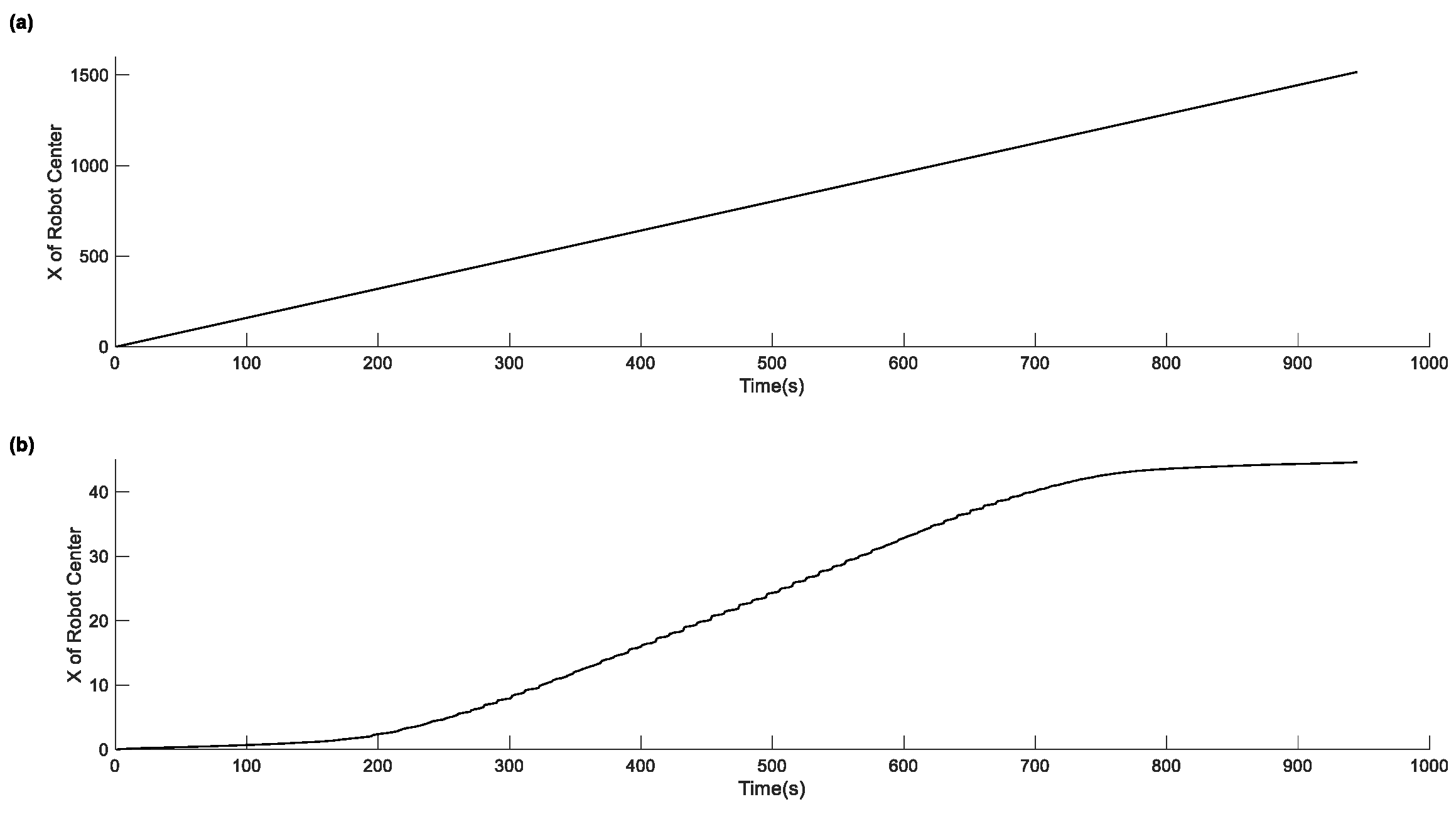
4.1. Datasets
4.2. Comparative Experiment Setting
- LR;
- KNN;
- DT;
- SGRF;
- PFRF;
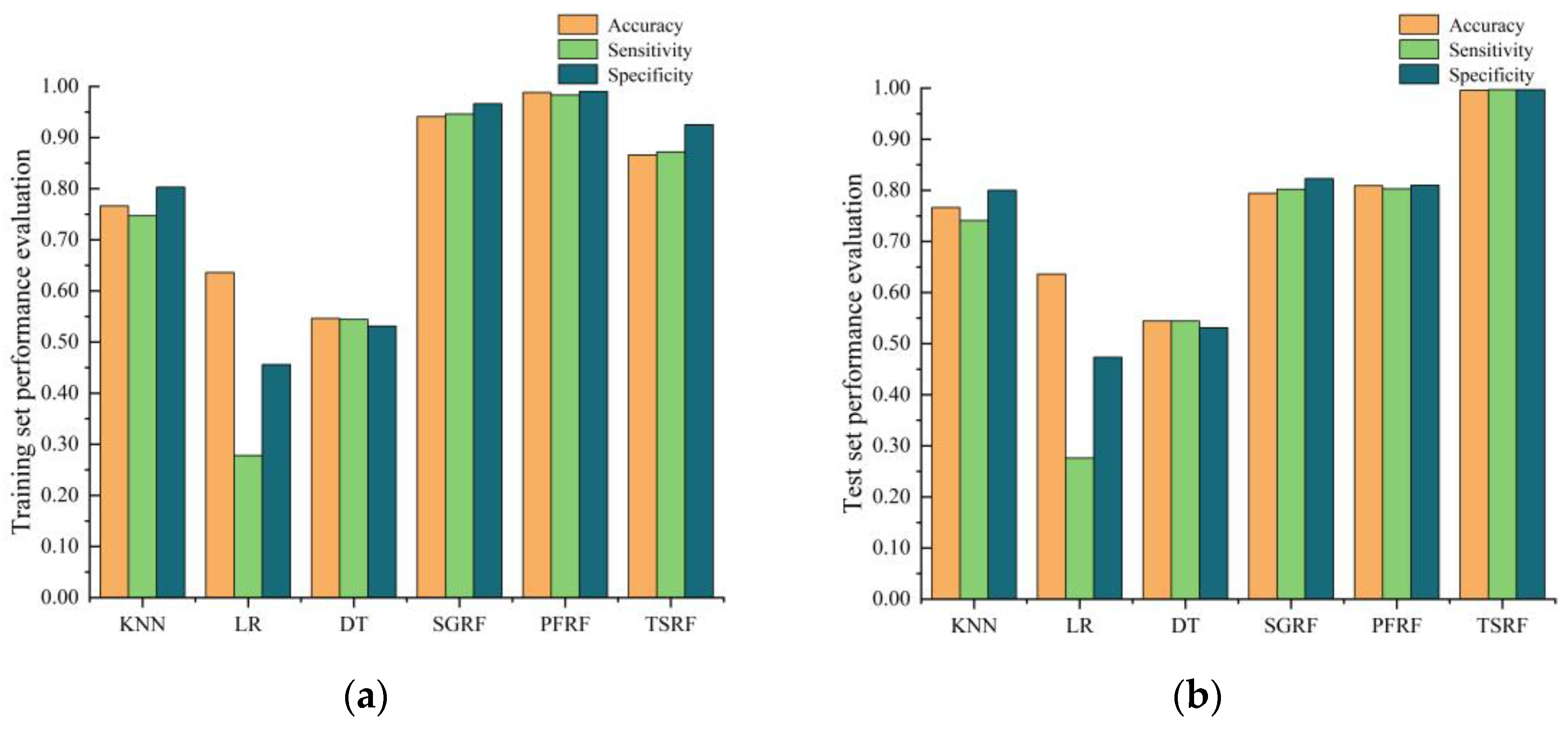
4.3. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ono, K.; Hayashi, T.; Fujii, M.; Shibasaki, N.; Sonehara, M. Development for industrial robotics applications. IHI Eng. Rev. 2009, 42, 103–107. [Google Scholar]
- Li, G.; Luo, Y. Industrial Robots’ Application in Processing Production Line of Mechanical Parts. J. Phys. Conf. Ser. 2019, 1176, 052051. [Google Scholar] [CrossRef]
- Song, Q.; Zhao, Q. Recent advances in robotics and intelligent robots applications. Appl. Sci. 2024, 14, 4279. [Google Scholar] [CrossRef]
- Cong, Q.; Shi, X.; Xiong, Y.; Wang, J.; Yang, Z.; Tian, W. A novel bionic gripper based on the front tarsi of scutigers. Trans. Can. Soc. Mech. Eng. 2022, 46, 427–435. [Google Scholar] [CrossRef]
- Pan, Y.; Fan, J.; Liu, G.; Liu, Y.; Zhao, J. Design and hydrodynamic analysis of controllable soft-body extension-driven flippers inspired by swimming frog flippers. Eng. Appl. Comput. Fluid Mech. 2024, 18, 2342504. [Google Scholar] [CrossRef]
- Mar-Castro, E.; May-Rodríguez, S.A.; Núñez-Cruz, R.S.; Antonio-Yañez, E.D.; Aparicio-Lastiri, L.M.; Herrera-Vidal, J. Development of a Vertical Submerging and Emerging Bat-Ray-Inspired Underwater Vehicle. Biomimetics 2024, 9, 582. [Google Scholar] [CrossRef]
- Lee, J.H.; Michelis, M.Y.; Katzschmann, R.; Manchester, Z. Aquarium: A fully differentiable fluid-structure interaction solver for robotics applications. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 11272–11279. [Google Scholar]
- Zhang, C.; Chen, B.; Li, X. Fuzzy Failure Modes, Effect and Criticality Analysis on Electromechanical Actuators. Actuators 2024, 13, 510. [Google Scholar] [CrossRef]
- Gao, G.B.; Wang, J.S.; Yue, W.H.; Peng, J.H. Fault Diagnosis and Maintain of Manufacturing Equipment Based on Vulnerability. J. Mech. Eng. 2020, 56, 141–149. [Google Scholar]
- Isermann, R. Model-based fault-detection and diagnosis–status and applications. Annu. Rev. Control 2005, 29, 71–85. [Google Scholar] [CrossRef]
- Chen, J.; Patton, R.J. Robust Model-Based Fault Diagnosis for Dynamic Systems; Springer Science & Business Media: Heidelberg, Germany, 2012; Volume 3. [Google Scholar]
- Gertler, J. Fault Detection and Diagnosis in Engineering Systems; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Asif, U. Improving the navigability of a hexapod robot using a fault-tolerant adaptive gait. Int. J. Adv. Robot. Syst. 2012, 9, 34. [Google Scholar] [CrossRef]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:1312.6199. [Google Scholar]
- Dobson, J.E. On reading and interpreting black box deep neural networks. Int. J. Digit. Humanit. 2023, 5, 431–449. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, H.; Qin, Z.; Moiseev, G.V.; Huo, J. Research on self-recovery control algorithm of quadruped robot fall based on reinforcement learning. Actuators 2023, 12, 110. [Google Scholar] [CrossRef]
- Mehta, D.; Salvi, A.; Krovi, V. Rough terrain path tracking of an ackermann steered platform using hybrid deep reinforcement learning. In Proceedings of the 2024 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 15–19 July 2024; pp. 685–690. [Google Scholar]
- Zhu, J.; Wei, Y.; Kang, Y.; Jiang, X.; Dullerud, G.E. Adaptive deep reinforcement learning for non-stationary environments. Sci. China Inf. Sci. 2022, 65, 202204. [Google Scholar] [CrossRef]
- Yang, B.-S.; Di, X.; Han, T. Random forests classifier for machine fault diagnosis. J. Mech. Sci. Technol. 2008, 22, 1716–1725. [Google Scholar] [CrossRef]
- Ma, S.; Chen, M.; Wu, J.; Wang, Y.; Jia, B.; Jiang, Y. Intelligent fault diagnosis of HVCB with feature space optimization-based random forest. Sensors 2018, 18, 1221. [Google Scholar] [CrossRef]
- Yang, C.; Yuan, H.; Zhang, F.; Xie, M.; Wang, Y.; Jiang, G.M. Convective initiation nowcasting in South China using physics-augmented random forest models and geostationary satellites. Earth Space Sci. 2024, 11, e2024EA003571. [Google Scholar] [CrossRef]
- Seifert, S. Application of random forest based approaches to surface-enhanced Raman scattering data. Sci. Rep. 2020, 10, 5436. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.X.; Feng, S.Y.; Liu, Z.L. Geological structure recognition model based on improved random forest algorithm. Coal Sci. Technol. 2023, 51, 149–156. [Google Scholar]
- Xu, B.; Ye, Y.; Nie, L. An improved random forest classifier for image classification. In Proceedings of the 2012 IEEE international Conference on Information and Automation, Seoul, Republic of Korea, 20–24 August 2012; pp. 795–800. [Google Scholar]
- Xu, B.; Guo, X.; Ye, Y.; Cheng, J. An improved random forest classifier for text categorization. J. Comput. 2012, 7, 2913–2920. [Google Scholar] [CrossRef]
- Scornet, E.; Biau, G.; Vert, J.-P. Consistency of random forests. Ann. Statist. 2015, 43, 1716–1741. [Google Scholar] [CrossRef]
- Scornet, E. On the asymptotics of random forests. J. Multivar. Anal. 2016, 146, 72–83. [Google Scholar] [CrossRef]
- Mousaei, A.; Naderi, Y.; Mekhilef, S.; Golestan, S.; Iqbal, A. Optimal Placement of Electric Vehicle Charging Stations Using Machine Learning: A Comprehensive Review; SSRN: Rochester, NY, USA, 2025. [Google Scholar]
- Mousaei, A.; Naderi, Y.; Bayram, I.S. Advancing state of charge management in electric vehicles with machine learning: A technological review. IEEE Access 2024, 12, 43255–43283. [Google Scholar] [CrossRef]

| Feature Name | Technical Definition | Mathematical Formulation |
|---|---|---|
| Kinetic Energy Index | Quantifies rotational kinetic energy of joint motion | |
| Torque Ratio Coefficient | Ratio of principal torque components in Cartesian space | |
| Trajectory Curvature Metric | Measures path deviation via Frenet–Serret formulas | |
| Motion Stability Indicator | Characterizes gait consistency through signal dispersion | |
| Spatial Orientation Angle | Direction cosine relative to robot base frame |
| Methods | KNN | LR | DT | SGRF | PFRF | TSRF |
|---|---|---|---|---|---|---|
| accuracy | 76.6% | 63.6% | 53.1% | 97.9% | 98.8% | 86.6% |
| specificity | 74.7% | 27.8% | 52.9% | 97.1% | 98.3% | 87.0% |
| sensitivity | 80.3% | 45.6% | 52.0% | 98.1% | 99.0% | 92.4% |
| Methods | KNN | LR | DT | SGRF | PFRF | TSRF |
|---|---|---|---|---|---|---|
| accuracy | 76.6% | 63.6% | 53.1% | 80.9% | 80.8% | 99.7% |
| specificity | 74.1% | 27.6% | 53.0% | 80.2% | 80.3% | 99.8% |
| sensitivity | 80.0% | 47.3% | 51.2% | 81.0% | 81.0% | 99.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Q.; Men, Y.; Zhang, K.; Yu, M.; Liu, Y. Real-Time Joint Fault Detection and Diagnosis of Hexapod Robot Based on Improved Random Forest. Processes 2025, 13, 2762. https://doi.org/10.3390/pr13092762
Fang Q, Men Y, Zhang K, Yu M, Liu Y. Real-Time Joint Fault Detection and Diagnosis of Hexapod Robot Based on Improved Random Forest. Processes. 2025; 13(9):2762. https://doi.org/10.3390/pr13092762
Chicago/Turabian StyleFang, Qilei, Yifan Men, Kai Zhang, Man Yu, and Yin Liu. 2025. "Real-Time Joint Fault Detection and Diagnosis of Hexapod Robot Based on Improved Random Forest" Processes 13, no. 9: 2762. https://doi.org/10.3390/pr13092762
APA StyleFang, Q., Men, Y., Zhang, K., Yu, M., & Liu, Y. (2025). Real-Time Joint Fault Detection and Diagnosis of Hexapod Robot Based on Improved Random Forest. Processes, 13(9), 2762. https://doi.org/10.3390/pr13092762






