Economic Optimal Scheduling of Virtual Power Plants with Vehicle-to-Grid Integration Considering Uncertainty

Abstract

To mitigate the risks posed by uncertainties in renewable energy output and Electric Vehicle (EV) travel patterns on the scheduling of Virtual Power Plants (VPPs), this paper proposes an optimal scheduling model for a VPP incorporating EVs based on Information Gap Decision Theory (IGDT). First, a Monte Carlo load forecasting model is established based on the behavioral characteristics of EV users, and a Sigmoid function is introduced to quantify the dynamic relationship between user response willingness and VPP incentive prices. Second, within the VPP framework, an economic optimal scheduling model considering multi-source collaboration is developed by integrating wind power, photovoltaics, gas turbines, energy storage systems, and EV clusters with Vehicle-to-Grid (V2G) capabilities. Subsequently, to address the uncertain parameters within the model, IGDT is employed to construct a bi-level decision-making mechanism that encompasses both risk-averse and opportunity-seeking strategies. Finally, a case study on a VPP is conducted to verify the correctness and effectiveness of the proposed model and algorithm. The results demonstrate that the proposed method can effectively achieve a 7.94% reduction in the VPP’s comprehensive dispatch cost under typical scenarios, exhibiting superiority in terms of both economy and stability.

1. Introduction

Distributed energy sources (DERs) are widely used in the construction of new power systems due to their multiple advantages, such as being green, flexible, and renewable [1,2,3]. At the same time, they exhibit randomness and volatility due to environmental factors. In the future, the large-scale, high-proportion integration of distributed energy will pose significant challenges to the stability of the power system and energy security. Therefore, establishing a more flexible and resilient new power system has become an urgent task. A Virtual Power Plant (VPP) aggregates and controls controllable loads such as wind power, photovoltaics, energy storage, and electric vehicle (EV), participating in the electricity market through advanced communication technologies [4,5]. Through complementary advantages and optimal allocation within the VPP, it is possible to reduce the randomness and volatility of renewable energy within the system on one hand and to achieve multi-energy complementarity on the power side and flexible interaction on the load side on the other [6]. Therefore, studying the optimal scheduling and operation methods of VPPs has important practical value for the optimized utilization of distributed energy.

Current research on VPPs has explored various facets of their operation, including dynamic aggregation and economic dispatch [7]. For instance, Chen et al. [8] developed an optimal dispatch strategy considering the spatio-temporal coupling of hydropower. However, this model is primarily tailored for basin-wide hydro–wind–PV systems and is less applicable to the diverse resource mix typically found in urban VPPs. Pan et al. [9] designed a coordinated bidding strategy for VPPs in energy and peak-shaving markets using a Stackelberg game model. While innovative, this approach may oversimplify the complex interplay between multiple agents in real-world scenarios, where their strategic behaviors are not always hierarchical.

With the rapid expansion of the EV industry, the potential of EV clusters as distributed energy storage resources has garnered considerable attention [10]. Numerous studies have investigated the coordinated dispatch of EVs within VPPs. Li et al. [11] proposed a Stackelberg game-based interval optimization model for a VPP with EVs. Chen et al. [12] modeled EVs as mobile energy storage units and employed the whale optimization algorithm for scheduling, while Wang et al. [13] proposed a sampling-then-clustering management strategy for EV charging and discharging. A common limitation across these studies is the inadequate modeling of the relationship between user behavior and economic incentives; they often overlook how users’ willingness to participate dynamically responds to price signals, which is crucial for realistic demand-side management. Additionally, Bharti et al. [14] proposed a lookup table method to estimate and model the charging behavior of EVs, which circumvents complex real-time computations and significantly accelerates simulation speeds. However, as the study was based on data from the Delhi region in India, its generalizability and scalability require further validation.

A central challenge in VPP scheduling is managing the uncertainty associated with high penetrations of renewable energy and variable loads. Conventional methods have distinct drawbacks. The two-point estimation method, used by Sun et al. [15], is computationally simple but suffers from poor accuracy, limiting its practical applicability. Scenario-based methods, as applied by Ge et al. [16], can describe uncertainty with high fidelity but are computationally intensive and depend on accurately defined probability distributions, which are often difficult to obtain. Stochastic optimization, such as the chance-constrained programming proposed by Sun et al. [3], is effective but introduces a degree of subjectivity, as the optimal solution is highly sensitive to the assumed probability distributions of the uncertain parameters. Similarly, the robust optimization approach, whether based on Wasserstein distance ambiguity sets [17] or traditional robust formulations [18], often leads to overly conservative solutions that sacrifice economic efficiency to ensure system security against worst-case scenarios. In contrast to these methods, Information Gap Decision Theory (IGDT) offers a non-probabilistic framework for decision-making under severe uncertainty. It does not require knowledge of probability distributions and instead quantifies the gap between what is known and what needs to be known for a decision to succeed. By evaluating the robustness of a strategy against adverse uncertainty (risk aversion) and its potential to capitalize on favorable outcomes (opportunity seeking), IGDT provides a flexible and computationally efficient tool for decision-makers.

Therefore, this paper proposes an optimal scheduling model for a VPP including EVs based on IGDT. The main contributions of this study are as follows:

• A Novel EV Participation Model: A Monte Carlo method is used to forecast EV charging loads based on statistical travel data. Crucially, a Sigmoid function is introduced to quantitatively model the dynamic relationship between EV users’ willingness to participate in V2G services and the incentive prices offered by the VPP, enabling a more realistic model of demand-side response.
• A Bi-Directional Uncertainty-Aware Dispatch Framework: Information Gap Decision Theory (IGDT) is employed to develop a bi-level optimal scheduling model. This framework allows the VPP operator to formulate dispatch strategies from both risk-averse (robust) and opportunity-seeking perspectives, providing flexibility to navigate the trade-off between operational cost and resilience against forecast errors in renewable generation and load.
• Comprehensive Multi-Source Coordination: The proposed VPP model holistically integrates a diverse set of assets, including wind turbines, PV arrays, gas turbines, battery energy storage, and V2G-enabled EV clusters. The model optimizes the coordinated operation of these resources to minimize total system cost while satisfying all technical constraints, thereby maximizing economic efficiency and grid stability.

The remainder of this paper is organized as follows: Section 2 constructs a Monte Carlo probabilistic forecasting model for EVs’ charging load based on user travel characteristics and subsequently quantifies the travel patterns and charging/discharging behaviors of EVs by considering user willingness. Building on this foundation, Section 3 develops an optimal dispatch model for a VPP that incorporates Vehicle-to-Grid (V2G) capabilities. In Section 4, IGDT is introduced to manage system uncertainties from both risk-averse and opportunity-seeking perspectives, dynamically adjusting the uncertainty interval via forecast reference values and deviation factors to provide bi-directional dispatch strategies for decision-makers. Section 5 validates the effectiveness and superiority of the proposed method in addressing source-load uncertainty through a case study. Finally, Section 6 presents the conclusions and offers suggestions for future research.

2. Electric Vehicle Load Forecasting Model

The “China Electric Vehicle Big Data Research Report”, released by the National Big Data Alliance of Electric Vehicles, provides a statistical analysis of real-time operational data from EVs in 2019. A normal distribution is used to fit the travel characteristics of EVs. The daily driving mileage of a user tends to follow a log-normal distribution, with its probability density function as

$$f_d(x)={\displaystyle \frac{1}{{\sigma }_d\sqrt{2\pi }}}\exp \left[-{\displaystyle \frac{{(\ln x-{\mu }_d)}^2}{2{{\sigma }_d}^2}}\right]{\displaystyle \frac{{\partial }^2\mathrm{\Omega }}{\partial u\partial v}}$$

(1)

where ${\mu }_d$ is the expected value of the driving distance in kilometers and ${\sigma }_d$ is the standard deviation.

The start time of a user’s trip $T_{out}$ follows a normal distribution with the probability density function:

$$f_o=\left\{\begin{array}{l}{\displaystyle \frac{1}{{\sigma }_o\sqrt{2\pi }}}\exp \left[-{\displaystyle \frac{{(\ln x-{\mu }_o)}^2}{2{{\sigma }_o}^2}}\right],\hspace{1em}\hspace{1em}0\le x\le {\mu }_o+12\\ {\displaystyle \frac{1}{{\sigma }_o\sqrt{2\pi }}}\exp \left[-{\displaystyle \frac{{(x-24-{\mu }_o)}^2}{2{{\sigma }_o}^2}}\right],\hspace{1em}\hspace{1em}{\mu }_o+12\le x\le 24\end{array}\right.$$

(2)

where ${\mu }_o$ is the expected value of the travel start time in hours and ${\sigma }_o$ is its standard deviation.

The end time of the user’s travel for the day $T_{in}$ follows a normal distribution with the probability density function:

$$f_r=\left\{\begin{array}{l}{\displaystyle \frac{1}{{\sigma }_r\sqrt{2\pi }}}\exp \left[-{\displaystyle \frac{{(\ln x-{\mu }_r)}^2}{2{{\sigma }_r}^2}}\right],\hspace{1em}\hspace{1em}0\le x\le {\mu }_r+12\\ {\displaystyle \frac{1}{{\sigma }_r\sqrt{2\pi }}}\exp \left[-{\displaystyle \frac{{(x-24-{\mu }_r)}^2}{2{{\sigma }_r}^2}}\right],\hspace{1em}\hspace{1em}{\mu }_r+12\le x\le 24\end{array}\right.$$

(3)

where ${\mu }_r$ is the expected value of the return end time in hours and ${\sigma }_r$ is its standard deviation.

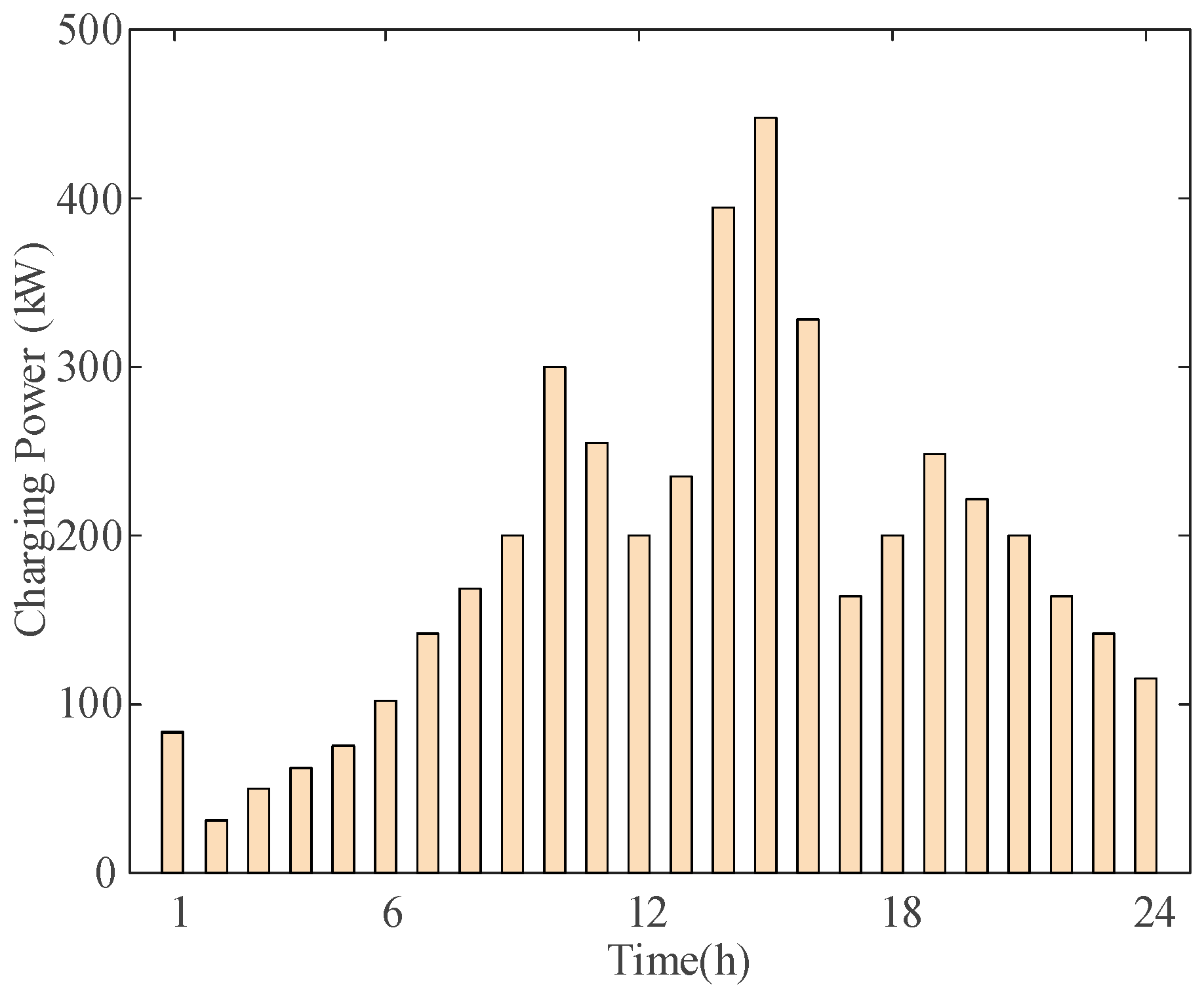
Taking a charging station in Nanjing, China, as an example, its EV charging data is shown in Figure 1. The Monte Carlo method is used to predict the EV charging load. The process involves inputting basic parameters such as charging power, discharging power, charging efficiency, discharging efficiency, and maximum daily mileage to generate the initial state of charge and charging start time. These are then used to calculate the charging duration [19], thereby obtaining the charging or discharging load of a single EV.

Whether an EV owner is willing to follow the dispatch commands of the VPP is highly subjective. To accurately represent the user’s willingness to participate, this paper uses the Sigmoid function to model user willingness. This model can effectively reflect the relationship between the EV user’s willingness and the VPP’s incentive price [20]. The specific formula is as follows:

$$\Psi ={\displaystyle \frac{{\Psi }_{\max }}{1+e^{-k(p-p_0)}}}$$

(4)

where $\Psi$ represents the EV user’s willingness, $\Psi \in [0,1]$, representing the expected proportion of a user’s maximum dispatchable charging/discharging power that they are willing to provide for VPP dispatch at a specific incentive price p. ${\Psi }_{\max }$ is the maximum willingness, k controls the steepness of the curve, and $p_0$ is the midpoint of the curve. The values of parameters such as k and p₀ in this study are based on existing literature and common assumptions [21]. In practical applications, the values will vary depending on the user group, region and market environment, and they need to be calibrated with actual data.

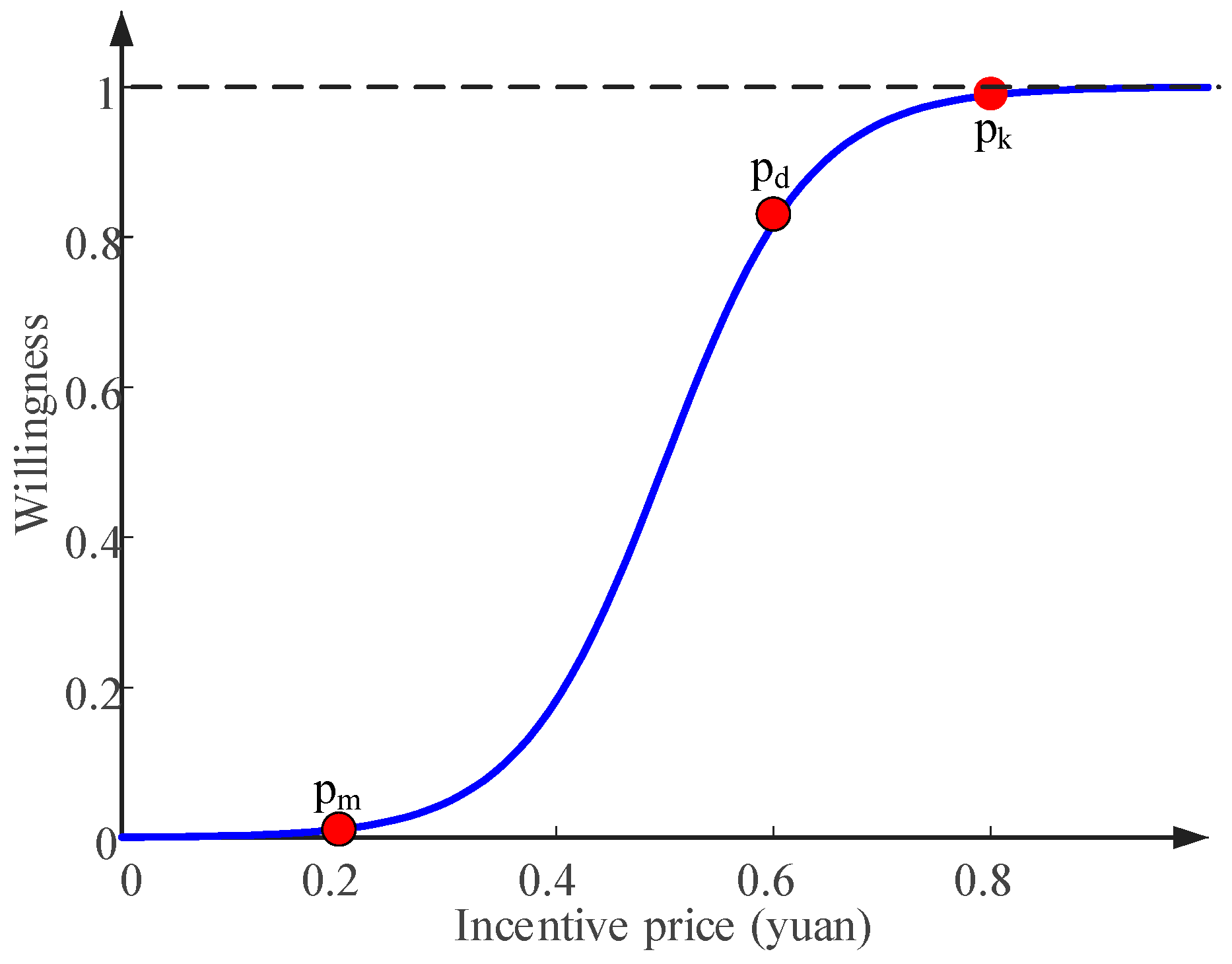
The curve of EV user willingness versus the VPP incentive price is shown in Figure 2. When the price is below the minimum effective price $p_m$, the owner’s willingness is close to zero, indicating their unwillingness to participate. When the price exceeds the saturation price $p_k$, the owner’s willingness approaches its maximum value, and further price increases will not affect it. When the price is at the recommended incentive price $p_d$, the willingness exceeds 0.8, and most EV users are willing to accept the VPP’s dispatch commands.

At this point, the total EV charging load $P_t^{EV,c}$ and total discharging load $P_t^{EV,d}$ can be expressed as

$$P_t^{EV,c}={\displaystyle \sum _{i=1}^n{\Psi }_i{P}_{i,t}^{EV,c}}$$

(5)

$$P_t^{EV,d}={\displaystyle \sum _{i=1}^n{\Psi }_i{P}_{i,t}^{EV,d}}$$

(6)

where ${\Psi }_i$ represents the willingness of the i-th EV user and $P_{i,t}^{EV,c},P_{i,t}^{EV,d}$ are the charging and discharging powers of the i-th EV at time t, respectively.

3. VPP Optimal Dispatch Model with EVs

3.1. VPP Framework with EVs

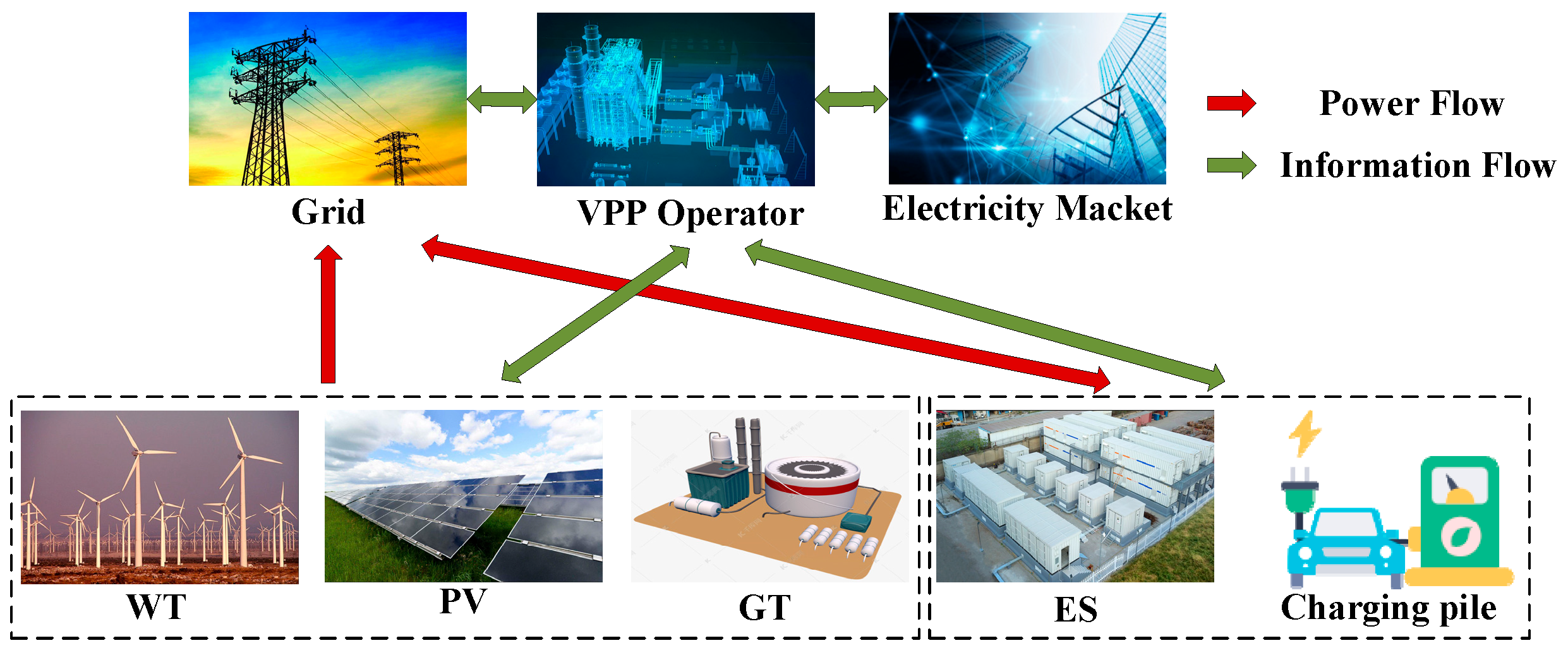
The VPP model studied in this paper integrates DERs such as wind turbines (WTs), photovoltaics (PV), gas turbines (GTs), energy storage systems (ESs), charging piles, and EVs. By coordinating user-side loads and distributed power sources, a VPP framework including EVS is established. The entire framework is shown in Figure 3. The power grid and natural gas network are the main energy supply sources for the VPP. The renewable energy generation units are wind turbine and photovoltaic units. The gas turbine uses gas to supply electricity to the user-side load. The GTs and ESs have fast regulation capabilities, complementing the non-dispatchable nature of renewable energy, which can effectively suppress the fluctuations of wind and solar power and increase the utilization of renewable energy. V2G technology enables the dispatch of EVs to mitigate the fluctuations of renewable energy generation, reduce the impact of renewable energy randomness on the power system, and enable the system to operate efficiently, stably, and safely.

3.2. Objective Function

The model’s operating cost includes the gas turbine generation cost $C_t^{GT}$, the cost of purchasing electricity from the grid $C_t^{grid}$, the operation and maintenance cost of wind and solar power $C_t^{pw}$, the ES loss cost $C_t^d$, and the EV dispatch cost $C_t^{EV}$. The objective function is to minimize the total operating cost of the VPP system, which can be expressed as

$$\min C={\displaystyle \sum _{t=1}^T(}{C}_t^{GT}+C_t^{grid}+C_t^{pw}+C_t^d+C_t^{EV})$$

(7)

$$C_t^{GT}=c^{GT}{P}_t^{GT}+{\displaystyle \frac{c^{gas}}{{\eta }^e{Q}^g}}{P}_t^{GT}$$

(8)

$$C_t^{grid}=c_t^{grid}{P}_t^{grid}$$

(9)

$$C_t^{pw}=c^w{P}_t^w+c^s{P}_t^s$$

(10)

$$C_t^{EV}=c_t^{EV,d}{P}_t^{EV,d}-c_t^{EV,c}{P}_t^{EV,c}$$

(11)

$$C_t^d=C_t^{dy}+C_t^{dn}$$

(12)

$$C_t^{dy}=c^{ES,o}\times (P_t^{ES,c}+P_t^{ES,d})+c^{ES,m}\times E$$

(13)

$$C_t^{dn}=c^{ES,loss}\times \left[\left(1-{\eta }^c\right)\times P_t^{ES,c}+\left(1-{\eta }^d\right)\times P_t^{ES,d}\right]$$

(14)

where C is the economic cost of the VPP in one dispatch cycle and T is 24 h;

$c^{GT}$ is the GT operation and maintenance management factor, $P_t^{GT}$ is the actual output of the GT, $c^{gas}$ is the price of gas, ${\eta }^e$ is the generation efficiency of the gas turbine, and $Q^e$ is the calorific value of natural gas;

$c_t^{grid}$ is the electricity purchase price at time t and $P_t^{grid}$ is the purchased power at time t;

$c^w$ and $c^s$ are the operation and maintenance coefficients for wind turbines and photovoltaics and $P_t^w$,$P_t^s$ are the aggregated power of wind and photovoltaics;

$c_t^{EV,c}$ and $c_t^{EV,d}$ are the charging and discharging price coefficients for EVs at time t;

$C_t^{dy}$ and $C_t^{dn}$ are the loss cost and operation/maintenance cost of the ES at time t, $c^{ES,o}$ is the operating cost coefficient, $c^{ES,m}$ is the maintenance cost coefficient, E is the capacity of the ES, $c^{ES,loss}$ is the energy loss cost coefficient, $P_t^{ES,c}$ and $P_t^{ES,d}$ are the charging and discharging powers at time t, and ${\eta }^c$, ${\eta }^d$ are the charging and discharging efficiencies of the ES.

3.3. Constraints

The VPP purchases electricity and natural gas resources from the main grid and gas network and supplies energy to multi-energy users through various energy conversion devices. Its power balance constraint is as follows:

$$P_t^L=P_t^{grid}+P_t^w+P_t^s+P_t^{GT}+P_t^{ES,d}-P_t^{ES,s}$$

(15)

where $P_t^L$ is the electricity load of the VPP at time t.

The output constraint for the gas turbine is as follows:

$$P^{PT,\min }\le P_t^{GT}\le P^{PT,\max }$$

(16)

where $P^{GT,\min }$ and $P^{GT,\max }$ are the minimum and maximum outputs of the gas turbine.

The constraints for wind and photovoltaic power are as follows:

$$0\le P_t^w\le P_t^{w,\max }$$

(17)

$$0\le P_t^s\le P_t^{s,\max }$$

(18)

where $P_t^{w,\max }$ and $P_t^{s,\max }$ are the maximum available outputs of wind and photovoltaic power at time t.

The charging/discharging and capacity constraints for EVs are as follows:

$$0\le P_t^{EV,c}\le P^{EV,c,\max }$$

(19)

$$0\le P_t^{EV,d}\le P^{EV,d,\max }$$

(20)

where $P^{EV,c,\max }$ and $P^{EV,d,\max }$ are the maximum charging and discharging powers of the EV cluster.

The power constraint for purchasing from the electricity market is as follows:

$$0\le P_t^{grid}\le P^{\mathrm{grid},\max }$$

(21)

where $P_t^{grid,\max }$ is the maximum power purchase limit.

The ES constraints are as follows:

$$0\le P_t^{ES,c}\le P^{ES,c,\max }$$

(22)

$$0\le P_t^{ES,d}\le P^{ES,d,\max }$$

(23)

$$S^{\min }\le S_t\le S^{\max }$$

(24)

$$S_t=S_{t-1}\left(1-\delta \right)+{\displaystyle \frac{\left(P_t^{ES,c}{\eta }_c-P_t^{ES,d}{\eta }_d\right)\mathsf{\Delta }t}{E}}$$

(25)

where $P^{ES,c,\max }$ and $P^{ES,d,\max }$ are the maximum discharging and charging powers of the ES; $S^{\min }$ and $S^{\max }$ are the minimum and maximum state of charge of the ES, respectively; $S_t$ and $S_{t-1}$ are the remaining capacity state of the ES at time t and t − 1, respectively; and $\delta$ is the self-discharge rate of the ES.

4. VPP Model Based on IGDT

4.1. Introduction to IGDT

Information Gap Decision Theory (IGDT) is used to study the allowable range of variation for uncertain parameters while satisfying preset objectives. It can be used for decision-making under uncertainty when the predicted values of input parameters are known. It includes a robust model and an opportunity model, which correspond to the two different strategies a decision-maker might adopt when facing risks [21].

When uncertainty exists, decision-makers need to adopt appropriate strategies to handle the resulting impacts. IGDT mainly consists of three parts: the system model, operational requirements, and the uncertainty set model.

4.2. System Model

For a cost optimization problem, the system model is as follows:

$$\left\{\begin{array}{l}\min B(w,d)\\ s.t.\mathrm{ }H(w,d)=0\\ \hspace{1em}\hspace{1em}\mathrm{G}(w,\mathrm{d})\ge 0\end{array}\right.$$

(26)

where w is the uncertain parameter, d is the decision variable, B(w, d) is the objective function, and H(w, d) and G(w, d) are the equality and inequality constraints, respectively.

4.3. Uncertainty Modeling

In IGDT, the fluctuation range of an uncertain parameter w around its predicted value $\tilde{w}$ can be described by the following model [22]:

$$\left\{\begin{array}{l}w\in U(\alpha ,\tilde{w})\\ U(\alpha ,\tilde{w})=\left\{w\right.:\left|{\displaystyle \frac{w-\tilde{w}}{\tilde{w}}}\right|\le \left.\alpha \right\}\end{array}\right.$$

(27)

where $\alpha$ represents the fluctuation magnitude of the uncertain parameter, $\alpha \ge 0$; $U(\alpha ,\tilde{w})$ indicates that the deviation of the uncertain parameter w from its predicted value does not exceed $\alpha$.

Taking wind and photovoltaic power output as the uncertain parameters, their fluctuation ranges can be expressed according to Equation (27) as

$$\begin{array}{l}U({\alpha }_w,\widetilde{P_t^w})=\\ \hspace{1em}\hspace{1em}\left\{P_t^w:(1-{\alpha }_w)\right.\widetilde{P_t^w}\le P_t^w\le (1+{\alpha }_w)\left.\widetilde{P_t^w}\right\}\end{array}$$

(28)

$$\begin{array}{l}U({\alpha }_s,\widetilde{P_t^{pv}})=\\ \hspace{1em}\hspace{1em}\left\{P_t^{pv}:(1-{\alpha }_s)\right.\widetilde{P_t^{pv}}\le P_t^{pv}\le (1+{\alpha }_s)\left.\widetilde{P_t^{pv}}\right\}\end{array}$$

(29)

where $\widetilde{P_t^s},\widetilde{P_t^w}$ are the predicted outputs of the wind farm and photovoltaic plant and ${\alpha }_w,{\alpha }_s$ are their corresponding fluctuation magnitudes.

When multiple sources of uncertainty are present in the model, it is necessary to aggregate their individual fluctuation ranges into a single comprehensive metric to represent the total system uncertainty. The weighted sum approach is a common and effective method to achieve this. It allows the VPP operator to assign different levels of significance to each uncertain parameter via weight factors reflecting their relative volatility or impact on the system. In this method, the fluctuation magnitudes of multiple uncertain parameters can be converted into a comprehensive fluctuation range α, expressed as:

$$\left\{\begin{array}{l}\alpha =k_w{\alpha }_w+k_s{\alpha }_s\\ k_w+k_s=1\end{array}\right.$$

(30)

where $k_w,k_s$ represent the weight factors for ${\alpha }_w$ and ${\alpha }_s$. Their specific values can be selected according to actual conditions. In this research, $k_w,k_s$ are both assigned a value of 0.5 [23].

4.4. Operational Requirements

The IGDT dispatch model is a bi-level optimization model. In the robust model, the lower-level problem seeks to identify the worst-case scheduling cost, while the upper-level problem maximizes the uncertainty radius ${\alpha }_r$ that the system can tolerate, subject to the constraint that this worst-case cost does not exceed a predefined limit. Conversely, in the opportunity model, the lower-level problem determines the best-case scheduling cost, and the upper-level problem minimizes the uncertainty radius ${\alpha }_o$ required to achieve an operating cost that is at or below a desired target value. In an uncertain environment, the robust model represents the system’s ability to withstand the maximum change in uncertain parameters, while the opportunity model quantifies the potential gains realized from favorable deviations in uncertain parameters. The corresponding mathematical models for these two strategies are as follows [24,25]:

$$(a)\left\{\begin{array}{l}\max \{{\alpha }_r:\underset{w\in U({\alpha }_r,\tilde{w})}{\max }f(w,d)\le f_r\}\\ s.t.\\ \hspace{1em}{f}_r=(1+{\theta }_r)f_d\\ \hspace{1em}H(w,d)=0\\ \hspace{1em}G(w,d)\ge 0\end{array}\right.(b)\left\{\begin{array}{l}\min \{{\alpha }_o:\underset{w\in U({\alpha }_o,\tilde{w})}{\min }f(w,d)\le f_o\}\\ s.t.\\ \hspace{1em}{f}_o=(1-{\theta }_o)f_d\\ \hspace{1em}H(w,d)=0\\ \hspace{1em}G(w,d)\ge 0\end{array}\right.$$

(31)

where $f_d$ is the objective function value under the deterministic model. ${\theta }_r,{\theta }_o$ are the deviation factors: ${\theta }_r$ indicates the worst-case cost $f_r=(1+{\theta }_r)f_d$ that the decision-maker can accept in the robust model, while ${\theta }_o$ indicates the desired optimal cost $f_o=(1-{\theta }_o)f_d$ in the opportunity model.

For a given d, $\max f(w,d)$ and $\min f(w,d)$ are functions of the uncertainty parameter w.

4.5. Algorithm Flow

• Replace the uncertain parameters with their predicted values $\widetilde{P_t}$ and solve the original deterministic system model to obtain the objective function value $f_d$.
• Set the subjective deviation factors ${\theta }_r,{\theta }_o$ for the robust and opportunity models, respectively.
• Solve the bi-level optimization models with uncertainty to obtain the prediction error $\alpha$ and the corresponding dispatch plan.
• Calculate the variation interval of the uncertain parameters under different plans. End.

The flow chart of scheduling is shown in Figure 4.

5. Case Study Analysis

The economic optimal dispatch model of a VPP including EVs based on IGDT is a mixed-integer linear programming problem. The experiments were conducted on a computer with a 64-bit operating system, 8.0 GB of memory, and an Intel(R) Core(TM) i5-1035G1 processor. The software environment was MATLAB R2021a with the Gurobi 11.0.3 solver. Monte Carlo scenario generation used the MATLAB Parallel Computing Toolbox (Parfor). This paper selects the operational data of a typical day from an actual VPP demonstration project in Jiangsu Province. The VPP system consists of a 900 kW wind farm, a 500 kW photovoltaic station, two 440 kW gas turbines, a 400 kW energy storage system, and 50 public charging piles with V2G capability. The load includes residential, general commercial, and industrial loads.

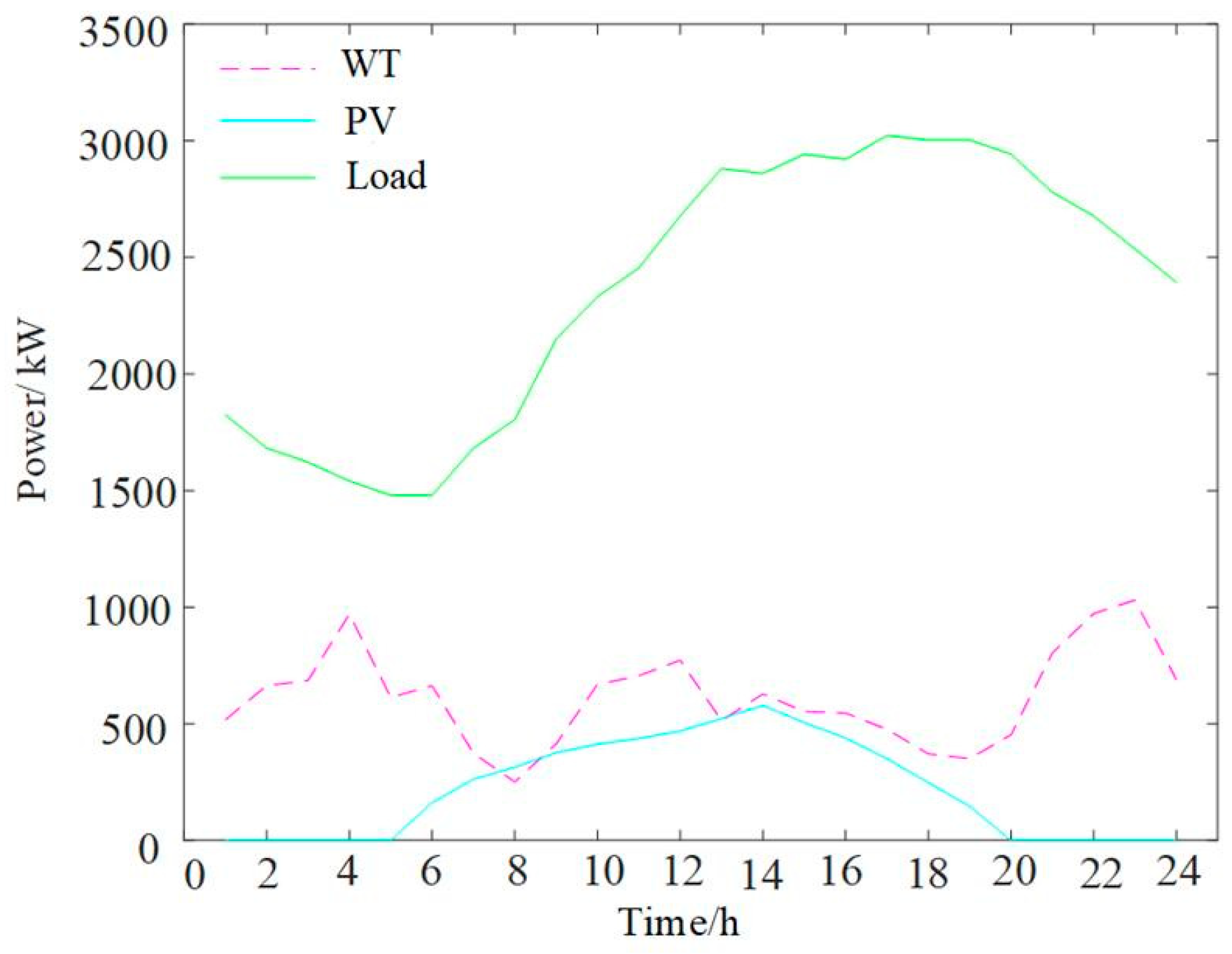
Detailed parameters for WT, PV, GT, ES, together with EV parameter values and distributions, are shown in

Table 1. VPP system parameters.

Parameters	$P_t^{w,\max }$	$P_t^{s,\max }$	$P_t^{GT,\max }$	$P_t^{GT,\min }$	$P_t^{EV,c,\max }$$/P_t^{EV,d,\max }$	$S^{max}$	$S^{min}$
Values	900 kW	500 kW	880 kW	88 kW	150 kW	400 kW h	0 kW h
Parameters	$c^{gas}$	$Q^e$	${\eta }^e$	$c^{GT}$	$c^{ES,m}$	$c^{ES,o}$	$c^{ES,loss}$
Values	2.5 ¥/m3	9.7 kWh/m3	40%	0.12 ¥/kW	0.009	0.05	0.0253
Parameters	${\eta }_c$$/{\eta }_d$	$c^w$	$c^s$	$P_{i,t}^{EV,c}$$/P_{i,t}^{EV,d}$	SOC	$t_s$	$t_c$
Values or Distruibution	5 kW	0.03	0.01	5 kW	N (40, 0.01)	N (17.9, 1.92)	N (1.12, 1.56)

; the time-of-use electricity prices are in

Table 2. TOU electricity price.

Name	Period	Price
Peak	10:00~15:00, 18:00~21:00	0.84
Mid-peak	7:00~10:00, 15:00~18:00, 21:00~24:00	0.53
Off-peak	24:00~07:00	0.27

; and the WT, PV output forecasts and load forecast are shown in Figure 5.

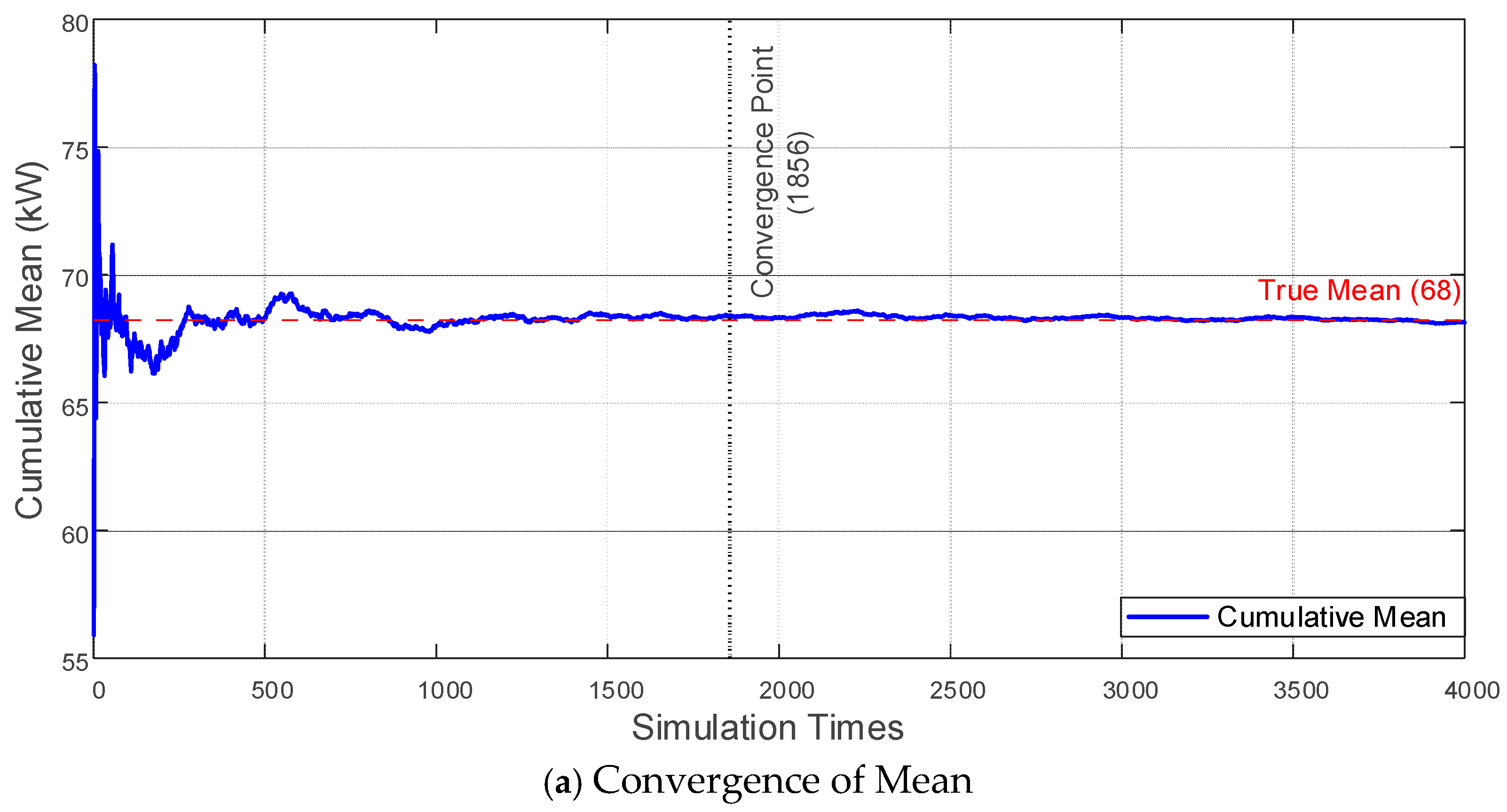
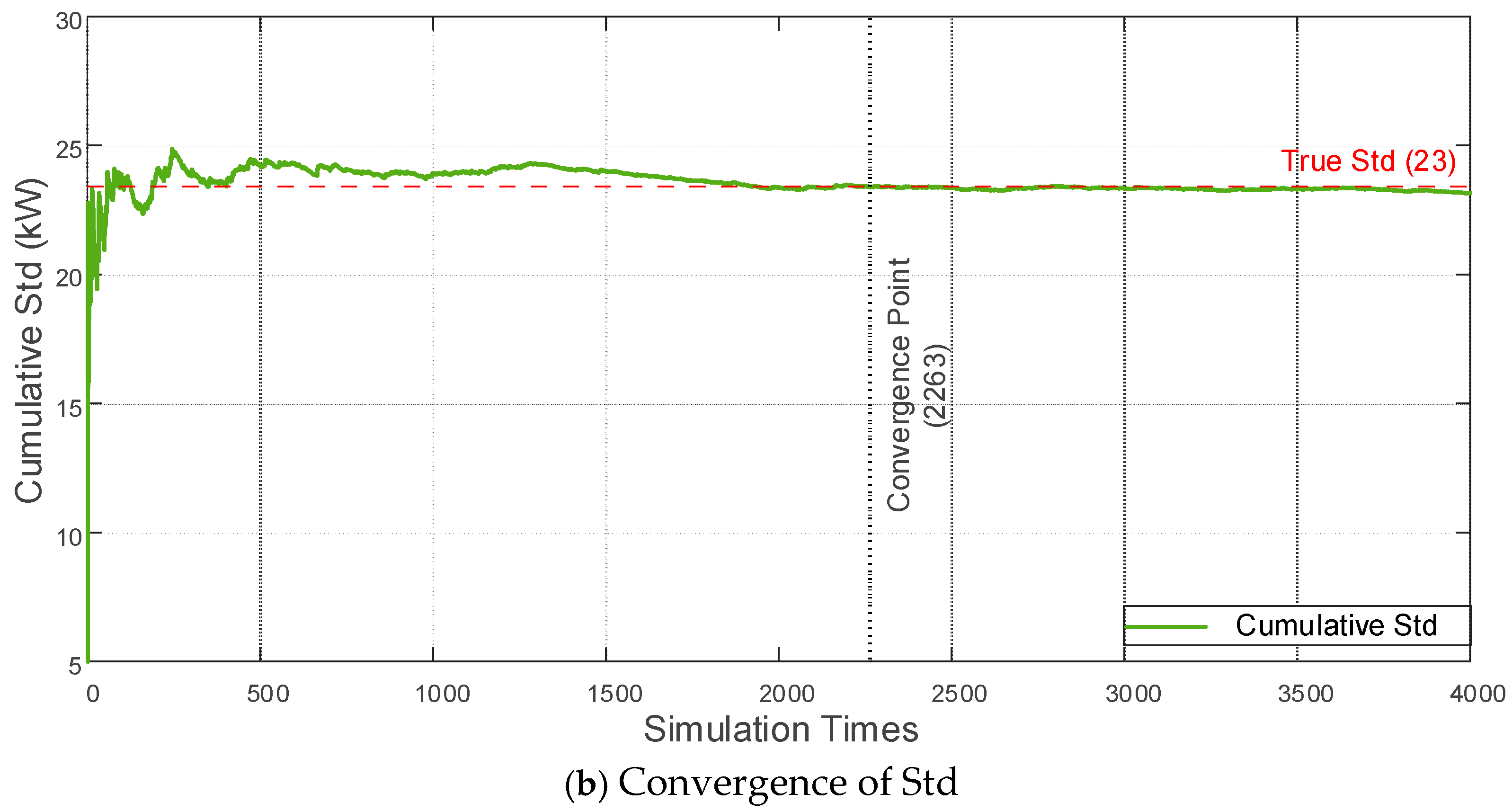
To ensure the statistical robustness of the EV charging load forecast, this study performed 4000 Monte Carlo simulations for the 50-EV cluster. The mean and standard deviation of the generated charging load profile, shown in Figure 6, were observed to stabilize after approximately 2300 simulations, confirming that the total number of runs was sufficient to reliably capture the stochastic nature of EV charging behavior.

5.1. VPP Optimal Dispatch Based on IGDT in an Uncertain Environment

By substituting the system parameters and the wind and load forecast values into the deterministic dispatch model, the global optimal solution is found to be $f_d$ = 11,229.6 yuan.

Figure 6 shows the optimal dispatch results corresponding to the optimal compromise solution obtained from the IGDT model, which comprehensive dispatching cost is 11,432.1 yuan. A positive power value indicates energy supply, while a negative value indicates energy consumption. As shown in Figure 7, To minimize VPP operating costs, VPP operators always tend to utilize lower-priced DERs during dispatch. From 00:00 to 06:00, the electricity price is in the off-peak period. During this time, V2G guides EV users to charge, and the ES enters a charging state. From 06:00 to 08:00, the GT output increases significantly, while EVs and the ES continue to charge during the mid-peak period. During peak hours, the VPP reduces electricity purchases through optimal dispatch, instead using natural gas and the ESS to offset the economic burden of high peak electricity prices. The GT output increases significantly, and the ES discharges to meet load demand. Simultaneously, under the guidance of the time-of-use price strategy and V2G, EVs act as a power source for the system, reducing the peak load and lowering the VPP’s operating cost during peak hours.

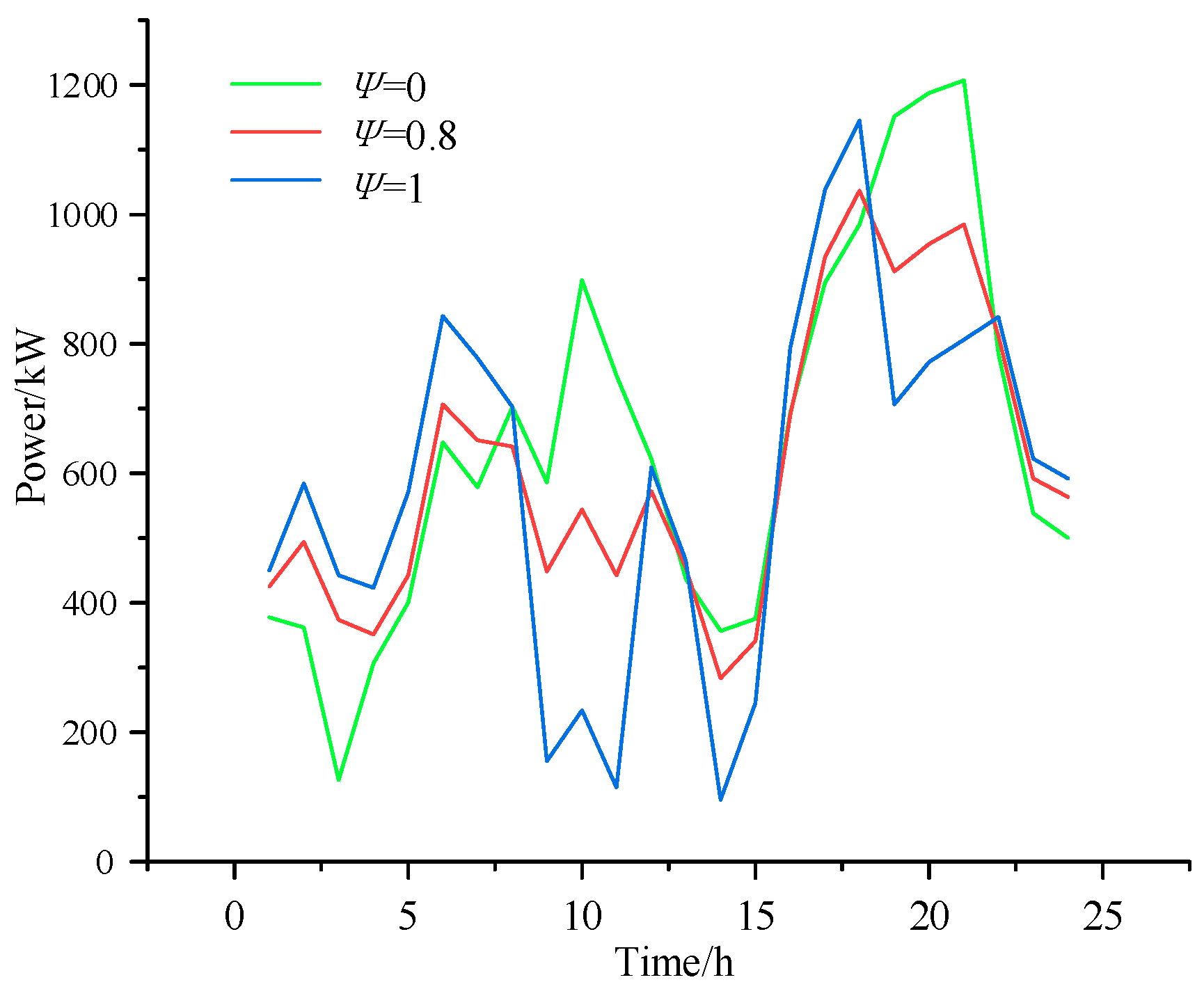
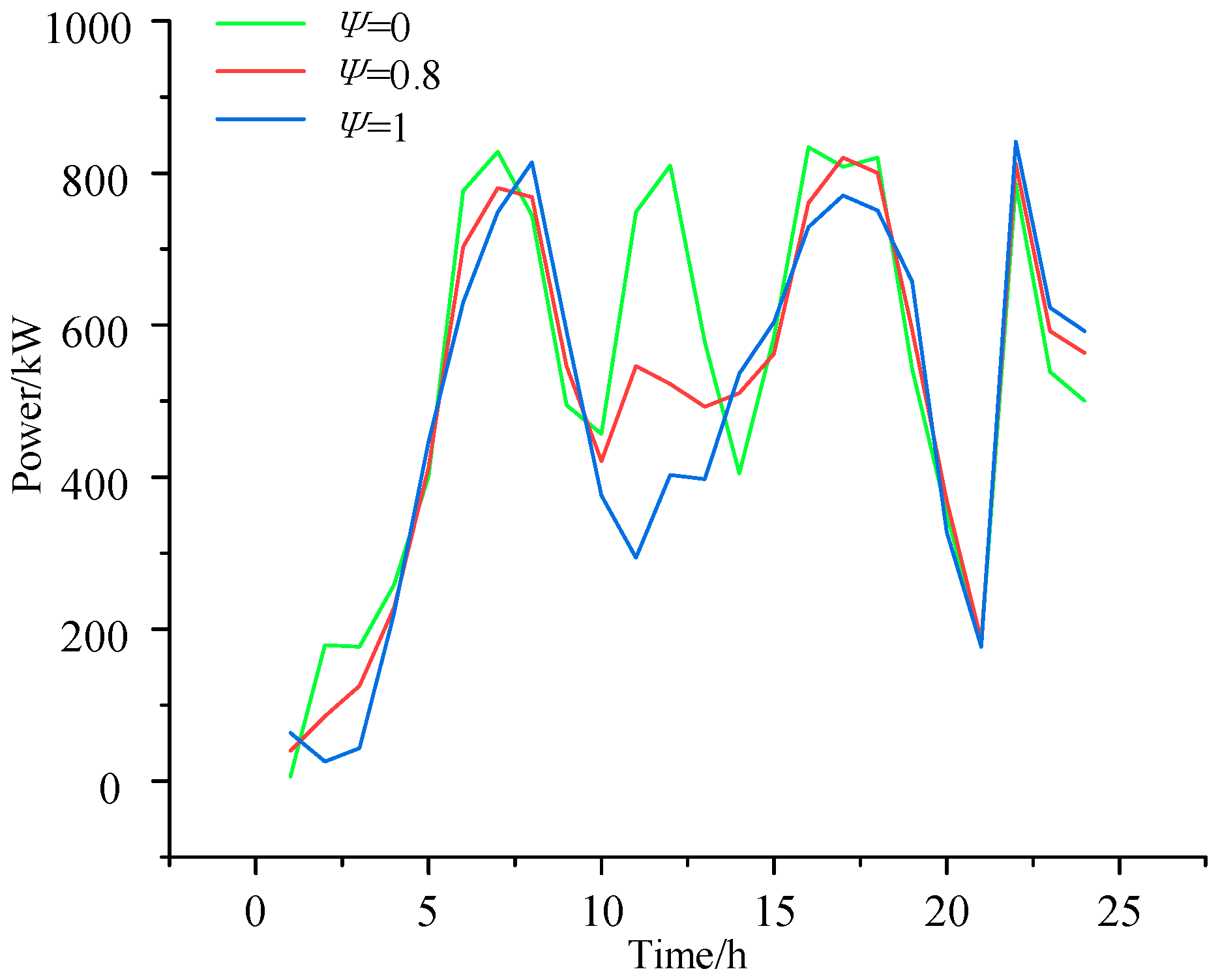
5.2. Impact of EV Forecasting Model on VPP Dispatch Model

In the model constructed in this paper, the total optimized cost is primarily driven by the costs of purchasing electricity and gas. To analyze the impact of EV integration on the system cost, the purchased power and GT output are compared for different EV user willingness levels. The willingness is set to 0 (no EV users accept VPP control), 0.8 (most users are willing to participate), and 1 (all users follow VPP dispatch), as shown in Figure 8 and Figure 9.

When V2G participates in the system’s optimal dispatch, the peak load is significantly reduced. EV charging during peak hours is shifted to off-peak hours, which increases the load during the off-peak period. Since the off-peak electricity price is lower, the system chooses to purchase more power from the main grid to reduce operating costs. Comparative analysis shows that when the user willingness is 0.8, 80% of EV users are willing to participate in control, reducing the 24 h power purchase by 1898.5 kW and natural gas consumption by 293.9 m³, lowering the system dispatch cost by 906.4 yuan (7.94%). When the user willingness is 1, meaning all users accept VPP dispatch, the 24 h power purchase is reduced by 2315.3 kW and natural gas consumption by 376.9 m³, decreasing the system dispatch cost by 1132.9 yuan (9.92%). The cost comparison for the three scenarios is shown in

Table 3. Cost comparison.

Optimal Dispatch System	Power Purchase Cost/yuan	Gas Purchase Cost/yuan	EV Dispatch Cost/yuan	Total Cost/yuan
Ψ = 0	6458.3	4953.8	0	11,412.1
Ψ = 0.8	5491.2	4201.7	812.8	10,505.7
Ψ = 1	5249.5	4013.7	1016	10,279.2

.

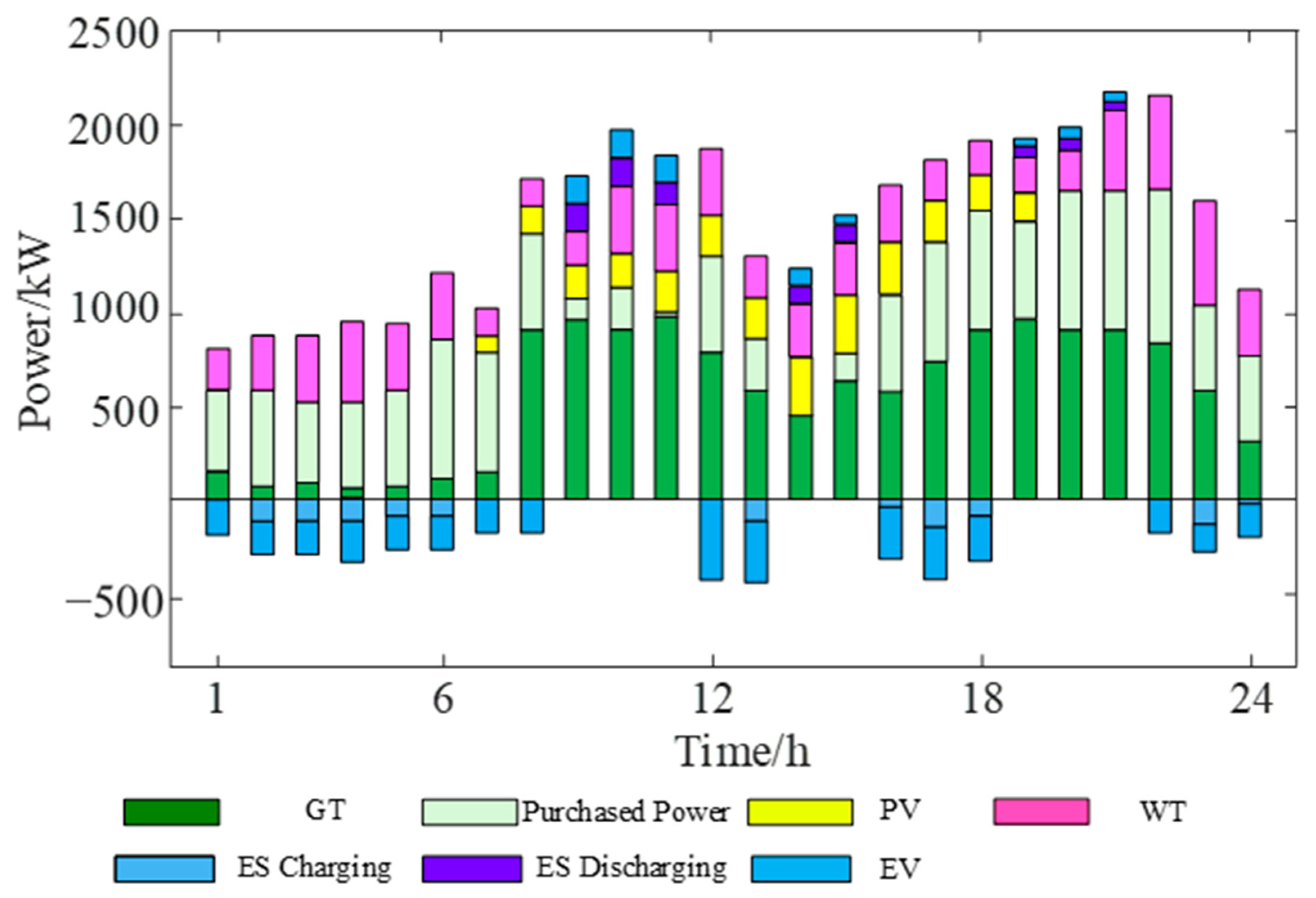
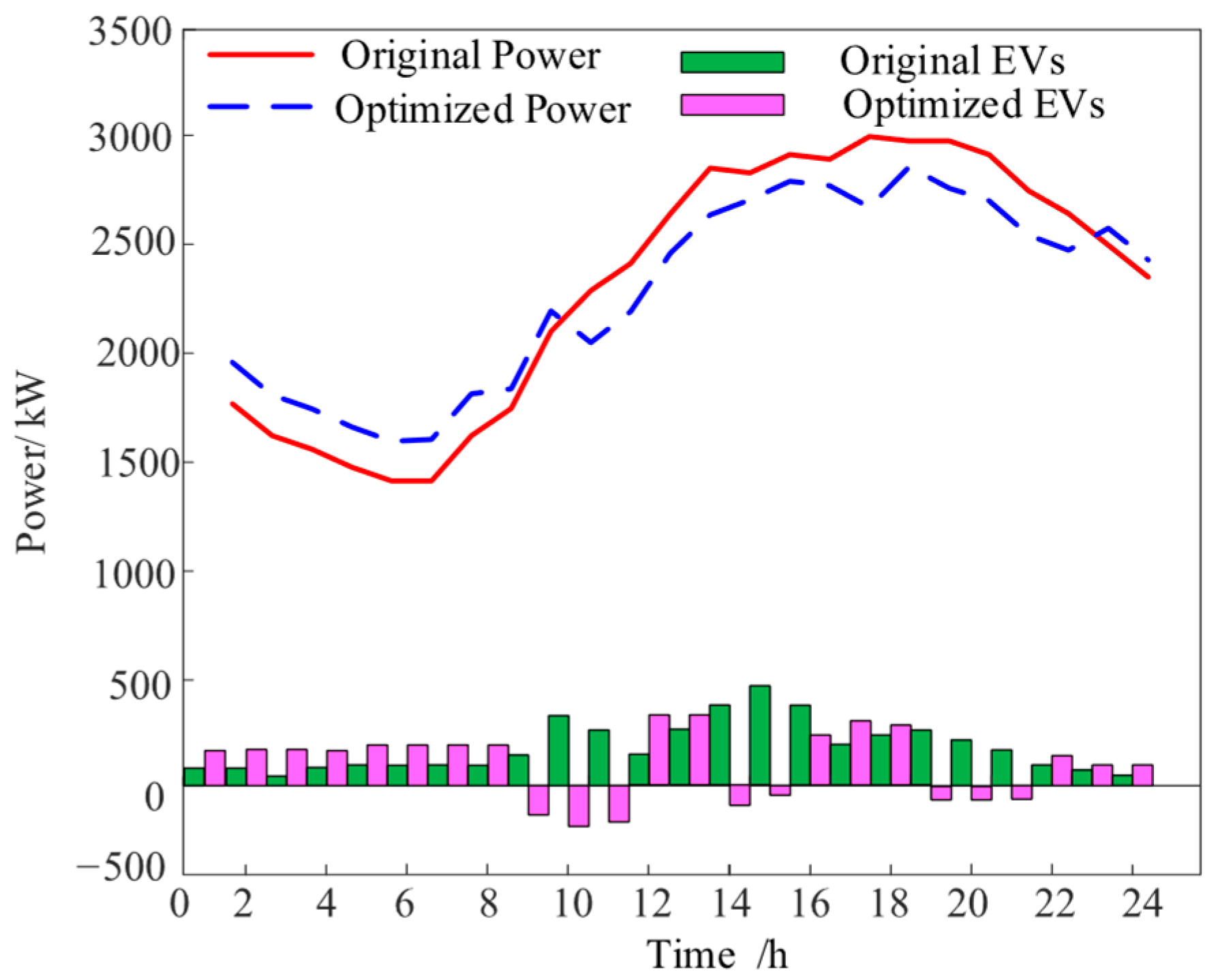
Figure 10 shows a comparison of EV charging/discharging and the load before and after optimization. Analysis of the bar chart shows that EVs play a positive role, reducing the peak-to-valley load difference by 24.55%. During peak hours such as 08:00–11:00, 13:00–15:00, and 18:00, EVs discharge, playing a peak-shaving role on the load curve and reducing the amount of electricity the VPP purchases from the main grid. While meeting the needs of EV owners, V2G effectively shifts the load from peak hours to mid-peak and off-peak periods. The EV charging peak load from 13:00 to 15:00 is distributed to the noon and afternoon of the mid-peak period, and the peak from 18:00 to 22:00 is moved to the period from 22:00 to the early morning of the next day, achieving the goal of peak shaving and valley filling.

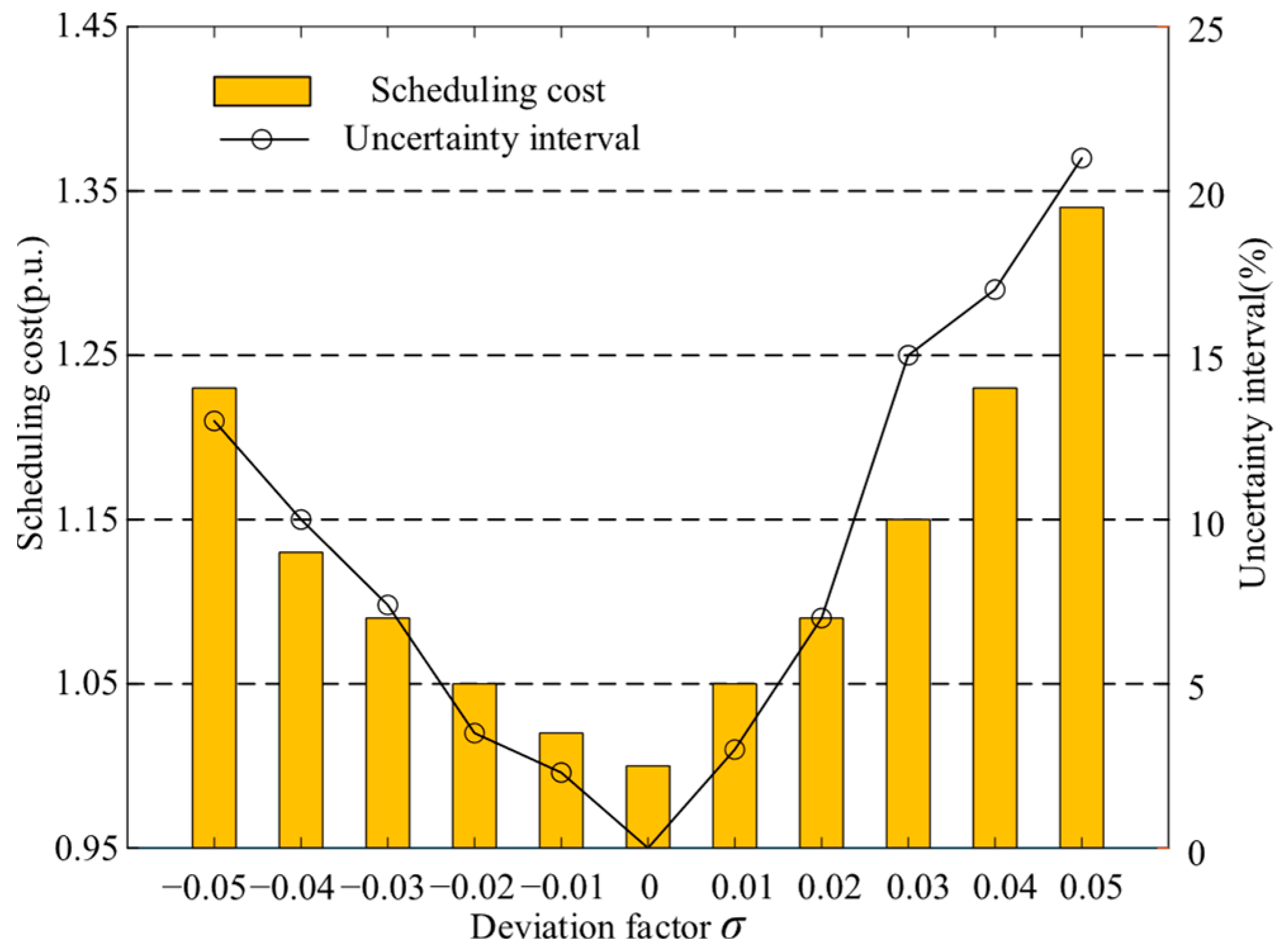
5.3. Impact of Deviation Factor on IGDT Dispatch Results

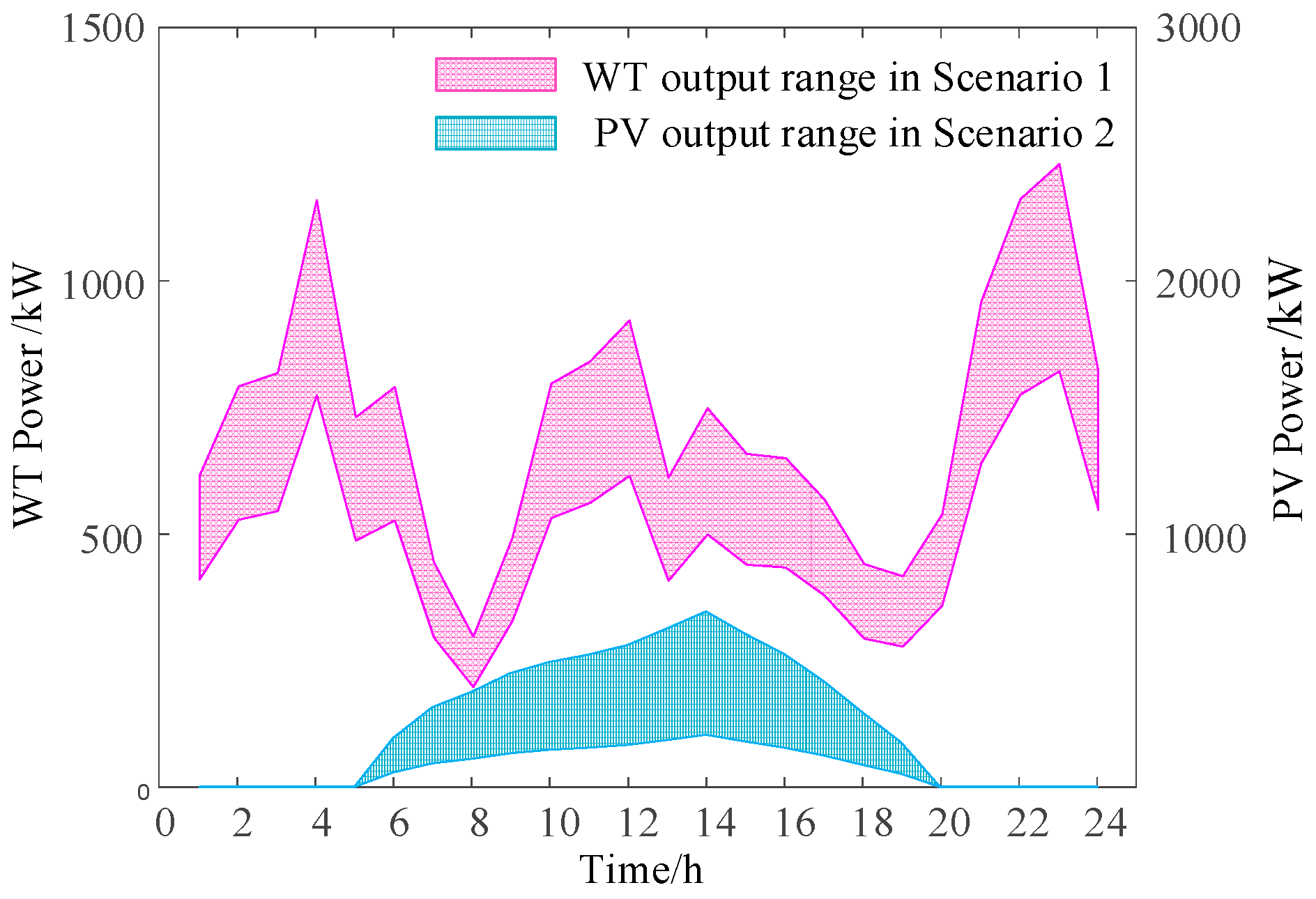
To analyze the impact of wind and solar output uncertainty within the system, three different uncertainty scenarios were set, as shown in

Table 4. Three uncertainty scenarios.

Scenario	Wind Power	Photovoltaic	Renewable Energy Penetration
Scenario1	√	×	39.5%
Scenario2	×	√	21.9%
Scenario3	√	√	61.4%

, where “√” indicates that the model considers the uncertainty factor and “×” indicates that it does not.

Let the fluctuation magnitude of the uncertain parameter in the IGDT robust dispatch model be ${\alpha }_r$, and in the IGDT opportunity dispatch model, let it be ${\alpha }_o$. Taking a deviation factor of 0.05 as an example, the pessimistic and optimistic dispatch costs for the system are 12,003.7 yuan and 10,860.4 yuan, respectively. In the model, the fluctuation magnitudes considering wind power uncertainty can be obtained as ${\alpha }_r^w=18.65\%$, ${\alpha }_o^w=21.15\%$, and those considering photovoltaic uncertainty ${\alpha }_r^{pv}=49.89\%$, ${\alpha }_o^{pv}=52.17\%$. The uncertain output range for wind and photovoltaic power is shown in Figure 11.

The value of the deviation factor needs to be chosen based on historical data, risk preference, and strategic goals, so that the decision can both handle uncertainty risks and seize potential opportunities. It is important to clarify that these deviation factors are not calibrated by the model but are set by the VPP operator as strategic inputs. For a given scheduling horizon, these values are static. For this purpose, the deviation factor coefficient varied from −0.05 to 0.05. The uncertainty radius and system operating cost of the IGDT dispatch model are shown in Figure 12. As seen in the figure, the uncertainty radius continuously increases with the increase in the risk-aversion coefficient, and the system operating cost also increases. This is because in the IGDT robust model, uncertainty pushes the objective expectation in an unfavorable direction. A larger uncertainty radius indicates greater robustness against uncertainty but a higher system operating cost. Conversely, in the IGDT opportunity model, uncertainty moves the objective expectation in a favorable direction. In the opportunity model, achieving a more ambitious cost target requires a larger uncertainty radius. The dispatch plan in this case can better cope with the long-term uncertainty of wind and load, and the VPP can choose an appropriate aversion coefficient based on the cost it can bear.

5.4. Comparative Analysis of IGDT and Stochastic Optimization

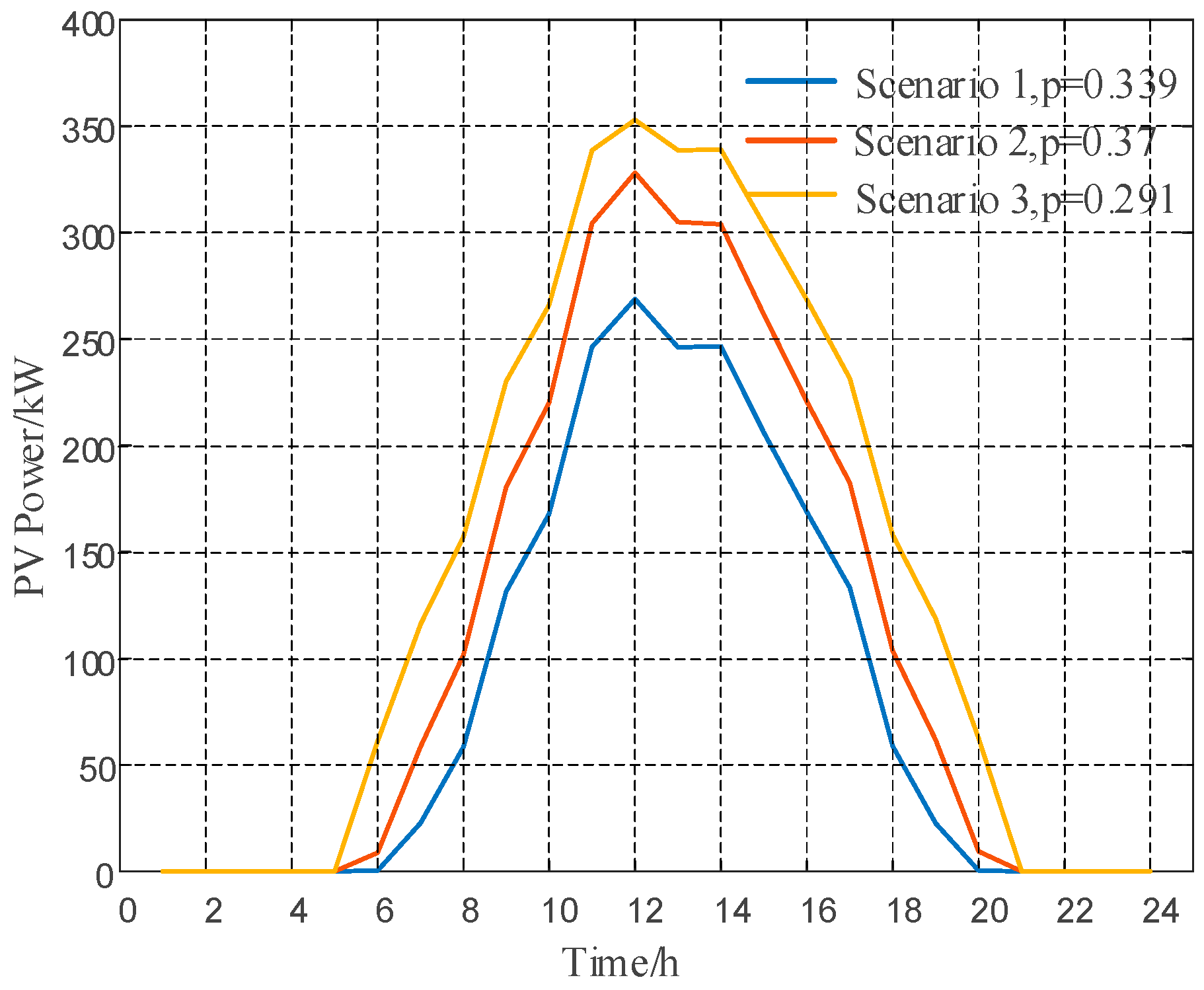
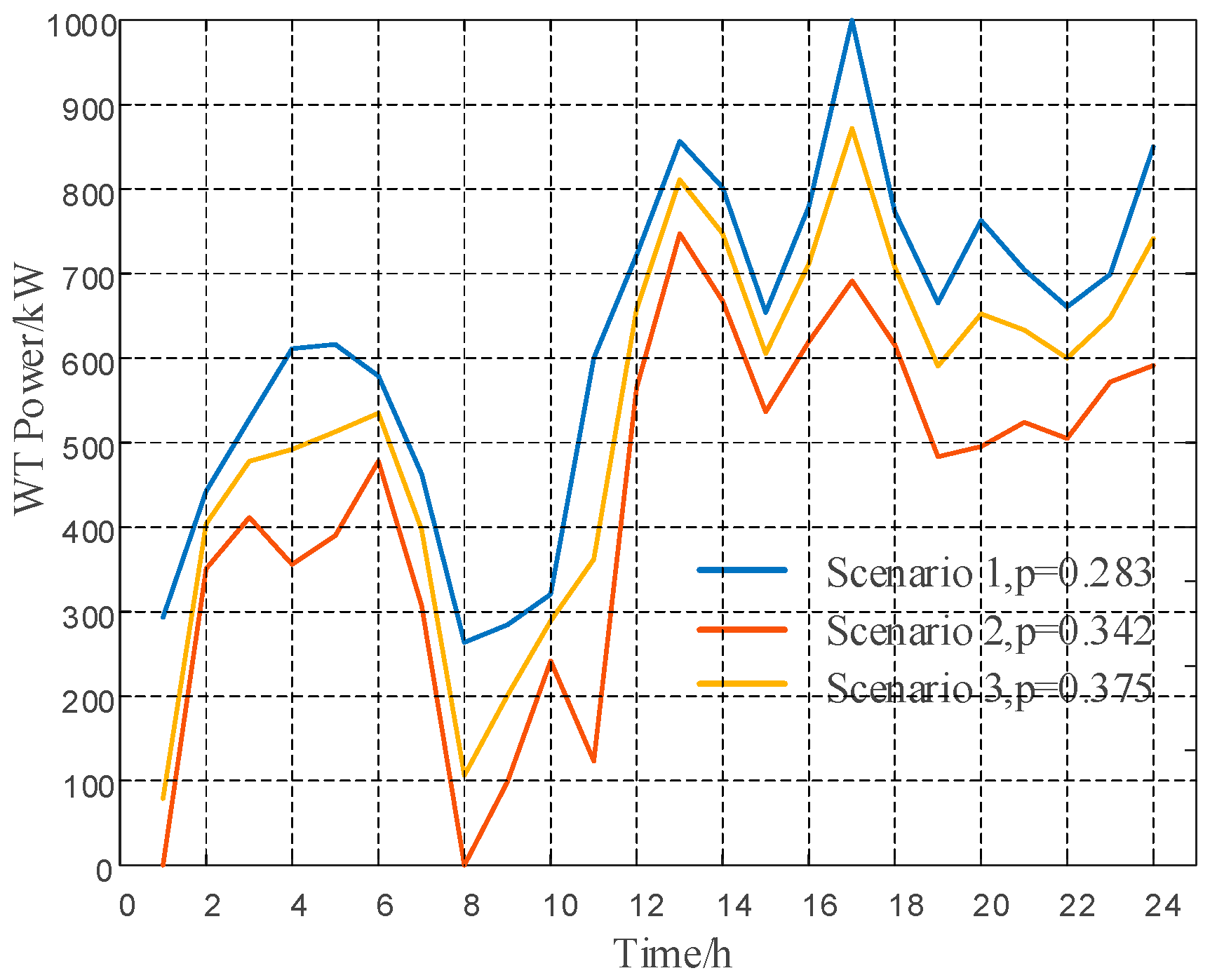
This section compares IGDT with the Monte Carlo and robust optimization methods to verify the differences between the IGDT model proposed in this paper and traditional stochastic optimization methods in handling wind power uncertainty. The Monte Carlo method was used to generate 1000 scenarios, where wind power output follows a Beta distribution with shape parameters α = 2.5, β = 3.0, and a forecast reference value of 1000 kW; photovoltaic output follows a Beta distribution with shape parameters α = 3.0, β = 2.8, and a forecast reference value of 360 kW. The K-means clustering method was then used to cluster these into three typical scenarios [26,27]. The clustering results for photovoltaic and wind power are shown in Figure 13 and Figure 14.

Robust optimization aims to minimize the total operating cost in the worst-case scenario. The values for the relevant uncertain parameters are shown in

Table 5. Robust optimization parameters.

Parameter	Value	Model
Wind power fluctuation range	±25% of predicted value	$\mathrm{\Delta }{P}_t^w=0.25{\overline{P}}_t^w$
Photovoltaic fluctuation range	±25% of predicted value	$\mathrm{\Delta }{P}_t^{pv}=0.25{\overline{P}}_t^{pv}$
Load fluctuation range	±15% of predicted value	$\mathrm{\Delta }{P}_t^{load}=0.15{\overline{P}}_t^{load}$

.

To verify the model’s practicality, the performance of IGDT, Monte Carlo, and robust optimization was compared based on actual operational data from a typical day of a VPP demonstration project in Jiangsu Province, China, as shown in

Table 6. Actual operating parameters.

Parameter	Value	Unit
Actual wind power output	832 ± 121	kW
Actual photovoltaic output	378 ± 89	kW
System load	2150 ± 205	kW
Electricity purchase cost	0.84/0.53/0.27	yuan/kWh
Natural gas price	2.52	yuan/m3

.

The performance of the method proposed in this paper was compared with other stochastic optimization methods in terms of average cost, worst-case cost, uncertainty radius, and computation time. Ten uncertainty scenarios were randomly selected to compute the average cost and worst-case cost. The comparison results between IGDT and traditional stochastic optimization are shown in

Table 7. IGDT compared with other stochastic optimization methods.

Method	Uncertainty Radius (%)	Average Cost (yuan)	Worst-Case Cost (yuan)	Time (s)
Monte Carlo	22.64	11,656.3	12,487.1	597
Robust Optimization	25.00	12,014.8	12,156.4	139
IGDT	18.65	11,395.2	12,277.6	53

.

As can be seen from Table 7, despite demonstrating superior performance in terms of average cost, the Monte Carlo method exhibits the highest worst-case cost and incurs a marked increase in computational time. Robust optimization has the strongest ability to withstand wind and solar load uncertainty, but its average cost is also the highest, trading economy for system stability. IGDT demonstrates superior economic efficiency and computational speed over other stochastic optimization methods, reducing average dispatching costs by a range of 2.24% to 5.16%, with calculation times decreasing by 61.8% to 91.1%. This indicates that IGDT has a lower algorithmic complexity, making its computation time acceptable for day-ahead scenarios. Meanwhile, it is crucial to recognize that because IGDT operates based on the predicted values of uncertain parameters and quantifies their deviation through an uncertainty radius α, it exhibits a lower tolerance to prediction errors concerning renewable energy and load uncertainties. Consequently, this necessitates either more accurate forecasting models or enhanced real-time control capabilities to manage deviations.

6. Conclusions

This paper proposed an optimal dispatch model for a multi-source VPP based on IGDT, which effectively integrates the V2G capabilities of EVs to manage source-load uncertainties. The simulation results validate the model’s effectiveness in enhancing both the economic and secure operation of the power system. By strategically scheduling the charging and discharging cycles of EVs, the model successfully reduced the peak-to-valley load difference by 24.55%, thereby improving net load curve stability and reducing operational pressures. Quantitatively, the inclusion of V2G capabilities led to a 7.94% reduction in the VPP’s comprehensive dispatch cost under typical scenarios, demonstrating the significant economic benefits of leveraging EV flexibility. Furthermore, the proposed IGDT-based approach proved superior to conventional uncertainty handling methods; compared to stochastic and robust optimization, it not only reduced average dispatching costs by a range of 2.24% to 5.16% but also drastically improved computational performance, with calculation times decreasing by 61.8% to 91.1%.

Despite these compelling results, the study has certain limitations. The EV participation model, while effective, simplifies user behavior and does not fully account for complex factors such as battery degradation costs or the heterogeneity of driver responses to incentives. Similarly, the IGDT method’s performance is inherently dependent on the accuracy of the initial forecast, and its non-probabilistic nature may not be suitable for all risk management frameworks. Future research should therefore focus on developing more sophisticated models of EV user behavior, potentially using agent-based modeling or machine learning to capture more realistic participation patterns. Another promising direction is to explore hybrid uncertainty models that combine the computational efficiency of IGDT with the probabilistic insights of scenario-based methods, thereby providing VPP operators with a more robust and comprehensive decision-making tool for navigating highly uncertain energy landscapes.