Numerical Study on the Energy-Harvesting Performance of Multiple Flapping Foils
Abstract
1. Introduction
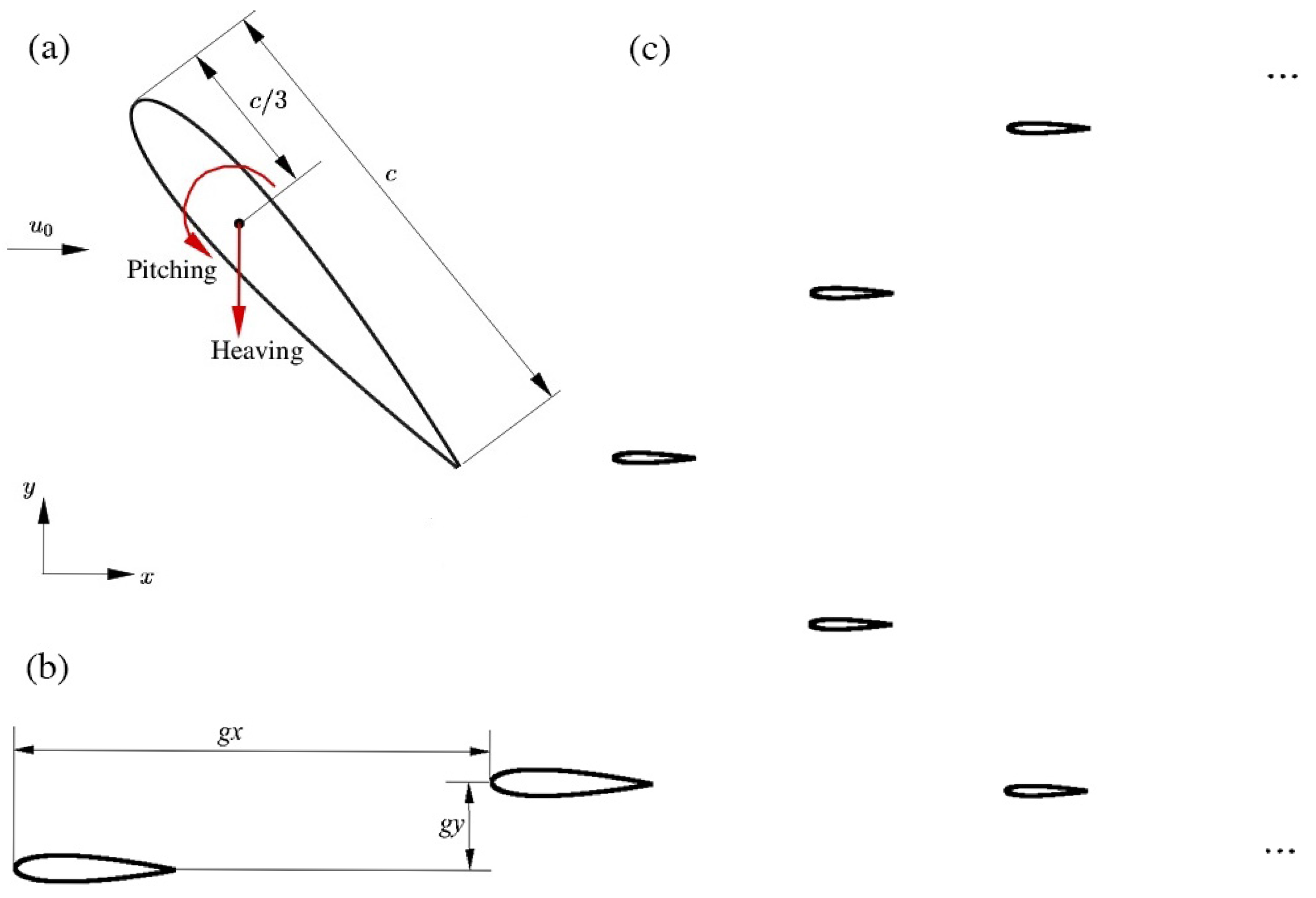
2. Physical Problem
3. Numerical Methods
3.1. LBM for the Fluid Flow
3.2. The IB Method for FSI
4. Results and Discussions
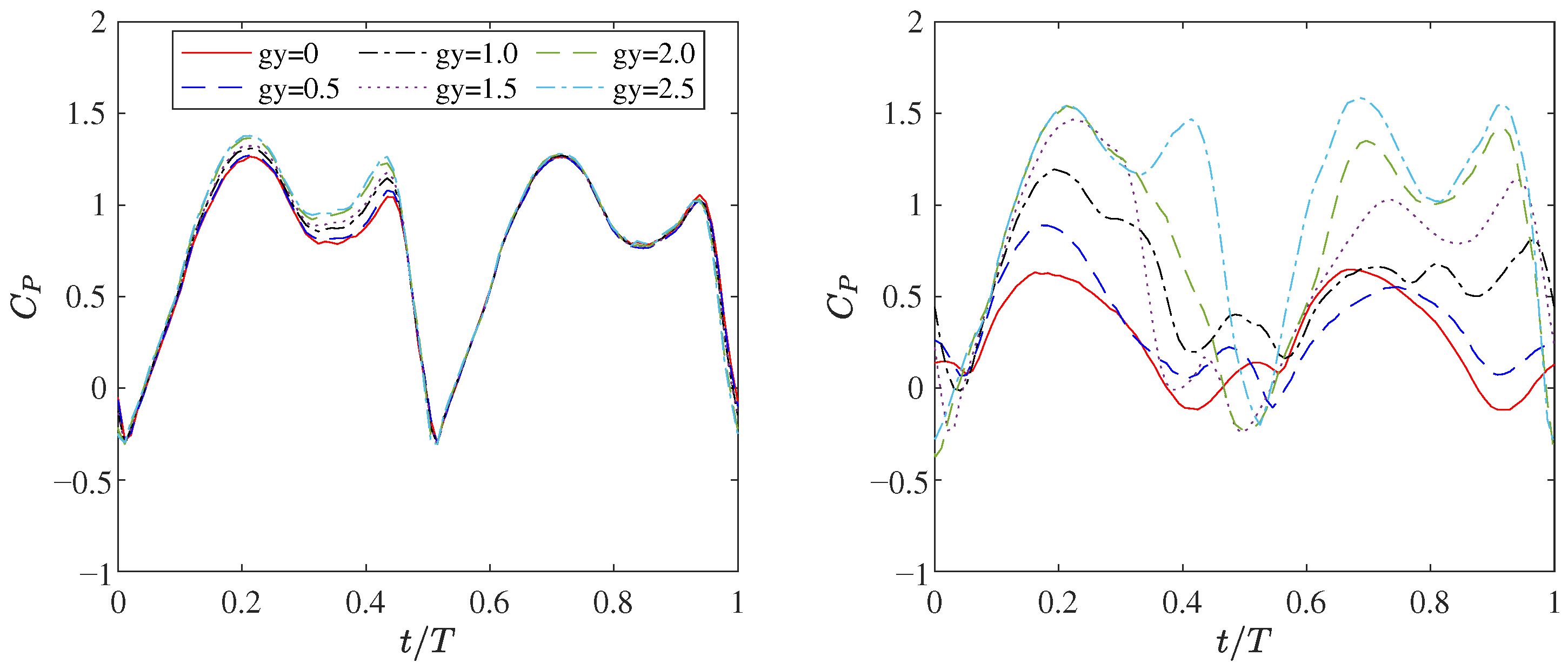
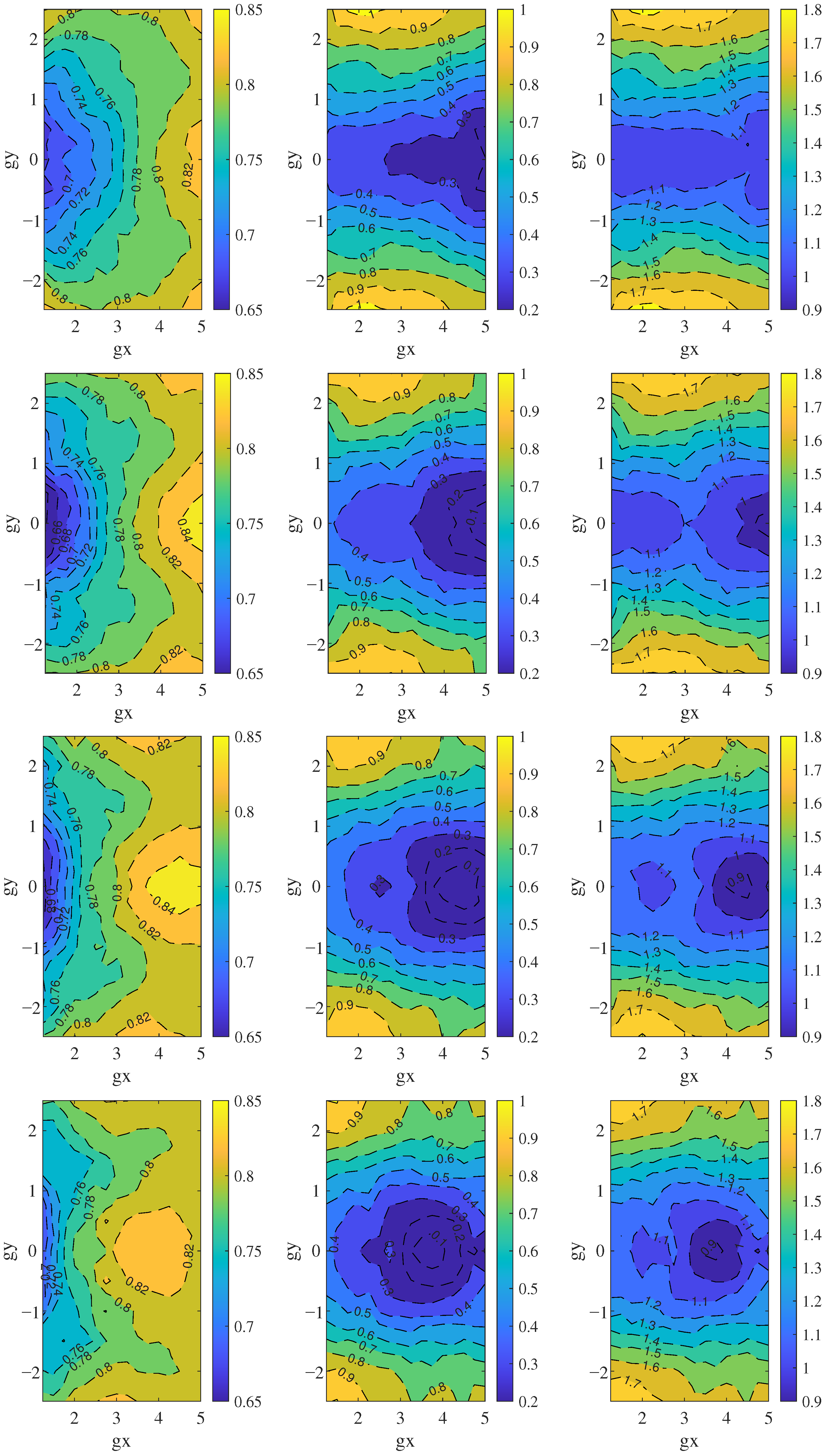
4.1. Effects of the Spatial Arrangements of Two Staggered Foils
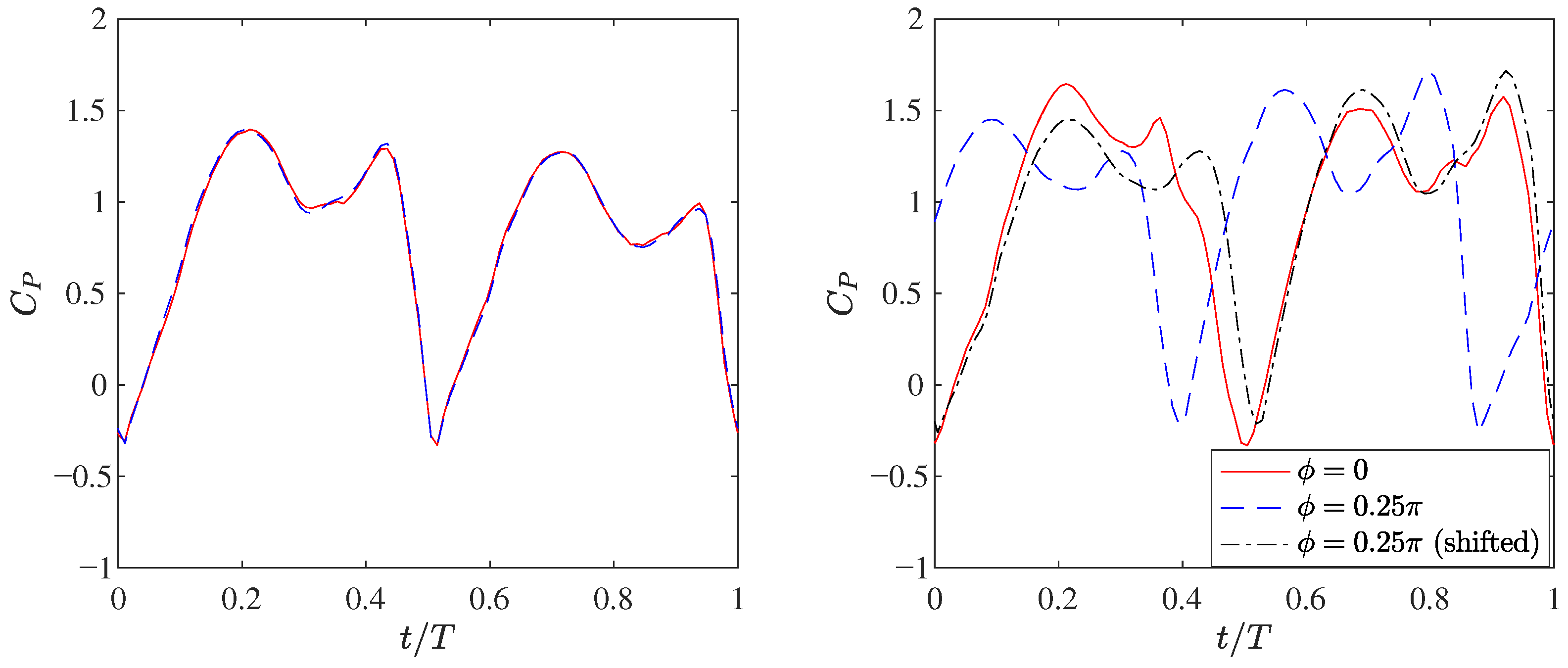
4.2. Effects of Phase Difference of Two Staggered Foils
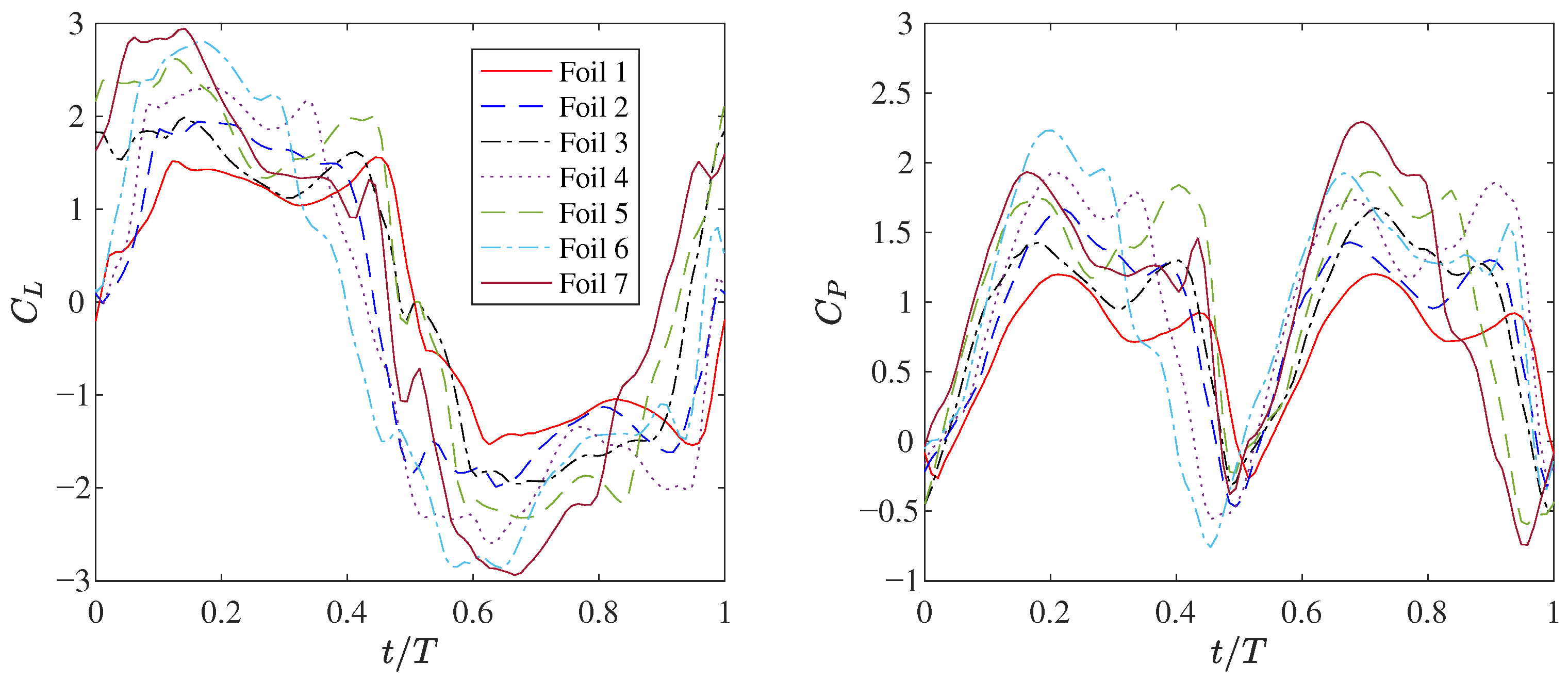
4.3. Energy-Harvesting Performance of Multiple Flapping Foils
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational fluid dynamics |
| DVM | Discrete vortex method |
| FSI | Fluid–structure interaction |
| IBM | Immersed boundary method |
| LBM | Lattice Boltzmann method |
| LEV | Leading edge vortex |
| MRT | Multi-relaxation-time |
| TEV | Trailing edge vortex |
| UPM | Unsteady panel method |
References
- Olabi, A.; Abdelkareem, M.A. Renewable energy and climate change. Renew. Sustain. Energy Rev. 2022, 158, 112111. [Google Scholar] [CrossRef]
- Yang, X.; Pang, J.; Teng, F.; Gong, R.; Springer, C. The environmental co-benefit and economic impact of China’s low-carbon pathways: Evidence from linking bottom-up and top-down models. Renew. Sustain. Energy Rev. 2021, 136, 110438. [Google Scholar] [CrossRef]
- Young, J.; Lai, J.C.; Platzer, M.F. A review of progress and challenges in flapping foil power generation. Prog. Aerosp. Sci. 2014, 67, 2–28. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, X.; Tian, X.; Li, X.; Lu, W. A review on fluid dynamics of flapping foils. Ocean Eng. 2020, 195, 106712. [Google Scholar] [CrossRef]
- Lewis, M.; Neill, S.; Robins, P.; Hashemi, M. Resource assessment for future generations of tidal-stream energy arrays. Energy 2015, 83, 403–415. [Google Scholar] [CrossRef]
- McKinney, W.; DeLaurier, J. The Wingmill: An oscillating-wing windmill. J. Energy 1981, 5, 109–115. [Google Scholar] [CrossRef]
- Davids, S.T. A Computational and Experimental Investigation of a Flutter Generator. Ph.D. Thesis, Naval Postgraduate School, Monterey, CA, USA, 1999. [Google Scholar]
- Lindsey, K. A Feasibility Study of Oscillating-Wing Power Generators. Ph.D. Thesis, Naval Postgraduate School, Monterey, CA, USA, 2002. [Google Scholar]
- Wang, L.; Liu, Z.; Rajamuni, M. Recent progress of lattice Boltzmann method and its applications in fluid-structure interaction. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 2461–2484. [Google Scholar] [CrossRef]
- Hoke, C.M.; Young, J.; Lai, J.C. Enhancing the power-extraction efficiency of a flapping foil by active morphing. AIAA J. 2023, 61, 4056–4069. [Google Scholar] [CrossRef]
- Liu, W.; Xiao, Q.; Zhu, Q. Passive flexibility effect on oscillating foil energy harvester. AIAA J. 2016, 54, 1172–1187. [Google Scholar] [CrossRef]
- Liu, Z.; Lai, J.C.; Young, J.; Tian, F.B. Discrete vortex method with flow separation corrections for flapping-foil power generators. AIAA J. 2017, 55, 410–418. [Google Scholar] [CrossRef]
- Wu, S.; Wang, L. Numerical Study on the Energy Harvesting Performance of a Flapping Foil with Attached Flaps. Processes 2024, 12, 1963. [Google Scholar] [CrossRef]
- Kinsey, T.; Dumas, G. Optimal tandem configuration for oscillating-foils hydrokinetic turbine. J. Fluids Eng. 2012, 134, 031103. [Google Scholar] [CrossRef]
- Karakas, F.; Fenercioglu, I. Effect of phase angle on tandem flapping-wing power generation. Int. J. Energy Prod. Manag. 2017, 2, 95–105. [Google Scholar] [CrossRef]
- Young, J.; Tian, F.B.; Liu, Z.; Lai, J.C.; Nadim, N.; Lucey, A.D. Analysis of unsteady flow effects on the Betz limit for flapping foil power generation. J. Fluid Mech. 2020, 902, A30. [Google Scholar] [CrossRef]
- Zheng, M.; Bai, Y. The configuration effect of flapping foils for energy harvesting. Phys. Fluids 2022, 34, 113608. [Google Scholar] [CrossRef]
- Xiao, Q.; Zhu, Q. A review on flow energy harvesters based on flapping foils. J. Fluids Struct. 2014, 46, 174–191. [Google Scholar] [CrossRef]
- Kinsey, T.; Dumas, G. Parametric study of an oscillating airfoil in a power-extraction regime. AIAA J. 2008, 46, 1318–1330. [Google Scholar] [CrossRef]
- Liu, Z.; Tian, F.B.; Young, J.; Lai, J. Flapping foil power generator performance enhanced with a spring-connected tail. Phys. Fluids 2017, 29, 123601. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C. Analysis of lattice Boltzmann equation for microscale gas flows: Relaxation times, boundary conditions and the Knudsen layer. Int. J. Comput. Fluid Dyn. 2008, 22, 465–473. [Google Scholar] [CrossRef]
- Tian, F.B.; Luo, H.; Zhu, L.; Liao, J.C.; Lu, X.Y. An efficient immersed boundary-lattice Boltzmann method for the hydrodynamic interaction of elastic filaments. J. Comput. Phys. 2011, 230, 7266–7283. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.; Mei, R.; Shyy, W. A multi-block lattice Boltzmann method for viscous fluid flows. Int. J. Numer. Methods Fluids 2002, 39, 99–120. [Google Scholar] [CrossRef]
- Kim, Y.; Peskin, C.S. Penalty immersed boundary method for an elastic boundary with mass. Phys. Fluids 2007, 19, 053103. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, Q.; Li, Z.; Li, Y.; Feng, X. Partial confinement effects on the performance of a flapping foil power generator. Phys. Fluids 2023, 35, 027108. [Google Scholar] [CrossRef]
- Tian, F.B.; Dai, H.; Luo, H.; Doyle, J.F.; Rousseau, B. Fluid–structure interaction involving large deformations: 3D simulations and applications to biological systems. J. Comput. Phys. 2014, 258, 451–469. [Google Scholar] [CrossRef] [PubMed]
- Mittal, R.; Dong, H.; Bozkurttas, M.; Najjar, F.; Vargas, A.; Von Loebbecke, A. A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. J. Comput. Phys. 2008, 227, 4825–4852. [Google Scholar] [CrossRef] [PubMed]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef]
- Wang, L.; Tian, F.B. Numerical simulation of flow over a parallel cantilevered flag in the vicinity of a rigid wall. Phys. Rev. E 2019, 99, 053111. [Google Scholar] [CrossRef]







| 1.25 | 0.774 | 0.134 | −45.9% |
| 2.0 | 0.766 | 0.232 | −40.6% |
| 3.0 | 0.749 | 0.281 | −38.7% |
| 4.0 | 0.781 | 0.272 | −37.3% |
| 5.0 | 0.814 | 0.274 | −35.2% |
| 0.0 | 0.749 | 0.281 | −38.7% |
| 0.5 | 0.750 | 0.348 | −34.6% |
| 1.0 | 0.764 | 0.589 | −19.5% |
| 1.5 | 0.771 | 0.665 | −14.5% |
| 2.0 | 0.784 | 0.808 | −5.2% |
| 2.5 | 0.789 | 0.993 | 6.1% |
| N | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 (baseline) | 0.850 | - | - | - | - | - | - | - |
| 3 | 0.733 | 0.956 | 0.963 | - | - | - | - | 4.1% |
| 5 | 0.703 | 0.903 | 0.900 | 1.047 | 1.062 | - | - | 8.6% |
| 7 | 0.692 | 0.878 | 0.877 | 1.046 | 1.036 | 1.028 | 1.031 | 10.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Wang, L. Numerical Study on the Energy-Harvesting Performance of Multiple Flapping Foils. Processes 2025, 13, 2739. https://doi.org/10.3390/pr13092739
Wu S, Wang L. Numerical Study on the Energy-Harvesting Performance of Multiple Flapping Foils. Processes. 2025; 13(9):2739. https://doi.org/10.3390/pr13092739
Chicago/Turabian StyleWu, Shihui, and Li Wang. 2025. "Numerical Study on the Energy-Harvesting Performance of Multiple Flapping Foils" Processes 13, no. 9: 2739. https://doi.org/10.3390/pr13092739
APA StyleWu, S., & Wang, L. (2025). Numerical Study on the Energy-Harvesting Performance of Multiple Flapping Foils. Processes, 13(9), 2739. https://doi.org/10.3390/pr13092739





