Research on the Formation-Wellbore Temperature Profile Characteristics Under the Co-Existence of Kick and Leakage Condition
Abstract
1. Introduction
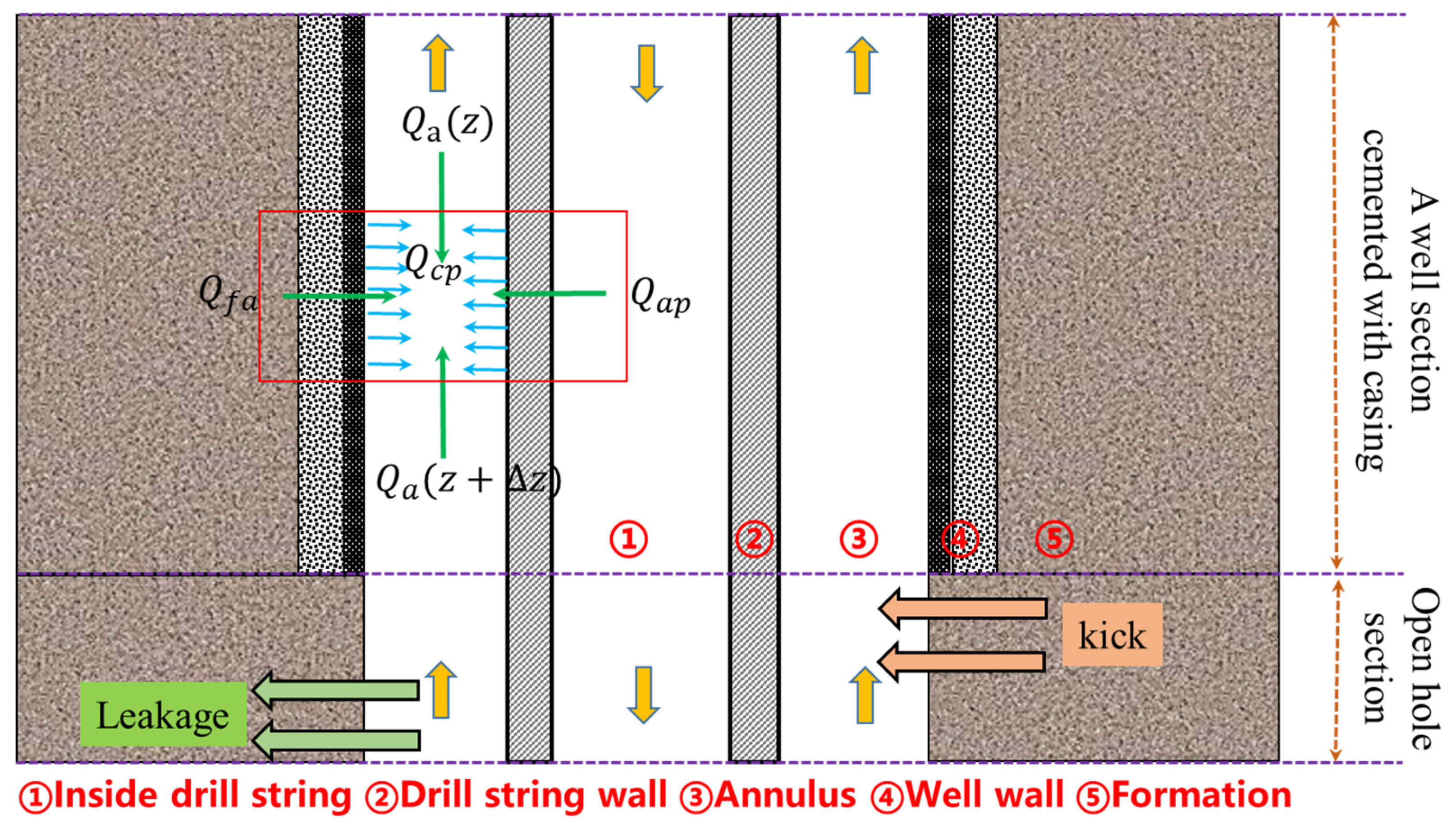
2. Physical Model
- Case 1. A single-point leakage at the bottom and a single-point kick (SK) at the upper bare borehole.
- Case 2. A continuous leakage (CL) at the bottom and a single-point kick at the upper bare borehole.
- Case 3. A single-point leakage at the bottom and a continuous kick (CK) at the upper bare borehole.
- Case 4. A continuous leakage at the bottomhole and a continuous kick at the upper bare borehole.
- Heat convection caused by drilling fluids flow in the annulus and drilling string.
- Variable mass flow and heat convection due to formation fluid intrusion into the annulus.
- Heat loss and convection due to mud leakage in the annulus.
- Heat transfer between formation and wellbore.
3. Mathematical Model
- (1)
- The thermophysical properties of solid media (pipe, cement and formation) are considered constant and do not depend on temperature changes.
- (2)
- There is one-dimensional axial flow in the wellbore.
- (3)
- The effect of cuttings on heat exchange between wellbore and formation is ignored
- (4)
- To reduce computational complexity, the wellbore wall is modeled as a homogeneous medium, and the multi-layer radial heat transfer within the “casing–cement–formation” system is neglected.
3.1. Heat Transfer Model in Drill String
3.2. Heat Transfer Model of Drill String Wall
3.3. Heat Transfer Model of the Annulus
3.4. Heat Transfer Model of the Well Wall
3.5. Heat Transfer Model of the Formation
3.6. Auxiliary Model
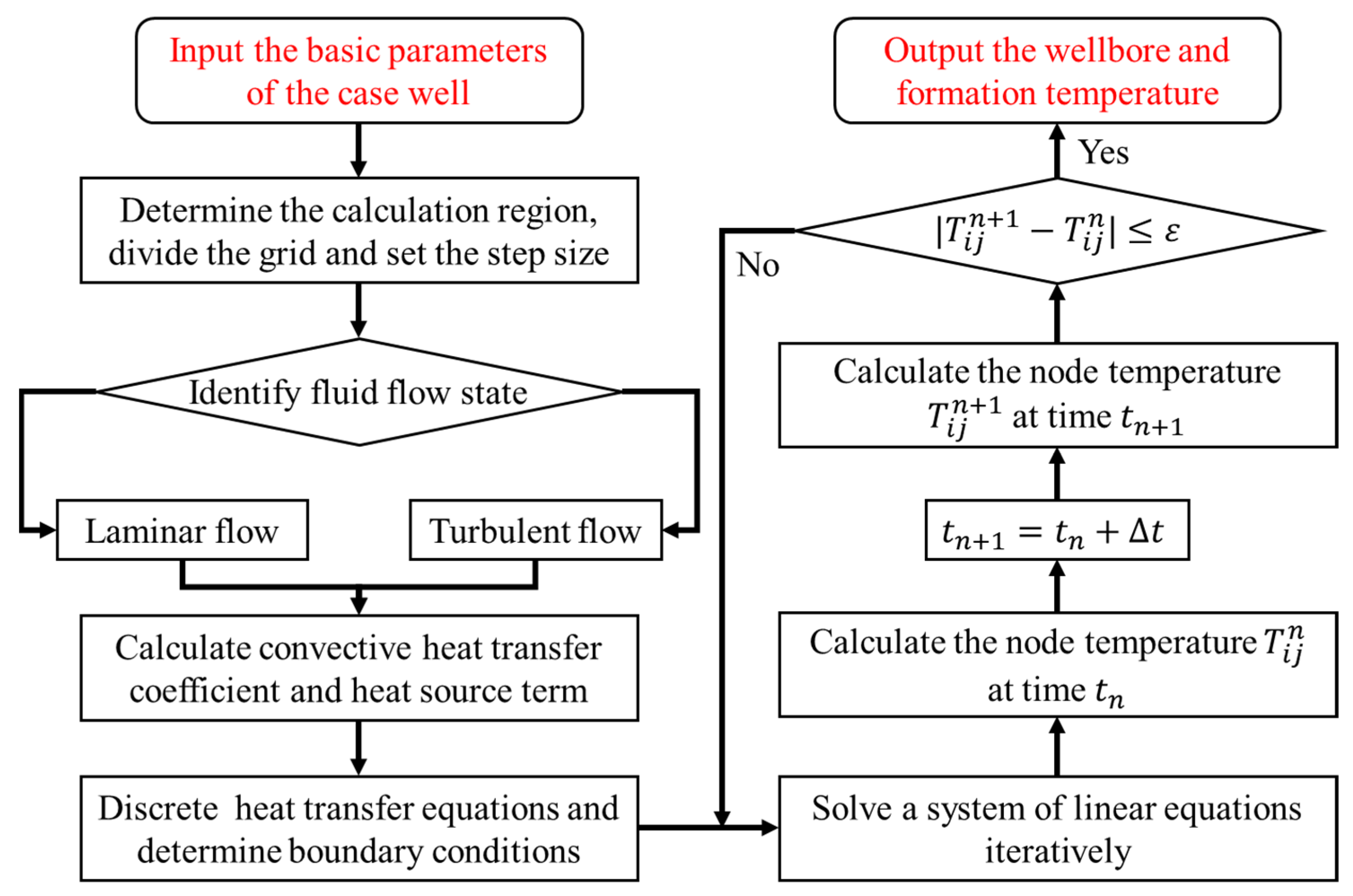
4. Model Solution
4.1. Initial Condition
4.2. Boundary Condition
4.3. Solution Process
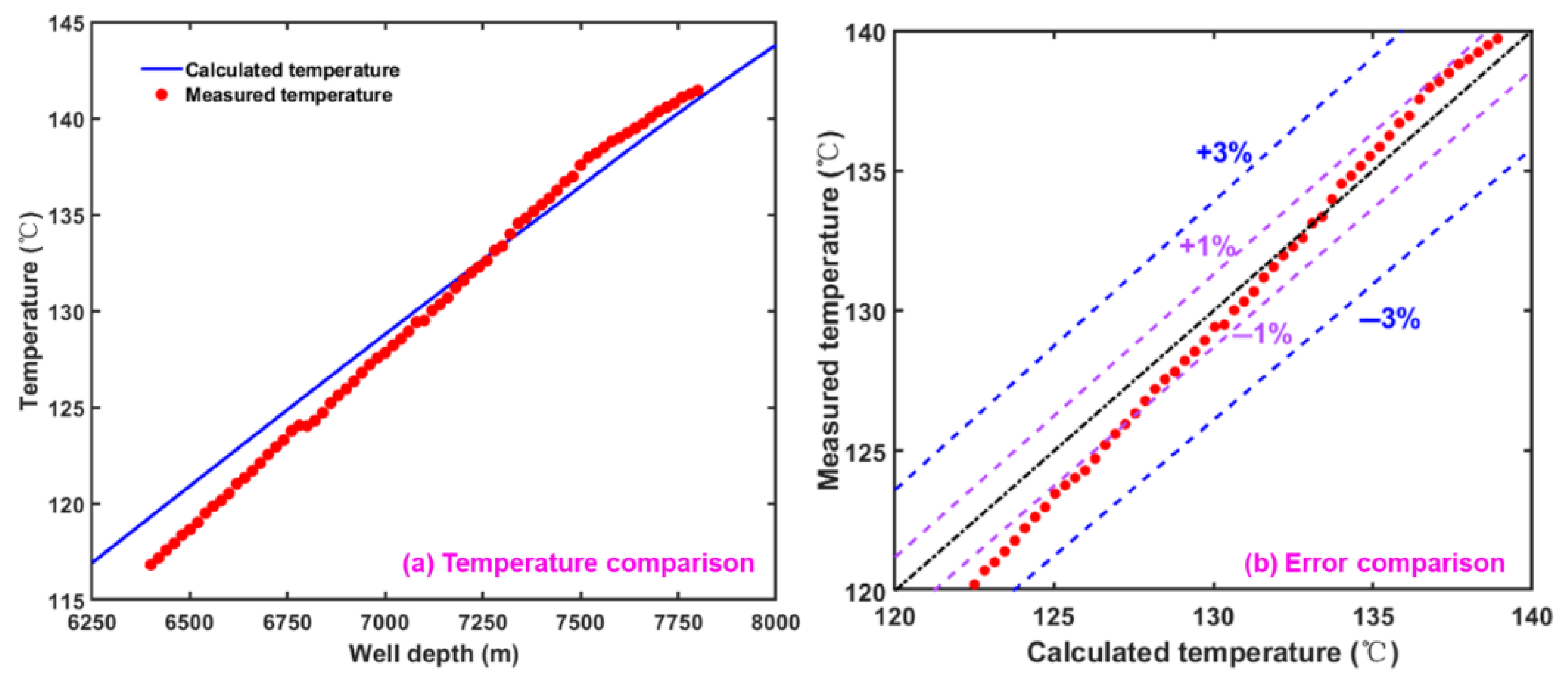
5. Model Validation
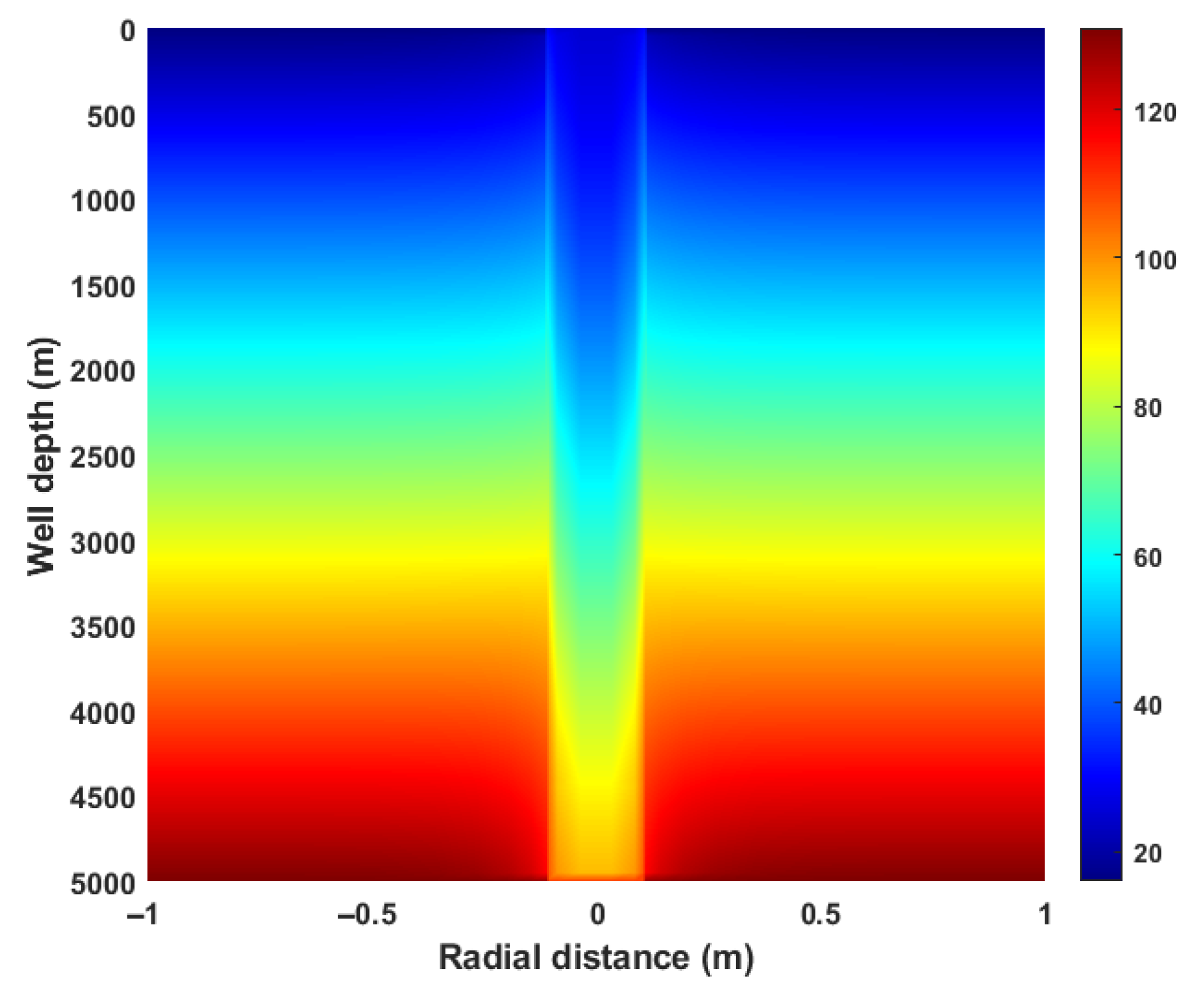
6. Results and Discussion
6.1. Annulus Temperature
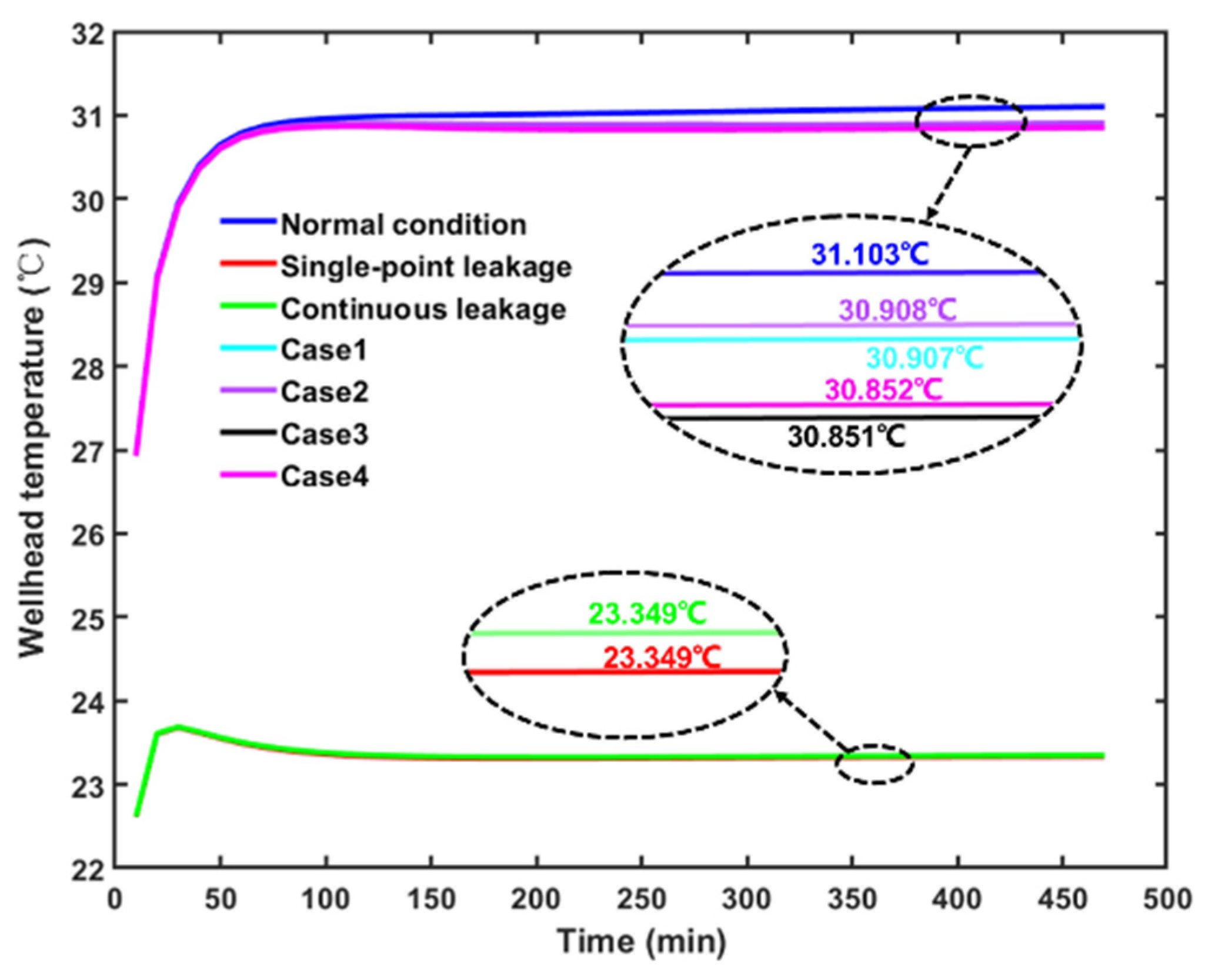
6.2. Wellhead Temperature
6.3. The Temperature of the Bottom Hole
6.4. Temperature Difference Between Inside the Drill String and Annulus
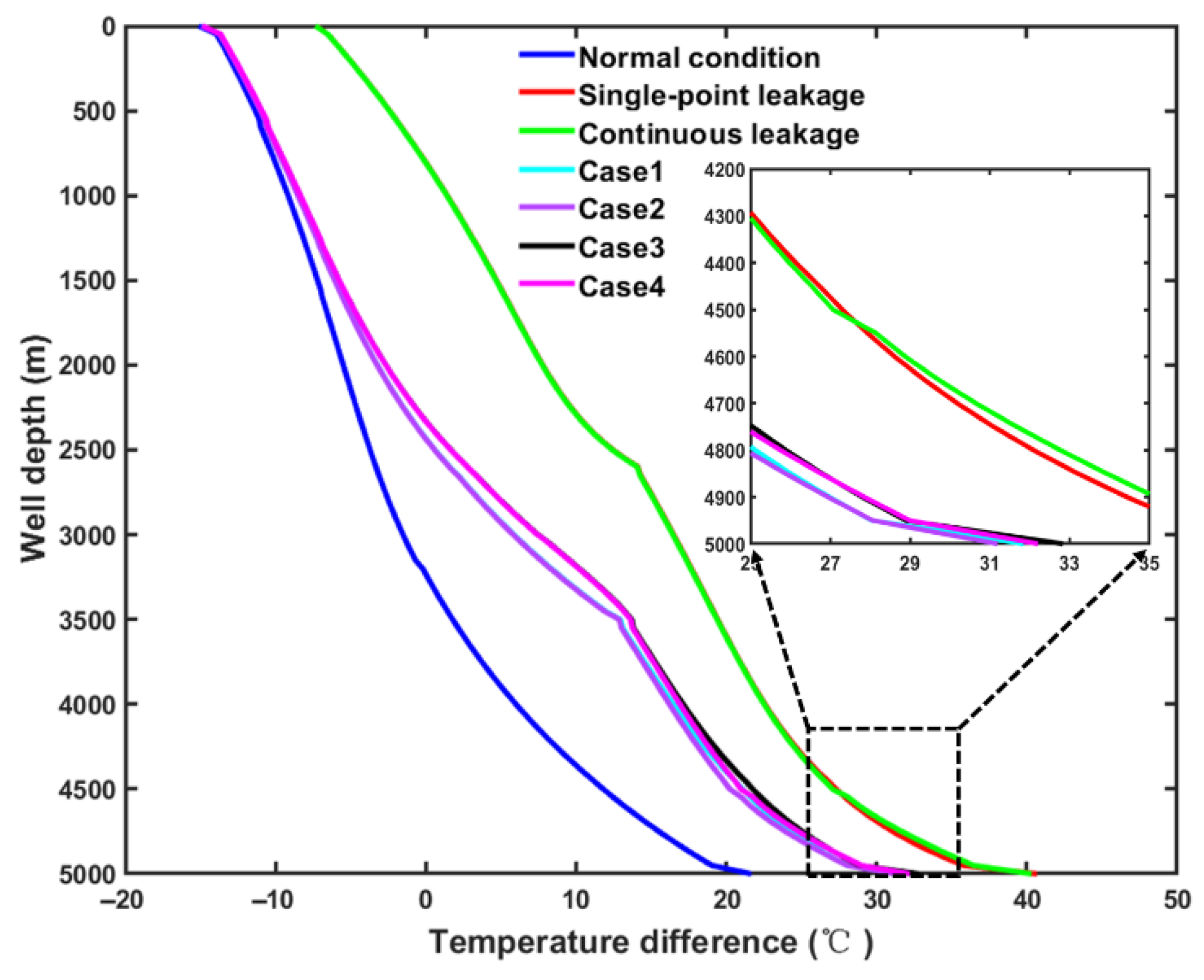
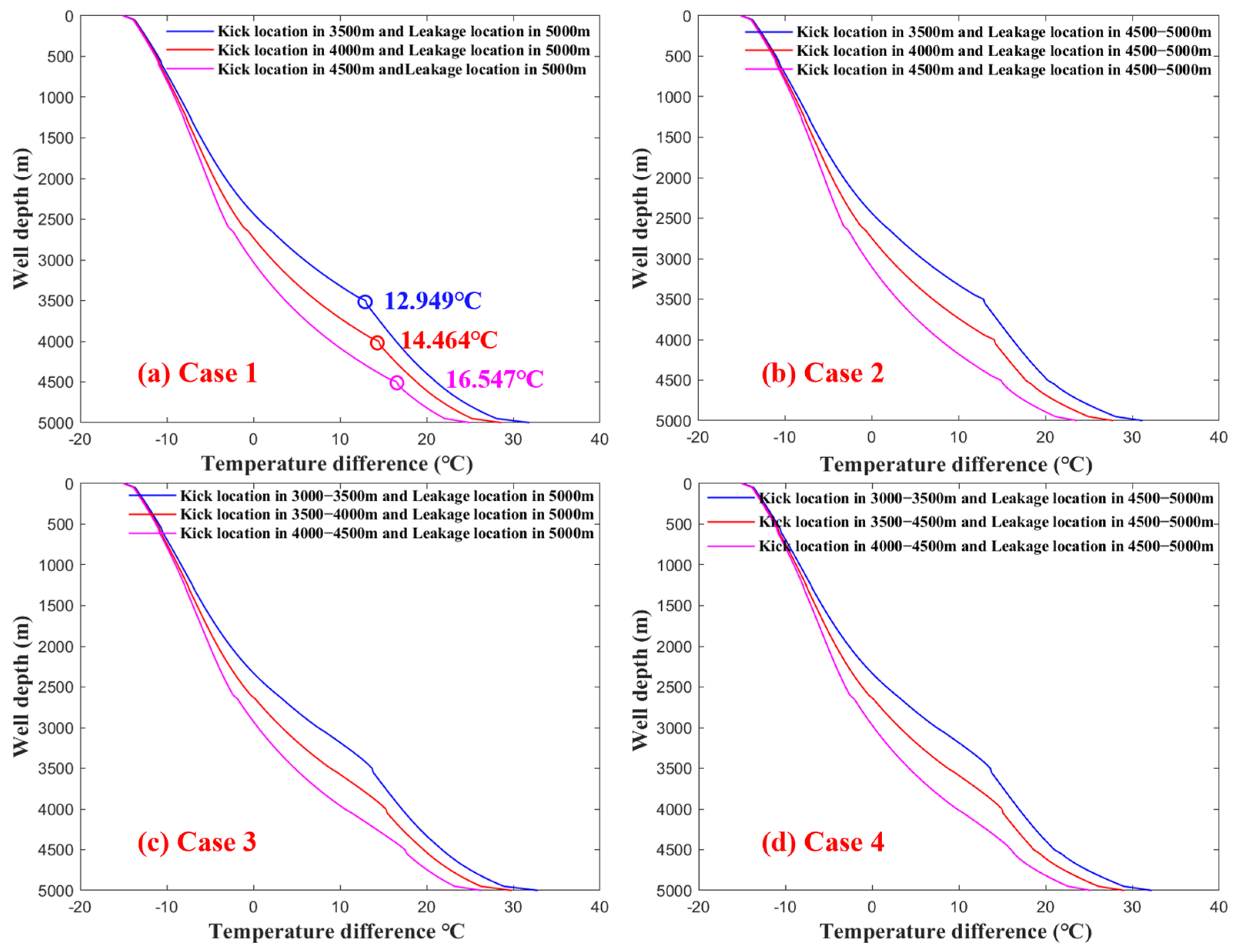
6.5. Temperature Difference Between Formation and Annulus
7. Discussion
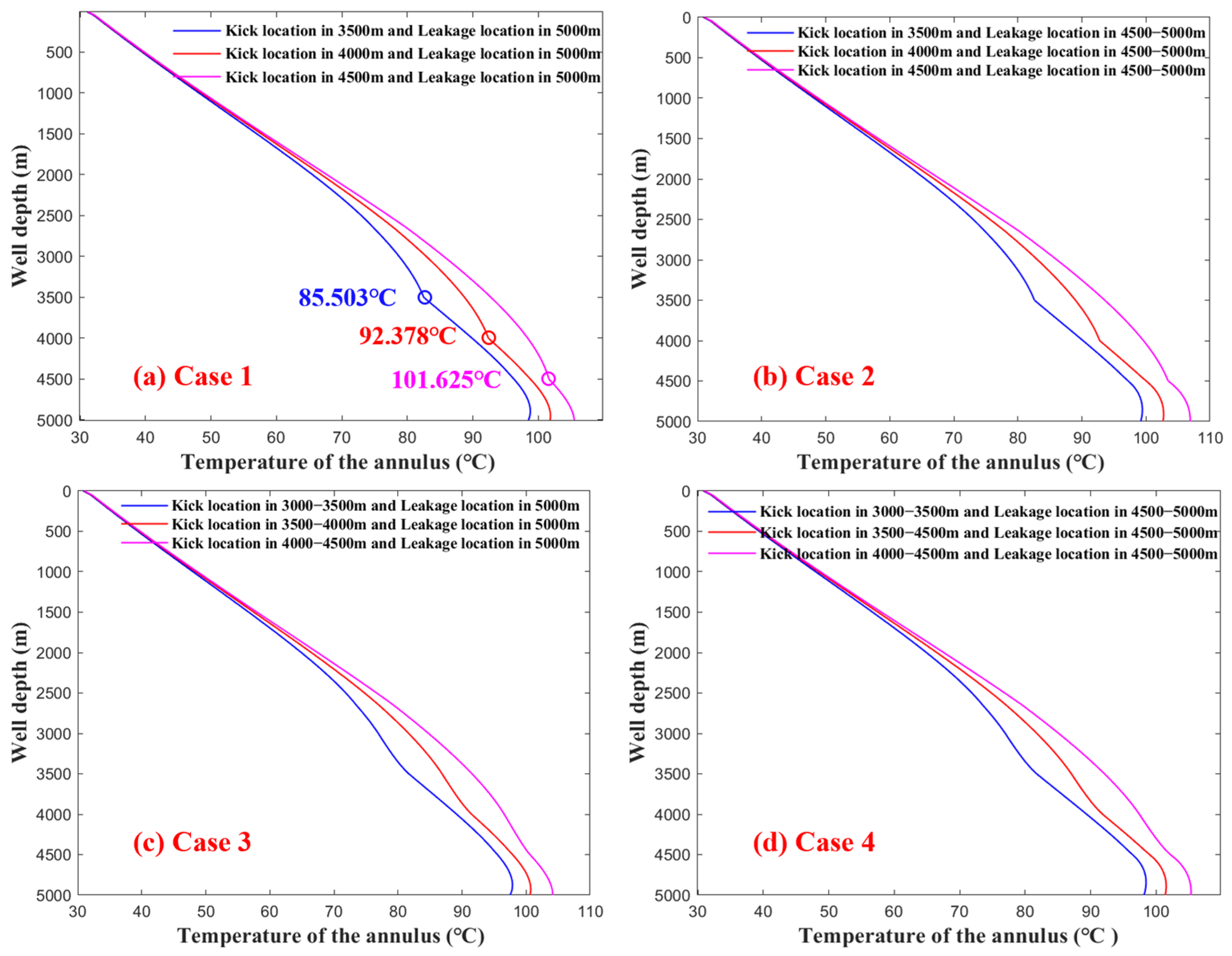
7.1. Influence of Kick Location on Annulus Temperature
7.2. Influence of Kick Depth on Drill String–Annulus Temperature Differential
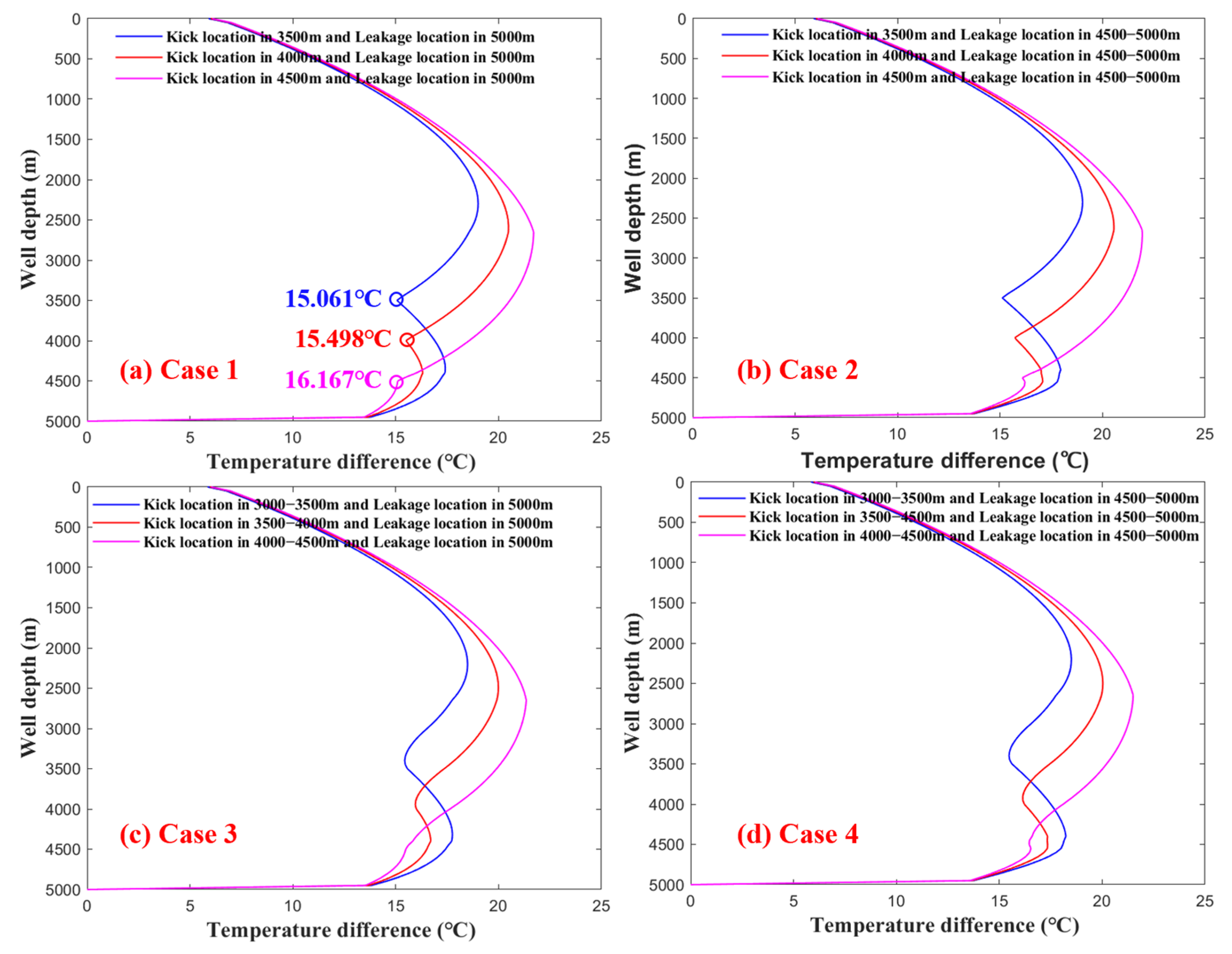
7.3. Influence of Kick Depth on Annulus–Formation Temperature Difference
8. Conclusions
- (1)
- The annular temperature under single-point leakage, continuous leakage, and combined kick–leakage conditions is lower than that under normal conditions. Both the bottom hole and wellhead temperatures in the single-point and continuous leakage cases are significantly reduced compared to the normal case. However, the wellhead temperature difference between the combined kick–leakage condition and the normal condition is minimal. Moreover, the type of leakage (single-point or continuous) has limited impact on the annular temperature profile when kick and leakage coexist.
- (2)
- The temperature difference between the interior of the drill string and the annulus under kick, leakage, and combined kick–leakage conditions exhibits a wavy trend of alternating increases and decreases with depth. The curves for single-point and continuous leakage cases are nearly identical, with only minor deviations in the open-hole section. The drill string–annulus temperature difference in the combined kick–leakage condition is notably greater than that under normal conditions.
- (3)
- As the kick location gets closer to the bottom hole, the annular temperature increases and the temperature difference between annulus and formation decreases. Above the bare borehole section, the temperature difference between inside the drill string and annulus keeps decreasing as the distance between the kick and leakage location gradually increases.
- (4)
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nomenclature | |
| Density, kg/m3 | |
| Viscous friction power, W/m | |
| Fluid rate, m3/s | |
| Temperature, °C | |
| Surface temperature, °C | |
| Temperature of injected drilling fluid | |
| Convective heat transfer coefficient, W/(m2 °C) | |
| H | Depth of bottom hole, m |
| Thermal conductivity, W/(m °C) | |
| Specific heat, J/(kg °C) | |
| Axial coordinate, m | |
| Radial coordinate, m | |
| velocity, m/s | |
| Time, s | |
| Nusselt number | |
| Reynolds number | |
| Prandtl number | |
| Liquidity index | |
| Pipe diameter, m | |
| Hydraulic diameter, m | |
| Hydraulic diameter of drill string, m | |
| Hydraulic diameter of annulus, m | |
| Friction coefficient | |
| Cross-sectional area of drill string, m2 | |
| Cross-sectional area of annulus, m2 | |
| Roughness of pipe | |
| Parameter of friction coefficient | |
| Geothermal gradient, °C/m | |
| Subscript | |
| l | Liquid phase |
| p | Drill string |
| w | Drill string wall |
| a | Annuals |
| c | Casing |
| pi | Drill string inner wall |
| po | Drill string outer wall |
| ci | Casing inner wall |
| co | Casing outer wall |
| kick | Kick |
| loss | Leakage |
References
- Kaiser, M.J. Modeling the time and cost to drill an offshore well. Energy 2009, 34, 1097–1112. [Google Scholar] [CrossRef]
- Nian, Y.L.; Cheng, W.L. Evaluation of geothermal heating from abandoned oil wells. Energy 2018, 142, 592–607. [Google Scholar] [CrossRef]
- Jia, H.; Kang, Z.; Zhu, J.; Ren, L.; Cai, M.; Wang, T.; Xu, Y.; Li, Z. High density bromide-based nanocomposite gel for temporary plugging in fractured reservoirs with multi-pressure systems. J. Pet. Sci. Eng. 2021, 205, 108778. [Google Scholar] [CrossRef]
- Magzoub, M.I.; Salehi, S.; Hussein, I.A.; Nasser, M.S. Loss circulation in drilling and well construction: The significance of applications of crosslinked polymers in wellbore strengthening: A review. J. Pet. Sci. Eng. 2020, 185, 106653. [Google Scholar] [CrossRef]
- Yin, H.; Liu, P.; Li, Q.; Wang, Q.; Dao, D. A new approach to risk control of gas kick in high-pressure sour gas wells. J. Nat. Gas Sci. Eng. 2015, 26, 142–148. [Google Scholar] [CrossRef]
- Liu, G.; Meng, Z.; Luo, D.; Wang, J.; Gu, D.; Yang, D. Experimental evaluation of interlayer interference during commingled production in a tight sandstone gas reservoir with multi-pressure systems. Fuel 2020, 262, 116557. [Google Scholar] [CrossRef]
- Stone, R.; Tian, S. Sometimes Neglected Hydraulic Parameters of Underbalanced and Managed-Pressure Drilling. In Proceedings of the SPE/IADC Managed Pressure Drilling and Underbalanced Operations Conference and Exhibition, Abu Dhabi, United Arab Emirates, 28–29 January 2008; Society of Petroleum Engineers: Richardson, TX, USA, 2008. [Google Scholar]
- Iversen, F.P.; Gravdal, J.E.; Nygaard, G.H.; Gjeraldstveit, H.; Carlsen, L.A.; Low, E.; Munro, C.; Torvund, S. Feasibility study of managed-pressure drilling with automatic choke control in depleted HP/HT field. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006; Society of Petroleum Engineers: Richardson, TX, USA, 2006. [Google Scholar]
- Wu, X.; Wan, F.; Chen, Z.; Han, L.; Li, Z. Drilling and completion technologies for deep carbonate rocks in the Sichuan Basin: Practices and prospects. Nat. Gas Ind. B 2020, 7, 547–556. [Google Scholar] [CrossRef]
- Jia, H.; Chen, H.; Guo, S. Fluid loss control mechanism of using polymer gel pill based on multi-crosslinking during overbalanced well workover and completion. Fuel 2017, 210, 207–216. [Google Scholar] [CrossRef]
- Kamel, M.A.; Elkatatny, S.; Mysorewala, M.F.; Al-Majed, A.; Elshafei, M. Adaptive and real-time optimal control of stick–slip and bit wear in autonomous rotary steerable drilling. J. Energy Resour. Technol. 2018, 140, 032908. [Google Scholar] [CrossRef]
- Vajargah, A.K.; van Oort, E. Early kick detection and well control decision-making for managed pressure drilling automation. J. Nat. Gas Sci. Eng. 2015, 27, 354–366. [Google Scholar] [CrossRef]
- Feng, Y.; Gray, K.E. Review of fundamental studies on lost circulation and wellbore strengthening. J. Pet. Sci. Eng. 2017, 152, 511–522. [Google Scholar] [CrossRef]
- Jinsheng, S.U.N.; Yingrui, B.A.I.; Cheng, R.; Lyu, K.; Liu, F.; Feng, J.; Lei, S.; Zhang, J.; Hao, H. Research progress and prospect of plugging technologies for fractured formation with severe lost circulation. Pet. Explor. Dev. 2021, 48, 732–743. [Google Scholar] [CrossRef]
- Yang, H.; Li, J.; Liu, G.; Wang, C.; Li, M.; Jiang, H. Numerical analysis of transient wellbore thermal behavior in dynamic deepwater multi-gradient drilling. Energy 2019, 179, 138–153. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiong, Y.; Gao, Y.; Liu, L.; Wang, M.; Peng, G. Wellbore temperature profile during circulation stage when well-kick occurs in a continuous formation from the bottom hole. Energy 2018, 164, 964–977. [Google Scholar] [CrossRef]
- Espinosa-Paredes, G.; Espinosa-Martínez, E.G. A feedback-based inverse heat transfer method to estimate unperturbed temperatures in wellbores. Energy Convers. Manag. 2009, 50, 140–148. [Google Scholar] [CrossRef]
- Li, M.; Liu, G.; Li, J.; Zhang, T.; He, M. Thermal performance analysis of drilling horizontal wells in high temperature formations. Appl. Therm. Eng. 2015, 78, 217–227. [Google Scholar] [CrossRef]
- Li, G.; Yang, M.; Meng, Y.; Wen, Z.; Wang, Y.; Yuan, Z. Transient heat transfer models of wellbore and formation systems during the drilling process under well kick conditions in the bottom hole. Appl. Therm. Eng. 2016, 93, 339–347. [Google Scholar] [CrossRef]
- Yang, M.; Li, X.; Deng, J.; Meng, Y.; Li, G. Prediction of wellbore and formation temperatures during circulation and shut-in stages under kick conditions. Energy 2015, 91, 1018–1029. [Google Scholar] [CrossRef]
- Yang, M.; Meng, Y.; Li, G.; Li, Y.; Chen, Y.; Zhao, X.; Li, H. Estimation of wellbore and formation temperatures during the drilling process under lost circulation conditions. Math. Probl. Eng. 2013, 2013, 579091. [Google Scholar] [CrossRef]
- Luheshi, M.N. Estimation of formation temperature from borehole measurements. Geophys. J. Int. 1983, 74, 747–776. [Google Scholar]
- Tekin, S. Estimation of the Formation Temperature from the Inlet and Outlet Mud Temperatures While Drilling Geothermal Formations. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2010. [Google Scholar]
- Fomin, S.; Hashida, T.; Chugunov, V.; Kuznetsov, A.V. A borehole temperature during drilling in a fractured rock formation. Int. J. Heat Mass Transf. 2005, 48, 385–394. [Google Scholar] [CrossRef]
- Zhang, Z.; Wei, Y.; Xiong, Y.; Peng, G.; Wang, G.; Lu, J.; Zhong, L.; Wang, J. Influence of the location of drilling fluid loss on wellbore temperature profile during drilling. Energy 2022, 244, 123031. [Google Scholar] [CrossRef]
- Espinosa-Paredes, G.; Garcia-Gutierrez, A. Thermal behavior of geothermal wells using mud and air–water mixtures as drilling fluids. Energy Convers. Manag. 2004, 45, 1513–1527. [Google Scholar] [CrossRef]
- Chen, N.H. An explicit equation for friction factor in pipe. Ind. Eng. Chem. Fundam. 1979, 18, 296–297. [Google Scholar] [CrossRef]
- Zhang, G.; Li, J.; Yang, H.; Huang, H. A new detection method of co-existence of well kick and loss circulation based on thermal behavior of wellbore-formation coupled system. Int. J. Hydrogen Energy 2024, 58, 239–258. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Owusu, A.B. A modified Ester-branched thickener for rheology and wettability during CO2 fracturing for improved fracturing property. Environ. Sci. Pollut. Res. 2019, 26, 20787–20797. [Google Scholar] [CrossRef] [PubMed]
- Qingchao, L.; Jingjuan, W.; Qiang, L.; Fuling, W. Sediment Instability Caused by Gas Production from Hydrate-Bearing Sediment in Northern South China Sea by Horizontal Wellbore: Sensitivity Analysis. Nat. Resour. Res. 2025, 34, 1667–1699. [Google Scholar] [CrossRef]
- Petersen, J.; Bjørkevoll, K.S.; Lekvam, K. Computing the danger of hydrate formation using a modified dynamic kick simulator. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 27 February–1 March 2001; Society of Petroleum Engineers: Richardson, TX, USA, 2001. [Google Scholar]
- Rao, B.K. Heat transfer to non-Newtonian flows over a cylinder in cross flow. Int. J. Heat Fluid Flow 2000, 21, 693–700. [Google Scholar] [CrossRef]





| Configuration | Hole Diameter (mm) | Casing OD (mm) | Casing ID (mm) | Depth (m) |
|---|---|---|---|---|
| Surface casing | 406.40 | 273.05 | 258.65 | 1200.00 |
| Technical casing | 258.65 | 244.50 | 224.00 | 2500.00 |
| Open-hole section | 215.90 | / | / | 5000.00 |
| Tool Type | OD (mm) | ID (mm) | Individual Length (m) | Total Length (m) |
|---|---|---|---|---|
| Main drill string | 149.20 | 129.50 | 4728.00 | 4728.00 |
| Heavy-weight pipe | 127.00 | 76.20 | 85.60 | 272.00 |
| Drill collar | 158.80 | 57.20 | 184.70 | 186.40 |
| Downhole stabilizer | 212.00 | 159.00 | 1.40 | 1.70 |
| Polycrystalline Diamond Compact bit | 215.90 | / | 0.30 | 0.30 |
| Medium | Density (kg/m3) | Specific Heat (J/kg·°C) | Thermal Conductivity (W/m·°C) |
|---|---|---|---|
| Drilling mud | 1200 | 2500 | 1.75 |
| Steel tubular/Casing assembly | 8000 | 400 | 43.75 |
| Cement sheath | 2140 | 2000 | 0.70 |
| Geological formation | 2640 | 800 | 2.25 |
| Variable Name | Numerical Entry |
|---|---|
| Borehole total depth | 5000 m |
| Yield point of drilling mud | 10 Pa |
| Fluidity index (n) | 0.65 |
| Consistency coefficient | 0.34 Pa·sn |
| Inlet temperature of circulating mud | 25 °C |
| Surface temperature | 16 °C |
| Geothermal gradient | 2.3 °C/100 m |
| Drilling fluid displacement | 15 L/s |
| Drill-pipe rotation rate | 60 r/min |
| Rate of penetration | 5.00 m/h |
| Bit diameter | 215.90 mm |
| Scenario | Kick Rate (m3/s) | Leakage Rate (m3/s) | Kick Position (m) | Leakage Position (m) |
|---|---|---|---|---|
| Case 1 | 0.01 | 0.01 | 3500 | 5000 |
| Case 2 | 0.01 | 0.01 | 3500 | 4500–5000 |
| Case 3 | 0.01 | 0.01 | 3000–3500 | 5000 |
| Case 4 | 0.01 | 0.01 | 3000–3500 | 4500–5000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Li, M.; Wang, H.; Hao, W.; Liu, K.; Li, Y.; Zhang, H.; Zhang, G. Research on the Formation-Wellbore Temperature Profile Characteristics Under the Co-Existence of Kick and Leakage Condition. Processes 2025, 13, 2730. https://doi.org/10.3390/pr13092730
Chen Y, Li M, Wang H, Hao W, Liu K, Li Y, Zhang H, Zhang G. Research on the Formation-Wellbore Temperature Profile Characteristics Under the Co-Existence of Kick and Leakage Condition. Processes. 2025; 13(9):2730. https://doi.org/10.3390/pr13092730
Chicago/Turabian StyleChen, Yufei, Mu Li, Hao Wang, Weiwei Hao, Kerou Liu, Yafei Li, Hui Zhang, and Geng Zhang. 2025. "Research on the Formation-Wellbore Temperature Profile Characteristics Under the Co-Existence of Kick and Leakage Condition" Processes 13, no. 9: 2730. https://doi.org/10.3390/pr13092730
APA StyleChen, Y., Li, M., Wang, H., Hao, W., Liu, K., Li, Y., Zhang, H., & Zhang, G. (2025). Research on the Formation-Wellbore Temperature Profile Characteristics Under the Co-Existence of Kick and Leakage Condition. Processes, 13(9), 2730. https://doi.org/10.3390/pr13092730






