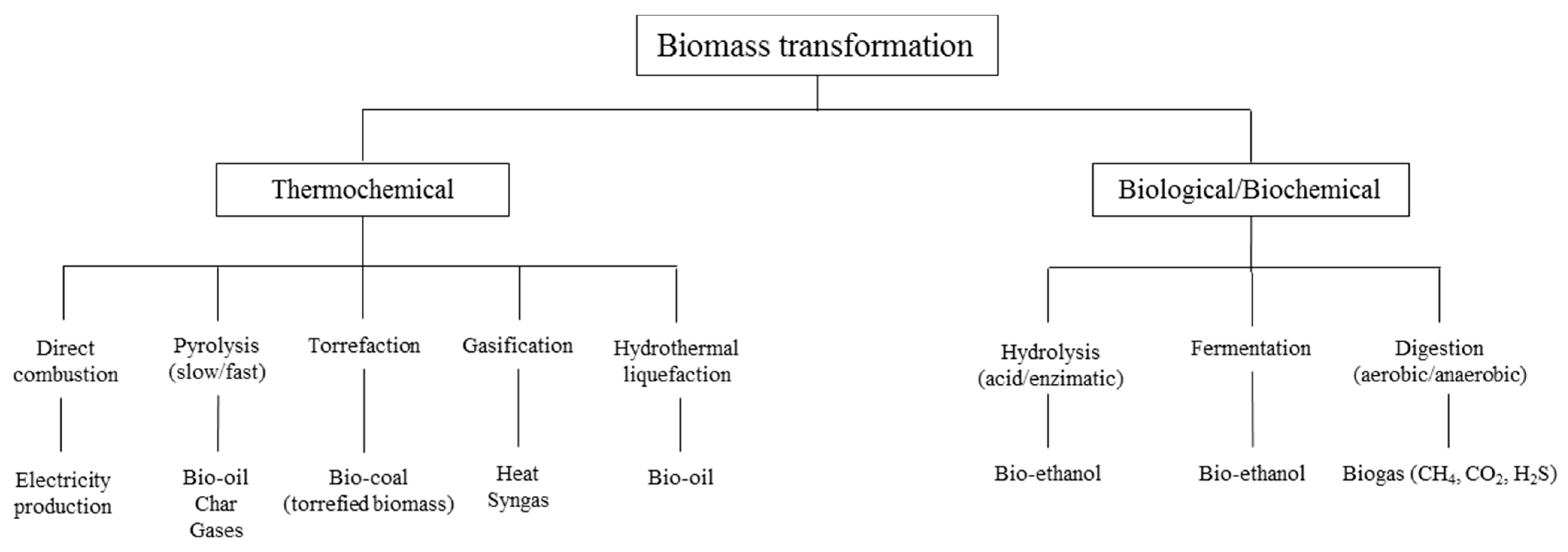
Review of Biomass Gasification Technologies with a Particular Focus on a Downdraft Gasifier
Abstract
1. Introduction
2. Biomass Types Used as Feed
2.1. Particle Size
2.2. Cellulose, Hemicellulose, and Lignin Content
- Sargassum horneri: 28.29–39.88%; 16.75–22.64%; 22.10–27.20%.
- Corn stalk: 30.60–33.10%; 25.80–27.65%; 14.60–15.90%.
- Hemicellulose: 95.39 (kJ mol−1); cellulose: 199.66 (kJ mol−1); lignin: 174.40 (kJ mol−1).
2.3. Proximate and Ultimate Analysis for Different Types of Biomasses
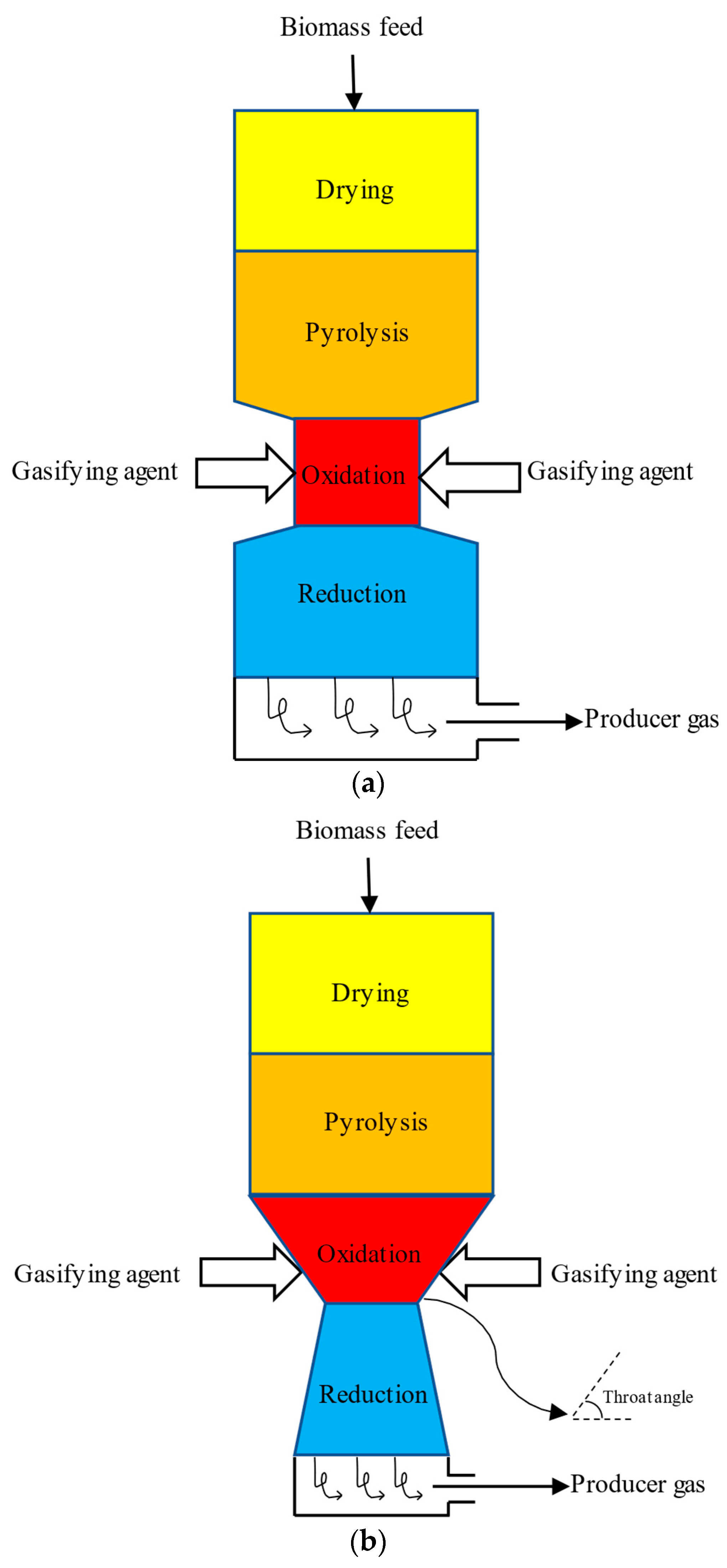
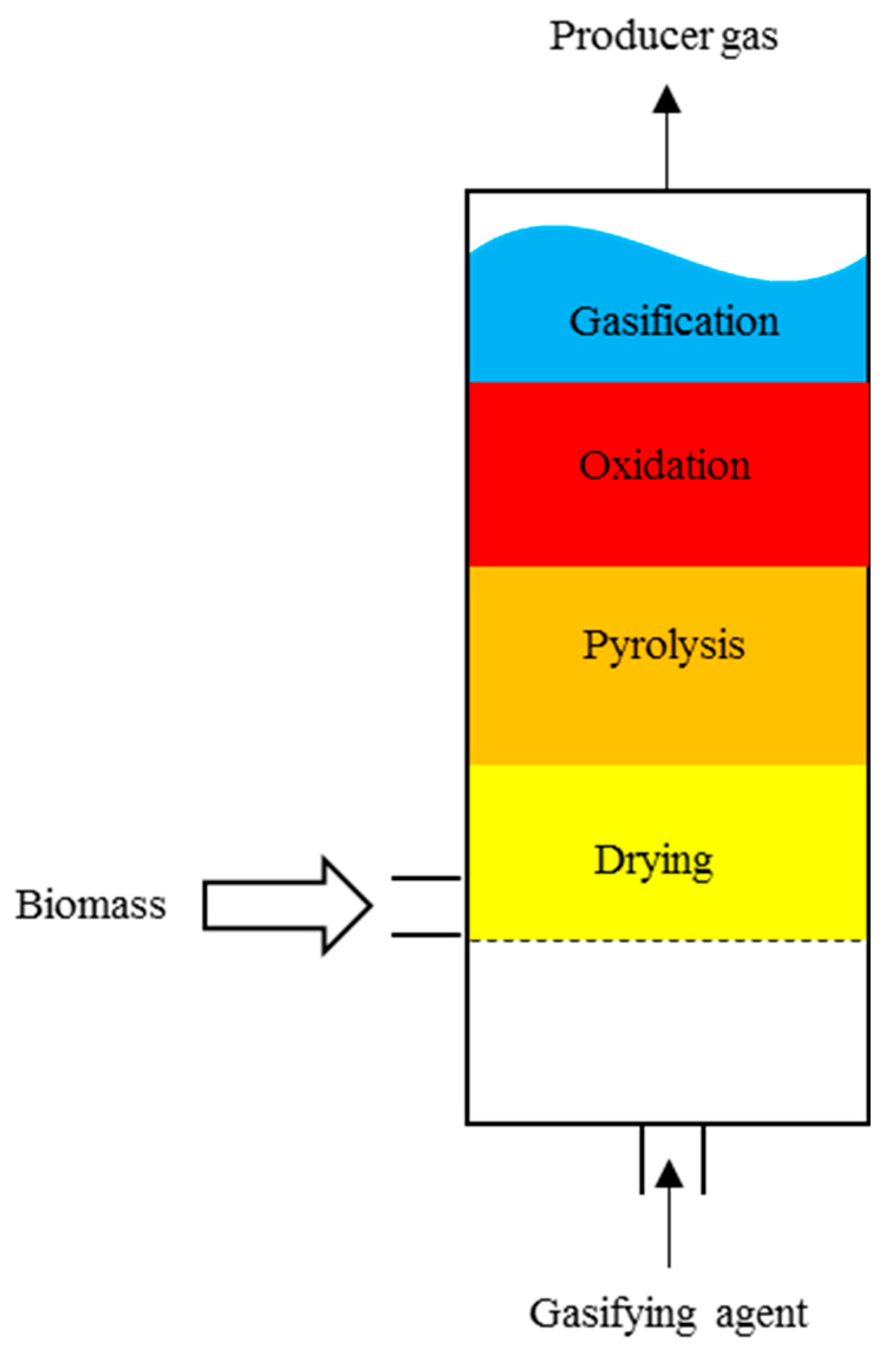
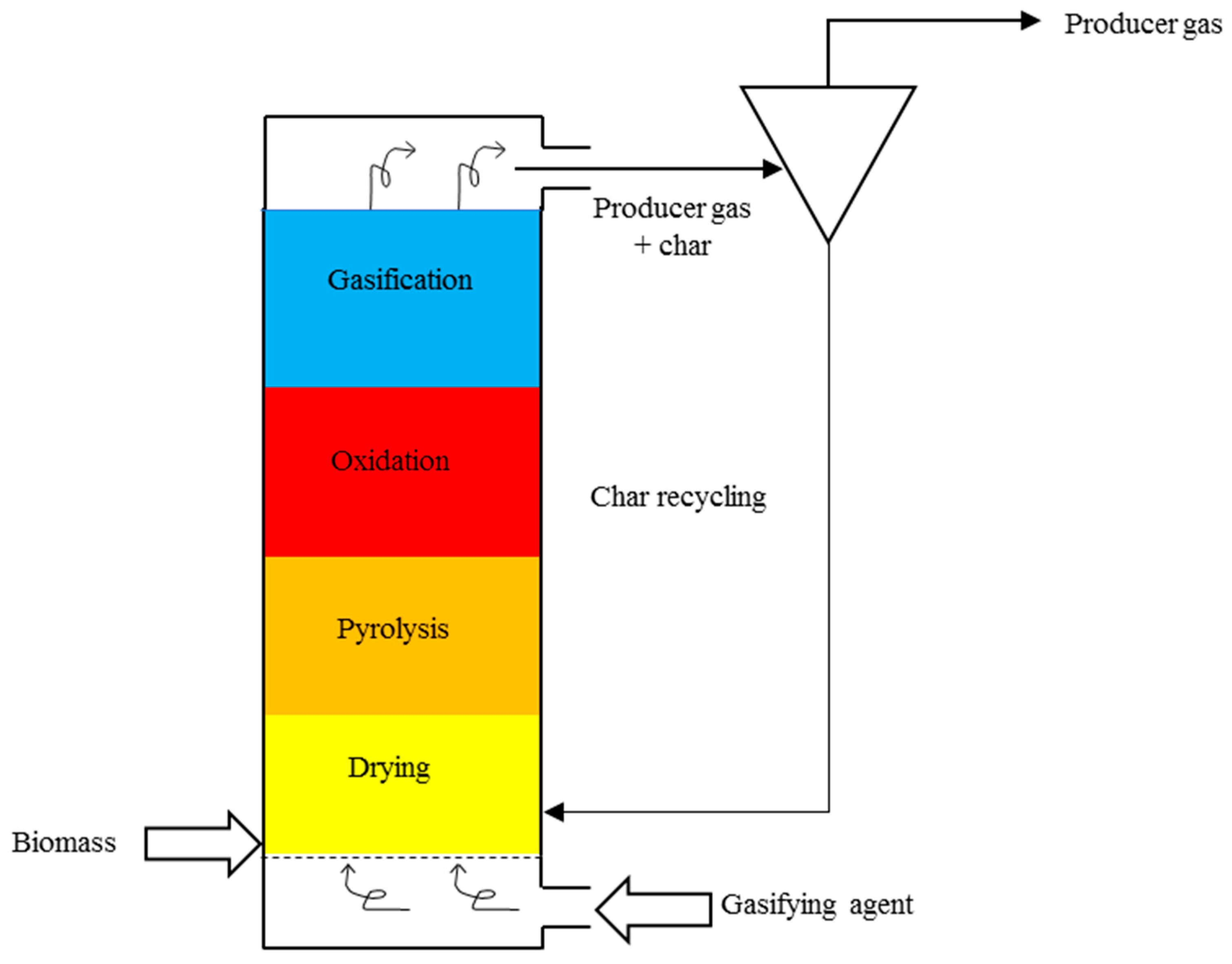
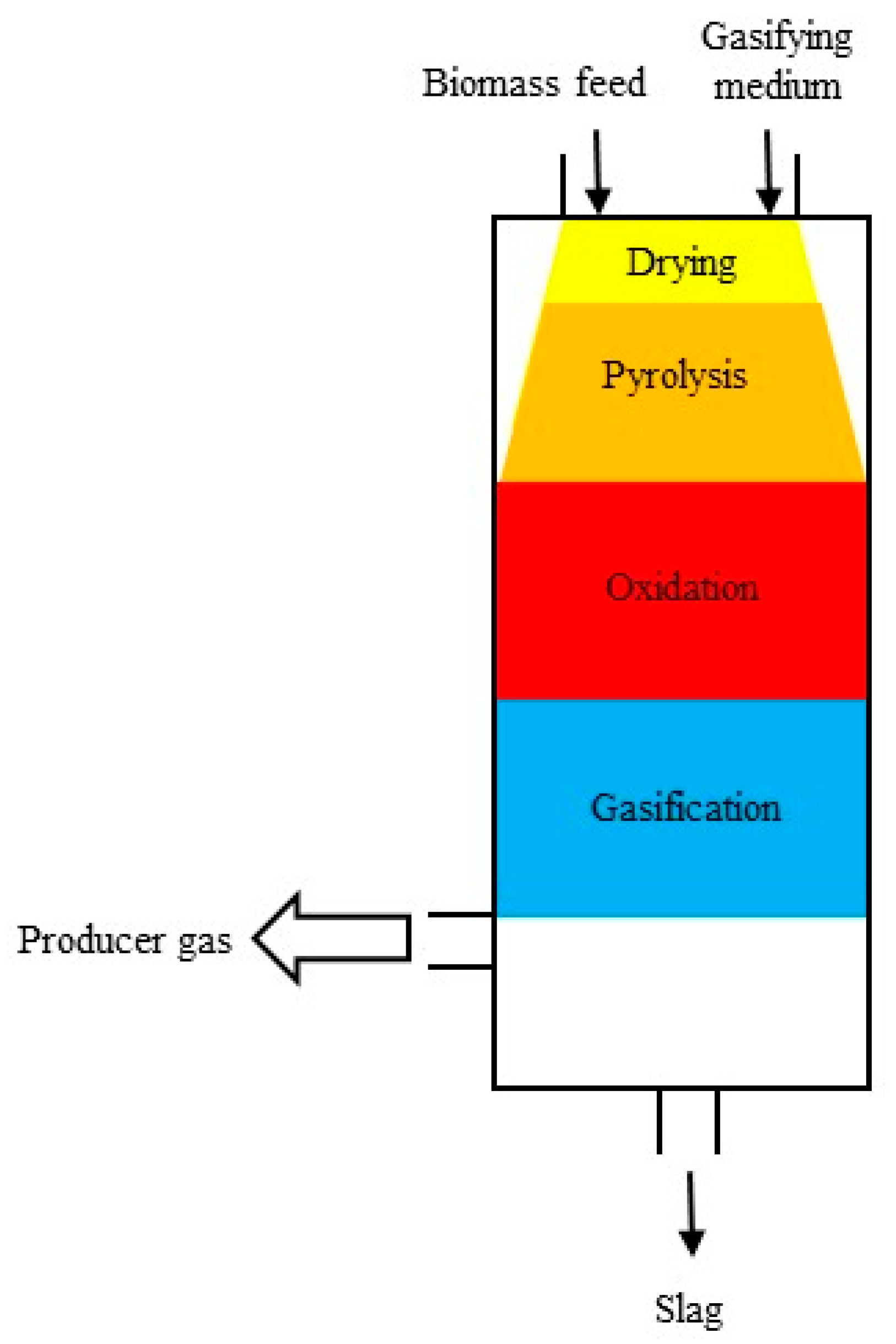
3. Reactors Used for Gasification
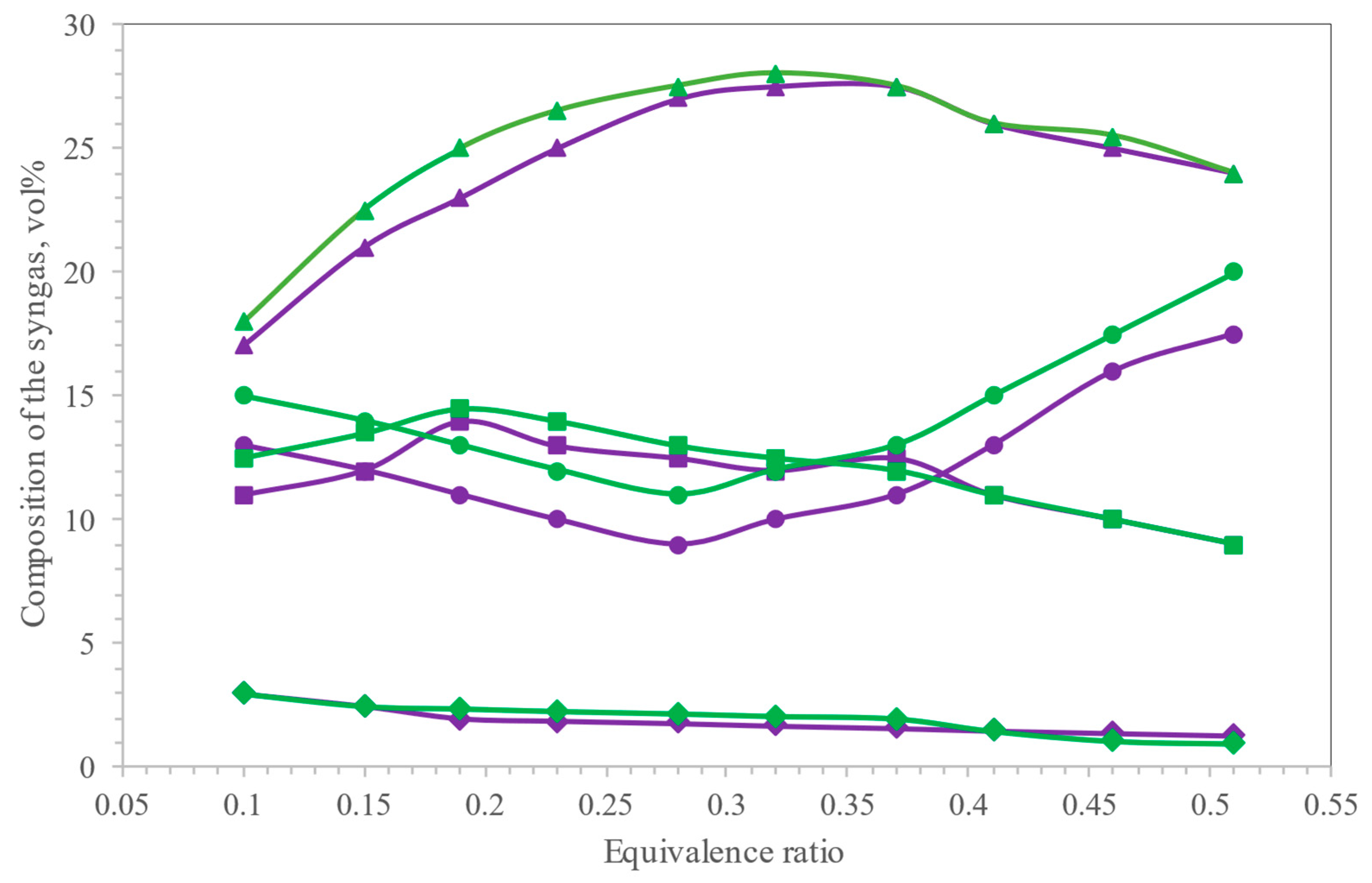
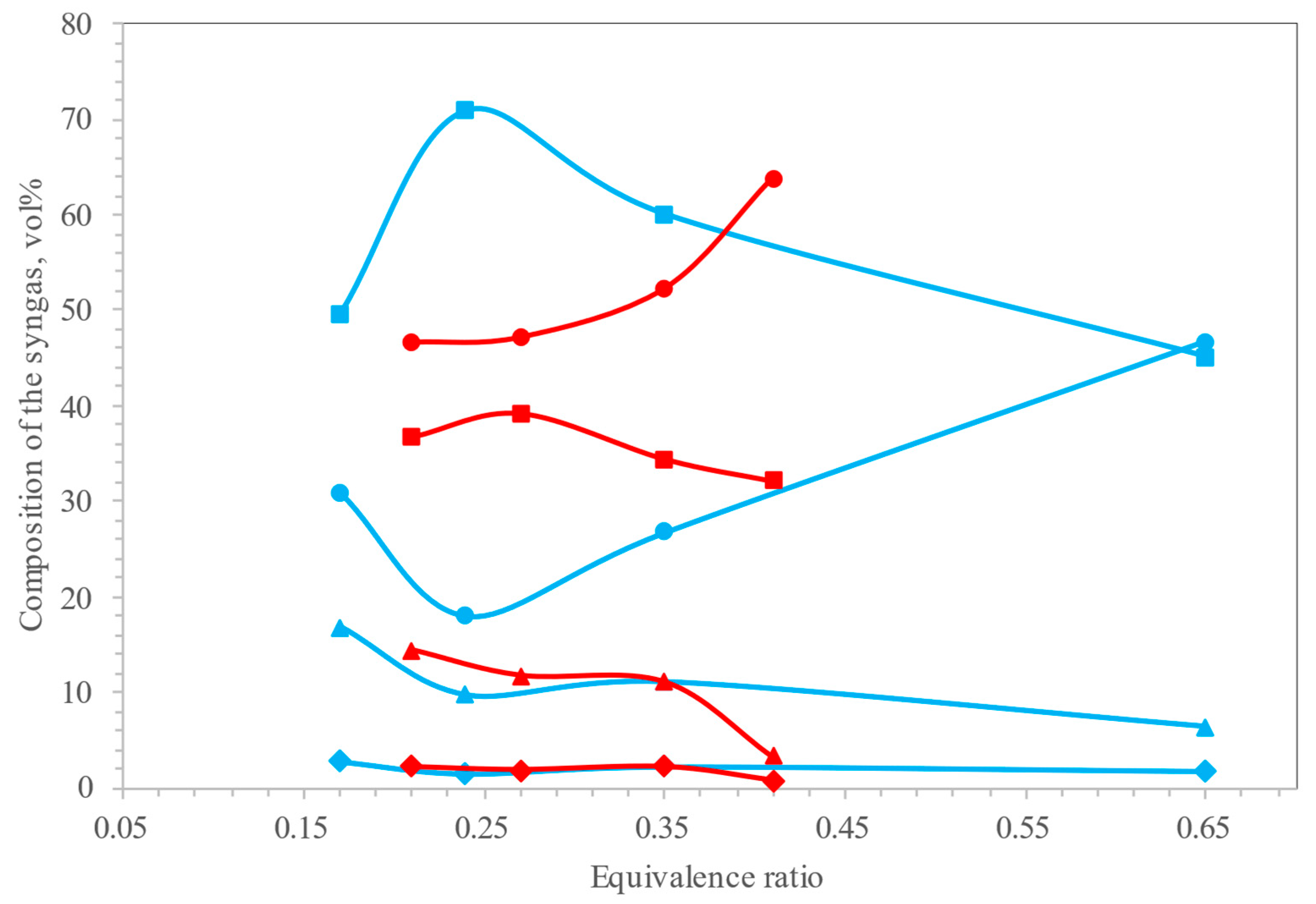
4. Gasifying Medium
5. Syngas Cleaning
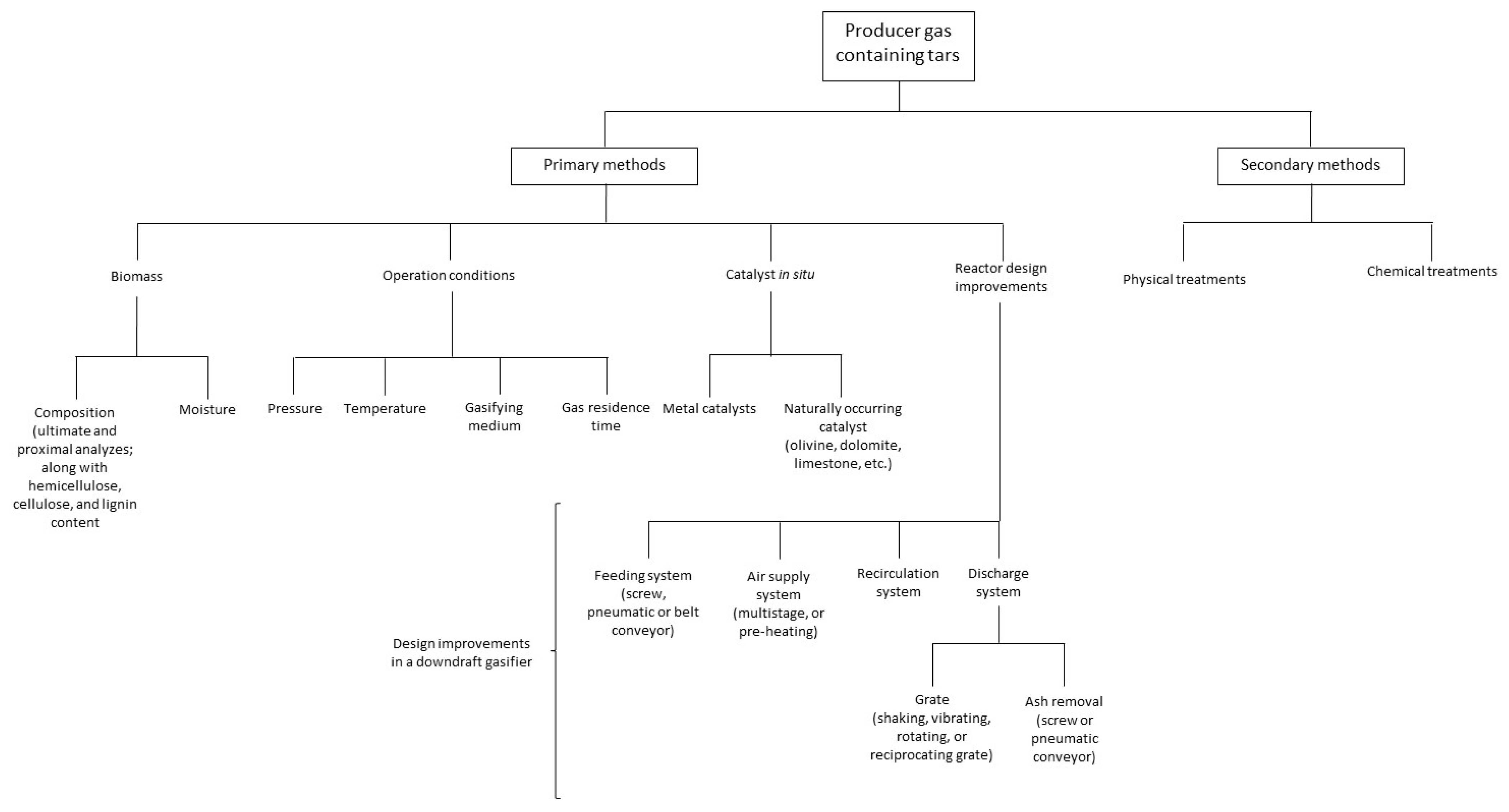
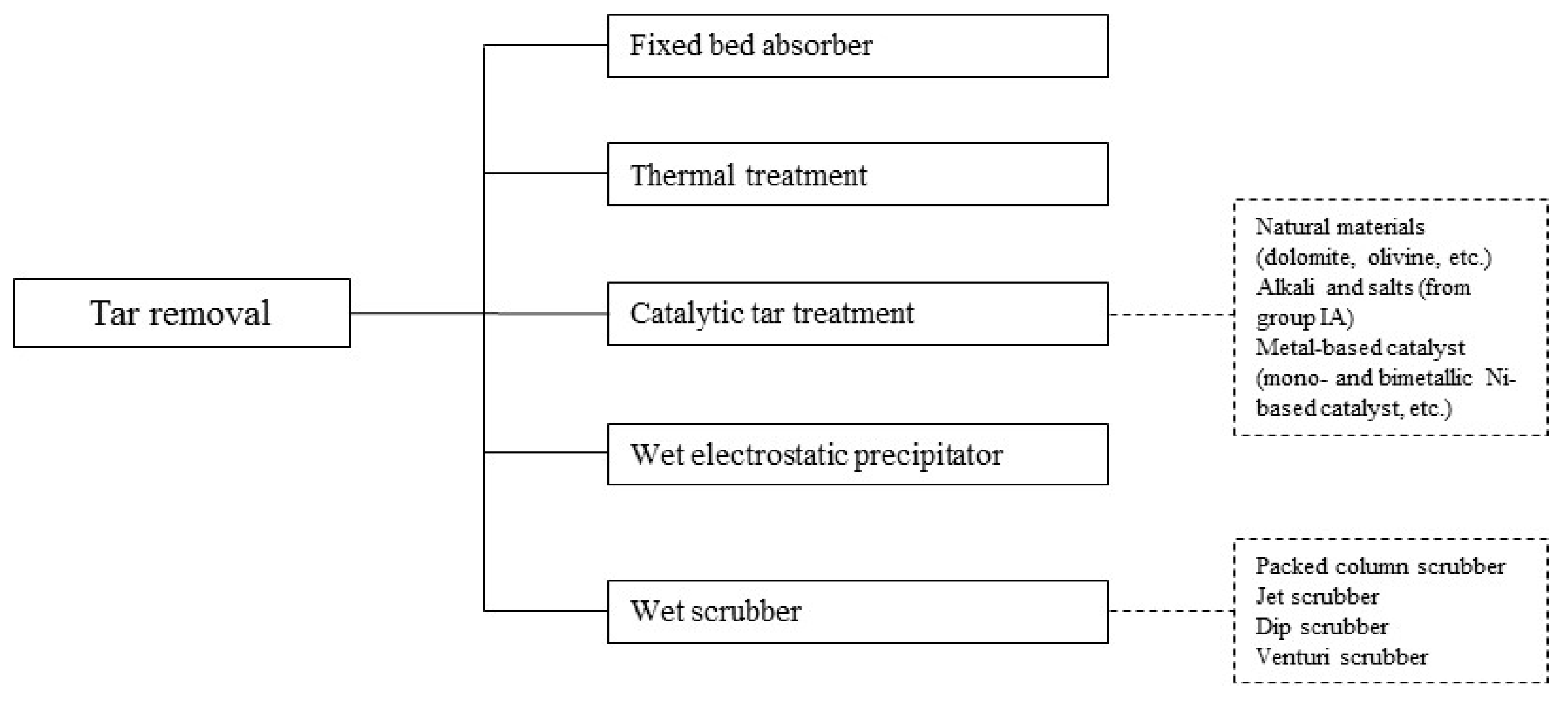
5.1. Tar Mitigation Techniques
5.2. Physical/Mechanical Processes
5.3. Tar Removal
5.3.1. Wet Scrubbers
5.3.2. Wet Electrostatic Precipitators (Wet ESPs)
5.3.3. Fixed Bed Adsorber
5.3.4. Thermal Treatment
5.3.5. Catalytic Tar Treatment
5.4. Recent Tar Mitigation Techniques
6. Influence of Pressure Drop and Heat Transfer in Gasification
- (a)
- Solid–gas heat transfer coefficient.
- (b)
- Radiation absorption coefficient.
- (c)
- Bed–wall heat transfer coefficient.
7. Uses and Applications of the Producer Gas
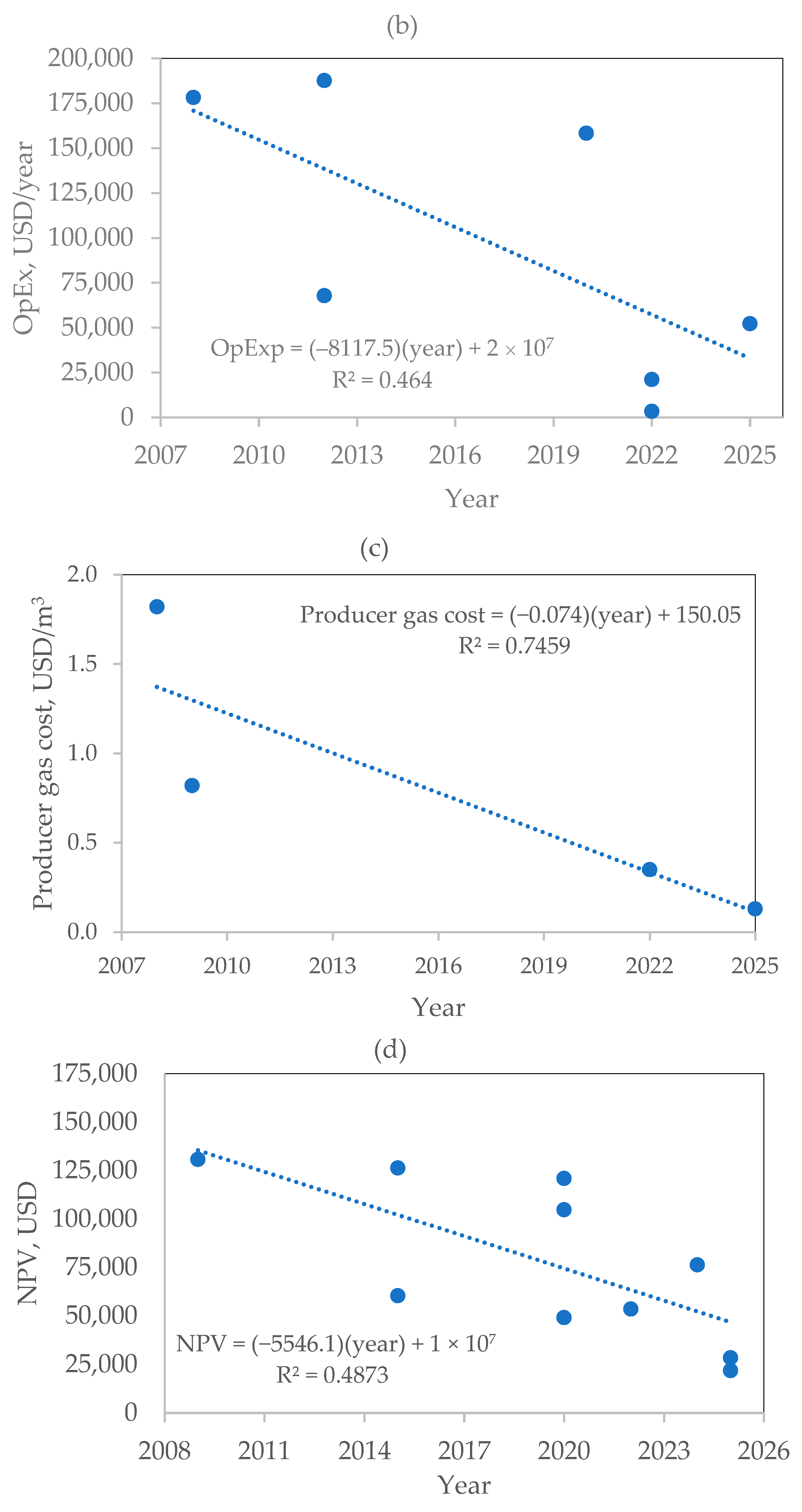
8. Economic Feasibility of Biomass Gasification
Technological Maturity and Economical Parameters for Biomass Gasification in Downdraft Gasifiers
9. Modeling of the Gasification Reactions and Reactor Focused on Downdraft Gasifiers
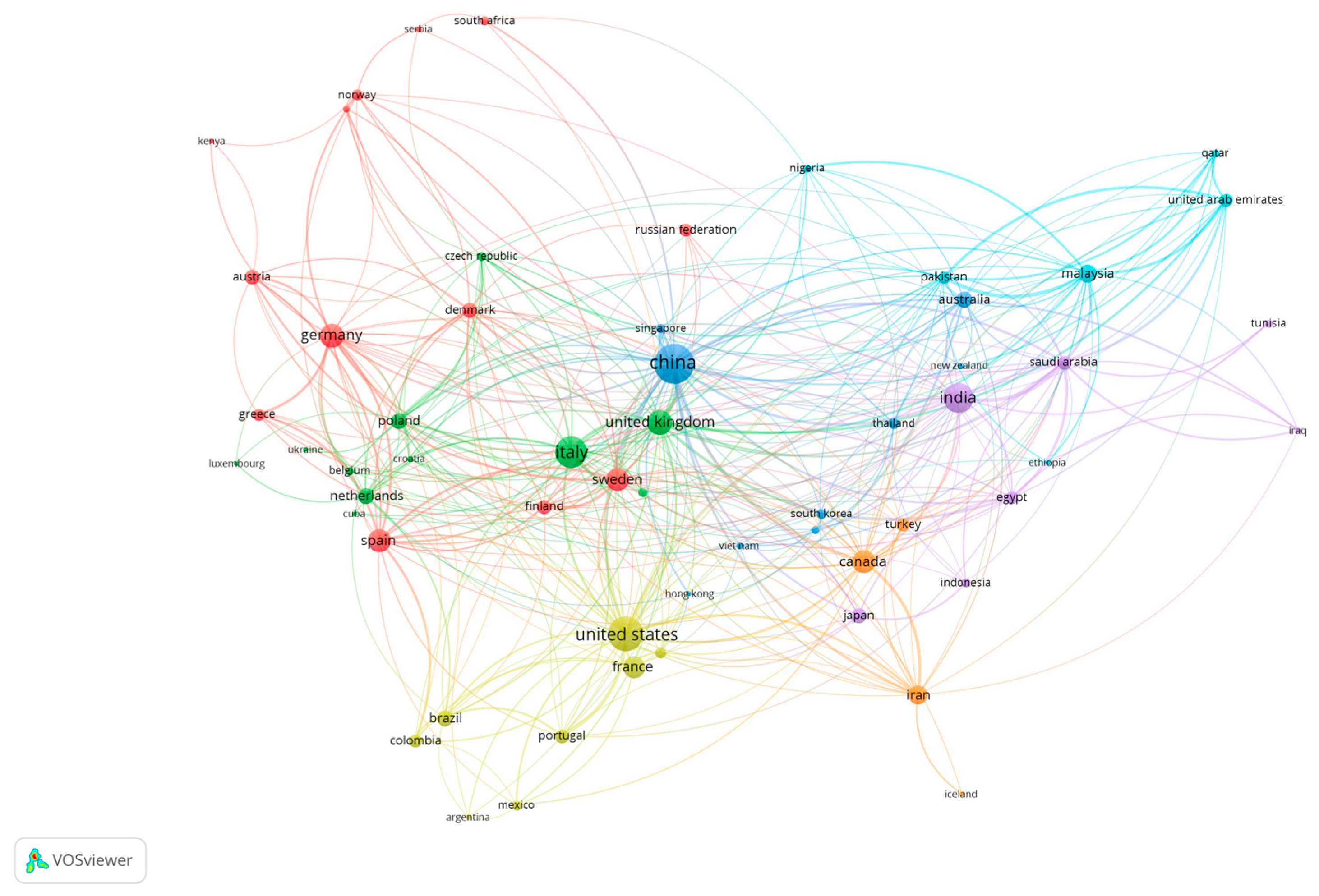
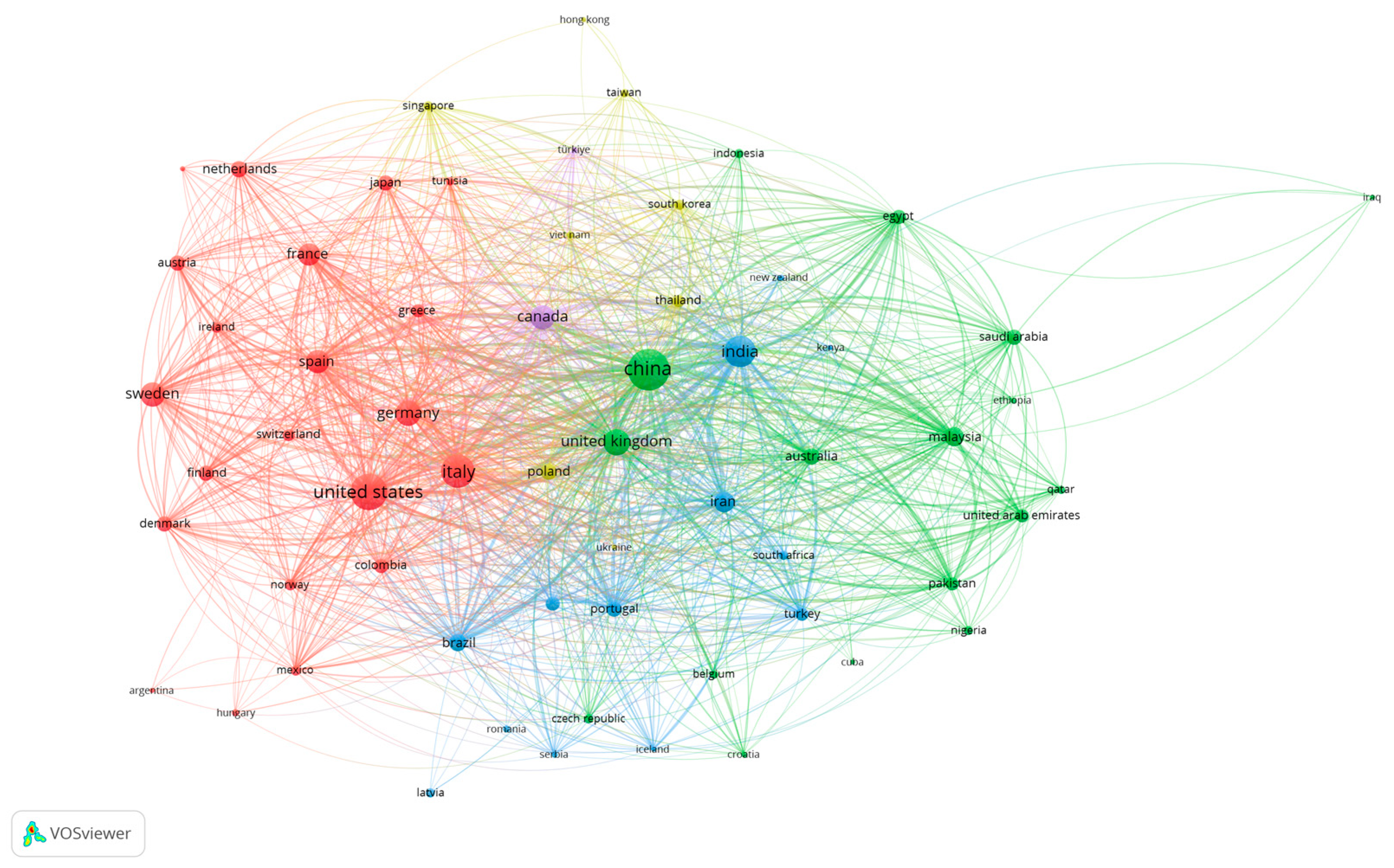
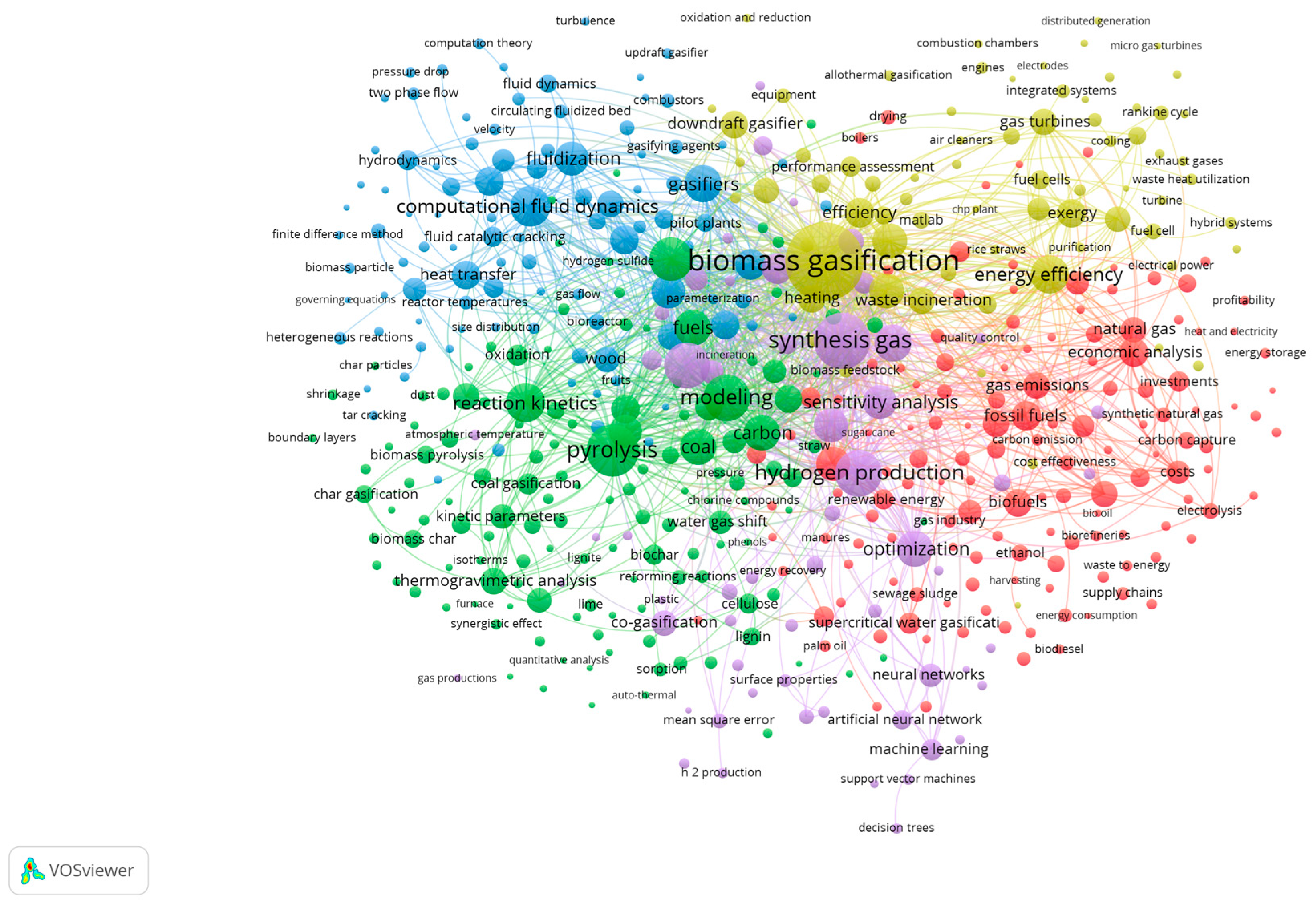
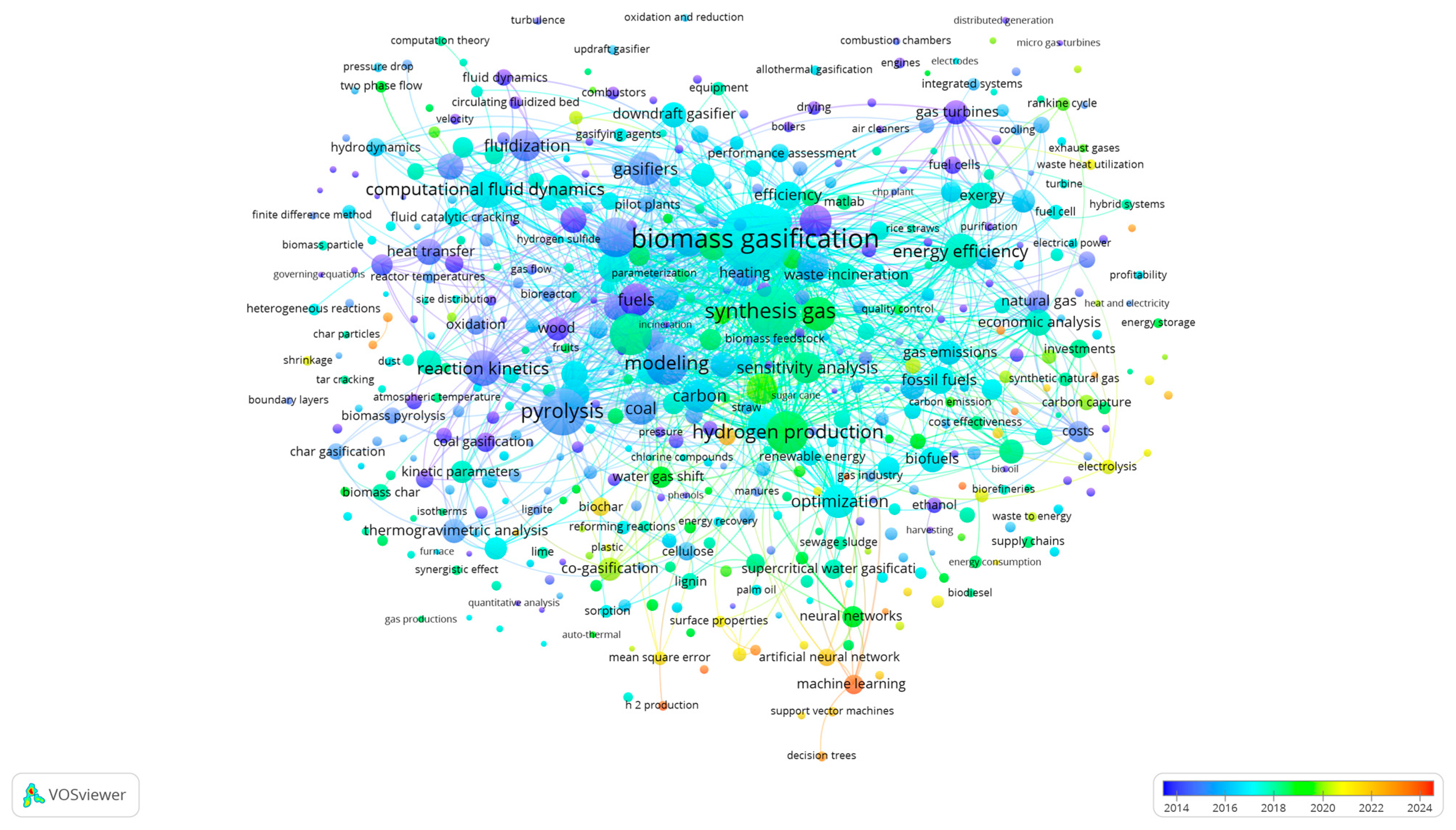
9.1. Bibliometric Analysis: Network Visualization for Co-Authorship, Bibliographic Coupling, Network and Overlay Visualization Maps
9.2. Equilibrium Models
9.2.1. Stoichiometric Models
9.2.2. Non-Stoichiometric Models
9.3. Kinetic and Reactor Models
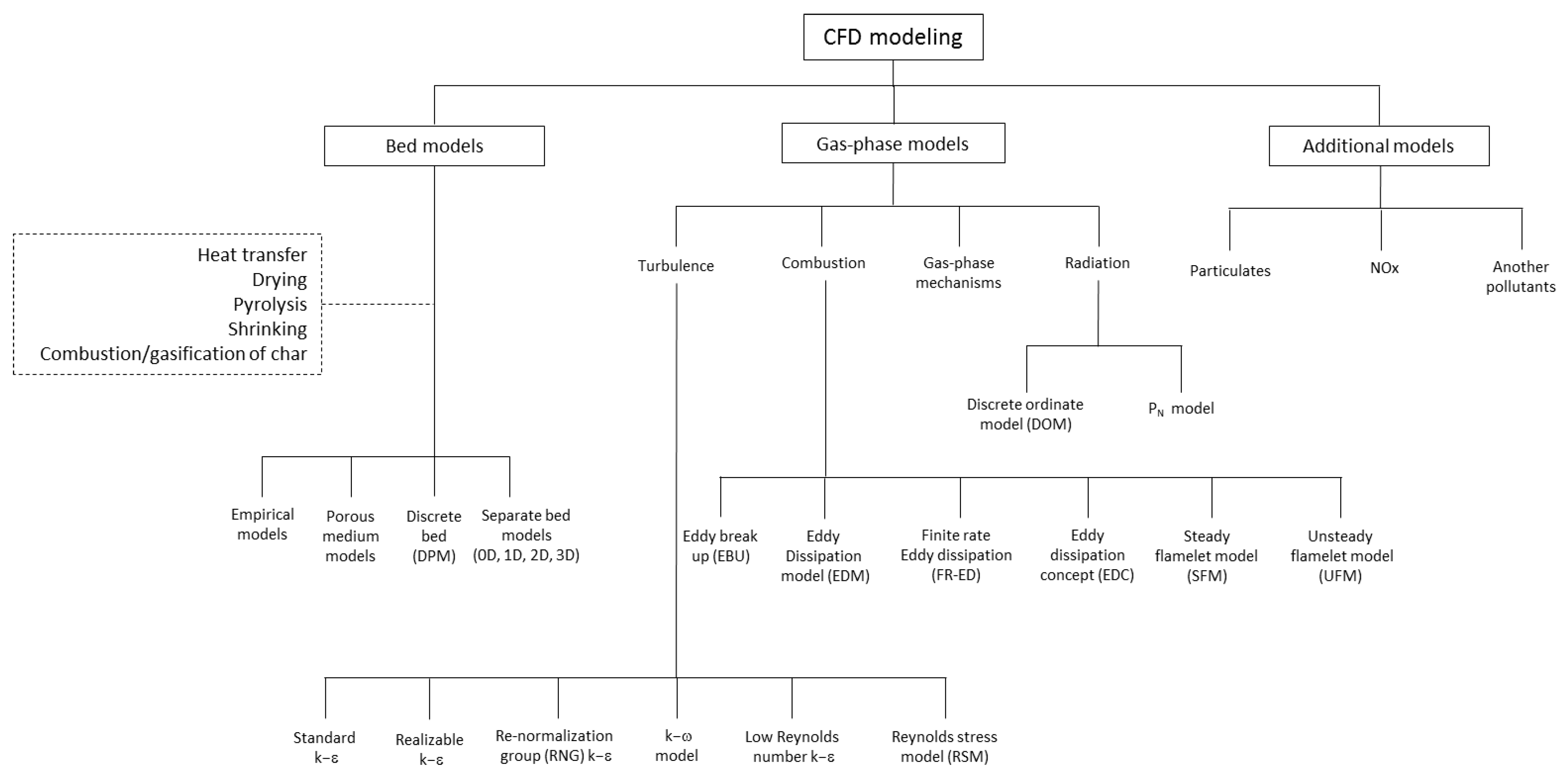
9.4. Models Based on Computational Fluid Dynamics (CFD)
- (1)
- The standard k–ε model, which is known for its numerical stability and is used to describe the fluid flow under both reacting and non-reacting conditions, such as in chemical reactors and furnaces.
- (2)
- The realizable k–ε model can be modified to enhance its accuracy in simulating fluid rotation and high strain rates. This modification involves adjusting the eddy viscosity and dissipation rate parameters, which are derived from the standard model.
- (3)
- The renormalization group (RNG) k–ε model has been proven to be more accurate for strain and swirl flows, as derived from the Navier–Stokes equation.
- (4)
- The low Reynolds number k-ε model, which necessitates a highly refined grid in the proximity of the wall, a consequence of its interaction with the fluid.
9.5. Other Programs/Techniques Used for Simulation of Biomass Gasification
10. Summary and Perspectives
11. Concluding Remarks
Funding
Conflicts of Interest
Abbreviations
| Formation enthalpy for reactants in (kJ mol−1) | |
| Formation enthalpy for products in (kJ mol−1) | |
| Gibbs function for species I in (kJ mol−1) | |
| Gibbs function for species i in (kJ mol−1) | |
| Difference of enthalpy among temperature T and standard conditions in (kJ mol−1) | |
| Difference of enthalpy among reactants temperature To and standard conditions in (kJ mol−1) | |
| H | Specific enthalpy in (J kg−1) |
| hw | Evaporation enthalpy of water of the dry solid fuel in (kJ mol−1) |
| xr | Number of moles for reactants |
| xp | Number of moles for products |
| xtar | Number of moles of tar |
| xchar | Number of moles of char |
| xi | Number of moles of species i |
| yi | Concentration of species i in (wt%) |
| Yi | Mass fraction of species i in (kg kg−1) |
| Mi | Molar mass of species i in (kg mol−1) |
| a | Number of moles of air entering the gasifier |
| Pi | Partial pressure of species I in (Pa) |
| Ki | Equilibrium constant of reaction i |
| ν | Superficial gas velocity in (m s−1) |
| υi | Stoichiometric coefficient of species i (positive for products and negative for reactants). For υi,j, it is the stoichiometric coefficient of species i in the j reaction |
| Srj,i | Stoichiometric coefficient of reactants i in reaction j |
| Spj,i | Stoichiometric coefficient of products i in reaction j |
| z | Axial distance in (m) |
| Rx | Formation rate of species x in (mol m−3 s−1) |
| Po | Atmospheric pressure in (Pa) |
| P | Total pressure in (Pa) |
| n | Summation of all species nx |
| nt | Number of moles of raw gas at temperature T (K) per mole of biomass |
| ni | Number of moles of species i |
| ri | Reaction rate of species i in (mol m−3 s−1) |
| rc | Reaction rate of char in (mol m−3 s−1) |
| rj | Production of chemical species j (j = CO, CO2, H2, H2O, O2, and N2) |
| cx | Molar heat capacity in (J mol−1 K−1) |
| cP,I | Specific heat capacity for species I in (J g−1 K−1) (where c for char, g for gas phase) |
| fp | Pyrolysis fraction |
| φ | Actual air to stoichiometric air ratio |
| α | Fraction of unreacted carbon |
| βi | Correction factors for equilibria constants |
| χi | Non-equilibrium mole fraction of species i |
| χeq,I | Equilibrium mole fraction of species i |
| Molar flow rate of species i | |
| λi | Thermal conductivity for i in (W m−1 K−1) (where c for char, b for porous bed char, g for gas phase) |
| Sc | Specific gravity of char |
| μ | Dynamic viscosity in (kg m−1 s−1) |
| K | Permeability in (m2) |
| Uc | Char velocity in (m s−1) |
| Cc | Char concentration in (mol m−3) |
| Ug | Gas phase velocity in (m s−1) |
| Us | Solid phase velocity in (m s−1) |
| Cg | Gas phase concentration in (mol m−3) |
| mi | Mass in kg for species i (i = C6H9O4, CH0.26O0.09, and CH1.88O0.7, which corresponds to biomass, char, and tar) |
| mH | Mass of hydrogen in (kg) |
| ṁ | Mass flowrate in (kg s−1) |
| Mg | Molar mass of gas phase in (g mol−1) |
| Mc | Molar mass of char in (g mol−1) |
| Mi | Molar mass of species i in (kg mol−1) (where j = C6H9O4, CH0.26O0.09, and H2O) |
| Mj | Molar mass of species j in (kg mol−1) (where j = H2, O2, N2, CO, CO2, CH4, H2O, and CH1.88O0.7, where CH1.88O0.7 is tar) |
| MCO | Molar mass of CO in (g mol−1) |
| ωi | Char conversion rate |
| CC,0 | Initial molar concentration of char in (mol m−3) |
| ε | Porosity |
| ep | Char particle thickness in (m) |
| τ | Tortuosity |
| δ | Molar ratio of nitrogen to oxygen (3.76 for standard air) |
| η | Gasification efficiency in (%) |
| Dj,N2 | Diffusion coefficient of species j in nitrogen as gas solvent in (m2 s−1) (where j = CO, CO2, H2, H2O, O2, and N2) |
| Dj | Diffusion coefficient of species j in (m2 s−1) |
| Heat lost by convection in (kW m−3) | |
| Heat of reaction in (kJ mol−1) | |
| X | Char conversion |
| z | Bed height in (cm) or (mm) |
| ρi, ρP | Density for species i in (kg m−3) (for P as subscript, it is the solid mass density) |
| εp | Porosity of particle |
| θP | Solids fraction volume |
| Shi | Sherwood number for species i |
| Sci | Schmidt number for species i |
| Re | Reynolds number |
| dP | Particle biomass diameter in (mm) or (m) |
| Ac | Surface area of char in (m2) |
| Kc,i | Kinetic constant considering intrinsic kinetics for species i (for i = O2, CO2, and H2O) |
| η | Effectiveness factor |
| Ai | Species i in the system |
| kj, ko | Pre-exponential factor in (s−1) in the Arrhenius equation |
| ANN | Artificial neural networks |
| CapEx | Capital expenditures in (USD) |
| CFD | Computational fluid dynamics |
| CGE | Cold gas efficiency in (%) |
| CHP | Combined heat and power |
| CRF | Char reactivity factor |
| ER | Equivalence ratio |
| FT | Fischer–Tropsch synthesis |
| HHV | Higher heating value in (MJ kg−1) |
| ICE | Internal combustion engines |
| IRR | Internal rate of return in (%) |
| LCOE | Levelized cost of electricity |
| LHV | Lower heating value in (MJ kg−1) |
| NPV | Net present value in (USD) |
| O&M | Plant operation and maintenance in (USD) |
| OpEx | Operational expenditures in (USD) |
| PAHs | Polycyclic aromatic hydrocarbons |
| PBP | Payback period in (years) |
References
- Wu, X.; McLaren, J.; Madl, R.; Wang, D. Biofuels from Lignocellulosic Biomass. In Sustainable Biotechnology: Sources of Renewable Energy; Singh, O.V., Harvey, S.P., Eds.; Springer: Chambersburg, PA, USA, 2010; pp. 19–41. [Google Scholar] [CrossRef]
- Lourinho, G.; Alves, O.; Garcia, B.; Rijo, B.; Brito, P.; Nobre, C. Costs of gasification technologies for energy and fuel production: Overview, analysis, and numerical estimation. Recycling 2023, 8, 49. [Google Scholar] [CrossRef]
- Renewable Energy Technologies: Costs Analysis Series. Biomass for Power Generation. IRENA Working Paper. 2012. Available online: https://www.researchgate.net/publication/303169841_Renewable_energy_technologies_cost_analysis_series_Biomass_for_Power_Generation (accessed on 16 May 2025).
- Situmorang, Y.A.; Zhao, Z.; Yoshida, A.; Abudula, A.; Guan, G. Small-scale biomass gasification systems for power generation (<200 kW): A review. Renew. Sustain. Energy Rev. 2020, 117, 109486. [Google Scholar] [CrossRef]
- Zhang, K.; Chang, J.; Guan, Y.; Chen, H.; Yang, Y.; Jiang, J. Lignocellulosic biomass gasification technology in China. Renew. Energy 2013, 49, 175–184. [Google Scholar] [CrossRef]
- Kushwah, A.; Reina, T.R.; Short, M. Modelling approaches for biomass gasifiers: A comprehensive overview. Sci. Total Environ. 2022, 834, 155243. [Google Scholar] [CrossRef]
- Kirsanovs, V.; Blumberga, D.; Veidenbergs, I.; Rochas, C.; Vigants, E.; Vigants, G. Experimental investigation of downdraft gasifier at various conditions. Energy Procedia 2017, 128, 332–338. [Google Scholar] [CrossRef]
- Leung, D.Y.C.; Yin, X.L.; Wu, C.Z. A review on the development and commercialization of biomass gasification technologies in China. Renew. Sustain. Energy Rev. 2004, 8, 565–580. [Google Scholar] [CrossRef]
- Buragohain, B.; Mahanta, P.; Moholkar, V.S. Biomass gasification for decentralized power generation: The Indian perspective. Renew. Sustain. Energy Rev. 2010, 14, 73–92. [Google Scholar] [CrossRef]
- Ma, L.; Wang, T.; Liu, Q.; Zhang, X.; Ma, W.; Zhang, Q. A review of thermal-chemical conversion of lignocellulosic biomass in China. Biotechnol. Adv. 2012, 30, 859–873. [Google Scholar] [CrossRef]
- Martínez, J.D.; Mahkamov, K.; Andrade, R.V.; Lora, E.E.S. Syngas production in downdraft biomass gasifiers and its application using internal combustion engines. Renew. Energy 2012, 38, 1–9. [Google Scholar] [CrossRef]
- Shahabuddin, M.; Alam, M.T.; Krishna, B.B.; Bhaskar, T.; Perkins, G. A review on the production of renewable aviation fuels from the gasification of biomass and residual wastes. Bioresour. Technol. 2020, 312, 123596. [Google Scholar] [CrossRef]
- Ferreira, S.; Monteiro, E.; Brito, P.; Vilarinho, C. A Holistic review on biomass gasification modified equilibrium models. Energies 2019, 12, 160. [Google Scholar] [CrossRef]
- Alauddin, Z.A.B.Z.; Lahijani, P.; Mohammadi, M.; Mohamed, A.R. Gasification of lignocellulosic biomass in fluidized beds for renewable energy development: A review. Renew. Sustain. Energy Rev. 2010, 14, 2852–2862. [Google Scholar] [CrossRef]
- Pérez, J.F.; Melgar, A.; Benjumea, P.N. Effect of operating and design parameters on the gasification/combustion process of waste biomass in fixed bed downdraft reactors: An experimental study. Fuel 2012, 96, 487–496. [Google Scholar] [CrossRef]
- Lv, P.M.; Xiong, Z.H.; Chang, J.; Wu, C.Z.; Chen, Y.; Zhu, J.X. An experimental study on biomass air–steam gasification in a fluidized bed. Bioresour. Technol. 2004, 95, 95–101. [Google Scholar] [CrossRef] [PubMed]
- Anca-Couce, A. Reaction mechanisms and multi-scale modelling of lignocellulosic biomass pyrolysis. Prog. Energy Combust. Sci. 2016, 53, 41–79. [Google Scholar] [CrossRef]
- Gani, A.; Naruse, I. Effect of cellulose and lignin content on pyrolysis and combustion characteristics for several types of biomass. Renew. Energy 2007, 32, 649–661. [Google Scholar] [CrossRef]
- Jayah, T.H.; Aye, L.; Fuller, R.J.; Stewart, D.F. Computer simulation of a downdraft wood gasifier for tea drying. Biomass Bioenergy 2003, 25, 459–469. [Google Scholar] [CrossRef]
- Pereira, E.G.; Da Silva, J.N.; De Oliveira, J.L.; Machado, C.S. Sustainable energy: A review of gasification technologies. Renew. Sustain. Energy Rev. 2012, 16, 4753–4762. [Google Scholar] [CrossRef]
- Parthasarathy, P.; Narayanan, K.S. Hydrogen production from steam gasification of biomass: Influence of process parameters on hydrogen yield—A review. Renew. Energy 2014, 66, 570–579. [Google Scholar] [CrossRef]
- Cortazar, M.; Santamaria, L.; Lopez, G.; Alvarez, J.; Zhang, L.; Wang, R.; Bi, X.; Olazar, M. A Comprehensive review of primary strategies for tar removal in biomass gasification. Energy Conv. Manag. 2023, 276, 116496. [Google Scholar] [CrossRef]
- Moiceanu, G.; Paraschiv, G.; Voicu, G.; Dinca, M.; Negoita, O.; Chitoiu, M.; Tudor, P. Energy consumption at size reduction of lignocellulose biomass for bioenergy. Sustainability 2019, 11, 2477. [Google Scholar] [CrossRef]
- Luo, S.; Xiao, B.; Guo, X.; Hu, Z.; Liu, S.; He, M. Hydrogen-rich gas from catalytic steam gasification of biomass in a fixed bed reactor: Influence of particle size on gasification performance. Int. J. Hydrogren Energy 2009, 34, 1260–1264. [Google Scholar] [CrossRef]
- Tian, Y.; Zhou, X.; Lin, S.; Bai, J.; Xu, M. Syngas production from air-steam gasification of biomass with natural catalysts. Sci. Total Environ. 2018, 645, 518–523. [Google Scholar] [CrossRef]
- Erkiaga, A.; Lopez, G.; Amutio, M.; Bilbao, J.; Olazar, M. Influence of operating conditions on the steam gasification of biomass in a conical spouted bed reactor. Chem. Eng. J. 2014, 237, 259–267. [Google Scholar] [CrossRef]
- Acharya, B.; Sule, I.; Dutta, A. A review on advances of torrefaction technologies for biomass processing. Biomass Conv. Bioref. 2012, 2, 349–369. [Google Scholar] [CrossRef]
- Ayub, Y.; Zhou, J.; Ren, J.; He, C. An innovative integration of torrefaction, gasification, and solid oxide fuel cell for carbon-neutral utilization of biomass waste: Process development, economic, exergy, advanced exergy, and exoergonomics analysis. Energy Conv. Manag. 2023, 292, 117426. [Google Scholar] [CrossRef]
- Reschmeier, R.; Karl, J. Experimental study of wood char gasification kinetics in fluidized beds. Biomass Bioenergy 2016, 85, 288–299. [Google Scholar] [CrossRef]
- Yang, H.; Yan, R.; Chen, H.; Zheng, C.; Lee, D.H.; Liang, D.T. In-depth investigation of biomass pyrolysis based on three major components: Hemicellulose, cellulose and lignin. Energy Fuels 2006, 20, 388–393. [Google Scholar] [CrossRef]
- Carmo-Calado, L.; Hermoso-Orzáes, M.J.; La Cal-Herrera, J.; Brito, P.; Terrados-Cepeda, J. Techno-economic evaluation of downdraft fixed be gasification of almond shell and husk as a process step in energy production for decentralized solutions applied in biorefinery systems. Agronomy 2023, 13, 2278. [Google Scholar] [CrossRef]
- Ai, N.; Jiang, Y.; Omar, S.; Wang, J.; Xia, L.; Ren, J. Rapid measurement of cellulose, hemicellulose, and lignin contents in Sargassum horneri by Near-Infrarred Spectroscopy and characteristics variables selection methods. Molecules 2022, 27, 335. [Google Scholar] [CrossRef]
- Salmén, L. Micromechanical understanding of the cell-wall structure. Comptes Rendus Biol. 2004, 327, 873–880. [Google Scholar] [CrossRef]
- Nanda, S.; Mohammad, J.; Reddy, S.N.; Kozinski, J.A.; Dalai, A.K. Pathways of lignocellulosic biomass conversion to renewable fuels. Biomass Convers. Biorefin. 2014, 4, 157–191. [Google Scholar] [CrossRef]
- Babinszki, B.; Sebestyén, Z.; Jakab, E.; Czirok, I.S.; Wang, L.; Skreiberg, Ø.; Czégény, Z. Impact of water leaching of biomass on the composition of torrefaction condensates. J. Anal. Appl. Pyrol. 2025, 189, 107092. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, S.; Qin, Y.; Wang, W.; Vassilev, S.V.; He, C.; Wei, Y.; Vassileva, C.G. Insights into chemical evolution mechanism of different biomass during torrefaction based on the properties of torrefied solid, liquid, and gaseous products. Energy 2025, 318, 134912. [Google Scholar] [CrossRef]
- Díez, D.; Urueña, A.; Piñero, R.; Barrio, A.; Tamminen, T. Determination of hemicellulose, cellulose, and lignin content in different of biomasses by thermogravimetric analysis and pseudocomponent kinetic model (TGA-PKM method). Processes 2020, 8, 1048. [Google Scholar] [CrossRef]
- Nawab, S.; Zahoor; Shah, S.B.; Rahman, M.U.; Keerio, H.A.; Rahman, I. Optimizing bamboo biomass for sustainable isobutanol production using genetically engineered Escherichia coli. Biochem. Eng. J. 2025, 217, 109669. [Google Scholar] [CrossRef]
- Ajorloo, M.; Ghodrat, M.; Scott, J.; Strezov, V. Evaluating the role of feedstock composition and component interactions on biomass gasification. Fuel 2025, 381, 133528. [Google Scholar] [CrossRef]
- Rego, F.; Dias, A.P.S.; Casquilho, M.; Rosa, F.C.; Rodrigues, A. Fast determination of lignocellulosic composition of poplar biomass by thermogravimetry. Biomass Bioenergy 2019, 122, 375–380. [Google Scholar] [CrossRef]
- Zhou, H.; Long, Y.; Meng, A.; Li, Q.; Zhang, Y. The pyrolysis simulation of five biomass species by hemi-cellulose, cellulose and lignin based on thermogravimetric curves. Thermochim. Acta 2013, 566, 36–43. [Google Scholar] [CrossRef]
- Skreiberg, A.; Skreiberg, Ø.; Sandquist, J.; Sørum, L. TGA and macro-TGA characterisation of biomass fuels and fuel mixtures. Fuel 2011, 90, 2182–2197. [Google Scholar] [CrossRef]
- Yeo, J.Y.; Chin, B.L.F.; Tan, J.K.; Loh, Y.S. Comparative studies on the pyrolysis of cellulose, hemicellulose, and lignin based on combined kinetics. J. Energy Inst. 2019, 92, 27–37. [Google Scholar] [CrossRef]
- Channiwala, S.A.; Parikh, P.P. A unified correlation for estimating HHV of solid, liquid and gaseous fuels. Fuel 2002, 81, 1051–1063. [Google Scholar] [CrossRef]
- Jenkins, B.M.; Baxter, L.L.; Miles, T.R.; Miles, T.R. Combustion properties of biomass. Fuel Process. Technol. 1998, 54, 17–46. [Google Scholar] [CrossRef]
- Suárez, J.A.; Luengo, C.A.; Fonseca Felfli, F.; Bezzon, G.; Beatón, P.A. Thermochemical properties of Cuban biomass. Energy Sources 2000, 22, 851–857. [Google Scholar] [CrossRef]
- Biagini, E.; Barontini, F.; Tognotti, L. Development of a bi-equilibrium model for biomass gasification in a downdraft bed reactor. Bioresour. Technol. 2016, 201, 156–165. [Google Scholar] [CrossRef] [PubMed]
- Morey, R.V.; Hatfield, D.L.; Sears, R.; Haak, D.; Tiffany, D.G.; Kaliyan, N. Fuel properties of biomass feed streams at ethanol plants. Appl. Energ. Agricult. 2009, 25, 57–64. [Google Scholar] [CrossRef]
- Munir, S.; Daood, S.S.; Nimmo, W.; Cunliffe, A.M.; Gibbs, B.M. Thermal analysis and devolatilization kinetics of cotton stalk, sugar cane bagasse and shea meal under nitrogen and air atmospheres. Bioresour. Technol. 2009, 100, 1413–1418. [Google Scholar] [CrossRef]
- Sharma, A.K. Equilibrium modeling of global reduction reactions for a downdraft (biomass) gasifier. Energy Conv. Manag. 2008, 49, 832–842. [Google Scholar] [CrossRef]
- Monir, M.U.; Abd Aziz, A.; Kristanti, R.A.; Yousuf, A. Co-gasification of empty fruit bunch in a downdraft reactor: A pilot scale approach. Bioresour. Technol. Rep. 2018, 1, 39–49. [Google Scholar] [CrossRef]
- Bonelli, P.R. Slow pyrolysis of nutshells: Characterization of derived chars and of process kinetics. Energ. Source 2003, 25, 767–778. [Google Scholar] [CrossRef]
- Yoon, S.J.; Son, Y.I.; Kim, Y.K.; Lee, J.G. Gasification and power generation characteristics of rice husk and rice husk pellet using a downdraft fixed-bed gasifier. Renew. Energy 2012, 42, 163–167. [Google Scholar] [CrossRef]
- Keche, A.J.; Gaddale, A.P.R.; Tated, R.G. Simulation of biomass gasification in downdraft gasifier for different biomass fuels using ASPEN PLUS. Clean Technol. Environ. Policy 2015, 17, 465–473. [Google Scholar] [CrossRef]
- Kraisornkachit, P.; Vivanpatarakij, S.; Amornraksa, S.; Simasatitkul, L.; Assabumrungrat, S. Performance evaluation of different combined systems of biochar gasifier, reformer and CO2 capture unit for synthesis gas production. Int. J. Hydrogren Energy 2016, 41, 13408–13418. [Google Scholar] [CrossRef]
- Viana, H.F.; Rodrigues, A.R.; Godina, R.; Matias, J.C.O.; Nunes, L.J.R. Evaluation of the Physical, Chemical and thermal properties of Portuguese maritime pine biomass. Sustainability 2018, 10, 2877. [Google Scholar] [CrossRef]
- Ali, S.A.M.; Razzak, S.A.; Hossain, M.M. Apparent kinetics of high temperature oxidative decomposition of microalgal biomass. Bioresour. Technol. 2015, 175, 569–577. [Google Scholar] [CrossRef]
- Wander, P.R.; Altafini, C.R.; Barreto, R.M. Assessment of a small sawdust gasification unit. Biomass Bioenergy 2004, 27, 467–476. [Google Scholar] [CrossRef]
- Zhou, Y. Experimental and Aspen Plus modeling research on bio-char and syngas co-production by gasification of biomass waste: The products and reaction energy balance evaluation. Biomass Convers. Biorefin. 2023, 14, 5387–5398. [Google Scholar] [CrossRef]
- Venugopal, D.; Lakshmanan, T.; Natarajan, A. Investigation of gasification reactions and H2/CO ratio analysis for rice husk air gasification simulation. Therm. Sci. 2023, 27, 881–890. [Google Scholar] [CrossRef]
- Pinto, F.; André, R.; Miranda, M.; Neves, D.; Varela, F.; Santos, J. Effect of gasification agent on co-gasification of rice production wastes mixtures. Fuel 2016, 180, 407–416. [Google Scholar] [CrossRef]
- Mendiburu, A.Z.; Carvalho, J.A.; Zanzi, R.; Coronado, C.R.; Silveira, J.L. Thermochemical equilibrium modeling of a biomass downdraft gasifier: Constrained and unconstrained non-stoichiometric models. Energy 2014, 71, 624–637. [Google Scholar] [CrossRef]
- Viswanathan, K.; Abbas, S.; Wu, W. Syngas analysis by hybrid modeling of sewage sludge gasification in downdraft reactor: Validation and optimization. Waste Manag. 2022, 144, 132–143. [Google Scholar] [CrossRef] [PubMed]
- Bijesh, R.; Arun, P.; Muraleedharan, C. Modified stoichiometric equilibrium model for sewage sludge gasification and its validation based on experiments in a downdraft gasifier. Biomass Convers. Biorefin. 2023, 13, 9023–9043. [Google Scholar] [CrossRef]
- Zabaniotou, A.; Ioannidou, O.; Skoulou, V. Rapeseed residues utilization for energy and 2nd generation biofuels. Fuel 2008, 87, 1492–1502. [Google Scholar] [CrossRef]
- Tilouche, R.; Garma, R.; Binous, H.; Bellagi, A. Valorization of Tunisian olive pomace by steam gasification: Thermodynamic study using Mathematica and Aspen Plus. Biomass Convers. Biorefin. 2023, 14, 16499–16514. [Google Scholar] [CrossRef]
- Yin, C.Y. Prediction of higher heating values of biomass from proximate and ultimate analyses. Fuel 2011, 90, 1128–1132. [Google Scholar] [CrossRef]
- Wang, L.; Weller, C.L.; Jones, D.D.; Hanna, M.A. Contemporary issues in thermal gasification of biomass and its application to electricity and fuel production. Biomass Bioenergy 2008, 32, 573–581. [Google Scholar] [CrossRef]
- Pfeifer, C.; Koppatz, S.; Hofbauer, H. Steam gasification of various feedstocks at a dual fluidised bed gasifier: Impacts of operation conditions and bed materials. Biomass Convers. Biorefin. 2011, 1, 39–53. [Google Scholar] [CrossRef]
- Hasler, P.; Nussbaumer, T. Gas cleaning for IC engine applications from fixed bed biomass gasification. Biomass Bioenergy 1999, 16, 385–395. [Google Scholar] [CrossRef]
- Milne, T.A.; Evans, R.J.; Abatzoglou, N. Biomass Gasifier “Tars”: Their Nature, Formation, and Conversion; National Renewable Energy Laboratory: Golden, CO, USA, 1998. [Google Scholar]
- Lettner, F.; Timmerer, H.; Haselbacher, P. Guideline for safe and eco-friendly biomass gasification. In Biomass Gasification—State of the Art Description; Graz University of Technology: Graz, Austria, 2007. [Google Scholar]
- Han, J.; Kim, H. The reduction and control technology of tar during biomass gasification/pyrolysis: An overview. Renew. Sustain. Energy Rev. 2008, 12, 397–416. [Google Scholar] [CrossRef]
- van der Drift, A.; van Doorn, J.; Vermeulen, J.W. Ten residual biomass fuels for circulating fluidized-bed gasification. Biomass Bioenergy 2001, 20, 45–56. [Google Scholar] [CrossRef]
- Puig-Arnavat, M.; Bruno, J.C.; Coronas, A. Review and analysis of biomass gasification models. Renew. Sustain. Energy Rev. 2010, 14, 2841–2851. [Google Scholar] [CrossRef]
- Du, J.; Wu, F.; Ma, X. Progress in research of process intensification of spouted beds: A comprehensive review. Chin. J. Chem. Eng. 2023, 62, 238–260. [Google Scholar] [CrossRef]
- Pail, A.V.; Peters, E.A.J.F.; Kuipers, J.A.M. Computational study of particle temperature in a bubbling spout fluidized bed with hot gas injection. Powder Technol. 2015, 284, 475–485. [Google Scholar] [CrossRef]
- Briesemeister, L.; Kremling, M.; Fendt, S.; Spliethoff, H. Air-blown entrained-flow gasification of biomass: Influence of operating conditions. Energy Fuels 2017, 31, 10924–10932. [Google Scholar] [CrossRef]
- Hailu, A. Development and performance analysis of top lit updraft: Natural draft gasifier stoves with various feed stocks. Heliyon 2022, 8, e10163. [Google Scholar] [CrossRef] [PubMed]
- Tremel, A.; Spliethoff, H. Gasification kinetics during entrained flow gasification—Part III: Modeling and optimisation of entrained flow gasifiers. Fuel 2013, 107, 170–182. [Google Scholar] [CrossRef]
- Murthy, B.N.; Sawarkar, A.N.; Deshmukh, N.A.; Mathew, T.; Joshi, J.B. Petroleum coke gasification: A review. Can. J. Chem. Eng. 2014, 92, 441–468. [Google Scholar] [CrossRef]
- Hrbek, J. Status Report on Thermal Biomass Gasification in Countries Participating in IEA Bioenergy Task 33; IEA Bioenergy: Paris, France, 2016. [Google Scholar]
- Gil, J.; Corella, J.; Aznar, M.P.; Caballero, M.A. Biomass gasification in atmospheric and bubbling fluidized bed: Effect of the type of gasifying agent on the product distribution. Biomass Bioenergy 1999, 17, 389–403. [Google Scholar] [CrossRef]
- Rapagnà, S.; Jan, N.; Kiennemann, A.; Foscolo, P.U. Steam-gasification of biomass in a fluidised-bed of olivine particles. Biomass Bioenergy 2000, 19, 187–197. [Google Scholar] [CrossRef]
- Devi, L.; Ptasinski, K.J.; Janssen, F.J.J.G. A review of the primary measures for tar elimination in biomass gasification processes. Biomass Bioenergy 2003, 24, 125–140. [Google Scholar] [CrossRef]
- Narváez, I.; Orío, A.; Aznar, M.P.; Corella, J. Biomass basification with air in an atmospheric bubbling fluidized bed. Effect of six operational variables on the quality of the produced raw gas. Ind. Eng. Chem. Res. 1996, 35, 2110–2120. [Google Scholar] [CrossRef]
- Kinoshita, C.M.; Wang, Y.; Zhou, J. Tar formation under different biomass gasification conditions. J. Anal. Appl. Pyrolysis 1994, 29, 169–181. [Google Scholar] [CrossRef]
- Guan, G.; Kaewpanha, M.; Hao, X.; Abudula, A. Catalytic steam reforming of biomass tar: Prospects and challenges. Renew. Sustain. Energy Rev. 2016, 58, 450–461. [Google Scholar] [CrossRef]
- Luo, S.; Xiao, B.; Hu, Z.; Liu, S.; Guo, X.; He, M. Hydrogen-rich gas from catalytic steam gasification of biomass in a fixed bed reactor: Influence of temperature and steam on gasification performance. Int. J. Hydrogren Energy 2009, 34, 2191–2194. [Google Scholar] [CrossRef]
- Gao, K.; Chen, G.; Yan, B.; Ti, S.; Wang, H.; Si, G.; Qi, T. Modeling of biomass thermal decomposition/gasification in a downdraft gasifier under low pressure by Aspen plus. Therm. Sci. Eng. Prog. 2025, 59, 103229. [Google Scholar] [CrossRef]
- Doherty, W.; Reynolds, A.; Kennedy, D. The effect of air preheating in a biomass CFD gasifier using ASPEN Plus simulation. Biomass Bioenergy 2009, 33, 1158–1167. [Google Scholar] [CrossRef]
- Kumar, A.; Pandey, D.S.; Mondal, T. Experimental investigation of process parameters for hydrogen-rich syngas production from rice husk gasification. Sustain. Chem. Clim. Action 2025, 6, 100061. [Google Scholar] [CrossRef]
- Renganathan, T.; Yadav, M.V.; Pushpavanam, S.; Voolapalli, R.K.; Cho, Y.S. CO2 utilization for gasification of carbonaceous feedstocks: A thermodynamic analysis. Chem. Eng. Sci. 2012, 83, 159–170. [Google Scholar] [CrossRef]
- García, L.; Salvador, M.L.; Arauzo, J.; Bilbao, R. CO2 as a gasifying agent for gas production from pine sawdust at low temperatures using a Ni/Al coprecipitated catalyst. Fuel Process. Technol. 2001, 69, 157–174. [Google Scholar] [CrossRef]
- Lahijani, P.; Zainal, Z.A.; Mohamed, A.R.; Mohammadi, M. CO2 gasification reactivity of biomass char: Catalytic influence of alkali, alkaline earth and transition metal salts. Bioresour. Technol. 2013, 144, 288–295. [Google Scholar] [CrossRef]
- Huang, Y.; Yin, X.; Wu, C.; Wang, C.; Xie, J.; Zhou, Z.; Ma, L.; Li, H. Effects of metal catalysts on CO2 gasification reactivity of biomass char. Biotechnol. Adv. 2009, 27, 568–572. [Google Scholar] [CrossRef]
- Mortensen, P.M.; Dybkjær, I. Industrial scale experience on steam reforming of CO2-rich gas. Appl. Catal. A-Gen. 2015, 495, 141–151. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, G.; Schurz, M.; Steffen, K.; Meyer, B. Kinetic study on CO2 gasification of brown coal and biomass chars: Reaction order. Fuel 2016, 173, 311–319. [Google Scholar] [CrossRef]
- Bui, H.H.; Wang, L.; Tran, K.Q.; Skreiberg, Ø. CO2 gasification of charcoals produced at various pressures. Fuel Process. Technol. 2016, 152, 207–214. [Google Scholar] [CrossRef]
- Bikane, K.; Yu, J.; Shah, S.M.; Long, X.; Paterson, N.; Pini, R.; Millan, M. High pressure CO2 gasification of Morupule coal: Kinetics and morphological development of chars. Chem. Eng. J. 2023, 462, 142136. [Google Scholar] [CrossRef]
- Zhang, S.; Wu, M.; Qian, Z.; Li, Q.; Zhang, Y.; Zhou, H. CO rich syngas production from catalytic CO2 gasification-reforming of biomass components on Ni/CeO2. Fuel 2024, 357, 130087. [Google Scholar] [CrossRef]
- Hong, W.Y. A techno-economic review on carbon capture, utilisation and storage systems for achieving a net-zero CO2 emission future. Carbon Capture Sci. Technol. 2022, 3, 100044. [Google Scholar] [CrossRef]
- Wang, M.; Luo, J. A coupled electrochemical system for CO2 capture, conversion and product purification. eScience 2023, 3, 100155. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, Y.; Bie, X.; Li, Q.; Zhang, Y.; Zhou, H. Mechanisms in CO2 gasification and co-gasification of combustible solid waste: A critical review. Gas Sci. Eng. 2024, 128, 205368. [Google Scholar] [CrossRef]
- Rakesh, N.; Dasappa, S. A critical assessment of tar generated during biomass gasification—formation, evaluation, issues and mitigation strategies. Renew. Sustain. Energy Rev. 2018, 91, 1045–1064. [Google Scholar] [CrossRef]
- Neubauer, Y. Strategies for tar reduction in fuel-gases and synthesis-gases from biomass gasification. J. Sustain. Energy Environ. 2011, 67, 71. [Google Scholar]
- Meng, J.; Wang, X.; Zhao, Z.; Zheng, A.; Huang, Z.; Wei, G.; Lv, K.; Li, H. Highly abrasion resistant thermally fused olivine as in-situ catalysts for tar reduction in a circulating fluidized bed biomass gasifier. Bioresour. Technol. 2018, 268, 212–220. [Google Scholar] [CrossRef]
- Wolfesberger, U.; Aigner, I.; Hofbauer, H. Tar content and composition in producer gas of fluidized bed gasification of wood—Influence of temperature and pressure. Environ. Prog. Sustain. Energy 2009, 28, 372–379. [Google Scholar] [CrossRef]
- Motta, I.L.; Miranda, N.T.; Maciel Filho, R.; Wolf Maciel, M.R. Biomass gasification in fluidized beds: A review of biomass moisture content and operating pressure effects. Renew. Sustain. Energy Rev. 2018, 94, 998–1023. [Google Scholar] [CrossRef]
- Kurkela, E.; Kurkela, M.; Hiltunen, K. The effects of wood particle size and different process variables on the performance of steam-oxygen blown circulating fluidized-bed gasifier. Environ. Prog. Sustain. Energy 2014, 33, 681–687. [Google Scholar] [CrossRef]
- Berrueco, C.; Recari, J.; Matas Güell, B.; del Alamo, G. Pressurized gasification of torrefied woody biomass in a lab scale fluidized bed. Energy 2014, 70, 68–78. [Google Scholar] [CrossRef]
- Mayerhofer, M.; Mitsakis, P.; Meng, X.; de Jong, W.; Spliethoff, H.; Gaderer, M. Influence of pressure, temperature and steam on tar and gas in allothermal fluidized bed gasification. Fuel 2012, 99, 204–209. [Google Scholar] [CrossRef]
- Li, C.; Suzuki, K. Tar property, analysis, reforming mechanism and model for biomass gasification—An overview. Renew. Sustain. Energy Rev. 2009, 13, 594–604. [Google Scholar] [CrossRef]
- Costa, M.; La Villetta, M.; Massarotti, N. Optimal tuning of a thermo-chemical equilibrium model for downdraft biomass gasifiers. Chem. Engineer. Trans. 2015, 43, 439–444. [Google Scholar] [CrossRef]
- Vera, D.; Jurado, F.; Carpio, J. Study of a downdraft gasifier and externally fired gas turbine for olive industry wastes. Fuel Process. Technol. 2011, 92, 1970–1979. [Google Scholar] [CrossRef]
- Abuadala, A.; Dincer, I.; Naterer, G.F. Exergy analysis of hydrogen production from biomass gasification. Int. J. Hydrogren Energy 2010, 35, 4981–4990. [Google Scholar] [CrossRef]
- Font Palma, C. Modelling of tar formation and evolution for biomass gasification: A review. Appl. Energy 2013, 111, 129–141. [Google Scholar] [CrossRef]
- Sharma, R.K.; Hajaligol, M.R. Effect of pyrolysis conditions on the formation of polycyclic aromatic hydrocarbons (PAHs) from polyphenolic compounds. J. Anal. Appl. Pyrolysis 2003, 66, 123–144. [Google Scholar] [CrossRef]
- Scheer, A.M.; Mukarakate, C.; Robichaud, D.J.; Nimlos, M.R.; Carstensen, H.H.; Barney Ellison, G. Unimolecular thermal decomposition of phenol and d5-phenol: Direct observation of cyclopentadiene formation via cyclohexadienone. J. Chem. Phys. 2012, 136, 044309. [Google Scholar] [CrossRef] [PubMed]
- Simell, P.A.; Hepola, J.O.; Outi, A.; Krause, I. Effects of gasification gas components on tar and ammonia decomposition over hot gas cleanup catalysts. Fuel 1997, 76, 1117–1127. [Google Scholar] [CrossRef]
- Shen, Y.; Yoshikawa, K. Recent progresses in catalytic tar elimination during biomass gasification or pyrolysis—A review. Renew. Sustain. Energy Rev. 2013, 21, 371–392. [Google Scholar] [CrossRef]
- Susastriawan, A.A.P.; Saptoadi, H.; Purnomo. Small-scale downdraft gasifiers for biomass gasification: A review. Renew. Sustain. Energy Rev. 2017, 76, 979–1003. [Google Scholar] [CrossRef]
- Ramasubramanian, S.; Chandrasekaran, M. Optimisation of catalytic steam for tar mitigation in biomass producer gas. Int. J. Ambient. Energy 2020, 41, 621–626. [Google Scholar] [CrossRef]
- Akia, M.; Farshad, Y.; Elahe, M.; Dezhi, H.; Hamidreza, A. A review on conversion of biomass to biofuel by nanocatalysts. Biofuel Res. J. 2014, 1, 16–25. [Google Scholar] [CrossRef]
- Shanmuganandam, K.; Ramanan, M.V. Ni-Ce/SiO2 nanocomposite: Characterization and catalytic activity in the cracking of tar in biomass gasifiers. Energ. Source. Part A 2016, 38, 2418–2425. [Google Scholar] [CrossRef]
- Phuphuakrat, T.; Namioka, T.; Yoshikawa, K. Absorptive removal of biomass tar using water and oily materials. Bioresour. Technol. 2011, 102, 543–549. [Google Scholar] [CrossRef] [PubMed]
- Paethanom, A.; Nakahara, S.; Kobayashi, M.; Prawisudha, P.; Yoshikawa, K. Performance of tar removal by absorption and adsorption for biomass gasification. Fuel Process. Technol. 2012, 104, 144–154. [Google Scholar] [CrossRef]
- Meng, S.; Li, W.; Li, Z.; Song, H. Recent progress of the transition metal-based catalysts in the catalytic biomass gasification: A mini-review. Fuel 2023, 353, 129169. [Google Scholar] [CrossRef]
- Corella, J.; Toledo, J.M.; Padilla, R. Olivine or dolomite as in-bed additive in biomass gasification with air in a fluidized bed: Which is better? Energy Fuels 2004, 18, 713–720. [Google Scholar] [CrossRef]
- Christodoulou, C.; Grimekis, D.; Panopoulos, K.D.; Pachatouridou, E.P.; Iliopoulou, E.F.; Kakaras, E. Comparing calcined and un-treated olivine as bed materials for tar reduction in fluidized bed gasification. Fuel Process. Technol. 2014, 124, 275–285. [Google Scholar] [CrossRef]
- Marinkovic, J.; Thunman, H.; Knutsson, P.; Seemann, M. Characteristics of olivine as a bed material in an indirect biomass gasifier. Chem. Eng. J. 2015, 279, 555–566. [Google Scholar] [CrossRef]
- Weerachanchai, P.; Horio, M.; Tangsathitkulchai, C. Effects of gasifying conditions and bed materials on fluidized bed steam gasification of wood biomass. Bioresour. Technol. 2009, 100, 1419–1427. [Google Scholar] [CrossRef]
- Xu, D.; Xiong, Y.; Ye, J.; Su, Y.; Dong, Q.; Zhang, S. Performances of syngas production and deposited coke regulation during co-gasification of biomass and plastic wastes over Ni/γ-Al2O3 catalyst: Role of biomass to plastic ratio in feedstock. Chem. Eng. J. 2020, 392, 123728. [Google Scholar] [CrossRef]
- Chai, Y.; Gao, N.; Wang, M.; Wu, C. H2 production from co-pyrolysis/gasification of waste plastics and biomass under novel catalyst Ni-CaO-C. Chem. Eng. J. 2020, 382, 122947. [Google Scholar] [CrossRef]
- Tomishige, K.; Kimura, T.; Nishikawa, J.; Miyazawa, T.; Kunimori, K. Promoting effect of the interaction between Ni and CeO2 on steam gasification of biomass. Catal. Commun. 2007, 8, 1074–1079. [Google Scholar] [CrossRef]
- Tarifa, P.; Ramírez Reina, T.; González-Castaño, M.; Arellano-García, H. Catalytic upgrading of biomass-gasification mixtures using Ni-Fe/MgAl2O4 as a bifunctional catalyst. Energy Fuels 2022, 36, 8267–8273. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Niu, Y. Biomass to hydrogen-rich syngas via tar removal from steam gasification with La1-XCeXFeO3/dolomite as a catalyst. Int. J. Hydrogren Energy 2022, 47, 21997–22009. [Google Scholar] [CrossRef]
- Gai, D.; Shi, J.; Cui, X.; Zhao, P.; Zuo, W.; Zhang, J.; Jia, G.; Huang, Z. Catalytic performance and mechanism of A-site vacancy deficient perovskite catalyst over tar cracking during biomass pyrolysis. J. Clean. Prod. 2023, 405, 136876. [Google Scholar] [CrossRef]
- Asadullah, M.; Miyazawa, T.; Ito, S.; Kunimori, K.; Koyama, S.; Tomishige, K. A comparison of Rh/CeO2/SiO2 catalysts with steam reforming catalysts, dolomite and inert materials as bed materials in low throughput fluidized bed gasification systems. Biomass Bioenergy 2004, 26, 269–279. [Google Scholar] [CrossRef]
- Zhang, S.; Shang, Y.; Wang, J.; Chen, H.; Xiong, Y.; Zhang, H. Study on the construction of char-supported NiFe-NiFe2O4 catalyst and its catalytic cracking mechanism of biomass tar under relative low temperature. Fuel 2023, 346, 128412. [Google Scholar] [CrossRef]
- Rönkkönen, H.; Simell, P.; Reinikainen, M.; Krause, O.; Niemelä, M.V. Catalytic clean-up of gasification gas with precious metal catalysts—A novel catalytic reformer development. Fuel 2010, 89, 3272–3277. [Google Scholar] [CrossRef]
- Yin, S.F.; Xu, B.Q.; Zhou, X.P.; Au, C.T. A mini-review on ammonia decomposition catalysts for on-site generation of hydrogen for fuel cell applications. Appl. Catal. A-Gen. 2004, 277, 1–9. [Google Scholar] [CrossRef]
- Wang, L.; Hisada, Y.; Koike, M.; Li, D.; Watanabe, H.; Nakagawa, Y.; Tomishige, K. Catalyst property of Co–Fe alloy particles in the steam reforming of biomass tar and toluene. Appl. Catal. B-Environ. 2012, 121–122, 95–104. [Google Scholar] [CrossRef]
- Tang, W.; Cao, J.P.; Wang, Z.Y.; Jiang, W.; Zhao, X.Y.; He, Z.M.; Wang, Z.H.; Bai, H. Preparation of highly dispersed lignite-char-supported cobalt catalyst for stably steam reforming of biomass tar at low temperature. Fuel 2023, 334, 126814. [Google Scholar] [CrossRef]
- Tian, B.; Mao, S.; Guo, F.; Bai, J.; Shu, R.; Lin, Q.; Liu, Q. Monolithic biochar-supported cobalt-based catalysts with high-activity and superior-stability for biomass tar reforming. Energy 2022, 242, 122970. [Google Scholar] [CrossRef]
- Dasappa, S.; Mukunda, H.S.; Paul, P.J.; Rajan, N.K.S. Biomass to Energy: The Science and Technology of the IISc Bio-Energy Systems; Indian Institute of Science: Bangalore, India, 2003. [Google Scholar]
- Boerrigter, H.; Van Paasen, S.V.B.; Bergman, P.C.A.; Könemann, J.W.; Emmen, R.; Wijnands, A. OLGA Tar Removal Technology. Energy Research Centre of the Netherlands, 2005. ECN-C--05-009. Available online: https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://publications.tno.nl/publication/34628499/3j51fW/c05009.pdf&ved=2ahUKEwjVlZGLxomPAxXIwzgGHf-XNR4QFnoECBcQAQ&usg=AOvVaw1tjMCa5ifgO-cgdGiDay9K (accessed on 21 May 2025).
- Hofbauer, H.; Rauch, R.; Loeffler, G.; Kaiser, S.; Fercher, E.; Tremmel, H. Six Years Experience with the FICFB-Gasification Process. 2002, pp. 982–985. Available online: https://www.researchgate.net/publication/228797225_Six_Years_Experience_with_the_FICFB-Gasification_Process (accessed on 16 May 2025).
- Bull, D. Performance Improvements to A Fast Internally Circulating Fluidized Bed (FICFB) Biomass Gasifier for Combined Heat and Power Plants. Master’s Thesis, University of Canterbury, Christchurch, New Zealand, 2008. [Google Scholar]
- Zhang, X.; Pan, J.; Wang, L.; Sun, H.; Zhu, Y.; Chen, H. Simulated biomass tar removal mechanism by a Quench Coupled with ADsoprtion Technology (QCADT). Chin. J. Chem. Eng. 2020, 28, 279–285. [Google Scholar] [CrossRef]
- Qin, Y.; Campen, A.; Wiltowski, T.; Feng, J.; Li, W. The influence of different chemical composition in biomass on gasification tar formation. Biomass Bioenergy 2015, 83, 77–84. [Google Scholar] [CrossRef]
- Qi, Y.; Muhammad, U.; Zhang, W.; Song, Y.; Zhang, M.; Wang, M.; Xu, C.; Xu, Y.; Cai, S.; Han, C.; et al. A comprehensive evaluation of recent advancement in municipal solid waste gasification: Research status, technical challenges and perspectives. Sep. Purif. Technol. 2025, 358, 130443. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Chu, Z.; Fang, Y. Thermodynamic analysis of integrated sorption-enhanced staged-gasification of biomass and in-situ CO2 utilization by methane reforming process based on calcium looping. Energy Conv. Manag. 2023, 278, 116710. [Google Scholar] [CrossRef]
- Ducom, G.; Tagutchou, J.P.; Gautier, M.; Gaignaire, C.; Méhu, J.; Gourdon, R. Olive mill solid waste in a pilot-scale downdraft gasifier with three-stage air supply: Performance, mass-energy balance and fate of inorganic elements. Fuel 2023, 340, 127469. [Google Scholar] [CrossRef]
- Dogru, M.; Howarth, C.R.; Akay, G.; Keskinler, B.; Malik, A.A. Gasification of hazelnut shells in a downdraft gasifier. Energy 2002, 27, 415–427. [Google Scholar] [CrossRef]
- Ouedraogo, H.; Sidibe, S.D.S.; Richardson, Y.; Zoungrana, L. Optimizing gasification in downdraft fixed-bed gasifier through experimental and kinetic modeling. Case Stud. Therm. Eng. 2025, 68, 105910. [Google Scholar] [CrossRef]
- Salem, A.M.; Paul, M.C. CFD modelling of spatiotemporal evolution of detailed tar species in a downdraft gasifier. Biomass Bioenergy 2023, 168, 106656. [Google Scholar] [CrossRef]
- Wibowo, W.A.; Pranolo, S.H.; Sunarno, J.N.; Purwadi, D. Effect of biomass feed size and air flow rate on the pressure drop of gasification reactor. J. Teknol. 2014, 68, 7–12. [Google Scholar] [CrossRef]
- Qi, X.B.; Zhang, H.; Zhu, J. Friction between gas-solid flow and circulating fluidized bed downer wall. Chem. Eng. J. 2008, 142, 318–326. [Google Scholar] [CrossRef]
- Van Swaaij, W.P.M.; Buurman, C.; van Bruegel, J.W. Shear stress on the wall of a dense gas-solid riser. Chem. Eng. Sci. 1970, 25, 1818–1820. [Google Scholar] [CrossRef]
- Hartge, E.U.; Li, Y.; Werther, J. Analysis of the local structure of the two phase flow in a fast fluidized bed. In Circulating Fluidized Bed Technology; Basu, P., Ed.; Pergamon: Oxford, UK, 1986; pp. 153–160. [Google Scholar] [CrossRef]
- Issangya, A.S.; Bai, D.; Bi, H.T.; Lim, K.S.; Zhu, J.; Grace, J.R. Suspension densities in a high-density circulating fluidized bed riser. Chem. Eng. Sci. 1999, 54, 5451–5460. [Google Scholar] [CrossRef]
- Pérez, J.F.; Benjumea, P.N.; Melgar, A. Sensitivity analysis of a biomass gasification model in fixed bed downdraft reactors: Effect of model and process parameters on reaction front. Biomass Bioenergy 2015, 83, 403–421. [Google Scholar] [CrossRef]
- Shin, D.; Choi, S. The combustion of simulated waste particles in a fixed bed. Combust. Flame 2000, 121, 167–180. [Google Scholar] [CrossRef]
- Reed, T.B.; Walt, R.; Ellis, S.; Das, A.; Deutsch, S. Superficial velocity—The key to downdraft gasification. In Biomass. A Growth Opportunity in Green Energy and Value-Added Products. United Kingdom; Overend, R.P., Chornet, E., Eds.; Pergamon: Oxford, UK, 1999; pp. 1001–1007. [Google Scholar]
- Yamazaki, T.; Kozu, H.; Yamagata, S.; Murao, N.; Ohta, S.; Shiya, S.; Ohba, T. Effect of superficial velocity on tar from downdraft gasification of biomass. Energy Fuels 2005, 19, 1186–1191. [Google Scholar] [CrossRef]
- Rauch, R.; Hrbek, J.; Hofbauer, H. Biomass gasification for synthesis gas production and applications of the syngas. WIREs Energy Environ. 2014, 3, 343–362. [Google Scholar] [CrossRef]
- Yang, J.; Ma, W.; Chen, D.; Holmen, A.; Davis, B.H. Fischer-Tropsch synthesis: A review of the effect of CO conversion on methane selectivity. Appl. Catal. A-Gen. 2014, 470, 250–260. [Google Scholar] [CrossRef]
- Soukup, G.; Pfeifer, C.; Kreuzeder, A.; Hofbauer, H. In situ CO2 capture in a dual fluidized bed biomass steam gasifier-bed material and fuel variation. Chem. Eng. Technol. 2009, 32, 348–354. [Google Scholar] [CrossRef]
- Gogate, M.R. Methanol-to-olefins process technology: Current status and future prospects. Pet. Sci. Technol. 2019, 37, 559–565. [Google Scholar] [CrossRef]
- Ekbom, T.; Costa de Paiva, T.; Müller-Langer, F. Assessments of Successes and Lessons Learned for Biofuels Deployment. Report Work Package 3. Case Studies Technologies. 2023. Available online: https://task39.ieabioenergy.com/publications-new/ (accessed on 26 November 2024).
- Reche López, P.; Gómez González, M.; Ruiz Reyes, N.; Jurado, F. Optimization of biomass fuelled systems for distributed generation using Particle Swarm Optimization. Electr. Power Syst. Res. 2008, 78, 1448–1455. [Google Scholar] [CrossRef]
- Kirkels, A.F.; Verbong, G.P.J. Biomass gasification: Still promising? A 30-year global overview. Renew. Sustain. Energy Rev. 2011, 15, 471–481. [Google Scholar] [CrossRef]
- McKendry, P. Energy production from biomass (part 3): Gasification technologies. Bioresour. Technol. 2002, 83, 55–63. [Google Scholar] [CrossRef]
- Fracaro, G.P.M.; Souza, S.N.M.; Medeiros, M.; Formentini, D.F.; Marques, C.A. Economic feasibility of biomass gasification for small-scale electricity generation in Brazil. In Proceedings of the World Renewable Energy Congress, Linköping, Sweden, 8–13 May 2011. [Google Scholar]
- Porcu, A.; Sollai, S.; Marotto, D.; Mureddu, M.; Ferrara, F.; Pettinau, A. Techno-economic analysis of a small-scale biomass-to-energy BFB gasification-based system. Energies 2019, 12, 494. [Google Scholar] [CrossRef]
- Indrawan, N.; Simkins, B.; Kumar, A.; Huhnke, R.L. Economics of distributed power generation via gasification of biomass and municipal solid waste. Energies 2020, 13, 3703. [Google Scholar] [CrossRef]
- Shahbeig, H.; Shafizadeh, A.; Rosen, M.A.; Sels, B.F. Exergy sustainability analysis of biomass gasification: A critical review. Biofuel Res. J. 2022, 33, 1592–1607. [Google Scholar] [CrossRef]
- Biomass for Heat and Power. Opportunity and Economics. Available online: https://group.vattenfall.com/siteassets/corporate/news_and_media/doc/biomass_report_-_final_-_compressed.pdf_13413687.pdf (accessed on 29 May 2025).
- Available online: https://demoplants21.best-research.eu/projects/displaymap/XQ62ks (accessed on 29 May 2025).
- Available online: https://www.inflationtool.com/us-dollar (accessed on 29 May 2025).
- Parathesi, M.; Singh Vincent, C.J.; Winsly, B.W. Parametric optimization and economic assessment of tyre waste co-gasification with agricultural biomass in a downdraft gasifier using RSM-CCD technique. Energy 2025, 318, 134786. [Google Scholar] [CrossRef]
- Campos, C.F.C.; de Sá Machado, V.A.; Soares, O.L.; Boloy, R.A.M. Techno-economic analysis and eco-efficiency indicators of a biomass-solar hybrid renewable energy system for João Pinheiro City. Discov. Sustain. 2024, 5, 41. [Google Scholar] [CrossRef]
- Umar, H.A.; Sulaiman, S.A. Parametric optimization through the use of Box-Behnken design in the co-gasification of oil palm trunk and frond for syngas production. Fuel 2022, 310, 122234. [Google Scholar] [CrossRef]
- Aguado, R.; Vera, D.; López-García, D.A.; Torreglosa, J.P.; Jurado, F. Techno-economic assessment of a gasification plant for distributed cogeneration in the agrifood sector. Appl. Sci. 2021, 11, 660. [Google Scholar] [CrossRef]
- Eliasu, A.; Derkyi, N.S.A.; Gyamfi, S. Techno-economic analysis of municipal solid waste gasification for electricity generation. Int. J. Energy Econ. Policy 2022, 12, 342–348. [Google Scholar] [CrossRef]
- Elsner, W.; Wysocki, M.; Niegodajew, P.; Borecki, R. Experimental and economic study of small-scale CHP installation equipped with downdraft gasifier and internal combustion engine. Appl. Energy 2017, 202, 213–227. [Google Scholar] [CrossRef]
- Abdoulmoumine, N.; Kulkarni, A.; Adhikari, S.; Taylor, S.; Loewenstein, E. Economic analysis of municipal power generation from gasification of urban green wastes: Case study of Fultondale, Alabama, USA. Biofuels Bioprod. Bioref. 2012, 6, 521–533. [Google Scholar] [CrossRef]
- Buchholz, T.; da Silva, I.; Furtado, J. Power from wood gasifiers in Uganda: A 250 kW and 10 kW case study. Proc. Inst. Civ. Eng.-Energy 2012, 165, 181–196. [Google Scholar] [CrossRef]
- Wei, L.; Pordesimo, L.O.; Filip To, S.D.; Herndon, C.W.; Batchelor, W.D. Evaluation of micro-scale syngas production costs through modeling. Trans. ASABE 2009, 52, 1649–1659. [Google Scholar] [CrossRef]
- Kim, H.; Parajuli, P.B.; Yu, F.; Columbus, E.P. Economic analysis and assessment of syngas production using a modeling approach. In Proceedings of the ASABE Annual International Meeting, Louisville, KY, USA, 7–10 August 2011. [Google Scholar] [CrossRef]
- Halba, A.; Arora, P.; Saroj, R.K.; Navle, P.; Halan, S. Transforming paper dust into electricity and biochar via gasification: Experimental, emission, and economic insights. Energy Conv. Manag. 2025, 326, 119503. [Google Scholar] [CrossRef]
- Isgiyarta, J.; Sudarmanta, B.; Prakoso, J.A.; Jannah, E.N.; Saleh, A.R. Micro-grid oil palm plantation waste gasification power plant in Indonesia: Techno-economic and socio-environmental analysis. Energies 2022, 15, 1782. [Google Scholar] [CrossRef]
- Copa, J.R.; Tuna, C.E.; Silveira, J.L.; Boloy, R.A.M.; Brito, P.; Silva, V.; Cardoso, J.; Eusébio, D. Techno-economic assessment of the use of syngas generated from biomass to feed an internal combustion engine. Energies 2020, 13, 3097. [Google Scholar] [CrossRef]
- Jia, J.; Zang, G.; Paul, M.C. Energy, exergy, and economic (3E) evaluation of a CCHP system with biomass gasifier, solid oxide fuel cells, micro-gas turbine, and absorption chiller. Int. J. Energy Res. 2021, 45, 15182–15199. [Google Scholar] [CrossRef]
- Jia, J.; Shu, L.; Zang, G.; Xu, L.; Abudula, A.; Ge, K. Energy analysis and techno-economic assessment of a co-gasification of woody biomass and animal manure, solid oxide fuel cells and micro gas turbine hybrid system. Energy 2018, 149, 750–761. [Google Scholar] [CrossRef]
- Proenza Pérez, N.; Blanco Machin, E.; Travieso Pedroso, D.; Roberts, J.J.; Santana Antunes, J.; Silveira, J.L. Biomass gasification for combined heat and power generation in the Cuban context: Energetic and economic analysis. Appl. Therm. Eng. 2015, 90, 1–12. [Google Scholar] [CrossRef]
- Rathore, N.S.; Panwar, N.L.; Chiplunkar, Y.V. Design and techno economic evaluation of biomass gasifier for industrial thermal applications. Afr. J. Environ. Sci. Technol. 2009, 3, 6–12. [Google Scholar]
- van Eck, N.J.; Waltman, L. Software survey: VOSviewer, a computer program for bibliometric mapping. Scientometrics 2010, 84, 525–538. [Google Scholar] [CrossRef]
- Gagliano, A.; Nocera, F.; Patania, F.; Cristina, M.; Castaldo, D. A robust numerical model for characterizing the syngas composition in a downdraft gasification process. Comptes Rendus Chim. 2016, 19, 441–449. [Google Scholar] [CrossRef]
- Trninić, M.; Stojiljković, D.; Manić, N.; Skreiberg, Ø.; Wang, L.; Jovović, A. A mathematical model of biomass downdraft gasification with an integrated pyrolysis model. Fuel 2020, 265, 116867. [Google Scholar] [CrossRef]
- Azzone, E.; Morini, M.; Pinelli, M. Development of an equilibrium model for the simulation of thermochemical gasification and application to agricultural residues. Renew. Energy 2012, 46, 248–254. [Google Scholar] [CrossRef]
- Huang, H.J.; Ramaswamy, S. Modeling biomass gasification using thermodynamic equilibrium approach. Appl. Biochem. Biotechnol. 2009, 154, 14–25. [Google Scholar] [CrossRef]
- Sharma, A.K. Equilibrium and kinetic modeling of char reduction reactions in a downdraft biomass gasifier: A comparison. Sol. Energy 2008, 82, 918–928. [Google Scholar] [CrossRef]
- Hameed, S.; Ramzan, N.; Rahman, Z.; Zafar, M.; Riaz, S. Kinetic modeling of reduction zone in biomass gasification. Energy Conv. Manag. 2014, 78, 367–373. [Google Scholar] [CrossRef]
- Ibrahim, A.; Veremieiev, S.; Gaskell, P.H. An advanced, comprehensive thermochemical equilibrium model of a downdraft biomass gasifier. Renew. Energ. 2022, 194, 912–925. [Google Scholar] [CrossRef]
- Talero, G.; Kansha, Y. Simulation of the steam gasification of Japanese waste wood in an indirectly heated downdraft reactor using PRO/IITM: Numerical comparison of stoichiometric and kinetic models. Energies 2022, 15, 4181. [Google Scholar] [CrossRef]
- Buragohain, B.; Mahanta, P.; Moholkar, V.S. Thermodynamic optimization of biomass gasification for decentralized power generation and Fischer–Tropsch synthesis. Energy 2010, 35, 2557–2579. [Google Scholar] [CrossRef]
- Gambarotta, A.; Morini, M.; Zubani, A. A non-stoichiometric equilibrium model for the simulation of the biomass gasification process. Appl. Energy 2018, 227, 119–127. [Google Scholar] [CrossRef]
- Antonopoulos, I.S.; Karagiannidis, A.; Gkouletsos, A.; Perkoulidis, G. Modelling of a downdraft gasifier fed by agricultural residues. Waste Manag. 2012, 32, 710–718. [Google Scholar] [CrossRef] [PubMed]
- Mahinpey, N.; Gomez, A. Review of gasification fundamentals and new findings: Reactors, feedstock, and kinetic studies. Chem. Eng. Sci. 2016, 148, 14–31. [Google Scholar] [CrossRef]
- Gradel, A.; Honke, R.; Wünning, J.G.; Plessing, T.; Jess, A. Modeling of biomass gasification in a downdraft gasifier with integrated tar adsorption. Chem. Eng. Technol. 2019, 42, 1895–1906. [Google Scholar] [CrossRef]
- Ephraim, A.; Pozzobon, V.; Louisnard, O.; Minh, D.P.; Nzihou, A.; Sharrock, P. Simulation of biomass char gasification in a downdraft reactor for syngas production. AIChE J. 2016, 62, 1079–1091. [Google Scholar] [CrossRef]
- Yucel, O.; Hastaoglu, M.A. Kinetic modeling and simulation of throated downdraft gasifier. Fuel Process. Technol. 2016, 144, 145–154. [Google Scholar] [CrossRef]
- Gordillo, E.D.; Belghit, A. A downdraft high temperature steam-only solar gasifier of biomass char: A modelling study. Biomass Bioenergy 2011, 35, 2034–2043. [Google Scholar] [CrossRef]
- Gøbel, B.; Henriksen, U.; Jensen, T.C.; Qvale, B.; Houbak, N. The development of a computer model for a fixed bed gasifier and its use for optimization and control. Bioresour. Technol. 2007, 98, 2043–2052. [Google Scholar] [CrossRef]
- Babu, B.V.; Sheth, P.N. Modeling and simulation of reduction zone of downdraft biomass gasifier: Effect of char reactivity factor. Energy Conv. Manag. 2006, 47, 2602–2611. [Google Scholar] [CrossRef]
- Tinaut, F.V.; Melgar, A.; Pérez, J.F.; Horrillo, A. Effect of biomass particle size and air superficial velocity on the gasification process in a downdraft gasifier fixed bed gasifier. An experimental and modelling study. Fuel Process. Technol. 2008, 89, 1079–1089. [Google Scholar] [CrossRef]
- Bruch, C.; Peters, B.; Nussbaumer, T. Modelling wood combustion under fixed bed conditions. Fuel 2003, 82, 729–738. [Google Scholar] [CrossRef]
- Wang, Y.; Kinoshita, C.M. Kinetic model of biomass gasification. Sol. Energy 1993, 51, 19–25. [Google Scholar] [CrossRef]
- Giltrap, D.L.; McKibbin, R.; Barnes, G.R.G. A steady state model of gas-char reactions in a downdraft biomass gasifier. Sol. Energy 2003, 74, 85–91. [Google Scholar] [CrossRef]
- Teixeira, G.; Van de Steene, L.; Ponthieux, A.; Salvador, S. Prediction of the gasification kinetics of a single wood char particle from a limited set of parameters. Fuel 2014, 123, 194–204. [Google Scholar] [CrossRef]
- Teixeira, G.; Van de Steene, L.; Salvador, S.; Gelix, F.; Dirion, J.L.; Paviet, F. Gasification of continuous wood char bed: Modelling and experimental approach. Chem. Engineer. Trans. 2014, 37, 247–252. [Google Scholar] [CrossRef]
- Carmona, O.M.; Vederza, A.; Morales, A.D.; Lenis, Y.A. Steady and transient state behavior of a gasification process under fixed-bed downdraft configuration. Heliyon 2024, 10, e34781. [Google Scholar] [CrossRef]
- Jia, J.; Xu, L.; Abudula, A.; Sun, B. Effects of operation parameters on performance of a downdraft gasifier in steady and transient state. Energy Conv. Manag. 2018, 155, 138–146. [Google Scholar] [CrossRef]
- Dernbecher, A.; Dieguez-Alonso, A.; Ortwein, A.; Tabet, F. Review on modelling approaches based on computational fluid dynamics for biomass combustion systems. Biomass Convers. Biorefin. 2019, 9, 129–182. [Google Scholar] [CrossRef]
- Bryden, K.M.; Ragland, K.W.; Rutland, C.J. Modeling thermally thick pyrolysis of wood. Biomass Bioenergy 2002, 22, 41–53. [Google Scholar] [CrossRef]
- Mehrabian, R.; Zahirovic, S.; Scharler, R.; Obernberger, I.; Kleditzsch, S.; Wirtz, S.; Scherer, V.; Lu, H.; Baxter, L.L. A CFD model for thermal conversion of thermally thick biomass particles. Fuel Process. Technol. 2012, 95, 96–108. [Google Scholar] [CrossRef]
- Peters, B. Classification of combustion regimes in a packed bed of particles based on the relevant time and length scales. Combust. Flame 1999, 116, 297–301. [Google Scholar] [CrossRef]
- Kurz, D.; Schnell, U.; Scheffknecht, G. CFD simulation of wood chip combustion on a grate using an Euler-Euler approach. Combust. Theory Model. 2012, 16, 251–273. [Google Scholar] [CrossRef]
- Miltner, M.; Miltner, A.; Harasek, M.; Friedl, A. Process simulation and CFD calculations for the development of an innovative baled biomass-fired combustion chamber. Appl. Therm. Eng. 2007, 27, 1138–1143. [Google Scholar] [CrossRef]
- Knaus, H.; Richter, S.; Unterberger, S.; Schnell, U.; Maier, H.; Hein, K.R.G. On the application of different turbulence models for the computation of fluid flow and combustion processes in small scale wood heaters. Exp. Therm. Fluid Sci. 2000, 21, 99–108. [Google Scholar] [CrossRef]
- Pandey, B.; Prajapati, Y.K.; Sheth, P.N. CFD analysis of the downdraft gasifier using species-transport and discrete phase model. Fuel 2022, 328, 125302. [Google Scholar] [CrossRef]
- Prasertcharoensuk, P.; Hernandez, D.A.; Bull, S.J.; Phan, A.N. Optimisation of a throat downdraft gasifier for hydrogen production. Biomass Bioenergy 2018, 116, 216–226. [Google Scholar] [CrossRef]
- Porteiro, J.; Collazo, J.; Patiño, D.; Granada, E.; Moran Gonzalez, J.C.; Míguez, J.L. Numerical modeling of a biomass pellet domestic boiler. Energy Fuels 2009, 23, 1067–1075. [Google Scholar] [CrossRef]
- Westbrook, C.K.; Dryer, F.L. Simplified reaction mechanisms for the oxidation of hydrocarbon fuels in flames. Combust. Sci. Technol. 1981, 27, 31–43. [Google Scholar] [CrossRef]
- Jones, W.P.; Lindstedt, R.P. Global reaction schemes for hydrocarbon combustion. Combust. Flame 1988, 73, 233–249. [Google Scholar] [CrossRef]
- Kim, S.; Shin, D.; Choi, S. Comparative evaluation of municipal solid waste incinerator designs by flow simulation. Combust. Flame 1996, 106, 241–251. [Google Scholar] [CrossRef]
- Yepes Maya, D.M.; Silva Lora, E.E.; Vieyra Andrade, R.; Ratner, A.; Martínez Angel, J.D. Biomass gasification using mixtures of air, saturated steam, and oxygen in a two-stage downdraft gasifier. Assessment using a CFD modeling approach. Renew. Energy 2021, 177, 1014–1030. [Google Scholar] [CrossRef]
- Ngamsidhiphongsa, N.; Ponpesh, P.; Shotipruk, A.; Arpornwichanop, A. Analysis of the Imbert downdraft gasifier using a species-transport CFD model including tar-cracking reactions. Energy Conv. Manag. 2020, 213, 112808. [Google Scholar] [CrossRef]
- Ngamsidhiphongsa, N.; Ghoniem, A.F.; Arpornwichanop, A. Detailed kinetic mechanism of devolatization stage and CFD modeling of downdraft gasifiers using pelletized palm oil empty fruit bunces. Renew. Energy 2021, 179, 2267–2276. [Google Scholar] [CrossRef]
- Tavares, R.; Monteiro, E.; Tabet, F.; Rouboa, A. Numerical investigation of optimum operating conditions for syngas and hydrogen production from biomass gasification using Aspen Plus. Renew. Energy 2020, 146, 1309–1314. [Google Scholar] [CrossRef]
- Kaushal, P.; Tyagi, R. Advanced simulations of biomass gasification in a fluidized bed reactor using ASPEN PLUS. Renew. Energy 2017, 101, 629–636. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, C.; Cai, L.; Long, X. Steady state modelling of steam-gasification of biomass for H2-rich syngas production. Energy 2022, 238 Part A, 121616. [Google Scholar] [CrossRef]
- Hu, Y.; Pang, K.; Cai, L.; Liu, Z. A multi-stage co-gasification system of biomass and municipal solid waste (MSW) for high quality syngas production. Energy 2021, 221, 119639. [Google Scholar] [CrossRef]
- Puig-Gamero, M.; Pio, D.T.; Tarelho, L.A.C.; Sánchez, P.; Sanchez-Silva, L. Simulation of biomass gasification in bubbling fluidized bed reactor using aspen plus®. Energy Conv. Manag. 2021, 235, 113981. [Google Scholar] [CrossRef]
- Tungalag, A.; Lee, B.; Yadav, M.; Akande, O. Yield prediction of MSW gasification including minor species through ASPEN plus simulation. Energy 2020, 198, 117296. [Google Scholar] [CrossRef]
- Han, J.; Liang, Y.; Hu, J.; Qin, L.; Street, J.; Lu, Y.; Yu, F. Modeling downdraft biomass gasification process by restricting chemical reaction equilibrium with Aspen Plus. Energy Conv. Manag. 2017, 153, 641–648. [Google Scholar] [CrossRef]
- Pala, L.P.R.; Wang, Q.; Kolb, G.; Hessel, V. Steam gasification of biomass with subsequent syngas adjustment using shift reaction for syngas production: An Aspen Plus model. Renew. Energy 2017, 101, 484–492. [Google Scholar] [CrossRef]
- Vikram, S.; Rosha, P.; Kumar, S.; Mahajani, S. Thermodynamic analysis and parametric optimization of steam-CO2 based biomass gasification system using Aspen PLUS. Energy 2022, 241, 122854. [Google Scholar] [CrossRef]
- Chaiwatanodom, P.; Vivanpatarakij, S.; Assabumrungrat, S. Thermodynamic analysis of biomass gasification with CO2 recycle for synthesis gas production. Appl. Energy 2014, 114, 10–17. [Google Scholar] [CrossRef]
- Adnan, M.A.; Susanto, H.; Binous, H.; Muraza, O.; Hossain, M.M. Feed compositions and gasification potential of several biomasses including a microalgae: A thermodynamic modeling approach. Int. J. Hydrogren Energy 2017, 42, 17009–17019. [Google Scholar] [CrossRef]
- Ajorloo, M.; Ghodrat, M.; Scott, J.; Strezov, V. Recent advances in thermodynamic analysis of biomass gasification: A review on numerical modelling and simulation. J. Energy Inst. 2022, 102, 395–419. [Google Scholar] [CrossRef]
- Oladokun, O.; Nyakuma, B.; Luing, W.S.; Oladimeji, E.; Abatan, O.; Ayeni, A.O.; Agboola, O.; Ayoola, A.A.; Ojewunmi, M.O.; Efeovbokhan, V.E.; et al. Gasific: A Python tool for biomass gasification process. In Advanced Manufacturing in Biological, Petroleum, and Nanotechnology Processing; Ayeni, A.O., Oladokun, O., Orodu, O.D., Eds.; Springer: Chambersburg, PA, USA, 2022; pp. 335–353. [Google Scholar] [CrossRef]
- Available online: https://www.openfoam.com/documentation/user-guide (accessed on 29 May 2025).
- Yan, B.; Zhao, S.; Li, J.; Chen, G.; Tao, J. A conceptual framework for biomass gasifier design using a semi-empirical model and heuristic algorithm. Chem. Eng. J. 2022, 427, 130881. [Google Scholar] [CrossRef]



| Reaction Type | Reaction Example | Enthalpy of Reaction, MJ kmol−1 |
|---|---|---|
| Homogeneous reactions | ||
| Hydrogen oxidation | H2 + ½ O2 → H2O | −242 |
| CO oxidation | CO + ½ O2 → CO2 | −283 |
| Steam methane reforming | CH4 + H2O ↔ CO + 3H2 | 206 |
| Water–gas shift | CO + H2O ↔ H2 + CO2 | −41 |
| Combustion | C + O2 → CO2 | −394 |
| Partial combustion | C + ½O2 → CO | −111 |
| Methanation | CO + 3H2 ↔ CH4 + H2O | −227 |
| Heterogeneous reactions | ||
| Water–gas | C + H2O ↔ H2 + CO | 131 |
| Boudouard | C + CO2 ↔ 2CO | 172 |
| Hydrogasification | C + 2H2 ↔ CH4 | −75 |
| Biomass Type | Hemicellulose, wt% | Cellulose, wt% | Lignin, wt% | Others, wt% | Reference |
|---|---|---|---|---|---|
| Black locust wood | 16.40 | 34.20 | 25.80 | 23.60 | [35] |
| Corn straw | 29.72 ± 0.83 | 34.03 ± 1.27 | 22.00 ± 0.58 | 14.25 ± 0.37 | [36] |
| Pine bark | 18.30 (22.62) a | 21.90 (27.07) a | 40.70 (50.31) a | 18.00 | [37] |
| Poplar | 21.70 (23.77) a | 42.70 (46.77) a | 26.90 (29.46) a | 7.20 | [37] |
| Rape straw | 16.90 | 27.90 | 21.1 | 34.10 | [35] |
| Spruce bark | 13.90 (15.67) a | 29.70 (33.48) a | 45.10 (50.84) a | 10.12 | [37] |
| Walnut shell | 19.29 ± 0.76 | 18.32 ± 0.65 | 41.50 ± 1.35 | 20.89 ± 0.63 | [36] |
| Wheat straw | 23.80 (29.10) a | 37.50 (45.84) a | 20.50 (25.06) a | [37] | |
| Wheat straw | 22.90 | 33.90 | 19.10 | 24.10 | [35] |
| Willow | 22.60 (24.57) a | 44.30 (48.15) a | 25.10 (27.28) a | 10.30 | [37] |
| Bamboo | 17.23 ± 0.43 | 44.45 ± 0.07 | 18.53 ± 0.32 | [38] | |
| Pine sawdust | 19.0 | 59.0 | 22.0 | [39] | |
| Wheat straw | 45.0 | 22.0 | 33.0 | [39] |
| Source | Proximate Analysis, wt% | Ultimate Analysis, wt% | Ref. | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Moisture | Volatiles | Fixed Carbon | Ash | C | H | N | O | S | LHV, (MJ kg−1) | ||
| Alfalfa stem | 78.92 | 15.81 | 5.27 | 47.17 | 5.99 | 2.68 | 38.19 | 0.20 | 16.8 | [45] | |
| Almond hulls | 73.80 | 20.07 | 6.13 | 47.53 | 5.97 | 1.13 | 39.16 | 0.06 | 17.0 | [45] | |
| Bamboo wood | 11.50 a | 86.80 | 11.24 | 1.95 | 48.76 | 6.32 | 0.20 | 42.77 | 18.5 | [44] | |
| Coconut shell | 8.20 a | 77.19 | 22.10 | 0.71 | 50.22 | 5.64 | 0.41 | 42.94 | 18.0 | [44] | |
| Coffee husk | 78.50 | 19.10 | 2.40 | 47.50 | 6.40 | 43.70 | 17.8 | [46] | |||
| Corn cobs | 10.1 a | 80.06 | 17.82 | 2.12 | 47.60 | 6.10 | 0.52 | 45.78 | 17.1 | [47] | |
| Corn stover | 66.58 | 26.65 | 6.73 | 45.48 | 5.52 | 0.69 | 41.52 | 0.04 | 16.2 | [48] | |
| Cotton stalk | 76.10 | 18.80 | 5.10 | 47.07 | 4.58 | 1.15 | 42.10 | 15.7 | [49] | ||
| Douglas fir bark | 56.2 | 5.9 | 36.7 | 19.9 | [50] | ||||||
| Empty fruits bunch | 5.5 | 69.0 | 18.5 | 7.0 | 42.33 | 5.28 | 1.46 | 50.84 | 0.08 | 14.0 | [51] |
| Eucalyptus wood | 16.40 a | 75.35 | 21.30 | 3.35 | 46.04 | 5.82 | 0.30 | 44.49 | 16.8 | [44] | |
| Hazelnut shell | 68.90 | 30.00 | 1.10 | 50.90 | 5.90 | 0.40 | 42.80 | 17.9 | [52] | ||
| Larch sawdust | 2.6 | 76.7 | 19.9 | 0.8 | 48.5 | 6.4 | 0.1 | 44.7 | 0.3 | 17.9 | [53] |
| Mango wood (Mangifera indica) | 82.30 | 16.34 | 1.36 | 50.18 | 6.35 | 0.13 | 43.34 | 17.2 | [54] | ||
| Mangrove | 5.3 | 36.26 | 56.4 | 2.04 | 66.46 | 4.37 | 0.03 | 29.14 | 22.8 | [55] | |
| Maritime pinewood (wood stem) b | 85.7 | 14.0 | 0.22 | 45.60 | 6.70 | 0.13 | 46.40 | 0.03 | 19.5 | [56] | |
| Microalgae (Nannochloropsis oculata) | 6.71 | 78.94 | 7.95 | 6.4 | 47.50 | 6.15 | 46.35 | 13.6 | [57] | ||
| Neem wood (Azadirachta indica) | 82.35 | 16.35 | 1.35 | 50.20 | 6.38 | 0.14 | 43.28 | 18.5 | [54] | ||
| Peanut shell | 84.90 | 13.40 | 1.70 | 47.40 | 6.10 | 2.10 | 44.40 | 16.8 | [52] | ||
| Pine sawdust (Pinus elliotti) | 10.66 | 73.74 | 15.30 | 0.30 | 50.91 | 6.13 | 0.23 | 42.14 | 18.1 | [58] | |
| Pinewood pellet | 10.8 | 69.8 | 18.3 | 1.1 | 49.8 | 6.03 | 0.21 | 42.86 | [59] | ||
| Rice husk | 9.95 | 55.54 | 14.99 | 19.52 | 49.07 | 3.79 | 0.63 | 46.42 | 0.09 | [60] | |
| Rice husk | 3.6 | 60.0 | 20.1 | 16.3 | 38.5 | 5.5 | 0.4 | 36.6 | 0.2 | 14.9 | [53] |
| Rice husk | 9.5 | 67.6 | 6.3 | 16.6 | 49.2 | 2.2 | 0.44 | 48.02 | 0.06 | 13.2 | [61] |
| Rice husk pellet | 9.2 | 65.1 | 16.4 | 9.30 | 46.60 | 6.20 | 0.70 | 37.40 | 0.10 | 15.6 | [53] |
| Rice straw | 65.47 | 15.83 | 18.67 | 38.24 | 5.20 | 0.87 | 36.26 | 0.18 | 13.6 | [45] | |
| Rubber wood | 80.1 | 19.2 | 0.7 | 50.6 | 6.5 | 0.2 | 42.0 | 17.7 | [19] | ||
| Sawdust pellets | 9.50 | 80.63 | 17.27 | 2.10 | 48.91 | 5.80 | 0.18 | 45.11 | 18.4 | [62] | |
| Sewage sludge | 6.48 | 50.09 | 4.39 | 39.04 | 29.50 | 4.67 | 5.27 | 20.21 | 1.31 | 11.5 | [63] |
| Sewage sludge | 13.25 | 45.50 | 10.65 | 30.60 | 21.56 | 4.11 | 2.89 | 21.43 | 1.81 | [64] | |
| Soya residue | 3.44 | 43.59 | 5.60 | 0.35 | 50.46 | 19.6 | [65] | ||||
| Sugarcane bagasse | 51.01 a | 83.66 | 13.15 | 3.20 | 45.48 | 5.96 | 45.21 | 0.15 | 16.9 | [44] | |
| Sunflower residue | 9.6 | 42.60 | 5.47 | 0.19 | 51.74 | 20.3 | [65] | ||||
| Switch grass | 76.69 | 14.34 | 8.97 | 46.68 | 5.82 | 0.77 | 37.38 | 0.19 | 16.3 | [45] | |
| Tunisian olive pomace | 23.45 | 75.28 c | 1.27 | 53.60 | 6.93 | 1.48 | 37.98 | 21.3 | [66] | ||
| Vine pruning | 17.6 a | 80.84 | 16.54 | 2.62 | 50.84 | 5.82 | 0.88 | 42.46 | 18.2 | [47] | |
| Wheat straw | 8.87 a | 82.12 | 10.98 | 6.90 | 42.95 | 5.35 | 46.99 | 16.2 | [44] | ||
| Reactor Characteristics | Commonly Used Feedstock | Particle Size, mm | Moisture Content (Wet Basis), wt% | |
|---|---|---|---|---|
| Fixed bed | ||||
| Updraft | The fuel is preheated, resulting in high efficiency. This gasifier requires a high flame temperature. The producer gas may contain some dust and impurities. | Chipped wood, dried sewage sludge, rice husks [3] | 6–100 [3] | <20 [3] |
| Downdraft | The producer gas reaches high temperatures, resulting in a reduced quantity of tars produced. | Wood chips, nut shells, pellets [3] | Up to 50 [3] | <15 [3] |
| Cross-draft | The temperature in the combustion zone exceeds 1500 °C. This gasifier is primarily used for processing charcoal. | Briquettes (eucalyptus, bamboo, etc.) [79] | Variable | <15 [79] |
| Fluidized bed | ||||
| Stationary fluidized bed | During fast pyrolysis, silica sand or olivine is used as bed material. Increasing the head space can reduce the amount of tar produced. Ash and char can be separated from the producer gas by a cyclone. | Bagasse, low alkali content fuels, mostly wood residues with high moisture content [3] | Up to 50 [3] | <60 [3] |
| Circulating fluidized bed | The producer gas is separated from the bed material and ash through a cyclone and returned to the gasifier. The gasifier can be scaled up due to the increased cross-sectional area. | Wood and chipped agricultural residues [3] | 6–50 [3] | 15–50 [3] |
| Circulating fluidized two-bed | Gasification takes place in one fluidized bed, while the bed material is circulated to the second bed and then to the gasification reactor. | Wood and chipped agricultural residues [3] | 6–50 [3] | 15–50 [3] |
| Entrained flow | ||||
| Entrained flow | Gasification occurs quickly with a low amount of tar. It is possible to operate at high temperatures (up to 1200 °C) and pressures (up to 100 bar). Biomass with a low ash melting point can be used as feed. Design requires materials that can withstand harsh operating conditions. | Coal and pet coke finely pulverized [80]. The adaptation of the entrained flow gasifier to biomass is still under development | Distinct values on micrometers scale [81] | |
| Reaction | −ΔH01173 a, kJ mol−1 |
|---|---|
| −876 b | |
| −123 c | |
| 713 | |
| 104 c | |
| −1105 b | |
| 73 | |
| Ref. | Catalyst and Composition | Main Results/Observations |
|---|---|---|
| [138] | La0.8Sr0.2Ni0.8Fe0.2O3 Preparation method: Sol-gel synthesis | Bamboo sawdust was used as feed. Pyrolysis of biomass was conducted at 700 °C using approximately 0.6 g of catalyst. The syngas yield was 475 (mL g−1), and the total gas yield was 606.7 (mL g−1) |
| [140] | NiFe-NiFe2O4/char Preparation method: in situ carbothermal reduction of Ni/Fe metal chloride impregnated sawdust. Ni: 0.42 wt%; Fe: 0.11 wt%; C: 89.20 wt%; O: 10.27 wt% | Tar conversion: 92.54% and 81.8% after three cycles of reuse (at T = 600 °C). |
| [144] | Co0.15-C2H3O2− Preparation method: Ion exchange method Co: 16 wt% | Tar model: toluene. Toluene conversion: 20.6% and 15.6% after 100 h of time on stream (0.1 g of catalyst at T = 400 °C, GHSV = 12,000 (mL h−1 g−1), and steam–to–carbon ratio = 0.68). |
| [145] | CoNi supported on monolithic biochar. Preparation method: Impregnation and carbonization. Co: 2.4 wt%; Ni: 2.49 wt%; C: 93.92 wt%; O: 1.19 wt% | Pyrolysis and cracking of pinewood at 600 °C and 700 °C, respectively, carried out in a two-stage fixed bed reactor. Tar conversion: 91% (after five cycles of reuse). |
| [136] | Ni-Fe/MgAl2O4 Preparation method: Successive wet impregnation. Ni: 2–10 wt%; Fe: 30 wt%; Mg: 10 wt% | Biomass gasification carried out with 200 mg of catalyst, volume ratio of CO2 (15%):H2 (0–60%):CH4 (0–15%), WHSV of 30 (L g−1 h−1), temperature between 400 and 700 °C. |
| [137] | La0.8Ce0.2FeO3/dolomite Preparation method: Sol-gel synthesis La0.8Ce0.2FeO3 represents the 10 wt% of the dolomite mass | Biomass gasification carried out with 8 g of pine wood and 4 g of catalyst at 850 °C. |
| [143] | CoFe/α-Al2O3 Preparation method: Co-impregnation Co: 12 wt%; Fe/Co molar ratio: 0.25 | Tar model: toluene. H2/CO ratio of 4.6 (for steam reforming of toluene). Toluene conversion: 62.7% [H2 flow of 3.8 (mmol min−1)]. |
| [141] | Precious metal (Rh, Pd, Ir, Ru, Pt) and Ni over modified ZrO2 Preparation method: Incipient wetness Rh, Pd, Ir, Ru, or Pt: 0.5 wt%; Ni: 8 wt% | Tar model: toluene/naphthalene (90/10). Tar conversion: ~95% (with Rh and Ni catalysts above 850 °C). Ammonia conversion: 75% with Ni catalysts. |
| [136] | Ni/CeO2/α-Al2O3 Preparation method: Co-impregnation Ni: 4 wt%; CeO2: 30 wt% | Tar model: cedar wood gasified. H2/CO ratio of 2.8 (for cedar wood steam gasification), low tar and coke amounts. |
| [120] | Ni/α–Al2O3 Preparation method: Impregnation Ni: 13.3 wt% | Tar model: toluene. Toluene conversion: ~100% (at P = 2 MPa and T = 900 °C). |
| Feedstock | Production Cost | Transport Cost | Total Costs |
|---|---|---|---|
| Wood chips from local energy crops (Europe) | 60–94 (88–139) | 60–94 (88–139) | |
| Wood chips (Brazil) | 71 (106) | ||
| Wood chips from forest residues (Scandinavian) transported to continental Europe | 64–77 (94–113) | 34–38 (50–56) | 98–115 (144–170) |
| Local agricultural residues (Europe) | 55–68 (81–100) | 55–68 (81–100) | |
| Pellets transported from USA to Europe | 100–119 (147–175) | 56–63 (83–93) | 157–182 (231–268) |
| Bagasse | Brazil: 11–13 (16–19) India: 12–14 (17–20) | Brazil: 11–13 (16–19) India: 12–14 (14–20) | |
| Charcoal mill (Brazil) | 95 (142) | 95 (142) | |
| Rice husk (India) | 22–30 (31–43) | 22–30 (31–43) |
| Owner | Location | Startup | Feedstock | Output | Contact |
|---|---|---|---|---|---|
| Azienda Agricola San Vittore | Vigevano, Italy | Wood chips | 0.5 MWel 0.4 MWth | ||
| Azienda Tenca dei Fratelli Zanotti/AB energy | Orzinuovi, Italy | 2009 | Forestry waste | 0.3 MWel | Available upon request |
| Ciamber | Forno di Zoldo, Italy | Lignocellulosics | 1.0 MWel 0.8 MWth | ||
| Comune Quingentole | Quingentole, Italy | 2006 | Wood chips | 0.07 MWel 0.14 MWth | www.comune.quingentole.mn.it (accessed on 29 May 2025) |
| Duchi Fratelli Societa Agricola/Agroenergia | Gadesco Pieve Delmona, Italy | 2010 | Wood chips | 0.96 MWel 3.2 MWth | |
| Glock Energie GmbH | Griffen, Austria | 2019 | Wood chips | 0.30 MWel 0.66 MWth | Available upon request |
| GRESCO Power Solution GmbH | Bad Wildungen, Germany | 2014 | Wood chips | 0.3 MWel 0.5 MWth | Available upon request |
| H.H. Kaeser GmbH | Gasel, Switzerland | 2015 | Wood chips | 0.14 MWel 0.24 MWth Investment including CHP gasifier unit, connection to heating device and power | Available upon request |
| Hotel Haffhus | Ueckermuende, Germany | 2018 | Wood chips (ISO 17225-4 A1 P16S-P31S) | 0.018 MWel 0.044 MWth | www.glock-oeko.com (accessed on 29 May 2025) |
| HS Energieanlagen GmbH | Neufahrn bei Freising, Germany | Waste wood Clean wood | 0.11 MWel 0.25 MWth | ||
| Josef Bucher AG Escholzmatt | Escholzmat, Switzerland | 2015 | Wood chips | 0.13 MWel 0.26 MWth | Available upon request |
| Ligento Nuernberg | Nürnberg, Germany | Wood chips | 0.14 MWel 0.24 MWth | Available upon request | |
| Nurmes | Nurmes, Finland | 2012 | Wood chips | 0.04 MWel 0.10 MWth | https://www.efarm.fi/kohteet/e-farm-kuittilan-tila-nurmes/ (accessed on 29 May 2025) |
| Qalovis Altenberge | Altenberge, Germany | 2012 | Wood pellets | 0.036 MWel 0.12 MWth | Available upon request |
| Spanner Bamberg | Landkreis Bamberg, Germany | 2011 | Wood pellets Wood chips | 0.045 MWel 0.120 MWth | |
| Spanner Landshut | Landkreis Landshut, Germany | 2011 | Wood chips | 0.025 MWel 0.500 MWth | Available upon request |
| Special Purpose Vehicule (MGGE) | Mont-Godinne, Belgium | 2018 | Clean wood chips Recycled wood | 0.75 MWel 1.20 MWth | https://xylowatt.com/ (accessed on 29 May 2025) |
| Steiner A. & Cie AG | Ettiswill, Switzerland | 2013 | Wood chips | 0.045 MWel 0.105 MWth | Available upon request |
| Wegscheid Aschaffenburg | Landkreis Aschaffenburg, Germany | 2011 | Wood pellets Wood chips | 0.12 MWel 0.23 MWth | Available upon request |
| Wegscheid Bamberg | Bamberg, Germany | 2011 | Wood pellets Wood chips | 0.12 MWel 0.23 MWth | Available upon request |
| Wegscheid Bayreuth | Bayreuth, Germany | Wood pellets Wood chips | 0.125 MWel | Available upon request | |
| Wegscheid Passau | Landkreis Passau, Germany | 2009 | Wood pellets Wood chips | 0.12 MWel 0.23 MWth | Available upon request |
| WUN Bioenergy | Schönbrunn, Germany | 2012 | Wood pellets Wood chips | 0.36 MWel 0.54 MWth | Available upon request |
| Owner | Locality | Status | Input | Output | Use |
|---|---|---|---|---|---|
| Charwood Energy + consortium | Cognac, France | Planed (TRL 9) | Lignocellulosics | Clean syngas | Direct use in furnace |
| Wegscheid Demo | Wegscheid, Germany | Operational (TRL 6-7) | Wood pellets Wood chips | 0.125 MWel 0.23 MWth | CHP |
| Year | CapEx, USD/Year | OpEx, USD/Year | Syngas Production Cost a, USD/Nm3 | Lifetime, Years | Main Application or Product | Reference |
|---|---|---|---|---|---|---|
| 2025 | 7035.86 | 52,254.06 | 0.13 | 10 | Syngas | [182] |
| 2024 | 14,185.14 | 10 | ICE | [183] | ||
| 2022 | 1396.30 | 3401.00 | 0.35 | 10 | Syngas | [184] |
| 2022 | 21,214.16 | 15 | CHP | [185] | ||
| 2022 | 21,121.00 | ICE | [186] | |||
| 2020 | 6975.13 | 158,305.00 | 20 | ICE | [177] | |
| 2017 | 21,317.81 | 20 | CHP | [187] | ||
| 2012 | 72,485.00 | 187,704.03 | 20 | ICE | [188] | |
| 2012 | 47,554.30 | 67,845.44 | ICE | [189] | ||
| 2009 | 0.82 | 20 | Syngas | [190] | ||
| 2008 | 178,212.00 | 1.82 | 20 | Syngas | [191] |
| Year | NPV, USD | PBP, Years | IRR, % | Reference |
|---|---|---|---|---|
| 2025 | 21,861.71 | 4.1 | 17.85 | [182] |
| 2025 | 28,399.35 | 12.09 | 14.00 | [192] |
| 2024 | 76,329.34 | 5.14 | 24.07 | [183] |
| 2022 | 53,586.30 | 6.0 | 9.72 | [193] |
| 2020 | 104,884.28 | 7.7 | 10.90 | [177] |
| 2020 | 49,123.80 a | 9.2 | 19.34 | [194] |
| 2020 | 121,032.49 | 6.91 | 16.63 | [195] |
| 2015 | 126,427.21 b | 6.01 | 18.15 | [196] |
| 2015 | 60,421.01 | 3.0 | 23.00 | [197] |
| 2009 | 130,794.37 | 2.92 | [198] |
| Country | Documents | Citations | Ratio Citations/Document |
|---|---|---|---|
| China | 332 | 10,357 | 31.2 |
| United States | 261 | 7321 | 28.0 |
| Italy | 214 | 5853 | 27.4 |
| India | 191 | 7197 | 37.7 |
| United Kingdom | 136 | 5780 | 42.5 |
| Germany | 122 | 4144 | 34.0 |
| Canada | 115 | 4658 | 40.5 |
| Sweden | 115 | 4149 | 36.1 |
| Spain | 111 | 4467 | 40.2 |
| France | 100 | 2874 | 28.7 |
| Ref. | Considerations | Main Reactions and Equations |
|---|---|---|
| [64] | Model type: stoichiometric equilibrium model for sewage sludge in a downdraft gasifier. Biomass source: Sewage sludge Tar is formed by C2H2, C2H4, C2H6, C6H6. Main results: chemical composition of gas. Yield of producer gas, carbon conversion efficiency, and cold gas efficiency. | CcHhOoNnSs + wH2O(l) + qH2O(g) + m(O2 + 3.76N2) → x1H2 + x2CO + x3CO2 + x4CH4 + x5H2O(g) + x6H2S + x7C2H2 + x8C2H4 + x9C2H6 + x10C6H6 + c(1 − α)C + x11N2 Tar in wt% is given by: Mass balance equations: x2 + x3 + x4 + 2x7 + 2x8 + 2x9 + 6x10 + c(1 − α) − c = 0 2x1 + 4x4 + 2x5 + 2x6 + 2x7 + 4x8 + 6x9 + 6x10 − h − 2w − 2q = 0 x2 + 2x3 + x5 − o − 2m − w − q = 0 2x11 − n − 2 × 3.76m = 0 x6 − s = 0 x1 + x2 + x3 + x4 + x5 + x6 + xtar + x11 = 1 Equilibrium reactions: (r1) C + CO2 ↔ 2CO (r2) C + H2O ↔ CO + H2 (r3) CO + H2O ↔ CO2 + H2 with equilibrium constant as (r4) C + 2H2 ↔ CH4 with equilibrium constant as (r5) S + H2 ↔ H2S |
| [206] | Model type: stoichiometric equilibrium model in the reduction zone of a downdraft gasifier. Biomass source: Several sources, such as rubber wood, wood pellets and chips, rice husk, bamboo, etc. Tar is represented by C6H6.2O0.2 and C. Main results: chemical composition of syngas, tar, and char yields, gasification temperature, cold gas efficiency, and lower heating value. | Global reaction: CHhOoNnSs + wH2O + a(O2 + 3.76N2) → x1H2 + x2CO + x3CO2 + x4CH4 + x5N2 + x6NH3 + x7H2S + x8H2O + x9C6H6.2O0.2 + x10C where: , , , , , with , and Mass balance equations: x2 + x3 + x4 + 6x9 + x10 = 1 2x1 + 4x4 + 3x6 + 2x7 + 2x8 + 6.2x9 = h + 2w x2 + 2x3 + x8 + 0.2x9 = o + w + 2a 2x5 + x6 = n + 7.52a X7 = s Equilibrium reactions: (r1) C + 2H2 ↔ CH4 with equilibrium constant as (r2) CO + H2O ↔ CO2 + H2 with equilibrium constant as (r3) C + CO2 ↔ 2CO with equilibrium constant as (r4) N2 + 3H2 ↔ 2NH3 with equilibrium constant as |
| [207] | Model type: stoichiometric model in a downdraft gasifier. Biomass source: Japanese cedar considered as CH1.49O0.73. Main results: effects of steam–to–biomass ratios and the temperature. | Reactions: (r1) CH1.49O0.73 → 0.34C + 0.75CH1.79O0.77 (r2) 0.75 CH1.79O0.77 → 0.099CO + 0.077CO2 + 0.08H2 +0.004CH4 + 0.3931CH1.43O0.53 + 0.26H2O (r3) CH1.43O0.53 → 0.526CO + 0.0987CO2 + 0.18CH4 + 0.08H2 + 0.248CH1.43O0.53 Equilibrium reactions: (r4) C + CO2 ↔ 2CO with equilibrium constant (r5) C + H2O ↔ CO + H2 with equilibrium constant (r6) CO + H2O ↔ CO2 + H2 with equilibrium constant |
| [201] | Model type: zero–dimensional thermodynamic equilibrium model in a downdraft gasification Biomass type: corn cob, pine bark, rubber wood, almond shell, wood pellets and chips, and sawdust. Tar content was limited to 6 g Nm3. Main results: Sensitivity analysis for gasification temperature, equivalence ratio, air preheating, amount of steam, oxygen enrichment degree, etc. | For pyrolysis reactions, the equations for products after drying are: With: For gasification reactions, the equations for products after pyrolysis are: Equilibrium constant for the water–gas shift reaction is: Equilibrium constant for the methanation reaction is: Equilibrium constant for the methane steam reforming reaction is: |
| [200] | Model type: global stoichiometric equilibrium for a downdraft gasifier. Biomass type: rubber wood and pellets Tar is considered as C6H6O0.2 with thermochemical properties as benzene. Char is considered as carbon with thermochemical properties as graphite. Main results: chemical composition of producer gas, lower heating value, and equilibrium temperature. | Global reaction: CHhOoNn + wH2O + m(O2 + 3.76N2) → x1H2 + x2CO + x3CO2 + x4H2O + x5CH4 + x6N2 + xtartar + xcharchar Independent equilibrium reactions: (r1) C + 2H2 ↔ CH4 with equilibrium constant as: and nt is total number of moles (r2) CO + H2O ↔ CO2 + H2 with equilibrium constant as: Mass balance equations: x2 + x3 + x5 + 6xtar + xchar = 1 2x1 + 2x4 + 4x5 + 6xtar = h + 2w x2 + 2x3 + x4 + 0.2xtar = o + w + 2m |
| [205] | Model type: equilibrium and kinetic models under isothermal and non-isothermal behavior for reduction zone in a downdraft gasifier Biomass type: bagasse, wood sawdust, Douglas fir bark, peanut hull, and rice husk Main results: chemical composition of producer gas | Global reaction: CHhOo + wH2O + yO2+ zN2 → x1C + x2H2 + x3CO + x4H2O + x5CO2 + x6CH4 + x7N2 Initial conditions: x7 = z x1 + x3 + x5 + x6 = 1 2x2 + 2x4 + 4x6 = h + 2w x3 + x4 + x5 = o + 2y + w Equilibrium constants calculated through Gibbs function as: Kinetic model: (r1) C + CO2 ↔ 2CO with (r2) C + H2O ↔ CO + H2 with (r3) C + 2H2 ↔ CH4 with (r4) CH4 + H2O ↔ CO + 3H2 with (r5) CO + H2O ↔ CO2 + H2 with With equilibrium constants as in [50] |
| [202] | Model type: global stoichiometric equilibrium for a downdraft gasifier. Biomass type: corn and sunflower stalks, rapeseed straw. Char is considered as carbon, and the factor α is the carbon fraction in equilibrium. Main results: chemical composition of producer gas, lower heating value, equilibrium temperature, and cold gas efficiency. | Global reaction: CHhOo + wH2O(l) + qH2O(g) + m(O2 + δN2) → x1H2 + x2CO + x3CO2 + x4H2O + x5CH4 + 3.76δN2 + (1 − α)C(s) (r1) C + 2H2 ↔ CH4 with equilibrium constant as: (r2) CO + H2O ↔ CO2 + H2 with equilibrium constant as: Mass balance equations: x2 + x3 + x5 = α 2x1 + 2x4 + 4x5 = h + 2(w + q) x2 + 2x3 + x4 = o + 2m + w + q Energy balance equation: |
| [203] | Model type: thermodynamic equilibrium model. Biomass type: rubber wood, sawdust, and biomass solid waste Char may be considered or not in model. Main results: chemical composition of producer gas | Global reaction: CHhOoNnSs + wH2O(l) + mO2 +gN2 → x1H2 + x2CO + x3CH4 + x4CO2 + x5H2O(g) + (n/2 + g)N2 + x6C(s) + sH2S (r1) CH4 + H2O ↔ CO +3H2 with equilibrium constant as: (r2) CO + H2O ↔ CO2 + H2 with equilibrium constant as: (r3) C(s) + H2O ↔ CO + H2 with equilibrium constant as: x2 + x3 + x4 = 1 (if char is not considered, i.e., x6 = 0) x2 + x3 + x4 + x6 = 1 (if char is considered) 2x1 + 4x3 + 2x5 + 2s = h + 2w o + w + 2m = x2 + 2x4 + x5 Equilibrium constants for modified model: where β1 is determined by fixing CH4 fraction in dry gas at its average value of experimental data where β2 is determined by fixing CO fraction in dry gas at its average value of experimental data |
| [50] | Model type: equilibrium model of global reduction reactions for a downdraft gasifier. Biomass source: Douglas fir bark Main results: chemical composition of dry gas. Parametric studies on moisture content, pressure, equivalence ratio, and initial reaction temperature in reduction zone affecting the dry gas composition and temperature, heating value, unconverted char, gasification efficiency, and absorbed heat in reduction zone. | Global reaction: C6HhOoNnSs + H2O + O2+ 3.76N2 → CO + CO2 + H2 + H2O + CH4 + C + N2 + SO2 Kinetic model (r1) CO + H2O ↔ CO2 + H2 (r2) CH4 + H2O ↔ CO + 3H2 (r3) C + CO2 ↔ 2CO (r4) C + H2O ↔ CO + H2 (r5) C + 2H2 ↔ CH4 Approximations: Mass balance where i = CO, CO2, H2, H2O, CH4, C, N2, SO2 and j = 1,2,3…rn Heat of absorption in reduction zone |
| [204] | Model type: equilibrium and kinetic model for reduction zone in a downdraft gasifier Biomass source: rubber wood where z (in mm) is the downward distance traveled by the particle Main results: chemical composition of dry gas, temperature and calorific value of producer gas, conversion efficiency, absorbed heat in reduction zone, and gasifier power output | Global reaction: C6HhOo + H2O + O2+ 3.76N2 → CO + CO2 + H2 + H2O + CH4 + C(char) + N2 Kinetic model (r1) C + CO2 ↔ 2CO with and (r2) C + 2H2O ↔ CO + H2 with and (r3) C + 2H2 ↔ CH4 with and (r4) CH4 + H2O ↔ CO + 3H2 with and |
| Ref. | Considerations | Main Reactions and Equations |
|---|---|---|
| [60] | Model type: non-stoichiometric equilibrium model for a downdraft gasifier Biomass source: rice husk Main results: Gas lower heating value and gasification efficiency, and chemical composition of producer gas. Maximum gasification efficiency is 58.57% at 725 °C and equivalence ratio of 0.25 with LHV | Assumptions: Equivalence ratios of 0.25, 0.35, and 0.45 Gas lower heating value in (kJ Nm−3): where CO, H2, and CH4 are in mol% Rice husk lower heating value in (kJ kg−1): where C, H, O, N, S are in wt% Gasification efficiency (%): where Y is in (Nm3 kg−1) Reactions involved: (r1) C + H2O → CO + H2 (r2) CO + H2O → CO2 + H2 (r3) C + CO2 → 2CO |
| [66] | Model type: non-stoichiometric equilibrium model Biomass source: Tunisian olive pomace Main results: sensitivity analysis of temperature, pressure, and steam/biomass molar ratio in the feed was studied and their influence on gas composition, syngas yield, syngas quality (H2/CO), and carbon conversion | Assumptions: Tar is not considered to be formed Char is only formed by carbon Volatile products are H2, CO, CO2, CH4, H2O, N2, NO, NO2 Biomass gasification proceeds as: CcHhOoNn + wH2O → x1CH4 + x2H2 + x3H2O + x4CO + x5CO2 + x6NO + x7NO2 +x8N2 + x9C with: c = x1 + x4 + x5 + x9 h + 2w = 4x1 + 2x2 + 2x3 o + w = x3 + x4 + 2x5 + x6 + 2x7 n = x6 + x7 + 2x8 Subject to the elemental conservation constraints per one mole of: |
| [209] | Model type: non-stoichiometric equilibrium model Biomass source: forest waste considered as CH1.4O0.85N0.02S0.00004 Main results: Chemical composition of syngas considering the ammonia and hydrogen sulfide contents. | Biomass gasification proceeds as: CHhOoNnSs + wH2O(l) + qH2O(g) + m(O2 + δN2) → x1CO + x2CO2 + x3O2 + x4CH4 + x5H2 +x6H2O + x7N2 + x8NO + x9NO2 + x10NH3 + x11HCN +x12H2S + x13SO2 + x14SO3 + x15COS + (1 − α)C Subject to the elemental conservation constraints: |
| [210] | Model type: non-stoichiometric model for a downdraft gasifier Biomass source: olive wood, Miscanthus, and cardoon, and olive wood had the best performance Main results: chemical composition of producer gas, lower heating value | Assumptions: Low tar amount is produced Pressure drop is negligible Gas behavior is ideal Carbon is converted into gas Equivalence ratio of 0.45 Heating values are calculated as: where C, H, S, O, N, and Ash content is in (wt%) |
| [208] | Model type: non-stoichiometric equilibrium model Biomass source: rice husk and bamboo and saw dusts Main results: Optimum parameters for Fischer–Tropsch synthesis decentralized power generation were reported | Assumptions: Gas behavior is ideal Equivalence ratios: 0 to 1.0 Temperatures: 400 to 1000 °C Saw dust formula as: CH1.193N0.007O0.585 Rice husk formula as: CH1.699N0.003O0.828 Bamboo dust formula as: CH1.657N0.018O0.904 Higher heating value in (MJ kg−1): where C, H, O, N, S, and Ash are in (wt%) on dry basis |
| Reference and Assumptions | Kinetics | Reactor Model |
|---|---|---|
| [212] Biomass: wood pellets (C6H9O4), with char as CH0.26O0.09 and tar as CH1.88O0.7. Reactor model: One-dimension discretization of transient downdraft gasifier. Main results: CO and CO2 composition at different temperatures (700–850 °C), char conversion, and parametric study at steady state conditions to obtain the temperature profiles, gas and tar yields, and conversion of char at different bed heights and air-to-fuel ratios. | (r1) mbm → wcmbm + wg1mbm + wtmbm (r2) CH0.26O0.09 + 1.02O2 → CO2 + 0.13H2O (r3) CH0.26O0.09 + CO2 → 2CO + 0.09H2O + 0.04H2 (r4) CH0.26O0.09 + 0.91H2O → CO + 1.04H2 (r5) mt → wCOmt + wCO2mt + wCH4mt (r6) H2 + ½O2 → H2O (r7) CO + ½O2 → CO2 (r8) CH4 + 1.5O2 → CO + 2H2O (r9) CH1.88O0.7 + 0.62O2 → CO + 0.94H2O (r10) CO + H2O ↔ CO2 + H2 | Mass balance for solid species Mass balance for gas species Energy balance for solid species Energy balance for gas species Porosity variation equation for i= C6H9O4, CH0.26O0.09 where γ, M, U, λ, cp, r, ρ, ε, and , are the mass concentration in kg m−1, molar mass in (kg mol−1), U is velocity in (m s−1), heat conductivity in (W m−1 K−1), thermal capacity in (J kg−1 K−1), molar reaction rate per volume in (mol s−1 m−3), density in (kg m−3), particle porosity dimensionless, heat flow in (J s−1), respectively, and subscripts i, s, g, p, ws, gs wg, sg, are referred to species i, solid, gas, solid particle, wall to solid transfer, gas to solid transfer, wall to gas transfer, solid particle to gas transfer. Considerations: z = 0.2 m, ε = 0.47, CO2 flowrate (NTP) = 2.15 (m3 h−1), N2 flowrate (NTP) = 4 (m3 h−1) |
| [213] Biomass: char from pyrolysis of wood Reactor model: one-dimensional steady state downdraft gasifier. Solution method: finite volume discretization in OpenFOAM. Main results: sensitivity analysis to study the influence of reactor inlet temperature and gas composition on char conversion, temperature profile of the bed, and syngas composition. | (r1) C + O2 → CO2 (r2) C + CO2 → 2CO (r3) C + H2O → CO + H2 (r4) CO + H2O ↔ CO2 + H2 Char conversion rate for reactions r1–r3 defined as ωi CC,0 is the initial concentration of char | Continuity equation (including Darcy’s law) where j = N2, CO2, H2O, CO, H2, O2 where K, P, μ, T, R, is permeability in (m2), pressure in (Pa), dynamic viscosity in (kg m−1 s−1), temperature in (K), universal gas constant (8.314 J mol−1 K−1), respectively. Mass balance for gas species where Dj,N2 is the diffusion coefficient of species j into nitrogen; τ: tortuosity Mass balance for solid species (char) where Uc: velocity of solid char in (m s−1); Cc: concentration of char in (mol m−3); rc: reaction rate of char in (mol m−3 s−1) where where X: char conversion. Energy balance where where cp,g: specific heat capacity of gas phase in (J g−1 K−1), M: molar mass of gas phase in (g mol−1); Mc: molar mass of char in (mol s−1); λb: thermal conductivity of the porous bed char in (W m−1 K−1); λg: thermal conductivity of the gas phase in (W m−1 K−1); λc: thermal conductivity of the char in (W m−1 K−1) Considerations: z = 65 cm; εp = 0.75; particle thickness (ep) = 5.5 × 10−3 m |
| [214] Biomass: wood pellets. Reactor model: one-dimensional unsteady state Imbert gasifier. Solution method: finite differences. Main results: transient behavior of temperature, syngas concentration, temperature at solid bed, and application of the model to different geometries. | (r1) H2Ol → H2Ov CcHhOo → x1CO + x2CO2 +x3H2 + x4CH4 + x5H2O + x6C6H6O + x7C10H8 + x8C6H6 with and (r2) C6H6O → CO + 0.4C10H8 +0.15C6H6 + 0.1CH4 + 0.75H2 with and (r3) C10H8 → 7.38C + 0.275C6H6 + 0.97CH4 + 2.235H2 with and Oxidation zone: (r4) CH4 + 1.5O2 → CO + 2H2O with and (r5) CO + ½O2 → CO2 with and (r6) H2 + ½O2 → H2O with and (r7) H2O → H2 + ½ O2 with and (r8) 2C + O2 → 2CO with and (r9) C + O2 → CO2 with and (r10) C6H6O + 4O2 → 6CO + 3H2 with and (r11) C6H6 + 4.5O2 → 6CO + 3H2O with and (r12) C10H8 + 7O2 → 10CO + 4H2O with and Reduction zone: (r13) CO + H2O → CO2 + H2 with and (r14) CH4 + H2O → CO + 3H2 with and (r15) C + CO2 → 2CO with and (r16) C+ H2O → CO + H2 with and (r17) C + 2H2 → CH4 with and (r18) C6H6O + 3H2O → 2CO + CO2 + 2.95CH4 + 0.05C + 0.1H2 with and (r19) C6H6 + 2H2O → 1.5C +2.5CH4 + 2CO with and | Mass conservation for biomass (wood): Mass conservation for moisture in the solid phase: Mass conservation for char: Mass conservation of gas (i = O2, CO, CO2, H2O, CH4, H2, tar, N2, and k = O2, H2O, N2) Mass conservation for the total gas: Energy conservation for the solid phase: Energy conservation for the gas phase: Energy conservation for the inner wall: Energy conservation for the exit gas: Energy conservation for the exiting gas: where the subscripts for s, m, c, g, w, ea, we, gt, and wt, correspond to solid, moisture, char, gas, wall, exiting gas to ambient, wall to exiting flow, total heat transfer, and total heat transfer from the wall to gas and solid phases, respectively; ρ is density in (kg m−3); Ac is cross-section area in (m2); W is mass flow per unit length in (kg m−1); U is superficial velocity in (m s−1); t is time in (s); T is temperature in (K); k is thermal conductivity in (kW m−1 K−1); q″ is heat flux in (kW m−2); q‴ is heat flux in (kW m−3), H is specific enthalpy in (kJ kg−1); z is axial coordinate; ΔH is heat of reaction in (kJ kmol−1); is mass flowrate in kg s m−1, r is reaction rate in (kmol s m−3); V is volume in (m3); M is molecular weight in (kg kmol−1). Considerations: Bed diameter: 0.1 m; ε = 0.5; dp = 0.01 m; moisture: 7.28 wt%; ρs0 = 416 (kg m−3) |
| [215] Biomass: biochar Reactor model: dynamic and steady state downdraft gasifier. Solution method: implicit finite volume and the upwind method. Main results: dynamic and steady state profiles for temperature and concentration of gas and solid phases | (r1) CO + H2O ↔ CO2 + H2 (r2) H2O + C ↔ H2 + CO (r3) CH4 + H2O ↔ CO + 3H2 (r4) CO2 + C ↔ 2 CO where and z is the axial position in (mm) | Mass balance in the gas phase for species i: where νij: stoichiometric coefficient of i in reaction j; Ug: gas input velocity in (m s−1); rj: reaction rate of species j; z: axial direction or bed height in (m); ε: bed porosity. Mass balance for solids: where M: mass of solids in (kg); t: time in (s), ṁ: mass flowrate in (kg s−1). Heat balance in the gas phase for species i: where Tg: gas temperature in (K); Ci: concentration of species i in (kg m−3) Heat balance for solids: where hse: convection heat coefficient between solids and gas in (kJ s−1m−2 K−1); As: solid face area in the cross section in (m2); Te: emulsion gas temperature in (K); Ts: solids temperature in (K); AR: bed cross area in (m2). Radiative flux density: where Qr: radiative flux density in the bed in (W m−2); K: extinction coefficient in (m−1); σ: Stefan-Boltzmann constant in (W m−2 K−4). Considerations: Gasifier 1: z = 0.083 m, diameter = 0.15 m; ε = 0.5; T steam = 473 K; steam velocity: 0.14–0.28 (m s−1) Gasifier 2: z = 0.236 m, diameter = 0.15 m; ε = 0.5; T steam = 473 K; steam velocity: 0.69 (m s−1) |
| [216] Char assumption: Biomass: char of beech chips (CH0.28O0.04). Reactor model: dynamic one-dimensional fixed bed reactor. Solution method: finite volume discretization Main results: temperature profiles, syngas composition and volume, cold gas efficiency, and LHV and HHV. | (r1) CO + H2O ↔ CO2 + H2 | Mass balance (char, gas, and ash content of the char): where is the mass of char per unit length in (kg m−1), is the char mass flowrate in (kg m−1 s−1), is the char converted during gasification per unit length where is the mass flowrate of char, is the gas obtained per unit length. where is mass of ash per unit length, is the ash mass flowrate. Energy balance: where is the mass per unit length, u is the internal energy, is the mass flowrate, H is the specific enthalpy, heat exchanged per unit length. Equilibrium constant for water–gas shift reaction: where T is temperature in (K). |
| [217] Biomass: Douglas fir bark (H3.03O1.17). Reactor model: steady state reduction zone of downdraft gasifier. Solution method: explicit finite differences. Main results: composition of producer gas and temperature profiles as the CRF varied. | (r1) C + CO2 ↔ 2CO (r2) C + H2O ↔ CO + H2 (r3) C + 2H2 ↔ CH4 (r4) CH4 + H2O ↔ CO + 3H2 | Energy balance: where nx, ν, cx, P, T, ρ, and z, are molar density of species x in (mol m−3), superficial gas velocity in (m s−1), molar heat capacity in (J mol−1 K−1), total pressure in (Pa), temperature in (K), density in (kg m−3), and axial distance in (m), respectively. Considerations: z = 245 mm; νo = 1.175 (m s−1); To = 1400 K; Po = 1.005 atm; fp = 0.3; CRF = 1, 10, 100, 1000, exponential and linear variations |
| Ref. | Considerations | Main Reactions in the Model |
|---|---|---|
| [157] | Model type: Discrete phase model based on the Lagrangian approach, standard k − ε for turbulence. Reactor type: Imbert downdraft gasifier. Biomass source: Rubber wood, Neem. Tar is considered as benzene, naphthalene, toluene, and phenol. Main results: The formation of tar species and their residence time. Production of syngas was also modeled. Grid consisted of 90,770 cells. Reactor dimensions of 950 (mm) height and 218 (mm) diameter. Activation energy is given in (kJ mol−1). | Oxidation: (r1) 2C + O2 → 2CO with and (r2) CO + ½ O2 → CO2 with and (r3) 2H2 + O2 → 2H2O with and (r4) CH4 + 2O2 → CO2 + 2H2O with and Gasification: (r5) C + CO2 → 2CO with and (r6) C + H2O → CO + H2 with and (r7) ½ C + H2 → ½ CH4 with and (r8) CH4 + H2O → CO + 3H2 with and (r9) CO + H2O → CO2 + H2 with and (r10) CO2 + H2 → CO + H2O with and Tar conversion: (r11) C7H8 → 0.17C10H8 + 0.89C6H6 + 0.67H2 with and (r12) C10H8 → 10C + 4H2 with and (r13) C10H8 + 4H2O → C6H6 + 4CO +5H2 with and (r14) C7H8 + H2 → C6H6 + CH4 with and (r15) C6H6 + 5H2O → 5CO + CH4 + 6H2 with and (r16) C6H6 + 7.5O2 → 6CO + 3H2 with and (r17) C7H8 + 3O2 → 6CO + 3H2 with and (r18) C7H8 + 9O2 → 7CO2 + 4H2O with and (r19) C6H6O → CO + 0.4C10H8 + 0.15C6H6 + 0.1CH4 + 0.75H2 with and |
| [234] | Model type: 2D steady-state, discrete phase model based on the Euler–Lagrangian approach, P1 radiation model, standard k − ε for turbulence. Reactor type: Imbert downdraft gasifier. Biomass source: biomass pellets. Char is carbon. Main results: Parametric study of the effect of equivalence ratio in temperature, gas production rate. Cold gas efficiency of 71.8% at ER of 0.25. Grid consisted of 88,642 cells. Reactor dimensions of 1083 (mm) height and 435 (mm) diameter. Activation energy is given in (kJ mol−1). | (r1) CcHhOoNn → x1CO + x2H2 + x3CH4 + x4CO2 + x5H2O + x6N2 (r2) 2C + O2 → 2CO with and (r3) CO + ½O2 → CO2 with and (r4) 2H2 + O2 → 2H2O with and (r5) CH4 + 1.5O2 → CO + 2H2O with and (r6) C + CO2 → 2CO with and (r7) C + H2O → CO + H2 with and (r8) C + 2H2 → CH4 with and (r9) CH4 + H2O → CO + 3H2 with and (r10) CO + H2O → CO2 + H2 with and (r11) CO2 + H2 → CO + H2O with and |
| [239] | Model type: 3D, P1 radiation model, realizable k − ε model for turbulence. Reactor type: Downdraft gasifier. Biomass source: Miscanthus briquettes. Main results: Temperature profile, syngas composition, and LHV. High predictability for different feedstocks. Grid consisted of 383,031 cells. Reactor dimensions of 900 (mm) height and 500 (mm) diameter. | Oxidation: (r1) C + ½ O2 → CO (r2) C + O2 → CO2 Gasification: (r3) C + CO2 → 2CO (r4) C + H2O → CO + H2 (r5) C + 2H2 → CH4 Gas-phase reactions: (r6) CO + ½ O2 → CO2 (r7) H2 + ½ O2 → H2O (r8) CH4 + H2O → CO + 3H2 (r9) CO + H2O → CO2 + H2 |
| [240] | Model type: 2D, porous media model to represent the packed bed, RNG k − ε model for turbulence. Reactor type: Imbert downdraft gasifier. Biomass source: Olive wood. Tar is considered as phenol, naphthalene, and benzene, while char is carbon. Main results: The influence of ratio of throat to gasifier diameters and the height to air nozzle from the throat on the tar concentration and cold gas efficiency was studied. Grid consisted of 20,000 cells. Reactor dimensions of 1370 (mm) height and 600 (mm) diameter. Activation energy is given in (kJ mol−1). | Pyrolysis including tar cracking: (r1) CcHhOo → x1CO + x2CO2 +x3H2 + x4CH4 + x5H2O + x6C6H6O + x7C10H8 + x8C6H6 with and (r2) C6H6O → CO + 0.4C10H8 +0.15C6H6 + 0.1CH4 + 0.75H2 with and (r3) C10H8 → 7.38C + 0.275C6H6 + 0.97CH4 + 2.235H2 with and Oxidation: (r4) CH4 + 1.5O2 → CO + 2H2O with and (r5) CO + ½O2 → CO2 with and (r6) H2 + ½O2 → H2O with and (r7) H2O → H2 + ½ O2 with and (r8) 2C + O2 → 2CO with and (r9) C + O2 → CO2 with and (r10) C6H6O + 4O2 → 6CO + 3H2 with and (r11) C6H6 + 4.5O2 → 6CO + 3H2O with and (r12) C10H8 + 7O2 → 10CO + 4H2O with and Reduction: (r13) CO + H2O → CO2 + H2 with and (r14) CH4 + H2O → CO + 3H2 with and (r15) C + CO2 → 2CO with and (r16) C+ H2O → CO + H2 with and (r17) C + 2H2 → CH4 with and (r18) C6H6O + 3H2O → 2CO + CO2 + 2.95CH4 + 0.05C + 0.1H2 with and (r19) C6H6 + 2H2O → 1.5C +2.5CH4 + 2CO with and |
| [241] | Model type: 2D, porous media model to represent the packed bed, RNG k − ε model for turbulence. Reactor type: Imbert downdraft gasifier. Biomass source: Oil palm residues. Tar is considered as phenol, hydroxyacetaldehyde, naphthalene, and benzene, while char is carbon. Main results: The effect of the equivalence ratio on the gas composition, tar concentration, and cold gas efficiency. Grid consisted of 20,000 cells. Reactor dimensions of 1370 (mm) height and 600 (mm) diameter. | Set of reactions as reported by [163] |
| [234] | Model type: 3D, Eulerian-Eulerian approach, standard k − ε model for turbulence Reactor: throat downdraft gasifier Biomass source: wood considered as C6H10.5O5N0.05 Main results: The ratio of diameters of throat-to-gasifier of 0.4, and the air inlet nozzles at 100 (mm) above the throat to give 31.2 mol% of H2 and H2/CO ratio of 1.25. Reactor dimensions of 550 (mm) height and 200 (mm) diameter. Activation energy given in (kJ mol−1). | Pyrolysis: (r1) CcHhOoNn → x1CO + x2CO2 + x3CH4 + x4H2 + x5Char + x6Ash with and Oxidation: (r2) C + O2 → CO2 with and (r3) C + ½ O2 → CO with and (r4) H2 + ½ O2 → H2O with and Reduction: (r5) C + CO2 → 2CO with and (r6) C + H2O → CO + H2 with and (r7) C + 2H2 → CH4 with and (r8) CH4 + H2O → CO + 3H2 with and (r9) CO + H2O → CO2 + H2 with and |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trejo, F. Review of Biomass Gasification Technologies with a Particular Focus on a Downdraft Gasifier. Processes 2025, 13, 2717. https://doi.org/10.3390/pr13092717
Trejo F. Review of Biomass Gasification Technologies with a Particular Focus on a Downdraft Gasifier. Processes. 2025; 13(9):2717. https://doi.org/10.3390/pr13092717
Chicago/Turabian StyleTrejo, Fernando. 2025. "Review of Biomass Gasification Technologies with a Particular Focus on a Downdraft Gasifier" Processes 13, no. 9: 2717. https://doi.org/10.3390/pr13092717
APA StyleTrejo, F. (2025). Review of Biomass Gasification Technologies with a Particular Focus on a Downdraft Gasifier. Processes, 13(9), 2717. https://doi.org/10.3390/pr13092717






