Comparative Simulation of Solar Adsorption and Absorption Cooling Systems with Latent Heat Storage with Erythritol and MgCl2·6H2O
Abstract
1. Introduction
2. Materials and Methods
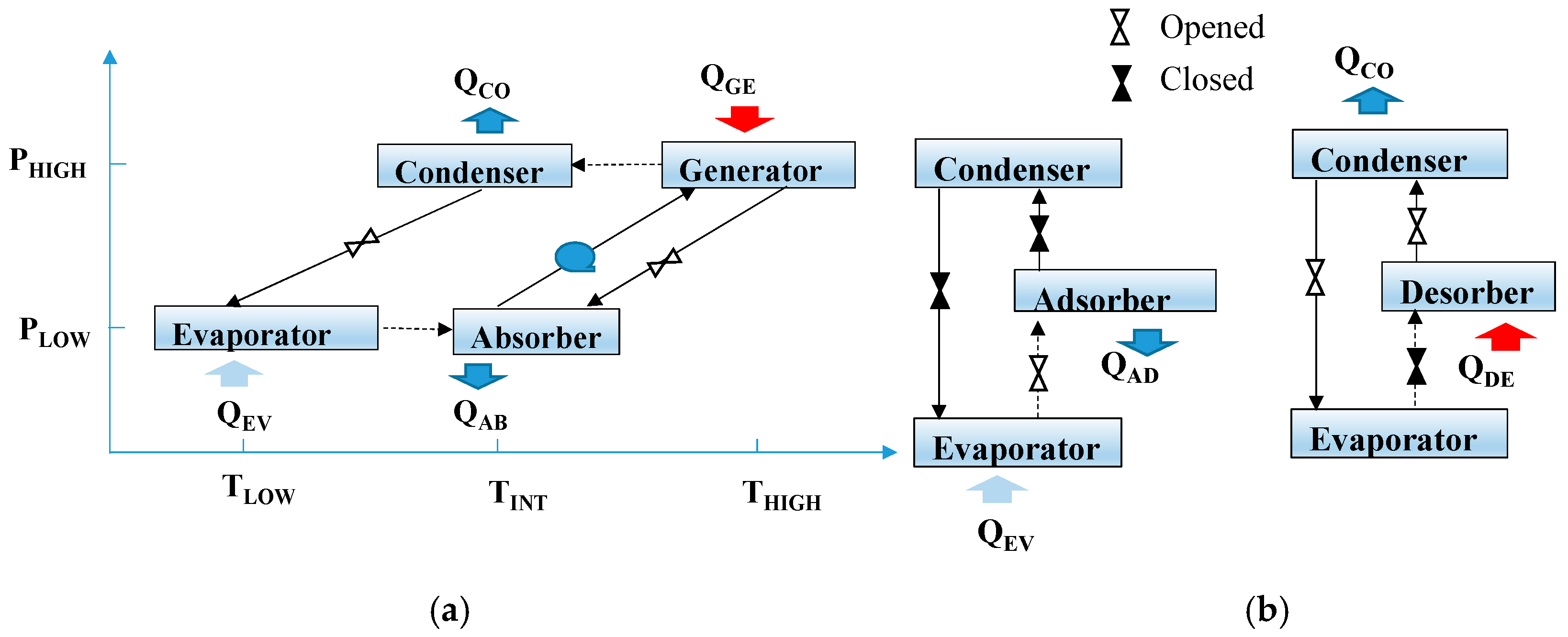
2.1. Adsorption and Absorption Cycles
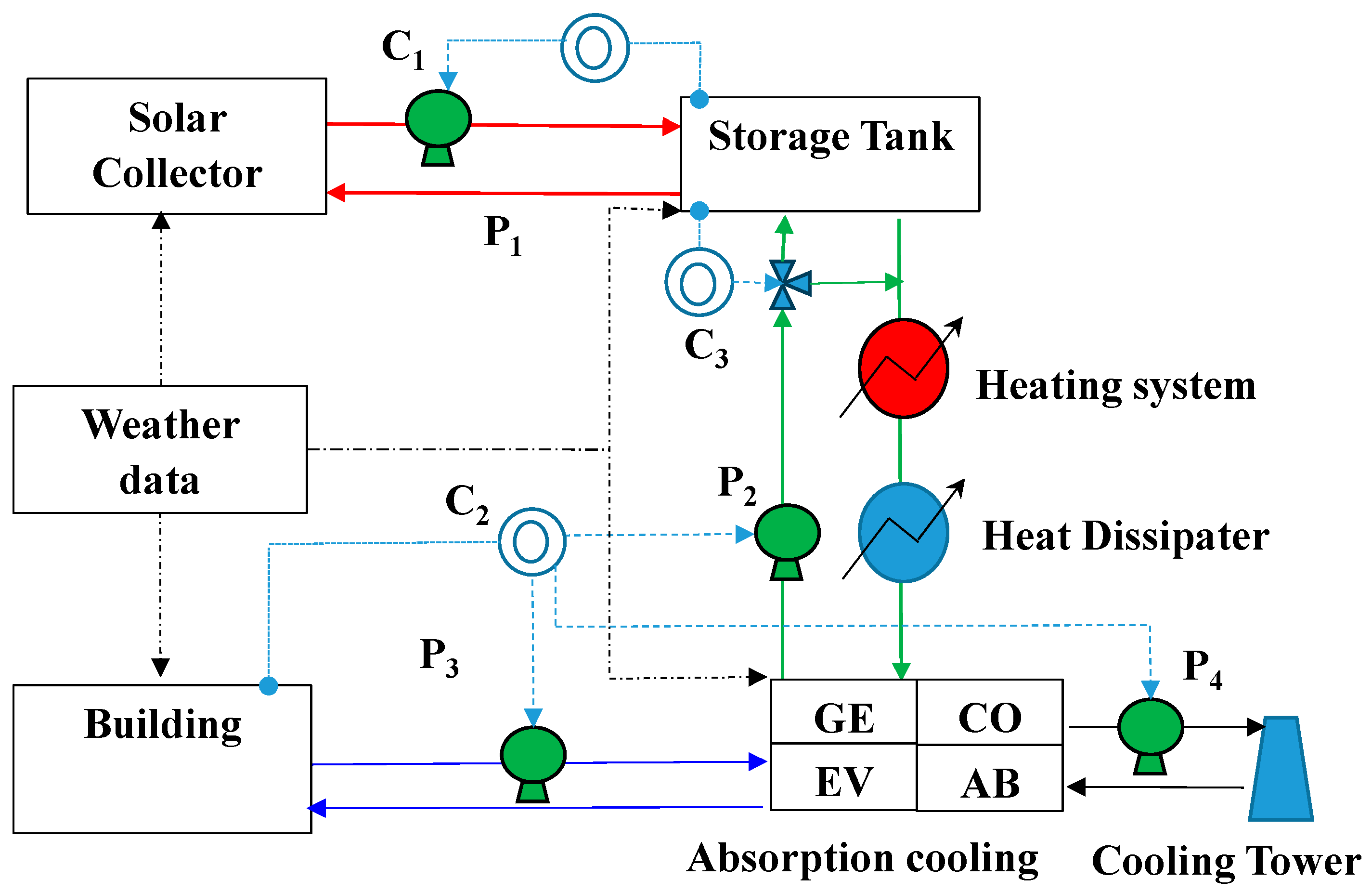
2.2. Description of the Solar Cooling System
2.3. Mathematical Model of the Latent Heat Storage Tank
- Isothermal condition is considered in the phase change.
- The PCM thermophysical properties are independent of temperature.
- PCM is homogeneous and isotropic.
- The thermal resistance of the metal wall in the plates is not taken into account.
- Input and output transport properties of the HF are considered the same.
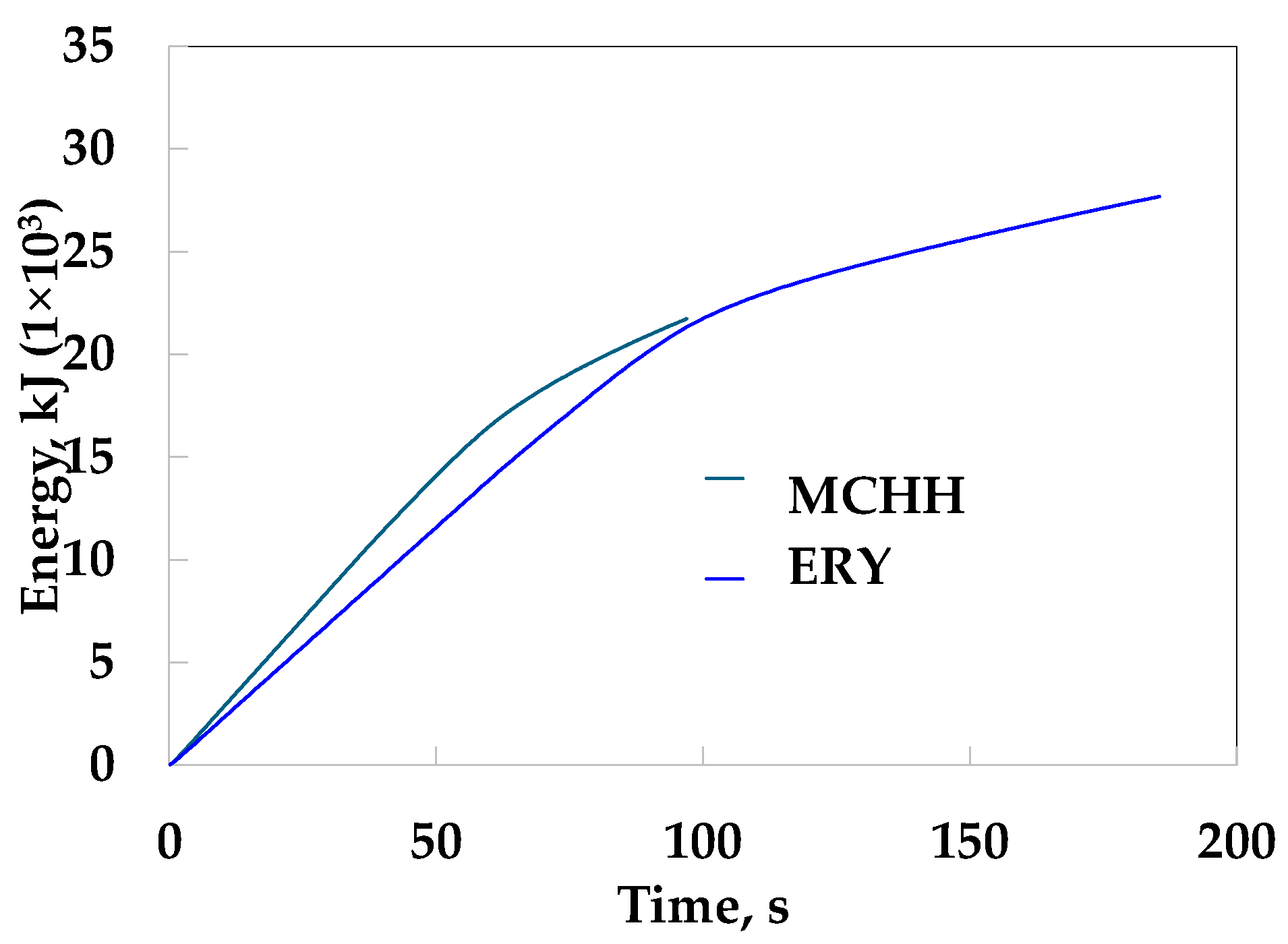
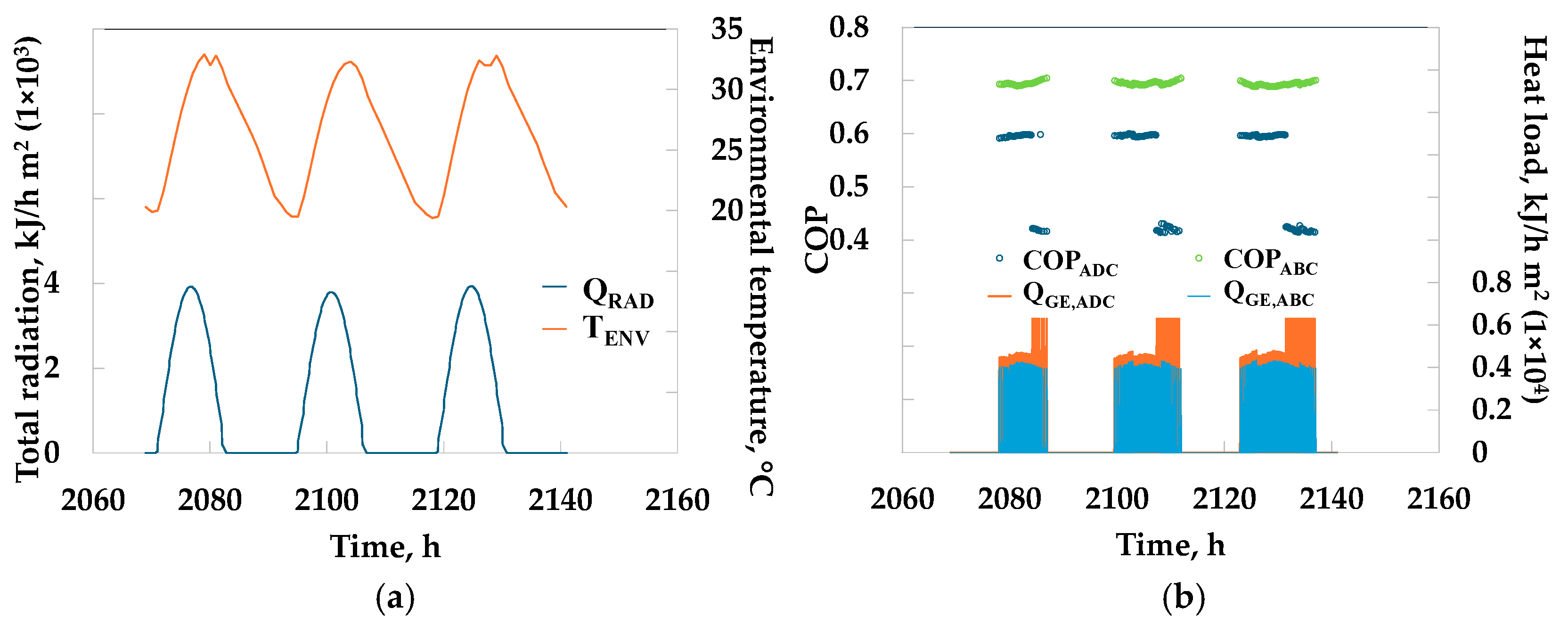
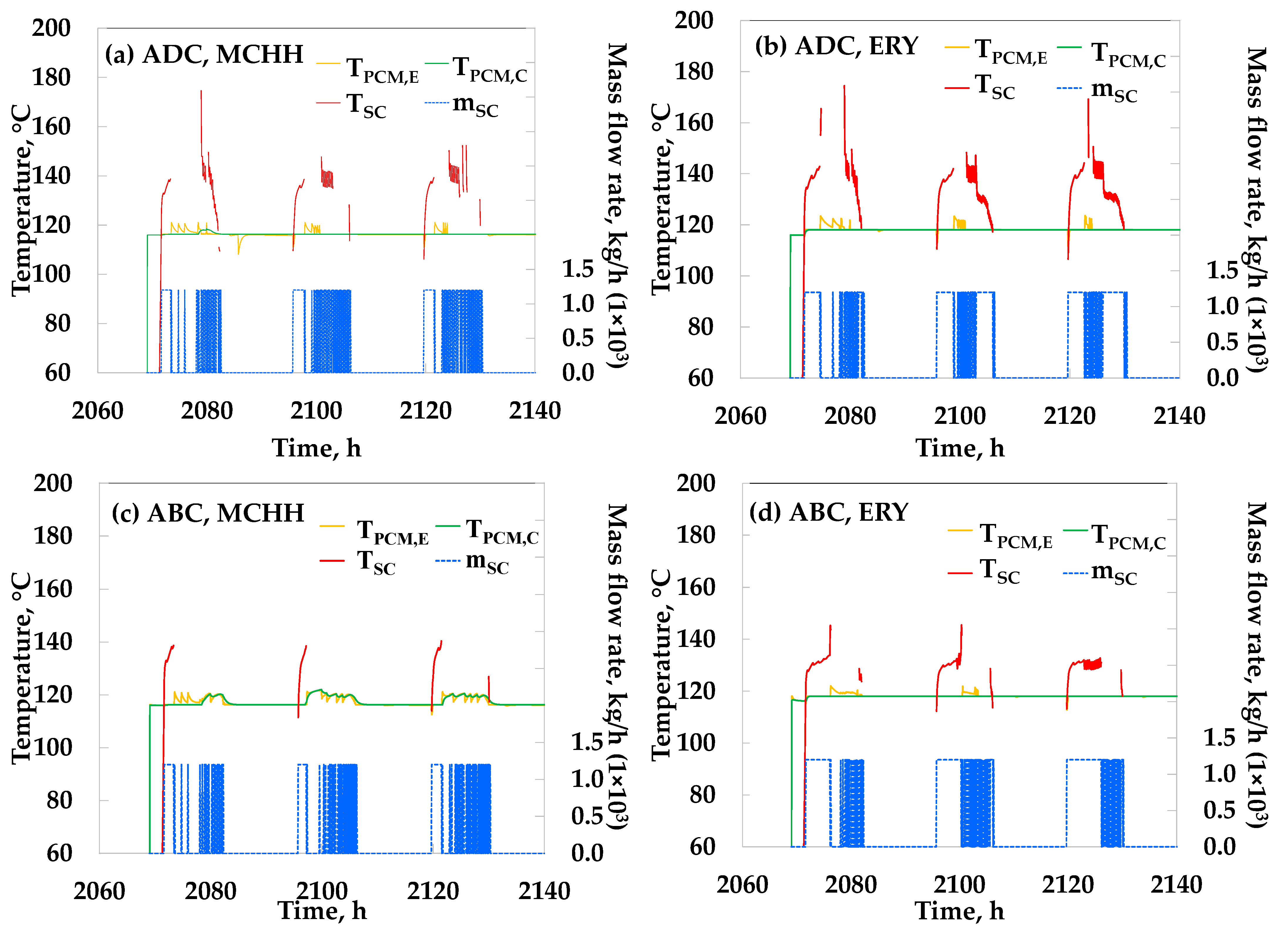
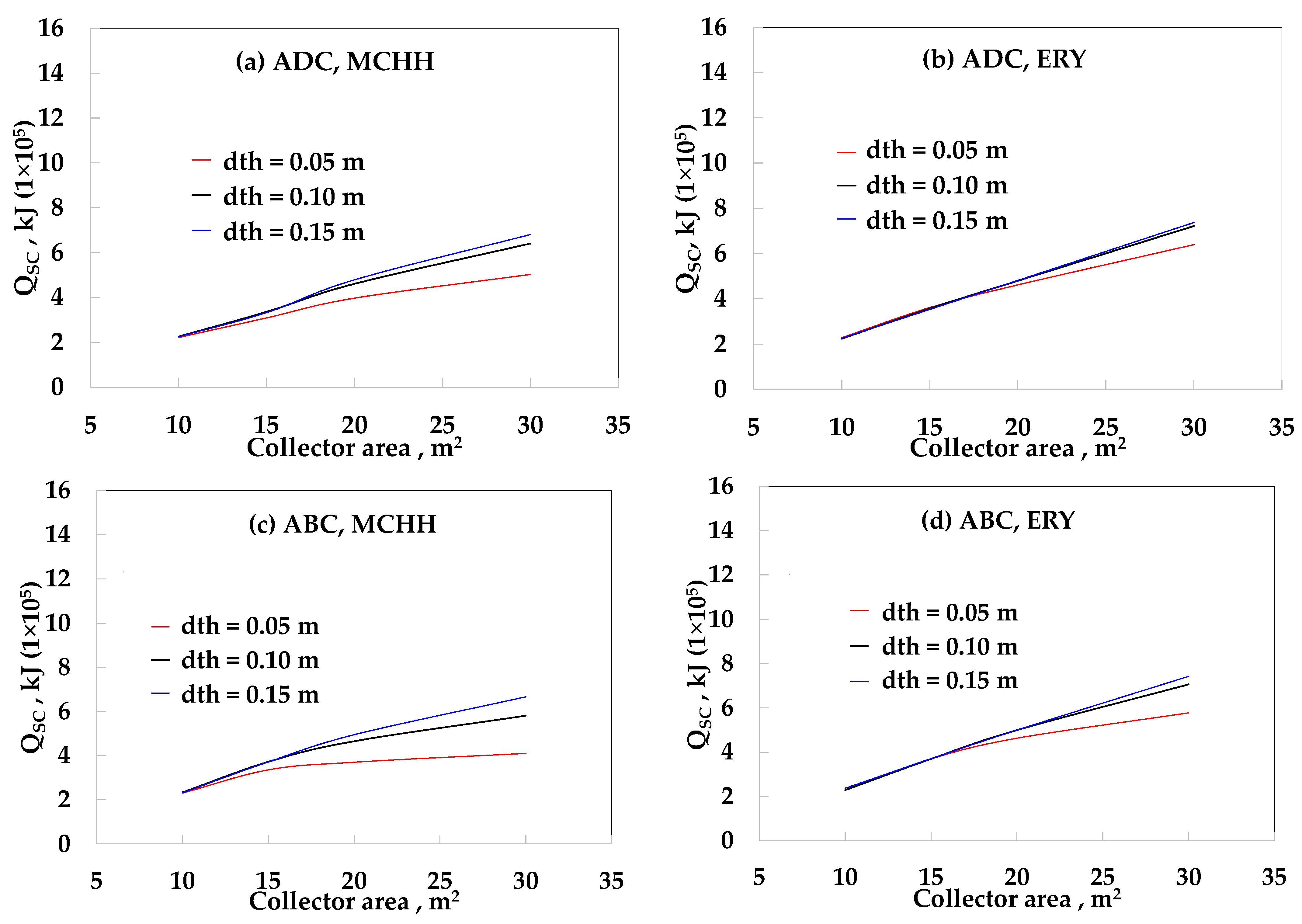
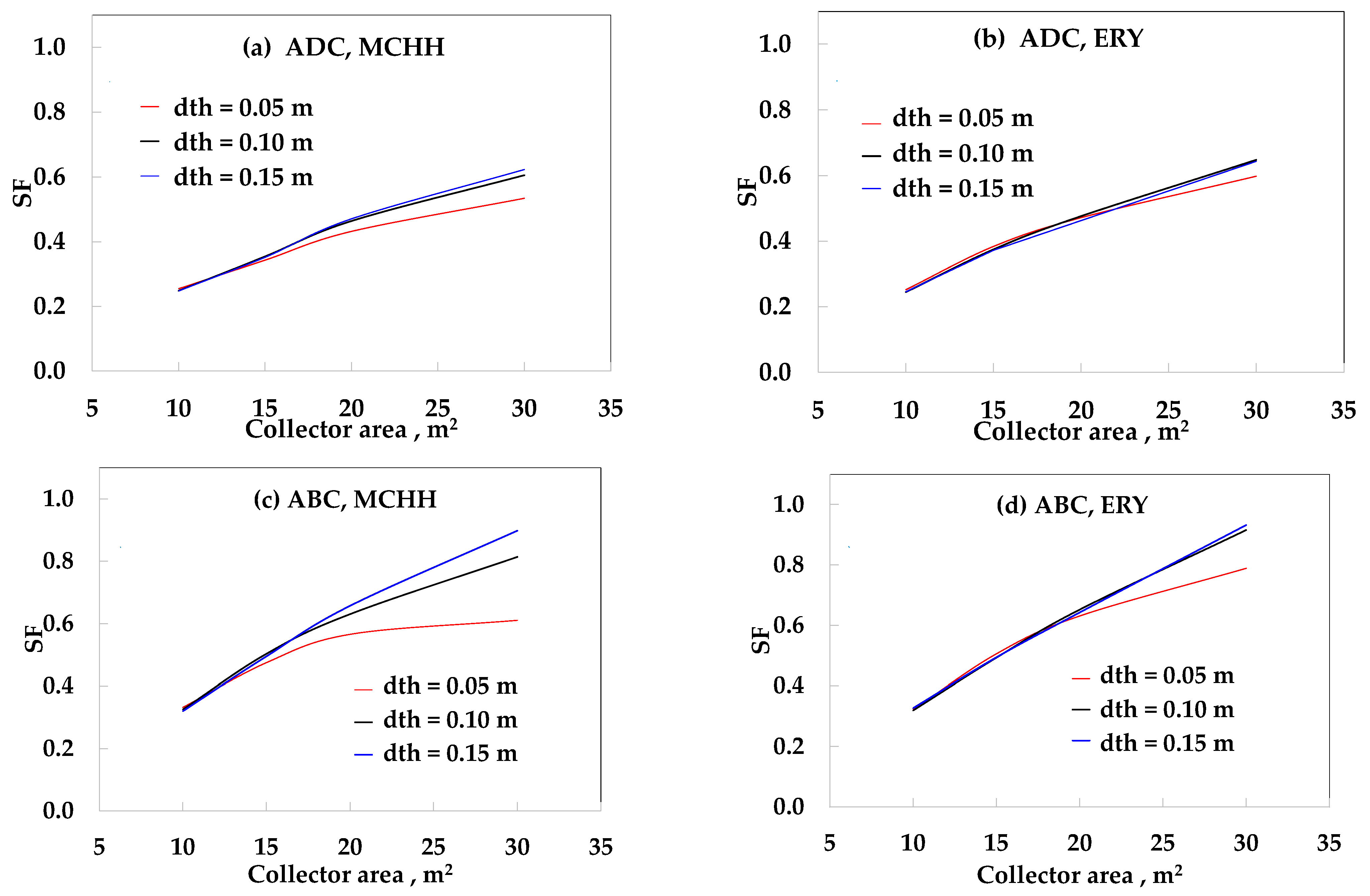
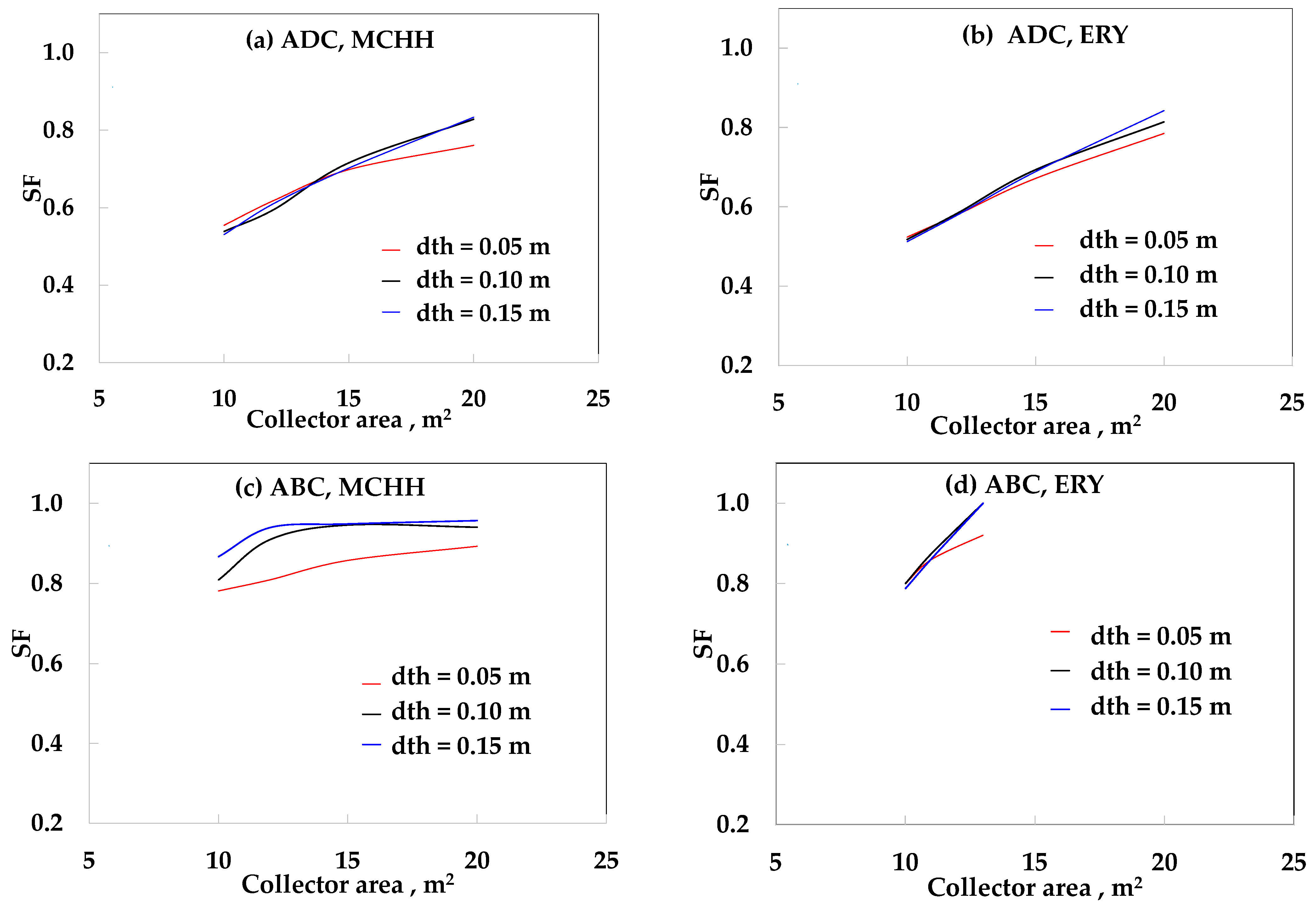
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| A | Area |
| ABC | Absorption cooling |
| ADC | Adsorption cooling |
| COP | Coefficient of operation |
| ERY | Erythritol |
| ed | Energy density, kJ/m3 |
| DISCH | Discharge |
| dth | Thickness of the PCM, m |
| F′(τα) | Collector (F′) (transmittance) (absorptance) product |
| h | Enthalpy, kJ/kg |
| HF | Heating fluid |
| htc | Heat transfer coefficient, kW/m2 °C |
| k | Thermal conductivity, kW/m °C |
| LHST | Latent heat storage tank |
| m | Mass flow rate, |
| MCHH | Magnesium chloride hexahydrate |
| PCM | Phase change material |
| Q | Energy, kJ |
| T | Temperature, °C |
| t | Time, s |
| Subscript | |
| SC | Solar collector |
| L | Liquid |
| S | Solid |
| Greek letter | |
| ε | Effectiveness |
| α | Thermal diffusivity, m2/s |
References
- Al-Falahi, A.; Alobaid, F.; Epple, B. Thermo-Economic Comparisons of Environmentally Friendly Solar Assisted Absorption Air Conditioning Systems. Appl. Sci. 2021, 11, 2442. [Google Scholar] [CrossRef]
- Al-Alili, Y.; Hwang, Y.; Radermacher, R. Review of solar thermal air conditioning technologies. Int. J. Refrig. 2014, 39, 4–22. [Google Scholar] [CrossRef]
- Fan, Z.; Infante, C.A.; Mosaffa, A.H. Numerical modelling of high temperature latent heat thermal storage for solar application combining with double-effect H2O/LiBr absorption refrigeration system. Sol. Energy 2014, 110, 398–409. [Google Scholar] [CrossRef]
- Pintaldi, S.; Sethuvenkatraman, S.; White, S.; Rosengarten, G. Energetic evaluation of thermal energy storage options for high efficiency solar cooling systems. Appl. Energy 2017, 188, 160–177. [Google Scholar] [CrossRef]
- Zhou, L.; Li, X.; Zhao, Y.; Dai, Y. Performance assessment of a single/double hybrid effect absorption cooling system driven by linear Fresnel solar collectors with latent thermal storage. Sol. Energy 2017, 151, 82–94. [Google Scholar] [CrossRef]
- Cerezo, J.; Lara, F.; Romero, R.J.; Rodríguez, A. Analysis and Simulation of an Absorption Cooling System Using a Latent Heat Storage Tank and a Tempering Valve. Energies 2021, 14, 1376. [Google Scholar] [CrossRef]
- Mehmood, S.; Lizana, J.; Friedrich, D. Solar-Driven Absorption Cooling System with Latent Heat Storage for Extremely Hot Climates. Energy Convers. Manag. 2023, 297, 117737. [Google Scholar] [CrossRef]
- Migla, L.; Bogdanovics, R.; Lebedeva, K. Performance Improvement of a Solar-Assisted Absorption Cooling System Integrated with Latent Heat Thermal Energy Storage. Energies 2023, 16, 5307. [Google Scholar] [CrossRef]
- Hosseini, L. Desing and Analysis of a Solar Assisted Absorption Cooling System Integrated with Latent Heat Storage. Master’s Thesis, Delft Universisty of Technology, Delft, The Nederlands, 2011. [Google Scholar]
- Poshtiri, A.H.; Jafari, A. 24-hour cooling of a building by a PCM-integrated adsorption system. Int. J. Refrig. 2017, 79, 57–75. [Google Scholar] [CrossRef]
- Kuczyńska, A.; Szaflik, W. Absorption and adsorption chillers applied to air conditioning systems. Arch. Thermodyn. 2010, 31, 77–94. [Google Scholar] [CrossRef]
- A Transient System Simulation Program, Solar Energy Laboratory. TRNSYS 18. Available online: http://sel.me.wisc.edu/trnsys/ (accessed on 1 July 2025).
- Solar Energy Laboratory. Multi-zone Building Modeling with Type 56 and TRNBuild, TRNSYS 16, Volume 6; University of Wisconsin: Madison, WI, USA, 2007; Available online: https://web.mit.edu/parmstr/Public/Documentation/06-MultizoneBuilding.pdf (accessed on 1 July 2025).
- TESS-Thermal Energy Systems Specialists. HVAC Library Mathematical Reference, TESSLibs 17, TRNSYS 17, Volume 6; TESS–Thermal Energy Systems Specialists: Madison, WI, USA, 2014. [Google Scholar]
- Solar Energy Laboratory. Mathematical Reference, TRNSYS 16, Volume 5; University of Wisconsin: Madison, WI, USA, 2006. Available online: https://web.mit.edu/parmstr/Public/Documentation/05-MathematicalReference.pdf (accessed on 1 July 2025).
- Solar Rating & Certification Corporation. Technical Data. Solar Concentration Model LH-3-2M. 2018. Available online: https://solar-rating.org/ (accessed on 1 July 2021).
- Solar Rating & Certification Corporation. Directory of SRCC Certified Solar Collector Ratings; Solar Rating & Certification Corporation: Washington, DC, USA, 2009. [Google Scholar]
- Klein, S.A. EES, Engineering Equation Solver; Professional Version; FChart Software: Madison, WI, USA, 2017; Available online: https://www.fchart.com/ees/ (accessed on 1 July 2025).
- Höhlein, S.; König-Haagen, A.; Brüggemann, D. Thermophysical Characterization of MgCl2·6H2O, Xylitol and Erythritol as Phase Change Materials (PCM) for Latent Heat Thermal Energy Storage (LHTES). Materials 2017, 10, 444. [Google Scholar] [CrossRef] [PubMed]
- Sigma-Aldrich. Available online: https://www.sigmaaldrich.com (accessed on 1 July 2025).
- El-Sebaii, A.A.; Al-Heniti, S.; Al-Agel, F.; Al-Ghamdi, A.A.; Al-Marzouki, F. One thousand thermal cycles of magnesium chloride hexahydrate as a promising PCM for indoor solar cooking. Energy Convers. Manag. 2011, 52, 1771–1777. [Google Scholar]
- Agyenim, F.; Eames, P.; Smyth, M. Experimental study on the melting and solidification behaviour of a medium temperature phase change storage material (Erythritol) system augmented with fins to power a LiBr/H2O absorption cooling system. Renew. Energy 2011, 36, 108–117. [Google Scholar] [CrossRef]


| Component | TSET (°C) | TCHILLED (°C) | TCOOLING (°C) | TGE (°C) |
|---|---|---|---|---|
| ABC | 6.7 | 5.5–10.0 | 26.6–32.2 | 108.9–116.1 |
| ADC | 6.7 | 5.0–12.0 | 10.0–35.0 | 65.0–95.0 |
| Component | Type | Description |
|---|---|---|
| Parabolic trough collector | 1288 | This subroutine models a concentrating solar collector. The efficiency parameters for the PT are F′(τα) = 0.611, C1 = 1.42, C2 = 0.021, C3 = 0.0, C4 = 0.0, C5 = 6.653, C6 = 0.0 [16]. |
| Evacuated tube collector | 71 | Intercept efficiency = 0.418; Negative first-order efficiency coefficient = 4.212 kJ/h m2 K [17]. |
| Weather data | 15-2 | The weather data processor reads data at regular intervals from an external weather data file, interpolates it at time steps of less than one hour, and provides the processed data to other TRNSYS components. Meteorological data were used for Temixco, Mexico. |
| Heating system | 6 | This component increases the temperature of a flow stream using either internal or external control. Data provided: Overall heat coefficient = 2.58 kJ/h m2 K, efficiency = 0.98. |
| Heat dissipater | 92 | This component reduces the temperature of a flow stream using either internal or external control. Data provided: Overall heat coefficient = 2.58 kJ/h m2 K, efficiency = 0.98. |
| Cooling tower | 510 | “This type models a closed-circuit cooling tower. A closed-loop evaporative cooler that removes heat from a liquid stream by evaporating water over coils, with the working fluid fully isolated from air and water contact”. |
| C1 and C3 | 2b | This component is an on/off differential controller that switches off or on when it has a value of 0 or 1, depending on the upper and lower temperature differences, as well as the dead-band temperature differences. |
| C2 | 1503 | This models three ON/OFF control functions to control a fluid cooling system. |
| P1, P2, P3, P4 | 3d | This component computes a mass flow rate using a variable control function. Data provided: Conversion coefficient = 0.05. |
| Component | Tmelting (°C) | Heat Fusion (kJ/kg) | Cp (kJ/kg °C) | k (W/m K) | (kg/m3) | Thermal Diffusivity (m2/s, 1 × 104) | Energy Density (kJ/m3) |
|---|---|---|---|---|---|---|---|
| ERY | 118.1 | 337 | cpS = 1.34 (20 °C) cpL = 2.87 (150 °C) | kS = 0.89 (20 °C) kL = 0.33 (140 °C) | S = 1440.4 (20 °C) L = 1289.1 | αS = 4.61 αL = 0.89 | edS = 0.234 edL = 0.261 |
| MCHH | 115.1–117.4 | 166.9 | cpS = 1.83 (100 °C) cpL = 2.57 (120 °C) | kS = 0.70 (110 °C) kL = 0.63 (120 °C) | S = 1595.5 (20 °C) L = 1455.7 | αS = 2.39 αL = 1.6 | edS = 0.105 edL = 0.115 |
| Parameter | Value |
|---|---|
| PCM Thickness (dth), m | 0.05 |
| Total flow rate of heating fluid, kg/s | 0.55 |
| Wide channel, m | 8.99 |
| Height channel, m | 0.005 |
| Longitude channel, m | 0.16 |
| Isolation, m | 0.10 |
| Case | SFMAX (dth = 0.05 m) | SFMAX (dth = 0.10 m) | SFMAX (dth = 0.15 m) |
|---|---|---|---|
| ADC-ET-MCHH | 0.53 | 0.61 | 0.62 |
| ADC-ET-ERY | 0.60 | 0.64 | 0.64 |
| ADC-PT-MCHH | 0.76 | 0.83 | 0.83 |
| ADC-PT-ERY | 0.78 | 0.81 | 0.84 |
| ABC-ET-MCHH | 0.61 | 0.81 | 0.90 |
| ABC-ET-ERY | 0.79 | 0.92 | 0.93 |
| ABC-PT-MCHH | 0.89 | 0.94 | 0.96 |
| ABC-PT-ERY | 0.92 | 1.00 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romero, R.J.; Lara, F.; Venegas-Reyes, E.; Montiel-Gonzalez, M.; Cerezo, J. Comparative Simulation of Solar Adsorption and Absorption Cooling Systems with Latent Heat Storage with Erythritol and MgCl2·6H2O. Processes 2025, 13, 2655. https://doi.org/10.3390/pr13082655
Romero RJ, Lara F, Venegas-Reyes E, Montiel-Gonzalez M, Cerezo J. Comparative Simulation of Solar Adsorption and Absorption Cooling Systems with Latent Heat Storage with Erythritol and MgCl2·6H2O. Processes. 2025; 13(8):2655. https://doi.org/10.3390/pr13082655
Chicago/Turabian StyleRomero, Rosenberg J., Fernando Lara, Eduardo Venegas-Reyes, Moisés Montiel-Gonzalez, and Jesús Cerezo. 2025. "Comparative Simulation of Solar Adsorption and Absorption Cooling Systems with Latent Heat Storage with Erythritol and MgCl2·6H2O" Processes 13, no. 8: 2655. https://doi.org/10.3390/pr13082655
APA StyleRomero, R. J., Lara, F., Venegas-Reyes, E., Montiel-Gonzalez, M., & Cerezo, J. (2025). Comparative Simulation of Solar Adsorption and Absorption Cooling Systems with Latent Heat Storage with Erythritol and MgCl2·6H2O. Processes, 13(8), 2655. https://doi.org/10.3390/pr13082655










