Effect of Back Wear-Ring Clearance on the Internal Flow Noise in a Centrifugal Pump
Abstract
1. Introduction
2. Research Model and Methods
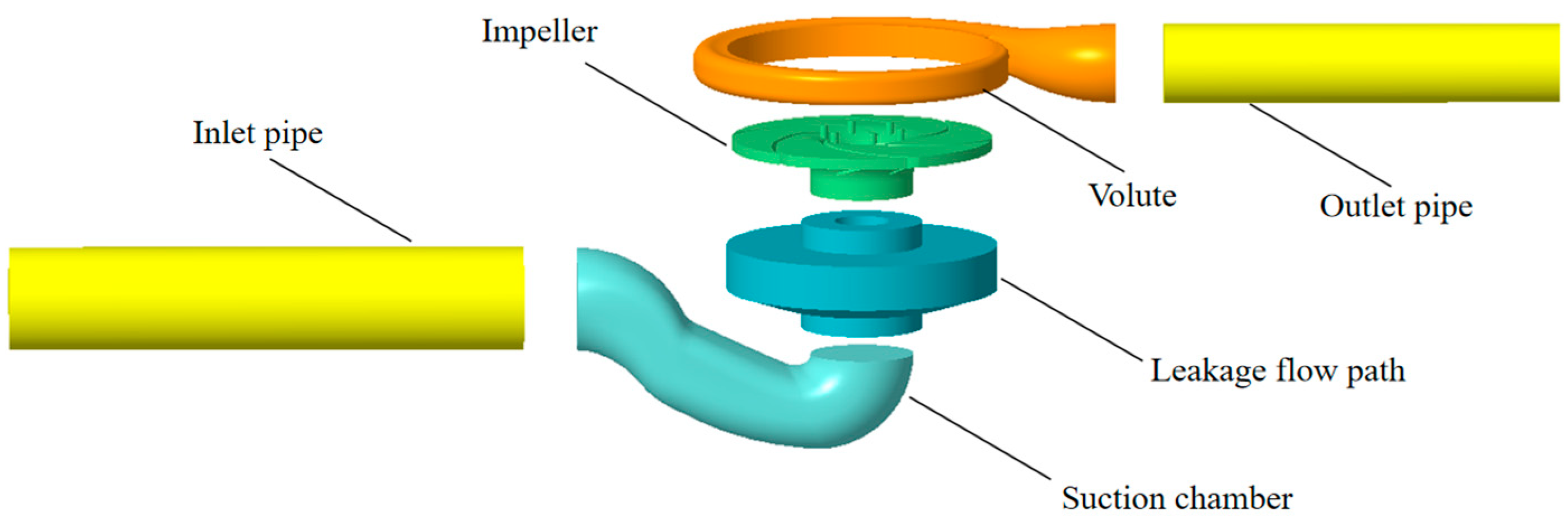
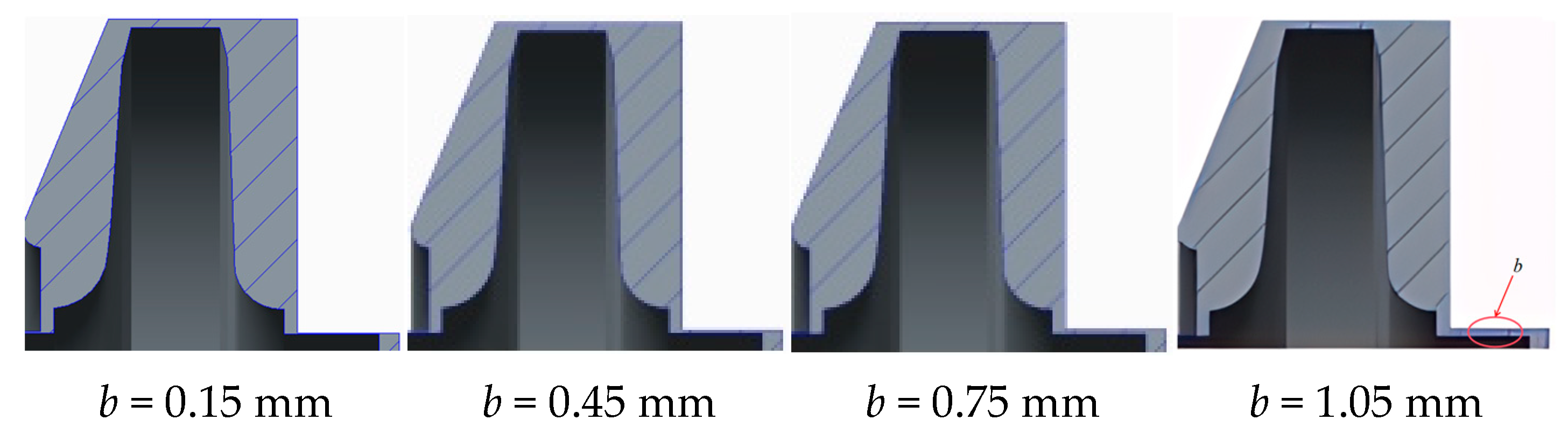
2.1. Research Model
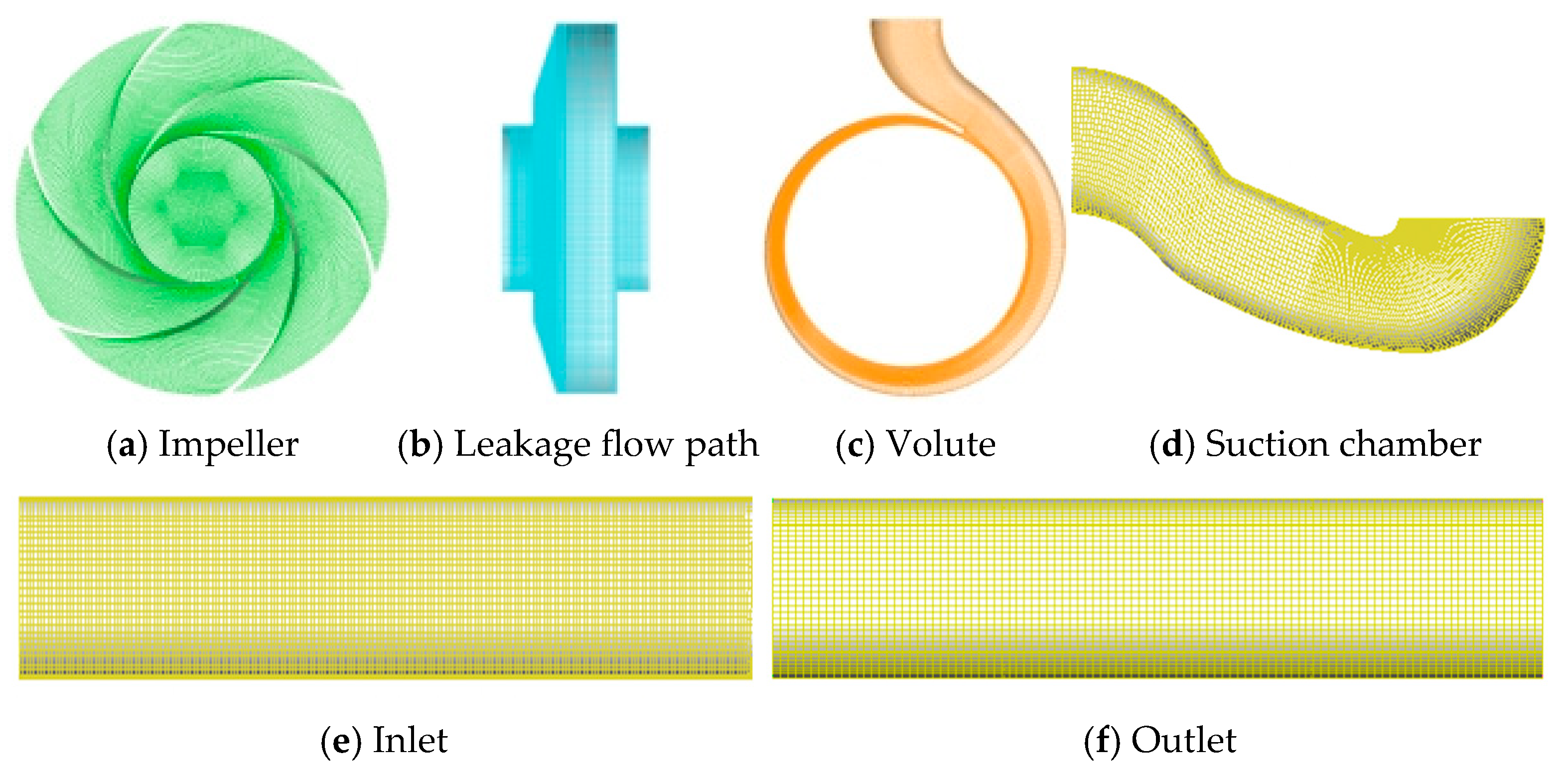
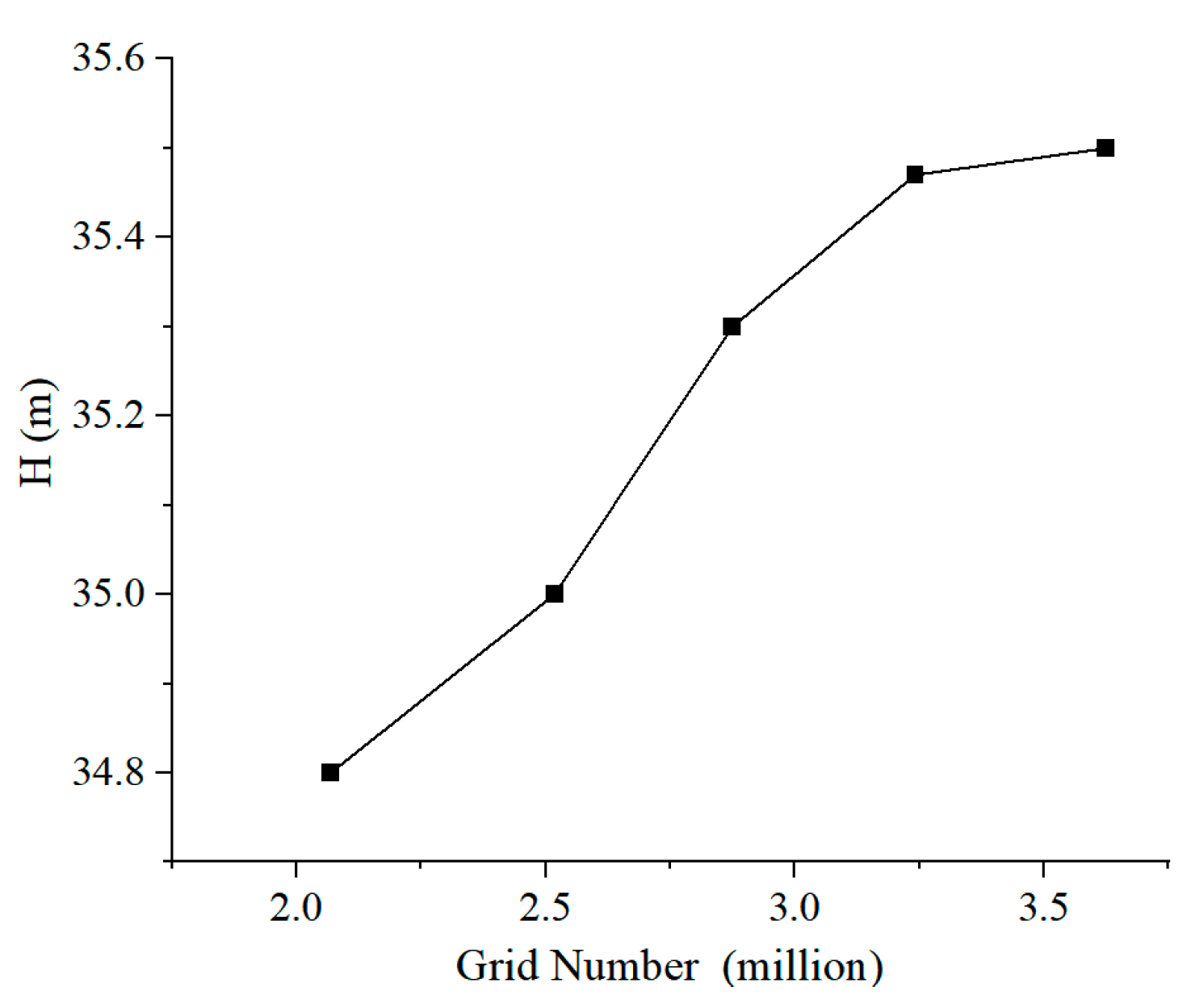
2.2. Grid Generation
2.3. Methods for Flow Field Simulation
2.3.1. Turbulence Model
2.3.2. Boundary Conditions
2.3.3. RMS of Pressure Pulsations
2.3.4. Pressure Pulsation Coefficient
2.4. Methods for Flow Noise Simulation
2.4.1. Acoustic Grid Division
2.4.2. Acoustic Simulation Theory
2.4.3. Sound Power Level
2.4.4. Sound Pressure Level
2.5. Experimental Verification
3. Flow Field Results and Discussion
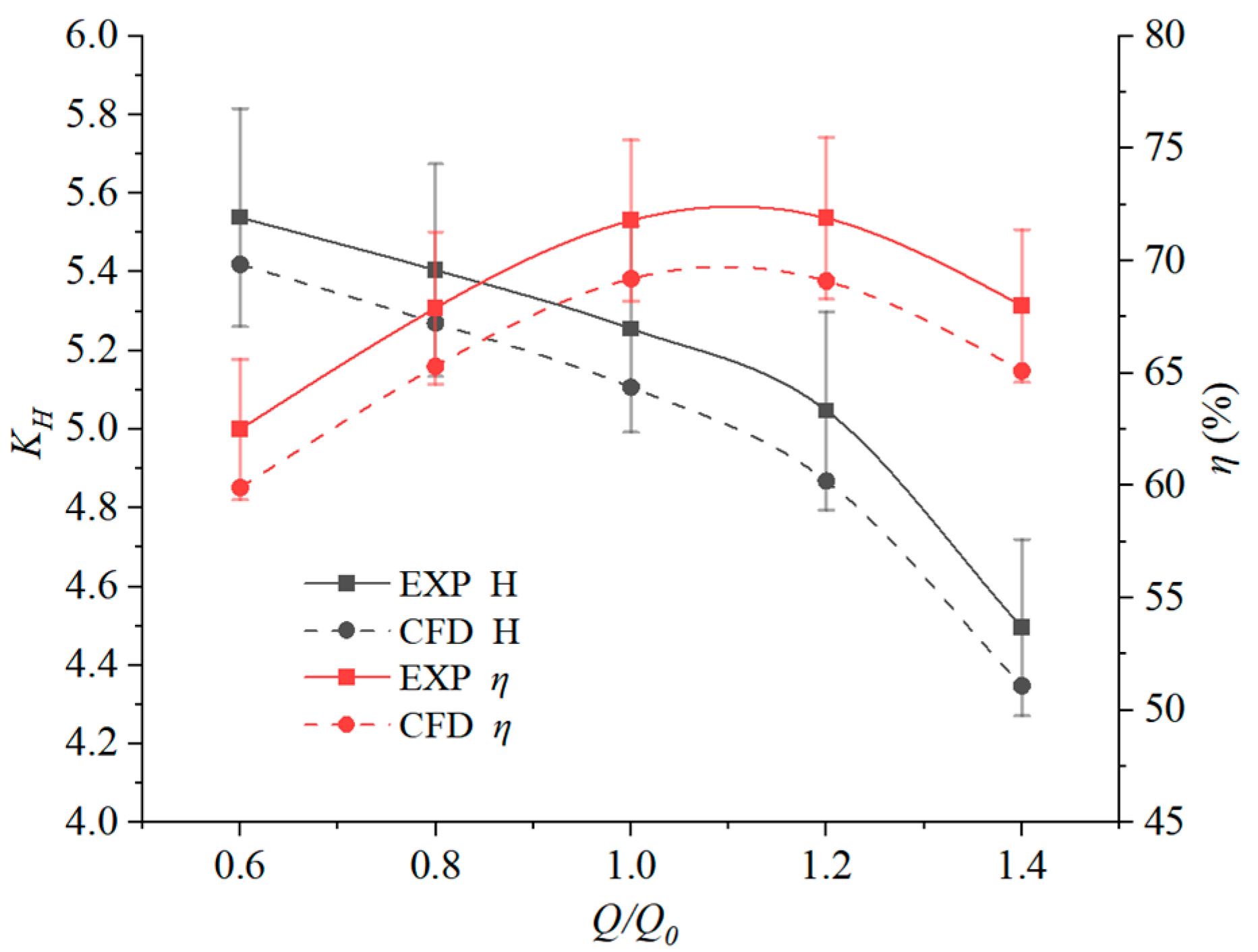
3.1. CFD Method Validation
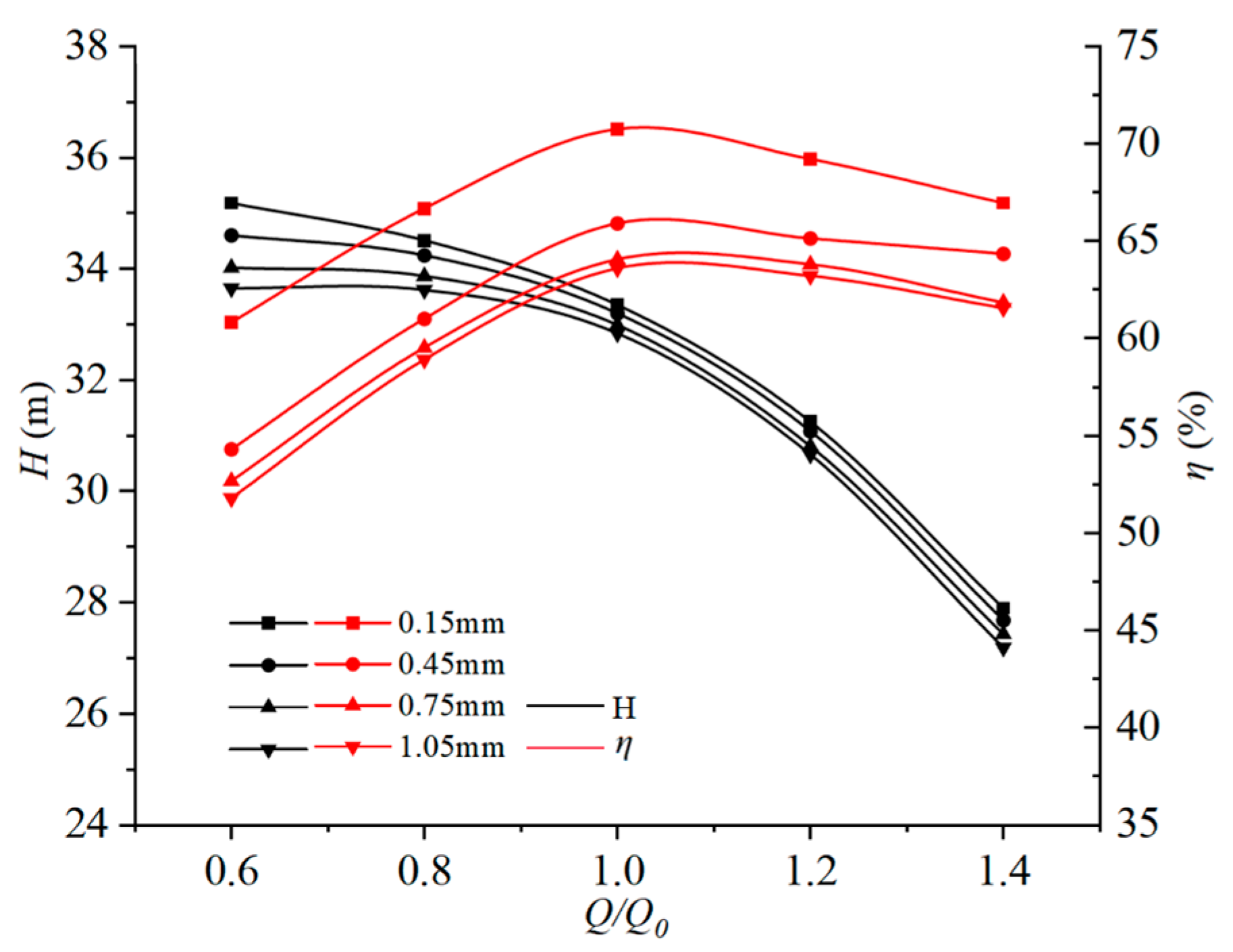
3.2. Energy Performance Analysis
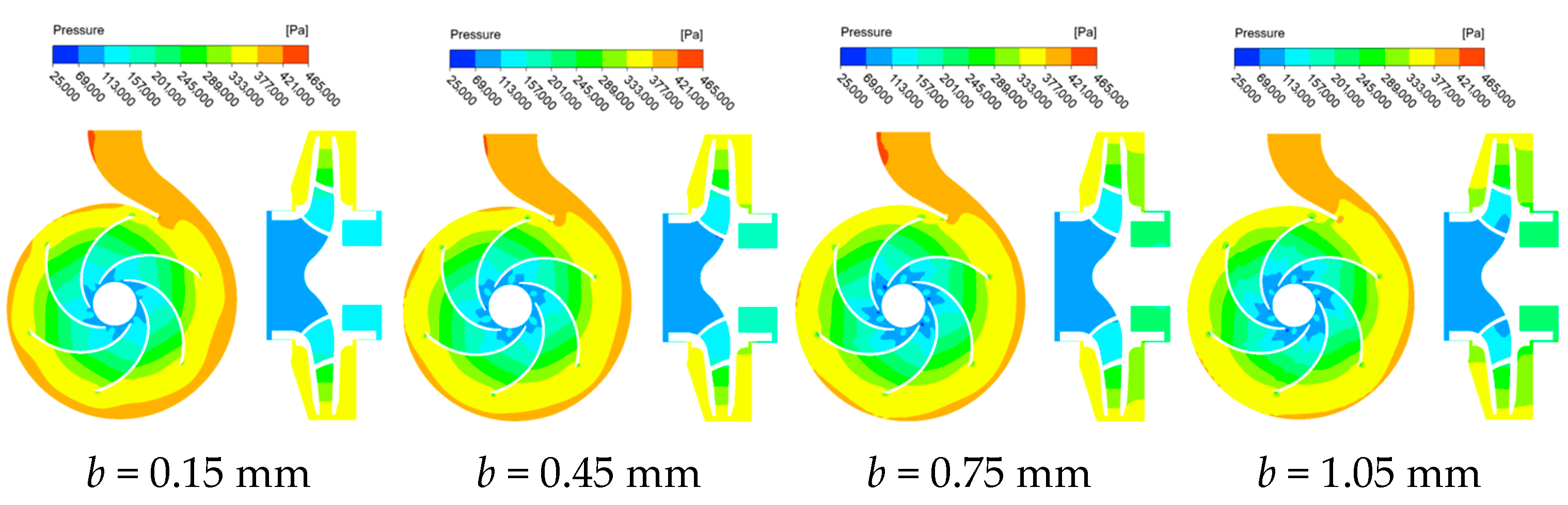
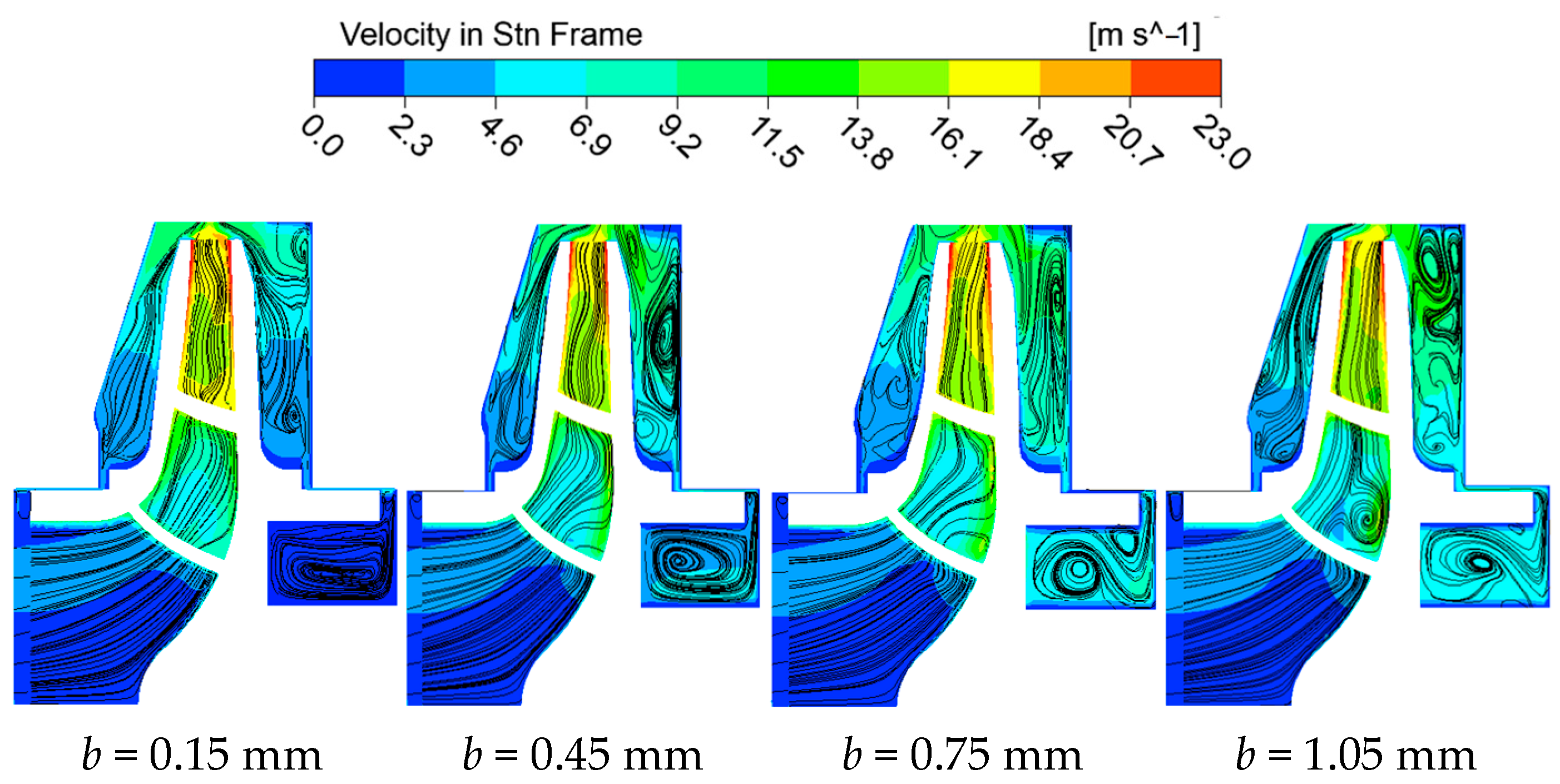
3.3. Internal Flow Field Analysis
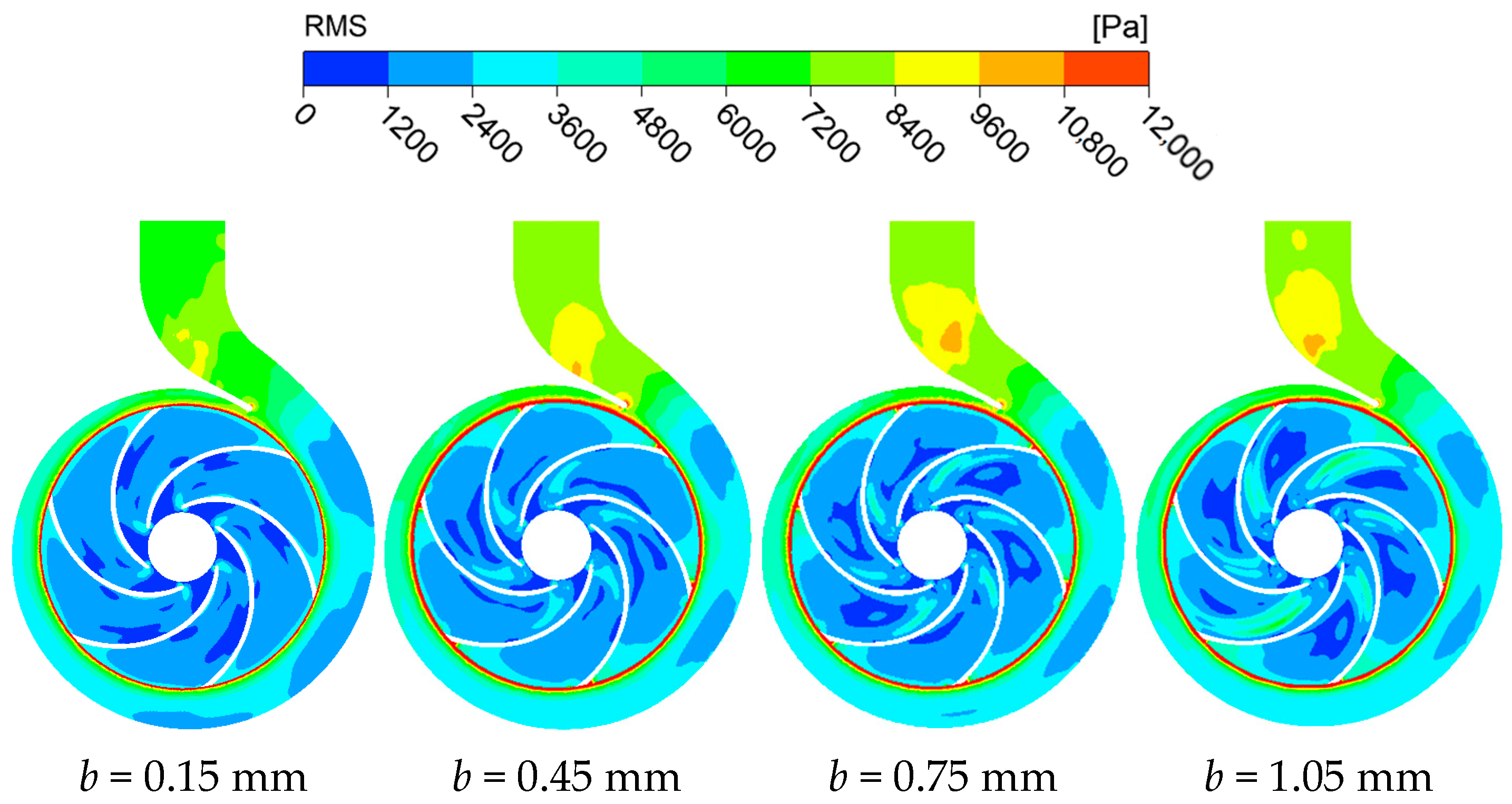
3.4. Pressure Pulsation Analysis
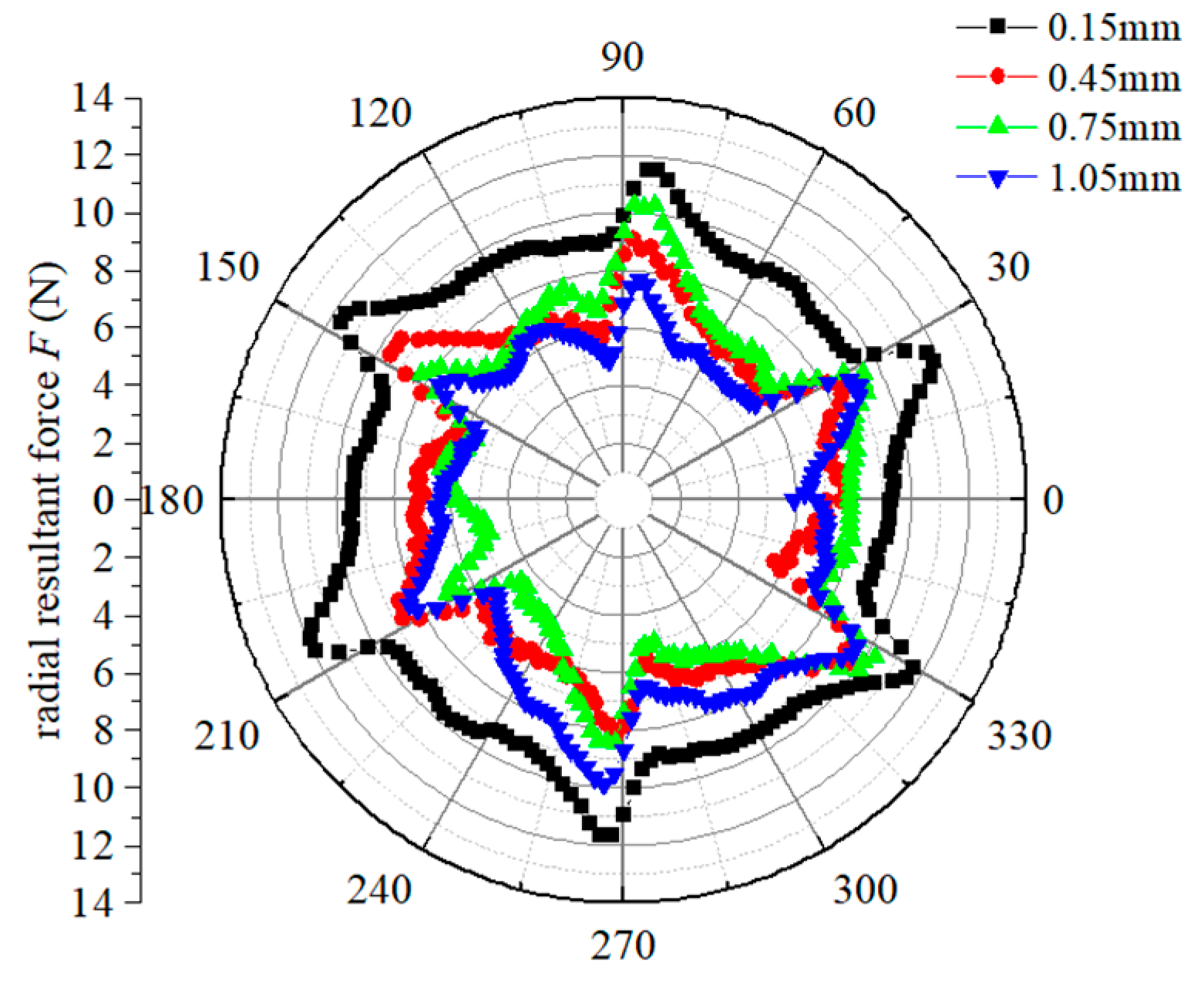
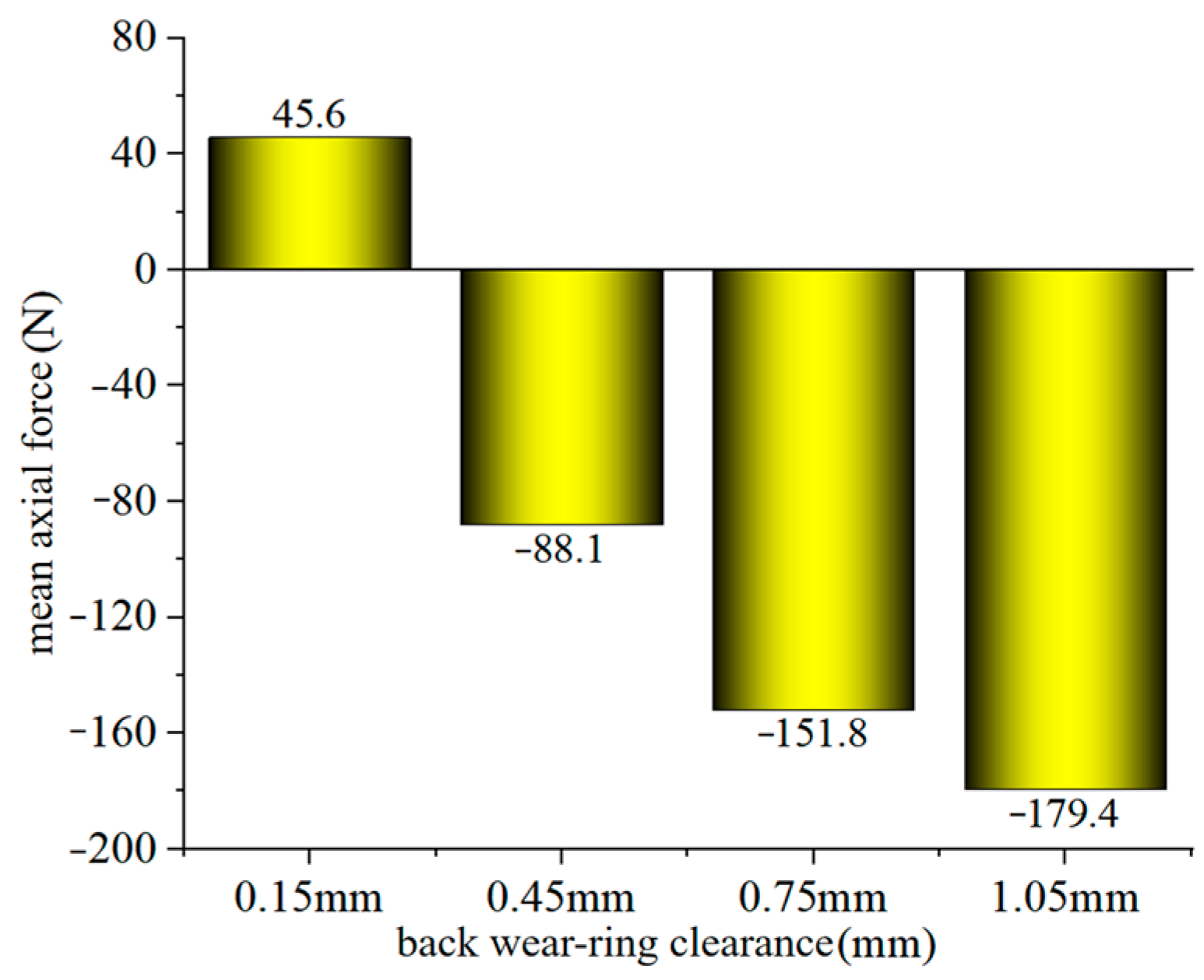
3.5. Dynamic Characteristic Analysis
4. Sound Field Results and Discussion
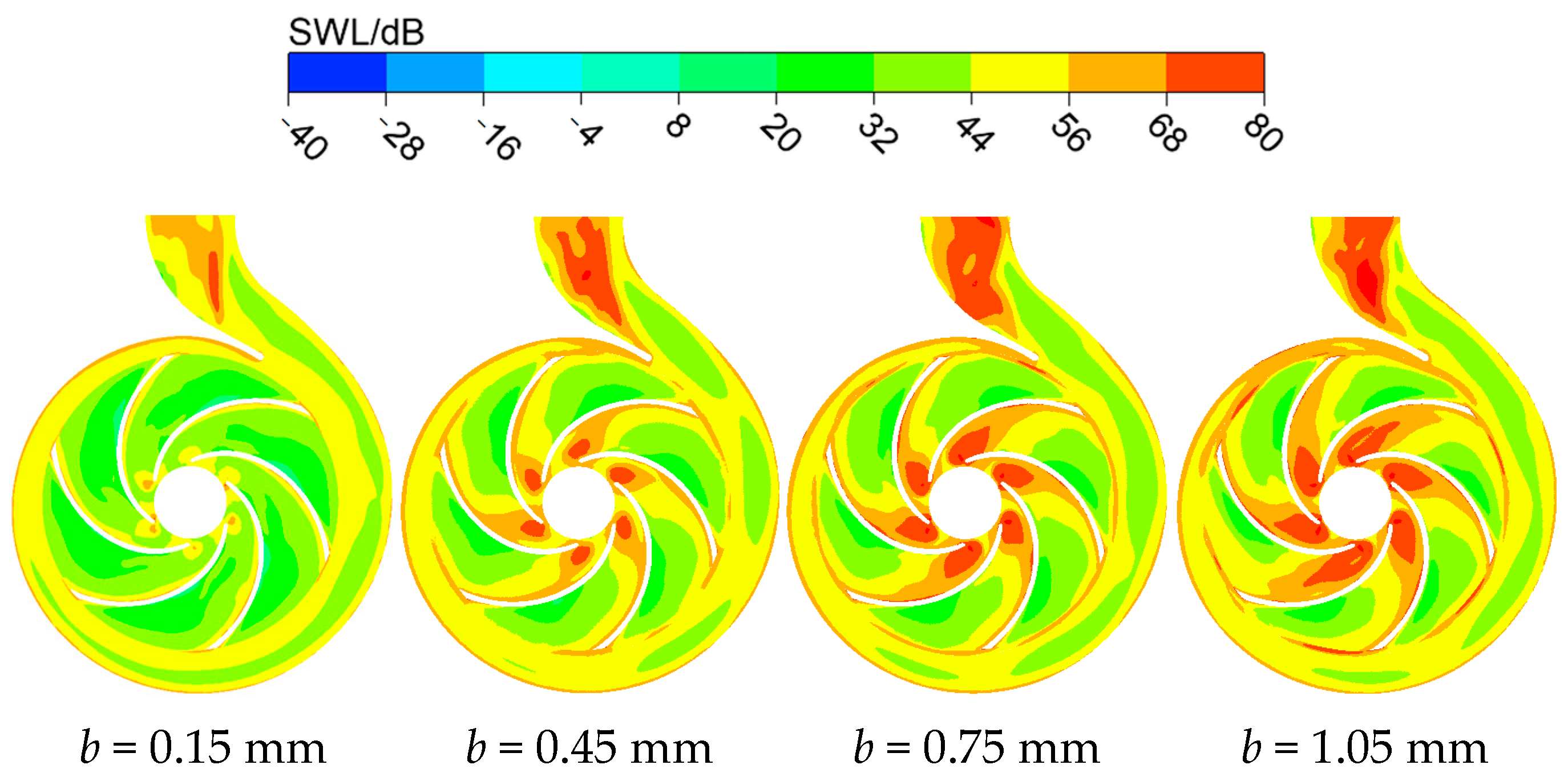
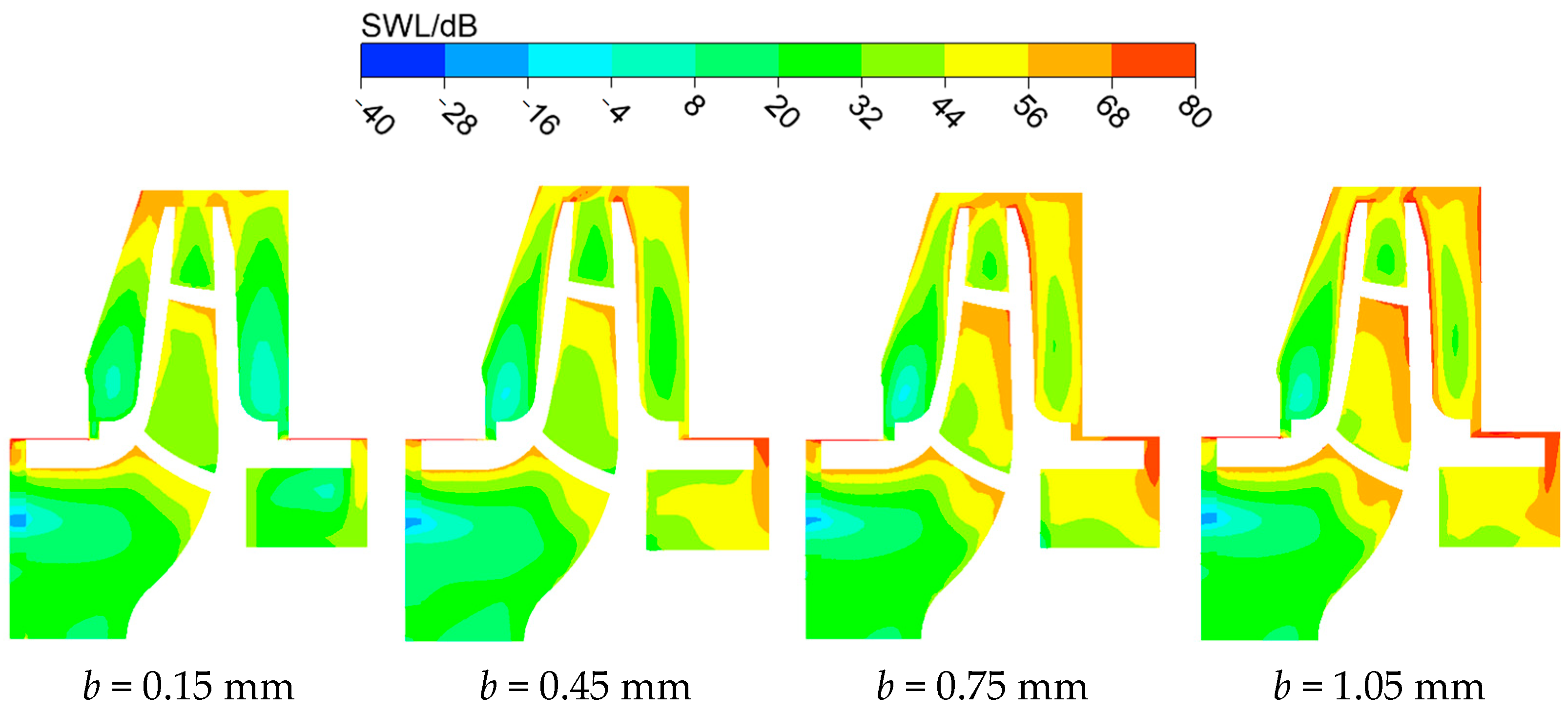
4.1. Sound Source Intensity Analysis
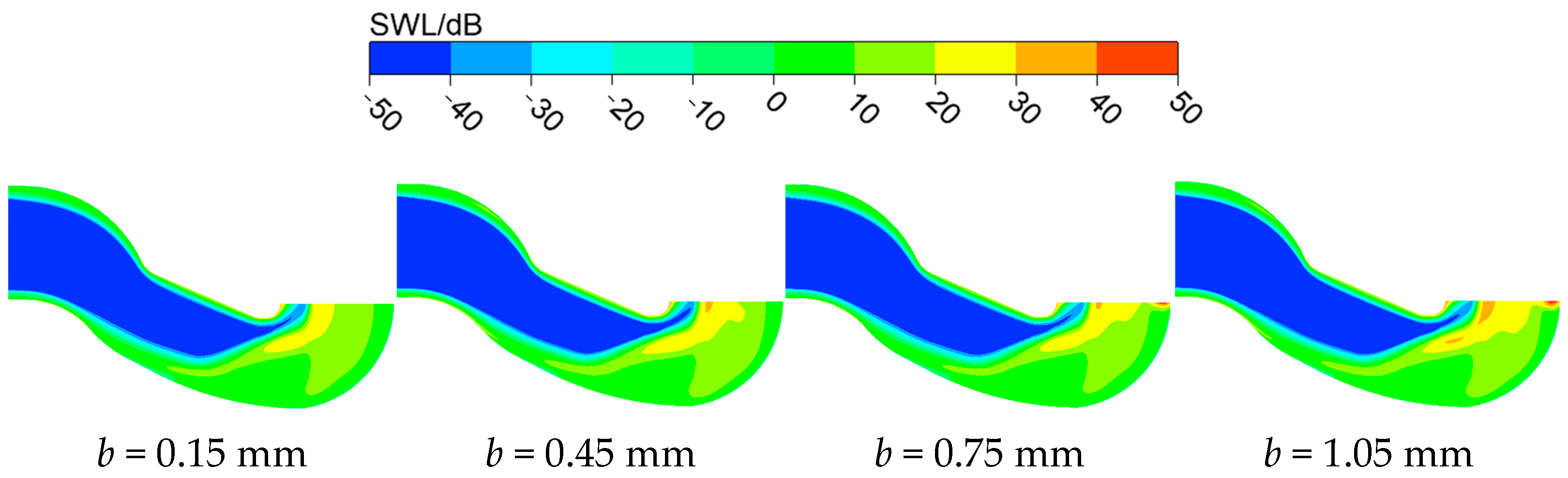
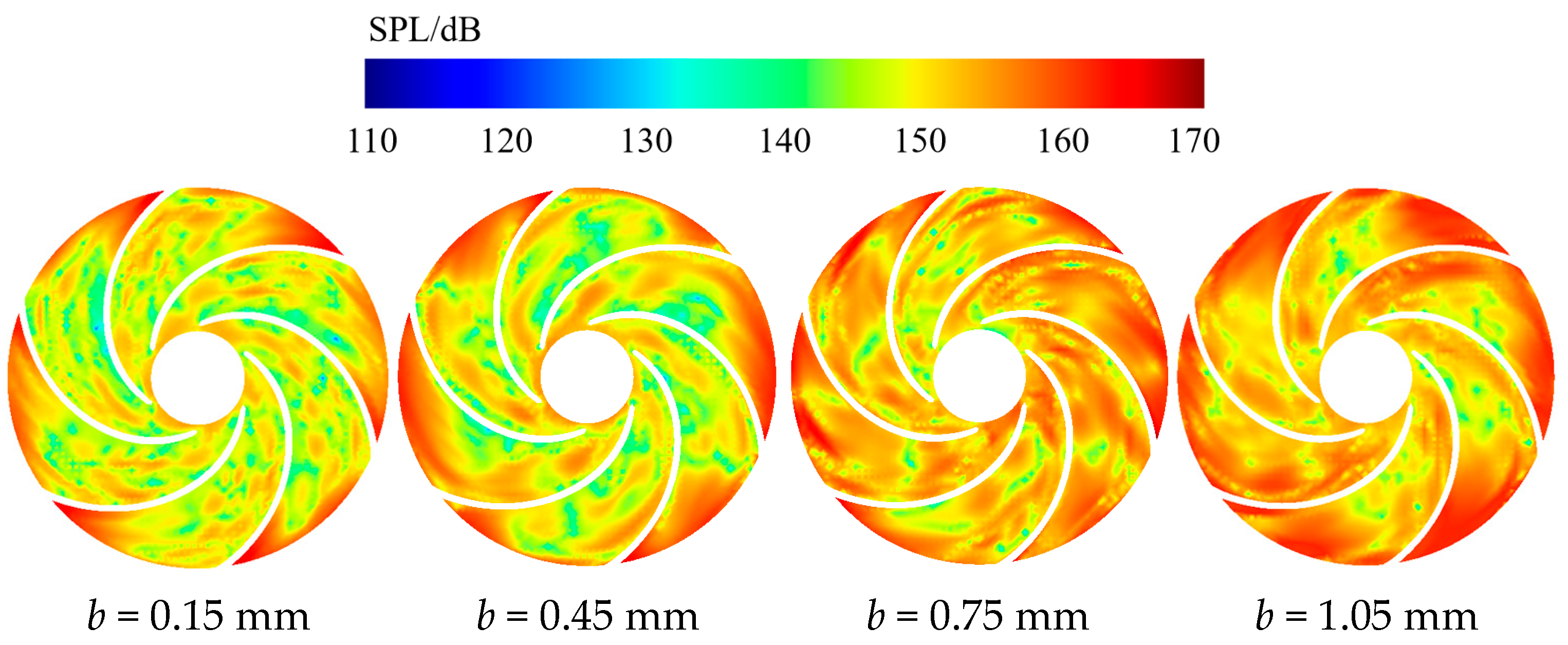
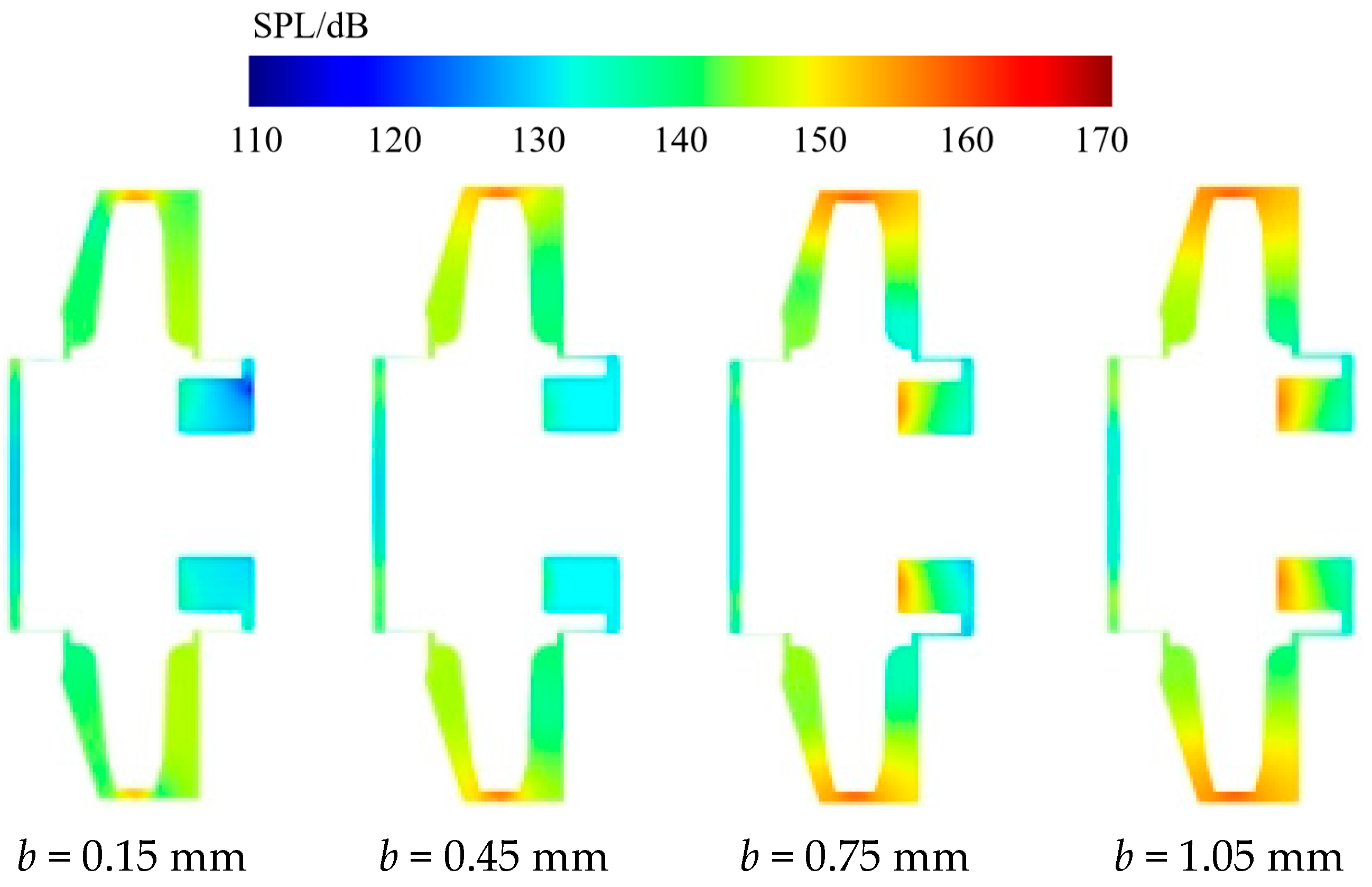
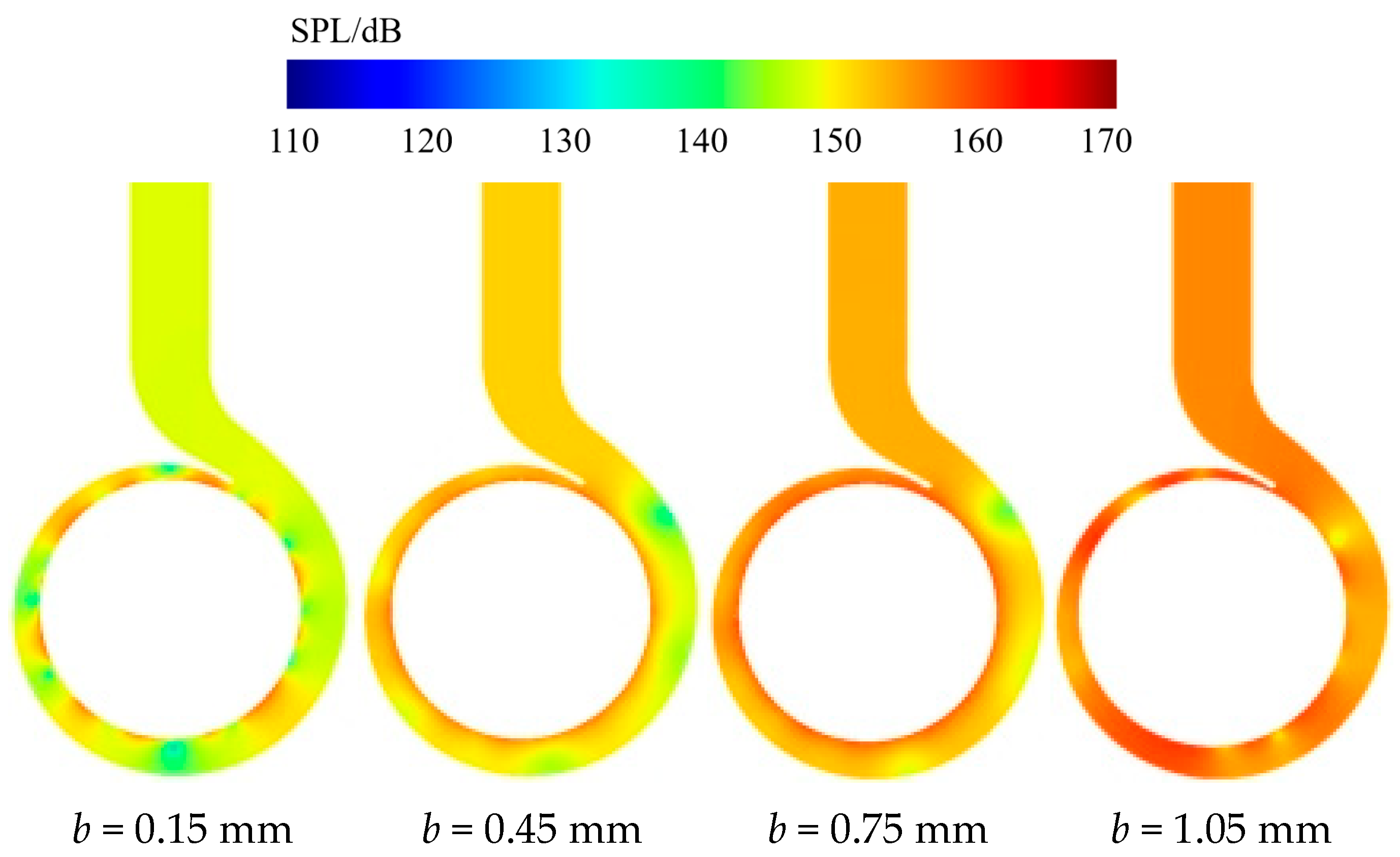
4.2. Sound Pressure Level Contour Analysis
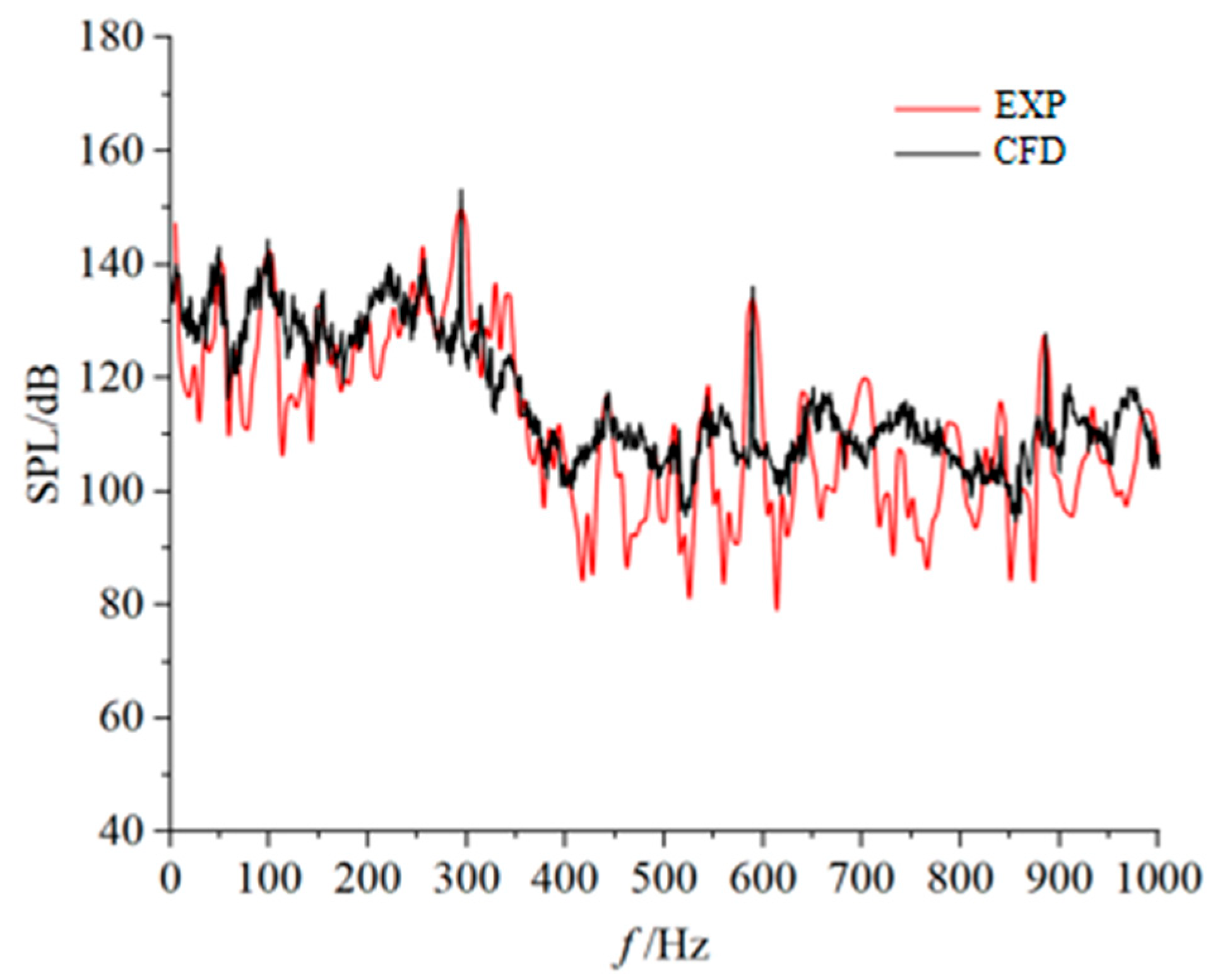
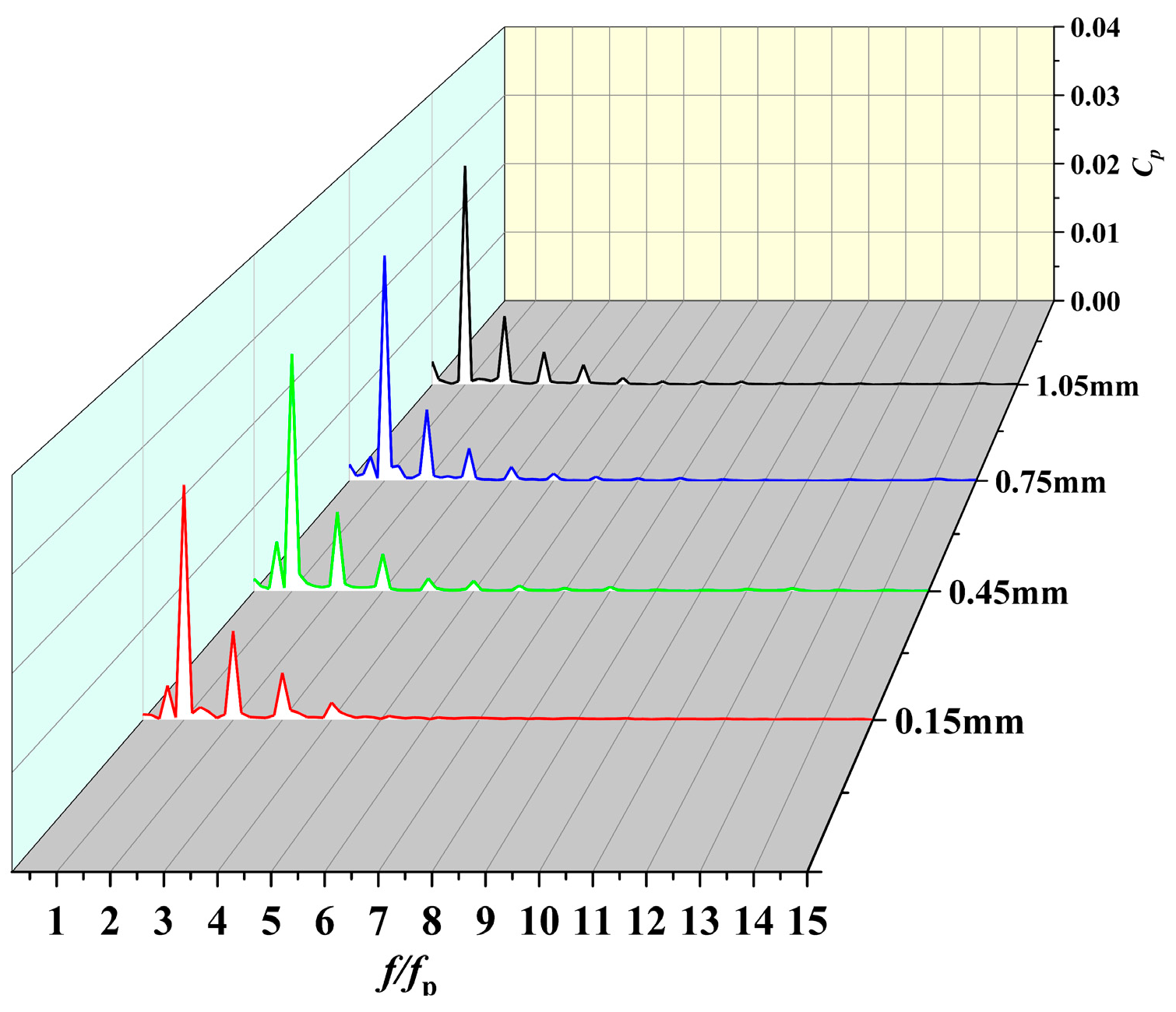
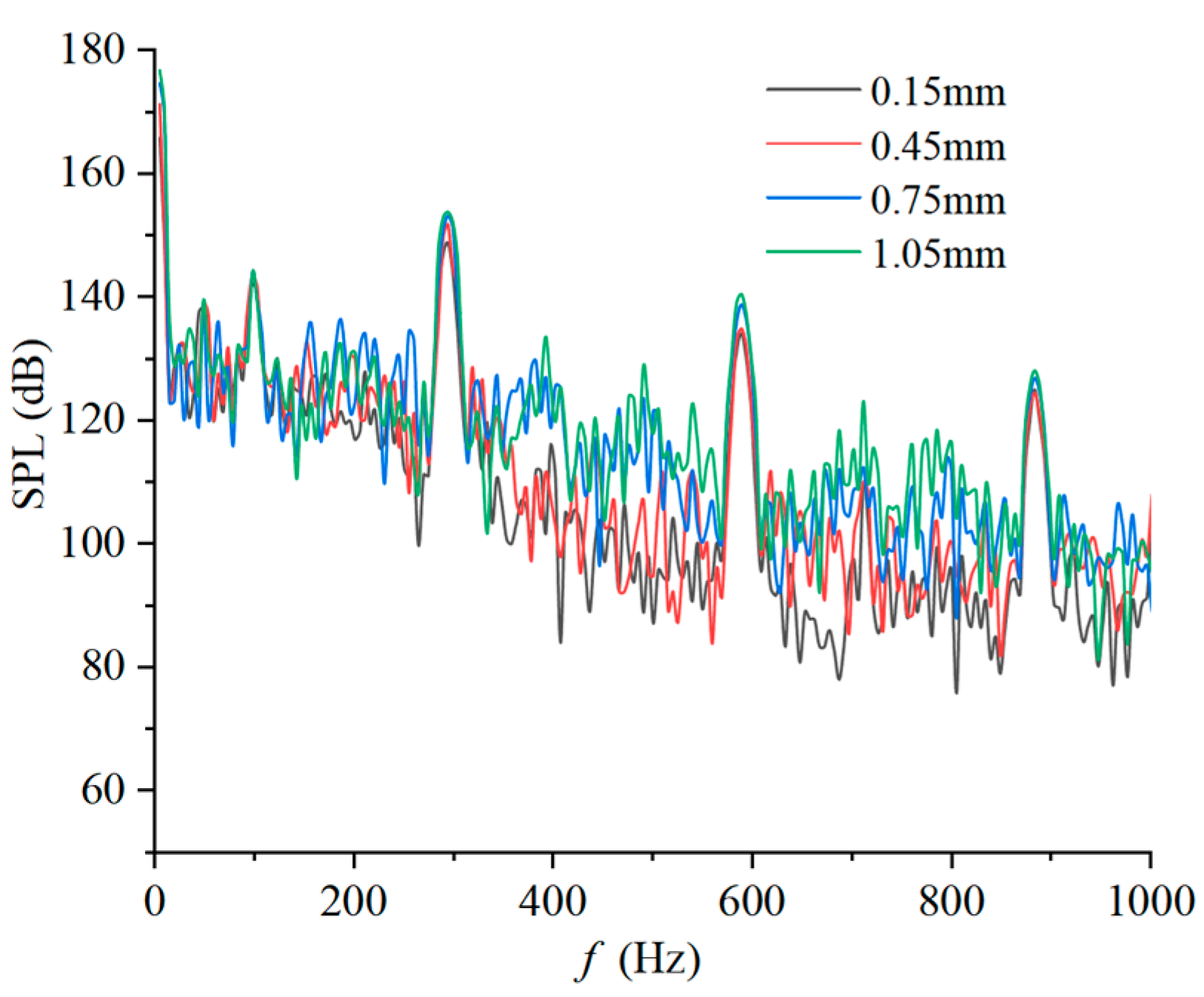
4.3. Sound Pressure Level Frequency Spectrum Curve Analysis
5. Conclusions
- 1
- With increasing back wear-ring clearance, both the head and efficiency of the centrifugal pump gradually decrease, though the head exhibits a relatively smaller reduction magnitude. For the 1.05 mm clearance scheme compared to 0.15 mm, the head decreases by 4.35% and efficiency reduces by 14.86%.
- 2
- With increased clearance, the low-pressure region at the impeller inlet enlarges, high-pressure areas develop around the balance holes, and pressure in the rear pump chamber drops markedly. Flow velocity within the rear chamber increases with multiple vortices developing; the high-RMS zone near the suction surface widens, while pressure fluctuations at the volute outlet intensify. The dominant frequency of pressure pulsations at the wear-ring clearance is the blade passing frequency (295 Hz), with its pulsation coefficient amplitude increasing by 12.9% under larger clearances.
- 3
- With enlarged back wear-ring clearance, radial force decreases by 38.6% (0.15→1.05 mm clearance) and loses 92% of its periodic component amplitude due to pressure field asymmetry. Axial force reverses 180° with magnitude increasing by 224% (from +45.6 N to −88.1 N at 0.45 mm clearance), while further clearance enlargement to 1.05 mm causes an additional 31% rise (to −115.3 N).
- 4
- Increasing back wear-ring clearance from 0.15 mm to 1.05 mm causes minor suction chamber changes but critically amplifies rotor–stator interface SWL by 62%, volute tongue energy density by 38%, and back ring outlet pulsation by 41%. High-intensity zones expand 112% near balance holes, while suction surface SPL rises 18.3 dB. Overall OASPL increases by 1.8 dB with 38% spatial expansion of high-SPL regions at rotor–stator interfaces.
- 5
- Across all clearances, the blade passing frequency (295 Hz) remains the dominant SPL frequency within the pump. As clearance increases from 0.15 mm to 1.05 mm, the overall internal SPL rises, with SPL at the blade frequency progressively increasing. Specifically, total SPL at 1.05 mm clearance is 1.8% higher than at 0.15 mm. For frequencies exceeding 350 Hz, SPL fluctuates between 80 and 140 dB.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| b | Back wear-ring clearance, mm |
| BPF | Blade Passing Frequency, Hz |
| c | Speed of sound in fluid, m/s |
| co | Reference sound speed in undisturbed fluid, m/s |
| Cp | Dimensionless pressure pulsation coefficient |
| CFD | Computational Fluid Dynamics, Method |
| f | Frequency, Hz |
| fmax | Maximum calculation frequency, Hz |
| FEM | Finite Element Method, Method |
| H | Pump head, m |
| k | Turbulent kinetic energy, m2/s2 |
| L | Acoustic grid size, m |
| Lp | Sound power level, dB |
| n | Rotational speed, rpm |
| OASPL | Overall Sound Pressure Level, dB |
| P | Instantaneous pressure, Pa |
| Po | Reference sound pressure, Pa |
| Pa | Sound power, W |
| Pref | Reference sound power, W |
| Qo | Design flow rate (25 m3/h), m3/h |
| RMS | Root Mean Square of pressure pulsation |
| SAS | Scale-Adaptive Simulation turbulence model, Model |
| SWL | Sound Power Level, dB |
| SPL | Sound Pressure Level, dB |
| SST | Shear Stress Transport turbulence model, Model |
| Tij | Lighthill stress tensor, N/m2 |
| u | Circumferential speed at impeller outer diameter, m/s |
| ut | Turbulent velocity, m/s |
| ω | Turbulent vortex frequency, rad/s |
| ρ | Fluid density, kg/m3 |
| ρ0 | Fluid density in undisturbed medium, kg/m3 |
| ε | Turbulent energy dissipation rate, m2/s3 |
| Δf | Frequency resolution (bin width), Hz |
References
- Yang, T.; Li, D.; Zhao, Y.-N.; Zhu, S.-C. Application of centrifugal pump and energy saving technical transformation. Chem. Manag. 2022, 12, 114–116. [Google Scholar]
- Luo, X.-Q.; Wu, D.-Z. The progress and development trend of pump technology. J. Hydroelectr. Power 2020, 39, 1–17. [Google Scholar] [CrossRef]
- Huo, Y.-W.; Yu, M.; Luo, X.-W.; Zhang, Y.; Ma, B.; Liu, D.-S.; Gao, J.-L. Research and technical development of centrifugal pump noise. Ship Sci. Technol. 2022, 44, 7–12. [Google Scholar]
- Luo, X.-W.; Ye, W.-X.; Song, X.-Y.; Geng, C. Future Fluid Machinery Technology Supporting the “Dual Carbon” Goal. J. Tsinghua Univ. (Nat. Sci. Ed.) 2022, 62, 678–692. [Google Scholar] [CrossRef]
- Yan, N.; Wang, X.; Wu, X.; Zhu, J. Study on the form of sealing ring and its sealing characteristics of centrifugal pump. J. Phys. Conf. Ser. 2024, 2752, 012117. [Google Scholar] [CrossRef]
- Mou, J.-G.; Chen, Z.-F.; Gu, Y.-Q.; Fan, T. Effect of sealing ring clearance on pump performance. World Pumps 2016, 2016, 38–41. [Google Scholar] [CrossRef]
- Wang, C.; Shi, W.-D.; Zhang, L.; Hu, Y.-C. Calculation formula optimization and effect of ring clearance on axial force of multistage pump. Math. Probl. Eng. 2013, 2023, 749375. [Google Scholar] [CrossRef]
- Zhao, W.-G.; Qiang, H.-H.; Xu, Q.; Liu, M. Influence of geometric parameters of front wear-ring of vertical self-priming pump on its self-priming performance. J. Irrig. Mech. Eng. 2024, 42, 333–341. [Google Scholar]
- Fu, Q.; Chen, Y.; Huang, Q.; Zhu, R.; Wang, X.; Lin, B. Influence of front ring clearance on internal flow characteristics of centrifugal pump. J. Chongqing Univ. Technol. (Nat. Sci.) 2022, 36, 203–209. [Google Scholar]
- Ayad, A.-F.; Abdalla, H.-M.; Aly, E.-A. Effect of semi-open impeller side clearance on the centrifugal pump performance using CFD. Aerosp. Sci. Technol. 2015, 47, 247–255. [Google Scholar] [CrossRef]
- Zhu, X.-Y.; Zhang, X.-Z.; Liu, J.-Y.; Zhang, Q. Numerical study on the influence of ring clearance on the performance of chemical canned motor pump. J. Shandong Jianzhu Univ. 2024, 39, 56–65. [Google Scholar]
- Luo, Y.; Zhang, W.; Fan, Y.; Han, Y.; Li, W.; Acheaw, E. Analysis of vibration characteristics of centrifugal pump mechanical seal under wear and damage degree. Shock. Vib. 2021, 2021, 1070–9622. [Google Scholar] [CrossRef]
- Isaev, N.; Budaev, G.; Danilovet, D.; Dobrokhodov, K. Investigation of the influence of wear in impeller seals on the axial force in double suction pumps. IOP Conf. Ser. Mater. Sci. Eng. 2020, 779, 012051. [Google Scholar] [CrossRef]
- Will, B.-C.; Benra, F.-K.; Dohmen, H.-J. Investigation of the flow in the impeller side clearances of a centrifugal pump with volute casing. J. Therm. Sci. 2012, 21, 197–208. [Google Scholar] [CrossRef]
- Cai, Y.; Xie, Z.; Yang, F.; Yan, M.; Mou, C.; Huang, Z.; Jin, Y.; Mou, J.; Gu, Y. Study on the Influence of Bionic Structure on the Sealing Performance of Centrifugal Pump Sealing Ring. Lubricants 2025, 13, 26. [Google Scholar] [CrossRef]
- Liu, H.-L.; Ding, J. Investigation into transient flow in a centrifugal pump with wear ring clearance variation. Adv. Mech. Eng. 2015, 6, 693097. [Google Scholar] [CrossRef]
- Zhang, N.; Gao, B.; Li, Z.; Ni, D.; Yang, M.; Jiang, Q. Experimental study on the effect of centrifugal pump mouth ring clearance on pressure pulsation characteristics. J. Eng. Thermophys. 2019, 40, 1520–1525. [Google Scholar]
- Mauro, G.; Pascal, B.; Sergio, A.; Mirasso, A.E. An application of the scale-adapted simulation to the unsteady flow across a tube bundle. Int. J. Heat Fluid Flow 2022, 96, 109007. [Google Scholar] [CrossRef]
- Song, Z.; Chen, Y.; Yu, T.; Wang, X.; Cao, H.; Li, Z.; Lang, X.; Xu, S.; Lu, S.; Jiang, C. Influence of the Trailing Edge Shape of Impeller Blades on Centrifugal Pumps with Unsteady Characteristics. Processes 2024, 12, 508. [Google Scholar] [CrossRef]
- Zhang, N.; Dong, H.; Zheng, F.; Gad, M.; Li, D.; Gao, B. Investigation of the Impact of Rotor-Stator Matching Modes on the Pressure Pulsations of the Guide Vane Centrifugal Pump. Ann. Nucl. Energy 2025, 214, 111189. [Google Scholar] [CrossRef]
- Li, N. On sound propagation characteristics of waterjet duct based on acoustic finite element method. Shipping 2023, 34, 50–55. [Google Scholar] [CrossRef]
- Lighthill, M.-J. On sound generated aerodynamically: Part I: General theory. Proc. R. Soc. Lond. 1952, 211, 564–587. [Google Scholar] [CrossRef]
- Ennouri, M.; Kanfoudi, H.; Bel Hadj Taher, A.; Zgolli, R. Numerical flow simulation and cavitation prediction in a centrifugal pump using an SST-SAS turbulence model. J. Appl. Fluid Mech. 2019, 12, 25–39. [Google Scholar] [CrossRef]
- Proudman, I. The generation of noise by isotropic turbulence. Proc. R. Soc. A 1952, 214, 119–132. [Google Scholar] [CrossRef]
- Lilley, G.-M. The radiated noise from isotropic turbulence. Theor. Comput. Fluid Dyn. 1994, 6, 281–301. [Google Scholar] [CrossRef]
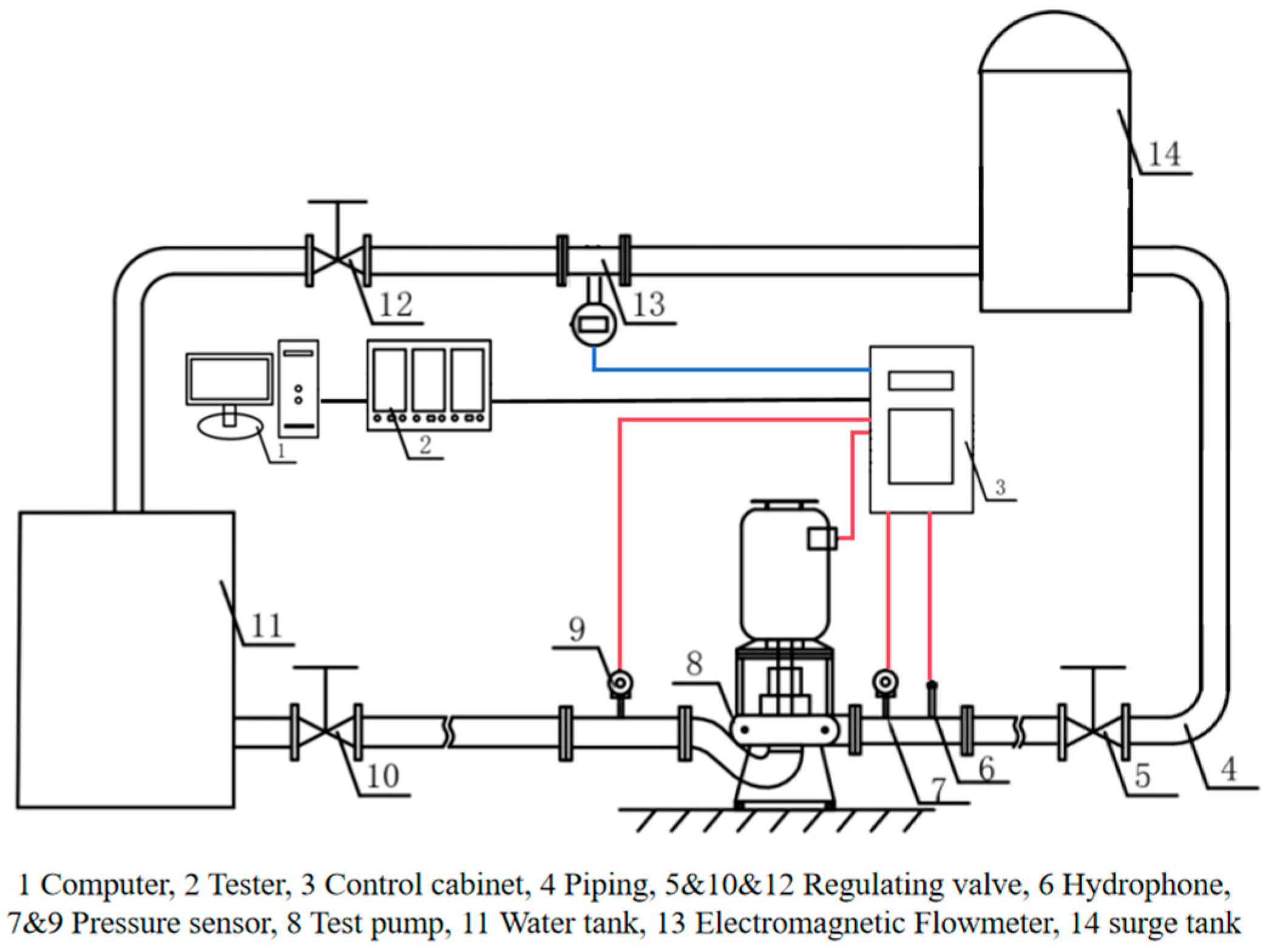
| Instrument Name | Model | Range | Accuracy |
|---|---|---|---|
| Electromagnetic Flowmeter | DXLD-50 | 0.1~85 m3/h | ±0.2% |
| Static pressure sensor | MEA3000 | 0~1 MPa | ±0.1% |
| Hydrophone | RHSA-10 | 20 Hz~200 kHz | ±2 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, P.; Tan, M.; Wu, X.; Liu, H.; Wu, D. Effect of Back Wear-Ring Clearance on the Internal Flow Noise in a Centrifugal Pump. Processes 2025, 13, 2641. https://doi.org/10.3390/pr13082641
Zhou P, Tan M, Wu X, Liu H, Wu D. Effect of Back Wear-Ring Clearance on the Internal Flow Noise in a Centrifugal Pump. Processes. 2025; 13(8):2641. https://doi.org/10.3390/pr13082641
Chicago/Turabian StyleZhou, Pengxuan, Minggao Tan, Xianfang Wu, Houlin Liu, and Denghao Wu. 2025. "Effect of Back Wear-Ring Clearance on the Internal Flow Noise in a Centrifugal Pump" Processes 13, no. 8: 2641. https://doi.org/10.3390/pr13082641
APA StyleZhou, P., Tan, M., Wu, X., Liu, H., & Wu, D. (2025). Effect of Back Wear-Ring Clearance on the Internal Flow Noise in a Centrifugal Pump. Processes, 13(8), 2641. https://doi.org/10.3390/pr13082641






