A Robust Fuzzy Adaptive Control Scheme for PMSM with Sliding Mode Dynamics

Abstract

A key trade-off persists in the control of permanent magnet synchronous motors (PMSMs): achieving fast finite-time convergence often exacerbates control chattering, while conventional chattering-suppression methods can compromise the system’s dynamic response. The existing literature often addresses these challenges in isolation. The core original contribution of this research lies in proposing a novel robust fuzzy adaptive control scheme that effectively resolves this trade-off through a synergistic design. The contributions are as follows: (1) A novel reaching law is formulated to significantly accelerate error convergence, achieving finite-time stability and improving upon conventional reaching law designs. (2) A super-twisting sliding mode observer is integrated into the control loop, providing accurate real-time estimation of load torque disturbances, which is used for feedforward compensation to drastically improve the system’s disturbance rejection capability. (3) A fuzzy adaptive mechanism is developed to dynamically tune key gains in the sliding mode law. This approach effectively suppresses chattering without sacrificing response speed, enhancing system robustness. (4) The stability and convergence of the proposed controller are rigorously analyzed. Simulations, comparing the proposed method with conventional adaptive sliding mode control (ASMC), demonstrate its marked superiority in control accuracy, transient behavior, and disturbance rejection. This work provides an integrated solution that balances rapidity and smoothness for high-performance motor control, offering significant theoretical and engineering value.

1. Introduction

Due to their high efficiency, high power density, excellent reliability, and wide speed regulation range, permanent magnet synchronous motors (PMSMs) are widely adopted in high-performance application fields such as industrial automation, electric vehicles, and aerospace systems. Nevertheless, PMSMs are characterized by nonlinear dynamics and strong coupling, making their control particularly challenging in real-world scenarios. Their performance is often affected by variations in internal parameters—such as resistance, inductance, and permanent magnet flux linkage—caused by factors like temperature fluctuations and magnetic saturation. Moreover, external disturbances, including load torque variations and supply voltage fluctuations, can further degrade system stability. These combined uncertainties limit the effectiveness of conventional control strategies in achieving high precision, fast dynamic response, and robust performance. Consequently, developing advanced control methodologies to optimize the system’s dynamic and steady-state characteristics of PMSMs holds substantial theoretical and practical value [1,2].

To enhance the control performance of PMSMs, various control strategies have been introduced in the recent literature. Vector control enables precise decoupling of current components, while direct torque control (DTC) is known for its fast dynamic response [3]. Proportional–integral (PI) control is widely adopted due to its simplicity and ease of implementation [4]. Neural network-based controllers are capable of handling complex nonlinear behaviors [5], and active disturbance rejection control (ADRC) offers strong disturbance rejection capabilities [6]. Among these approaches, sliding mode control (SMC) has demonstrated distinctive advantages in PMSM applications, attributed to its strong robustness, rapid response, and high adaptability to parameter variations and external disturbances [7]. By designing a specific sliding surface, SMC guides the system states to evolve along a predefined trajectory, thereby achieving effective and robust control of the motor system.

Most conventional sliding mode control (SMC) schemes rely on asymptotic stability, which implies that system stability is achieved only as time approaches infinity—a condition that is impractical for real-time applications [8,9]. To address this limitation, various accelerated convergence techniques have been developed. For instance, Ref. [10] proposed a fast terminal sliding mode structure that initiates system motion directly on the sliding surface, thereby significantly reducing error convergence time. In [11], an improved reaching law was introduced to enable finite-time convergence to the sliding surface. Although these approaches enhance convergence speed, their settling time remains dependent on the original conditions, making it difficult to achieve uniform dynamic behavior under varying operating conditions. To overcome this issue, we propose a fixed-time sliding mode control strategy, which guarantees convergence to the sliding surface within a predefined fixed time, independent of the initial state [12].

Despite the numerous advantages of sliding mode control (SMC), the chattering phenomenon remains a significant challenge in practical applications. Chattering is typically caused by fluctuations in control gains and the high-frequency switching nature of the control law [13]. To mitigate this issue, several approaches have been proposed. In [14], a recursive fast terminal sliding mode structure was introduced to enforce system trajectories to begin directly on the sliding surface, thereby accelerating the convergence of tracking errors. An improved dual-power reaching law was proposed. In [15], where state-dependent power terms were incorporated to introduce variable-speed convergence characteristics, enabling finite-time reachability of the sliding surface. However, these methods often struggle to simultaneously satisfy the requirements of rapidity and accuracy under diverse operating conditions. To resolve this issue, we propose an adaptive fuzzy sliding mode control strategy, in which critical parameters of the control law are dynamically tuned using an adaptive fuzzy algorithm. This approach enhances the system’s ability to cope with model uncertainties and complex disturbances, thereby enhancing the control accuracy, dynamic response, and robustness of PMSM systems [16,17]. Similarly, another recent work by Yang combined a prescribed performance control strategy with a fixed-time sliding mode controller to enhance the dynamic response and minimize speed errors in motor systems [18]. In [19], a model-free adaptive fuzzy sliding-mode observer was proposed, which innovatively uses fuzzy rules to compensate for observer errors without relying on an accurate system model. However, many of these advanced methods still face challenges in achieving a balance between fast convergence and chattering suppression, or they rely on complex algorithms that are difficult to implement. This highlights an existing gap for a control strategy that synergistically combines guaranteed finite-time convergence, robust chattering suppression, and practical implementation simplicity, which is the primary motivation for our work.

This paper proposes a novel control scheme for PMSMs based on adaptive fuzzy sliding mode control. The method integrates the adaptability of fuzzy logic control, the fast response and determinism of sliding mode control, and the robustness of adaptive control to construct a composite control strategy. By dynamically tuning key parameters of the sliding mode control law via an adaptive fuzzy algorithm, the proposed approach achieves effective compensation for system uncertainties and varying operating conditions, thereby enhancing the robustness, control accuracy, and dynamic performance of PMSM systems.

This work makes the following key contributions: (1) A fixed-time sliding mode control strategy is introduced to accelerate convergence speed, independent of initial conditions. (2) A hybrid control strategy combining adaptive and fuzzy control is developed to suppress chattering and improve system robustness under complex disturbances. (3) Both simulation and experimental verification highlight the efficacy and superiority of the proposed control strategy.

2. Mathematical Model of PMSMs

Configuration and Structure of the PMSM

To better comprehend the system’s operational behavior of PMSMs and to design effective control schemes, it is essential to establish an accurate mathematical model. The PMSM model is mainly composed of two components: the electrical subsystem and the mechanical subsystem. The following subsections present the current equations, torque expression, and mechanical motion equation. Figure 1 shows the structure of PMSM.

In the PMSM modeling framework, the voltage–current equations describe the dynamic relationship between the stator voltages and currents. By transforming the three-phase system into the $d-q$ rotating reference frame, the system’s voltage–current dynamics are formulated as follows:

$$\left\{\begin{array}{l}{v}_d=R_i{i}_d+L_d{\displaystyle \frac{d{i}_d}{dt}}-w_e{L}_q{i}_q\hfill \\ v_q=R_i{i}_q+L_q{\displaystyle \frac{d{i}_q}{dt}}+w_e\left(L_d{i}_d+{\lambda }_m\right)\hfill \end{array}\right.$$

(1)

where $i_q$ and $i_d$ are the corresponding axis currents; $v_q$ and $v_d$ denote the voltages along the quadrature and direct axes, respectively; $L_q$ and $L_d$ are the corresponding axis inductances; $w_e$ is the electrical angular velocity; $R_i$ denotes the stator resistance; ${\lambda }_m$ denotes the flux linkage generated by the permanent magnets. The voltage–current dynamics in the $d-q$ reference frame reveal the distribution and coupling behavior of stator currents with respect to the rotating magnetic field, thereby providing physical insight into the direct regulation of flux and torque.

In a PMSM, the electromagnetic torque is chiefly produced by the interplay of the stator current and magnetic flux, and it is calculated as follows:

$$T_e={\displaystyle \frac{3}{2}}p\left[{\lambda }_m{i}_q+\left(L_d-L_q\right)i_d{i}_q\right]$$

(2)

where $p$ represents the motor’s pole pair count. According to the torque equation, the magnitude of the electromagnetic torque is directly associated with the permanent magnet flux linkage ${\lambda }_m$ and the q-axis current $i_q$, and is also affected by the d-axis current $i_d$, the inductances $L_d$ and $L_q$.

The mechanical dynamics of the motor are characterized by the interaction between the load torque and the electromagnetic torque. The mechanical motion equation encapsulates the combined influence of the electromagnetic torque, load torque, and frictional forces, indicating that the variation in rotational speed is governed by the resultant torque obtained after the electromagnetic torque counteracts frictional resistance and the load torque. The governing equation can be expressed as:

$$J{\displaystyle \frac{d{w}_m}{dt}}=T_e-T_L-B{w}_m$$

(3)

where $J$ denotes the rotor’s moment of inertia, $w_m$ is the mechanical angular velocity of the rotor, $T_e$ represents the electromagnetic torque, $T_L$ is the load torque, and $B$ is the rotational friction coefficient.

3. Adaptive Fuzzy Sliding Mode Reaching Law

3.1. Reaching Law Design

The reaching law is a critical component in sliding mode control. Its purpose is to drive the system from any original position to the sliding surface rapidly and then ensure convergence along the surface toward the target. An appropriate reaching law should not only guarantee a fast convergence rate but also minimize chattering, thereby enhancing the system’s robustness. The conventional exponential reaching law is stated as:

$$\dot{s}=-\epsilon sgn\left(s\right)-ks$$

(4)

In the equation, $s$ denotes the sliding surface function, while $\epsilon$ and $k$ are positive constants that determine the speed at which the control system approaches the sliding surface. Increasing the value of $\epsilon$ can improve the convergence rate, thereby enhancing the dynamic performance; however, it may also exacerbate the chattering phenomenon. Based on the exponential reaching law and incorporating fuzzy control and adaptive control concepts, we propose the following adaptive fuzzy sliding mode reaching law:

$$\dot{s}=-\epsilon m{\left|s\right|}^{a}tanh\left(s\right)-k^{\ast }{\left|s\right|}^{c}sgn\left(s\right)$$

(5)

To intuitively compare the dynamic characteristics of the two approaches, Figure 2 plots the phase trajectories of the proposed reaching law and a conventional one.

The sliding mode convergence law shown in Equation (5) can be split into the following two parts:

$$\begin{array}{c}{u}_1\left(s\right)=-\epsilon m{\left|s\right|}^{a}tanh\left(s\right)\\ u_2\left(s\right)=-k^{\ast }{\left|s\right|}^{c}sgn\left(s\right)\end{array}$$

$u_1\left(s\right)$ is referred to as the strong reaching term, primarily responsible for providing a substantial convergence driving force when the state variables are separated from the sliding surface (i.e., when $\left|s\right|$ is large).

$u_2\left(s\right)$ is referred to as the weak reaching term, which serves to maintain continuous convergence and effectively suppress chattering when the system state nears the sliding surface (i.e., as $\left|s\right|$ tends to zero).

When the state variables are significantly separated from the sliding surface, $\left|s\right|$ is large, and $tanh\left(s\right)\approx sgn\left(s\right)$; therefore, the strong reaching term can be approximated as:

$$u_1\left(s\right)\approx -\epsilon m{\left|s\right|}^a\mathrm{sgn}\left(s\right)$$

At this time, due to the rapid growth of ${\left|s\right|}^a$, this term dominates the system’s convergence behavior, providing a larger reaching torque that accelerates the system’s convergence to the sliding surface. Meanwhile, owing to the nonlinear amplification characteristic of this term, the reaching time can be effectively shortened, thereby enhancing the dynamic performance during the reaching phase.

In the course of approaching the sliding mode surface (i.e., $\left|s\right|$ tends to zero), the strong reaching term gradually diminishes, with $u_1\left(s\right)\to 0$. At this stage, under the setting of $0<c<1$, the weak reaching term $u_2\left(s\right)$ can still provide a certain magnitude of reaching effect.

To further reduce rapid control switching in the vicinity of the sliding surface and mitigate the risk of chattering, this study employs a fuzzy algorithm to dynamically adjust the gain parameters, decreasing them as the state variables gradually reach the sliding surface. This design significantly weakens the switching intensity near the sliding surface, enhances the smoothness after the system enters the sliding mode, and enhances the system’s performance in steady-state conditions.

3.2. The Adjustment Model of the Tuning Factor m

To achieve a trade-off between fast convergence in the reaching phase and smooth steady-state behavior, the following adjustment mechanism is adopted in this study:

$$\dot{m}=-p\cdot m\cdot \left|s\right|-w\cdot m$$

(6)

In this model, $\dot{m}$ denotes the time derivative of the tuning factor $m$, while $p$ is a positive constant that controls the sensitivity of $m$ to variations in $s$. The parameter $w$ is another positive constant that enables the system to decay independently to some extent.

When $s$ is large, the term $-p\cdot m\cdot \left|s\right|$ exerts a strong influence on the rate of change of $m$, enabling rapid adjustment of $m$ and facilitating fast convergence toward the sliding surface. Conversely, when $s$ is small, the variation rate of $m$ decreases but does not vanish, due to the independent decay effect introduced by $-w\cdot m$. This helps to further suppress excessive control adjustment or chattering near the sliding surface.

From Equation (6), it can be observed that the term $-p\cdot m\cdot \left|s\right|$ combines exponential decay with an integral control strategy; the exponential decay enhances the convergence rate, while the integral component ensures the smooth handling of long-term error, preventing overshoot and chattering. This effectively improves both the convergence performance and the resilience of the system.

The decay term $-w\cdot m$ independently regulates the attenuation of $m$, providing an additional damping effect as the system approaches the sliding surface, which further reduces the likelihood of excessive control action or chattering near the sliding surface.

By introducing this model, the tuning factor $m$ can be dynamically adjusted in real time based on the evolution of the system error. Compared with conventional fixed-gain approaches, this error-driven suppressive tuning law achieves a better dynamic balance between convergence assurance and steady-state oscillation reduction, thereby significantly enhancing system robustness and control smoothness.

3.3. Fuzzy Control Model

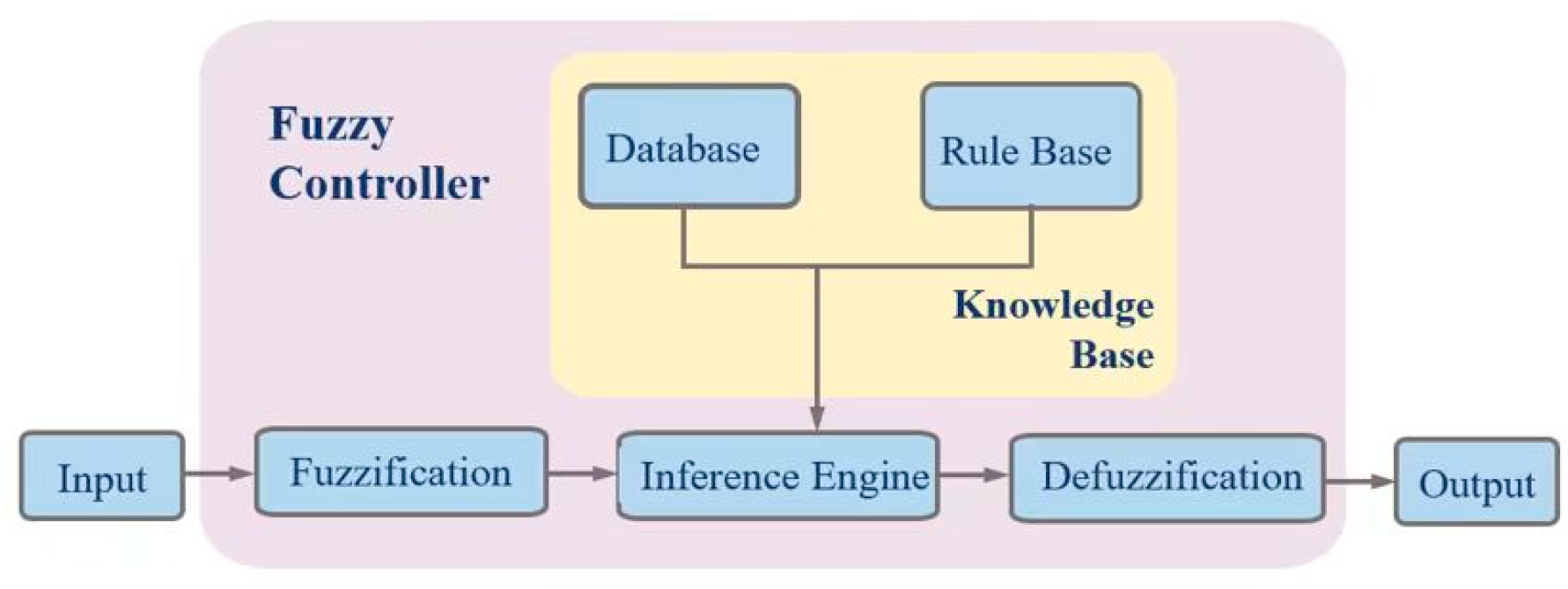
To further improve the system’s resilience and optimize the performance of the reaching law, a fuzzy control algorithm is incorporated to adaptively regulate the control gain $k^{\ast }$ within the reaching law. Figure 3 shows the working principle of fuzzy control:

In this design, the universes of discourse for the fuzzy controller’s parameters are carefully defined based on the actual operating characteristics of the motor and its drive system, ensuring the effectiveness and robustness of fuzzy inference across the full operating range.

First, through experimental analysis of the motor system’s dynamic response, the value ranges of the control error $e$ and its rate of change (which may be chosen as either $\dot{e}$ or the sliding mode variable $s$) are obtained under both steady-state conditions and representative disturbances. Based on the experimental data, a normal distribution is assumed to model the statistical behavior of the error. The interval of $\pm 3\sigma$ is then selected as the primary operating range, which defines the universes of discourse for the fuzzy controller’s input variables.

This method effectively covers the system’s behavior within a 99.7% confidence level, ensuring the generality and practical applicability of the fuzzy control scheme.

Secondly, real-time system error and sliding mode reaching law serve as input variables to the fuzzy controller. By introducing a dual-input fuzzy rule base, both the state error and the approach behavior toward the sliding surface are considered simultaneously, enabling multidimensional adaptive adjustment of the control gain.

Each input variable is categorized into five fuzzy linguistic terms: positive big (PB), positive small (PS), zero (ZO), negative small (NS), and negative big (NB). The output is a fuzzy quantity used for the dynamic tuning of the control gain, which is categorized into five fuzzy levels: TINY, SMALL, SECONDARY, BIG, and HUGE, abbreviated in the rule table as TI, SM, SE, BI, and HU, respectively. The fuzzy rules are shown in

Table 1. Fuzzy inference rule base for the adaptive gain.

s/e	NB	NS	ZO	PS	PB
NB	HU	BI	SE	BI	HU
NS	BI	SE	SM	SE	BI
ZO	SE	SM	TI	SM	SE
PS	BI	SE	SM	SE	BI
PB	HU	BI	SE	BI	HU

.

Based on extensive simulations and experimental results, and considering the varying adjustment magnitudes required during the sliding mode reaching process, a fuzzy control rule table has been formulated (see Table 1). The underlying principle is as follows:

When the error $e$ or the sliding mode reaching variable $s$ is large, the fuzzy inference yields a relatively high control gain (BI or HU) to promptly eliminate significant dynamic deviations. As the system error gradually decreases and approaches zero, the controller outputs a smaller gain (SM or TI) to reduce the switching intensity near the sliding surface and avoid the introduction of undesired high-frequency dynamics.

Moreover, to further enhance the smoothness of the adjustment, symmetric triangular membership functions are employed for fuzzifying the input variables. This design improves the sensitivity of the inference process to small perturbations, thereby strengthening the system’s fine-tuning capability.

3.4. Stability Analysis of the Controller

Stability analysis of the adaptive fuzzy sliding mode control begins with the definition of the Lyapunov function: $V\left(s\right)=s^2$. Taking its time derivative yields:

$$\dot{V}\left(s\right)=2s\dot{s}$$

(7)

Combining with Equation (5), we obtain:

$$\begin{gathered} \dot{V}\left(s\right)=2s\left[-\epsilon m{\left|s\right|}^a\tan \mathrm{h}(s)-k^{\ast }{\left|s\right|}^{c}sgn\left(s\right)\right] \\ =-2\epsilon m{\left|s\right|}^{a+1}\left|\tan \mathrm{h}(s)\right|-2k^{\ast }{\left|s\right|}^{c+1}\le 0 \end{gathered}$$

In summary, the adaptive fuzzy sliding mode controller has been proven stable.

4. Design of PMSM Sliding Mode Controller

This chapter aims to design an online observer capable of real-time and accurate estimation of unknown load torque. By introducing the observed disturbance value as a feedforward compensation signal into the main controller, the system can anticipate and compensate for disturbances before they have a significant impact, thereby achieving active “cancellation” of the disturbance.

4.1. System Model for Observer Design

In the PMSM drive system analyzed in this paper, minor effects such as frictional damping are neglected, and the dynamics of the motor’s rotating part can be simplified as:

$$J\dot{w}=K_t{i}_q-T_L$$

(8)

The electromagnetic torque coefficient is defined as $K_t=1.5P_n{\psi }_f$. This simplified model neglects frictional damping and other higher-order nonlinear effects, highlighting the direct driving effect of $i_q$ on the speed variation, while treating $T_L$ as an unknown but bounded disturbance.

To achieve effective estimation of the unmeasurable load disturbance and enhance the system’s adaptability to external disturbances and model uncertainties, this study treats the unknown disturbance as a state variable. An augmented state-space model is constructed to facilitate the observer design. Specifically, the state vector is defined as:

$$x=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}\omega \\ T_L\end{array}\right]$$

Then the system can be rewritten as:

$$\left\{\begin{array}{l}{\dot{x}}_1={\displaystyle \frac{K_t}{J}}{i}_q-{\displaystyle \frac{1}{J}}{x}_2\hfill \\ {\dot{x}}_2=h\left(t\right)\hfill \end{array}\right.$$

(9)

where $h\left(t\right)$ refers to the load torque’s rate of change, which is an unknown but bound function. Since the rotor speed ${\omega }_r$ is accessible via direct measurement with sensors, the system output is naturally defined as $y={\omega }_r$.

Based on this, this study designs a super-twisting sliding mode observer to simultaneously evaluate the motor speed and the unknown load torque. Its structure is as follows:

$$\left\{\begin{array}{l}{\dot{\widehat{x}}}_1={\displaystyle \frac{K_t}{J}}{i}_q-{\displaystyle \frac{1}{J}}{\widehat{x}}_2+k_1|e_1{|}^{{\displaystyle \frac{1}{2}}}\mathrm{sgn}\left(e_1\right)\hfill \\ {\dot{\widehat{x}}}_2=k_2\mathrm{sgn}\left(e_1\right)\hfill \end{array}\right.$$

(10)

All correction actions of the observer are derived from the computable speed observation error $e_1$:

$$e_1=x_1-{\widehat{x}}_1=\omega -{\widehat{\omega }}_1$$

(11)

The design of this observer fully leverages the output error $e_1$ as the sole feedback signal to drive the update of the two-dimensional state estimates. By injecting a sliding mode compensation based on $e_1$, the system achieves strong robustness. In the first equation, a super-twisting nonlinear term involving $|e_1{|}^{1/2}$ is introduced into the speed estimation. Compared with conventional linear sliding terms, this term provides a stronger convergence force when the error is large, accelerating convergence, while adaptively reducing the gain when the error is small, thereby effectively suppressing chattering. The second equation integrates the sign function $\mathrm{sgn}\left(e_1\right)$ to dynamically reconstruct the unknown disturbance in real time, enabling the load torque estimate to rapidly follow once the speed converges.

Compared with classical Luenberger observers or conventional sliding mode observers, the super-twisting sliding mode structure adopted in this study offers a balanced combination of fast convergence and chattering suppression. Its coupled second-order dynamics take full advantage of the system’s physical characteristics. By utilizing the sliding mode convergence of the speed observation error to indirectly drive the disturbance estimation process, high-precision reconstruction of the load disturbance is achieved. This significantly enhances the system’s adaptability and robustness under load transients or parameter uncertainties.

The structure of this observer not only reflects the multi-derivative convergence mechanism of sliding mode observation in mathematical form but also avoids the need for high-order derivative computations and excessive sensors in practical implementation. This simplifies the hardware structure and lays a solid foundation for subsequent compensation control based on the estimated values.

To further verify the stability of the proposed observer, the following sections will conduct a rigorous convergence analysis of the error dynamics using the Lyapunov method.

4.2. Stability Analysis of the Observer

Lyapunov stability analysis is employed to investigate the error dynamics of the proposed super-twisting sliding mode observer and assess its convergence properties. To facilitate the analysis, new state variables are introduced as follows:

$${\zeta }_1=|e_1{|}^{{\displaystyle \frac{1}{2}}}\mathrm{sgn}\left(e_1\right),{\zeta }_2=e_2$$

where $e_2=x_2-{\widehat{x}}_2$ represents the torque observation error, i.e., the estimation error between the actual load torque and its observed value.

A quadratic Lyapunov candidate function is selected in the following form:

$$V\left(\zeta \right)={\zeta }^{T}P\zeta$$

(12)

where

$$P=\left[\begin{array}{cc}{\displaystyle \frac{k_1^2}{2}}+2k_2& -{\displaystyle \frac{k_1}{2J}}\\ -{\displaystyle \frac{k_1}{2J}}& {\displaystyle \frac{1}{J^2}}\end{array}\right]$$

To ensure that $V\left(\zeta \right)$ is a strictly positive definite function, the matrix $P$ must be positive definite. According to the leading principal minor criterion for symmetric matrices, this condition is satisfied as long as:

$$\begin{gathered} {\displaystyle \frac{k_1^2}{2}}+2k_2>0 \\ \det \left(P\right)={\displaystyle \frac{1}{J^2}}\left({\displaystyle \frac{k_1^2}{4}}+2k_2\right)>0 \end{gathered}$$

Therefore, if the gains $k_1, k_2>0$ are chosen to satisfy the following condition:

$${\displaystyle \frac{k_1^2}{4}}+2k_2>0$$

(13)

then $P$ is a positive definite matrix, and consequently $V\left(\zeta \right)$ is a function of positive definite with respect to $\zeta$.

The time derivative of $V\left(\zeta \right)$ is:

$$\dot{V}\left(\zeta \right)={\dot{\zeta }}^{T}P\zeta +{\zeta }^{T}P\dot{\zeta }=2{\dot{\zeta }}^{T}P\zeta$$

(14)

The error system dynamics are:

$$\begin{array}{c}{\dot{\zeta }}_1=-{\displaystyle \frac{1}{2J\left|{\zeta }_1\right|}}{\zeta }_2-{\displaystyle \frac{k_1}{2\left|{\zeta }_1\right|}}{\zeta }_1\\ {\dot{\zeta }}_2=h\left(t\right)-k_2{\displaystyle \frac{{\zeta }_1}{\left|{\zeta }_1\right|}}\end{array}$$

Substituting it into Equation (14):

$$\dot{V}\left(\zeta \right)=-{\displaystyle \frac{1}{\left|{\zeta }_1\right|}}{\zeta }^{\mathrm{T}}Q\zeta +{\displaystyle \frac{h\left(t\right)}{J}}\left(-{\displaystyle \frac{k_1}{J}}{\zeta }_1+{\displaystyle \frac{2}{J}}{\zeta }_2\right)$$

(15)

where

$$Q=\left[\begin{array}{cc}{\displaystyle \frac{k_1}{2}}\left({\displaystyle \frac{k_1^2}{2}}+2k_2-{\displaystyle \frac{k_2}{J}}\right)& 0\\ 0& {\displaystyle \frac{k_1}{2J^2}}\end{array}\right]$$

By selecting appropriate gains $k_1$ and $k_2$, matrix $Q$ can be ensured to be diagonal and positive definite; that is, there exists $\alpha >0$ such that:

$${\zeta }^{\mathrm{T}}Q\zeta \ge \alpha \Vert \zeta {\Vert }^2$$

(16)

On the other hand, the disturbance term satisfies

$$\begin{array}{cc}\left|{\displaystyle \frac{h\left(t\right)}{J}}\left(-{\displaystyle \frac{k_1}{J}}{\zeta }_1+{\displaystyle \frac{2}{J}}{\zeta }_2\right)\right|& \le {\displaystyle \frac{\left|h\left(t\right)\right|}{J}}\left({\displaystyle \frac{k_1}{J}}\left|{\zeta }_1\right|+{\displaystyle \frac{2}{J}}\left|{\zeta }_2\right|\right)\hfill \\ & \le H_{max}{c}_1\Vert \zeta \Vert \hfill \end{array}$$

(17)

where $H_{\max }$ is the known upper bound of $h\left(t\right)$, and $c_1$ is a constant determined by the gains and $J$.

In summary, it can be concluded that:

$$\dot{V}\left(\zeta \right)\le -{\displaystyle \frac{1}{\left|{\zeta }_1\right|}}{\zeta }^{T}Q\zeta +H_{max}{c}_1\Vert \zeta \Vert \le -W\left(\zeta \right)+H_{max}{c}_1\Vert \zeta \Vert$$

(18)

where $W\left(\zeta \right)={\displaystyle \frac{1}{\left|{\zeta }_1\right|}}{\zeta }^{T}Q\zeta$ is a function that is positive definite.

In order to guarantee that the system maintains convergence under bounded disturbances, increasing $k_2$ (specifically ensuring $k_2>J{H}_{\max }$) allows the negative term $W\left(\zeta \right)$ to dominate, thereby further guaranteeing that:

$$\dot{V}\left(\zeta \right)\le -W_0\left(\zeta \right)$$

(19)

where $W_0\left(\zeta \right)$ is another positive definite function.

Therefore, according to Lyapunov stability theory, the system’s error dynamics are asymptotically bounded and, under ideal conditions, converge to zero, thereby rigorously proving the stability and robustness of the designed super-twisting SMC-based observer.

5. PMSM SMC Design

Sliding Mode Controller

Based on the PMSM detailed in the Configuration and Structure of the PMSM Section, the simplified dynamics of the motor can be derived by combining the voltage equations and the mechanical equations as follows:

$$J\dot{w}=1.5p_n{\psi }_f{i}_q-T_L$$

(20)

where $\dot{\omega }$ is the derivative of the motor’s rotational speed; $p_n$ denotes the number of pole pairs; ${\psi }_f$ is the permanent magnet flux linkage; $i_q$ is the motor’s torque-producing current component; and $T_L$ is the load torque. $J$ is the moment of inertia.

For subsequent analysis and to facilitate controller design, the following state variables are introduced:

$$\left\{\begin{array}{l}{x}_1={\omega }_d-\omega \hfill \\ x_2=x_1=-\dot{\omega }\hfill \end{array}\right.$$

(21)

where ${\mathsf{\omega }}_d$ denotes the desired mechanical angular velocity, which can be obtained from Equation (20) as:

$$\left\{\begin{array}{l}{\dot{x}}_1=-\dot{\omega }={\displaystyle \frac{1}{J}}\left(T_L-1.5p_n{\psi }_f{i}_q\right)\hfill \\ {\dot{x}}_2=-\ddot{\omega }=-{\displaystyle \frac{1.5p_n{\psi }_f}{J}}{i}_q\hfill \end{array}\right.$$

(22)

To further simplify, define the input variables $u={\dot{i}}_q$, $\rho ={\displaystyle \raisebox{1ex}{$1.5p_n{\psi }_f$}\!\left/ \!\raisebox{-1ex}{$J$}\right.}$, and, on the basis of the system model, the following state equations are obtained:

$$\left[\begin{array}{c}{\dot{x}}_1\\ {\dot{x}}_2\end{array}\right]=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\left[\begin{array}{c}0\\ -\rho \end{array}\right]u$$

(23)

To ensure the system converges rapidly and robustly to the desired state, the following linear sliding surface is selected:

$$s=\gamma x_1+x_2$$

(24)

where $\gamma >0$ functions as a design parameter for adjusting the sliding surface’s slope. The design of this sliding surface integrates the position error $x_1$ and the velocity error $x_2$, balancing steady-state accuracy with dynamic response speed.

By computing the derivative of the sliding surface, we obtain:

$$\dot{s}=\gamma x_2+{\dot{x}}_2=\gamma x_2-\rho u$$

(25)

To guarantee the system attains the sliding surface in bounded time from any initial state, an enhanced reaching law incorporating super-twisting and saturation terms as in Equation (5) is adopted. Combining this with the expression for $\dot{s}$, the control law can be derived as:

$$u={\displaystyle \frac{1}{\rho }}\left[\gamma x_2+\epsilon m{\left|s\right|}^a\tan \mathrm{h}\left(s\right)+k^{\ast }{\left|s\right|}^c\mathrm{sgn}\left(s\right)\right]$$

(26)

By integrating, the reference feedback component of the q-axis current is given by:

$$i_{q,fb}={\displaystyle \frac{1}{\rho }}{\displaystyle \int \left[\gamma x_2+\epsilon m{\left|s\right|}^a\tan \mathrm{h}\left(s\right)+k^{\ast }{\left|s\right|}^c\mathrm{sgn}\left(s\right)\right]dt}$$

(27)

To boost the system’s capability to withstand disturbances, a load torque feedforward compensation based on the STSMO (super-twisting sliding mode observer) designed in Section 4 is introduced:

$$i_{q,ff}^{\ast }={\displaystyle \frac{{\widehat{T}}_L}{K_t}}={\displaystyle \frac{{\widehat{T}}_L}{1.5P_n{\psi }_f}}$$

(28)

Thus, the composite reference current command is obtained as:

$$i_q^{\ast }=i_{q,fb}+i_{q,ff}^{\ast }$$

(29)

Through this structure, the sliding mode controller suppresses internal model errors and minor disturbances via feedback, while the feedforward component actively compensates for external load disturbances, achieving faster response and reduced steady-state error. The synergy of both parts significantly enhances the system’s resilience to external perturbations and parameter variations. The structure diagram of the system is shown in Figure 4.

6. Simulation Results Analysis

To verify the dynamic performance and controller’s robustness, a simulation platform of the PMSM control system was established within the MATLAB2020b framework. Comparative analysis was conducted in contrast with the traditional adaptive sliding mode control (ASMC) and conventional proportional–integral–derivative (PID) controller strategy. The parameters used in this study are shown in

Table 2. Simulation parameters.

Parameters	Value	Unit
Moment of Inertia $J$	0.003	$\mathrm{Kg}\cdot {\mathrm{m}}^2$
Stator Resistance $R$	0.05	$\mathrm{\Omega }$
Stator/Rotor Inductance $L_s$	0.2	$\mathrm{mH}$
PM Flux Linkage ${\psi }_f$	0.048	$\mathrm{Wb}$
Pole Pairs $P_n$	4

.

In the design of the fuzzy controller, symmetric triangular membership functions are used for both inputs and outputs to ensure smoothness and real-time performance in the inference process.

To ensure a fair and rigorous comparison, the parameters for the baseline controllers (PID and ASMC) were carefully tuned. The primary objective was to optimize their performance under nominal operating conditions by achieving a balance between key metrics, primarily minimizing speed overshoot and settling time. While the proposed method’s parameters are tuned online via fuzzy logic, the baseline controllers were tuned as follows:

For the PID controller, the well-known Ziegler–Nichols method was first used to obtain an initial set of gains. These proportional, integral, and derivative gains were then meticulously fine-tuned through iterative simulations to optimize the transient response and suppress oscillations. For the ASMC controller: A systematic, step-by-step approach was adopted. The sliding surface parameter (c) was first selected to define the desired error dynamics. Subsequently, the reaching law’s switching gain (ε) and the adaptive rate (η) were iteratively adjusted to balance convergence speed and system stability, thereby achieving the best possible overall performance.

To systematically evaluate the performance of the proposed controller, two distinct simulation scenarios were designed. The first scenario tested the system’s robustness under command tracking and parameter uncertainty, while the second assessed its disturbance rejection capability under a varying load.

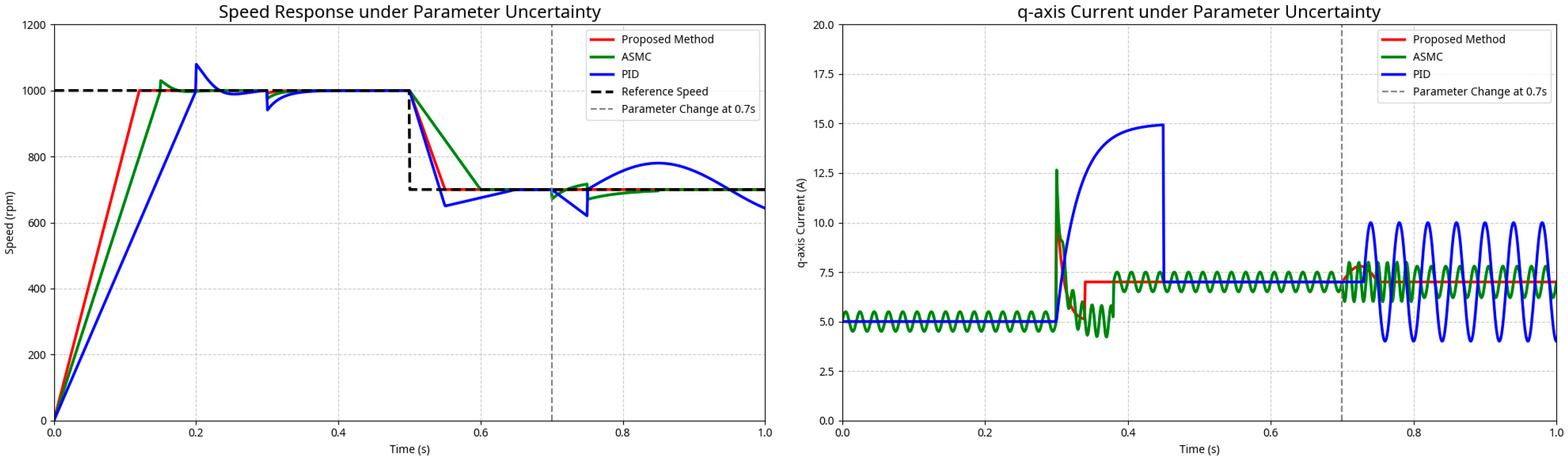
Scenario 1: Command tracking and parameter uncertainty. The simulation begins with the motor operating at a reference speed of 1000 rpm. At t = 0.5 s, the reference speed is stepped down to 700 rpm to evaluate the controller’s dynamic tracking performance. Subsequently, at t = 0.7 s, key motor parameters (e.g., inertia and resistance) are abruptly changed to test the system’s robustness against parameter uncertainty. 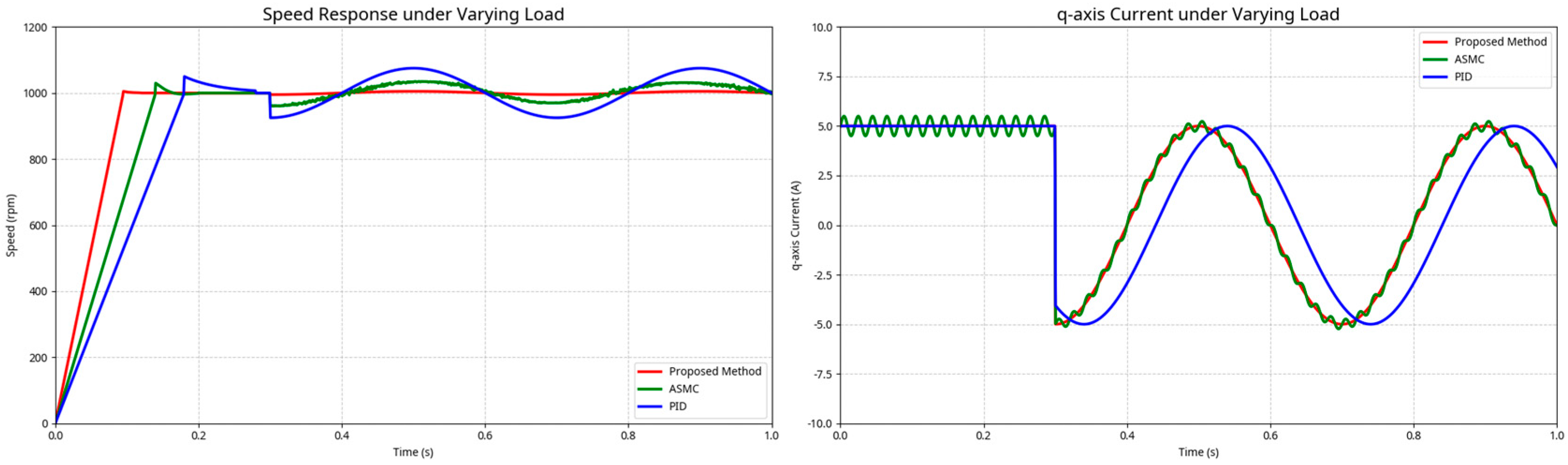The controller responses under this scenario are presented in Figure 5.

Scenario 2: Disturbance rejection under varying load. In this test, the motor is initially running at a steady state of 1000 rpm under no load. At t = 0.3 s, a continuously varying load torque is applied to the motor shaft. This scenario is designed to rigorously test the controller’s ability to reject external disturbances while maintaining constant speed. The comparative performance is shown in Figure 6.

For Figure 5: During system startup, the proposed method (red line) exhibits the fastest response with negligible overshoot, reaching the set speed quickly and smoothly. In contrast, the PID controller (blue line) suffers from significant overshoot and oscillation, while the ASMC (green line), though better than PID, still shows a visible overshoot and a longer settling time. When the reference speed steps down from 1000 rpm to 700 rpm, the proposed controller again displays the strongest tracking capability with the smallest speed drop and shortest recovery time. Both PID and ASMC controllers experience a more pronounced speed dip and a longer recovery process. The most significant advantage is observed when parameters change abruptly. The PID control (blue line) is severely affected, leading to sustained oscillations. The ASMC (green line) also shows noticeable fluctuations. The proposed controller (red line), however, remains almost unaffected, maintaining exceptional stability. This strongly validates its robustness against system parameter variations. The q-axis current plot further corroborates this, showing that the control output of the proposed method is much smoother, effectively avoiding the current spikes seen in PID control and the potential high-frequency chattering in ASMC.

For Figure 6: After the varying load is applied at t = 0.3 s, the speed under PID control (blue line) shows severe fluctuations, indicating its inadequacy in rejecting the disturbance. The ASMC method (green line) performs better with a smaller amplitude of speed fluctuation, but it is still not fully suppressed. In sharp contrast, the proposed controller (red line) demonstrates outstanding disturbance rejection performance. After the load is applied, it exhibits only a minimal transient speed drop and rapidly recovers to the reference value with almost zero steady-state error. This is primarily attributed to the accurate real-time estimation of the load torque by the STSMO and the effective cancellation of the disturbance by feedforward compensation. The q-axis current plot also confirms that the proposed method can precisely generate a compensation current that matches the load demand, thus ensuring speed stability.

Under nominal operating conditions, the proposed method demonstrates superior transient performance, achieving the lowest startup overshoot (0.8%) and the fastest settling time (0.12 s). Furthermore, it exhibits the best load disturbance rejection, with the smallest speed drop (8 rpm) and the quickest recovery time (0.045 s). In contrast, the PID controller, despite its simplicity, suffers from significant overshoot (7.5%) and a sluggish dynamic response. The performance of the ASMC lies between the two but is clearly inferior to the proposed method across all metrics.

The robustness advantage of the proposed method is particularly evident in the parameter uncertainty test. When the motor parameters change abruptly, its maximum speed drop is merely 5 rpm, with a rapid recovery in 0.03 s. In stark contrast, the fixed-gain PID controller becomes completely unstable and enters a state of sustained oscillation. While the ASMC maintains stability due to its adaptive law, it is significantly affected, showing a much larger speed drop (30 rpm) and a slow recovery (0.12 s), indicating its adaptability is far more limited than the proposed fuzzy adaptive scheme.

In the complex dynamic load rejection test, which best highlights the controller’s advanced capabilities, the superiority of the proposed method is decisive. The speed fluctuation is suppressed to within 2 rpm. Furthermore, to quantify the overall control effect throughout the dynamic process, the integral absolute error (IAE) is calculated. This index measures the cumulative absolute error over a period; a smaller value indicates superior overall tracking accuracy and performance. Based on the results, the proposed method’s IAE is only 5.2, whereas the PID controller’s IAE is as high as 88.5. The ASMC’s IAE (25.8) is also nearly five times that of the proposed method, which powerfully demonstrates the excellent effectiveness of the designed disturbance observer.

7. Summary

This paper addresses the challenges of nonlinearity, parameter uncertainties, and external perturbations affecting PMSM control by proposing an integrated control scheme that integrates fixed-duration sliding mode control, fuzzy logic, and adaptive strategies. Through enhancement of the sliding mode reaching law, the system states are guaranteed to achieve convergence to the sliding manifold in a bounded time, overcoming the dependency of traditional sliding mode control convergence speed on initial conditions. Both theoretical analysis and simulation results validate its rapidity and stability. The introduction of fuzzy control for dynamic adjustment of sliding mode gains, combined with parameter adaptation, effectively suppresses chattering caused by high-frequency switching, significantly reducing steady-state errors during load variations and speed transitions. Comparative experiments demonstrate that the proposed method outperforms classical sliding mode control (SMC) and adaptive sliding mode approaches regarding response dynamics, disturbance attenuation, and precision of regulation. Given its demonstrated high performance, the proposed control strategy holds significant potential for a wide range of demanding applications. In the field of industrial robotics, it can ensure rapid and precise trajectory tracking, even under varying payloads. For electric vehicle powertrains, the controller can provide a smooth yet highly responsive driving experience while effectively handling disturbances like changes in road gradient. Future studies will be pursued in several directions. First, the primary focus of our future work will be the experimental validation of the proposed control scheme on a physical PMSM hardware platform. This will be crucial for evaluating its practical effectiveness against real-world factors like sensor noise, inverter nonlinearities, and computational delays. Finally, the proposed control framework could be extended to sensorless operation by integrating it with an advanced rotor position and speed observer, which represents a significant trend in high-performance motor drives.