An Interpretable Model for Cardiac Arrhythmia Classification Using 1D CNN-GRU with Attention Mechanism

Abstract

Accurate classification of cardiac arrhythmias remains a crucial task in biomedical signal processing. This study proposes a hybrid deep learning approach called 1D CNN-eGRU that integrates one-dimensional convolutional neural network models (1D CNN) and a gated recurrent unit (GRU) architecture with an attention mechanism for the precise classification of cardiac arrhythmias based on ECG Lead II signals. To enhance the classification of cardiac arrhythmias, we also address data imbalances in the MIT-BIH arrhythmia dataset by introducing a hybrid data balancing method that blends resampling and class-weight learning. Additionally, we apply Sig-LIME, a refined variant of LIME tailored for signal datasets, to provide comprehensive insights into model decisions. The suggested hybrid 1D CNN-eGRU approach, a fusion of 1D CNN-GRU along with an attention mechanism, is designed to acquire intricate temporal and spatial dependencies in ECG signals. It aims to distinguish between four distinct arrhythmia classes from the MIT-BIH dataset, addressing a significant challenge in medical diagnostics. Demonstrating strong performance, the proposed hybrid 1D CNN-eGRU model achieves an overall accuracy of 0.99, sensitivity of 0.93, and specificity of 0.99. Per-class evaluation shows precision ranging from 0.80 to 1.00, sensitivity from 0.83 to 0.99, and F1-scores between 0.82 and 0.99 across four arrhythmia types (normal, supraventricular, ventricular, and fusion). The model also attains an AUC of 1.00 on average, with a final test loss of 0.07. These results not only demonstrate the model’s effectiveness in arrhythmia classification but also underscore the added value of interpretability enabled through the use of the Sig-LIME technique.

1. Introduction

Cardiac arrhythmia is a common manifestation of cardiovascular disease (CVD) that poses a significant health concern and contributes to high mortality rates worldwide. It involves irregular heart rhythms that can result in serious complications such as an escalated risk of stroke or sudden cardiac death [1].

The predominant approach for identifying arrhythmias is electrocardiography (ECG), which monitors the electrical activities of the heart throughout time [2]. ECG signals are typically acquired from multiple leads, each providing various insights into the heart’s electrical functions [3]. Lead II explicitly plays a frequent role in arrhythmia diagnosis. With the annual worldwide recording of over 300 million ECGs and this number showing continuous growth, the importance of this diagnostic method is clear [4].

The widespread adoption of ECG stems from its non-invasive and cost-effective nature, enabling the identification of various cardiovascular irregularities such as atrial fibrillation (AF), premature atrial contractions (PAC), and myocardial infarctions (MI) [5,6]. Nonetheless, the analysis of ECG signals presents a challenge, especially with more intricate arrhythmias [2].

Diagnosing cardiac arrhythmia via ECG signal interpretation has conventionally been reported to physicians based on their clinical exposure. This conventional method involves a subjective correlation between a patient’s ECG pattern and an established taxonomy of medical conditions which depends on a subjective interpretation of medical literature [7,8]. While the traditional approach of ECG signal interpretation has shown some effectiveness, it often suffers from errors and wrong classification [2]. As a result, there is an increasing need to automate medical processes in order to enhance the quality of patient care and reduce overall healthcare costs. This leads to the development of alternative methods for analyzing ECG signals using machine learning and deep learning techniques [9,10].

Deep learning models including recurrent neural networks (RNNs) and convolutional neural networks (CNNs) have attracted significant attention due to their strong ability to learn complex data patterns [11,12]. Thus, CNNs and RNNs have been used in various areas of biomedical signal processing (e.g., classification of arrhythmias based on ECG signals) [2]. The main advantage of deep learning is its ability to extract meaningful features directly from raw data, which allows the capture of subtle signal characteristics that may be difficult to identify manually [13]. While traditional approaches often struggle with the high unpredictability of ECG signals [2], deep learning models have the capability to handle such challenges and manage large-scale ECG analysis [1].

Several literature studies have shown the strong potential of DL models in automated arrhythmia classification using ECG signals. CNNs, in particular, effectively learn spatial features from ECG recordings. Kachuee, et al. [14] developed a deep CNN model that classified five arrhythmia types according to the AAMI EC57 standard, achieving classification accuracies of 93.4% for arrhythmias and 95.9% for myocardial infarction (MI). Romdhane, et al. [15] proposed a CNN model optimized with a focal loss function to address class imbalance, enhancing the detection of minority heartbeat classes. Their method, evaluated on the INCART and MIT-BIH datasets, yielded 98.41% accuracy, 98.38% F1-score, 98.37% precision, and 98.41% sensitivity. Ahmed, et al. [16] introduced a one-dimensional CNN architecture for arrhythmia detection, reporting performance metrics of 99% accuracy, 94% sensitivity, and 99% precision.

Recurrent neural networks (RNNs), particularly LSTM, are proficient in modeling temporal dependencies within ECG signals. Singh, et al. [17] employed LSTMs on the MIT-BIH Arrhythmia Database to distinguish between regular and irregular beats, demonstrating superior performance compared to other RNN models. Several studies have also explored hybrid architectures that combine CNNs and RNNs. Xu, et al. [18] proposed a model integrating convolutional layers, Squeeze-and-Excitation residual blocks, and bidirectional LSTMs. This architecture achieved 95.90% sensitivity, 96.34% specificity, and a classification time of 6.23 s across five ECG classes. Similarly, Maurya, et al. [19] developed a cascaded model combining LSTM and RNN layers for classifying 12-lead ECG signals, achieving 89.9% accuracy, 93.46% sensitivity, and 84.36% specificity. More recently, Sarankumar, et al. [20] introduced a BiGRU-based autoencoder model that achieved 97.76% accuracy and 98.31% specificity on the CPSC 2018 dataset, illustrating the effectiveness of bidirectional modeling and latent feature compression.

Despite the promising accuracy achieved by deep learning models in arrhythmia classification, several critical limitations remain unaddressed, particularly regarding interpretability, data imbalance, and the absence of attention mechanisms [21,22].

First and foremost, interpretability remains a fundamental challenge. While the CNN- and LSTM-based models discussed in the literature (e.g., Kachuee, et al. [14]; Ahmed, et al. [16]) demonstrate strong classification performance, they largely operate as “black boxes.” In clinical settings, such opacity impedes the trust and acceptance of these models among healthcare professionals, who must often justify diagnostic decisions. Especially in jurisdictions where explainability is legally mandated [23], the inability to understand or audit model reasoning presents a significant barrier to clinical adoption [24]. Most of the reviewed studies provide limited insight into the internal decision-making pathways of their models, neglecting the crucial requirement for transparent and accountable AI in medicine. Secondly, the issue of data imbalance persists across the reviewed works. Arrhythmia datasets such as MIT-BIH and INCART often exhibit skewed class distributions, where common arrhythmias are overrepresented and rarer ones are underrepresented. This imbalance can bias models toward majority classes, diminishing their diagnostic reliability for rare but clinically significant arrhythmias [25]. Although Romdhane, et al. [15] attempt to address this through the use of focal loss, such strategies are underutilized or insufficiently validated in other studies. Inadequate handling of data imbalance may inflate overall accuracy metrics while masking poor performance on minority classes, which is unacceptable in high-stakes clinical diagnostics [26]. Finally, the lack of attention mechanisms in many of the proposed models limits their capacity to capture salient temporal or spatial features in ECG signals. Attention mechanisms—particularly those embedded within transformer or hybrid CNN-RNN architectures—have shown promise in selectively weighting important signal segments, enhancing both performance and interpretability. Yet the majority of studies rely solely on convolutional or sequential encoders without incorporating attention-based enhancements. This omission represents a missed opportunity to improve model focus, reduce noise sensitivity, and provide visualizable attention maps that could further support explainability and clinician validation.

As can be noticed, illuminating the decision-making mechanisms employed by deep learning models becomes imperative to safeguard the accuracy, impartiality, absence of bias, and ethical conduct of predictions, especially considering their potential profound impact on individuals’ lives [27].

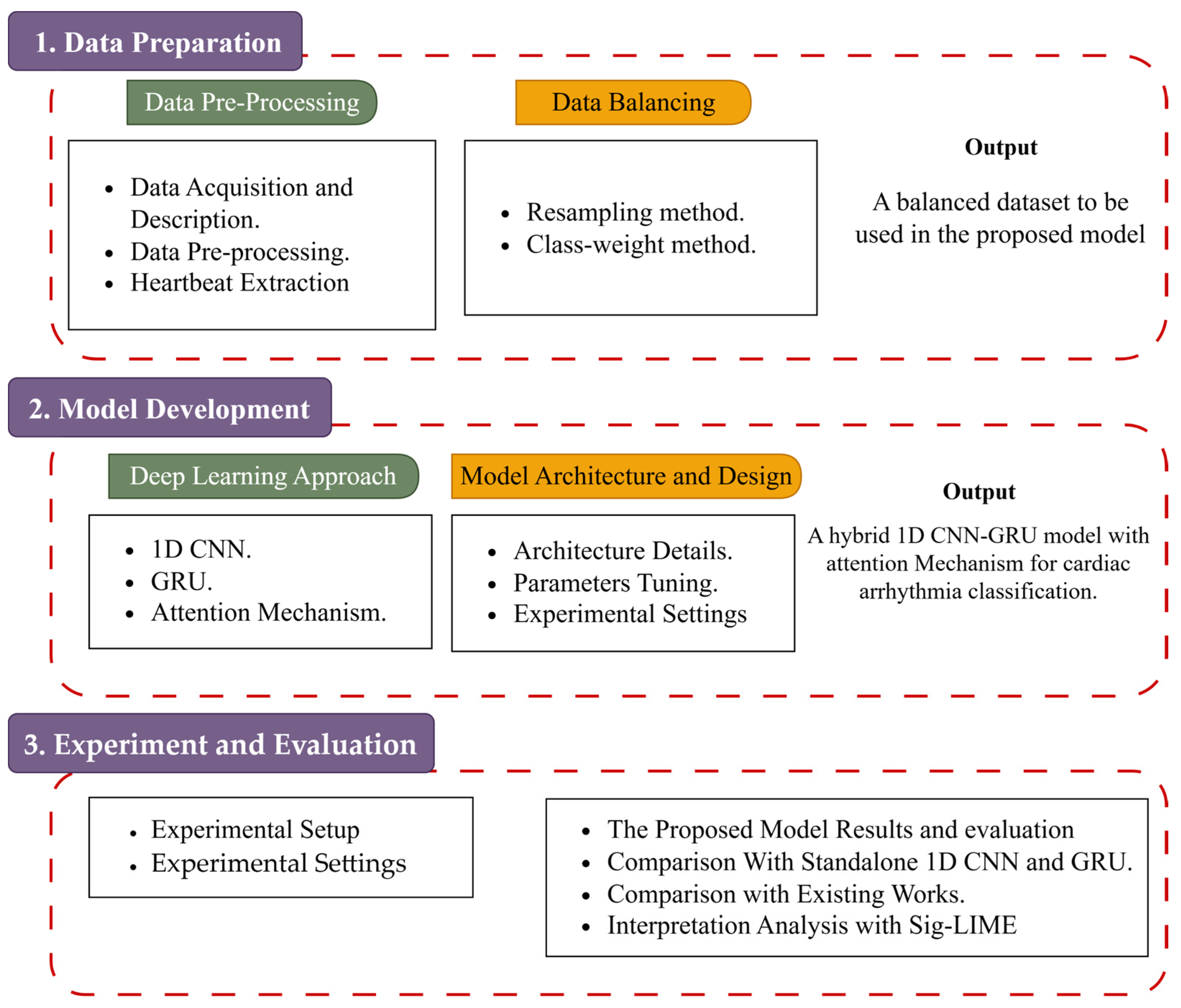
This paper aims to develop a reliable and interpretable deep learning model capable of accurately classifying a wide range of cardiac arrhythmias using single-lead electrocardiogram (ECG) signals, specifically Lead II. The proposed approach addresses key challenges in automated ECG analysis, including class imbalance, the need for robust feature extraction, and the lack of model transparency in clinical applications. The primary contributions of this study are outlined as follows:

• Proposing a hybrid data balancing technique that combines resampling methods with class-weighted learning to address class imbalance in the MIT-BIH arrhythmia dataset.
• Developing a hybrid 1D CNN-eGRU deep learning model with consideration for effective spatial–temporal feature extraction from ECG lead II signals.
• Employing the Sig-LIME as a signal-specific interpretability method to enhance the transparency and trustworthiness of the model’s predictions.

The remainder of this paper is organized as follows: Section 2 presents the materials and methods used in this study including the architecture of the 1D CNN-eGRU model. Section 3 presents and discusses the experimental results. Finally, Section 4 concludes the paper by summarizing the key findings and suggesting directions for future research.

2. Materials and Methods

The proposed system consists of dataset preparation, data preprocessing, and the deep learning architecture that will be utilized for cardiac arrhythmia classification. The article pipeline is shown in Figure 1.

2.1. Data Preparation

The code is publicly available in Kaggle: https://www.kaggle.com/code/talal92/mit-original-data-preprocessing (accessed on 12 March 2024). The data preparation phase serves as the critical foundation in the context of empirical research and data-driven analysis. This section explores the essential processes of data acquisition, preprocessing, data balancing, and splitting. Through these preparatory steps, data is transformed from its raw and ECG record state into a format that is conducive to rigorous academic investigation and statistical analysis.

2.1.1. Dataset Description

The study utilized original ECG signals sourced from the MIT-BIH dataset [28] as the primary data for classifying four types of arrhythmias based on the Association for the Advancement of Medical Instrumentation (AAMI) standard EC57 [29]. This dataset is widely acknowledged and frequently employed in cardiac arrhythmia analysis, comprising 48 half-hour ECG recordings, each containing Lead II and Lead V5 signals. Amongst 47 subjects, 25 subjects exhibited varying arrhythmias while 22 subjects had normal ECGs. These signals, sampled at 360 Hz with 11-bit resolution, underwent bandpass filtering between 0.1 Hz and 100 Hz. Annotation by two cardiologists resulted in beat classifications: normal (N), supraventricular ectopic (S), ventricular ectopic (V), or fusion (F).

2.1.2. Data Pre-Processing

The preparation of data for model training in cardiac arrhythmia classification involves a meticulous sequence of steps aimed at optimizing data usability and relevance. This process encompasses several key stages.

• Standardization and Signal Extraction: The first step involves transforming the 48 ECG recordings into arrays of equal size. This transformation ensures consistency in the input data format, and it allows the deep learning model to effectively process and analyze signals.
• Extracting Lead II: Lead II is commonly chosen for arrhythmia classification due to its ability to capture key cardiac information. In this step, Lead II signals are specifically extracted to focus on the most informative input which allows them to detect meaningful patterns that are strongly associated with various arrhythmia.
• Signal Optimization and Segmentation: The extracted ECG signals are first scaled to enhance the quality and consistency of the data. This normalization step ensures that the model interprets the signals more effectively. After scaling, the signals are segmented into individual heartbeats which enables the model to analyze the ECG on a beat-by-beat basis. As a result, the detecting and classifying of different arrhythmias will be improved by learning the distinctive features of each heartbeat.

2.1.3. Heartbeat Extraction Methodology

To analyze arrhythmias more effectively, individual heartbeats need to be extracted from the ECG signals through a clear and structured process. In this study, we use an efficient approach to extract heartbeats from Lead II of the MIT-BIH dataset. The process includes three main steps:

• R Peak Detection: The R peak represents the tallest point in the QRS complex and corresponds to the depolarization of the heart’s ventricles. Accurately detecting these peaks is crucial for tasks like arrhythmia detection, heart rate analysis, and diagnosing various heart conditions.
• Heartbeat Segmentation: Once the R peaks are identified, the ECG signal is segmented into individual heartbeats. Each segment is carefully centered around its respective R peak and consists of 180 data points which capture the key characteristics that are needed for accurate classification. This beat-by-beat segmentation ensures the model receives a comprehensive representation of each heartbeat.
• Labeling: After segmentation, each heartbeat is labeled based on the AAMI (Association for the Advancement of Medical Instrumentation) standard classification. This results in a labeled dataset containing 89,694 normal (N) beats, 2814 supraventricular (S) beats, 6487 ventricular (V) beats, and 779 fusion (F) beats. The AAMI standard ensures a consistent and reliable framework for arrhythmia classification.

The resulting dataset comprises categorized heartbeats for distinct arrhythmia types, each presented as a 180-feature window. Despite effectively capturing essential cardiac regions, such as the QRS Complex and T-wave, a notable class imbalance is evident among the classes. Specifically, ‘F’ exhibits 779 samples while ‘N’ encompasses 89,694 samples. This imbalance poses potential implications for the performance of machine learning models, necessitating dataset balancing to ensure equitable representation among classes during subsequent model training.

2.2. Data Balancing Technique

Imbalanced datasets cause models to favor majority classes while overlooking minority ones. This imbalance can lead to poor performance in detecting less frequent but clinically significant arrhythmia. To mitigate this issue, two complementary techniques are applied: resampling and class-weight adjustments. Resampling helps balance the class distribution, while class weighting guides the model to place greater emphasis on underrepresented classes during training. A combination of these methods is considered good practice because different imbalance scenarios may respond better to specific strategies [30]. By addressing the data imbalance from multiple angles, the model is better equipped to learn meaningful patterns across all arrhythmia types, which leads to more reliable classification results. Algorithm 1 shows the pseudocode of the proposed hybrid data balancing.

Algorithm 1: The pseudocode of the proposed hybrid data balancing
	Input: Class F (C0), Class N (C1), Class S (C2), Class V (C3), Total Number of Samples (TN), Total Number of Classes (C)
	Output: Resampled F (R0), Resampled N (R1), Resampled S (R2), Resampled V (R3), ClassWeight $[W_0$$,W_1,W_2,W_3$]
	Start Algorithm
	//  Class Weight Technique
1	Initialize ClassWeight as an empty list
2	For i from 0 to 3 do
3	$W_i={\displaystyle \frac{TN}{C\ast C_i}}$
4	$\mathrm{ClassWeight}.\mathrm{append}(W_i$)
5	End For
	//  Resampling Technique
6	Initialize R0, R1, R2, R3 as an empty list
7	For i from 0 to 3 do
8	For j from 0 to 30,000 do
9	$\mathrm{idx}=\mathrm{random}\mathrm{integer}\mathrm{between}0\mathrm{and}\mathrm{length}(C_i$)
10	$R_i$$.\mathrm{append}(C_i$[idx])
11	End For
12	End For
13	$\mathbf{Return}{R}_i$ and ClassWeight
14	End Algorithm

The hybrid data balancing technique incorporates the benefits of both the class-weight method and data resampling. This hybrid approach enables faster learning from the minority classes to be more robust with different data distributions.

2.2.1. Class-Weight Learning

Class-weight learning is a technique used to address data imbalance by assigning different levels of importance to classification errors during model training. Instead of treating all errors equally, it adjusts the learning process to reflect the higher cost of misclassifying minority class samples—an especially important consideration in many real-world applications where these rare cases can carry greater clinical significance [31].

Implementing class-weight learning often entails modifying the objective function within the classification algorithm to encompass the misclassification cost. This adaptation involves providing a penalty term into the objective function, mirroring the proportional cost of misclassifying individual classes.

To address the class imbalance present in the MIT-BIH dataset, we utilized the class-weight technique [32]. This method modifies the model cost function, and it assigns greater weight to minority classes which helps counter the dataset imbalance during model training. For a binary or multi-class classification problem, the class weights were computed using the following formula [33]:

$$W_{c\in C}={\displaystyle \frac{T{N}_{All}}{C\times {TN}_c}}$$

(1)

In the context of a dataset with $C$ classes, where $W_{c\in C}$ denotes the weight of class c, $T{N}_{All}$ represents the overall number of samples in the data, $C$ is the class number, and ${TN}_c$ is total number of samples in class $c$.

This approach encourages the model to prioritize learning to discern minority classes more accurately, consequently enhancing the overall classification performance [34].

2.2.2. Resampling Technique

Real-world datasets often suffer from class imbalance, where one class is significantly underrepresented relative to others. This imbalance is problematic as it can cause classification bias and poor model performance [35]. Resampling methods are a common strategy in machine learning to counteract class imbalance, typically involving either over-sampling the minority class or under-sampling the majority class. Over-sampling duplicates minority class samples randomly, while under-sampling involves random removal of majority class samples. These techniques strive to mitigate the impact of imbalanced data on the performance of the model.

Given a binary or multi-class classification problem, the mathematical formula used to resample the classes is as follows:

$$R_{c\in C}=\mathrm{b}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{i}\mathrm{n}\mathrm{g}\left(D_c,r\right)$$

(2)

In the context of a dataset with $C$ classes, where $R_{c\in C}$ denotes the resampled dataset for class $c$, $D_c$ represents the samples in class $c$, and $r$ corresponds to the total number of samples to generate. This means that for each class $c$, a resampled dataset $R_{c\in C}$ is generated by applying bootstrapping (sampling with replacement) to the data subset $D_c$.

It is noteworthy that data resampling was carried out exclusively on the training dataset to address class imbalance. Specifically, the majority class ‘N’ was under-sampled to 30,000 samples, while the minority classes ‘S’, ‘V’, and ‘F’ were each over-sampled to 30,000 samples. The testing dataset remained unchanged to accurately assess the performance of the machine learning model on new data without any data leakage. This approach ensures that the training dataset is balanced, preserving data integrity and maintaining an unbiased testing dataset representative of real-world conditions.

2.3. The Proposed Hybrid Cardiac Arrhythmia Classification Approach Based on 1D CNN-GRU and Attention Mechanism

This section presents a hybrid model architecture designed to leverage the complementary strengths of a one-dimensional convolutional neural network (1D CNN), gated recurrent units (GRU), and attention mechanism. The rationale for employing this hybrid architecture is its potential to effectively capture both spatial and temporal dependencies inherent in ECG signals. Within this framework, the 1D CNN serves as a feature extractor to identify crucial patterns within the data. Concurrently, the GRU functions as a sequence modeler that can contribute to the model’s ability to estimate posterior probabilities for arrhythmia presence based on input sequences [36]. Furthermore, the integration of an attention mechanism is crucial in enhancing model performance. This mechanism enables the model to dynamically focus computational resources on the most relevant segments of the input sequence, thereby prioritizing important features and improving interpretability. This strategic integration aims to significantly enhance classification accuracy and model robustness, further underscoring the prowess of the proposed hybrid 1D CNN-eGRU model in accurately diagnosing arrhythmias.

2.3.1. One-Dimensional Convolutional Neural Network

A variation of convolutional neural networks called one-dimensional convolutional neural networks (1D CNNs) is made especially for handling one-dimensional signals such as time series or sparse data [37]. The general design of 1D CNN is depicted in Figure 2.

The 1D CNNs operate similarly to 2D-CNNs except they are tailored to handle one-dimensional data, employing 1D convolutional filters instead of 2D filters. One-dimensional CNNs have fewer parameters, making them computationally efficient compared to 2D-CNNs [37]. They excel in capturing temporal relationships in signal data and extracting local characteristics that are resilient to minor temporal shifts. Thus, 1D CNNs are ideal for analyzing time series data with temporal dependencies. Overall, these characteristics of CNNs make them an effective analytical technique for analyzing and classifying various types of signal data, including the time series data like ECG signals. Formula (3), used for a 1D CNN, can be expressed as [38]

$$y_i=f\left(\sum _{j=1}^k{w}_j{x}_{i+j-1}+b\right)$$

(3)

where $x_{i+j-1}$ is the $j$th input element in a window of size $k$ that centers on the $i$th element, $w_j$ is the weight associated with that input, $b$ is a bias term, and $f$ is an activation function. Each input element is multiplied by the associated weight $w_j$. Then, the resulting products are added up. The final output $y_i$ is obtained by adding a bias term $b$ to this sum and then passing the result through an activation function $f$.

One-dimensional CNNs can also be used in conjunction with other architectures of neural networks like recurrent neural networks to process sequential data.

2.3.2. Gated Recurrent Unit

The Gated Recurrent Unit (GRU) is a type of recurrent neural network (RNN) architecture that was introduced by Cho, et al. [39] in 2014 as efficient alternative to the Long Short-Term Memory (LSTM) network. The GRU is specifically designed to model temporal dependencies in sequential data [40]. It utilizes two primary gating mechanisms: an update gate and a reset gate. The update gate determines the proportion of information from the previous hidden state that should be retained and passed to the current hidden state. Conversely, the reset gate controls how much of the previous hidden state’s information is disregarded when computing the candidate hidden state for the current time step. These gating mechanisms allow the GRU to selectively manage the flow of information to enable it to effectively capture long-range dependencies by adaptively updating its hidden state based on the sequence context. The internal operations of the GRU are detailed in Figure 3.

GRU can enhance the capability of RNNs to catch and model complex dependencies over long sequences since it can effectively manage information flow and incorporate these gating mechanisms. This makes it valuable architecture for applications based on sequential data analysis such as time series prediction, speech recognition, and natural language processing. The GRU can be defined mathematically as follows [41]:

$$\begin{gathered} z_t=\sigma \left(W_z{x}_t+U_z{h}_{t-1}+b_z\right) \\ {r}_t=\sigma \left(W_r{x}_t+U_r{h}_{t-1}+b_r\right) \\ {\tilde{h}}_t=\tanh \left(W_h{x}_t+U_h\left(r_t\odot h_{t-1}\right)+b_h\right) \\ {h}_t=\left(1-z_t\right)\odot h_{t-1}+z_t\odot \widetilde{h_t} \end{gathered}$$

(4)

The equations presented above represent the computations involved in the GRU architecture. In these equations, $x_t$ represents the input at time step $t$, $h_{t-1}$ represents the previous hidden state, $z_t$ corresponds to the update gate, $r_t$ denotes the reset gate, $\widetilde{h_t}$ represents the candidate hidden state, $h_t$ represents the current hidden state, $\sigma$ represents the sigmoid activation function, $\odot$ represents the element-wise multiplication operation, and $W$ and $U$ are weight matrices while $b$ represents the bias vectors that are learned during training. These equations describe the functionality of the update gate, reset gate, candidate hidden state, and current hidden state, respectively. The update gate controls the flow of information from the previous hidden state to the current hidden state, while the reset gate determines which parts of the input and previous hidden state should be discarded, the candidate hidden state estimates a new hidden state based on the input and previous hidden state, and the current hidden state is computed as a weighted combination of the previous hidden state and the candidate hidden state. The implementation of GRU has contributed to enhancing numerous applications such as sequential and time-series data analysis [42].

2.3.3. Attention Mechanism

The attention mechanism is a crucial component in modern neural network architectures, significantly improving their ability to handle sequential data by dynamically focusing on the most significant portions of the input. In the context of our hybrid model, the attention mechanism makes the model more capable of catching intricate dependencies in ECG signals, leading to more accurate arrhythmia classification.

The attention mechanism operates by giving diverse weights to various segments of the input sequence, allowing the model to concentrate on the most informative segments. The main concept is to calculate a weighted total of the input features, where each feature’s importance is indicated by its weight (attention score). The attention mechanism can be explained mathematically as follows.

(1)

Score Calculation: First, a score is computed for each input feature, which reflects its relevance. Various scoring functions can be used, such as dot product, scaled dot product, or additive functions. For simplicity, we use the dot product in this explanation.

$$\mathrm{Score}(h_t,s_{t-1})=h_t^T{s}_{t-1}$$

(5)

where the GRU’s hidden state at time step $t$ is represented by $h_t$ while $s_{t-1}$ is the previous hidden state or context vector.

(2)

Computing Attention Weights: The scores are then normalized using a Softmax function to obtain the attention weights.

$${\sigma }_t={\displaystyle \frac{exp\left(score\left(h_t,s_{t-1}\right)\right)}{\sum _{t\prime }exp\left(score\left(h_t,s_{t-1}\right)\right)}}$$

(6)

Here, ${\sigma }_t$ represents the attention weight for the hidden state $h_t$.

(3)

Computing Context Vector: The weighted sum of the input features is used to calculate the context vector $c_t$.

$$c_t=\sum _{t\prime }{\sigma }_t{h}_{t\prime }$$

(7)

(4)

Producing Output: The attention mechanism’s final output is a combination of the context vector and the current hidden state, often concatenated or passed through a feedforward neural network, where $f$ is a function that combines the context vector and the current hidden state.

$$o_t=f(c_t,s_t)$$

(8)

Overall, 1D CNN is effective in feature extraction and computational efficiency but has limitations in handling long-term dependencies in the sequential data. While 1D CNNs efficiently extract local features, their fixed-length convolutional filters inherently limit their ability to capture long-range temporal dependencies effectively [43]. GRUs, conversely, are specifically designed to model such sequential dependencies through their gating mechanisms, which regulate information flow over time. However, GRUs can be computationally intensive and may require longer training durations compared to CNNs [44]. Therefore, integrating 1D CNNs and GRUs into hybrid architecture presents a compelling strategy. This approach aims to leverage the CNN’s feature extraction capabilities for spatial patterns and the GRU’s strength in modeling temporal dynamics in order to potentially enhance predictive performance and mitigate the computational demands of purely recurrent models [45]. The inclusion of an attention mechanism further refines this architecture by enabling the model to dynamically allocate focus to the most salient segments of the input sequence, thereby improving its capacity to capture intricate dependencies.

2.3.4. The Proposed Hybrid Model Architecture and Design

The integration of the proposed model architecture involves combining the CNN and GRU layers cohesively with interconnections, incorporating an attention mechanism to enhance performance. CNN’s output feeds seamlessly into the GRU in order to ensure a continuous flow of information from spatial processing to temporal analysis. This integration allows end-to-end training to facilitate the suggested model to learn intricate representations directly from raw ECG signals [36].

The architecture of the suggested hybrid 1D CNN-eGRU model combines the strengths of 1D CNNs and GRUs to effectively catch spatial and temporal dependencies within ECG signals. As illustrated in Figure 4, the structure of proposed hybrid 1D CNN-eGRU model comprises the following components:

• CNN Component: It has two convolutional layers. Leaky ReLU activation, max-pooling, dropout, and batch-normalization layers come after each of the two convolutional layers. This arrangement facilitates hierarchical feature learning from input ECG signals, extracting relevant local features crucial for arrhythmia classification. The Leaky ReLU activation helps mitigate the vanishing gradient problem, enhancing the learning process.
• GRU Component: This component aids in modeling temporal dependencies within ECG signals. It utilizes the two GRU layers of a recurrent neural network. It captures evolving patterns over time by keeping a hidden state that includes data from earlier time steps.
• Attention Mechanism: This component consists of two attention mechanisms, each applied after the GRU layer. The attention mechanism can increase the performance of the CNN model by dynamically concentrating on the most significant portions of the input sequence. This mechanism computes a weighted total of the input features, where each feature’s importance is indicated by its weight, thereby improving interpretability and performance.
• Fully Connected Layer: This component comprises two dense layers—the first layer with 512 nodes and ReLU activation, introducing non-linearity, and the second layer with four nodes that represent the four arrhythmia classes, utilizing softmax activation to generate class probabilities.

Algorithm 2 depicts the pseudocode of the suggested hybrid 1D CNN-eGRU. The backpropagation and gradient descent optimization algorithms are utilized through the model training stage. The sparse cross-entropy is the loss function that is employed to measure the dissimilarity between the true labels and the anticipated probability. During training, the model learns the optimal weights and biases that minimize the loss function and increase the model performance.

This enhanced model architecture leverages the complementary strengths of CNNs for spatial feature extraction, GRUs for temporal dependency modeling, and the attention mechanism for focusing on critical parts of the sequence, thus significantly improving the accuracy and interpretability of arrhythmia classification.

Algorithm 2: The pseudocode of the proposed hybrid 1D CNN-eGRU model
	Input: InputData, TestData, filter = [124, 64], kernel = [10, 5], blocks = 2, ClassWeight, Unite = [124, 64]
	Output: Classification_results
	Start Algorithm
	// Phase 1: Model Architecture
1	model = Sequential ()
2	For (i in range (blocks)) do
3	model. Add (Conv1D(filter[i], (kernel[i],), activation = ‘relu’)
4	model. Add (MaxPooling1D (2))
5	model. Add (Dropout (0.2))
6	model. Add (BatchNormalization ())
7	model. Add (GRU(Units[i], return_sequences = True))
8	model. Add (BatchNormalization ())
9	End For
10	model. Add (Attention())
11	$\mathrm{model}.\mathrm{Add}\left(\mathrm{LayerNormalization}\right(\mathrm{epsilon}=1\times {10}^{-6}$))
12	model. Add (Flatten ())
13	model. Add (Dense (512, activation = ‘relu’)
14	model. Add (Dense (4, activation = ‘softmax’)
	//Phase 2, Compile the model
15	model. Compile (loss = ‘sparse_categorical_crossentropy’, optimizer = Adam (learning_rate = 0.001), metrics = [‘accuracy’])
	//Phase 3: Train the model
16	model. Fit (InputData, batch_size = 512, epochs = 100, validation_split = 0.20, class_weight = ClassWeight)
	//Phase 4: Predict arrhythmias classification for testing data
17	Classification_results = model. Predict (test_data)
18	Return Classification_results
	End Algorithm

3. Results and Discussion

The Results and Discussion Section unveils the empirical findings garnered from the implemented methodologies for cardiac arrhythmia classification based on ECG signals. This section meticulously presents and interprets the performance outcomes of the developed models, emphasizing their efficacy in classifying arrhythmias.

3.1. Experimental Setup

The experimental setup utilized for conducting our study is explained in this section. All experiments were performed on a computing system equipped with an Intel^® Xeon(R) CPU E3-1226 v3 @ 3.30 GHz × 4 processor (Intel Corporation, Santa Clara, CA, USA), an NVIDIA GeForce GTX 1070 GPU, a 1TB hard disk, and 23.4 GB of RAM (NVIDIA, Santa Clara, CA, USA). The software environment was based on Python 3.12.6 that was managed using the Anaconda distribution, with Jupyter Lab and Spyder that were utilized for interactive development and experimentation. Essential libraries were used in the experiments: NumPy for numerical computations, Pandas for data manipulation and processing, SciPy for scientific computing tasks, Scikit-learn 1.7.1 for implementing machine learning models and evaluation metrics, WFDB package 4.3.0 for accessing and processing physiological signal data, and TensorFlow 2.15.0 for developing and training the deep learning models.

The carefully curated experimental setup enabled the efficient execution of our research tasks, ensuring reliable results and fostering reproducibility. The hardware’s computational power, combined with the versatile software and essential libraries, facilitated a seamless and robust research environment for exploring the proposed explainable deep learning classification approach.

3.2. Experimental Setting

In our pursuit of enhancing the performance of the hybrid 1D CNN-eGRU suggested for cardiac arrhythmia classification, we systematically fine-tuned critical hyperparameters using a trial-and-error approach. We selected and adjusted hyperparameters including filter size, kernel size, dropout rate, GRU, dense nodes, decay rate, learning rate, training epochs, and batch size. The goal was to identify the best combination that would maximize the performance measures. We conducted a series of experiments, adjusting one or more hyperparameters while keeping others constant, recording the model’s performance metrics in each case. These experiments spanned 100 epochs, enabling a comprehensive exploration of hyperparameter effects on performance.

After each experiment, we rigorously analyzed the results, with a focus on accuracy, F1-score, recall, and precision. We identified the hyperparameters with the most significant impact on performance, leading to the selection of optimal values. The best parameters of the suggested hybrid 1D CNN-eGRU are outlined in

Table 1. The best parameters of the suggested CNN-eGRU.

Parameter	Value
Filter	124, 64
Dropout	0.200
Kernel size	10, 5
kernel_regularizer	0.001
GRU Unites	124, 64
Dense Node	512, 4
Learning rate	0.001
Decay_rate	0.900
Decay_steps	5000
Batch size	512
Epoch	100

.

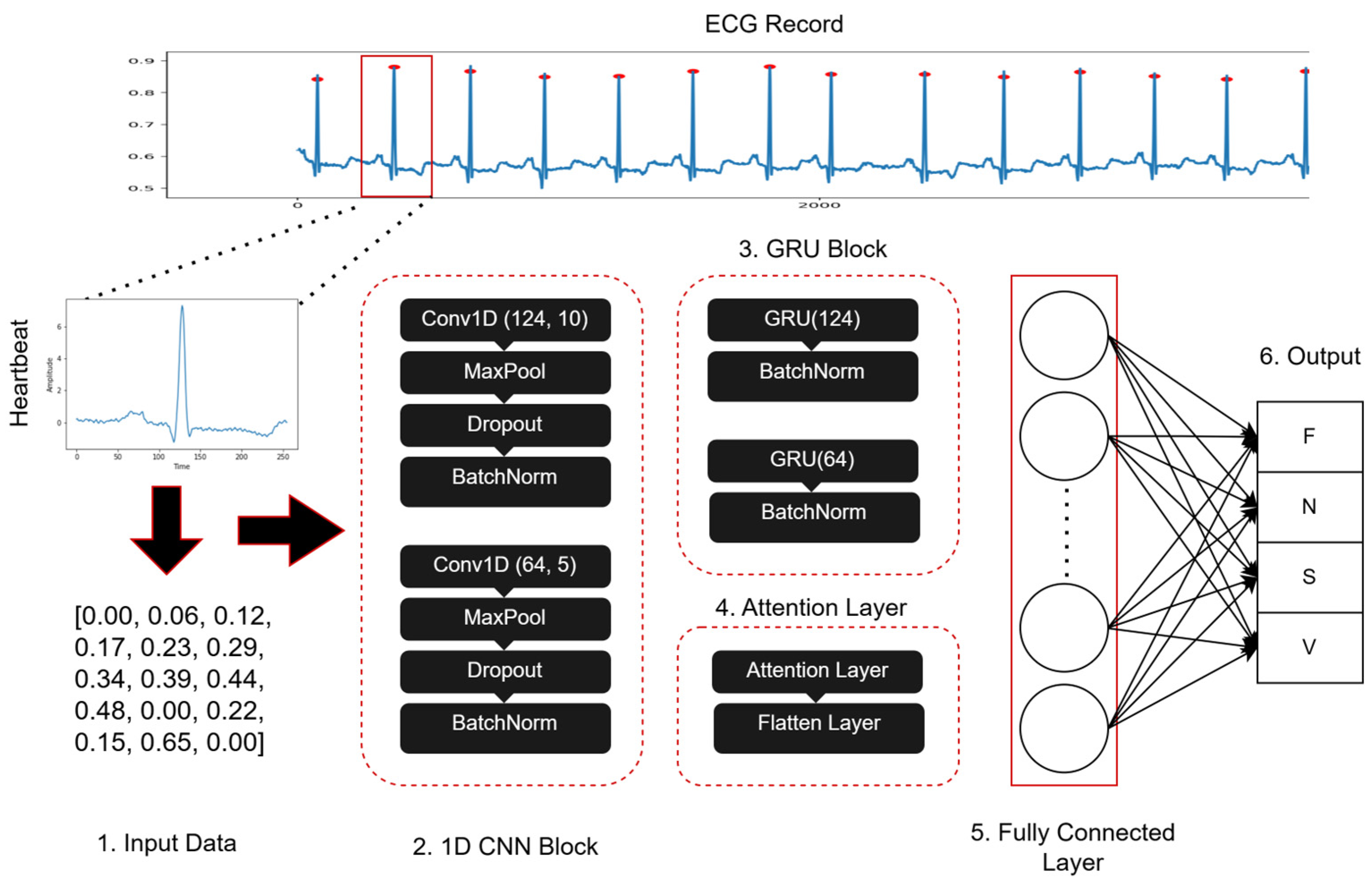
The model architecture incorporated two 1D CNN layers, with filter sizes of 124 and 64, respectively. These filters are responsible for extracting relevant features and capturing intricate relationships within the ECG data to aid in accurate arrhythmia classification. The receptive field of the convolutional filters is determined by the kernel size, which is set to 10 and 5 for the first and second CNN layers, respectively. It specifies the number of adjacent data points considered during the convolution operation to enable the model to catch local patterns and variations in the signals of ECG. A dropout layer with a rate of 0.2 was added to the model in order to avoid overfitting. During training, this layer arbitrarily sets a portion of inputs to zero to avoid the network from overly relying on specific features and promoting generalization. Additionally, a kernel regularizer with a value of 0.001 was applied to the convolutional and dense layers to avoid overfitting by punishing high weight values, thereby increasing the capability of generalization.

In the model architecture, two GRU layers also were included with 124 and 64 units. The GRU algorithm facilitated the extraction of sequential features and long-term dependencies within the ECG data, increasing the ability of the model to capture temporal dynamics crucial for accurate arrhythmia classification. An attention mechanism was integrated into the model to further enhance its performance. This mechanism dynamically focuses on the most significant portions of the input sequence, computing a weighted total of the input features, where each feature’s importance is indicated by its weight. This process increases the model’s interpretability and performance by emphasizing critical features for arrhythmia classification.

The fully connected layer consisted of two dense layers. The first dense layer comprised 512 nodes, which introduced non-linearity through the Rectified Linear Unit (ReLU) activation function. This layer enabled CNN to learn complex combinations of features extracted by previous layers, enhancing its discriminative capabilities. The second dense layer produced class probabilities using the softmax activation function and had four nodes, corresponding to the four arrhythmia classes.

The Adam optimizer was used to train the model at a learning rate of 0.001. The learning rate is an important parameter that controls the rate at which the model’s weights are updated during training. It defines the size of the adjustments made to the model’s parameters at each iteration, significantly impacting the speed and convergence of the training process. Higher learning rates can lead to overshooting, where the adjustments are too large, potentially hindering the convergence of the model. A decay rate of 0.9 and 5000 decay steps were applied to reduce the learning rate over time, ensuring more precise fine-tuning of the model’s parameters.

In each iteration, the number of samples processed is determined by the batch size, which is set to 512 in our experiments. This value was chosen to balance computational efficiency against available memory resources. The model was trained for a total of 100 epochs to represent 100 complete passes through the entire training dataset. This duration was determined to allow sufficient opportunity for the model to iteratively refine its internal parameters and learn the complex patterns necessary for accurate arrhythmia classification from the ECG data. These parameters collectively governed the training dynamics to help with optimal convergence and generalization performance.

3.3. Evaluation Metrics

In order to test and assess the performance of the suggested hybrid 1D CNN-eGRU, several performance metrics are utilized in our experiments:

• Accuracy: This measure demonstrates the ability of the model to accurately identify various arrhythmia classifications. Commonly, it computes the ratio of correctly classified samples to total samples.

$$Accuracy={\displaystyle \frac{TP+TN}{TP+FP+FN+TN}}$$

(9)

• Precision: This metric calculates the percentage of true positive predictions among all the positive predictions. It assesses the ability to avoid false positive errors and provides a measure of the correctness of the positively classified instances.

$$Precision={\displaystyle \frac{TP}{TP+FP}}$$

(10)

• Sensitivity (Recall): Sensitivity, also known as recall, quantifies the capacity of model to recognize all relevant examples of specific arrhythmia class. It measures the percentage of true positive predictions among the dataset’s real positive examples.

$$Sensitivity={\displaystyle \frac{TP}{TP+FN}}$$

(11)

• Specificity: Specificity denotes the ratio of correctly identified true negatives by the model among all actual negatives. It is also known as selectivity or the true negative rate, which quantifies the capacity of the model to precisely detect negative instances. Specifically, it assesses the accuracy in identifying examples that do not belong to the target class.

$$Specificity={\displaystyle \frac{TN}{TN+FP}}$$

(12)

• F1-score: The harmonic means of precision and sensitivity (recall) can be evaluated by the F1-score. The F1-score gives an overall assessment of the model’s performance in terms of both positive and negative predictions by combining precision and sensitivity into a single metric.

$$F1\text{-}score={\displaystyle \frac{2\ast recall\ast precision}{recall+precision}}$$

(13)

• ROC Curve and AUC: The Receiver Operating Characteristic (ROC) curve was used to graphically evaluate the classification performance across various discrimination thresholds. In the ROC, the True Positive Rate is plotted against the False Positive Rate. In addition, the Area Under the ROC Curve (AUC) quantifies the overall performance by calculating the area beneath this curve. A higher AUC value indicates a better ability of the model to distinguish between the different arrhythmia classes.

$$AUC={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{TP}{TP+FN}}+{\displaystyle \frac{TN}{TN+FP}}\right)$$

(14)

These measures together offer a comprehensive assessment of the deep learning model in classifying the cardiac arrhythmias.

3.4. Performance of the Proposed Hybrid Model

The hybrid 1D CNN-eGRU model demonstrated exceptional performance in the classification of four types of cardiac arrhythmia. In the training set, the model accomplished an overall accuracy of 100%. It indicates the ability of the proposed hybrid 1D CNN-eGRU model to accurately classify various arrhythmia classes. The validation and testing sets yielded impressive accuracy rates of 99%, further emphasizing the generalization capabilities and robustness of the proposed hybrid CNN-eGRU model. As depicted in Figure 5, the accuracy curve illustrates the performance of the proposed model throughout the training process.

The loss function scores of the 1D CNN-eGRU were notably low, with values of 0.02 and 0.07 in both the training and testing datasets, respectively. The testing dataset shows a slightly higher loss reflecting a modest increase in error when the model is applied to new data. This slight increase in loss is expected due to inherent differences between training and testing datasets.

The ROC curves, presented in Figure 6 for the training and testing, provide insights into the classification performance of the 1D CNN-eGRU for individual arrhythmia types. The AUC values in the training were 1.00 for all classes, indicating perfect discrimination between different classes. In the testing set, the AUC values were slightly lower but still high, with 0.99 for class F and class S and 1.00 for the remaining classes (N, V).

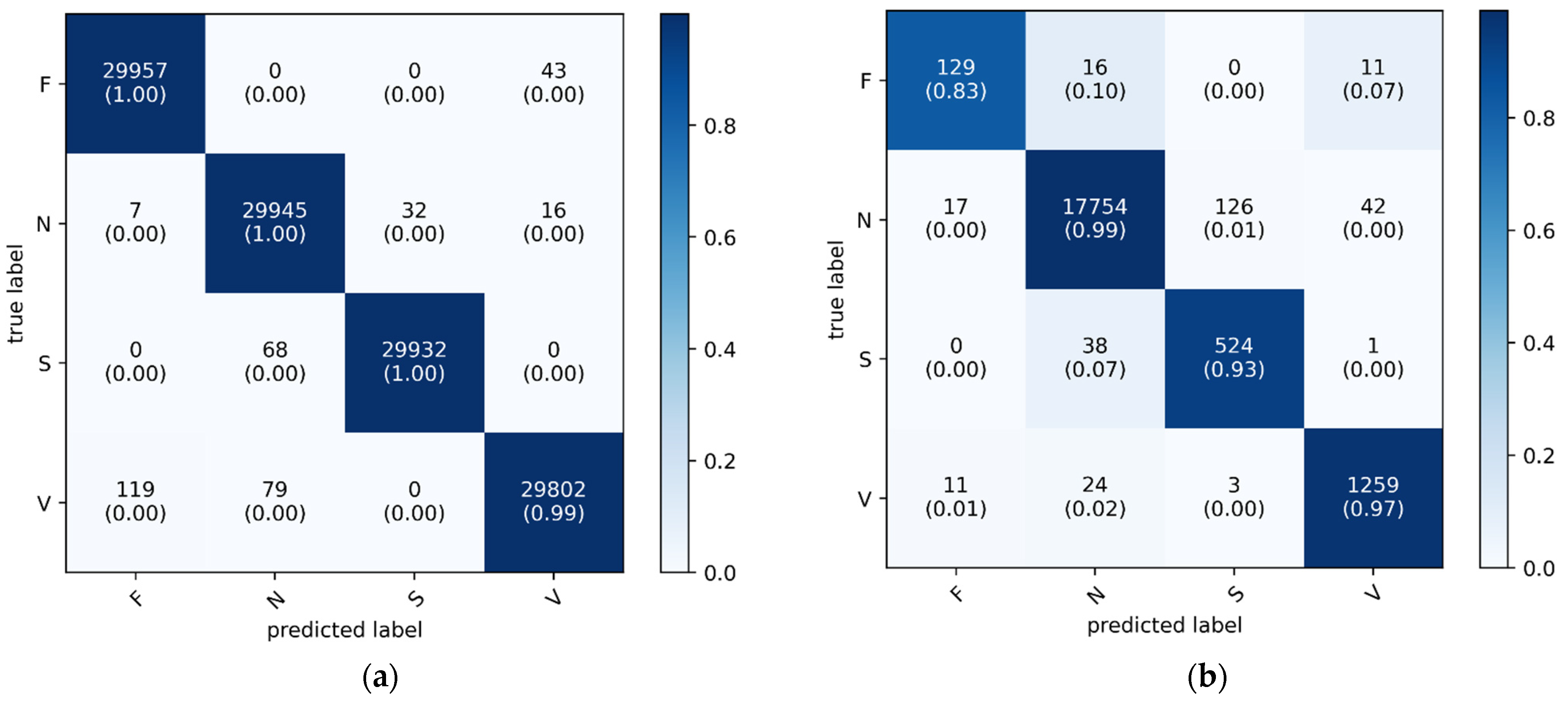
As shown in Figure 7, the confusion matrix displays the classification performance of the proposed 1D CNN-eGRU model on both the training (a) and testing (b) datasets. The y-axis represents the actual ground-truth labels for the four arrhythmia classes: fusion beats (F), normal beats (N), supraventricular beats (S), and ventricular beats (V). The x-axis corresponds to the predicted labels generated by the model. Each cell indicates the number of samples classified into each predicted class, with the diagonal cells representing correct classifications. These diagonal entries also include class-wise accuracy percentages in parentheses. A color bar is provided to illustrate the normalized accuracy values, using a blue gradient where darker shades indicate higher classification accuracy and lighter shades indicate lower agreement. This visualization highlights the model’s performance, with darker cells along the diagonal confirming accurate predictions and lighter off-diagonal cells revealing instances of misclassification.

Table 2. Evaluation metrics of the proposed 1D CNN-eGRU model for the testing dataset.

	Arrhythmia Class
	F	N	S	V	Avg
Precision	0.82	1.00	0.80	0.96	0.90
Sensitivity	0.83	0.99	0.93	0.97	0.93
F1-score	0.82	0.99	0.86	0.96	0.91
Specificity	1.00	0.97	0.99	1.00	0.99
AUC	0.99	1.00	0.99	1.00	1.00
Accuracy	0.99
Loss	0.07

offers a comprehensive comparison of various performance metrics for a classification model across four distinct classes (F, N, S, and V) for the testing dataset. These metrics encompass precision, sensitivity (recall), F1-score, specificity, AUC, accuracy, and loss. Each measure gives worthy insight into the performance of the model in accurately classifying instances of each class, thereby providing a thorough performance evaluation of the model. It is important to notice that we rounded all values in all tables to two decimal places.

Precision quantifies the proportion of true positive predictions among all positive predictions, with high precision indicating a low rate of false positives. In the testing dataset, precision values varied across classes, with class F and class S recording lower values (0.82 and 0.80, respectively) compared to other classes. This indicates that the model encounters some difficulty in distinguishing these classes in unseen data. Despite this, precision remained perfect for class N (1.00) and high for class V (0.96), resulting in an average precision of 0.90.

Sensitivity (Recall) measures the proportion of actual positive instances correctly identified by the model. The sensitivity values in the testing dataset remained high, with class N, S, and V achieving values above 0.90, while class F showed a lower sensitivity of 0.83. The overall average sensitivity of 0.93 indicates that the model is generally effective in identifying arrhythmia cases, though challenges exist for specific classes with lower sample representation.

F1-score, which balances precision and recall, showed similar patterns. The testing dataset recorded an F1-score of 0.82 for class F and 0.86 for class S, whereas the other classes performed significantly better. The average F1-score of 0.91 demonstrates that the model maintains an effective balance between precision and recall, although class imbalance slightly impacts its ability to generalize across all classes.

Specificity evaluates the capability of the model to correctly identify negative cases. The model performed exceptionally in this aspect since it achieved near-perfect specificity across all classes, with values ranging from 0.97 (class N) to 1.00 (class F and V). The average specificity of 0.99 confirms that the model is highly reliable in ruling out negative instances. This ensures minimal misclassification of normal ECG signals.

The AUC values provide insight into the ability of the model to differentiate between different arrhythmia classes. The model demonstrated excellent discriminative power since it achieved near-perfect AUC values (0.99–1.00) for all classes. The average AUC of 1.00 reflects the high robustness and effectiveness of the model in classification of the different arrhythmia categories.

The overall accuracy of 0.99 confirms that the model generalizes well to unseen data, correctly classifying the majority of testing samples. Additionally, the low loss value of 0.07 further indicates the stability and reliability of the trained model.

Despite its strong performance, the model exhibits slight limitations in precision and sensitivity, particularly for class F (156 samples) and class S (563 samples), which are underrepresented compared to other classes. Although a hybrid data balancing approach, including resampling and class weighting, was employed to mitigate class imbalance, the disparity in sample sizes remains a challenge.

3.5. Comparison with Standalone 1D CNN

To evaluate the effectiveness of the proposed 1D CNN-eGRU model, its performance was compared against a standalone 1D CNN model. The evaluation metrics, presented in

Table 3. Evaluation metrics of the 1D CNN model.

	Arrhythmia Class
	F	N	S	V	Avg
Precision	0.76	1.00	0.78	0.94	0.87
Sensitivity	0.85	0.99	0.93	0.97	0.93
F1-score	0.80	0.99	0.85	0.95	0.90
Specificity	0.99	0.97	0.99	0.99	0.99
AUC	0.99	1.00	0.99	1.00	0.99
Accuracy	0.98
Loss	0.16

, serve as a baseline to assess the advantages of integrating GRU layers with CNN.

In terms of precision, as can be observed from Table 2 and Table 3, the proposed 1D CNN-eGRU model achieved an average precision of 0.90, which is higher than the 0.87 obtained by the standalone 1D CNN model. This improvement is particularly noticeable in class F (0.82 vs. 0.76) and class S (0.80 vs. 0.78), indicating that the incorporation of GRU layers enhances the model’s ability to distinguish between arrhythmia types, particularly for minority classes.

As can be seen in Table 2 and Table 3, the sensitivity of both models remained comparable, with an average of 0.93 in both cases. However, the standalone CNN model demonstrated slightly lower sensitivity for class F (0.85 vs. 0.83 in the hybrid model). This result indicates that while CNN layers alone are effective at capturing spatial features, they may not fully capture the temporal dependencies of ECG signals, which are better handled by GRU layers.

The F1-score of the proposed hybrid model, which balances precision and recall, was 0.91 compared to 0.90 achieved by the standalone CNN model. The improvement is particularly evident in class F (0.82 vs. 0.80) and class S (0.86 vs. 0.85). These results confirm that the hybrid model maintains a better trade-off between precision and sensitivity, leading to more reliable classification performance.

In terms of specificity and AUC, both models exhibited strong performance. The specificity values remained high in both models (0.99 on average) to ensure minimal false positives. Similarly, AUC values were nearly identical between the two models. The proposed hybrid model achieved an average of 1.00 and the standalone CNN model reached 0.99. These results indicate that both architectures are highly capable of distinguishing between arrhythmia classes.

The most significant improvement was observed in accuracy and loss. The 1D CNN-eGRU model achieved a higher accuracy (0.99) compared to 0.98 in the standalone 1D CNN model. Additionally, the loss was significantly lower in the hybrid model (0.07) compared to 0.16 in the CNN-only model, indicating that the incorporation of GRU layers contributed to improved stability and convergence.

3.6. Comparison with Standalone GRU

A second comparative analysis was conducted between the proposed 1D CNN-eGRU model and a standalone GRU model. The performance metrics of the GRU-only architecture, presented in

Table 4. Evaluation metrics of the GRU model performance.

	Arrhythmia Class
	F	N	S	V	Avg
Precision	0.70	0.99	0.71	0.97	0.84
Sensitivity	0.83	0.98	0.92	0.96	0.92
F1-score	0.76	0.99	0.80	0.97	0.88
Specificity	0.99	0.96	0.99	0.99	0.98
AUC	0.98	0.99	0.99	1.00	0.99
Accuracy	0.98
Loss	0.16

, highlight the limitations of using GRU layers alone without CNN-based feature extraction.

As can be observed from Table 2 and Table 4, the precision of the proposed hybrid model (0.90) was significantly higher than that of the GRU model (0.84). This difference was particularly evident in class F (0.82 vs. 0.70) and class S (0.80 vs. 0.71), demonstrating that the CNN component plays a crucial role in improving classification accuracy, particularly for minority classes.

In terms of the sensitivity measure, the proposed hybrid 1D CNN-eGRU model showed slight improvement (0.93) compared to the GRU model (0.92). This highlights the ability of the model to correctly identify true positives for different arrhythmia classes.

The proposed hybrid 1D CNN-GRU model demonstrated superior performance across several key metrics compared to the standalone GRU model. It achieved higher overall accuracy (0.99 vs. 0.98) and also higher average F1-score (0.91 vs. 0.88). The F1-score improvement was notably influenced by enhanced precision in classifying specific arrhythmia classes (F and S). This indicates that the CNN component effectively extracted features that benefited the GRU’s sequential analysis. Furthermore, the hybrid model exhibited more efficient learning and potentially better generalization since it produced lower training loss (0.07 vs. 0.16). While both models achieved high specificity and AUC values that reflect strong capabilities in minimizing false positives and discriminating between classes, the hybrid model showed marginally higher average specificity (0.99 vs. 0.98). The near-identical AUC scores confirm the robust discriminative power of both architectures, yet the collective improvements in accuracy, F1-score, precision, and loss underscore the advantages of integrating CNN feature extraction with GRU sequence modeling for this arrhythmia classification task.

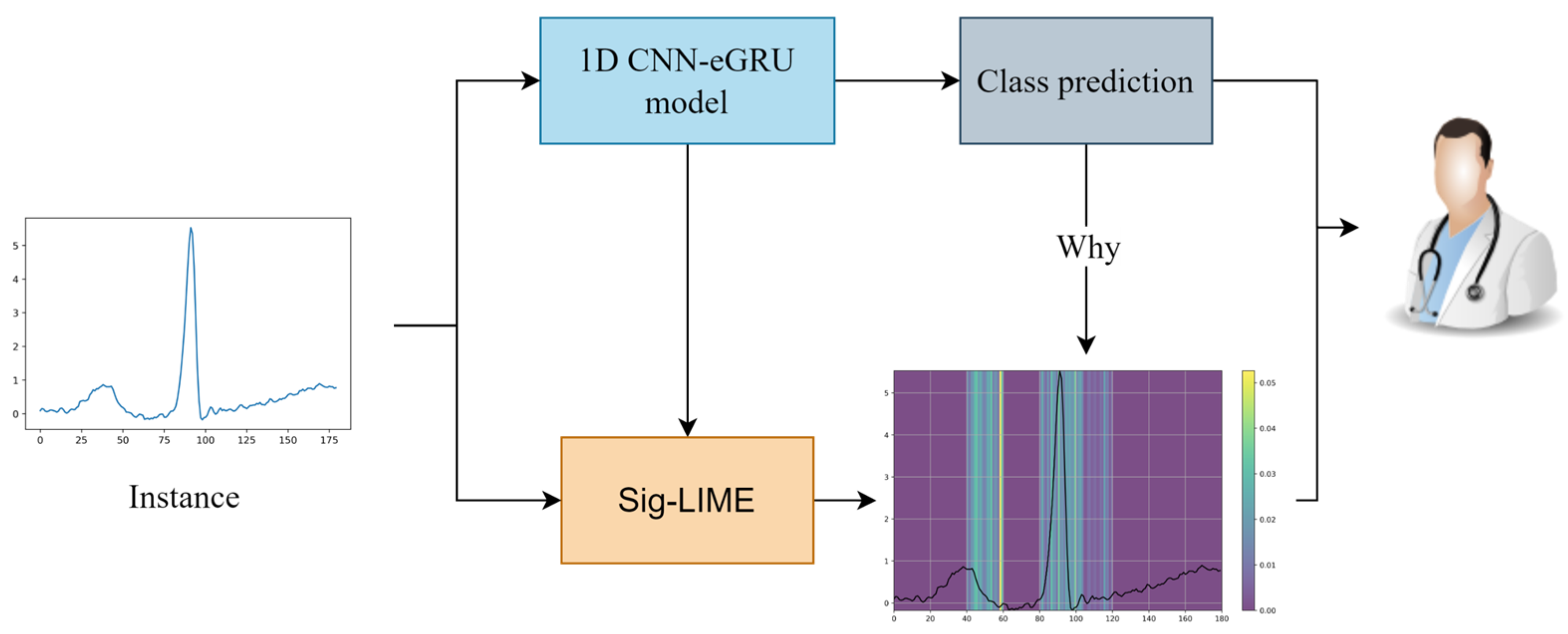
3.7. Interpretability Analysis with Sig-LIME

Sig-LIME (signal-based enhancement of LIME) [46] introduces an advanced version of the Local Interpretable Model-agnostic Explanations (LIME) [47] tailored for signal data, addressing limitations of the traditional LIME when applied to temporally dependent data. Sig-LIME leverages signal-specific features to generate more accurate and reliable explanations for machine learning models, particularly in fields requiring precise temporal data interpretation such as ECG analysis and other time-series data applications. The technique also tackles the issues of instability and local fidelity in LIME by integrating new data generation and weighting techniques, ensuring more consistent and faithful explanations.

Figure 8 illustrates the application of the Sig-LIME explanation technique to a 1D CNN-eGRU model used for classifying cardiac arrhythmia. The plot on the bottom right shows the Sig-LIME explanation for the input signal. The highlighted regions indicate the portions of the signal that contributed most to the model’s classification decision. These regions are where the model focused its attention to classify the signal as class N.

Figure 9 provides a comprehensive visual representation of the investigation’s extensive scope and the significant insights obtained through detailed analysis. Figure 9 illustrates the outcome of the Sig-LIME explanation technique using heatmaps, which highlights the features primarily situated around the QRS complex. This observation is visually apparent, as Sig-LIME consistently emphasizes the regions of the P-wave, QRS complex, and T-wave to differentiate between classes and classify various arrhythmias. Notably, the QRS complex is crucial in diagnosing a wide range of cardiac pathologies, including arrhythmias [48], thus substantiating the representations generated by Sig-LIME. The explanations demonstrate the proposed model’s capability to utilize these areas to effectively distinguish between different classes.

3.8. Comparison with Existing Works

This section presents a comparative analysis of the proposed 1D CNN-eGRU classifier against several existing deep learning-based models reported in recent literature. The evaluation is based on three primary performance metrics: accuracy, sensitivity, and specificity.

Table 5. Comparison of the proposed 1D CNN-eGRU model and the existing works.

Author	Classifier	Classes	Accuracy	Sensitivity	Specificity
Rasti et al. [49]	1D CNN	2	0.97	0.96	0.98
Hassan et al. [50]	CNN-BiLSTM	5	0.98	0.91	0.91
Essa et al. [51]	CNN-LSTM	4	0.96	0.69	0.95
Xu et al. [18]	CNN-BiLSTM	5	0.96	0.96	0.96
Guo et al. [52]	DenseNet-GRU	5	0.92	0.82	0.96
Hannun et al. [53]	1D CNN	12	0.95	0.77	0.97
Singh et al. [17]	RNN-LSTM	2	0.88	0.92	0.83
Kachuee et al. [14]	RISNet	5	0.93	0.93	N/A
Acharya, et al. [54]	1D CNN	5	0.94	0.97	0.92
Shadmand et al. [55]	BBNN	2	0.98	0.73	0.99
Our work	1D CNN-eGRU	4	0.99	0.94	0.99

summarizes the results, and the percentage differences are discussed to highlight the improvements achieved by the proposed model.

The proposed 1D CNN-eGRU classifier consistently demonstrates superior performance across most key metrics. When compared to the standard 1D CNN model [49], our approach yields a 2.06% increase in accuracy (0.97 vs. 0.99), a slight 2.08% reduction in sensitivity (0.96 vs. 0.94), and a 1.02% improvement in specificity (0.98 vs. 0.99).

Against the CNN-BiLSTM classifier developed by Hassan et al. [50], the proposed model achieves a 1.02% higher accuracy, a 3.30% increase in sensitivity, and a substantial 8.79% improvement in specificity. Similarly, when compared to the CNN-LSTM approach reported by Essa et al. [51], our model shows a 3.12% improvement in accuracy, a notable 36.23% gain in sensitivity, and a 4.21% increase in specificity.

Compared to the CNN-BiLSTM model by Xu et al. [18], the 1D CNN-eGRU architecture delivers a 3.12% higher accuracy (0.96 vs. 0.99), a 2.08% reduction in sensitivity, and a 3.12% enhancement in specificity.

Finally, in comparison with the DenseNet-GRU model [52], our proposed method achieves a 7.61% improvement in accuracy, a 14.63% increase in sensitivity (0.82 vs. 0.94), and a 3.12% rise in specificity. When evaluated against another 1D CNN model reported by [53], the proposed model outperforms it with a 4.21% higher accuracy, a 22.08% increase in sensitivity, and a 2.06% improvement in specificity.

Additional comparisons further validate the robustness of the proposed model. Our 1D CNN-eGRU classifier shows significant improvement over the RNN-LSTM model proposed by Singh et al. [17], with a 12.50% increase in accuracy, a 2.17% improvement in sensitivity, and a 19.28% gain in specificity. Compared to RISNet by Kachuee et al. [14], our classifier achieves a 6.45% higher accuracy and a 1.08% increase in sensitivity; however, specificity was not reported in RISNet.

When evaluated against the 1D CNN model by [54], our approach shows a 5.32% improvement in accuracy and a 7.61% increase in specificity, though it demonstrates a 3.09% lower sensitivity. Finally, when compared with the BBNN architecture developed by Shadmand et al. [55], our model attains a 1.02% improvement in accuracy and a remarkable 28.77% increase in sensitivity, with both models achieving an identical specificity of 0.99.

In addition to improved classification performance, our approach offers enhanced model interpretability through the integration of the Sig-LIME technique. By applying Sig-LIME, we are able to generate localized explanations for model predictions, highlighting the ECG signal regions that most influenced the decision. This capability addresses a critical gap in many existing deep learning approaches, which often operate as black-box models.

3.9. Discussion

The results in Table 2 highlight the effectiveness of the CNN-eGRU hybrid architecture in accurately classifying arrhythmias while also identifying areas for further enhancement, particularly in handling class imbalances. The high specificity, AUC, and overall accuracy reinforce the model’s strong predictive capabilities, making it a reliable tool for automated ECG-based arrhythmia classification.

Compared to the baseline 1D CNN model, the results in Table 2 and Table 3 demonstrate that the proposed hybrid CNN-eGRU model outperforms the standalone 1D CNN model in precision, F1-score, accuracy, and loss reduction, particularly benefiting underrepresented classes (F and S). While sensitivity, specificity, and AUC values remained comparable, the lower loss and higher precision in the hybrid model suggest that integrating GRU layers enhances the overall classification performance.

Compared to the standalone GRU model, the results in Table 2 and Table 4 demonstrate that the proposed hybrid model significantly outperforms the standalone GRU model in precision, F1-score, and accuracy, confirming the importance of CNN layers in feature extraction. The lower loss and improved classification performance in underrepresented classes (F and S) emphasize the advantage of combining CNN with GRU for ECG classification. The standalone GRU model struggled with precision, suggesting that sequential dependencies alone are insufficient without effective feature extraction from CNN layers.

To make our proposed 1D CNN-eGRU model produce more accurate, meaningful, and trust-worthy local explanations for classifying cardiac arrhythmia, the Sig-LIME explanation technique is employed in the proposed 1D CNN-eGRU model. As illustrated in Figure 9, the Sig-LIME explanations demonstrate that the proposed 1D CNN-eGRU model can utilize the P-wave, QRS and T-wave to effectively distinguish between different arrhythmia types.

When the proposed hybrid 1D CNN-eGRU model is compared to the existing works, the results in Table 5 demonstrate that the proposed hybrid CNN-eGRU model achieves superior performance and outperforms most of the previous works in terms of accuracy, sensitivity, and specificity. This indicates that integrating GRU and attention mechanism contributes to enhancing the performance of the proposed hybrid CNN-eGRU in the arrhythmia classification. Furthermore, compared to most of the existing works which often works as black-box models, the proposed 1D CNN-eGRU model utilizes the Sig-LIME to enhance the interpretability, transparency and trustworthiness of the model’s predictions.

4. Conclusions

This study proposed a novel deep learning architecture combining a one-dimensional Convolutional Neural Network (1D CNN) with a Gated Recurrent Unit (GRU) and an attention mechanism to enhance the classification of cardiac arrhythmias from ECG Lead II signals. A key innovation of this work lies in the hybrid data balancing strategy, which integrates resampling techniques with class-weighted learning to mitigate class imbalance in the MIT-BIH arrhythmia dataset. Furthermore, Sig-LIME was employed as a model-agnostic interpretability technique, offering transparent explanations of the model’s predictions and improving its applicability in clinical settings.

The proposed 1D CNN-eGRU model achieved excellent performance, with an overall accuracy and specificity of 0.99 and a sensitivity of 0.94 on the test set. These results surpass several state-of-the-art models reported in the literature such as CNN-LSTM [51], DenseNet-GRU [52], and RISNet [14], particularly in sensitivity and robustness across minority classes. By combining high predictive performance with interpretability, this study contributes to the growing body of research on trustworthy AI in healthcare. Future work will explore the scalability and generalizability of the model on larger and more diverse ECG datasets and assess its feasibility in real-time clinical deployment.