Small-Signal Stability Analysis of Converter-Interfaced Systems in DC Voltage Timescale Based on Amplitude/Frequency Operating Points
Abstract
1. Introduction
- (1)
- A universal linearized modeling method for amplitude–frequency operating points is proposed, which can be used for both qualitative and quantitative analysis of the stability mechanisms of internal voltage amplitude and internal voltage frequency.
- (2)
- The amplitude–frequency stability mechanism is analyzed using the SISO method. The influence of controller bandwidth at different DC voltage timescales on the Self-stable path and En-stable path is quantitatively evaluated. It is revealed that the instability of grid-connected converter systems is caused by insufficient damping provided by either the Self-stable path or the En-stable path.
- (3)
- The research results provide a mechanistic explanation for adjusting the control parameters of grid-connected converter systems under different DC voltage timescale bandwidths.
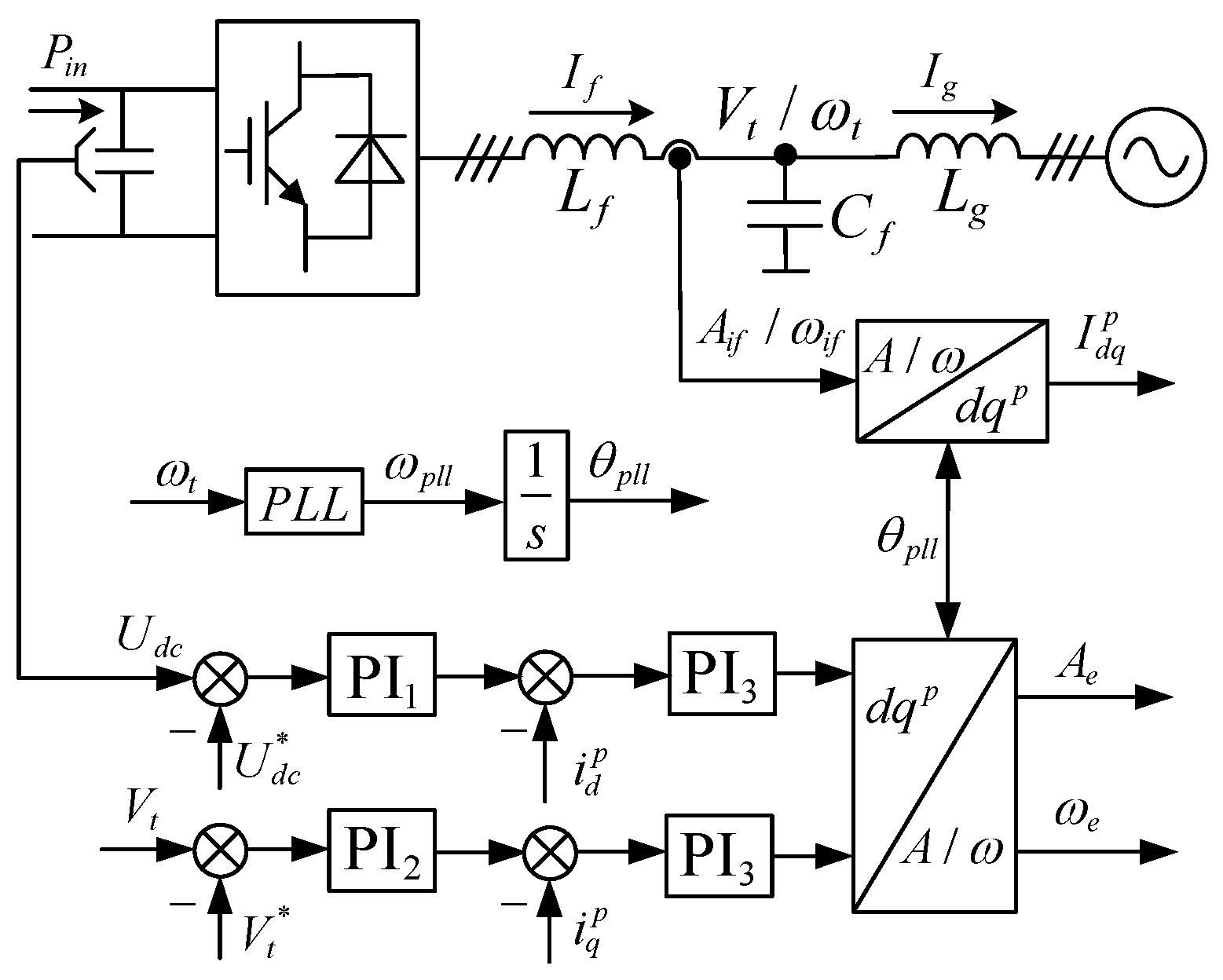
2. Small-Signal Modeling of Converter-Interfaced Systems in DC Voltage Timescale Based on Amplitude/Frequency Operating Points
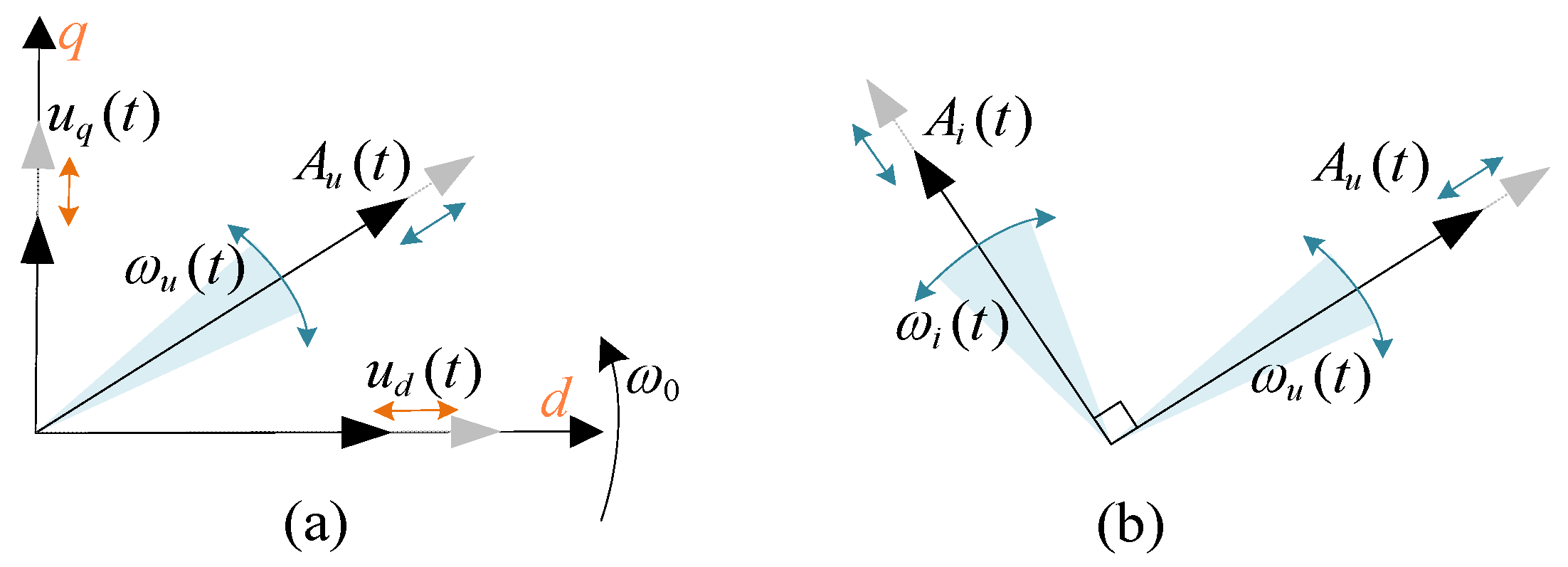
2.1. Modeling of AC Networks Based on Amplitude–Frequency Operating Points
2.2. Small-Signal Modeling of VSC
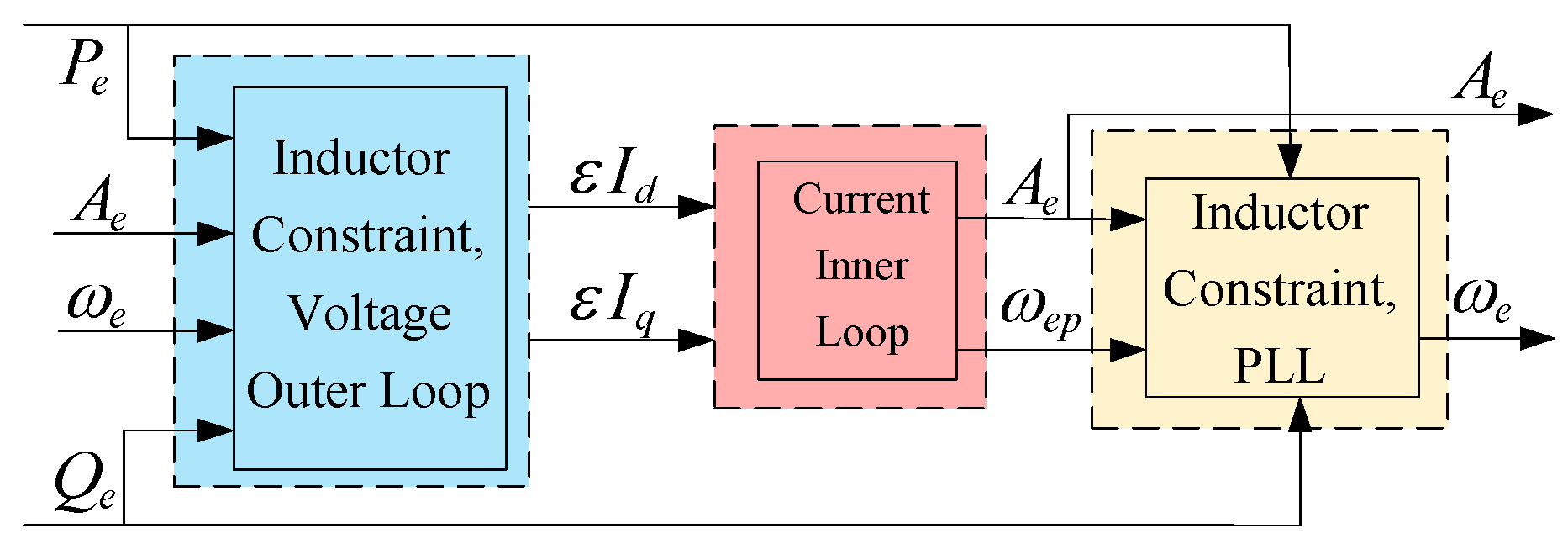
2.3. Reduced-Order DC Voltage Timescale Model for Converter-Interfaced Systems
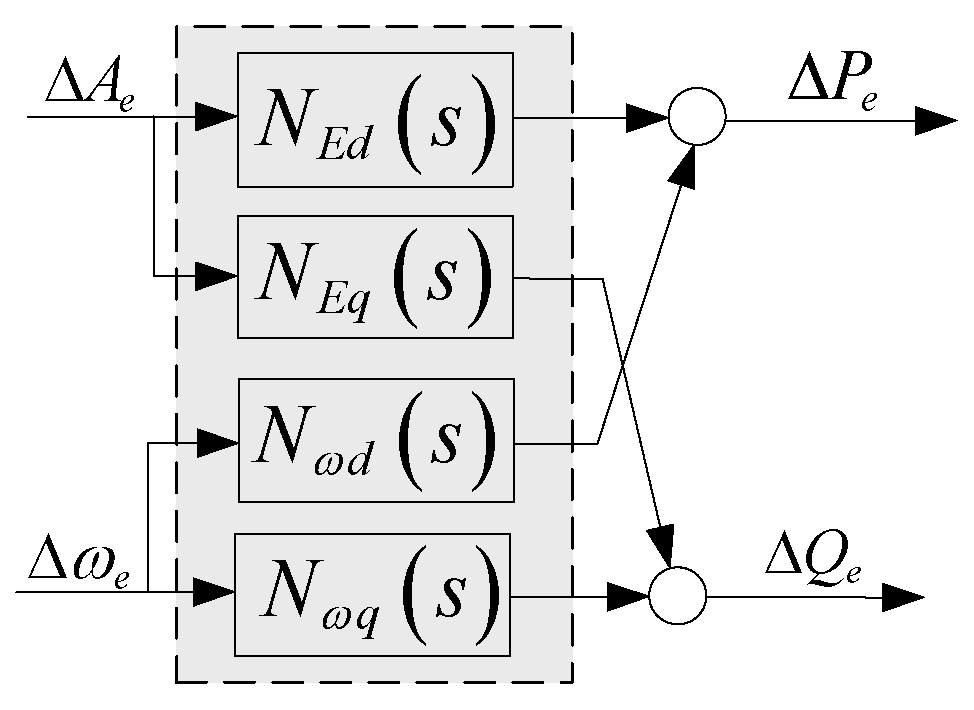
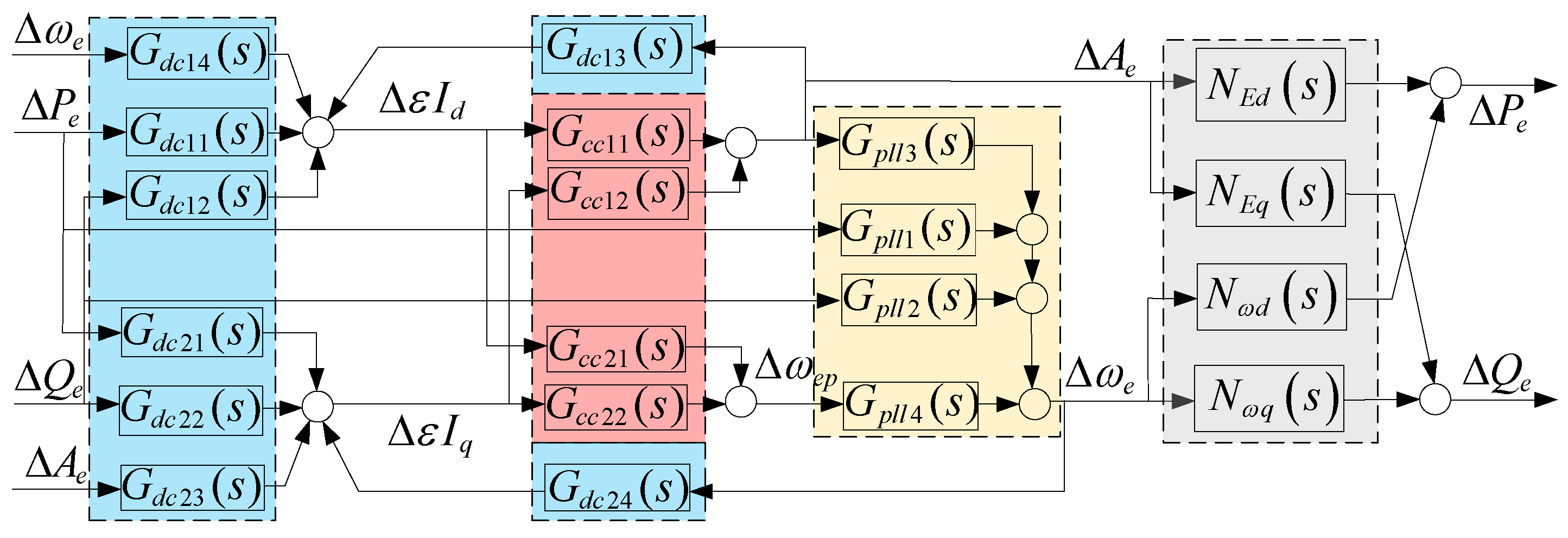
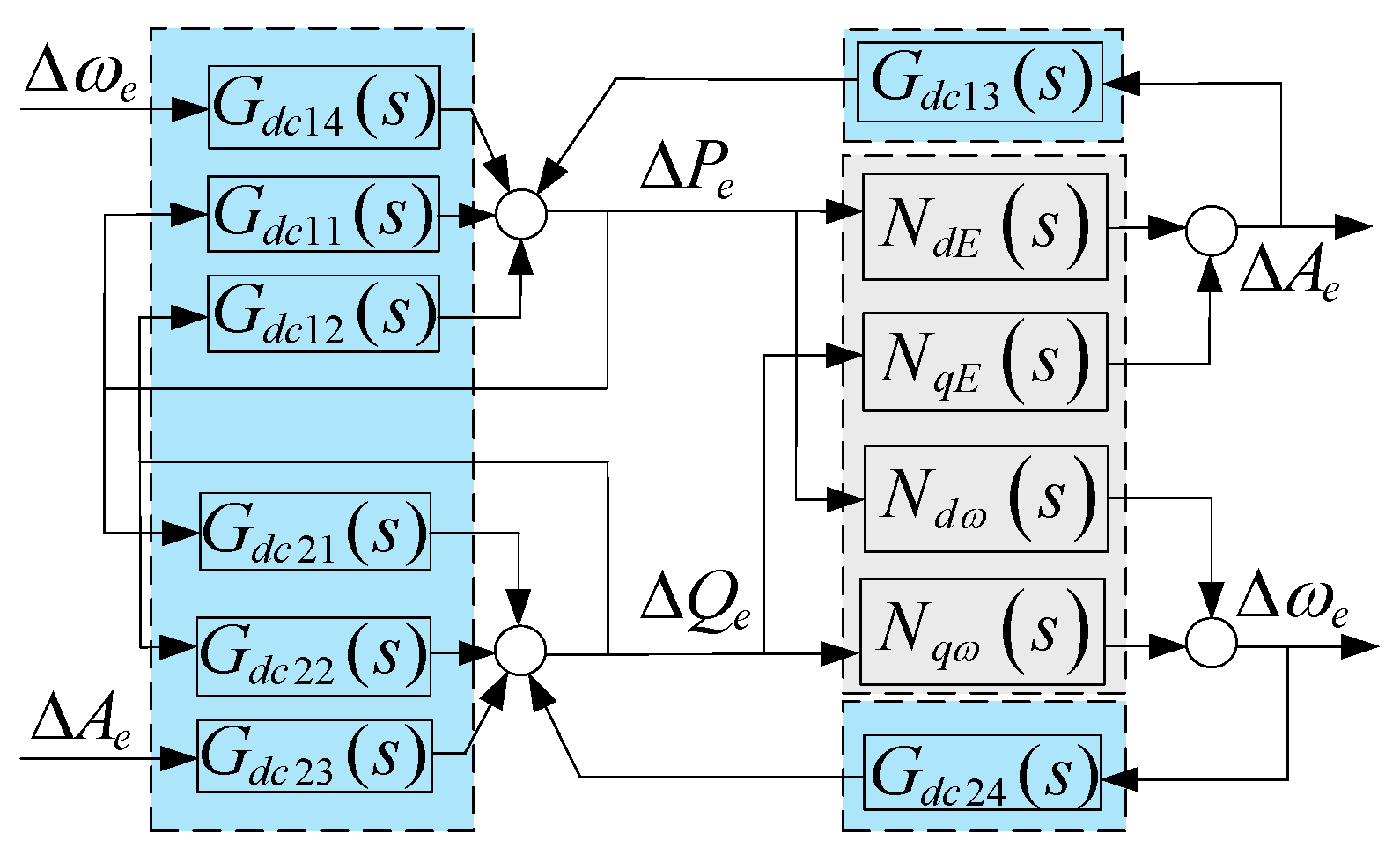
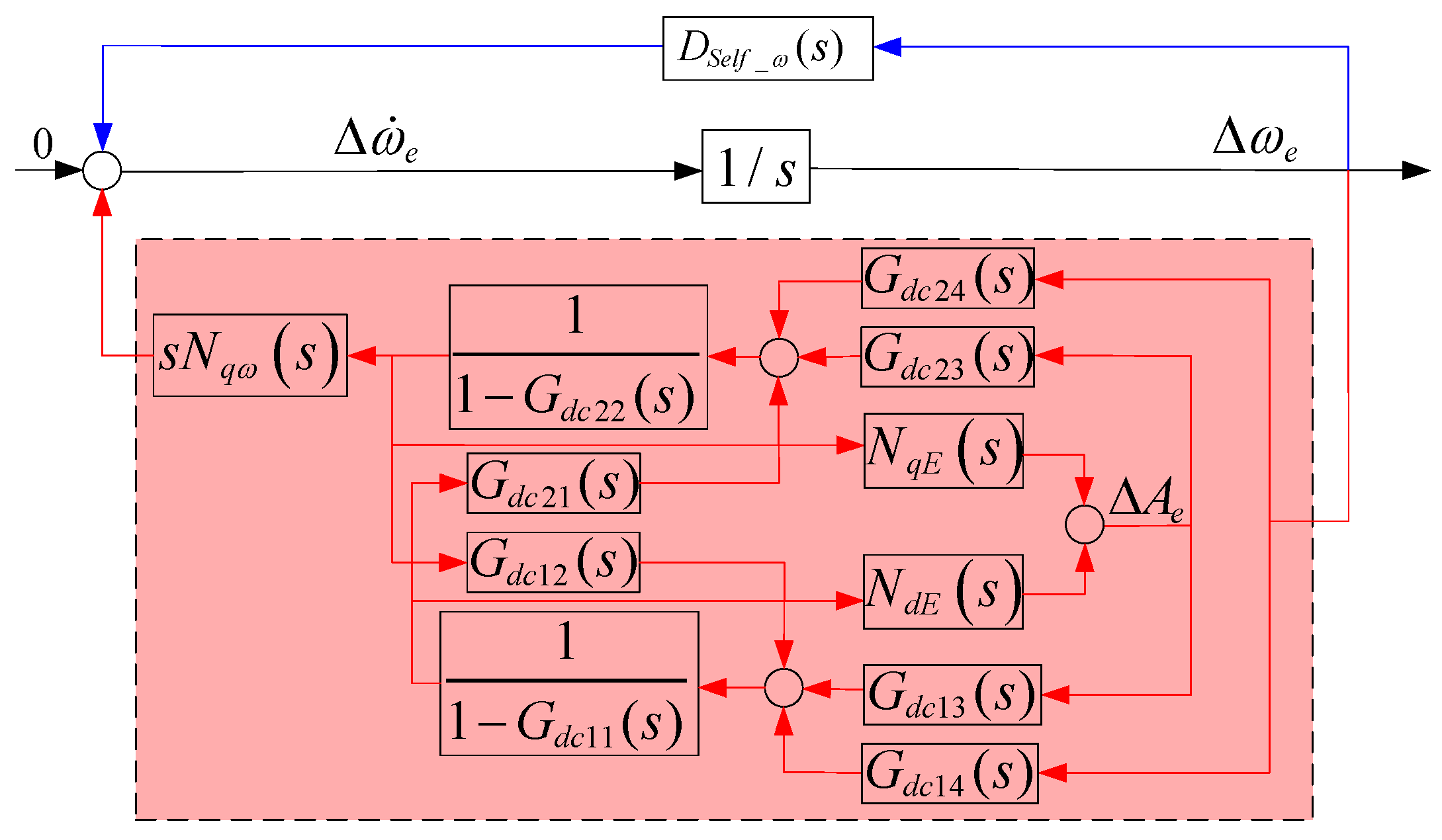
3. Self-Stable/En-Stable Path Analysis for Converter-Interfaced Systems
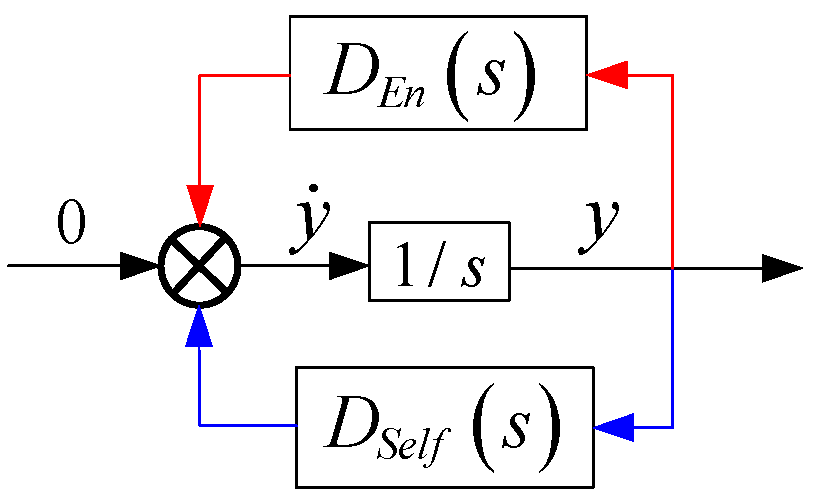
3.1. Self-Stable/En-Stable Path Analysis Method
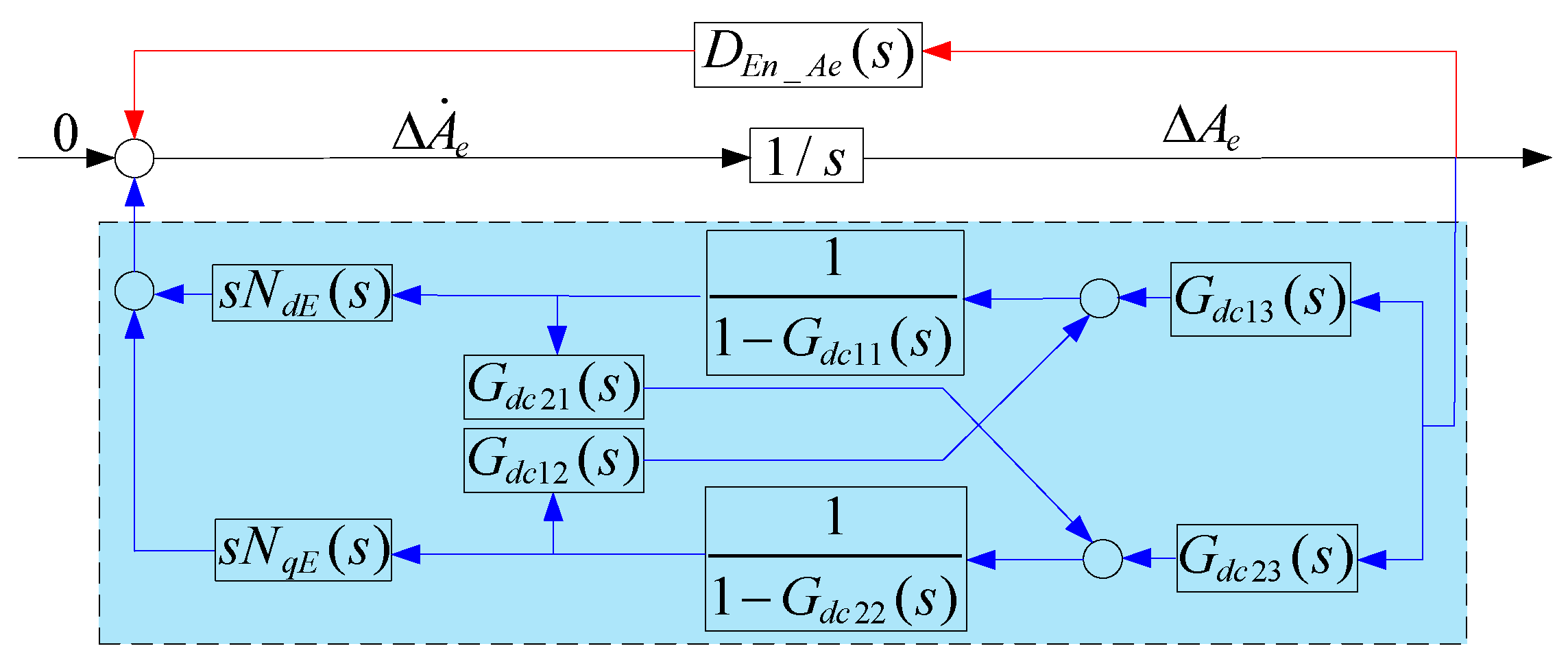
3.2. Self-Stable and En-Stable Paths of Internal Voltage Amplitude in Converter-Interfaced Systems
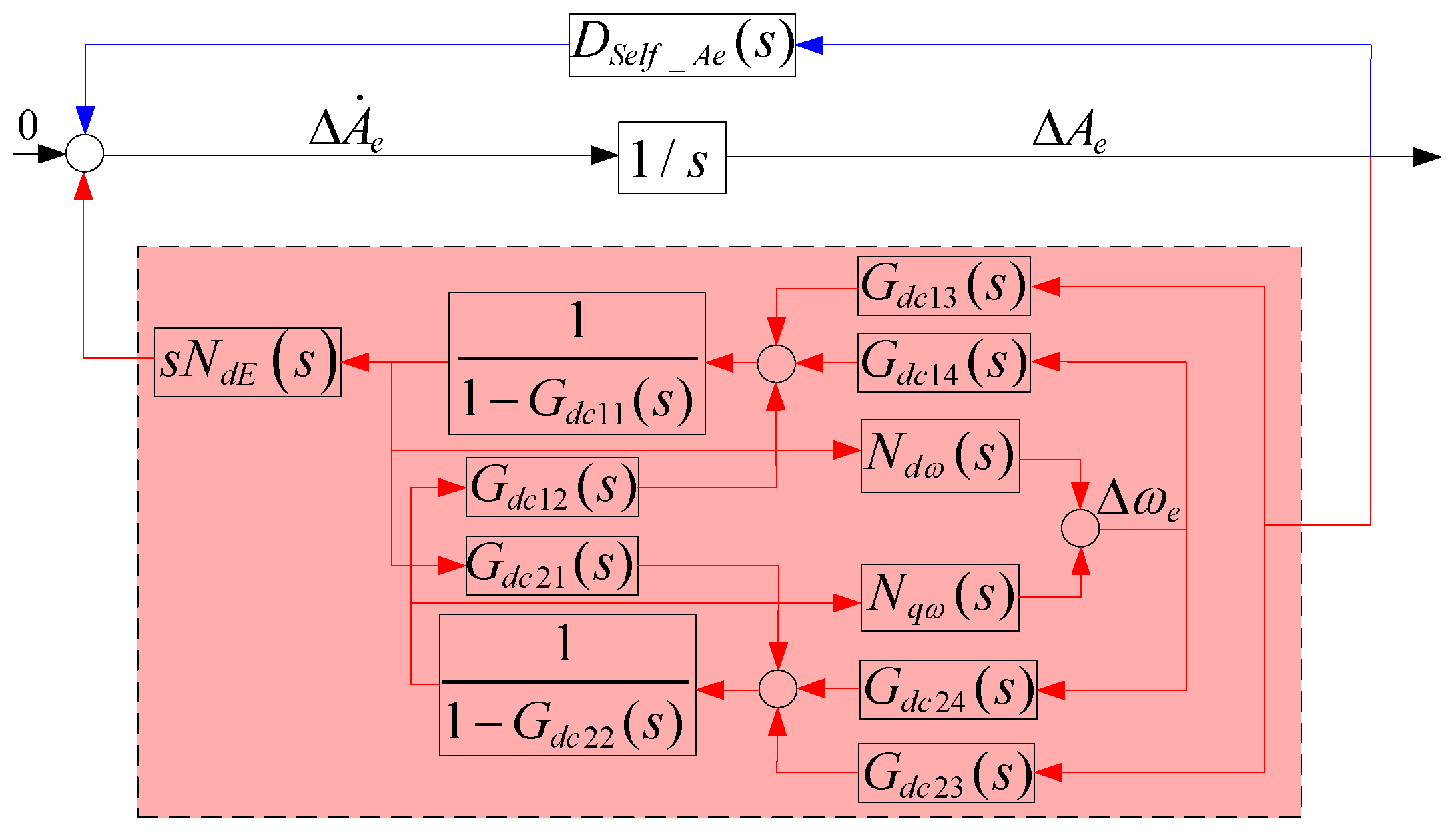
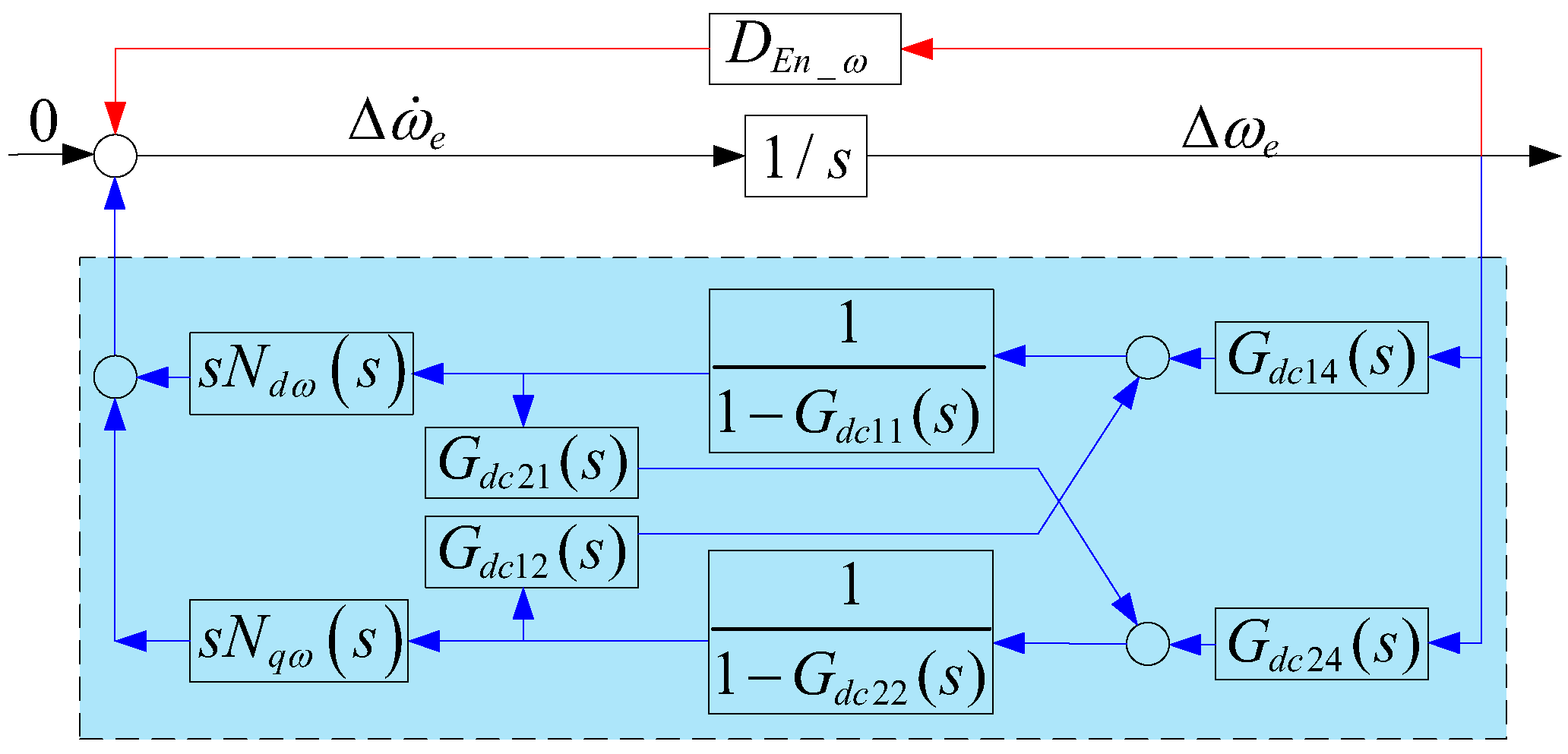
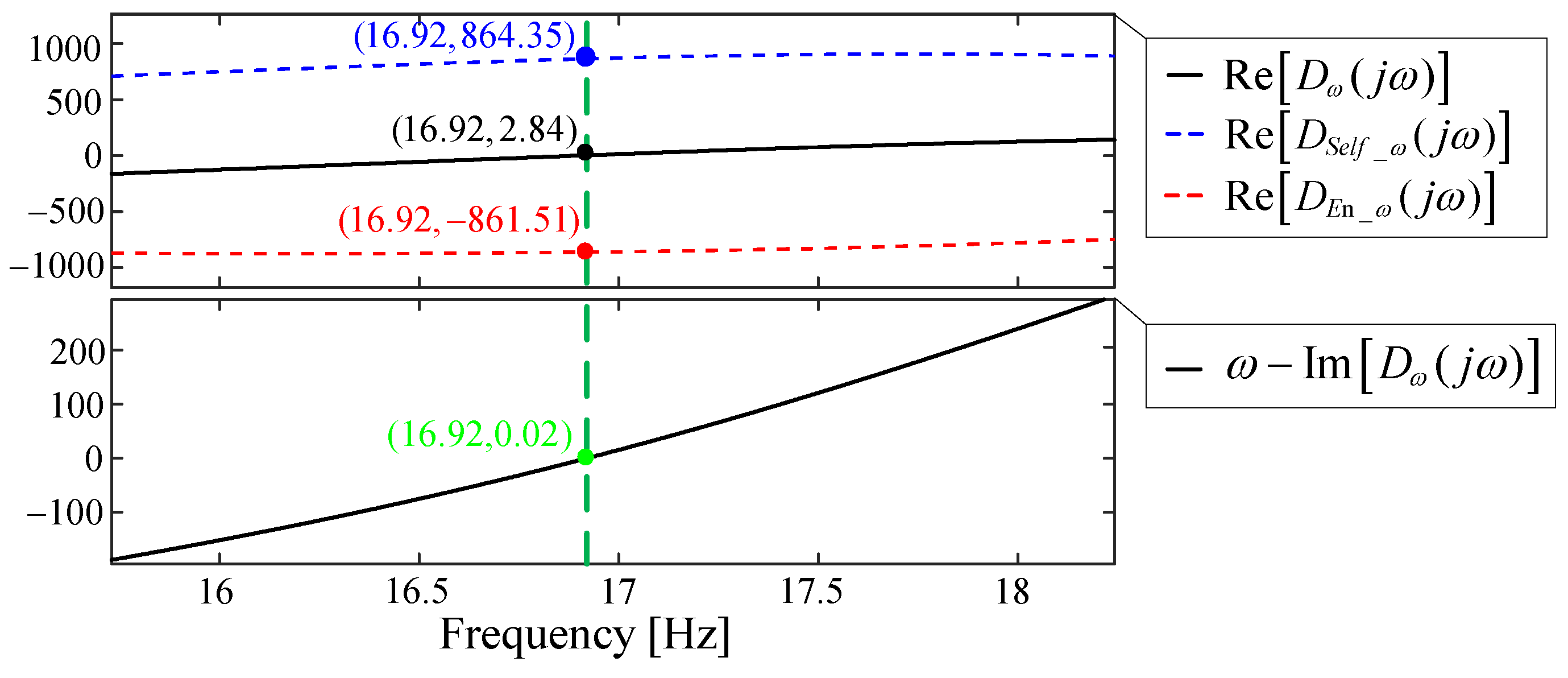
3.3. Self-Stable and En-Stable Paths of Internal Voltage Frequency in Converter-Interfaced Systems
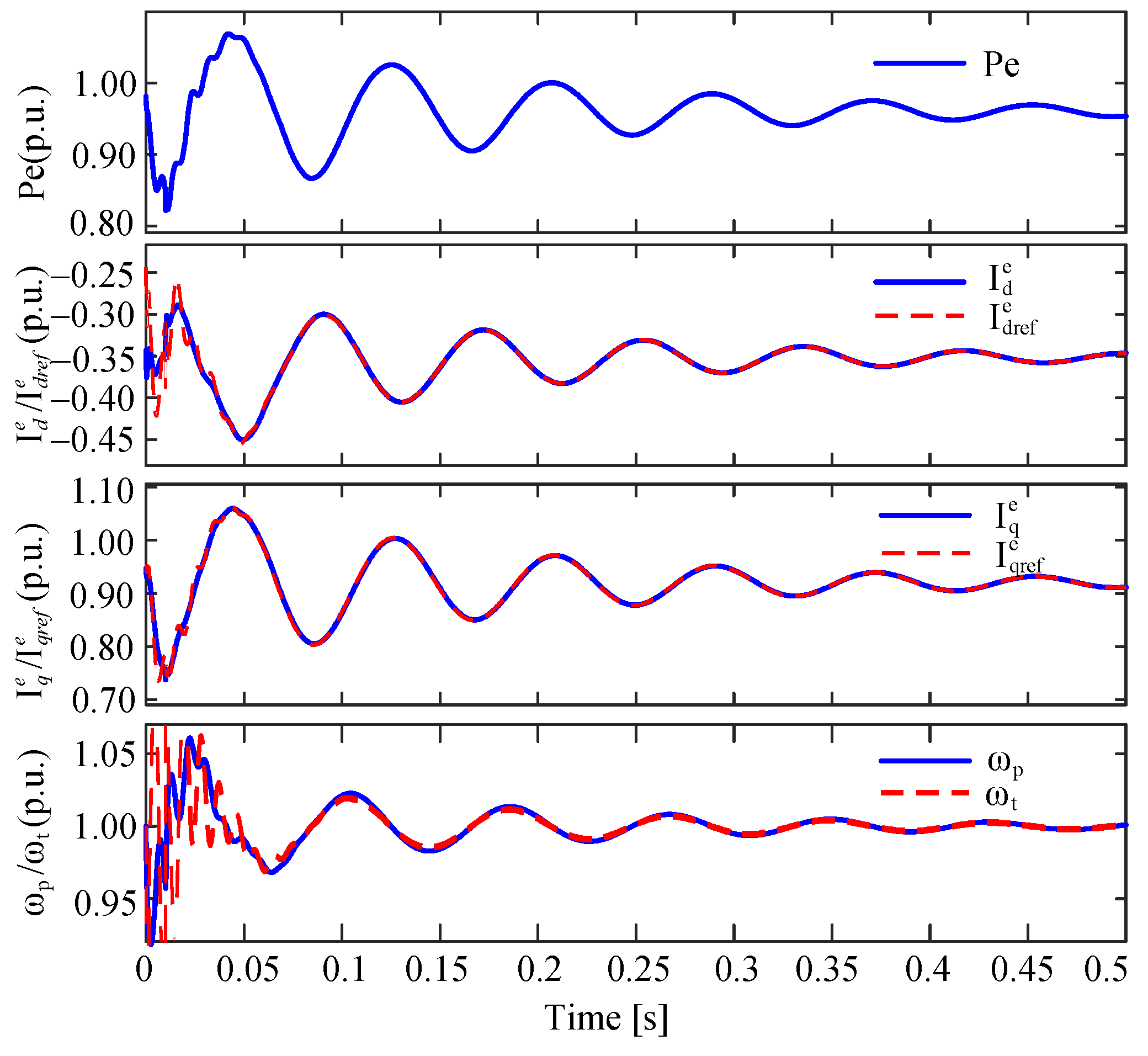
4. Case Study
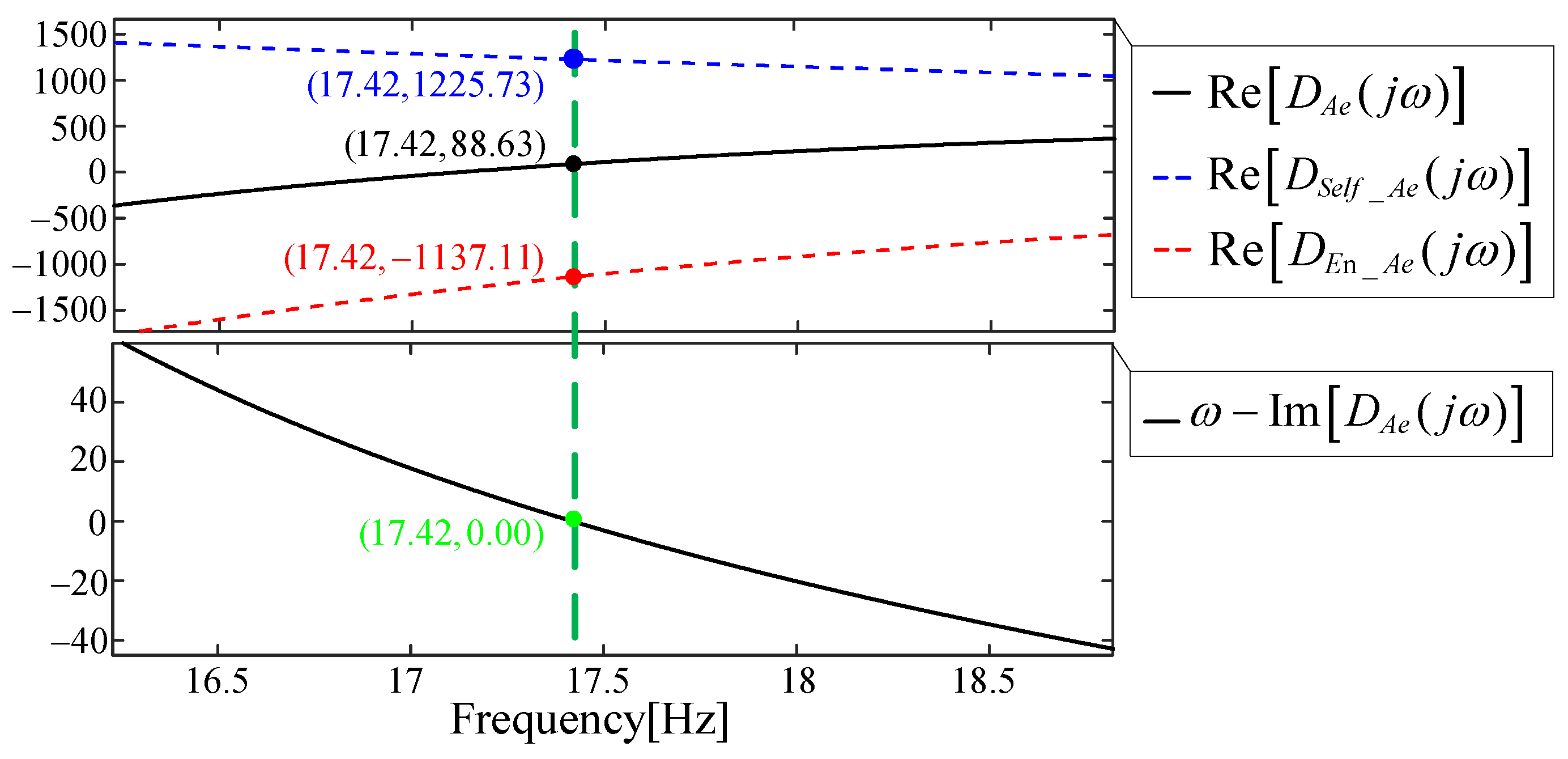
4.1. Stability of Internal Voltage Amplitude in Converter-Interfaced Systems
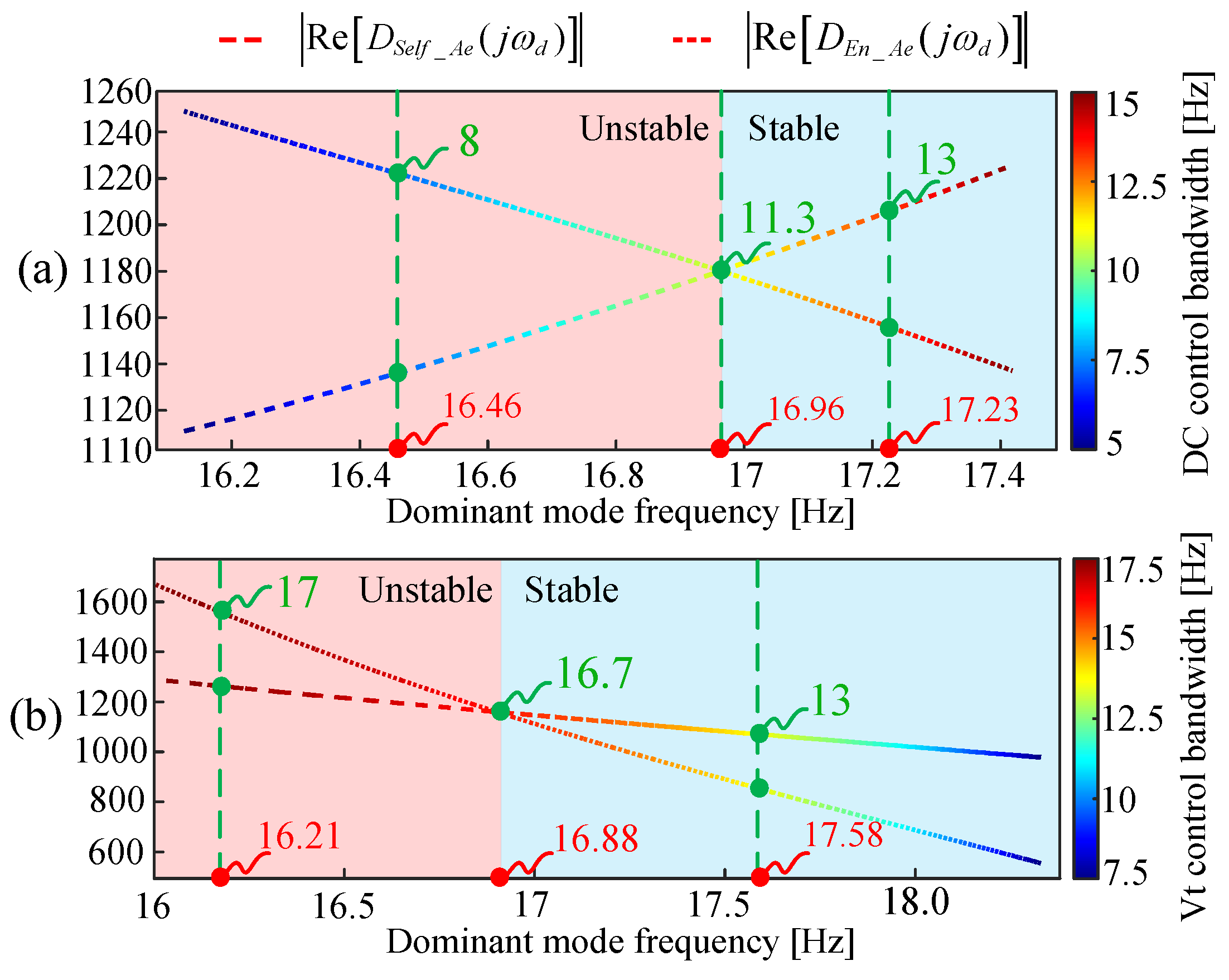
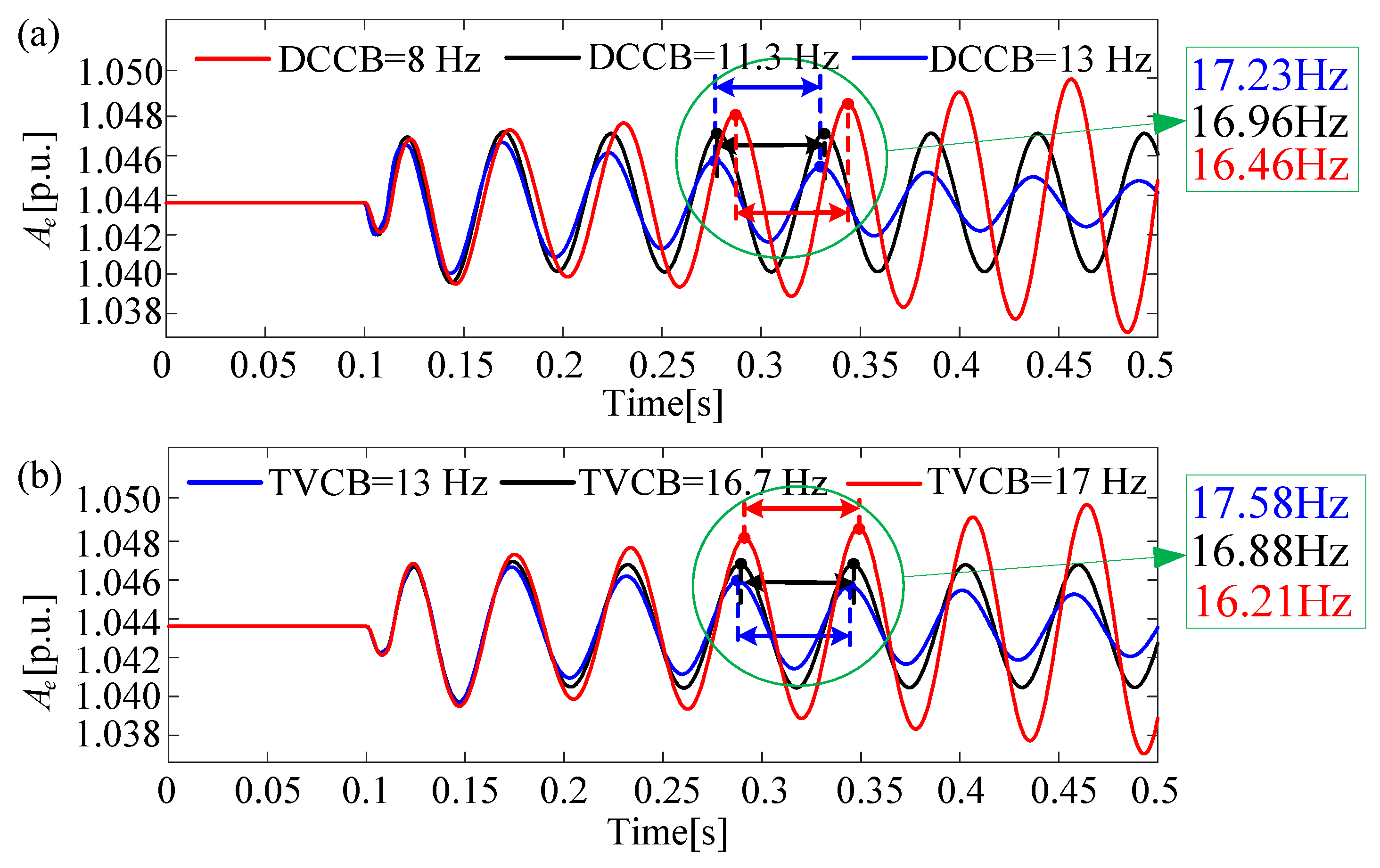
4.1.1. Influence of DCCB on the Amplitude Stability of Internal Voltage in Converter-Interfaced Systems
4.1.2. Influence of TVCB on the Amplitude Stability of Internal Voltage in Converter-Interfaced Systems
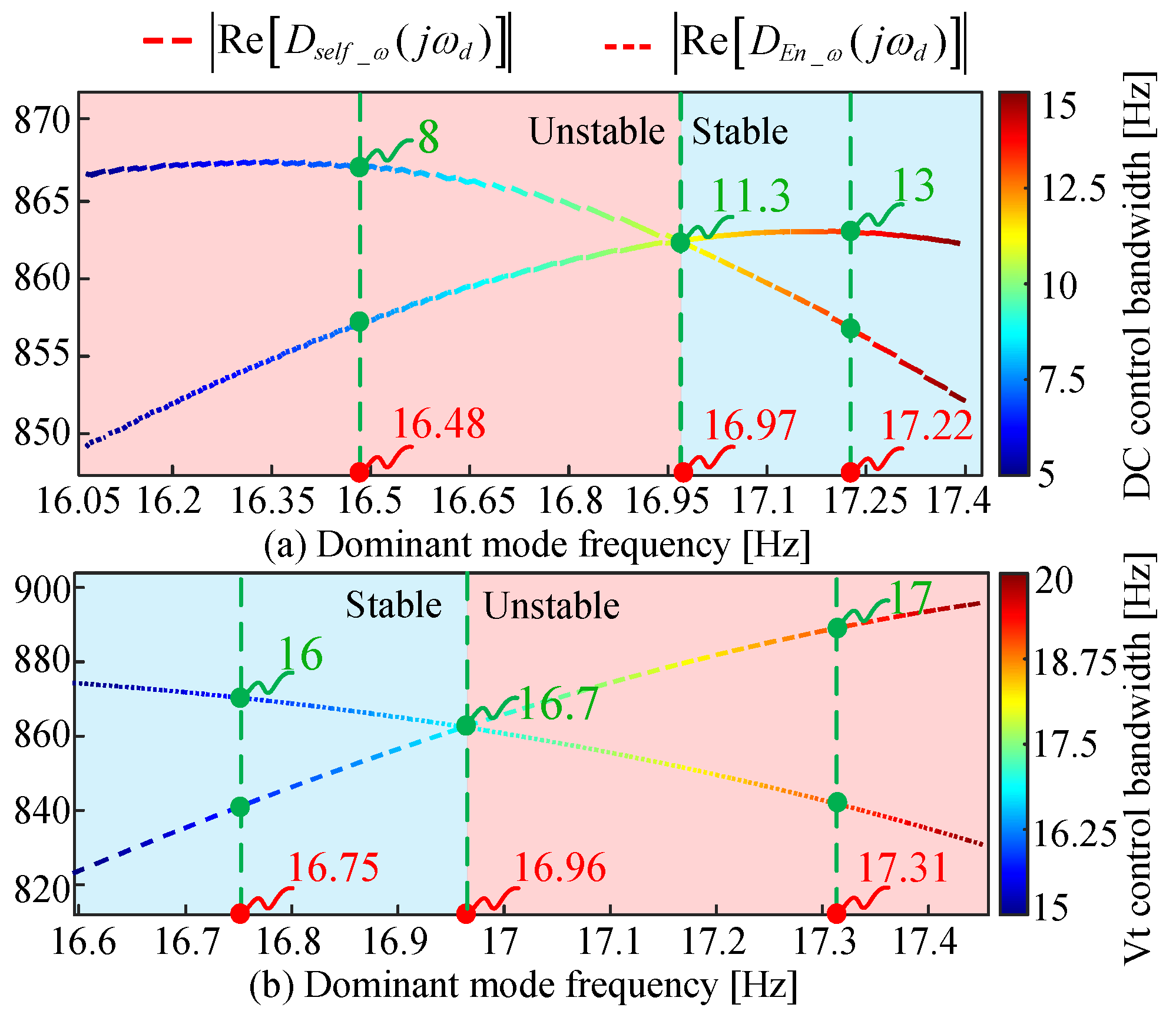
4.2. Stability of Internal Voltage Frequency in Converter-Interfaced Systems
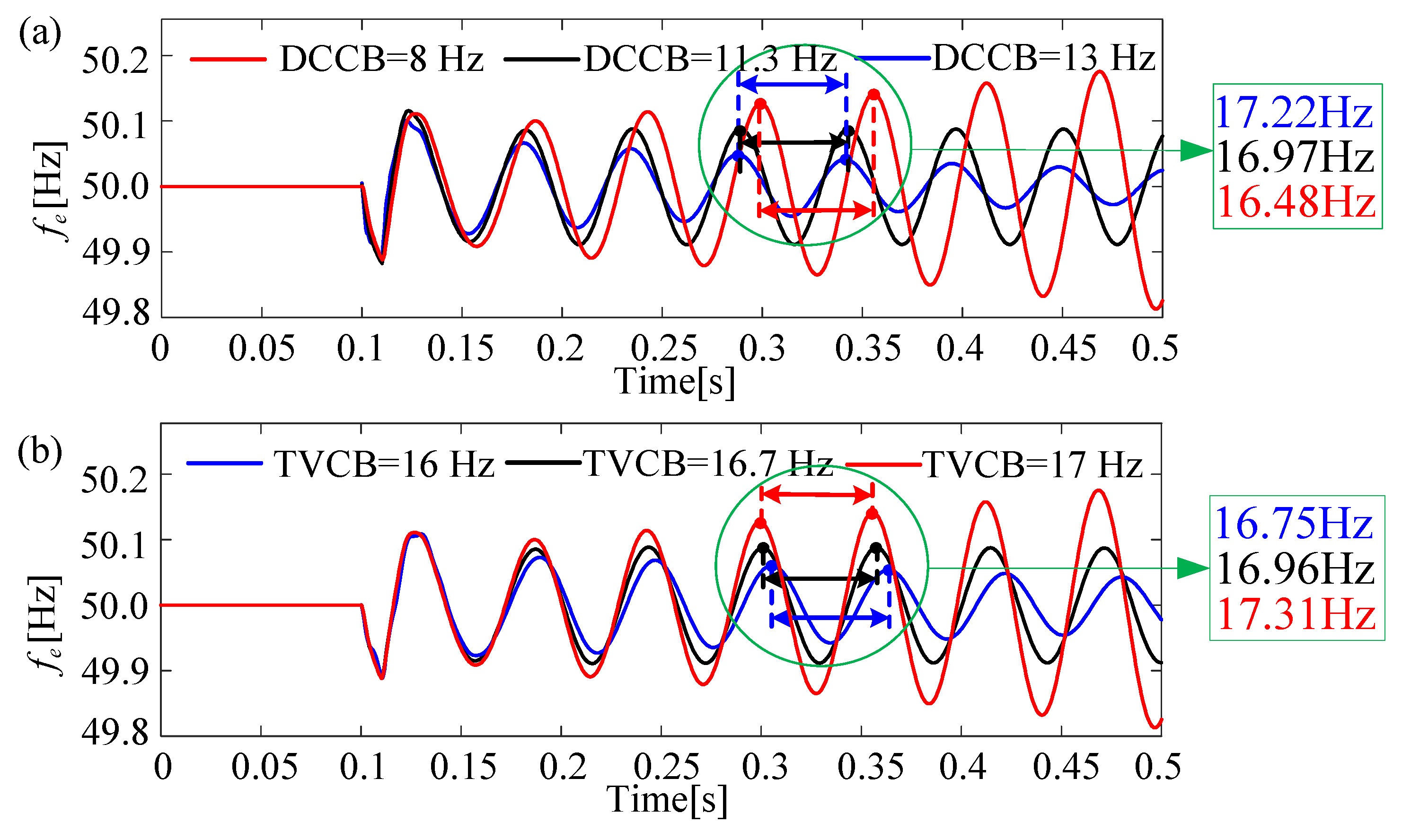
4.2.1. Influence of DCCB on the Frequency Stability of Internal Voltage in Converter-Interfaced Systems
4.2.2. Influence of TVCB on the Frequency Stability of Internal Voltage in Converter-Interfaced Systems
5. Conclusions
6. Limitations and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Parameters of Converter-Interfaced Systems
| Name | Parameter | Name | Parameter |
|---|---|---|---|
| Sbase | 100 kVA | Ubase | 690 V |
| DC side power (Pdc) | 0.96 p.u. | DC side voltage (Udc) | 1200 V |
| DC side capacitor (Cdc) | 1.68 mF | Filter inductance (Lf) | 0.15 p.u. |
| Grid frequency | 50 Hz | Filter capacitor (Cf) | 0.08 p.u. |
| Line inductance (Lg) | 0.6 p.u. | DC voltage control | PI1: 2/200 |
| Terminal voltage control | PI2: 1/100 | Current control | PI3: 1.2/800 |
| PLL | PI4: 90/20,000 | \ | \ |
Appendix B. Derivation Process of Equations (2)–(5)
Appendix C. Small-Signal Model of Converter-Interfaced Systems
References
- Hu, J.; Guo, Z.; Zhu, J.; Kurths, J.; Hou, Y.; Du, B.; Wu, Z.; Zhao, G.; Liu, Y.; Xin, K.; et al. Electromagnetic Dynamic Stability Analysis of Power Electronics-Dominated Systems Using Eigenstructure-Preserved LTP Theory. Nat. Commun. 2025, 16, 6852. [Google Scholar] [CrossRef] [PubMed]
- Peng, Q.; Fang, J.; Yang, Y.; Liu, T.; Blaabjerg, F. Maximum Virtual Inertia from DC-Link Capacitors Considering System Stability at Voltage Control Timescale. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 79–89. [Google Scholar] [CrossRef]
- Du, W.; Wang, Y.; Wang, H.F.; Ren, B.; Xiao, X. Small-Disturbance Stability Limit of a Grid-Connected Wind Farm with PMSGs in the Timescale of DC Voltage Dynamics. IEEE Trans. Power Syst. 2021, 36, 2366–2379. [Google Scholar] [CrossRef]
- Xu, Y.; Nian, H.; Chen, L. Small-Signal Modeling and Analysis of DC-Link Dynamics in Type-IV Wind Turbine System. IEEE Trans. Ind. Electron. 2021, 68, 1423–1433. [Google Scholar] [CrossRef]
- Cheng, Y.; Fan, L.; Rose, J.; Huang, S.-H.; Schmall, J.; Wang, X.; Xie, X.; Shair, J.; Ramamurthy, J.R.; Modi, N.; et al. Real-World Subsynchronous Oscillation Events in Power Grids with High Penetrations of Inverter-Based Resources. IEEE Trans. Power Syst. 2023, 38, 316–330. [Google Scholar] [CrossRef]
- Narayanan, V.; Kewat, S.; Singh, B. Solar PV-BES Based Microgrid System with Multifunctional VSC. IEEE Trans. Ind. Appl. 2020, 56, 2957–2967. [Google Scholar] [CrossRef]
- Hu, J.; Yuan, H.; Yuan, X. Modeling of DFIG-Based WTs for Small-Signal Stability Analysis in DVC Timescale in Power Electronized Power Systems. IEEE Trans. Energy Convers. 2017, 32, 1151–1165. [Google Scholar] [CrossRef]
- Markovic, U.; Stanojev, O.; Aristidou, P.; Hug, G. Partial Grid Forming Concept for 100% Inverter-Based Transmission Systems. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–9 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Ma, F.; Xin, H.; Wu, D.; Liu, Y.; Chen, X. Assessing Small-Signal Grid Strength of 100% Inverter-Based Power Systems. IEEE Trans. Power Deliv. 2024, 39, 2784–2796. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, X.; Hu, J. Effect of Reactive Power Control on Stability of DC-Link Voltage Control in VSC Connected to Weak Grid. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–5. [Google Scholar]
- Huang, Y.; Yuan, X.; Hu, J.; Zhou, P.; Wang, D. DC-Bus Voltage Control Stability Affected by AC-Bus Voltage Control in VSCs Connected to Weak AC Grids. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 445–458. [Google Scholar] [CrossRef]
- Yuan, H.; Yuan, X.; Hu, J. Modeling of Grid-Connected VSCs for Power System Small-Signal Stability Analysis in DC-Link Voltage Control Timescale. IEEE Trans. Power Syst. 2017, 32, 3981–3991. [Google Scholar] [CrossRef]
- Huang, J.; Yuan, X.; Wang, S. Cascaded multi-timescale modeling method of power electronic-interfaced device based on stimulation-response relationships of components for multi-timescale dynamic analysis of power systems. Proc. CSEE 2024, 45, 5467–5480. [Google Scholar]
- Huang, J.; Yuan, X.; Wang, S. Power-Imbalance Stimulation and Internal-Voltage Response Relationships Based Modeling Method of PE-Interfaced Devices in DC Voltage Control Timescale. IEEE Access 2023, 11, 105214–105224. [Google Scholar] [CrossRef]
- Askarov, A.; Bay, Y.; Ufa, R.; Radko, P.; Ilyushin, P.; Suvorov, A. Signatures and Mechanism Analysis of Converter-Grid Subsynchronous Oscillations. Mathematics 2024, 12, 3884. [Google Scholar] [CrossRef]
- Zhang, X.; Li, M.; Xu, D. PCC Voltage Perturbation Path Analysis and Compensation for Grid-Connected Voltage-Source Converter under Weak Grid. IEEE Trans. Ind. Electron. 2021, 68, 12331–12339. [Google Scholar] [CrossRef]
- Wang, D.; Liang, L.; Shi, L.; Hu, J.; Hou, Y. Analysis of Modal Resonance between PLL and DC-Link Voltage Control in Weak-Grid Tied VSCs. IEEE Trans. Power Syst. 2019, 34, 1127–1138. [Google Scholar] [CrossRef]
- Lu, D.; Wang, X.; Blaabjerg, F. Impedance-Based Analysis of DC-Link Voltage Dynamics in Voltage-Source Converters. IEEE Trans. Power Electron. 2019, 34, 3973–3985. [Google Scholar] [CrossRef]
- Zhao, M.; Yuan, X.; Hu, J. Modeling of DFIG Wind Turbine Based on Internal Voltage Motion Equation in Power Systems Phase-Amplitude Dynamics Analysis. IEEE Trans. Power Syst. 2018, 33, 1484–1495. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Cao, Y.; Wang, L.; Blaabjerg, F. Frequency and Voltage Stability Analysis of Grid-Forming Virtual Synchronous Generator Attached to Weak Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2662–2671. [Google Scholar] [CrossRef]
- Wang, S.; Yuan, X. Small-Disturbance Linearization Method for Converter Interfaced AC Power Systems Based on Operating Points of Internal-Voltage Amplitude/Frequency and Networks’ Active/Reactive Current. Proc. CSEE 2024, 44, 1081–1094. [Google Scholar] [CrossRef]
- Yang, H.; Yi, Y.; Li, S.; Zhou, Y. Active/Reactive Power Separation Mechanisms for Different Signal-Modulated Power Devices Based on Time-Varying Amplitude/Frequency Rotating Vectors in Dynamic Processes. Processes 2025, 13, 1907. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Blaabjerg, F.; Chen, Z. Harmonic Instability Assessment Using State-Space Modeling and Participation Analysis in Inverter-Fed Power Systems. IEEE Trans. Ind. Electron. 2017, 64, 806–816. [Google Scholar] [CrossRef]
- Hu, J.; Wang, W.; Li, Y.; Guo, J. Cross-Timescale Interaction Analysis between Voltage-Control and Rotor-Speed-Control Timescales in DFIG-WTs-Dominated Power Systems. IEEE Trans. Power Syst. 2025, 40, 2764–2776. [Google Scholar] [CrossRef]
- Wu, G.; Sun, H.; Zhang, X.; Egea-Alvarez, A.; Zhao, B.; Xu, S.; Wang, S.; Zhou, X. Parameter Design Oriented Analysis of the Current Control Stability of the Weak-Grid-Tied VSC. IEEE Trans. Power Deliv. 2021, 36, 1458–1470. [Google Scholar] [CrossRef]
- He, L.; Liu, D.; Tao, H.; Shen, Y.; Ren, J.; Wang, Y.; Li, J.; Xu, Y. Small-Signal Stability Analysis of Grid-Connected System for Renewable Energy Based on Network Node Impedance Modelling. Processes 2025, 13, 1292. [Google Scholar] [CrossRef]
- Liu, H.; Xie, X.; He, G.; Liu, C. Synchronous reference frame based impedance model and stability criterion for grid-connected renewable energy generation systems. Proc. CSEE 2017, 37, 4002–4007. [Google Scholar] [CrossRef]
- Li, S.; Yan, Y.; Yuan, X. SISO Equivalent of MIMO VSC-Dominated Power Systems for Voltage Amplitude and Phase Dynamic Analyses in Current Control Timescale. IEEE Trans. Energy Convers. 2019, 34, 1454–1465. [Google Scholar] [CrossRef]
- Wu, Y.; Wu, H.; Zhao, F.; Zhou, Z.; Wang, X. Reference-Frame Selection on Impedance Modeling of VSCs with Fundamental Frequency Dynamics. IEEE Trans. Power Electron. 2025, 40, 10059–10076. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Z.; Liu, J.; Boroyevich, D.; Burgos, R. Small-Signal Modeling and Stability Prediction of Parallel Droop-Controlled Inverters Based on Terminal Characteristics of Individual Inverters. IEEE Trans. Power Electron. 2020, 35, 1045–1063. [Google Scholar] [CrossRef]
- Yu, J.; Wang, S.; Liu, Z.; Li, J.; Liu, J.; Shang, J. Accurate Small-Signal Terminal Characteristic Model and SISO Stability Analysis Approach for Parallel Grid-Forming Inverters in Islanded Microgrids. IEEE Trans. Power Electron. 2023, 38, 6597–6612. [Google Scholar] [CrossRef]
- Yuan, X.; Li, S. An amplitude/frequency modulation based method of voltage source converter for power systems dynamic analysis in current control timescale. Proc. CSEE 2020, 40, 4732–4744. [Google Scholar] [CrossRef]
| Previous Approaches and Limitations | Our Innovative Approach and Advantages | |
|---|---|---|
| 1. Modeling Operating Point | Method: Primarily uses static DC values in the dq reference frame as operating points. Limitation: dq components lack intuitive physical meaning and are difficult to directly relate to the system’s energy and power dynamics. | Method: Uses the amplitude and frequency of the AC voltage as core state variables and operating points. Advantage: The operating points directly reflect the system’s energy state, providing clear physical meaning and an intuitive foundation for mechanism analysis. |
| 2. Stability Analysis Framework | Method: (a) MIMO state-space analysis (e.g., eigenvalues). (b) SISO impedance analysis. Limitation: (a) Accurate but acts as a “black box,” lacking physical insight and offering little guidance for design. (b) Intuitive but often requires oversimplification, potentially ignoring critical dynamic couplings. | Method: Proposes the “Self-stable/En-stable” path analytical framework. Advantage: Unifies analytical rigor with physical intuition. Through mathematical decoupling, it preserves the complete coupling information of the MIMO system while leveraging the intuitiveness of SISO tools for physical mechanism analysis. |
| 3. Oscillation Mechanism Revelation | Limitation: Typically identifies unstable modes but cannot clearly explain the root causes of oscillation, especially how interactions between different dynamics (e.g., amplitude and frequency) lead to instability. | Method: Performs quantitative analysis by decomposing the system into Self-stable and En-stable paths. Advantage: Clearly and quantitatively reveals the root causes of oscillation. For example, this study is the first to uncover the “dual” relationship between the stability mechanisms of amplitude and frequency. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, J.; Wang, S.; Hu, J. Small-Signal Stability Analysis of Converter-Interfaced Systems in DC Voltage Timescale Based on Amplitude/Frequency Operating Points. Processes 2025, 13, 2583. https://doi.org/10.3390/pr13082583
Lyu J, Wang S, Hu J. Small-Signal Stability Analysis of Converter-Interfaced Systems in DC Voltage Timescale Based on Amplitude/Frequency Operating Points. Processes. 2025; 13(8):2583. https://doi.org/10.3390/pr13082583
Chicago/Turabian StyleLyu, Jin, Sicheng Wang, and Jiabing Hu. 2025. "Small-Signal Stability Analysis of Converter-Interfaced Systems in DC Voltage Timescale Based on Amplitude/Frequency Operating Points" Processes 13, no. 8: 2583. https://doi.org/10.3390/pr13082583
APA StyleLyu, J., Wang, S., & Hu, J. (2025). Small-Signal Stability Analysis of Converter-Interfaced Systems in DC Voltage Timescale Based on Amplitude/Frequency Operating Points. Processes, 13(8), 2583. https://doi.org/10.3390/pr13082583






