Dynamic Interaction Mechanism Between Periphytic Algae and Flow in Open Channels
Abstract
1. Introduction
2. Theory and Methods
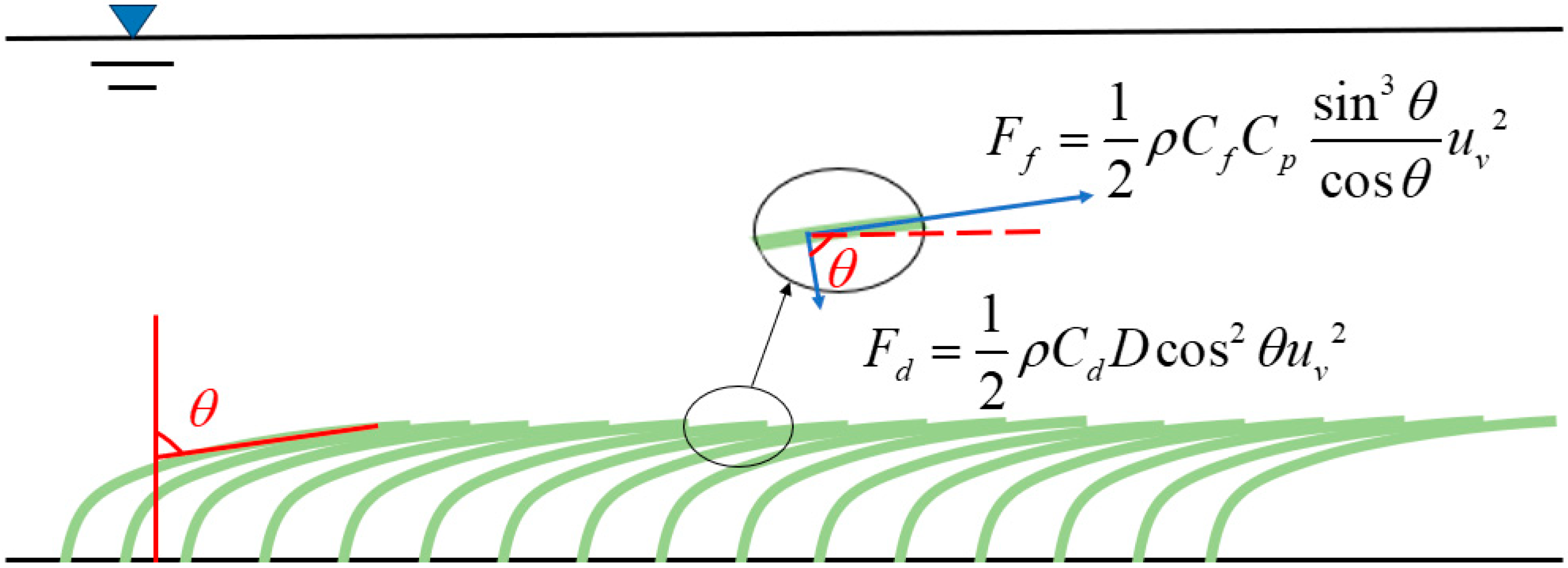
2.1. Resistance Characteristics of the Periphytic Algae Layer
2.2. Analytical Solution for Velocity Distribution
2.2.1. Analytical Solution for Velocity Distribution in the Periphytic Algae Layer
2.2.2. Analytical Solution for Velocity Distribution in the Free Water Layer
2.3. Error Analysis Method
3. Experiment
4. Results and Discussion
4.1. Velocity Model Validation
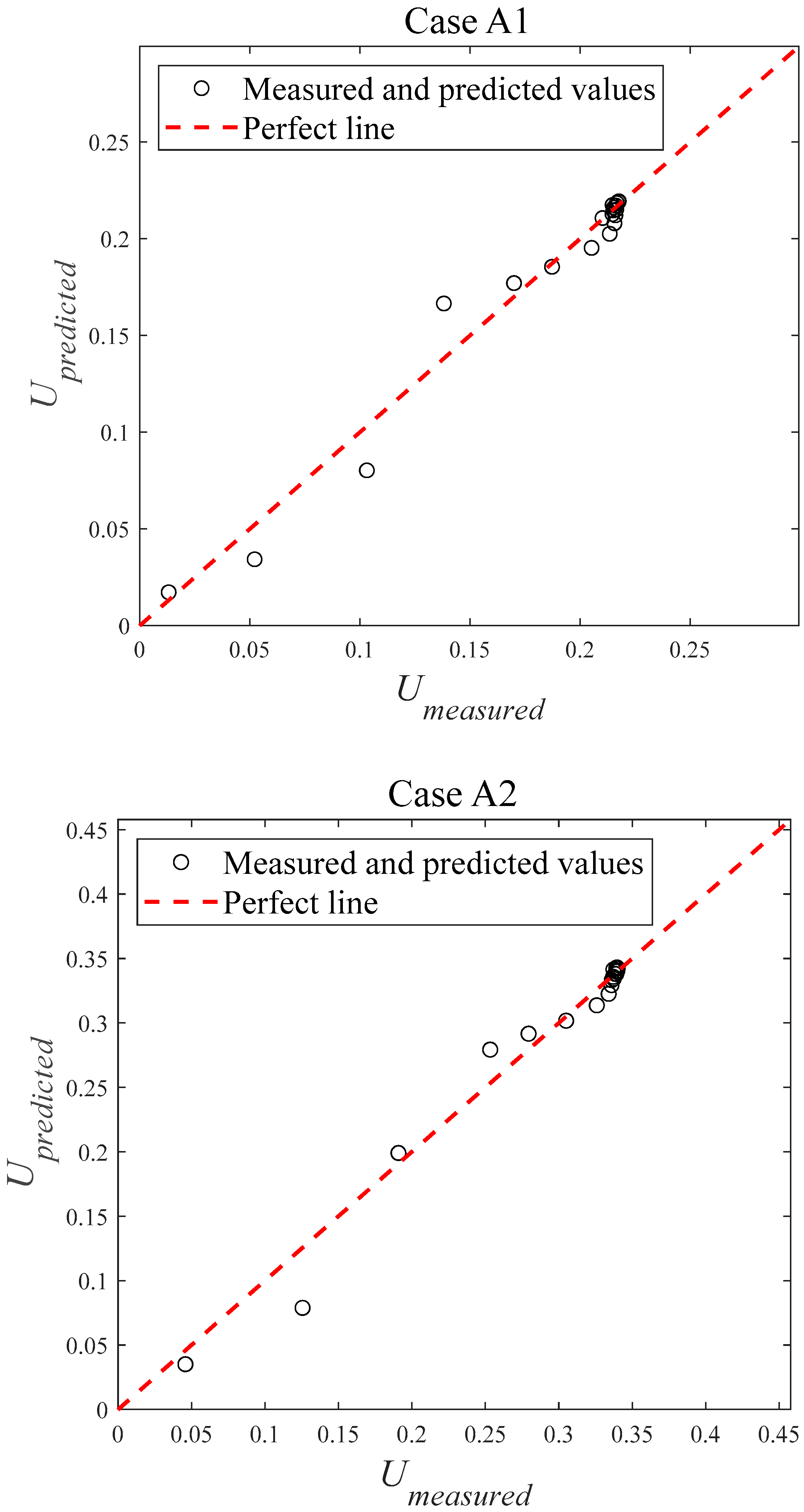
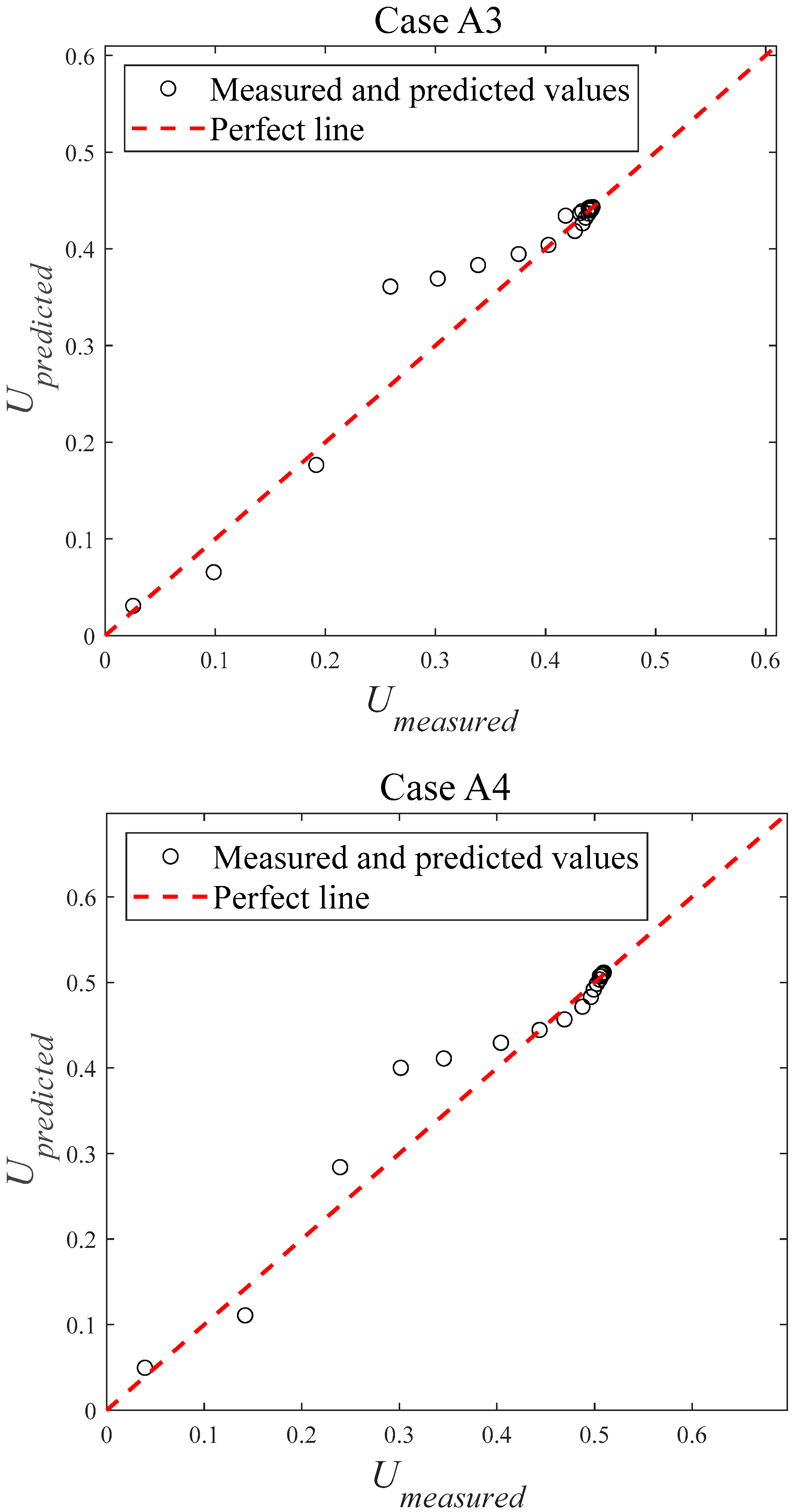
4.2. Error Analysis
4.3. Parameter Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fan, X.; Gao, S.; Zhang, Y.; Qin, B.; Xu, H.; Ding, S. Stimulation of high-concentration dissolved nitrogen and reactive phosphorus in Lake Taihu sediments on the initiation and maintenance of cyanobacterial blooms. Sci. Total Environ. 2022, 851, 158088. [Google Scholar] [CrossRef]
- Sun, L.; Wu, L.; Liu, X.; Huang, W.; Zhu, D.; Wang, Z.; Guan, R.; Liu, X. Reducing the risk of benthic algae outbreaks by regulating the flow velocity in a simulated South–North water diversion open channel. Int. J. Environ. Res. Public Health 2023, 20, 3564. [Google Scholar] [CrossRef]
- Hennequin, L.M.; Kim, S.; Monroe, E.A.; Eckles, T.P.; Beck, N.; Mays, W.D.; Fennell, P.S.; Hallett, J.P.; George, A.; Davis, R.W. Reclamation of nutrients, carbon, and metals from compromised surface waters fated to the Salton Sea: Biomass production and ecosystem services using an attached periphytic algae flow-way. Algal Res. 2022, 66, 102757. [Google Scholar] [CrossRef]
- Azim, M.E. Photosynthetic Periphyton and Surfaces. In Encyclopedia of Inland Waters; Academic Press: Cambridge, MA, USA, 2009; pp. 184–191. [Google Scholar] [CrossRef]
- Hansson, L.A. Factors regulating periphytic algal biomass. Limnol. Oceanogr. 1992, 37, 322–328. [Google Scholar] [CrossRef]
- Zulkifly, S.; Hanshew, A.; Young, E.B.; Lee, P.; Graham, M.E.; Graham, M.E.; Piotrowski, M.; Graham, L.E. The epiphytic microbiota of the globally widespread macroalga Cladophora glomerata (Chlorophyta, Cladophorales). Am. J. Bot. 2012, 99, 1541–1552. [Google Scholar] [CrossRef] [PubMed]
- Dodds, W.K.; Gudder, D.A. The ecology of Cladophora. J. Phycol. 1992, 28, 415–427. [Google Scholar] [CrossRef]
- Michalak, I.; Messyasz, B. Concise review of Cladophora spp.: Macroalgae of commercial interest. J. Appl. Phycol. 2021, 33, 133–166. [Google Scholar] [CrossRef]
- Battin, T.J.; Kaplan, L.A.; Denis Newbold, J.; Hansen, C.M. Contributions of microbial biofilms to ecosystem processes in stream mesocosms. Nature 2003, 426, 439–442. [Google Scholar] [CrossRef]
- Pan, M.; Li, H.; Han, X.; Jiang, S.; Diao, Y.; Ma, W.; Li, X.; Qin, J.; Yao, J.; Wang, Z. Impact of hydrodynamic conditions on the production and distribution of extracellular polymeric substance in river biofilms. Water 2023, 15, 3821. [Google Scholar] [CrossRef]
- Salant, N.L. ‘Sticky business’: The influence of streambed periphyton on particle deposition and infiltration. Geomorphology 2011, 126, 350–363. [Google Scholar] [CrossRef]
- Gerbersdorf, S.U.; Koca, K.; de Beer, D.; Chennu, A.; Noss, C.; Risse-Buhl, U.; Weitere, M.; Eiff, O.; Wagner, M.; Aberle, J.; et al. Exploring flow-biofilm-sediment interactions: Assessment of current status and future challenges. Water Res. 2020, 185, 116182. [Google Scholar] [CrossRef]
- Battin, T.J.; Besemer, K.; Bengtsson, M.M.; Romani, A.M.; Packmann, A.I. The ecology and biogeochemistry of stream biofilms. Nat. Rev. Microbiol. 2016, 14, 251–263. [Google Scholar] [CrossRef]
- Zhang, L.; Shen, T.; Cheng, Y.; Zhao, T.; Li, L.; Qi, P. Temporal and spatial variations in the bacterial community composition in Lake Bosten, a large, brackish lake in China. Sci. Rep. 2020, 10, 304. [Google Scholar] [CrossRef]
- Paerl, H.W.; Fulton, R.S.; Moisander, P.H.; Dyble, J. Harmful freshwater algal blooms, with an emphasis on cyanobacteria. Sci. World J. 2001, 1, 76. [Google Scholar] [CrossRef]
- Pranta, A.D.; Rahaman, M.T.; Ahmed, M.S.; Arefin Rafi, M.S. Navigating eutrophication in aquatic environments: Understanding impacts and unveiling solutions for effective wastewater management. Res. Ecol. 2023, 5, 11–18. [Google Scholar] [CrossRef]
- Balaji-Prasath, B.; Wang, Y.; Su, Y.P.; Hamilton, D.P.; Lin, H.; Zheng, L.; Zhang, Y. Methods to control harmful algal blooms: A review. Environ. Chem. Lett. 2022, 20, 3133–3152. [Google Scholar] [CrossRef]
- Brenckman, C.M.; Parameswarappa Jayalakshmamma, M.; Pennock, W.H.; Ashraf, F.; Borgaonkar, A.D. A Review of Harmful Algal Blooms: Causes, Effects, Monitoring, and Prevention Methods. Water 2025, 17, 1980. [Google Scholar] [CrossRef]
- Al-Thani, R.F.; Yasseen, B.T. Comparative Phycoremediation Potential of Micro-Green Algae and Dinoflagellates in Coastal and Inland Qatar. Processes 2025, 13, 2190. [Google Scholar] [CrossRef]
- El Bouaidi, W.; Enaime, G.; Loudiki, M.; Yaacoubi, A.; Douma, M.; Ounas, A.; Lübken, M. Adsorbents used for microcystin removal from water sources: Current knowledge and future prospects. Processes 2022, 10, 1235. [Google Scholar] [CrossRef]
- Correll, D.L. The role of phosphorus in the eutrophication of receiving waters: A review. J. Environ. Qual. 1998, 27, 261–266. [Google Scholar] [CrossRef]
- Paerl, H.W.; Otten, T.G. Harmful cyanobacterial blooms: Causes, consequences, and controls. Microb. Ecol. 2013, 65, 995–1010. [Google Scholar] [CrossRef]
- Son, D.H.; Fujino, T. Modeling approach to periphyton and nutrient interaction in a stream. J. Environ. Eng. 2003, 129, 834–843. [Google Scholar] [CrossRef]
- Fovet, O.; Belaud, G.; Litrico, X.; Charpentier, S.; Bertrand, C.; Dauta, A.; Hugodot, C. Modelling periphyton in irrigation canals. Ecol. Model. 2010, 221, 1153–1161. [Google Scholar] [CrossRef]
- Vogel, S. Drag and flexibility in sessile organisms. Am. Zool. 1984, 24, 37–44. [Google Scholar] [CrossRef]
- Nikora, V. Hydrodynamics of aquatic ecosystems: An interface between ecology, biomechanics and environmental fluid mechanics. River Res. Appl. 2010, 26, 367–384. [Google Scholar] [CrossRef]
- Schoelynck, J.; Meire, D.; Bal, K.; Buis, K.; Troch, P.; Bouma, T.; Meire, P.; Temmerman, S. Submerged macrophytes avoiding a negative feedback in reaction to hydrodynamic stress. Limnologica 2013, 43, 371–380. [Google Scholar] [CrossRef]
- Reiter, M.A. The effect of a developing algal assemblage on the hydrodynamics near substrates of different sizes. Arch. Hydrobiol. 1989, 115, 221–244. [Google Scholar] [CrossRef]
- Hondzo, M.; Wang, H. Effects of turbulence on growth and metabolism of periphyton in a laboratory flume. Water Resour. Res. 2002, 38, 13-1–13-9. [Google Scholar] [CrossRef]
- Leonard, L.A.; Luther, M.E. Flow hydrodynamics in tidal marsh canopies. Limnol. Oceanogr. 1995, 40, 1474–1484. [Google Scholar] [CrossRef]
- Sand-Jensen, K.; Mebus, J.R. Fine-scale patterns of water velocity within macrophyte patches in streams. Oikos 1996, 76, 169–180. [Google Scholar] [CrossRef]
- Matson, P.G.; Boyer, G.L.; Bridgeman, T.B.; Bullerjahn, G.S.; Kane, D.D.; McKay, R.M.; McKindles, K.M.; Raymond, H.A.; Snyder, B.K.; Stumpf, R.P.; et al. Physical drivers facilitating a toxigenic cyanobacterial bloom in a major Great Lakes tributary. Limnol. Oceanogr. 2020, 65, 2866–2882. [Google Scholar] [CrossRef]
- Horner, R.R.; Welch, E.B.; Seeley, M.R.; Jacoby, J.M. Responses of periphyton to changes in current velocity, suspended sediment and phosphorus concentration. Freshw. Biol. 1990, 24, 215–232. [Google Scholar] [CrossRef]
- Poff, N.L.; Voelz, N.J.; Ward, J.V.; Lee, R.E. Algal colonization under four experimentally-controlled current regimes in high mountain stream. J. N. Am. Benthol. Soc. 1990, 9, 303–318. [Google Scholar] [CrossRef]
- Biggs, B.J.; Goring, D.G.; Nikora, V.I. Subsidy and stress responses of stream periphyton to gradients in water velocity as a function of community growth form. J. Phycol. 1998, 34, 598–607. [Google Scholar] [CrossRef]
- Huai, W.X.; Zhang, J.; Katul, G.G.; Cheng, Y.G.; Tang, X.; Wang, W.J. The structure of turbulent flow through submerged flexible vegetation. J. Hydrodyn. 2019, 31, 274–292. [Google Scholar] [CrossRef]
- Jia, F.C.; Han, Y.; Wang, W.J.; Li, J.J.; Zhao, Z.; Du, J.Y. Flow structure and spectral characteristics in regions with highly flexible vegetation. J. Hydrol. 2025, 660, 133357. [Google Scholar] [CrossRef]
- Huai, W.X.; Li, S.; Katul, G.G.; Liu, M.Y.; Yang, Z.H. Flow dynamics and sediment transport in vegetated rivers: A review. J. Hydrodyn. 2021, 33, 400–420. [Google Scholar] [CrossRef]
- Yang, L.; Fang, H.Z.; Yang, Z.H.; Huai, W.X. Longitudinal dispersive coefficient in channels with aquatic vegetation: A review. J. Hydrodyn. 2023, 35, 379–395. [Google Scholar] [CrossRef]
- Wang, W.J.; Huai, W.X.; Zeng, Y.H.; Zhou, J.F. Analytical solution of velocity distribution for flow through submerged large deflection flexible vegetation. Appl. Math. Mech. 2015, 36, 107–120. [Google Scholar] [CrossRef]
- Hoerner, S.F. Fluid Dynamic Drag; Author: Midland Park, NJ, USA, 1965; pp. 16–35. [Google Scholar]
- Niklas, K.J. Plant Biomechanics: An Engineering Approach to Plant Form and Function; University of Chicago Press: Chicago, IL, USA, 1992. [Google Scholar]
- Wu, F.S. Characteristics of flow resistance in open channels with non-submerged rigid vegetation. J. Hydrodyn. Ser. B 2008, 20, 239–245. [Google Scholar] [CrossRef]
- Rainey, R.C.T. Aspects of the hydrodynamic loading on towed arrays and flexible risers. Engineering Structures 1989, 11, 248–253. [Google Scholar] [CrossRef]
- Gaylord, B.; Blanchette, C.A.; Denny, M.W. Mechanical consequences of size in wave-swept algae. Ecol. Monogr. 1994, 64, 287–313. [Google Scholar] [CrossRef]
- Luhar, M.; Nepf, H.M. Flow-induced reconfiguration of buoyant and flexible aquatic vegetation. Limnol. Oceanogr. 2011, 56, 2003–2017. [Google Scholar] [CrossRef]
- Tsujimoto, T.; Kitamura, T.; Fujii, Y. Hydraulic resistance of flow with flexible vegetation in open channel. J. Hydrosci. Hydraul. Eng. 1996, 14, 47–56. [Google Scholar]
- Kouwen, N.; Fathi-Moghadam, M. Friction factors for coniferous trees along rivers. J. Hydraul. Eng. 2000, 126, 732–740. [Google Scholar] [CrossRef]
- Oplatka, M. Stabilität von Weidenverbauungen an Flussufern. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 1998. [Google Scholar]
- Righetti, M.; Armanini, A. Flow resistance in open channel flows with sparsely distributed bushes. J. Hydrol. 2002, 269, 55–64. [Google Scholar] [CrossRef]
- Harder, D.L.; Speck, O.; Hurd, C.L.; Speck, T. Reconfiguration as a prerequisite for survival in highly unstable flow-dominated habitats. J. Plant Growth Regul. 2004, 23, 98–107. [Google Scholar] [CrossRef]
- Chapman, J.A.; Wilson, B.N.; Gulliver, J.S. Drag force parameters of rigid and flexible vegetal elements. Water Resour. Res. 2015, 51, 3292–3302. [Google Scholar] [CrossRef]
- White, F.M.; Majdalani, J. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 2006; Volume 3, pp. 433–434. [Google Scholar]
- Liu, M.Y.; Huai, W.X.; Yang, Z.H.; Zeng, Y.H. A genetic programming-based model for drag coefficient of emergent vegetation in open channel flows. Adv. Water Resour. 2020, 140, 103582. [Google Scholar] [CrossRef]
- Cheng, N.S.; Nguyen, H.T. Hydraulic radius for evaluating resistance induced by simulated emergent vegetation in open-channel flows. J. Hydraul. Eng. 2011, 137, 995–1004. [Google Scholar] [CrossRef]
- Suryanarayana, N.V.; Arici, Ö. Design and Simulation of Thermal Systems; McGraw-Hill Professional: New York, NY, USA, 2003. [Google Scholar]
- Li, J.J.; Wang, W.J.; Dong, F.; Peng, W.Q.; Fan, J.J.; Zhao, H.Q.; Chou, Q.C.; Huang, A.P. New drag force formula of bending stems in deriving analytical solutions of velocity profile for flow through flexible vegetation. Water Resour. Res. 2024, 60, e2023WR035951. [Google Scholar] [CrossRef]
- Rota, G.F.; Monti, A.; Olivieri, S.; Rosti, M.E. Dynamics and fluid–structure interaction in turbulent flows within and above flexible canopies. J. Fluid Mech. 2024, 989, A11. [Google Scholar] [CrossRef]
- Dijkstra, J.T.; Uittenbogaard, R.E. Modeling the interaction between flow and highly flexible aquatic vegetation. Water Resour. Res. 2010, 46, W12547. [Google Scholar] [CrossRef]
- Aliaga, J.; Aberle, J. Bed shear stress and near-bed flow through sparse arrays of rigid emergent vegetation. Water Resour. Res. 2024, 60, e2023WR035879. [Google Scholar] [CrossRef]
- Yang, W.; Choi, S.U. Impact of stem flexibility on mean flow and turbulence structure in depth-limited open channel flows with submerged vegetation. J. Hydraul. Res. 2009, 47, 445–454. [Google Scholar] [CrossRef]
- Nikora, V.I.; Goring, D.G.; Biggs, B.J.F. Some observations of the effects of micro-organisms growing on the bed of an open channel on the turbulence properties. J. Fluid Mech. 2002, 450, 317–341. [Google Scholar] [CrossRef]
- Wang, W.J.; Zhao, Y.F.; Ren, S.; Liu, X.B.; Dong, F.; Li, J.J.; Fan, J.J.; Wu, W.Q. Analytical solutions of flow velocity profile based on the morphological response of flexible vegetation. J. Hydrol. 2023, 624, 129839. [Google Scholar] [CrossRef]
- Kármán, T. Mechanische änlichkeit und turbulenz. Nachrichten Von Der Ges. Der Wiss. Zu Göttingen Math.-Phys. Kl. 1930, 1930, 58–76. [Google Scholar]
- Barenblatt, G.I.; Chorin, A.J.; Prostokishin, V.M. Scaling laws for fully developed turbulent flow in pipes: Discussion of experimental data. Proc. Natl. Acad. Sci. USA 1997, 94, 773–776. [Google Scholar] [CrossRef]
- Fu, H.; Yang, K.L.; Wang, T.; Guo, X.L. Analysis of parameter sensitivity and value for logarithmic velocity distribution formula. J. Hydraul. Eng. 2013, 44, 489–494. [Google Scholar]
- Zhang, J.; Mi, Z.; Wang, H.; Wang, W.; Li, Z.; Guan, M. A multiple-fluids-mechanics-based model of velocity profiles in currents with submerged vegetation. Front. Mar. Sci. 2023, 10, 1163456. [Google Scholar] [CrossRef]
- Alves, A.M.; de Gestinari, L.M.S.; de Oliveira, I.S.; Brito, K.L.M.; Moura, C.W.D.N. The genus Cladophora (Chlorophyta) in the littoral of Bahia, Brazil. Nova Hedwig. 2012, 95, 337. [Google Scholar] [CrossRef]




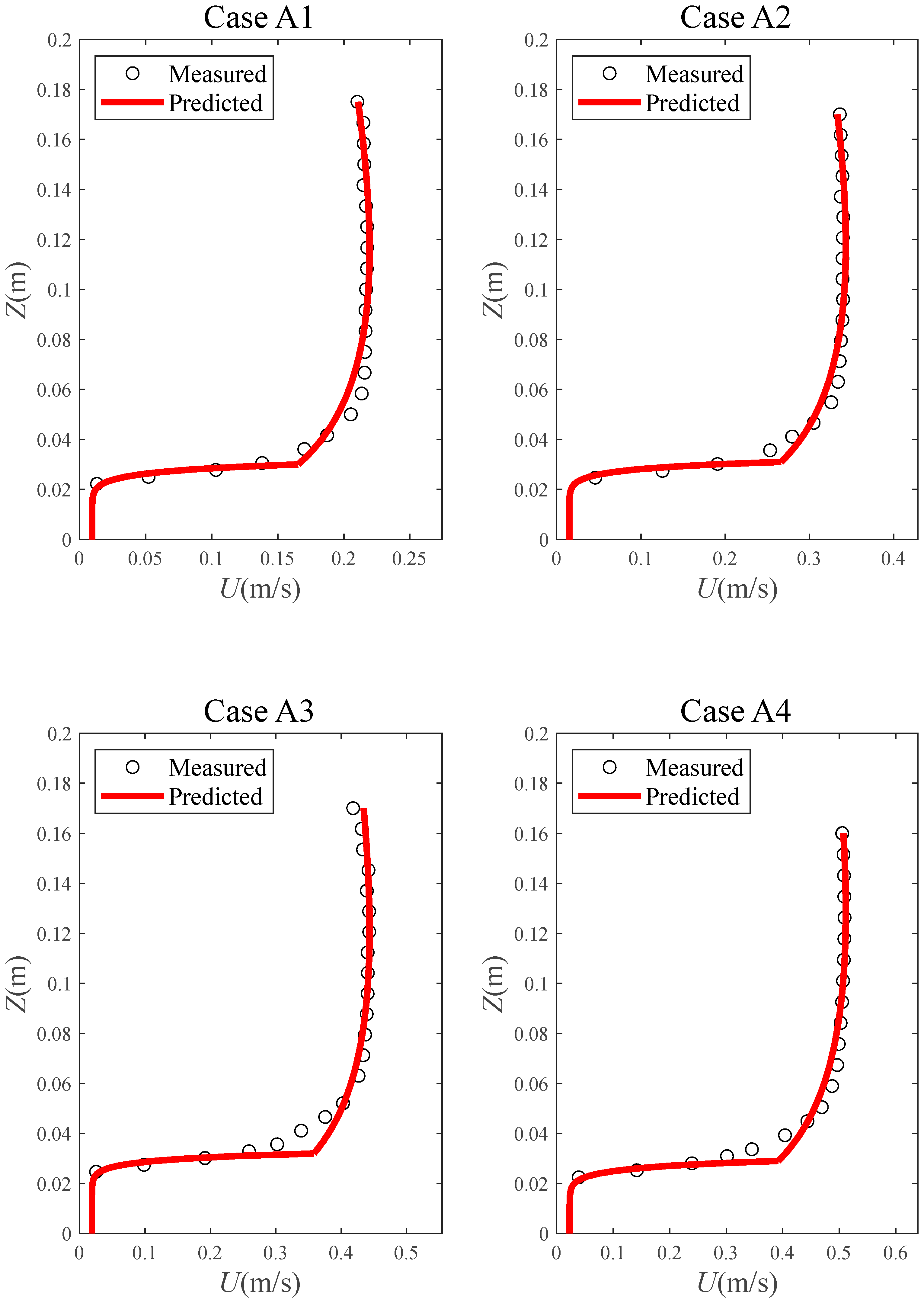
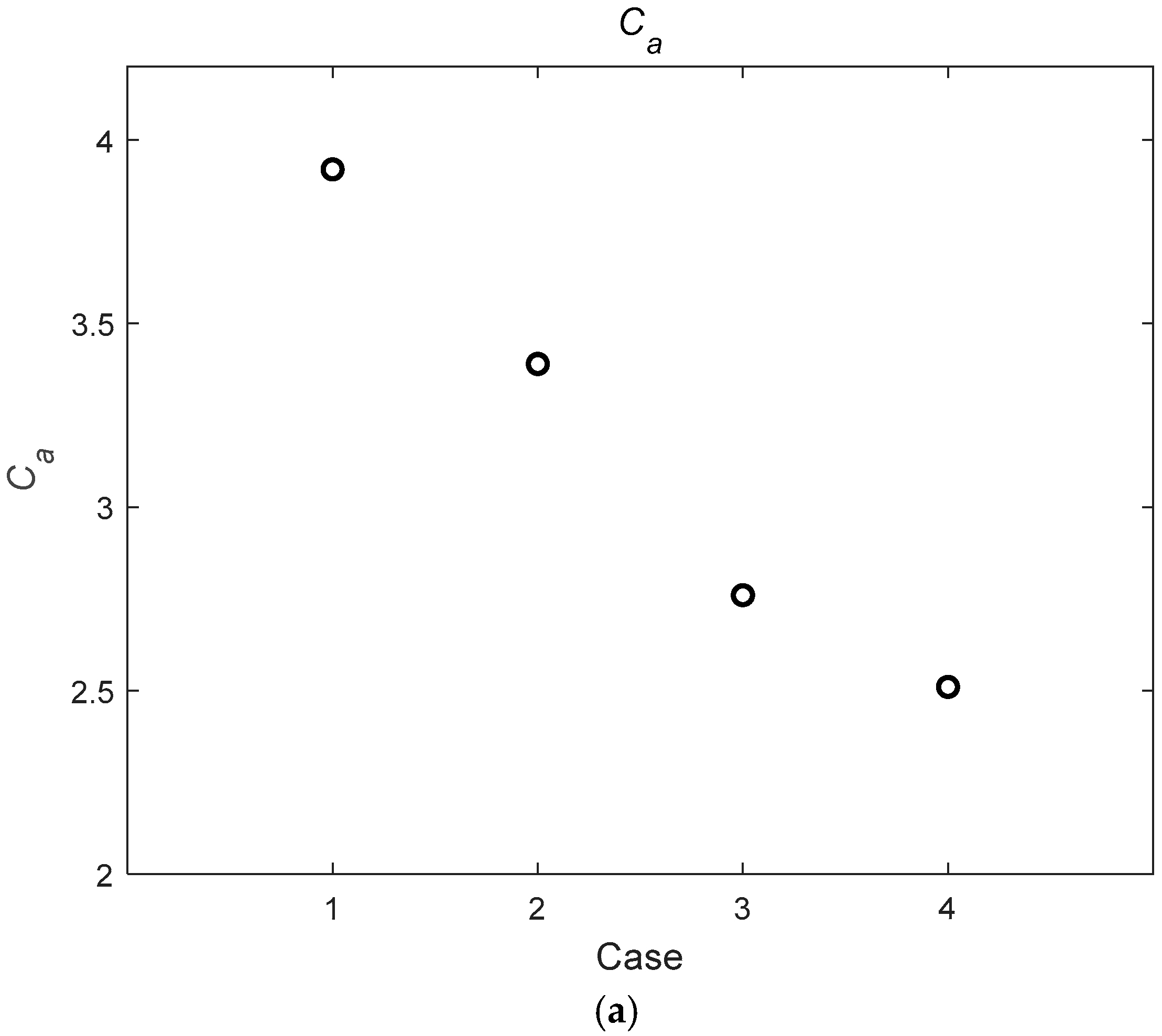
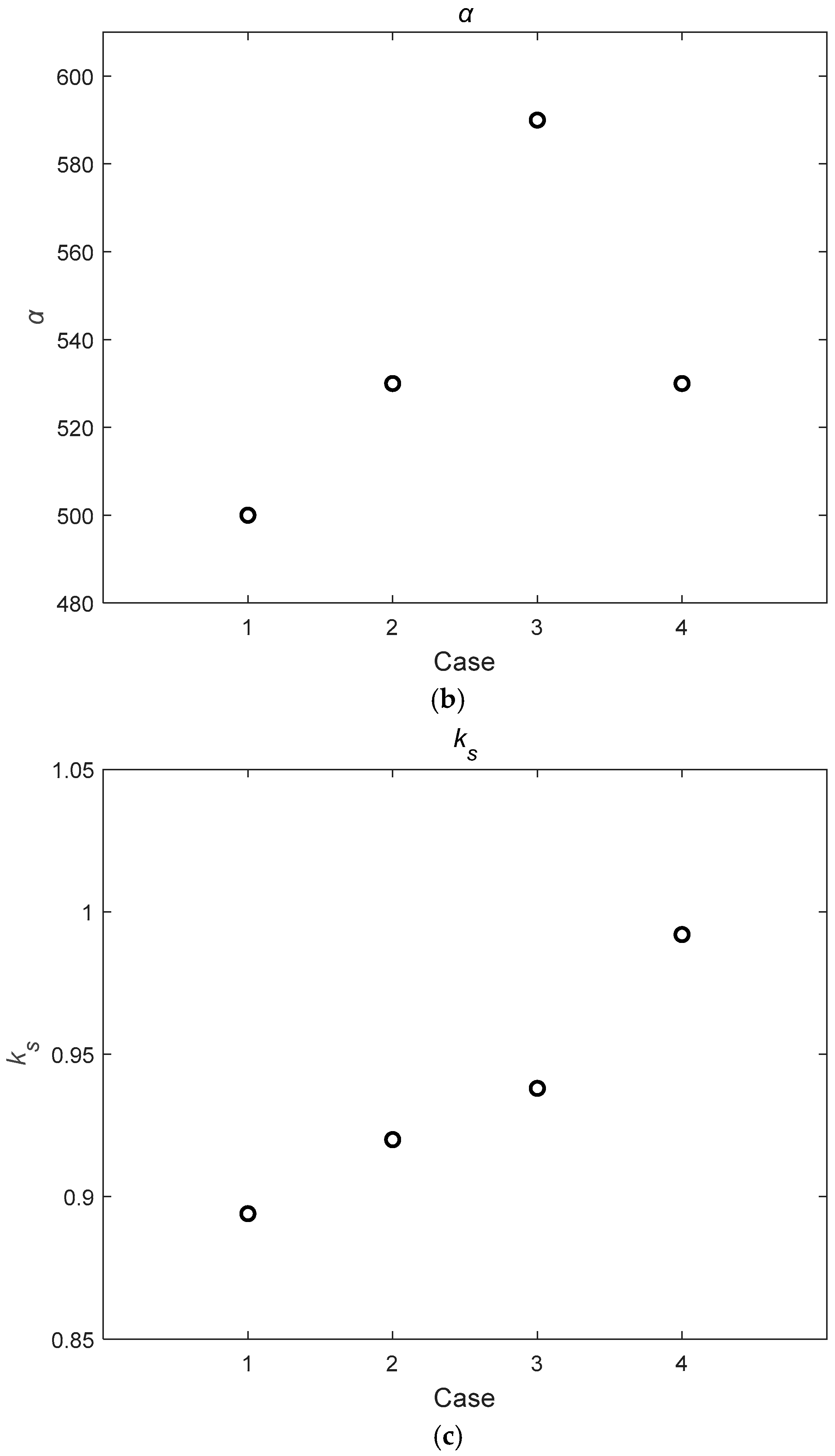
| Case | Q (m3/s) | hw (m) | hv (m) | D (mm) | m (1/m2) | Re | |
|---|---|---|---|---|---|---|---|
| A1 | 0.0172 | 0.175 | 0.030 | 0.05 | 1,200,000 | 97,348 | 5841 |
| A2 | 0.0273 | 0.170 | 0.031 | 0.05 | 1,200,000 | 158,935 | 9854 |
| A3 | 0.0356 | 0.170 | 0.032 | 0.05 | 1,200,000 | 207,609 | 13,287 |
| A4 | 0.0407 | 0.160 | 0.029 | 0.05 | 1,200,000 | 252,806 | 14,663 |
| Case | AE | RE | RMSE | nRMSE | R2 |
|---|---|---|---|---|---|
| A1 | 0.0060 | 6.21% | 0.0096 | 5.16% | 0.9740 |
| A2 | 0.0078 | 4.64% | 0.0131 | 4.39% | 0.9796 |
| A3 | 0.0157 | 7.12% | 0.0294 | 8.00% | 0.9448 |
| A4 | 0.0164 | 6.63% | 0.0297 | 6.97% | 0.9543 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.-Y.; Wang, W.-J.; Dong, F.; Han, Y.; Yu, J.-L.; Jia, F.-C.; Zheng, C.-L. Dynamic Interaction Mechanism Between Periphytic Algae and Flow in Open Channels. Processes 2025, 13, 2551. https://doi.org/10.3390/pr13082551
Xu M-Y, Wang W-J, Dong F, Han Y, Yu J-L, Jia F-C, Zheng C-L. Dynamic Interaction Mechanism Between Periphytic Algae and Flow in Open Channels. Processes. 2025; 13(8):2551. https://doi.org/10.3390/pr13082551
Chicago/Turabian StyleXu, Ming-Yang, Wei-Jie Wang, Fei Dong, Yu Han, Jun-Li Yu, Feng-Cong Jia, and Cai-Ling Zheng. 2025. "Dynamic Interaction Mechanism Between Periphytic Algae and Flow in Open Channels" Processes 13, no. 8: 2551. https://doi.org/10.3390/pr13082551
APA StyleXu, M.-Y., Wang, W.-J., Dong, F., Han, Y., Yu, J.-L., Jia, F.-C., & Zheng, C.-L. (2025). Dynamic Interaction Mechanism Between Periphytic Algae and Flow in Open Channels. Processes, 13(8), 2551. https://doi.org/10.3390/pr13082551






