Microfluidic Investigation on the Diffusion Law of Nano Displacement Agent in Porous Media
Abstract
1. Introduction
2. Determination of Nano-Displacement Agent Type
3. Establishment of Correlation Between Surfactant Concentration and RGB Value
3.1. Base Solution Preparation and Colorimetric Reaction
3.2. Materials and Equipment
3.3. Experimental Procedure

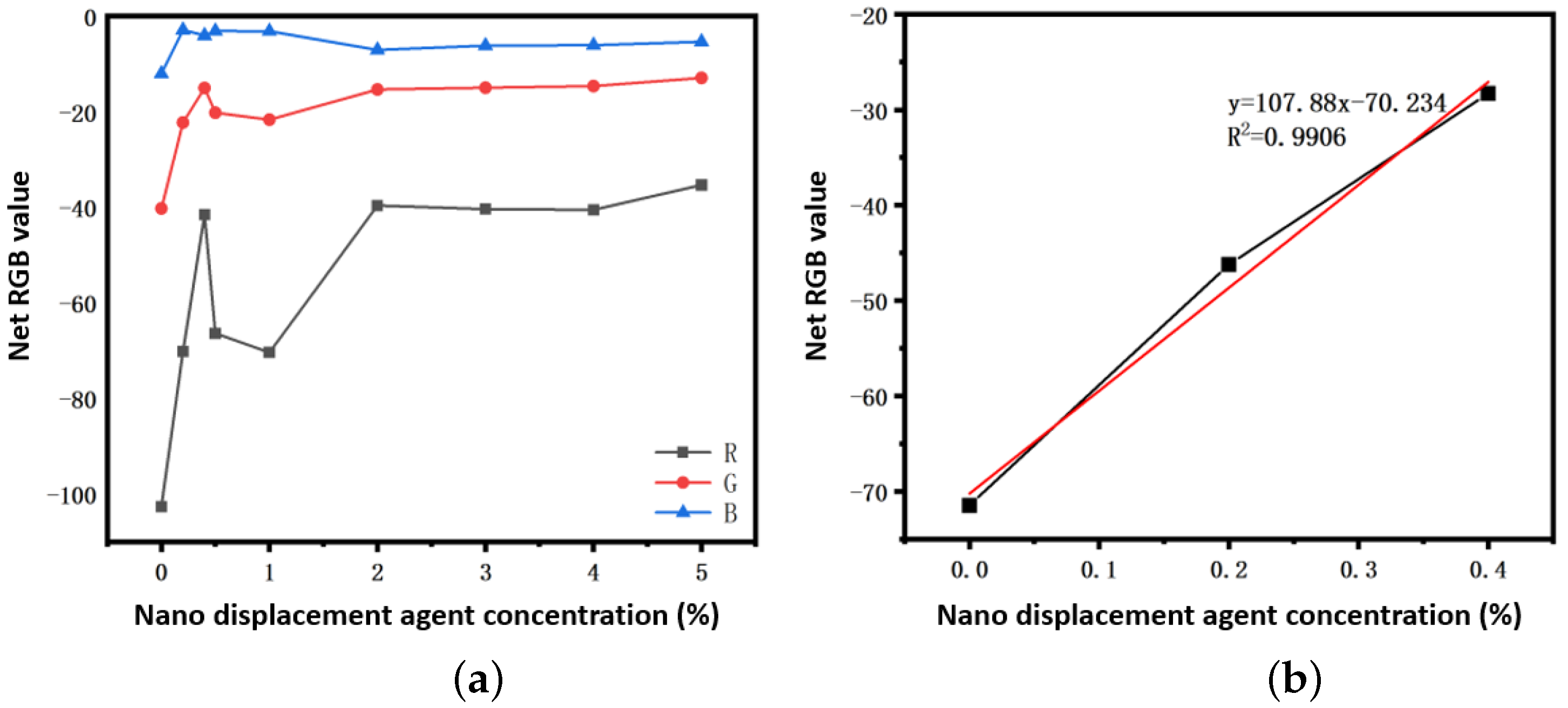
3.4. Establishment of the Concentration–RGB Standard Curve
4. Diffusion Characteristics of Nano-Displacement Agent Within Micropores
4.1. Experimental Procedures
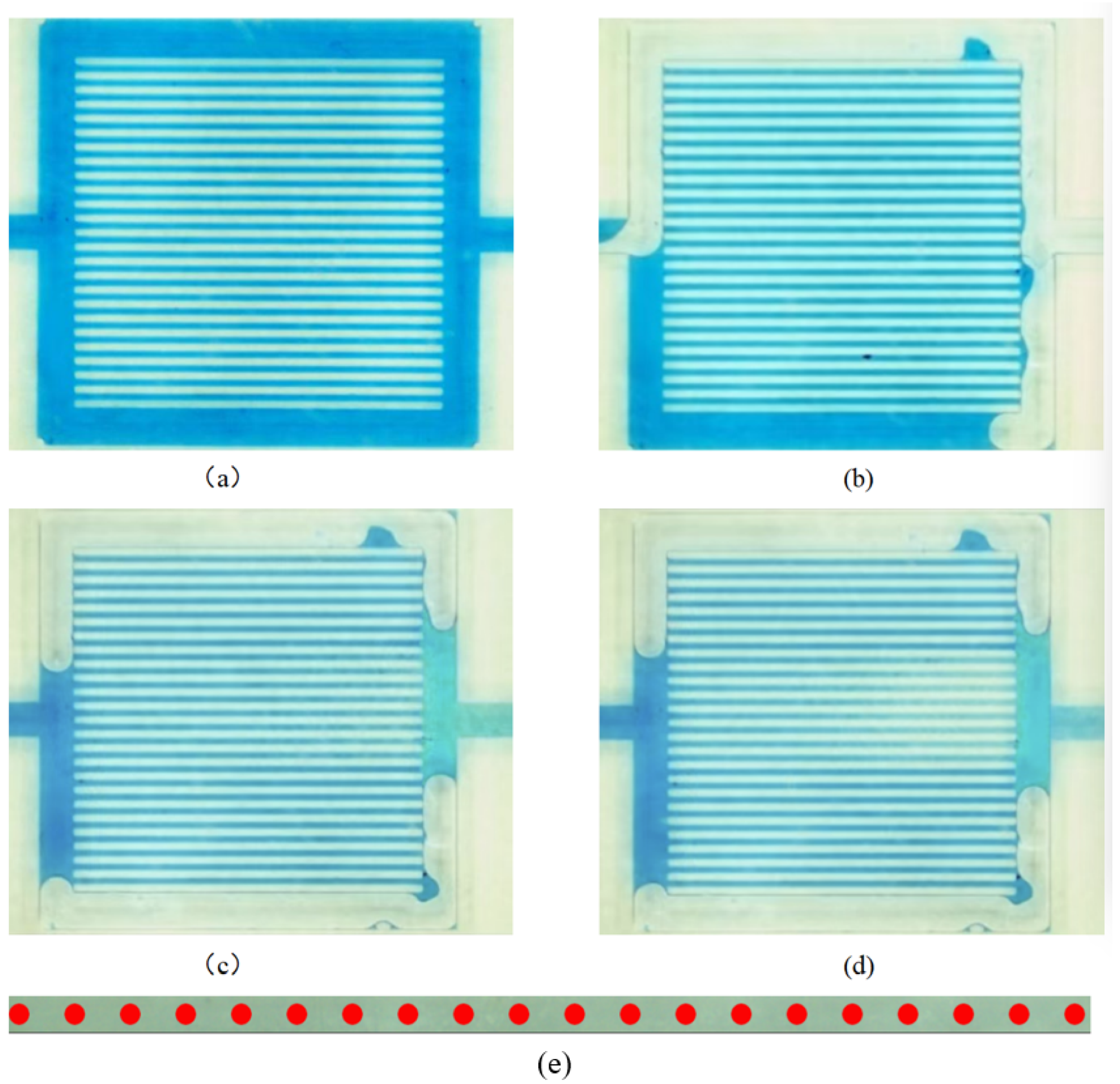
4.2. Diffusion Characteristics of Nano-Displacement Agent Within Micropores
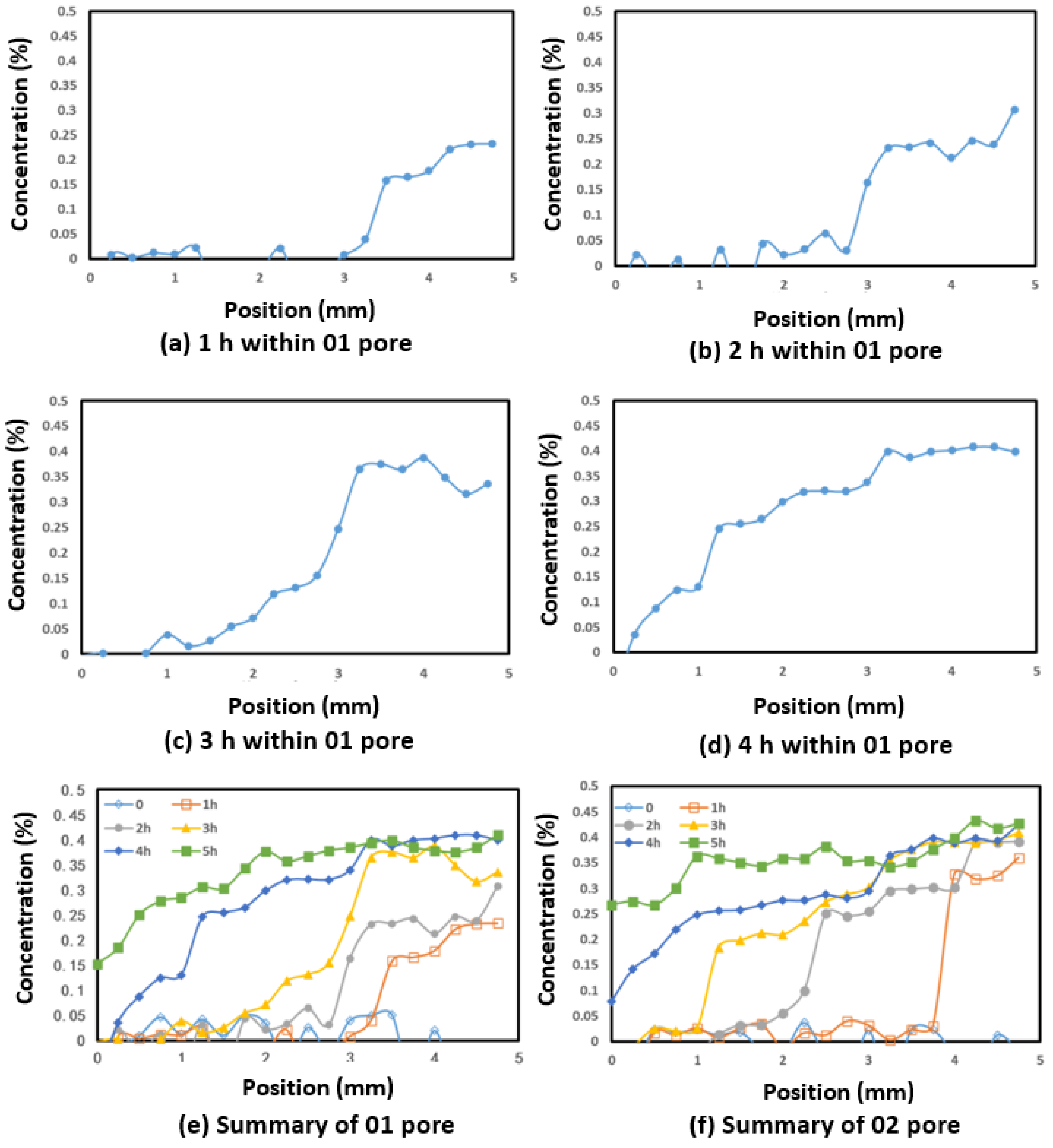
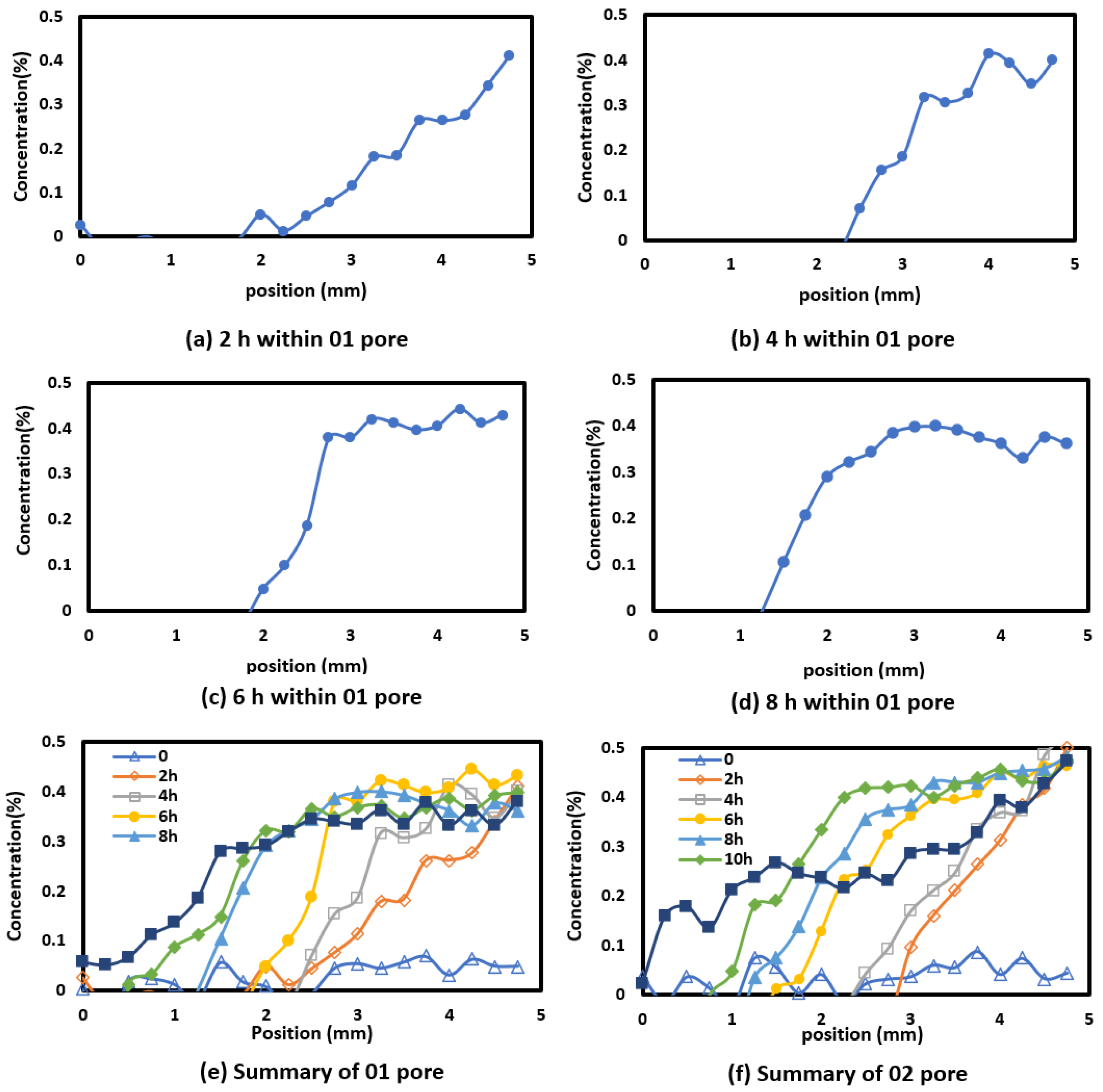
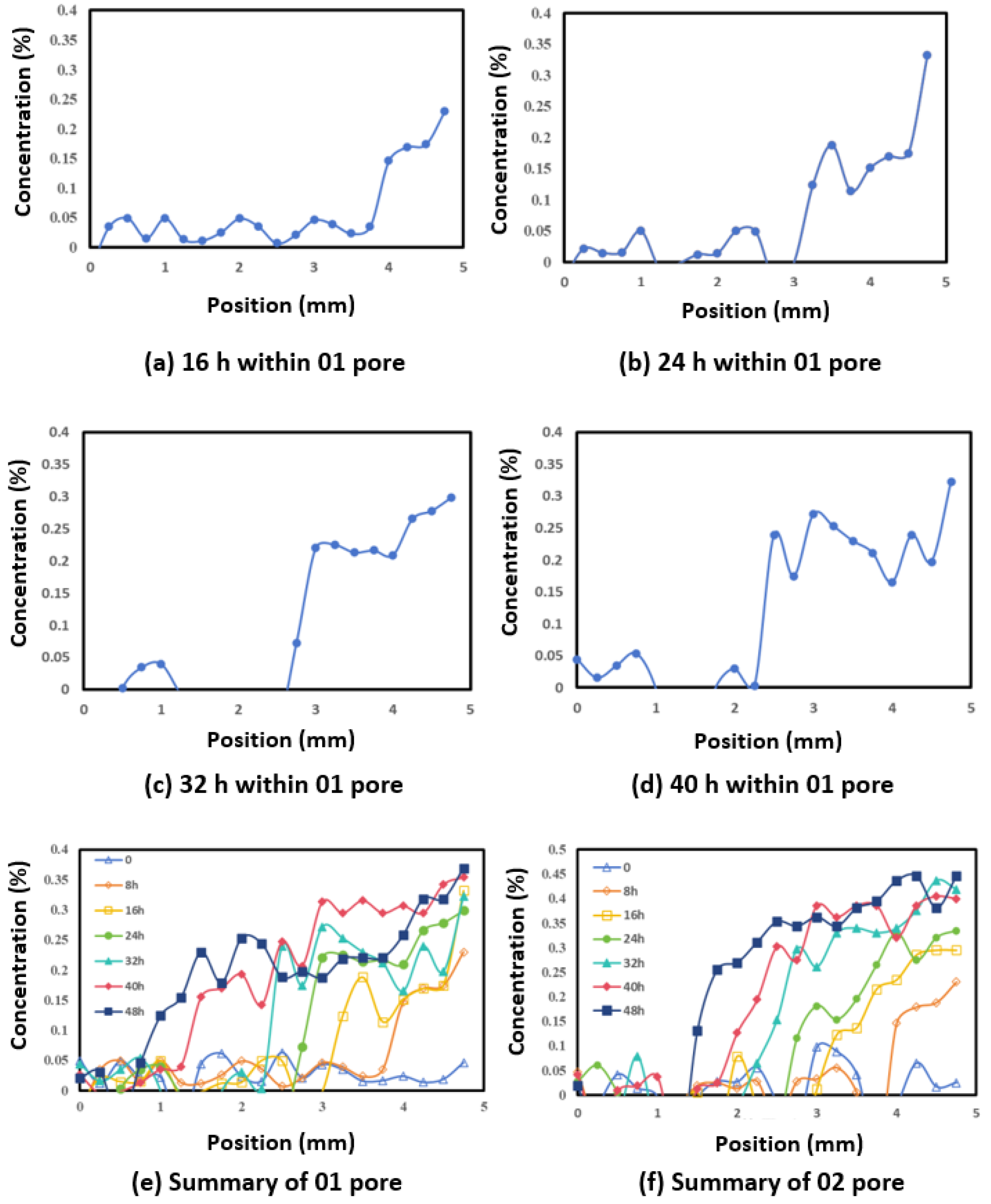
4.3. Diffusion Within 100 μm Pores
4.4. Diffusion Within 50 μm Pores
4.5. Diffusion Within 20 μm Pores
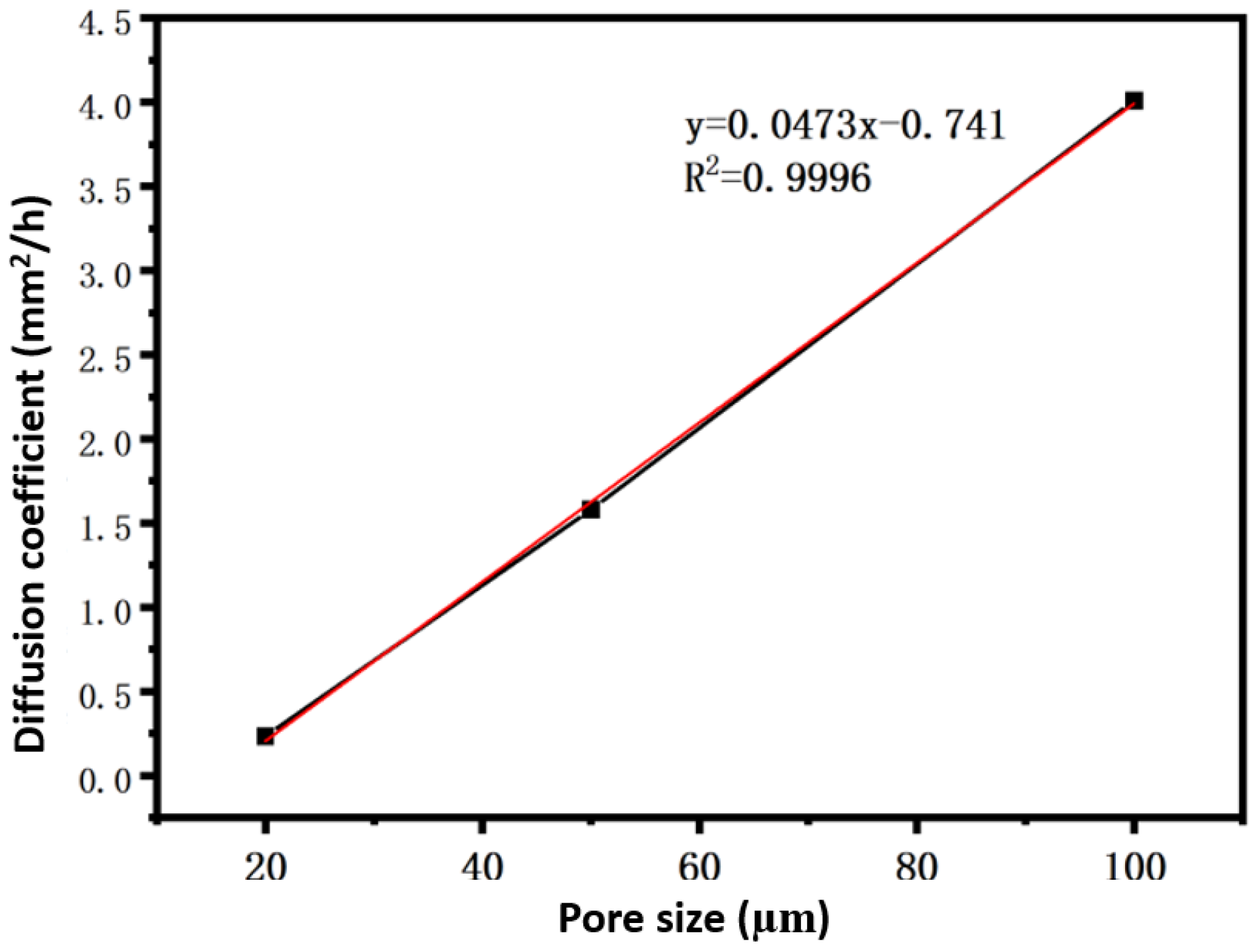
4.6. Determination of the Diffusion Coefficient
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IFT | interfacial tension |
| RGB | red green blue |
| EOR | enhanced oil recovery |
| PDMS | Polydimethylsiloxane |
Appendix A
References
- Li, M.; Wu, S.; Zhu, R.; Hu, S.; Wang, P.; Cai, Y.; Zhang, S. Heterogeneity and sedimentary characteristics of shale laminae of fine-grained sediments in alkaline lacustrine strata in the Permian Fengcheng Formation, Mahu Sag, NW China. Energies 2024, 17, 962. [Google Scholar] [CrossRef]
- Kuang, L.; Tang, Y.; Lei, D.; Chang, Q.; Ouyang, M.; Hou, L.; Deguang, L. Formation conditions and exploration potential of tight oil in the permian saline lacustrine dolomitic rock, Junggar Basin, NW China. Pet. Explor. Dev. 2012, 39, 700–711. [Google Scholar] [CrossRef]
- Chaohua, G.; Mingzhen, W.; Hong, L. Study of gas production from shale reservoirs with multi-stage hydraulic fracturing horizontal well considering multiple transport mechanisms. PLoS ONE 2018, 13, e0188480. [Google Scholar]
- Wang, C.; Gao, H.; Qi, Y.; Li, X.; Zhang, R.; Fan, H. Investigation on the mechanisms of spontaneous imbibition at high pressures for tight oil recovery. ACS Omega 2020, 5, 12727–12734. [Google Scholar] [CrossRef]
- Bai, J.; Liu, H.; Wang, J.; Qian, G.; Peng, Y.; Gao, Y.; Yan, L.; Fu-Lin, C. CO2, water and N2 injection for enhanced oil recovery with spatial arrangement of fractures in tight-oil reservoirs using Huff-N-Puff. Energies 2019, 12, 823. [Google Scholar] [CrossRef]
- Tu, J.; Sheng, J.J. Effect of pressure on imbibition in shale oil reservoirs with wettability considered. Energy Fuels 2020, 34, 4260–4272. [Google Scholar] [CrossRef]
- Wan, T.; Sheng, J.J. Enhanced recovery of crude oil from shale formations by gas injection in zipper-fractured horizontal wells. Pet. Sci. Technol. 2015, 33, 1605–1610. [Google Scholar] [CrossRef]
- Tian, W.; Wu, K.; Gao, Y.; Chen, Z.; Gao, Y.; Li, J. A critical review of enhanced oil recovery by imbibition: Theory and practice. Energy Fuels 2021, 35, 5643–5670. [Google Scholar] [CrossRef]
- Cao, Y.; Pan, Y.; Yang, S.; Zhao, X. Nanomaterials of displacement performance in low permeability reservoirs: A comprehensive review of experimental research and model evaluation. Phys. Fluids 2025, 37, 071307. [Google Scholar] [CrossRef]
- Ding, M.; Xue, X.; Wang, Y.; Zhang, C.H.; Qiu, S.Z. Mobilization of tight oil by spontaneous imbibition of surfactants. Pet. Sci. 2024, 21, 4176–4188. [Google Scholar] [CrossRef]
- Sun, Y.; Xin, Y.; Lv, F.; Dai, C.L. Experimental study on the mechanism of adsorption-improved imbibition in oil-wet tight sandstone by a nonionic surfactant for enhanced oil recovery. Pet. Sci. 2021, 18, 1115–1126. [Google Scholar] [CrossRef]
- Alvarez, J.O.; Neog, A.; Jais, A.; Schechter, D.S. Impact of surfactants for settability alteration in stimulation fluids and the potential for surfactant EOR in unconventional liquid reservoirs. In Proceedings of the SPE Unconventional Resources Conference, Vienna, Austria, 25–27 February 2014. [Google Scholar]
- Zhang, F.; Saputra, I.W.; Niu, G.; Adel, I.A.; Xu, L.; Schechter, D.S. Upscaling laboratory result of surfactant-assisted spontaneous imbibition to the field scale through scaling group analysis, numerical simulation, and discrete fracture network model. In Proceedings of the SPE Improved Oil Recovery Conference, Tulsa, OK, USA, 14–18 April 2018. [Google Scholar]
- Chen, W.; Geng, X.; Liu, W.; Ding, B.; Xiong, C.; Sun, J.; Wang, C.; Jiang, K. A comprehensive review on screening, application, and perspectives of surfactant-based chemical-enhanced oil recovery methods in unconventional oil reservoirs. Energy Fuels 2023, 37, 4729–4750. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Z.; Gao, M.; Xu, Z.; Adenutsi, C.D.; You, Q. New insights into the synergism between silica nanoparticles and surfactants on interfacial properties: Implications for spontaneous imbibition in tight oil reservoirs. J. Pet. Sci. Eng. 2022, 215, 110647. [Google Scholar] [CrossRef]
- Zhao, X.; Gao, Y.; Pan, Y.; Yang, Z. Progress on the Application of Nanomaterial Expansion in Oil Displacement. Appl. Sci. 2025, 15, 6484. [Google Scholar] [CrossRef]
- Li, B. Investigation into Stimulation Mechanism of CO2 Pre-Pad Energized Fracturing in Jimusar Shale Oil Reservoir. Ph.D. Thesis, China University of Petroleum, Beijing, China, 2023. (In Chinese). [Google Scholar]
- Gu, C.; Qin, R.; Di, Q.; Jiang, F.; Liu, Z.; Chen, H. Simulation and visualization experiment of manganese ion diffusion and damage to gel in a porous media-gel system. Pet. Explor. Dev. 2019, 46, 367–373. [Google Scholar] [CrossRef]
- Wang, C. Fractal Models of Single-Phase Gas Diffusion and Gas-Liquid Two-Phase Diffusion in Porous Media. Ph.D. Thesis, Kunming University of Science and Technology, Kunming, China, 2021. (In Chinese). [Google Scholar]
- Winanda, D.F.; Adisasmito, S. Addition of surfactants to Low Salinity Waterflooding in microfluidics system to increase oil recovery. Pet. Res. 2022, 7, 486–494. [Google Scholar] [CrossRef]
- Zou, G. Study on the Transport law Of Fracturing Fluid in Shale Gas Reservoirs. Ph.D. Thesis, University of Science and Technology Beijing, Beijing, China, 2023. (In Chinese). [Google Scholar]
- Liu, D. Microscopic Imbibition Effects in Shale Reservoir and Its Impact on Production. Ph.D. Thesis, China University of Petroleum, Beijing, China, 2021. (In Chinese). [Google Scholar]
- Yu, F.; Gao, Z.; Zhu, W.; Wang, C.; Liu, F.; Xu, F.; Jiang, H.; Li, J. Experiments on imbibition mechanisms of fractured reservoirs by microfluidic chips. Pet. Explor. Dev. 2021, 48, 1162–1172. [Google Scholar] [CrossRef]
- Wang, X.; He, A.; Ju, M.; Xu, Y.; Zhang, Y.; Xu, C. Improving Imbibition Recovery Efficiency in Tight Oil Reservoir Based On Microfluidic Method. Sci. Technol. Eng. 2021, 21, 6272–6277. (In Chinese) [Google Scholar]
- Xu, D. Study on Methods and Mechanisms of Enhanced Imbibition Efficiency for Changqing Tight Oil Reservoirs. Ph.D. Thesis, China University of Petroleum, Beijing, China, 2021. (In Chinese). [Google Scholar]
- Wang, X.; Liu, Y.; Yi, F.; Bo, H.; Wu, W.; Chen, W.; Fang, Y.; Caili, D. Characteristics of Crude Oil Utilization Improved by Imbibition of Surfactant in Matrix-fracture Dual Media. Oilfield Chem. 2022, 39, 108–114. (In Chinese) [Google Scholar]
- Zhokh, A. Size-controlled non-Fickian diffusion in a combined micro- and mesoporous material. Chem. Phys. 2019, 520, 27–31. [Google Scholar] [CrossRef]
- Kang, K.; Abdelfatah, E.; Pournik, M. Nanoparticles transport in heterogeneous porous media using continuous time random walk approach. J. Pet. Sci. Eng. 2019, 177, 544–557. [Google Scholar] [CrossRef]
- Coll, C.; Martinez-Manez, R.; Marcos, M.D.; Sancenon, F.; Soto, J. A simple approach for the selective and sensitive colorimetric detection of anionic surfactants in water. Angew. Chem. Int. Ed. Engl. 2007, 46. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X. Colorimetric and fluorometric detection of anionic surfactants with water soluble sensors. Sens. Actuators B Chem. 2015, 209, 258–264. [Google Scholar] [CrossRef]
- Lee, S.; Manjunatha, D.H.; Jeon, W.; Ban, C. Cationic Surfactant-Based Colorimetric Detection of Plasmodium Lactate Dehydrogenase, a Biomarker for Malaria, Using the Specific DNA Aptamer. PLoS One 2014, 9, e100847. [Google Scholar] [CrossRef] [PubMed]
- Smirnova, S.V.; Apyari, V.V. Aqueous Two-Phase Systems Based on Cationic and Anionic Surfactants Mixture for Rapid Extraction and Colorimetric Determination of Synthetic Food Dyes. Sensors 2023, 23, 3519. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Wang, X.; L, W.; Wu, X.; Li, J. Molecular Imprinting: Perspectives and Applications. Chem. Soc. Rev. 2016, 45, 2137–2211. [Google Scholar] [CrossRef] [PubMed]
- Korzhan, L.; Kulichenko, S.; Lelyushok, S. Smart Colorimetric Determination of Ionic Surfactants With Bromothymol Blue at the Presence of Nonionic Surfactant Triton X-100. Methods Objects Chem. Anal. 2023, 18, 136–142. [Google Scholar] [CrossRef]
- Jia, L.; Sun, W.; Li, W.; Dong, Y.; Wu, L.; Saldaña, M.; Gao, Y.; Jin, Y.; Sun, W. A Colour Indicator Film Based on Bromothymol Blue/Poly(Lactic Acid)/Polyvinylpyrrolidone for Detecting Bacteria. Packag. Technol. Sci. 2023, 36, 549–556. [Google Scholar] [CrossRef]
- Hu, Y.; Chaoneng, Z.; Jinzhou, Z.; Gao, D.; Fu, C. Mechanisms of fracturing fluid spontaneous imbibition behavior in shale reservoir: A review. J. Nat. Gas Sci. Eng. 2020, 82, 103498. [Google Scholar] [CrossRef]
- Liu, G.; Zhao, Z.; Sun, M.; Li, J.; Hu, G.; Wang, X. New insights into natural gas diffusion coefficient in rocks. Pet. Explor. Dev. 2012, 39, 597–604. [Google Scholar] [CrossRef]
- Achour, S.H.; Okuno, R. A single-phase diffusion model for gas injection in tight oil reservoirs. J. Pet. Sci. Eng. 2022, 213, 110469. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Bai, S.; Xiao, W.; Gao, S. Microfluidic Investigation on the Diffusion Law of Nano Displacement Agent in Porous Media. Processes 2025, 13, 2546. https://doi.org/10.3390/pr13082546
Liu J, Bai S, Xiao W, Gao S. Microfluidic Investigation on the Diffusion Law of Nano Displacement Agent in Porous Media. Processes. 2025; 13(8):2546. https://doi.org/10.3390/pr13082546
Chicago/Turabian StyleLiu, Jiahui, Shixun Bai, Weixiong Xiao, and Shengwu Gao. 2025. "Microfluidic Investigation on the Diffusion Law of Nano Displacement Agent in Porous Media" Processes 13, no. 8: 2546. https://doi.org/10.3390/pr13082546
APA StyleLiu, J., Bai, S., Xiao, W., & Gao, S. (2025). Microfluidic Investigation on the Diffusion Law of Nano Displacement Agent in Porous Media. Processes, 13(8), 2546. https://doi.org/10.3390/pr13082546





