Study on Quantifying Soil Thermal Imbalance in Shallow Coaxial Borehole Heat Exchangers
Abstract
1. Introduction
- 1.
- The current studies mainly reflect the degree of accumulation through soil temperature rise, lacking standardized quantitative evaluation metrics.
- 2.
- The current studies fail to reflect the trend of soil temperature changes during long-term operation of the system.
- 3.
- There is a shortage of comprehensive analyses on various design and operating factors on the thermal accumulation of a shallow borehole array.
2. Methods
2.1. Basic Assumptions
- (1)
- The initial soil temperature is assumed to be based on the geothermal gradient;
- (2)
- The inlet temperature or heat flux density of the circulating fluid in the pipe is assumed to be constant;
- (3)
- The influences of evaporation, diffusion, and condensation of the circulating fluid within the pipe, along with groundwater seepage, are neglected in the thermal conduction analysis of the rock and soil;
- (4)
- The rock and soil are treated as a homogeneous medium characterized by constant and uniform thermal properties, such as thermal conductivity, specific heat capacity, and thermal diffusivity.
2.2. Mathematical Model
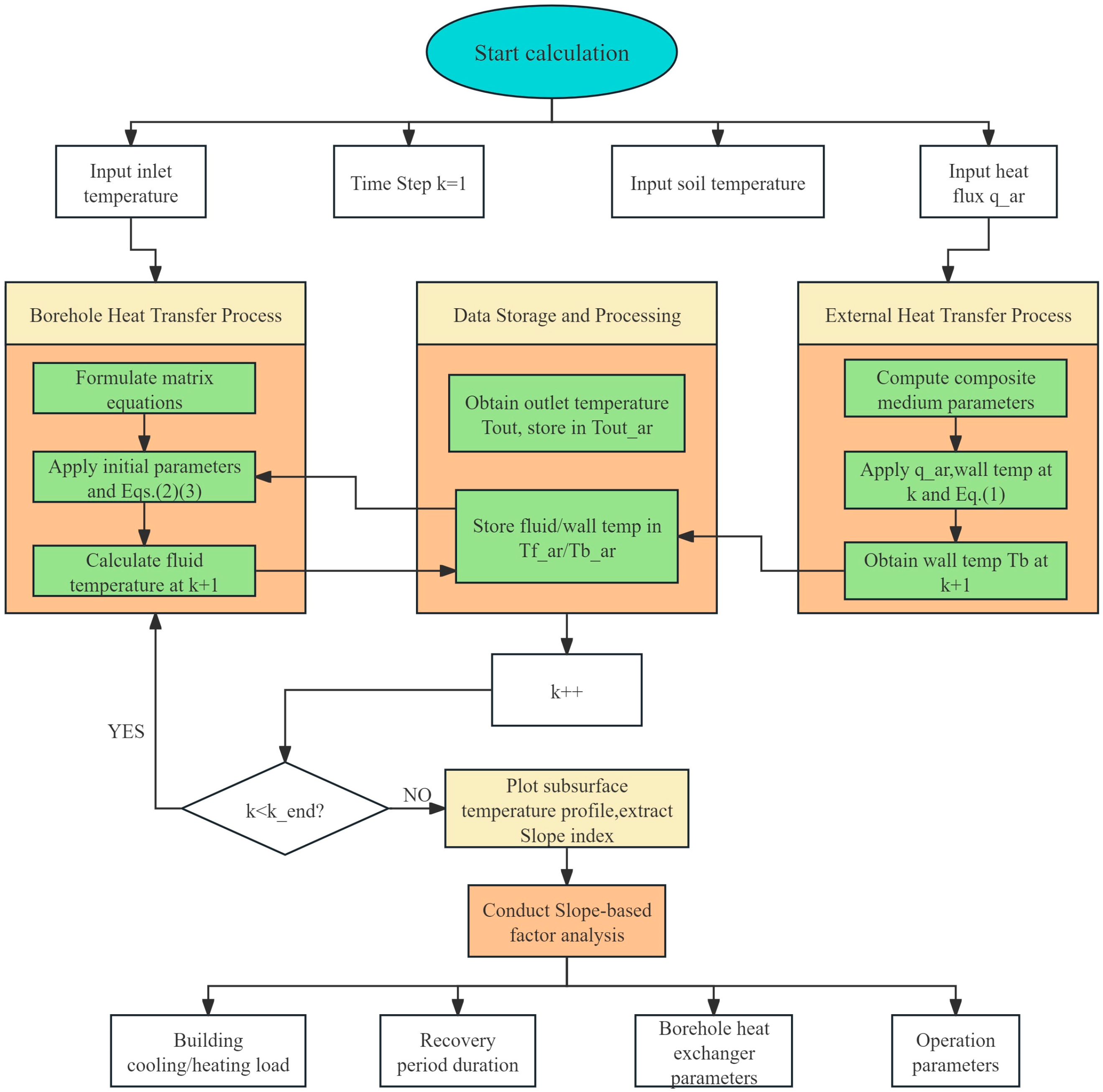
2.3. Calculation Process
3. Results
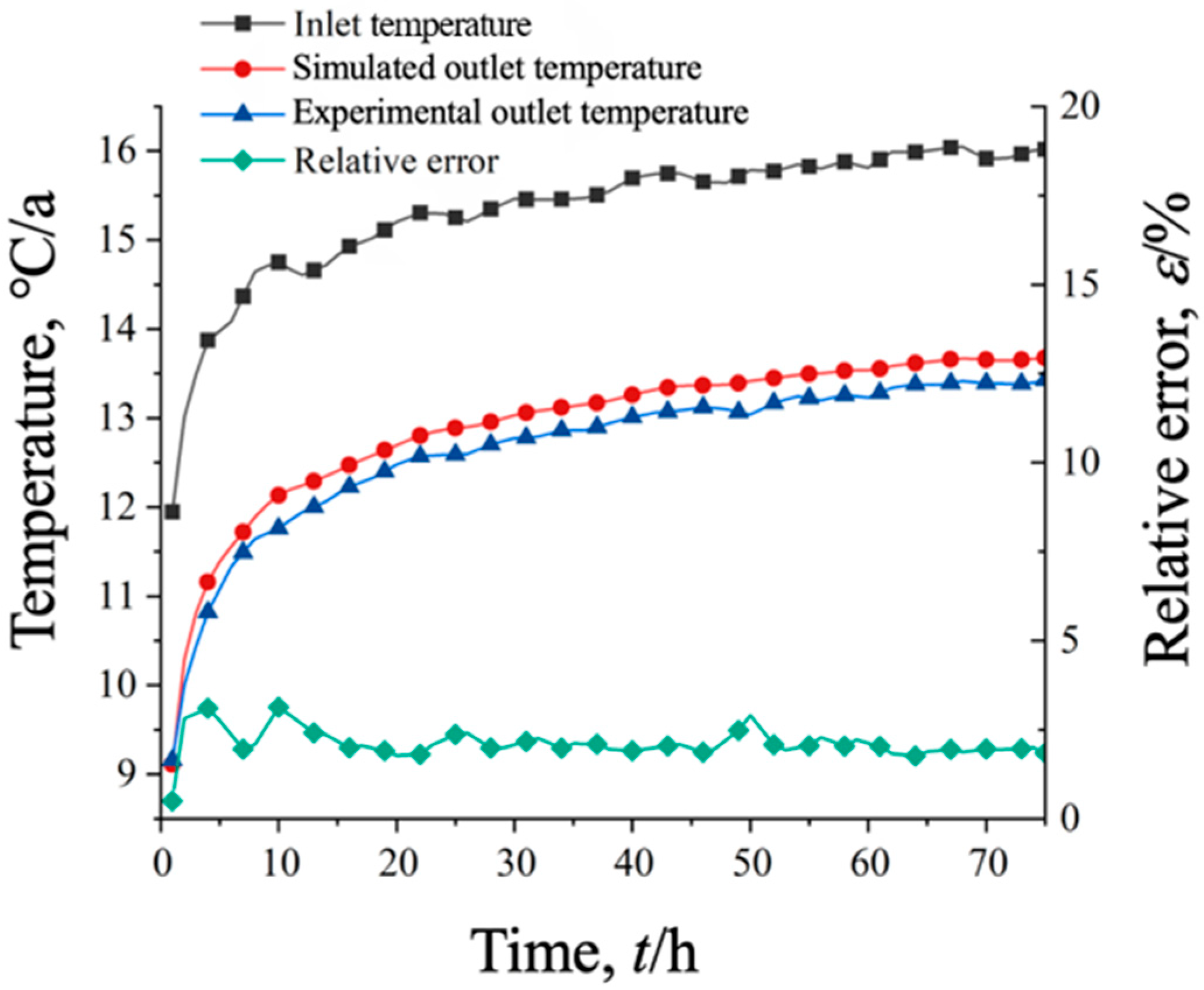
3.1. Model Validation
3.2. The Heat Accumulation Evaluation Metric
4. Discussion
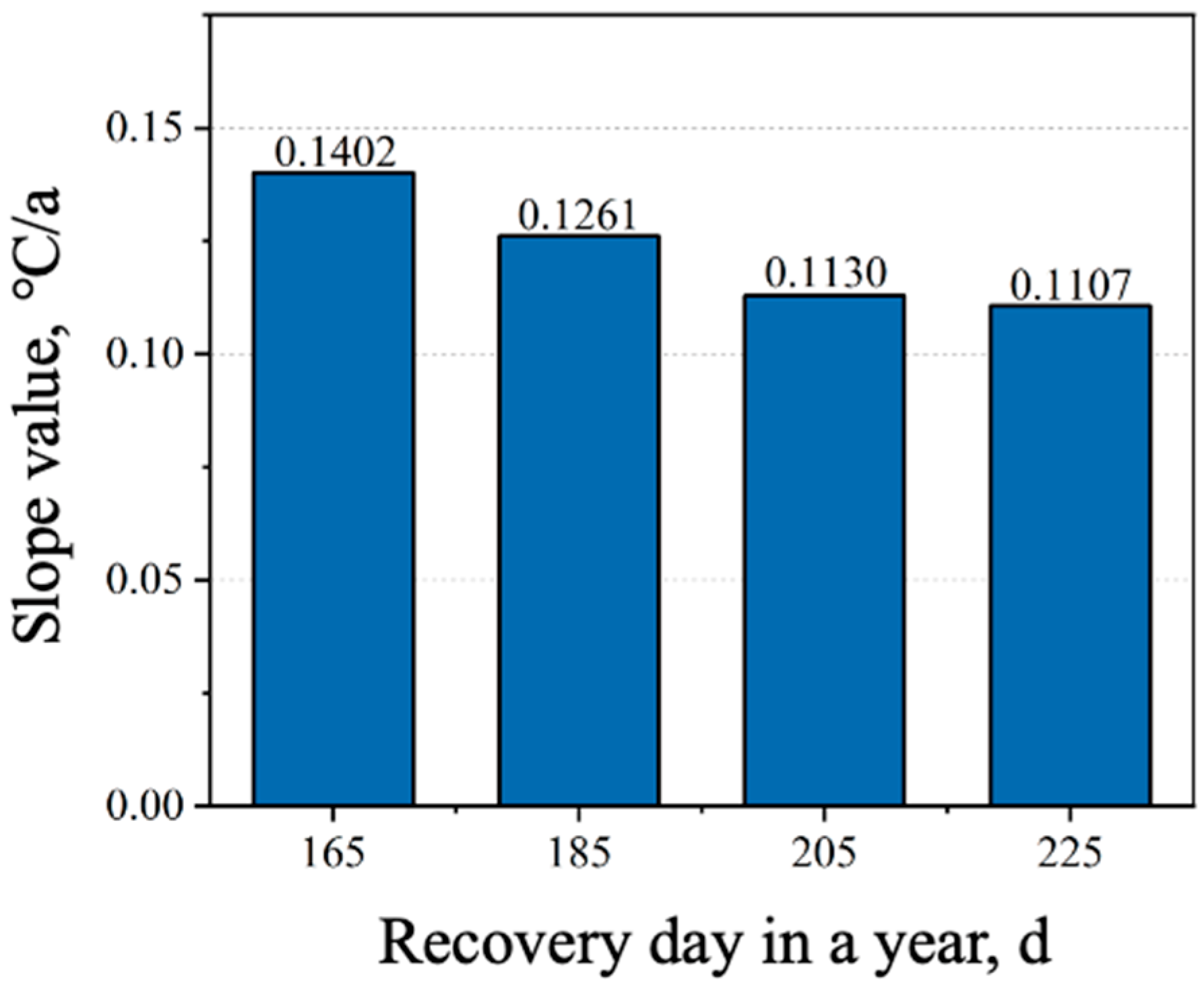
4.1. Building Cooling/Heating Loads and Recovery Period Duration
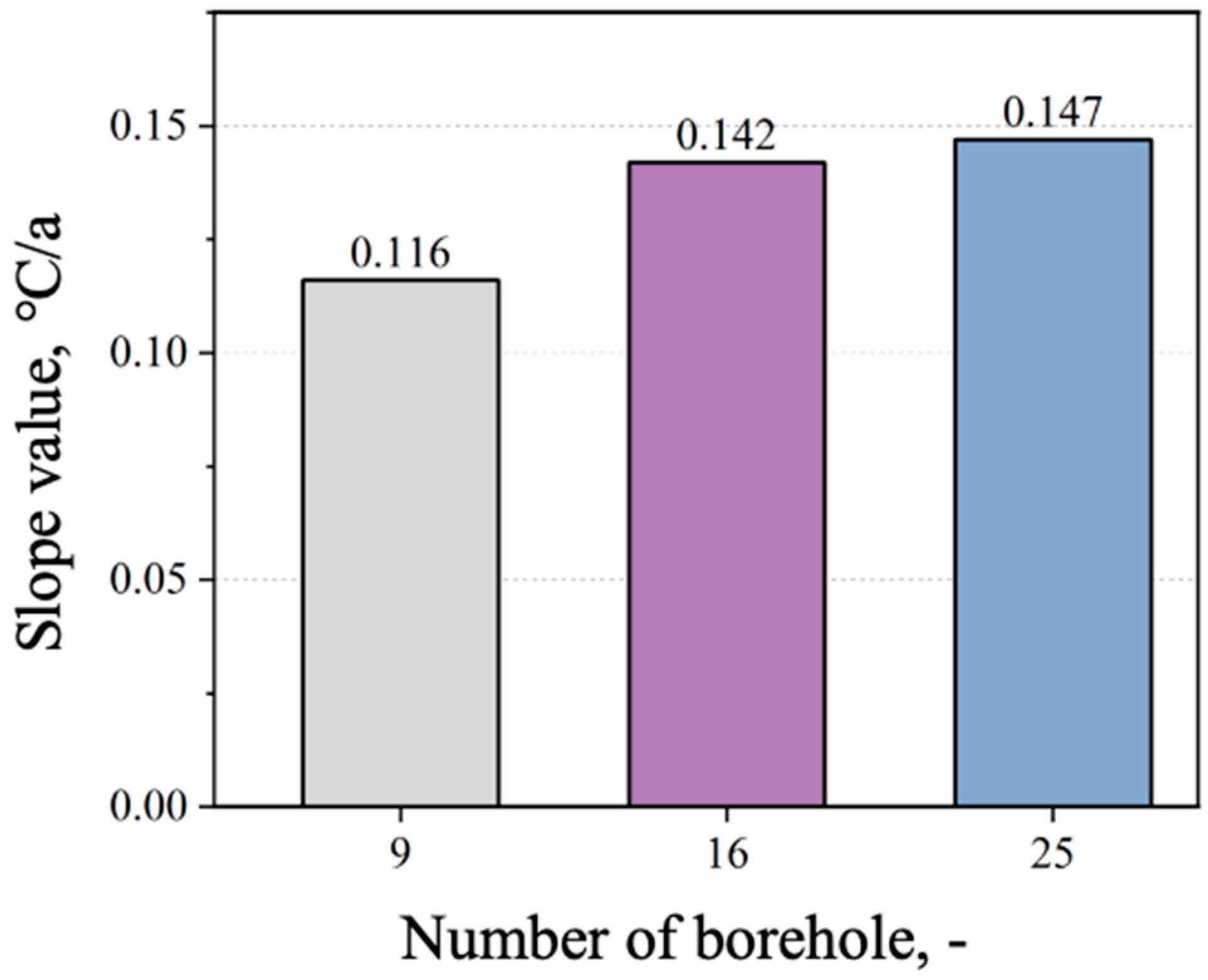
4.2. Borehole Spacing and Density
4.3. Vertical Borehole Depth
4.4. Backfill Thermal Conductivity
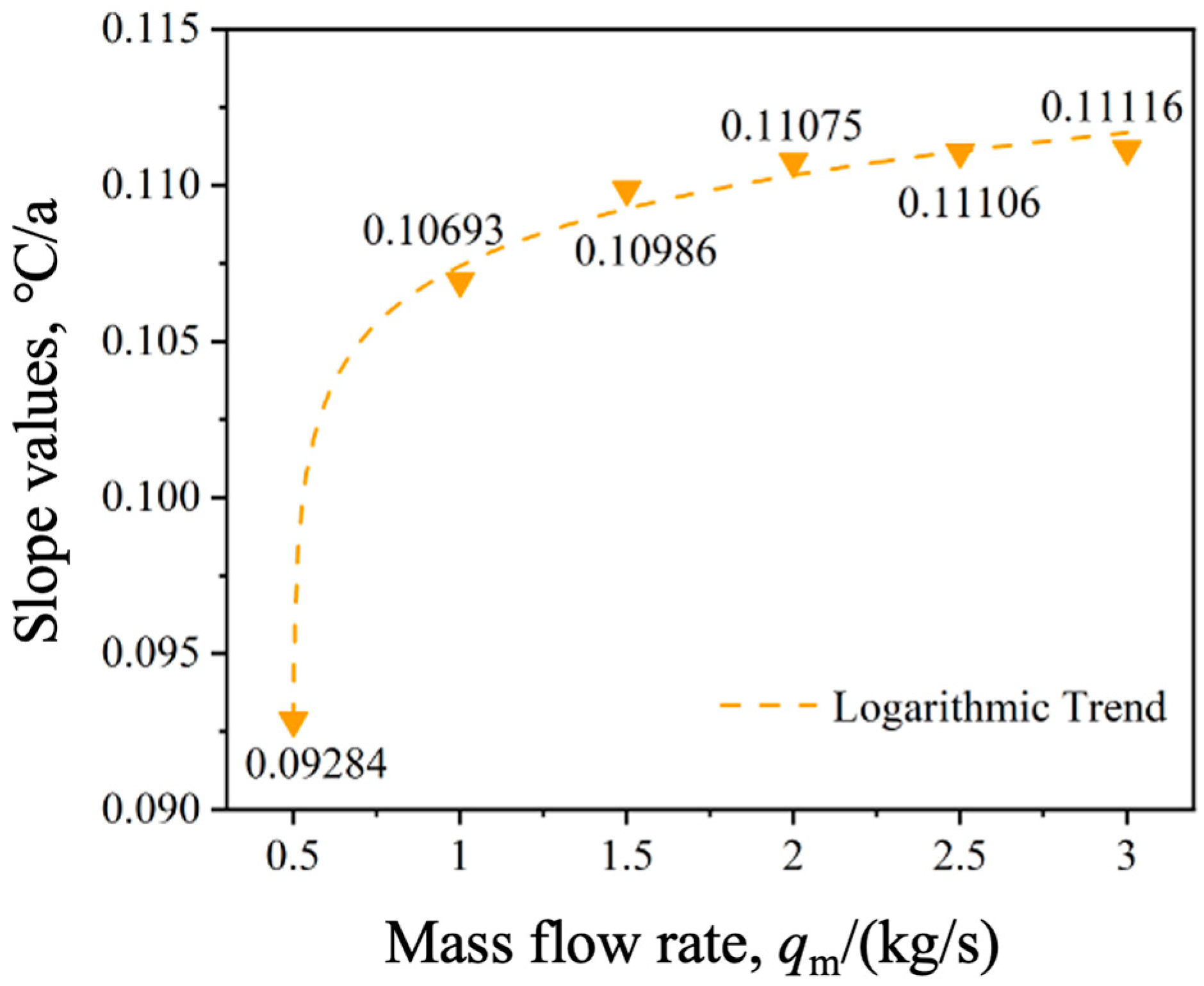
4.5. Circulating Water Flow Rate
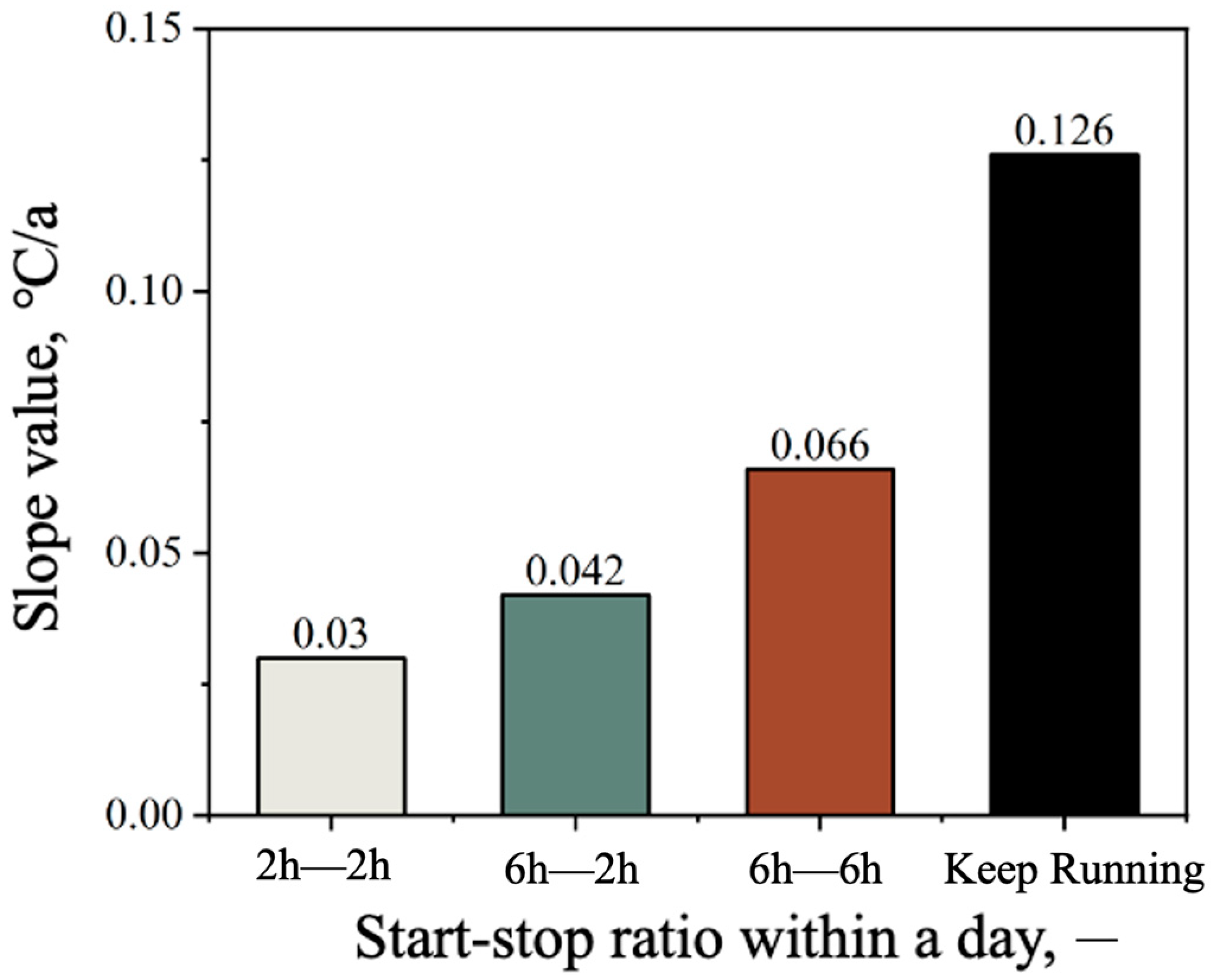
4.6. Operating Mode
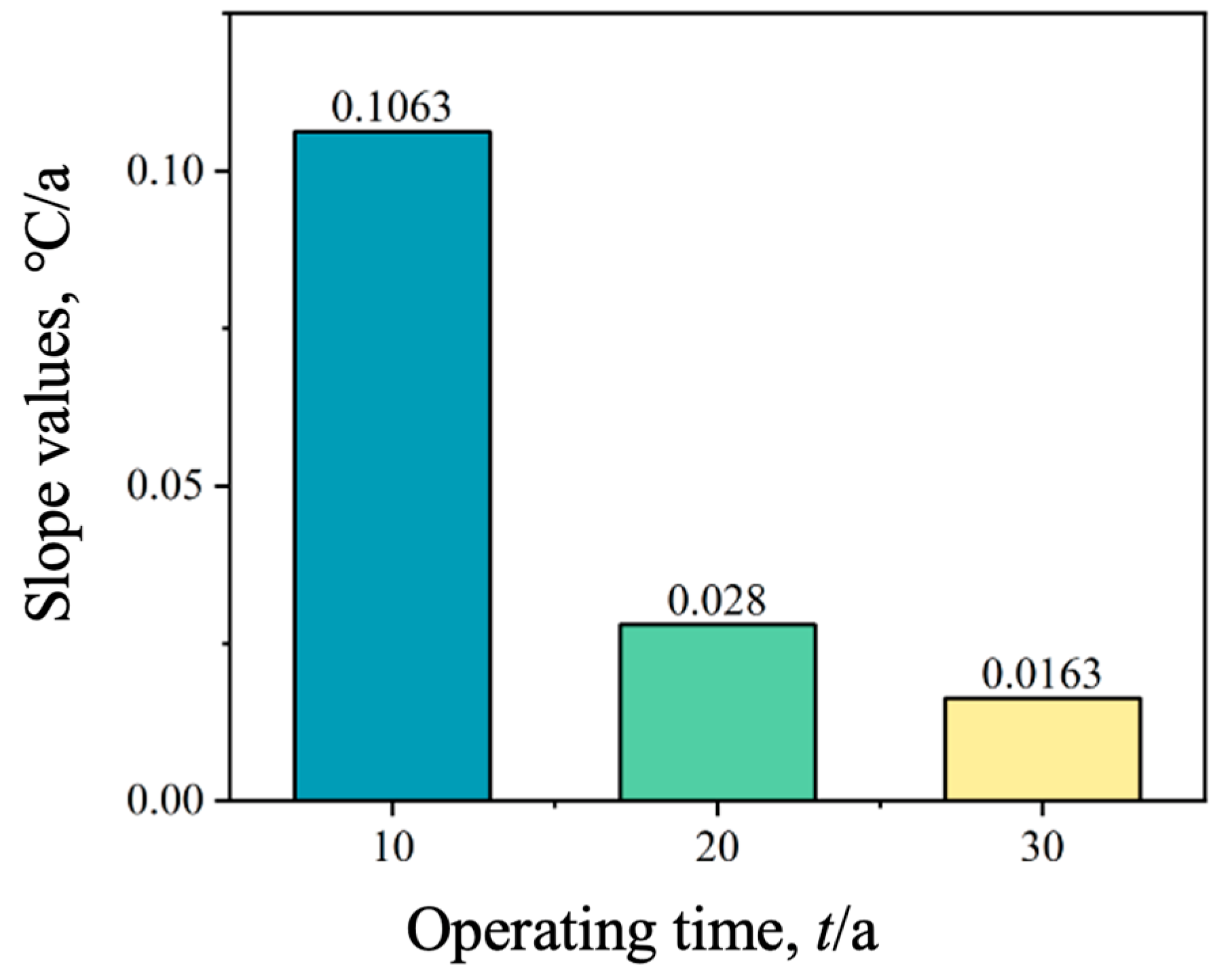
4.7. Operating Years
5. Conclusions
5.1. Conclusion
- 1.
- The simulation results of the shallow CBHE heat transfer model show good agreement with the experimental measurements. Once the system reaches steady-state operation, the maximum error is 3.61%, remaining within a 5% margin.
- 2.
- The linear trend Slope extracted from subsurface temperature profiles serves as the heat accumulation evaluation metric. Its sign and magnitude precisely quantify both the directionality (heat or cold accumulation) and severity of subsurface thermal imbalance. Based on this metric, a quantitative analysis of the relevant influencing factors was conducted.
- 3.
- Extending recovery periods, increasing borehole spacing, deepening vertical boreholes, enhancing backfill thermal conductivity, reducing circulating flow rates, and implementing intermittent operation all mitigate subsurface thermal accumulation. Among these factors, increasing borehole depth had the most pronounced effect: when the depth was increased from 100 m to 200 m, a reduction of 1.076 °C in the average annual temperature rise was observed.
5.2. Outlook
- 1.
- The model does not consider the impact of groundwater seepage. In future research, the existing model can be coupled with groundwater seepage to improve simulation accuracy. Considering that convective heat transfer may influence the results in a noticeable way, future studies should investigate the effect of groundwater flow rate and temperature on the thermal accumulation of bore fields.
- 2.
- This study assumes constant cooling/heating loads during long-term system operation, whereas actual engineering applications exhibit significant dynamic load fluctuations. Since the main purpose of this study was to reveal the relationship between various design and operation parameters and the thermal accumulation index, and considering that the thermal load profile in the real world is a more complex curve, future research should address this limitation through advanced methodologies.
- 3.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Amasyali, K.; El-Gohary, N.M. A Review of Data-Driven Building Energy Consumption Prediction Studies. Renew. Sustain. Energy Rev. 2018, 81, 1192–1205. [Google Scholar] [CrossRef]
- Liu, J.; Wang, F.; Gao, Y.; Zhang, Y.; Cai, W.; Wang, M.; Wang, Z. Influencing Factors Analysis and Operation Optimization for the Long-Term Performance of Medium-Deep Borehole Heat Exchanger Coupled Ground Source Heat Pump System. Energy Build. 2020, 226, 110385. [Google Scholar] [CrossRef]
- Lund, J.W.; Huttrer, G.W.; Toth, A.N. Characteristics and Trends in Geothermal Development and Use, 1995 to 2020. Geothermics 2022, 105, 102522. [Google Scholar] [CrossRef]
- Yuan, Y.; Cao, X.; Sun, L.; Lei, B.; Yu, N. Ground Source Heat Pump System: A Review of Simulation in China. Renew. Sustain. Energy Rev. 2012, 16, 6814–6822. [Google Scholar] [CrossRef]
- Urresta, E.; Moya, M.; Campana, C.; Cruz, C. Ground Thermal Conductivity Estimation Using the Thermal Response Test with a Horizontal Ground Heat Exchanger. Geothermics 2021, 96, 102213. [Google Scholar] [CrossRef]
- Rybach, L.; Eugster, W.J. Sustainability Aspects of Geothermal Heat Pump Operation, with Experience from Switzerland. Geothermics 2010, 39, 365–369. [Google Scholar] [CrossRef]
- Yiqiu, T.; Chi, Z.; Huijie, L.; Hao, S.; Huining, X. Experimental and Numerical Analysis of the Critical Heating Strategy for Hydronic Heated Snow Melting Airfield Runway. Appl. Therm. Eng. 2020, 178, 115508. [Google Scholar] [CrossRef]
- Chi, Z.; Yiqiu, T.; Fengchen, C.; Qing, Y.; Huining, X. Long-Term Thermal Analysis of an Airfield-Runway Snow-Melting System Utilizing Heat-Pipe Technology. Energy Convers. Manag. 2019, 186, 473–486. [Google Scholar] [CrossRef]
- Hein, P.; Kolditz, O.; Görke, U.-J.; Bucher, A.; Shao, H. A Numerical Study on the Sustainability and Efficiency of Borehole Heat Exchanger Coupled Ground Source Heat Pump Systems. Appl. Therm. Eng. 2016, 100, 421–433. [Google Scholar] [CrossRef]
- Rostami, S.; Ahmadi, N. In the Study of the Effects of the Pipe Design of a Heat Exchanger on the Thermo-Fluid Characteristics and Exergy Destruction. Processes 2025, 13, 835. [Google Scholar] [CrossRef]
- Muneeshwaran, M.; Kim, H.J.; Tayyab, M.; Li, W.; Nawaz, K.; Yang, C.-M. Flow Maldistribution in Plate Heat Exchangers—Impact, Analysis, and Solutions. Renew. Sustain. Energy Rev. 2025, 207, 114905. [Google Scholar] [CrossRef]
- Thomson, W. Mathematical and Physical Papers, 1st ed.; Cambridge University Press: Cambridge, UK, 2011; ISBN 978-1-108-02898-1. [Google Scholar]
- Zeng, H.Y.; Diao, N.R.; Fang, Z.H. A Finite Line-source Model for Boreholes in Geothermal Heat Exchangers. Heat Trans. Asian Res. 2002, 31, 558–567. [Google Scholar] [CrossRef]
- Hurley, M.J.; Gottuk, D.; Hall, J.R.; Harada, K.; Kuligowski, E.; Puchovsky, M.; Torero, J.; Watts, J.M.; Wieczorek, C. (Eds.) SFPE Handbook of Fire Protection Engineering; Springer: New York, NY, USA, 2016; ISBN 978-1-4939-2564-3. [Google Scholar]
- Man, Y.; Yang, H.; Diao, N.; Liu, J.; Fang, Z. A New Model and Analytical Solutions for Borehole and Pile Ground Heat Exchangers. Int. J. Heat Mass Transf. 2010, 53, 2593–2601. [Google Scholar] [CrossRef]
- Luo, Y.; Guo, H.; Meggers, F.; Zhang, L. Deep Coaxial Borehole Heat Exchanger: Analytical Modeling and Thermal Analysis. Energy 2019, 185, 1298–1313. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, M. Development of a Numerical Model for the Simulation of Vertical U-Tube Ground Heat Exchangers. Appl. Therm. Eng. 2009, 29, 920–924. [Google Scholar] [CrossRef]
- Mottaghy, D.; Dijkshoorn, L. Implementing an Effective Finite Difference Formulation for Borehole Heat Exchangers into a Heat and Mass Transport Code. Renew. Energy 2012, 45, 59–71. [Google Scholar] [CrossRef]
- Cai, W.; Wang, F.; Liu, J.; Wang, Z.; Ma, Z. Experimental and Numerical Investigation of Heat Transfer Performance and Sustainability of Deep Borehole Heat Exchangers Coupled with Ground Source Heat Pump Systems. Appl. Therm. Eng. 2019, 149, 975–986. [Google Scholar] [CrossRef]
- Cui, P.; Yang, H.; Fang, Z. Numerical Analysis and Experimental Validation of Heat Transfer in Ground Heat Exchangers in Alternative Operation Modes. Energy Build. 2008, 40, 1060–1066. [Google Scholar] [CrossRef]
- Kuzmic, N.; Law, Y.L.E.; Dworkin, S.B. Numerical Heat Transfer Comparison Study of Hybrid and Non-Hybrid Ground Source Heat Pump Systems. Appl. Energy 2016, 165, 919–929. [Google Scholar] [CrossRef]
- Penrod, E.B.; Prasanna, K.V. Design of a flat-plate collector for a solar earth heat pump. Pergamon 1962, 6, 9–22. [Google Scholar] [CrossRef]
- Fan, R.; Jiang, Y.; Yao, Y.; Ma, Z. Theoretical Study on the Performance of an Integrated Ground-Source Heat Pump System in a Whole Year. Energy 2008, 33, 1671–1679. [Google Scholar] [CrossRef]
- Qian, H.; Wang, Y. Modeling the Interactions between the Performance of Ground Source Heat Pumps and Soil Temperature Variations. Energy Sustain. Dev. 2014, 23, 115–121. [Google Scholar] [CrossRef]
- Yang, J.; Xu, L.; Hu, P.; Zhu, N.; Chen, X. Study on Intermittent Operation Strategies of a Hybrid Ground-Source Heat Pump System with Double-Cooling Towers for Hotel Buildings. Energy Build. 2014, 76, 506–512. [Google Scholar] [CrossRef]
- Yang, H.; Cui, P.; Fang, Z. Vertical-Borehole Ground-Coupled Heat Pumps: A Review of Models and Systems. Appl. Energy 2010, 87, 16–27. [Google Scholar] [CrossRef]
- Beier, R.A.; Acuña, J.; Mogensen, P.; Palm, B. Transient Heat Transfer in a Coaxial Borehole Heat Exchanger. Geothermics 2014, 51, 470–482. [Google Scholar] [CrossRef]
- Gao, W.; Masum, S.; Jiang, L. Technical Performance Comparison of Horizontal and Vertical Ground-Source Heat Pump Systems. J. GeoEnergy 2023, 2023, 6106360. [Google Scholar] [CrossRef]
- Cheng, N.; Zhou, C.; Luo, Y.; Shen, J.; Tian, Z.; Sun, D.; Fan, J.; Zhang, L.; Deng, J.; Rosen, M.A. Thermal Behavior and Performance of Shallow-Deep-Mixed Borehole Heat Exchanger Array for Sustainable Building Cooling and Heating. Energy Build. 2023, 291, 113108. [Google Scholar] [CrossRef]
- Wang, P.; Wang, Y.; Gao, W.; Xu, T.; Wei, X.; Shi, C.; Qi, Z.; Bai, L. Uncovering the Efficiency and Performance of Ground-Source Heat Pumps in Cold Regions: A Case Study of a Public Building in Northern China. Buildings 2023, 13, 1564. [Google Scholar] [CrossRef]
- Shao, Q.; Zhang, C.; Wang, B.; Chen, T.; Sun, M.; Yin, H. Research on the Influence of Underground Seepage on Regional Heat Accumulation of Ground Source Heat Pump Heat Exchanger. Thermal Sci. Eng. Prog. 2024, 48, 102391. [Google Scholar] [CrossRef]
- Zhao, Y.; Gao, J.; Wu, F.; Sun, Y.; Liu, A.; Yu, Z.; Zhang, X. Study on the Thermal Imbalance Characteristics and Optimal Operation Strategy of Ground Source Heat Pump System in Hot Summer and Cold Winter Areas. Energy Convers. Manag. 2025, 343, 120184. [Google Scholar] [CrossRef]
- Rad, F.M.; Fung, A.S.; Leong, W.H. Feasibility of Combined Solar Thermal and Ground Source Heat Pump Systems in Cold Climate, Canada. Energy Build. 2013, 61, 224–232. [Google Scholar] [CrossRef]
- Chang, L.; Kong, L.; Jing, Y.; Zhang, W.; Fu, S.; Lu, X.; Yao, H.; Xie, X.; Cui, P. Dynamic Simulation of Solar-Assisted Medium-Depth Ground Heat Exchanger Direct Heating System. Buildings 2025, 15, 1690. [Google Scholar] [CrossRef]
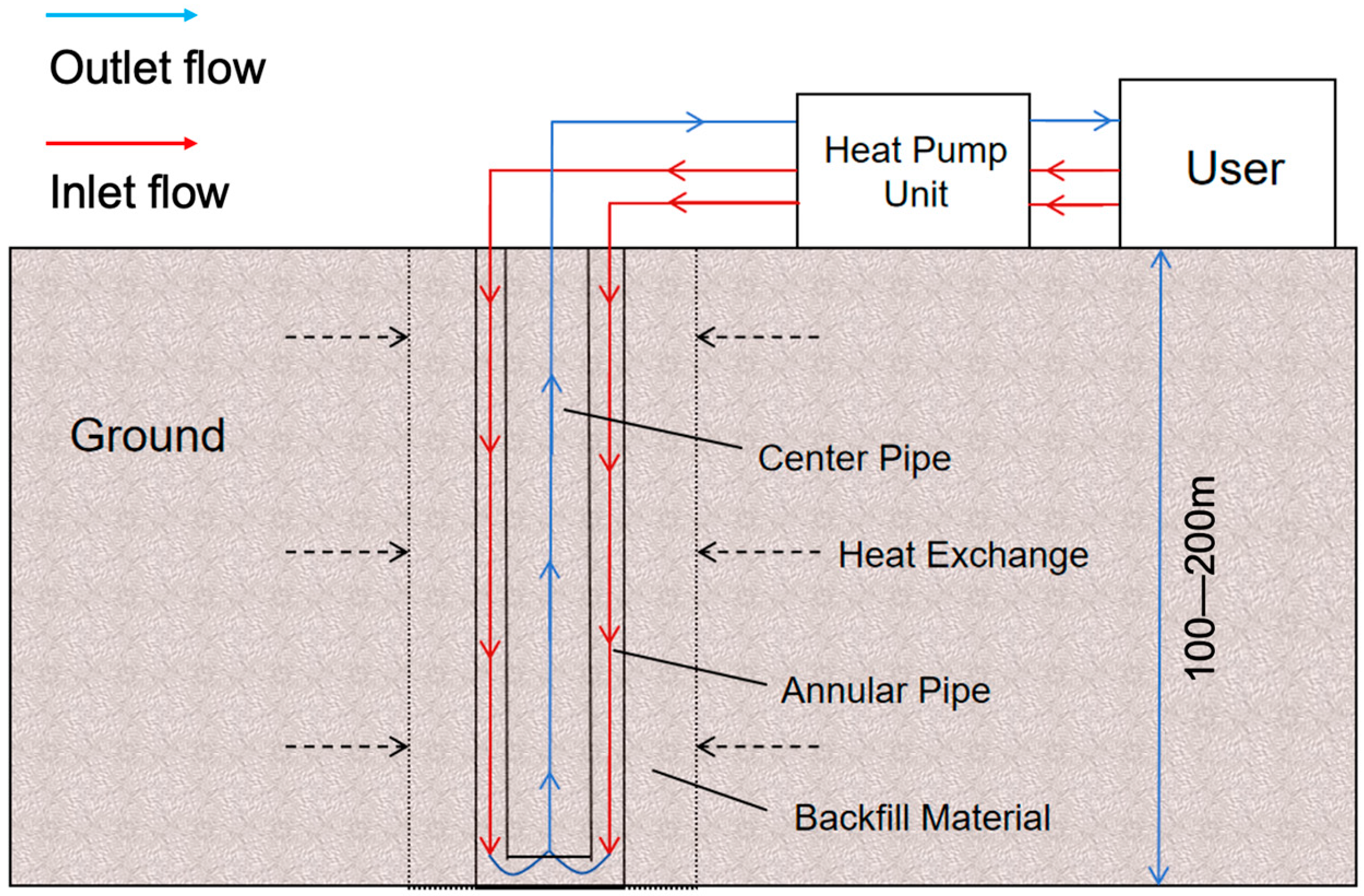





| Conditions | |||
|---|---|---|---|
| Drilling diameter, db | 115 mm | Specific heat capacity of circulating water, cf | |
| Drilling depth, H | 170 m | Thermal conductivity of circulating water, λf | 0.574 W/(m·K) |
| Outer diameter of descent pipe, dao | 114 mm | Volume flow rate of circulating water, qV | 0.58 × 10−3 m3/s |
| Inter diameter of descent pipe, dai | 113.2 mm | Specific heat capacity of backfill material, cins | 2.5 × 106 J/(kg·°C) |
| Outer diameter of ascend pipe, dco | 40 mm | Thermal conductivity of backfill materials, λins | 3.25 W/(m·K) |
| Inter diameter of ascend pipe, dci | 35.2 mm | Spatial step, Δz | 3.4 m |
| Density of circulating water, ρf | 995.7 kg/m3 | Time step, Δτ | 3600 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, R.; He, W.; Zhou, C.; Hu, Y.; Liu, Y.; Han, T.; Luo, Y.; Wang, M. Study on Quantifying Soil Thermal Imbalance in Shallow Coaxial Borehole Heat Exchangers. Processes 2025, 13, 2543. https://doi.org/10.3390/pr13082543
Liu R, He W, Zhou C, Hu Y, Liu Y, Han T, Luo Y, Wang M. Study on Quantifying Soil Thermal Imbalance in Shallow Coaxial Borehole Heat Exchangers. Processes. 2025; 13(8):2543. https://doi.org/10.3390/pr13082543
Chicago/Turabian StyleLiu, Rujie, Wei He, Chaohui Zhou, Yue Hu, Yuce Liu, Tao Han, Yongqiang Luo, and Meng Wang. 2025. "Study on Quantifying Soil Thermal Imbalance in Shallow Coaxial Borehole Heat Exchangers" Processes 13, no. 8: 2543. https://doi.org/10.3390/pr13082543
APA StyleLiu, R., He, W., Zhou, C., Hu, Y., Liu, Y., Han, T., Luo, Y., & Wang, M. (2025). Study on Quantifying Soil Thermal Imbalance in Shallow Coaxial Borehole Heat Exchangers. Processes, 13(8), 2543. https://doi.org/10.3390/pr13082543







