Intelligent Collaborative Optimization Method for Multi-Well Plunger Gas Lifting Process on Platform
Abstract
1. Introduction
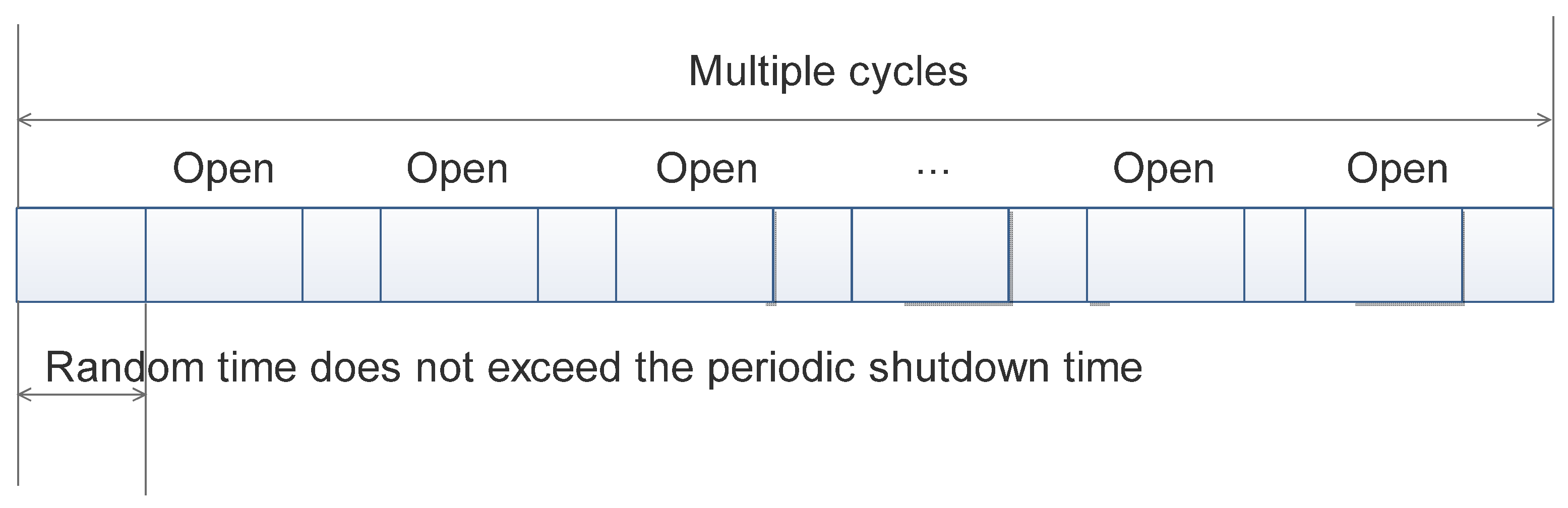
- (1)
- Under the current POC gas production process control mode, there are many types of on-site measure well controllers, and the failure rate of controllers is relatively high.
- (2)
- Frequent data packet loss is caused by network latency, leading to delayed algorithm execution.
- (3)
- After multi-level configuration transmission of a large amount of data, data loss and configuration errors exist.
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Mathematical Modeling
- (1)
- Objective 1—Maximize daily gas production: Calculate the cumulative gas production during 24 h or the maximum operational cycle (if exceeding 24 h), then turn it into the equivalent daily production rate using temporal scaling. This converted value constitutes the first fitness component.
- (2)
- Objective 2—Stabilize production with minimized fluctuations: Determine the mean gas production rate over the operative period. Divide the period into n intervals and compute the absolute deviation between each interval’s average rate and the global mean. The fitness component derives from minimizing the average deviation across all intervals: fitness component 2 = 1/(average deviation/minimum observed deviation).
- (3)
- Multi-objective formulation: Implement weighted aggregation using parameter α: composite fitness = α × (total gas production/maximum achievable production) + (1 − α) × (1/(average deviation/minimum deviation)).
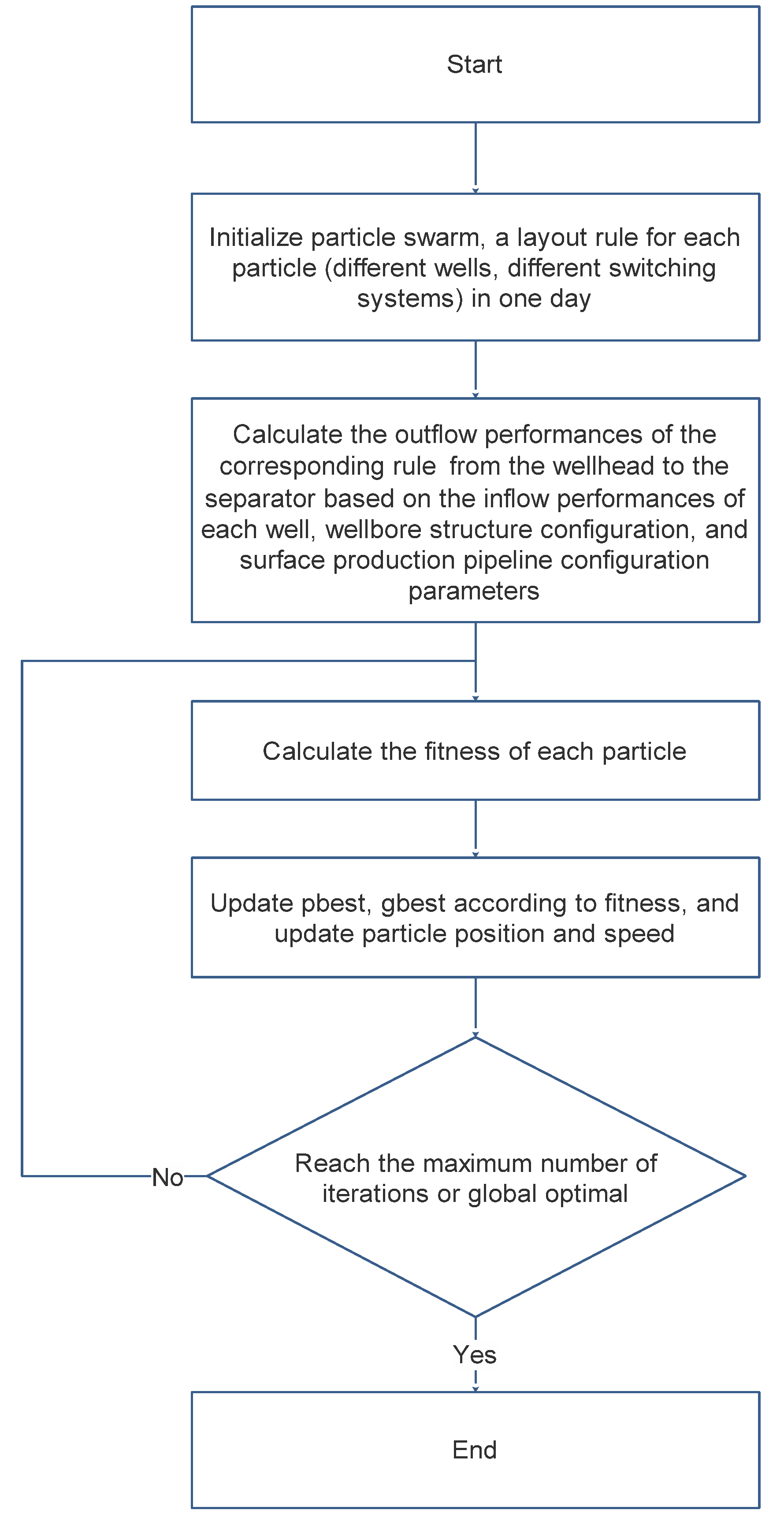
2.2.2. Model Establishment and Solution Method
3. Results
3.1. Gas Production Rates Under Different Well Schedules
3.2. Platform-Wide Optimization
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kannan, S.K.; Boyer, M.; Yuan, G.; Lu, H.; Fai-Yengo, G. Modeling and Optimization of Gas-Assisted Plunger Lift GAPL by a Transient Simulator: A Case Study of a Permian Shale Well. In Proceedings of the SPE Eastern Regional Meeting, Charleston, WV, USA, 15–17 October 2019; SPE: Richardson, TX, USA, 2019. [Google Scholar] [CrossRef]
- Hashmi, G.M.; Hasan, A.R.; Kabir, C.S. Simplified Modeling of Plunger-Lift Assisted Production in Gas Wells. J. Nat. Gas Sci. Eng. 2018, 52, 454–460. [Google Scholar] [CrossRef]
- Mei, H.P.; Li, K.; Hao, J.; Gao, Y.; Wang, Q. Optimization of Plunger Lift System and Intelligent Operation in Gas Fields. Petrochem. Ind. Appl. 2020, 39, 111–113. [Google Scholar]
- Wang, X.H.; He, T.H.; Tu, L.H.; Ai, B.B.; Zhang, L.; Wang, Y.H. Optimization of Production Systems for Plunger-Lift-Assisted Gas Wells. Inn. Mong. Petrochem. Ind. 2019, 45, 55–58. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Z.; Tang, T.; Li, Q.; Jin, S.; Sun, Y.; Liu, H. Research on Production Pattern Optimization of Intermittent Wels. Chem. Technol. Fuels Oils 2021, 57, 133–142. [Google Scholar] [CrossRef]
- Nandola, N.N.; Kaisare, N.S.; Gupta, A. Online Optimization for a Plunger Lift Process in Shale Gas Wells. Comput. Chem. Eng. 2018, 108, 89–97. [Google Scholar] [CrossRef]
- Lin, P.; Bai, P.; Wang, Y.J.; Wang, Y.X.; Wang, X.; Wang, P.H. Research on Intelligent Optimization of Plunger-Lift Wells. Inn. Mong. Petrochem. Ind. 2021, 47, 46–49. [Google Scholar] [CrossRef]
- Liu, P.; Chen, M.; He, Z.; Luo, W.; Miao, S. Study on a Gas Plunger Lift Model for Shale Gas Wells and Its Effective Application. FDMP-Fluid Dyn. Mater. Process. 2022, 18, 933–955. [Google Scholar] [CrossRef]
- Miao, S.; Liu, X.; Feng, X.; Shi, H.; Luo, W.; Liu, P. A Dynamic Plunger Lift Model for Shale Gas Wells. FDMP-Fluid Dyn. Mater. Process. 2023, 19, 1735–1751. [Google Scholar] [CrossRef]
- Liu, M.P.; Gao, X.L.; Li, D.L.; Hong, L.; Huang, S. Study on Backpressure Effects in Plunger-Lift Drainage Gas Recovery Technology. Inn. Mong. Petrochem. Ind. 2021, 47, 75–77. [Google Scholar] [CrossRef]
- Wang, L.; Yang, S.Z.; Jin, J.S.; Zhang, Z.X.; Hao, S. Analysis of Intermittent Gas Production Constraints in Low-Pressure Gas Wells and Countermeasures. Inn. Mong. Petrochem. Ind. 2018, 44, 117–120. [Google Scholar] [CrossRef]
- Liu, E.B.; Li, C.J.; Yang, Y. Optimal Energy Consumption Analysis of Natural Gas Pipeline. Sci. World J. 2014, 2014, 506138. [Google Scholar] [CrossRef] [PubMed]
- Liu, E.B.; Kuang, J.C.; Peng, S.B.; Liu, Y.T. Transient Operation Optimization Technology of Gas Transmission Pipeline: A Case Study of West-East Gas Transmission Pipeline. IEEE Access 2019, 7, 112131–112141. [Google Scholar] [CrossRef]
- Shah, S.; Khan, H.R.; Rahman, A.; Butt, S. Production Optimization in Well-6 of Habiganj Gas Field, Bangladesh: A Prospective Application of Nodal Analysis Approach. J. Pet. Explor. Prod. Technol. 2020, 10, 3557–3568. [Google Scholar] [CrossRef]
- Hoffmann, A. Short-Term Model-Based Production Optimization for a Gas Field in North Africa. J. Model. Optim. 2018, 10, 65–80. [Google Scholar] [CrossRef][Green Version]
- Zheng, D.M.; He, S.H.; Xu, W.J.; Zhang, X.J. Intelligent Plunger-Lift Technology in Daniudi Gas Field. Well Test. 2020, 29, 19–26. [Google Scholar] [CrossRef]
- Liu, H.M.; Li, M.; Liu, Q.P.; Zhang, L.Y. Research and Application of Plunger-Lift Technology in Fuling Shale Gas Field. Pet. Drill. Tech. 2020, 48, 102–107. [Google Scholar] [CrossRef]
- Li, J.L.; Liao, R.Q.; Luo, W.; Han, Y. Study on Optimal Gas Distribution for Continuous Gas Lift Well Groups. J. Pet. Gas 2016, 38, 8. [Google Scholar] [CrossRef]
- Wang, Q.R.; Wang, J.X.; Li, M.W.; Yu, F.; Cai, D.G.; Zeng, L.J. Influencing Factors and Regime Optimization Methods of Plunger Technology in Shale Gas Wells. J. Nat. Gas Technol. Econ. 2023, 17, 36–41. [Google Scholar]
- Du, L.; Wang, C.K. Research on Plunger Gas Lift Technology for Water Drainage and Gas Production. Liaoning Chem. Ind. 2022, 51, 860–862. [Google Scholar] [CrossRef]
- Zhang, C.; Jin, D.Q.; Li, S.H.; Zhang, J.Z. Application Research on New Plunger Gas Lift System in Sulige Gas Field. Drill. Prod. Technol. 2017, 40, 74–76+10. [Google Scholar] [CrossRef]







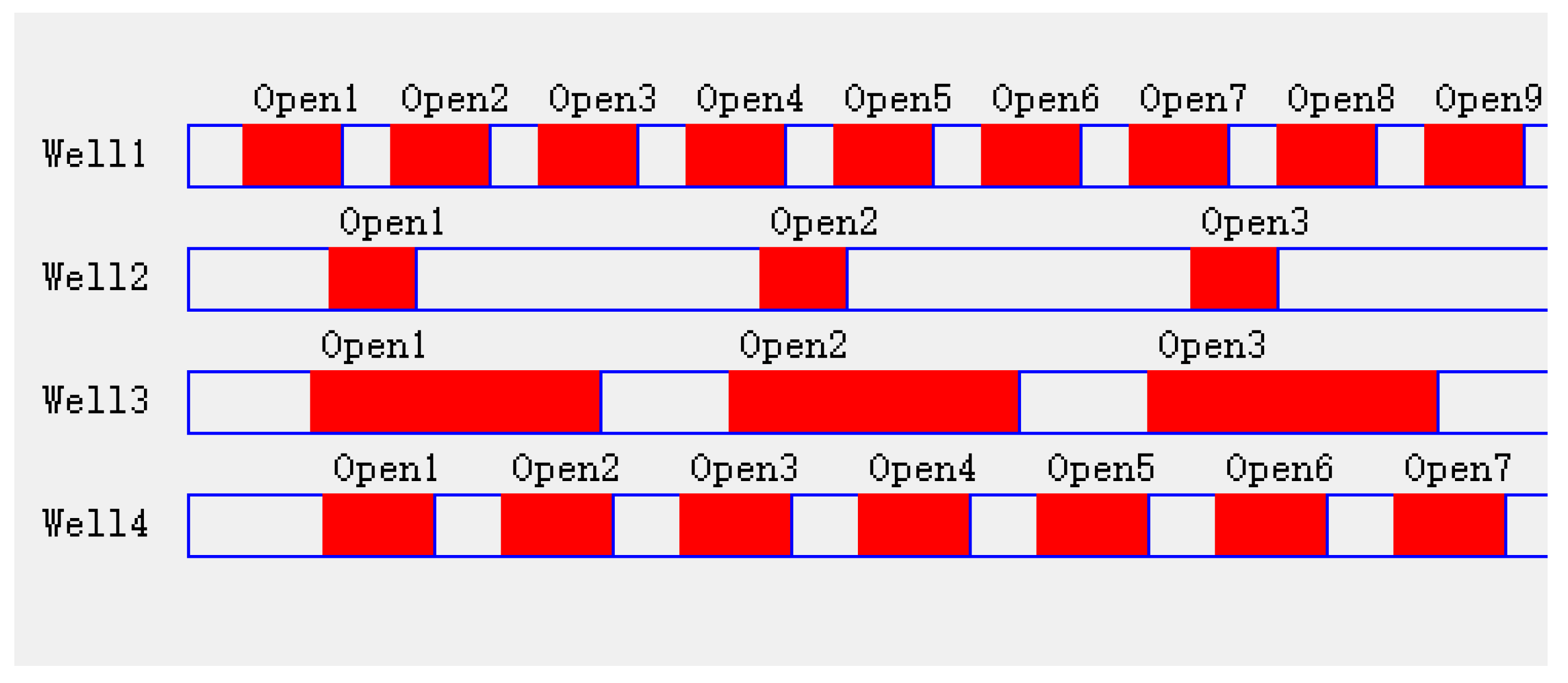
| Well ID | Well 1 | Well 2 | Well 3 | Well 4 | |
|---|---|---|---|---|---|
| Formation Pressure * | MPa | 10 | 10 | 10 | 10 |
| Gas Productivity Index * | 104 m3/d/MPa2 | 0.01043 | 0.0263 | 0.0133 | 0.029 |
| Liquid Productivity Index/WGR * | m3/d/MPa | 0.0761 | 0.2849 | 0.1818 | 0.18 |
| Tubing Inner Diameter | mm | 50.6 | 50.6 | 50.6 | 50.6 |
| Tubing Depth | m | 3500 | 3500 | 3500 | 3500 |
| Casing Inner Diameter | mm | 114.3 | 114.3 | 114.3 | 114.3 |
| Reservoir Temperature | °C | 100 | 100 | 100 | 100 |
| Surface Temperature | °C | 15 | 15 | 15 | 15 |
| Formation Water Specific Gravity | - | 1.02 | 1.02 | 1.02 | 1.02 |
| Gas Specific Gravity | - | 0.7 | 0.7 | 0.7 | 0.7 |
| Water Production | m3/d | 0.5 | 1 | 1 | 1 |
| Gas Production | 104 m3/d | 0.928 | 1.525 | 1.063 | 2.265 |
| Plunger Mass | kg | 3.3 | 3.3 | 3.3 | 3.3 |
| Anchor Depth(TVD) | m | 3300/3250 | 3200/3220 | 3250/3280 | 3280/3340 |
| Current Operating Schedule | min | Afterflow 25 min Close 60 min | Afterflow 10 min Close 55 min | Afterflow 50 min Close 65 min | Afterflow 230 min Close 60 min |
| Plunger Rise Time | min | 150 | 90 | 90 | 120 |
| Casing Pressure Before Opening | MPa | 2.79 | 4.36 | 2.89 | 3.7 |
| Casing Pressure Before Shut-in | MPa | 2.35 | 3.7 | 2.69 | 3.39 |
| Tubing Pressure Before Opening | MPa | 2.48 | 3.62 | 2.53 | 3.63 |
| Tubing Pressure Before Shut-in | MPa | 1.4 | 1.28 | 1.22 | 1.83 |
| Pipeline Delivery Pressure | MPa | 1.59 | 1.6 | 1.6 | 1.6 |
| Well ID | Cycle Time (min) | Opening Duration (min) | Shut-in Duration (min) | Gas Production Rate (104 m3/d) | Liquid Production Rate (m3/d) | Notes |
|---|---|---|---|---|---|---|
| Well 1 | 235 | 175 | 60 | 9272 | 0.53 | Current system |
| 235 | 155 | 80 | 9355 | 0.53 | ||
| 235 | 135 | 100 | 9763 | 0.55 | ||
| 235 | 115 | 120 | 9054 | 0.51 | ||
| 215 | 155 | 60 | 9071 | 0.52 | ||
| 215 | 135 | 80 | 9175 | 0.52 | ||
| 215 | 115 | 100 | 9247 | 0.52 | ||
| 195 | 135 | 60 | 9175 | 0.52 | ||
| 195 | 115 | 80 | 9116 | 0.52 | ||
| 195 | 95 | 100 | 9004 | 0.51 | ||
| Well 2 | 155 | 100 | 55 | 16761 | 1.2 | Current system |
| 155 | 90 | 65 | 17,741 | 1.26 | ||
| 155 | 70 | 85 | 16,729 | 1.17 | ||
| 175 | 120 | 55 | 15,066 | 1.07 | ||
| 175 | 100 | 75 | 17,392 | 1.23 | ||
| 175 | 80 | 95 | 16,366 | 1.14 | ||
| 135 | 80 | 55 | 16,028 | 1.14 | ||
| 135 | 70 | 65 | 17,658 | 1.25 | ||
| 135 | 60 | 75 | 17,108 | 1.2 | ||
| 195 | 140 | 55 | 15,664 | 1.11 | ||
| 195 | 120 | 75 | 17,462 | 1.24 | ||
| 195 | 100 | 95 | 16,562 | 1.16 | ||
| Well 3 | 205 | 140 | 65 | 10630 | 1.02 | Current system |
| 205 | 120 | 85 | 10,587 | 1.02 | ||
| 205 | 130 | 75 | 10,680 | 1.03 | ||
| 205 | 150 | 55 | 10,666 | 1.02 | ||
| 205 | 100 | 105 | 10,338 | 0.98 | ||
| 225 | 160 | 65 | 10,617 | 1.02 | ||
| 225 | 140 | 85 | 10,577 | 1.01 | ||
| 225 | 120 | 105 | 10,358 | 0.98 | ||
| 185 | 120 | 65 | 10,774 | 1.04 | ||
| 185 | 100 | 85 | 10,584 | 1.01 | ||
| 185 | 80 | 105 | 10,302 | 0.98 | ||
| 165 | 100 | 65 | 10,805 | 1.05 | ||
| 145 | 80 | 65 | 10,806 | 1.05 | ||
| 125 | 60 | 65 | 10,777 | 1.04 | ||
| 160 | 80 | 80 | 10,628 | 1.02 | ||
| Well 4 | 410 | 350 | 60 | 24200 | 1.09 | Current system |
| 410 | 330 | 80 | 24,130 | 1.09 | ||
| 410 | 300 | 110 | 23,454 | 1.05 | ||
| 460 | 400 | 60 | 24,002 | 1.08 | ||
| 460 | 380 | 80 | 24,010 | 1.09 | ||
| 460 | 360 | 100 | 23,668 | 1.07 | ||
| 360 | 300 | 60 | 24,497 | 1.12 | ||
| 360 | 280 | 80 | 24,209 | 1.1 | ||
| 360 | 260 | 100 | 23,725 | 1.07 |
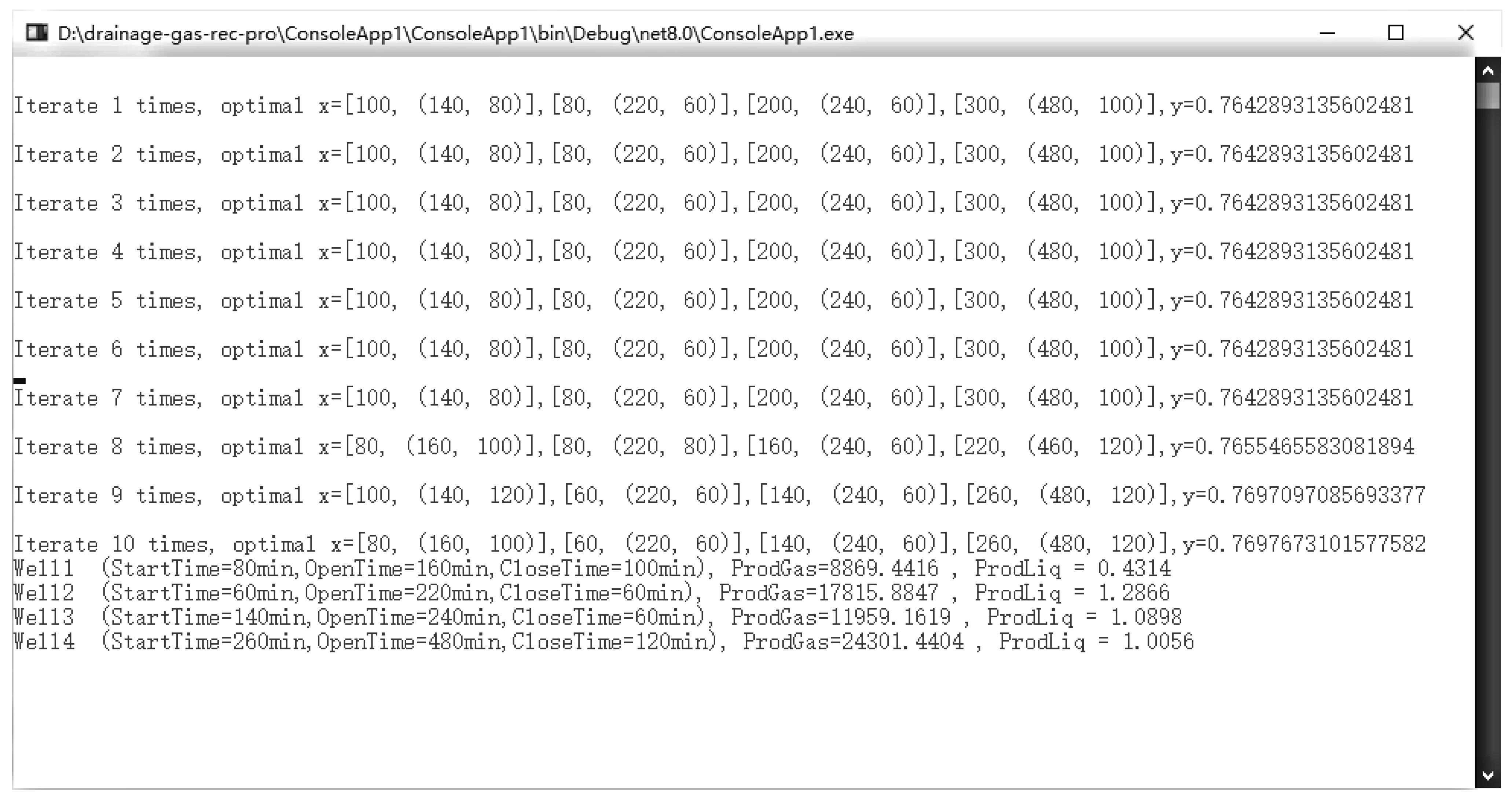
| On-Site Production of Wells (m3/d) | The Output of the Software Correction Simulation (m3/d) | Output After Optimizing the Work Schedule (m3/d) | |
|---|---|---|---|
| Well 1 | 8626.53 | 9272 | 9280 |
| Well 2 | 16,966.98 | 16,761 | 15,250 |
| Well 3 | 12,410.17 | 10,630 | 10,630 |
| Well 4 | 24,301.44 | 24,200 | 22,650 |
| Total | 62,305.12 | 60,863 | 57,810 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Wang, Q.; Wang, Y.; Huang, C.; He, T.; Tang, T.; Luo, W. Intelligent Collaborative Optimization Method for Multi-Well Plunger Gas Lifting Process on Platform. Processes 2025, 13, 2534. https://doi.org/10.3390/pr13082534
Yang Z, Wang Q, Wang Y, Huang C, He T, Tang T, Luo W. Intelligent Collaborative Optimization Method for Multi-Well Plunger Gas Lifting Process on Platform. Processes. 2025; 13(8):2534. https://doi.org/10.3390/pr13082534
Chicago/Turabian StyleYang, Zhi, Qingrong Wang, Yunfu Wang, Chencheng Huang, Tianbao He, Tang Tang, and Wei Luo. 2025. "Intelligent Collaborative Optimization Method for Multi-Well Plunger Gas Lifting Process on Platform" Processes 13, no. 8: 2534. https://doi.org/10.3390/pr13082534
APA StyleYang, Z., Wang, Q., Wang, Y., Huang, C., He, T., Tang, T., & Luo, W. (2025). Intelligent Collaborative Optimization Method for Multi-Well Plunger Gas Lifting Process on Platform. Processes, 13(8), 2534. https://doi.org/10.3390/pr13082534






