A Coordinated Operation Optimization Model for Multiple Microgrids and Shared Energy Storage Based on Asymmetric Bargaining Negotiations
Abstract
1. Introduction
2. Methods
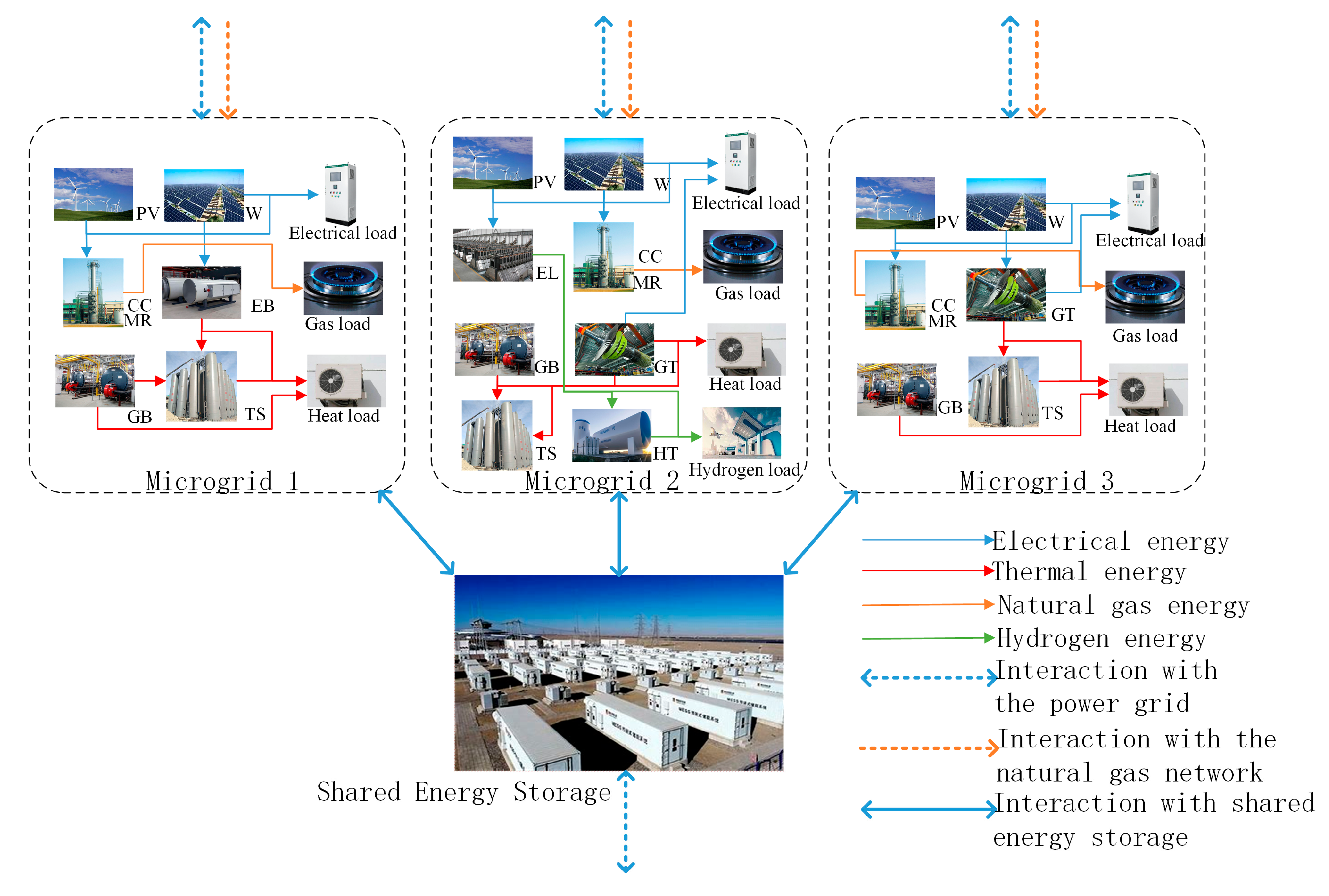
2.1. Cooperative Operating Architecture
2.2. Microgrid and SES Operation Optimization Model
2.2.1. Microgrid Operation Optimization Model
- (1)
- Objective function
- (2)
- Operating constraints
2.2.2. SES Operation Optimization Model
- (1)
- Objective function
- (2)
- Operating constraints
2.3. Multiple Microgrids and SES Coordinated Optimization Model
2.3.1. Symmetric Bargaining Model
2.3.2. Asymmetric Bargaining Model
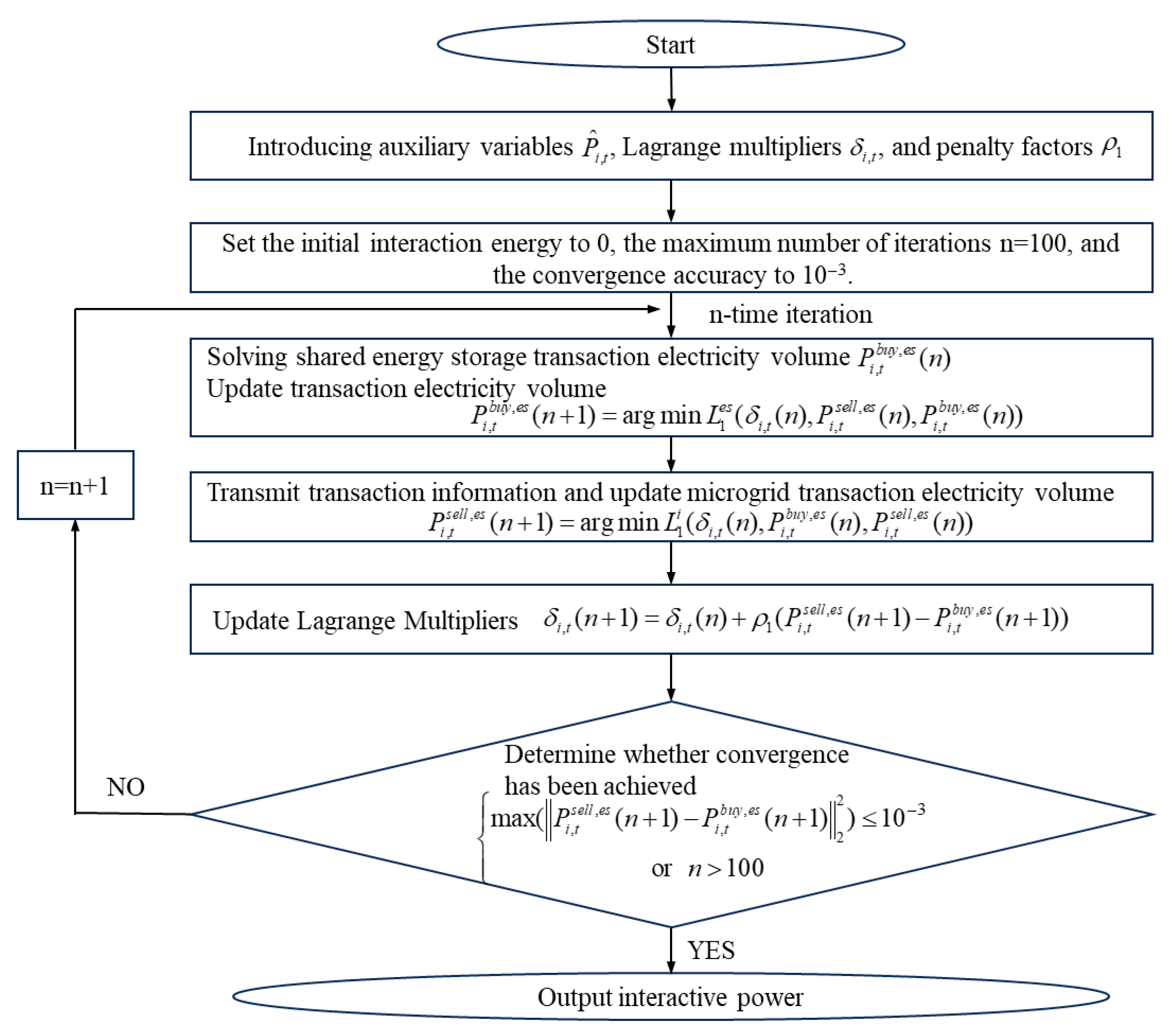
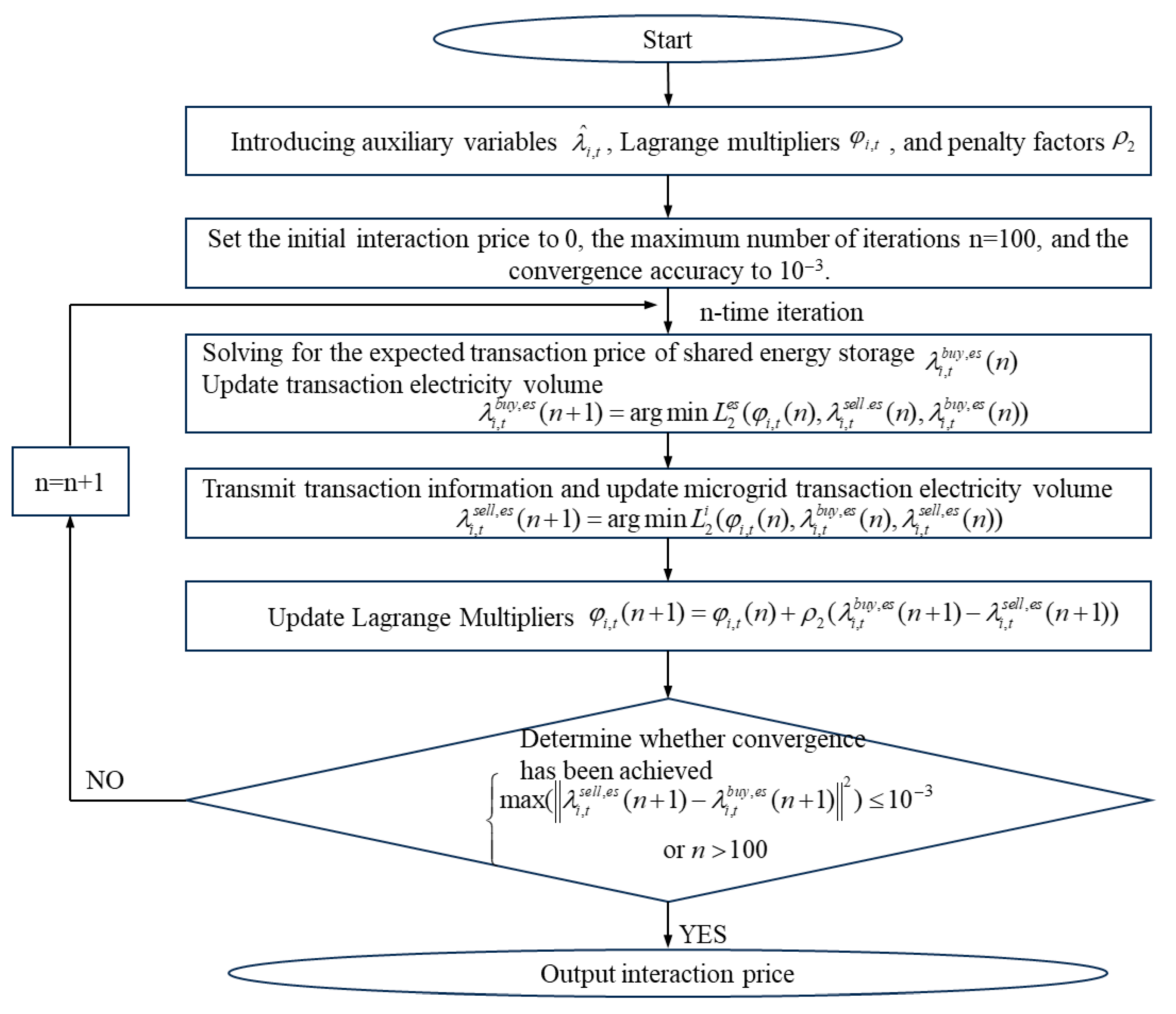
2.3.3. Model Solution
- (1)
- Solutions to the problem of maximizing alliance profits
- (2)
- Solutions to the problem of electricity price negotiations
2.4. Excess Profit Distribution Satisfaction Model
3. Results
3.1. Basic Data
3.2. Results Analysis
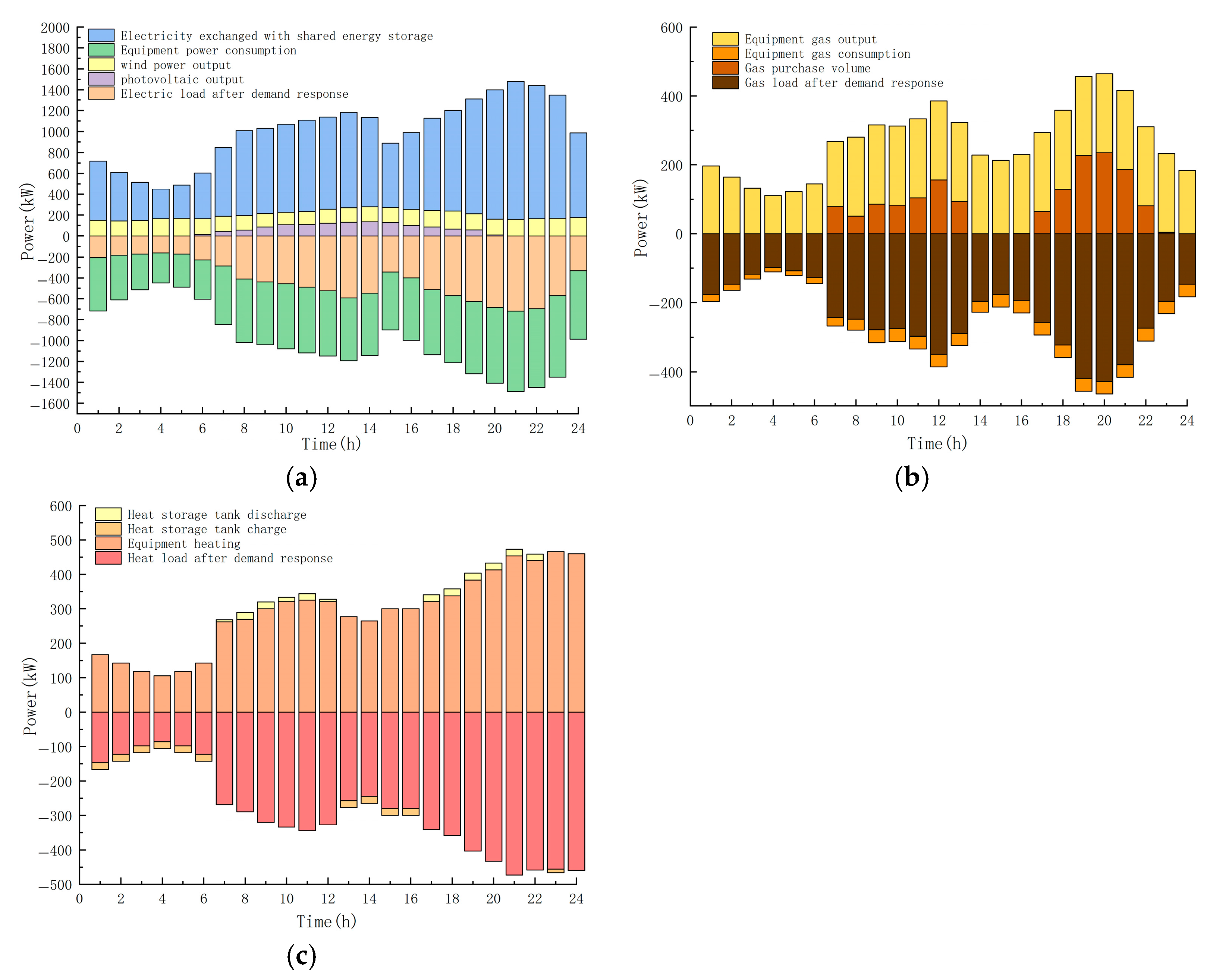
3.2.1. Operation Results
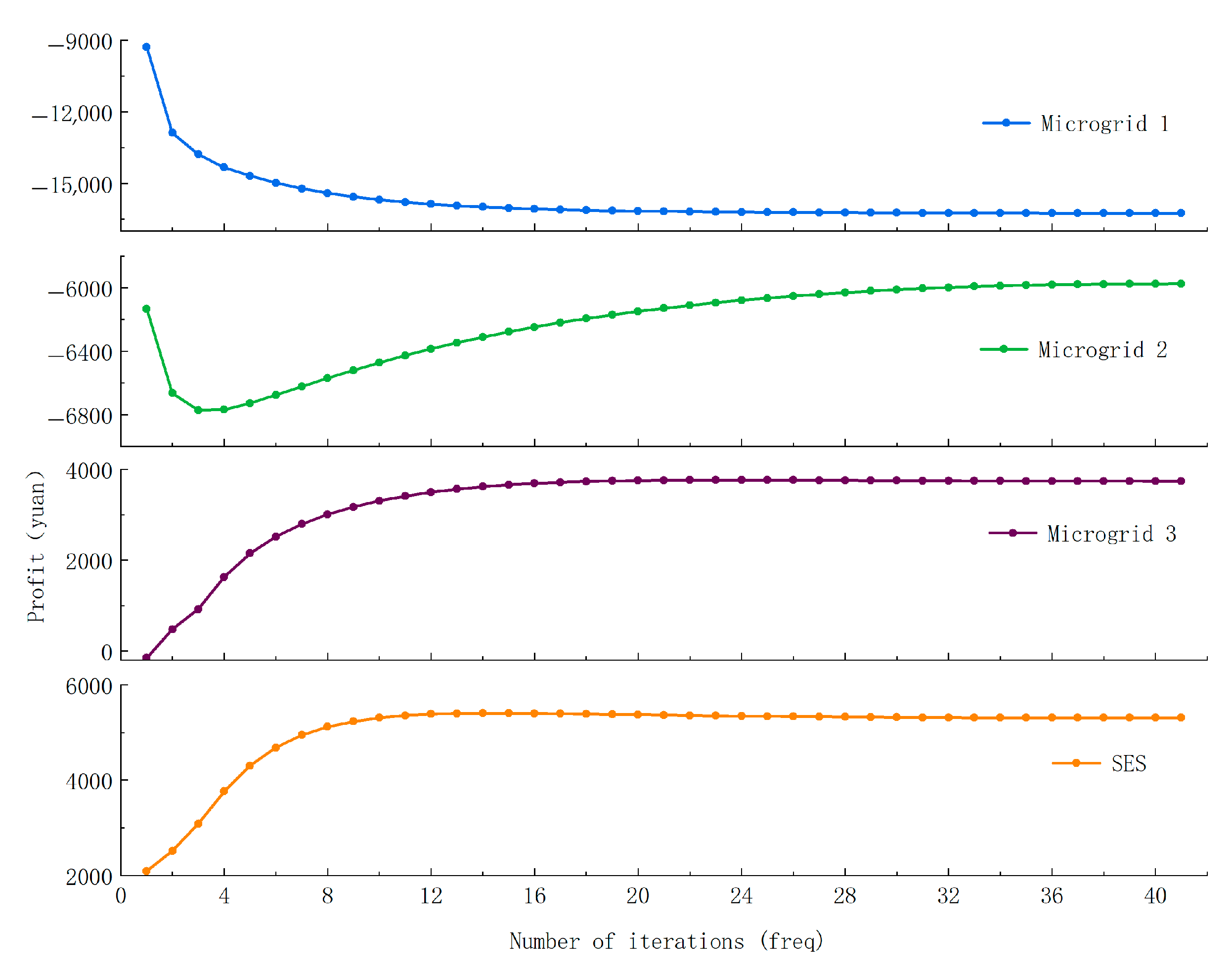
3.2.2. Algorithm Convergence
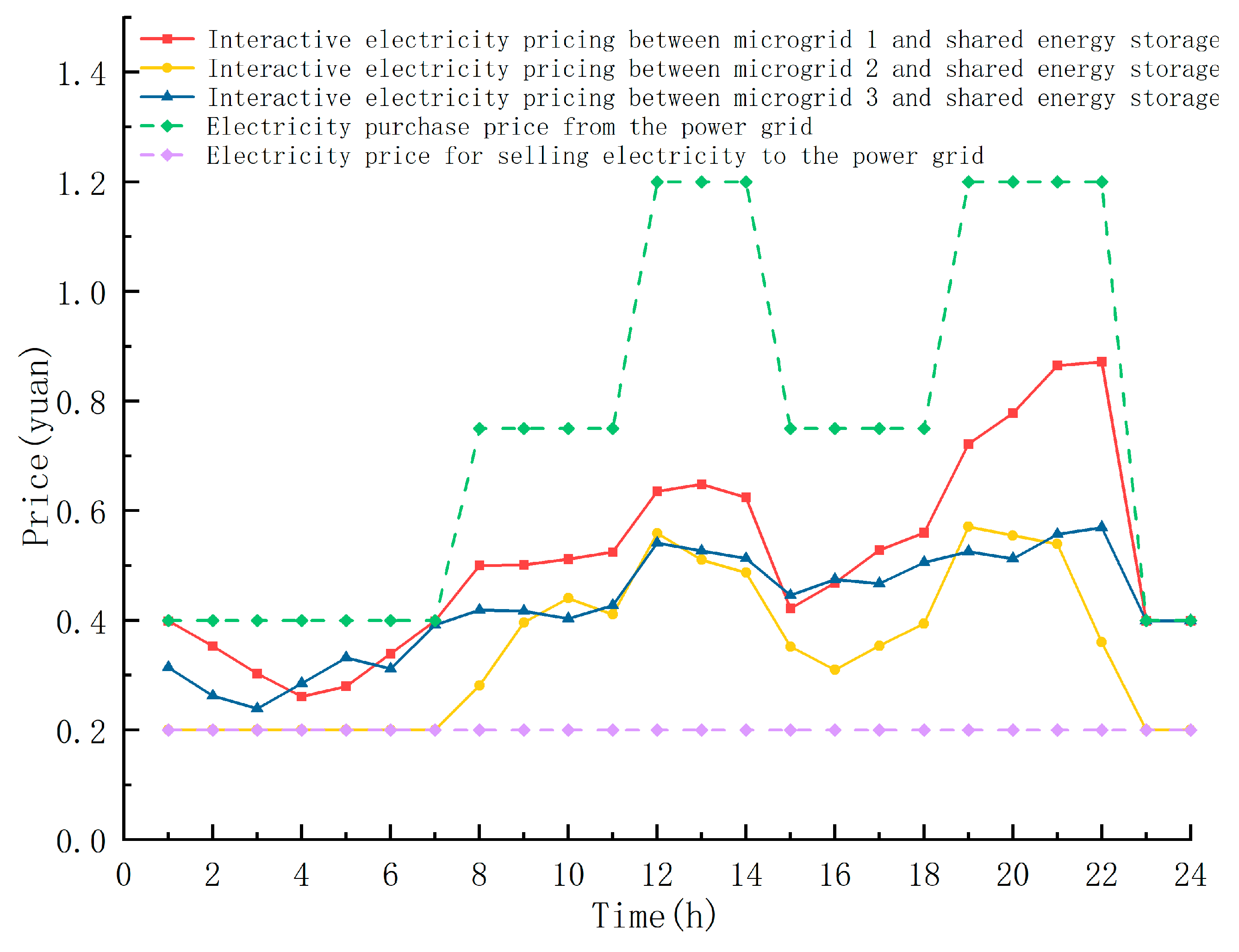
3.2.3. Electricity Price Negotiation Comparison
4. Discussion
- (1)
- After group coordination, SES interacts with the PG and various microgrids to achieve dynamic responses to the differentiated needs of microgrids, promoting the local consumption of new energy in the microgrids and effectively improving the operational efficiency of all entities.
- (2)
- Asymmetric pricing based on energy contribution enables the reasonable allocation of cooperative benefits, maintaining the enthusiasm of all entities to participate in group cooperation. Microgrids with higher renewable energy generation can obtain higher benefits during the allocation process, thereby encouraging microgrid entities to further expand their installed renewable energy capacity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lv, R.; Huang, Z.; Wei, Y.; Li, Y. Research on master-slave game based optimal scheduling of multi-MG shared energy storage. Mod. Electron. Tech. 2024, 47, 46–50. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C.; Hao, Y. Microgrid Alliance Two-stage Optimal Scheduling Considering Demand Response and Shared Energy Storage. Smart Power 2024, 52, 48–55. [Google Scholar]
- Yu, S.; Zhou, S.; Qin, J. Layout optimization of China’s power transmission lines for renewable power integration considering flexible resources and grid stability. Int. J. Electr. Power Energy Syst. 2022, 135, 107507. [Google Scholar] [CrossRef]
- Dai, R.; Esmaeilbeigi, R.; Charkhgard, H. The utilization of shared energy storage in energy systems: A comprehensive review. IEEE Trans. Smart Grid 2021, 12, 3163–3174. [Google Scholar] [CrossRef]
- Cao, M.; Xie, C.; Li, F.; Yin, C.; Zhang, G.; Gao, Y. Co-optimized Operation of Multi-integrated Energy Microgrids-shared Energy Storage Plants Based on Two-stage Robustness. Power Syst. Technol. 2024, 48, 4493–4502. [Google Scholar] [CrossRef]
- Zhao, S.; Liu, Y.; Xu, J.; Peng, C.; Yan, L.; Collaborative Scheduling Strategy for Islanded Oilfield Microgrid Clusters Considering Shared Energy Storage. South. Power Syst. Technol. 2025, pp. 1–14. Available online: http://kns.cnki.net/kcms/detail/44.1643.TK.20250422.0650.010.html (accessed on 6 August 2025).
- Yuan, B.; Liu, Z.; Wei, M.; Yang, C.; Xi, P. An Optimization Study on the P2P Game for the Shared Energy Storage Joint Microgrid Cluster Based on IGDT. Power Syst. Clean Energy 2024, 40, 20–29. [Google Scholar]
- Ge, S.; Cheng, X.; Liu, H.; Li, J.; Li, J. Market Design of P2P Electricity Carbon Coupling Transaction Among Multi-microgrids in a Zone. High Volt. Eng. 2023, 49, 1341–1349. [Google Scholar] [CrossRef]
- Yao, L.; Wang, W.; Lin, H.; Liu, J. Day-ahead Optimal Scheduling of Wind-powered Microgrid Cluster with Source-storage Collaboration Taking into Account Low-carbon Economic Operation. J. Chin. Soc. Power Eng. 2024, 44, 462–474. [Google Scholar] [CrossRef]
- Ma, R.; Xia, X.; Yan, Z.; Zhang, S.; Zhu, D. The Optimization Strategy for Joint Scheduling of Microgrids Cluster and Shared Energy Storage Based on Bi-Level Cooperation Game. Power Syst. Clean Energy 2025, 41, 133–139. [Google Scholar]
- Zhou, H.; Chang, X.; Chang, C. Dual-Layer Optimization of Configuration and Dispatch for Comprehensive Energy Multi-Microgrid Configuration with Shared Energy Storage. China Electr. Equip. Ind. 2025, 3, 9–18. [Google Scholar]
- Li, Z.; Zhang, C.; Wang, R.; Zhang, Z.; Deng, L.; Optimization Configuration and Benefit Analysis of Hydrogen Shared Energy Storage in Integrated Energy Microgrid Cluster. South. Power Syst. Technol. 2025, pp. 1–13. Available online: http://kns.cnki.net/kcms/detail/44.1643.TK.20250328.1133.009.html (accessed on 6 August 2025).
- Tian, Y.; Liang, N.; Xu, H.; Lu, J.; Shang, Y.; Luo, S. Optimal scheduling of electricity-carbon joint multilateral trading in regional power grid based on Nash negotiation. Electr. Power Eng. Technol. 2025, 44, 108–119. [Google Scholar]
- Lu, J.; Liang, N.; Xu, H.; Xu, Y.; Tian, Y.; Shang, Y. Coordinated Optimal Dispatch of Multiple Integrated Energy Systems Under Dynamic Carbon-Green Certificate Trading Interaction Mechanism. Autom. Electr. Power Syst. 2025, 49, 52–60. [Google Scholar]
- Gong, J.; Dong, J. An Independent Energy Storage Electricity Insurance Service Model Based on Asymmetric Nash Bargaining Game. Mod. Electr. Power 2025, 1–12. [Google Scholar] [CrossRef]
- Wang, P.; Yu, Y.; Zhao, Y.; Xin, L.; Wang, H. Optimization Strategy for Collaborative Market Participation of Photovoltaic Prosumers and Shared Energy Storage Based on Nash Bargaining. Power Syst. Technol. 2025, 49, 642–652. [Google Scholar] [CrossRef]
- Zheng, J.; He, S.; Wang, W.; Yuan, Z.; Cheng, Z.; Fan, X. Distributionally Robust Thermoelectricity Trading Optimization For Multiple-Integrated Energy Service Providers Based on Asymmetric Nash Bargaining. Acta Energiae Solaris Sin. 2024, 45, 121–133. [Google Scholar] [CrossRef]
- Sun, J.; Ke, D.; Xu, J.; Liao, S.; Sun, Y. Multi-energy Cooperative Optimization and Profit Distribution Strategy in Low-grade Heat Source Area Considering the Flexibility of Heat Pump. High Volt. Eng. 2025, 51, 158–168. [Google Scholar] [CrossRef]
- Jiang, D.; Guo, Y.; Liang, K.; Niu, J.; Shi, K.; Yang, C. Cooperative Game of Multi-Power-Gas Interconnection System Considering New Energy Consumption and Low Carbon Emission. Acta Energiae Solaris Sin. 2023, 44, 58–67. [Google Scholar] [CrossRef]
- Yu, H.; Shen, Y.; Lin, S.; Li, D.; Xu, L. Optimization Strategies for Energy Sharing in Commercial Building Clusters Considering User Psychology. Power Syst. Technol. 2022, 46, 4423–4436. [Google Scholar] [CrossRef]
- Ju, L.; Liu, L.; Han, Y.; Yang, S.; Li, G.; Lu, X.; Liu, Y.; Qiao, H. Robust Multi-objective optimal dispatching model for a novel island micro energy grid incorporating biomass waste energy conversion system, desalination and power-to-hydrogen devices. Appl. Energy 2023, 343, 121176. [Google Scholar] [CrossRef]
- Wu, J.; Lou, P.; Guan, M.; Huang, Y.; Zhang, Y.; Cao, Y. Operation Optimization Strategy of Multi-microgrids Energy Sharing Based on Asymmetric Nash Bargaining. Power Syst. Technol. 2022, 46, 2711–2723. [Google Scholar] [CrossRef]
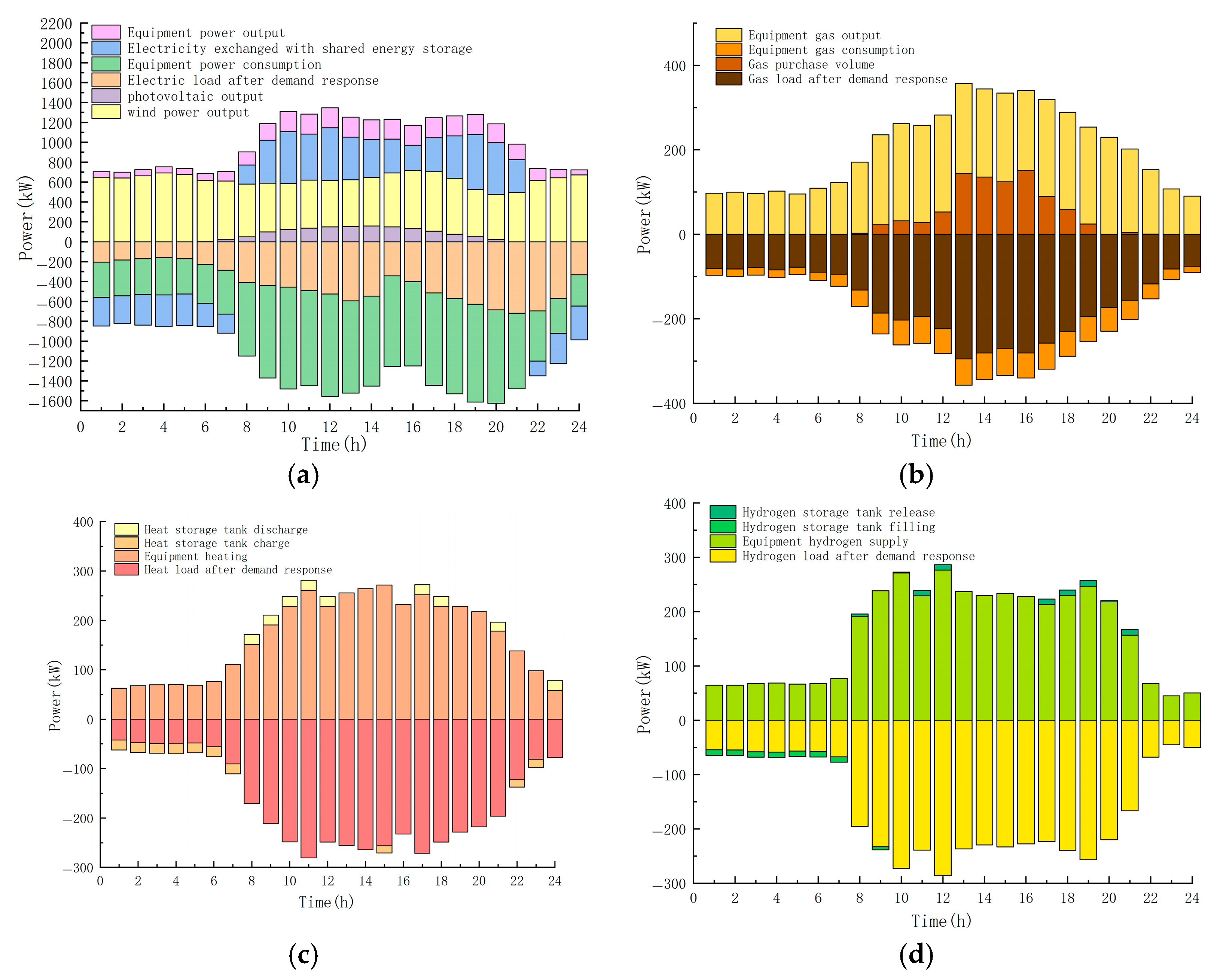
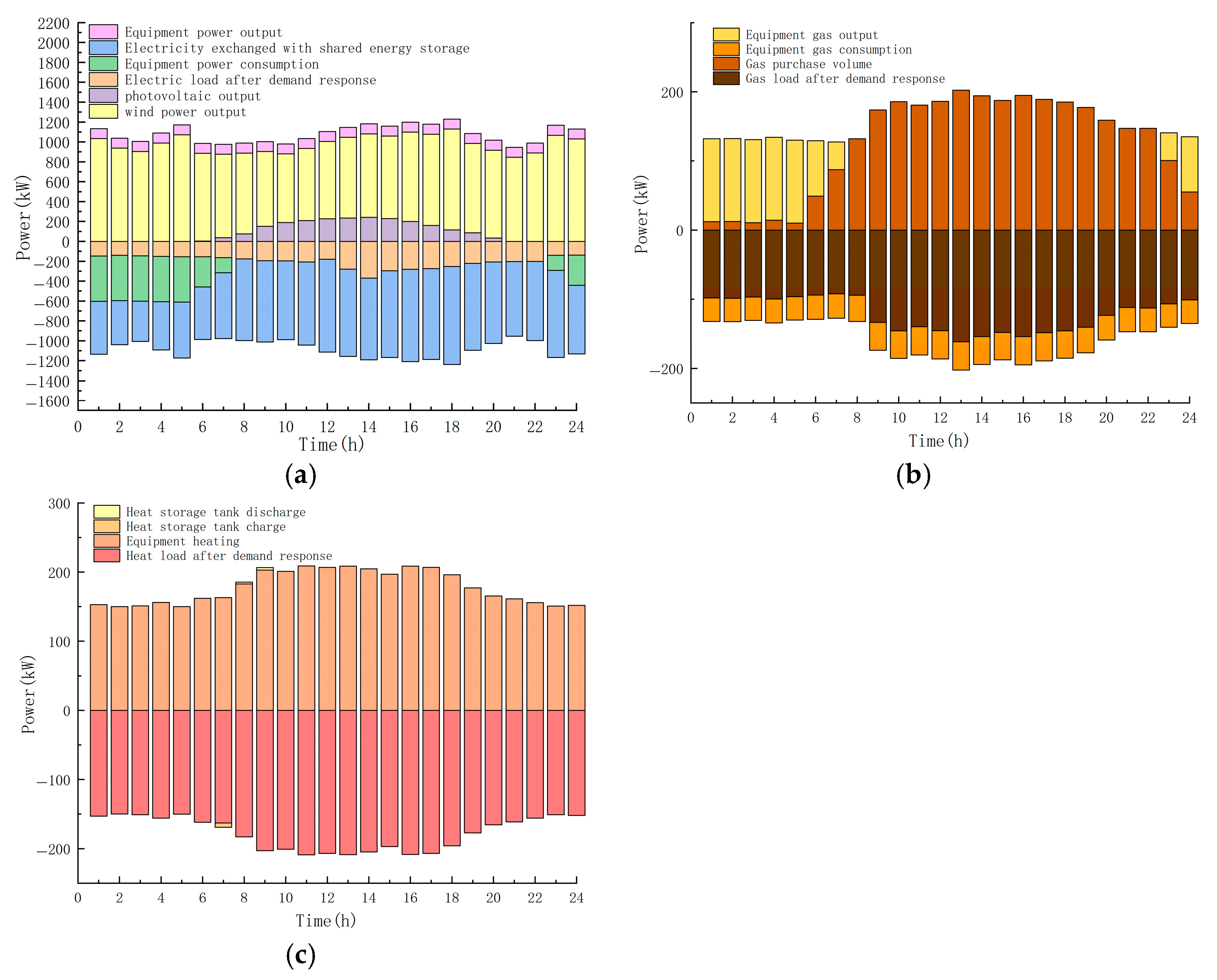
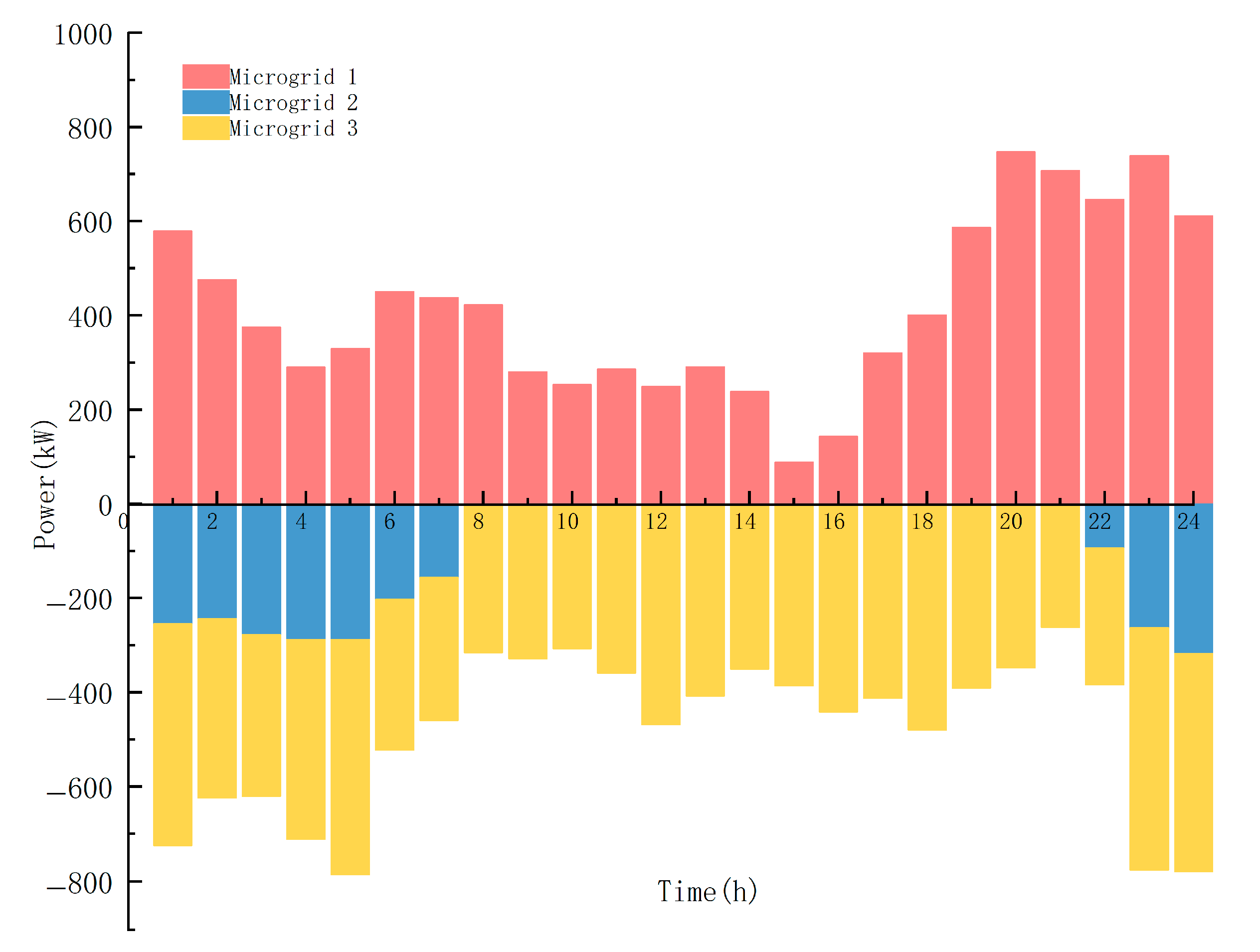
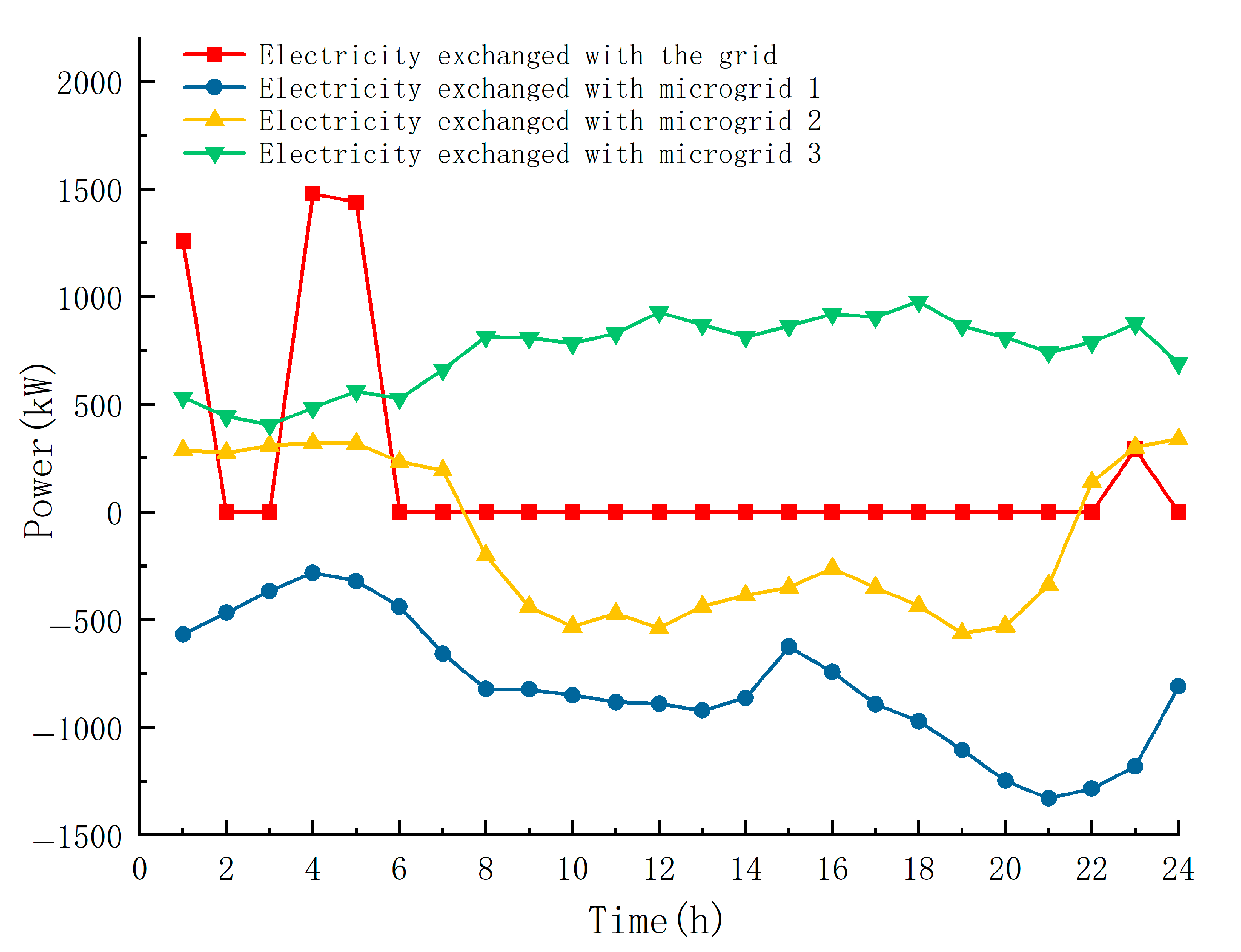
| Equipment | Microgrid 1 | Microgrid 2 | Microgrid 3 | Operating Costs |
|---|---|---|---|---|
| WP | 400 kW | 1000 kW | 1800 kW | 0.013 yuan/kW |
| PV | 400 kW | 400 kW | 800 kW | 0.014 yuan/kW |
| GT | / | 500 kW | 400 kW | 0.053 yuan/kW |
| GB | 400 kW | 500 kW | 400 kW | 0.037 yuan/kW |
| EB | 300 kW | / | / | 0.046 yuan/kW |
| EL | / | 500 kW | / | 0.125 yuan/m3 |
| CC | 300 m3 | 500 m3 | 500 m3 | 0.015 yuan/m3 |
| MR | 300 m3 | 500 m3 | 500 m3 | 0.141 yuan/m3 |
| HT | / | 100 m3 | / | 0.012 yuan/m3 |
| TS | 200 kW | 200 kW | 200 kW | 0.018 yuan/kW |
| Category | Time Period | Price |
|---|---|---|
| Distribution network electricity sales price | 23:00–07:00 | 0.4 |
| 08:00–11:00, 15:00–18:00 | 0.75 | |
| 12:00–14:00, 19:00–22:00 | 1.2 | |
| Distribution network electricity purchase price | All day | 0.2 |
| Natural gas price | All day | 1.8 |
| Carbon emission factor | All day | 0.047 |
| Shiftable load compensation coefficient | All day | 0.2 |
| Reducible load compensation factor | All day | 0.35 |
| Increasable load compensation coefficient | All day | 0.25 |
| Scenario | Microgrid 1 (Yuan) | Microgrid 2 (Yuan) | Microgrid 3 (Yuan) | SES (Yuan) |
|---|---|---|---|---|
| non-cooperative operation | −17,454.76 | −6823.58 | 468.52 | / |
| symmetric cooperative bargaining | −14,796.58 | −4149.958 | 3108.33 | 2669.20 |
| asymmetric cooperative bargaining | −16,247.67 | −5975.345 | 3742.65 | 5307.68 |
| Scenario | Microgrid 1 | Microgrid 2 | Microgrid 3 | SES |
|---|---|---|---|---|
| symmetric cooperative bargaining | 0.249809883 | 0.251261088 | 0.248083511 | 0.250845518 |
| asymmetric cooperative bargaining | 0.113478864 | 0.079742807 | 0.307801866 | 0.498976463 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Tan, Z.; Zhou, X.; Li, J.; Hu, Y.; Wu, H.; Ju, L. A Coordinated Operation Optimization Model for Multiple Microgrids and Shared Energy Storage Based on Asymmetric Bargaining Negotiations. Processes 2025, 13, 2514. https://doi.org/10.3390/pr13082514
Wang Y, Tan Z, Zhou X, Li J, Hu Y, Wu H, Ju L. A Coordinated Operation Optimization Model for Multiple Microgrids and Shared Energy Storage Based on Asymmetric Bargaining Negotiations. Processes. 2025; 13(8):2514. https://doi.org/10.3390/pr13082514
Chicago/Turabian StyleWang, Yao, Zhongfu Tan, Xiaotong Zhou, Jia Li, Yingying Hu, Huimin Wu, and Liwei Ju. 2025. "A Coordinated Operation Optimization Model for Multiple Microgrids and Shared Energy Storage Based on Asymmetric Bargaining Negotiations" Processes 13, no. 8: 2514. https://doi.org/10.3390/pr13082514
APA StyleWang, Y., Tan, Z., Zhou, X., Li, J., Hu, Y., Wu, H., & Ju, L. (2025). A Coordinated Operation Optimization Model for Multiple Microgrids and Shared Energy Storage Based on Asymmetric Bargaining Negotiations. Processes, 13(8), 2514. https://doi.org/10.3390/pr13082514





