Abstract
This study proposes a MPL (microporous layer)–GDL (gas diffusion layer) microstructure reconstruction method based on a novel random reconstruction algorithm. Then the Shan–Chen multi-component and multi-phase lattice Boltzmann method (SC-LBM) is used to systematically describe the influence of different contact angle distributions on the drainage characteristics of the GDL of proton exchange membrane fuel cells (PEMFCs). Meanwhile, the breakthrough time of liquid water, steady-state time, and liquid water saturation are compared. The results show that with the increase in contact angle, the time for the first droplet breakthrough and the steady-state time are significantly shortened, and the saturation of liquid water gradually decreases at the steady state, indicating that increasing hydrophobicity can effectively improve the drainage capacity of the GDL. Several double-gradient and three-gradient contact angle distribution schemes are studied, and it is found that the gradient structure with increasing contact angles along the direction of water flow will lead to prolonged steady-state time and elevated water saturation, which is not conducive to drainage. This study analyzes the drainage process under different wettability gradients considering aspects such as the droplet morphology evolution, flow path, and water distribution mechanism, clarifying the key role of gradient design in GDL water management. This work also provides a theoretical basis and design guidelines for wettability optimization in the GDL of PEMFCs.
1. Introduction
To effectively suppress the side effects of fossil fuels, the critical transition to the large-scale employment of renewable energy is unavoidable. However, most renewable energy sources are intermittent and geographically constrained, resulting in temporal and spatial gaps between the energy availability and the consumption of the end-users. To tackle these problems, it is necessary to deploy appropriate energy conversion devices for power grids [1]. Hydrogen energy holds significant potential in the clean energy transition and is an effective pathway for achieving large-scale deep decarbonization. Electrolysis of water for green hydrogen production is not only one of the ways to obtain hydrogen energy but also contributes to addressing the intermittency and variability of renewable energy sources. Under the dual impetus of the “dual-carbon” goals and the development of new energy vehicles, PEMFCs are gradually becoming a key direction in the future transportation field due to their high energy density, zero emissions, and rapid response characteristics [2,3].
However, as the current density increases, if the water produced by the cathode catalytic layer cannot be promptly discharged through the MPL and GDL to the gas channel (GC), it will accumulate in the pores of the GDL, forming a continuous or semi-continuous water film. This will seriously impede the transport of oxygen to the catalytic layer, leading to hypoxia at the catalytic active sites. This further leads to a sharp decline in battery performance and even causes the “flooding” phenomenon [4,5,6,7]. Therefore, optimizing the pore structure and surface wettability of the GDL to achieve efficient drainage is of crucial significance for ensuring the stable operation of PEMFCs at high current densities.
As the core component of PEMFCs, the GDL not only provides channels for electron conduction and gas diffusion in the catalytic layer but also must have appropriate hydrophobicity to ensure the timely discharge of the generated liquid water [8]. If the overall or local hydrophobicity of the GDL is insufficient and the pore size distribution is uneven, liquid water is prone to form water storage zones inside, affecting the channels of reaction gases. In severe cases, it may even lead to stack failure [9]. Research shows that the key factors influencing the drainage performance of the GDL include its structural parameters (such as its porosity, thickness, and fiber diameter) [10,11,12,13,14], compression degree [15], and wettability (contact angle) distribution between the GDL and MPL [16,17,18].
In terms of the structural parameters, Jeon et al. [12] conducted a multiphase LBM simulation study and found that although thickening the GDL could reduce the formation of water droplets on the ribs, it would prolong the breakthrough time of water. Meanwhile, the differences in fiber structure also affect the water saturation and breakthrough position. Gao et al. [19] and Xia et al. [20] respectively expounded the comprehensive influence of the thickness and porosity of the GDL on battery performance through a three-dimensional non-isothermal simulation and three-channel model; moderately increasing the thickness and improving the porosity can promote the uniform distribution of gas and liquid, but too large or too small an increase is not conducive to water discharge. Anyanwu et al. [14] and Yang et al. [13] investigated the influence of the fiber diameter and curvature on droplet permeation and movement behavior based on VOF and random reconstruction methods. They pointed out that small-diameter fibers are conducive to droplet acceleration but may reduce the permeability. An increase in fiber curvature can improve the connectivity, but it will lead to an increase in water saturation. Shangguan et al. [10] compared the water transport characteristics of GDLs with different porosity gradients through a VOF simulation and found that the V-shaped gradient structure had the lowest saturation and the best drainage efficiency. Huang et al. [21] and Ruijie et al. [22] further investigated the influence of the gradient porosity on the current density and pressure drop under different flow channel designs, both demonstrating that the gradient design can significantly enhance the oxygen utilization rate and drainage performance.
At the wettability level, Wang et al. [17] reconstructed the two-dimensional GDL structure with a real PTFE distribution using a random algorithm and investigated the effects of different PTFE contents and gradient distributions on liquid water transport by using a multiphase pseudo-potential LBM. The study found that when the PTFE content was 10 wt%, the effective porosity of the GDL was the highest, and the steady-state time was the shortest. Moreover, a reasonable gradient PTFE distribution can increase the effective porosity rates by 4.2% and 5.8% respectively, and shorten the steady-state time. The change in partition size has no obvious effect on the overall porosity and water saturation, but it can shorten the steady-state time. Zhang et al. [23] reconstructed the microstructure of a TGP-H-060 GDL using micro-CT scanning and simulated the liquid water transport under six PTFE distribution conditions through a multiphase LBM. The results show that the overall high contact angle drainage is the best. In a double-layer structure, the low contact angle of the Lay2-A bottom layer leads to easy water accumulation, the high contact angle of the Lay2-B bottom layer inhibits the invasion of generated water, and the low contact angle of the upper layer enhances drainage. In a three-layer structure, the contact angle of the middle layer dominates the drainage force. Zhou et al. [24] reconstructed the microstructure of a GDL through a random algorithm and considered the compression deformation based on the finite element method. They used a three-dimensional VOF model to simulate the two-phase flow and studied the influence of different PTFE treatment depths and gradients along the thickness direction and the in-plane direction on water management. The research found that for a GDL with a single gradient along the thickness direction, the drainage can be accelerated when the wetness of the fibers close to the CL increases. For the direction within the plane, the “hydrophobic under the flow channel and hydrophilic under the rib” scheme they proposed can take into account the transmission performance of both gas and water. Ira et al. [16] investigated the liquid water transport behavior of mixed wettability GDLs under different hydrophilic fiber ratios and compression ratios by using the GDL model derived from the Shan–Chen pseudo-potential multiphase LBM combined with the random reconstruction algorithm. The research found that hen the hydrophilic fibers in the GDL exceed 10%, discontinuous water clusters will form in the GDL, resulting in an increase in GDL water saturation, an extension of the steady-state time, and an increase in GC droplets. Hydrophilic fibers can promote improved drainage if they are distributed under the flow channel, at the GDL–GC interface, or in line with the flow direction. However, when hydrophilic fibers are located at the MPL–GDL interface or under the ribs, this will aggravate water accumulation.
In conclusion, although previous studies have revealed the transport mechanism of liquid water within the GDL and at the MPL–GDL interface from multiple perspectives such as the GDL thickness, porosity, fiber structure, wettability, and MPL thickness, most of them are limited to single structures or uniform wettability designs, making it difficult to fully reproduce the entire process of liquid water from generation to discharge in the MPL–GDL–GC overall system. Moreover, systematic research on the stepped wettability zoning design along the flow direction is still relatively scarce. In view of these factors, this study proposes a two-dimensional MPL–GDL–GC microstructure reconstruction method based on a novel random reconstruction algorithm to conduct an overall modeling of MPL-GDL-GC MPL, GDL and GC, and different settings (including MPL-GDL-GC fiber diameter, porosity, and contact angle) are used for the microstructure of each part. The Shan–Chen multi-component and multi-phase LBM is used to design and compare the two-segment and three-segment contact angle gradient distribution schemes from the inlet to the outlet. This paper will conduct an in-depth assessment of the influence of different contact angle distributions on drainage characteristics from aspects such as the liquid water flow paths, droplet morphology, and liquid water distribution. The aim is to explore the paths and mechanisms of liquid water discharge under different GDL wettability conditions through the coupling design of the overall structure of the MPL–GDL–GC and the gradient wettability, and to provide a scientific explanation for the drainage differences of GDLs in PEMFCs. It provides a reference for the future wettability partition optimization of GDLs.
2. Numerical Model
2.1. Multi-Component and Multi-Phase LB Model
In mesoscopic fluid modeling, the lattice Boltzmann method (LBM) simulates fluid dynamics characteristics based on the collision–migration process of lattice points [25]. The core of this method lies in evolving the particle distribution function to implicitly match the macroscopic Navier the Stokes equations. For gas diffusion layers (GDLs) with extremely complex pore structures, the LBM has been proven to effectively and accurately capture the complex process of water–gas two-phase flow. More importantly, by adjusting the intensity of the interaction forces among the liquid–gas–solid phases, this method can precisely set the contact angle [26], which gives it a significant advantage in the study of evaluating the drainage capacity of GDLs with different hydrophilic or hydrophobic characteristics. Therefore, the multi-component and multi-phase LBM has been widely adopted as the core approach for studying water management issues within GDLs. Based on the above background, this study decided to adopt the LBM for simulations. The specific model is based on the BGK (Bhatnagar–Gross–Krook) equation with a single relaxation time and integrates the multi-component and multi-phase modeling method proposed by Shan and Chen.
For the multi-component and multi-phase SC-LBM, the lattice Boltzmann distribution function satisfies the following discrete evolution equation [27]:
where fi(k)(x,t) represents the distribution function of the kth component along the grid direction ei at position x and time t; fi(k),eq(x,t) represents the equilibrium distribution functions of the kth component, which can be written in the common second-order approximate form [28]:
Here, ei represents the discrete velocity. For the D2Q9 model, ei (see Figure 1) is defined as follows:
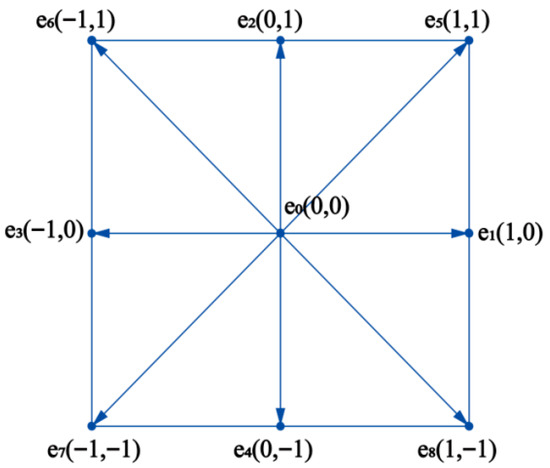
Figure 1.
The D2Q9 model of the lattice Boltzmann method.
In Equation (1), τk is the collision time related to viscosity ν:
In Equation (2), wi represents the grid weight and is related to the grid model. In the D2Q9 model, w0 = 4/9, w1~4 = 1/9, w5~8 = 1/36; cs represents the speed of sound in a fluid, and in the D2Q9 model, cs2 = 1/3; ρk and ukeq are the local macroscopic density and equilibrium velocity of the kth component, respectively. The calculation equations are as follows:
Here, Fk represents the total interaction force of the kth component at grid point x, which consists of three forces, including the fluid–fluid interaction force (F1), the fluid–solid interaction force (F2), and the externally applied force (F3). The calculation formula is as follows:
Since external forces are not taken into account in this article, F3 = 0.
The calculation formula for the fluid–fluid interaction force (F1) is as follows:
Here, ψk(x,t) is the potential function of the SC model, usually taking the form ψk(x,t) = 1 − exp(−ρk). Gk,k′ represents the strength of the interaction force between the kth component and the k′th component.
The calculation formula for the fluid–solid interaction force (F2) is as follows:
In this equation, Gw represents the strength of the force between the fluid and the solid; s(x + ei∆t,t) is a judgment parameter, and its value is 1 when the adjacent nodes are solid. When the adjacent nodes are fluid, it is 0.
Here, u represents the macroscopic velocity of the mixed fluid, and the calculation formula is as follows:
In this equation, ρkuk represents the momentum density of the kth component, and the calculation formula is as follows:
The total density ρ of the mixed fluid is given by the following equation:
While the total pressure p of the mixed fluid can be calculated as follows [29]:
2.2. Computational Domain
This paper mainly studies the influence of the GDL wettability distribution on drainage characteristics. Variables such as the porosity and fiber structure remain unchanged in different groups of simulations. Traditional GDLs use carbon fiber paper or carbon cloth as the base material, and usually only a small amount (about 10%) of polytetrafluoroethylene (PTFE) is coated between the fibers [30]. The contact angle of the treated GDL fibers is approximately 110°. To make the transmission of gas and liquid from the CL to GDL smoother and to ensure a more uniform distribution of reaction gas on the surface of the CL, an MPL is often added between the CL and GDL. Together, the GDL and MPL form a porous transport layer (PTL). The MPL is a hydrophobic porous structure [16,31], and usually has a larger contact angle than the GDL. Therefore, in this paper, the contact angle of the MPL is set at 120°. The overall computing domain is shown in Figure 2.
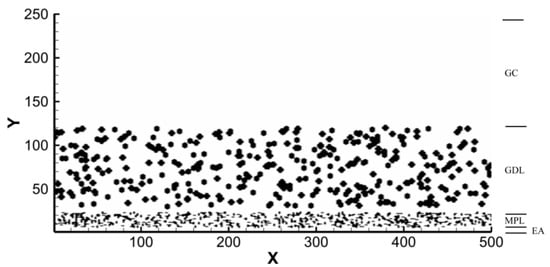
Figure 2.
The two-dimensional computational domain of the MPL, GDL, and GC.
The length X of the computational domain is 500 μm, and the thickness Y is 250 μm. In this paper, 1 μm represents the length of 1 grid length (∆x), so the size of the computational domain is 500∆x × 250∆x. The overall computing domain consists of four parts, namely the entry area (EA), MPL, GDL, and GC. Among them, the thickness of the EA is 5∆x, that of the MPL is 20∆x, that of the GDL is 100∆x, and that of the GC is 125∆x. The GDL and MPL are respectively constructed by randomly distributed circular particles with diameters of 7 μm and 2 μm. The porosity of the GDL is 0.74 [32], and that of the MPL is 0.64 [16]. In the simulation, the contact angles of GDL fibers are set at 80°, 100°, 110°, and 120°, while that of the MPL is 120°.
2.3. Initial and Boundary Conditions
At the beginning of the simulation, air fills the entire computing domain, and liquid water is injected into the domain from the bottom at Y = 1. To reduce the influence of the boundary, an inlet area with a thickness of 5∆x is set as a buffer during the simulation. The Zou–He [33] boundary condition is adopted for the bottom entrance area and the top exit area of the computational domain, and the water injection rate is set to 1 × 10−4 [34]. Periodic boundary conditions are used on both the left and right sides, while rebound boundary conditions are adopted for MPL and GDL particles. In the GDL porous structure, the flow of liquid water is mainly driven by capillary force, while viscous force and gravity can be ignored. Therefore, in this study, when using the SC model, the density and viscosity of liquid water and air are set to equal values [35,36]. Detailed information on the computational domain and simulation conditions of this paper is presented in Table 1.

Table 1.
Values of all parameters in the simulation in the lattice unit.
3. Model Validation
To ensure the accuracy of the LBM model used in this study, two verification experiments are conducted in this paper, namely for surface tension verification and contact angle verification experiments, and the corresponding Gc values and Gw values are obtained simultaneously.
3.1. Surface Tension Verification
In the SC model, Gc is a key parameter that controls the intensity of the interaction force between different fluids. If the Gc value is small, the components of different fluids will not separate from each other but will mix with each other. To verify this phenomenon, in this study, a circular droplet with a radius of 20 lattices is placed in a 100 × 100 computational domain, and periodic boundary conditions are adopted on all four sides of the computational domain. We set the initial density of fluid 1 (liquid) within the droplet to 2.0 and outside the droplet to 1 × 10−5 [37]; fluid 2 (gas) is the opposite [37], and then the morphological changes of the droplet in space are observed.
When Gc continues to increase, although it can maintain the separation of gas and liquid phases, it will make the numerical calculation unstable and overly magnify the density difference between the two phases [31,38]. Therefore, the author continued to simulate the separation of the two phases of Gc from 0 to 5.5 and plotted the variation curve of the density of fluid 1 (liquid) with the increase in Gc, and selected Gc = 4.0 based on this theory, as shown in Figure 3.
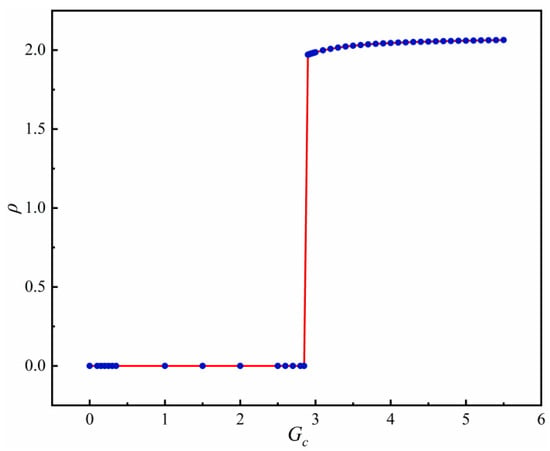
Figure 3.
The variation curve of the density of fluid 1 with the increase in Gc.
Next, this paper further verifies the compliance of the model with Laplace’s law. According to this law, the pressure difference between the inside and outside of a droplet is directly proportional to the interfacial tension and inversely proportional to the droplet radius, which can be expressed by the following equation:
Here, Pin represents the pressure inside the droplet and Pout represents the pressure outside the droplet; σ represents surface tension, and R is the radius of the droplet. The pressure value is calculated by Equation (13). Therefore, in this study, Gc is fixed at 4.0, and droplets with radii increasing from 15 to 30 are placed in a 100 × 100 computational domain. Under the effect of surface tension, the pressure difference between the inside and outside of the droplets is calculated after the operation stabilizes. The linear fit of ∆P and 1/R is then plotted (Figure 4). This indicates that the pressure difference inside and outside the droplet and 1/R can be regarded as a linear relationship. Therefore, the simulation results of the code are in perfect agreement with Laplace’s law.
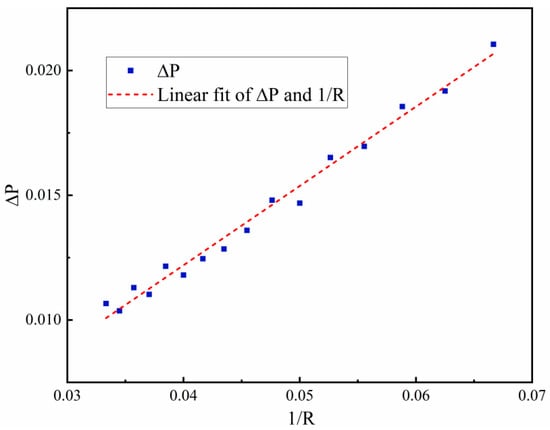
Figure 4.
The linear fit of ∆P and 1/R.
3.2. Contact Angle Verification
The contact angle refers to the angle between the solid–liquid interface, the interior of the liquid, and the gas–liquid interface at the junction of solid, liquid, and gas phases. It is determined by the wettability of the solid surface. When the solid surface is hydrophilic, the contact angle is less than 90°, and the liquid is prone to adsorb and form a film on the solid surface. When the surface of a solid shows hydrophobicity, the contact angle is greater than 90°, and the liquid is prone to aggregate into droplets on the solid surface. As shown in Figure 5, the liquid forms droplets on the hydrophobic surface.
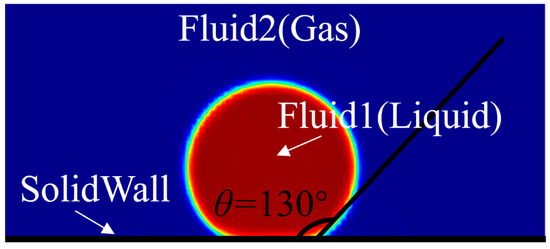
Figure 5.
A droplet on a solid wall (contact angle of 130°).
As shown in Equation (9), in the SC model, the hydrophilicity and hydrophobicity of the solid wall to the fluid can be adjusted by regulating the value of Gw. To obtain the precise correspondence between Gw and the contact angle, this study conducted the following contact angle verification simulation. At the beginning of the simulation, a rectangular droplet with a length of 40 and a width of 20 is placed on a horizontal solid wall. The size of the calculation domain is 100 × 100 grids. The left and right sides of the calculation area are set as periodic boundary conditions, and the upper and lower sides are set as solid rebound boundary conditions. As in the surface tension verification of Section 3.1, the initial densities of fluid 1 inside and outside the droplet are set at 2 and 1 × 10−5, respectively, while the opposite is true for fluid 2. After the droplet reaches a stable state, the shape of the droplet and the angle of the liquid–solid interface are recorded, and the contact angle is calculated using the method of Shan et al. [39].
The relationship between the contact angle and Gw is shown in Figure 6a. The contact angle gradually increases with the increase in Gw, which is highly consistent with the calculation results of Kim et al. [31]. Figure 6b shows a schematic diagram of a liquid droplet reaching a stable form on a solid wall under different Gw values.
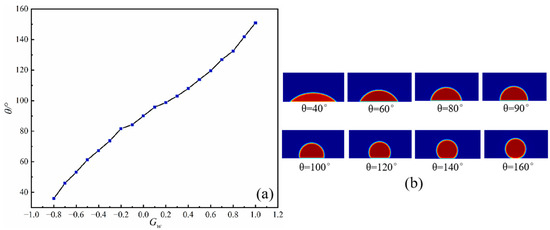
Figure 6.
(a) Line graph of the relationship between the contact angle and Gw. (b) Droplets formed on the solid surface at different Gw values.
4. Results and Discussion
4.1. Simulation of GDL Drainage with Uniform Moisture Distribution
This study first simulated uniform humidity GDLs with fiber contact angles of 100°, 110°, 120°, and 130°, which are respectively named case 1, case 2, case 3, and case 4 in this paper. Figure 7 shows the water distribution characteristics after the water discharge reaches stability in four cases (where red represents liquid water, light blue dots represent solid MPL and GDL particles, and the dark blue background represents gas air). It can be seen from the figure that the transmission path of liquid water shows a distinct capillary flow phenomenon, which indicates that the flow of liquid water in the GDL is mainly driven by capillary force. As the contact angle θ increases from 100° to 130°, the liquid phase distribution shows significant differences; under low contact angle conditions (θ = 100°, case 1), the liquid phase mainly exists in concentrated clusters, forming many large irregular clumps of liquid droplets. Different clusters are interconnected, resulting in interlinked water delivery channels and few and concentrated drainage paths, and the pores left for the gas are sealed, as marked in areas such as e, f, and g in Figure 7a. When θ is raised to 110° (case 2), the liquid phase disperses, the size of the main drainage channel decreases (areas such as h and i in Figure 7b), and the drainage path transitions to multiple branches. As the contact angle continues to increase, the water distribution on the highly hydrophobic surfaces (θ = 120°, 130°, case 3, case 4) shows a highly dispersed characteristic. The originally interconnected hydrophobic channels transform into a dispersed dendritic structure, presenting a fully covered and dispersed dendritic drainage path (Figure 7c,d).
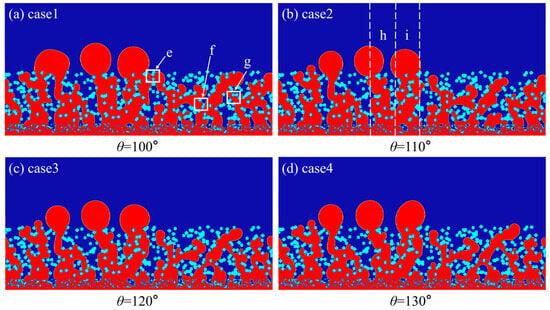
Figure 7.
Different contact angles for GDLs with stable-state water distribution: (a) θ = 100°; (b) θ = 110°; (c) θ = 120°; (d) θ = 130°.
Although the water distribution characteristics in the stable state of GDLs vary at different contact angles, the overall drainage process is relatively similar. This paper analyzes the GDL drainage process with tentacles at 110°. In the liquid water inlet area, the water phase (red) covers the bottom of the MPL fibers (light blue) with a continuous water film, forming a uniform wetting layer. In the initial stage (t = 10,000), after the liquid water enters the MPL structure, the water phase no longer fills uniformly in the porous structure but preferentially passes through the macroporous areas, forming pointed protrusions (areas such as e, f, and g in Figure 8a). This phenomenon is because the pore size affects the local capillary breakthrough pressure. An increase in pore radius leads to a decrease in resistance, thereby influencing the flow path of liquid water [40,41,42]. With the evolution of time (t = 50,000), the finger-like droplets gradually form a tree-like branch drainage network. At the same time, the mutual merging of some branches can be observed (such as the h and i regions in Figure 8b), which causes the cross-sectional area of the flow channel to increase several times and reduces the flow resistance. After the liquid water breaks through the GDL (t = 90,000), the water delivery channel is roughly formed (in the k, l, m, n, and other regions in Figure 8c), and the flow resistance is significantly reduced. The diameter of the main channel is expanded to the critical size, and a large amount of liquid water is discharged through the main channel. When a quasi-steady state is reached (t = 135,000), the GDL exhibits a bi-phase coexistence feature; a large amount of liquid water is concentrated in the main channel (with a diameter range of 15–20 μm), while the remaining water remains in the fiber-dense area in the form of liquid bridges or droplets, such as the p and q regions in Figure 8d. It is worth mentioning that during the process of liquid water discharge, the same finding as in the study by Guo et al. [43] can be observed. When liquid water is discharged through larger pores, the connected transport channels show a regression phenomenon. As shown in Figure 9b, as time t increases from 110,000 to 150,000, the regression phenomena of water masses c, d, and e can be observed. This is because when the drainage channel reaches the outlet, the fluid resistance inside the channel drops sharply, forming a local low-pressure area. Driven by the pressure difference, the water mass at the edge of the channel converges preferentially towards the main channel that has already been broken through, thereby causing the water mass to retreat.
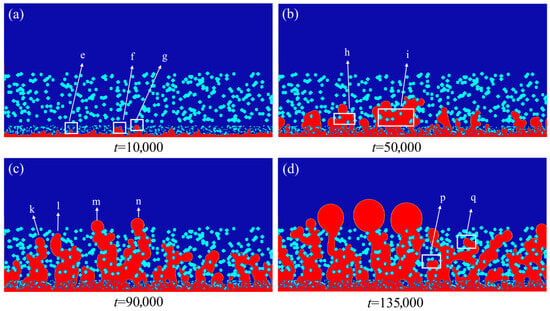
Figure 8.
The GDL drainage process with a contact angle of 110°: (a) t = 10,000; (b) t = 50,000; (c) t = 90,000; (d) t = 135,000.
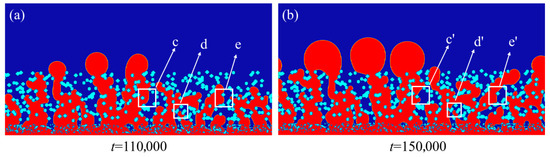
Figure 9.
Water mass regression phenomenon: (a) t = 110,000; (b) t = 150,000.
Figure 10a shows the breakthrough time and steady-state time of liquid water under four cases. It can be seen that as the contact angle of the uniform GDL increases, both the time of the droplet’s first breakthrough and the time of the liquid water’s steady state show a decreasing trend, which is consistent with the results in [31,43]. Compared with case 1, the first breakthrough times and the steady-state times of liquid water for case 2, case 3, and case 4 are reduced by 2.5% and 5.8%, 5.0% and 5.8%, and 6.25% and 5.11%, respectively. To further compare the drainage performance of DGLS with different contact angles, this paper plots the variations of liquid water saturation Stotal over time under four cases (Figure 10b). Stotal is defined as the ratio of the volume of liquid water in the PTL to the total volume of the entire void space. It can be seen that as time goes by, Stotal under all working conditions shows a three-stage characteristic of rapid increase, a slowdown in growth rate, and gradual stabilization; during the rapid accumulation stage in the early and middle stages, liquid water rapidly fills large pores driven by capillary forces, and the saturation of liquid water increases rapidly. In the middle and late stages, when liquid water flows through narrow pores, the flow resistance increases, and part of the liquid water flow is hindered by GDL fibers, slowing down the growth rate of liquid water saturation. When liquid water flows through all breakthrough points and enters the GC, the drainage path in the GDL has largely formed, and the increase in liquid water saturation has significantly slowed down and gradually entered a steady state. In this paper, the change in liquid water saturation ∆Stotal within an adjacent period (100 grid time) ≤ 0.5% is defined as a steady state [34]. It can also be observed that the larger the GDL contact angle, the smaller the saturation of liquid water in the steady state, which is consistent with the reports in [16,24,43]. Moreover, compared with case 1, the steady-state saturation of liquid water in case 2, case 3, and case 4 decreased by 6.57%, 8.17%, and 9.35%, respectively. These results indicate that increasing the GDL contact angle can improve the performance of liquid water drainage.
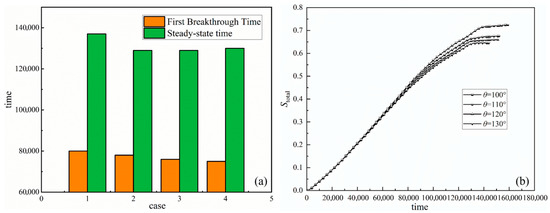
Figure 10.
(a) Liquid water first breakthrough times and steady-state times under four cases. (b) The curve of liquid water saturation varying with time.
4.2. GDL Drainage Simulation Based on Gradient Wetting Distribution
In this study, four different stepped humidity GDL structures are constructed, namely the double-gradient type GDL with contact angles of 100° in the front half and 120° in the second half of the GDL, and contact angles of 120° in the front half and 100° in the second half of the GDL. There is a three-gradient type GDL with contact angles of 100° at the front end, 110° at the middle end, and 120° at the rear end, as well as contact angles of 1020° at the front end, 110° at the middle end, and 110° at the rear end. In this article, they are respectively named case 5, case 6, case 7, and case 8. The differences among the four structures are shown in Table 2.

Table 2.
Structural zoning of double-gradient and triple-gradient wettability GDL.
Figure 11 and Figure 12 show the drainage process of liquid water under double-gradient humidity and triple-gradient humidity, respectively. By comparing case 5 with case 6, it can be observed that at the MPL–GDL junction, due to the larger contact angle at the entrance of case 6, its hydrophobicity increases, and the breakthrough pressure of water is greater, which leads to liquid water being more likely to accumulate at the MPL–GDL junction. The water mass here is prone to diffuse and aggregate in the horizontal direction, as shown in areas such as a and b in Figure 11. This is not conducive to the electrochemical reaction of the gas passing through the MPL on the GL. Therefore, the fiber contact angle at the MPL to GC interface should maintain a decreasing trend to avoid this situation. When liquid water diffuses into the GDL along the thickness direction, due to the fact that the rear part of the GDL is larger than the front part, the flow resistance of liquid water increases when it flows through the middle section of the GDL. This leads to lateral diffusion and polymerization of liquid water at the junction where the contact angle changes. As a result, more liquid water accumulates in the middle section of the GDL, and the gas transmission channel is blocked by the water bridge formed by polymerization. The probability of flooding within the GDL has significantly increased, as shown in areas such as c and d in Figure 11. The drainage conditions of case 7 and case 8 have the same trend (as shown in Figure 12). Studies have shown that an increase in the GDL contact angle along the direction of water flow will increase the possibility of flooding and is not conducive to the discharge of liquid water, which is consistent with the research results in [43,44].
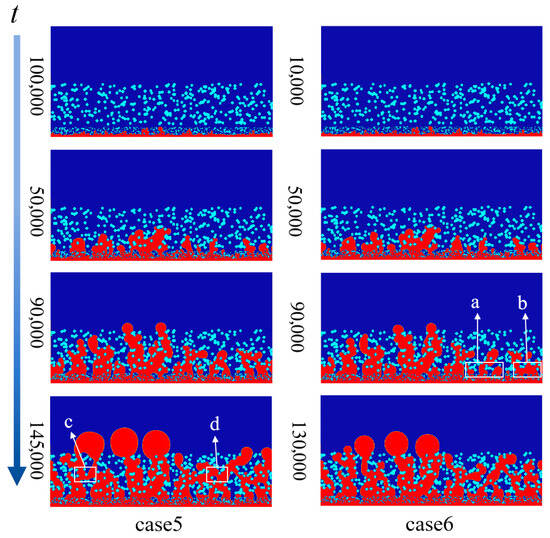
Figure 11.
The drainage process of liquid water with double-gradient wettability.
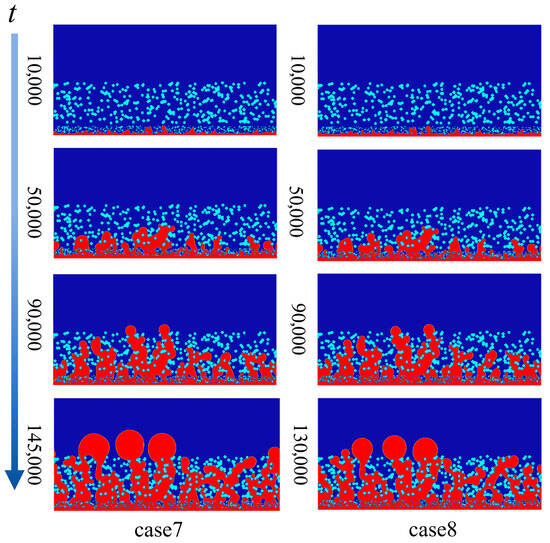
Figure 12.
The drainage process of liquid water with triple-gradient wettability.
Figure 13a shows the liquid water breakthrough times and steady-state times under four cases and compares them with case 2. It can be seen that when the average contact angle inside the GDL is 110°, the double-gradient and triple-gradient wetting GDLs differ from the uniform wetting GDLs in the first liquid water breakthrough time and steady-state time. Compared with the uniform wettability in case 2, the steady-state times of case 5 and case 7, which have an increased contact angle gradient along the drainage direction, increase by 3.88% and 3.88% respectively, while the changes of case 6 and case 8, which have a decreased contact angle gradient along the drainage direction, are not significant. Figure 13b shows the variation and a comparison of liquid water saturation over time between four types of gradient wettability GDLs and uniform wettability GDLs. Before reaching the steady-state time, the overall liquid water saturation rates within the five types of GDL do not differ much, but after reaching the steady-state time, it can be seen that the steady-state water saturation rates of case 5 and case 7 with an increased contact angle gradient along the drainage direction are higher than the uniform wettability GDL of case 2, which is consistent with the results in [43], increasing by 2.99% and 2.48% respectively, while the changes in case 6 and case 8 with a decreased contact angle gradient along the drainage direction are not significant. When the average GDL and the humidity at the inlet and outlet are the same, the greater the gradient, the smaller the difference in GDL drainage compared to uniform humidity. This section of the study also indicates that an increase in the contact angle gradient along the drainage direction is not conducive to the drainage performance of the GDL.
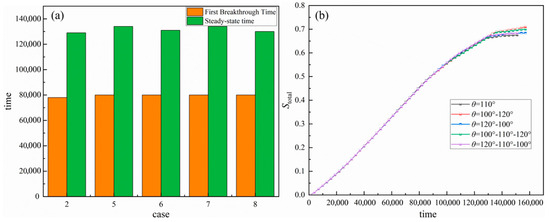
Figure 13.
(a) Liquid water first breakthrough times and steady-state times under four cases. (b) Variations of liquid water saturation with time between gradient wettability GDLs and uniform wettability GDLs.
5. Conclusions
This study developed a pore-scale model based on the multi-component and multi-phase lattice Boltzmann method, and conducted an in-depth analysis and discussion of the liquid water flow path, breakthrough time, water saturation, steady-state time, and droplet growth of GDLs with various wettability distributions containing MPLs. The main conclusions are as follows:
(1) As the GDL contact angle increases from 100° to 130°, the first breakthrough time of liquid water decreases by approximately 2.5% to 6.3%, the steady-state time decreases by approximately 5.1% to 5.8%, and the steady-state water saturation decreases by approximately 6.6% to 9.4%. This indicates that enhancing the overall hydrophobicity of the GDL can accelerate the breakthrough of capillary fingers and reduce the water film residue.
(2) Gradient GDLs with increasing contact angles along the drainage direction (100°→120° and 100°→110°→120°) will cause water cluster aggregation at the MPL–GDL junction and the middle section, resulting in an extension of the steady-state time by approximately 3.9% and an increase in steady-state saturation by about 2.5–3.0%, thereby weakening the drainage efficiency.
Author Contributions
N.X.: Writing—review and editing, supervision, funding acquisition. H.C.: Software, conceptualization, resources. J.L.: Visualization, validation. C.Z.: Methodology, investigation, writing—original draft. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (grant number 52206037).
Data Availability Statement
The original contributions presented in this study are included in the article materials. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Mei, J.; Meng, X.; Tang, X.; Li, H.; Hasanien, H.; Alharbi, M.; Dong, Z.; Shen, J.; Sun, C.; Fan, F.; et al. An Accurate Parameter Estimation Method of the Voltage Model for Proton Exchange Membrane Fuel Cells. Energies 2024, 17, 2917. [Google Scholar] [CrossRef]
- Mo, S.; Du, L.; Huang, Z.; Chen, J.; Zhou, Y.; Wu, P.; Meng, L.; Wang, N.; Xing, L.; Zhao, M.; et al. Recent Advances on PEM Fuel Cells: From Key Materials to Membrane Electrode Assembly. Electrochem. Energy Rev. 2023, 6, 28. [Google Scholar] [CrossRef]
- Sankar, K.; Aguan, K.; Jana, A.K. A proton exchange membrane fuel cell with an airflow cooling system: Dynamics, validation and nonlinear control. Energy Convers. Manag. 2019, 183, 230–240. [Google Scholar] [CrossRef]
- Na, J.; Park, G.; Park, J.; Yang, S.; Oh, H.-M.; Baek, J.; Kim, D.; Youn, J.; Lim, J.; Park, T. Visualization of initial evolution of flooding in proton exchange membrane fuel cells with parallel flow channels. Int. J. Hydrogen Energy 2025, 114, 239–249. [Google Scholar] [CrossRef]
- Han, S.H.; Choi, N.H.; Choi, Y.D. Study on the flooding phenomena and performance enhancement of PEM fuel cell applying a Concus-Finn condition. Renew. Energy 2012, 44, 88–98. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, X.; Gong, F.; Liu, Z.; Zhang, Z.; Wang, C. Water flooding diagnosis of proton exchange membrane fuel cell based on current density scanning. J. Electroanal. Chem. 2024, 952, 117929. [Google Scholar] [CrossRef]
- Song, W.; Yu, H.; Shao, Z.; Yi, B.; Lin, J.; Liu, N. Effect of polytetrafluoroethylene distribution in the gas diffusion layer on water flooding in proton exchange membrane fuel cells. Chin. J. Catal. 2014, 35, 468–473. [Google Scholar] [CrossRef]
- Yang, D.; Garg, H.; Andersson, M. Numerical simulation of two-phase flow in gas diffusion layer and gas channel of proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2023, 48, 15677–15694. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, S. Numerical study and prediction of water transfer in gas diffusion layer of proton exchange membrane fuel cells under vibrating conditions. Int. J. Energy Res. 2022, 46, 18781–18795. [Google Scholar] [CrossRef]
- Shangguan, X.; Li, Y.; Qin, Y.; Cao, S.; Zhang, J.; Yin, Y. Effect of the porosity distribution on the liquid water transport in the gas diffusion layer of PEMFC. Electrochim. Acta 2021, 371, 137814. [Google Scholar] [CrossRef]
- Chen, L.; Luan, H.-B.; He, Y.-L.; Tao, W.-Q. Pore-scale flow and mass transport in gas diffusion layer of proton exchange membrane fuel cell with interdigitated flow fields. Int. J. Therm. Sci. 2012, 51, 132–144. [Google Scholar] [CrossRef]
- Jeon, D.H. Effect of gas diffusion layer thickness on liquid water transport characteristics in polymer electrolyte membrane fuel cells. J. Power Sources 2020, 475, 228578. [Google Scholar] [CrossRef]
- Yang, D.; Andersson, M.; Garg, H. Effect of fiber curvature on gas diffusion layer two-phase dynamics of proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2024, 85, 635–651. [Google Scholar] [CrossRef]
- Anyanwu, I.S.; Niu, Z.; Jiao, D.; Najmi, A.-U.-H.; Liu, Z.; Jiao, K. Liquid Water Transport Behavior at GDL-Channel Interface of a Wave-Like Channel. Energies 2020, 13, 2726. [Google Scholar] [CrossRef]
- Yan, S.; Yang, M.; Sun, C.; Xu, S. Liquid Water Characteristics in the Compressed Gradient Porosity Gas Diffusion Layer of Proton Exchange Membrane Fuel Cells Using the Lattice Boltzmann Method. Energies 2023, 16, 6010. [Google Scholar] [CrossRef]
- Ira, Y.; Bakhshan, Y.; Khorshidimalahmadi, J. Effect of wettability heterogeneity and compression on liquid water transport in gas diffusion layer coated with microporous layer of PEMFC. Int. J. Hydrogen Energy 2021, 46, 17397–17413. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, H.; Zhang, Z.; Li, H.; Wang, X. Lattice Boltzmann simulation of a gas diffusion layer with a gradient polytetrafluoroethylene distribution for a proton exchange membrane fuel cell. Appl. Energy 2022, 320, 119248. [Google Scholar] [CrossRef]
- Molaeimanesh, G.R.; Akbari, M.H. Role of wettability and water droplet size during water removal from a PEMFC GDL by lattice Boltzmann method. Int. J. Hydrogen Energy 2016, 41, 14872–14884. [Google Scholar] [CrossRef]
- Gao, W.; Li, Q.; Sun, K.; Chen, R.; Che, Z.; Wang, T. Effects of gas diffusion layer thickness on PEM fuel cells with composite foam-rib flow fields. Int. Commun. Heat Mass Transf. 2024, 153, 107394. [Google Scholar] [CrossRef]
- Xia, L.; Ni, M.; He, Q.; Xu, Q.; Cheng, C. Optimization of gas diffusion layer in high temperature PEMFC with the focuses on thickness and porosity. Appl. Energy 2021, 300, 117357. [Google Scholar] [CrossRef]
- Huang, Y.-X.; Cheng, C.-H.; Wang, X.-D.; Jang, J.-Y. Effects of porosity gradient in gas diffusion layers on performance of proton exchange membrane fuel cells. Energy 2010, 35, 4786–4794. [Google Scholar] [CrossRef]
- Zhu, R.; Zhan, Z.; Zhang, H.; Du, Q.; Chen, X.; Xiang, X.; Wen, X.; Pan, M. Effects of Cathode GDL Gradient Porosity Distribution along the Flow Channel Direction on Gas-Liquid Transport and Performance of PEMFC. Polymers 2023, 15, 1629. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Li, Y.; Lv, X.; Zhou, Z.; Wu, W.-T.; Wei, L.; Hu, C.; Lyu, J.; Li, Y.; Song, Y. Study of liquid water dynamics in Zoned PEMFC GDLs with different wettability. Fuel 2025, 394, 135171. [Google Scholar] [CrossRef]
- Zhou, X.; Wu, L.; Niu, Z.; Bao, Z.; Sun, X.; Liu, Z.; Li, Y.; Jiao, K.; Liu, Z.; Du, Q. Effects of surface wettability on two-phase flow in the compressed gas diffusion layer microstructures. Int. J. Heat Mass Transf. 2020, 151, 119370. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef]
- Hao, L.; Cheng, P. Lattice Boltzmann simulations of water transport in gas diffusion layer of a polymer electrolyte membrane fuel cell. J. Power Sources 2010, 195, 3870–3881. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- He, X.; Luo, L.-S. Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 1997, 56, 6811–6817. [Google Scholar] [CrossRef]
- He, X.; Doolen, G.D. Thermodynamic foundations of kinetic theory and Lattice Boltzmann models for multiphase flows. J. Stat. Phys. 2002, 107, 309–328. [Google Scholar] [CrossRef]
- Yoshimune, W.; Kato, A.; Yamaguchi, S.; Hibi, S.; Kato, S. Comprehensive Analysis of Wettability in Waterproofed Gas Diffusion Layers for Polymer Electrolyte Fuel Cells. ACS Appl. Mater. Interfaces 2024, 16, 36489–36497. [Google Scholar] [CrossRef]
- Kim, K.N.; Kang, J.H.; Lee, S.G.; Nam, J.H.; Kim, C.-J. Lattice Boltzmann simulation of liquid water transport in microporous and gas diffusion layers of polymer electrolyte membrane fuel cells. J. Power Sources 2015, 278, 703–717. [Google Scholar] [CrossRef]
- Mukherjee, P.P.; Wang, C.-Y.; Kang, Q. Mesoscopic modeling of two-phase behavior and flooding phenomena in polymer electrolyte fuel cells. Electrochim. Acta 2009, 54, 6861–6875. [Google Scholar] [CrossRef]
- Zou, Q.; He, X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar] [CrossRef]
- Chen, W.; Jiang, F. Impact of PTFE content and distribution on liquid–gas flow in PEMFC carbon paper gas distribution layer: 3D lattice Boltzmann simulations. Int. J. Hydrogen Energy 2016, 41, 8550–8562. [Google Scholar] [CrossRef]
- Deng, H.; Hou, Y.; Jiao, K. Lattice Boltzmann simulation of liquid water transport inside and at interface of gas diffusion and micro-porous layers of PEM fuel cells. Int. J. Heat Mass Transf. 2019, 140, 1074–1090. [Google Scholar] [CrossRef]
- Shan, X. Simulation of Rayleigh-B\’enard convection using a lattice Boltzmann method. Phys. Rev. E 1997, 55, 2780–2788. [Google Scholar] [CrossRef]
- Huang, H.; Thorne, D.T., Jr.; Schaap, M.G.; Sukop, M.C. Proposed approximation for contact angles in Shan-and-Chen-type multicomponent multiphase lattice Boltzmann models. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2007, 76, 066701. [Google Scholar] [CrossRef]
- Chen, L.; Luan, H.-B.; Tao, W.-Q. Liquid water dynamic behaviors in the GDL and GC of PEMFCs using lattice Boltzmann method. Front. Heat Mass Transf. 2010, 1, 023002. [Google Scholar] [CrossRef]
- Huang, H.; Sukop, M.; Lu, X. Shan and Chen-Type Multi-Component Multiphase Models. In Multiphase Lattice Boltzmann Methods: Theory and Application; Wiley-Blackwell: Hoboken, NJ, USA, 2015; pp. 71–93. [Google Scholar]
- Wang, H.; Yang, G.; Li, S.; Shen, Q.; Su, F.; Jiang, Z.; Liao, J.; Pan, X. Pore-Scale Modeling of Mass Transport in Partially Saturated Cathode Gas Diffusion Layers of Proton Exchange Membrane Fuel Cell. Energy Fuels 2022, 36, 8422–8431. [Google Scholar] [CrossRef]
- Liao, J.; Yang, G.; Shen, Q.; Li, S.; Jiang, Z.; Wang, H.; Sheng, Z.; Zhang, G.; Zhang, H. Effects of the Structure, Wettability, and Rib-Channel Width Ratio on Liquid Water Transport in Gas Diffusion Layer Using the Lattice Boltzmann Method. Energy Fuels 2021, 35, 16799–16813. [Google Scholar] [CrossRef]
- Yang, M.; Jiang, Y.; Liu, J.; Xu, S.; Du, A. Lattice Boltzmann method modeling and experimental study on liquid water characteristics in the gas diffusion layer of proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2022, 47, 10366–10380. [Google Scholar] [CrossRef]
- Guo, L.; Chen, L.; Zhang, R.; Peng, M.; Tao, W.-Q. Pore-scale simulation of two-phase flow and oxygen reactive transport in gas diffusion layer of proton exchange membrane fuel cells: Effects of nonuniform wettability and porosity. Energy 2022, 253, 124101. [Google Scholar] [CrossRef]
- Yu, J.; Froning, D.; Reimer, U.; Lehnert, W. Polytetrafluorethylene effects on liquid water flowing through the gas diffusion layer of polymer electrolyte membrane fuel cells. J. Power Sources 2019, 438, 226975. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).