Abstract
This study presents TeS v.3, a thermodynamic equilibrium simulator integrated with an artificial intelligence agent (AI), ThermoAgent, to enhance the analysis of complex chemical systems. Developed in Python, the simulator employs Gibbs energy minimization for isothermal reactors and entropy maximization for adiabatic reactors. ThermoAgent leverages the LangChain framework to interpret natural language commands, autonomously execute simulations, and query a scientific knowledge base through a Retrieval-Augmented Generation (RAG) approach. The validation of TeS v.3 demonstrated high accuracy, with coefficients of determination (R2 > 0.95) compared to reference simulation data and strong correlation (R2 > 0.88) with experimental data from the steam methane reforming (SMR) process. The SMR analysis correctly distinguished the high conversions in isothermal reactors from the limited conversions in adiabatic reactors, due to the reaction temperature drop. ThermoAgent successfully executed simulations and provided justified analyses, combining generated data with information from reference publications. The successful integration of the simulator with the AI agent represents a significant advancement, offering a powerful tool that accurately calculates equilibrium and accelerates knowledge extraction through intuitive interaction.
1. Introduction
Chemical process engineering has continuously evolved in the pursuit of efficiency, safety, and sustainability. Process modeling and simulation have established themselves as a fundamental pillar of modern chemical engineering [1], enabling virtual experiments that provide critical insights into process behavior before physical construction or the implementation of operational changes [2].
The thermodynamic framework forms the core of any chemical process simulator. Accurate prediction of physicochemical properties, as well as phase and chemical equilibria, serves as the foundation upon which all simulations are built. Therefore, selecting an appropriate thermodynamic package is the most critical decision to ensure the validity and accuracy of the results [3].
For reactive systems, thermodynamic analysis defines the theoretical limits of conversion and selectivity. Several authors have reported excellent results using approaches based on Gibbs free energy minimization, such as Barros et al. [4] in the supercritical gasification of black liquor. In addition to Gibbs minimization for isothermal reactors [5,6,7], entropy maximization offers an alternative perspective for adiabatic systems, proving effective in predicting thermal behavior [8]. Freitas et al. [9] demonstrated this methodology for processes under constant pressure and enthalpy.
The steam methane reforming (SMR) process serves as an exemplary case for validating thermodynamic simulators. As the dominant technological route for large-scale hydrogen production [5,10], it is extensively documented in the literature. Conducted under severe conditions (700–1000 °C, 3–25 bar), it exhibits prominent equilibrium limitations [5,11] and operational challenges such as catalyst deactivation and coke formation, making it a rigorous benchmark for equilibrium simulation tools [12].
Alongside the advancement of first-principles-based models, chemical process engineering is undergoing a transformation driven by artificial intelligence (AI) and machine learning (ML). This new era marks a shift from purely mechanistic approaches to data-driven models and, more promisingly, to hybrid models that integrate physical knowledge with data analysis [13,14]. While the application of AI faces unique challenges, such as limited availability of high-quality data and severe consequences of modeling errors, its potential to accelerate innovation is undeniable.
This work positions AI as a complementary tool capable of enriching analyses and enhancing knowledge extraction from thermodynamic simulation results. The integration of AI techniques helps overcome the limitations of traditional approaches, offering new ways to visualize complex solution spaces, uncover patterns in high-dimensional domains, and accelerate optimization processes.
The present study addresses the development of a thermodynamic equilibrium simulator for complex reactive systems, using the SMR process as a case study. The main objective is to develop and validate a robust tool based on Gibbs free energy minimization for isothermal reactors and entropy maximization for adiabatic reactors, demonstrating how AI agents can serve as auxiliary analytical instruments, providing meaningful insights into the behavior of simulated processes.
2. Literature Review
2.1. Process Simulation Software
Process simulation software has become an indispensable tool in chemical engineering, enabling engineers to model, analyze, and optimize complex chemical processes prior to their physical implementation. These software packages simulate mass and energy balances of process plants, with applications spanning design studies, debottlenecking, control system checkouts, dynamic simulation, operator training, and digital twin creation.
The simulation landscape encompasses both commercial and open-source solutions. Commercial simulators such as Aspen HYSYS, Aspen Plus, ProSim Plus, and UniSim are industry standards, offering comprehensive thermodynamic databases, robust algorithms, and user-friendly interfaces [15]. Open-source alternatives have gained traction, particularly in academia. DWSIM is a notable CAPE-OPEN compliant simulator offering capabilities previously restricted to commercial software, including Python integration for thermodynamic calculations and machine learning workflows [16,17]. Other platforms like COCO provide modular environments that enhance ecosystem flexibility [18,19].
Thermodynamic modeling is the foundation of accurate process simulation, governing phase and chemical reaction equilibria and energy balances that determine process feasibility and efficiency. Selecting appropriate thermodynamic models is the most critical aspect of simulator development [20]. Accuracy is paramount, as small inaccuracies, especially in reactive systems under extreme conditions like steam methane reforming, can propagate into significant design errors [21]. Modern platforms offer extensive model ranges, from classical equations of state such as Peng–Robinson (PR) and Soave–Redlich–Kwong (SRK), activity coefficient models like NRTL and UNIQUAC [22], to advanced molecular approaches such as PC-SAFT theory and group contribution methods [23]. Rigorous non-ideality treatment, including fugacity and activity calculations, enables reliable equilibrium predictions in complex systems.
Simulator evolution has been driven by computational advances and improved numerical methods. Sophisticated algorithms for solving complex, nonlinear equation systems, including successive substitution, Newton–Raphson, and quasi-Newton methods, are standard [24]. Ipopt (Interior Point OPTimizer) represents a significant advancement, becoming a cornerstone for large-scale nonlinear programming problems. Implementing primal-dual interior point methods, Ipopt excels in thermodynamic equilibrium calculations such as Gibbs energy minimization, enabling rapid determination of chemical and phase compositions in complex systems [25]. Its robustness in handling thousands of variables and constraints makes it invaluable for enterprise-wide dynamic optimization [26,27,28].
Modern process simulation paradigm emphasizes flexibility and integration, driven primarily by Python. Its open-source nature, extensive scientific libraries (NumPy, SciPy, Pandas), and robust machine learning ecosystem (TensorFlow, PyTorch, scikit-learn) make Python ideal for developing AI-integrated simulators [27]. This interoperability allows Python-based simulators to connect seamlessly with mathematical software, control systems, and solvers like Ipopt [28,29]. Open-source transparency and extensibility are crucial for field advancement, enabling researchers to implement custom thermodynamic models, validate computational methods, and develop specialized applications, overcoming proprietary software limitations [30].
2.2. AI Capabilities for Knowledge Enrichment for Process Evaluation
The integration of AI and ML in chemical engineering has opened new frontiers for process evaluation and optimization. AI empowers engineers with data-driven decision-making, optimization, and prediction capabilities for process simulation, product development, anomaly detection, predictive maintenance, and energy optimization.
AI’s fundamental capabilities lie in extracting knowledge and recognizing patterns in diverse data types. Machine learning algorithms, particularly neural networks, have demonstrated remarkable success in modeling complex nonlinear relationships in chemical processes [31]. Natural Language Processing (NLP) can analyze technical documentation to extract insights, while Computer Vision enables real-time equipment and product quality monitoring [32].
Predictive modeling is a promising application domain where ML algorithms learn from historical data to predict performance, equipment failures, or product quality [33]. The transformation toward renewable energy requires new paradigms for flexible plant design and functional materials, where AI-driven approaches offer significant advantages. Reviews have classified AI applications in process engineering, highlighting these technologies’ maturity [34].
AI-driven optimization algorithms, including genetic algorithms, particle swarm optimization (PSO), and reinforcement learning (RL), solve complex multi-objective problems that are computationally intensive for traditional methods [35]. PSO has established itself as a leading heuristic global optimization method [36,37]. Deep reinforcement learning offers promising approaches for energy and feedstock transformations [38].
Hybrid models combine first-principles models with AI techniques, leveraging mechanistic model interpretability while capturing complex phenomena through data-driven components. AI agents represent intelligent systems that autonomously perform analysis tasks, interpret results, and provide recommendations to engineers [33,39], building on historical concepts like expert systems [35].
Despite significant potential, AI application faces challenges. Engineers require careful validation of AI-based approaches due to large financial and safety implications. Data quality and availability are critical factors, as steady-state operations limit training data diversity for ML algorithms.
AI integration with process simulation software represents natural evolution. AI-enhanced simulators automatically adjust parameters, suggest optimal conditions, and identify improvements [40]. This synergy promises to accelerate innovation while maintaining industrial rigor and reliability [31].
2.3. The Steam Methane Reforming Process
Steam methane reforming is the dominant and most mature technology for large-scale hydrogen production, accounting for most of the world’s dedicated output [5]. The hydrogen generated is a fundamental chemical feedstock, serving as an essential raw material in the production of ammonia (for fertilizers) and methanol and in oil refineries for hydrotreating and hydrocracking processes. The ubiquity and economic importance of SMR make it a process of immense industrial and academic relevance.
The chemistry of the SMR process is traditionally described by a set of reversible reactions that occur simultaneously in a catalytic reactor. The two primary reactions that form the basis for thermodynamic analysis are the reforming reaction and the water–gas shift (WGS) reaction [41]. The first, highly endothermic, converts methane and steam; the second, which is exothermic, increases the hydrogen yield by consuming the carbon monoxide formed. Kinetic models, such as the one proposed by Xu and Froment [42], often utilize a set of three reactions to fully describe the system. The foundational reactions are presented in Equations (1)–(3).
The process is endothermic, meaning that an increase in temperature favors the conversion of methane into products. A significant operational challenge in the SMR process is the deposition of coke on the catalyst surface, which leads to deactivation [43]. A common method used to overcome this issue is to increase the H2O/CH4 ratio in the feed, which diminishes the formation of solid carbon. Coke formation can occur through several reactions, but at high temperatures (above 910 K), the primary route is methane cracking (Equation (4)).
Given these characteristics, the SMR process is selected as the ideal case study for this work. It serves as a rigorous benchmark for several key reasons:
- Its vast industrial relevance ensures that findings are meaningful.
- It is strongly limited by thermodynamic equilibrium, making it a perfect test for an equilibrium-based simulator.
- Its inherent complexity, arising from multiple simultaneous reactions and severe operating conditions, provides a robust challenge.
- The wide availability of experimental and industrial data in the literature allows for thorough model validation.
Therefore, the SMR process will be used to develop and validate the thermodynamic equilibrium simulator and to demonstrate the application of AI agents as auxiliary instruments for complex process analysis.
3. Methodology
This section presents the thermodynamic and computational framework underlying the TeS simulator. The described methodologies generate high-fidelity equilibrium data that supports subsequent analyses. An AI agent enhances this framework by interpreting simulation outputs, identifying complex patterns, and directly interacting with thermodynamic models. This capability enables autonomous simulations and systematic exploration of the solution space, facilitating the extraction of knowledge beyond traditional approaches.
3.1. Calculation of Equilibrium Compositions in Isothermal Reactors at Constant Pressure: Thermodynamic Study Applying Gibbs Energy Minimization
The combined chemical and phase equilibrium problem, formulated as the minimization of the total Gibbs free energy of the system at constant pressure and temperature, can be expressed as shown in Equation (5) [44], considering a mixture that may contain solid, liquid, and gaseous phases.
Additionally, at the Gibbs energy minimum, the system must satisfy the following constraints:
- I.
- Non-negativity of the number of moles (Equation (6)):
- II.
- Conservation of atoms (Equation (7)):
In all cases considered in this study, the only solid component included is solid carbon, and this phase is assumed to behave ideally. Another important assumption is that, for all systems discussed in this work, the φ–φ (phi-phi) approach is employed for the prediction of non-ideal behavior.
3.2. Calculation of Equilibrium Compositions and Temperatures in Adiabatic Reactors at Constant Pressure: Thermodynamic Study Applying Entropy Maximization
At constant pressure and enthalpy (P and H), the thermodynamic equilibrium of a reactive multicomponent system can be determined by the maximization of the system’s entropy, as expressed in Equation (8) [45].
The entropy maximization methodology must comply with the same constraints employed in the Gibbs free energy minimization approach; however, the system’s enthalpy must also be conserved. Equation (9) describes this enthalpy conservation, where the sum of the enthalpies along the reaction pathway must equal the sum of the enthalpies of the components in the initial state.
Further details on process modeling of reactive systems using minG and maxS can be found in the works of Mitoura et al. [5,46,47] and Freitas and Guirardello [8,9,48].
3.3. Considerations on Non-Idealities of the Reaction System
The TeS simulator offers the use of both the PR and SRK equations of state to assess system non-ideality. The PR equation is well-known for its balance of simplicity and accuracy, having been developed to perform as well as or better than the SRK equation by modifying the attractive pressure term of the semi-empirical Van der Waals equation [49].
For this study, only the PR equation of state will be used to predict non-idealities. Equation (10) presents the polynomial form of compressibility factor Z for the PR EoS.
The dimensionless coefficients A and B encapsulate the dependence on pressure, temperature, and mixture composition and are defined as shown in Equations (11) and (12), respectively.
The mixture energy parameter (am) is calculated using a quadratic mixing rule that accounts for the interactions between all pairs of components (i and j) in the mixture, as shown in Equation (13). The mixture co-volume parameter (bm) is calculated as a linear average of the individual component contributions, weighted by their molar fractions yi, as shown in Equation (14).
For a given thermodynamic state (T, P, and composition), the values of A and B are calculated, and the corresponding cubic equation is solved for Z. If there is only one real root, the system exists as a single phase. If three distinct real roots are obtained, the largest root corresponds to the compressibility factor of the vapor phase (Zg), and the smallest to that of the liquid phase (Zl). The intermediate root has no physical meaning, as it represents a thermodynamically unstable state. Equation (15) presents the fugacity coefficient calculations for the Peng–Robinson equation for both liquid and vapor phases.
3.4. Strategies for Solving Equilibrium Problems
For the SMR process simulations, six components (H2O, H2, CH4, CO2, CO, and C) were initially considered, selected based on the kinetic model reported by Xu and Froment [42]. All thermodynamic properties, as well as the polynomials for heat capacity calculations, were obtained from Introduction to Chemical Engineering Thermodynamics by Joe Mauk Smith, Michael M. Abbott, and Hendrick C. Van Ness [50].
The simulations were carried out using TeS v.3, a standalone computational platform developed in Python for solving thermodynamic equilibrium problems. TeS v.3 integrates advanced optimization technologies by employing the Pyomo framework for NLP modeling and Ipopt as a robust solver for large-scale nonlinear optimization problems [51,52], enabling the identification of optimal solutions for both minG and maxS formulations.
The software does not require prior installation and provides an intuitive interface where users can input thermodynamic data, component compositions, and choose between different equations of state (Peng–Robinson or Soave–Redlich–Kwong), as well as the truncated virial equation beyond the ideal gas term. Additionally, users can restrict the formation of specific components, vary feed compositions, and define operating pressure and temperature. Simulation outputs include customizable tables and graphical visualizations, such as response surfaces and correlation matrices, ensuring both flexibility and comprehensive analysis capabilities.
3.5. Architecture for Integrating Thermodynamic Models with an AI Agent
The previous sections provided information about the modeling employed to solve equilibrium problems. At the programming language level, each methodology, minG and maxS, is implemented as Python modules and can be invoked through simple function calls. The next step in this study is to develop an AI agent capable of consuming these previously described modules to perform thermodynamic equilibrium calculations. Figure 1 presents the proposed architecture for the AI agent, called ThermoAgent, which can execute simulations and retrieve information from documents previously specified by the user to enrich the context.
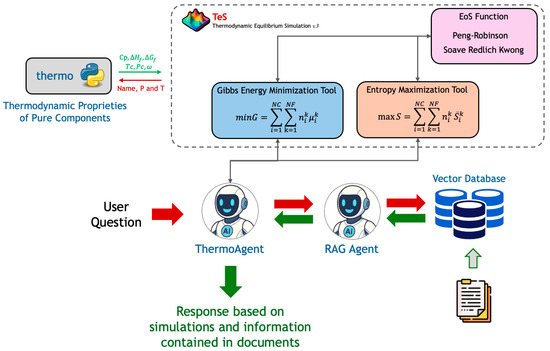
Figure 1.
ThermoAgent architecture proposal.
Autonomous AI agents have been a prominent research focus in both academia and industry. They possess the capability to make decisions based on a predefined set of information [52]. ThermoAgent acts as the central orchestrator of the system, designed and built using the LangChain framework. When a user submits a query, ThermoAgent analyzes the request and determines the most appropriate tool to employ. The primary tools at its disposal are the thermodynamic calculation modules developed in this work, which are part of TeS v.3. These tools include the following:
- Gibbs Energy Minimization Tool: Invokes the minG module to simulate isothermal reactors, calculating the equilibrium composition at a given temperature and pressure.
- Entropy Maximization Tool: Invokes the maxS module to simulate adiabatic reactors, determining both the final equilibrium composition and temperature.
An important point to highlight is that tool selection is entirely driven by the user’s prompt. ThermoAgent is instructed to sequentially follow the user’s request, and it can execute multiple tools to produce the final answer. For example, in an isothermal reactor simulation, ThermoAgent first queries the minG tool to simulate the process. Based on the simulation results and the user’s question, it then formulates a query to the RAG Agent. Combining the outputs from the RAG Agent and the minG tool, ThermoAgent generates and returns the final response to the user.
These simulation tools are powered by robust implementations of the Peng–Robinson EoS and utilize the open-source thermo version 0.4.2 library for the fundamental thermodynamic properties of pure components.
For queries that require contextual or descriptive information rather than numerical calculation, ThermoAgent delegates the task to a specialized RAG Agent. This agent is connected to a knowledge base built from relevant technical documents, articles, and textbooks. For this work, the knowledge base is indexed into a vector database using FAISS, which creates a temporary, local instance for each user session. The RAG Agent retrieves the most relevant information from this database and provides it as context for generating a comprehensive answer.
The reasoning capabilities of both ThermoAgent and the RAG Agent, as well as the final synthesis of all responses, are powered by the gpt-4.1-mini LLM (Large Language Model), accessed through the Azure OpenAI. This integrated architecture allows ThermoAgent to deliver hybrid responses that seamlessly combine rigorous, first-principles thermodynamic calculations with knowledge extracted from a specialized document corpus, providing deep and contextually rich insights into the system’s behavior.
4. Results
The previous sections provided details on the approach used for equilibrium calculations as well as the assumptions adopted. This section aims to present the results obtained by applying the described methodologies. Initially, results are shown to validate the TeS v.3 simulations; thus, Section 4.1, Section 4.2, and Section 4.3 present outcomes generated by TeS v.3 without the assistance of AI, with the goal of verifying the steam methane reforming process and demonstrating the tool’s predictive accuracy. Section 4.4 is dedicated to results obtained with the support of ThermoAgent.
4.1. Validation of Thermodynamic Modeling
4.1.1. Validation with Simulated Data
To validate the results reported by TeS v.3, both simulated and experimental data from previous studies on the SMR process are used. As an initial verification, Figure 2 presents the results generated by TeS v.3 alongside simulated data reported by Freitas and Guirardello [53], Ávila et al. [54], and Seo et al. [55].
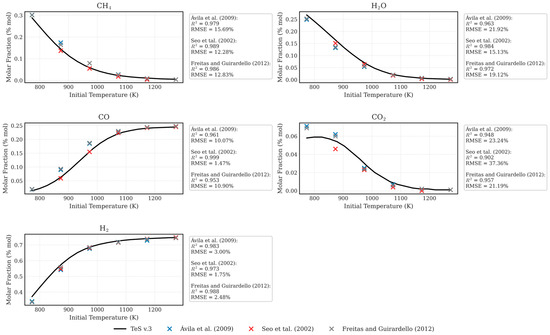
Figure 2.
Validation of simulated data with TeS with data simulated by Freitas and Guirardello [53], Ávila et al. [54], and Seo et al. [55].
Ávila et al. [54] evaluated the SMR process using two distinct calculation methodologies: the evaluation of equilibrium constants through Lagrange multipliers, which was solved using Scilab. The data presented in this work refer to the methodology based on Lagrange multipliers. The authors reported the molar ratios of CH4, H2, CO, and CO2 at 10 atm with a H2O/CH4 ratio equal to 1, for temperatures ranging from 773 to 1273 K.
Seo et al. [55] used Aspen Plus™ under conditions similar to those presented by Ávila et al. [54]. Freitas and Guirardello [53] investigated the SMR process using a robust approach based on the truncated Virial equation (truncated in the second term) to account for non-idealities. The simulations were performed using GAMS with CONOPT 3 as the solver. The SMR process was evaluated under the same conditions as those considered by the previously mentioned authors.
To validate the results obtained with TeS v.3, simulations were reproduced under the exact conditions described by the referenced authors. The outcomes, presented in Figure 2, show excellent agreement between TeS v.3 predictions and the literature data. For all evaluated cases, TeS v.3 achieved coefficients of determination (R2) above 0.9.
The primary benchmark in this validation was the comparison with the results reported by Freitas and Guirardello [53], who employed the CONOPT 3 solver, renowned for its robustness in solving highly nonlinear problems similar to those addressed by Ipopt. In these comparisons, TeS v.3 consistently delivered R2 values exceeding 0.95.
This thorough validation with simulated data confirms the accuracy and reliability of TeS v.3 for thermodynamic equilibrium calculations. The strong alignment with results from established academic studies and commercial software, evidenced by R2 consistently greater than 0.9, highlights the predictive capability of the model. Particularly, the high agreement with the benchmark data from Freitas and Guirardello [56], with R2 surpassing 0.95, underscores the numerical precision of TeS v.3 when compared to results generated using the robust CONOPT 3 solver.
4.1.2. Validation with Experimental Data
More important than validating simulated data against simulations reported by other authors is the validation of simulated data against experimental data, which is essential. Figure 3 presents a comparison between the simulated data obtained using TeS v.3 and the experimental data reported by Rakass et al. [56]. The experiments conducted by Rakass et al. [56] were carried out at 1 atm, with a H2O/CH4 molar ratio of 2:1 and temperatures ranging from 300 to 800 °C. The authors employed unsupported nickel powder as the catalyst.
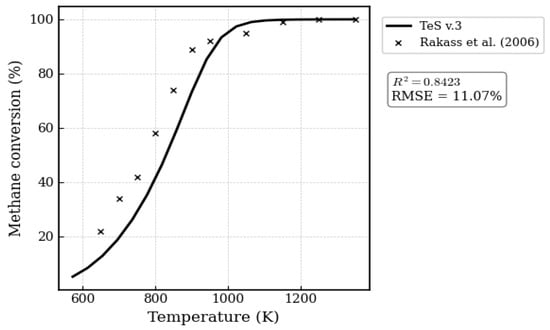
Figure 3.
Validation of TeS-simulated data with experimental data reported by Rakass et al. [56].
Discrepancies between simulated and experimental data are to be expected, especially in this case, since the authors employed a catalyst to drive the reaction an effect that cannot be captured by the methodology implemented in TeS v.3. Nevertheless, the results obtained with TeS v.3 show good agreement with the experimental data reported by Rakass et al. [56], achieving an R2 value greater than 0.84.
In addition to the experimental data reported by Rakass et al. [56], the simulated results from TeS v.3 were also evaluated against data presented by Khzouz and Gkanas [57]. The authors investigated the SMR process at temperatures ranging from 500 to 700 °C, at 1 atm, using a feed composition with a steam-to-carbon (S/C) ratio of 2. The experiments were conducted with a 10% nickel catalyst supported on alumina (Ni/Al2O3).
In addition to the experimental data, Khzouz and Gkanas [57] also reported simulated results by applying the Gibbs energy minimization approach under the same conditions as those used in their experiments. As verified in Figure 4, the results obtained with TeS v.3 demonstrate a high degree of accuracy and predictive capability. The simulator’s outputs show excellent agreement with the simulated thermodynamic equilibrium data from Khzouz and Gkanas [57], achieving a coefficient of determination of over 0.98. This near-perfect correlation primarily validates the fundamental thermodynamic engine of TeS v.3, confirming its ability to accurately replicate established equilibrium models.
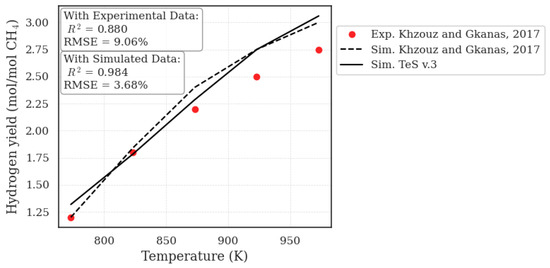
Figure 4.
Validation of TeS v.3-simulated data with simulated and experimental data reported by Khzouz and Gkanas [57].
Furthermore, it is essential to highlight that TeS v.3 is designed as a purely thermodynamic simulator and, as such, does not account for the kinetic effects inherent to catalytic processes. Even with this scope, the simulator shows good agreement with the experimental data (R2 = 0.88), successfully modeling the process’s real-world trends. Therefore, the divergence between the ideal equilibrium predicted by TeS v.3 and the physical experiment’s outcome is an expected result. This gap can be confidently attributed to the kinetic and mass transport limitations imposed by the catalyst in the experimental setup, phenomena that are intentionally outside the scope of a pure equilibrium simulation.
4.1.3. Conclusions About Validations
The validation confirms TeS v.3 as a robust and reliable tool for thermodynamic analysis of the SMR process. The simulator showed strong agreement with commercial software, academic models, and open-source tools, achieving high coefficients of determination (R2 > 0.95) and low deviations, validating both its thermodynamic framework and numerical implementation.
When compared with experimental data, TeS v.3 effectively captured real process trends, despite not accounting for catalytic kinetics. The deviations observed align with expectations, confirming that TeS predicts the ideal thermodynamic equilibrium and serves as a theoretical benchmark.
With the validity of TeS established, the following sections apply the minG and maxS methodologies to investigate the SMR process under various operating conditions.
4.2. Evaluation of the Process Conditioned to Isothermal Reactors
The results presented in this section were generated using TeS v.3, employing the Peng–Robinson EoS to account for non-ideal behavior and allowing for the formation of components in both phases using minG. The SMR process was investigated over a temperature range of 773–1273 K, pressures from 1 to 10 bar, and methane feed compositions ranging from 0.5 to 3.0 mol, while the amount of steam in the feed was fixed at 1 mol. A total of 8000 simulations were performed in approximately 3 min.
A response surface is a useful tool for analyzing the combined effects of multiple variables on an outcome. In TeS v.3, this analysis is supported. Figure 5 shows the effects of temperature and pressure on key component formation in the SMR process for a fixed methane feed of 1 mol.
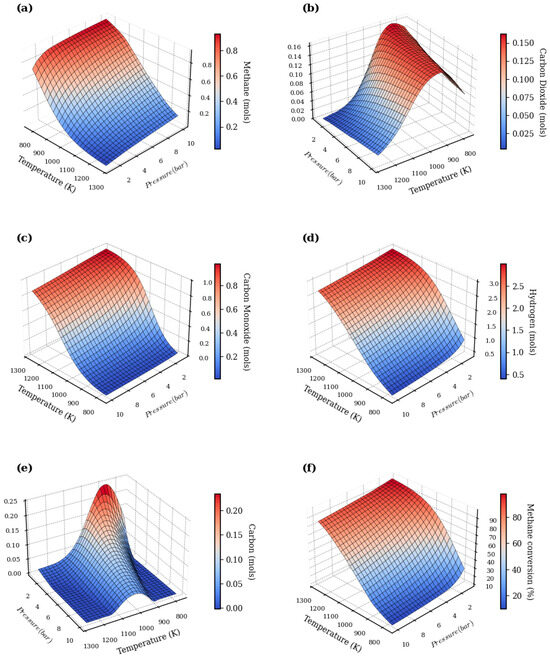
Figure 5.
Combined effects of pressure and temperature on product formation throughout the methane steam reforming process. (a): methane; (b): carbon dioxide; (c): carbon monoxide; (d): hydrogen; (e): carbon; (f): methane conversion.
The evaluation of the reactants, particularly methane (Figure 5a), reveals that its molar fraction consistently decreases with increasing temperature. This indicates a conversion approaching 100% under the most severe conditions, a typical behavior of endothermic reactions. SMR is conventionally carried out at high temperatures (700–1000 °C) and moderate pressures (3–25 bar), where the thermodynamic equilibrium shifts toward product formation at higher temperatures and lower pressures. Increasing the pressure, on the other hand, exerts a slight adverse effect by shifting the equilibrium away from the desired products [58,59,60].
As a result, the formation of products exhibits distinct behaviors. Hydrogen production (Figure 5d), the main product of interest, is significantly enhanced at high temperatures and low pressures, reaching molar fractions above 0.6. This trend aligns with Le Chatelier’s principle, as the reactions involved lead to an increase in the number of gas-phase moles [60]. The equilibrium of the reforming reaction and the water–gas shift reaction governs the optimal conditions for hydrogen yield [61].
In contrast, carbon monoxide (Figure 5c) presents a more complex profile, with a peak concentration at intermediate temperatures (900–1000 K). This reflects the competitive balance between its formation via reforming (CH4 + H2O → CO + 3H2) and its consumption via the WGS reaction (CO + H2O → CO2 + H2). The same WGS reaction governs the formation of carbon dioxide (Figure 5b), which also reaches a maximum at intermediate temperatures and is notably favored by higher pressures. The equilibrium constant for the WGS reaction decreases as temperature increases, explaining the observed trends.
Beyond the gaseous products, a critical issue is the deposition of solid carbon (Figure 5f), which shows a pronounced maximum around 900 K. This phenomenon is attributed to the competition between carbon-forming reactions—favored at lower temperatures (such as the Boudouard reaction: 2CO → C + CO2, and methane decomposition: CH4 → C + 2H2) and carbon-gasifying reactions (C + H2O → CO + H2, and C + CO2 → 2CO), which become dominant at higher temperatures. Carbon deposition is favored below 700 °C, while at temperatures above 700 °C, the Boudouard equilibrium shifts toward CO, reducing solid carbon formation [62]. In summary, the results show that for an S/C ratio of 1:1, the conditions that maximize hydrogen production and minimize carbon formation correspond to high temperatures (>1000 K) and low pressures (<5 bar).
A very useful way to examine potential correlations between process variables is through Pearson and Spearman correlation matrices. Pearson correlation assesses linear relationships between continuous variables, assuming data normality and being sensitive to outliers. In contrast, Spearman correlation is a non-parametric measure that evaluates monotonic relationships based on the ranked values of variables, making it more robust to nonlinear distributions and outliers. By analyzing both, it becomes possible to capture not only linear patterns but also more general trends between variables, providing a broader understanding of the system’s interactions. TeS v.3 enables the evaluation of simulated results through both Pearson and Spearman correlation matrices, enhancing the analysis and interpretation of the system’s thermodynamic behavior.
Figure 6 presents the Pearson and Spearman correlation matrices for the variables involved in the SMR process. The quantitative analysis of the relationships between operational variables (temperature, pressure, and steam-to-carbon ratio) and the products of the steam methane reforming process, as presented in the Pearson and Spearman correlation matrices, confirms and reinforces the thermodynamic principles previously discussed. The correlation coefficients quantify both the direction and strength of trends, providing a robust summary of the system’s behavior.
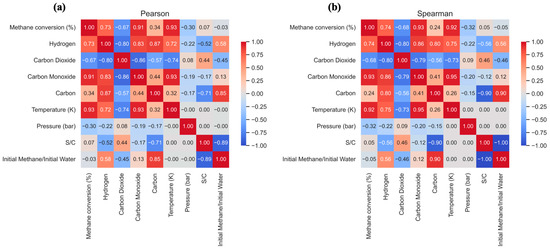
Figure 6.
Pearson (a) and Spearman (b) correlation matrix on the variables of the methane steam reforming process in an isothermal reactor (minG).
Temperature emerges as the most influential variable, showing a very strong positive correlation with methane conversion (+0.93) and carbon monoxide formation (+0.93), as well as a strong positive correlation with hydrogen production (+0.72). This trend reflects the strongly endothermic nature of the steam reforming reaction (CH4 + H2O ⇌ CO + 3H2). According to Le Chatelier’s principle, increasing temperature shifts the equilibrium toward heat consumption, favoring the forward reaction and leading to higher conversion and greater yields of H2 and CO. Conversely, the strong negative correlation between temperature and carbon dioxide formation (–0.74) is attributed to the exothermic nature of the water–gas-shift reaction (CO + H2O ⇌ CO2 + H2), where higher temperatures shift the equilibrium to the left, consuming CO2 and decreasing its molar fraction under high-temperature conditions.
The steam/carbon (S/C) ratio plays a critical role in modulating both selectivity and process stability. Its very strong negative correlation with carbon formation (–0.71) is particularly relevant from an industrial standpoint. Excess steam suppresses carbon deposition by promoting the gasification reaction and shifting the overall equilibrium away from the methane decomposition pathway. Additionally, the S/C ratio shows a moderate positive correlation with hydrogen (+0.52) and carbon dioxide (+0.44) production and a negative correlation with carbon monoxide (–0.17). This is because excess H2O shifts the WGS equilibrium to the right, converting more CO into CO2 and H2, thereby improving hydrogen yield at the expense of CO.
Pressure exhibits weaker, though still noticeable, negative correlations with methane conversion (–0.30), hydrogen (–0.22), and carbon monoxide formation (–0.19). The reforming reaction increases the total number of gas-phase moles (2 moles of reactants to 4 moles of products), and Le Chatelier’s principle indicates that increasing pressure shifts the equilibrium toward the side with fewer moles, the reactants thus disfavoring conversion and product yields.
In summary, the correlation matrices quantitatively validate the thermodynamic model of the SMR process. They show that optimizing hydrogen production requires a careful balance of operational conditions: high temperatures are essential for conversion, while a high S/C ratio is critical not only for maximizing hydrogen yield but also for preventing coke formation and ensuring process integrity. Although pressure has a thermodynamically adverse effect, its influence is less pronounced, allowing for industrial operation at moderate pressures for practical and economic reasons.
4.3. Evaluation of the Process Conditioned to Adiabatic Reactors
The results presented in this section were generated using TeS v.3, which employed the Peng–Robinson equation of state to account for non-ideal behavior and allowed for the formation of components in both gas and liquid phases via the maxS methodology. The SMR process was explored across a temperature range of 800–1500 K, pressures from 1 to 10 bar, and methane feed compositions ranging from 0.5 to 3.0 mol, with the steam feed fixed at 1 mol. A total of 8000 simulations were completed in approximately 4.5 min.
An initial observation is that the simulation time required for maxS is longer than that for minG, due to the inclusion of an additional constraint, enthalpy conservation, which increases the overall complexity of the optimization problem. Another relevant point is the tendency for maxS to result in higher equilibrium temperatures. This outcome reflects the adiabatic nature of the reactor modeled in maxS, which lacks external thermal support, unlike an isothermal reactor. As a result, the SMR process tends to exhibit improved performance at higher temperatures under maxS conditions, in contrast to the minG approach.
Figure 7 presents the equilibrium compositions and temperature for the SMR process under adiabatic conditions at 1 bar, with 1 mol of methane in the feed.
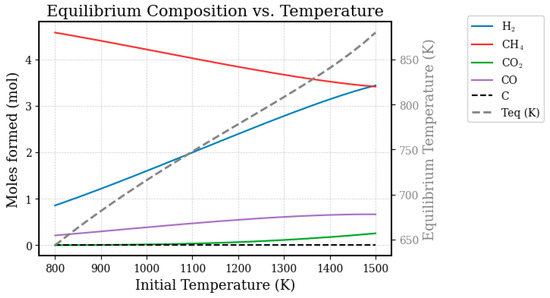
Figure 7.
Product formation and equilibrium temperature as a function of temperature for the steam reforming process of methane conditioned in an adiabatic reactor (maxS).
The results presented in Figure 7 highlight a fundamental and limiting characteristic of this type of operation: the high amount of residual methane in the outlet stream, indicating low reactant conversion even at very high inlet temperatures. This behavior is mainly attributed to the self-limiting nature of the process, which combines adiabatic operation with the strongly endothermic character of the reforming reaction [42,63,64]
Although the feed enters the reactor at an elevated temperature, the reaction consumes heat from the system itself, resulting in a sharp temperature drop, as illustrated by the dashed line representing the equilibrium temperature (Teq). Chemical equilibrium is thus established at this significantly lower outlet temperature, where methane conversion is thermodynamically less favorable [65,66].
As a direct consequence, the product formation trends reflect this limitation: hydrogen and carbon monoxide production increase only gradually with rising inlet temperature, since Teq, although also increasing, remains at a level that restricts the advancement of the reaction. This observation aligns with previous thermodynamic studies showing the critical dependence of methane conversion on system temperature [67].
Figure 7 also indicates that solid carbon formation is thermodynamically inhibited under these conditions, which is consistent with the literature reporting that carbon deposition is favored at lower temperatures and higher C/H ratios [68].
In summary, Figure 7 demonstrates the main drawback of a simple adiabatic reactor, emphasizing that achieving the high conversions required in industrial practice demands a continuous heat supply to maintain elevated system temperatures and overcome this intrinsic thermodynamic barrier [69].
In addition to the initial temperature, it is also important to assess the effect of feed composition on the equilibrium temperature of the reaction system. Figure 8 presents the behavior of the equilibrium temperature as a function of the H2O/CH4 molar ratio at 1 bar simulated using TeS v.3 and data reported simulated by Freitas and Guirardello [53] at same conditions.
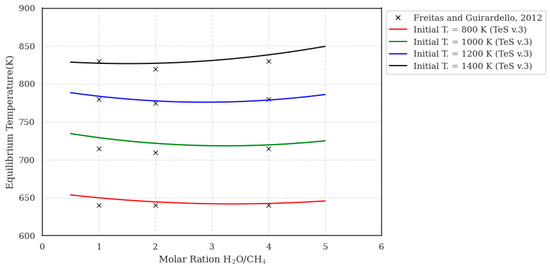
Figure 8.
Equilibrium temperature as a function of the H2O/CH4 feed ratio for the steam methane reforming process under adiabatic reactor conditions (maxS).
The results presented in Figure 8 illustrate the behavior of the equilibrium temperature during the SMR process operating under adiabatic conditions at 1 bar. The most prominent feature observed is the sharp drop in temperature between the reactor inlet and outlet. This phenomenon is a direct consequence of the strongly endothermic nature of the reforming reaction, which, occurring in a system without heat exchange with the surroundings, consumes the energy of the reactive mixture itself, reducing its temperature until chemical equilibrium is reached. The figure also demonstrates that an increase in the H2O/CH4 molar ratio causes a slight rise in the equilibrium temperature. This behavior is explained by the fact that, with the steam flow fixed, a higher S/C ratio implies a lower amount of methane in the feed, which reduces the overall extent of the endothermic reaction and, consequently, the total heat consumed. The validity of the employed model is confirmed by the excellent agreement (R2 > 0.98) between the results simulated by TeS v.3 and the reference data from Freitas and Guirardello [53], indicating that the energy balance and chemical equilibrium of the adiabatic reactor are accurately described.
In order to investigate the combined effects of process variables on the equilibrium temperature behavior throughout the SMR process, Figure 9 shows the combined effects of these variables on the outlet equilibrium temperature of an adiabatic SMR reactor. The results presented in Figure 9a were simulated by fixing the methane feed at 1 mol, while for Figure 9b, the pressure was fixed at 1 bar.
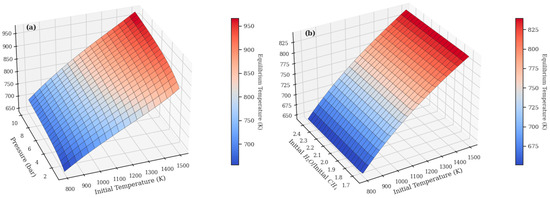
Figure 9.
Combined effects of initial temperature and pressure (a) and initial temperature and H2O/CH4 molar ratio (b) on the equilibrium temperature of the SMR process in an adiabatic reactor (maxS).
Analysis of Figure 9a reveals that, for a given initial temperature, an increase in pressure results in a higher equilibrium temperature. This seemingly counterintuitive trend is a direct consequence of Le Chatelier’s principle: since the reforming reaction involves an increase in the number of gas moles, high pressure inhibits methane conversion. Given the reaction’s strongly endothermic nature, lower conversion means less heat is consumed from the system, resulting in a less pronounced temperature drop and, consequently, a higher Teq. Similarly, Figure 9b shows that an increase in the H2O/CH4 molar ratio also raises the final equilibrium temperature. In this case, increasing the steam-to-carbon ratio dilutes the concentration of the limiting reactant (methane), which decreases the overall extent of the endothermic reaction that can occur. Again, with less reaction, less heat is consumed, and the outlet temperature remains higher. Therefore, Figure 10 effectively illustrates that the outlet temperature of an adiabatic SMR reactor is governed by the extent of the endothermic conversion, which can be modulated by both pressure and the stoichiometric ratio of the reactants.
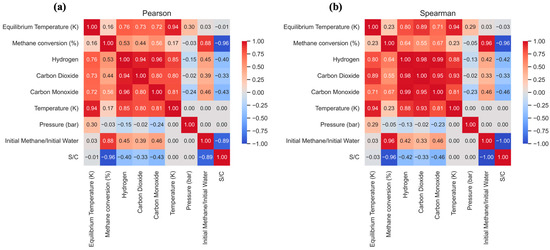
Figure 10.
Pearson (a) and Spearman (b) correlation matrix for the variables of the methane steam reforming process in an adiabatic reactor (maxS).
Finally, Figure 10 presents the Pearson and Spearman correlation matrices, which serve as a quantitative and conclusive summary of the behavior of the adiabatic SMR reactor, synthesizing all previous observations.
The analysis of these coefficients numerically confirms the complex interdependence of the variables. The most revealing result is the very weak correlation between initial temperature (K) and methane conversion (%), with a coefficient of only +0.17 (Pearson). This low value quantitatively substantiates the discussion from previous figures regarding the self-limiting nature of the adiabatic reactor. It confirms that simply increasing the inlet temperature is an inefficient strategy for enhancing conversion, as the adiabatic temperature drop imposes a thermodynamic constraint.
Moreover, the matrix elucidates the underlying relationships between variables. A very strong positive correlation (+0.94) is observed between initial temperature and equilibrium temperature. This, together with the strong positive correlation (+0.76) between Teq and hydrogen formation, delineates the causal sequence: increasing the inlet temperature raises the final operating temperature, which in turn accounts for the modest increase in hydrogen production. The effect of pressure corroborates the analysis in Figure 10a, exhibiting a positive correlation with Teq (+0.30) and a negative correlation with conversion (−0.15), confirming that pressure suppresses the endothermic reaction, resulting in lower conversion but a less pronounced temperature decline.
The strongest correlation within the system is associated with the S/C ratio, displaying a pronounced negative correlation with carbon formation (−0.89), thereby underscoring its critical role as an inhibitor of coke deposition, a conclusion consistent across all analyses.
As the main conclusion, the performance of an adiabatic reforming reactor is governed by its internal energy balance. Process variables modulate the extent of the endothermic reaction, which dictates the final equilibrium temperature and, consequently, the achievable conversion and selectivity, highlighting the intrinsic limitations of this configuration compared to externally heated systems.
4.4. Process Evaluation with the Help of the AI Agent
As a final step in this study, the ThermoAgent feature will be employed to generate insights based on simulations using the equilibrium calculation modules previously described, given that the preceding sections have confirmed their validity.
As illustrated in Figure 1, ThermoAgent is capable of integrating the equilibrium calculation modules and receives user prompts as input. For this study, three scientific articles were used to enrich the contextual knowledge and to support the construction of the Retrieval-Augmented Generation (RAG) Agent knowledge base. The selected articles are as follows:
- Reaction Mechanism Development for Methane Steam Reforming on a Ni/Al2O3 Catalyst, Richter et al. [70];
- Catalytic Hydrogen Production from Methane: A Review on Recent Progress and Prospect, Chen et al. [12];
- Analytical and Numerical Thermodynamic Equilibrium Simulations of Steam Methane Reforming: A Comparison Study, Varandas et al. [59].
All the referenced articles are open access and are used solely as contextual sources for knowledge retrieval within ThermoAgent. As such, they are not used for training machine learning models, and this process does not infringe upon any data protection policies or intellectual property rights.
The first use case evaluated by ThermoAgent is defined as follows:
“Please simulate the steam methane reforming process considering the following components: CH4, H2O, H2, CO, CO2, and C. The feed consists of 2 mol of steam and 1 mol of methane. Evaluate the process across a temperature range of 700–1200 K at 1 bar in an isothermal reactor.”
This prompt was processed by ThermoAgent using the previously validated thermodynamic equilibrium modules (only minG for this example). The system automatically parsed the input parameters, selected the appropriate computational module, and carried out the simulation.
The text below presents the response generated by ThermoAgent:
“Here is the simulation of the steam methane reforming process in an isothermal reactor at 1 bar, with temperature ranging from 700 to 1200 K. The feed consists of 1 mol of CH4 and 2 mol of H2O. The Table 1 shows the equilibrium molar amounts of the components: Table 1. Results for SMR with 1 mole of methane and 2 moles of water at 1 bar.
Table 1. Results for SMR with 1 mole of methane and 2 moles of water at 1 bar.
As temperature increases, methane and water decrease, while hydrogen and carbon monoxide increase, consistent with the steam reforming reaction. Solid carbon formation is negligible at equilibrium. Let me know if you need further analysis or graphs.”
Overall, ThermoAgent responded very satisfactorily to the task. The statement that increasing temperature favors solid carbon formation is strongly supported by the findings of Varandas et al. [59].
The next step involves extracting insights based on the simulated results. The subsequent prompt is presented below:
“What justifies the absence of solid carbon formation under the simulated conditions?”
As a response:
“The absence of solid carbon formation under the simulated conditions (1 bar pressure and temperature range 700–1200 K) in steam methane reforming (SMR) can be justified by the thermodynamic equilibrium and operational parameters typical of the process:
1. High Steam-to-Carbon Ratio: The feed contains excess steam (2 mol H2O per 1 mol CH4), which favors the reforming reactions and suppresses carbon deposition. Steam reacts with carbon precursors, converting them into CO and CO2, thus minimizing solid carbon formation.
2. Low Pressure: SMR is more favorable at low pressures (around 1 bar), which also helps reduce carbon deposition. Higher pressures tend to favor methane decomposition and carbon formation.
3. Coupling with Water-Gas Shift Reaction: The presence of steam and CO promotes the water-gas shift reaction (CO + H2O ⇄ CO2 + H2), which helps consume CO and maintain a gas-phase equilibrium, further reducing the likelihood of carbon formation.
In summary, the combination of high steam content, appropriate temperature range, low pressure, and equilibrium favoring gaseous products explains the negligible solid carbon formation in the simulation.
References from the literature support these points, indicating that carbon formation is minimized under typical SMR conditions and becomes significant only under conditions of low steam-to-carbon ratio, lower temperatures, or very high temperatures with different pressure conditions.
If you want, I can provide more detailed references or further analysis.”
Once again, the results are satisfactory for the given request. In summary, all the statements presented above are consistent with the selected reference texts, including the studies by Richter et al. [70], Chen et al. [12], and Varandas et al. [59], which provide both theoretical and experimental support for the thermodynamic behaviors observed in the simulations conducted using ThermoAgent.
Another relevant scenario would be comparing the behavior of the SMR process in isothermal and adiabatic reactors. For this case, ThermoAgent would need to consult the minG and maxS tools. The prompt presented for this request is as follows:
“Simulate the steam methane reforming process considering the following components: CH4, H2O, H2, CO, CO2, and C. The feed consists of 2 moles of steam and 1 mole of methane. Evaluate this process in isothermal and adiabatic reactors. Assess the hydrogen formation performance and the thermal behavior of the reaction system.”
As expected, ThermoAgent used the minG and maxS tools to simulate the process in isothermal and adiabatic reactors, respectively. In parallel, RAG Agent queried the process to gather context. The results are presented below:
“The simulation results for methane steam reforming (SMR) in isothermal and adiabatic reactors were satisfactory, using a 2:1 H2O to CH4 feed ratio. Figure 11 compares hydrogen formation in both scenarios, while Figure 12 illustrates thermal behavior for the adiabatic case.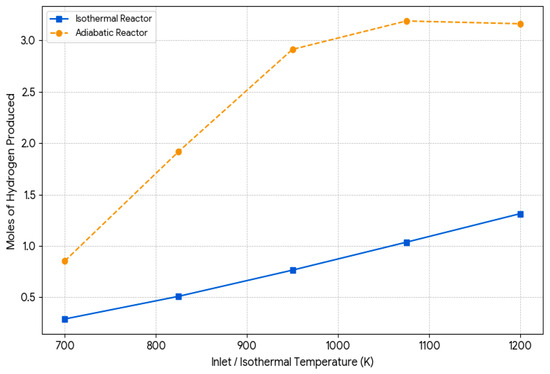 Figure 11. Hydrogen production vs. inlet temperature.
Figure 11. Hydrogen production vs. inlet temperature.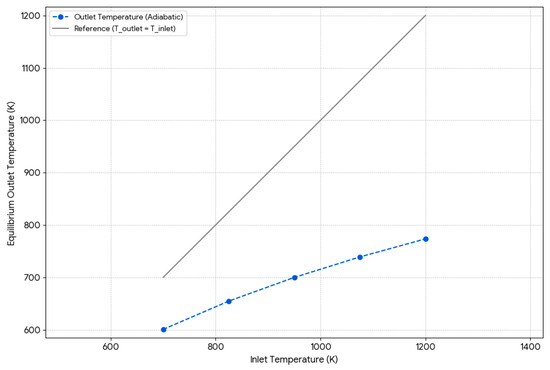 Figure 12. Temperatura profilein adiabatic reactor.
Figure 12. Temperatura profilein adiabatic reactor.
In the isothermal reactor, constant temperature is maintained through continuous heat supply, which strongly favors the endothermic reforming reaction (CH4 + H2O ⇌ CO + 3H2). The simulation shows that hydrogen production increases with temperature, confirming the reactor’s superior performance across all inlet temperatures. Based on Chen et al. [12], this is due to the reaction’s high enthalpy change (ΔH°(298K) = +206 kJ/mol), which shifts equilibrium toward hydrogen and CO under higher heat. Additionally, no carbon formation was observed, likely because favorable conditions allow gasification reactions (e.g., C + H2O ⇌ CO + H2) to prevent coke accumulation. In contrast, the adiabatic reactor, which does not exchange heat with the surroundings, showed a notable drop in outlet temperature, especially at higher inlet values. This temperature drop limits the extent of the endothermic reaction, reducing conversion and hydrogen yield compared to the isothermal reactor. Some carbon formation was detected at lower inlet temperatures, which may be due to local cooling favoring methane decomposition (CH4 ⇌ C + 2H2) over gasification, as described by Varandas et al. [59]. In conclusion, isothermal reactors offer better performance by continuously supplying the energy required for reforming, while adiabatic reactors are limited by intrinsic thermal drops, leading to lower efficiency under identical conditions.
The above results reveal ThermoAgent’s high potential for solving the requested equilibrium problems, but especially for justifying the results using the model’s knowledge base enriched by context generated by RAG Agent. ThermoAgent also displays the references used and graphically displays the results for the analyses requested by the user.
In general, ThermoAgent produced results that are consistent with the literature used as a reference and accurately simulated all the tested cases. The examples presented are merely illustrative; however, the tool is capable of performing much more complex simulations and generating advanced insights.
To validate the consistency of ThermoAgent’s responses, we adopted a simple yet effective testing approach. Although there are no well-established metrics for assessing agent performance, we designed a validation procedure based on repeated simulations and the use of a secondary agent to verify the outputs. This testing agent had access to the ground-truth answers for the requested problems, enabling the calculation of performance metrics. The results obtained are as follows:
- Total tests performed: 20;
- Accuracy of simulated data: 100%;
- Accuracy of tool selection: 100%;
- Accuracy of parameter selection: 100%;
- Quality of generated discussions: good.
These results confirm the reliability of ThermoAgent within the tested scope. The 100% accuracy in both tool and parameter selection demonstrates that, for example, when an isothermal reactor simulation was required, ThermoAgent consistently invoked the correct tool. Likewise, the simulated data perfectly matched the ground-truth values provided to the testing agent. While the architecture may still be susceptible to erroneous calls or parameter misselection under more complex or ambiguous scenarios, no such issues were observed in this study, reinforcing the robustness of ThermoAgent in the evaluated cases.
Beyond accuracy, ThermoAgent offers significant practical advantages. It allows users to simulate complex processes and formulate advanced queries using only natural language, eliminating the need for manual configuration or specialized commands. Moreover, the agent performs simulations and document retrieval in parallel, enabling it to simultaneously generate results, compare multiple scenarios, and retrieve relevant references. This integrated approach considerably reduces the time required for analysis while enhancing the depth and quality of the insights produced.
This validation completes the cycle proposed in this work. Initially, the methodologies for thermodynamic equilibrium calculations were validated against both simulated and experimental data, showing excellent agreement. Subsequently, the steam methane reforming process was analyzed using Gibbs energy minimization and entropy maximization to evaluate system behavior under different conditions. Finally, ThermoAgent demonstrated strong predictive capabilities and high potential to support users by performing simulations, comparing scenarios, retrieving references, and extracting knowledge from both documents and simulated data, all through simple natural language prompts.
5. Conclusions
This study detailed the development, validation, and application of TeS v.3, a thermodynamic equilibrium simulator designed for complex reacting systems, using steam methane reforming as a rigorous case study. Comprehensive validation demonstrated the simulator’s high accuracy and reliability, showing excellent agreement (coefficient of determination R2 > 0.95) with simulation data from an academic benchmark. Additionally, TeS v.3 exhibited a strong ability to capture trends observed in experimental data, with deviations consistent with kinetic and mass transport limitations inherent to catalytic systems, which are not accounted for in a pure equilibrium simulation.
The SMR process analysis revealed distinct and fundamental behaviors for both isothermal and adiabatic reactors. For isothermal reactors, the results confirmed that high temperatures and low pressures maximize hydrogen production, while solid carbon formation exhibits a complex behavior with a peak at intermediate temperatures (around 900 K). In contrast, the analysis of adiabatic reactors demonstrated the self-limiting nature of the process, where the significant temperature drop caused by the endothermic reaction severely limits methane conversion, even under high inlet temperatures. This limitation was quantitatively confirmed by the weak correlation (+0.17) between the initial temperature and conversion.
The central focus of this work was the successful demonstration of ThermoAgent, an AI agent integrated with TeS v3 simulator. ThermoAgent proved capable of interpreting natural language prompts to autonomously perform simulations, analyze results, and, importantly, leverage a knowledge base via an RAG system to provide precise and context-rich thermodynamic justifications in the thermodynamic study of the SMR process. The agent’s ability to perform goal-oriented simulations, such as maximizing carbon formation, illustrates its potential as an advanced analytical tool.
In summary, this work not only validates TeS v.3 as a robust and open-source tool for thermodynamic analysis but also introduces a new paradigm for process simulation where the synergy between first-principles-based models and artificial intelligence agents accelerates knowledge extraction, enriches analysis, and enhances the understanding of complex chemical systems.
6. Patents
The results presented in this article were developed using TeS (Thermodynamic Equilibrium Simulation) software. This software was developed by the authors of this text, and this article marks the first publication using this tool version (v.3). TeS was registered by the National Institute of Industrial Property with registration number BR512025000478-8.
Author Contributions
J.M.d.S.J.: project proposal, methodology, and software development. J.M.d.S.J.: research and validation. J.M.d.S.J.: development of results. J.M.d.S.J. and A.P.M. and A.C.D.d.F.: constant evaluation of results. A.P.M. and A.C.D.d.F.: supervision and guidance throughout the development of the article. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study were generated through simulations based on the previously described thermodynamic approach. As discussed throughout the text, the simulation tool used (TeS) was developed to support academic studies and research in general. The simulator is publicly available here and can be used by anyone interested. Access to the ThermoAgent repository is available upon request. Interested parties should contact the authors of this work.
Acknowledgments
The authors extend their gratitude to the dedicated faculty at the University of Campinas and the Federal University of Maranhão for their invaluable contributions to the personal and professional growth of countless people, as well as to all educators who actively promote the advancement of society.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Franco, I.C. Modeling and Simulation: Chemical Processes. J. Eng. Exact. Sci. 2021, 7, francoic2021-01. [Google Scholar] [CrossRef]
- Foo, D. Chemical Engineering Process Simulation; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Gmehling, J.; Kleiber, M.; Kolbe, B.; Rarey, J. Chemical Thermodynamics for Process Simulation; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Barros, T.V.; Carregosa, J.d.C.; Wisniewski, A., Jr.; Freitas, A.C.D.; Guirardello, R.; Ferreira-Pinto, L.; Bonfim-Rocha, L.; Jegatheesan, V.; Cardozo-Filho, L. Assessment of black liquor hydrothermal treatment under sub- and supercritical conditions: Products distribution and economic perspectives. Chemosphere 2022, 286, 131774. [Google Scholar] [CrossRef]
- Junior, J.M.d.S.; Gomes, J.G.; de Freitas, A.C.D.; Guirardello, R. An Analysis of the Methane Cracking Process for CO2-Free Hydrogen Production Using Thermodynamic Methodologies. Methane 2022, 1, 243–261. [Google Scholar] [CrossRef]
- Gomes, J.G.; Mitoura, J.; Guirardello, R. Thermodynamic analysis for hydrogen production from the reaction of subcritical and supercritical gasification of the C. Vulgaris microalgae. Energy 2022, 260, 125030. [Google Scholar] [CrossRef]
- Freitas, A.C.D.; Guirardello, R. Thermodynamic characterization of hydrocarbon synthesis from syngas using fischer-tropsch type reaction. Chem. Eng. Trans. 2015, 43, 1831–1836. [Google Scholar] [CrossRef]
- Freitas, A.C.D.; Guirardello, R. Use of CO2 as a co-reactant to promote syngas production in supercritical water gasification of sugarcane bagasse. J. CO2 Util. 2015, 9, 66–73. [Google Scholar] [CrossRef]
- Freitas, A.C.D.; Guirardello, R. Oxidative reforming of methane for hydrogen and synthesis gas production: Thermodynamic equilibrium analysis. J. Nat. Gas Chem. 2012, 21, 571–580. [Google Scholar] [CrossRef]
- Tabrizi, F.F.; Mousavi, S.A.H.S.; Atashi, H. Thermodynamic analysis of steam reforming of methane with statistical approaches. Energy Convers. Manag. 2015, 103, 1065–1077. [Google Scholar] [CrossRef]
- Pashchenko, D. Thermodynamic equilibrium analysis of steam methane reforming based on a conjugate solution of material balance and law action mass equations with the detailed energy balance. Int. J. Energy Res. 2020, 44, 438–447. [Google Scholar] [CrossRef]
- Chen, L.; Qi, Z.; Zhang, S.; Su, J.; Somorjai, G.A. Catalytic Hydrogen Production from Methane: A Review on Recent Progress and Prospect. Catalysts 2020, 10, 858. [Google Scholar] [CrossRef]
- Dobbelaere, M.R.; Plehiers, P.P.; Van de Vijver, R.; Stevens, C.V.; Van Geem, K.M. Machine Learning in Chemical Engineering: Strengths, Weaknesses, Opportunities, and Threats. Engineering 2021, 7, 1201–1211. [Google Scholar] [CrossRef]
- Xu, W.; Wang, Y.; Zhang, D.; Yang, Z.; Yuan, Z.; Lin, Y.; Yan, H.; Zhou, X.; Yang, C. Transparent AI-assisted chemical engineering process: Machine learning modeling and multi-objective optimization for integrating process data and molecular-level reaction mechanisms. J. Clean. Prod. 2024, 448, 141412. [Google Scholar] [CrossRef]
- Seider, W.D.; Lewin, D.R.; Seader, J.D.; Widagdo, S.; Gani, R.; Ng, K.M. Product and Process Design Principles: Synthesis, Analysis and Evaluation; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Sandrock, C.; de Vaal, P.L. Dynamic Simulation of Chemical Engineering Systems Using OpenModelica and CAPE-OPEN; 2009; pp. 859–864. Available online: https://www.sciencedirect.com/science/article/abs/pii/S1570794609701439 (accessed on 1 August 2025).
- Tangsriwong, K.; Lapchit, P.; Kittijungjit, T.; Klamrassamee, T.; Sukjai, Y.; Laoonual, Y. Modeling of chemical processes using commercial and open-source software: A comparison between Aspen Plus and DWSIM. IOP Conf. Ser. Earth Environ. Sci. 2020, 463, 012057. [Google Scholar] [CrossRef]
- Andreadou, C.; Martinopoulos, G. CAPE-OPEN simulation of waste-to-energy technologies for urban cities. Int. J. Sustain. Energy 2018, 37, 96–104. [Google Scholar] [CrossRef]
- Alqaheem, Y.; Alobaid, M. Development of a membrane process in CAPE-OPEN to CAPE-OPEN (COCO) simulator for carbon dioxide separation. Results Eng. 2024, 22, 102239. [Google Scholar] [CrossRef]
- Ferro, V.R.; De Riva, J.; Sanchez, D.; Ruiz, E.; Palomar, J. Conceptual design of unit operations to separate aromatic hydrocarbons from naphtha using ionic liquids. COSMO-based process simulations with multi-component “real” mixture feed. Chem. Eng. Res. Des. 2015, 94, 632–647. [Google Scholar] [CrossRef]
- Kontogeorgis, G.M.; Folas, G.K. Thermodynamic Models for Industrial Applications: From Classical and Advanced Mixing Rules to Association Theories; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Prausnitz, J.M.; Lichtenthaler, R.N.; De Azevedo, E.G. Molecular Thermodynamics of Fluid-Phase Equilibria; Pearson Education: London, UK, 1998. [Google Scholar]
- Gross, J.; Sadowski, G. Perturbed-chain SAFT: An equation of state based on a perturbation theory for chain molecules. Ind. Eng. Chem. Res. 2001, 40, 1244–1260. [Google Scholar] [CrossRef]
- Bonnans, J.-F.; Gilbert, J.C.; Lemaréchal, C.; Sagastizábal, C.A. Numerical Optimization: Theoretical and Practical Aspects; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Biegler, L.T.; Zavala, V.M. Large-scale nonlinear programming using IPOPT: An integrating framework for enterprise-wide dynamic optimization. Comput. Chem. Eng. 2009, 33, 575–582. [Google Scholar] [CrossRef]
- Cortes, Y.; Kummar, D.; Singh, V.; Guest, J. An Open Source Process Simulation Environment on Python for Automated Preliminary Techno-Economic Analysis. In Proceedings of the 2018 AIChE Annual Meeting, AIChE, Pittsburgh, PA, USA, 28 October–2 November 2018. [Google Scholar]
- Dimian, A.C.; Bildea, C.S.; Kiss, A.A. Integrated Design and Simulation of Chemical Processes; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Dunning, I.; Huchette, J.; Lubin, M. JuMP: A modeling language for mathematical optimization. SIAM Rev. 2017, 59, 295–320. [Google Scholar] [CrossRef]
- McKinney, W. Data structures for statistical computing in Python. SciPy 2010, 445, 51–56. [Google Scholar]
- Qin, S.J.; Chiang, L.H. Advances and opportunities in machine learning for process data analytics. Comput. Chem. Eng. 2019, 126, 465–473. [Google Scholar] [CrossRef]
- Venkatasubramanian, V. The promise of artificial intelligence in chemical engineering: Is it here, finally? AIChE J. 2019, 65, 466–478. [Google Scholar] [CrossRef]
- Schweidtmann, A.M.; Esche, E.; Fischer, A.; Kloft, M.; Repke, J.; Sager, S.; Mitsos, A. Machine learning in chemical engineering: A perspective. Chemie Ingenieur Technik 2021, 93, 2029–2039. [Google Scholar] [CrossRef]
- Gao, H.; Zhu, L.-T.; Luo, Z.-H.; Fraga, M.A.; Hsing, I.-M. Machine learning and data science in chemical engineering. Ind. Eng. Chem. Res. 2022, 61, 8357–8358. [Google Scholar] [CrossRef]
- Henao, C.A.; Maravelias, C.T. Surrogate-based superstructure optimization framework. AIChE J. 2011, 57, 1216–1232. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A comprehensive survey on particle swarm optimization algorithm and its applications. Math. Probl. Eng. 2015, 2015, 931256. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization: An overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Gao, Q.; Schweidtmann, A.M. Deep reinforcement learning for process design: Review and perspective. Curr. Opin. Chem. Eng. 2024, 44, 101012. [Google Scholar] [CrossRef]
- Villa, L.; Brusamarello, C.Z. Application of machine learning in monitoring fouling in heat exchangers in chemical engineering: A systematic review. Can. J. Chem. Eng. 2025, 103, 1786–1801. [Google Scholar] [CrossRef]
- Rosen, A.S.; Iyer, S.M.; Ray, D.; Yao, Z.; Aspuru-Guzik, A.; Gagliardi, L.; Notestein, J.M.; Snurr, R.Q. Machine learning the quantum-chemical properties of metal–organic frameworks for accelerated materials discovery. Matter 2021, 4, 1578–1597. [Google Scholar] [CrossRef]
- Satterfield, C.N. Heterogeneous Catalysis in Industrial Practice; 1991. Available online: https://www.osti.gov/biblio/5495428 (accessed on 1 August 2025).
- Xu, J.; Froment, G.F. Methane steam reforming, methanation and water-gas shift: I. Intrinsic kinetics. AIChE J. 1989, 35, 88–96. [Google Scholar] [CrossRef]
- Hou, K.; Hughes, R. The kinetics of methane steam reforming over a Ni/α-Al2O catalyst. Chem. Eng. J. 2001, 82, 311–328. [Google Scholar] [CrossRef]
- Castillo, J.; Grossmann, I.E. Computation of phase and chemical equilibria. Comput. Chem. Eng. 1981, 5, 99–108. [Google Scholar] [CrossRef]
- Rossi, C.C.R.S.; Berezuk, M.E.; Cardozo-Filho, L.; Guirardello, R. Simultaneous calculation of chemical and phase equilibria using convexity analysis. Comput. Chem. Eng. 2011, 35, 1226–1237. [Google Scholar] [CrossRef]
- Junior, J.M.D.S.; Mariano, A.P. Gasification of Lignocellulosic Waste in Supercritical Water: Study of Thermodynamic Equilibrium as a Nonlinear Programming Problem. Eng 2024, 5, 1096–1111. [Google Scholar] [CrossRef]
- Santos, J.M.D.; De Sousa, G.F.B.; Vidotti, A.D.S.; De Freitas, A.C.D.; Guirardello, R. Optimization of glycerol gasification process in supercritical water using thermodynamic approach. Chem. Eng. Trans. 2021, 86, 847–852. [Google Scholar] [CrossRef]
- Freitas, A.C.D.; Guirardello, R. Comparison of several glycerol reforming methods for hydrogen and syngas production using Gibbs energy minimization. Int. J. Hydrogen Energy 2014, 39, 17969–17984. [Google Scholar] [CrossRef]
- Peng, D.-Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Smith, J.M.; Van Ness, H.C.; Abbott, M.M.; Swihart, M.T. Introduction to Chemical Engineering Thermodynamics; McGraw-Hill: Singapore, 2018. [Google Scholar]
- Hart, W.E.; Laird, C.D.; Watson, J.-P.; Woodruff, D.L.; Hackebeil, G.A.; Nicholson, B.L.; Siirola, J.D. Pyomo-Optimization Modeling in Python; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Wang, L.; Ma, C.; Feng, X.; Zhang, Z.; Yang, H.; Zhang, J.; Chen, Z.; Tang, J.; Chen, X.; Lin, Y.; et al. A survey on large language model based autonomous agents. Front. Comput. Sci. 2024, 18, 186345. [Google Scholar] [CrossRef]
- Carlos Daltro de Freitas, A. Análise Termodinâmica de Processos de Reforma do Metano e da Síntese Fischer-Tropsch. Master’s Thesis, Universidade Estadual de Campinas, São Paulo, Brazil, 2012. [Google Scholar] [CrossRef]
- Ávila-Neto, C.N.; Dantas, S.C.; Silva, F.A.; Franco, T.V.; Romanielo, L.L.; Hori, C.E.; Assis, A.J. Hydrogen production from methane reforming: Thermodynamic assessment and autothermal reactor design. J. Nat. Gas Sci. Eng. 2009, 1, 205–215. [Google Scholar] [CrossRef]
- Seo, Y.-S.; Shirley, A.; Kolaczkowski, S.T. Evaluation of thermodynamically favourable operating conditions for production of hydrogen in three different reforming technologies. J. Power Sources 2002, 108, 213–225. [Google Scholar] [CrossRef]
- Rakass, S.; Oudghiri-Hassani, H.; Rowntree, P.; Abatzoglou, N. Steam reforming of methane over unsupported nickel catalysts. J. Power Sources 2006, 158, 485–496. [Google Scholar] [CrossRef]
- Khzouz, M.; Gkanas, E.I. Experimental and Numerical Study of Low Temperature Methane Steam Reforming for Hydrogen Production. Catalysts 2017, 8, 5. [Google Scholar] [CrossRef]
- Kogler, M.; Köck, E.-M.; Klötzer, B.; Schachinger, T.; Wallisch, W.; Henn, R.; Huck, C.W.; Hejny, C.; Penner, S. High-Temperature Carbon Deposition on Oxide Surfaces by CO Disproportionation. J. Phys. Chem. C 2016, 120, 1795–1807. [Google Scholar] [CrossRef]
- Varandas, B.; Oliveira, M.; Borges, A. Analytical and Numerical Thermodynamic Equilibrium Simulations of Steam Methane Reforming: A Comparison Study. Reactions 2024, 5, 246–259. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, G.; Zhang, H.; Liu, Q.; Zhou, J. Thermodynamic analysis and optimization for steam methane reforming hydrogen production system using high temperature gas-cooled reactor pebble-bed module. J. Nucl. Sci. Technol. 2021, 58, 1359–1372. [Google Scholar] [CrossRef]
- Castro-Dominguez, B.; Mardilovich, I.; Ma, L.-C.; Ma, R.; Dixon, A.; Kazantzis, N.; Ma, Y. Integration of Methane Steam Reforming and Water Gas Shift Reaction in a Pd/Au/Pd-Based Catalytic Membrane Reactor for Process Intensification. Membranes 2016, 6, 44. [Google Scholar] [CrossRef]
- Yang, L.; Ge, X. Biogas and Syngas Upgrading. Adv. Bioenergy 2016, 1, 125–188. [Google Scholar] [CrossRef]
- Rostrup-Nielsen, J.R. Syngas in perspective. Catal. Today 2002, 71, 243–247. [Google Scholar] [CrossRef]
- Rostrup-Nielsen, J.R. Production of synthesis gas. Catal. Today 1993, 18, 305–324. [Google Scholar] [CrossRef]
- Christensen, T.S.; Primdahl, I.I. Improve syngas production using autothermal reforming. Hydrocarb. Process. 1994, 73. Available online: https://www.osti.gov/biblio/7270244 (accessed on 1 August 2025).
- Shah, N.; Panjala, D.; Huffman, G.P. Hydrogen production by catalytic decomposition of methane. Energy Fuels 2001, 15, 1528–1534. [Google Scholar] [CrossRef]
- Hoang, D.L.; Chan, S.H.; Ding, O.L. Kinetic and modelling study of methane steam reforming over sulfide nickel catalyst on a gamma alumina support. Chem. Eng. J. 2005, 112, 1–11. [Google Scholar] [CrossRef]
- Rostrup-Nielsen, J.; Trimm, D.L. Mechanisms of carbon formation on nickel-containing catalysts. J. Catal. 1977, 48, 155–165. [Google Scholar] [CrossRef]
- Aasberg-Petersen, K.; Dybkjær, I.; Ovesen, C.V.; Schjødt, N.C.; Sehested, J.; Thomsen, S.G. Natural gas to synthesis gas–catalysts and catalytic processes. J. Nat. Gas Sci. Eng. 2011, 3, 423–459. [Google Scholar] [CrossRef]
- Richter, J.; Rachow, F.; Israel, J.; Roth, N.; Charlafti, E.; Günther, V.; Flege, J.I.; Mauss, F. Reaction Mechanism Development for Methane Steam Reforming on a Ni/Al2O3 Catalyst. Catalysts 2023, 13, 884. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).