An Energy System Modeling Approach for Power Transformer Oil Temperature Prediction Based on CEEMD and Robust Deep Ensemble RVFL

Abstract

Accurate prediction of transformer oil temperature is crucial for load optimization scheduling and timely early warning of thermal faults in power transformers. This paper proposes a transformer oil temperature prediction method based on Complementary Ensemble Empirical Mode Decomposition (CEEMD), Outlier-Robust Ensemble Deep Random Vector Functional Link Network (ORedRVFL), and error correction. CEEMD is used to decompose the oil temperature data into multiple subsequences, enhancing the regularity and predictability of the data. Regularization and norm improvements are introduced to edRVFL to obtain a more robust ORedRVFL model. The Tent initialization-based Differential Evolution algorithm (TDE) is employed to optimize the model parameters and predict each subsequence. Finally, error correction is applied to the prediction results. Taking the main transformer of a hydropower station in Yunnan, China as an example, the experimental results show that the proposed method improves the prediction accuracy by 5.05% and 4.13% in winter and summer oil temperature predictions, respectively. Moreover, the model’s degradation is significantly reduced when random noise is added, which verifies its robustness. This method provides an efficient and accurate solution for transformer oil temperature prediction.

1. Introduction

Transformers are extremely critical in all aspects of power systems, including generation, transmission, distribution, and utilization of electricity. Their normal operation is the foundation for the efficient functioning and reliable power supply quality of the power system [1]. During operation, transformers generate heat, and high temperatures can accelerate the aging of and even damage to insulation materials, leading to failures. Due to their unique internal structure and environment, the measurement of hot-spot temperatures is subject to random errors, making it difficult to monitor accurately [2]. Accurate oil temperature predictions can assist power system operators in allocating loads more rationally and optimizing the operational efficiency of transformers [3]. Abnormal increases in transformer oil temperature are usually signs of impending failure [4]. By improving the accuracy of predictions, we can detect potential failure risks earlier [5], thereby taking preventive measures to avoid equipment damage and power outages [6]. Accurate oil temperature predictions can assist power system operators in allocating loads more rationally and optimizing the operational efficiency of transformers [7]. Therefore, proposing an accurate method for accurately forecasting transformer oil temperature holds substantial importance.

During operation, transformers generate heat. Excessively high temperatures can accelerate the aging process of insulating materials, potentially leading to their damage [8]. Due to the unique internal structure and working environment of transformers, random errors may occur in the measurement of hot-spot temperatures inside the transformer, rendering accurate monitoring unfeasible [9]. Therefore, it is of great significance to propose an accurate method for predicting transformer oil temperature [10].

The current approaches to measuring transformer oil temperature primarily consist of direct temperature measurement and thermal circuit modeling, numerical computation, and intelligent model algorithms [11]. Direct temperature measurement involves installing temperature sensors on the transformer to collect temperature data in real time [12]. Although this method provides direct temperature readings, it faces challenges in insulation treatment. Even with the aid of fiber-optic technology, which enables its application, the cost is high and the maintenance is complex [13]. Therefore, despite its ability to provide direct temperature measurements, this method has certain limitations in terms of cost, maintenance, response speed, and accuracy, and is not widely used at present [14].

The thermal equivalent circuit method predicts oil temperature by analyzing the heat generation and dissipation processes within the transformer and constructing a thermal circuit model of the heat transfer process [15,16]. The numerical computation method mainly involves building a physical model of the transformer’s interior, employing the finite element method or the finite volume method. These methods discretize continuous equations and then iteratively solve for the temperature field distribution to simulate and calculate the temperature distribution inside the transformer [17]. Both of these methods can accurately predict temperature changes during transformer operation and have certain applications. However, they inevitably face some issues. For example, although the thermal circuit model is physically well-defined and can intuitively reflect the heat transfer and distribution within the transformer, its construction and parameter calculation are relatively complex [18]. Its accuracy depends on appropriate parameters and boundary conditions, requiring a large amount of experimental and field measurement data, which introduces significant uncertainty [19]. The finite element method requires discretization of both time and space domains, while the finite volume method needs continuous iteration and correction during prediction. Although these methods can significantly improve simulation convergence and accuracy, they consume a large amount of computational resources and time and rely heavily on empirical formulas [20].

Based on the aforementioned characteristics, experts have increasingly utilized machine learning models for transformer oil temperature prediction. Zou et al. [21]. verified the effectiveness of Long Short-Term Memory (LSTM) [22] in estimating the upper oil temperature of transformers. Gunda et al. [23] formulated a linear discrete model for the hot-spot temperature of transformer windings based on the Kalman filter algorithm, predicting the hot-spot temperature of oil-immersed transformers under different operating loads and concluding that the winding hot-spot temperature is correlated with season, ambient temperature, and load. Oliveira [24] analyzed the temperature characteristics of oil-immersed transformers and used a BP neural network as the prediction model to accurately predict the hot-spot temperature of a 2000 KVA oil-immersed transformer. Li Ghnatios et al. [25] validated the effectiveness of self-supervised pre-training methods regarding top-oil temperature determination of transformers, proposing a dual-channel pre-trained temporal attention network model that showed significant results in single time-step prediction of transformer top oil temperature. Juarez-Balderas et al. [26] proposed a transformer hot-spot temperature prediction model based on Artificial Neural Networks (ANNs), which was verified by experimental data through Finite Element Method (FEM) simulations and demonstrated accurate prediction results.

Although the methods proposed by the above scholars have achieved good prediction results, the temperature of transformer oil changes with the variation in the transformer load rate, and thus it has a high degree of uncertainty [27]. Single models are often sensitive to the distribution of historical data and struggle to capture the underlying patterns within this data [28]. Therefore, when the complexity of historical data increases, the prediction accuracy of single models often decreases significantly [29]. As a result, many scholars have combined data preprocessing techniques with prediction models. Feng et al. [30] performed principal component analysis on the main feature quantities to determine the transformer’s hot-spot temperature windings, achieving input index reconstruction and obtaining better prediction results. Zhang et al. [31] used Ensemble Empirical Mode Decomposition (EEMD) to reduce data noise and constructed a deep learning model for predicting the hot-spot temperature of transformers using LSTM.

Existing transformer oil temperature forecasting approaches require a significant amount of historical data and are sensitive to data disturbances. However, in practical applications, the amount of data available for modeling and calculation is often limited, and certain training data may be biased due to unknown factors, making it difficult to improve the prediction model through extensive training. To address the above issues, this paper introduces a novel approach for predicting the top oil temperature of transformers, grounded in CEEMD decomposition, ORedRVFL prediction, and error correction:

(1)

For the first time, CEEMD is combined with ORedRVFL for oil temperature prediction, addressing the three bottlenecks of traditional methods: noise sensitivity, overfitting to outliers, and blind parameter tuning.

(2)

The Huber norm regularization layer is introduced in edRVFL for the first time to suppress the interference of outliers and enhance the model’s generalization ability.

(3)

Tent chaotic initialization is used instead of random initialization to avoid premature convergence of the DE algorithm and optimize the hyperparameters of the ORedRVFL model, thereby improving the model’s prediction accuracy.

(4)

A recursive correction mechanism for residual components is established to eliminate cumulative prediction bias, enabling the model to maintain high precision in complex data environments and enhancing its reliability in practical applications.

2. Methods

2.1. Complementary Ensemble Empirical Mode Decomposition

Complementary Ensemble Empirical Mode Decomposition (CEEMD) [32] reduces reconstruction errors and significantly improves the mode mixing phenomenon found in Empirical Mode Decomposition (EMD) [33]. Ma et al. [34] proposed that, when performing signal decomposition, the noise amplitude is usually set to 0.1 or 0.3 times the signal standard deviation, and an ensemble size is generally chosen between 50 and 200. These parameter settings have achieved good results in prediction tasks. Xiong [35] et al. suggested that, when using CEEMD for signal preprocessing, the choice of noise amplitude and ensemble size has a significant impact on model performance. The noise amplitude is typically between 0.05 and 0.2 times the signal standard deviation, and an ensemble size between 50 and 150 is more appropriate. These parameter ranges have been proven effective in wind power prediction. Therefore, we used these parameters as an initial reference. The illustrative representation of the CEEMD decomposition algorithm is illustrated in Figure 1. First, the original oil temperature data are corrupted by additive positive and negative Gaussian white noise with a magnitude $o(t)$. The detailed procedure is outlined as follows:

$$\left\{\begin{array}{l}{o}_i^{+}(t)=o(t)+{\phi }_i^{+}(t)\\ o_i^{-}(t)=o(t)+{\phi }_i^{-}(t)\end{array}\right.$$

(1)

where ${\phi }_i^{+}(t)$ and ${\phi }_i^{-}(t)$ represent the bipolar white noise components for the i-th instance, respectively. $o_i^{+}(t)$ and $o_i^{-}(t)$ represent the oil temperature data after adding positive and negative white noise, respectively.

Using the EMD algorithm to decompose the signal after adding white noise, the expression formula for the decomposed sequence is as follows:

$$\left\{\begin{array}{l}{o}_i^{+}(t)={\displaystyle {\sum }_{j=1}^n{R}_{ij}^{+}(t)+r_i^{+}(t)}\\ o_i^{-}(t)={\displaystyle {\sum }_{j=1}^n{R}_{ij}^{-}(t)+r_i^{-}(t)}\end{array}\right.$$

(2)

where $R_{ij}(t)$ represents the j-th Intrinsic Mode Function (IMF) component obtained from the decomposition of the i-th signal, and $r_i$ represents the residue obtained from the dissection of the j-th signal.

Finally, the average value of each IMF component obtained from the decomposition is calculated to obtain the final decomposition result of the CEEMD algorithm. The process unfolds in the following manner:

$$\left\{\begin{array}{l}{R}_j(t)={\displaystyle \frac{1}{2N}}{\displaystyle \sum _{i=1}^N\left[R_{ij}^{+}(t)+R_{ij}^{-}(t)\right]}\\ Se={\displaystyle \frac{1}{2N}}{\displaystyle \sum _{i=1}^N(r_i^{+}+r_i^{-})}\end{array}\right.$$

(3)

where N denotes the number of white noise instances, $R_j(t)$ (for j = 1, …, m) represents the j-th component obtained from the final decomposition, and $Se$ is the residue after decomposition.

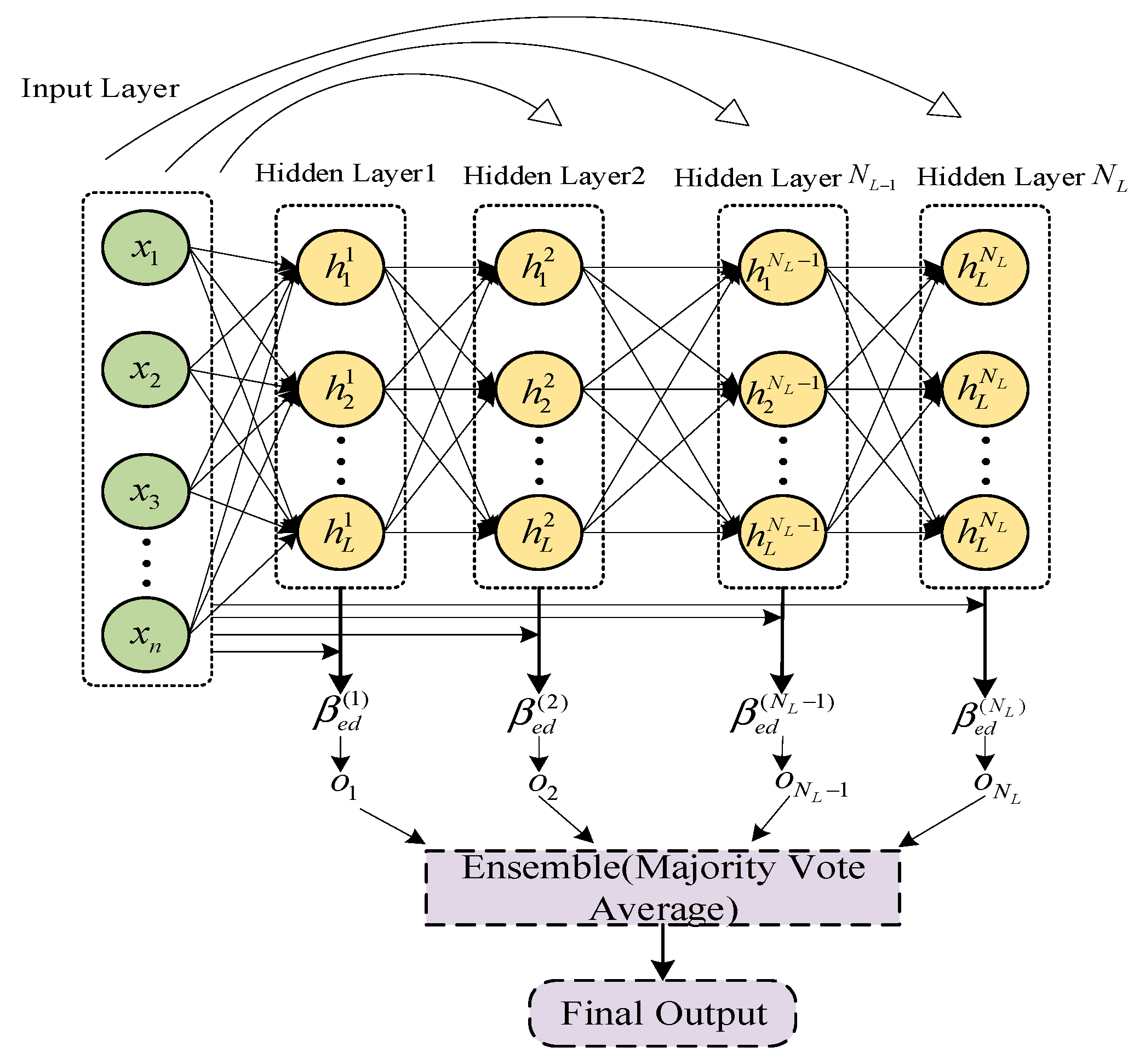
2.2. Robust Deep Ensemble RVFL

Similar to the ELM model, RVFL is a type of feedforward neural network [35]. The framework structure can be seen in Figure 2. In the RVFL model, the input data from the input layer traverses the nodes in the hidden layer, where it undergoes a nonlinear mapping, and the concluding result is output through the output function. The RVFL network can be described as in Equation (4):

$$f\left(x\right)={\displaystyle {\sum }_{j=1}^J{\beta }_j}g\left({\omega }_j^{T}X+b_j\right)+{\displaystyle {\sum }_{j=J+1}^{J+N}{\beta }_j{x}_j}$$

(4)

where $\mathrm{g}(·)$ serves as the activation function, and ${\omega }_j$ represents the weight associated with the j-th hidden node. $X=[x_1,x_2,\dots ,x_N]$ is the input matrix, $b_j$ is the threshold, and ${\beta }_j$ is the weight of the output layer.

The edRVFL (Ensemble Deep Random Vector Functional Link) [36] model is an ensemble deep learning framework that combines the advantages of deep learning, ensemble methods, and the IF–THEN properties of fuzzy inference systems (FIS) to generate rich feature representations for training. To tackle the challenge of outliers in the transformer oil temperature data affecting prediction accuracy, this paper proposes a robust edRVFL model. By introducing regularization and balancing the training error and weight relationship through norms, the model reduces the interference of outliers and enhances its robustness. The ORedRVFL network is described as in Equation (5):

$$h_L(x)={\displaystyle \sum _{j=1}^L\left(\begin{array}{l}{(H^{T}H+\frac{2}{C\mu I})}^{-1}·\\ H^T(y-e_i+\frac{{\lambda }_i}{\mu })g({\omega }_{j}X+b_j)\end{array}\right)}$$

(5)

where$L$ indicates the number of hidden layer nodes, $H$ represents the output matrix of the hidden layer, $C$ is the regularization coefficient, $\mu$ is the penalty parameter, $e$ represents the training error, and $\lambda$ is the extended Lagrange multiplier series.

2.3. Tent Chaotic Differential Evolution Algorithm (TDE)

The Differential Evolution (DE) algorithm optimizes the objective function by simulating the mutation, crossover, and selection operations in biological evolution. The implementation steps of the DE algorithm are as follows:

(1) Initialization

First, initialize the algorithm population. After initialization, each individual is represented as follows:

$$x_{i,G}\left(i=1,2,\dots ,NP\right)$$

(6)

where $i$ denotes the individual index, $G$ represents the generation number, and $NP$ is the population size.

In the differential evolution algorithm, let the bounds of the parameter variables be $g{x}_j^{(L)}<x_j<x_j^U$. The expression for $x_{ji,0}$ is as follows:

$$x_{ji,0}=rand[0,1]\times (x_j^{(U)}-x_j^{(L)})+x_j^L$$

(7)

(2) Mutation

Following population initialization, the mutation operation is performed. For each candidate solution $x_{i,G}\left(i=1,2,\dots ,NP\right)$, the mutation vector is generated as follows:

$$v_{i,G+1}=x_{r_1,G}+F\cdot (x_{r_2,G}-x_{r_3,G})$$

(8)

where $F$ is the mutation operator and is a real constant factor between 1 and 2.

(3) Crossover

The crossover process increases the heterogeneity among solution candidates by executing crossover between the mutant vector and the target vector, thereby avoiding randomness and ensuring that the trial vector is altered. The specific process is as follows:

$$u_{i,G+1}=(u_{1_i,G+1},u_{2_i,G+1},\dots ,u_{D_i,G+1})$$

(9)

$$u_{ji,G+1}=\left\{\begin{array}{l}{v}_{ji,G+1} if \mathrm{rand}(j)<=\mathrm{CR} \mathrm{or} j=\mathrm{rnbr}(i)\\ x_{ji,G+1} if x\ne 0 \mathrm{and} \mathrm{j}\ne \mathrm{rnbr}(i)\end{array}\right.$$

(10)

where $\mathrm{rand}(j)$ denotes the $j-th$ estimate of the stochastic-number generator, $\mathrm{rnbr}(i)$ represents a stochastically drawn sequence, and $CR$ functions as the crossover mechanism.

(4) Selection

The selection operation in the Differential Evolution algorithm is based on the greedy criterion: the trial vector is compared with the target vector $x_{i,G}$. If the trial vector has a higher fitness, it is selected for the next generation; otherwise, the original target vector is retained.

(5) Handling of Boundary Conditions

If, during the mutation process, a solution is generated outside the feasible domain, the mutant vector is redefined within the feasible solution range. The specific process is as follows:

$$u_{ji,G+1}=rand[0,1]\cdot (x_j^{(U)}-x_j^{(L)})+x_j^{(L)}$$

(11)

where: $i=1,2,\dots ,NP;j=1,2,\dots ,D$

The random initialization of the original algorithm is prone to population clustering, which affects the convergence speed. In this paper, the Tent map, which has better randomness and uniformity, is used to initialize the individuals in the algorithm. The specific expression is as follows:

$$r_{j+1}=\left\{\begin{array}{l}\psi r_j\hspace{1em}\hspace{1em}\hspace{1em}{r}_j<0.5\\ \psi (1-r_j)\hspace{1em}{r}_j\ge 0.5\end{array}\right.$$

(12)

$$x_{i,G}=lb+(ub-lb)\cdot r_j$$

(13)

where$r_j$ denotes a uniformly distributed random value between the specified range [0, 1], $\psi$ is a chaotic parameter in the interval (0, 2], and $lb$ and $ub$ signify the lower and upper extents of the solution range, respectively.

2.4. Error Correction Model

In practical prediction, the inherent errors of models are often overlooked, but the potential information they contain can be mined and utilized [37]. Therefore, this paper proposes to correct the preliminary prediction results to further improve the prediction accuracy. The procedure for error correction is described as follows:

Step 1: Calculate the error sequence. The error sequence is obtained, where $o_i$ represents the $i-th$ true value spanning from the coolant’s chill floor to its thermal ceiling sequence, and $p_i$ represents the $i-th$ predicted value from the oil’s coolest skin to its searing core sequence. The formulation for the error sequence $e_i$ is as follows:

$$e_i=o_i-p_i$$

(14)

Step 2: Train the ELM error model. After reasonably partitioning the error sequence, it is used as the input for training and predicting the error model to obtain the predicted error value for the $i-th$ sample.

Step 3: Add the $i-th$ transformer oil temperature predicted value $p_i$ and the $i-th$ predicted error value $y_i$ to obtain the $i-th$ error-corrected transformer oil temperature predicted value. Finally, the final predicted sequence of transformer oil temperature ${\widehat{y}}_i$ is obtained as shown in Equation (15):

$${\widehat{y}}_i=p_i+y_i$$

(15)

2.5. Construction of the Transformer Top Oil Temperature Prediction Model

The structure of the hybrid transformer top oil temperature forecasting model unveiled in this paper, namely TDE-CEEMD-ORedRVFL-EC, is presented in Figure 3. The implementation process is described as follows:

Step 1: Use the transformer oil temperature data from December 2023 to February 2024 as the winter prediction dataset and the data from June to August 2024 as the summer dataset. Model each of these datasets separately.

Step 2: Decompose the historical transformer oil temperature data using CEEMD to make the sub-sequences more stationary. Then, set the first 70% of each sub-sequence component as the training set and the last 30% as the testing set.

Step 3: Introduce regularization and norms to improve edRVFL to ORedRVFL, enhancing robustness. Input the data from Step 2 into ORedRVFL to generate preliminary predictions.

Step 4: Calculate the prediction error from Step 3, establish a correction model, adjust the initial predictions, and obtain more accurate final results.

Step 5: To rigorously benchmark the model’s performance, set ELM, BP, LSTM, edRVFL, ORedRVFL, and CEEMD-ORedRVFL as control group models and conduct comparisons.

Figure 3. Flowchart of the overall prediction model.

Figure 3. Flowchart of the overall prediction model.

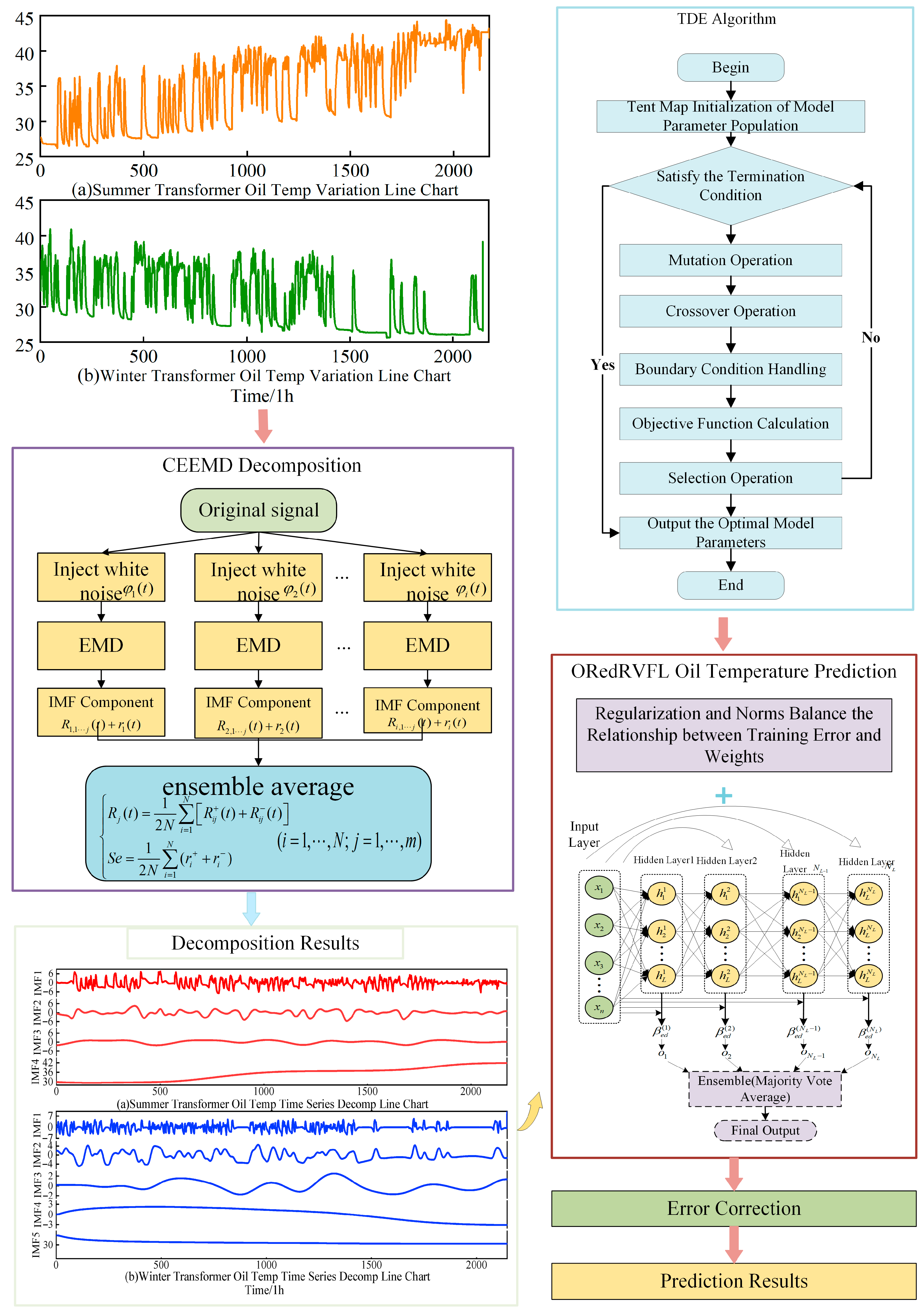
3. Data Preprocessing

3.1. Dataset Introduction

The hourly-level transformer oil temperature data from December 2023 to February 2024 (winter) and June to August 2024 (summer) of the main transformer at a hydropower station in Yunnan, China, were selected to verify the model. The sampling interval was 1 h. There were 2145 data points for the winter dataset and 2173 for the summer dataset. Figure 4 illustrates the variation in the oil temperature data sequences for the two seasons, and

Table 1. Transformer oil temperature history data information.

Data Name	Summer	Winter
Maximum Value	44.381	40.922
Minimum Value	26.166	25.631
Average Value	34.9936	30.8591

provides their maximum, minimum, and average values.

3.2. Data Decomposition and Partitioning

The decomposition results of the oil temperature data by the CEEMD algorithm are presented in Figure 5, where Figure 5a shows the winter decomposition result and Figure 5b shows the summer decomposition result. Under the decomposition of the CEEMD algorithm, the winter oil temperature data are segmented into four IMF components, and the summer oil temperature data are broken down into five IMF elements. The frequency of the transformer oil temperature data components decomposed by the CEEMD algorithm gradually decreases, the regularity is enhanced, and the trend becomes more stable.

3.3. Random Noise Data

To verify the prediction performance and robustness of the ORedRVFL model under random noise and complex data conditions, this paper randomly generated 150 and 152 random noises (with an amplitude of ±5, accounting for 10% of the length of the training dataset) in the winter and summer datasets, respectively, to simulate the interference of transformer oil temperature sensors leading to inaccurate measurements. Figure 6 shows the line charts for the two sets of noise.

4. Experimental Results and Analysis

4.1. The Performance Comparison of Algorithms

The Tent mapping initialization method is based on the good randomness and uniformity characteristics of the Tent mapping, which can generate a more uniformly distributed initial population, thereby significantly enhancing the algorithm’s global search ability and performance. The TDE algorithm has been compared with four other algorithms, namely, Artificial Bee Colony Optimization (ASO), Particle Swarm Optimization (PSO), Harris Hawks Optimization (HHO), and Differential Evolution (DE) on three benchmark functions (F1, F9, and F14). Performance comparison results of the algorithms are given in

Table 2. Performance comparison chart for the algorithms.

Benchmark Function	Algorithm	Average Value	Standard Deviation	Optimal Solution
$f_1$	ASO	7.89 × 10−5	0.000249401	2.94 × 10−15
	PSO	0.85220533	0.330388366	0.362945255
	HHO	11566.65089	3885.164694	5835.221608
	DE	3.89 × 10−15	3.36 × 10−15	5.90 × 10−16
	TDE	6.16 × 10−62	1.53 × 10−61	2.51 × 10−75
$f_9$	ASO	42.21042681	6.548604671	35.82220426
	PSO	56.32590351	14.01800727	41.41953517
	HHO	297.6034322	19.8717627	268.7495013
	DE	5.357551215	5.168711573	1.59 × 10−12
	TDE	0	0	0
$f_{14}$	ASO	1.794378737	1.023738232	0.998003838
	PSO	1.494226808	0.843210368	0.998003838
	HHO	1.295816676	0.669811166	0.998003838
	DE	5.598097203	4.530763325	0.998003839
	TDE	1.097406545	0.314338957	0.998003838

, with the best performance results and the corresponding algorithm are indicated in bold. The convergence curves of the five algorithms are given in Figure 7. Experimental results also show that the TDE algorithm with Tent mapping initialization performs excellently on multiple test functions, especially in complex multimodal and high-dimensional optimization problems, where it demonstrates faster convergence speed and higher solution quality.

From Figure 7, it can be seen that the TDE (purple curve) demonstrates the best convergence performance across all test functions. At the end of the iterations, the fitness value of TDE is the lowest, indicating that it has found the optimal solution or a solution close to the optimal one. This suggests that TDE has superior global search capabilities compared to other algorithms. Additionally, the curve of TDE shows good stability during the iteration process, with no significant fluctuations, indicating that the algorithm is relatively stable during the search process and less likely to get stuck in local optima. The performance comparison chart of the algorithms is shown in Table 2.

4.2. Evaluation Metrics

In the field of data prediction, evaluation metrics serve as the fundamental yardsticks for gauging both model performance and the fidelity of forecasted outcomes. The evaluation metrics used in this paper and their calculation formulas are detailed in

Table 3. Evaluation indicators and their formulas.

Assessment Indicators	Formula
Root Mean Square Error (RMSE)	$\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{i=1}^n{(x_i-y_i)}^2}}$
Mean Absolute Error (MAE)	${\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{i=1}^n\left|x_i-y_i\right|}$
Mean Absolute Percentage Error (MAPE)	${\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{i=1}^n\left|\frac{x_i-y_i}{x_i}\right|}\times 100\%$
Correlation Coefficient (R)	${\displaystyle \frac{{\displaystyle {\sum }_{i=1}^n(x_i-\overline{x})}(y_i-\overline{y})}{\sqrt{{{\displaystyle {\sum }_{i=1}^n(x_i-\overline{x})}}^2{\displaystyle {\sum }_{i=1}^n{(y_i-\overline{y})}^2}}}}$

where $x_i$ captures the actual observed value, $\overline{x}$ represents the average of the ground-truth values, $y_i$ captures the model’s forecasts value, $\overline{y}$ represents the average of the predicted values, and $n$ denotes the sample count.

.

4.3. Experimental Design and Result Analysis

To validate the forecasting capability of the CEEMD-ORedRVFL-EC model, this paper conducted predictions of the real hourly transformer top oil temperature for both summer and winter using MATLAB 2023a, supplied by MathWorks, Inc., with its headquarters located in Natick, MA, USA. and compared the results with those from LSTM, BP, ELM, edRVFL, ORedRVFL, and CEEMD-ORedRVFL as control groups.

Table 4. Evaluation indexes of transformer oil temperature prediction results.

Season	Model	RMSE	MAE	R	MAPE
Summer	ELM	0.98499	0.78857	0.96842	0.01959
	BP	0.90876	0.70660	0.97154	0.01764
	LSTM	0.80409	0.58828	0.97539	0.01472
	edRVFL	0.76446	0.46345	0.97497	0.01180
	ORedRVFL	0.75688	0.47819	0.97529	0.01216
	CEEMD-ORedRVFL	0.71868	0.45684	0.97730	0.01167
	CEEMD-ORedRVFL-EC	0.71304	0.45326	0.97762	0.01159
Winter	ELM	0.87662	0.43601	0.93748	0.01489
	BP	0.76791	0.47134	0.95918	0.01688
	LSTM	0.74059	0.30142	0.95684	0.01028
	edRVFL	0.70246	0.19226	0.95971	0.00625
	ORedRVFL	0.69605	0.21843	0.96084	0.00724
	CEEMD-ORedRVFL	0.66732	0.23765	0.96607	0.00796
	CEEMD-ORedRVFL-EC	0.65980	0.21371	0.96619	0.00708

presents each model’s individual prediction errors, and Figure 8 shows the fitting line charts of some models.

From the metrics in Table 4, the results reveal that the forecast performance of the proposed model is better in winter than in summer. This is due to the higher volatility of electricity usage in summer, which leads to more complex and variable transformer oil temperature data, thereby validating the authenticity of this data. The RMSE results show that the edRVFL model outperforms all single-model control groups in terms of prediction accuracy. The introduction of robust methods in the ORedRVFL model leads to better prediction accuracy than that of the edRVFL model. In both summer and winter predictions, the RMSE of the ORedRVFL model’s performance improves by 0.992% and 0.913%, respectively, relative to the edRVFL model, proving that the ORedRVFL model demonstrates an advantage in dealing with complex data. Compared with the ORedRVFL model, the CEEMD-ORedRVFL model exhibits marked improvements in prediction accuracy, with RMSE reductions of 5.047% and 4.128% in winter and summer, respectively. This demonstrates that the decomposition algorithm markedly enhances the prediction performance of the ORedRVFL model. The CEEMD-ORedRVFL-EC model, which incorporates an error-correction model grounded in the CEEMD-ORedRVFL model, further improves the prediction accuracy. Its prediction metrics are improved by 0.785% and 0.501% in summer and winter oil temperature predictions, respectively, compared with the CEEMD-ORedRVFL model. This proves that the application of the error-correction approach can further boost the predictive reliability of the CEEMD-ORedRVFL thermal profile of the transformer oil prediction model. As can be seen from Figure 8, the predictive outcomes of the CEEMD-ORedRVFL-EC model have the highest degree of overlap with the true data curve.

To verify the robustness of the ORedRVFL model, this paper conducted simulation experiments on the summer and winter transformer oil temperature data with added random noise (the random noise information is described in Section 3.3). The experimental process was the same as that without added noise, and the result metrics and fitting results are presented in

Table 5. Evaluation metrics for oil temperature prediction results with the addition of random noise.

Season	Model	RMSE	MAE	R	MAPE
Summer	ELM	1.23618	0.97025	0.95088	0.02391
	BP	1.19375	0.98887	0.96861	0.02436
	LSTM	0.94845	0.75448	0.96998	0.01883
	edRVFL	0.87346	0.56784	0.96918	0.01434
	ORedRVFL	0.77231	0.50869	0.97470	0.01289
	CEEMD-ORedRVFL	0.77126	0.50902	0.97489	0.01289
	CEEMD-ORedRVFL-EC	0.77079	0.49497	0.97467	0.01255
Winter	ELM	1.10196	0.66029	0.90071	0.02298
	BP	0.93037	0.66356	0.94384	0.02381
	LSTM	0.92479	0.54066	0.93744	0.01898
	edRVFL	0.85924	0.47096	0.94070	0.01629
	ORedRVFL	0.71107	0.24781	0.95968	0.00832
	CEEMD-ORedRVFL	0.70846	0.26364	0.95973	0.00894
	CEEMD-ORedRVFL-EC	0.70462	0.23483	0.96130	0.00784

and Figure 9, respectively.

Table 4 presents the prediction error results for the summer and winter transformer oil temperature predictions after adding random noise, and Figure 8 shows the fitting line charts of the main comparison models for the summer and winter transformer oil temperature predictions after adding random noise. The metrics in Table 4 indicate that the prediction results of all models deteriorated to varying degrees after the addition of random noise. Specifically, the BP model deteriorated by 31.36% and 21.16% in summer and winter oil temperature predictions, respectively; LSTM deteriorated by 17.95% and 24.87%; edRVFL deteriorated by 14.26% and 22.32%; while ORedRVFL deteriorated by only 2.04% and 2.16%. This demonstrates that the degradation of the ORedRVFL model is significantly lower compared to other models. Thanks to the incorporation of decomposition and error correction, the CEEMD-ORedRVFL-EC model shows improved accuracy over the ORedRVFL model. As can be clearly seen from Figure 8, the prediction result curve of the CEEMD-ORedRVFL-EC model almost overlaps with the true values, while the single-model control groups all exhibit significant deviations. This demonstrates that the robustness enhancement of the proposed CEEMD-ORedRVFL-EC model in this paper is highly effective.

Figure 10 shows the bar charts of the RMSE metrics for each model in both seasons with and without added noise, where (a) and (b) are for summer, and (c) and (d) are for winter. Figure 10 suggests that the developed model yields the lowest RMSE, with prediction results closer to the actual values. Comparing the figures with and without noise, it is observable that the RMSE of the control group models significantly increases after adding noise, while the proposed model only manifests a marginal increase. This demonstrates that the proposed model is capable of consistently delivering accurate predictions even in the presence of random noise, showing strong robustness and the ability to handle complex oil temperature data.

5. Diebold-Mariano Test

The Diebold-Mariano test (DM test) is a non-parametric method for comparing the predictive accuracy of two forecasting models. It assesses whether there is a significant difference in predictive performance by comparing the forecast errors of the two models, with the null hypothesis being that the predictive accuracy of the two models is the same [38]. This test is applicable to a variety of loss functions and in this study, we primarily used the Mean Squared Error (MSE).

After conducting the DM test on the oil temperature dataset with added random noise, comparing our proposed model (CEEMD-ORedRVFL-EC) with several other models, the results are shown in

Table 6. Significance Analysis of the Proposed Model CEEMD-ORedRVFL-EC Compared with Other Benchmark Models.

Season	Model	DM
Summer	CEEMD-ORedRVFL	0.5599
	ORedRVFL	2.9853
	edRVFL	4.8496
	LSTM	7.6922
	BP	13.736
	ELM	11.8441
Winter	CEEMD-ORedRVFL	1.3716
	ORedRVFL	2.2922
	edRVFL	2.5265
	LSTM	2.7642
	BP	6.254
	ELM	6.2713

.

In both summer and winter data, the DM values of the proposed model compared with each benchmark model are greater than 0, intuitively demonstrating its superiority in predictive performance. In the summer data, the DM values of the proposed model compared with ORedRVFL, edRVFL, LSTM, BP, ELM, and other models are all greater than 2.576, proving that its prediction accuracy is significantly higher than these models at the 5% significance level. In the winter data, the DM values of the proposed model compared with most benchmark models are greater than 1.96, indicating that its prediction accuracy is significantly better than these models at the 1% significance level. Overall, the proposed model has higher prediction accuracy than other models, proving that it has significant and outstanding performance advantages in the oil temperature prediction task and is the best-performing model currently.

Overall, the proposed model has significantly higher prediction accuracy than other models in the vast majority of cases, indisputably proving that the proposed model has significant and outstanding performance advantages in the oil temperature prediction task and is the best-performing model currently.

6. Conclusions

Aiming at the issues of low real-time performance and weak anti-interference capability in transformer oil temperature measurement and prediction, this paper presents a transformer-oil temperature forecasting approach rooted in the CEEMD-ORedRVFL-EC model. Using the main transformer’s historical oil-temperature data at a hydropower station in Yunnan, China, through experimental research conducted as a case study, the following insights are derived:

(1)

The CEEMD algorithm decomposes the oil temperature sequence into multiple sub-sequences with different frequencies, significantly enhancing the regularity and predictability of the data. Experiments show that, after the introduction of the decomposition algorithm, the model’s prediction accuracy for winter and summer oil temperatures increased by 5.05% and 4.13%, respectively.

(2)

The introduction of regularization and norm improvements to edRVFL resulted in the ORedRVFL model, which exhibited significantly reduced degradation when subjected to random noise. This validates its robustness and anti-interference capability.

(3)

The error correction mechanism further improved prediction accuracy, enabling the model to more accurately reflect the actual changes in transformer oil temperature.

(4)

Based on the experimental results, the proposed model’s predictive accuracy surpasses that of other control group models, achieving more accurate transformer oil temperature prediction.