A Dual-Stage and Dual-Population Algorithm Based on Chemical Reaction Optimization for Constrained Multi-Objective Optimization
Abstract
1. Introduction
- Innovative integration of CRO with a dual-stage and dual-population framework: Uniquely integrates the collision reaction mechanism of CRO with a tailored dual-stage and dual-population framework specifically designed for CMOPs. This fusion not only leverages CRO’s strengths in global and local search but also addresses its limitations in handling complex constraints and infeasible regions through a structured, phased approach.
- Enhanced molecular collision operators with structure repair strategy: Introduces novel molecular collision operators that incorporate a structure repair strategy to preserve high-quality solution structures during decomposition and synthesis reactions. This strategy prevents the loss of historically optimal structures throughout the reaction process, which enhances the algorithm’s search efficiency and stability.
- Dynamic stage transition mechanism based on population state: Implements a dynamic stage transition mechanism that switches from the first stage (objective optimization) to the second stage (constraint satisfaction) based on the actual state of the population. This mechanism ensures that the algorithm can adaptively respond to problem characteristics, which facilitates efficient convergence towards the CPF.
- Weak complementary mechanism for inter-population information exchange: Designs a weak complementary mechanism that promotes information exchange between the main and auxiliary populations without direct substitution of individuals. This mechanism harnesses the guiding potential of infeasible solutions while maintaining the feasibility and diversity of the main population, thereby enhancing the overall performance of the algorithm.
2. Related Work
2.1. Multi-Objective Evolutionary Algorithm Based on Chemical Reaction Optimization
2.2. Multi-Population Co-Evolution Constrained Optimization Method
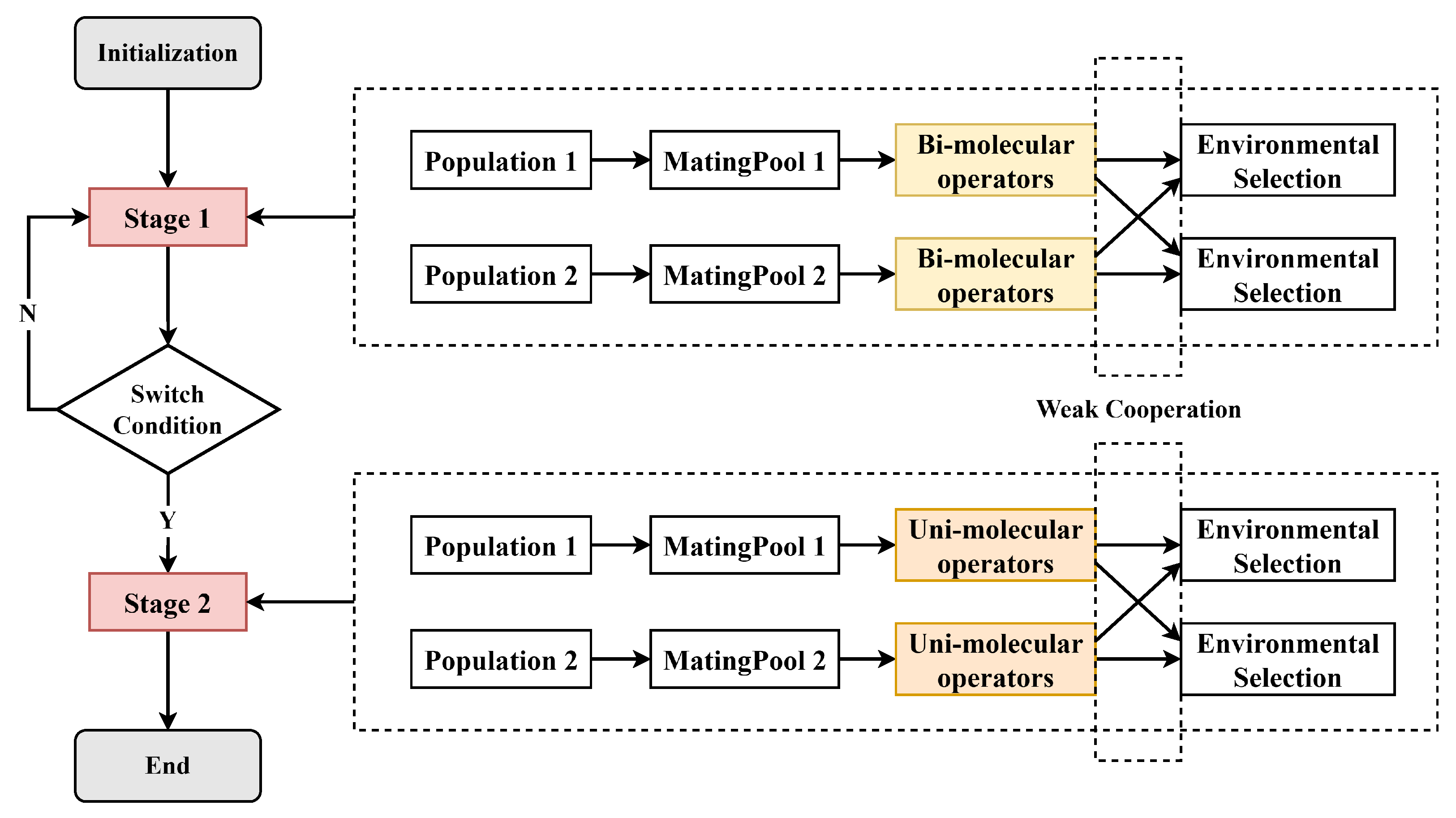
3. The Proposed Algorithm
3.1. Improvement of Molecular Collisions
3.1.1. Introduction of Structural Repair Strategy
3.1.2. Design of Directional Search Operators
3.2. Procedure of the Proposed DDCRO
| Algorithm 1 Main Procedure of DDCRO |
|
3.3. The Mechanism of Two-Stage
3.4. The Mechanism of Dual Population
3.4.1. Stage1—Pop 1 Environmental Selection
| Algorithm 2 Stage1-Pop1 Environmental Selection |
|
3.4.2. Stage2—Pop1 Environmental Selection
| Algorithm 3 Stage2-Pop1 Environmental Selection |
|
3.4.3. Pop2 Environmental Selection
3.5. Computational Complexity
4. Experimental Studies
4.1. Experimental Settings
4.1.1. Test Problems
4.1.2. Comparison Algorithms
4.1.3. Assessment Criteria
4.2. Experimental Results and Analysis
4.2.1. Comparisons on DTLZ
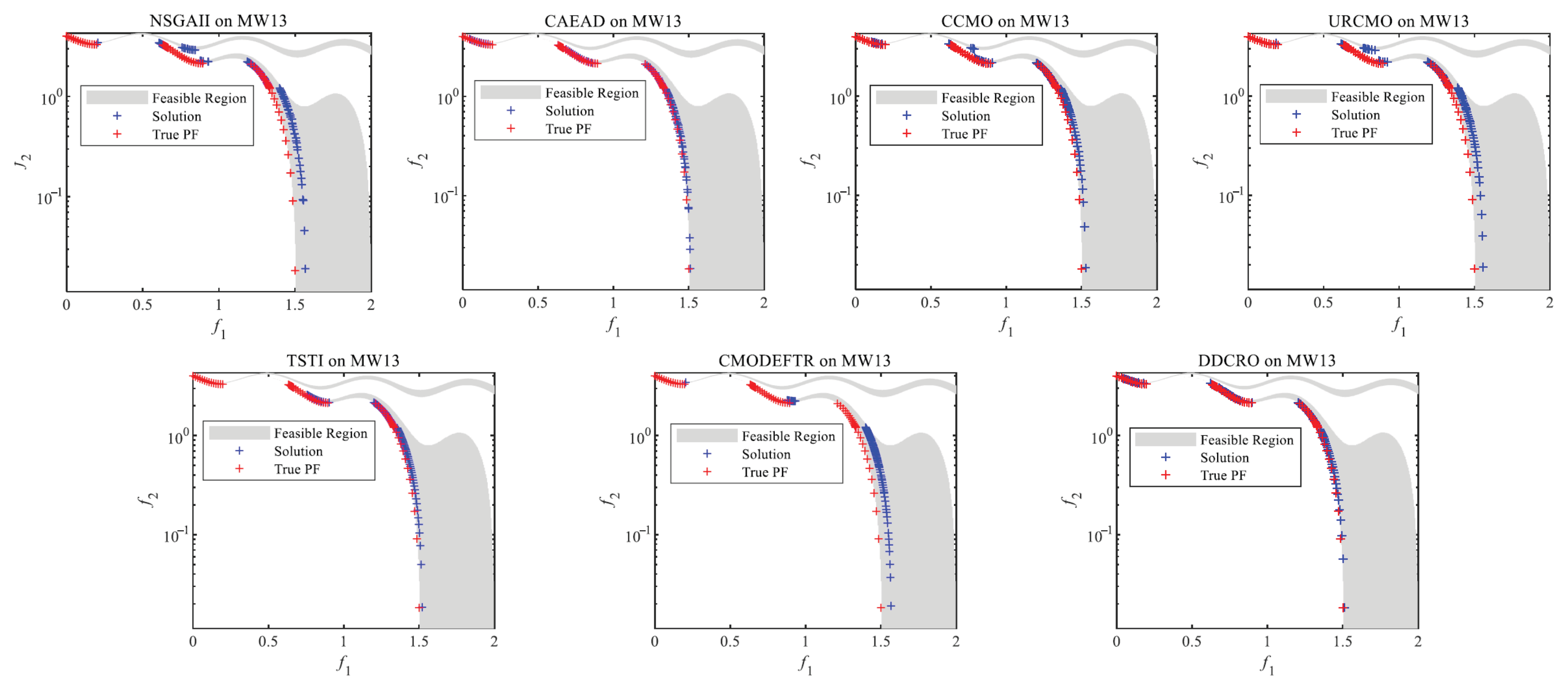
4.2.2. Comparisons on MW
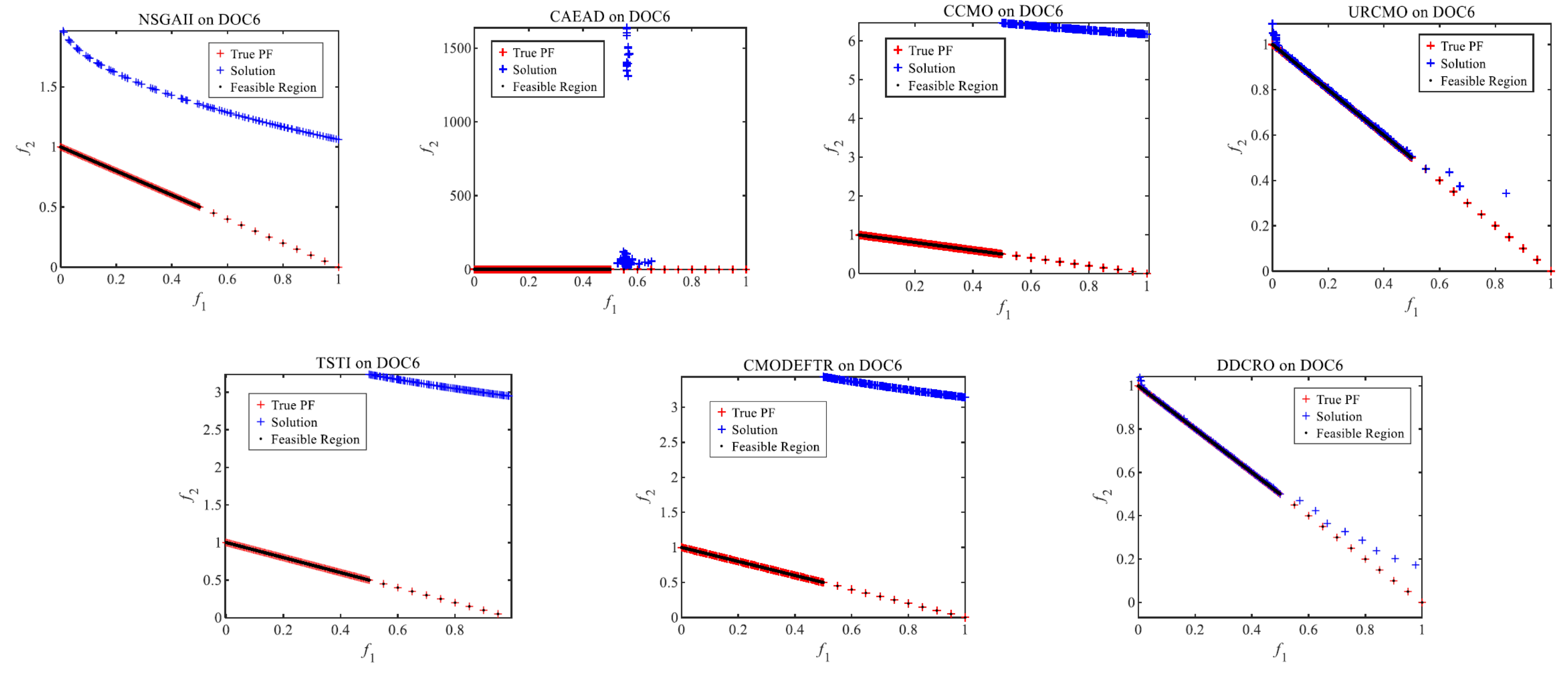
4.2.3. Comparisons on DOC
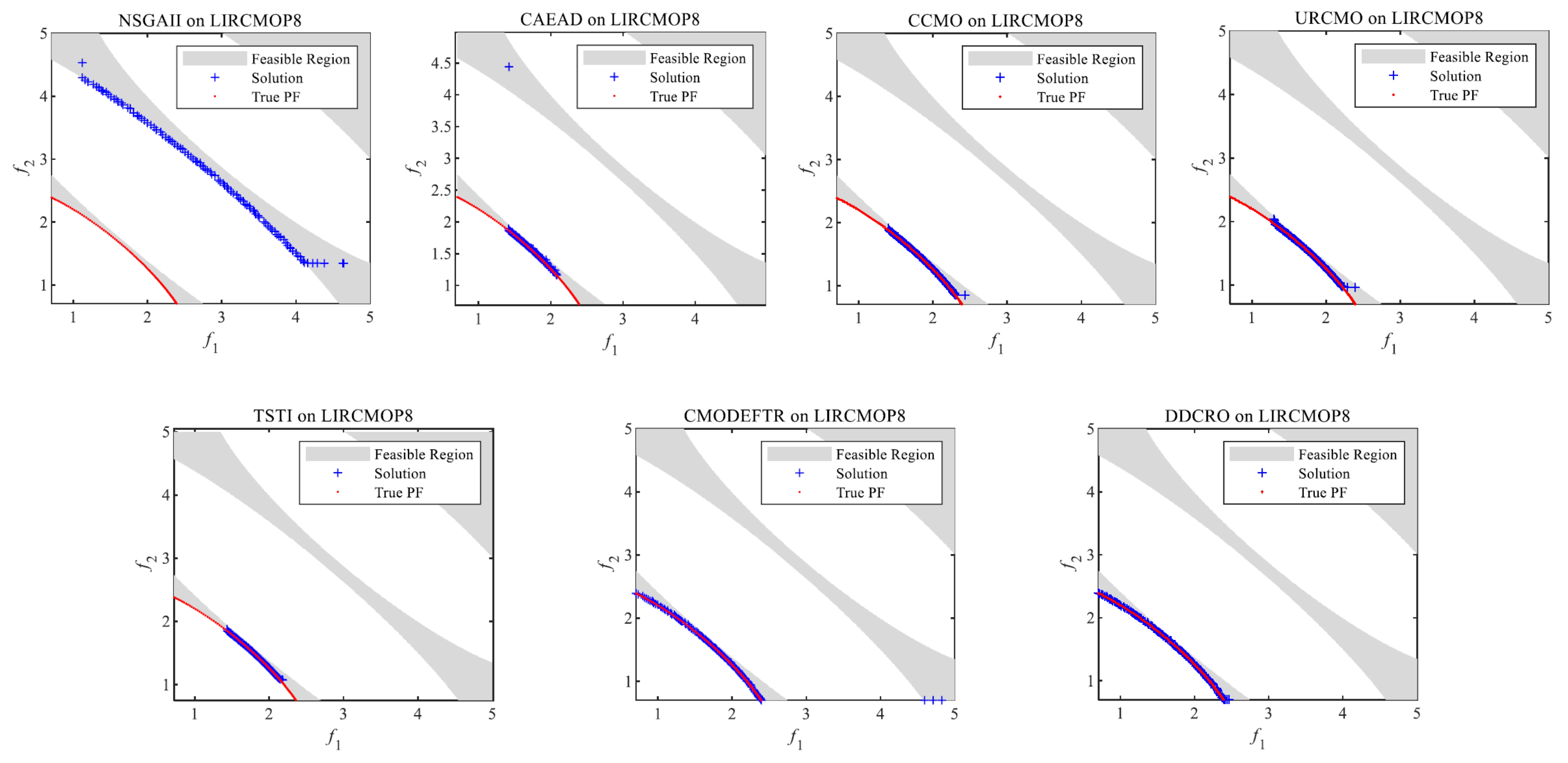
4.2.4. Comparisons on LIRCMOP
4.3. Comparisons on Real-World Problems
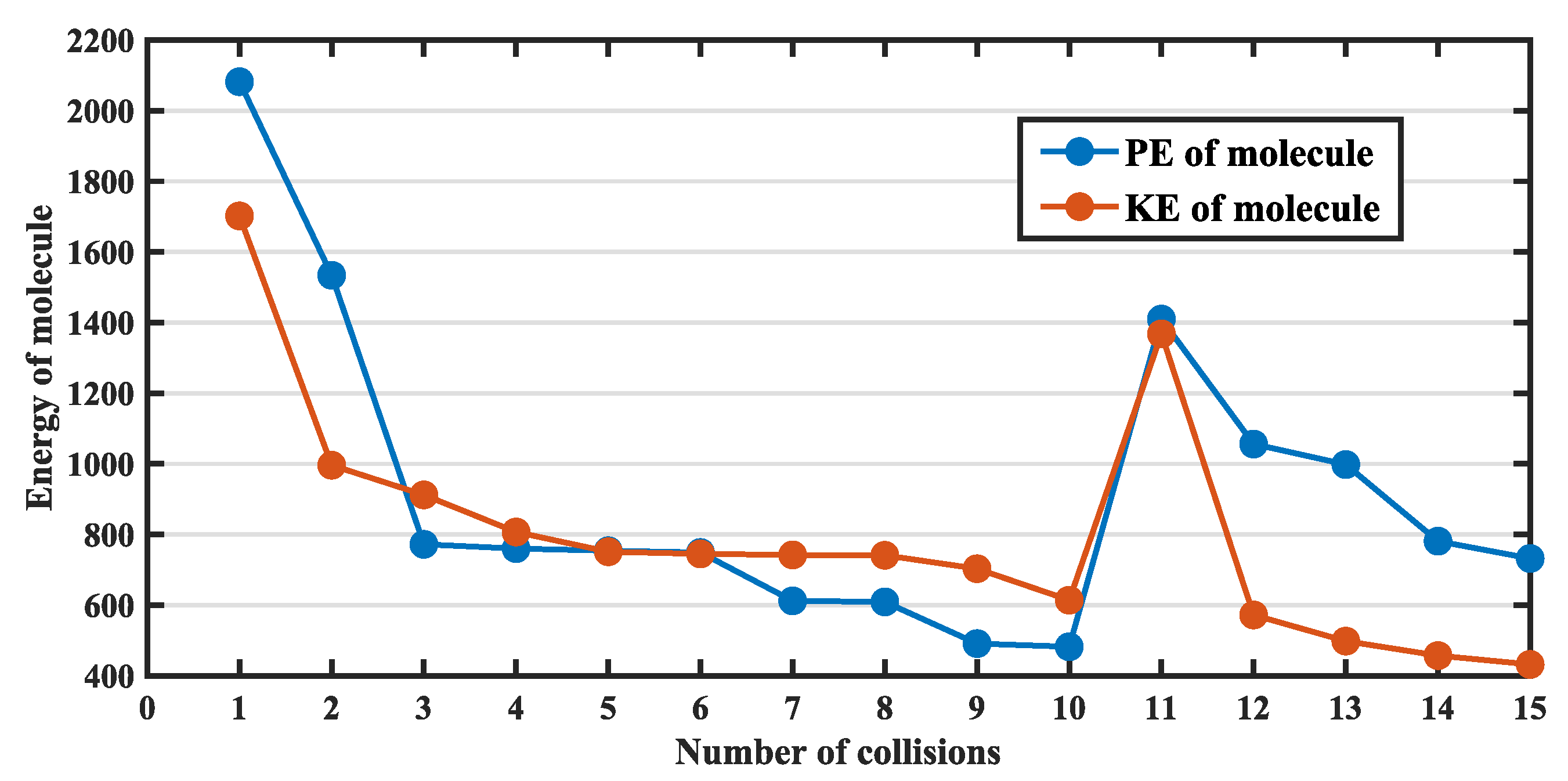
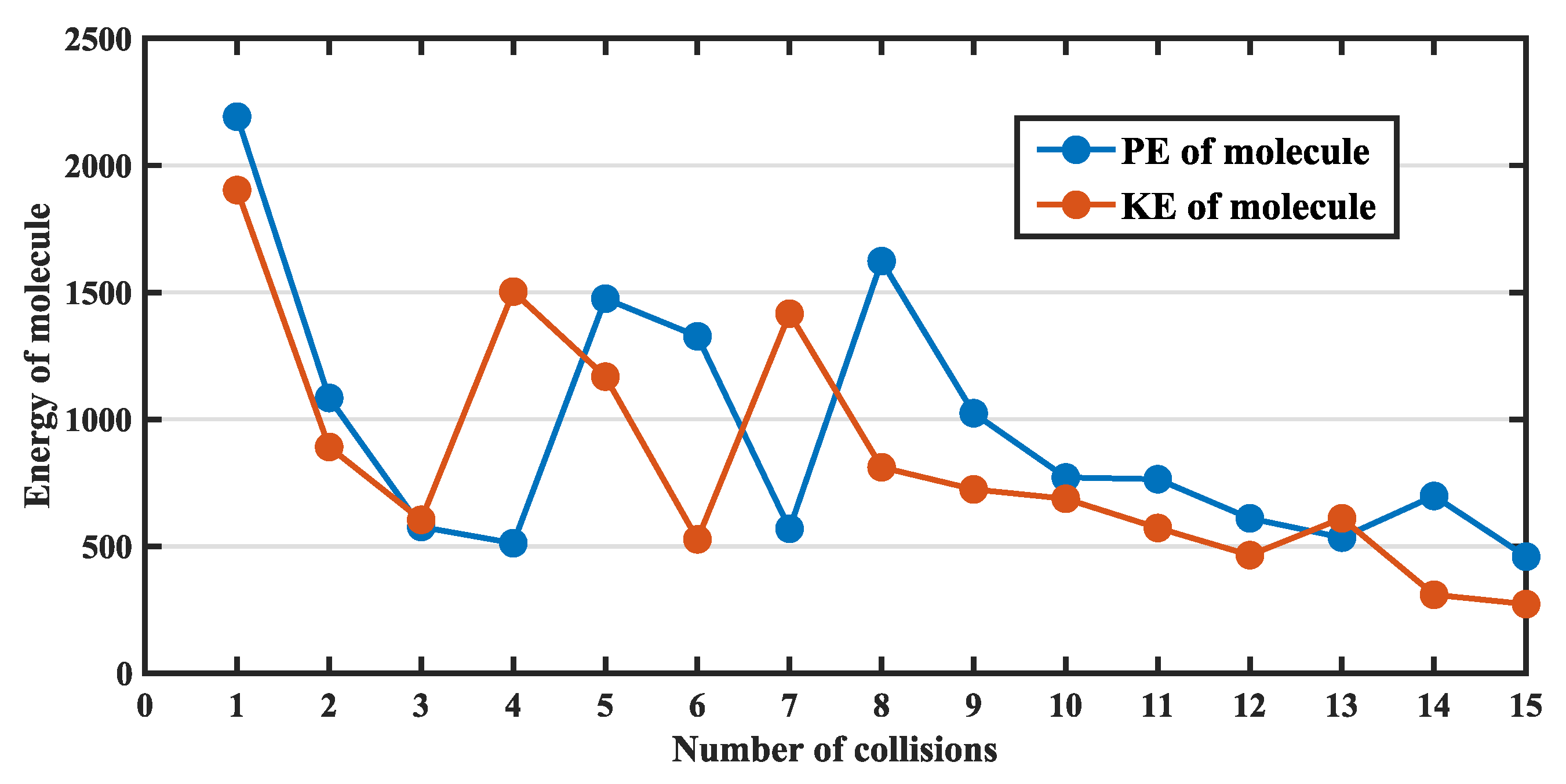
4.4. Effect Conflict Analysis of Molecular Collisions
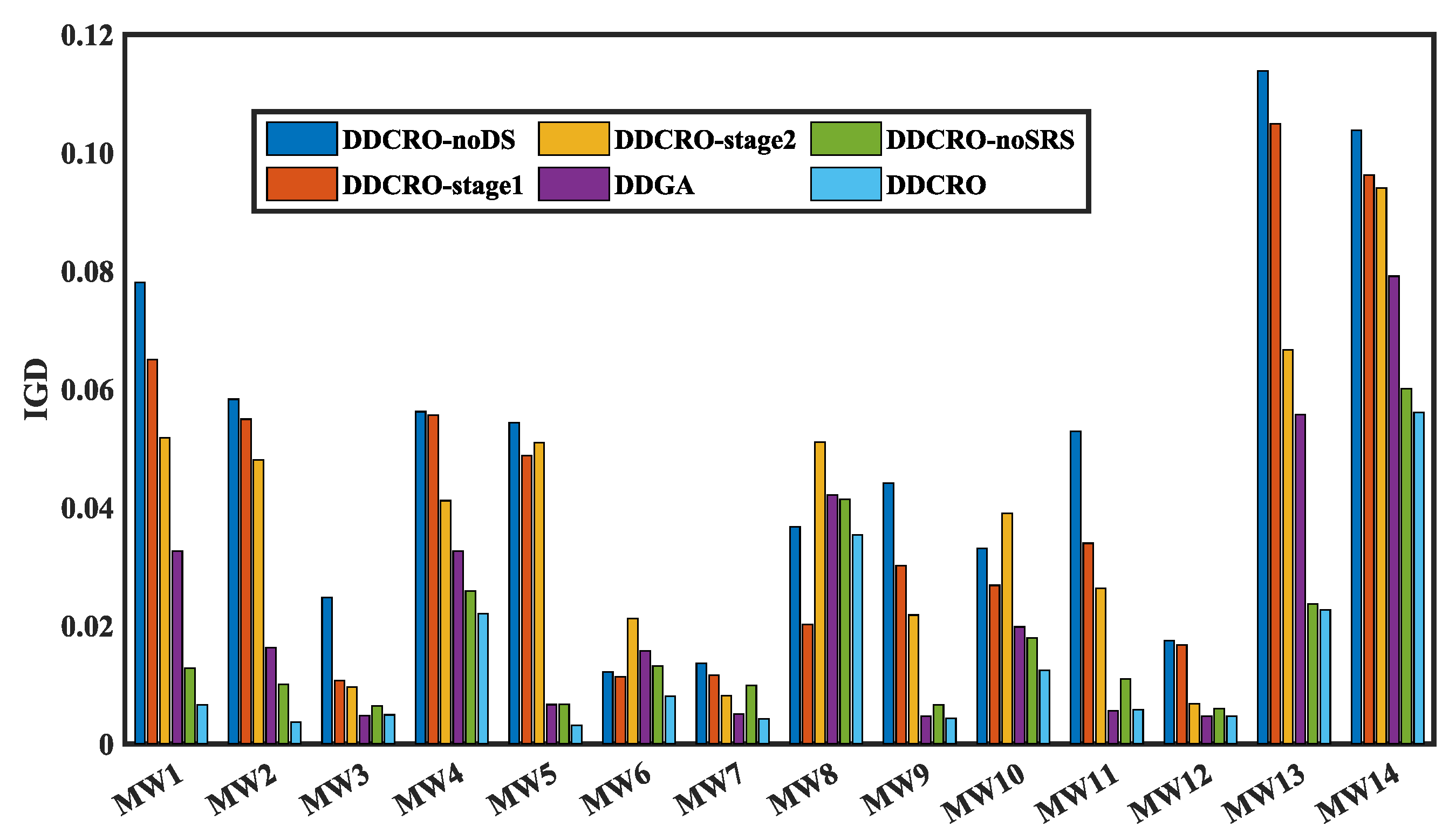
4.5. Ablation Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ali, I.M.; Essam, D.; Kasmarik, K. Novel binary differential evolution algorithm for knapsack problems. Inf. Sci. 2021, 542, 177–194. [Google Scholar] [CrossRef]
- Zuo, X.; Chen, C.; Tan, W.; Zhou, M. Vehicle scheduling of an urban bus line via an improved multiobjective genetic algorithm. IEEE Trans. Intell. Transp. Syst. 2014, 16, 1030–1041. [Google Scholar] [CrossRef]
- Ma, H.; Huang, X.; Hu, Z.; Chen, Y.; Qian, D.; Deng, J.; Hua, L. Multi-objective production scheduling optimization and management control system of complex aerospace components: A review. Int. J. Adv. Manuf. Technol. 2023, 127, 4973–4993. [Google Scholar] [CrossRef]
- Naqvi, S.S.A.; Jamil, H.; Iqbal, N.; Khan, S.; Lee, D.I.; Park, Y.C.; Kim, D.H. Multi-objective optimization of PI controller for BLDC motor speed control and energy saving in Electric Vehicles: A constrained swarm-based approach. Energy Rep. 2024, 12, 402–417. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Xia, Z.; Liu, Y.; Lu, J.; Cao, J.; Rutkowski, L. Penalty method for constrained distributed quaternion-variable optimization. IEEE Trans. Cybern. 2020, 51, 5631–5636. [Google Scholar] [CrossRef] [PubMed]
- Tetsuyuki, T.; Sakai, S. Constrained optimization by the ε constrained differential evolution with gradient-based mutation and feasible elites. In Proceedings of the IEEE Congress on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; p. r8. [Google Scholar]
- Liang, J.; Qiao, K.; Yu, K.; Qu, B.; Yue, C.; Guo, W.; Wang, L. Utilizing the relationship between unconstrained and constrained Pareto fronts for constrained multiobjective optimization. IEEE Trans. Cybern. 2022, 53, 3873–3886. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Li, H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; TIK Report; Computer Engineering and Networks Laboratory, ETH Zurich: Zurich, Switzerland, 2001; Volume 103. [Google Scholar]
- Yu, Q.; Yang, C.; Dai, G.; Peng, L.; Li, J. A novel penalty function-based interval constrained multi-objective optimization algorithm for uncertain problems. Swarm Evol. Comput. 2024, 88, 101584. [Google Scholar] [CrossRef]
- Zhou, P.; Zhang, S.; Chai, T. Adaptive constraint penalty-based multiobjective operation optimization of an industrial dynamic system with complex multiconstraint. IEEE Trans. Cybern. 2024, 54, 4724–4737. [Google Scholar] [CrossRef]
- Song, S.; Zhang, K.; Zhang, L.; Wu, N. A dual-population algorithm based on self-adaptive epsilon method for constrained multi-objective optimization. Inf. Sci. 2024, 655, 119906. [Google Scholar] [CrossRef]
- Ji, J.Y.; Zeng, S.; Wong, M.L. ε-Constrained multiobjective differential evolution using linear population size expansion. Inf. Sci. 2022, 609, 445–464. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Razzaghi, R.; Jalili, M.; Liebman, A. Multi-objective coordinated EV charging strategy in distribution networks using an improved augmented epsilon-constrained method. Appl. Energy 2024, 369, 123547. [Google Scholar] [CrossRef]
- Luo, W.; Yu, X.; Yen, G.G. Dual-stage and dual-population cooperative evolutionary algorithm for solving constrained multiobjective problems. Appl. Soft Comput. 2024, 160, 111703. [Google Scholar] [CrossRef]
- Dong, J.; Gong, W.; Ming, F.; Wang, L. A two-stage evolutionary algorithm based on three indicators for constrained multi-objective optimization. Expert Syst. Appl. 2022, 195, 116499. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, Q.; Lin, Q. A constrained multiobjective evolutionary algorithm with detect-and-escape strategy. IEEE Trans. Evol. Comput. 2020, 24, 938–947. [Google Scholar] [CrossRef]
- Ma, H.; Wei, H.; Tian, Y.; Cheng, R.; Zhang, X. A multi-stage evolutionary algorithm for multi-objective optimization with complex constraints. Inf. Sci. 2021, 560, 68–91. [Google Scholar] [CrossRef]
- Lam, A.Y.; Li, V.O. Chemical-reaction-inspired metaheuristic for optimization. IEEE Trans. Evol. Comput. 2009, 14, 381–399. [Google Scholar] [CrossRef]
- Abbassi, M.; Chaabani, A.; Said, L.B. An efficient chemical reaction algorithm for multi-objective combinatorial bi-level optimization. Eng. Optim. 2022, 54, 665–686. [Google Scholar] [CrossRef]
- Gu, Q.; Luo, J.; Li, X.; Lu, C. An adaptive evolutionary algorithm with coordinated selection strategies for many-objective optimization. Appl. Intell. 2023, 53, 9368–9395. [Google Scholar] [CrossRef]
- Liang, Z.; Zeng, J.; Liu, L.; Zhu, Z. A many-objective optimization algorithm with mutation strategy based on variable classification and elite individual. Swarm Evol. Comput. 2021, 60, 100769. [Google Scholar] [CrossRef]
- Bechikh, S.; Chaabani, A.; Said, L.B. An efficient chemical reaction optimization algorithm for multiobjective optimization. IEEE Trans. Cybern. 2014, 45, 2051–2064. [Google Scholar] [CrossRef]
- Ding, W.; Chen, M.; Dong, W.; Luo, F.; Gu, C. Chemical Reaction-inspired Dual-population Co-evolutionary Algorithm for Many-objective Optimization. Expert Syst. Appl. 2025, 289, 128257. [Google Scholar] [CrossRef]
- Islam, M.S.; Islam, M.R. A solution method to maximal covering location problem based on chemical reaction optimization (CRO) algorithm. Soft Comput. 2023, 27, 7337–7361. [Google Scholar] [CrossRef]
- Shaheen, A.; Sleit, A.; Al-Sharaeh, S. An improved chemical reaction optimization algorithm for solving traveling salesman problem. In Proceedings of the 2018 9th International Conference on Information and Communication Systems (ICICS), Irbid, Jordan, 3–5 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 37–42. [Google Scholar]
- De, A.; Pratap, S.; Kumar, A.; Tiwari, M. A hybrid dynamic berth allocation planning problem with fuel costs considerations for container terminal port using chemical reaction optimization approach. Ann. Oper. Res. 2020, 290, 783–811. [Google Scholar] [CrossRef]
- Talatahari, S.; Azizi, M.; Gandomi, A.H. Material generation algorithm: A novel metaheuristic algorithm for optimization of engineering problems. Processes 2021, 9, 859. [Google Scholar] [CrossRef]
- Li, K.; Chen, R.; Fu, G.; Yao, X. Two-archive evolutionary algorithm for constrained multiobjective optimization. IEEE Trans. Evol. Comput. 2018, 23, 303–315. [Google Scholar] [CrossRef]
- Yuan, Z.; Yang, L.; Tian, J.; Wei, X.; Li, K. Dual-population dual-stage evolutionary algorithm for complex constrained multiobjective optimization problems. J. Comput. Appl. 2024. [Google Scholar] [CrossRef]
- Li, W.; Gong, W.; Ming, F.; Wang, L. Constrained multi-objective evolutionary algorithm with an improved two-archive strategy. Knowl.-Based Syst. 2022, 246, 108732. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Y.; Hou, Z.; Zou, J.; Zheng, J. A novel multi-population evolutionary algorithm based on hybrid collaboration for constrained multi-objective optimization. Swarm Evol. Comput. 2024, 87, 101581. [Google Scholar] [CrossRef]
- Ming, M.; Trivedi, A.; Wang, R.; Srinivasan, D.; Zhang, T. A dual-population-based evolutionary algorithm for constrained multiobjective optimization. IEEE Trans. Evol. Comput. 2021, 25, 739–753. [Google Scholar] [CrossRef]
- Liu, Z.Z.; Wang, B.C.; Tang, K. Handling constrained multiobjective optimization problems via bidirectional coevolution. IEEE Trans. Cybern. 2021, 52, 10163–10176. [Google Scholar] [CrossRef] [PubMed]
- Fan, Z.; Li, W.; Cai, X.; Li, H.; Wei, C.; Zhang, Q.; Deb, K.; Goodman, E. Push and pull search for solving constrained multi-objective optimization problems. Swarm Evol. Comput. 2019, 44, 665–679. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, T.; Xiao, J.; Zhang, X.; Jin, Y. A coevolutionary framework for constrained multiobjective optimization problems. IEEE Trans. Evol. Comput. 2020, 25, 102–116. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhu, M.; Wang, J.; Zhang, Z.; Xiang, Y.; Zhang, J. Tri-goal evolution framework for constrained many-objective optimization. IEEE Trans. Syst. Man, Cybern. Syst. 2018, 50, 3086–3099. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: Handling constraints and extending to an adaptive approach. IEEE Trans. Evol. Comput. 2013, 18, 602–622. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Y. Evolutionary constrained multiobjective optimization: Test suite construction and performance comparisons. IEEE Trans. Evol. Comput. 2019, 23, 972–986. [Google Scholar] [CrossRef]
- Liu, Z.Z.; Wang, Y. Handling constrained multiobjective optimization problems with constraints in both the decision and objective spaces. IEEE Trans. Evol. Comput. 2019, 23, 870–884. [Google Scholar] [CrossRef]
- Fan, Z.; Li, W.; Cai, X.; Huang, H.; Fang, Y.; You, Y.; Mo, J.; Wei, C.; Goodman, E. An improved epsilon constraint-handling method in MOEA/D for CMOPs with large infeasible regions. Soft Comput. 2019, 23, 12491–12510. [Google Scholar] [CrossRef]
- Kumar, A.; Wu, G.; Ali, M.Z.; Luo, Q.; Mallipeddi, R.; Suganthan, P.N.; Das, S. A benchmark-suite of real-world constrained multi-objective optimization problems and some baseline results. Swarm Evol. Comput. 2021, 67, 100961. [Google Scholar] [CrossRef]
- Zou, J.; Sun, R.; Yang, S.; Zheng, J. A dual-population algorithm based on alternative evolution and degeneration for solving constrained multi-objective optimization problems. Inf. Sci. 2021, 579, 89–102. [Google Scholar] [CrossRef]
- Zeng, Z.; Zhang, X.; Hong, Z. A constrained multiobjective differential evolution algorithm based on the fusion of two rankings. Inf. Sci. 2023, 647, 119572. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X. PlatEMO: A MATLAB Platform for Evolutionary Multi-Objective Optimization. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]

| Test Suite | Test Problem | Objectives | Variables |
|---|---|---|---|
| DTLZ | C1/DC1/DC2/DC3-DTLZ1 | 3 | 7 |
| others | 3 | 12 | |
| MW | MW1–14 | 2 | 15 |
| DOC | DOC1 | 2 | 6 |
| DOC2 | 2 | 16 | |
| DOC3 | 2 | 10 | |
| DOC4–5 | 2 | 8 | |
| DOC6–7 | 2 | 11 | |
| DOC8 | 2 | 10 | |
| DOC9 | 2 | 11 | |
| LIRCMOP | LIRCMOP1–12 | 2 | 10 |
| LIRCMOP13–14 | 3 | 10 |
| Problem | NSGAII | CAEAD | CCMO | URCMO | TSTI | CMODE-FTR | DDCRO | |
|---|---|---|---|---|---|---|---|---|
| C1_DTLZ1 | IGD | 2.7961 (4.50)− | 2.2881 (1.43)− | 1.9909 (1.33)≈ | 2.2185 (6.81)− | 2.0018 (7.80)− | 2.6349 (0.00)≈ | 1.9655 (1.19) |
| HV | 8.1577 (1.12)− | 8.3624 (6.34)− | 8.3762 (1.40)≈ | 8.2152 (4.10)− | 8.4064 (1.91)≈ | 8.2191 (0.00)≈ | 8.3811 (9.97) | |
| C1_DTLZ3 | IGD | 6.0485 (3.96)− | 2.8450 (3.65)− | 5.4115 (5.31)≈ | 1.5810 (1.13)− | 8.0147 (5.65)− | 2.3152 (3.85)− | 5.3272 (8.45) |
| HV | 1.1382 (2.28)− | 7.2555 (1.27)− | 5.5600 (8.40)≈ | 3.7335 (1.91)− | 0.0000 (0.00)− | 7.7162 (1.08)− | 5.5878 (3.02) | |
| C2_DTLZ2 | IGD | 5.6409 (1.98)− | 5.5431 (2.69)− | 4.2781 (9.73)≈ | 4.3246 (9.06)≈ | 4.2097 (5.55)≈ | 5.5665 (1.62)− | 4.2093 (3.17) |
| HV | 4.8434 (2.95)− | 5.0360 (4.35)− | 5.1557 (8.27)− | 5.1180 (2.93)− | 5.1571 (2.38)≈ | 4.8158 (5.67)− | 5.1864 (9.17) | |
| C3_DTLZ4 | IGD | 1.2544 (4.08)− | 1.1157 (2.17)− | 9.5734 (1.34)≈ | 1.0654 (2.34)− | 9.6538 (9.78)≈ | 1.3089 (3.73)− | 9.5405 (8.10) |
| HV | 7.6724 (4.94)− | 7.8501 (1.03)− | 7.8922 (6.32)≈ | 7.8134 (2.23)− | 7.8923 (7.76)≈ | 7.6839 (7.16)− | 7.8994 (1.39) | |
| DC1_DTLZ1 | IGD | 1.4610 (6.77)− | 1.5260 (2.93)− | 1.1446 (7.72)≈ | 1.2004 (5.25)− | 1.1974 (9.56)≈ | 1.1554 (2.01)− | 1.1432 (9.27) |
| HV | 6.1347 (3.67)− | 6.2671 (9.53)− | 6.3070 (9.90)≈ | 6.2819 (1.69)− | 6.2738 (5.86)≈ | 4.5649 (3.02)− | 6.3171 (8.95) | |
| DC1_DTLZ3 | IGD | 4.4127 (3.56)− | 8.9060 (1.62)− | 3.4245 (7.21)≈ | 7.9188 (4.95)≈ | 8.1523 (5.92)≈ | 1.0252 (1.09)− | 3.5488 (1.14) |
| HV | 4.5791 (5.09)− | 2.8181 (2.18)− | 4.6879 (4.06)≈ | 3.7338 (1.07)≈ | 3.8028 (1.08)≈ | 8.9104 (1.77)− | 4.6700 (3.94) | |
| DC2_DTLZ1 | IGD | NaN
(NaN) | 3.7956 (2.98)− | 2.0391 (4.14)≈ | 3.1066 (8.71)− | 2.8059 (0.00)≈ | NaN (NaN) | 2.0044 (4.38) |
| HV | NaN (NaN) | 7.9008 (9.61)≈ | 8.3990 (1.71)≈ | 8.0620 (2.54)− | 8.1348 (0.00)≈ | NaN (NaN) | 8.4112 (3.23) | |
| DC2_DTLZ3 | IGD | NaN (NaN) | 5.6924 (9.65)≈ | 5.3675 (6.31)≈ | 5.7923 (4.28)≈ | NaN (NaN) | NaN (NaN) | 1.2851 (1.05) |
| HV | NaN (NaN) | 4.7510 (8.55)≈ | 4.3228 (1.61)− | 1.0134 (2.21)≈ | NaN (NaN) | NaN (NaN) | 5.5553 (1.58) | |
| DC3_DTLZ1 | IGD | 1.8108 (1.48)− | 2.2275 (4.27)− | 7.0380 (1.54)≈ | 9.7489 (1.81)≈ | 3.0917 (1.53)− | 4.9849 (6.46)− | 7.1917 (3.71) |
| HV | 1.8058 (2.34)− | 3.9322 (2.62)≈ | 5.3167 (1.46)≈ | 3.9911 (2.66)≈ | 6.6111 (6.16)− | 2.6532 (3.06)≈ | 5.3320 (4.62) | |
| DC3_DTLZ3 | IGD | 1.4270 (3.18)− | 1.1605 (2.15)≈ | 2.2225 (1.58)≈ | 4.8606 (1.49)≈ | 2.7253 (3.33)− | 2.1272 (2.69)− | 1.3855 (1.80) |
| HV | 0.0000 (0.00)− | 1.9122 (1.47)≈ | 3.5135 (8.50)≈ | 2.5569 (5.11)≈ | 0.0000 (0.00)− | 0.0000 (0.00)− | 2.4469 (1.35) | |
| 0/0/20 | 8/12/00 | 2/18/00 | 11/9/00 | 9/11/00 | 0/17/3 | |||
| Problem | NSGAII | CAEAD | CCMO | URCMO | TSTI | CMODE-FTR | DDCRO | |
|---|---|---|---|---|---|---|---|---|
| MW1 | IGD | 8.8883 (1.45)− | 2.0225 (6.17)≈ | 1.6301 (1.29)≈ | 1.7771 (2.58)≈ | 1.6596 (5.28)≈ | 3.6838 (3.53)− | 1.6166 (3.68) |
| HV | 4.1526 (1.17)≈ | 4.8882 (2.43)≈ | 4.8986 (1.02)≈ | 4.8971 (4.18)≈ | 4.8950 (6.63)≈ | 4.8657 (6.20)≈ | 4.8969 (2.11) | |
| MW2 | IGD | 2.4671 (3.02)− | 1.2472 (7.71)≈ | 2.0246 (7.25)≈ | 2.4547 (1.05)≈ | 1.6666 (5.24)≈ | 9.9745 (7.75)− | 9.7542 (6.86) |
| HV | 5.4660 (4.52)− | 5.7204 (1.35)≈ | 5.5418 (1.22)≈ | 5.4719 (1.53)≈ | 5.5961 (9.09)≈ | 4.5061 (9.76)− | 5.6692 (1.23) | |
| MW3 | IGD | 6.0297 (3.18)− | 5.5115 (3.80)≈ | 5.0220 (2.42)≈ | 5.0630 (2.22)≈ | 5.7086 (6.79)≈ | 5.7481 (6.44)− | 4.9940 (1.77) |
| HV | 5.4301 (4.90)− | 5.4384 (6.64)≈ | 5.4414 (4.63)≈ | 5.4420 (2.42)≈ | 5.4380 (9.08)≈ | 5.4461 (2.96)≈ | 5.4423 (3.89) | |
| MW4 | IGD | 6.5117 (4.68)≈ | 6.8851 (8.38)≈ | 6.3658 (1.49)≈ | 6.2140 (1.04)≈ | 1.3715 (1.72)≈ | 1.7708 (2.16)≈ | 5.9330 (8.21) |
| HV | 5.7905 (5.68)≈ | 5.7869 (9.96)≈ | 5.7923 (1.83)≈ | 5.7941 (1.06)≈ | 5.7114 (1.93)≈ | 5.6173 (3.32)≈ | 5.7969 (1.25) | |
| MW5 | IGD | 2.6810 (2.40)≈ | 1.9416 (4.25)− | 2.3415 (2.03)≈ | 6.6335 (2.03)+ | 2.7408 (3.44)− | 5.7111 (3.67)− | 3.3726 (3.73) |
| HV | 3.0361 (2.44)≈ | 3.1258 (2.43)− | 3.2358 (9.60)≈ | 3.2429 (1.20)+ | 2.1870 (1.14)− | 1.4690 (1.12)− | 3.2318 (1.23) | |
| MW6 | IGD | 2.0907 (1.12)− | 1.1971 (3.99)− | 2.8164 (7.15)− | 1.3571 (7.17)≈ | 1.2743 (2.11)≈ | 2.8905 (2.99)− | 4.0866 (2.67) |
| HV | 3.0148 (1.53)− | 3.1035 (5.24)− | 2.9163 (9.69)− | 3.1140 (9.73)≈ | 2.7096 (6.32)≈ | 1.8611 (1.19)− | 3.2608 (4.81) | |
| MW7 | IGD | 5.3408 (4.65)≈ | 7.4288 (8.46)− | 5.0896 (4.13)≈ | 4.7052 (4.41)≈ | 5.3385 (2.61)≈ | 9.4991 (1.77)− | 5.2352 (6.35) |
| HV | 4.1103 (4.54)≈ | 4.0898 (1.15)− | 4.1163 (5.70)≈ | 4.1196 (2.54)≈ | 4.1143 (5.30)≈ | 4.1257 (2.20)≈ | 4.1174 (1.04) | |
| MW8 | IGD | 2.9668 (1.86)≈ | 9.4994 (7.90)≈ | 2.0580 (1.22)≈ | 2.5545 (1.07)≈ | 2.3854 (7.38)≈ | 4.9277 (1.91)− | 2.1166 (7.10) |
| HV | 2.8146 (2.86)≈ | 3.1200 (1.25)≈ | 2.9535 (1.85)≈ | 2.8781 (1.61)≈ | 2.9040 (1.11)≈ | 2.5114 (3.01)− | 2.9445 (1.07) | |
| MW9 | IGD | 9.5797 (2.31)− | 8.8084 (6.27)− | 4.8282 (1.99)≈ | 5.5030 (6.19)≈ | 6.9900 (1.14)− | 5.3824 (9.78)≈ | 4.9346 (2.59) |
| HV | 3.8496 (5.05)− | 3.9184 (6.16)− | 3.9794 (7.56)≈ | 3.9400 (2.72)≈ | 3.9039 (2.34)− | 3.9463 (3.56)≈ | 3.9903 (2.90) | |
| MW10 | IGD | 1.2505 (1.00)≈ | 1.1542 (7.19)≈ | 1.6410 (9.40)≈ | 3.2628 (1.69)≈ | 6.4999 (5.80)≈ | 3.4954 (2.42)≈ | 3.5918 (2.11) |
| HV | 3.6196 (5.67)≈ | 4.4202 (9.72)≈ | 4.3581 (9.59)≈ | 4.2120 (1.37)≈ | 3.9905 (3.74)≈ | 2.4603 (1.12)≈ | 4.1867 (1.65) | |
| MW11 | IGD | 4.3943 (3.27)− | 1.5706 (3.92)− | 6.4006 (3.57)≈ | 6.2673 (1.31)≈ | 6.1445 (2.50)≈ | 7.5658 (2.94)≈ | 6.1887 (9.15) |
| HV | 3.3014 (8.08)− | 4.4209 (6.97)− | 4.4698 (2.75)≈ | 4.4729 (1.01)≈ | 4.4726 (4.86)≈ | 4.4640 (3.33)≈ | 4.4701 (1.41) | |
| MW12 | IGD | 3.8931 (4.43)− | 7.9188 (6.00)− | 4.9123 (4.20)≈ | 5.2133 (4.08)≈ | 5.6206 (1.47)≈ | 5.0237 (8.91)≈ | 4.9434 (1.59) |
| HV | 3.0191 (3.49)− | 6.0017 (3.37)− | 6.0427 (1.67)≈ | 6.0389 (1.04)≈ | 6.0343 (2.24)≈ | 6.0437 (3.54)≈ | 6.0430 (2.83) | |
| MW13 | IGD | 2.2901 (2.21)− | 3.9569 (3.57)≈ | 6.6127 (4.23)≈ | 9.5446 (3.38)− | 1.9761 (5.80)− | 1.7622 (2.19)− | 2.9415 (1.34) |
| HV | 4.0406 (2.86)− | 4.6042 (1.59)≈ | 4.4585 (2.24)≈ | 4.3144 (2.03)− | 3.8627 (1.81)− | 4.0737 (1.89)− | 4.6281 (4.63) | |
| MW14 | IGD | 1.9127 (2.02)≈ | 4.6069 (4.55)− | 1.6658 (2.18)≈ | 1.6059 (7.25)≈ | 1.7623 (3.00)≈ | 1.4583 (3.18)≈ | 1.7480 (5.67) |
| HV | 5.0152 (1.47)≈ | 4.1331 (1.03)− | 5.0356 (1.66)≈ | 5.0432 (6.52)≈ | 5.0269 (2.09)≈ | 5.0507 (1.66)≈ | 5.0293 (3.86) | |
| 0/15/13 | 0/14/14 | 2/26/00 | 2/24/02 | 6/22/00 | 0/13/15 | |||
| Problem | NSGAII | CAEAD | CCMO | URCMO | TSTI | CMODE-FTR | DDCRO | |
|---|---|---|---|---|---|---|---|---|
| DOC1 | IGD | 2.9253 (3.34)− | 8.2729 (2.68)− | 1.0472 (4.00)− | 1.1683 (2.20)+ | 3.8109 (4.12)− | 1.1068 (8.70)− | 7.4209 (1.641) |
| HV | 1.7695 (3.54)− | 0.0000 (0.00)− | 0.0000 (0.00)− | 2.9030 (1.03)+ | 6.7356 (1.35)≈ | 0.0000 (0.00)− | 9.0909 (4.011) | |
| DOC2 | IGD | NaN (NaN) | 1.1290 (1.48)− | NaN (NaN) | 3.9553 (9.18)− | NaN (NaN) | 3.4578 (6.94)− | 2.1205 (5.25) |
| HV | NaN (NaN) | 6.1105 (2.05)− | NaN (NaN) | 3.7072 (6.10)≈ | NaN (NaN) | 6.1145 (9.26)− | 6.2079 (9.50) | |
| DOC3 | IGD | 6.0806 (2.43)− | 2.9889 (5.62)≈ | 7.8636 (0.00)− | 1.0740 (1.95)− | 6.4069 (2.39)− | 7.3797 (5.30)− | 2.5982 (3.42) |
| HV | 0.0000 (0.00)− | 2.1173 (1.61)≈ | 0.0000 (0.00)− | 1.0533 (1.53)− | 0.0000 (0.00)− | 1.3189 (6.35)− | 2.2318 (1.21) | |
| DOC4 | IGD | 1.4097 (1.58)− | 3.4608 (1.24)− | 1.6812 (2.13)− | 4.0835 (9.57)+ | 2.6397 (2.81)− | 1.0652 (6.03)≈ | 7.8113 (1.314) |
| HV | 4.7278 (6.25)+ | 5.4256 (3.12)− | 8.4613 (1.07)≈ | 5.1678 (1.09)+ | 0.0000 (0.00)− | 4.2122 (8.42)≈ | 2.8087 (1.474) | |
| DOC5 | IGD | NaN (NaN) | 2.3946 (8.44)+ | NaN (NaN) | 1.3060 (3.41)≈ | 8.1993 (3.33)≈ | 9.5431 (7.52)− | 8.7037 (7.53) |
| HV | NaN (NaN) | 1.3613 (8.62)− | NaN (NaN) | 0.0000 (0.00)− | 0.0000 (0.00)− | NaN (NaN) | 1.5933 (2.76) | |
| DOC6 | IGD | 1.6480 (2.37)− | 3.0718 (1.04)− | 2.8738 (2.12)− | 3.9294 (8.91)≈ | 1.4032 (8.81)− | 1.8493 (1.54)− | 2.9024 (3.94) |
| HV | 6.6140 (8.60)≈ | 5.3306 (3.43)≈ | 0.0000 (0.00)− | 4.9828 (2.02)≈ | 2.9290 (5.86)≈ | 9.9672 (1.99)− | 5.3333 (8.20) | |
| DOC7 | IGD | 5.7742 (2.22)− | 3.7170 (6.79)− | 5.2305 (1.52)− | 6.4552 (3.02)− | 6.6391 (1.82)− | 5.9332 (9.99)− | 2.3762 (1.06) |
| HV | 0.0000 (0.00)− | 5.3605 (2.52)+ | 0.0000 (0.00)− | 4.6720 (5.50)≈ | 0.0000 (0.00)− | 0.0000 (0.00)− | 4.4292 (1.50) | |
| DOC8 | IGD | 8.0012 (7.68)− | 6.2107 (1.93)+ | 1.1374 (4.45)− | 4.0650 (7.61)− | 1.2127 (5.85)− | 1.3146 (6.82)− | 2.6482 (9.77) |
| HV | 0.0000 (0.00)− | 8.0093 (1.95)+ | 0.0000 (0.00)− | 0.0000 (0.00)− | 0.0000 (0.00)− | 0.0000 (0.00)− | 5.2764 (1.21) | |
| DOC9 | IGD | 1.9469 (8.49)≈ | 9.2808 (9.97)≈ | 2.0132 (1.11)≈ | 9.2210 (1.58)≈ | 1.1037 (1.73)≈ | 2.8189 (1.53)− | 7.6204 (9.33) |
| HV | 0.0000 (0.00)+ | NaN (NaN) | NaN (NaN) | NaN (NaN) | NaN (NaN) | NaN (NaN) | NaN (NaN) | |
| 2/14/2 | 5/9/04 | 0/16/2 | 8/6/04 | 0/14/4 | 0/16/2 | |||
| Problem | NSGAII | CAEAD | CCMO | URCMO | TSTI | CMODE-FTR | DDCRO | |
|---|---|---|---|---|---|---|---|---|
| LIRCMOP1 | IGD | 2.7449 (2.83)− | 4.3540 (7.39)− | 2.7039 (6.07)− | 9.9904 (6.64)≈ | 2.1876 (1.96)≈ | 2.6361 (4.14)− | 1.6329 (5.52) |
| HV | 1.1980 (4.59)≈ | 1.0044 (4.03)− | 1.1732 (2.06)− | 1.9313 (3.11)≈ | 1.4142 (3.46)≈ | 1.1921 (1.08)− | 2.3278 (3.89) | |
| LIRCMOP2 | IGD | 2.5970 (3.35)− | 1.8335 (4.95)− | 2.0220 (7.73)− | 4.1306 (1.69)+ | 1.8454 (2.22)− | 2.2267 (4.32)− | 1.2727 (1.53) |
| HV | 2.2756 (1.45)− | 2.7582 (4.05)− | 2.6006 (4.52)− | 3.6091 (1.97)+ | 2.6764 (1.01)≈ | 2.4536 (2.33)− | 3.5653 (5.87) | |
| LIRCMOP3 | IGD | 3.1570 (2.76)− | 2.9752 (6.46)≈ | 2.5325 (6.05)− | 9.2023 (6.54)− | 2.2847 (2.86)≈ | 2.4553 (6.84)− | 1.6157 (8.94) |
| HV | 9.7716 (7.23)− | 9.9980 (1.86)− | 1.1811 (1.77)≈ | 1.6650 (2.97)− | 1.2211 (5.85)− | 1.2205 (2.22)− | 2.0276 (3.66) | |
| LIRCMOP4 | IGD | 2.8082 (3.00)− | 3.0014 (4.86)− | 2.4722 (6.36)− | 1.0687 (8.14)− | 2.0825 (1.61)− | 2.0094 (4.89)− | 7.8443 (1.80) |
| HV | 1.9400 (1.33)− | 1.8673 (2.62)− | 2.0858 (3.30)− | 2.6692 (3.57)− | 2.2891 (1.65)≈ | 2.3137 (2.28)− | 3.1304 (1.09) | |
| LIRCMOP5 | IGD | 1.2185 (5.52)− | 1.2163 (1.40)− | 1.0537 (2.45)− | 3.3111 (1.83)− | 7.6531 (5.21)− | 2.7959 (2.68)− | 7.6998 (2.42) |
| HV | 0.0000 (0.00)− | 0.0000 (0.00)− | 1.4138 (7.84)− | 2.8917 (1.78)≈ | 7.6955 (8.97)− | 1.6260 (1.16)− | 2.9072 (1.98) | |
| LIRCMOP6 | IGD | 1.1048 (4.82)− | 1.3463 (1.19)− | 9.1878 (8.96)− | 2.3687 (3.46)− | 1.0955 (5.00)− | 3.2387 (2.63)− | 7.0283 (7.48) |
| HV | 2.5329 (5.07)− | 0.0000 (0.00)− | 1.2749 (1.33)− | 1.9506 (9.64)≈ | 2.5013 (5.00)− | 1.0974 (6.80)− | 1.9652 (1.87) | |
| LIRCMOP7 | IGD | 1.6731 (5.22)− | 1.8871 (1.06)+ | 1.0954 (2.30)− | 7.6530 (2.92)+ | 1.3837 (3.18)− | 1.0084 (1.34)− | 8.2893 (2.79) |
| HV | 2.3458 (1.45)− | 2.9195 (2.99)≈ | 2.5135 (6.52)≈ | 2.9424 (1.66)≈ | 2.4317 (1.01)≈ | 2.5397 (2.77)− | 2.9406 (1.49) | |
| LIRCMOP8 | IGD | 1.3234 (7.17)− | 2.6366 (5.27)+ | 1.5128 (3.01)− | 7.6717 (9.77)+ | 2.3944 (1.03)− | 1.2381 (3.59)− | 8.3020 (1.25) |
| HV | 5.7138 (1.14)− | 2.9386 (8.89)≈ | 2.4035 (9.93)≈ | 2.9422 (5.42)≈ | 2.2503 (9.15)≈ | 2.4606 (1.11)− | 2.9407 (9.81) | |
| LIRCMOP9 | IGD | 8.9381 (1.24)− | 5.4657 (7.93)≈ | 3.7897 (7.71)− | 2.0962 (2.02)≈ | 4.7970 (4.37)≈ | 3.9393 (1.02)− | 1.0897 (5.71) |
| HV | 1.3587 (5.40)− | 3.2977 (4.72)− | 4.4378 (4.03)− | 4.8093 (8.60)≈ | 3.7784 (2.28)≈ | 4.1103 (4.64)≈ | 5.2079 (4.55) | |
| LIRCMOP10 | IGD | 8.3474 (1.17)− | 2.5749 (1.12)− | 9.8981 (2.06)≈ | 9.9064 (1.89)− | 6.1928 (3.19)− | 8.8364 (6.56)− | 7.2569 (2.32) |
| HV | 1.1813 (9.21)− | 5.6856 (5.56)− | 6.6456 (4.22)− | 7.0388 (9.51)≈ | 3.7660 (1.90)− | 6.6076 (2.76)− | 7.0565 (1.28) | |
| LIRCMOP11 | IGD | 7.5204 (3.91)− | 1.8885 (9.12)− | 2.9826 (3.40)≈ | 4.2108 (3.51)− | 4.3844 (1.79)− | 5.0023 (3.17)≈ | 2.0630 (3.46) |
| HV | 2.2713 (2.64)− | 6.1236 (3.72)− | 6.7906 (1.72)≈ | 6.7366 (1.62)≈ | 4.4070 (8.59)− | 6.6706 (1.36)≈ | 6.8511 (1.66) | |
| LIRCMOP12 | IGD | 5.4822 (2.22)− | 4.3325 (4.61)− | 1.6727 (1.03)− | 1.1282 (1.71)− | 3.4805 (5.09)− | 1.8868 (6.90)− | 3.8137 (1.09) |
| HV | 3.4342 (1.05)− | 4.2233 (1.98)− | 5.4270 (5.70)− | 5.6502 (8.76)− | 4.4299 (2.82)− | 5.3174 (3.58)− | 6.2012 (2.65) | |
| LIRCMOP13 | IGD | 1.3265 (1.55)− | 1.0806 (6.35)+ | 9.7572 (1.15)+ | 1.0247 (5.55)+ | 1.0091 (6.13)≈ | 9.0807 (7.50)+ | 1.2242 (1.89) |
| HV | 1.0882 (2.18)− | 5.4657 (1.17)+ | 5.5171 (1.55)+ | 5.3486 (1.72)+ | 1.3891 (2.78)− | 5.6002 (9.06)+ | 5.1812 (3.13) | |
| LIRCMOP14 | IGD | 1.2835 (9.57)− | 1.1296 (2.20)+ | 1.0104 (1.28)+ | 9.8191 (6.51)+ | 9.7651 (5.89)≈ | 9.5164 (5.54)+ | 1.1578 (2.34) |
| HV | 6.8210 (3.69)− | 5.4635 (4.98)+ | 5.5153 (1.53)+ | 5.4960 (1.18)+ | 1.3948 (2.78)− | 5.5519 (2.66)≈ | 5.3737 (1.60) | |
| 0/27/1 | 6/18/4 | 4/18/6 | 11/9/08 | 0/18/10 | 3/21/4 | |||
| Problem | NSGAII | CAEAD | CCMO | URCMO | TSTI | CMODE-FTR | DDCRO | |
|---|---|---|---|---|---|---|---|---|
| RWMOP5 | HV | 2.4048 (6.85)− | 1.0000 (0.00)≈ | 3.6357 (4.36)− | 2.6605 (1.87)− | 3.8238 (1.57)− | 9.5594 (6.75)+ | 5.1425 (4.41) |
| RWMOP7 | HV | 4.8535 (3.21)− | 9.1229 (1.41)≈ | 4.7768 (1.44)− | 4.8150 (3.68)− | 4.7958 (1.11)− | 7.1772 (3.22)≈ | 9.2924 (5.09) |
| RWMOP9 | HV | 3.3229 (1.41)− | 4.6776 (1.94)− | 5.4123 (8.79)− | 5.5053 (1.09)− | 5.4269 (9.68)− | 1.7725 (3.24)− | 9.2311 (8.25) |
| RWMOP10 | HV | 9.3570 (5.35)+ | 5.6658 (2.82)− | 1.4404 (1.38)− | 1.4175 (4.35)− | 1.4478 (7.54)− | 1.0000 (0.00)+ | 8.3282 (9.00) |
| RWMOP11 | HV | 5.8765 (8.48)− | 2.6726 (3.72)− | 7.1295 (2.56)− | 1.7321 (4.14)− | 4.1360 (1.84)− | 1.0962 (3.06)− | 8.9073 (0.00) |
| RWMOP21 | HV | 8.2328 (2.16)+ | 9.3902 (4.13)+ | 2.9337 (1.35)+ | 2.9341 (2.10)+ | 3.0675 (9.40)+ | 3.7814 (1.98)+ | 2.6415 (2.68) |
| RWMOP25 | HV | 2.3374 (9.14)− | 4.7956 (2.25)− | 2.3656 (3.68)− | 2.3689 (9.66)− | 2.3765 (1.55)− | 3.6364 (4.27)− | 9.9735 (1.03) |
| RWMOP27 | HV | 2.8523 (7.58)≈ | 9.8338 (3.22)− | 1.6764 (7.50)− | 4.1701 (1.48)− | 3.1610 (8.43)≈ | 3.5569 (4.11)− | 3.7459 (8.05) |
| 2/5/1 | 1/5/2 | 1/7/0 | 1/7/0 | 1/6/1 | 3/4/1 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Guo, X.; Li, Y.; Li, N.; Zheng, R.; Dong, W.; Ding, W. A Dual-Stage and Dual-Population Algorithm Based on Chemical Reaction Optimization for Constrained Multi-Objective Optimization. Processes 2025, 13, 2484. https://doi.org/10.3390/pr13082484
Zhang T, Guo X, Li Y, Li N, Zheng R, Dong W, Ding W. A Dual-Stage and Dual-Population Algorithm Based on Chemical Reaction Optimization for Constrained Multi-Objective Optimization. Processes. 2025; 13(8):2484. https://doi.org/10.3390/pr13082484
Chicago/Turabian StyleZhang, Tianyu, Xin Guo, Yan Li, Na Li, Ruochen Zheng, Wenbo Dong, and Weichao Ding. 2025. "A Dual-Stage and Dual-Population Algorithm Based on Chemical Reaction Optimization for Constrained Multi-Objective Optimization" Processes 13, no. 8: 2484. https://doi.org/10.3390/pr13082484
APA StyleZhang, T., Guo, X., Li, Y., Li, N., Zheng, R., Dong, W., & Ding, W. (2025). A Dual-Stage and Dual-Population Algorithm Based on Chemical Reaction Optimization for Constrained Multi-Objective Optimization. Processes, 13(8), 2484. https://doi.org/10.3390/pr13082484






