Abstract
FeAl intermetallic compounds exhibit high application potential in high-voltage transmission lines to withstand external forces such as powerlines’ own gravity and wind force. The ordered crystal structure in FeAl intermetallic compounds endows materials with high strength, but the remarkable brittleness at room temperature restricts engineering applications. This contradiction is essentially closely related to the deformation mechanism at the nanoscale. Here, we performed molecular dynamics simulations to reveal anomalous grain size effects and deformation mechanisms in nanocrystalline FeAl intermetallic material. Models with grain sizes ranging from 6.2 to 17.4 nm were systematically investigated under uniaxial tensile stress. The study uncovers a distinctive inverse Hall-Petch relationship governing flow stress within the nanoscale regime. This behavior stems from high-density grain boundaries promoting dislocation annihilation over pile-up. Crucially, the material exhibits anomalous ductility at ultra-high strain rates due to stress-induced phase transformation dominating the plastic deformation. The nascent FCC phase accommodates strain through enhanced slip systems and inherent low stacking fault energy with the increasing phase fraction paralleling the stress plateau. Nanoconfinement suppresses the propagation of macroscopic defects while simultaneously suppressing room-temperature brittle fracture and inhibiting the rapid phase transformation pathways at extreme strain rates. These findings provide new theoretical foundations for designing high-strength and high-toughness intermetallic nanocompounds.
1. Introduction
The performance of cable protective coatings directly determines their long-term service reliability in complex environments [1,2,3]. While traditional coating materials, such as galvanized steel, pure aluminum, and epoxy resin, are widely used, they still have limitations [4,5]. FeAl alloy nanocoatings [6,7], due to their unique phase composition and performance advantages, have become a key research direction for the new generation of cable protective materials.
To investigate the mechanical properties and deformation mechanisms of FeAl alloys, numerous researchers have conducted extensive experimental studies. For example, M. M. Rajath Hegde [8] synthesized nanostructured FeAl alloy and found out the coexistence of elemental and alloy phases with increasing hardness during alloying. M.A. Morris-Muñoz [9] et al. prepared bulk nanocrystalline FeAl alloy and discovered that within the fine-grain size range of 40–100 nm, excellent particle bonding and high density can be achieved, resulting in superior combined strength and toughness properties.
Compared to coarse-grained crystals, nanocrystalline polycrystals with grain sizes below 100 nm exhibit unstable atomic arrangements at grain boundaries, leading to performance distinctly different from coarse-grained or microcrystalline materials of the same composition. Specifically, the Hall-Petch relationship [10,11], a classical theory of grain refinement strengthening, states that yield strength is inversely proportional to the square root of grain size. However, whether this relationship still holds when grain size is refined to the nanoscale has been a major research focus in recent years. Niu [12] et al. found that the grain size significantly influences the mechanical behavior of polycrystalline titanium in a dual-zone manner. A critical grain size of 19.96 nm defines the dual zone of the Hall-Petch relationship. When the grain size falls below 19.96 nm, the peak stress decreases with further grain refinement, exhibiting an inverse Hall-Petch relationship, otherwise obeying the classical relation. Song [13] et al. systematically explored a similar regulation with Ti3Al nanocrystalline alloys with a critical grain size of 8 nm. Chen [14] et al., using molecular dynamics simulations, observed that the tensile strength of AlMg polycrystalline alloys follows the Hall-Petch relationship for grain sizes above 10 nm but exhibits an inverse Hall-Petch relationship below 10 nm. This strong correlation between size, mechanism, and performance suggests that the grain size effect and detail deformation mechanisms can govern the mechanical properties of nanostructured materials. Whether the FeAl nanocrystal falls into the same route is still a mystery.
Therefore, our study employs molecular dynamics to simulate the tensile process of nanocrystalline FeAl alloys under various grain sizes, aiming to systematically analyze their deformation mechanisms and microstructural evolution perspectives at the atomistic level. Our study will provide comprehensive atomistic insights that are crucial for rationally designing FeAl nanocoatings with optimized strength-toughness combinations tailored for complex service environments, moving beyond the empirical correlations often established in prior reports and providing foundational theoretical guidance for next-generation material development.
2. Methods
This study relies on the classical molecular dynamics (MD) code LAMMPS [15] Version 29 August 2024 (Large-scale Atomic/Molecular Massively Parallel Simulator) software, with atomic motion states visualized using OVITO [16]. The potential function describes the interactions between atoms in the system. In this study, the modified embedded atom method (MEAM) [17,18] and interatomic potentials were adopted for molecular dynamics simulations. This potential function is a modified model extended from the EAM potential by introducing bond-angle directionality. Compared with other potential functions, MEAM can adapt to more complex local atomic environments and fully account for the characteristics of electron density distribution. The polycrystalline FeAl models were generated using the ATOMSK [19] version beta-0.13.1 software. The modeling process began by constructing a body-centered cubic FeAl intermetallic compound unit cell. Subsequently, the Voronoi tessellation algorithm within ATOMSK was employed to create polycrystalline structures with varying average grain sizes. Although the simulated grain sizes in Table 1 (6.2–17.4 nm) are numerically close, this range deliberately spans and falls below typical critical sizes reported for inverse Hall-Petch transitions in other nanocrystalline systems [12,13,14]. In this procedure, N nodes were initially placed randomly within the simulation box volume, with each node defining the center of a future grain. Red lines connected adjacent nodes, and the perpendicular bisectors of these connections were constructed to form closed polyhedral shapes. Each resulting polyhedron enclosed the space of an individual grain, with the blue lines signifying the grain boundaries. A unique crystallographic orientation was then assigned to each grain. Atoms, based on the initial BCC FeAl unit cell, were placed within each grain according to its assigned orientation. Atoms located outside the boundaries of their respective grains were subsequently deleted. This process resulted in a fully atomistic polycrystalline FeAl model. Figure 1 illustrates the complete modeling and visualization workflow. The generated FeAl polycrystal models were finally used to simulate tensile deformation processes.

Table 1.
The model parameters of polycrystalline alloys with different average grain size.
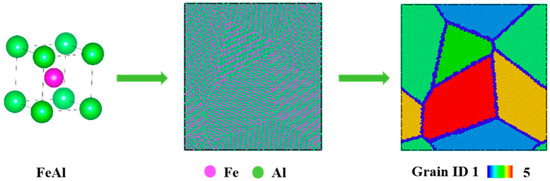
Figure 1.
Schematic diagram of the nanocrystalline FeAl alloys model.
To construct a reasonable initial configuration, periodic boundary conditions were applied throughout the simulation. Before sample loading, the model was first subjected to energy minimization using the conjugate gradient method, with an energy convergence criterion of 10−15 eV and a force convergence criterion of 10−15 eV/Å. Subsequently, under the isothermal-isobaric (NPT) ensemble, the Nosé-Hoover thermostat was used to maintain the system in a thermodynamic equilibrium state at 300 K for 100 ps. This step aimed to eliminate non-physical contacts and residual internal stress in grain boundary regions. The time step selected for the simulation was 1 fs. During the loading stage, strain was introduced via uniaxial tension along the y-axis, with a constant nominal strain rate of 1 × 109 s−1. The x and z directions were maintained under zero-pressure conditions, and the entire process was conducted at a constant temperature of 300 K. During deformation, the evolution of atomic configurations was visualized and structurally characterized using OVITO software 3.13.0 combined with Polyhedral Template Matching [20]; the dynamic evolution of the dislocation core line network was analyzed using the dislocation extraction algorithm (DXA) [21].
3. Results and Discussion
3.1. Grain Size Effect
To explore the mechanical behavior and deformation mechanisms of the alloy material, the stress-strain diagrams of samples with different grain sizes are presented in Figure 2a. These curves offer a critical insight into the fundamental mechanical properties of the materials. From the picture, all samples, irrespective of grain size, exhibit similar characteristic stress-strain behavior: stress initially increases linearly with strain until reaching a peak stress point. This peak signifies the transition from elastic to plastic deformation, clearly demarcating the elastic and plastic regimes of the curve. Further analysis of the peak stress (Figure 2c) reveals that its value increases with increasing grain size, albeit in a non-linear manner. For instance, as the grain size increases from 6.2 nm to 8.1 nm, the peak stress rises from 4.63 GPa to 5.20 GPa, representing a 12.3% increase. However, when the grain size increases further from 8.1 nm to 14.9 nm, the peak stress increases marginally from 5.20 GPa to 5.41 GPa, a mere 4.6% increase. Notably, beyond a grain size of approximately 8.1 nm (e.g., within the 8.1 nm to 14.9 nm range), the peak stress becomes relatively insensitive to further increases in grain size. This phenomenon is intrinsically linked to the nature of FeAl as a brittle intermetallic compound. At room temperature, FeAl inherently exhibits limited dislocation mobility. At smaller grain sizes, while an increased density of grain boundaries could theoretically impede dislocation slip, the inherent restriction on dislocation activity is already severe, diminishing the additional hindering effect of fine grains. Conversely, as grain size increases, the reduced grain boundary density provides more space for the limited dislocation motion. This allows the material to accommodate greater dislocation slip, thereby resisting external loads and leading to the observed increase in peak stress with grain size. However, once the grain size exceeds a critical threshold (around 8.1 nm), the strengthening effect arising from increased dislocation slip space saturation ceases, and the peak stress ceases to increase significantly.
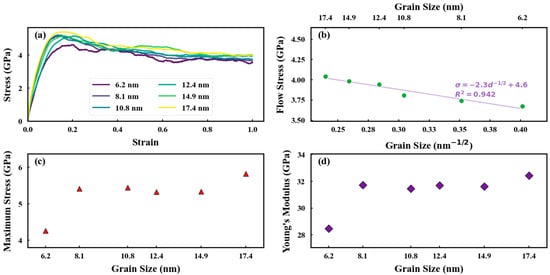
Figure 2.
(a) Stress-strain curves corresponding to different grain sizes; (b) Young’s modulus; (c) maximum stress; (d) Flow stress corresponding to different grain sizes.
Regarding the material’s stiffness, Figure 2d shows that Young’s modulus also increases with increasing grain size. Young’s modulus characterizes the stiffness in the elastic regime and is fundamentally governed by atomic bonding forces. However, in nanocrystalline materials, grain boundaries exert a significant constraining effect on elastic deformation and, coupled with dislocation mobility, modulate the macroscopic modulus. The grain boundary regions, characterized by disordered atomic arrangements, typically possess a lower elastic modulus than the grain interiors. In specimens with smaller grains, the high volume fraction of grain boundaries introduces substantial regions of reduced stiffness and atomic disorder. This not only diminishes the overall efficiency of interatomic force transmission but also lowers the macroscopic Young’s modulus due to the “softer” nature of these regions. This is evidenced by the sample with a grain size of 6.2 nm (Figure 2d), which exhibits a significantly lower Young’s modulus (28.6 GPa) compared to other grain sizes, likely due to its highest grain boundary volume fraction. The trend of systematically decreasing grain boundary fraction with increasing grain size, clearly shown in Figure 3, further confirms that the reduction in the proportion of “softer” grain boundary regions is the fundamental reason for the slight increase in Young’s modulus with increasing grain size. We also found increasing temperature leads to a significant decrease in both the ultimate stress and flow stress of polycrystalline FeAl alloys in Figures S1 and S2.
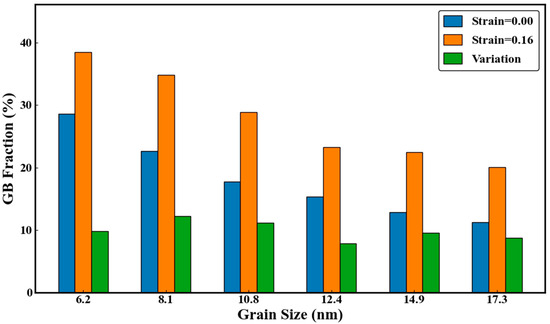
Figure 3.
Grain boundary fraction percentage and difference before and after stretching at different grain sizes.
Further observation reveals that the variations of Young’s modulus and peak stress with grain size follow highly consistent trends. This consistency arises from two key factors: Firstly, the crucial strain corresponding to the attainment of peak stress remains remarkably stable at approximately 16% for all samples, indicating that the critical strain for macroscopic plastic yielding is independent of grain size. Secondly, as previously discussed, the numerical changes in both properties are strongly correlated with the grain boundary volume fraction. A decrease in grain boundary fraction enhances both the macroscopic Young’s modulus and the peak stress. Consequently, their trends with changing grain size naturally exhibit this parallelism.
If we consider the average stress within the strain range of 0.4 to 0.5 as the flow stress under plastic flow conditions, the relationship between the average flow stress and grain size is plotted with green dots in Figure 2c. From the figure, it can be observed that within the grain size range of 6.2 nm to 17.4 nm, the variation in flow stress follows an inverse Hall-Petch relationship:
where d is the grain size, σ represents the flow stress, which in this context is equivalent to the yield strength. The Hall-Petch constant (K) is −2.34 GPa·nm1/2, which is an empirical constant characterizing the extent to which grain boundaries impede dislocation motion. A negative value of K indicates that the grain boundaries do not hinder dislocation motion; contrarily, they facilitate coordinated dislocation movement. The intersection value of 4.58 represents the theoretical yield strength of the material when the grain size approaches infinity.
As opposed to the classical Hall-Petch theory, our study found that neither stable dislocation pile-up near the grain boundaries nor the deformation mechanisms were observed in previous studies, including grain boundary sliding [13] or dislocation motion [12,14]. Throughout the tensile deformation process (Figure 4), the core phenomenon observed is that dislocation lines continuously interact with grain boundaries during motion and are effectively absorbed and annihilated by the latter. This means that as deformation progresses, dislocation density does not accumulate and increase at grain boundaries; instead, it gradually decreases. A similar effect was also observed in Lu’s [22] work, where in small-grained materials with a high proportion of grain boundaries, dislocations are rapidly absorbed, thereby activating softening mechanisms such as grain boundary sliding. Notably, the rate of this dislocation disappearance exhibits strong grain size dependence. Smaller grain sizes result in higher grain boundary density and larger surface area, leading to greater efficiency in dislocation absorption and annihilation by grain boundaries, which in turn accelerates the decay of dislocation density. Thus, under the dominance of this newly observed dynamic mechanism, the overall resistance of the material to plastic deformation decreases as the grain size reduces. The absence of the dislocation pile-up in the nanocrystalline structure is formally aligned with the inverse Hall-Petch relationship [23]. It highlights the critical role of grain boundaries in regulating the dynamic evolution of dislocations and their decisive influence on the strength and toughness behavior of materials.
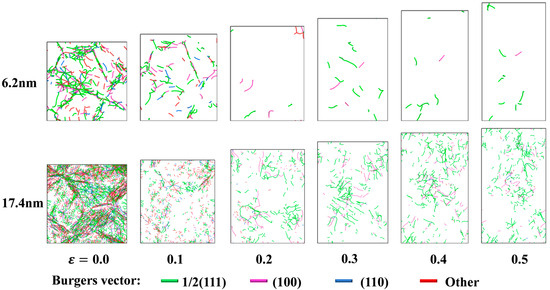
Figure 4.
Atomic structure evolution with different strain sizes (upper: 6.2 nm; lower: 17.4 nm). Lines of different colors represent different dislocation lines with distinct Burgers vectors.
3.2. Analysis of Deformation Mechanisms
Although FeAl alloys typically exhibit significant room-temperature brittleness, the stress-strain curve in this study reveals exceptional ductility in the modeled material. Analysis of the polycrystalline model’s atomic evolution (Figure 5) shows extensive stress-induced phase transformation from BCC to FCC during the tension process. This crystal restructuring occurs through coordinated shear displacements rather than conventional dislocation slip, enabling efficient energy dissipation and manifesting macroscopically as sustained deformation under near-constant flow stress. Furthermore, no discernible grain boundary sliding phenomena were observed (S4). Our newly observed plastic deformation mechanism differs fundamentally from the interface or grain boundary design strategies reported in the literature. Li [24] et al. reported the transmission of interfacial sliding at the sub-micron scale, enabling co-deformation of the brittle FeAl2 phase. Su [25] et al engineered 2–10 nm Co-rich grain boundaries in nanocrystalline CoAl (Co60Al40) to turn them into dislocation nucleation sites, which triggered the propagation of <100> and 1/2<111> dislocations into the grain interiors, enabling a transition from brittle shear fracture to homogeneous plastic deformation. The core of both strategies lies in overcoming brittleness limitations by regulating dislocation activity. In contrast, the nanocrystalline FeAl in our study exhibits a unique phase transformation-dominated plastic deformation mechanism under ultra-high strain rates. Especially when the grain size reaches 17.4 nm, the material undergoes a significant stress-induced phase transformation from BCC to FCC during tensile deformation.

Figure 5.
Atomic structure snapshots of the model with a grain size of 17.4 nm at different strains. Different colors of the particles in the snapshots represent different crystal phases. BCC is in blue, FCC is in green, HCP is in red, and the grain boundary is in light gray.
The phase transformation alters the brittleness of FeAl nanocrystalline material, leading to high ductility. The inherent brittleness of pristine B2-FeAl stems from its ordered structure impeding dislocation motion [26,27,28]. In contrast, the newly formed FCC phase offers critical deformability advantages, including more independent slip systems, lower dislocation resistance, and a stacking fault energy that is conducive to dislocation dissociation and cross-slip. These properties allow transformed regions to accommodate further plasticity through conventional dislocation mechanisms. Moreover, significant stress concentrations at BCC/FCC interfaces resulting from lattice mismatch spontaneously nucleate dislocations into the nascent FCC phase, accelerating plastic flow. The increasing FCC volume fraction directly correlates with the stress-strain profile (Figure 6), confirming stress-induced phase transformation, not traditional dislocation or grain-boundary sliding. The initiation, propagation, and growth of the FCC phase govern macroscopic plastic flow, producing the characteristic stress plateau and ductile-like behavior observed.
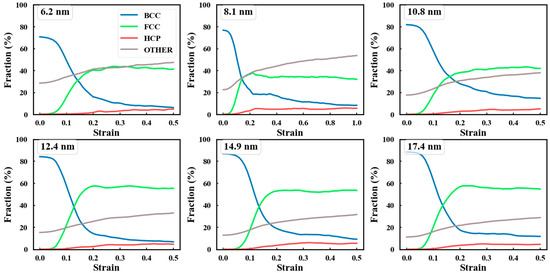
Figure 6.
Evolution of atomic structure with varying grain sizes.
This phase transformation-dominated deformation mechanism fundamentally arises from the combined effects of the inherently extreme strain rates and nanoscale dimensions characteristic of MD simulations [29,30]. These extreme conditions compel the material to adopt the fastest deformation pathway, which is stress-induced shear-driven martensitic transformation. This transformation occurs instantaneously, on picosecond-to-nanosecond timescales without requiring atomic diffusion, precisely aligning with MD time scales. It thus becomes the core mechanism efficiently coordinating macroscopic plastic strain, explaining the synchronized progression of FCC phase fraction growth with the stress-strain curve. Simultaneously, the ultra-high strain rate effectively suppresses the key slow processes responsible for FeAl’s room-temperature brittleness and thermally activated dislocation slip and subcritical crack growth. The material lacks the time needed for dislocations to overcome the inherently high slip resistance of the B2 structure or for microcracks to propagate to critical size slowly. Furthermore, the nanoscale dimension eliminates the critical-sized defects that inevitably occur in macroscopic materials and trigger catastrophic brittle fracture. The high surface-to-volume ratio enables free surfaces to act as soft regions, alleviating stress concentrations, nucleating dislocations, or accommodating local plasticity. Additionally, the relatively homogeneous stress states at small scales and the ease of coordinating transformation across multiple grains effectively suppress deformation localization. Therefore, the synergy of high strain rate and nanoscale dimensions masks the physical origins of FeAl’s brittleness under realistic conditions, while forcibly activating and significantly amplifying a rapid deformation mechanism that is difficult to dominate or may even be suppressed, during a slow, practical loading process. The influence of grain size must also be understood within this framework. The mismatch between MD simulation and the FeAl’s actual brittleness reflects a competition between grain boundary softening effects in small grains and increased resistance to transformation initiation in larger grains. Meanwhile, it does not alter the fundamental role of phase transformation as the dominant plasticity mechanism.
4. Conclusions
This work employs molecular dynamics simulations to systematically investigate the deformation mechanisms and grain size effects in nanocrystalline FeAl under ultra-high strain rates (109 s−1). The study provides the first direct evidence that the dual role of grain boundaries in dislocation evolution is the core factor constructing the inverse Hall-Petch relationship. At the nanoscale, high-density grain boundaries transition from dislocation barriers into dislocation annihilation sinks. By accelerating dislocation absorption, they drive the flow stress to exhibit inverse Hall-Petch behavior, resulting in a significant weakening of conventional dislocation strengthening with grain refinement.
More critically, the synergistic interplay between strain rate and scale dictates the selection of plastic deformation pathways. The extreme strain rate suppresses room-temperature brittle mechanisms inherent to B2-FeAl, while simultaneously forcing the activation of stress-induced BCC to FCC phase transformation. Concurrently, the nanoscale dimensions promote this transformation as the dominant mechanism for accommodating macroscopic plasticity by inhibiting defect propagation and enhancing stress homogeneity.
These findings offer a novel theoretical foundation for understanding the complex interplay between grain size, strain rate, and deformation mechanisms in nanostructured intermetallic compounds. This is particularly relevant for demanding applications such as advanced protective coatings in extreme environments, including high-voltage transmission lines under violent wind-induced galloping, ice shedding impacts, and foreign object collisions. Following the mechanisms, the newly designed coatings would combine high impact resistance with superior overall mechanical performance, demonstrating substantial innovative value for practical application.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/pr13082462/s1, Figure S1: Stress-strain curves of samples with different temperatures with a grain size of 17.4 nm; Figure S2: a. maximum stress; b. Young's modulus corresponding to different temperatures with grain size of 17.4 nm; Figure S3: Atomic structure snapshots of the model with a grain size of 17.4 nm at different temperatures before deforming; Figure S4: Comparison of the grain boundary (GB) network in the strained states, illustrating GB movement.
Author Contributions
Conceptualization, X.L.; methodology, X.L.; formal analysis, P.C. and L.H.; investigation, L.H.; writing-original draft preparation, K.G.; writing-review and editing, K.G. and J.Y.; supervision, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a self-funded project of the Inner Mongolia Power (Group) Co., Ltd., Inner Mongolia Power Research Institute (Inner Mongolia Power Research Institute [2023] Issue 81, Project No. 2023-ZC-1-02).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed at the corresponding authors.
Conflicts of Interest
Authors Xiaoming Liu and Peng Chen were employed by the company Inner Mongolia Power (Group) Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Sharun, V.; Rajasekaran, M.; Shanmugam, S.K.; Tripathi, V.; Rajneesh Sharma, G.; Puthilibai, G.; Sudhakar, M.; Negash, K. Study on Developments in Protection Coating Techniques for Steel. Adv. Mater. Sci. Eng. 2022, 2022, 1–10. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, Q.; Cui, B.; Wu, K. Study on Reliability and Selection of Silicone Grease Used for Coating at the Interface Between Cable and Accessory. IEEE Trans. Dielectr. Electr. Insul. 2022, 29, 2354–2362. [Google Scholar] [CrossRef]
- Aljibori, H.; Al-Amiery, A.; Kadhum, A. Advances in corrosion protection coatings: A comprehensive review. Int. J. Corros. Scale Inhib. 2023, 12, 1476–1520. [Google Scholar] [CrossRef]
- Liu, H.; Yan, L.; Wang, F. Synthesis of antioxidant functionalized nano-TiO2 for improving fire resistance and UV-shielding behavior of intumescent fire-retardant coatings for cable. Prog. Org. Coat. 2024, 194, 108622. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, W.; Chen, J.; Skrzypkowski, K.; Zagórski, K.; Zagórska, A. Investigation into Effects of Coating on Stress Corrosion of Cable Bolts in Deep Underground Environments. Materials 2024, 17, 3563. [Google Scholar] [CrossRef]
- Huang, J.; Xie, H.; Luo, L.M.; Zan, X.; Liu, D.G.; Wu, Y.C. Preparation and properties of FeAl/Al2O3 composite tritium permeation barrier coating on surface of 316L stainless steel. Surf. Coat. Technol. 2020, 383, 125282. [Google Scholar] [CrossRef]
- Yin, B.; Liu, G.; Zhou, H.; Chen, J.; Yan, F. Microstructures and properties of plasma sprayed FeAl/CeO2/ZrO2 nano-composite coating. Appl. Surf. Sci. 2010, 256, 4176–4184. [Google Scholar] [CrossRef]
- Rajath Hegde, M.M.; Surendranathan, A.O. Phase transformation, structural evolution, and mechanical property of nanostructured feal as a result of mechanical alloying. Powder Metall. Met. Ceram. 2009, 48, 641–651. [Google Scholar] [CrossRef]
- Morris-Muñoz, M.A.; Dodge, A.; Morris, D.G. Structure, strength and toughness of nanocrystalline FeAl. Nanostructured Mater. 1999, 11, 873–885. [Google Scholar] [CrossRef]
- Petch, N.J. The Cleavage Strength of Polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Hall, E.O. The Deformation and Ageing of Mild Steel: III Discussion of Results. Proc. Phys. Society Sect. B 1951, 64, 747. [Google Scholar] [CrossRef]
- Niu, Y.; Jia, Y.; Lv, X.; Zhu, Y.; Wang, Y. Molecular dynamics simulations of polycrystalline titanium mechanical properties: Grain size effect. Mater. Today Commun. 2024, 40, 109558. [Google Scholar] [CrossRef]
- Song, H.; Gao, T.; Gao, Y.; Liu, Y.; Xie, Q.; Chen, Q.; Xiao, Q.; Liang, Y.; Wang, B. Hall–Petch relationship in Ti3Al nano-polycrystalline alloys by molecular dynamics simulation. J. Mater. Sci. 2022, 57, 20589–20600. [Google Scholar] [CrossRef]
- Chen, J.; Li, R.; Wang, B.; Liu, G. Effect of grain size on tensile deformation behavior of nano-polycrystalline Al and Al–Mg alloys with grain boundary segregation of Mg. J. Mater. Res. Technol. 2024, 33, 6328–6339. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Baskes, M.I. Modified embedded-atom potentials for cubic materials and impurities. Phys. Rev. B 1992, 46, 2727–2742. [Google Scholar] [CrossRef]
- Lee, B.-J.; Baskes, M.I. Second nearest-neighbor modified embedded-atom-method potential. Phys. Rev. B 2000, 62, 8564–8567. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Larsen, P.M.; Schmidt, S.; Schiøtz, J. Robust structural identification via polyhedral template matching. Model. Simul. Mater. Sci. Eng. 2016, 24, 055007. [Google Scholar] [CrossRef]
- Stukowski, A.; Bulatov, V.V.; Arsenlis, A. Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sci. Eng. 2012, 20, 085007. [Google Scholar] [CrossRef]
- Lu, X.; Dong, C.; Guo, X.; Ren, J.; Xue, H.; Tang, F.; Ding, Y. Effects of grain size and temperature on mechanical properties of nano-polycrystalline Nickel-cobalt alloy. J. Mater. Res. Technol. 2020, 9, 13161–13173. [Google Scholar] [CrossRef]
- Naik, S.N.; Walley, S.M. The Hall–Petch and inverse Hall–Petch relations and the hardness of nanocrystalline metals. J. Mater. Sci. 2020, 55, 2661–2681. [Google Scholar] [CrossRef]
- Li, L.-L.; Su, Y.; Beyerlein, I.J.; Han, W.-Z. Achieving room-temperature brittle-to-ductile transition in ultrafine layered Fe-Al alloys. Sci. Adv. 2020, 6, eabb6658. [Google Scholar] [CrossRef]
- Su, R.; Neffati, D.; Cho, J.; Shang, Z.; Zhang, Y.; Ding, J.; Li, Q.; Xue, S.; Wang, H.; Kulkarni, Y.; et al. High-strength nanocrystalline intermetallics with room temperature deformability enabled by nanometer thick grain boundaries. Sci. Adv. 2021, 7, eabc8288. [Google Scholar] [CrossRef]
- Wang, H.; Kou, R.; Yi, H.; Figueroa, S.; Vecchio, K.S. Mesoscale hetero-deformation induced (HDI) stress in FeAl-based metallic-intermetallic laminate (MIL) composites. Acta Mater. 2021, 213, 116949. [Google Scholar] [CrossRef]
- Zamanzade, M.; Barnoush, A.; Motz, C. A Review on the Properties of Iron Aluminide Intermetallics. Crystals 2016, 6, 10. [Google Scholar] [CrossRef]
- Meyers, M.A.; Mishra, A.; Benson, D.J. Mechanical properties of nanocrystalline materials. Prog. Mater. Sci. 2006, 51, 427–556. [Google Scholar] [CrossRef]
- Dong, S.; Liu, X.-Y.; Zhou, C. Atomistic modeling of plastic deformation in B2-FeAl/Al nanolayered composites. J. Mater. Sci. 2021, 56, 17080–17095. [Google Scholar] [CrossRef]
- Guo, Y.-F.; Wang, Y.-S.; Zhao, D.-L. Atomistic simulation of stress-induced phase transformation and recrystallization at the crack tip in bcc iron. Acta Mater. 2007, 55, 401–407. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).