Abstract
Coarse-grained soils serve as essential fill materials in earth–rock dam engineering, where their mechanical properties critically influence dam deformation and stability, directly impacting project safety. Artificial intelligence (AI) techniques are emerging as powerful tools for predicting the mechanical properties of coarse-grained soils. However, AI-based prediction models for these properties face persistent challenges, particularly in parameter tuning—a process requiring substantial computational resources, extensive time, and specialized expertise. To address these limitations, this study proposes a novel prediction model that integrates Adaptive Simulated Annealing (ASA) with an improved Particle Swarm Optimization (PSO) algorithm to optimize the Elman Neural Network (ENN). The methodology encompasses three key aspects: First, the standard PSO algorithm is enhanced by dynamically adjusting its inertial weight and learning factors. The ASA algorithm is then employed to optimize the Adaptive PSO (APSO), effectively mitigating premature convergence and local optima entrapment during training, thereby ensuring convergence to the global optimum. Second, the refined PSO algorithm optimizes the ENN, overcoming its inherent limitations of slow convergence and susceptibility to local minima. Finally, validation through real-world engineering case studies demonstrates that the ASA-PSO-optimized ENN model achieves high accuracy in predicting the mechanical properties of coarse-grained soils. This model provides reliable constitutive parameters for stress–strain analysis in earth–rock dam engineering applications.
1. Introduction
Coarse-grained soils are widely distributed, abundantly available, and easily quarried. Recognized for their high bearing capacity, excellent compactability, superior permeability, high compressive strength, and low deformability, they are extensively utilized in critical infrastructure projects including earth–rock dams, deep excavations, and railway subgrades. Notably, they constitute over 90% of fill materials in earth–rock dam construction [1]. Consequently, the mechanical properties of coarse-grained soils directly govern dam deformation and stability [2,3] thereby influencing the design, construction, lifelong safety, and reliability of such projects. Accurate prediction of their mechanical parameters is therefore essential.
The strength and deformation characteristics of coarse-grained soils are of paramount importance. Conventional triaxial testing serves as a primary and reliable method for analyzing their stress–strain relationship curves. According to testing standards, the ratio of the specimen diameter to the maximum particle size (D/dmax) must exceed 5. However, with technological advances in dam construction and increasing dam heights, fill materials now reach maximum particle sizes of 800–1200 mm. Developing testing equipment capable of accommodating such large-scale specimens is prohibitively expensive and technically challenging [4].
1.1. Literature Review
With the rapid advancement of computer technology and artificial intelligence, computer-simulated triaxial compression tests have become widely used in geotechnical engineering. Additionally, machine learning-based prediction models for the mechanical properties of coarse-grained soils are gaining significant traction in civil and hydraulic engineering.
In computational simulations of triaxial tests, the dominant approaches are the Discrete Element Method (DEM) for analyzing large-scale discrete particle movements and Particle Flow Code (PFC) technology, which is grounded in DEM principles for granular material behavior [5,6]. PFC-based simulations of triaxial compression tests on coarse-grained soils—used to derive stress–strain relationships—have achieved considerable maturity with extensive research outcomes. For instance, T. G. Sitharam [7] employed DEM to investigate the influence of maximum particle size, fabric, and gradation on mechanical properties from a microscopic perspective. Zhou et al. [8] developed a Stochastic Granular Discontinuous Deformation (SGDD) model to simulate rockfill triaxial specimens at the mesoscale, successfully reproducing internal particle movement patterns through numerical simulations and experimental validation. Alaei E. et al. [9] established a rockfill material model using PFC2D based on DEM fundamentals. Their particle breakage and triaxial tests on a rockfill dam demonstrated the model’s capability to capture strength, deformation, and fragmentation behaviors, confirming its accuracy. Cheng et al. [10] utilized 3D particle flow software (PFC3D) to simulate gradation characteristics, constructing a particle flow model for deformation behavior of coarse-grained soils. Model parameters representing mesoscopic mechanical properties were calibrated via triaxial tests, validating the model’s efficacy. A particle gradation generation method was employed to piecewise reconstruct gradation curves, closely approximating realistic particle size distributions.
Concurrently, machine learning techniques have been employed for mechanical property prediction due to their powerful nonlinear fitting capabilities: Early work by Ellis et al. [11] compiled datasets from triaxial tests on eight sand types to train artificial neural networks for stress–strain relationship prediction. Zhu et al. [12] investigated correlations between soil gradation and compaction characteristics using neural networks, revealing strong relationships between Weibull distribution parameters and porosity. Zhou, Li et al. [13,14] employed six supervised machine learning models (including random forest, regression, and Artificial Neural Network) to predict rockfill shear strength, demonstrating high consistency between predicted and experimental results.
Despite extensive research by numerous scholars on prediction methods for the mechanical properties of coarse-grained soils, these methods still face several significant challenges.
First, regarding conventional triaxial testing: Current engineering practice commonly involves scaling down in situ coarse-grained soils to fit laboratory apparatus sizes. Mathematical constitutive models are then constructed to characterize the mechanical behavior of the prototype soil. However, regardless of the scaling technique employed, the scaled soil samples inevitably exhibit altered particle size distributions (gradations) and mechanical properties. Consequently, these models fail to accurately capture the engineering characteristics of the prototype soil, potentially compromising design reliability and the safe, stable operation of engineered structures.
Second, concerning numerical simulation: The lack of systematic and comprehensive theories governing particle motion and contact behavior hinders the development of particle contact models. Existing models are inadequate for the quantitative analysis and prediction of coarse-grained soil mechanics. Consequently, substantial discrepancies persist between numerical simulations of soil mechanical behavior and experimental observations. Furthermore, the Discrete Element Method (DEM) struggles to accurately simulate the mechanical properties of the fraction of coarse-grained soil with particles smaller than 5 mm.
Third, for machine learning approaches: Predicting the mechanical characteristics of coarse-grained materials using machine learning necessitates a foundation of authentic triaxial test data. The predictive performance of these models is critically dependent on both the quantity and quality of this data. In practical engineering applications, the impracticality of performing direct laboratory tests on large-sized coarse-grained soils leads to severely constrained datasets. This scarcity severely constrains the construction of robust machine learning models, further undermining their generalizability and interpretability [15].
1.2. Contribution
To address the aforementioned challenges, this paper proposes a novel prediction model for the mechanical parameters of dam materials, termed the ASA-PSO-ENN model. This model combines a Simulated Annealing (SA) algorithm with an Adaptive Particle Swarm Optimization (APSO) algorithm to optimize an Elman Neural Network (ENN) architecture.
Firstly, improvements were made to the standard Particle Swarm Optimization (PSO) algorithm concerning both the inertia weight and learning factors. The SA algorithm was then employed to optimize the APSO algorithm, effectively mitigating its tendency to converge prematurely towards local optima during training [16,17]. This combined approach ensures convergence towards the global optimal solution.
Secondly, the enhanced PSO algorithm (APSO optimized by SA) was employed to optimize the Elman Neural Network architecture. This addresses inherent limitations of the ENN, such as slow convergence speed and susceptibility to local minima [18,19].
Finally, the ASA-PSO-ENN model was trained using input parameters derived from laboratory triaxial tests, specifically, the gradation of the dam material, confining pressure, axial strain, and dry density. The model’s output variable is the deviatoric stress. The trained model was subsequently applied to predict the mechanical parameters of dam materials in actual engineering projects. These predictions were rigorously validated against measured values to validate the model’s rationality and applicability.
The primary objective of this research is to introduce a novel method for predicting the mechanical parameters of coarse-grained materials. This methodology is designed to generate more physically realistic input parameters for numerical simulations of earth–rockfill dam deformation. Furthermore, it offers valuable reference and technical support for optimizing dam zoning design and effectively controlling dam deformation and stability.
1.3. Organization
The organization of this paper is as follows: Section 2 introduces the fundamental principles and framework of the proposed ASA-PSO-ENN model. Section 3 details the establishment and training process of the coarse-grained soil mechanical property prediction model. Section 4 discusses the experimental results from applying this model to predict the stress–strain relationship of sand–gravel dam materials in a practical engineering case, including a comparative assessment between the predicted and experimentally measured values of deviatoric stress vs. axial strain vs. volumetric strain relationships. Section 5 summarizes the main findings and provides discussion, while Section 6 analyzes the study’s limitations and future research directions.
2. Materials and Methods
2.1. Fundamental Principles of the ASA-PSO-ENN Model
This study employs an Elman Neural Network (ENN) to construct a prediction model for the mechanical parameters of coarse-grained materials. To overcome inherent limitations of neural networks, including a slow convergence rate and the tendency to converge to local optima, we propose an adaptive Simulated Annealing–Particle Swarm Optimization (SA-PSO) algorithm for ENN optimization. The resulting ASA-PSO-ENN model’s computational architecture is shown in Figure 1, with its implementation algorithm executing the following sequence:.
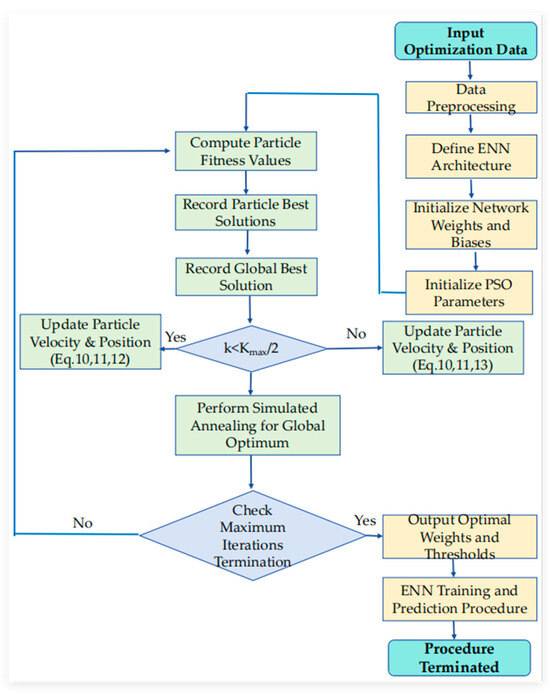
Figure 1.
Flowchart of the coarse-grained soil mechanical parameter prediction model based on SA-PSO-optimized ENN.
Step 1: Data Preprocessing. Discretize the stress–strain relationship curve data. Normalize the data using Equation (16). Partition the dataset into training and testing sets.
Step 2: Construct the ENN Model. Initialize the structure of the Elman Neural Network.
Step 3: Initialize PSO Parameters. Set the PSO algorithm parameters, including the maximum iteration count (Kmax), population size (N), inertia weight (ω), and learning factors (c1, c2).
Step 4: Initialize PSO Population. Initialize the positions of the PSO population particles. Define the mean squared error (MSE) of the ENN predictions as the fitness function for the PSO algorithm. Record the personal best (Pbest) and global best (Gbest) values.
Step 5: Iterative Optimization. Perform iterative optimization until the maximum iteration count (Kmax) is reached, terminating the PSO loop. During each iteration:
(a) Update the particle velocities and positions using adaptively adjusted inertia weights and learning factors.
(b) Update the recorded Pbest and Gbest values.
(c) Monitor for Premature Convergence. If premature convergence is detected, invoke the Simulated Annealing (SA) operation to enable the algorithm to escape local optima. The process aims to ultimately locate the global optimal solution.
Step 6: Assign Optimized Parameters to ENN. Assign the optimized weights and threshold parameters obtained from the PSO to the Elman Neural Network.
Step 7: Train and Predict. Train the Elman Neural Network optimized by the adaptive SA-PSO algorithm and perform predictions.
2.2. Multilayer Dynamic Recurrent Neural Network (Elman Neural Network, ENN)
The Elman Neural Network (ENN), proposed by Elman [20] in 1990, is a classic multilayer dynamic recurrent neural network. As illustrated in Figure 2, its network topology consists of an input layer, a hidden layer, and an output layer, where the contexts and functions of these layers are similar to those of feedforward neural networks.
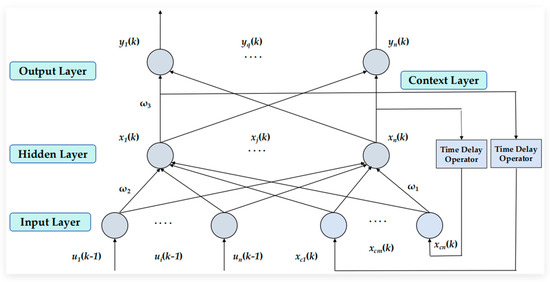
Figure 2.
Topological structure of the Elman Neural Network (ENN).
A key feature of the ENN is the incorporation of a delay operator (also called a context layer) within the hidden layer, which stores and memorizes the output of the hidden layer from the previous time step. This stored information is then fed back as an additional input to the hidden layer at the next time step, forming a recurrent feedback loop. This mechanism enhances the network’s ability to process dynamic and time-dependent information, providing the ENN strong temporal adaptability. As a result, the network’s output more closely matches the temporal dynamics of the data, enhancing prediction accuracy for sequential or time-evolving patterns.
The mathematical formulation of the Elman Neural Network (ENN) structural model is expressed as follows:
where
- x(k), xc(k), and y(k) are the output vectors of the hidden layer, context layer, and output layer at time step k;
- u(k − 1) is the input layer vector at time step k − 1;
- g(·) is the transfer function of the output layer, defined as a linear combination of hidden layer outputs;
- f(·) is the transfer function of the hidden layer, typically implemented as a Sigmoid function;
- ω1, ω2, and ω3 are the synaptic weight matrices for the context-to-hidden layer, input-to-hidden layer, and hidden-to-output layer connections, respectively;
- MSE is the objective function for neural network weight adjustment;
- y(k) is the actual value at time step k;
- yt(k) is the predicted value at time step k.
2.3. Particle Swarm Optimization (PSO)
Particle Swarm Optimization (PSO), a swarm intelligence optimization algorithm proposed by Kennedy and Eberhart in 1995 [21], simulates collective foraging behaviors observed in bird flocks; the fundamental computational principle is illustrated in Figure 3. This population-based stochastic optimization algorithm works by facilitating information exchange among candidate solutions within the search space. During initialization, N particles are deployed, where each particle represents a candidate solution characterized by three state parameters: position, velocity, and fitness value. Through iterative updates, particles dynamically adjust their trajectories by synthesizing individual historical best positions (Pbest) and the swarm’s global best position (Gbest) [22]. For a D-dimensional search space, the velocity and position of particle i at iteration k + 1 evolve according to:
where
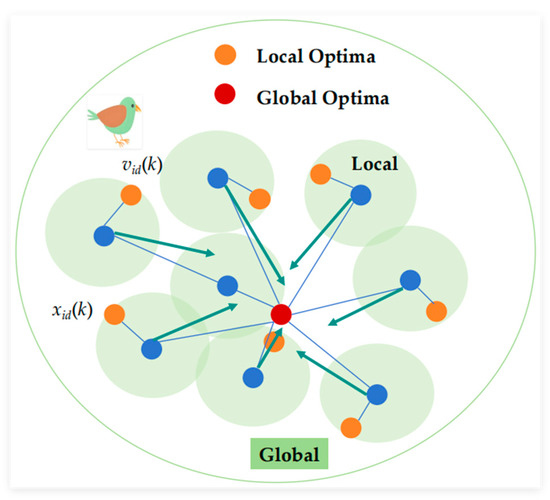
Figure 3.
Schematic diagram of Particle Swarm Optimization operational principle.
- i = 1, 2, …, N;
- d = 1, 2, …, D;
- k is the iteration count;
- ω is the inertia weight governing particle momentum;
- c1 and c2 are the acceleration coefficients: c1 = self–cognitive factor directing particles toward individual historical best positions (Pbest); c2 = social–cognitive factor facilitating information exchange within the swarm, guiding particles toward the global best position (Gbest);
- r1 and r2 are uniformly distributed random variables in [0, 1] enhancing population diversity;
- vid(k) and xid(k) are the velocity of particle i along dimension D at iteration k;
- Pbest,id(k) is the historical optimal position of particle i along dimension D through iteration k;
- Gbest,id(k) is the historical optimal position of the entire swarm along dimension D through iteration k.
In Particle Swarm Optimization (PSO), the optimization process occurs through particles exploring the search space, with each velocity update iteration comprising three fundamental components. First, the momentum retention term perpetuates a fraction of the particle’s prior velocity, governed by the inertia weight ω [23]. This component reflects the influence of historical motion states and critically balances global exploration versus local exploitation capabilities. Second, the cognitive acceleration component, regulated by coefficient c1, quantifies individual reliance on personal historical experience through self–cognitive behavior [24]. Third, the social acceleration component under coefficient c2 facilitates collective intelligence by enabling information exchange among swarm particles. This tripartite mechanism collectively enables particles to dynamically adjust their positions and velocities by balancing individual experience with swarm intelligence, driving convergence toward optimal solutions. Consequently, the inertia weight (ω) and acceleration coefficients (c1, c2) constitute pivotal parameters determining algorithmic performance [25,26].
Particle Swarm Optimization (PSO) has gained widespread adoption across diverse optimization domains owing to its operational advantages, including minimal parameter tuning requirements, rapid convergence characteristics, and straightforward implementation. However the algorithm demonstrates inherent limitations, including susceptibility to local optima entrapment, premature convergence phenomena, and oscillatory behavior during late-stage optimization. To mitigate these deficiencies, this work implements a dual modification strategy: (1) adaptive refinement of the inertia weight (ω) and acceleration coefficients (c1, c2) and (2) integration of a simulated annealing approach. This hybrid architecture effectively prevents local optima entrapment while preserving robust global exploration throughout the optimization process.
2.4. Adaptive Particle Swarm Optimization (APSO)
2.4.1. Adaptive Inertia Weight Adjustment
The inertia weight (ω) is a critical parameter in Particle Swarm Optimization (PSO) that fundamentally regulates the algorithm’s search behavior by controlling particles’ momentum preservation from previous velocity states. An optimal ω value fundamentally balances local exploitation and global exploration capabilities: empirical evidence confirms that elevated ω values enhance the global search scope at the expense of excessive particle velocities that may overshoot optimal regions, whereas diminished ω values intensify local search precision while heightening susceptibility to local optima entrapment and premature convergence [27,28]. Mathematically, ω exhibits a positive correlation with the convergence rate and global search capability and a negative correlation with local search precision.
To enhance the optimization performance of the Particle Swarm Optimization algorithm and prevent convergence to local optima, this study employs a hyperbolic tangent function with domain-constrained inputs x ∈ [−5, 5] to achieve nonlinear adaptive adjustment of the inertia weight [29]. The adaptive inertia weight formulation is defined as follows:
where
- k is the Current iteration index;
- Kmax is the Maximum iteration count;
- ωmax and ωmin are the Initial exploration intensity and Final exploitation intensity. Empirical studies [30,31] confirm that configuring ωmax = 0.95 and ωmin = 0.40 yields significant performance enhancements in convergence efficiency and solution precision.
The adaptive inertia weight function in this study employs a phase-dependent nonlinear decay strategy, as illustrated in Figure 4. During the initial exploration phase, the inertia weight undergoes systematic annealing, maintaining sufficient momentum to enable wide-ranging global search. This deliberate preservation effectively mitigates premature convergence risks by allowing comprehensive solution space exploration. During intermediate iterations, the inertia weight transitions to a quasi-linear decay regime, establishing an optimal balance where global exploration gradually yields to intensified local exploitation. In the terminal optimization phase, the decay rate decelerates significantly, focusing computational resources on meticulous local refinement to pinpoint the global optimum with enhanced precision.
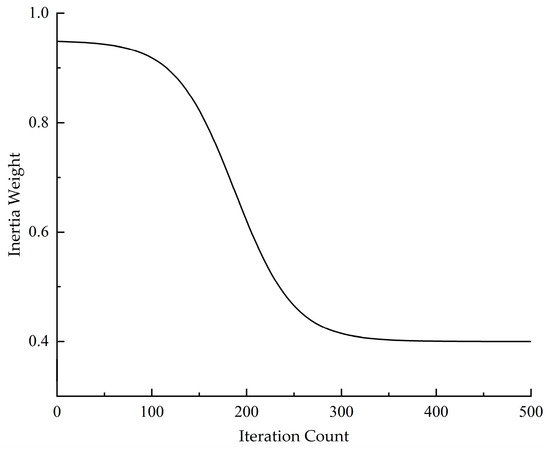
Figure 4.
Variation profile of adaptive inertia weight adjustment.
2.4.2. Adaptive Acceleration Coefficients
Particle Swarm Optimization exhibits progressive convergence during iterations, where diminishing swarm diversity impedes optimization efficacy. To augment swarm diversity, this work implements second-order oscillatory processing on particle velocity updates, improving the global–local convergence balance. The improved optimization algorithm prioritizes global exploration by emphasizing particle self–cognitive capabilities and enhancing traversal, thereby reducing the probability of becoming trapped in local optima.
As iterations progress, the algorithm enhances inter-particle communication, allowing the globally best solution (Gbest) to exert a more substantial influence on each particle’s search behavior. This drives intensified local exploitation around the vicinity of Gbest. Concurrently, the inertia weight (ω) decreases progressively, while the cognitive learning factor (c1) diminishes, and the social learning factor (c2) increases, further refining the search focus toward promising regions. The learning factors adopt the following adaptive strategy:
where c1max and c1min represent the maximum and minimum values of the cognitive learning factor, while c2max and c2min denote the corresponding bounds for the social learning factor. As demonstrated in Reference [32] and validated through extensive experimental results, the cognitive learning factor c1 decreases linearly from 2.50 to 1.25, whereas the social learning factor c2 increases linearly from 1.25 to 2.50 throughout the iterations (i.e., c1max = 2.50, c1min = 1.25; c2max = 2.50, c2min = 1.25). This adaptive strategy effectively balances global exploration and local exploitation capabilities.
The corresponding modified particle swarm optimization algorithm can be mathematically formulated as follows:
The values of the second-order oscillation factors ξ1 and ξ2 are set as follows [33,34]:
In the second-order oscillatory particle swarm optimization algorithm, Equation (12) is employed in the initial phase to achieve oscillatory convergence and enhance global exploration capability, while Equation (13) is adopted in the later phase to accomplish asymptotic convergence and improve the local refinement capability.
2.4.3. Simulated Annealing (SA)
The Simulated Annealing (SA) algorithm, proposed by Metropolis in the 1950s through studies of solid-state annealing processes, employs the Metropolis criterion [35] as its core mechanism. This criterion uniquely permits acceptance of both superior solutions and—with probability determined by the temperature parameter—inferior solutions during the cooling process. This property enhances the algorithm’s ability to escape local optima. In this study, we integrate adaptive particle swarm optimization with simulated annealing to effectively reduce the probability of premature convergence to local optima. The Metropolis criterion defines the probability of accepting a new solution for a system transitioning from state i to state j at temperature T based on their internal energy difference as:
In this formulation, Ei(k) and Ej(k) represent the internal energies (i.e., the fitness values of the current particle) in states i and j, respectively; Ti denotes the annealing temperature at the current state; and ΔE = Ej(k) − Ei(k) corresponds to the internal energy increment. When Ej(k) < Ei(k), the system unconditionally accepts the new state (probability = 1). Conversely, when Ej(k) ≥ Ei(k), the inferior solution (worse state) is accepted with a probability p = exp(−ΔE/Ti) [36,37,38]. This annealing process executes multiple iterative cycles to progressively identify optimal solutions. To maintain solution accuracy, the temperature parameter follows a carefully controlled gradual decay schedule. The annealing operation is systematically applied after each complete iteration cycle.
The simulated annealing (SA) algorithm is a global optimization method inspired by the metallurgical annealing process, which probabilistically converges to the globally optimal solution of the objective function (see Algorithm Principle in Figure 5). In optimization problems, the internal energy can be abstracted as a fitness function. At higher temperatures, the algorithm exhibits a greater probability of accepting inferior solutions. As the temperature gradually decreases, this acceptance probability correspondingly reduces, enabling the algorithm to escape local optima and ultimately converge to the global optimum. In this study, we incorporate the SA mechanism into the adaptive particle swarm optimization algorithm. During the optimization process, this hybrid approach intentionally accepts temporally degraded solutions within a controlled range with a specified probability, thereby facilitating escape from local optima and ensuring convergence to the global optimal solution.
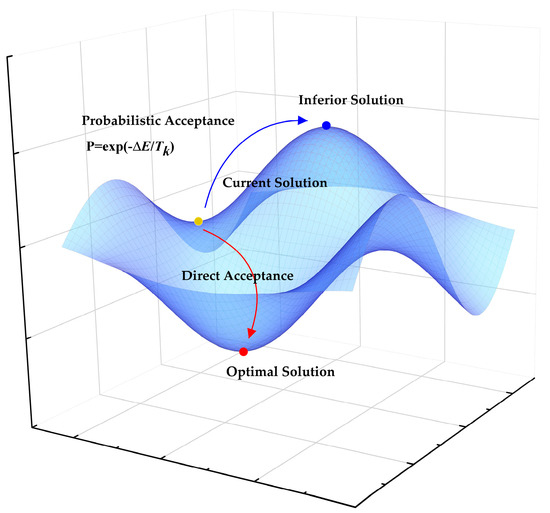
Figure 5.
Schematic diagram of the simulated annealing algorithm principle.
Implementation Procedure of SA Algorithm:
Step 1: Initialize annealing temperature T0, generate a random initial solution A0, and compute its fitness value f(A0).
Step 2: Perturb the current solution A0 to generate a new feasible solution A1. Calculate fitness value f(A1) and compute the fitness difference:
Δf = f(A1) − f(A0)
Step 3: Evaluate Metropolis criterion: If min{1, exp(−Δf/Ti)}) >random [0, 1], accept solution A1. Here, random [0, 1] denotes a uniformly distributed random number in [0, 1].
Step 4: Annealing operation: Update temperature via Ti+1 = βTi (where β is the cooling coefficient, 0 < β < 1). Terminate if convergence criteria are satisfied; otherwise, repeat Steps 2–3 until convergence.
2.5. Adaptive Simulated Annealing—Particle Swarm Optimization (ASA-PSO)
The standard PSO algorithm is prone to local optima and premature convergence during optimization. In contrast, the mutation characteristics of SA enable effective escape from local optima to achieve global optimality. Motivated by this, we propose the ASA-PSO algorithm (see flowchart in Figure 6). This enhanced algorithm builds upon particle swarm optimization while integrating simulated annealing mechanisms, collectively improving solution accuracy through three key innovations:
Figure 6.
Flowchart of the adaptive ASA-PSO algorithm.
First, to balance global and local optimization capabilities in PSO, we introduce a nonlinear inertia weight adjustment strategy based on the hyperbolic tangent function. By linking the inertia weight to the tanh function within the domain [−5, 5], it adapts dynamically during iterations:
- During initial stages, weights decrease gradually to enhance global exploration and mitigate premature convergence;
- Mid-optimization exhibits near-linear weight reduction, transitioning focus toward local exploitation;
- Final stages feature diminished weight decay rates to intensify local search precision.
Second, addressing population diversity degradation in PSO, we develop a second-order oscillatory velocity update strategy. This mechanism enhances particle trajectory ergodicity and strengthens cognitive capabilities, thereby maintaining swarm diversity. The proposed methodology significantly mitigates premature convergence phenomena, substantially reduces susceptibility to local optima entrapment, and enhances global search capability.
Finally, we integrate SA’s perturbation mechanism and search strategy into adaptive PSO (APSO), forming the novel hybrid ASA-PSO algorithm. This fusion combines SA’s global exploration strengths with APSO’s computational efficiency, enabling rapid convergence while enhancing global search capabilities. As a result, the proposed algorithm attains enhanced solution precision while reliably preventing premature convergence phenomena.
Based on the aforementioned framework, the procedural steps of the proposed ASA-PSO algorithm are formally delineated in Table 1.

Table 1.
Procedural steps of the ASA-PSO algorithm.
The complete algorithmic workflow of the adaptive ASA-PSO method is illustrated in Figure 6.
3. ASA-PSO-ENN Prediction Model for Mechanical Properties of Coarse-Grained Soils
3.1. Dataset Construction
Considering the credibility of real-world data significantly enhances model prediction accuracy, all training and testing datasets for this study originate from triaxial compression test results rather than simulated data. Data primarily derive from triaxial tests on gravel materials in typical concrete-faced rockfill dams in China. The dataset incorporates the following characteristics: specimen gradation (maximum particle size: 60 mm), confining pressure, and dry density.
These parameters were collected to investigate the stress–strain relationships of coarse-grained soils, with corresponding stress–strain curves serving as data labels. Given the bijective functional relationship between stress and strain, axial strain is designated as the independent variable and deviatoric stress as the dependent variable, where axial strain undergoes feature transformation for analysis.
For stress–strain curve data collection, we extracted coordinate points from graphical plots using GetData Graph Digitizer (v2.26.0.20). Given the continuous nature of stress–strain relationships, discrete sampling was performed to facilitate model input processing. The abscissa (axial strain) was sampled at 0.3% intervals, with the maximum strain threshold set at 15% based on experimental determination of specimen failure at this deformation level [39,40]. Figure 7 illustrates the discretized stress–strain curves. Since some specimens failed before reaching 15% axial strain, each experimental curve yielded a maximum of 50 data points. The discretized dataset ultimately comprised 875 data points from all triaxial tests.
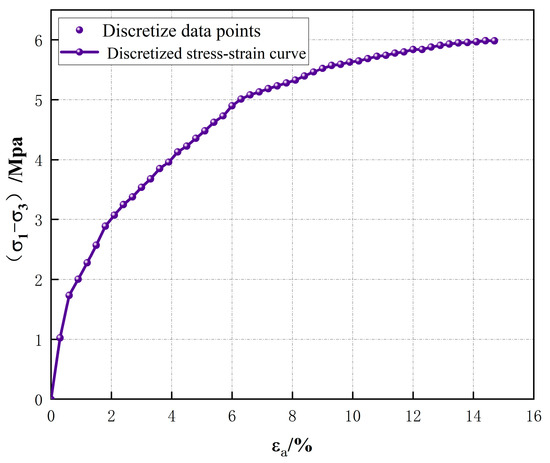
Figure 7.
Discretization of stress–strain curves.
3.2. Data Preprocessing
The parameters in the constructed coarse-grained soil mechanical properties dataset (e.g., gradation, dry density, confining pressure) serve as dominant controlling factors influencing mechanical behavior. These parameters exhibit varying dimensions and units, resulting in significant numerical disparities among features. Directly using raw data as model inputs would severely compromise prediction accuracy. To eliminate dimensional influences, we implement z-score standardization for data normalization, transforming values into mapped results z. Post-normalization data conform to a standard normal distribution. The normalization function is expressed as:
where
- x is the sample data;
- μ is the sample mean;
- σ is the standard deviation of the sample data.
3.3. Model Establishment
3.3.1. Parameter Configuration
From the preprocessed valid dataset, we randomly partitioned 426 samples for training and reserved 106 samples as the testing set, maintaining an 80:20 split ratio. To validate the prediction accuracy improvement of the proposed model, the ASA-PSO-ENN model was compared against ENN, PSO-ENN, and APSO-ENN models using the testing dataset. The parameters in Table 2 were used to establish the base ENN model. Subsequently, PSO, APSO, and ASA-PSO algorithms were respectively employed to optimize the initial weights and thresholds of the neural network. In this study, PSO, APSO, and ASA-PSO implement distinct adjustment strategies for particle motion, with their parameter configurations summarized in Table 3.

Table 2.
Parameter configuration for ENN model.

Table 3.
Parameter configuration for PSO, APSO, and ASA-PSO algorithms.
3.3.2. Model Evaluation Metrics
To rigorously validate the accuracy of the coarse-grained soil mechanical property prediction model developed with our improved particle swarm optimization algorithm, four evaluation metrics have been introduced: Coefficient of Determination (R2); Mean Squared Error (MSE, Equation (4)); Root Mean Squared Error (RMSE); Mean Absolute Error (MAE).
where
- y(k) is the measured value at data point k;
- yt(k) is the predicted value at data point k;
- yp(k) is the mean value of all measured data points in the test set;
- N is the total number of samples in the test set.
4. Results
4.1. Model Training and Testing
To evaluate the effectiveness and precision of the proposed algorithm, both conventional PSO and ASA-PSO implementation utilized the mean squared error (MSE) as the fitness function. The evolutionary curves of PSO and ASA-PSO are presented in Figure 8. Analysis reveals that adaptive adjustment of inertia weight and learning factors enables standard PSO to partially escape local optima. Building upon APSO, the integration of simulated annealing further enhances local optima avoidance capabilities and improves global optimum search accuracy. Additionally, the proposed algorithm achieves accelerated convergence rates while maintaining solution precision.
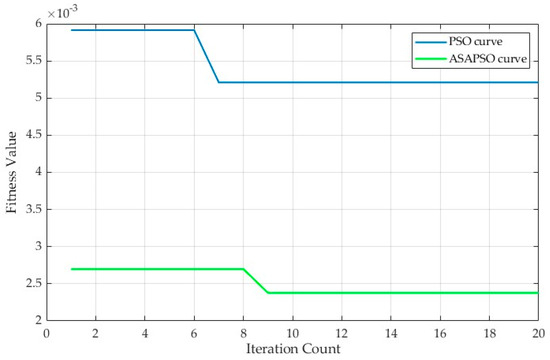
Figure 8.
Evolutionary curves of the model algorithms.
To demonstrate the predictive capability of the ASA-PSO-ENN model, a comparative analysis was conducted using 106 data points from the test set. Figure 9 presents the predicted deviatoric stress results from different models, with the training sample number on the x-axis and the predicted deviatoric stress values on the y-axis. By comparing the predictions of the ELMAN neural network, PSO-Elman, and the proposed ASA-PSO-ENN algorithm against the actual values, it is evident that the ASA-PSO-ENN model achieves the best fit with the true values, demonstrating significantly higher prediction accuracy than the other two comparative algorithms. These results further validate the superior performance of the ASA-PSO-ENN model in predicting deviatoric stress.
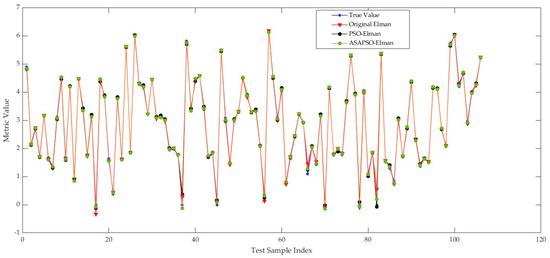
Figure 9.
Comparative visualization of predictive versus experimental values for Elman neural networks pre- and post-PSO optimization.
As shown in Figure 10, the evaluation metrics of different prediction models are compared. The results indicate that the optimized ASA-PSO-ENN prediction model proposed in this study exhibits significantly lower MAE, MSE, and RMSE values compared to both the standard ENN and PSO-ENN algorithms, demonstrating superior predictive performance. Furthermore, the optimized model achieves a correlation coefficient of 0.9799, representing improvements of approximately 11.8% and 9.1% over the ENN and PSO-ENN algorithms, respectively. The experimental results demonstrate that the ASA-PSO-optimized ENN model achieves superior computational efficiency and faster convergence rates in practical implementations, proving particularly effective for predicting coarse-grained soil mechanical properties.
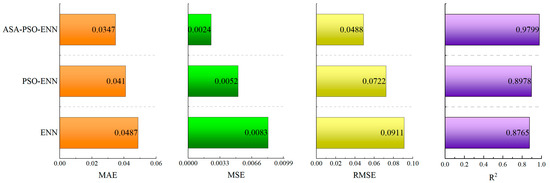
Figure 10.
Comparison of error evaluation metrics among different prediction models.
4.2. Engineering Verification
Based on the proposed ASA-PSO-ENN prediction model for the mechanical parameters of coarse-grained soils, real triaxial test data of sandy gravel materials from an earth–rock dam project were selected to validate the model. Input parameters including different gradations, dry densities, confining pressures, and axial strains were fed into the pre-trained ASA-PSO-ENN prediction model to forecast the deviatoric stress and volumetric strain. The relationships between predicted versus actual deviatoric stress–strain and volumetric strain–strain for the sandy gravel materials are plotted in Figure 11a and b, respectively. In the figures, the horizontal axis represents axial strain, while the vertical axis displays the predicted values of deviatoric stress and volumetric change. The blue curves represent the measured results (i.e., true values) of deviatoric stress and volumetric strain from the triaxial compression tests, while the orange curves depict the predicted results (i.e., predicted values) generated by the ASA-PSO-ENN model. It is evident that the proposed ENN model optimized by the ASA-PSO algorithm demonstrates high predictive capability for the mechanical parameters of coarse-grained soils.
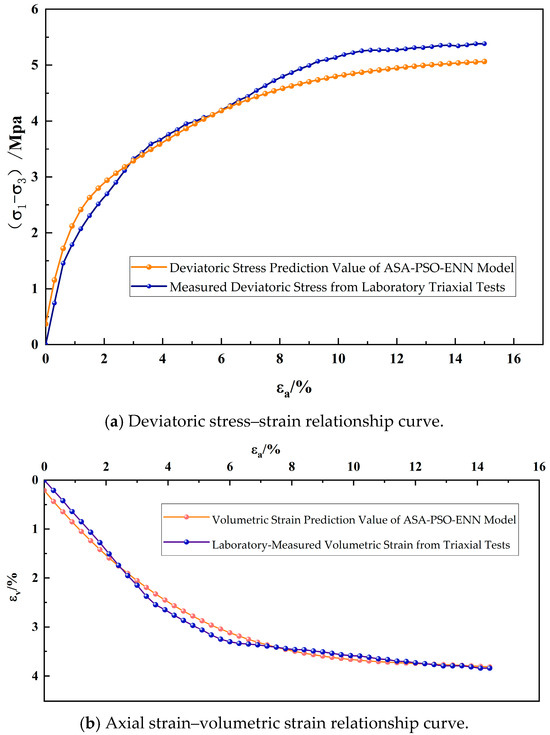
Figure 11.
Comparison of deviatoric stress–axial strain–volumetric strain relationships between laboratory tests and ASA-PSO-ENN model predictions.
5. Conclusions and Discussions
As the primary fill material for earth–rock dams, the mechanical properties of coarse-grained soils exert direct impacts on dam safety assessments. This study proposes a predictive model for the mechanical parameters of coarse-grained soils by optimizing an Elman Neural Network (ENN) using the combined Adaptive Simulated Annealing and Particle Swarm Optimization (ASA-PSO) algorithm. The key conclusions are as follows:
- (1)
- A hyperbolic tangent function-based nonlinear inertia weight adjustment strategy was adopted to enable the adaptive variation of the particle swarm optimization (PSO) algorithm during the iterative process, effectively balancing its global and local optimization capabilities. The proposed second-order oscillatory strategy for particle velocity updates enhances the traversal behavior of particle motion by introducing an oscillation mechanism, thereby strengthening the particles’ self–cognitive ability and maintaining population diversity. This approach effectively prevents premature convergence and reduces the risk of the algorithm becoming trapped in local optima. By integrating the perturbation mechanism and search strategy of simulated annealing (SA) into the adaptive particle swarm algorithm (APSO), a novel hybrid optimization algorithm (ASA-PSO) was developed. This hybrid algorithm not only ensures rapid convergence but also enhances global search capability, further improving solution accuracy and effectively mitigating premature convergence. Validation through practical engineering cases demonstrates that the Elman neural network (ENN) model optimized by the fusion of simulated annealing and the improved PSO algorithm achieves high accuracy and strong stability in predicting the mechanical properties of coarse-grained materials, indicating significant engineering application value.
- (2)
- The developed ASA-PSO-ENN model in this study can accurately predict the deviatoric stress–axial strain–volumetric strain relationship of coarse-grained materials, thereby enabling the determination of key parameters for the Duncan E-B nonlinear model. These parameters can be directly applied to the finite element analysis (FEA) constitutive model of geotechnical structures such as earth–rock dams, significantly improving the accuracy of deformation numerical analysis and enhancing the engineering application value. Furthermore, the model exhibits excellent rapid prediction capabilities. During actual construction, by inputting real-time field-monitored compaction parameters of fill materials into the trained model, the mechanical property parameters of the compacted fill under current rolling conditions can be quickly obtained. Through real-time comparison with design target values, the model provides timely and reliable technical guidance for construction personnel to dynamically adjust compaction operations (e.g., roller passes and intensity).
- (3)
- In recent years, artificial intelligence and machine learning technologies have been widely applied in engineering prediction fields, with algorithms such as LSTM, LightGBM, and SVM demonstrating extensive utility across various domains. LSTM, leveraging its strength in temporal sequence modeling, is commonly employed for dynamic system predictions (e.g., meteorology, transportation). Light GBM excels in efficiency and interpretability, making it particularly suitable for structured data processing (e.g., finance, healthcare). SVM, owing to its superior performance in small-sample classification, stands out in high-dimensional data applications (e.g., image and biological data analysis). Zhang et al. [41] systematically reviewed the technological evolution from traditional machine learning to deep learning and large-scale models for seismic response analysis of earth–rock dams, highlighting the advantages and limitations of different approaches.
The proposed ASA-PSO-ENN hybrid model in this study incorporates several innovative features: First, an adaptive strategy (ASA) is introduced to dynamically optimize the inertia weight parameters of the particle swarm, significantly enhancing the model’s temporal response capability. Second, by combining the nonlinear mapping ability of neural networks with the global optimization strength of the particle swarm algorithm, the model achieves high-precision capture of complex patterns. Finally, the recurrent feedback structure of ENN ensures model stability under data perturbations while maintaining excellent temporal generalization performance.
Engineering case studies demonstrate that the model exhibits superior accuracy and robustness in predicting the deviatoric stress–axial strain–volumetric strain relationship of coarse-grained soils (e.g., gravelly sands), providing a novel technical pathway for parameter prediction in geotechnical applications.
- (4)
- The deformation characteristic parameters of dam coarse-grained materials are primarily determined through laboratory triaxial tests. However, in the construction of high rockfill dams, the increasing particle size of dam materials is constrained by testing equipment dimensions, leading to significant scale effects in laboratory test results. Furthermore, as the filling height of earth–rock dams increases, the compaction density of dam materials varies across different elevation zones, resulting in corresponding variations in mechanical properties along the dam height. If the mechanical parameters obtained during the construction phase are still used for dam deformation analysis, the results often fail to accurately reflect actual dam deformations.
Therefore, the application of the proposed ASA-PSO-ENN model for predicting mechanical properties of coarse-grained materials enables the estimation of reasonable mechanical parameters that account for both scale effects and elevation-dependent non-uniform compaction. Consequently, dam deformation analyses based on these predicted parameters will yield more accurate and rational results.
6. Limitations and Future Research Directions
The ASA-PSO-ENN model for predicting mechanical properties of coarse-grained soils established in this study has the following limitations that need to be addressed in future research:
- (1)
- Data-related limitations
First, the model’s training relies on triaxial test data, making its prediction accuracy inherently dependent on the quality of experimental data. Thus, rigorous data screening and preprocessing are critical. Currently, the limited dataset scale constrains model performance; expanding the dataset would significantly enhance prediction accuracy and reliability.
Secondly, the scope of application of this model is limited to coarse-grained materials with a maximum particle size of 60 mm. For the scenarios involving dam materials with a particle size of 800 to 1200 mm in actual water conservancy projects, it is necessary to consider the scale effect to establish a quantitative conversion model between the prototype gradation and the laboratory gradation, mathematically map the prototype gradation to the corresponding laboratory gradation, and use the ASA-PSO-ENN prediction model to predict the physical and mechanical characteristic parameters of the prototype gradation.
Finally, while the model accounts for key parameters such as gradation, dry density, and confining pressure, further improvements in assessment precision and generalizability demand the integration of multi-project, multi-material databases. Such expansion would strengthen the model’s engineering applicability and predictive robustness.
- (2)
- Applicability limitations
The gradation characteristics serve as critical input parameters for the proposed model. The model was developed based on triaxial test data of gravelly sands, which feature hard, rounded particles with negligible breakage during compaction. Consequently, the gradation characteristics remain consistent between pre- and post-compaction states, as well as with the original quarry materials.
However, for crushed rockfill materials (e.g., blasted aggregates), significant particle breakage occurs during compaction, leading to substantial changes in gradation characteristics. This mechanism fundamentally limits the prediction accuracy of the current model. Future studies should:
- Systematically investigate the evolution patterns of gradation parameters under compaction;
- Optimize model parameters to account for particle breakage effects;
- Develop enhanced prediction models to improve accuracy.
Such advancements will provide more reliable theoretical support for mechanical parameter prediction across diverse coarse-grained materials.
- (3)
- Comparative analysis of intelligent algorithms
While other advanced nonlinear modeling algorithms (LSTM, LightGBM, SVM) have demonstrated excellent performance across various domains, their systematic application in evaluating mechanical properties of coarse-grained soils (particularly deviatoric stress–strain–volumetric strain relationships) remains unexplored. Notable applications in related fields include the following: Zhou et al. [13] employed Random Forest and Cubist algorithms to develop predictive models for accurate assessment of shear strength characteristics in rockfill materials; Wang et al. [42] enhanced ionospheric prediction accuracy through a Residual Attention-Bi Conv LSTM model incorporating residual attention mechanisms; Mu et al. [43] proposed a BKA-CNN-SVM hybrid model combining optimization algorithms with deep learning for rockburst intensity prediction; Wang et al. [44] significantly improved gas concentration prediction reliability using a variable-weight combined LSTM-LightGBM model.
Although neural network approaches (e.g., our ASA-PSO-ENN model) show promising predictive capabilities in this domain, their inherent “black-box” nature presents limitations: obscured interpretability of relationships between input variables and prediction results; heightened risk of overfitting; potential compromise of generalization performance.
Future research should leverage the proven successes of these alternative algorithms to:
- Develop novel assessment methodologies with enhanced prediction accuracy;
- Establish interpretable mapping relationships between material parameters and mechanical responses;
- Optimize model architectures to balance computational efficiency with physical meaningfulness.
Author Contributions
Experimental work and data analysis; Methodology and manuscript writing, H.W.; Manuscript review, J.L.; Model construction and analysis, Y.Z.; Experimental data collection, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by: 1. The National Natural Science Foundation of China [Grant No. 52369012] (“Regulation process study of winter irrigation on soil water, heat, salt and nitrogen during seasonal freeze–thaw period in Xinjiang”); 2. The Science and Technology Bureau of Xinjiang Production and Construction Corps [Grant No. 2022DB020] (“Support Programme for Innovation and Development of Key Industries in Southern Xinjiang”); 3. The Science and Technology Bureau of Xinjiang Production and Construction Corps [Grant No. 2024AB079] (“Research and Demonstration of Prefabricated Frost-Resistant Structures and Intelligent Monitoring Systems for Hydraulic Structures in Irrigation Areas”).
Data Availability Statement
Data Availability Statement: The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Acknowledgments
The authors would like to express their sincere gratitude to the relevant departments of the Alta Sh Hydropower Project for providing the essential data and materials that supported this research.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PSO | Particle Swarm Optimization |
| APSO | Adaptive Particle Swarm Optimization |
| SA | Simulated Annealing |
| ENN | Elman Neural Net |
| ASA-PSO | Adaptive Simulated Annealing–Particle Swarm Optimization |
| ANN | Artificial Neural Network |
| AI | Artificial intelligence |
| LSTM | Long Short-Term Memory |
| GBM | Light Gradient-Boosting Machine |
| BKA | Bidirectional Kernel Attention |
| CNN | Convolutional Neural Network |
| SVM | Support Vector Machine |
References
- Jiang, J.; Zuo, Y.; Cheng, Z.; Pan, J. Strength characteristics of coarse-grained materials with different densities by large-scale true triaxial tests. Rock Soil Mech. 2020, 41, 2601–2608. (In Chinese) [Google Scholar] [CrossRef]
- Liu, M.; Shi, X. Brief introduction of engineering property for coarse grained soil. IOP Conf. Ser. Earth Environ. Sci. 2019, 267, 032047. [Google Scholar] [CrossRef]
- Ventini, R.; Flora, A.; Lirer, S.; Mancuso, C. On the effect of grading and degree of saturation on rockfill volumetric deformation. In Geotechnical Research for Land Protection and Development; Springer: Cham, Switzerland, 2019; Volume 40, pp. 462–471. [Google Scholar] [CrossRef]
- Ai, X.; Wang, G.; Kong, X.; Cui, B.; Hu, B.; Ma, H.; Xu, C. The scale effect of coarse-grained materials by triaxial test simulation. Adv. Civ. Eng. 2021, 2021, 6665531. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Itasca Consulting Group. Particle Flow Code in 3 Dimensions: User’s Guide; Itasca Consulting Group: Minneapolis, MN, USA, 2008. [Google Scholar]
- Sitharam, T.G.; Nimbkar, M.S. Micromechanical modelling of granular materials: Effect of particle size and gradation. Geotech. Geol. Eng. 2000, 18, 91–117. [Google Scholar] [CrossRef]
- Zhou, W.; Chang, X.; Zhou, C.; Zhu, K. A random discontinuous deformation model for meso-mechanical simulation of rockfill materials and its application. Chin. J. Rock Mech. Eng. 2009, 28, 491–499. (In Chinese) [Google Scholar]
- Alaei, E.; Mahboubi, A. A discrete model for simulating shear strength and deformation behaviour of rockfill material, considering the particle breakage phenomenon. Granul. Matter 2012, 14, 707–717. [Google Scholar] [CrossRef]
- Chen, C.; Liu, X.; Luo, Z.; Song, Z. Influence of particle size distribution on strength and deformation characteristics of coarse-grained soils. J. Eng. Geol. 2016, 24, 1191–1198. (In Chinese) [Google Scholar] [CrossRef]
- Ellis, G.W.; Yao, C.; Zhao, R.; Penumadu, D. Stress-strain modeling of sands using artificial neural networks. J. Geotech. Eng. 1995, 121, 429–435. [Google Scholar] [CrossRef]
- Zhu, S.; Ye, H.; Yang, Y.; Ma, G. Research and application on large-scale coarse-grained soil filling characteristics and gradation optimization. Granul. Matter 2022, 24, 121. [Google Scholar] [CrossRef]
- Zhou, J.; Li, E.; Wei, H.; Li, C.; Qiao, Q.; Armaghani, D.J. Random forests and cubist algorithms for predicting shear strengths of rockfill materials. Appl. Sci. 2019, 9, 1621. [Google Scholar] [CrossRef]
- Li, C.; Zhang, J.; Mei, X.; Zhou, J. Supervised intelligent prediction of shear strength of rockfill materials based on data driven and a case study. Transp. Geotech. 2024, 45, 101229. [Google Scholar] [CrossRef]
- Cui, P.; Athey, S. Stable learning establishes some common ground between causal inference and machine learning. Nat. Mach. Intell. 2022, 4, 110–115. [Google Scholar] [CrossRef]
- Mughal, M.A.; Ma, Q.; Xiao, C. Photovoltaic cell parameter estimation using hybrid particle swarm optimization and simulated annealing. Energies 2017, 10, 1213. [Google Scholar] [CrossRef]
- Bilandi, N.; Verma, H.K.; Dhir, R. hPSO-SA: Hybrid particle swarm optimization-simulated annealing algorithm for relay node selection in wireless body area networks. Appl. Intell. 2021, 51, 1410–1438. [Google Scholar] [CrossRef]
- Jia, W.; Zhao, D.; Zheng, Y.; Hou, S. A novel optimized GA–Elman neural network algorithm. Neural Comput. Appl. 2019, 31, 449–459. [Google Scholar] [CrossRef]
- Ruiz, L.; Rueda, R.; Cuéllar, M.; Pegalajar, M. Energy consumption forecasting based on Elman neural networks with evolutive optimization. Expert Syst. Appl. 2018, 92, 380–389. [Google Scholar] [CrossRef]
- Elman, J.L. Finding structure in time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, Y.; Wang, W.; Liu, B. Compaction density evaluation model of sand-gravel dam based on Elman neural network with modified particle swarm optimization. Front. Phys. 2022, 9, 806231. [Google Scholar] [CrossRef]
- Liu, B. Particle Swarm Optimization Algorithm and Its Engineering Applications; Publishing House of Electronics Industry: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Xu, C.; Zhang, J.; Ma, P. A particle swarm optimization algorithm balancing global and local search capabilities. Microelectron. Comput. 2016, 33, 134–138. (In Chinese) [Google Scholar] [CrossRef]
- Yang, X.; Yuan, J.; Yuan, J.; Mao, H. A modified particle swarm optimizer with dynamic adaptation. Appl. Math. Comput. 2007, 189, 1205–1213. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q.; Zhang, Y. Improvement and application of particle swarm optimization algorithm based on the parameters and the strategy of co-evolution. Appl. Math. Inf. Sci. 2015, 9, 1355. [Google Scholar] [CrossRef]
- Ge, H.-W.; Qian, F.; Liang, Y.-C.; Du, W.-L.; Wang, L. Identification and control of nonlinear systems by a dissimilation particle swarm optimization-based Elman neural network. Nonlinear Anal. Real World Appl. 2008, 9, 1345–1360. [Google Scholar] [CrossRef]
- Hua, Y.; Wang, S.; Bai, G.; Li, B. Improved particle swarm optimization algorithm based on nonlinear decreasing inertia weight. J. Chongqing Technol. Bus. Univ. (Nat. Sci. Ed.) 2021, 38, 1–9. (In Chinese) [Google Scholar] [CrossRef]
- Yan, Q.; Ma, R.; Ma, Y.; Wang, J. An adaptive simulated annealing particle swarm optimization algorithm. J. Xidian Univ. 2021, 48, 120–127. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Q.; Qin, H.; Qi, C.; Wang, Q. Temperature prediction method based on XGBoost improved by adaptive SA-PSO. Electron. Meas. Technol. 2023, 46, 67–72. (In Chinese) [Google Scholar] [CrossRef]
- Xiao, B.; Li, D.; Mu, G.; Dong, G. Power quality disturbance classification model based on CNN optimized by SA-PSO algorithm. Electr. Power Autom. Equip. 2024, 44, 185–190. (In Chinese) [Google Scholar] [CrossRef]
- Su, M.; Xiao, B.; Yue, L. Energy-saving optimization of urban rail train ATO based on improved PSO-SA algorithm. Transducer Microsyst. Technol. 2023, 42, 64–67+76. (In Chinese) [Google Scholar] [CrossRef]
- Ma, Q.; Lei, X.; Zhang, Q. Mobile Robot Path Planning with Complex Constraints Based on the Second-Order Oscillating Particle Swarm Optimization Algorithm. In Proceedings of the 2009 WRI World Congress on Computer Science and Information Engineering, Los Angeles, CA, USA, 31 March–2 April 2009; pp. 244–248. [Google Scholar] [CrossRef]
- Hu, J.; Zeng, J. Second-order oscillating particle swarm optimization algorithm. J. Syst. Simul. 2007, 05, 997–999. (In Chinese) [Google Scholar]
- Wang, Y.; Cui, L.; Tian, P.; Qin, L.; Zeng, X. Research on ECT image reconstruction method based on simulated annealing particle swarm optimization algorithm. Chin. J. Sens. Actuators 2024, 37, 484–491. (In Chinese) [Google Scholar]
- Shao, L.; Wang, Z.; Li, C. Mine ventilation optimization algorithm based on simulated annealing and improved particle swarm optimization. J. Syst. Simul. 2021, 33, 2085–2094. (In Chinese) [Google Scholar] [CrossRef]
- Meng, X.; Wang, W.; Xiang, Z. Dynamic compensation method for FOG navigation system based on particle swarm optimization and simulated annealing algorithm. Infrared Laser Eng. 2014, 43, 1555–1560. (In Chinese) [Google Scholar]
- Hafez, A.; Abdelaziz, A.; Hendy, M.; Ali, A. Optimal sizing of off-line microgrid via hybrid multi-objective simulated annealing particle swarm optimize. Comput. Electr. Eng. 2021, 94, 107294. [Google Scholar] [CrossRef]
- Lin, P.; Ratnam, R.; Sankari, H.; Garg, A. Mechanism of microstructural variation under cyclic shearing of Shantou marine clay: Experimental investigation and model development. Geotech. Geol. Eng. 2019, 37, 4163–4210. [Google Scholar] [CrossRef]
- Zhang, Y.; Hua, Y.; Zhang, X.; He, J.; Jia, M.; Cao, L.; An, Z. Enhancing stability and interpretability in the study of strength behavior for coarse-grained soils. Comput. Geotech. 2024, 171, 106333. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Wang, H.Y.; Li, B.; Zhou, F.; Han, L. Research advances in AI-based seismic response analysis methods for earth-rock dams. Earth Sci. Front. 2025, 1–19. (In Chinese) [Google Scholar] [CrossRef]
- Wang, H.; Liu, H.; Yuan, J.; Le, H.; Li, L.; Chen, Y.; Shan, W.; Yuan, G. Residual Attention-BiConvLSTM: A novel global ionospheric TEC map prediction model. Chin. J. Geophys. 2025, 68, 413–430. (In Chinese) [Google Scholar]
- Mu, H.W.; Zhou, Z.H.; Zheng, F.P.; Liu, J.; Zeng, S.; Duan, Y. Rockburst intensity prediction based on BKA-CNN-SVM model. Chin. J. High Press. Phys. 2025, 39, 105–118. (In Chinese) [Google Scholar]
- Wang, X.; Xu, N.; Meng, X.; Chang, H. Prediction of gas concentration based on LSTM-LightGBM variable weight combination model. Energies 2022, 15, 827. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).