Service Composition Optimization Method for Sewing Machine Cases Based on an Improved Multi-Objective Artificial Hummingbird Algorithm
Abstract
1. Introduction
- Many multi-objective optimization algorithms lack sufficient optimization capabilities when solving manufacturing resource service combination optimization problems and are prone to falling into local optima.
- Sewing machine cases are manufacturing equipment with relatively complex characteristic information, and an optimal model for the complex service composition of sewing machine cases has not yet been fully established.
2. Materials and Methods
2.1. Materials
2.2. Classification of Manufacturing Tasks
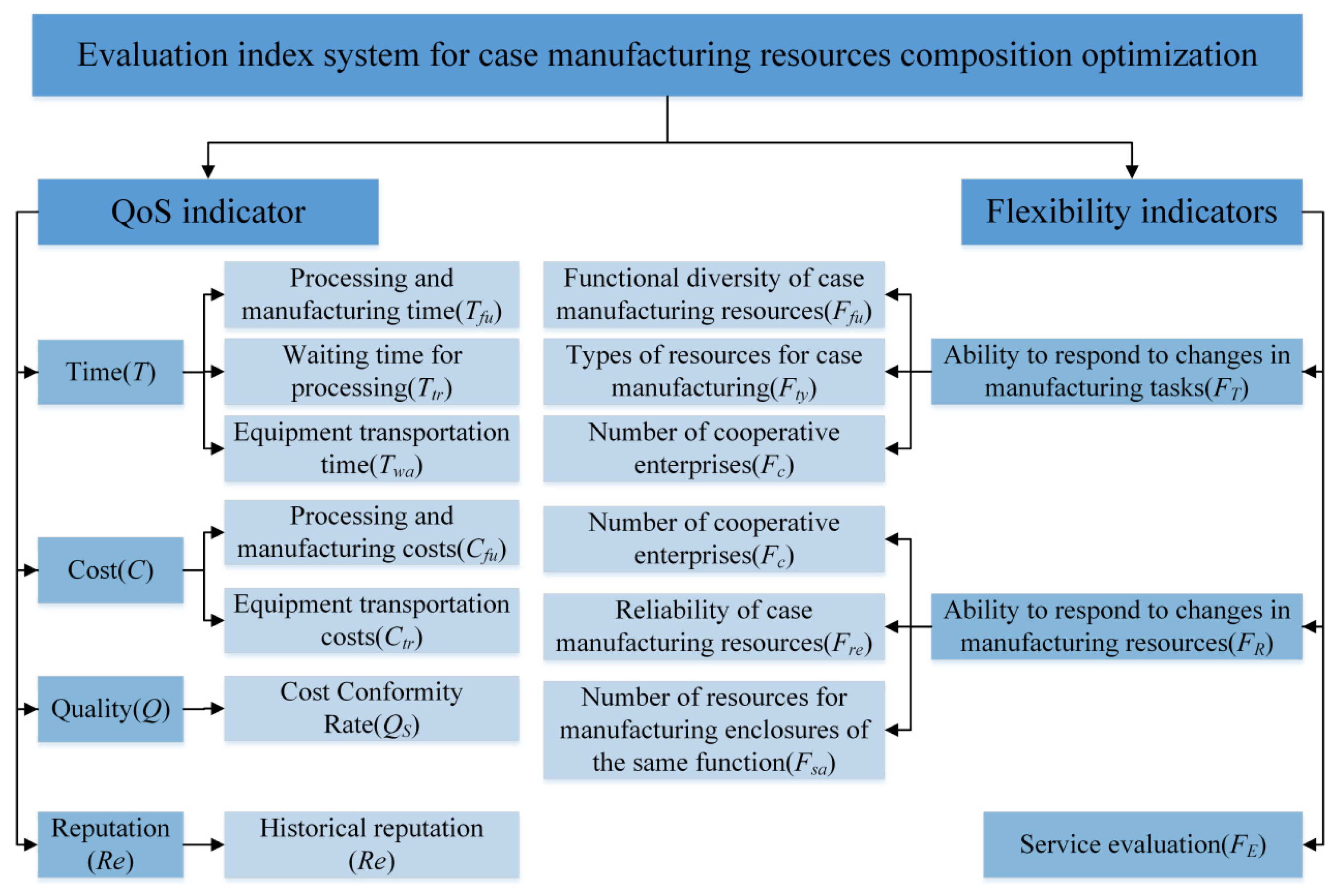
2.3. Evaluation Indicator System for Manufacturing Service Composition Optimization
- Time indicator T: Includes processing and manufacturing time Tfu, processing waiting time Ttr, and equipment transportation time Twa.
- Cost indicator C: Includes processing and manufacturing costs Cfu and equipment transportation costs Ctr.
- Quality indicator Q: Refers to the quality acceptance rate of manufacturing service providers completing relevant manufacturing tasks, expressed as Qs.
- Reputation indicator Re: Used to indicate the historical reputation of manufacturing services.
- Ability to respond to changes in manufacturing tasks FT: Refers to the ability of manufacturing resource providers to successfully complete manufacturing tasks even when the content of the tasks changes after they have been assigned. The quality of this ability directly affects the efficiency of manufacturing resource composition optimization, so it is included in the flexibility indicators. The ability to respond to changes in manufacturing tasks includes the diversity of manufacturing resource functions Ffu, the types of manufacturing resources Fty, and the number of cooperating enterprises Fc.
- Manufacturing resource change response capability FR: Refers to the ability of the manufacturing resource provider to successfully complete a manufacturing task after it has been assigned, even if the manufacturing resources participating in the manufacturing service withdraw from the service for some reason. The quality of this ability directly affects the stability of completing manufacturing tasks in the process of manufacturing resource composition optimization, so it is included in the flexibility indicators, including the number of cooperative enterprises Fc, the reliability of manufacturing resources Fre, and the number of manufacturing resources with the same function Fsa.
- Service evaluation FE: This refers to the historical service evaluation of various manufacturing resources, that is, the satisfaction evaluation given by service demanders to the provision of manufacturing resources during the manufacturing service process. It represents the service attitude, service capacity, service level, speed of problem handling, quality of problem handling, and attitude toward problems of manufacturing services. The higher the service evaluation, the stronger the ability of manufacturing services to respond to changes in manufacturing tasks and manufacturing resources. Therefore, service evaluation is included in the soft indicators.
2.4. Consideration of a Dual-Objective Service Composition Optimization Model with QoS Indicators and Flexibility Indicators
- Time T, perform the cumulative aggregation operation as shown in Formula (2):
- 2.
- Cost C, perform cumulative aggregation operation, as shown in Formula (3):
- 3.
- Quality Q, perform cumulative aggregation operation, as shown in Formula (4):
- 4.
- Reputation Re, perform cumulative aggregation operations, as shown in Formula (5):
- For FT, the ability to respond to changes in manufacturing tasks, perform cumulative aggregation operations, as shown in Formula (7):
- 2.
- For FR, perform cumulative aggregation operations as shown in Formula (8):
- 3.
- For FE, perform cumulative aggregation operation as shown in Formula (9):
- The QoS indicator for manufacturing services is calculated as shown in Formula (11):
- 2.
- The indicator for manufacturing service flexibility is calculated as shown in Formula (12):
2.5. ORAHA_DE Algorithm
2.5.1. Introduction to the MOAHA
- Axial flight
- 2.
- Diagonal flight
- 3.
- Omnidirectional flight
- Guided foraging
- 2.
- Field foraging
- 3.
- Migratory feeding
2.5.2. Improvement Strategy
- The MOAHA has a problem of low initial population diversity during the initialization process, which leads to a high degree of randomness and uneven distribution in the initial population. This can cause uneven distribution on the Pareto front. By embedding an opposition-based learning strategy [35] into the MOAHA’s population initialization process, it is possible to quickly increase the diversity of the population in the initial stage by generating solutions that are opposite to the current solution. As shown in Formula (20):
- 2.
- To address the issue that the search capability of the MOAHA may not be sufficient to cover the entire solution space, a roulette wheel selection strategy [36] is embedded in the MOAHA to introduce a certain degree of randomness into the selection process, giving individuals with lower fitness a certain chance of being selected. The roulette wheel selection strategy can select a global leader σ from an external archive to guide the population individuals to search in the best region. This strategy helps prevent the algorithm from becoming trapped in local optima too early and enhances its global search capabilities. The probabilities for each hypercube in the roulette wheel selection strategy are as follows, as shown in Formula (21):
- 3.
- To address the slow convergence speed of the MOAHA, the characteristics of Lévy flight long steps to escape local optima and short steps for searching are embedded in the MOAHA. This enables the MOAHA to obtain a solution set closer to the true Pareto front when solving multi-objective optimization problems, while also improving population diversity and convergence speed. The specific operation is as follows:
- Mutation
- b.
- Intersection
- c.
- Selection
- d.
- Lévy flight improved differential evolution strategy
2.6. Set Encoding Position
2.7. ORAHA_DE Algorithm Process Framework Diagram
- Initialize parameters, including setting the hummingbird population size, iteration count, external archive size, search space dimension, and access table;
- The elite opposition-based learning strategy is integrated into the multi-objective hummingbird algorithm. By generating opposition solutions that are opposite to the current solution, the objective function values of all hummingbirds are evaluated, and the current solution is added to the external archive;
- Determine whether the number of solutions in the archive exceeds the maximum value. If it exceeds the maximum number of solutions, execute the dynamic congestion distance elimination strategy. If it does not exceed the maximum number of solutions, proceed to step 4;
- Determine whether the iteration termination condition has been met. If so, save the archive and terminate the algorithm. If not, perform a non-dominated sorting update on the population and proceed to step 5;
- Check if the rand value is greater than 0.5. If so, execute the guided foraging strategy. If not, select the leader improvement domain foraging operation using the roulette wheel selection strategy. Upon completion, update the access table;
- Execute the Lévy flight-enhanced differential evolution strategy, add the population to the archive, and synchronously update the dominance relationships;
- Determine whether mod (t, 2n) = 0 is true. If so, execute the migration foraging strategy and synchronously update the dominance relationship. If not, return to step 3 and re-enter the loop.
2.8. Algorithm Performance Indicators
- GD [39] is used to measure the distance between the Pareto frontier found by the algorithm and the true Pareto frontier, as shown in Formula (31):
- 2.
- HV [40] is used to measure the hypervolume covered by the Pareto frontier, as shown in Equation (32):
3. Results
3.1. Algorithm Performance Comparison
3.1.1. Benchmark Function Comparison
3.1.2. Wilcoxon Signed-Rank Test
3.1.3. Friedman Test
3.2. Case Studies
3.2.1. Comparison of Convergence Speed and Time
3.2.2. Optimal Solution Distribution
4. Discussion
5. Conclusions
- Compared with the other five multi-objective optimization algorithms, the GD indicator of the ORAHA_DE algorithm had the smallest value in seven of the nine different test functions, with a minimum value of 4.35 × 10−2, indicating that the Pareto frontier found by the ORAHA_DE algorithm was closer to the true Pareto frontier and significantly better than the other five algorithms. The HV indicator had the maximum value in all nine test functions, with a maximum value of 1.77 × 10−1, indicating that the Pareto frontier found by the ORAHA_DE algorithm was of higher quality. The Wilcoxon signed-rank test shows that the GD and HV values of the ORAHA_DE algorithm are significantly better than those of other algorithms in most test functions. The Friedman test shows that the ORAHA_DE algorithm ranks first in both the GD and HV indicators, and the p-value is much less than 0.05, indicating that there is a significant difference between the ORAHA_DE algorithm and the other five algorithms, and that its overall performance is the best. Additionally, Figure 6 and Figure 7 demonstrate that the ORAHA_DE algorithm exhibits relatively higher stability across different test functions.
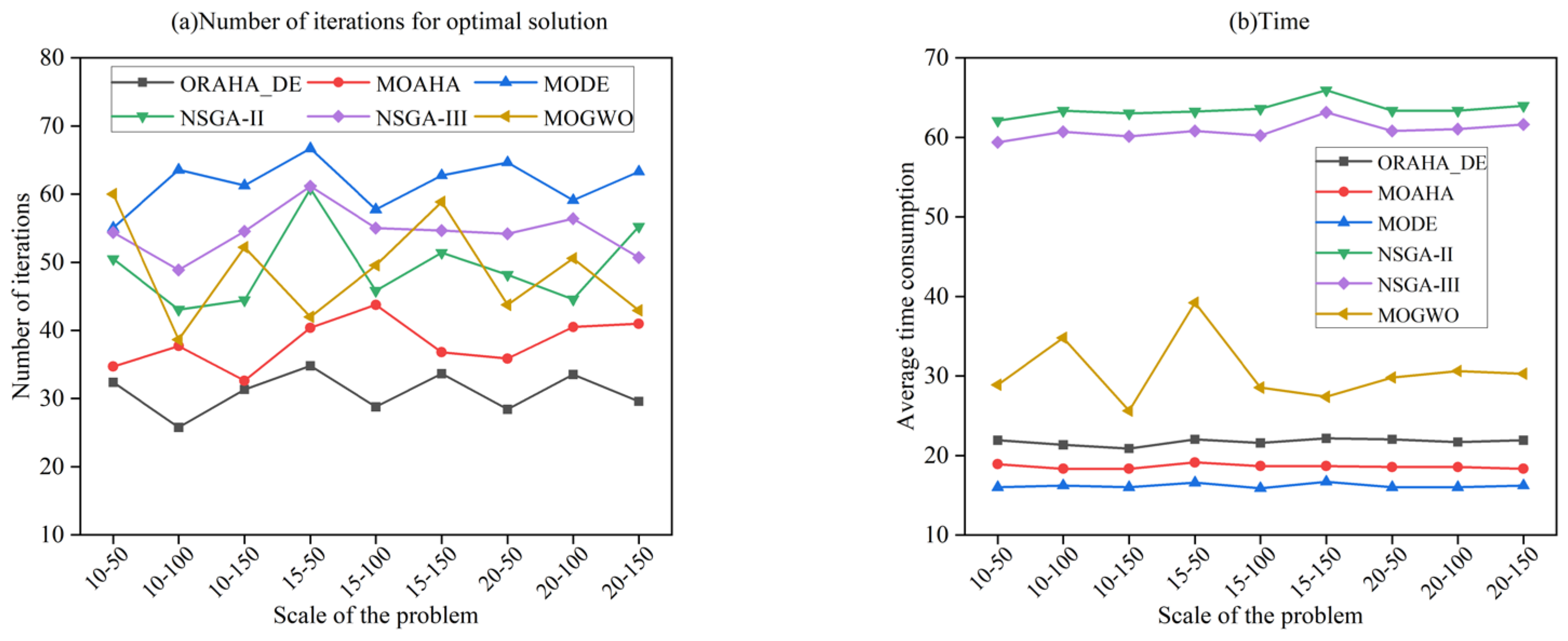
- When solving nine different-scale sewing machine cases composition optimization problems, the average number of iterations for the optimal solution of the ORAHA_DE algorithm was around 30, while that of the MOAHA was around 40. However, the number of iterations for the optimal solution of the other four algorithms ranged from 45 to 75, which was higher than that of the ORAHA_DE algorithm. By testing the time consumed in solving nine different-scale sewing machine cases manufacturing composition optimization problems, we can conclude that the ORAHA_DE algorithm takes slightly longer than the MODE algorithm and the MOAHA to find the optimal solution, but much less time than the NSGA-II and NSGA-III algorithms. The average time taken by the ORAHA_DE algorithm to solve nine different-sized sewing machine cases manufacturing problems is between 20.88 and 22.15 s. As the dataset size increases from (10–50) to (20–150), the ORAHA_DE algorithm achieves the optimal solution with an average of 30 ± 5 iterations and an average solution time of 21.5 ± 0.65 s across different problem scales. Compared to other algorithms, it consistently demonstrates a certain advantage, indicating that this algorithm maintains its performance even as the number of processes increases, the number of candidate services grows, and when the dataset is expanded, the quality of the solution set remains virtually unaffected, suggesting that the performance of this method is not significantly impacted by dataset expansion.
- By comparing the optimal solutions of different algorithms in service composition optimization problems, it can be concluded that the optimal solution obtained by the ORAHA_DE algorithm is superior to other algorithms. When the QoS indicator is high, there is also a high flexibility indicator. In the composition optimization problems of sewing machine cases with 10, 15, and 20 processes, the optimal solution values of the QoS indicator are concentrated between (0.86–0.90), (0.83–0.91), and (0.87–0.92), respectively, while the optimal solution values for the flexibility indicator are concentrated between (28.23–29.07), (41.35–42.83), and (53.86–55.43), respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Camarinha-Matos, L. Collaborative networked organizations: Status and trends in manufacturing. Annu. Rev. Control 2009, 33, 199–208. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, S.; Chen, G. Combining social network and collaborative filtering for personalised manufacturing service recommendation. Int. J. Prod. Res. 2013, 51, 6702–6719. [Google Scholar] [CrossRef]
- Cheng, Y.; Bi, L.; Tao, F. Hypernetwork-based manufacturing service scheduling for distributed and collaborative manufacturing operations towards smart manufacturing. J. Intell. Manuf. 2020, 31, 1707–1720. [Google Scholar] [CrossRef]
- Leng, J.; Jiang, P. Evaluation across and within collaborative manufacturing networks: A comparison of manufacturers’ interactions and attributes. Int. J. Prod. Res. 2018, 56, 5131–5146. [Google Scholar] [CrossRef]
- Zhang, X.; Ming, X.; Bao, Y. Networking-enabled product service system (N-PSS) in collaborative manufacturing platform for mass personalization model. Comput. Ind. Eng. 2022, 163, 107805. [Google Scholar] [CrossRef]
- Tao, F.; Zhao, D.; Yefa, H. Correlation-aware resource service composition and optimal-selection in manufacturing grid. Eur. J. Oper. Res. 2010, 201, 129–143. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Z.; Jiang, X. An optimal selection method of cloud manufacturing resource for guide roller based on combination algorithm. J. Imaging Sci. Technol. 2024, 68, 1. [Google Scholar] [CrossRef]
- Fazeli, M.; Farjami, Y.; Nickray, M. An ensemble optimisation approach to service composition in cloud manufacturing. Int. J. Comput. Integr. Manuf. 2019, 32, 83–91. [Google Scholar] [CrossRef]
- Hu, Q.; Qi, H.; Jia, Y. A two-phase method to optimize service composition in cloud manufacturing. Computing 2024, 106, 2261–2291. [Google Scholar] [CrossRef]
- Cai, A.; Guo, Z.; Guo, S. Optimization strategy of knowledge service composition in cloud manufacturing environment. Comput. Integr. Manuf. Syst. 2019, 25, 421–430. [Google Scholar] [CrossRef]
- Song, C.; Zheng, H.; Han, G. Cloud edge collaborative service composition optimization for intelligent manufacturing. IEEE Trans. Ind. Inform. 2022, 19, 6849–6858. [Google Scholar] [CrossRef]
- Rodriguez-Mier, P.; Mucientes, M.; Lama, M. Hybrid optimization algorithm for large-scale QoS-aware service composition. IEEE Trans. Serv. Comput. 2015, 10, 547–559. [Google Scholar] [CrossRef]
- Sodhro, A.H.; Malokani, A.S.; Sodhro, G.H.; Muzammall, M.; Zongwei, L. An adaptive QoS computation for medical data processing in intelligent healthcare applications. Neural Comput. Appl. 2020, 32, 723–734. [Google Scholar] [CrossRef]
- Badawy, M.M.; Ali, Z.H.; Ali, H.A. QoS provisioning framework for service-oriented internet of things (IoT). Clust. Comput. 2020, 23, 575–591. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Z.; Zhang, G. A QoS-guaranteed intelligent routing mechanism in software-defined networks. Comput. Netw. 2021, 185, 107709. [Google Scholar] [CrossRef]
- Yu, Y.; Li, S.; Ma, J. Time-aware cloud manufacturing service selection using unknown QoS prediction and uncertain user preferences. Concurr. Eng. 2021, 29, 370–385. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, Y.; Sun, S. A comprehensive survey on NSGA-II for multi-objective optimization and applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Ranjan, S.; Gupta, R.; Nanda, S. Threshold based constrained θ-NSGA-III algorithm to solve many-objective optimization problems. Inf. Sci. 2025, 697, 121751. [Google Scholar] [CrossRef]
- Shu, X.; Liu, Y.; Liu, J. Multi-objective particle swarm optimization with dynamic population size. J. Comput. Des. Eng. 2023, 10, 446–467. [Google Scholar] [CrossRef]
- Makhadmeh, S.; Alomari, O.; Mirjalili, S. Recent advances in multi-objective grey wolf optimizer, its versions and applications. Neural Comput. Appl. 2022, 34, 19723–19749. [Google Scholar] [CrossRef]
- Khodadadi, N.; Mirjalili, S.; Zhao, W. Multi-Objective Artificial Hummingbird Algorithm//Advances in Swarm Intelligence: Variations and Adaptations for Optimization Problems; Springer International Publishing: Cham, Switzerland, 2022; pp. 407–419. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.; Saremi, S. Grasshopper optimization algorithm for multi-objective optimization problems. Appl. Intell. 2018, 48, 805–820. [Google Scholar] [CrossRef]
- Basu, M. Economic environmental dispatch using multi-objective differential evolution. Appl. Soft Comput. 2011, 11, 2845–2853. [Google Scholar] [CrossRef]
- Gao, Z.; Liu, S.; Qian, S.; Zhu, L.; Shi, G.; Zhao, J. A Resource Composition Optimization Algorithm Based on Improved Polar Bear Optimization Algorithm for Manufacturing Wallboard for Coating Machine. Coatings 2025, 15, 418. [Google Scholar] [CrossRef]
- Li, F.; Zhang, L.; Liu, Y. QoS-aware service composition in cloud manufacturing: A Gale–Shapley algorithm-based approach. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 2386–2397. [Google Scholar] [CrossRef]
- Zhang, Y.; Cui, G.; Wang, Y. An optimization algorithm for service composition based on an improved FOA. Tsinghua Sci. Technol. 2015, 20, 90–99. [Google Scholar] [CrossRef]
- Zhang, C.; Ning, J.; Wu, J. A multi-objective optimization method for service composition problem with sharing property. Swarm Evol. Comput. 2019, 49, 266–276. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, B.; Wang, S. A dynamic ant-colony genetic algorithm for cloud service composition optimization. Int. J. Adv. Manuf. Technol. 2019, 102, 355–368. [Google Scholar] [CrossRef]
- Seghir, F. Fdmoabc: Fuzzy discrete multi-objective artificial bee colony approach for solving the non-deterministic QoS-driven web service composition problem. Expert Syst. Appl. 2021, 167, 114413. [Google Scholar] [CrossRef]
- Zhu, L.; Jiang, Z.; Shi, J.; Jin, C. An overview of turn-milling technology. Int. J. Adv. Manuf. Technol. 2015, 81, 493–505. [Google Scholar] [CrossRef]
- Ivanov, V.; Evtuhov, A.; Dehtiarov, I.; Trojanowska, J. Fundamentals of Manufacturing Engineering Using Digital Visualization; Springer Nature: Berlin, Germany, 2025. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, B.; Wang, S.; Liu, W.; Jin, T. An improved grey wolf optimizer algorithm for energy-aware service composition in cloud manufacturing. Int. J. Adv. Manuf. Technol. 2019, 105, 3079–3091. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Mirjalili, S.; Wang, L.; Khodadadi, N.; Mirjalili, S.M. An effective multi-objective artificial hummingbird algorithm with dynamic elimination-based crowding distance for solving engineering design problems. Comput. Methods Appl. Mech. Eng. 2022, 398, 115223. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, L.; Mirjalili, S. Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications. Comput. Methods Appl. Mech. Eng. 2022, 388, 114194. [Google Scholar] [CrossRef]
- Mahdavi, S.; Rahnamayan, S.; Deb, K. Opposition based learning: A literature review. Swarm Evol. Comput. 2018, 39, 1–23. [Google Scholar] [CrossRef]
- Mirjalili, S.; Saremi, S.; Mirjalili, S.; Coelho, L.d.S. Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization. Expert Syst. Appl. 2016, 47, 106–119. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341. [Google Scholar] [CrossRef]
- Wang, Y.; Ran, S.; Wang, G. Role-oriented binary grey wolf optimizer using foraging-following and lévy flight for feature selection. Appl. Math. Model. 2024, 126, 310–326. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, B.; Wang, S.; Zhang, Z.; Tang, X. Bi-objective service composition and optimal selection for cloud manufacturing with QoS and robustness criteria. Appl. Soft Comput. 2022, 128, 109530. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, S.; Pu, R.; Zhou, P.; Chen, G.; Li, K.; Lv, D. An adaptive robust service composition and optimal selection method for cloud manufacturing based on the enhanced multi-objective artificial hummingbird algorithm. Expert Syst. Appl. 2024, 244, 122823. [Google Scholar] [CrossRef]









| Arithmetic | Parameters |
|---|---|
| ORAHA_DE | Maximum number of iterations: 300, Population size: 100, External archive size: 50, Migration factor: 100, Lévy flight step factor: ε = 0.3, β = 1.5 |
| MOAHA | Maximum number of iterations: 300, Population size: 100, External archive size: 50, Migration factor: 100 |
| MODE | Maximum number of iterations: 300, Population size: 100, External archive size: 50, Scaling factor: 0.5, Crossover probability: 0.2 |
| NSGA-II | Maximum number of iterations: 300, Population size: 100, External archive size: 50, Crossover ratio: 0.6, Variation ratio: 0.4, Variation rate: 0.02 |
| NSGA-III | Maximum number of iterations: 300, Population size: 100, External archive size: 50, Crossover ratio: 0.6, Variation ratio: 0.4, Variation rate: 0.02 |
| MOGWO | Maximum number of iterations: 300, Population size: 100, External archive size: 50, Number of grids per dimension: 10, Expansion rate: 0.1, Leader selection pressure: 3, Deletion selection pressure: 2 |
| GD | ZDT1 | ZDT2 | UF1 | UF2 | UF3 | UF4 | UF5 | UF6 | UF7 | |
|---|---|---|---|---|---|---|---|---|---|---|
| ORAHA_DE | Mean | 9.11 × 10−2 | 4.35 × 10−2 | 4.18 × 10−2 | 5.52 × 10−2 | 3.52 × 10−1 | 5.44 × 10−2 | 1.66 × 10−1 | 3.27 × 10−1 | 8.56 × 10−2 |
| Std | 2.18 × 10−2 | 1.61 × 10−2 | 1.23 × 10−2 | 1.12 × 10−2 | 2.91 × 10−2 | 6.40 × 10−3 | 1.54 × 10−2 | 7.12 × 10−2 | 2.41 × 10−2 | |
| MOAHA | Mean | 1.32 × 10−1 | 6.81 × 10−2 | 3.62 × 10−2 | 1.82 × 10−1 | 5.56 × 10−1 | 5.74 × 10−2 | 2.96 × 10−1 | 5.77 × 10−1 | 1.28 × 10−1 |
| Std | 2.45 × 10−2 | 2.87 × 10−2 | 8.40 × 10−3 | 4.11 × 10−2 | 7.86 × 10−2 | 1.19 × 10−2 | 1.99 × 10−2 | 8.85 × 10−2 | 3.04 × 10−2 | |
| MODE | Mean | 3.55 × 10−1 | 1.77 × 10−1 | 7.45 × 10−2 | 4.25 × 10−1 | 1.02 × 100 | 1.03 × 10−1 | 8.67 × 10−1 | 1.53 × 100 | 2.56 × 10−1 |
| Std | 3.19 × 10−2 | 3.12 × 10−2 | 1.01 × 10−3 | 1.57 × 10−2 | 1.83 × 10−1 | 1.03 × 10−2 | 3.11 × 10−2 | 1.26 × 10−1 | 2.18 × 10−2 | |
| NSGA-II | Mean | 1.01 × 10−1 | 5.63 × 10−2 | 5.34 × 10−2 | 1.1 × 10−1 | 3.31 × 10−1 | 4.74 × 10−2 | 2.97 × 10−1 | 4.72 × 10−1 | 1.23 × 10−1 |
| Std | 3.54 × 10−2 | 1.46 × 10−2 | 9.90 × 10−3 | 2.37 × 10−2 | 2.09 × 10−2 | 5.50 × 10−3 | 4.16 × 10−2 | 8.34 × 10−2 | 1.09 × 10−2 | |
| NSGA-III | Mean | 9.78 × 10−2 | 4.62 × 10−3 | 4.89 × 10−2 | 1.11 × 10−1 | 3.74 × 10−1 | 4.64 × 10−2 | 2.38 × 10−1 | 3.49 × 10−1 | 1.10 × 10−1 |
| Std | 1.75 × 10−2 | 1.48 × 10−2 | 1.32 × 10−2 | 3.63 × 10−2 | 2.82 × 10−2 | 8.00 × 10−3 | 6.18 × 10−2 | 1.27 × 10−1 | 1.59 × 10−2 | |
| MOGWO | Mean | 5.69 × 10−1 | 2.21 × 10−1 | 8.52 × 10−2 | 5.75 × 10−1 | 1.14 × 100 | 1.42 × 10−2 | 1.26 × 100 | 1.66 × 100 | 2.64 × 10−1 |
| Std | 6.91 × 10−2 | 6.53 × 10−2 | 2.71 × 10−2 | 1.84 × 10−2 | 1.06 × 10−1 | 1.28 × 10−2 | 1.12 × 10−1 | 6.41 × 10−2 | 4.62 × 10−2 |
| HV | ZDT1 | ZDT2 | UF1 | UF2 | UF3 | UF4 | UF5 | UF6 | UF7 | |
|---|---|---|---|---|---|---|---|---|---|---|
| ORAHA_DE | Mean | 1.77 × 10−1 | 1.26 × 10−1 | 9.52 × 10−2 | 8.68 × 10−2 | 7.56 × 10−2 | 1.16 × 10−1 | 6.09 × 10−2 | 7.32 × 10−2 | 1.67 × 10−1 |
| Std | 1.49 × 10−3 | 6.90 × 10−3 | 4.00 × 10−3 | 7.30 × 10−3 | 3.90 × 10−3 | 8.60 × 10−3 | 7.80 × 10−3 | 1.90 × 10−3 | 5.80 × 10−3 | |
| MOAHA | Mean | 1.59 × 10−1 | 1.09 × 10−1 | 8.98 × 10−2 | 7.33 × 10−2 | 6.65 × 10−2 | 1.06 × 10−1 | 4.68 × 10−2 | 5.64 × 10−2 | 1.49 × 10−1 |
| Std | 2.90 × 10−3 | 6.00 × 10−3 | 3.50 × 10−3 | 8.20 × 10−3 | 4.50 × 10−3 | 2.20 × 10−3 | 1.23 × 10−2 | 5.40 × 10−3 | 7.80 × 10−3 | |
| MODE | Mean | 1.35 × 10−1 | 8.15 × 10−2 | 6.79 × 10−2 | 4.25 × 10−2 | 3.65 × 10−2 | 6.68 × 10−2 | 2.34 × 10−2 | 3.06 × 10−2 | 1.16 × 10−1 |
| Std | 5.40 × 10−3 | 4.00 × 10−3 | 4.80 × 10−3 | 4.40 × 10−3 | 3.40 × 10−3 | 5.80 × 10−3 | 5.50 × 10−3 | 2.50 × 10−3 | 2.80 × 10−3 | |
| NSGA-II | Mean | 1.67 × 10−1 | 1.03 × 10−1 | 9.25 × 10−2 | 7.29 × 10−2 | 7.28 × 10−2 | 1.09 × 10−1 | 4.75 × 10−2 | 6.74 × 10−2 | 1.64 × 10−1 |
| Std | 1.50 × 10−3 | 2.80 × 10−3 | 2.50 × 10−3 | 1.40 × 10−3 | 3.20 × 10−3 | 1.18 × 10−2 | 7.40 × 10−3 | 3.70 × 10−3 | 5.40 × 10−3 | |
| NSGA-III | Mean | 1.69 × 10−1 | 1.06 × 10−1 | 9.26 × 10−2 | 7.67 × 10−2 | 7.33 × 10−2 | 1.16 × 10−1 | 5.19 × 10−2 | 6.90 × 10−2 | 1.60 × 10−1 |
| Std | 3.80 × 10−3 | 3.30 × 10−3 | 1.60 × 10−3 | 7.30 × 10−3 | 4.60 × 10−3 | 8.50 × 10−3 | 8.40 × 10−3 | 4.60 × 10−3 | 3.40 × 10−3 | |
| MOGWO | Mean | 1.21 × 10−1 | 6.54 × 10−2 | 4.35 × 10−2 | 3.44 × 10−2 | 2.67 × 10−2 | 5.80 × 10−2 | 1.34 × 10−2 | 1.98 × 10−2 | 1.06 × 10−1 |
| Std | 7.10 × 10−3 | 2.60 × 10−3 | 4.20 × 10−3 | 2.30 × 10−3 | 3.50 × 10−3 | 6.40 × 10−3 | 3.00 × 10−3 | 3.00 × 10−3 | 4.20 × 10−3 |
| ORAHA_DE VS | ZDT1 | ZDT2 | UF1 | UF2 | UF3 | UF4 | UF5 | UF6 | UF7 | +/≈/− | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MOAHA | Sign | + | + | ≈ | + | + | ≈ | + | + | + | 7/2/0 |
| MODE | + | + | + | + | + | + | + | + | + | 9/0/0 | |
| NSGA-II | + | ≈ | ≈ | + | ≈ | ≈ | + | + | + | 5/4/0 | |
| NSGA-III | + | ≈ | ≈ | + | + | ≈ | + | ≈ | + | 5/4/0 | |
| MOGWO | + | + | + | + | + | + | + | + | + | 9/0/0 |
| ORAHA_DE VS | ZDT1 | ZDT2 | UF1 | UF2 | UF3 | UF4 | UF5 | UF6 | UF7 | +/≈/− | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MOAHA | Sign | + | + | ≈ | ≈ | ≈ | ≈ | ≈ | ≈ | + | 3/6/0 |
| MODE | + | ≈ | + | + | + | + | + | + | + | 8/1/0 | |
| NSGA-II | ≈ | + | ≈ | + | ≈ | ≈ | + | ≈ | ≈ | 3/6/0 | |
| NSGA-III | ≈ | + | ≈ | ≈ | + | ≈ | ≈ | + | ≈ | 3/6/0 | |
| MOGWO | + | + | + | + | + | + | + | + | + | 9/0/0 |
| Metric | Algorithms | Mean Rank | Final Priority | Chi-Square | p-Value |
|---|---|---|---|---|---|
| GD | ORAHA_DE | 1.78 | 1 | 7.45 | 5.11 × 10−5 |
| MOAHA | 3.78 | 4 | |||
| MODE | 4.67 | 5 | |||
| NSGA-II | 2.89 | 3 | |||
| NSGA-III | 2.67 | 2 | |||
| MOGWO | 5.22 | 6 | |||
| HV | ORAHA_DE | 5.94 | 1 | 4.22 × 101 | 2.20 × 10−16 |
| MOAHA | 3.33 | 4 | |||
| MODE | 2.00 | 5 | |||
| NSGA-II | 3.89 | 3 | |||
| NSGA-III | 4.83 | 2 | |||
| MOGWO | 1.00 | 6 |
| Manufacturing Resources | T | C | Q | Re | F |
|---|---|---|---|---|---|
| CMR1-1 | 0.40 | 0.76 | 0.86 | 0.89 | 42 |
| CMR1-2 | 0.34 | 0.75 | 0.92 | 0.91 | 46 |
| CMR1-3 | 0.37 | 0.81 | 0.88 | 0.87 | 40 |
| CMR2-1 | 0.73 | 0.51 | 0.90 | 0.83 | 54 |
| CMR2-2 | 0.78 | 0.56 | 0.88 | 0.78 | 49 |
| CMR3-1 | 0.59 | 0.30 | 0.93 | 0.84 | 44 |
| CMR3-2 | 0.52 | 0.35 | 0.90 | 0.80 | 42 |
| CMR4-1 | 0.31 | 0.44 | 0.89 | 0.81 | 38 |
| … | … | … | … | … | … |
| CMR18-1 | 0.47 | 0.55 | 0.82 | 0.67 | 29 |
| CMR18-2 | 0.44 | 0.56 | 0.85 | 0.63 | 33 |
| CMR18-3 | 0.42 | 0.64 | 0.81 | 0.68 | 30 |
| CMR19-1 | 0.59 | 0.49 | 0.85 | 0.90 | 42 |
| CMR19-2 | 0.61 | 0.57 | 0.87 | 0.89 | 51 |
| CMR19-3 | 0.51 | 0.45 | 0.87 | 0.91 | 50 |
| CMR20-1 | 0.50 | 0.54 | 0.95 | 0.92 | 37 |
| CMR20-2 | 0.52 | 0.59 | 0.94 | 0.90 | 34 |
| Indicator | Quality of Service Indicators QoS | Flexible Indicators | |||
|---|---|---|---|---|---|
| T | C | Q | Re | ||
| Evaluation Interval | [0.20, 0.86] | [0.20, 0.86] | [0.60, 0.95] | [0.60, 0.95] | [24, 56] |
| Causality | negative | negative | positive | positive | positive |
| Scale | Quality of Service Indicators QoS | T | C | Q | Re | F |
|---|---|---|---|---|---|---|
| 10–50 | CMR1-8-CMR2-9-CMR3-1-CMR4-11-CMR5-13-CMR6-1-CMR7-1 -CMR8-10-CMR9-9-CMR10-5 | 0.24 | 0.23 | 0.92 | 0.91 | 28.23 |
| 10–100 | CMR1-4-CMR2-22-CMR3-5-CMR4-1-CMR5-3-CMR6-1-CMR7-16 -CMR8-13-CMR9-19-CMR10-25 | 0.25 | 0.23 | 0.92 | 0.87 | 28.23 |
| 10–150 | CMR1-7-CMR2-1-CMR3-1-CMR4-1-CMR5-6-CMR6-5-CMR7-21 -CMR8-9-CMR9-8-CMR10-16 | 0.26 | 0.26 | 0.92 | 0.82 | 27.73 |
| 15–50 | CMR1-5-CMR2-1-CMR3-7-CMR4-3-CMR5-3-CMR6-11-CMR7-3-CMR8-6 -CMR9-8-CMR10-1-CMR11-4-CMR12-12-CMR13-18-CMR14-6-CMR15-2 | 0.27 | 0.25 | 0.93 | 0.90 | 41.35 |
| 15–100 | CMR1-8-CMR2-8-CMR3-2-CMR4-1-CMR5-3-CMR6-13-CMR7-20-CMR8-15 -CMR9-19-CMR10-2-CMR11-18-CMR12-17-CMR13-3-CMR14-2-CMR15-5 | 0.30 | 0.30 | 0.89 | 0.92 | 41.13 |
| 15–150 | CMR1-4-CMR2-6-CMR3-9-CMR4-1-CMR5-21-CMR6-13-CMR7-2-CMR8-5 -CMR9-4-CMR10-6-CMR11-8-CMR12-4-CMR13-1-CMR14-1-CMR15-9 | 0.25 | 0.29 | 0.89 | 0.90 | 40.12 |
| 20–50 | CMR1-7-CMR2-11-CMR3-13-CMR4-8-CMR5-12-CMR6-2-CMR7-1-CMR8-9 -CMR9-6-CMR10-4-CMR11-5-CMR12-13-CMR13-11-CMR14-15-CMR15-3 -CMR16-13-CMR17-17-CMR18-6-CMR19-3-CMR20-1 | 0.22 | 0.22 | 0.94 | 0.94 | 53.19 |
| 20–100 | CMR1-12-CMR2-19-CMR3-11-CMR4-1-CMR5-3-CMR6-11-CMR7-9-CMR8-5 -CMR9-12-CMR10-6-CMR11-1-CMR12-4-CMR13-7-CMR14-8-CMR15-13 -CMR16-21-CMR17-14-CMR18-10-CMR19-17-CMR20-12 | 0.22 | 0.26 | 0.88 | 0.94 | 52.89 |
| 20–150 | CMR1-2-CMR2-6-CMR3-11-CMR4-21-CMR5-15-CMR6-10-CMR7-7-CMR8-1 -CMR9-19-CMR10-10-CMR11-15-CMR12-13-CMR13-24-CMR14-16-CMR15-12 -CMR16-23-CMR17-15-CMR18-10-CMR19-10-CMR20-1 | 0.24 | 0.22 | 0.90 | 0.92 | 53.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, G.; Liu, S.; Shi, K.; Zhu, L.; Gao, Z.; Zhang, J. Service Composition Optimization Method for Sewing Machine Cases Based on an Improved Multi-Objective Artificial Hummingbird Algorithm. Processes 2025, 13, 2433. https://doi.org/10.3390/pr13082433
Shi G, Liu S, Shi K, Zhu L, Gao Z, Zhang J. Service Composition Optimization Method for Sewing Machine Cases Based on an Improved Multi-Objective Artificial Hummingbird Algorithm. Processes. 2025; 13(8):2433. https://doi.org/10.3390/pr13082433
Chicago/Turabian StyleShi, Gan, Shanhui Liu, Keqiang Shi, Langze Zhu, Zhenjie Gao, and Jiayue Zhang. 2025. "Service Composition Optimization Method for Sewing Machine Cases Based on an Improved Multi-Objective Artificial Hummingbird Algorithm" Processes 13, no. 8: 2433. https://doi.org/10.3390/pr13082433
APA StyleShi, G., Liu, S., Shi, K., Zhu, L., Gao, Z., & Zhang, J. (2025). Service Composition Optimization Method for Sewing Machine Cases Based on an Improved Multi-Objective Artificial Hummingbird Algorithm. Processes, 13(8), 2433. https://doi.org/10.3390/pr13082433






