Structural, Thermophysical, and Magnetic Properties of the γ′-Fe4N System: Density Functional Theory and Experimental Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Electronic Structure Calculations
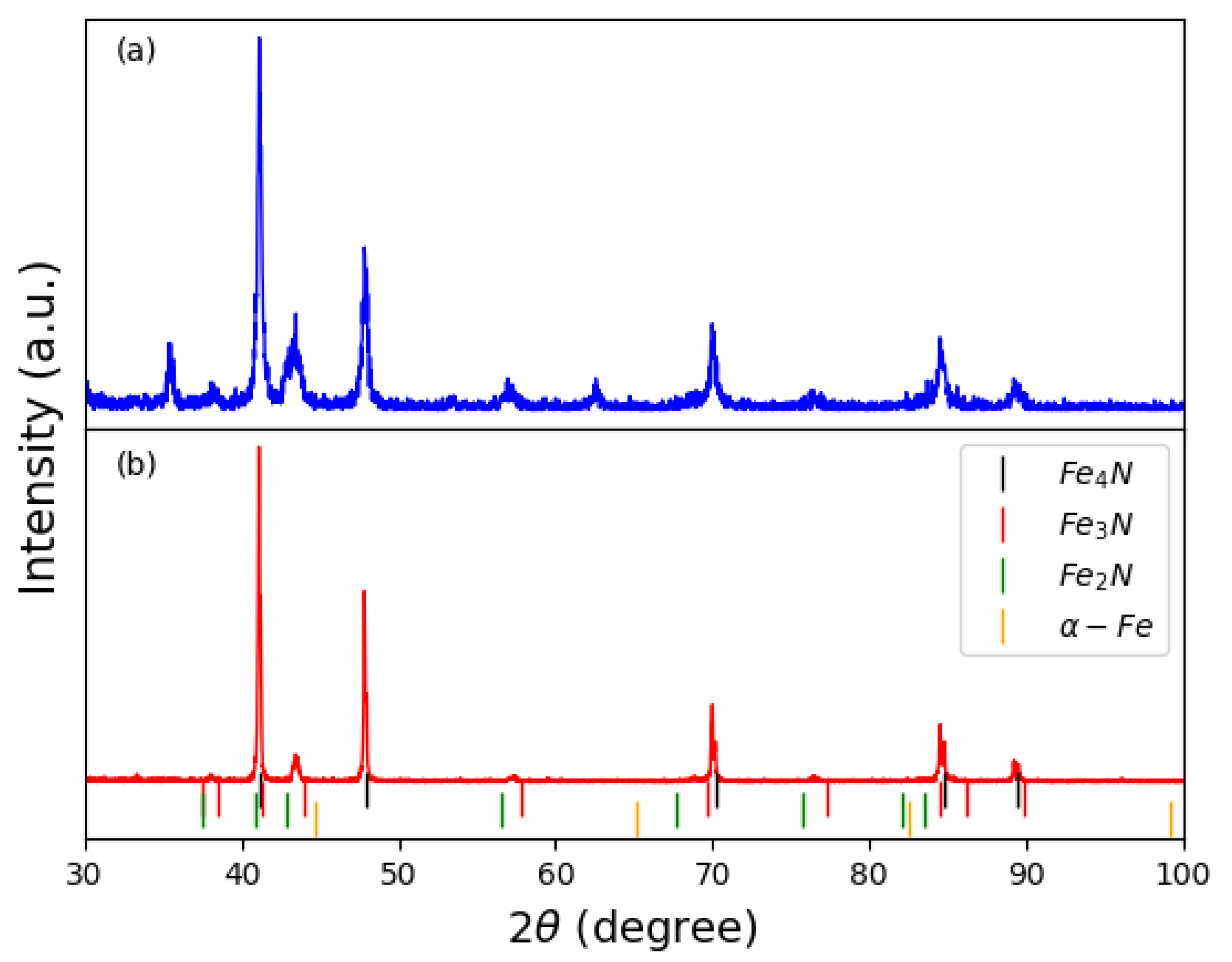
2.2. Experimental Details
3. Results
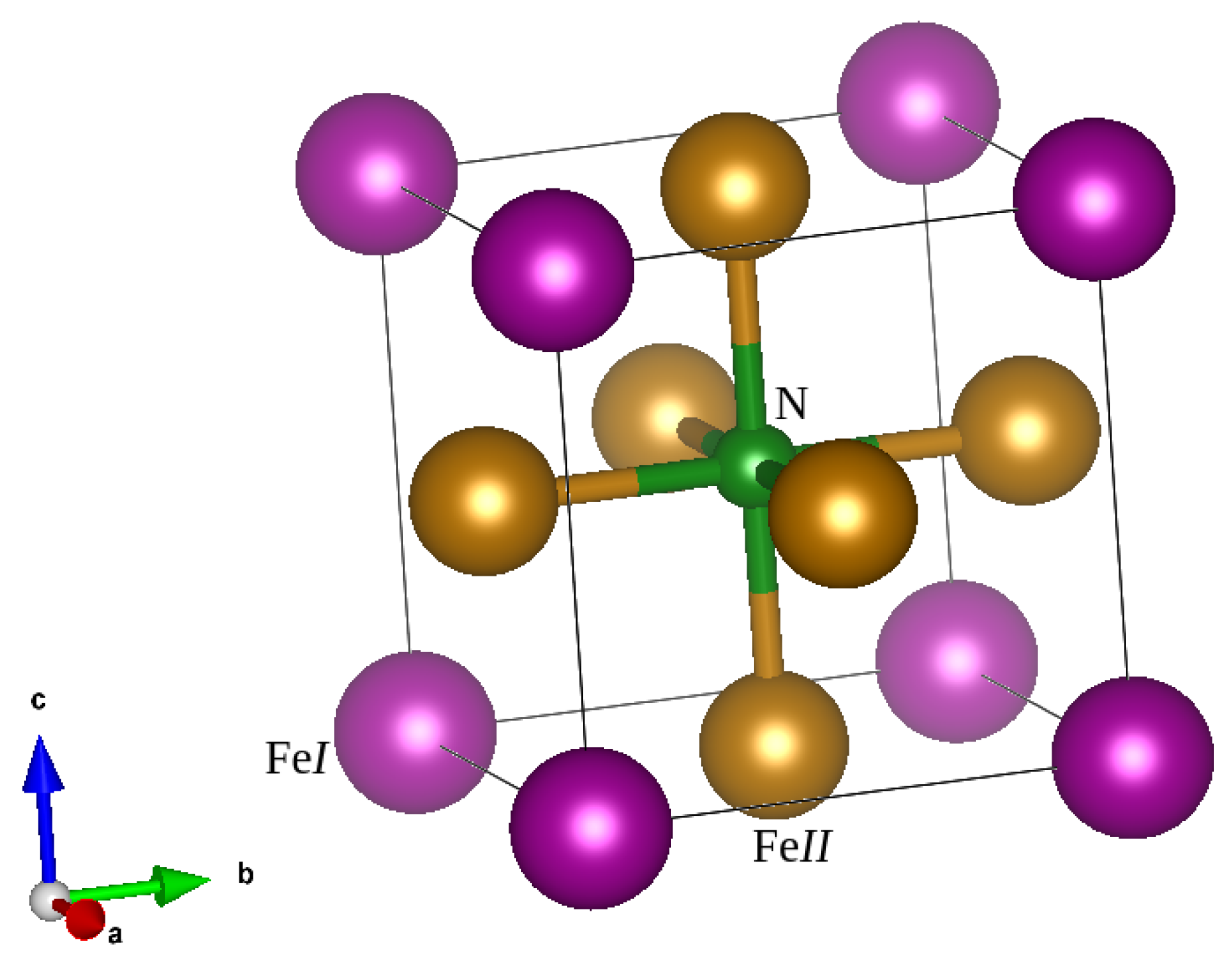
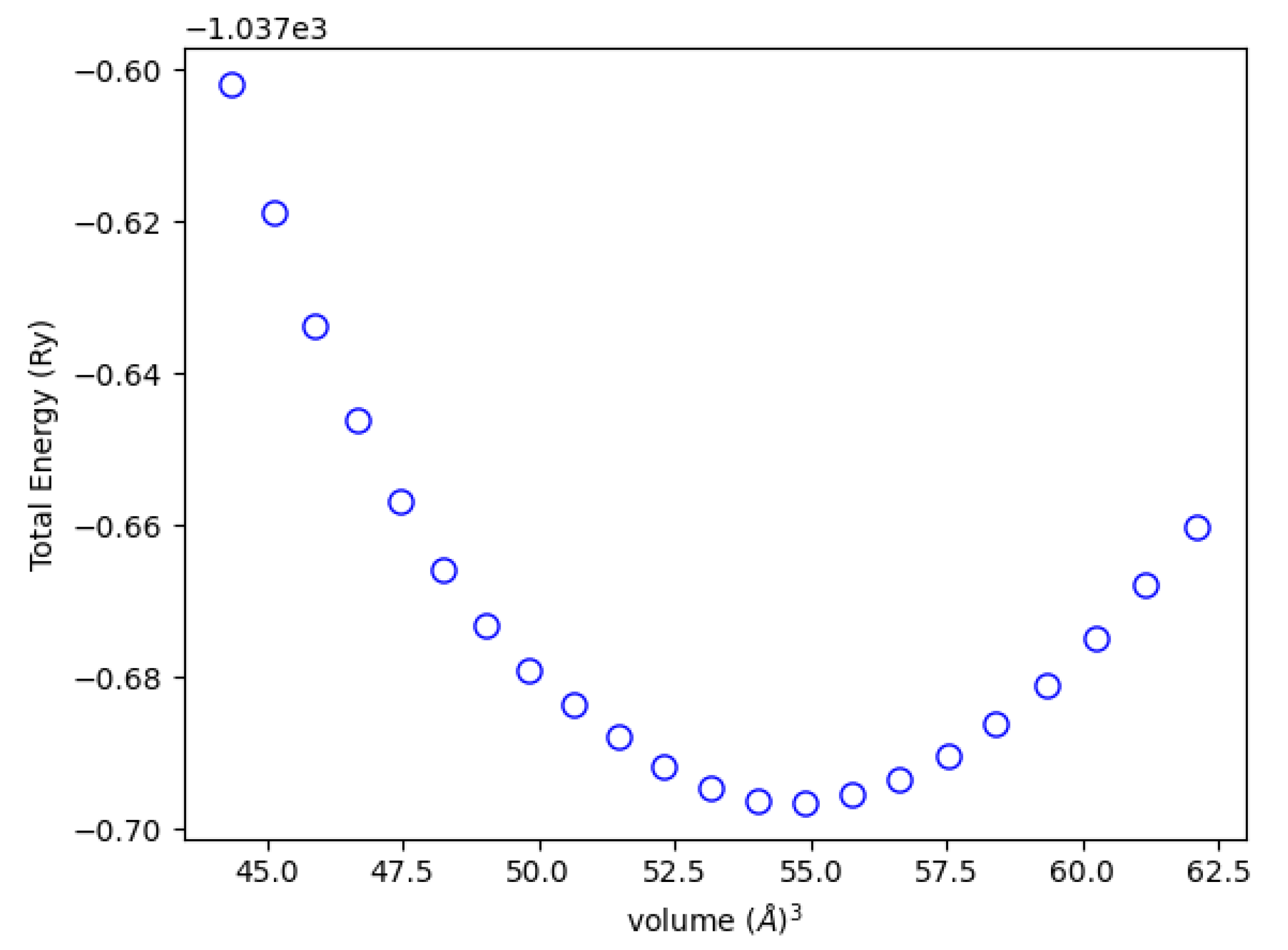
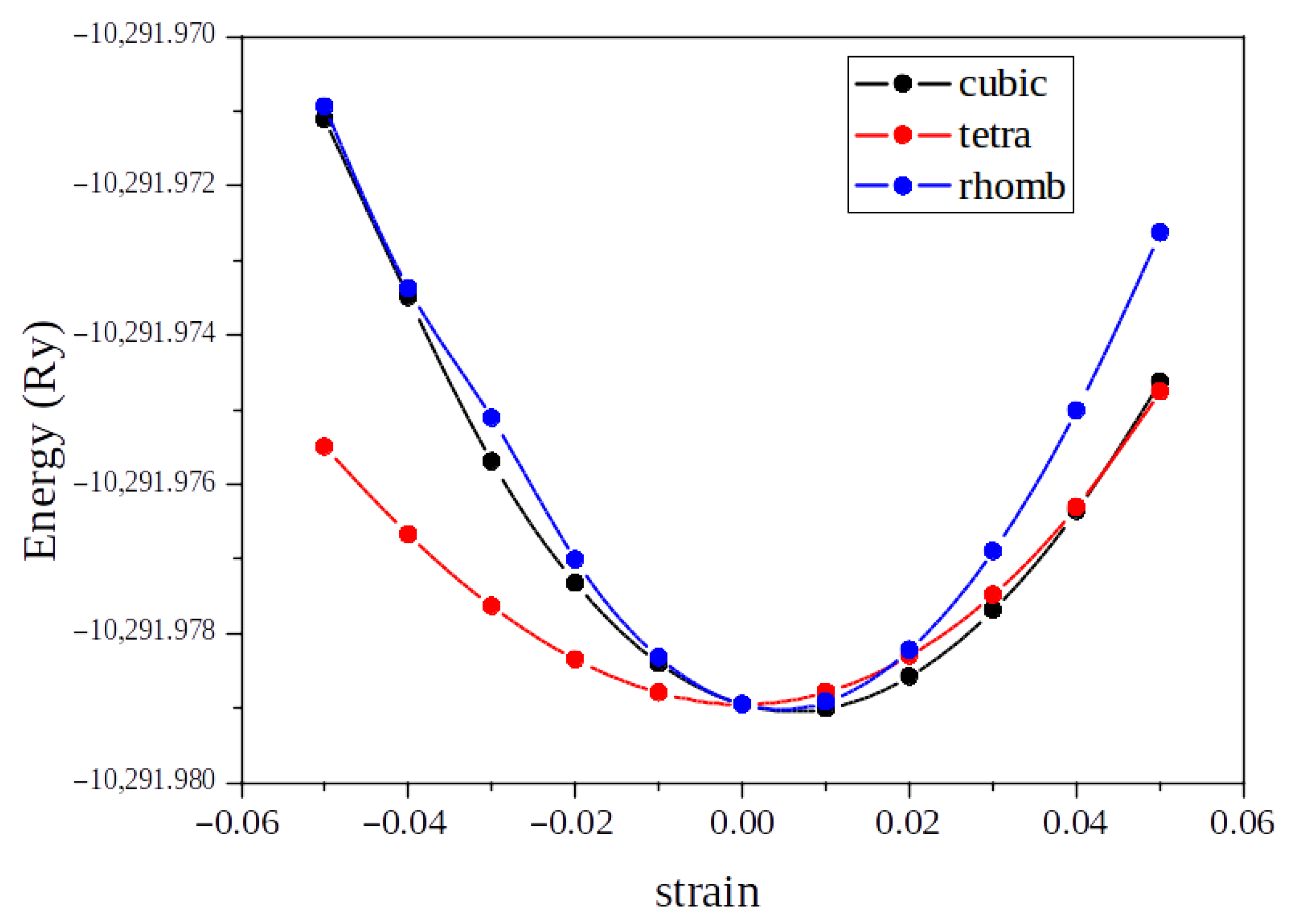
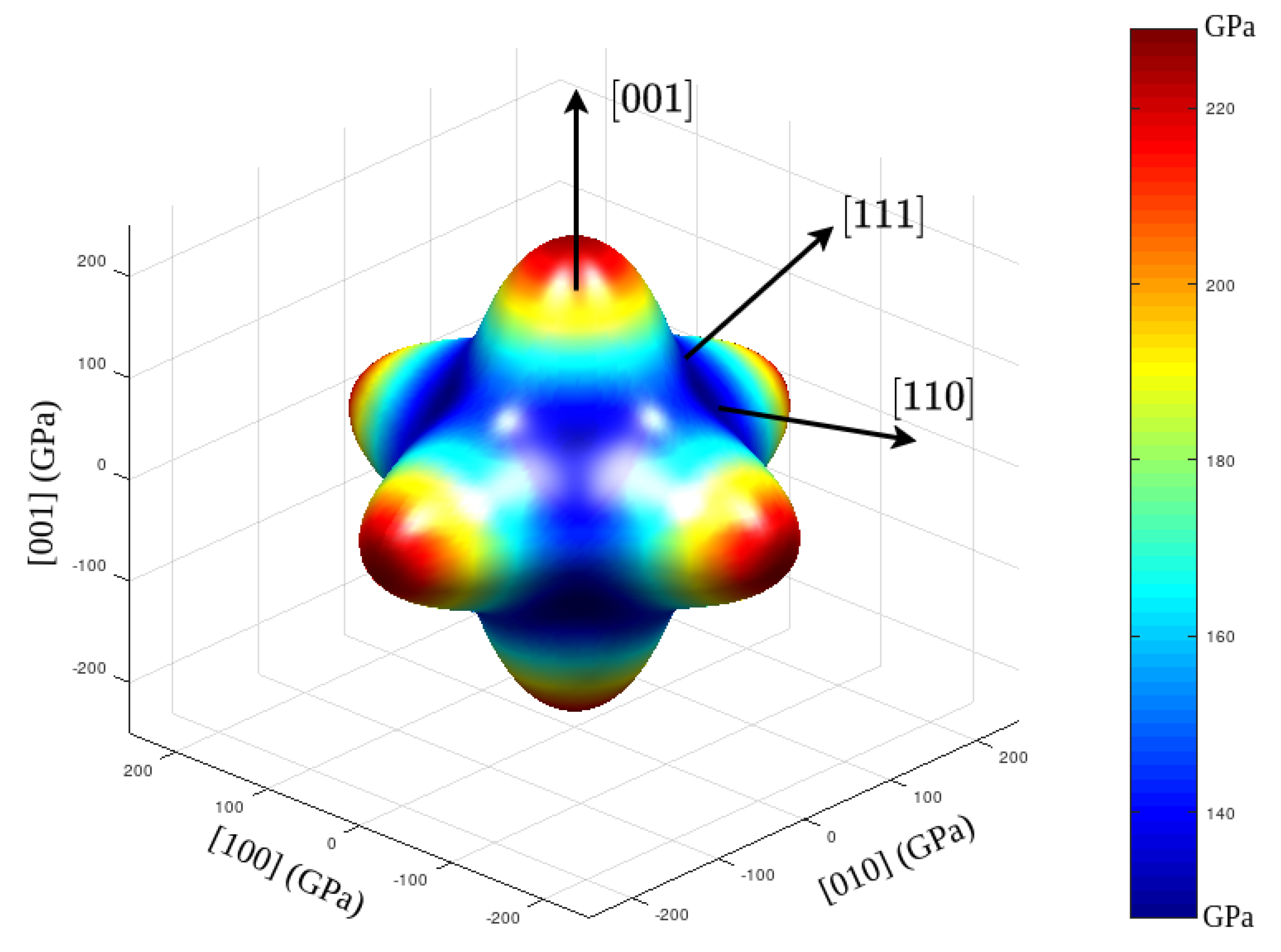
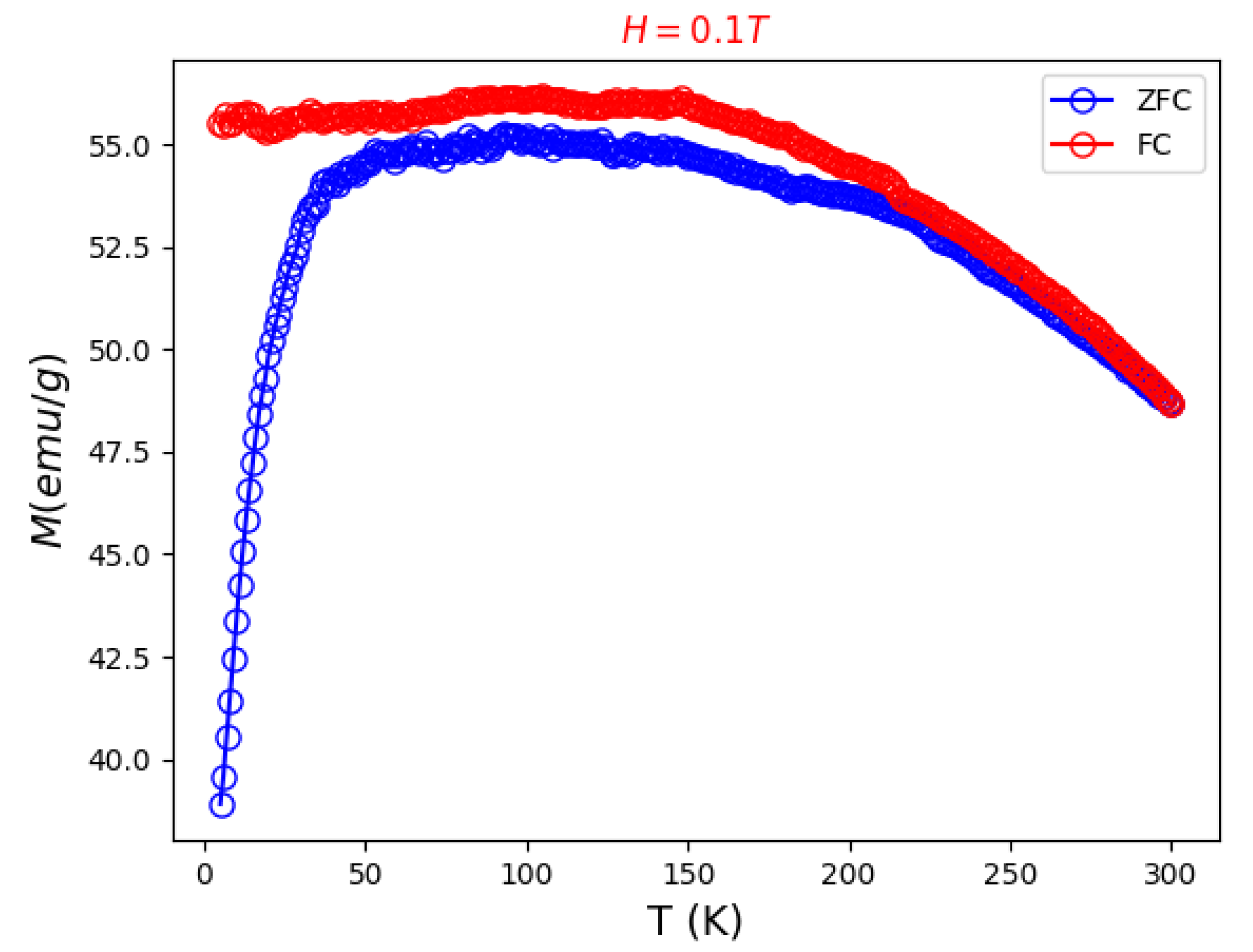
3.1. Structural and Elastic Properties
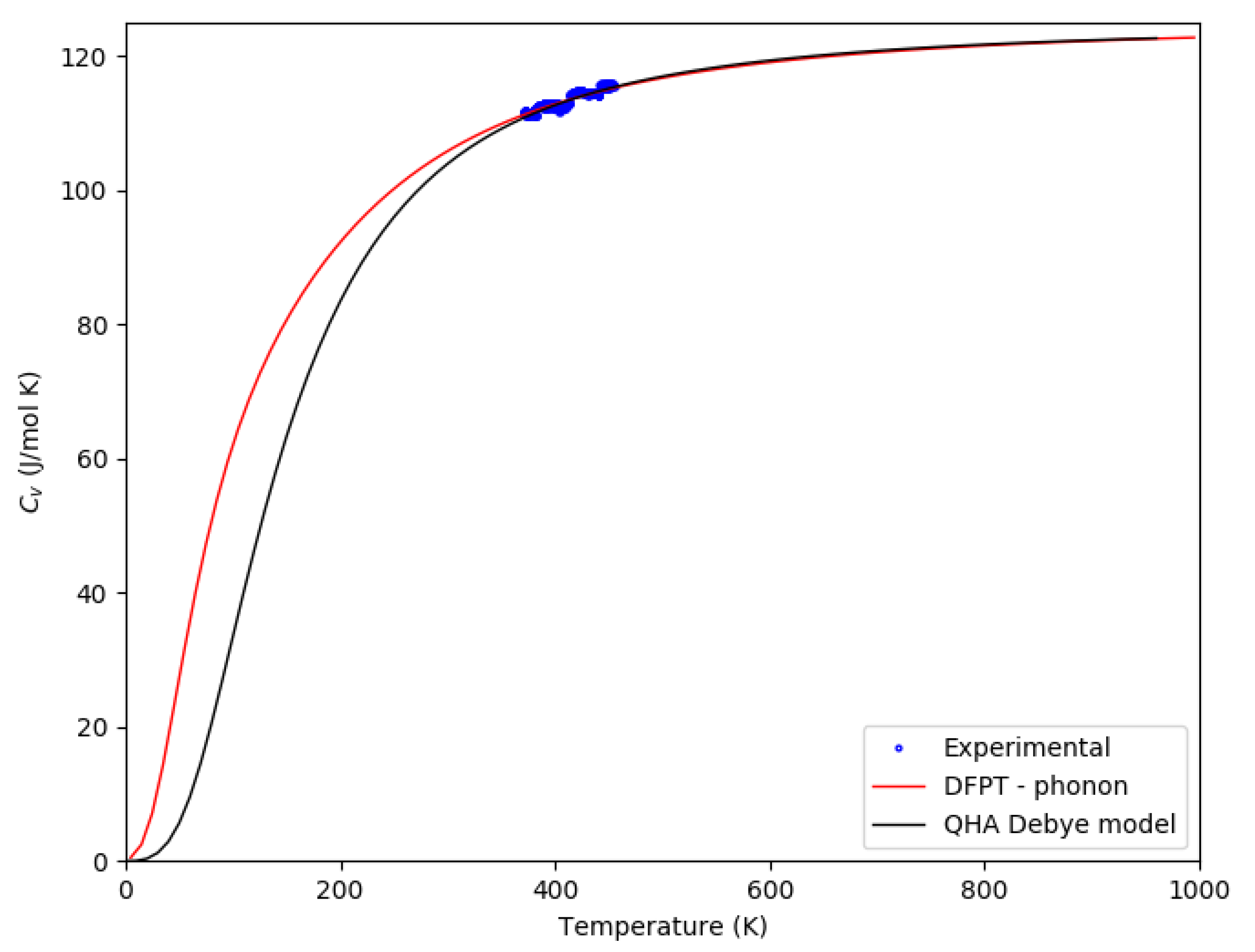
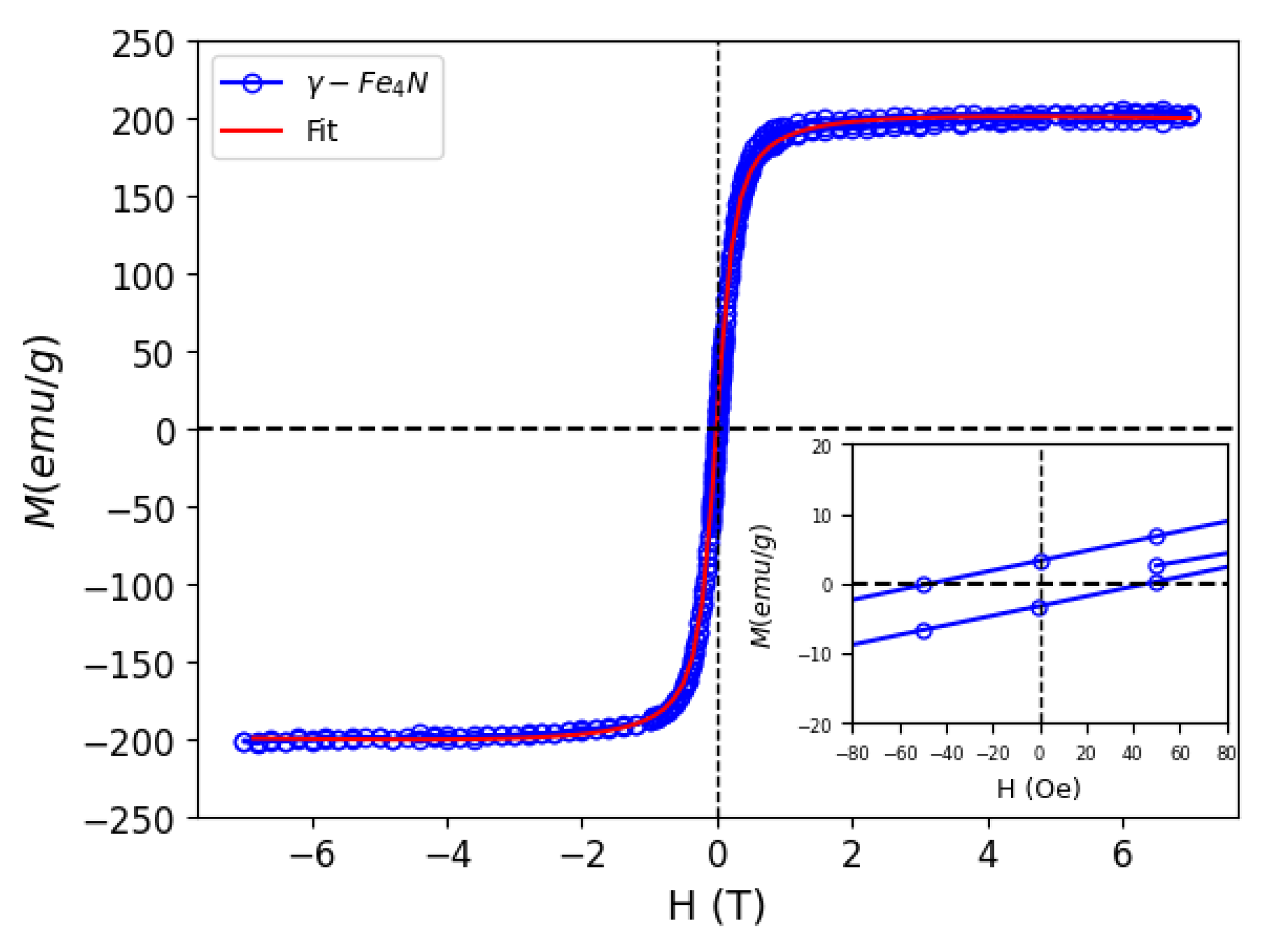
3.2. Thermophysical and Magnetic Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhattacharyya, S. Iron Nitride Family at Reduced Dimensions: A Review of Their Synthesis Protocols and Structural and Magnetic Properties. J. Phys. Chem. C 2015, 119, 1601–1622. [Google Scholar] [CrossRef]
- Brumovský, M.; Oborná, J.; Micić, V.; Malina, O.; Kašlík, J.; Tunega, D.; Kolos, M.; Hofmann, T.; Karlický, F.; Filip, J. Iron Nitride Nanoparticles for Enhanced Reductive Dechlorination of Trichloroethylene. Environ. Sci. Technol. 2022, 56, 4425–4436. [Google Scholar] [CrossRef] [PubMed]
- Wojciechowski, P.; Lewandowski, M. Iron Nitride Thin Films: Growth, Structure, and Properties. Cryst. Growth Des. 2022, 22, 4618–4639. [Google Scholar] [CrossRef]
- Andriamandroso, D.; Demazeau, G.; Pouchard, M.; Hagenmuller, P. New ferromagnetic materials for magnetic recording: The iron carbonitrides. J. Solid State Chem. 1984, 54, 54–60. [Google Scholar] [CrossRef]
- Siberchicot, B.; Matar, S.F.; Fournes, L.; Demazeau, G.; Hagenmuller, P. Influence of the substitution of manganese for iron in the Fe4N lattice on particle formation and magnetic properties. J. Solid State Chem. 1990, 84, 10–15. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yui, T.; Yamaki, K.; Kakeya, I.; Kadowaki, K.; Suemasu, T. Epitaxial growth of ferromagnetic Fe3N films on Si(111) substrates by molecular beam epitaxy. J. Cryst. Growth 2007, 301–302, 597–601. [Google Scholar] [CrossRef]
- Arabczyk, W.; Pelka, R.; Kocemba, I.; Brzoza-Kos, A.; Wyszkowski, A.; Lendzion-Bieluń, Z. Study of Phase Transformation Processes Occurring in the Nanocrystalline Iron/Ammonia/Hydrogen System by the Magnetic Permeability Measurement Method. J. Phys. Chem. C 2022, 126, 7704–7710. [Google Scholar] [CrossRef]
- Wood, J.C.; Nozik, A.J. Direction of the Magnetic Easy Axis in γ′-Fe4N. Phys. Rev. B 1971, 4, 2224. [Google Scholar] [CrossRef]
- Costa-Krämer, J.L.; Borsa, D.M.; García-Martín, J.M.; Martín-González, M.S.; Boerma, D.O.; Briones, F. Structure and magnetism of single-phase epitaxial γ′-Fe4N. Phys. Rev. B 2004, 69, 144402. [Google Scholar] [CrossRef]
- Bartels, O.; Becker, K.D. A High-Temperature Mössbauer Study of the Iron Nitrides. Z. Phys. Chem. 2009, 221, 11–12. [Google Scholar] [CrossRef]
- Maeda, Y.; Imamura, K.; Ohtake, M.; Isogami, S.; Kawai, T.; Futamoto, M.; Kirino, F.; Inaba, N. Large magnetostriction in γ′-Fe4N single-crystal thin film. J. Magn. Magn. Mater. 2023, 585, 170942. [Google Scholar] [CrossRef]
- Li, W.; Li, W.; Chen, J.; Ying, Y.; Yu, J.; Zheng, J.; Qiao, L.; Li, J.; Che, S. Migration of N element and evolution of microstructure in spark plasma sintered bulk γ′-Fe4N. J. Alloys Compd. 2022, 928, 167201. [Google Scholar] [CrossRef]
- Shi, X.; Du, L.; Xiao, K.; Ping, Q.; Sun, X.; Mi, W. Demonstrating Current-Driven Anomalous Hall Resistivity in Epitaxial Pt(3 nm)/Fe4N(≤6 nm)/MgO Heterostructures toward Spintronic Devices. ACS Appl. Nano Mater. 2024, 7, 13952–13958. [Google Scholar] [CrossRef]
- Shi, X.; Wu, M.; Lai, Z.; Li, X.; Gao, P.; Mi, W. Bending Strain-Tailored Magnetic and Electronic Transport Properties of Reactively Sputtered γ′-Fe4N/Muscovite Epitaxial Heterostructures toward Flexible Spintronics. ACS Appl. Mater. Interfaces 2020, 12, 27394–27404. [Google Scholar] [CrossRef]
- Chen, X.; Shi, X.; Zhang, Z.; Liu, X.; Jin, C.; Mi, W. Manipulation of Magnetic Properties and Magnetoresistance in Co/Cu/γ′-Fe4N/Mica Flexible Spin Valves via External Mechanical Strains. ACS Appl. Electron. Mater. 2022, 4, 276–286. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Z.; Yang, H. Magnetic and Electrochemical Properties of γ′-Fe4N Nanoparticles with Cuboidal and Rodlike Morphologies. J. Phys. Chem. C 2023, 127, 728–735. [Google Scholar] [CrossRef]
- Li, X.; Chen, C.; Gao, T.; Xiao, D. Boosting lithium/sodium ion storage by synergistic effect between nanostructured Fe4N-Fe3C and 3D interconnected graphitic C3N4. J. Alloys Compd. 2024, 981, 173661. [Google Scholar] [CrossRef]
- Wu, M.; Wang, J.; Xing, B.; Zhu, H. Hydrogen diffusion in Fe4N: Implication for an effective hydrogen diffusion barrier. Int. J. Hydrogen Energy 2023, 48, 29418–29423. [Google Scholar] [CrossRef]
- Ma, Y.; Bae, J.W.; Kim, S.H.; Klug, M.J.; Li, K.; Vogel, D.; Ponge, D.; Rohwerder, M.; Gault, B.; Raabe, D. Reducing Iron Oxide with Ammonia: A Sustainable Path to Green Steel. Adv. Sci. 2023, 10, 2300111. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Q.; Yu, M.; Wang, W.; Liu, S.; Liang, X.; Wang, C.; Dai, Y.; Xu, Y. Porous and flake-like γ′-Fe4N @ iron oxides with enhanced microwave absorption performance. Ceram. Int. 2021, 47, 8315–8321. [Google Scholar] [CrossRef]
- Mahboubi, F.; Samandi, M.; Dunne, D.; Bloyce, A.; Bell, T. Plasma nitriding of microalloyed steel. Surf. Coat. Technol. 1995, 71, 135–141. [Google Scholar] [CrossRef]
- Berg, M.; Budtz-Jørgensen, C.V.; Reitz, H.; Schweitz, K.O.; Chevallier, J.; Kringhøj, P. On plasma nitriding of steels. Surf. Coat. Technol. 2000, 124, 25. [Google Scholar] [CrossRef]
- Zhang, X.; Su, K.; Chen, X.; Li, J.; Wang, B.; Luo, Z.; Qian, D.; Li, J.; Liu, J. A Hybrid of the Fe4N–Fe Heterojunction Supported on N-Doped Carbon Nanobelts and Ketjen Black Carbon as a Robust High-Performance Electrocatalyst. J. Phys. Chem. Lett. 2022, 13, 11118–11127. [Google Scholar] [CrossRef] [PubMed]
- Wang, L. Influence of compound layer on the corrosion resistance of low alloy steel in a 3.5% NaCl solution. Eng. Res. Express 2024, 6, 025407. [Google Scholar] [CrossRef]
- Reis, J.S., Jr.; Sousa Brito, M.C.; de Oliveira, P.A.; Libório, M.S.; Monção, R.M.; Nunes, M.S.; Júnior, C.A.; Rossino, L.A.; Costa, T.H.C.; Feitor, M.C.; et al. Influence of Quenching and Tempering on the Tribological and Corrosion Behavior of Plasma-Nitrided Society of Automotive Engineers 52100. Steel Res. Int. 2024, 95, 2300512. [Google Scholar]
- Kusmanov, S.A.; Tambovskii, I.V.; Korableva, S.S.; Silkin, S.A.; Smirnov, A.A.; Kusmanova, I.A.; Gorokhov, I.S. Increase in Hardness and Corrosion Resistance of a Medium-Carbon Steel Surface Using Cathodic Plasma Electrolytic Nitriding. Surf. Eng. Appl. Electrochem. 2022, 58, 323–329. [Google Scholar] [CrossRef]
- Breton, H.; Komabayashi, T.; Thompson, S.; Potts, N.; McGuire, C.; Suehiro, S.; Anzellini, S.; Ohishi, Y. Static compression of Fe4N to 77 GPa and its implications for nitrogen storage in the deep Earth. Am. Mineral. 2019, 104, 1781–1787. [Google Scholar] [CrossRef]
- Litasov, K.D.; Shatskiy, A.; Ponomarev, D.S.; Gavryushkin, P.N. Equations of state of iron nitrides ε-Fe3Nx and γ-Fe4Ny to 30 GPa and 1200K and implication for nitrogen in the Earth’s core. J. Geophys. Res. Solid Earth 2017, 122, 3574–3584. [Google Scholar] [CrossRef]
- Zhuang, Y.; Su, X.; Salke, N.P.; Cui, Z.; Hu, Q.; Zhang, D.; Liu, J. The effect of nitrogen on the compressibility and conductivity of iron at high pressure. Geosci. Front. 2021, 12, 983–989. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Prandini, G.; Marrazzo, A.; Castelli, I.E.; Mounet, N.; Marzari, N. Precision and efficiency in solid-state pseudopotential calculations. npj Comput. Mater. 2018, 4, 72. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Murnaghan, F.D. Finite Deformations of an Elastic Solid. Am. J. Math. 1937, 59, 235–260. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809. [Google Scholar] [CrossRef]
- Shirane, G.; Takei, W.J.; Ruby, S.L. Mössbauer Study of Hyperfine Fields and Isomer Shifts in Fe4N and (Fe,Ni)4N. Phys. Rev. 1962, 126, 49. [Google Scholar] [CrossRef]
- Jacobs, H.; Rechenbach, D.; Zachwieja, U. Structure determination of γ′-Fe4N and ε-Fe3N. J. Alloys Compd. 1997, 227, 10–17. [Google Scholar] [CrossRef]
- Kurian, S.; Bhattacharyya, S.; Desimoni, J.; Peltzer y Blancá, E.L.; Gil Rebaza, A.V.; Gajbhiye, N.S. Investigation of γ′-Fe4N–GaN Nanocomposites: Structural and Magnetic Characterization, Mössbauer Spectroscopy and Ab Initio Calculations. J. Phys. Chem. C 2010, 114, 17542–17549. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Hashimoto, H.; Song, M.; Mitsuishi, K.; Furuya, K. Phase transformation from Fe4N to Fe3O4 due to electron irradiation in the transmission electron microscope. Acta Mater. 2004, 52, 1669–1674. [Google Scholar] [CrossRef]
- Panda, R.N.; Gajbhiye, N.S. Magnetic properties of nanocrystalline γ′-Fe4N and ε-Fe3N synthesized by citrate route. IEEE Trans. Magn. 1998, 34, 542–548. [Google Scholar] [CrossRef]
- Gajbhiye, N.S.; Panda, R.N.; Ninghthoujam, R.S.; Bhattacharyya, S. Magnetism of nanostructured iron nitride (Fe–N) systems. Phys. Status Solidi C 2004, 1, 3252–3259. [Google Scholar] [CrossRef]
- Jacobs, H.; Bock, J. Einkristallzüchtung von γ′-Fe4N in überkritischem ammoniak. J. Less-Common Met. 1987, 134, 215–220. [Google Scholar] [CrossRef]
- Gil Rebaza, A.V.; Mudarra Navarro, A.M.; Martínez, J.; Peltzer y Blancá, E.L. First principles and experimental studies of the structural and magnetic ground state of the ternary compound MnFe3N. J. Alloys Compd. 2016, 683, 32–37. [Google Scholar] [CrossRef]
- Takahashi, T.; Takahashi, N.; Tamura, N.; Nakamura, T.; Yoshioka, M.; Inami, W.; Kawata, Y. Growth of Fe4N epitaxial layers displaying anomalous light reflectivity modulated by an external magnetic field. J. Mater. Chem. 2001, 11, 3154–3157. [Google Scholar] [CrossRef]
- Grache, S.Y.; Borsa, D.M.; Boerma, D.O. On the growth of magnetic Fe4N films. Surf. Sci. 2002, 515, 359–368. [Google Scholar] [CrossRef]
- Hill, R. On discontinuous plastic states, with special reference to localized necking in thin sheets. J. Mech. Phys. Solids 1952, 1, 19–30. [Google Scholar] [CrossRef]
- Gressmann, T.; Wohlschlögel, M.; Shang, S.; Welzel, U.; Leineweber, A.; Mittemeijer, E.J.; Liu, Z.-K. Elastic anisotropy of γ′-Fe4N and elastic grain interaction in γ′-Fe4N1-y layers on α-Fe: First-principles calculations and diffraction stress measurements. Acta Mater. 2007, 55, 5833–5843. [Google Scholar] [CrossRef]
- Takahashi, T.; Burghaus, J.; Music, D.; Dronskowski, R.; Schneider, J.M. Elastic properties of Fe4N probed by nanoindentation and ab initio calculation. Acta Mater. 2012, 60, 2054. [Google Scholar] [CrossRef]
- Ma, X.G.; Jiang, J.J.; Liang, P.; Wang, J.; Ma, Q.; Zhang, Q.K. Structural stability and magnetization of γ′-Fe4N and CoFe3N compounds. J. Alloys Compd. 2009, 480, 475–480. [Google Scholar] [CrossRef]
- Zhao, E.; Xiang, H.; Meng, J.; Wu, Z. First-principles investigation on the elastic, magnetic and electronic properties of MFe3N (M=Fe, Ru, Os). Chem. Phys. Lett. 2007, 449, 96. [Google Scholar] [CrossRef]
- Peltzer y Blancá, E.L.; Desimoni, J.; Christensen, N.E.; Emmerich, H.; Cottenier, S. The magnetization of γ′-Fe4N: Theory vs. experiment. Phys. Status Solidi B 2009, 246, 909–928. [Google Scholar] [CrossRef]
- Yang, C.L.; Abd-Elmeguid, M.M.; Micklitz, H.; Michels, G.; Otto, J.W.; Kong, Y.; Xue, D.S.; Li, F.S. Pressure effects on the electronic properties and the magnetic ground state of Fe4N. J. Magn. Magn. Mater. 1999, 151, L19–L23. [Google Scholar] [CrossRef]
- Yan, M.F.; Wu, Y.Q.; Liu, R.L. Plasticity and ab initio characterization on Fe4N produced on the surface of nanocrystallized 18Ni-maraging steel plasma nitrided at lower temperature. Appl. Surf. Sci. 2009, 255, 8902–8906. [Google Scholar] [CrossRef]
- Adler, J.F.; Williams, Q. A high-pressure X-ray diffraction study of iron nitrides: Implications for Earth’s core. J. Geophys. Res. Solid Earth 2005, 110, B01203. [Google Scholar] [CrossRef]
- Guo, K.; Rau, D.; Von Appen, J.; Prost, Y.; Schnelle, W.; Dronskowski, R.; Niewa, R.; Schwarz, U. High pressure high-temperature behavior and magnetic properties of Fe4N: Experiment and theory. High Pressure Res. 2013, 33, 1–13. [Google Scholar] [CrossRef]
- Adhikari, V.; Liu, Z.T.Y.; Szymanski, N.J.; Khatri, I.; Gall, D.; Sarin, P.; Khare, S.V. First-principles study of mechanical and magnetic properties of transition metal (M) nitrides in the cubic M4N structure. J. Phys. Chem. Solids 2018, 120, 197–206. [Google Scholar] [CrossRef]
- Chen, J.-S.; Yu, C.; Lu, H. Phase stability, magnetism, elastic properties and hardness of binary iron nitrides from first principles. J. Alloys Compd. 2015, 625, 224–230. [Google Scholar] [CrossRef]
- Tan, X.; Wang, S.; Chen, Y.; Zhou, Y.; Li, Z. Design, preparation and characterization of iron nitride magnetic abrasives. J. Alloys Compd. 2019, 774, 443–450. [Google Scholar] [CrossRef]
- Ishimatsu, N.; Maruyama, H.; Kawamura, N.; Suzuki, M.; Ohishi, Y.; Ito, M.; Nasu, S.; Kawakami, T.; Shimomura, O. Pressure-induced magnetic transition in Fe4N probed by Fe K-edge XMCD measurement. J. Phys. Soc. Jpn. 2003, 72, 2372–2376. [Google Scholar] [CrossRef]
- Lv, Z.Q.; Gao, Y.; Sun, S.H.; Qv, M.G.; Wang, Z.H.; Shi, Z.P.; Fu, W.T. Electronic, magnetic and elastic properties of γ′-Fe4N (X=B/C/N) from density functional theory calculations. J. Magn. Magn. Mater. 2013, 333, 39–45. [Google Scholar] [CrossRef]
- Yurkova, A.I.; Byakova, A.V.; Belots’ky, A.V.; Milman, Y.V.; Dub, S.N. Deformation Structure, Friction, Hardness, Nano Grain Structure, Nanoindentation, Nitriding, Plasticity Characteristic δ-A, Severe Plastic Deformation (SPD), Young’s Modulus. Mater. Sci. Forum 2006, 503–504, 645–650. [Google Scholar] [CrossRef]
- Zheng, S.; Sun, Y.; Bloyce, A.; Bell, T. Characterization of plasma nitrided andl pvd-tin duplex treated armco iron and en40b steel by nanoindentation. Mater. Manuf. Process. 1995, 10, 815–824. [Google Scholar] [CrossRef]
- Schröter, W.; Spengler, A. Zum E-Modul von nitridhaltigen Schichten auf Stahl. HTM J. Heat Treat. Mater. 1996, 51, 356–362. [Google Scholar] [CrossRef]
- Pellizzari, M.; Molinari, A.; Straffelini, G. Thermal fatigue resistance of plasma duplex-treated tool steel. Surf. Coat. Technol. 2001, 142–144, 1109–1115. [Google Scholar] [CrossRef]
- Arnaud, P.; Heripre, E.; Douit, F.; Aubin, V.; Fouvry, S.; Guiheux, R.; Branger, V.; Miche, G. Micromechanical tensile test investigation to identify elastic and toughness properties of thin nitride compound layers. Surf. Coat. Technol. 2021, 421, 127303. [Google Scholar] [CrossRef]
- Weber, T.; de Wit, L.; Saris, F.W.; Königer, A.; Rauschenbach, B.; Wolf, G.K.; Krauss, S. Hardness and corrosion resistance of single-phase nitride and carbide on iron. Mater. Sci. Eng. A 1995, 199, 205–210. [Google Scholar] [CrossRef]
- Otero-de-la-Roza, A.; Luaña, V. Gibbs2: A new version of the quasi-harmonic model code. I. Robust treatment of the static data. Comput. Phys. Commun. 2011, 182, 1708–1720. [Google Scholar] [CrossRef]
- Otero-de-la-Roza, A.; Abbasi-Pérez, D.; Luaña, V. Gibbs2: A new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features and implementation. Comput. Phys. Commun. 2011, 182, 2232–2248. [Google Scholar] [CrossRef]
- Francisco, E.; Recio, J.M.; Blanco, M.A.; Martín Pendás, A.; Costales, A. Quantum-mechanical study of thermodynamic and bonding properties of MgF2. J. Phys. Chem. A 1998, 102, 1595–1601. [Google Scholar] [CrossRef]
- Francisco, E.; Blanco, M.A.; Sanjurjo, G. Atomistic simulation of SrF2 polymorphs. Phys. Rev. 2001, 63, 094107. [Google Scholar] [CrossRef]
- Flórez, M.; Recio, J.M.; Francisco, E.; Blanco, M.A.; Martín Pendás, A. First-principles study of the rocksalt–cesium chloride relative phase stability in alkali halides. Phys. Rev. 2002, 66, 144112. [Google Scholar] [CrossRef]
- Baroni, S.; de Gironcoli, S.; Dal Corso, A.; Giannozzi, P. Phonons and related crystal properties from density-functional pertubation theory. Rev. Mod. Phys. 2001, 73, 515. [Google Scholar] [CrossRef]
- Petretto, G.; Dwaraknath, S.; Miranda, H.P.C.; Winston, D.; Giantomassi, M.; van Setten, M.J.; Gonze, X.; Persson, K.A.; Hautier, G.; Rignanese, G.M. High-throughput density-functional pertubation theory phonons for inorganic material. Sci. Data 2018, 5, 180065. [Google Scholar] [CrossRef]
- Guan, P.W.; Houchins, G.; Viswanathan, V. Uncertainty quantification of DFT-predicted finite temperature thermodynamic properties within the Debye model. J. Chem. Phys. 2019, 151, 244702. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, X.; Li, M.; Liu, C.; Li, H.; Meng, X.; Mehmood Ur Rehman, K. Preparation and soft magnetic properties of γ′-Fe4N particles. J. Mater. Sci. 2017, 29, 1254–1257. [Google Scholar] [CrossRef]
- Chen, S.K.; Jin, S.; Kammlott, G.W.; Tiefel, T.H.; Johnson, D.W., Jr.; Gyorgy, E.M. Synthesis and magnetic properties of Fe4N and (Fe, Ni)4N sheets. J. Magn. Magn. Mater. 1992, 110, 65–72. [Google Scholar] [CrossRef]
- Dirba, I.; Yazdi, M.B.; Radetinac, A.; Komissinskiy, P.; Flege, S.; Gutfleisch, O.; Alff, L. Growth, structure, and magnetic properties of γ′-Fe4N thin films. J. Magn. Magn. Mater. 2015, 379, 151–155. [Google Scholar] [CrossRef]
- Qi, Q.; O’Donnell, K.; Touchais, E.; Coey, J.M.D. Mössbauer spectra and magnetic properties of iron nitrides. Hyperfine Interact. 1994, 94, 2067–2073. [Google Scholar] [CrossRef]
- Xiao, J.Q.; Chien, C.L. Radio frequency reactive sputtered iron nitrides using ammonia gas: Structure and magnetic properties. Appl. Phys. Lett. 1994, 64, 384–386. [Google Scholar] [CrossRef]
- Guillaud, C.; Creveaux, H. Magnetisme—Preparation et proprietes magnetiques du compose defini Fe4N. C. R. Seances Acad. Sci. Vie Acad. 1946, 222, 1170–1172. [Google Scholar]
- Atiq, S.; Ko, H.-S.; Siddiqi, S.A.; Shin, S.-C. Effect of epitaxy and lattice mismatch on saturation magnetization of γ′-Fe4N thin films. Appl. Phys. Lett. 2008, 92, 222507. [Google Scholar] [CrossRef]
- Jiang, Y.; Jiang, L. Synthesis of γ-Fe4N powder in liquid nitrogen. AIP Adv. 2019, 9, 035215. [Google Scholar] [CrossRef]
- Frazer, B.C. Magnetic structure of Fe4N. Phys. Rev. 1958, 112, 751. [Google Scholar] [CrossRef]
- Gallego, J.M.; Boerma, D.O.; Miranda, R.; Ynduráin, F. 1D Lattice Distortions as the Origin of the (2×2)p4gm Reconstruction in γ′-Fe4N(100): A Magnetism-Induced Surface Reconstruction. Phys. Rev. Lett. 2005, 95, 136102. [Google Scholar] [CrossRef]
| Parameter | This Work | Theoretical Data | Experimental Data |
|---|---|---|---|
| (GPa) | 325.4 | 307.2 [47], 313.0 [48], | |
| 306 [49], 337 [50] | |||
| (GPa) | 131.3 | 134.1 [47], 137.0 [48], | |
| 99 [49], 131 [50] | |||
| (GPa) | 50.1 | 46.0 [47], 46.0 [48], | |
| 47 [49], 58.5 [50] | |||
| B (GPa) | 196.0 | 191.8 [47], 196.0 [48], 200 [51] | 196.0 [48], 198.0 [52] |
| 168 [49], 194.1 [53], 199.4 [50] | 155.0 [54] 155.8 [55], 144.4 [29] | ||
| 195.8 [56], 198.7 [57], 190.6 [58] | 141 [59], 169 [27], 162 [28] | ||
| E (GPa) | 184.9 | 161.5 [47], 162.0 [48], 168.9 [53] | 159.0 [48], 165.0 [48] |
| 195.6 [60], 197.0 [50], 156.4 [56] | 172.0 [61], 200.0 [62] | ||
| 184.0 [49], 168.5 [47], 173.8 [57] | 211.0 [63], 204 [64], 195 [65] | ||
| 178.0 [58] | |||
| G (GPa) | 65.5 | 63.6 [60], 59.4 [47], 59.0 [48] | 59.0 [48] |
| 70.0 [49], 73.6 [50], 57.2 [56] | |||
| 62.2 [47], 70 [49], 62.3 [53] | |||
| 64.2 [57] | |||
| v | 0.318 | 0.325 [47], 0.360 [48], 0.321 [53] | 0.360 [48] |
| 0.325 [60], 0.37 [56], 0.34 [58] | |||
| 0.350 [57], 0.320 [49], 0.336 [50] | |||
| H (GPa) | 8.5 | 10.15 [53], 6.01 [57] | 6.6 [66], 6.76 [58], 8.0 [48] |
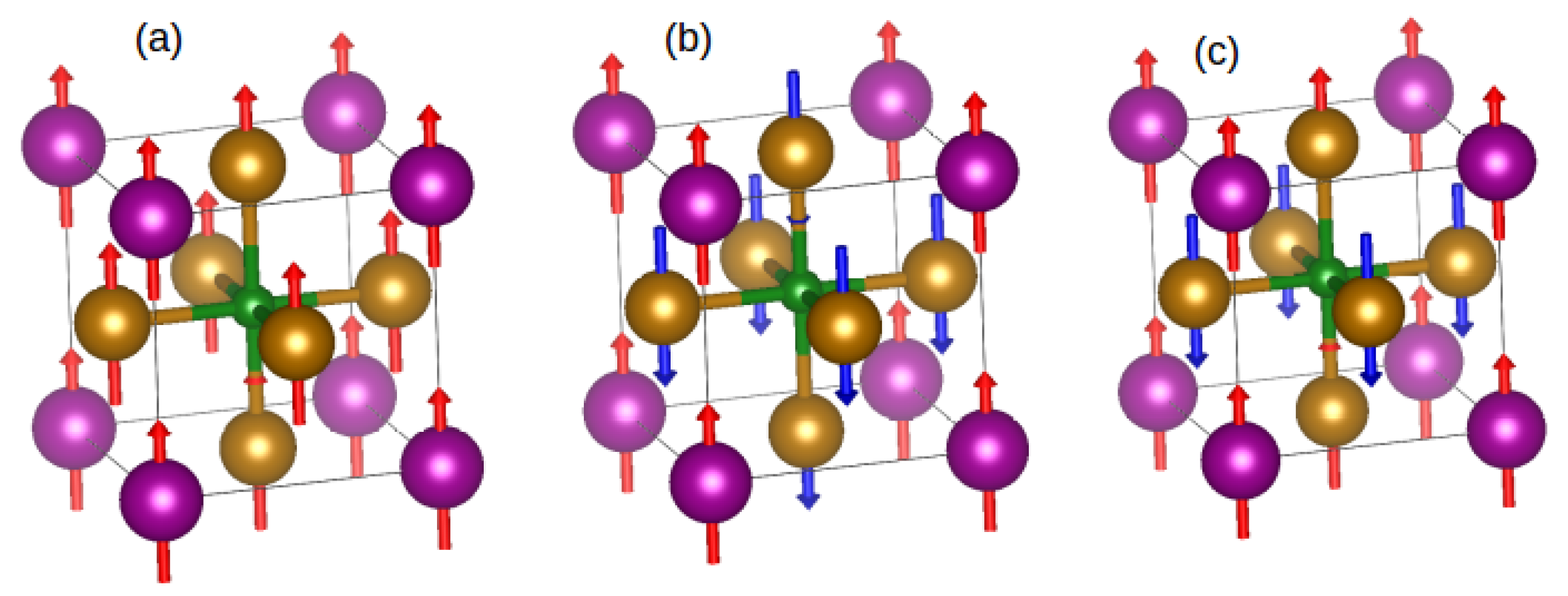
| FM | AF01 | AF02 | |
|---|---|---|---|
| (meV) | 0.0 | 1022.1 | 695.6 |
| 9.80 | 4.33 | −1.65 | |
| 3.00 | −2.12 | −2.60 | |
| 2.00 | 1.99 | −1.91/1.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñoz Medina, G.A.; Mudarra Navarro, A.M.; Deluque Toro, C.E.; Gil Rebaza, A.V. Structural, Thermophysical, and Magnetic Properties of the γ′-Fe4N System: Density Functional Theory and Experimental Study. Processes 2025, 13, 2402. https://doi.org/10.3390/pr13082402
Muñoz Medina GA, Mudarra Navarro AM, Deluque Toro CE, Gil Rebaza AV. Structural, Thermophysical, and Magnetic Properties of the γ′-Fe4N System: Density Functional Theory and Experimental Study. Processes. 2025; 13(8):2402. https://doi.org/10.3390/pr13082402
Chicago/Turabian StyleMuñoz Medina, Guillermo A., Azucena M. Mudarra Navarro, Crispulo E. Deluque Toro, and Arles V. Gil Rebaza. 2025. "Structural, Thermophysical, and Magnetic Properties of the γ′-Fe4N System: Density Functional Theory and Experimental Study" Processes 13, no. 8: 2402. https://doi.org/10.3390/pr13082402
APA StyleMuñoz Medina, G. A., Mudarra Navarro, A. M., Deluque Toro, C. E., & Gil Rebaza, A. V. (2025). Structural, Thermophysical, and Magnetic Properties of the γ′-Fe4N System: Density Functional Theory and Experimental Study. Processes, 13(8), 2402. https://doi.org/10.3390/pr13082402







