Abstract
In the process of CNC machining, reducing energy consumption, production costs, and improving machining quality are critical strategies for enhancing product competitiveness. Based on an analysis of machine tool processing mechanisms, calculation models for energy consumption, manufacturing cost, and quality (represented by surface roughness) in CNC lathes were established. These models were optimized using the Egret Swarm Optimization Algorithm (ESOA), which integrates three core strategies: waiting, random search, and bounding mechanisms. With the objectives of minimizing energy consumption, manufacturing cost, and maximizing quality, cutting parameters (e.g., cutting speed, feed rate, and depth of cut) were selected as optimization variables. A multi-objective ESOA (MOESOA) framework was applied to resolve trade-offs among conflicting objectives, and the effectiveness of the proposed method was validated through a case study. The simulation results show that the optimization of cutting parameters is beneficial to energy conservation during the machining process, although it may increase costs. Additionally, under the three-objective optimization, the improvement of surface roughness is relatively limited. The further two-objective (energy consumption and cost) optimization model demonstrates better convergence while ensuring that the surface roughness meets the basic requirements. This method provides an effective tool for optimizing cutting parameters.
1. Introduction
Globally, energy saving and consumption reduction have become crucial strategies for many countries to face the pressure of the energy crisis and environmental degradation. Minimizing energy consumption remains a significant challenge in the contemporary industrial field [1]. As the cornerstone of industrial manufacturing and the primary energy consumer, machine tools play pivotal roles throughout production processes. Notably, the average energy utilization efficiency of machine tools remains below 30%, with substantial energy wastage exacerbating ecological pollution and excessive carbon emissions [2,3]. Given this context, optimizing cutting parameters in machine tools to achieve energy efficiency, cost reduction, and high-quality output presents extensive research potential. This approach has profound significance for environmental preservation and resource sustainability.
Research on the energy consumption optimization of machine tools can generally be categorized into two categories. The first category primarily centers on enhancing mechanical structures and adopting advanced cutting technologies. Examples include the development of multi-axis linkage machine tools [4] and thermal characteristic optimization studies [5]. The second category, in contrast, focuses on investigating the coupling relationship between processing parameters and energy consumption. The goal is to construct accurate energy consumption models and optimize parameters for energy conservation [6,7]. Among these, the first category emphasizes improvements in hardware technology, often requiring the renewal or replacement of machine tool equipment. This approach not only entails high replacement costs but also limits its widespread adoption due to the significant research and verification thresholds involved. By comparison, improving energy efficiency based on existing equipment represents a more practical alternative. In this context, achieving energy conservation through the optimization of low-cost cutting parameters plays a crucial role in reducing energy consumption and manufacturing costs within the manufacturing industry [8,9].
In the field of cutting parameter optimization, the primary research objectives are to construct a mathematical model of the processing procedure and determine optimal parameters. Existing literature addresses this challenge by constructing mathematical models from two main perspectives. First, energy consumption models are established based on empirical formulas. For instance, Liu Z [10] et al. developed a machine tool energy consumption model by selecting optimal cutting parameters (e.g., cutting speed, feed rate, and cutting depth) under various cutting conditions. Zhou C [11] et al. combined plunge milling to investigate the relationship between 34CrNi3Mo high-strength steel and cutting parameters. Zhao SZ [12] et al. utilized micro-cutting technology to analyze the cutting mechanism and failure criteria of metallographic structures at a microscopic level, optimizing the cutting parameters for 45# steel. These studies rely on processing data to analyze and model the energy consumption mechanisms of CNC machine tools. However, with advancements in numerical control, high-speed cutting, and precision manufacturing technologies, the application scope of these predictive models is limited, making it challenging to meet the technical requirements of energy-efficient and low-cost processing.
To address the deficiencies of the aforementioned research, another approach focuses on constructing mathematical models related to variables and employing high-quality parameter optimization methods. To achieve this, various intelligent optimization algorithms have been widely applied to optimize numerical control cutting parameters and reduce unit production costs. These algorithms include the Genetic Algorithm (GA) [13], Simulated Annealing Algorithm (SA/PA) [14], and Scatter Search Algorithm (SSA) [15], among others. However, these methods prioritize economic benefits while neglecting processing quality, often leading to trade-offs between competing objectives, which limits their effectiveness in practical applications. Product quality, manufacturing costs, and energy consumption are typically conflicting targets. For example, achieving high product quality significantly increases control costs and energy usage. Consequently, single-objective optimization algorithms exhibit certain limitations [16].
To overcome these limitations, multi-objective optimization methods have emerged and developed rapidly. Common multi-objective optimization methods include the Multi-objective genetic algorithm (MOGA) [17,18], black hole-continuous ant colony algorithm [19], whale optimization algorithm [20], non-dominated sorting genetic algorithm II (NSGA-II) [21], among others. Among these, the multi-objective egret swarm optimization algorithm (MOESOA) is a novel swarm intelligence optimization algorithm inspired by the foraging behavior of egret flocks [22]. This algorithm solves optimization problems by simulating the collective intelligent behavior during the foraging process of egret groups and utilizing information exchange and collaboration among individuals. Specifically, MOESOA employs waiting, random walk, and bounding strategies for parameter optimization. It dynamically adjusts search strategies and introduces a leader mechanism to help the group escape local optima quickly. MOESOA is regarded as one of the most effective algorithms for handling multi-objective optimization problems. The optimization of cutting parameters based on energy conservation, low cost, and high quality represents a typical multi-objective optimization problem, necessitating the identification of the Pareto front within the feasible solution set as the optimal solution set. Therefore, in this paper, an energy-saving and low-cost cutting parameter model for machining processes is constructed and solved using MOESOA. Finally, the superiority and effectiveness of the algorithm in solving multi-objective optimization problems were validated through case studies.
2. Multi-Objective Optimization Model Based on Energy Saving, Low-Cost and High Quality
2.1. Variables
Based on the principles of multi-performance balance and practical requirements [23], this paper focuses on achieving the highest quality, the lowest cost, and the minimum energy consumption simultaneously. A multi-objective optimization model for energy-saving, low-cost, and high-quality machining is constructed accordingly. In this model, the three elements of cutting (cutting speed, cutting depth, and feed rate) are the basis for determining the cutting process and cutting objectives. Consequently, within this model, these three crucial cutting parameters are chosen as decision variables.
2.2. Objectives
To establish an energy consumption assessment model for the processing phase, it is first necessary to define the boundaries of the energy consumption assessment [24,25]. From the perspective of energy consumption forms, energy consumption can be categorized into direct energy consumption and indirect energy consumption. Specifically, direct energy consumption encompasses the energy used by machine tools and auxiliary facilities, whereas indirect energy consumption includes the internal energy consumption of cutting tools and cutting fluids.
From the production cycle standpoint, direct energy consumption in processing primarily originates from startup energy consumption, cutting energy consumption, and tool change energy consumption, among others. In terms of load-related relationships, direct energy consumption can further be subdivided into constant energy consumption and variable energy consumption of machine tools. Here, constant energy consumption is independent of the load, while variable energy consumption fluctuates with the load [26,27].
After defining the boundaries of energy consumption assessment, taking the power consumption of the Bridgeport Torque cutting automatic gun bed as an example (as shown in Figure 1), a statistical energy consumption model for the machine tool is established. This model enables more precise representation and evaluation of the energy efficiency of different machine tools during the processing stage, thereby providing data support for energy efficiency optimization and the development of energy-saving strategies.
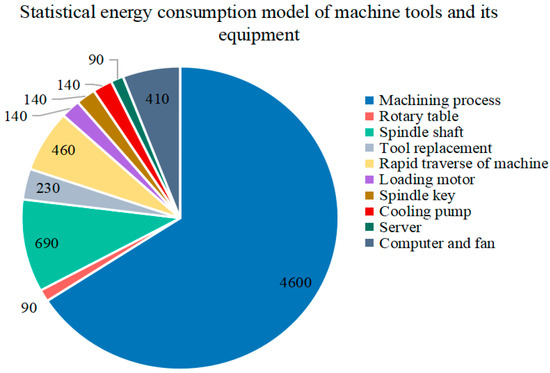
Figure 1.
Statistical energy consumption model for machine tools.
Considering the complexity of the energy consumption assessment process and the significance of data accuracy, this paper focuses on the energy consumption incurred during the machining of a single part by machine tools and develops a comprehensive processing energy consumption evaluation function model. The entire machining process is treated as a multi-cycle system, encompassing the startup phase, cutting cycle, and standby cycle. Among these, the target of the energy consumption assessment is the total energy consumption of the entire machining process. During this process, the primary components of energy consumption include startup energy consumption, cutting energy consumption, tool change energy consumption, the embodied energy of cutting tools, and the embodied energy of cutting fluids. Consequently, the total energy consumption generated during machining can be represented by Equation (1).
In Equation (1), the starting energy consumption refers to the energy consumed by the machine tool during its initial startup phase. Given the complex energy consumption characteristics during this stage, the total energy is generally closely correlated with the spindle speed of the machine tool and remains relatively constant. Therefore, the specific value of starting energy consumption can be determined through experimental measurement. By integrating the research findings of Liu et al. presented in refs. [28,29], Equation (2) can subsequently be derived.
In Equation (2), represents the quadratic function of the starting energy, while n indicates the rotational speed of the main shaft (r/min).
The cutting of energy consumption can be determined by multiplying the power consumed by the machine tool during workpiece processing by the total processing time. The corresponding expression is presented in Equation (3).
In Equation (3), represents the idle power (kJ) of the machine tool; denotes the cutting speed (m/min); indicates the cutting depth (mm); signifies the feed rate (mm/r); represents the correction coefficient for the material’s strength and hardness affecting the main cutting force; denotes the influence coefficient of cutting parameters on the main cutting force; represents the coefficient of additional load loss.
The cutting time in Equation (3) can be determined using Equation (4).
In Equation (4), represents the cut-in length (mm) of the cutting tool; denotes the cutting length (mm) of the cutting tool; indicates the cutting length of the workpiece (mm).
Tool change energy consumption refers to the energy consumed during the process of changing cutting tools. It can be assessed as the product of the machine tool’s idle power and the tool change time, as calculated using Equation (5).
The energy footprint of a cutting tool refers to the energy consumption during its use, which is calculated by multiplying the idle power of the machine tool by the tool change time. Specifically, it can be calculated by Equation (6).
In Equation (6), represents the internal energy (kJ) of each cutting edge; indicates the number of cutting edges used in the processing.
The tool life in Equation (6) can be estimated by the following formula: .
In Equation (6), represents the coefficient of the tool life.
The energy footprint of cutting fluid refers to the calculation based on the specific internal energy of the cutting fluid and the volume used in the manufacturing process, which can be specifically calculated by Equation (7).
In Equation (7), represents the specific internal energy (kJ/kg) of the auxiliary material; denotes the density of the auxiliary material (kg/L); indicates the consumption rate of auxiliary materials (L/s).
Based on the above discussion, a new equation can be derived to represent the energy consumed in the turning operation. For more details, refer to Equation (8).
In Equation (8), represents the diameter of the workpiece (mm).
Cost objective C: The processing cost of each processing procedure can be expressed by Equation (9).
Quality Objective: In the machining operation, the surface roughness of the workpiece is commonly utilized as a key indicator reflecting the quality outcome of the process. Consequently, in this study, surface roughness is adopted as the quality objective. Based on the chamfer radius of different cutting tools, the roughness of the workpiece after turning can be estimated using Equations (10)–(12).
When the chamfer radius is extremely small (approaching zero), the rough surface can be determined using Equation (10).
In Equation (10), represents the angle of the main cutting edge of the cutting tool; represents the angle of the secondary cutting edge of the cutting tool.
If the chamfer radius is relatively large while the feed rate is small, the rough surface can be calculated using Equation (11).
In Equation (11), represents the chamfer radius of the cutting tool.
If the chamfer radius is relatively small while the feed rate is large, the surface roughness can be calculated by Equation (12):
To sum up, the objective of the optimization problem can be expressed as Equation (13).
2.3. Constraints
The machine tool’s performance constrains the cutting parameters during machine tool processing, and all cutting variables must remain within the machine tool’s operational limits. This general relationship can be expressed using Equation (14).
In Equation (14), represents the cutting speed (m/min); denotes the feed rate (mm/r); indicates the cutting depth (mm).
3. Case Study Based on the Multi-Objective Egret Swarm Optimization Algorithm
3.1. The Multi-Objective Egret Swarm Optimization Algorithm
The MOESOA is one of the most widely used algorithms in multi-objective optimization simulation [30,31,32,33]. Compared with other algorithms, it exhibits three significant advantages. First, it integrates two distinct hunting strategies: the waiting strategy and the aggressive strategy, achieving an effective balance between exploration and exploitation. Second, an adaptive weight update mechanism has been incorporated, enabling dynamic adjustment of the search strategy during the optimization process to better adapt to the current search status. Third, the introduction of a leader mechanism enhances global search capabilities, effectively reducing the risk of being trapped in local optima [34,35,36]. Therefore, in this study, the MOESOA algorithm is employed to solve the Pareto optimal solution for the processing parameter optimization problem. The specific steps are as follows.
Step 1: Set the population size and the maximum iterations , where in [20, 200] and in [100, 5000]. The optimization objectives are set to minimize energy consumption , manufacturing cost , and product quality degradation . The objective function is expressed as Equation (15).
Step 2: Defined the structure of each individual in the population. The authors adopted real-number encoding to reduce potential coding errors in the optimization algorithm. Each individual structure includes the following elements: three decision variables (cutting depth, feed rate, and cutting speed), the objective functions (energy consumption , manufacturing cost , and product quality ), their corresponding constraint conditions, and the values of these constraints.
Step 3: Initialized a population of individuals by randomly assigning variable values within their respective ranges. Then, calculate the values of the three-objective functions and the constraints. Perform non-dominated sorting on the individuals to obtain the initial egret population, where the position of each egret represents a candidate solution in the solution space.
Step 4: Updated the iteration count .
Step 5: Checked whether the current iteration count . If true, proceed to Step 6; otherwise, go to Step 16.
Step 6: Implement the waiting strategy. Calculate and update the comprehensive gradient using Equation (15).
In Equation (15), , represents a random number within the range (0, 0.5), which serves to balance the weights of corrections in different directions within the comprehensive gradient.
indicates the direction correction corresponding to the best positions of the egret team.
indicates the direction correction corresponding to the best positions across all teams for the egret team.
Update the weights of the observation method using Equation (16).
represents the exponential moving mean of the gradient.
represents the exponential moving mean of the square of the gradient.
According to Equation (17), compute and return the expected position of egret .
In Equation (17), represents the current position of egret , and represents the upper and lower bound intervals of the solution space.
Step 7: Computed the global optimal solution and historical optimal solution for each individual in the particle swarm, where the number of iterations is denoted as .
Step 8: Utilized the social consciousness model to update both the individual and overall directions of the particle swarm .
Step 9: Developed two update strategies via random search and bounding mechanisms to adjust the positions of particles, thereby forming a new particle swarm . Under the random search strategy, calculate and return the expected position of egret using Equation (18).
In Equation (18), represents the random number used to synthesize the expected position of egret . Under the encirclement strategy, calculate and return the expected position of egret group using Equation (19).
In Equation (19), denotes the gap matrix between the current position and the best position of the egret team; denotes the gap matrix between the current position and the best positions of all egret teams.
Step 10: Evaluated the fitness value of the new particle swarm .
Step 11: Conducted non-dominated rank sorting on the new particle swarm and selected the non-dominated solutions to update the position information and fitness values of the particles, thereby obtaining the frontier set F formed by different non-dominated rank classifications, .
Step 12: Let the population .
Step 13: Checked whether condition is satisfied. If not, proceed to Step 15.
Step 14: Computed the congestion degree for the frontier set , and sort it in descending order based on congestion distance. Select the top elements from to construct the generation population .
Step 15: Recalculated the global and historical optimal solutions for individuals in the particle swarm , let , and then return to Step 6.
Step 16: Derived the Pareto optimal set for energy consumption , manufacturing cost , and product quality under varying iteration counts gen, along with the corresponding parameter set, .
The fundamental procedure of the algorithm is illustrated in Figure 2.
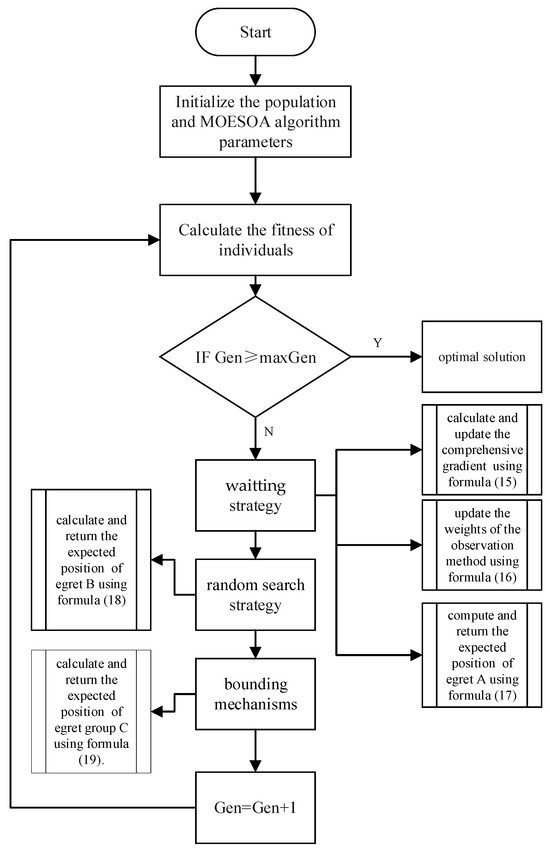
Figure 2.
The fundamental procedure of MOESOA.
3.2. Case Analysis
To investigate the influence of cutting parameters on energy consumption, cost, and cutting quality, this study uses turning operations as an example. It selects a 45# carbon steel cylindrical bar for machining. The cylindrical bar has a length of 200 mm and a diameter of 50 mm, and its raw material exhibits a tensile strength of 670 MPa. Machining is performed on a CNC lathe with two rotational speed settings: high and low levels. This study primarily focuses on rough machining, with the rotational speed range set between 100 and 1000 r/min. The cutting tool utilized in the optimization process is a YT15 75° cylindrical cemented carbide tool, and its detailed specifications are provided in Table 1.

Table 1.
Parameters of cutting tools.
To implement the optimization, several parameters and data must be determined in advance. First, the starting energy consumption, idle power, and additional load loss coefficient of the machine tool need to be obtained. These data were measured using the wideband power analyzer (model 3390) produced by HIOKI Corporation of Japan to determine the startup energy consumption and idle power. Second, referring to the mechanical engineering manual, the correlation coefficients in the optimization model (including and A are identified, and their specific values are presented in Table 2.

Table 2.
The coefficients of the optimized model.
In the table, represents the correction coefficient of the material’s strength and hardness to the main cutting force.
represents the correction coefficient of the cutting-edge angle of the cutting tool to the main cutting force.
represents the correction coefficient of the inclination angle of the cutting tool to the main cutting force.
represents the correction coefficient of the cutting-edge inclination angle of the cutting tool to the main cutting force.
Calculate the loss of cutting fluid. In this processing procedure, a mixture of 5% emulsifier and 95% water is used. Based on literature research, the consumption rate of pure emulsifiers is 0.95 L/min. A cutting blade weighing 10 g has an energy footprint of approximately 4100 kJ. In this study, paraffin is adopted as the basis for estimating the energy footprint of cutting fluid, with its internal energy being 72,885 kJ/kg, according to relevant studies [37].
Determine the production cost and material cost. The production cost is estimated at $0.051 per second, encompassing direct costs such as machine tool depreciation and workers’ wages, as well as indirect costs arising from management. Hard alloy cutting tools are purchased at $8.33 per piece, while pure emulsifiers are priced at $18.75 per liter. Furthermore, when considering the coefficients, it is necessary to clarify the constraint conditions. Specifically, due to the rotational speed limit of the machine tool, the allowable cutting speed range is between 45 and 120 m/min. The maximum feed depth and feed rate in the rough machining stage are set within the ranges of 2.5–7.6 mm and 0.15–0.75 mm/r, respectively [38]. Based on the above data, the following multi-objective optimization models can be established, as shown in Equations (20) and (21).
3.3. Analysis of Simulation Results Based on MOESOA
The MOSEOA algorithm is executed based on the Matlab2023b computing software. Through file exchange, the geometric data of CAD is exported in STEP format, and then a parsing script is written in Matlab2023b for processing. The calculation results are then exported as files and reimported into CAD. It has good compatibility with existing CAD/CAM software through file import and export. The integration with the actual ERP/MES system is also carried out through the import and export of files. Through simulation in MATLAB R2023a, the parameters of the mathematical model focusing on energy saving, low cost, and high quality were determined, thereby obtaining the optimal processing parameters, which were 2.5 mm for feed depth, 0.75 mm/r for feed rate, and 45 m/min for cutting speed, respectively. The corresponding optimal objective function values were 95.33, 3.85, and 9.84. The surface roughness value requirement for the part to be processed in this paper is 12.8 μm. The surface roughness values (9.84, 9.84, 9.51) obtained in the experiment are all less than 12.8 μm, which are within the allowable range. Surface profile is one of the key assessment contents. Usually, it can represent the processing quality of the product. The three-dimensional diagram of the surface roughness requirements is shown in Figure 3.
Figure 3.
The surface roughness requirements of the parts.
To demonstrate the performance of the optimization algorithm, we compared scheme 1 with the other two schemes, and the results are shown in Table 3. Among them, scheme 1 is the optimal result obtained by the optimization model considering three objectives; scheme 2 only considers the optimal solution obtained by the optimization model of cost and quality objectives. The variable selection in scheme 3 is based on the operator’s experience rather than determined by mathematical optimization methods. The optimization models of the three objectives in scheme 1 perform well in terms of energy conservation. Therefore, conducting optimization operations has a positive impact on energy conservation.

Table 3.
A Comparative study of experimental schemes.
Regarding the analysis of surface roughness, the Pareto frontiers under three optimization objectives are presented in Figure 4a, which indicates the data distribution among the three objectives. Through the methods introduced by Deb and Datta [39], combined with Figure 4b–d, there is a good equilibrium relationship between the energy consumption target and the cost target. Similarly, a good balance is also shown between the cost target and the quality target. However, there is a lack of obvious balance between the energy consumption target and the quality target. Furthermore, it can be seen from Table 3 that the parameter selection has little influence on the surface roughness, which might be because the parameters have been limited within a reasonable range.
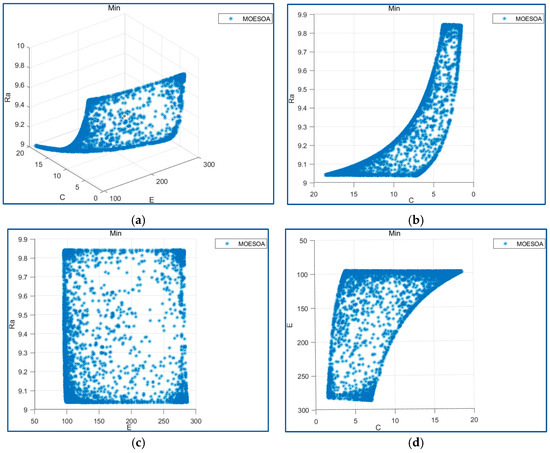
Figure 4.
The non-dominated frontier obtained by the MOESOA algorithm for processing parameter optimization. (a) Three views of MOESOA; (b) projection of cost and surface roughness; (c) projection of energy consumption and surface roughness; (d) projection of cost and surface roughness.
Therefore, the multi-objective optimization model considering energy consumption and processing costs may exhibit superior performance. After modifying the optimization model, the MOESOA is re-executed in the MATLAB R2023a environment, yielding the non-dominated frontier that accounts for both energy consumption and processing cost objectives, as illustrated in Figure 5.
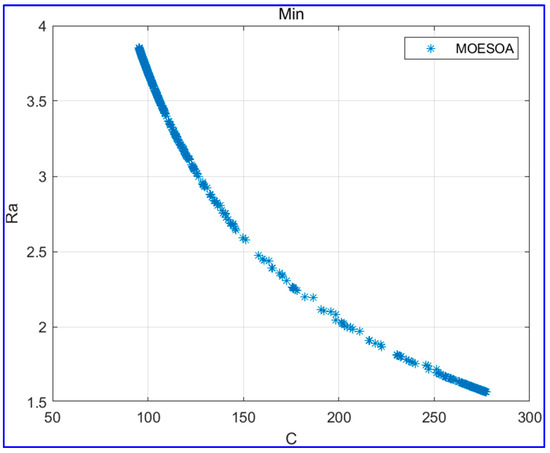
Figure 5.
The non-dominant frontier of energy consumption and manufacturing cost.
As shown in Figure 5, the optimization model with two objectives performs well in terms of convergence. Therefore, if the optimization of two objectives can achieve the same result as that of the optimization of three objectives, the former should be given priority. According to the optimal solution, the extreme point solutions obtained by the two-objective optimizations are (2.5, 0.75, 45, 95.33, and 3.85), and this result is consistent with the optimal solutions of the three-objective optimizations. Therefore, the optimization model considering energy consumption and cost can effectively replace the original three-objective optimization models and has the same optimal results and better convergence performance.
4. Conclusions
The three variables of cutting depth, feed rate, and cutting speed are taken as key variables in this paper. A model for energy conservation, low cost, and high quality was established to minimize energy consumption and cost while ensuring processing quality. The model is solved using the MOESOA algorithm, which incorporates three primary modules: the waiting strategy, the random walk strategy, and the bounding strategy. A complete algorithmic workflow is established accordingly. Simulation results based on the Matlab R2023a platform demonstrate that the algorithm achieves significant improvements in reducing energy consumption and cost.
Nevertheless, this study has certain limitations. While the algorithm performs well in optimizing energy consumption and cost, it is found that its effectiveness in improving surface roughness (an important indicator of processing quality) is relatively limited. It indicates that during the strongly coupled multi-objective optimization process aiming to achieve energy efficiency, low cost, and high quality simultaneously, the two-objective optimization exhibits a superior algorithm that may struggle to reconcile conflicts among these objectives under specific operating conditions fully. To address this issue, a dual-objective optimization model focusing solely on energy consumption and cost is further developed. Although this model exhibits improved convergence performance. Based on this simulation conclusion, this paper recommends adopting this model to optimize cutting parameters. While this study has made notable progress in developing an energy consumption model for the turning process, further in-depth research enhancement is required for achieved by suspending active optimization of processing quality, representing a strategic adjustment in objective prioritization. Therefore, in applications where high processing quality is critical, the suitability of this approach should be carefully evaluated. While progress has been made in modeling energy consumption in turning processes, the generalizability of the proposed model requires further validation across a broader range of machining scenarios.
Although this paper provides a reliable case study for MOESOA-based cutting parameter optimization, its potential for widespread industrial application needs to be explored in more diverse contexts. To enhance the practical relevance and general applicability of the research, future work will focus on the adaptability and scalability of both the model and algorithm. Specifically, the following directions are proposed: (1) extend the model to other machining processes in the future, such as milling and drilling, and vali-date its effectiveness in processing various engineering materials, including cast iron, composite materials, and high-temperature alloys; (2) investigate how the model adapts to the dynamic characteristics of different types and power levels of CNC machines (e.g., turning centers and machining centers), as well as the influence of varying tool geometries (e.g., rake angle and tool tip radius) on optimization outcomes; (3) examine the robustness of the model in geographically diverse production environments characterized by significant differences in technical infrastructure (e.g., legacy vs. advanced equipment) and economic constraints (e.g., regions with high vs. low electricity prices or labor costs), and explore corresponding adjustments to optimization strategies.
Based on the simulation results and the outlined future research directions, this paper recommends the proposed optimization model, particularly the dual-objective version, as an effective tool for optimizing cutting parameters. It also emphasizes the importance of selecting appropriate optimization objectives and calibrating the model according to the specific quality requirements of each application scenario. This study contributes phased achievements in energy consumption modeling and multi-objective optimization for turning processes, laying a solid foundation for future in-depth investigations in complex and diverse real-world industrial settings.
Author Contributions
Conceptualization, Y.Z. and Y.X.; methodology, Y.X.; software, Y.Z.; validation, Y.Z.; formal analysis, Y.Z.; investigation, X.Z.; data curation, Y.Z.; writing—original draft preparation, Y.Z.; writing—review and editing, Y.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Hunan Provincial Social Science Achievements Evaluation Committee General Project (Project number: XSP25YBZ152); The Education Department of Hunan Province (Project number: 23A0541); The Science and Technology Research Project of Jiangxi Provincial Department of Education in 2024 (Project number: 2409108). The funding is provided by the corresponding author.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zheng, J.; Jia, R.; Hu, X.; Qi, T.; Pan, Q.; Zhu, J.; Qiu, X.; Xia, Z.; Xv, B.; Deng, C. Regulating cutting fluid parameters for optimal energy and economic performance: Methods for efficient and Low-Energy electrical machining. Energy Convers. Manag. 2024, 314, 118707. [Google Scholar] [CrossRef]
- Nasseriyan, P.; Jafari, S.; Khajehpour, H.; Edalati, S. Toward a green steel production powered by a hybrid renewable energy system: Techno-economic and environmental assessment. Energy Convers. Manag. 2025, 332, 119716. [Google Scholar] [CrossRef]
- Li, T.; Kong, L.L.; Zhang, H.-C.; Iqbal, A. Recent research and development of typical cutting machine tool’s energy consumption model. J. Mech. Eng. 2014, 50, 102–111. [Google Scholar] [CrossRef]
- Wang, W.; Sun, J.; Yan, S.; Yuan, Y.; Xiao, T.; Chen, B.; Du, T.; Na, H. Multi-objective optimization analysis of on-demand design in multi-source heating system for low carbon development. Energy 2025, 324, 135917. [Google Scholar] [CrossRef]
- Sun, S.; Gao, Z.; Qiao, Y.; Wang, J. Research on thermal characteristic modeling and cooling system parameter optimization of high-speed motorized spindle. Manuf. Technol. Mach. Tool 2023, 10, 90–97. [Google Scholar] [CrossRef]
- Li, G.; Bai, X.; Wang, L.; Li, C.; Li, Y. Key technologies and development trends of multi-axis tool grinding software. China Mech. Eng. 2022, 33, 943–951. [Google Scholar]
- Lv, Q.; Wang, L.; Li, Z.; Song, W.; Bu, F.; Wang, L. Robust optimization for integrated production and energy scheduling in low-carbon factories with captive power plants under decision-dependent uncertainty. Appl. Energy 2025, 379, 124827. [Google Scholar] [CrossRef]
- Xing, J.L. Application of digital twin in mechanical processing technology and optimization of cutting parameters. Intern. Combust. Engine Parts 2024, 10, 107–109. [Google Scholar] [CrossRef]
- Yang, W.Y.; Li, B.T.; Chen, J.X. Consideration of tool material selection in the fuzzy optimization of CNC machining process parameters. Mach. China 2023, 28, 34–37. [Google Scholar]
- Liu, Z. Optimization analysis of process parameters for NC turning and milling. Mod. Manuf. Technol. Equip. 2022, 58, 142–144. [Google Scholar]
- Zhou, C.; Jiang, Z.H.; Zhang, Y.; Shao, Z.W.; Wang, D.Y. Influence of cutting parameters on cutting force of 34CrNi3Mo high strength steel processed by plunge milling. Tool Eng. 2022, 56, 111–114. [Google Scholar]
- Zhao, S.Z. Simulation Analysis of Steel Micro-Cutting Process and Optimization of Cutting Parameters from Macro and Micro Angles. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2022. Available online: https://kns.cnki.net/kcms2/article/abstract?v=Qc2UN8NgW0vHOK4GSuJhnno_9X1Y6iyL1EfEGY2pnTILNZKphehcdcOXd8l7qp9hAMDbLb6xKTtkQsAU0AkEqMRNBZrzZ00LF5Rd-RQBC7XhaTuR7iVhKW8BdV_0mDZvDse2mKe5KYxqzWZIN2j-NUZsvCY_r28NgLwxfXqUL50=&uniplatform=NZKPT (accessed on 1 March 2025).
- Wang, L.P.; Kong, X.Y.; Yu, G. Motor servo control parameter tuning for parallel and hybrid machine tools based on a genetic algorithm. J. Tsinghua Univ. Sci. Technol. 2021, 61, 1106–1114. [Google Scholar]
- Sel, A.; Gurkan, M.E.; Hamzaday, A. Energy-aware production lot-sizing and parallel machine scheduling with the product-specific machining tools and power requirements. Comput. Ind. Eng. 2024, 196, 110503. [Google Scholar] [CrossRef]
- Chen, M.C. Optimization machining economics models of turning operations using the scatter search approach. Int. J. Prod. Res. 2004, 42, 2611–2625. [Google Scholar] [CrossRef]
- Gontarz, S.; Patyk, R.; Bohdal, L.; Jackiewicz, D. Multiparameter optimization of mechanical cutting process of grain-oriented silicon steel. Acta Phys. Pol. A 2020, 137, 930–932. [Google Scholar] [CrossRef]
- Zhao, H.; Cao, Y.; Huang, L.; Zeng, M.; Meng, Z.; Lei, Y. Multi-objective optimization of cutting parameters of ZL205A aluminium alloy based on genetic algorithm. Ordnance Mater. Sci. Eng. 2023, 46, 58–65. [Google Scholar]
- Sarwade, J.M.; Bankar, S.; Janrao, S.; Sakure, K.; Patil, R.; Bokefode, S.; Kulal, N. A novel approach for iris recognition system using genetic algorithm. J. Artif. Intell. Technol. 2024, 4, 9–17. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, L.; Zhang, C.; Li, J.; He, K. Optimization of cutting parameters of CNC lathe using black hole-continuous ant colony algorithm. Mech. Sci. Technol. Aerosp. Eng. 2023, 42, 1705–1711. [Google Scholar]
- Yang, A.; Fang, T.; Serrano, E.A.; Liu, B.; Liu, F.; Chen, Z. Charging Pile Fault Prediction Model Based on GRU Network and WOA. J. Artif. Intell. Technol. 2025, 5, 57–65. [Google Scholar] [CrossRef]
- Xu, J.Y.; Zhong, G.Y.; Yang, S.F. Improved NSGA-II algorithm and its application in optimization of machining parameters. Comput. Eng. Appl. 2017, 53, 227–234. [Google Scholar]
- Chen, Z.; Francis, A.; Li, S.; Liao, B.; Xiao, D.; Ha, T.T.; Li, J.; Ding, L.; Cao, X. Egret swarm optimization algorithm: An evolutionary computation approach for model free optimization. Biomimetics 2022, 7, 144. [Google Scholar] [CrossRef] [PubMed]
- Kordonowy, D.N. A Power Assessment of Machining Tools; Massachusetts Institute of Technology: Cambridge, MA, USA, 2003. [Google Scholar]
- Yin, R.X.; Ke, J. Optimization of milling cutting parameters under carbon efficiency target. Mach. Des. Manuf. 2022, 1888, 012008. [Google Scholar] [CrossRef]
- Xu, X.; Li, F.; Kong, W.; Yu, W.; Zhou, J.; Zhou, L. Energy consumptions modeling and simulation of machine tools based on vericut. Chin. Mech. Eng. Soc. J. 2018, 29, 2533–2538. [Google Scholar]
- Zhang, H.; Li, S.; Yan, W.; Jiang, Z.; Zhu, S.; Ma, F. A data and model hybrid driven method for machining energy consumption prediction of boxy parts. Chin. Mech. Eng. Soc. J. 2023, 59, 97–108. [Google Scholar] [CrossRef]
- Han, J.; Xiong, F.S.; Yao, S.; Xu, R. Study on the energy consumption evaluation of nc machining tool paths exergy loss method. Mach. Des. Manuf. 2024, 118–124. [Google Scholar]
- Liu, F.; Liu, S. Multi-period energy model of electro-mechanical main driving system during the service process of machine tools. Chin. Mech. Eng. Soc. J. 2012, 48, 9. [Google Scholar] [CrossRef]
- Li, C.B.; Cao, H.J.; Liu, F. Key Technologies and Applications of Green Manufacturing in Machine Tools; China Mechine Press: Beijing, China, 2022. [Google Scholar]
- Wu, D.; Sotnikov, D.; Haajari, M.; Salmi, T. Minimizing conductor consumption in high-field hts solenoid design using adaptive ANN-based optimization algorithm. IEEE Trans. Appl. Supercond. 2025, 35, 4603505. [Google Scholar] [CrossRef]
- Hamdipour, A.; Basiri, A.; Zaare, M.; Mirjalili, S. Artificial rabbit’s optimization algorithm with automatically DBSCAN clustering algorithm to similarity agent update for features selection problems. J. Supercomput. 2024, 81, 150. [Google Scholar] [CrossRef]
- Buchibabu, P.; Somlal, J. Sustainable energy management in microgrids: A multi-objective approach for stochastic load and intermittent renewable energy resources. Electr. Eng. 2025, 107, 285–299. [Google Scholar] [CrossRef]
- Kulkarni, P.P.; Ghawghawe, N.D. Hybrid DA-PSO approach for optimal location and parameter settings for TCSC controller in power system. IET Gener. Transm. Distrib. 2020, 14, 1222–1232. [Google Scholar] [CrossRef]
- Wei, P.; Shang, M.; Zhou, J.; Shi, X. Efficient adaptive learning rate for convolutional neural network based on quadratic interpolation egret swarm optimization algorithm. Heliyon 2024, 10, e37814. [Google Scholar] [CrossRef] [PubMed]
- Simon, J.; Kapileswar, N.; Padmavathi, B.; Devi, K.D.; Kumar, P.P. Optimization of node deployment in underwater internet of things using novel adaptive long short-term memory-based egret swarm optimization algorithm. Int. J. Commun. Syst. 2024, 37, 22. [Google Scholar] [CrossRef]
- Ansho, P.M.; Nisha, M.G. Egret swarm optimized distributed power flow controller for power quality enhancement in grid connected hybrid system. J. Electr. Eng. Technol. 2024, 19, 2047–2057. [Google Scholar]
- Yuan, B.R.; Nie, Z.R.; Di, X.H.; Zuo, T.Y. Life cycle inventories of fossil fuels in China (II): Final life cycle inventories. Modern Chem. Ind. 2006, 26, 59–61. [Google Scholar]
- Kalpakjian, S.; Schmid, S.R. Manufacturing Engineering and Technology: Machining; Tsinghua University Press: Beijing, China, 2006. [Google Scholar]
- Deb, K.; Datta, R. Hybrid evolutionary multi-objective optimization and analysis of machining operations. Eng. Optim. 2012, 44, 685–706. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).