Bearing Fault Diagnosis Based on Multiscale Lightweight Convolutional Neural Network
Abstract
1. Introduction
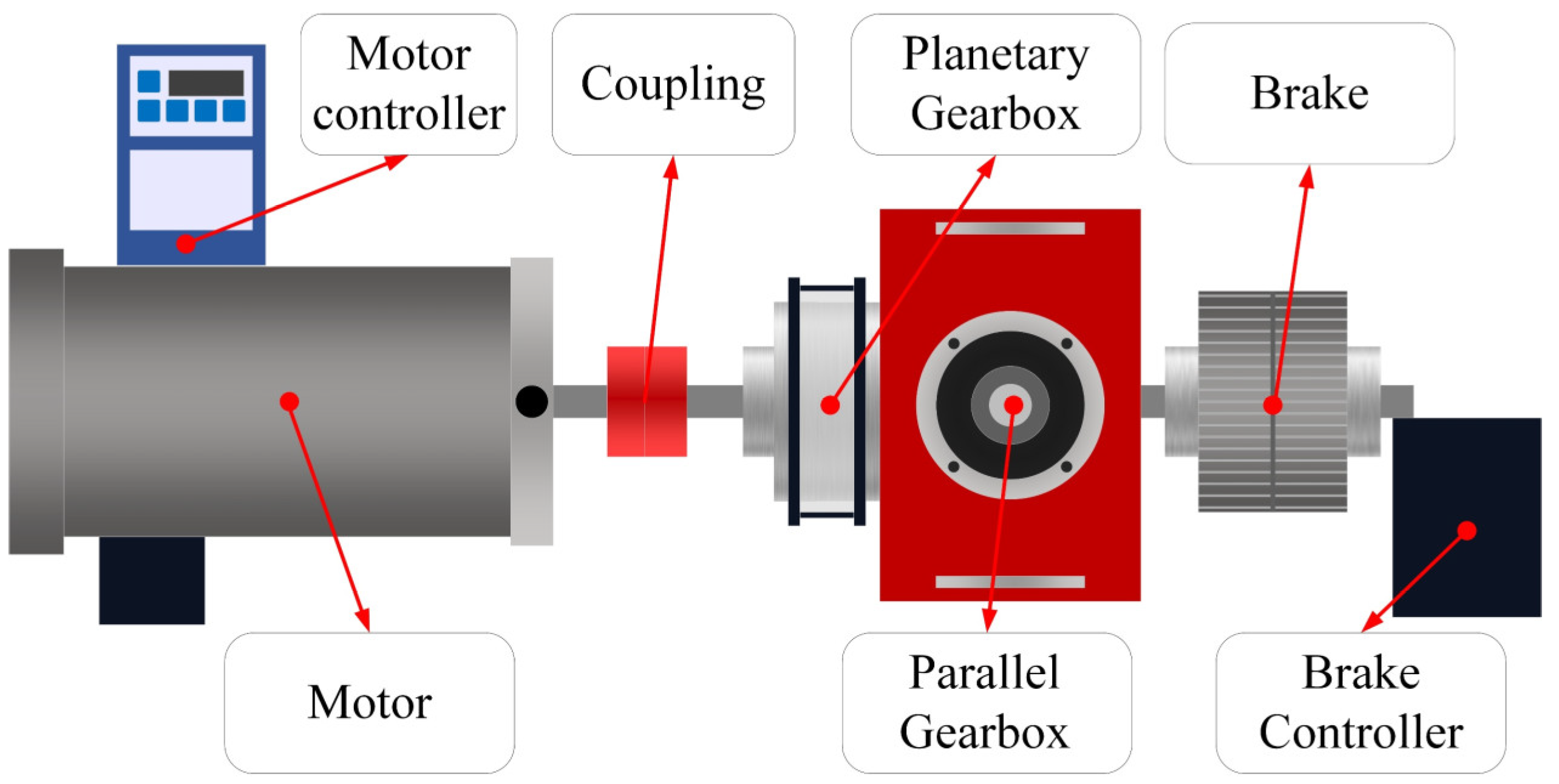
2. Experimental Setup
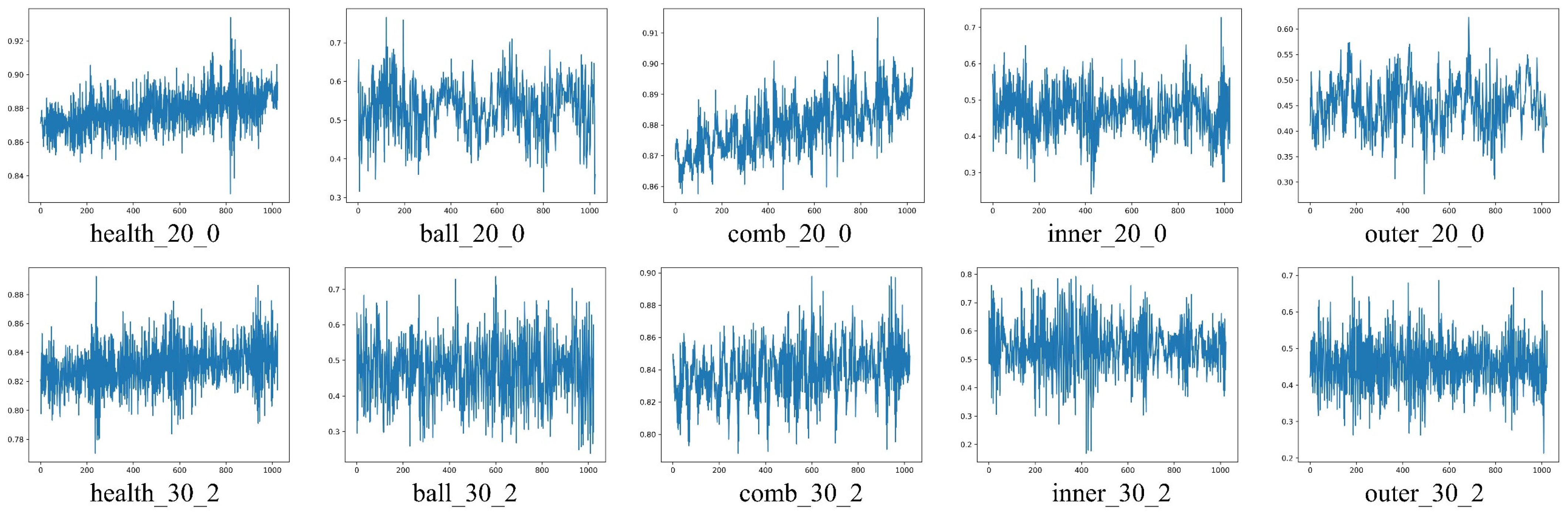
2.1. Dataset Information
2.2. Methods
2.2.1. Design of MGE-ResNet
2.2.2. Gramian Angular Field (GAF) Encoding
2.2.3. Ghost Module
2.2.4. Efficient Channel Attention (ECA) Module
2.2.5. GE (Ghost and ECA) Block
2.2.6. Multiscale Feature Fusion
3. Results
3.1. Validation of Datasets
3.2. Contrast Experiment
- (1)
- Accuracy
- (2)
- Recall and Precision
- (3)
- F1 Score
- (4)
- GFLOPs (Giga Floating-Point Operations)
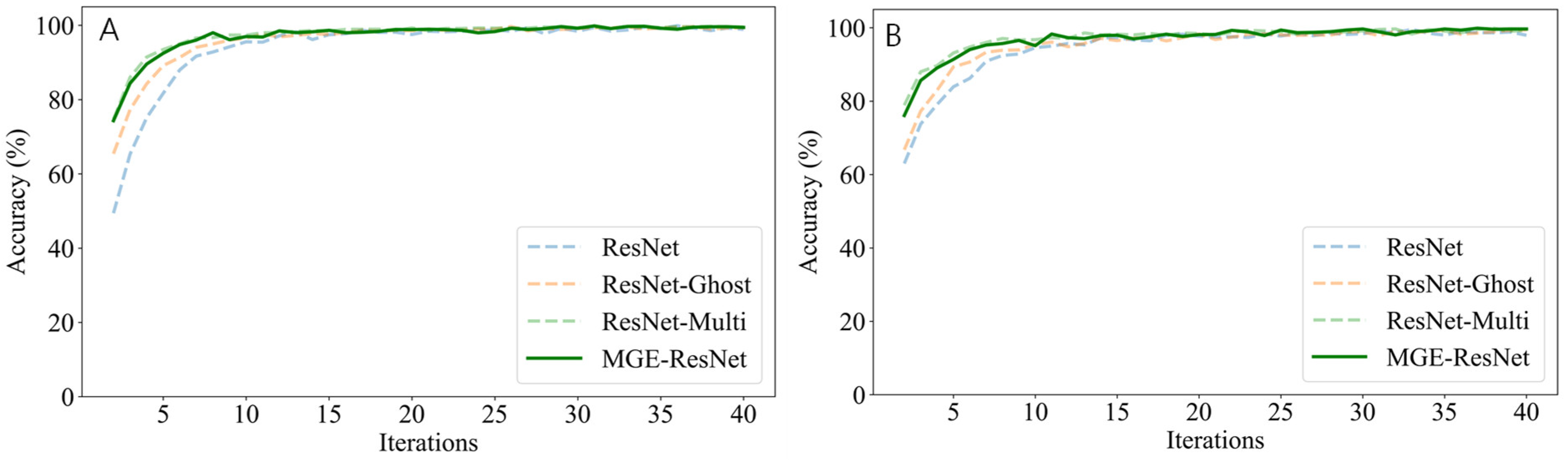
3.3. Ablation Experiment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bai, Y.; Cheng, W.; Wen, W.; Liu, Y. Application of time-frequency analysis in rotating machinery fault diagnosis. Shock Vib. 2023, 2023, 9878228. [Google Scholar] [CrossRef]
- Kankar, P.K.; Sharma, S.C.; Harsha, S.P. Fault diagnosis of ball bearings using machine learning methods. Expert Syst. Appl. 2011, 38, 1876–1886. [Google Scholar] [CrossRef]
- Ahmad, H.; Cheng, W.; Xing, J.; Wang, W.; Du, S.; Li, L.; Zhang, R.; Chen, X.; Lu, J. Deep learning-based fault diagnosis of planetary gearbox: A systematic review. J. Manuf. Syst. 2024, 77, 730–745. [Google Scholar] [CrossRef]
- He, M.; He, H. Deep learning based approach for bearing fault diagnosis. IEEE Trans. Ind. Appl. 2017, 53, 3057–3065. [Google Scholar] [CrossRef]
- Cai, Y.-P.; Li, A.-H.; Shi, L.-S.; Bai, X.-F.; Shen, J.-W. Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum Kurtosis. J. Vib. Shock. 2011, 30, 167–172. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Hu, A.-J.; Ma, W.-L.; Tang, G.-J. Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and Kurtosis criterion. Proc. Chin. Soc. Electr. Eng. 2012, 32, 106–111. [Google Scholar]
- Zhao, H.; Guo, S.; Gao, D. Singular value decomposition and variational modal decomposition based Fault feature extraction of bearing fault. J. Vib. Shock 2016, 35, 183–188. [Google Scholar]
- Tang, Z.; Wang, M.; Ouyang, T.; Che, F. A wind turbine bearing fault diagnosis method based on fused depth features in time–frequency domain. Energy Rep. 2022, 8, 12727–12739. [Google Scholar] [CrossRef]
- Tao, H.; Qiu, J.; Chen, Y.; Stojanovic, V.; Cheng, L. Unsupervised cross-domain rolling bearing fault diagnosis based on time-frequency information fusion. J. Frankl. Inst. 2023, 360, 1454–1477. [Google Scholar] [CrossRef]
- Xie, F.; Li, G.; Song, C.; Song, M. The early diagnosis of rolling bearings’ faults using fractional Fourier transform information fusion and a lightweight neural network. Fractal Fract. 2023, 7, 875. [Google Scholar] [CrossRef]
- Zou, F.; Zhang, H.; Sang, S.; Li, X.; He, W.; Liu, X. Bearing fault diagnosis based on combined multi-scale weighted entropy morphological filtering and bi-LSTM. Appl. Intell. 2021, 51, 6647–6664. [Google Scholar] [CrossRef]
- Lei, M.; Meng, G.; Dong, G. Fault detection for vibration signals on rolling bearings based on the symplectic entropy method. Entropy 2017, 19, 607. [Google Scholar] [CrossRef]
- Binti Shahrulhisham, N.N.H.; Chong, K.H.; Yaw, C.T.; Koh, S.P. Application of machine learning technique using support vector machine in wind turbine fault diagnosis. J. Phys. Conf. Ser. 2022, 2319, 012017. [Google Scholar] [CrossRef]
- An, X.L.; Jiang, D.X.; Li, S.H.; Chen, J. Fault diagnosis of direct-drive wind turbine based on support vector machine. J. Phys. Conf. Ser. 2011, 305, 012030. [Google Scholar] [CrossRef]
- Huang, Y. Fault diagnosis of spindle bearing in wind turbine based SVM. Instrumentation 2016, 23, 88–92. [Google Scholar]
- Xu, Y.-G.; Meng, Z.-P.; Lu, M. Fault diagnosis method of rolling bearing based on dual-tree complex wavelet packet transform and SVM. J. Aerosp. Power 2014, 29, 67–73. [Google Scholar]
- Xin, W.; Yan, W.-Y. Fault diagnosis of roller bearings based on variational mode decomposition and SVM. J. Vib. Shock 2017, 36, 252–256. [Google Scholar]
- Lei, N.; Huang, F.; Li, C. Rolling bearing fault diagnosis based on variational mode decomposition and weighted multidimensional feature entropy fusion. J. Vibroeng. 2024, 26, 590–614. [Google Scholar] [CrossRef]
- Li, L.; Meng, W.; Liu, X.; Fei, J. Research on rolling bearing fault diagnosis based on variational modal decomposition parameter optimization and an improved support vector machine. Electronics 2023, 12, 1290. [Google Scholar] [CrossRef]
- Gao, L.X.; Ren, Z.Q.; Zhang, J.Y.; Xu, Y.G.; Wang, Y. Rolling bearing fault diagnosis methods based on Fisher ratio and SVM. J. Beijing Univ. Technol. 2011, 37, 13–18. [Google Scholar]
- Cheng, J.S.; Yu, D.J.; Yang, Y. Fault diagnosis of roller bearings based on EMD and SVM. J. Aerosp. Power 2006, 21, 575–580. [Google Scholar]
- Guan, X.; Chen, G. Sharing pattern feature selection using multiple improved genetic algorithms and its application in bearing fault diagnosis. J. Mech. Sci. Technol. 2019, 33, 129–138. [Google Scholar] [CrossRef]
- Wu, G.; Ji, X.; Yang, G.; Jia, Y.; Cao, C. Signal-to-image: Rolling bearing fault diagnosis using ResNet family deep-learning models. Processes 2023, 11, 1527. [Google Scholar] [CrossRef]
- Sohaib, M.; Kim, C.-H.; Kim, J.-M. A hybrid feature model and deep-learning-based bearing fault diagnosis. Sensors 2017, 17, 2876. [Google Scholar] [CrossRef]
- Plakias, S.; Boutalis, Y.S. Fault detection and identification of rolling element bearings with attentive dense CNN. Neurocomputing 2020, 405, 208–217. [Google Scholar] [CrossRef]
- Liu, X.; Sun, W.; Li, H.; Hussain, Z.; Liu, A. The method of rolling bearing fault diagnosis based on multi-domain supervised learning of convolution neural network. Energies 2022, 15, 4614. [Google Scholar] [CrossRef]
- Qi, L.; Zhang, Q.; Xie, Y.; Zhang, J.; Ke, J. Research on wind turbine fault detection based on CNN-LSTM. Energies 2024, 17, 4497. [Google Scholar] [CrossRef]
- Velandia-Cardenas, C.; Vidal, Y.; Pozo, F. Wind turbine gearbox early fault detection using Mel-Frequency Cepstral Coefficients of vibration data. Struct. Control Health Monit. 2024, 2024, 7733730. [Google Scholar] [CrossRef]
- Wang, C.; Li, D. Fault early warning of fan gearbox bearing based on LSTM network. Electr. Power Sci. Eng. 2020, 36, 40–45. [Google Scholar]
- Khorram, A.; Khalooei, M.; Rezghi, M. End-to-end CNN + LSTM deep learning approach for bearing fault diagnosis. Appl. Intell. 2021, 51, 736–751. [Google Scholar] [CrossRef]
- Han, K.; Wang, Y.; Tian, Q.; Guo, J.; Xu, C.; Xu, C. Ghostnet: More features from cheap operations. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1580–1589. [Google Scholar]
- Wang, Q.; Wu, B.; Zhu, P.; Li, P.; Zuo, W.; Hu, Q. ECA-Net: Efficient channel attention for deep convolutional neural networks. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11534–11542. [Google Scholar]
- Li, C.; Mo, M.; Yan, R. Fault diagnosis of rolling bearing based on WHVG and GCN. IEEE Trans. Instrum. Meas. 2021, 70, 3519811. [Google Scholar] [CrossRef]
- Juhlin, M.; Sward, J.; Pesavento, M.; Jakobsson, A. Estimating faults modes in ball bearing machinery using a sparse reconstruction framework. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018; pp. 2330–2334. [Google Scholar]
- Pang, B.; He, Y.; Tang, G.-J.; Zhou, C.; Tian, T. Rolling bearing fault diagnosis based on optimal notch filter and enhanced singular value decomposition. Entropy 2018, 20, 482. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Li, C.; Peng, G.; Chen, Y.; Zhang, Z. A deep convolutional neural network with new training methods for bearing fault diagnosis under noisy environment and different working load. Mech. Syst. Signal Process. 2018, 100, 439–453. [Google Scholar] [CrossRef]
- Jin, Z.; Chen, D.; He, D.; Sun, Y.; Yin, X. Bearing fault diagnosis based on VMD and improved CNN. J. Fail. Anal. Prev. 2023, 23, 165–175. [Google Scholar] [CrossRef]
- Huang, J. Deep-learning-based rolling element bearing fault diagnosis considering noise utilizing enhanced VGG-16. In Proceedings of the 2024 IEEE 6th International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 26–28 July 2024; pp. 1547–1552. [Google Scholar]
- Mohiuddin, M.; Islam, M.S.; Islam, S.; Miah, M.S.; Niu, M.-B. Intelligent fault diagnosis of rolling element bearings based on modified AlexNet. Sensors 2023, 23, 7764. [Google Scholar] [CrossRef]











| Methodology | Representative Works | Advantages | Disadvantages |
|---|---|---|---|
| Traditional signal processing methods | Time-domain features, frequency-domain features, time–frequency-domain features, and signal distribution features [5,6,7,8]. Two FFT (fast Fourier transforms) deep frequency domain analyses [9]. The recursive feature elimination combined with the chi-square test [10]. Mean square value indicator [11]. Multiscale weighted entropy morphological filtering [12]. Nonlinear symplectic entropy measure analysis [13]. | Strong multidimensional feature extraction capability and wide adaptability. Effectively deal with non-smooth signals. | Relying on expert experience to design features. High computational complexity. Generalization ability for small samples and complex failure modes is limited. |
| Machine learning methods | SVM combined with residual analysis to predict fan bearing status [14,15,16]. Double-tree wavelet packet transform, SVM [17]. Variational modal decomposition, SVM [18,19,20]. Wavelet packet decomposition, SVM [21]. EMD, Autoregressive model, SVM [22,23]. | Reduction of dependence on expert knowledge. A higher degree of automation. High diagnosis accuracy is maintained with small samples. | Features need to be artificially designed. Weak model interpretability. Limited ability to process high-dimensional data. |
| Deep learning methods | Combining hybrid feature pooling with DNN based on SAE [25]. Attention-intensive convolutional neural network [26,27]. LSTM temperature prediction model [28,29,30]. Combining end-to-end convolutional neural network and LSTM [31]. Attention mechanisms, lightweight methods [32,33]. | End-to-end automatic feature extraction. Strong nonlinear modeling capability. Adaptation to complex working conditions. High diagnostic efficiency. | Reliance on massively labeled data. High consumption of computational resources. Poor model interpretability. |
| Method | Experiment 1 | Experiment 2 | ||
|---|---|---|---|---|
| Average Accuracy (%) | GFLOPs | Average Accuracy (%) | GFLOPs | |
| Method_1 | 81.46 ± 4.28 | 0.48 | 86.88 ± 2.15 | 0.48 |
| Method_2 | 88.50 ± 8.14 | 0.69 | 71.54 ± 7.68 | 0.69 |
| Method_3 | 96.81 ± 3.05 | 30.83 | 93.67 ± 5.46 | 30.83 |
| Method_4 | 97.94 ± 1.91 | 1.88 | 97.58 ± 2.10 | 1.88 |
| Method_5 | 95.65 ± 4.22 | 4.21 | 93.31 ± 6.85 | 4.21 |
| MGE-ResNet | 99.44 ± 0.42 | 1.99 | 99.54 ± 0.46 | 1.99 |
| Method | Experiment 1 | Experiment 2 | ||
|---|---|---|---|---|
| Average Accuracy (%) | GFLOPs | Average Accuracy (%) | GFLOPs | |
| ResNet | 98.64 ± 1.42 | 3.60 | 97.95 ± 1.85 | 3.60 |
| ResNet-Ghost | 98.62 ± 2.16 | 1.81 | 98.42 ± 0.92 | 1.81 |
| ResNet-Multi-Ghost | 98.91 ± 1.91 | 1.99 | 99.25 ± 0.66 | 1.99 |
| MGE-ResNet | 99.44 ± 0.42 | 1.99 | 99.54 ± 0.46 | 1.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Zhang, Z.; Zhong, Z.; Hou, J.; Chen, Z.; Cai, Z.; Kim, J.-H. Bearing Fault Diagnosis Based on Multiscale Lightweight Convolutional Neural Network. Processes 2025, 13, 1239. https://doi.org/10.3390/pr13041239
Cui Y, Zhang Z, Zhong Z, Hou J, Chen Z, Cai Z, Kim J-H. Bearing Fault Diagnosis Based on Multiscale Lightweight Convolutional Neural Network. Processes. 2025; 13(4):1239. https://doi.org/10.3390/pr13041239
Chicago/Turabian StyleCui, Yunhao, Zhihui Zhang, Zhidan Zhong, Jian Hou, Zhiyong Chen, Zhicheng Cai, and Jun-Hyun Kim. 2025. "Bearing Fault Diagnosis Based on Multiscale Lightweight Convolutional Neural Network" Processes 13, no. 4: 1239. https://doi.org/10.3390/pr13041239
APA StyleCui, Y., Zhang, Z., Zhong, Z., Hou, J., Chen, Z., Cai, Z., & Kim, J.-H. (2025). Bearing Fault Diagnosis Based on Multiscale Lightweight Convolutional Neural Network. Processes, 13(4), 1239. https://doi.org/10.3390/pr13041239








