Study on Critical Gas Flow Velocity to Prevent Sulfur Particle Deposition in Vertical Wells Considering Adhesive Forces
Abstract
1. Introduction
2. Critical Gas Flow Velocity Model
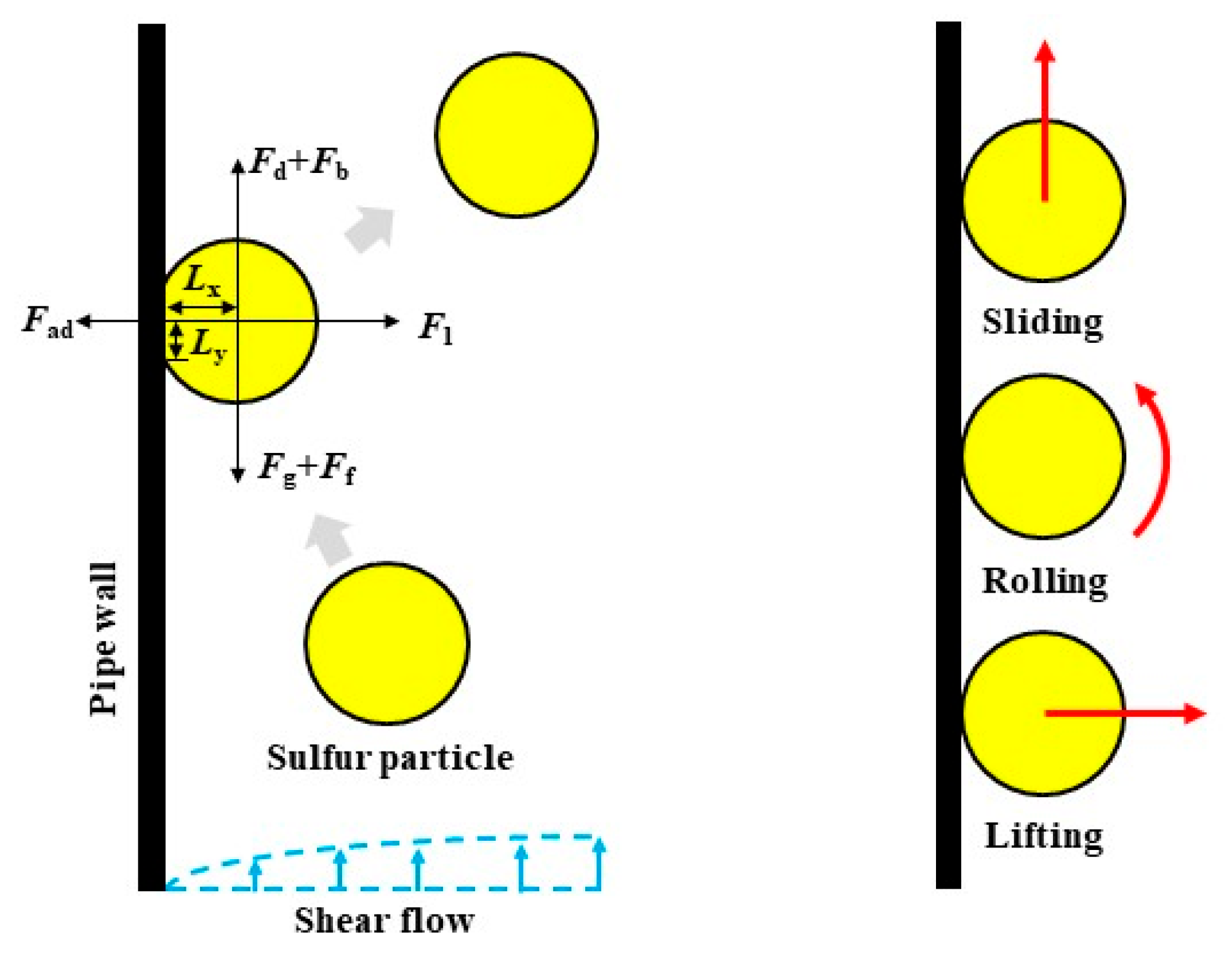
2.1. Mechanisms of Sulfur Particle Detachment from the Pipe Wall
2.2. Model Derivation
2.3. Calculation Parameter Settings and Solution Strategy
3. Results and Discussions
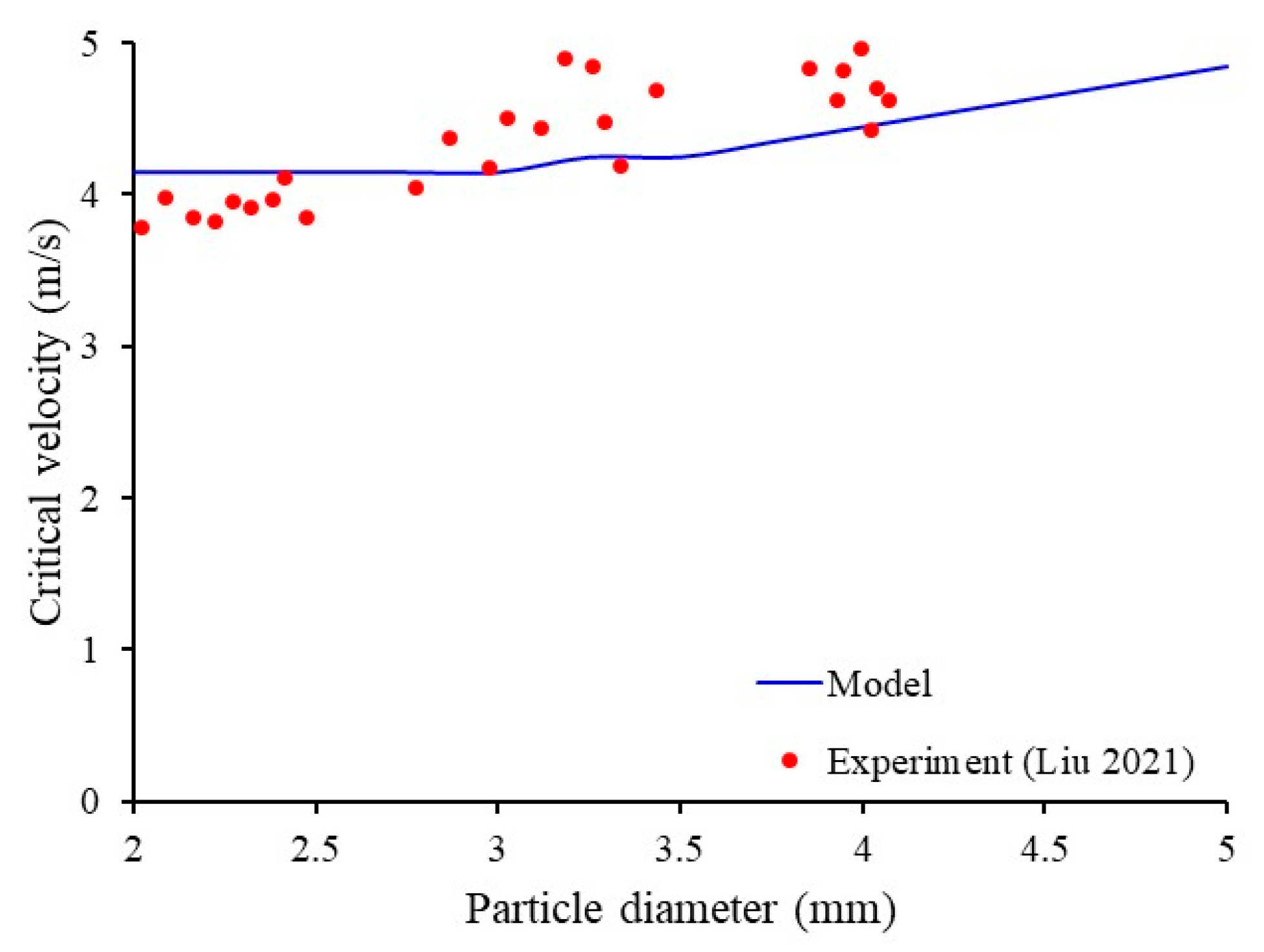
3.1. Validation
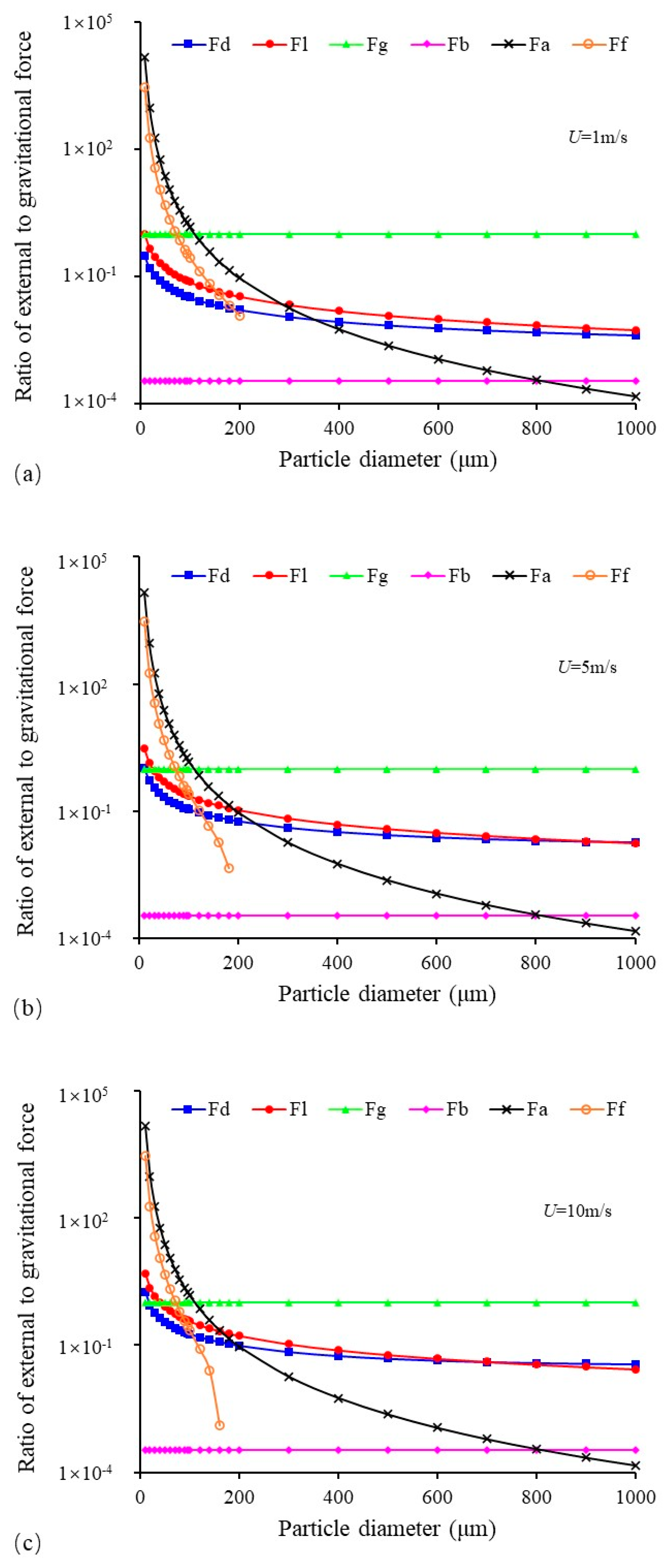
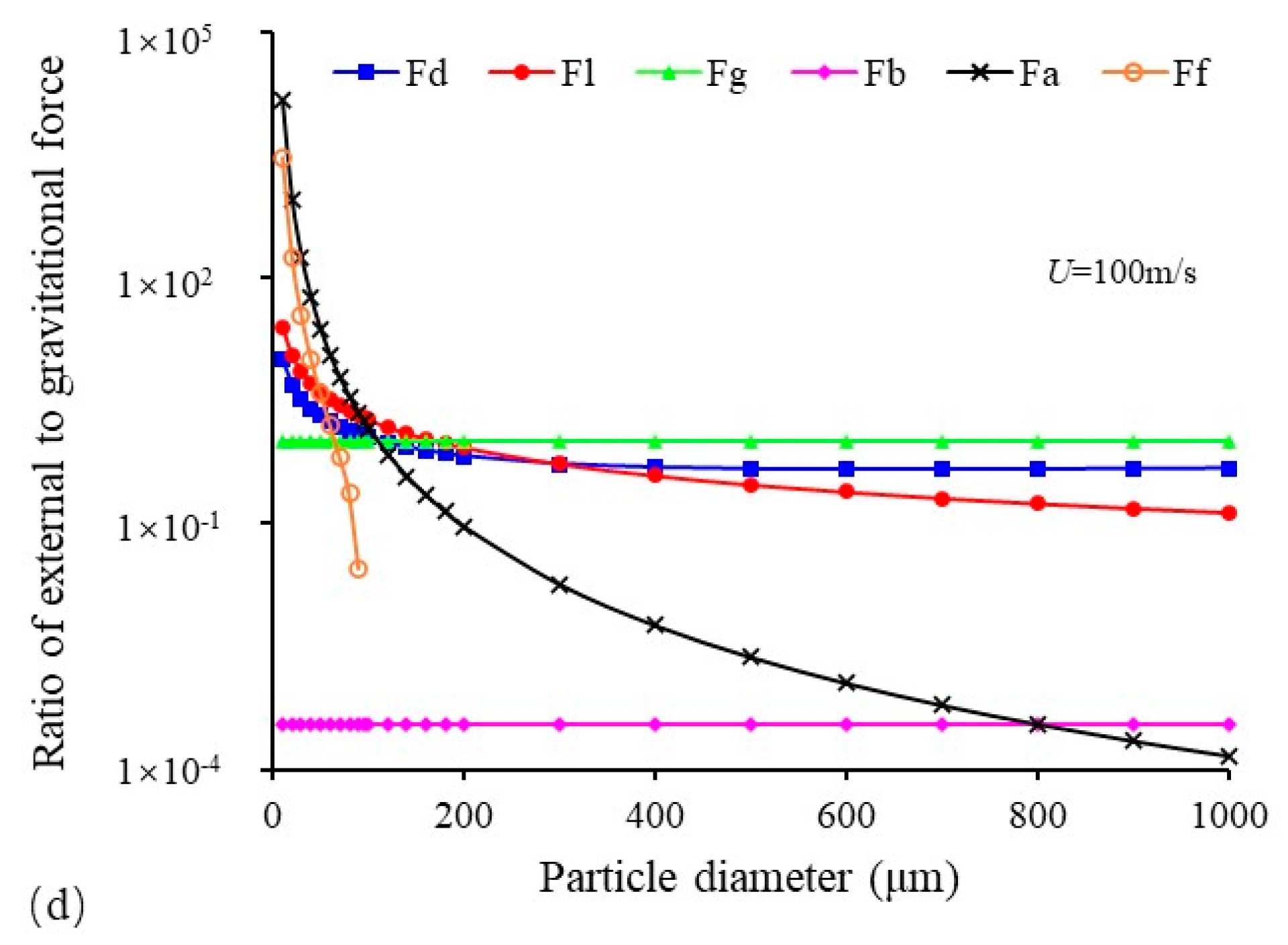
3.2. Forces Acting on Deposited Sulfur Particles
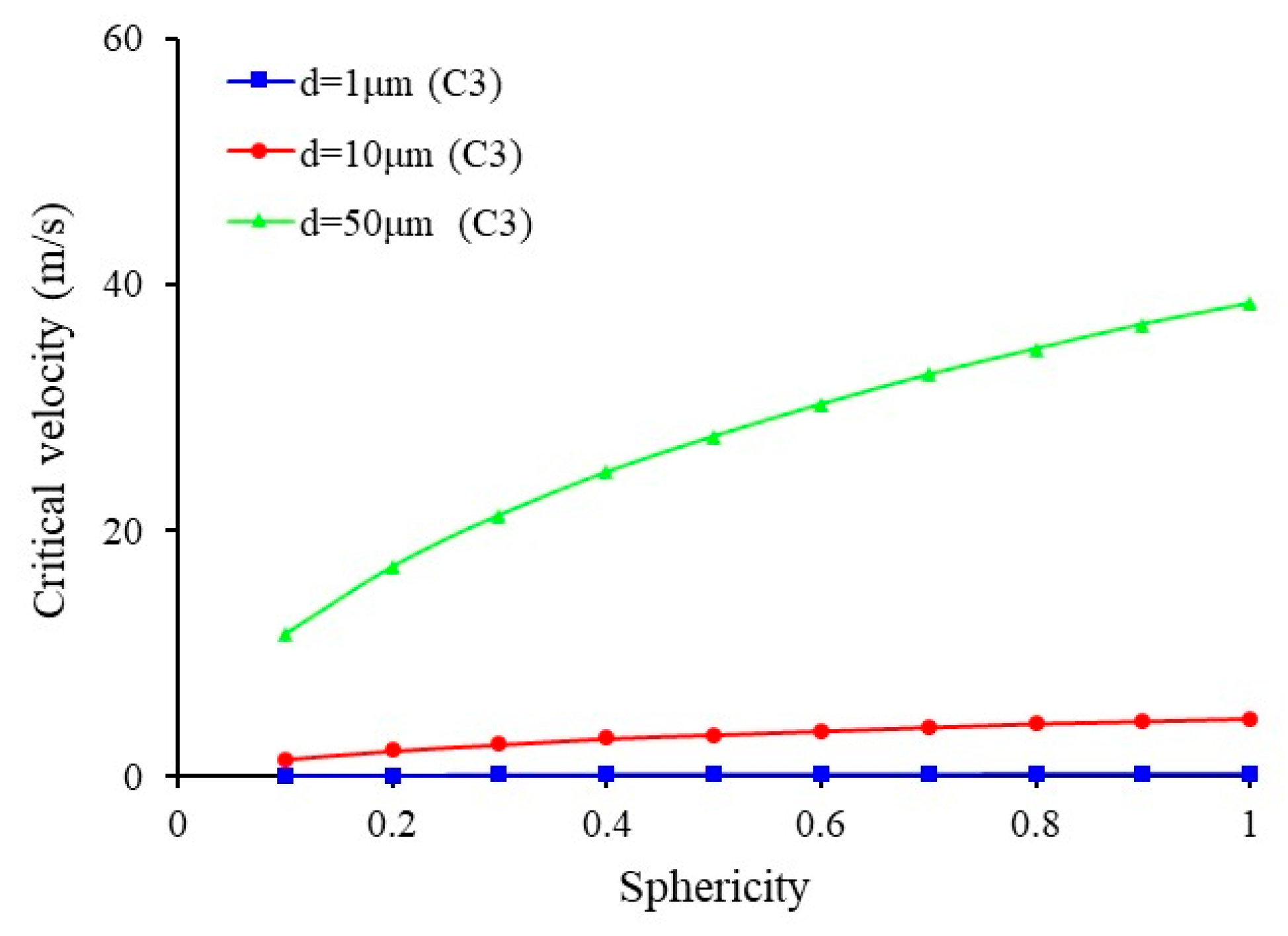
3.3. Effect of Size and Sphericity of Sulfur Particle
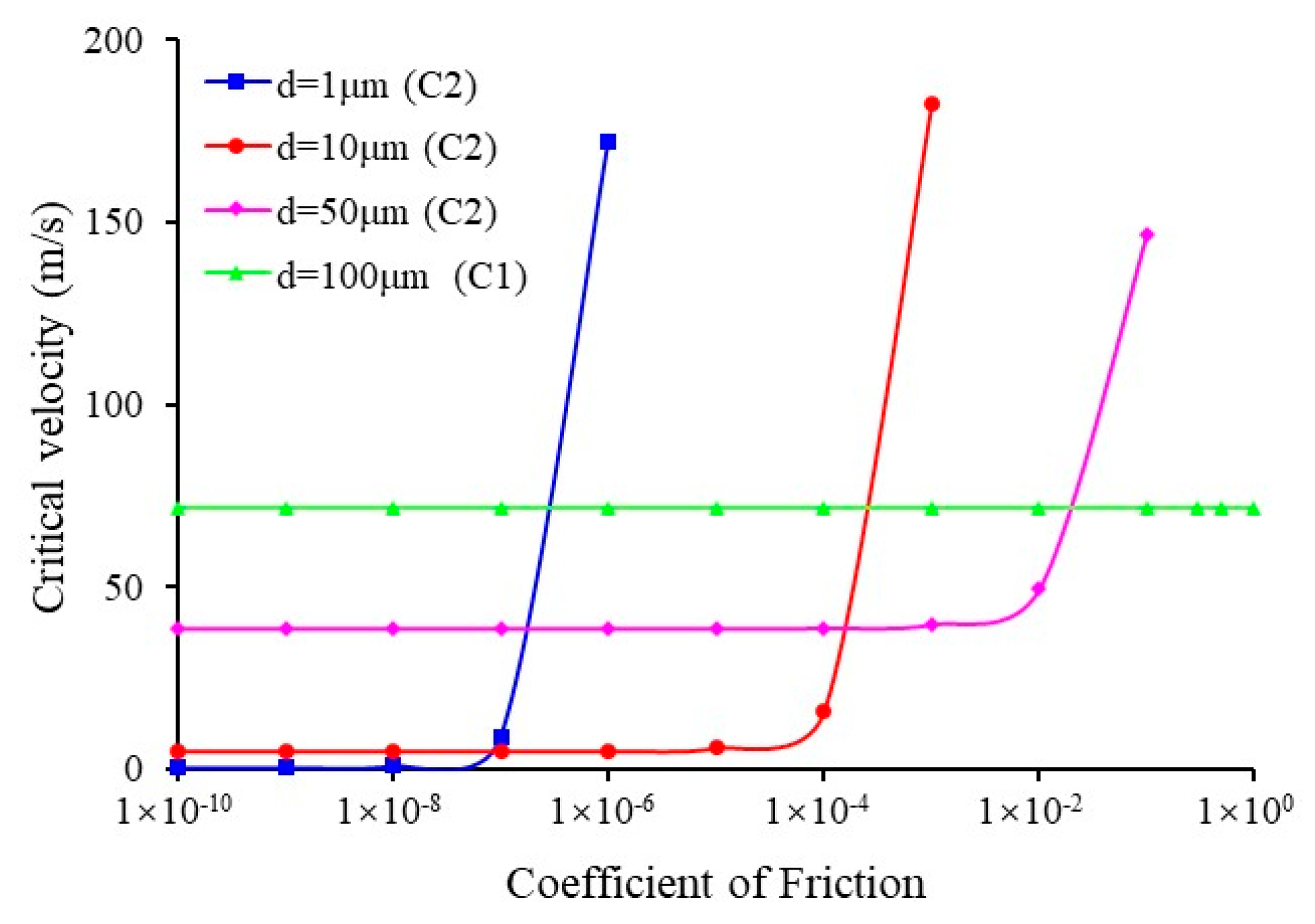
3.4. Effect of Coefficient of Friction and Moment of Sulfur Particle
3.5. Effect of Hamaker Constant
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Santos, J.P.L.; Lobato, A.L.; Moraes, C.; Santos, L.C.L. Determination of Elemental Sulfur Deposition Rates for Different Natural Gas Compositions. J. Pet. Sci. Eng. 2015, 135, 461–465. [Google Scholar] [CrossRef]
- Fu, D. Dynamic Characteristics and Countermeasures of Sulfur Plugging in Gas Wells of Puguang Gas Field. J. Southwest Pet. Univ. (Sci. Technol. Ed.) 2023, 45, 119–130. [Google Scholar] [CrossRef]
- Tang, Y.; Voelker, J.; Keskin, C.; Xu, Z.; Hu, B.; Jia, C. A Flow Assurance Study on Elemental Sulfur Deposition in Sour Gas Wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Denver, CO, USA, 30 October–2 November 2011. [Google Scholar] [CrossRef]
- Li, C.J.; Liu, G.; Jia, W.L. Elemental Sulfur Deposition in High Sulfur-Content Natural Gas Transmission Pipelines: A Review. Chin. Sci. Bull. 2018, 63, 816–827. (In Chinese) [Google Scholar] [CrossRef]
- Roberts, B. Flow Impairment by Deposited Sulfur: A Review of 50 Years of Research. J. Nat. Gas Eng. 2017, 2, 84–105. [Google Scholar] [CrossRef]
- Wen, S.; Jia, C.; Li, H.; Zhao, F.; Chen, Y. Development Concept and Management Model of PetroChina’s First International Cooperation Project of Onshore High-Sulfur Gas Field. Nat. Gas Ind. 2021, 41, 58–68. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Sun, T.; Li, K.; Zhou, J.; Luo, Y.; Zhu, G. Dynamic Characteristics and Carrying-Law Simulation of Sulfur Droplets in the Wellbore of High-Sulfur Gas Wells. Fault-Block Oil Gas Field 2023, 30, 458–465. [Google Scholar] [CrossRef]
- Gao, Z.; Gu, S.; Zeng, J. Sulfur Deposition Model in the Wellbore of High-Sulfur Gas Wells. Fault-Block Oil Gas Field 2022, 29, 139–144. [Google Scholar] [CrossRef]
- Ding, Y.; Jiang, D.; He, X.; Yue, P.; Feng, J.; He, J. Simulation of Sulfur Deposition in High-Sulfur Gas Well of Feixianguan Formation, Tieshanpo. In Proceedings of the 2024 International Petroleum and Petrochemical Technology Conference, Beijing, China, 25–27 March 2024. [Google Scholar] [CrossRef]
- Xiong, R.; Guo, J.; Kiyingi, W.; Hu, Y.; Qiao, X.; Wang, L.; Tan, B. Numerical Model of Asphaltene Deposition in Vertical Wellbores: Considerations of Particle Shape and Drag Force. Powder Technol. 2024, 448, 120284. [Google Scholar] [CrossRef]
- Guo, X.; Chen, Y.; Shi, J.; Yang, H.; Jia, H. Prediction of Sulfur Deposition in the Wellbore of High-Sulfur Deviated Wells. Pet. Geol. Oilfield Dev. Daqing 2021, 40, 57–64. [Google Scholar] [CrossRef]
- Guo, X.; Wang, P.; Ma, J.; Jia, C. Numerical Simulation of Sulfur Deposition in Wellbore of Sour-Gas Reservoir. Processes 2022, 10, 1743. [Google Scholar] [CrossRef]
- Huang, S.; Liu, J.; Wang, X.; Shi, S. Experimental Study and Modeling of Sulfur Particle Migration in High-Sulfur Gas Wells. Pet. Sci. Technol. 2025, 1–27. [Google Scholar] [CrossRef]
- Liu, W.; Huang, X.; Zhang, L.; He, J.; Cen, X. Analysis of Sulfur Deposition for High-Sulfur Gas Reservoirs. Pet. Sci. Technol. 2022, 40, 1716–1734. [Google Scholar] [CrossRef]
- Li, Q.; Zeng, D.; Li, T.; Zhang, R.; Shi, Z.; You, Y.; Zeng, J. Modeling Multiphase Transport and Sulfur Deposition in Wellbores with Application to Sour Gas Production. SPE J. 2025, in press. [CrossRef]
- Wang, Z.; Li, Z.; Pei, J.; Ma, N.; Zhang, J.; Sun, B. Simulation of Hydrate Particle Aggregation and Deposition in Gas-Dominated Flow. SPE J. 2024, 29, 1492–1509. [Google Scholar] [CrossRef]
- Wang, Z.; Peng, J.; Wang, X.; Liu, Z.; Chen, J.; Shi, H. Experiment on Sulfur-Carrying Particles in Gas–Liquid Two-Phase Flow and Prediction Method of Critical Velocity for Sulfur-Carrying Gas. Oil Drill. Prod. Technol. 2025, 47, 35–43. [Google Scholar] [CrossRef]
- Zeng, S.; Yang, X.; Zhang, Q.; Xu, C.; Liu, J.; Han, Y.; Liang, X.; Yao, G. Investigating on the Prediction Model of Sulfur Deposition in High Sour Gas Wells. Procedia Eng. 2012, 29, 4267–4272. [Google Scholar] [CrossRef]
- Xu, C.; Wang, J.; Zeng, S. Prediction Model of Sulfur Deposition in the High Sulfur Gas Well Bore. In Fuzzy Information and Engineering Volume 2; Cao, B., Li, T., Zhang, C., Eds.; Advances in Intelligent and Soft Computing Volume 62; Springer: Berlin/Heidelberg, Germany, 2009; pp. 439–446. [Google Scholar] [CrossRef]
- Hu, J.; Luo, W.; He, S.; Zhao, J.; Wang, X. Sulfur Glomeration Mechanism and Critical Velocity Calculation in Sour Gas Wellbore. Procedia Environ. Sci. 2011, 11, 1177–1182. [Google Scholar] [CrossRef]
- Li, S.; Yin, F.; Qi, Y.; Su, X.; Gao, Y. Critical Deposition Velocity of Hydrate Particles in Undulating Sections of Gas Pipelines. In Proceedings of the International Conference on Computational & Experimental Engineering and Sciences, Shenzhen, China, 26–29 May 2023. [Google Scholar] [CrossRef]
- Nicholas, J.W.; Dieker, L.E.; Sloan, E.D.; Koh, C.A. Assessing the Feasibility of Hydrate Deposition on Pipeline Walls: Adhesion-Force Measurements of Clathrate Hydrate Particles on Carbon Steel. J. Colloid. Interface Sci. 2009, 331, 322–328. [Google Scholar] [CrossRef]
- Fu, J.; Liu, Y.; Zhao, J.; Song, Y.; Liu, Z. Theoretical Model for Hydrate Removal in Gas-Dominated Pipelines. Energy Procedia 2019, 158, 5349–5354. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, N.; Zhang, J.; Pei, J.; Tong, S.; Sun, B. Numerical Modeling of Hydrate Particle Deposition in Pipes with Diameter Reduction. SPE J. 2023, 28, 522–539. [Google Scholar] [CrossRef]
- Hosseini, S.F.; Mozaffarian, M.; Dabir, B.; van den Akker, H.E. Coupled DEM–CFD Analysis of Asphaltene Particle Agglomeration in Turbulent Pipe Flow. Chem. Eng. J. 2024, 486, 150070. [Google Scholar] [CrossRef]
- Ma, N.; Wang, Z.; Zhang, J.; Liu, P.; Peng, Y. Simulation of Hydrate Migration and Deposition in Pipes with Diameter Reduction and Direction Variation. SPE J. 2024, 29, 3616–3634. [Google Scholar] [CrossRef]
- Zhang, L.; Jin, R.; Wang, J.; Yao, H.; Li, Y.; Yin, F.; Song, Y. Kinetic Properties and Dynamic Distribution of Hydrate Particles in a Water-Dominated System. Energy Fuels 2024, 38, 18457–18468. [Google Scholar] [CrossRef]
- Reichardt, H. Vollständige Darstellung der Turbulenten Geschwindigkeitsverteilung in Glatten Leitungen. Z. Angew. Math. Mech. 1951, 31, 208–219. [Google Scholar] [CrossRef]
- Rabinovich, E.; Kalman, H. Incipient Motion of Individual Particles in Horizontal Particle–Fluid Systems. Part B Theor. Analysis. Powder Technol. 2009, 192, 318–325. [Google Scholar] [CrossRef]
- O’Neill, M.E. A Sphere in Contact with a Plane Wall in a Slow Linear Shear Flow. Chem. Eng. Sci. 1968, 23, 1293–1298. [Google Scholar] [CrossRef]
- Hölzer, A.; Sommerfeld, M. New Simple Correlation Formula for the Drag Coefficient of Non-Spherical Particles. Powder Technol. 2008, 184, 361–365. [Google Scholar] [CrossRef]
- Brazhenko, V.; Mochalin, I. Terminal Velocity and Drag Coefficient of a Smooth Steel Sphere Moving in Water-Filled Vertical and Inclined Glass Pipes (Newton Regime). Powder Technol. 2024, 446, 120120. [Google Scholar] [CrossRef]
- Mollinger, A.M.; Nieuwstadt, F.T.M. Measurement of the Lift Force on a Particle Fixed to the Wall in the Viscous Sublayer of a Fully Developed Turbulent Boundary Layer. J. Fluid Mech. 1996, 316, 285–306. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar] [CrossRef]
- Hu, J.; Yang, X.; He, S.; Zhao, J. Distribution of Sulfur Deposition Near a Wellbore in a Sour Gas Reservoir. J. Geophys. Eng. 2013, 10, 015005. [Google Scholar] [CrossRef]
- Aarons, L.; Sundaresan, S. Shear Flow of Assemblies of Cohesive and Non-Cohesive Granular Materials. Powder Technol. 2006, 169, 10–21. [Google Scholar] [CrossRef]
- Burdick, G.M.; Berman, N.S.; Beaudoin, S.P. Hydrodynamic Particle Removal from Surfaces. Thin Solid Film. 2005, 488, 116–123. [Google Scholar] [CrossRef]
- Mortazavi, R. Re-Entrainment of Submicron Solid Particles. Ph.D. Thesis, Virginia Commonwealth University, Richmond, VA, USA, 2005. [Google Scholar] [CrossRef]
- Jassim, E.; Abdi, M.A.; Muzychka, Y. A New Approach to Investigate Hydrate Deposition in Gas-Dominated Flowlines. J. Nat. Gas Sci. Eng. 2010, 2, 163–177. [Google Scholar] [CrossRef]
- Liu, Z.X. Study on Hydrate Blockage Mechanism and Characteristic in Natural Gas Transportation Pipeline. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2021. [Google Scholar] [CrossRef]
- Wang, L.; Lu, T.; Li, Z.; Guo, X. Microscopic Mechanism and Percolation Model of Dynamic Deposition of Elemental Sulfur Particles in Acidic Gas Reservoirs. ACS Omega 2024, 9, 30159–30168. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| Gas density, kg/m3 | 0.72 |
| Gas viscosity, Pa·s | 0.0000252 |
| Pipe diameter, m | 0.0794 |
| Hamaker constant, J | 1.2 × 10−9 |
| Sulfur density, kg/m3 | 2070 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Hui, D.; Li, T.; Liu, W.; Zhang, R.; Zhou, M.; Yuan, S. Study on Critical Gas Flow Velocity to Prevent Sulfur Particle Deposition in Vertical Wells Considering Adhesive Forces. Processes 2025, 13, 2380. https://doi.org/10.3390/pr13082380
Zhang L, Hui D, Li T, Liu W, Zhang R, Zhou M, Yuan S. Study on Critical Gas Flow Velocity to Prevent Sulfur Particle Deposition in Vertical Wells Considering Adhesive Forces. Processes. 2025; 13(8):2380. https://doi.org/10.3390/pr13082380
Chicago/Turabian StyleZhang, Lianjin, Dong Hui, Tao Li, Wei Liu, Ruiduo Zhang, Mengfei Zhou, and Shan Yuan. 2025. "Study on Critical Gas Flow Velocity to Prevent Sulfur Particle Deposition in Vertical Wells Considering Adhesive Forces" Processes 13, no. 8: 2380. https://doi.org/10.3390/pr13082380
APA StyleZhang, L., Hui, D., Li, T., Liu, W., Zhang, R., Zhou, M., & Yuan, S. (2025). Study on Critical Gas Flow Velocity to Prevent Sulfur Particle Deposition in Vertical Wells Considering Adhesive Forces. Processes, 13(8), 2380. https://doi.org/10.3390/pr13082380





