Reliability Evaluation of New-Generation Substation Relay Protection Equipment Based on ASFSSA-LSTM-GAN
Abstract
1. Introduction
- A novel generative framework is proposed based on an LSTM-GAN architecture optimized by the ASFSSA, effectively addressing the issue of small sample size in fault data.
- The LSTM network, enhanced by ASFSSA, improves the generator’s ability to model temporal dependencies and escape local optima.
- A least squares-based reliability estimation method is employed to fit the reliability distribution model using both real and synthetic data.
- This work provides a practical solution for reliability assessment and life prediction of substation relay protection devices in data-scarce scenarios.
2. Reliability Distribution Model of Relay Protection Equipment
3. SFSSA Optimizes the GAN Model of LSTM
3.1. Principles of GAN Model
3.2. Generator Model Construction
3.2.1. ASFSSA Algorithm
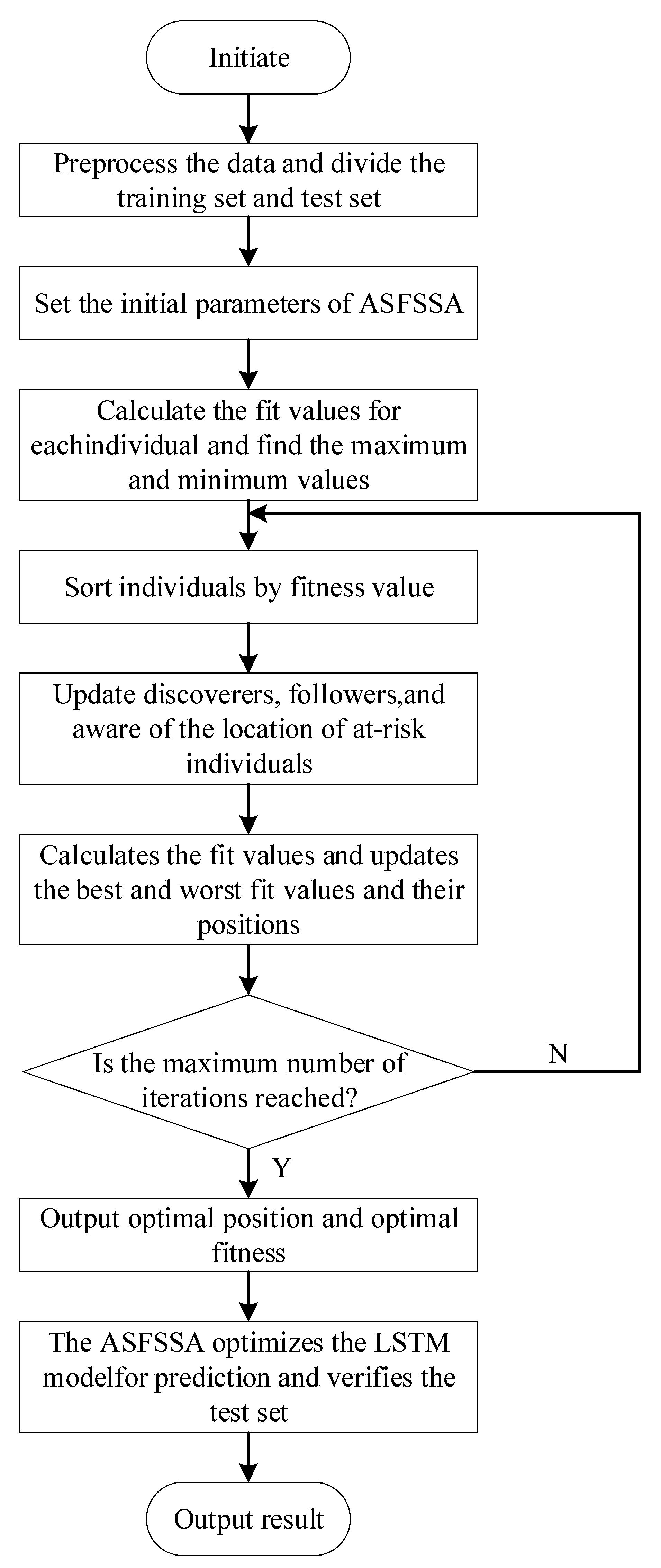
3.2.2. ASFSSA Optimizes the LSTM Algorithm
- 0.
- The initialization of sparrow swarm parameters involves setting the total population size (pop), the number of discoverers ( ), total iterations (), solution accuracy (E), and the weights and biases in the LSTM. The vector Z denotes the weights and biases in the LSTM, and its initialization can be expressed as follows:In the equations, ; is a function that transforms matrices into column vectors; represents the various weight matrices in the LSTM; and represents the various bias matrices in the LSTM.
- 1.
- The population individuals’ positions are initialized using tent mapping to generate pop sparrow individuals.
- 2.
- The position of each sparrow individual is assigned to the optimization parameters in the LSTM. The fitness value of each population individual is calculated using Equation (11), and the maximum fitness value and minimum fitness value are determined.
- 3.
- The population is then sorted, based on fitness values.
- 4.
- The top individuals are selected as discoverers, while the rest are followers. The discoverers’ positions are updated using Equations (6) and (7), after incorporating the strategy.
- 5.
- The positions of the followers are updated using Equation (9).
- 6.
- Equation (10) is used to update the positions of the sparrow individuals aware of danger.
- 7.
- After each iteration, the fitness value for each individual is recalculated, and the maximum fitness value , minimum fitness value , and their corresponding positions are updated.
- 8.
- Judge whether the algorithm has reached the maximum number of iterations or the solution’s precision. If it has, then output the optimization results; otherwise, return to step 4.
- 9.
- Assign the optimal position vector to the weights and bias parameters of the LSTM neural network, and train and predict with the LSTM, according to these parameters.
3.3. Construction of Discriminator Model
ASFSSA-LSTM-GAN Model
4. ASFSSA Optimizes the Reliability Assessment of GAN Model Relay Protection Equipment for LSTM
4.1. Statistical Mode 1: Reliability Evaluation Model
4.2. Statistical Mode 2: Reliability Evaluation Model
5. Analysis of Numerical Examples
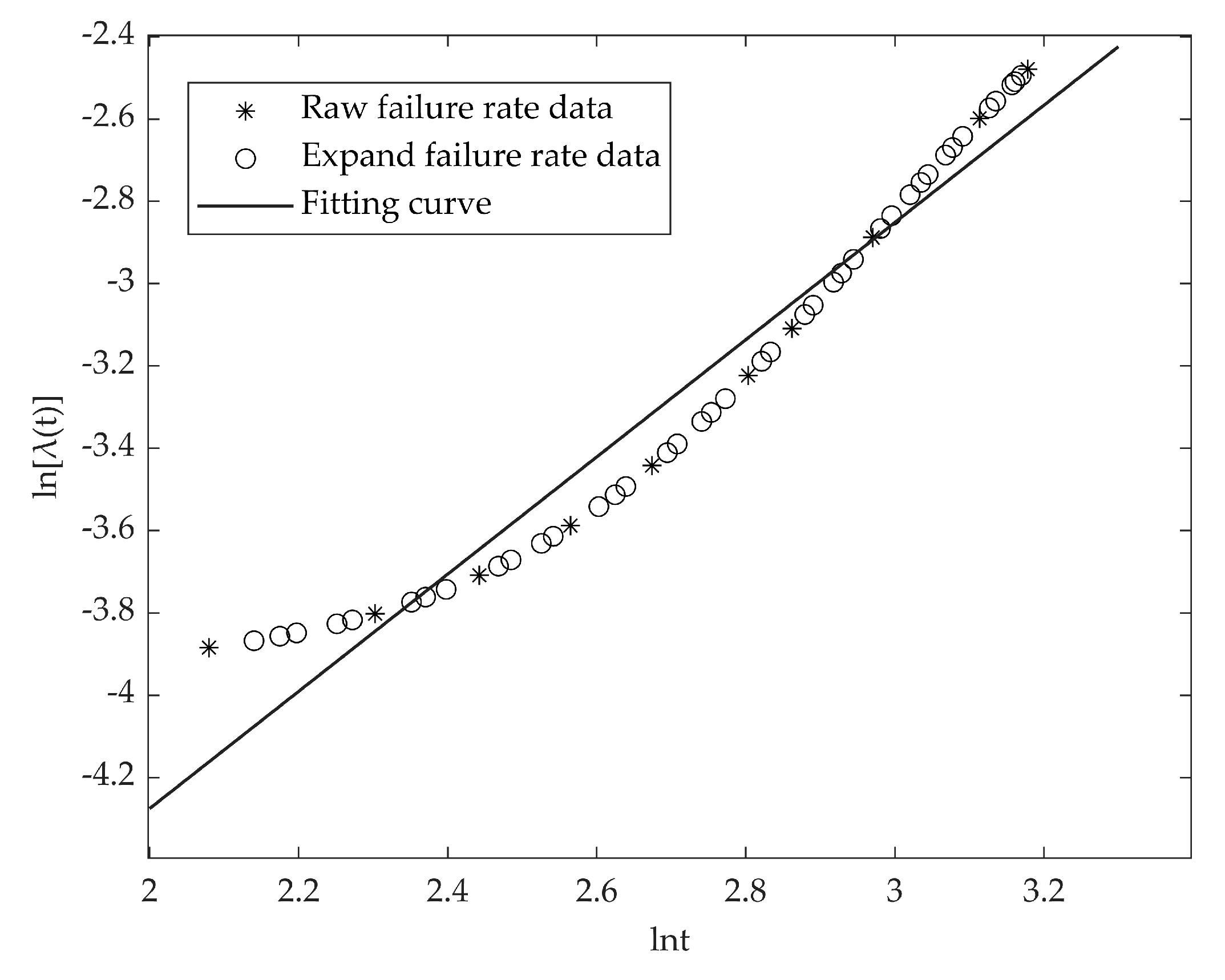
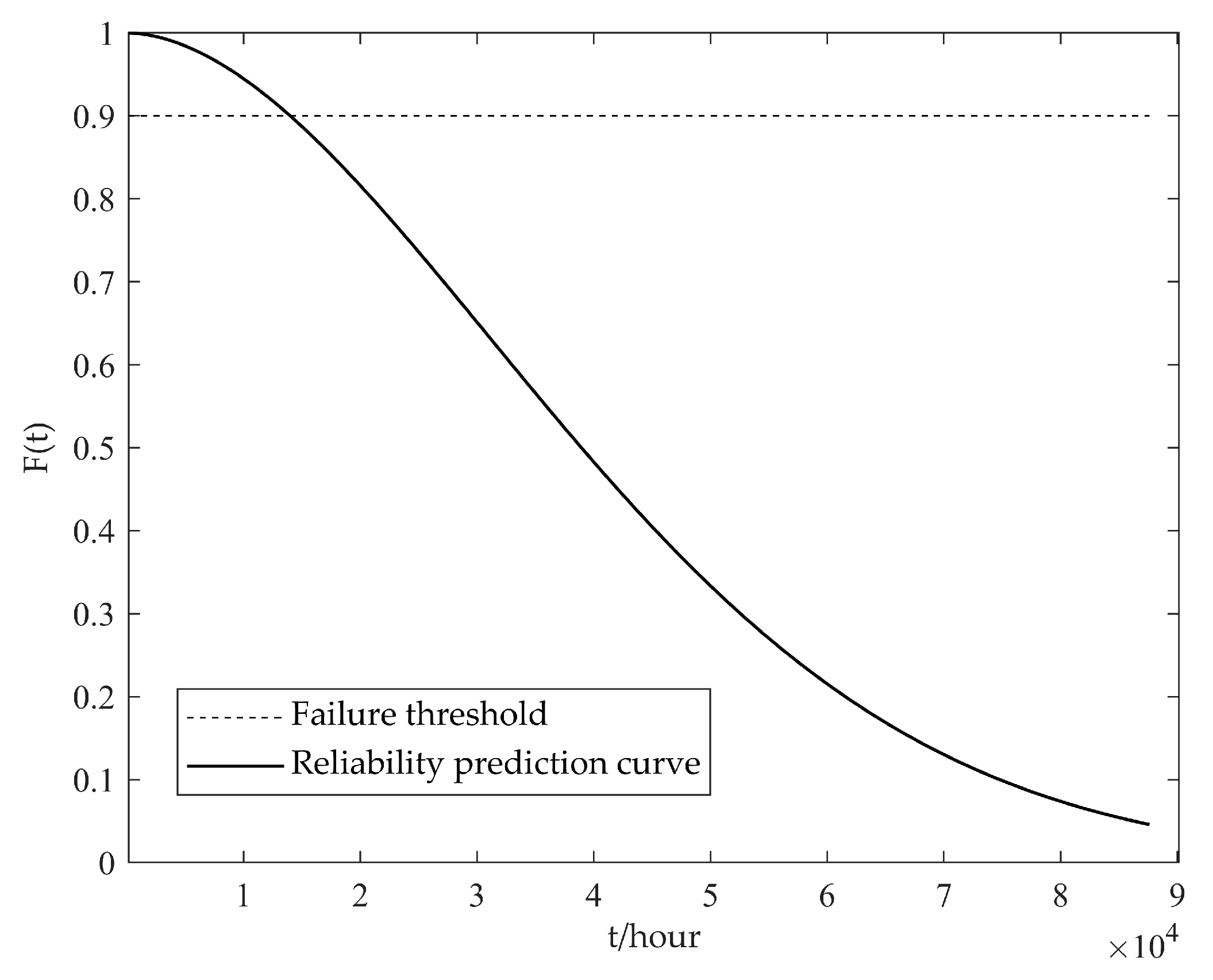
5.1. Statistical Mode 1: Example Analysis
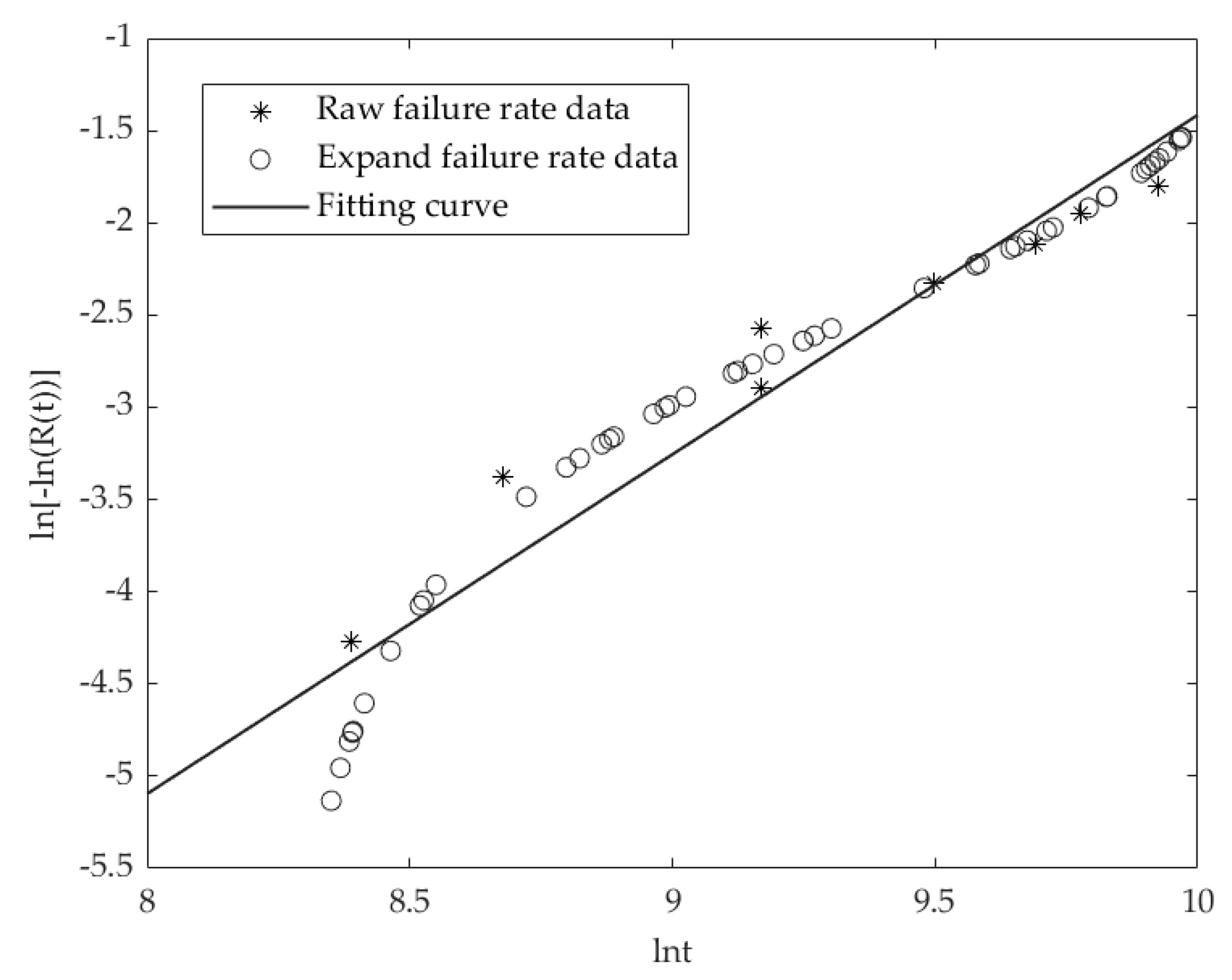
5.2. Statistical Mode 2: Example Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, L.; Cao, X.; Zhou, Y.; Lin, Z.; Zhou, J.; Guan, X.; Wu, Q. Frequency-Constrained Coordinated Scheduling for Asynchronous AC Systems under Uncertainty via Distributional Robustness. IEEE Trans. Netw. Sci. Eng. 2025, 1–13. [Google Scholar] [CrossRef]
- Dai, Z.; Wang, Z.; Jiao, Y.; Cao, S. Probabilistic Assessment Method for Failure Risk of Stepped Protection Philosophy. Trans. China Electrotech. Soc. 2012, 27, 175–182. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, X. Research on safe operation mode of power supply reliability in distribution network. China High New Technol. 2023, 22, 16–18. (In Chinese) [Google Scholar] [CrossRef]
- Guo, T.; Zhao, X.; Feng, B.; Chen, H. Network security risk and protection strategy of power distribution network automation system. Netw. Secur. Technol. Appl. 2023, 6, 124–125. (In Chinese) [Google Scholar]
- Wang, J.; Wu, D.; Zhu, Z.; Li, H.; Yang, L.; Tang, W.; Mu, C. Fine management practice for reliability analysis of low-voltage electrical equipment. Electr. Eng. 2023, 16, 182–184+188. (In Chinese) [Google Scholar] [CrossRef]
- Huang, K. Study on Residual Life Evaluation of High Voltage Circuit Breaker; North China Electric Power University: Beijing, China, 2013. (In Chinese) [Google Scholar]
- Gui, H. Study on Residual Life Evaluation of Power Transformer; North China Electric Power University: Beijing, China, 2014. [Google Scholar]
- Yi, Y. Life analysis of relay protection device and study on life influence mechanism. Power Syst. Prot. Control 2013, 41, 79–83. (In Chinese) [Google Scholar] [CrossRef]
- Tan, Z.; Xu, C.; Yin, Z.; Tian, X.; Lu, S. Research on AT traction network relay protection model based on Feeding Section. J. Phys. Conf. Ser. 2022, 2310, 012081. [Google Scholar] [CrossRef]
- Li, X.; Ge, D.; Lin, Z.; Wang, S.; Wang, J. Practical application of dynamic fault tree in reliability evaluation of reactor protection system. Nucl. Tech. 2021, 44, 73–80. (In Chinese) [Google Scholar] [CrossRef]
- Dai, Z.; Li, Z.; Jiao, Y.; Wang, Z. Reliability assessment of relay protection based on small sample failure data based on BP neural network. Electr. Power Autom. Equip. 2014, 34, 129–134. (In Chinese) [Google Scholar]
- Wang, J. Research on Real-Time Reliability and Risk Assessment of Relay Protection in Intelligent Substation; North China Electric Power University: Beijing, China, 2019. (In Chinese) [Google Scholar]
- Zhang, L.; Wang, G.; Cao, L.; Dai, Z.; Kou, B. Intelligent state evaluation and early warning of protection system based on GAN model and random forest algorithm. J. Electr. Power Sci. Technol. 2021, 36, 104–112. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, H.; Meng, R.; Fu, W.; Wang, Z.; Jia, J. Reliability prediction of LSTM network relay protection device. China Meas. Test 2023, 49, 164–170. (In Chinese) [Google Scholar]
- Nikpour, B.; Sinodinos, D.; Armanfard, N. Deep Reinforcement Learning in Human Activity Recognition: A Survey and Outlook. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 4267–4278. [Google Scholar] [CrossRef] [PubMed]
- Richter, D.J.; Calix, R.A.; Kim, K. A Review of Reinforcement Learning for Fixed-Wing Aircraft Control Tasks. IEEE Access 2024, 12, 103026–103048. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Reddi, V.J. Deep Reinforcement Learning for Cyber Security. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 3779–3795. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Lin, K.; Jain, A.K.; Zhou, J. Transfer Learning in Deep Reinforcement Learning: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 13344–13362. [Google Scholar] [CrossRef]
- Yang, X.; Xie, L.; Yang, Y.; Zhao, B.; Li, Y. A comparative study for parameter estimation of the Weibull distribution in a small sample size: An application to spring fatigue failure data. Qual. Eng. 2022, 35, 553–565. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, Y. Small sample Weibull reliability analysis based on least squares support vector machine. China Mech. Eng. 2012, 23, 1967–1971. (In Chinese) [Google Scholar]
- Jagadeesan, K.; Palanisamy, G. Atherosclerosis plaque tissue classification using self-attention-based conditional variational auto-encoder generative adversarial network using OCT plaque image. Biomed. Eng./Biomed. Tech. 2023, 68, 633–649. [Google Scholar] [CrossRef]
- Dong, X.; Miao, Z.; Man, L.; Shen, J.; Jin, Z.; Guo, Z.; Teoh, A.B.J. Reconstruct face from features based on genetic algorithm using GAN generator as a distribution constraint. Comput. Secur. 2023, 125, 103026. [Google Scholar] [CrossRef]
- Ouyang, C.; Qiu, Y.; Zhu, D. Adaptive Spiral Flying Sparrow Search Algorithm. Sci. Program. 2021, 2021, 6505253. [Google Scholar] [CrossRef]
- Wang, S.; Jia, H.; Shen, C.; Wu, Y.; Liu, J. Application of an optimized GAN model in 5G energy-saving timing. J. Taiyuan Univ. Technol. 2024, 55, 743–751. (In Chinese) [Google Scholar]
- Jing, Z.; Dai, B.; Wang, R.; Liu, S.; Jiang, Z. Reliability evaluation method of relay protection device based on long short-term memory network. Electr. Eng. 2023, 14, 115–117. (In Chinese) [Google Scholar] [CrossRef]


| Operating Year Limited to/Year | Average Failure Rate/(Times Year−1 Station−1) | Operating Year Limited to/Year | Average Failure Rate/(Times Year−1 Station−1) |
|---|---|---|---|
| 8 | 0.0185 | 16.5 | 0.0386 |
| 10 | 0.0184 | 17.5 | 0.0452 |
| 11.5 | 0.0236 | 19.5 | 0.0564 |
| 13 | 0.0389 | 22.5 | 0.1142 |
| 14.5 | 0.0217 | 24 | 0.1862 |
| Device ID | Reliability | Failure Time/h | Equipment Operation Condition |
|---|---|---|---|
| 1 | 0.9861 | maloperation | |
| 3 | 0.9663 | maloperation | |
| 18 | 0.9464 | maloperation | |
| 20 | 0.9266 | maloperation | |
| 25 | 0.9067 | maloperation | |
| 38 | 0.8869 | maloperation | |
| 39 | 0.8671 | maloperation | |
| 44 | 0.8472 | maloperation |
| MODEL | RMSE | MSE | R2 |
|---|---|---|---|
| BP | 0.00595 | 3.538 × 10−5 | 0.79798 |
| LSTM | 0.00565 | 3.189 × 10−5 | 0.8179 |
| LSTM-GAN | 0.00561 | 3.151 × 10−5 | 0.82009 |
| ASFSSA-LSTM-GAN | 0.00233 | 5.451 × 10−5 | 0.96888 |
| Data | Correlation Coefficient |
|---|---|
| Raw data | 0.8925 |
| BP network expansion data | 0.7643 |
| LSTM network expansion data | 0.9944 |
| LSTM-GAN network expansion data | 0.9878 |
| ASFSSA-LSTM-GAN network expansion data | 0.9759 |
| MODEL | RMSE | MSE | R2 |
|---|---|---|---|
| BP | 1034.43 | 1,070,043.88 | 0.9342 |
| LSTM | 897.90 | 806,223.14 | 0.9505 |
| LSTM-GAN | 826.09 | 682,422.06 | 0.9581 |
| ASFSSA-LSTM-GAN | 776.24 | 602,542.13 | 0.9630 |
| Data | Correlation Coefficient |
|---|---|
| Raw data | 0.9795 |
| BP network expansion data | 0.7549 |
| LSTM network expansion data | 0.9444 |
| LSTM-GAN network expansion data | 0.9702 |
| ASFSSA-LSTM-GAN network expansion data | 0.9758 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, B.; Chen, K.; Du, X.; Duan, W.; Wang, Y.; Hu, J.; Zou, H. Reliability Evaluation of New-Generation Substation Relay Protection Equipment Based on ASFSSA-LSTM-GAN. Processes 2025, 13, 2300. https://doi.org/10.3390/pr13072300
Tian B, Chen K, Du X, Duan W, Wang Y, Hu J, Zou H. Reliability Evaluation of New-Generation Substation Relay Protection Equipment Based on ASFSSA-LSTM-GAN. Processes. 2025; 13(7):2300. https://doi.org/10.3390/pr13072300
Chicago/Turabian StyleTian, Baojiang, Kai Chen, Xingwei Du, Wenyan Duan, Yibo Wang, Jiajia Hu, and Hongbo Zou. 2025. "Reliability Evaluation of New-Generation Substation Relay Protection Equipment Based on ASFSSA-LSTM-GAN" Processes 13, no. 7: 2300. https://doi.org/10.3390/pr13072300
APA StyleTian, B., Chen, K., Du, X., Duan, W., Wang, Y., Hu, J., & Zou, H. (2025). Reliability Evaluation of New-Generation Substation Relay Protection Equipment Based on ASFSSA-LSTM-GAN. Processes, 13(7), 2300. https://doi.org/10.3390/pr13072300





