Control Strategy of Distributed Photovoltaic Storage Charging Pile Under Weak Grid

Abstract

Distributed photovoltaic storage charging piles in remote rural areas can solve the problem of charging difficulties for new energy vehicles in the countryside, but these storage charging piles contain a large number of power electronic devices, and there is a risk of resonance in the system under weak grid conditions. Firstly, the topology of a photovoltaic storage charging pile is introduced, including a bidirectional DC/DC converter, unidirectional DC/DC converter, and single-phase grid-connected inverter. Then, the maximum power tracking control strategy based on improved conductance micro-increment is derived for a photovoltaic power generation system, and a constant voltage and constant current charge–discharge control strategy is derived for energy storage equipment. Additionally, a segmented reflective charging control strategy is introduced for charging piles, and the quasi-PR controller is introduced for single-phase grid-connected inverters. In addition, an improved second-order general integrator phase-locked loop (SOGI-PLL) based on feed-forward of the grid current is derived. Finally, a simulation model is built to verify the performance of the solar–storage charging pile and lay the technical groundwork for future integrated control strategies.

1. Introduction

In 2023, aimed at promoting the adoption of new energy vehicles (NEVs) in rural areas, the Chinese government launched “NEVs Going to the Countryside Campaign”. It is projected that by 2030, the total stock of NEVs in rural regions will exceed 70 million units [1]. Alongside this growth, NEV rural expansion requires the development of charging infrastructure. Currently, rural charging infrastructure is still in the early stages of development. High-power ultra-fast charging stations (e.g., 120 kW, 240 kW, 360 kW, 480 kW, or even 600 kW) are not yet suitable for rural areas [2].

Rural areas are typically distant from load centers and power generation facilities [3,4]. As a result, rural power grids face significant challenges such as long transmission lines, limited line capacity, and so on, making them unsuitable for large-scale EV charging station deployment. Additionally, these grids exhibit weak grid characteristics [5,6]. Thus, the deployment of large-scale NEV charging stations would impose significant stress on rural power grids [7]. The operation and maintenance costs of large-scale charging stations is relatively high. Moreover, charging stations are sparsely distributed, leading to increased labor costs for repairs. Additionally, regular maintenance and technological upgrades further raise operational costs for charging service providers [8,9]. Thus, home-based chargers are the predominant solution in rural areas.

Most AC charging piles have a power rating of approximately 6.6 kW, which imposes relatively high power capacity requirements for rural household grid connections [10,11]. Rural areas predominantly feature single-household courtyard residences, offering abundant idle rooftop resources [12,13]. This creates favorable conditions for deploying distributed home solar–storage-integrated charging systems [14]. Furthermore, solar–storage charging infrastructure can alleviate rural power shortages by leveraging time-of-use electricity pricing to increase household income through peak shaving and valley filling. This approach enables coordinated frequency regulation of the power system through the synergy of source, load, grid, and storage components [3].

However, rural power grids exhibit weak grid characteristics. Solar–storage-integrated charging piles incorporate a significant number of power electronic devices, and the high-frequency switching operations of these devices introduce higher-order harmonic currents into the grid. While LCL filters are commonly used to suppress high-frequency harmonics, they are prone to triggering resonance issues [15,16]. Moreover, maximum power point tracking (MPPT) control in the photovoltaic (PV) generation units of such charging piles typically relies on the output voltage of PV arrays as the reference. This approach is highly susceptible to environmental factors such as temperature and solar irradiance variations, leading to reduced tracking efficiency [17,18].

To address the aforementioned challenges, this study establishes a solar–storage-integrated charging pile model with the following advanced control strategies. Firstly, an improved incremental conductance (IC) maximum power point tracking (MPPT) control strategy is implemented to achieve precise power tracking under dynamic environmental conditions. Then, a quasi-proportional resonant controller is adopted to enable zero steady-state error tracking of single-phase sinusoidal voltage references [19]. Finally, a second-order generalized integrator (SOGI)-based PLL is designed to ensure accurate grid voltage synchronization while actively suppressing resonance risks inherent to weak grid operation [20].

Electric vehicle charging stations employ a segmented charging strategy. The pre-charging phase safeguards battery integrity, the segmented constant-current charging phase enables rapid energy replenishment, and the positive–negative pulse current charging phase mitigates battery polarization phenomena. This approach extends battery service life and cycle durability. Compared to conventional methods, this solution addresses infrastructure limitations in remote areas by eliminating dependency on grid installations, thereby promoting EV adoption in underserved regions. This dual-benefit approach reduces carbon emissions while enhancing resident mobility convenience.

By establishing a model of a photovoltaic (PV)–storage-integrated charging station in a weak grid environment, this study verifies that the proposed control method effectively addresses the charging challenges of new energy electric vehicles in remote rural areas characterized by weak grid conditions. The PV–storage charging station not only enhances residents’ economic benefits but also contributes to grid frequency stabilization. Furthermore, the proposed method significantly improves the adaptability of single-phase grid-connected inverters in weak grid scenarios and demonstrates robust performance. And all the methods are developed separately for different power electronic converters within the PV–storage-integrated charging station, laying the technical foundation for future coordinated control research.

2. Topology of the Photovoltaic Energy Storage System

Figure 1 illustrates the topology of a distributed household-level PV energy storage (ES) charging pile designed for rural areas. The system comprises a battery unit interfaced via a bidirectional Direct Current/Direct Current (DC/DC) converter, a PV array connected through a unidirectional DC/DC converter, a charging pile also linked through a unidirectional DC/DC converter, and a single-phase full-bridge inverter module.

The bidirectional DC/DC converter adopts a buck/boost topology, as illustrated in Figure 2a; the first unidirectional single-phase DC/DC converter employs a boost configuration, as shown in Figure 2b; and the single-phase full-bridge inverter follows the structural layout presented in Figure 2c.

In Figure 2b, i_pv denotes the output current of the PV array, while v_pv represents its output voltage. The parameter L corresponds to the filter inductance in the Boost converter circuit. In Figure 2c, U_dc and C_dc signify the voltage and capacitance of the DC bus, respectively. L₁ and L₂ are the two inductors within the LCL, and C is the corresponding filter capacitance. L_g indicates the equivalent grid-side reactance. The variable u_pcc refers to the voltage at the point of common coupling, u_g to the grid voltage, and u_inv to the output voltage of the grid-tied inverter. The currents i_L1 and i_L2 denote the respective currents flowing through inductors L₁ and L₂.

To streamline the analysis of the control strategy for the PV-ES charging pile, this study does not consider the optimal operational states of the PV and energy storage systems under varying economic returns. Instead, the PV system operates under a maximum power point tracking (MPPT) scheme, and the charging/discharging behavior of the energy storage unit is governed by the conditions outlined in

Table 1. Operational modes of the distributed photovoltaic–energy storage charging system.

Time-Differentiated Tariffs Period	State of Charge (SOC)	Operational Status of the Energy Storage System
Peak Period	SOC > 20%	Discharging
	SOC < 20%	Inactive
Flat Period	SOC < 80% Ppv − Pev > 0	Charging
	Otherwise	Inactive
Off-Peak Period	SOC < 80%	Charging
	SOC > 80%	Inactive

Note: P_pv denotes the output power of the photovoltaic system; P_ev denotes the charging demand of EV.

.

As indicated in Table 1, during peak pricing periods, the energy storage system engages in discharging provided the SOC exceeds 20%; if the SOC falls at or below this threshold, the system remains inactive. During flat-rate periods, the system charges only when certain conditions are met: the SOC is below 80%, and the photovoltaic output surpasses the electric vehicle’s power demand. Failing either condition results in system idleness. During off-peak periods, the energy storage unit enters the charging mode when its SOC remains below 80%; in all other cases, it remains inactive. Furthermore, the DC bus voltage is maintained and regulated through the operation of the single-phase grid-connected inverter.

3. Control Strategy Analysis of Optical Storage Charging Pile

3.1. Photovoltaic Array DC/DC Converter Control

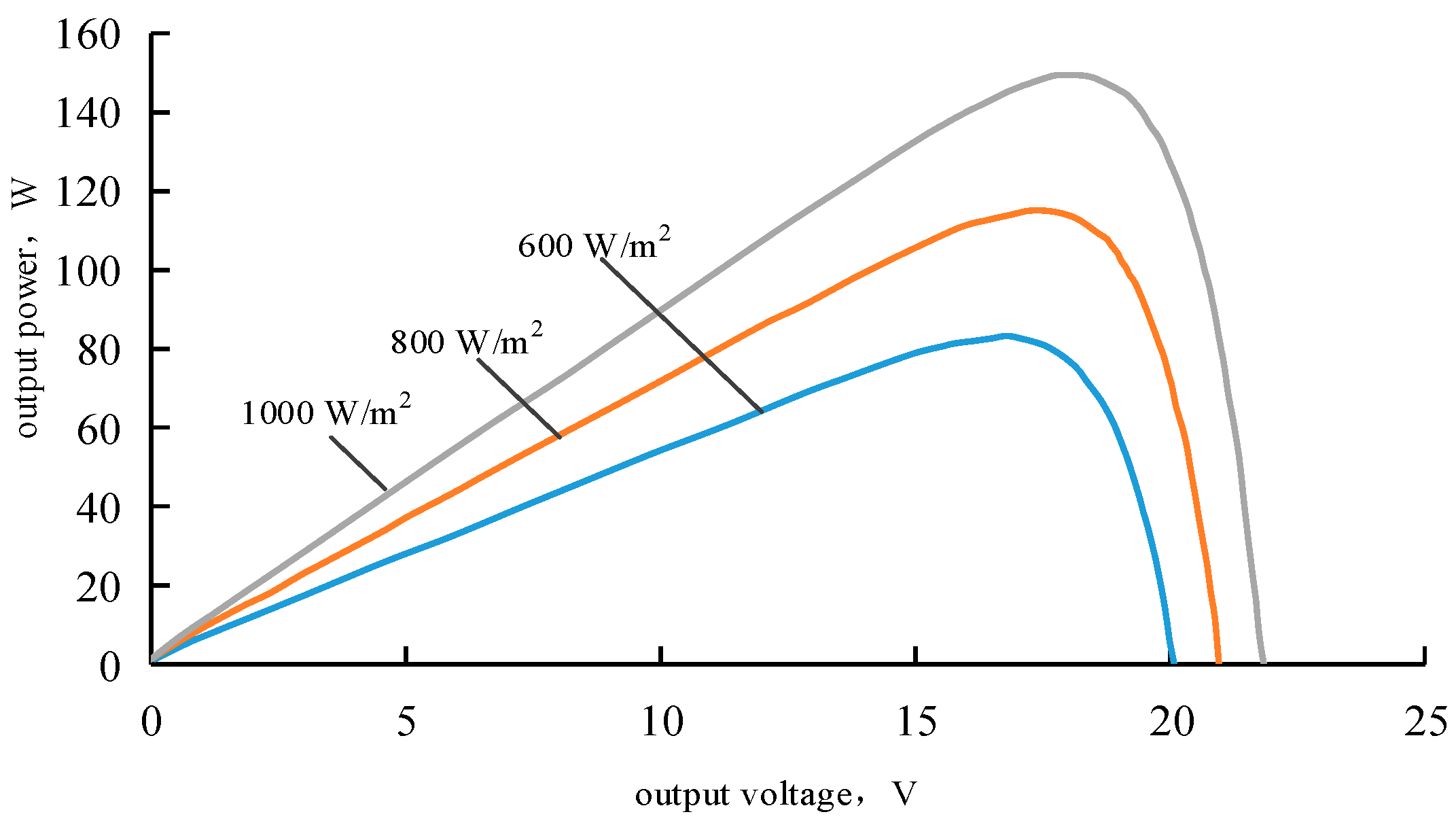
For a specific model of PV array at an ambient temperature of 25 °C with varying light intensities, Figure 3 illustrates the nonlinear relationship between the output power P_pv and the output voltage v_pv.

From Figure 3, it can be seen that the relationship between the output power and output voltage of the PV array is affected by the ambient temperature and light intensity.

The DC bus voltage is connected to the PV array through a Boost converter, and the maximum power tracking control strategies that are commonly used include the conductance increment method, the constant voltage method, and the perturbation observation method. Among them, the conductivity increment method is characterized as having high data memory requirements and high computational accuracy. The constant voltage method can be easily implemented. However, in areas where ambient temperatures are unstable, it cannot be guaranteed that the PV power system is working in the maximum power tracking mode. The perturbation observation method has fewer control parameters, but requires repeated adjustments to the output power.

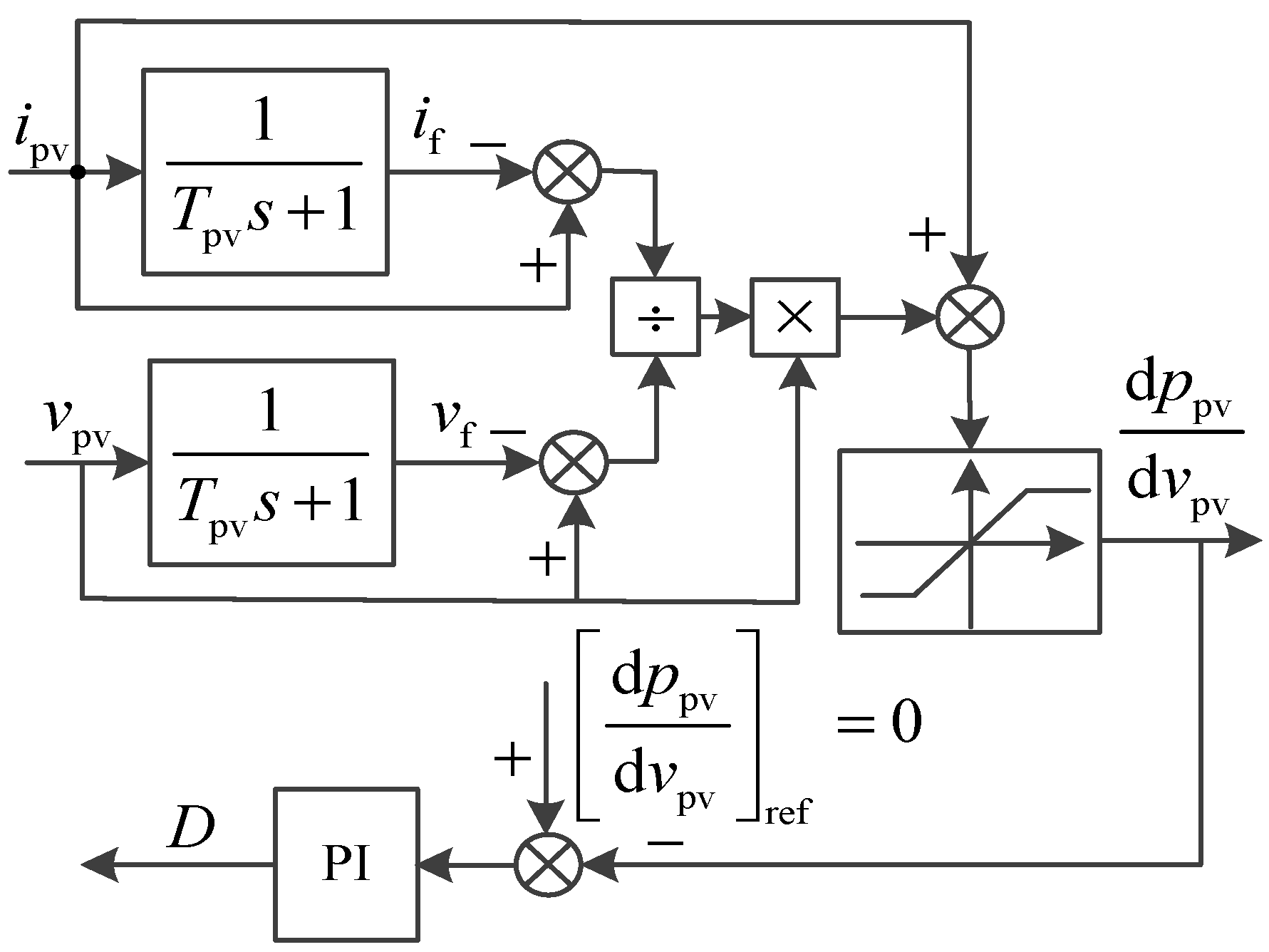
Based on the conductivity increment method, a control strategy for differentiating the output voltage of the PV array in the PV power generation system is proposed in this paper. The conductance micro-increment can be expressed as Equation (1).

$${\displaystyle \frac{\mathrm{d}{p}_{\mathrm{pv}}}{\mathrm{d}{v}_{\mathrm{pv}}}}={\displaystyle \frac{\mathrm{d}\left(v_{\mathrm{pv}}{i}_{\mathrm{pv}}\right)}{\mathrm{d}{v}_{\mathrm{pv}}}}=i_{\mathrm{pv}}+v_{\mathrm{pv}}{\displaystyle \frac{\mathrm{d}{i}_{\mathrm{pv}}}{\mathrm{d}{v}_{\mathrm{pv}}}}$$

(1)

where the micro-increment of the output current of the PV array with respect to the output voltage can be obtained through a low-pass filter, as demonstrated in Equations (2)–(4).

$$i_{\mathrm{f}}\left(s\right)={\displaystyle \frac{1}{Ts+1}}{i}_{\mathrm{pv}}\left(s\right)$$

(2)

$$s\cdot i_{\mathrm{f}}\left(s\right)={\displaystyle \frac{i_{\mathrm{pv}}\left(s\right)-i_{\mathrm{f}}\left(s\right)}{T}}$$

(3)

$${\displaystyle \frac{\mathrm{d}{p}_{\mathrm{pv}}}{\mathrm{d}{v}_{\mathrm{pv}}}}=i_{\mathrm{pv}}+v_{\mathrm{pv}}{\displaystyle \frac{\mathrm{d}{i}_{\mathrm{pv}}}{\mathrm{d}{v}_{\mathrm{pv}}}}\approx i_{\mathrm{pv}}+v_{\mathrm{pv}}{\displaystyle \frac{\mathrm{d}{i}_{\mathrm{f}}}{\mathrm{d}{v}_{\mathrm{f}}}}=i_{\mathrm{pv}}+v_{\mathrm{pv}}{\displaystyle \frac{i_{\mathrm{pv}}-i_{\mathrm{f}}}{v_{\mathrm{pv}}-v_{\mathrm{f}}}}$$

(4)

where i_f(s) denotes the low-frequency component of the PV array output current, and 1/T denotes the cutoff frequency of the low-pass filter, which can be set to 1000 Hz. v_f denotes the low-frequency component of the PV array output voltage.

Based on Equation (4), the conductance micro-increment of the PV array can be obtained through the method demonstrated in Figure 4. Therefore, the conductance micro-increment can be adopted as the control objective for realizing the maximum power tracking control of the PV power generation system.

3.2. Control Strategies for Energy Storage Devices

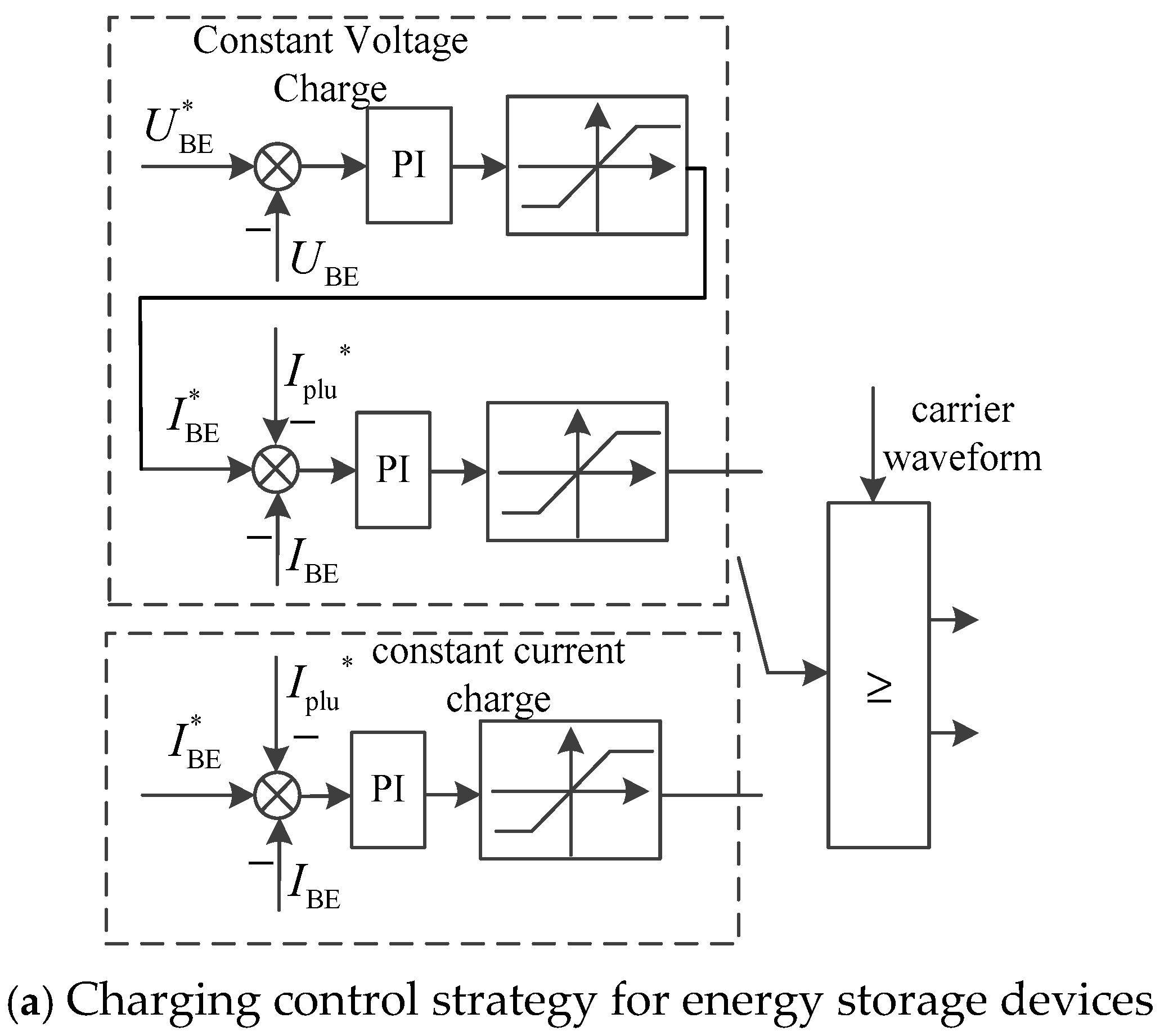
The energy storage device adopts a constant-current and constant-voltage control strategy. The charging process is divided into two stages: constant-current charging and constant-voltage charging. During the initial charging stage, charging is performed with a constant high current. When the terminal voltage of the energy storage device reaches the pre-set voltage value, a constant voltage control strategy is employed, during which the charging current is gradually reduced. Charging of the energy storage device is completed when the charging current decreases to the set value. When the energy storage device is discharged, constant-current discharge control is employed.

One of the functions of the energy storage device in the photovoltaic energy storage charging pile is to absorb the pulse current generated during the initiation of charging by a new energy vehicle, thereby mitigating sudden drops in the DC bus voltage that may cause system shutdown. The charging control strategy and discharging control strategy of the energy storage device are presented in Figure 5a,b, respectively.

3.3. Segmented Control Strategy for Electric Vehicle Charging Pile

Lithium iron phosphate batteries are predominantly employed in most new energy electric vehicles. The charging methods for charging piles are classified into AC charging and DC charging, with AC charging typically utilizing single-phase or three-phase power supplies featuring low rated currents. DC charging posts have high charging power and high current ratings. Lower power capacity is observed in residential power grids of rural areas; thus, AC charging piles are employed, with a typical charging duration ranging from 6 to 10 h.

Constant current charging, constant voltage charging, pulse charging, and reflex charging are employed in new energy electric vehicles. The use of a reflective charging method can remove the polarization phenomenon of the battery in new energy electric vehicles and increase the service life of the battery as well as the number of cycles of charging and discharging.

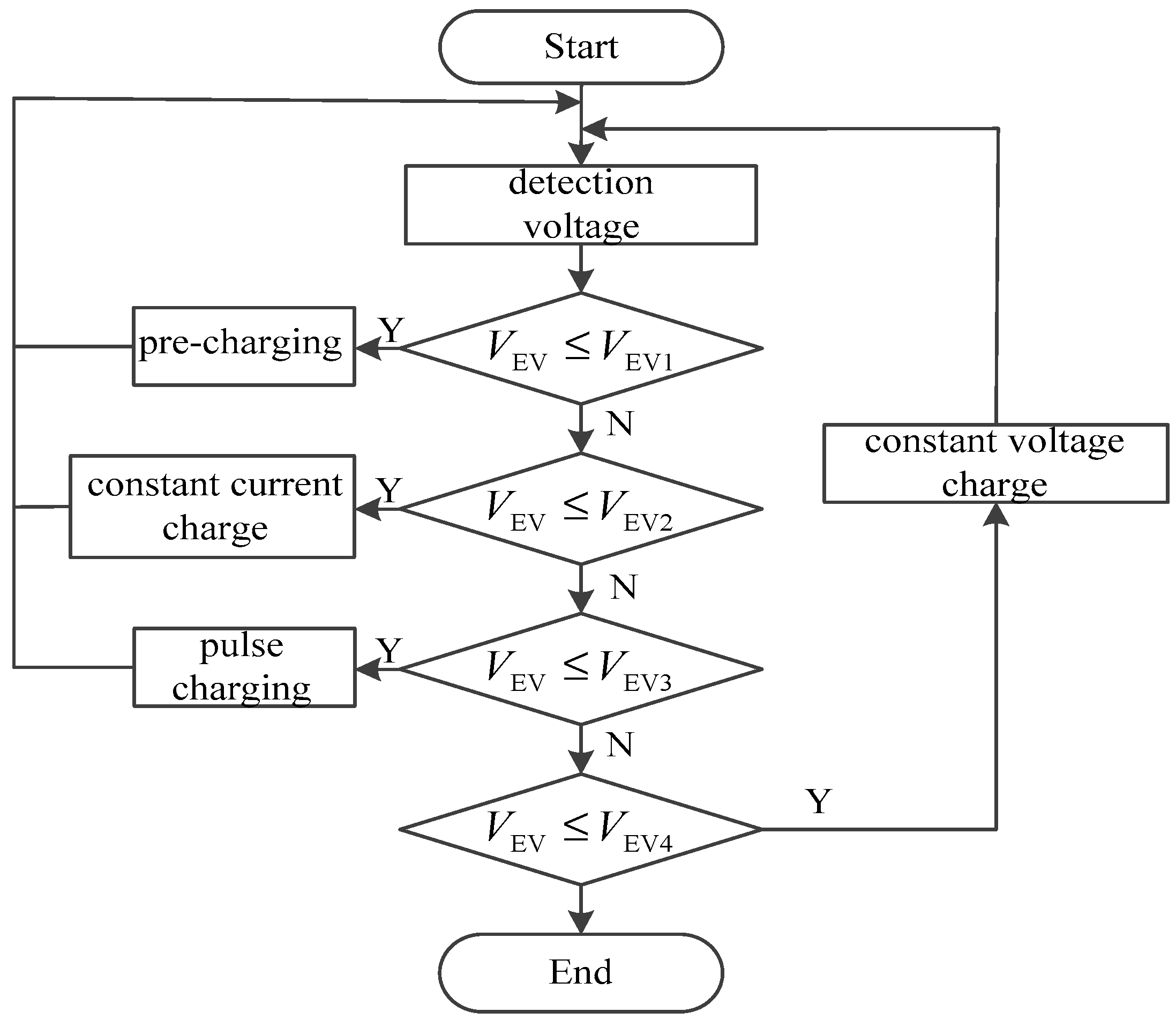
Considering both the charging time and service life of the battery, the segmented fast charging strategy is adopted. This approach employs different charging methods across distinct stages and can be divided into three stages.

In the pre-charging stage, the SOC of the battery is maintained below 10%, its primary function is battery protection. The segmented constant current (SCC) charging stage is recognized as the rapid charging stage. The high-current positive/negative pulse charging stage involves charging the battery with large-amplitude positive and negative pulse currents.

To ensure that the charge capacity of each charging segment is approximately equal for rechargeable battery cells, the state of charge (SOC) can be divided as follows: 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, and 99%.

The charging strategy of the charging pile is depicted in Figure 6.

3.4. Grid-Connected Inverter Control Strategy

The single-phase inverter topology is shown in Figure 2c. Considering the equivalent inductance L_g of the grid transmission line, the transfer function of the LCL filter is

$$G\left(s\right)={\displaystyle \frac{i_{L2}\left(s\right)}{u_{\mathrm{inv}}\left(s\right)}}={\displaystyle \frac{1}{C{L}_1\left(L_2+L_g\right)s^3+\left(L_1+L_2+L_g\right)s}}$$

(5)

From Equation (5), it can be seen that the grid inductive reactance affects the performance of the LCL filter due to the weak grid characteristics, which changes the resonant frequency.

When the PI controller is employed in the control system of a single-phase grid-connected inverter, steady-state errors in amplitude and phase are introduced during the tracking of sinusoidal signals, and the anti-interference capability is found to be weak. While strong anti-interference performance is exhibited and no steady-state errors are observed during sinusoidal signal tracking when a PR controller is employed, the gain of the PR controller is relatively low at non-fundamental frequencies, and system performance may deteriorate if the grid frequency shifts.

The quasi-PR controller offers the advantage of enabling sinusoidal signal tracking without steady-state errors and can mitigate the impact of grid fundamental frequency offset on the control system’s performance. The transfer function of the quasi-PR controller is as follows:

$$G_{\mathrm{PR}}\left(s\right)=K_{\mathrm{p}\_\mathrm{PR}}+{\displaystyle \frac{2K_{\mathrm{R}\_\mathrm{PR}}{\omega }_{0\_\mathrm{PR}}s}{s^2+2{\omega }_{0\_\mathrm{PR}}s+{\omega }_{0\_\mathrm{PR}}{{\omega }_{0\_\mathrm{PR}}}^2}}$$

(6)

where K_{p_PR}, K_{R_PR}, and ω_{0_PR} are, respectively, defined as the scaling coefficient, resonance coefficient, and fundamental angular frequency of the quasi-PR controller.

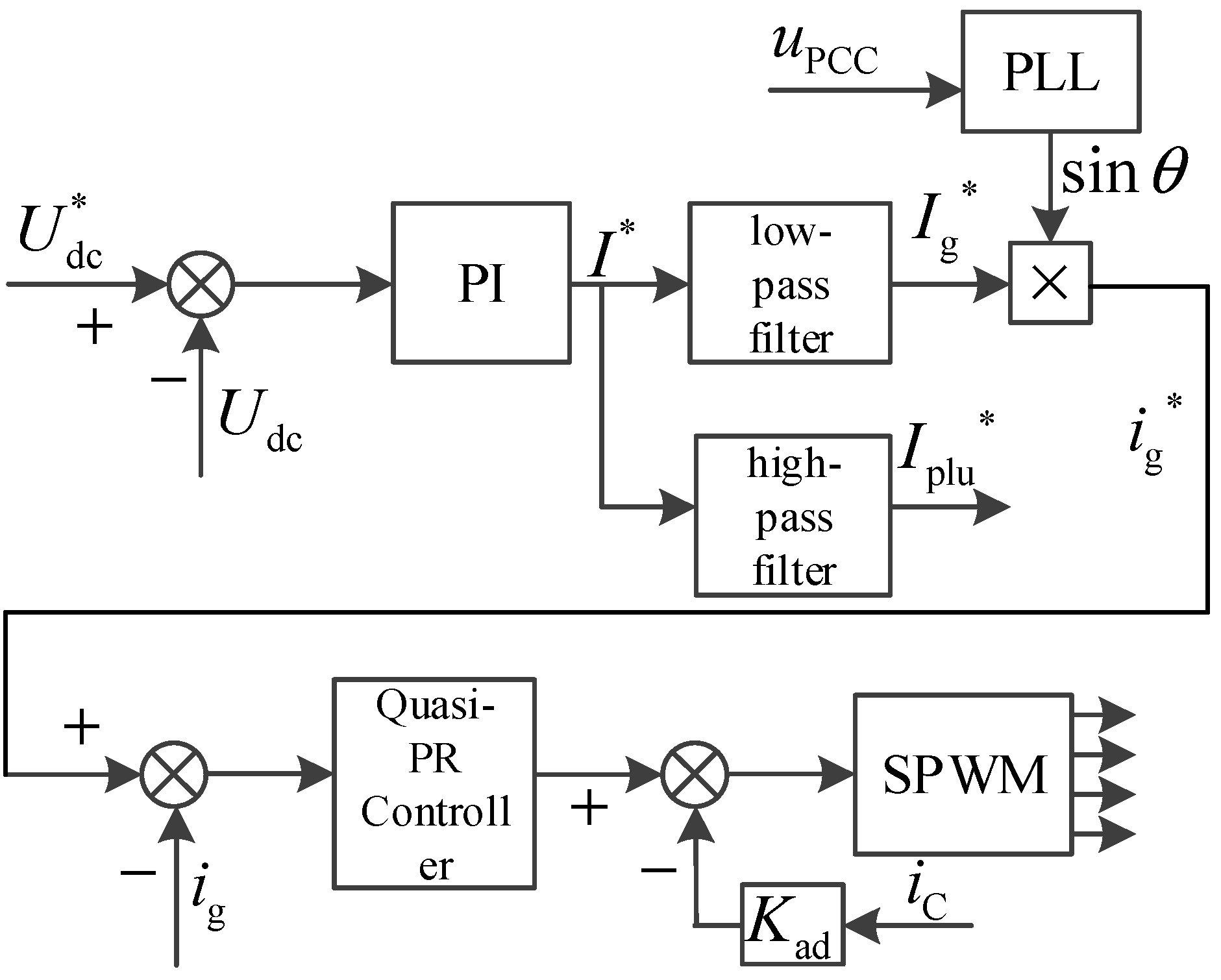
The single-phase grid-connected inverter control system employing a quasi-PR controller is depicted in Figure 7. I^* is the current reference value output by the DC bus voltage controller, I_g^* is the low-frequency component of the current reference value, and I_plu^* is the high-frequency component of the current reference value, where I_g^* is provided by the single-phase grid connected inverter and I_plu^* is provided by the battery system.

When the operating condition of a weak grid changes, the equivalent impedance L_g of the transmission line varies. The synchronization of the voltage phase angle at the point of common coupling (PCC) using a phase-locked loop (PLL) can be expressed as follows:

$$u_{\mathrm{pcc}}=u_{\mathrm{g}}+{\omega }_{\mathrm{g}}{L}_{\mathrm{g}}{i}_{\mathrm{L2}}$$

(7)

where ω_g is the angular frequency of the grid voltage. Equation (7) indicates a coupling relationship between the PLL and L_g. Therefore, using a conventional PLL may result in poor system stability or even system failure. The second-order generalized integrator phase-locked loop (SOGI-PLL) can reduce the system bandwidth, filter out high-order harmonics while having minimal impact on the fundamental component, and ensure the accuracy of phase angle detection at the PCC. The block diagram of SOGI-PLL is shown in Figure 8.

In the diagram, u_{pcc_α} and u_{pcc_β} represent the α-axis and β-axis components of u_pcc in the stationary two-phase coordinate system; u_{pcc_d} and u_{pcc_q} are the d-axis and q-axis components in the rotating two-phase coordinate system. u_q* denotes the reference value of u_{pcc_q}, Δu_q is the error of u_{pcc_q}, s is the differential operator, and k_ff is the first-order differential coefficient.

To further reduce the impact of the transmission line inductance on the PLL, a grid current feedforward module is adopted. This module can reduce the effect of the term ω_gL_gi_L2 in Equation (7) on the PLL. Since the current feedforward loop is added, the output of the SOGI_PLL is no longer the phase of u_pcc, as shown in Figure 9.

Therefore, a phase compensation module is added, which can be expressed as follows:

$${\phi }_{\mathrm{c}}=f\left(I_{\mathrm{ref}}\right)=\arctan {\displaystyle \frac{100\pi k_{\mathrm{ff}}{I}_{\mathrm{ref}}}{U_{\mathrm{m}}}}$$

(8)

where I_ref is the amplitude of i_L2, and U_m is the amplitude of U_g.

4. Simulation Results

To verify the proposed control strategy in this paper, a simulation model was built. Figure 10 shows the simulation model built through Matlab R2020b/simulation. Figure 10a shows the PV system, Figure 10b shows MPPT for PV system, Figure 10c shows the single-phase full-bridge inverter, Figure 10d shows the buck/boost converter, Figure 10e shows the SOGI-PLL, and Figure 10f shows the control strategy for a buck/boost converter.

The parameters in the simulation model are shown in

Table 2. The parameters in the simulation model.

Parameters	Value	Parameters	Value
DC bus voltage	400 V	L1	2.578 mH
RMS value of AC voltage	220 V	L2	0.357 mH
C in LCL filter	10.3 μF	Total charging time of battery	9 h
RMS value of output power of PV	4 kW	Rated charging current of charging pile	48 A
RMS value of upcc	400 V	RMS value of iL2	35 A

.

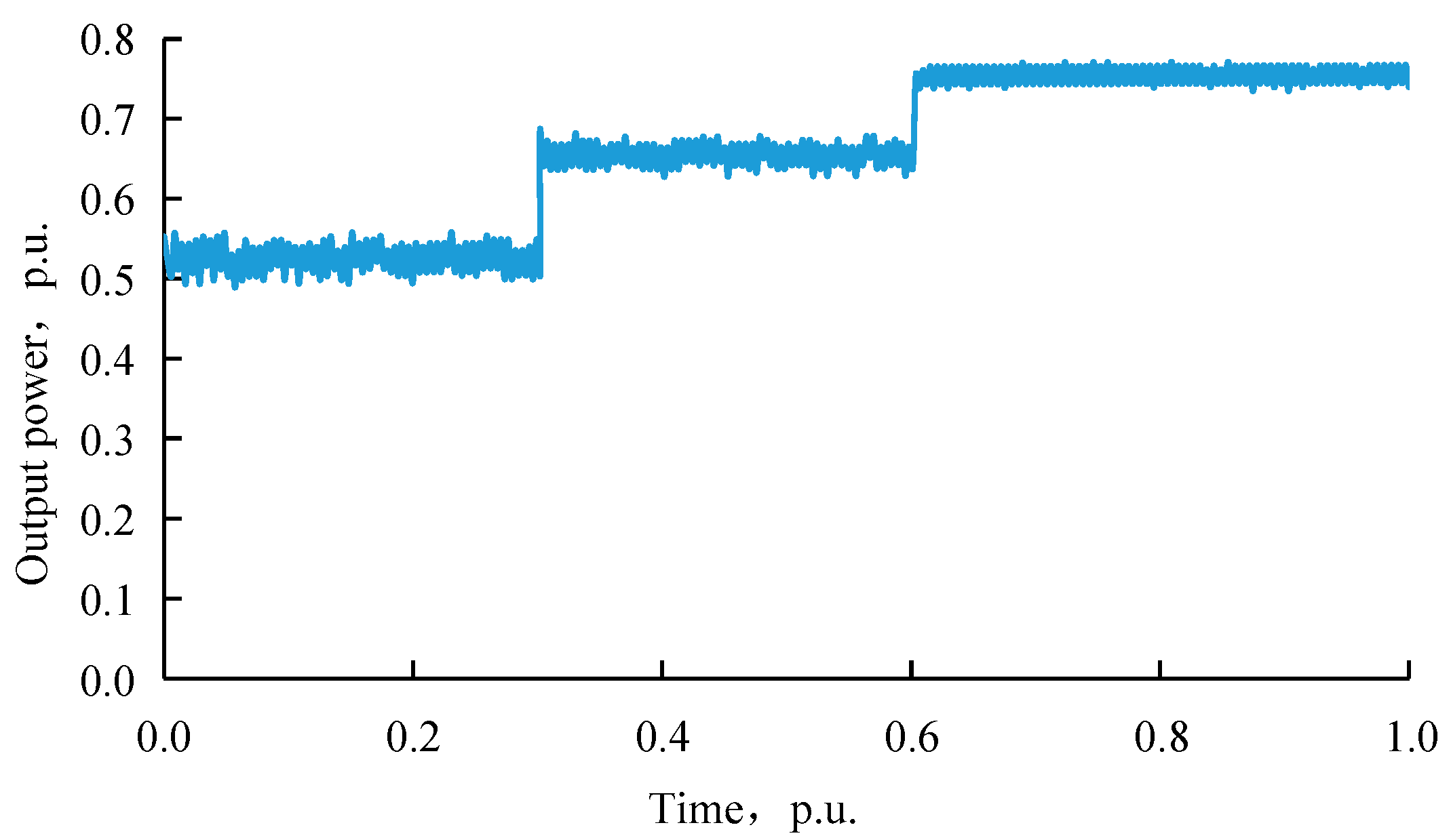
To verify the maximum power point tracking (MPPT) control strategy of the photovoltaic power generation system based on incremental conductance, the irradiance was set to increase from 600 W/m² to 800 W/m², and then to 1000 W/m². The output power curve of the photovoltaic power generation system under these conditions is shown in Figure 11. The rated time in Figure 11 is 6 h.

As shown in Figure 11, with the increase in irradiance intensity, the output power of the photovoltaic power generation system also increases, indicating that the maximum power point tracking can be effectively achieved.

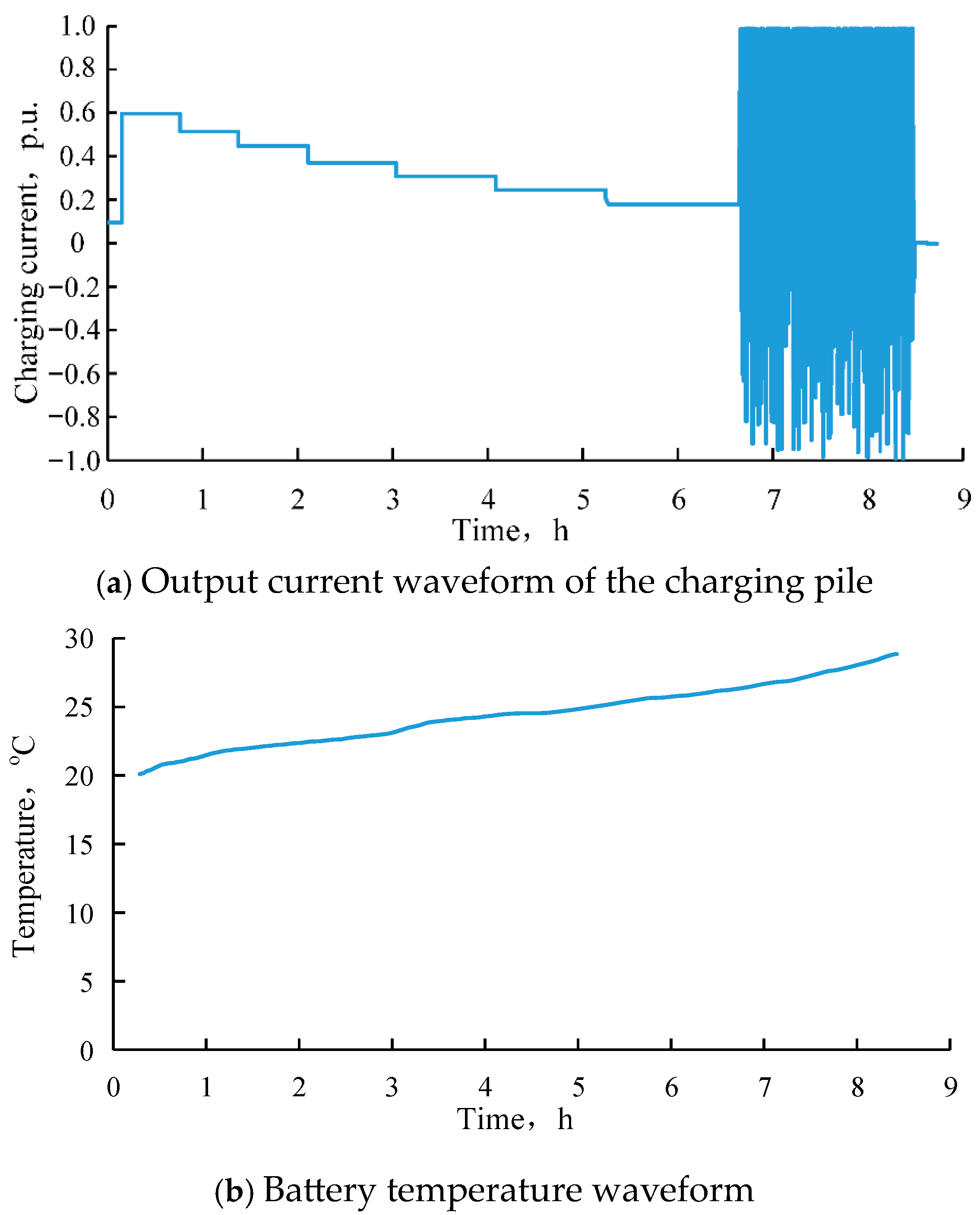
Figure 12a shows the output current waveform of the charging pile for the new energy electric vehicle, and Figure 12b illustrates the temperature rise in the battery during charging.

As shown in Figure 12, the charging process of the battery for the new energy electric vehicle is divided into four stages. First, a small current is used for pre-charging. Then, constant current charging is applied to raise the battery state of charge (SOC) to approximately 80%. After that, large positive and negative pulse currents are used to further charge the battery to around 98–99% SOC. Finally, constant current charging is applied again to increase the SOC to 99.9%, completing the charging process. From the battery temperature rise curve, it can be observed that the battery temperature increases gradually from room temperature (20 °C) to about 29 °C. The temperature rise is small, indicating that the method does not cause thermal damage to the battery.

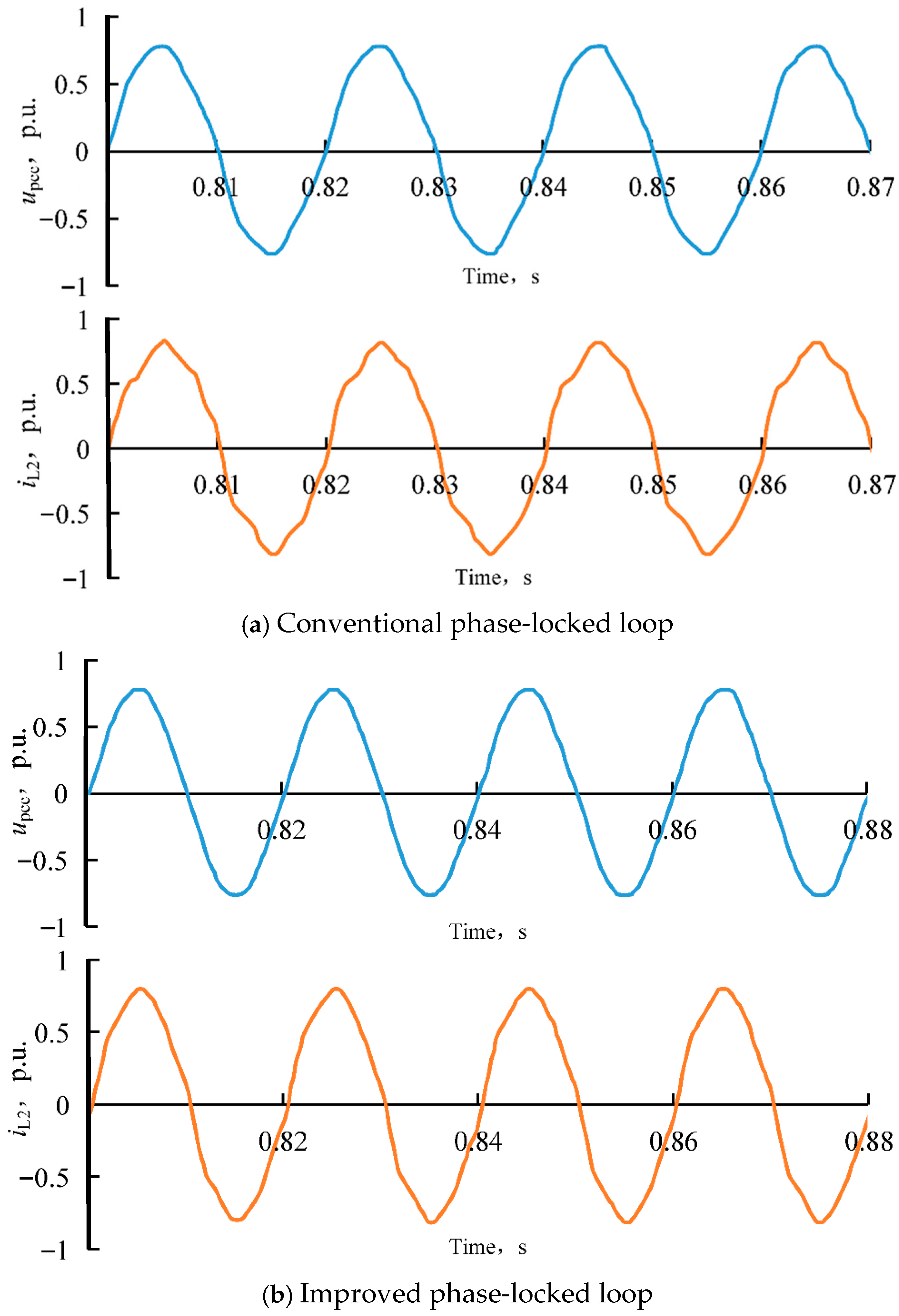
Figure 13a shows the output voltage and current waveforms of the single-phase grid-connected inverter when the transmission line impedance is set to 1 mH and a conventional phase-locked loop (PLL) is used. Figure 13b shows the waveforms when the proposed improved PLL is adopted.

As shown in Figure 13, when the improved PLL is applied, the output current of the grid-connected inverter exhibits lower harmonic content. In contrast, under the control system with a conventional PLL, the harmonic content of the inverter output current increases as L_g (the grid-side inductance) rises, indicating a greater influence of transmission line impedance under weak grid conditions.

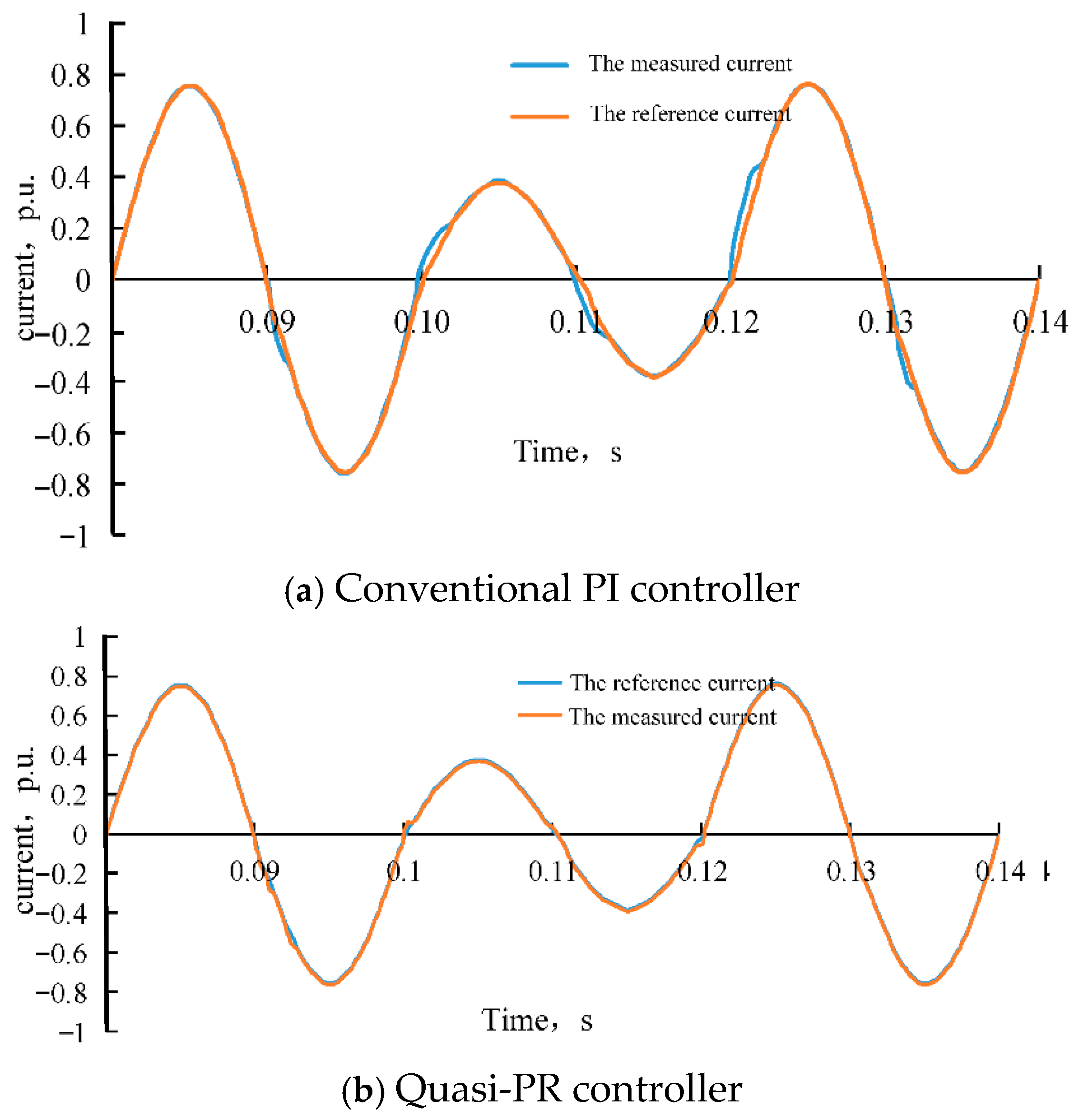
Figure 14a shows the output current of the single-phase grid-connected inverter when a conventional PI controller is used, under a scenario where the solar irradiance changes suddenly. Figure 14b presents the output current waveform when a quasi-PR controller is used under the same conditions.

As shown in Figure 14, the single-phase grid-connected inverter using the quasi-PR controller is able to track the reference current of the system without steady-state error.

5. Conclusions

The power grid in remote rural areas exhibits weak grid characteristics. Distributed photovoltaic–storage charging piles can effectively solve the charging difficulties of new energy electric vehicles in these regions. In the distributed system, the photovoltaic generation unit adopts a maximum power point tracking control strategy based on improved incremental conductance. The charging pile adopts a segmented charging control method. The single-phase grid-connected inverter uses a quasi-PR controller, and the phase-locked loop employs a SOGI-PLL with grid current feedforward compensation. With these control strategies, the distributed photovoltaic–storage charging pile can overcome the stability issues of power electronic equipment in weak grid conditions and exhibits strong robustness. This provides crucial technical underpinning for promoting electric vehicle (EV) proliferation in remote regions.

In subsequent research, we will undertake a dedicated study on coordinated control strategies for distributed solar–storage charging stations to further enhance their operational efficacy.