Acoustic Characterization of Leakage in Buried Natural Gas Pipelines
Abstract
1. Introduction
2. Simulation Methods
2.1. Computational Domain and Boundary Conditions
- (1)
- The spatial structure of the soil is assumed to remain unchanged throughout the leakage process. No chemical reactions occur between the leaking gas and the surrounding soil, and the influence of gravity on fluid flow within the porous medium is neglected.
- (2)
- The soil pores are considered to be filled with air, and the soil moisture content is neglected.
- (3)
- The natural gas inside the pipeline is modeled as pure methane, based on the fact that methane typically comprises 75–98% of natural gas.
2.2. Mathematical Model
2.2.1. Governing Equations
- (1)
- Species Transport Model
- (2)
- Realizable k-ε Model
- (3)
- LES Model
2.2.2. Acoustic Field Calculation Model
- (1)
- Broadband Noise Source Model
- (2)
- FW-H Model
2.3. Numerical Method
2.4. Mesh Independence Verification
3. Numerical Results and Discussion
3.1. Leakage Flow Field Analysis
3.1.1. Effect of Varying Pipeline Pressure on Flow Field Characteristics
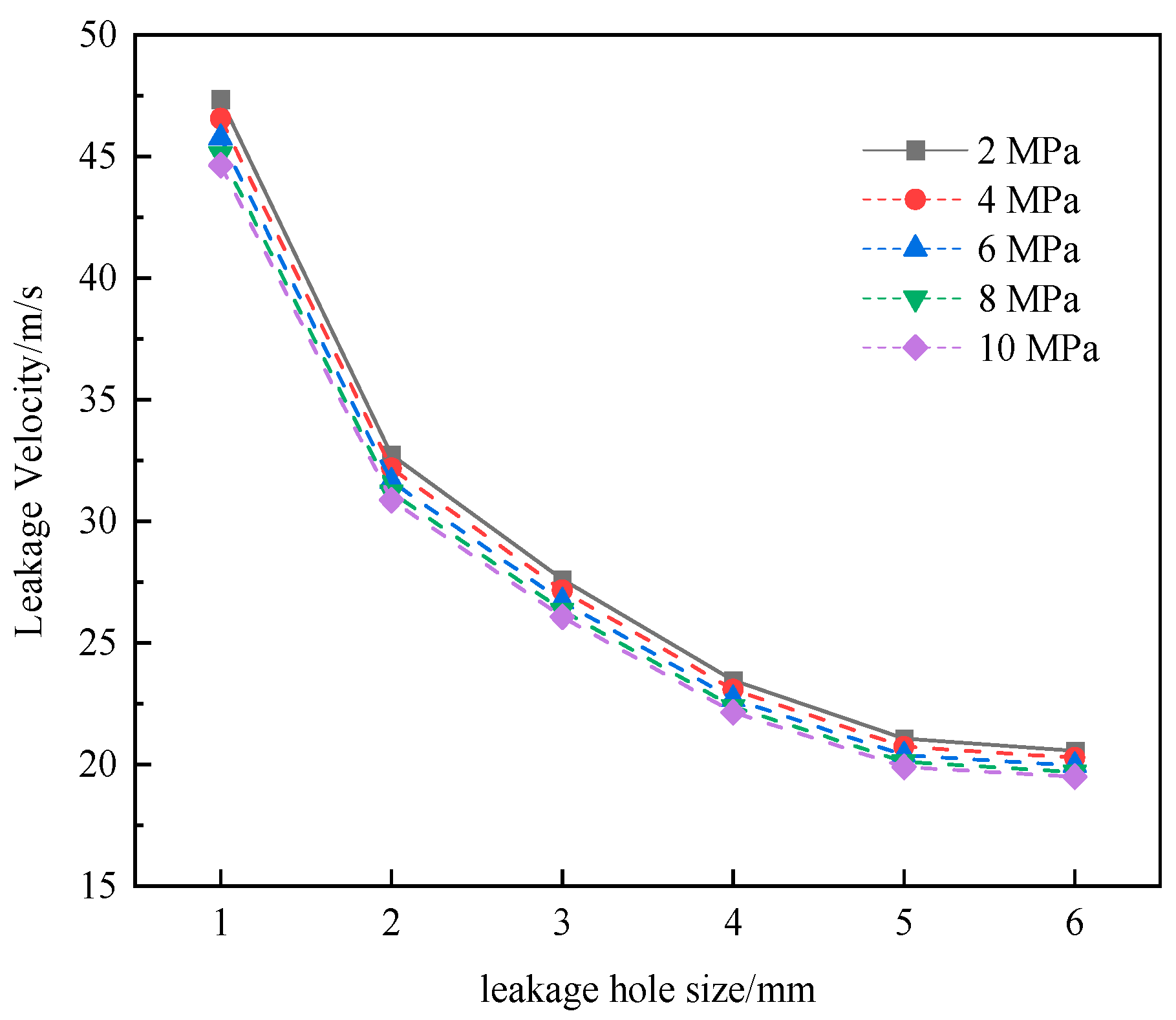
3.1.2. Influence of Leakage Hole Size on the Flow Field
3.1.3. Influence of Soil Type on the Flow Field
3.1.4. Influence of Leakage Direction on the Flow Field
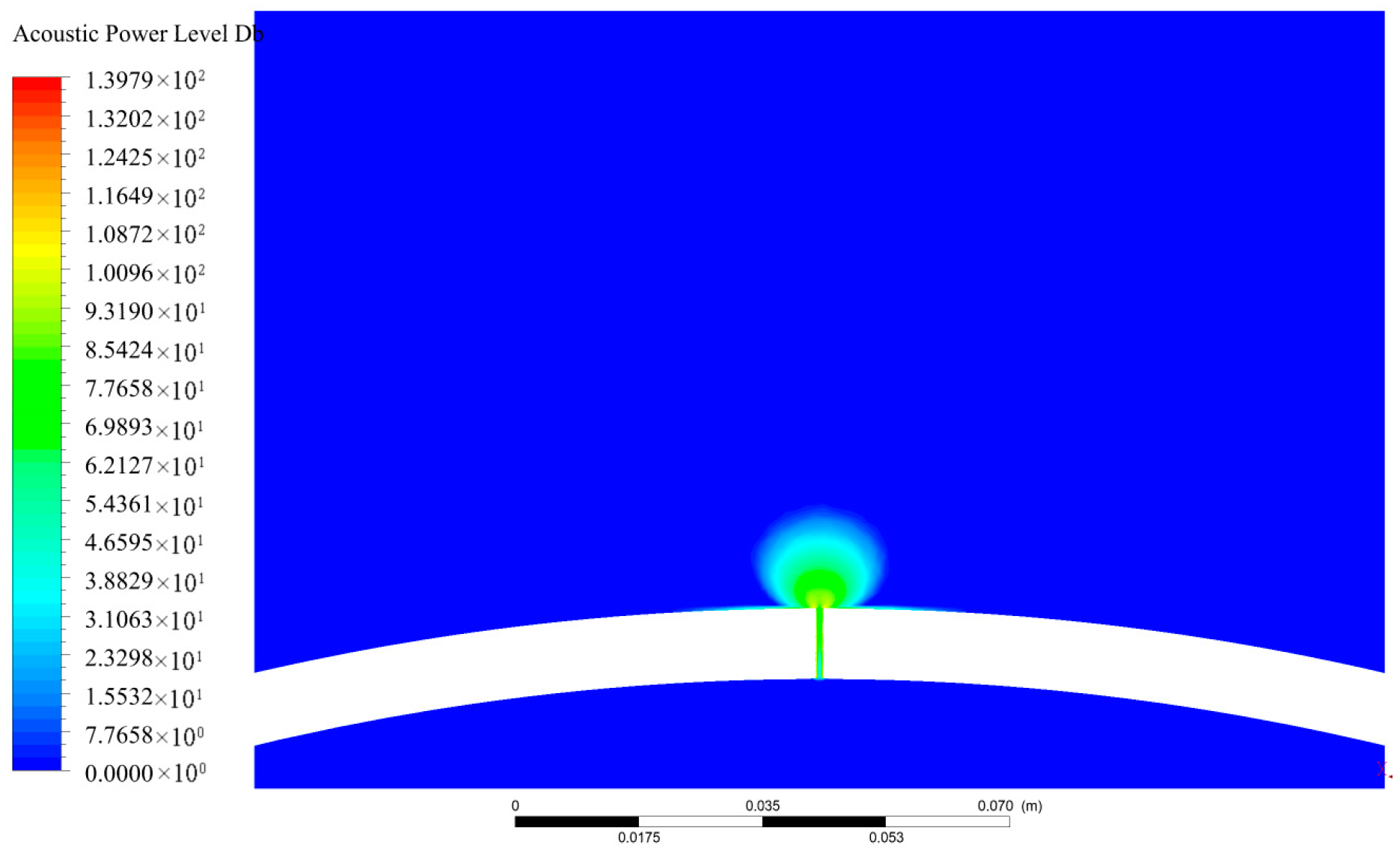
3.2. Analysis of Leakage Acoustic Source Characteristics
3.2.1. Influence of Pipeline Pressure on Acoustic Source Characteristics
3.2.2. Influence of Leakage Hole Size on Acoustic Source Characteristics
3.2.3. Influence of Soil Medium on Acoustic Source Characteristics
3.2.4. Influence of Leakage Direction on Acoustic Source Characteristics
3.3. Leakage Sound Field Characteristics
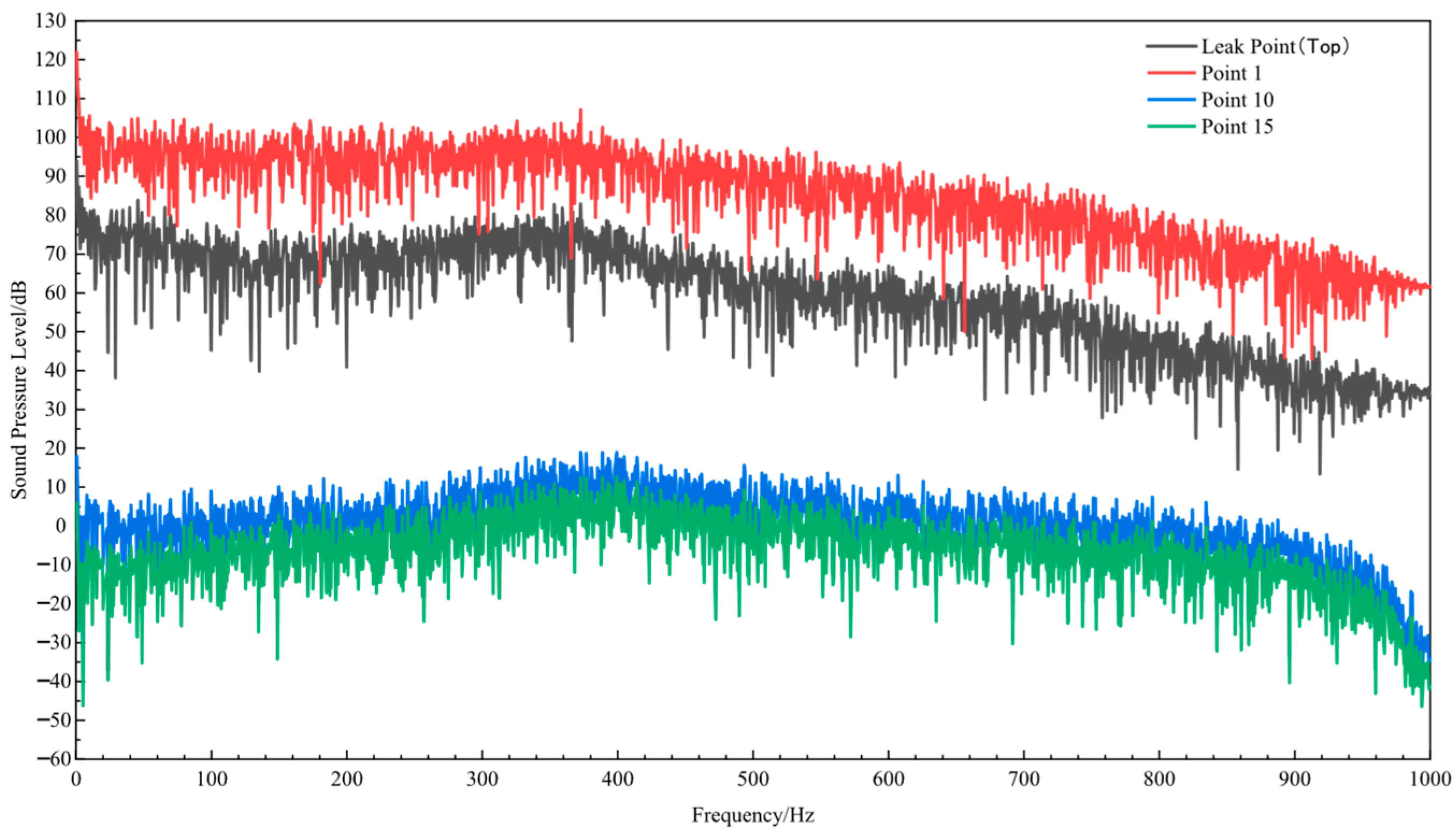
3.3.1. Influence of Pipeline Pressure on Sound Field Characteristics
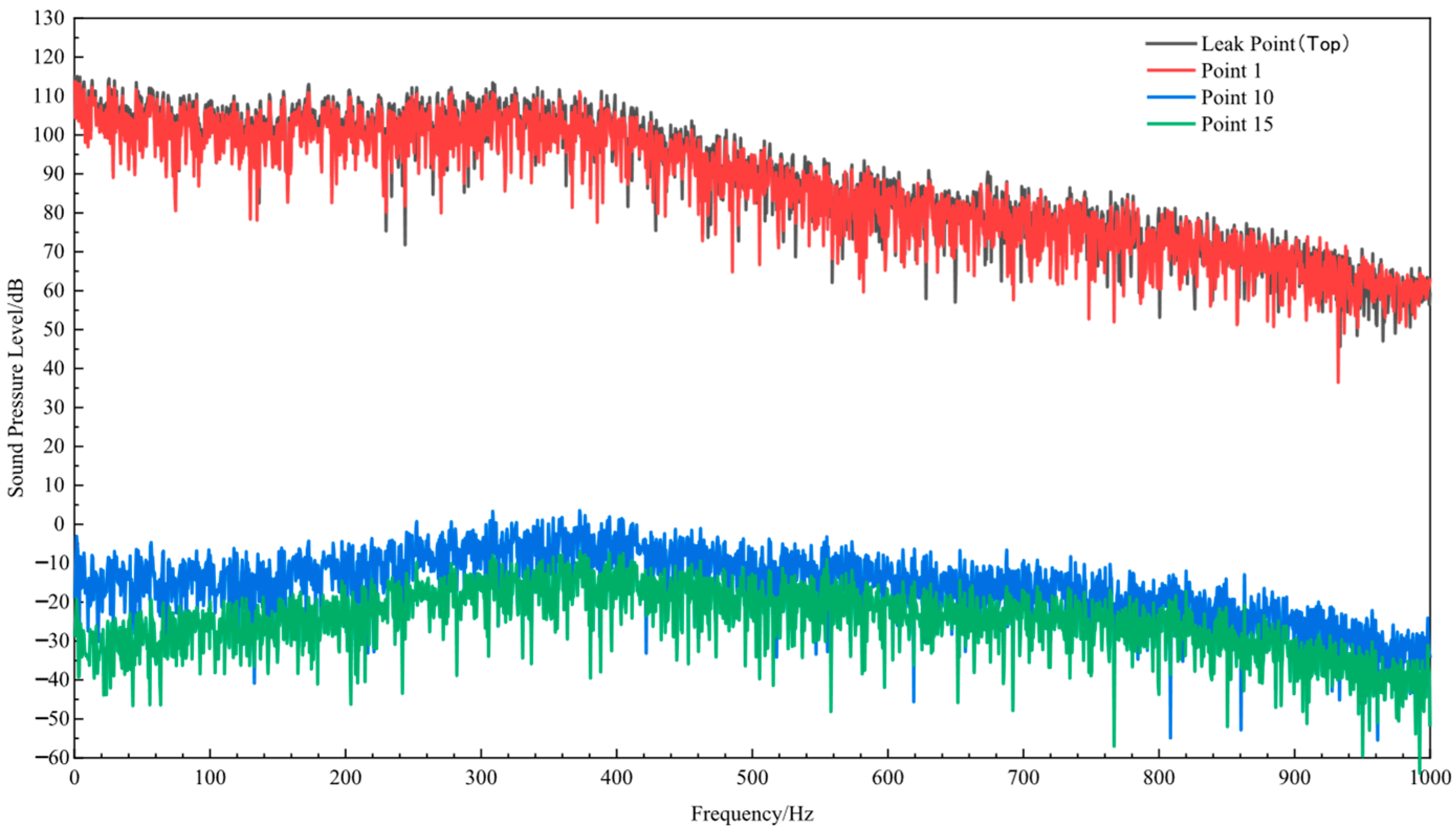
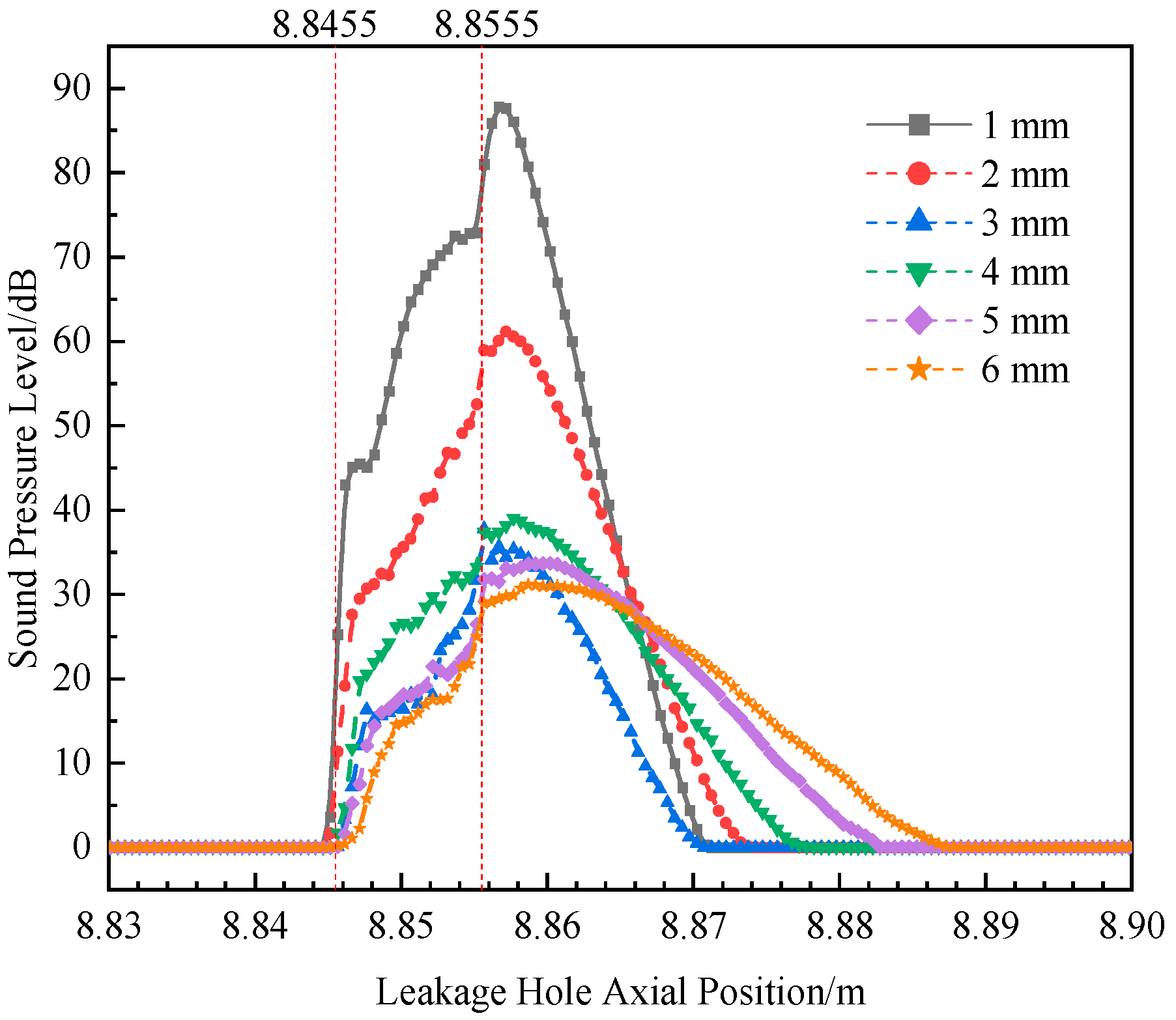
3.3.2. Influence of Leakage Hole Size on Sound Field Characteristics
3.3.3. Influence of Soil Medium on Sound Field Characteristics
3.3.4. Influence of Leakage Direction on Sound Field Characteristics
3.4. Relationship Between Leakage Noise and Flow Field Characteristics in Natural Gas Pipelines
4. Practical Considerations
5. Conclusions
- (1)
- Leakage noise in buried natural gas pipelines is primarily composed of dipole sources (caused by gas–solid interactions) and quadrupole sources (arising from turbulent stresses). These noise generation mechanisms can be effectively characterized through key flow field parameters.
- (2)
- The simulated results under different hole sizes and pipeline pressures reveal that leakage noise energy is predominantly concentrated in the 0–500 Hz frequency range, with SPL values ranging from approximately 20 dB to 160 dB. This confirms the feasibility of acoustic methods for leak detection. Additionally, within a spatial range of 1.5 m above and 4 m below the leakage hole, the overall SPL remains positive, offering a practical reference for sensor placement and experimental design.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rui, Z.; Han, G.; Zhang, H.; Wang, S.; Pu, H.; Ling, K. A New Model to Evaluate Two Leak Points in a Gas Pipeline. J. Nat. Gas Sci. Eng. 2017, 46, 491–497. [Google Scholar] [CrossRef]
- Aguilera, R.F. The Role of Natural Gas in a Low Carbon Asia Pacific. Appl. Energy 2014, 113, 1795–1800. [Google Scholar] [CrossRef]
- Global Energy Demand Rose by 2.3% in 2018, Its Fastest Pace in the Last Decade. International Energy Agency: Paris, France, 26 March 2019. Available online: https://www.iea.org/news/global-energy-demand-rose-by-23-in-2018-its-fastest-pace-in-the-last-decade (accessed on 8 June 2025).
- Halim, S.Z.; Yu, M.; Escobar, H.; Quddus, N. Towards a Causal Model from Pipeline Incident Data Analysis. Process Saf. Environ. Prot. 2020, 143, 348–360. [Google Scholar] [CrossRef]
- Wang, X.; Tan, Y.; Zhang, T.; Xiao, R.; Yu, K.; Zhang, J. Numerical Study on the Diffusion Process of Pinhole Leakage of Natural Gas from Underground Pipelines to the Soil. J. Nat. Gas Sci. Eng. 2021, 87, 103792. [Google Scholar] [CrossRef]
- Awalt, J. Global Pipeline Construction Outlook 2023: Asia, Europe Pipeline Plans Surge as Russia Sanctions Roil Energy Trade. Pipeline Gas J. 2023, 250. [Google Scholar]
- Weller, Z.D.; Hamburg, S.P.; von Fischer, J.C. A National Estimate of Methane Leakage from Pipelines in Natural Gas Local Distribution Systems. Environ. Sci. Technol. 2020, 54, 7515–7524. [Google Scholar] [CrossRef] [PubMed]
- Highwood Emissions Management. Leak Detection Methods for Natural Gas Gathering, Transmission, and Distribution Pipelines; Highwood Emissions Management: Calgary, Canada, 2022. [Google Scholar]
- Wehnert, P. Overview of Leak Detection Solutions for Improving Gas Safety. Trenchless Technology Magazine, 2021. [Google Scholar]
- Korlapati, N.V.S.; Khan, F.; Noor, Q.; Mirza, S.; Vaddiraju, S. Review and Analysis of Pipeline Leak Detection Methods. J. Pipeline Sci. Eng. 2022, 2, 100052. [Google Scholar] [CrossRef]
- Sivathanu, Y. Natural Gas Leak Detection in Pipelines—Technology Status Report; U.S. DOE NETL: Pittsburgh, PA, USA, 2004. [Google Scholar]
- PHMSA (Pipeline and Hazardous Materials Safety Administration). Pipeline Safety: Requirement of Leak Detection for Gas Pipelines. Dly. J. United States Gov. 2021, 86, 2210. [Google Scholar]
- Zhang, K.; Ma, R.; Chen, S.; Gong, Y. Simulation and Experimental Research on the Propagation Mechanisms of Acoustic Energy inside the Pipeline to Detect the Leakage. Geoenergy Sci. Eng. 2024, 243, 213410. [Google Scholar] [CrossRef]
- Zhang, Z.; Yuan, H.; Fu, M.; Chen, T.; Gao, Y.; Feng, G. Theoretical Investigation on the Characteristics of Leak Noise for Natural Gas Pipelines. J. Theor. Comput. Acoust. 2020, 28, 2050005. [Google Scholar] [CrossRef]
- Lin, T.; Wang, Z.; Hu, B.; Ji, Y.; Liang, X. Simulation and Experimental Study of Buried Natural Gas Pipeline Leak Detection Based on Sound Source Characteristics. Therm. Sci. 2024, 28, 101–113. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, X.; Zhang, Y. A Review on the Research and Application of Big Data Technology in Natural Gas Downstream. Oil Gas New Energy 2021, 33, 1–5. [Google Scholar]
- Zhang, J.; Lian, Z.; Zhou, Z.; Xiong, M.; Lian, M.; Zheng, J. Acoustic Method of High-Pressure Natural Gas Pipelines Leakage Detection: Numerical and Applications. Int. J. Press. Vessel. Pip. 2021, 194, 104540. [Google Scholar] [CrossRef]
- Han, B.; He, J.; Wang, J. Acoustic Detection and Localization Method for Natural Gas Pipeline Leakage. Noise Vib. Control. 2021, 41, 58–64, 146. [Google Scholar]
- Shang, W.; Xie, R. Research on Leakage Localization Detection Technology for Natural Gas Pipelines. Petrochem. Technol. 2015, 22, 143–144. [Google Scholar]
- Zhang, X.; Wang, J.; Li, H.; Liu, Y. Experimental Validation and CFD Analysis of Methane Leakage Behavior from a Buried High-Pressure Pipeline. J. Nat. Gas Sci. Eng. 2024, 113, 104220. [Google Scholar]
- Bagheri, M.; Sari, A. Study of Natural Gas Emission from a Hole on Underground Pipelines Using Optimal De-sign-Based CFD Simulations: Developing Comprehensive Soil Classified Leakage Models. J. Nat. Gas Sci. Eng. 2022, 102, 104583. [Google Scholar] [CrossRef]
- Yue, J.; Chen, Y.; He, L. Numerical Investigation of Natural Gas Leakage Diffusion and Risk Evaluation in Buried Pipelines near Underground Structures. Process Saf. Environ. Prot. 2024, 178, 859–873. [Google Scholar]
- Jin, H.; Zhang, L.; Liang, W.; Ye, Y.; Ding, Q. Numerical Simulation of Acoustic Source Characteristics and Propagation Mechanism in Natural Gas Pipeline Leakage. Acta Pet. Sin. 2014, 35, 172–177. [Google Scholar] [CrossRef]
- Martins, A.F.; Seleghim, P.R. Modeling and Experimental Validation of the Hydrodynamic Transient Associated with Leaks in Pipelines. In Proceedings of the 20th International Congress of Mechanical Engineering (COBEM 2009), Gramado, Brazil, 15–20 November 2009. [Google Scholar]
- Oh, Y.G.; Kim, J.T.; Park, J.H. Acoustic Characteristics of a Leak from a Crack in a Pressurized Pipe. Nucl. Eng. Des. 2018, 327, 198–211. [Google Scholar] [CrossRef]
- Uchendu, I.C.; Marburg, S.; McDonald, A.G. Leak Detection and Localisation in Pipelines Using Transient Acoustic Signals. In Proceedings of the ISMA2020 International Conference on Noise and Vibration Engineering, Leuven, Belgium, 7–9 September 2020. [Google Scholar]
- Xiao, W.; Joseph, P.F.; Li, F. Prediction of Leak Noise Spectra in Plastic and Metal Water Distribution Pipes. J. Sound Vib. 2020, 488, 115646. [Google Scholar] [CrossRef]
- Shi, X.; Fan, W.; Lin, B.; Wang, D. Simulation of Pipeline Leakage Flow and Sound Field Based on Fluent and LMS Virtual.Lab. In Proceedings of the 2nd China International Conference on Process Safety (AIChE), Qingdao, China, 28–29 August 2014. [Google Scholar]
- Liu, K. Numerical Simulation of Natural Gas Pipeline Leakage Considering Throttling Effect. Ph.D. Thesis, China University of Petroleum, Beijing, China, 2019. [Google Scholar]
- Peng, T.; Qian, R. A Review on the Theoretical Research of Large Eddy Simulation (LES). In Proceedings of the 8th National Academic Symposium on Modern Structural Engineering, Tianjin, China, 18–21 July 2008. [Google Scholar]
- Smagorinsky, J. General Circulation Experiments with Primitive Equations. Mon. Weather. Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Han, H. Numerical Simulation of Flow Field and Acoustic Field Characteristics in Pipeline Micro-Leakage. Master’s Thesis, North China Electric Power University, Beijing, China, 2018. [Google Scholar]
- Bergeron, R.G.; Kim, W.; Kim, J. Broadband Noise Prediction for Aerofoils with a Serrated Trailing Edge Based on Amiet’s Theory. J. Sound Vib. 2021, 512, 116352. [Google Scholar]
- Fiore, M.; Daroukh, M.; Montagnac, M. Broadband Noise Prediction of a Counter Rotating Open Rotor Based on LES Simulation with Phase-Lagged Assumption (Draft). J. Sound Vib. 2021, 514, 116431. [Google Scholar] [CrossRef]
- Hyeonu, H.; Mathew, S.; Jaehyung, J.; Arup, N. Acoustic Metasurface-Aided Broadband Noise Reduction in Automobile Induced by Tire-Pavement Interaction. Materials 2021, 14, 4240. [Google Scholar] [CrossRef]
- Wang, S.; Tang, J.; Qiu, X.; Burrentt, I.S. Broadband Noise Insulation of Windows Using Coiled-up Silencers Consisting of Coupled Tubes. Sci. Rep. 2021, 11, 14023. [Google Scholar] [CrossRef]
- Zawadzki, I.; Gély, A.; Rezgui, M.; Michel, R. Analytical Prediction of the Blade Trailing Edge Broadband Noise of a Plug Fan. J. Phys. Conf. Ser. 2021, 1909, 012035. [Google Scholar]
- Proudman, I. The Generation of Noise by Isotropic Turbulence. Proc. R. Soc. A 1952, 214, 119–132. [Google Scholar] [CrossRef]
- Sarkar, S.; Hussaini, M.Y. Computation of the Sound Generated by Isotropic Turbulence; DTIC: Fort Belvoir, VA, USA, 1993. [Google Scholar]
- Mostafapour, A.; Davoodi, S. A Theoretical and Experimental Study on Acoustic Signals Caused by Leakage in Buried Gas-Filled Pipe. Appl. Acoust. 2015, 87, 1–5. [Google Scholar] [CrossRef]
- Williams, J.E.F.; Hawkings, D.L. Sound Generation by Turbulence and Surfaces in Arbitrary Motion. Philos. Trans. R. Soc. A 1969, 264, 321–342. [Google Scholar] [CrossRef]
- Liu, C.; Li, Y.; Fu, J.; Liu, G. Experimental Study on Acoustic Propagation-Characteristics-Based Leak Location Method for Natural Gas Pipelines. Process Saf. Environ. Prot. 2015, 96, 43–60. [Google Scholar] [CrossRef]
























| Density /(kg/m3) | Specific Heat Capacity/J/(kg/K) | Thermal Conductivity / | Porosity /% | Surface Heat Transfer Coefficient / |
|---|---|---|---|---|
| 2650 | 840 | 0.018 | 0.45 | 11.6 |
| Boundary Location | Boundary Name | Boundary Type | Value |
|---|---|---|---|
| Pipeline Inlet | Inlet-Pipeline | Pressure inlet | 2–10 MPa |
| Pipeline Outlet | Outlet-Pipeline | Pressure outlet | 101,325 Pa |
| Ground Surface | Outlet-Top | Pressure outlet | 101,325 Pa |
| Periphery of the Computational Domain | Outlet-Around | Pressure outlet | 101,325 Pa |
| Bottom of the Computational Domain | Outlet-Bottom | Pressure outlet | 101,325 Pa |
| Interface Between Leakage Hole Fluid and Soil | Holefluid-Soilfluid | Interior | |
| Interface Between Leakage Hole Fluid and Soil | Holefluid-Pipefluid | Interior | |
| Outer Wall of the Pipeline | Wall-outside | Stationary wall | |
| Inner Wall of the Pipeline | Wall-inside | Stationary wall | |
| Side Wall of the Leakage Hole | Wall-hole | Stationary wall |
| Soil Type | Average Particle Diameter/mm | Porosity |
|---|---|---|
| Sandy | 0.5–1.0 | 0.25–0.45 |
| Loam | 0.05–0.5 | 0.43–0.54 |
| Clay | 0.01–0.05 | 0.3–0.6 |
| Soil Type | Particle Diameter /mm | Porosity | Viscous Resistance /1/m2 | Inertial Resistance /1/m |
|---|---|---|---|---|
| Sandy | 0.6 | 0.45 | 1.38 × 109 | 3.52 × 104 |
| Loam | 0.06 | 0.45 | 1.38 × 1011 | 3.52 × 105 |
| Clay | 0.01 | 0.45 | 4.98 × 1012 | 2.11 × 106 |
| Pipe Diameter /mm | Leakage Hole Diameter /mm | Pipeline Pressure /MPa | Leakage Hole Location | Soil Type | Burial Depth /m |
|---|---|---|---|---|---|
| 711 | 1 | 2–10 | Top | Loam | 1.5 |
| 711 | 2 | 2–10 | Top | Loam | 1.5 |
| 711 | 3 | 2–10 | Top | Loam | 1.5 |
| 711 | 4 | 2–10 | Top | Loam | 1.5 |
| 711 | 5 | 2–10 | Top | Loam | 1.5 |
| 711 | 6 | 2–10 | Top | Loam | 1.5 |
| 711 | 6 | 6 | Top | Sandy | 1.5 |
| 711 | 6 | 6 | Top | Clay | 1.5 |
| 711 | 6 | 6 | Bottom | Loam | 1.5 |
| 711 | 6 | 6 | Side | Loam | 1.5 |
| Case | Pipe Diameter /mm | Leakage Hole Diameter /mm | Pipeline Pressure /MPa | Leakage Location | Soil Type | Burial Depth /m |
|---|---|---|---|---|---|---|
| 1 | 711 | 6 | 2 | Top | Loam | 1.5 |
| 2 | 711 | 6 | 4 | Top | Loam | 1.5 |
| 3 | 711 | 6 | 6 | Top | Loam | 1.5 |
| 4 | 711 | 6 | 8 | Top | Loam | 1.5 |
| 5 | 711 | 6 | 10 | Top | Loam | 1.5 |
| 6 | 711 | 1 | 6 | Top | Loam | 1.5 |
| 7 | 711 | 2 | 6 | Top | Sandy | 1.5 |
| 8 | 711 | 3 | 6 | Top | Clay | 1.5 |
| 9 | 711 | 4 | 6 | Top | Loam | 1.5 |
| 10 | 711 | 5 | 6 | Top | Loam | 1.5 |
| 11 | 711 | 6 | 6 | Top | Sandy | 1.5 |
| 12 | 711 | 6 | 6 | Top | Clay | 1.5 |
| 13 | 711 | 6 | 6 | Bottom | Loam | 1.5 |
| 14 | 711 | 6 | 6 | Side | Loam | 1.5 |
| Receiver Point | x/m | y/m | z/m |
|---|---|---|---|
| Leak Point (Top) | 5.0 | 5.0 | 8.8555 |
| Point 1 | 5.0 | 5.0 | 8.856 |
| Point 2 | 2.5 | 5.0 | 8.856 |
| Point 3 | 0.0 | 5.0 | 8.856 |
| Point 4 | 7.5 | 5.0 | 8.856 |
| Point 5 | 10 | 5.0 | 8.856 |
| Point 6 | 5.0 | 2.5 | 8.856 |
| Point 7 | 5.0 | 0.0 | 8.856 |
| Point 8 | 5.0 | 7.5 | 8.856 |
| Point 9 | 5.0 | 10 | 8.856 |
| Point10 | 5.0 | 5.0 | 9.356 |
| Point 11 | 7.5 | 5.0 | 9.356 |
| Point 12 | 10 | 5.0 | 9.356 |
| Point 13 | 5.0 | 7.5 | 9.356 |
| Point 14 | 5.0 | 10 | 9.356 |
| Point 15 | 5.0 | 5.0 | 9.856 |
| Point 16 | 7.5 | 5.0 | 9.856 |
| Point 17 | 5.0 | 5.0 | 4.856 |
| Point 18 | 5.0 | 7.5 | 4.856 |
| Point 19 | 5.0 | 5.0 | 0.856 |
| Point 20 | 7.5 | 5.0 | 0.856 |
| Receiver Point | x/m | y/m | z/m |
|---|---|---|---|
| Leak Point (Top) | 5.0000 | 5.0000 | 8.8555 |
| Leak Point (Bottom) | 5.0000 | 5.0000 | 8.1445 |
| Leak Point (Side) | 5.3555 | 5.0000 | 8.5000 |
| Point 21 | 5.0000 | 5.0000 | 8.9555 |
| Point 22 | 5.0000 | 5.0000 | 9.0555 |
| Point 23 | 5.0000 | 5.0000 | 8.0445 |
| Point 24 | 5.0000 | 5.0000 | 7.9445 |
| Point 25 | 4.5445 | 5.0000 | 8.5000 |
| Point 26 | 4.4445 | 5.0000 | 8.5000 |
| Point 27 | 5.4555 | 5.0000 | 8.5000 |
| Point 28 | 5.5555 | 5.0000 | 8.5000 |
| No. | Acoustic Source Surface | Boundary Type |
|---|---|---|
| Source 1 | Holefluid-Soilfluid | Interior |
| Source 2 | Wall-Hole | Stationary wall |
| Source 3 | Holefluid-Soilfluid and Wall-Hole | Coupled |
| No. | Min. Element Size/mm | Max. Element Size/mm | Mesh Count | Min. Inverse Orthogonal Quality | Avg. Velocity at Leakage/m/s | Avg. SPL at Leakage/dB |
|---|---|---|---|---|---|---|
| 1 | 2.50 | 500 | 246,040 | 0.08 | 10.516 | 48.443 |
| 2 | 2.00 | 500 | 250,512 | 0.24 | 16.532 | 58.480 |
| 3 | 1.50 | 500 | 256,881 | 0.41 | 17.876 | 58.050 |
| 4 | 1.00 | 500 | 114,659 | 0.35 | 20.361 | 57.218 |
| 5 | 1.00 | 300 | 289,793 | 0.21 | 20.164 | 56.499 |
| 6 | 1.00 | 100 | 966,446 | 0.20 | 20.157 | 56.511 |
| 7 | 0.50 | 100 | 968,095 | 0.26 | 20.284 | 56.884 |
| 8 | 0.30 | 100 | 907,170 | 0.32 | 20.080 | 57.212 |
| 9 | 0.10 | 100 | 930,152 | 0.32 | 20.045 | 56.566 |
| 10 | 0.05 | 100 | 988,188 | 0.23 | 20.448 | 56.867 |
| Pipeline Pressure /MPa | Centerline SPL in Leakage Hole | SPL in Leakage Hole Fluid Domain | Overall SPL | |
|---|---|---|---|---|
| Max/dB | Average/dB | Max/dB | Max/dB | |
| 2 | 40.624 | 26.178 | 100.777 | 100.777 |
| 4 | 32.611 | 17.826 | 101.149 | 101.149 |
| 6 | 27.792 | 13.251 | 101.356 | 101.356 |
| 8 | 24.377 | 10.388 | 101.545 | 101.545 |
| 10 | 21.746 | 8.399 | 102.177 | 102.177 |
| Pipeline Pressure /mm | Centerline SPL in Leakage Hole | SPL in Leakage Hole Fluid Domain | Overall SPL | |
|---|---|---|---|---|
| Max/dB | Ave/dB | Max/dB | Max/dB | |
| 1 | 78.892 | 59.320 | 142.700 | 142.700 |
| 2 | 57.585 | 37.196 | 128.979 | 128.979 |
| 3 | 35.755 | 17.782 | 125.965 | 125.965 |
| 4 | 36.675 | 24.411 | 110.207 | 110.207 |
| 5 | 30.170 | 16.280 | 107.259 | 107.259 |
| 6 | 27.792 | 13.251 | 100.777 | 100.777 |
| Soil Type | Centerline SPL in Leakage Hole | SPL in Leakage Hole Fluid Domain | Overall SPL | |
|---|---|---|---|---|
| Max/dB | Ave/dB | Max/dB | Max/dB | |
| Sandy | 46.922 | 32.245 | 141.497 | 141.497 |
| Loam | 27.792 | 13.251 | 100.777 | 100.777 |
| Clay | 8.9679 | 1.924 | 58.472 | 58.472 |
| Leak Position | SPL on Leakage Hole Axes | Overall SPL | |
|---|---|---|---|
| Max/dB | Average/dB | Max/dB | |
| Top | 27.792 | 13.251 | 100.777 |
| Bottom | 26.680 | 9.442 | 105.103 |
| Side | 25.071 | 9.210 | 105.834 |
| Soil Type | Average Dynamic Pressure/Pa | Average Turbulent Kinetic Energy/(J/kg) | Overall SPL /dB |
|---|---|---|---|
| Sandy | 31,314 | 41.326 | 156.151 |
| Loam | 3415 | 4.109 | 132.414 |
| Clay | 361 | 0.355 | 107.739 |
| Leak Position | Average Dynamic Pressure/Pa | Average Turbulent Kinetic Energy/(J/kg) | Overall SPL /dB |
|---|---|---|---|
| Top | 3414.87 | 4.109 | 132.414 |
| Bottom | 3336.77 | 3.978 | 132.803 |
| Side | 3400.81 | 3.968 | 131.659 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.; Gu, X.; Zhang, X.; Zhang, K.; Zhang, H.; Xiong, Z. Acoustic Characterization of Leakage in Buried Natural Gas Pipelines. Processes 2025, 13, 2274. https://doi.org/10.3390/pr13072274
Cai Y, Gu X, Zhang X, Zhang K, Zhang H, Xiong Z. Acoustic Characterization of Leakage in Buried Natural Gas Pipelines. Processes. 2025; 13(7):2274. https://doi.org/10.3390/pr13072274
Chicago/Turabian StyleCai, Yongjun, Xiaolong Gu, Xiahua Zhang, Ke Zhang, Huiye Zhang, and Zhiyi Xiong. 2025. "Acoustic Characterization of Leakage in Buried Natural Gas Pipelines" Processes 13, no. 7: 2274. https://doi.org/10.3390/pr13072274
APA StyleCai, Y., Gu, X., Zhang, X., Zhang, K., Zhang, H., & Xiong, Z. (2025). Acoustic Characterization of Leakage in Buried Natural Gas Pipelines. Processes, 13(7), 2274. https://doi.org/10.3390/pr13072274





