Radial Temperature Distribution Characteristics of Long-Span Transmission Lines Under Forced Convection Conditions
Abstract
1. Introduction
2. Calculation of Layered Temperature of Large Span Conductors
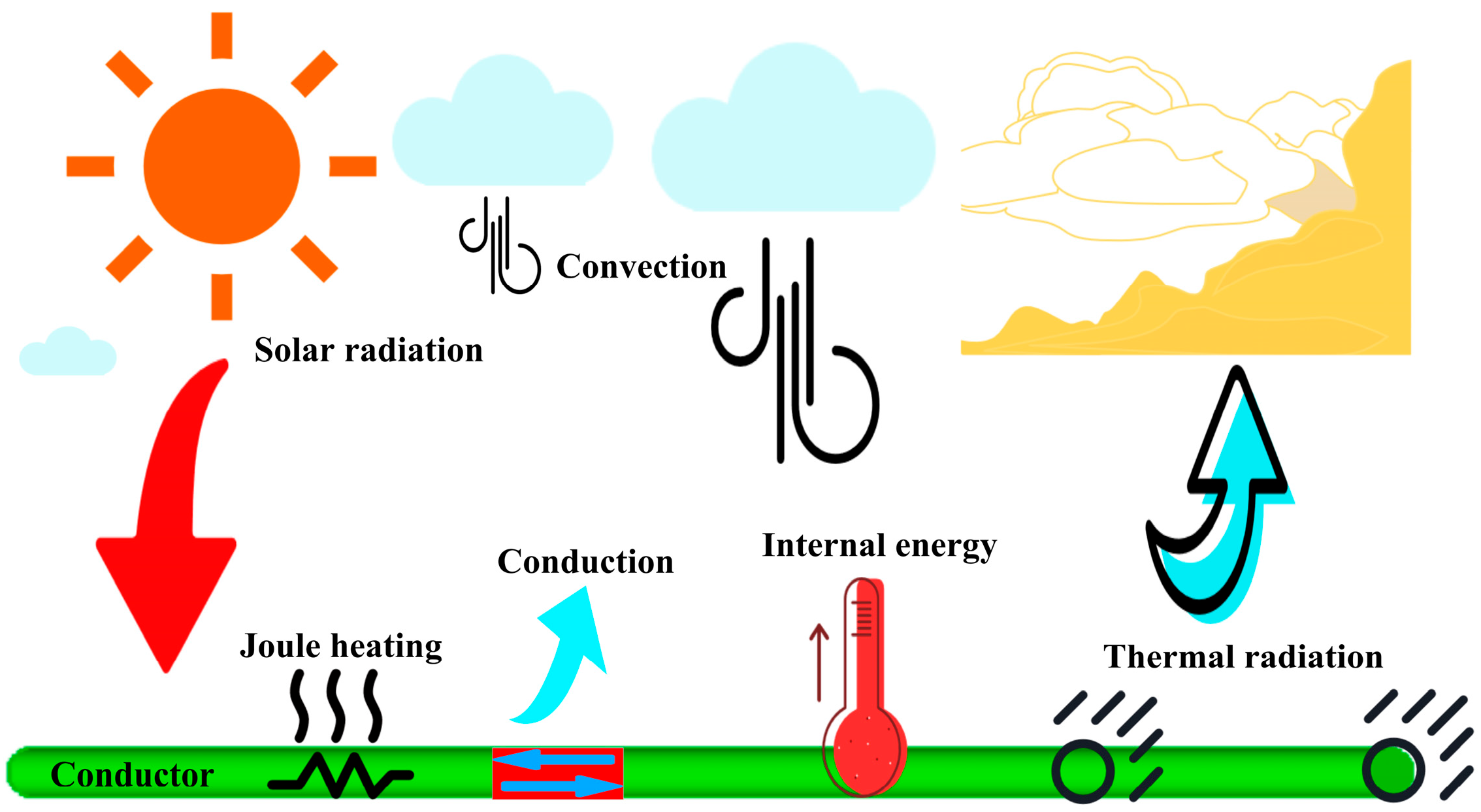
2.1. Wire Heat Dissipation Power
2.2. Radial Temperature Heat Balance Equation
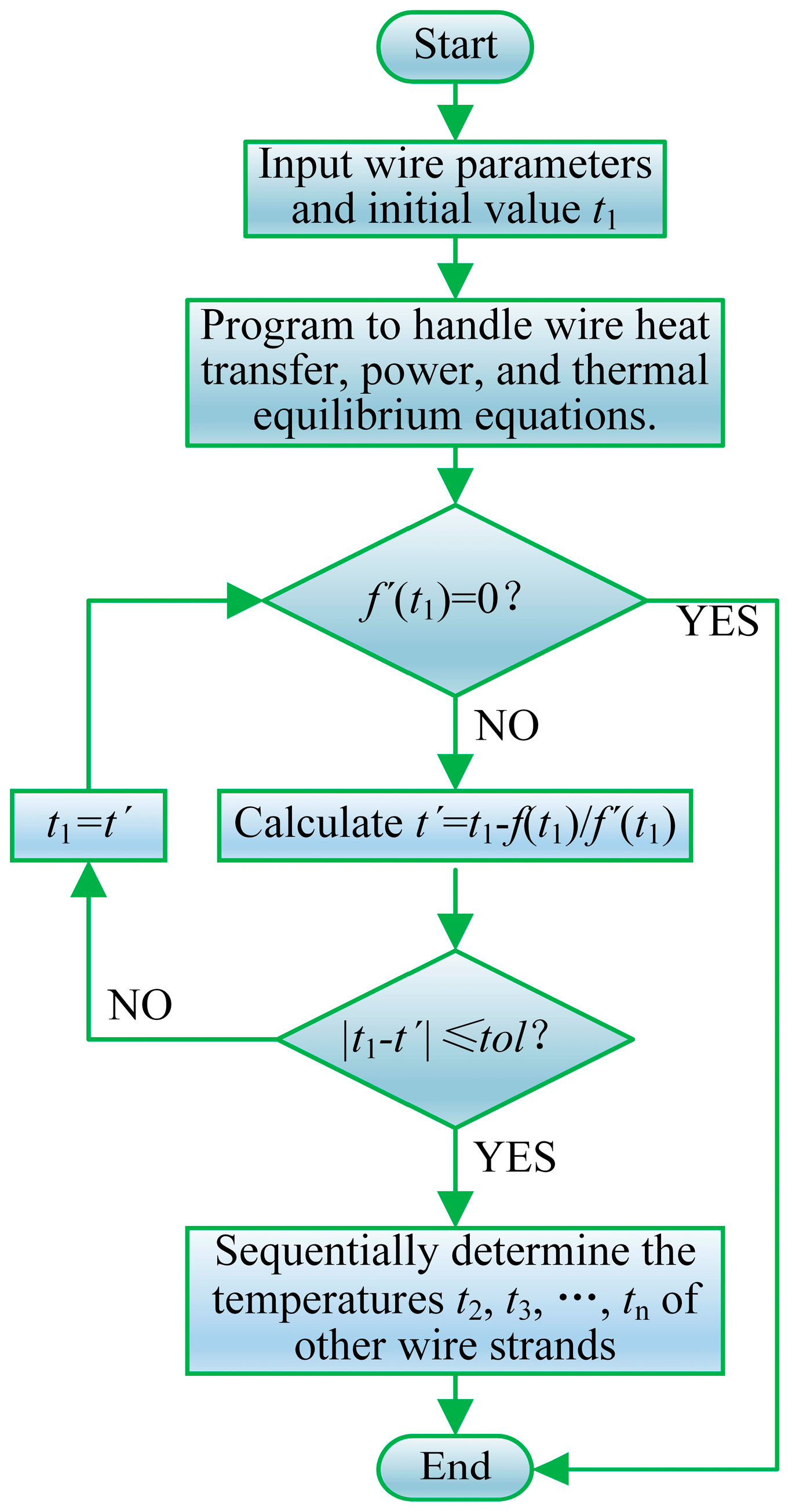
2.3. Analytical Model of Radial Temperature in Conductors
3. Finite Element Model of Radial Temperature Field of the Conductor
3.1. Basic Assumptions and Boundary Conditions
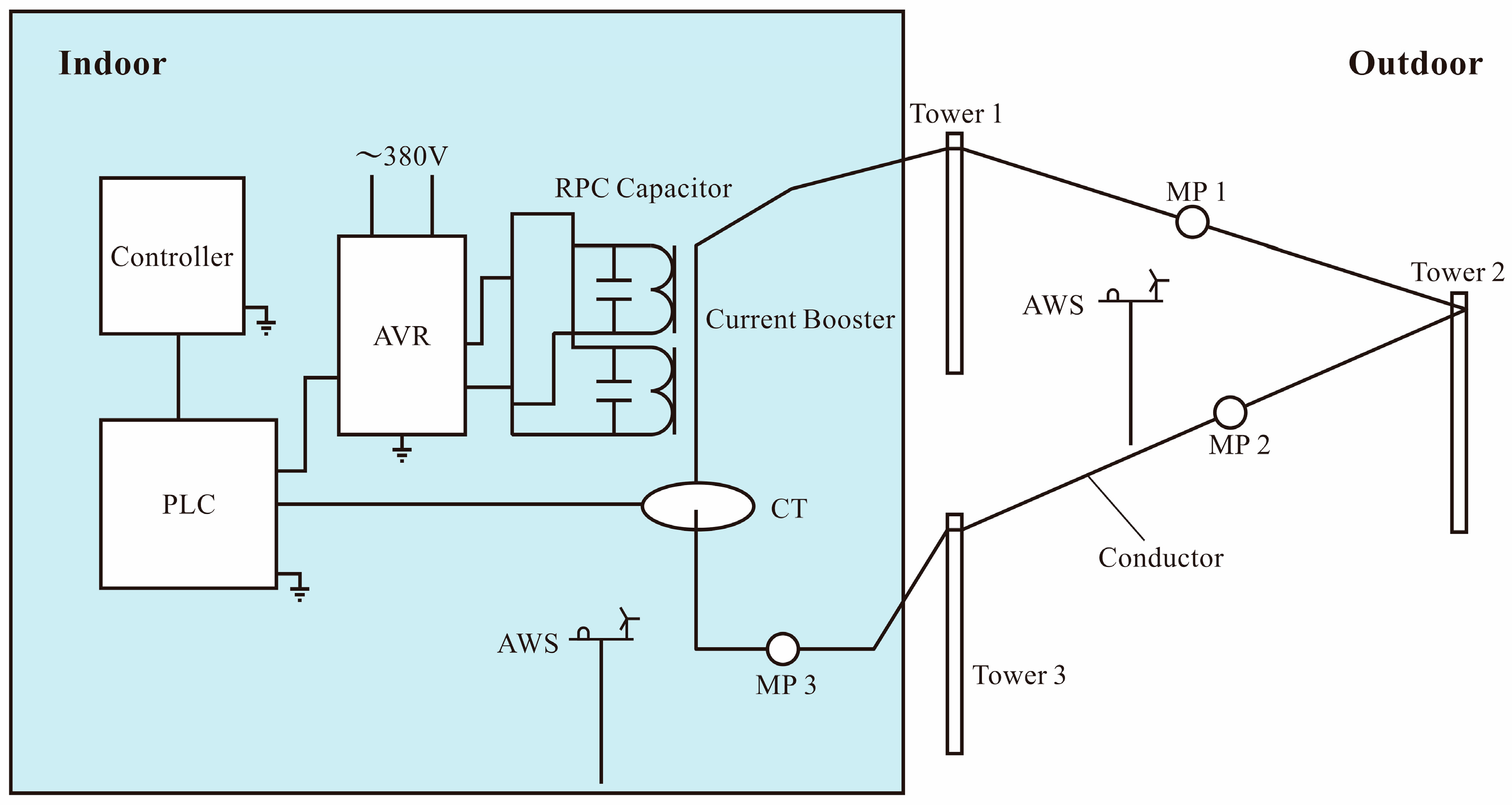
3.2. Model Building and Meshing
3.3. Calculation of Heat Source and Heat Dissipation
3.4. Verification of Iterative Method and Finite Element Method
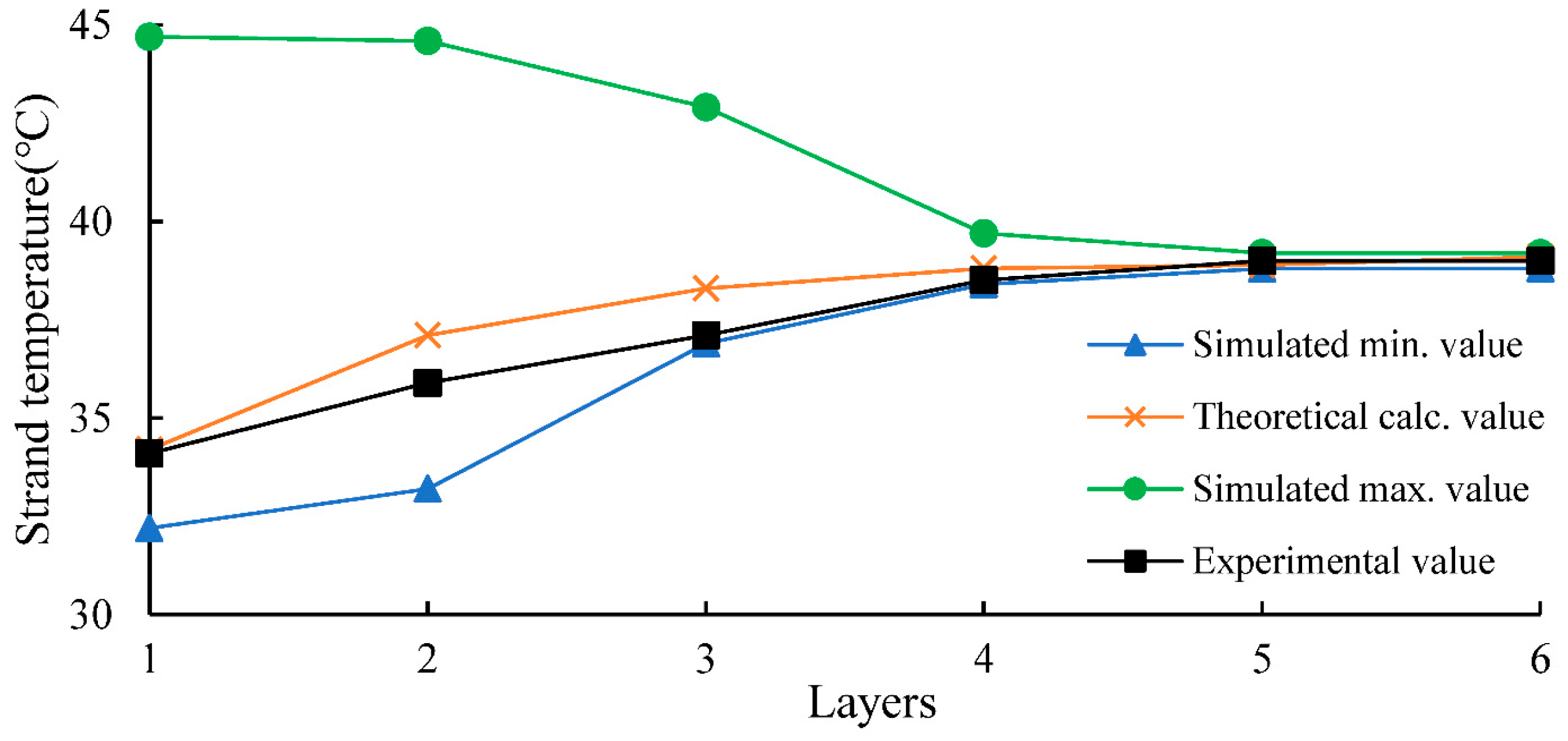
3.5. Radial Temperature Analysis
4. Analysis of Influencing Factors
4.1. Effect of Current Carrying Capacity on Radial Temperature of Conductor
4.2. Effect of Wind Speed on Radial Temperature of Conductor
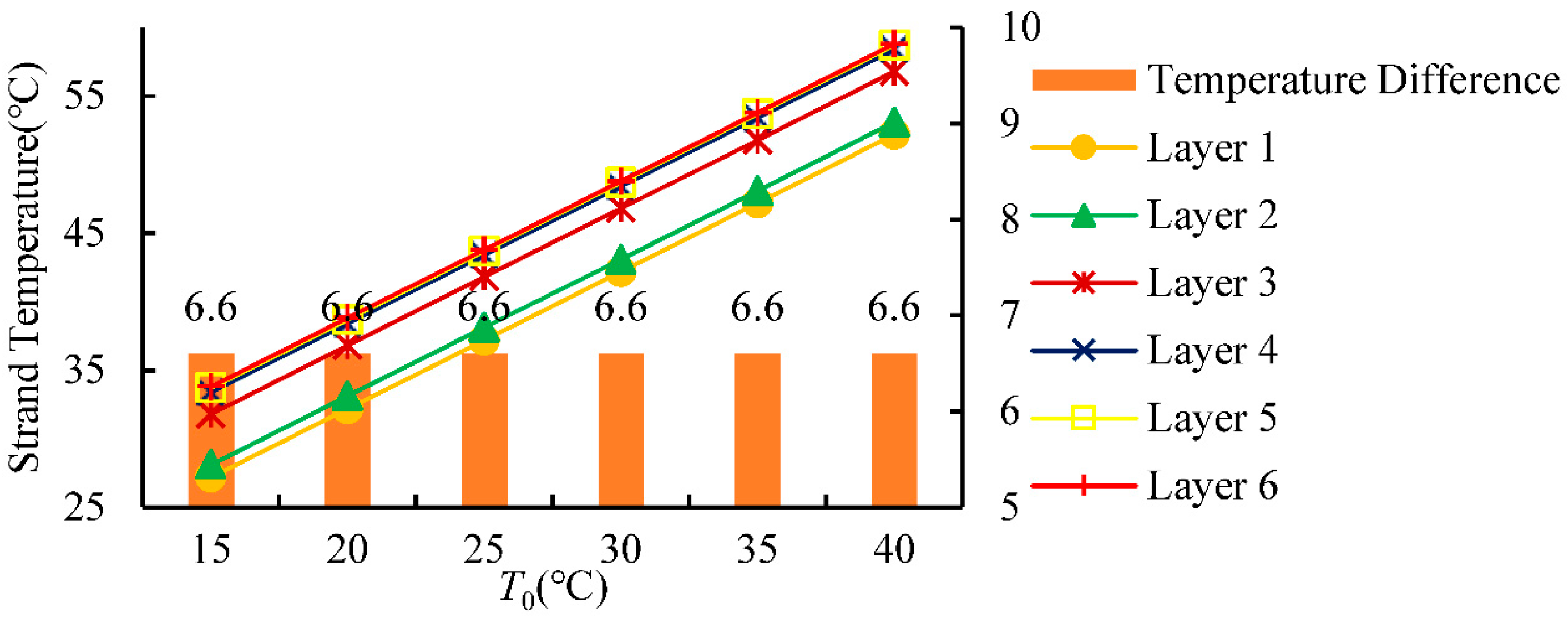
4.3. Effect of Ambient Temperature on Radial Temperature of Conductor
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Meyberg, R.A.; de Barros, M.T.C.; Lima, A.C.S. New approach for ampacity calculation of overhead lines with steel-cored conductors. IEEE Trans. Power Deliv. 2022, 38, 1011–1019. [Google Scholar] [CrossRef]
- Chen, S.L.; Black, W.Z.; Fancher, M.L. High-temperature sag model for overhead conductors. IEEE Trans. Power Deliv. 2003, 18, 183–188. [Google Scholar] [CrossRef]
- Erickson, E.; Slobodin, R.; Poshtan, M.; Taufik, T.; Callenes, J. Using power infrastructures for wildfire detection in California. In Proceedings of the 2020 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference, Washington, DC, USA, 17–20 February 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Wang, Y.; Mo, Y.; Wang, M.; Zhou, X.; Liang, L.; Zhang, P. Impact of conductor temperature time–space variation on the power system operational state. Energies 2018, 11, 760. [Google Scholar] [CrossRef]
- de Nazaré, F.V.B.; Werneck, M.M. Hybrid optoelectronic sensor for current and temperature monitoring in overhead transmission lines. IEEE Sens. J. 2012, 12, 1193–1194. [Google Scholar] [CrossRef]
- Voršič, Ž.; Maruša, R.; Pihler, J. New method for calculating the heating of the conductor. Energies 2019, 12, 2769. [Google Scholar] [CrossRef]
- Zhou, J.; Yao, K.; Huang, X.; Zhang, W.; Ashtaq, A.; Hao, Y.; Chen, Y. Temperature calculation and measurement on power cable conductor based on equivalent thermal circuit and BOTDA. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe, Genova, Italy, 11–14 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–4. [Google Scholar]
- Lei, M.; Liu, G.; Lai, Y.-T.; Li, J.-Z.; Li, W.; Liu, Y.G. Study on thermal model of dynamic temperature calculation of single-core cable based on Laplace calculation method. In Proceedings of the 2010 IEEE International Symposium on Electrical Insulation, San Diego, CA, USA, 6–9 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1–7. [Google Scholar]
- Feng, K.; Ying, Z.; Tong, X. Radial thermal circuit model for overhead conductors based on parameter identification under natural convection condition. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Ying, Z.; Kai, F.; Du, Z.; Liu, Y.; Wu, J. Thermal circuit modeling of the relationship between current and axial temperature for high voltage overhead conductor. Proc. CSEE 2015, 35, 2887–2895. [Google Scholar]
- Lee, H.B.; Lee, B.C.; Kim, J.H.; Nam, Y.H.; Kang, J.W. Improvement of the conductor temperature calculation algorithm for calculating the allowable current in the underground channel. Trans. Korean Inst. Electr. Eng. 2018, 67, 352–357. [Google Scholar]
- Yang, L.; Qiu, W.; Huang, J.; Hao, Y.; Fu, M.; Hou, S.; Li, L. Comparison of conductor-temperature calculations based on different radial-position-temperature detections for high-voltage power cable. Energies 2018, 11, 117. [Google Scholar] [CrossRef]
- Yang, X.; Zhu, S.; Qin, S.; Zhan, X.; Zhu, L. Analysis of temperature rise characteristics and current carrying capacity of overhead conductor. In Proceedings of the 2022 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Denver, CO, USA, 30 October–2 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 123–126. [Google Scholar]
- Kujovič, T.; Ries, R.; Mošať, M.; Gömöry, F. The critical current of REBCO coated conductors subjected to a mechanical loading at varying angles. IEEE Trans. Appl. Supercond. 2023, 33, 1–4. [Google Scholar] [CrossRef]
- Zhang, P.; Li, W.; Yang, K.; Feng, Y.; Cheng, P.; Wang, C.; Zhan, H. Condition estimate of contacts of current-carrying conductor in GIS based on the FEM calculation of temperature field. In Proceedings of the 2015 3rd International Conference on Electric Power Equipment—Switching Technology (ICEPE-ST), Busan, Republic of Korea, 25–28 October 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 69–73. [Google Scholar]
- Zunec, M.; Ticar, I.; Jakl, F. Determination of current and temperature distribution in overhead conductors by using electromagnetic-field analysis tools. IEEE Trans. Power Deliv. 2006, 21, 1524–1529. [Google Scholar] [CrossRef]
- Niu, H.; Jia, Y.; Ye, Y. Calculation of transient cable conductor temperature based on support vector machine optimized by particle swarm optimization algorithm. In Proceedings of the 2016 IEEE International Conference on High Voltage Engineering and Application, Chengdu, China, 19–22 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Hong, M.; Lu, Y.; Xin, Y. Cable conductor temperature prediction method based on nonlinear auto-regressive model with exogenous inputs neural network. In Proceedings of the 3rd International Conference on Intelligent Power and Systems, Shenzhen, China, 20–22 October 2023; pp. 266–271. [Google Scholar]
- IEEE Std 738-2023 (Revision of IEEE Std 738-2012); IEEE Standard for Calculating the Current-Temperature Relationship of Bare Overhead Conductors. IEEE: Piscataway, NJ, USA, 2013.
- CIGRE Working Group B2.43. Guide for Thermal Rating Calculation of Overhead Lines; CIGRE: Norwest, NSW, Australia, 2014. [Google Scholar]
- IEC 60853-1; Calculation of the Cyclic and Emergency Current Rating of Cables—Part 1: Cyclic Rating Factor for Cables Up to and Including 18/30 (36) kV. IEC: Geneva, Switzerland, 2014.
- Kanálik, M.; Margitová, A.; Beňa, Ľ. Temperature calculation of overhead power line conductors based on CIGRE Technical Brochure 601 in Slovakia. Electr. Eng. 2019, 101, 921–933. [Google Scholar] [CrossRef]
- Liang, Z.; Jiang, Y. Calculation of electric field and temperature of overhead transmission lines with covered conductors. In Proceedings of the 8th International Conference on Computer Science and Network Technology, Dalian, China, 20–22 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 50–54. [Google Scholar]
- Petrov, A.; Yang, J. AC Loss Modelling of a CORC Cable via an Analytical Equation and Finite Elements. IEEE Trans. Appl. Supercond. 2023, 33, 1–4. [Google Scholar] [CrossRef]
- Brakelmann, H.; Anders, G.J. Transient thermal response of power cables with temperature dependent losses. IEEE Trans. Power Deliv. 2020, 36, 2777–2784. [Google Scholar] [CrossRef]
- Zaręba, M.; Szczegielniak, T.; Jabłoński, P. Influence of the skin and proximity effects on the thermal field in a system of two parallel round conductors. Energies 2023, 16, 6341. [Google Scholar] [CrossRef]
- Black, W.Z.; Collins, S.S.; Hall, J.F. Theoretical model for temperature gradients within bare overhead conductors. IEEE Trans. Power Deliv. 1988, 3, 707–715. [Google Scholar] [CrossRef]
- Morgan, V.T. The radial temperature distribution and effective radial thermal conductivity in bare solid and stranded conductors. IEEE Trans. Power Deliv. 1990, 5, 1443–1452. [Google Scholar] [CrossRef]
- Jakl, F.; Žunec, M.; Tičar, I.; Uglešić, I. Distribution of current density in layers of overhead bare conductor. In Proceedings of the Power Systems and Communication Systems Infrastructures for the Future, Beijing, China, 23–27 September 2002; p. 56. [Google Scholar]
- Absi Salas, F.M.; Orlande, H.R.; Domingues, L.A.; Barbosa, C.R. Sequential estimation of the radial temperature variation in overhead power cables. Heat Transf. Eng. 2022, 43, 1610–1623. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Han, X.; Huang, X.; Zhao, X. Preliminary study on morgan transmission capacity simplified formula of transmission. J. Electr. Power Syst. Autom. 2009, 21, 92–96. [Google Scholar]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Introduction to Heat Transfer; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Li, Y. Calculation of Radial Temperature Difference in Overhead Conductors and Its Impact on Dynamic Capacity Enhancement; Huazhong University of Science and Technology: Wuhan, China, 2018. [Google Scholar]
- Liu, J.; Yang, H.; Yu, S.; Wang, S.; Shang, Y.; Yang, F. Real-time transient thermal rating and the calculation of risk level of transmission lines. Energies 2018, 11, 1233. [Google Scholar] [CrossRef]
- Maksić, M.; Djurica, V.; Souvent, A.; Slak, J.; Depolli, M.; Kosec, G. Cooling of overhead power lines due to the natural convection. Int. J. Electr. Power Energy Syst. 2019, 113, 333–343. [Google Scholar] [CrossRef]
- Argyros, I.K.; Ren, H. A relationship between the Lipschitz constants appearing in Taylor’s formula. Pure Appl. Math. 2011, 18, 345–351. [Google Scholar] [CrossRef][Green Version]
- Brazhenko, V.; Qiu, Y.; Cai, J.; Wang, D. Thermal Evaluation of Multilayer Wall with a Hat-Stringer in Aircraft Design. Stroj. Vestn. -J. Mech. Eng. 2022, 68, 635–641. [Google Scholar] [CrossRef]
- GB/T1179-2017; Round Wire Concentric Lay Overhead Electrical Stranded Conductors. Standardization Administration of the People’s Republic of China: Beijing, China, 2017.
- Huang, X.; Cui, Y.; Zhu, Y. Analysis of the surface convective heat transfer coefficient of icicle on transmission lines. High. Volt. Eng. 2019, 45, 1975–1981. [Google Scholar]
- Liu, Z.L.; Li, H.Z.; Liu, G. Analysis on radial temperature field of overhead conductor based on finite element simulation. Insul. Mater. 2021, 54, 84–90. [Google Scholar]
- Hu, J.; Xiong, X.F.; Wang, J. Radial and circumferential temperature calculation method for overhead transmission lines based on thermal network model. Trans. China Electrotech. Soc. 2019, 34, 139–152. [Google Scholar]







| Technical Specifications | Conductor Material | |
|---|---|---|
| Aluminum | Steel | |
| Cross-sectional area (mm2) | 499.5 | 282.88 |
| Structural composition | 48 | 37 |
| Diameter of single strand (mm) | 3.64 | 3.12 |
| Material density (kg/m3) | 2700 | 7800 |
| Specific heat capacity (J/(kg·K)) | 880 | 460 |
| Electrical resistivity (nΩ·m) | 16.98 | 26.34 |
| Temperature coefficient (°C−1) | 0.004 | 0.0065 |
| Thermal conductivity (W/(m·K)) | 226 | 45 |
| Technical Specifications | Conductor Material | |
|---|---|---|
| Aluminum | Steel | |
| Cross-sectional area (mm2) | 300.09 | 38.9 |
| Structural composition | 24 | 7 |
| Diameter of single strand (mm) | 3.99 | 2.66 |
| Material density (kg/m3) | 2790 | 7780 |
| Specific heat capacity (J/(kg·K)) | 881 | 470 |
| Electrical resistivity (nΩ·m) | 28.26 | 191.57 |
| Temperature coefficient (°C−1) | 0.00403 | 0.00455 |
| Thermal conductivity (W/(m·K)) | 170 | 43 |
| Current (A) | Experimental Value (°C) | Iteration Value (°C) | Absolute Value Error (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T1 | T2 | T3 | T4 | T1 | T2 | T3 | T4 | T1 | T2 | T3 | T4 | |
| 400 | 36.5 | 37.4 | 38.4 | 38.4 | 36.1 | 37.5 | 38.3 | 38.3 | 1.10 | 0.27 | 0.26 | 0.26 |
| 500 | 48 | 49.4 | 50.8 | 50.8 | 46.8 | 48.6 | 49.9 | 49.9 | 2.50 | 1.62 | 1.77 | 1.77 |
| 600 | 59 | 61.2 | 63.1 | 63.1 | 58.6 | 60.5 | 63.9 | 63.9 | 0.68 | 1.14 | 1.27 | 1.27 |
| 700 | 73.4 | 76.6 | 79.1 | 79.1 | 72.5 | 74.4 | 77.8 | 77.8 | 1.23 | 2.87 | 1.64 | 1.64 |
| Layers | Minimum Value of FEM (°C) | Theoretical Iteration Value (°C) | Maximum Value of FEM (°C) | Average Value of FEM (°C) | Average Value Error (%) |
|---|---|---|---|---|---|
| L1 (T1) | 32.2 | 34.2 | 44.7 | 35.1 | −2.63% |
| L2 (T2) | 33.1 | 37.1 | 44.6 | 36.8 | 0.81% |
| L3 (T3) | 36.9 | 38.3 | 42.9 | 37.9 | 1.04% |
| L4 (T4) | 38.4 | 38.8 | 39.7 | 38.8 | 0.00% |
| L5 (T5) | 38.8 | 38.9 | 39.2 | 39.0 | −0.26% |
| L6 (T6) | 38.8 | 39.1 | 39.2 | 39.0 | 0.26% |
| Type | Theoretical Iteration Method | FEM |
|---|---|---|
| Pre-processing time | 9 min | 21 min |
| Iterative computation time | 2 s | 11 min |
| Technical Specifications | Conductor Material | |
|---|---|---|
| Aluminum | Steel | |
| Cross-sectional area (mm2) | 240 | 30 |
| Structural composition | 24 | 7 |
| Diameter of single strand (mm) | 3.6 | 2.4 |
| Electrical resistivity (nΩ·m) | 28.26 | 191.57 |
| Temperature coefficient (°C−1) | 0.00403 | 0.00651 |
| Thermal conductivity (W/(m·K)) | 226 | 45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Song, C.; Chen, X.; Liu, Z. Radial Temperature Distribution Characteristics of Long-Span Transmission Lines Under Forced Convection Conditions. Processes 2025, 13, 2273. https://doi.org/10.3390/pr13072273
Wang F, Song C, Chen X, Liu Z. Radial Temperature Distribution Characteristics of Long-Span Transmission Lines Under Forced Convection Conditions. Processes. 2025; 13(7):2273. https://doi.org/10.3390/pr13072273
Chicago/Turabian StyleWang, Feng, Chuanxing Song, Xinghua Chen, and Zhangjun Liu. 2025. "Radial Temperature Distribution Characteristics of Long-Span Transmission Lines Under Forced Convection Conditions" Processes 13, no. 7: 2273. https://doi.org/10.3390/pr13072273
APA StyleWang, F., Song, C., Chen, X., & Liu, Z. (2025). Radial Temperature Distribution Characteristics of Long-Span Transmission Lines Under Forced Convection Conditions. Processes, 13(7), 2273. https://doi.org/10.3390/pr13072273







