Optimal Collaborative Scheduling Strategy of Mobile Energy Storage System and Electric Vehicles Considering SpatioTemporal Characteristics
Abstract
1. Introduction
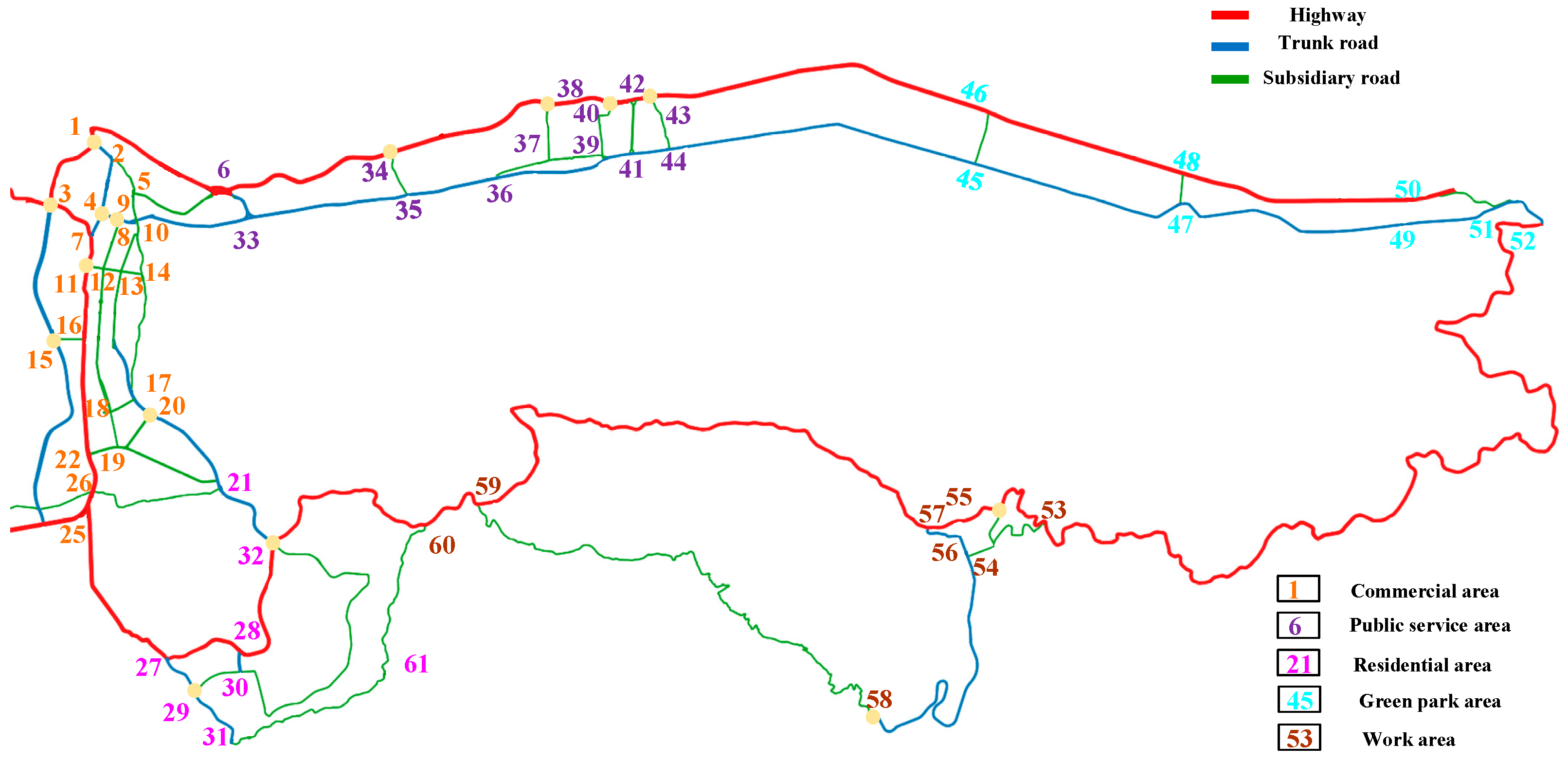
2. Road Network and Traffic Flow Modeling
2.1. Road Topology Model
2.2. Traffic Flow Model
2.2.1. Traffic-Following Model
2.2.2. Transportation Probability Matrix
3. Spatiotemporal Characteristics of Electric Vehicles and Evaluation Model of User Response Willingness
3.1. Temporal Characteristics of Electric Vehicles
3.2. Spatial Characteristics of Electric Vehicles
3.3. Evaluation Model of Electric Vehicle User Response Willingness
3.3.1. User Response Rate Model Considering Incentive Level
3.3.2. Positive Response Bias of Users
4. SpatioTemporal Joint Scheduling and Solution Method for Mobile Energy Storage Systems and Electric Vehicles
4.1. Charging and Discharging Model of Mobile Energy Storage System
4.2. Objective Function
4.2.1. Profits of Electric Vehicle Charging Station Operators
4.2.2. Comprehensive Cost of Electric Vehicle User
4.2.3. Total Voltage Deviation
4.3. Main Constraints
4.3.1. Constraints of Charging and Discharging Price
4.3.2. Constraints of Charging Demands
4.3.3. Grid Operation Constraints
4.4. Solving Method
5. Case Studies
5.1. Parameter Settings
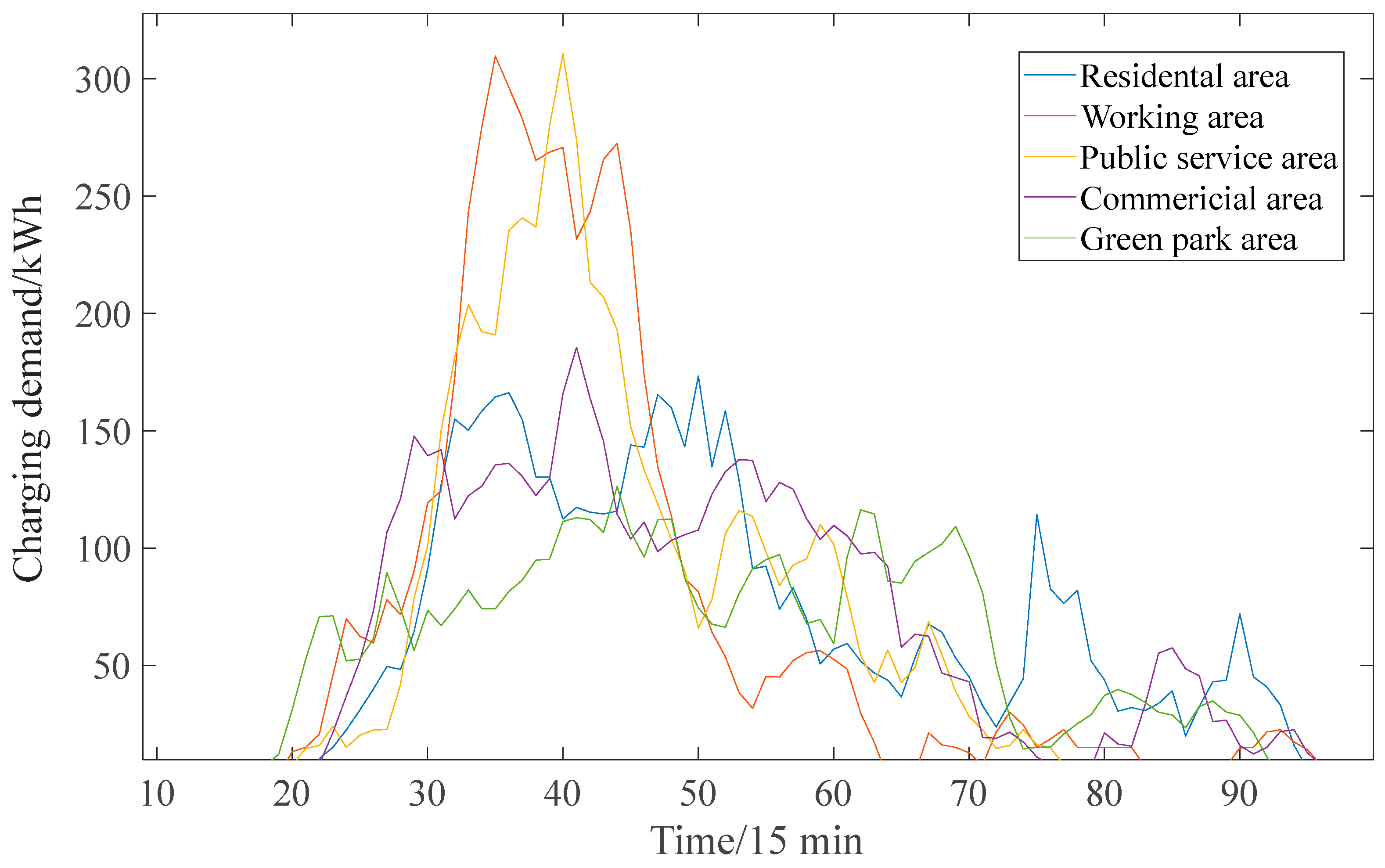
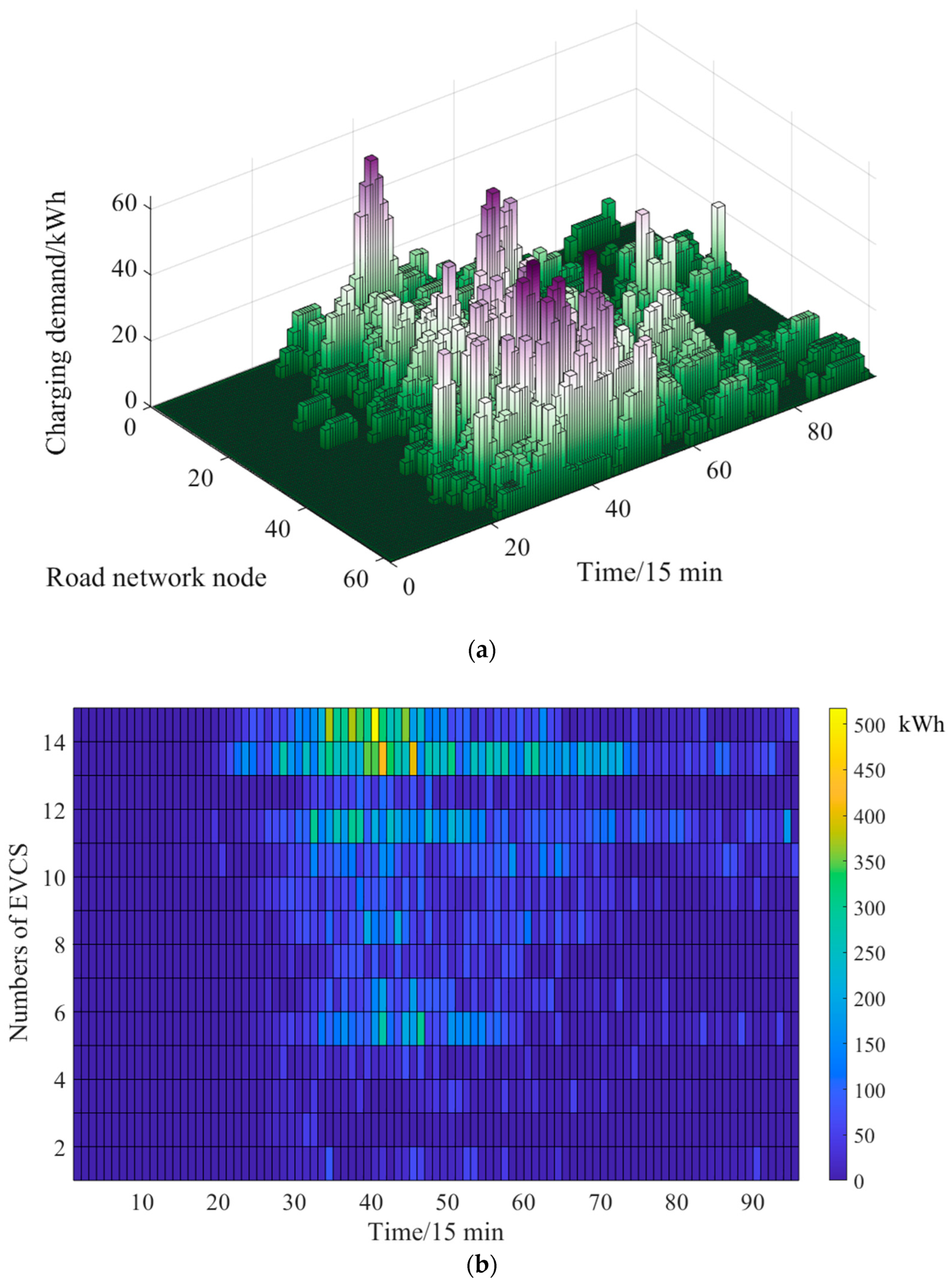
5.2. Analysis of Demand Prediction of Electric Vehicle Charging
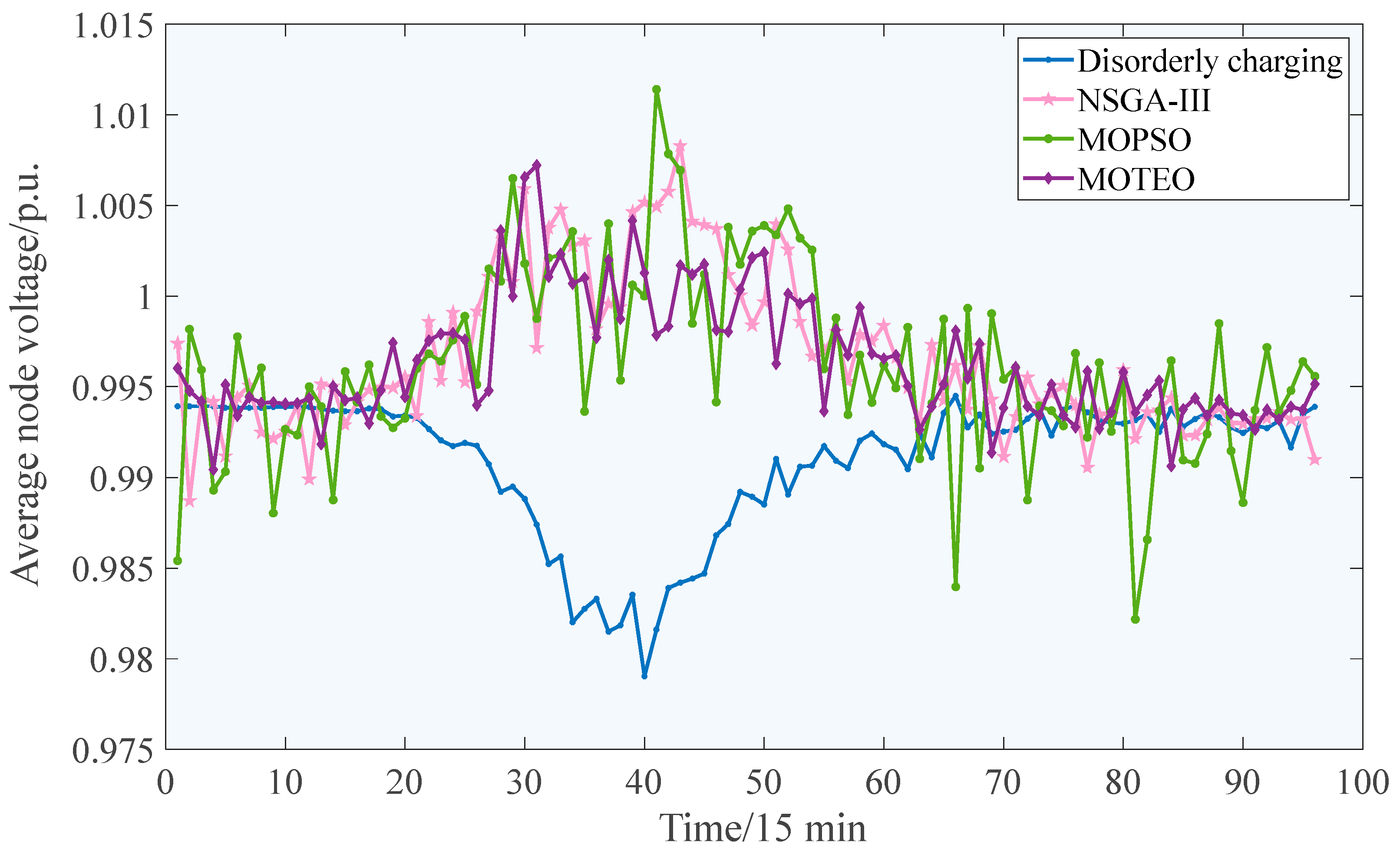
5.3. Analysis of Optimization Results
5.3.1. Comparison of Optimization Algorithms
5.3.2. Analysis of Pricing Strategy
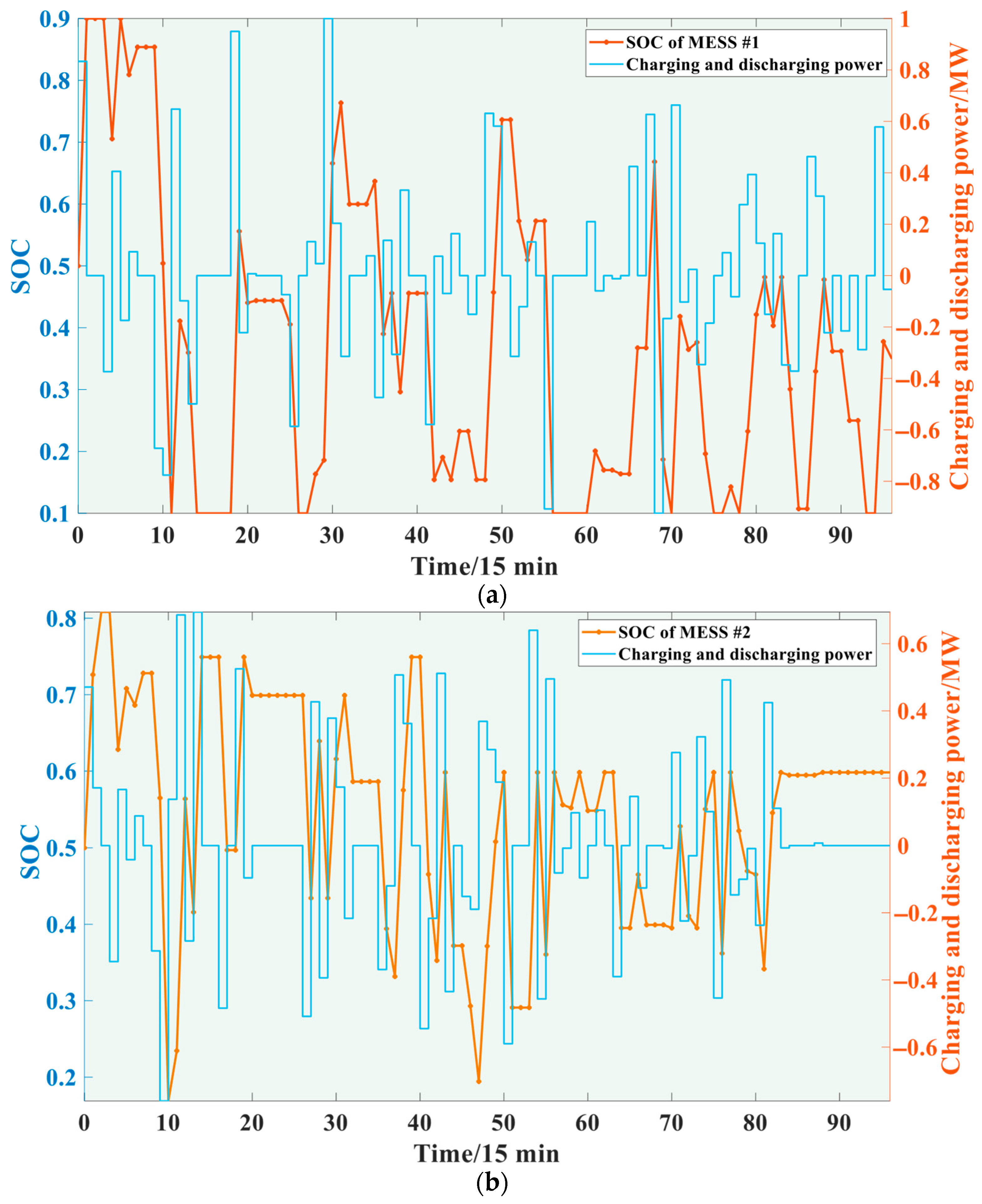
5.3.3. Analysis of Mobile Energy Storage System Scheduling
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Glossary
| Safe driving speed at time | |
| Speed of the preceding electric vehicle at time | |
| Optimal path | |
| Cooling power of the air conditioner | |
| Heating power of the air conditioner | |
| Incentive price | |
| Actual response rate | |
| Capacity of mobile energy storage system at time | |
| Charging power of mobile energy storage system at time | |
| Discharging power of mobile energy storage system at time | |
| State of charge of mobile energy storage system at time | |
| Charging price of the th electric vehicle charging station at time | |
| Discharging price of the th electric vehicle charging station at time | |
| Charging power of electric vehicles | |
| Discharging power of electric vehicles | |
| Purchasing price of distribution network at time | |
| Selling price of distribution network at time | |
| Voltage of node at time | |
| Charging demands of the th charging station at time | |
| Active power loss of node at time | |
| Charging power of node at time | |
| Discharging of node at time |
References
- Yang, B.; Li, J.; Shu, H.; Cai, Z.; Tang, B.; Huang, X.; Zhu, M. Recent advances of optimal sizing and location of charging stations: A critical overview. Int. J. Energy Res. 2022, 46, 17899–17925. [Google Scholar] [CrossRef]
- Zhang, K.; Xu, Y.; Sun, H. Bilevel optimal coordination of active distribution network and charging stations considering EV drivers’ willingness. Appl. Energy 2024, 360, 122790. [Google Scholar] [CrossRef]
- Yang, B.; Yu, L.; Chen, Y.; Ye, H.; Shao, R.; Shu, H.; Yu, T.; Zhang, X.; Sun, L. Modelling, applications, and evaluations of optimal sizing and placement of distributed generations: A critical state-of-the-art survey. Int. J. Energy Res. 2021, 45, 3615–3642. [Google Scholar] [CrossRef]
- He, B.; Yang, B.; Han, Y.; Zhou, Y.; Hu, Y.; Shu, H.; Su, S.; Yang, J.; Huang, Y.; Li, J.; et al. Optimal EVCS planning via spatial-temporal distribution of charging demand forecasting and traffic-grid coupling. Energy 2024, 313, 133885. [Google Scholar] [CrossRef]
- Jin, X.; Wu, Q.; Jia, H.; Hatziargyriou, N.D. Optimal integration of building heating loads in integrated heating/electricity community energy systems: A bi-level MPC approach. IEEE Trans. Sustain. Energy 2021, 12, 1741–1754. [Google Scholar] [CrossRef]
- Makaremi, S. A multi-output deep learning model for energy demand and port availability forecasting in EV charging infrastructure. Energy 2025, 317, 134582. [Google Scholar] [CrossRef]
- Aduama, P.; Zhang, Z.; Al-Sumaiti, A.S. Multi-feature data fusion-based load forecasting of electric vehicle charging stations using a deep learning model. Energies 2023, 16, 1309. [Google Scholar] [CrossRef]
- Arsalan, M.; Jacob, E.; Nie, Z.; Farzaneh, H. Analyzing the impact of battery technical performance and driving conditions on the overall economic feasibility of a Vehicle-to-Grid (V2G) system implemented in the Japan electric power exchange (JEPX) market. Energy Convers. Manag. X 2025, 26, 100980. [Google Scholar] [CrossRef]
- Yu, H.; Tu, J.; Shao, Z.; Jian, L. Accommodating more electric vehicles in old residential communities by enabling distributed vehicle-to-grid dispatching and coordinated system operation. Renew. Sustain. Energy Rev. 2025, 218, 115814. [Google Scholar] [CrossRef]
- Wu, Y.; Aziz, S.M.; Haque, M.H.; Kauschke, T. New staggered time-of-use tariffs to mitigate the impact of electric vehicle charging demand on distribution networks. Sustain. Energy Grids Netw. 2025, 42, 101628. [Google Scholar] [CrossRef]
- Meng, W.; Song, D.; Huang, L.; Chen, X.; Yang, J.; Dong, M.; Talaat, M.; Elkholy, M.H. Distributed energy management of electric vehicle charging stations based on hierarchical pricing mechanism and aggregate feasible regions. Energy 2024, 291, 130332. [Google Scholar] [CrossRef]
- Zhang, J.; Che, L.; Wan, X.; Shahidehpour, M. Distributed hierarchical coordination of networked charging stations based on peer-to-peer trading and EV charging flexibility quantification. IEEE Trans. Power Syst. 2022, 37, 2961–2975. [Google Scholar] [CrossRef]
- Meng, Q.; He, Y.; Gao, Y.; Hussain, S.; Lu, J.; Guerrero, J.M. Bi-level four-stage optimization scheduling for active distribution networks with electric vehicle integration using multi-mode dynamic pricing. Energy 2025, 327, 136316. [Google Scholar] [CrossRef]
- Yin, W.; Wen, T.; Zhang, C. Cooperative optimal scheduling strategy of electric vehicles based on dynamic electricity price mechanism. Energy 2023, 263, 125627. [Google Scholar] [CrossRef]
- Zhang, Z.; Lv, L.; Wang, X. Research on dynamic time-sharing tariff orderly charging strategy based on NSGA2 in PV-storage-charging stations. Electr. Power Syst. Res. 2023, 225, 109784. [Google Scholar]
- Lu, Z.; Ma, Y.; Han, D.; Xu, X.; Xia, S. Spatial–temporal scheduling of regional integrated energy systems with stationary-mobile energy storage systems based on improved Lyapunov optimization. J. Energy Storage 2025, 122, 116665. [Google Scholar] [CrossRef]
- Ghasemi, S.; Moshtagh, J. Distribution system restoration after extreme events considering distributed generators and static energy storage systems with mobile energy storage systems dispatch in transportation systems. Appl. Energy 2022, 310, 118507. [Google Scholar] [CrossRef]
- Farzin, H.; Chehrazi, F.; Saniei, M. Multi-objective planning of mobile energy storage unit in active distribution network considering reliability. J. Energy Storage 2025, 109, 115138. [Google Scholar] [CrossRef]
- Chen, T.; Xu, X.; Wang, H.; Yan, Z. Routing and scheduling of mobile energy storage system for electricity arbitrage based on two-layer deep reinforcement learning. IEEE Trans. Transp. Electrif. 2023, 9, 1087–1102. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, Z.; Mai, X.; Zhao, J.; Qiu, J.; Liu, G.; Dong, Z.Y.; Ghias, A.M.Y.M. Mobile battery energy storage system control with knowledge-assisted deep reinforcement learning. Energy Convers. Econ. 2022, 3, 381–391. [Google Scholar] [CrossRef]
- Chen, L.; He, H.; Jing, R.; Xie, M.; Ye, K. Energy management in integrated energy system with electric vehicles as mobile energy storage: An approach using bi-level deep reinforcement learning. Energy 2024, 307, 132757. [Google Scholar] [CrossRef]
- Wang, D.; Xu, H.; Dai, L.; Zhang, L.; Guo, J. Enhancing the utilization of renewable generation on the highway with mobile energy storage vehicles and electric vehicles. Electr. Power Syst. Res. 2024, 231, 110311. [Google Scholar] [CrossRef]
- Qian, T.; Fang, M.; Shu, W.; Shao, C. Real-Time Simulation Framework of Urban EVs Charging Loads Based on Micro-Level Modeling of Transportation Network. Proceedings of the CSEE. Available online: http://kns.cnki.net/kcms/detail/11.2107.TM.20250220.0916.002.html (accessed on 8 June 2025).
- Shao, Y.; Mu, Y.; Yu, X.; Dong, X.; Jia, H.; Wu, J.; Zeng, Y. A spatial-temporal charging load forecast and impact analysis method for distribution network using EVs-traffic-distribution model. Proc. CSEE 2017, 37, 5207–5219+5519. [Google Scholar]
- Yi, T.; Zhang, C.; Lin, T.; Liu, J. Research on the spatial-temporal distribution of electric vehicle charging load demand: A case study in China. J. Clean. Prod. 2020, 242, 118457. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, J.; Liu, Y.; Zhang, H.; Lv, G. Daily electric vehicle charging load profiles considering demographics of vehicle users. Appl. Energy 2020, 274, 115063. [Google Scholar] [CrossRef]
- Fiori, C.; Ahn, K.; Rakha, H.A. Power-based electric vehicle energy consumption model: Model development and validation. Appl. Energy 2016, 168, 257–268. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, Z.; Yang, X. Electric vehicle charging load prediction based on dynamic energy consumption model and user psychology. Mod. Electr. Power 2022, 39, 710–719. [Google Scholar]
- Chang, F.; Huang, M.; Zhang, W. Research on coordinated charging of electric vehicles based on TOU charging price. Power Syst. Technol. 2016, 40, 2609–2615. [Google Scholar]
- Zhou, X.; Huang, X.; Zhang, Y.; Tang, Y.; Yao, L.; Yang, J. Real-time scheduling and optimization model of electric vehicles based on fuzzy evaluation of demand response potential. Electr. Power Autom. Equip. 2022, 42, 30–37. [Google Scholar]
- Sun, W.; Liu, W.; Zhang, J. Collaborative optimization for dynamic reconfiguration of distribution network and mobile energy storage in background of high proportion of renewable energy. Autom. Electr. Power Syst. 2021, 45, 80–90. [Google Scholar]
- Li, J.; Yang, B.; Huang, J.; Guo, Z.; Wang, J.; Zhang, R.; Hu, Y.; Shu, H.; Chen, Y.; Yan, Y. Optimal planning of electricity-hydrogen hybrid energy storage system considering demand response in active distribution network. Energy 2023, 273, 127142. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.; Cao, P.; Zhu, T.; Shu, H.; Chen, J.; Zhang, J.; Zhu, J. Classification, summarization and perspectives on state-of-charge estimation of lithium-ion batteries used in electric vehicles: A critical comprehensive survey. J. Energy Storage 2021, 39, 102572. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, B.; Wu, P.; Wang, X.; Li, J.; Huang, Y.; Su, R.; He, G.; Yang, J.; Su, S.; et al. Optimal planning of electric-heating integrated energy system in low-carbon park with energy storage system. J. Energy Storage 2024, 99, 113327. [Google Scholar] [CrossRef]
- Heris, M.K. NSGA-III: Non-dominated Sorting Genetic Algorithm, the Third Version—MATLAB Implementation, Yarpiz, 2016. Available online: https://yarpiz.com/456/ypea126-nsga3 (accessed on 6 July 2025).
- Li, J.; Yang, B.; Hu, Y.; Zhang, R.; Shu, H. Location and capacity planning of electricity hydrogen hybrid energy storage system considering demand response. Power Syst. Technol. 2023, 47, 3698–3714. [Google Scholar]





| Ref. | Actual Traffic Network | Electric-Traffic Coupling Model | Dynamic Pricing | Vehicle-to-Grid | Scheduling Objects | Multiple Objectives | |
|---|---|---|---|---|---|---|---|
| Electric Vehicles | Mobile Energy Storage System | ||||||
| [9] | √ | √ | √ | √ | |||
| [10] | √ | √ | √ | √ | |||
| [11] | √ | √ | √ | √ | |||
| [12] | √ | √ | √ | √ | |||
| [13] | √ | √ | √ | ||||
| [14] | √ | √ | √ | √ | |||
| [15] | √ | √ | √ | ||||
| [16] | √ | √ | |||||
| [17] | √ | √ | √ | ||||
| [18] | √ | √ | |||||
| [19] | √ | √ | √ | ||||
| [20] | √ | ||||||
| [21] | √ | √ | √ | ||||
| [22] | √ | √ | √ | √ | √ | √ | |
| This paper | √ | √ | √ | √ | √ | √ | √ |
| Time Characteristic | Node Classification | Probability Distribution | Parameters |
|---|---|---|---|
| Starting time | - | Burr type XII distribution | α = 7.986, C = 6.696, K = 0.609 |
| Parking duration | Residential nodes | Stable distribution | α = 1.324, β = −0.51, γ = 66.379, δ = 535.77 |
| Work nodes | Burr type XII distribution | α = 3032.83, C = 1.043, K = 27.171 | |
| Other nodes | Generalized extreme value distribution | k = 0.765, α = 35.419, μ = 63.477 |
| Parameter | Value |
|---|---|
| /(kw) | 120 |
| /(kw) | 30 |
| /(CNY/kW·h) | 0.1042 |
| /(CNY/h) | 30 |
| 0.96 | |
| 0.96 | |
| /(kW·h) | 2000 |
| 1.07 | |
| 0.93 |
| Parameter | Value |
|---|---|
| electric vehicle weight/(kg) | 2073 |
| electric vehicle capacity/(kW·h) | 76.3 |
| Transmission efficiency | 0.92 |
| Motor efficiency | 0.91 |
| Algorithms | Electric Vehicle Charging Station Operator Profits/CNY | Average Cost of Electric Vehicle Users/CNY | Average Discharge Revenue/CNY | Voltage Deviation/p.u. |
|---|---|---|---|---|
| Initial state | 42,880.00 | 56.01 | - | 0.661 |
| Non-dominated sorting genetic algorithm-III | 95,408.52 | 30.99 | 40.37 | 0.248 |
| Multi-objective particle swarm optimization | 84,055.72 | 33.49 | 38.33 | 0.337 |
| Multi-objective thermal exchange optimization algorithm | 88,386.97 | 31.93 | 37.52 | 0.215 |
| Mobile Energy Storage System Numbers | Driving Path (Road Nodes) |
|---|---|
| #1 | 11→58→1→1→4→1→58→1→3→3→58→1→1→1→58→58→1→1→1→1→58→58→38→11 |
| #2 | 55→58→58→58→58→1→15→34→43→58→58→3→55→58→58→1→1→58→58→1→58→58→1→55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Yu, T. Optimal Collaborative Scheduling Strategy of Mobile Energy Storage System and Electric Vehicles Considering SpatioTemporal Characteristics. Processes 2025, 13, 2242. https://doi.org/10.3390/pr13072242
Sun L, Yu T. Optimal Collaborative Scheduling Strategy of Mobile Energy Storage System and Electric Vehicles Considering SpatioTemporal Characteristics. Processes. 2025; 13(7):2242. https://doi.org/10.3390/pr13072242
Chicago/Turabian StyleSun, Liming, and Tao Yu. 2025. "Optimal Collaborative Scheduling Strategy of Mobile Energy Storage System and Electric Vehicles Considering SpatioTemporal Characteristics" Processes 13, no. 7: 2242. https://doi.org/10.3390/pr13072242
APA StyleSun, L., & Yu, T. (2025). Optimal Collaborative Scheduling Strategy of Mobile Energy Storage System and Electric Vehicles Considering SpatioTemporal Characteristics. Processes, 13(7), 2242. https://doi.org/10.3390/pr13072242





