Kinematic Analysis of the Jaw Crusher Drive Mechanism: A Different Mathematical Approach

Abstract

This paper presents a detailed kinematic analysis of a double-toggle jaw crusher used for the primary crushing of hard and bulky materials. The study introduces an innovative mathematical modeling method for the motion of the mechanism’s components, eliminating the need for traditional decomposition into structural groups. General equations are developed to determine the positions, linear velocities, and angular displacements of the moving elements, providing a solid foundation for equipment design and study. The generated mathematical model was validated using real-world dimensions of an SMD-117-type jaw crusher and by comparison with simulation results obtained from Mathcad, Linkage, Roberts Animator, and GIM software. The results demonstrated a high degree of agreement between the calculated and simulated trajectories and linear velocities. The analysis of angular displacements and linear velocities confirmed the cyclic nature of the mechanism’s motion, characterized by sinusoidal variations and low oscillations, which are relevant for assessing variable loads. Through its rigorous approach and multi-source validation, the research makes a significant contribution to the development of more efficient, durable, and adaptable jaw crushers for modern industrial requirements.

1. Introduction

The process industry represents a fundamental component of the modern economy, playing a key role in transforming raw materials into finished products through a sequence of sophisticated technological operations. The performance of the equipment used in these processes directly influences product quality, energy efficiency, and operational sustainability. In this context, a detailed and advanced analysis of industrial machinery becomes a strategic priority for optimizing technological workflows and preventing costly failures.

The transformations undergone by raw materials during technological processes may be mechanical, thermal, chemical, biochemical, or electrochemical in nature. Among these, grinding represents an essential preliminary stage with a major impact on the efficiency and quality of subsequent processes. The purpose of this operation is to reduce the size of solid particles, thereby facilitating chemical reactions and heat and mass transfer, accelerating the homogenization of mixtures, and improving material handling [1]. In fields such as the chemical, pharmaceutical, food, and construction materials industries, grinding is indispensable for obtaining products with uniform physicochemical properties. This stage involves the use of specialized equipment, such as ball mills, hammer mills, crushers, or grinders. Each of them is selected based on the material’s characteristics and the desired degree of fineness. The proper selection of machinery and operating parameters is essential for minimizing losses, reducing energy consumption, and preventing the premature wear of downstream installations [2,3,4].

Jaw crushers are among the most used machines for the primary grinding of solid materials and are indispensable in industries such as mining, construction materials, cement production, and recycling. These machines operate based on a simple mechanism (inspired by human mastication) consisting of two distinct stages [5,6]:

• The material is introduced between two jaws, one fixed and one movable.
• Through the oscillatory motion of the movable jaw, the distance between the two jaws decreases, generating compressive forces on the material, which leads to its crushing and fragmentation.

The analysis of jaw crusher operation is essential for improving performance, reducing energy consumption, and extending the service life of wear-prone components, specifically the two jaws, which are the fixed jaw and the movable jaw. Parameters such as the nip angle, shaft rotation speed, feed opening size, and material characteristics significantly influence the efficiency of the crushing process performed by this type of equipment [7,8].

These machines are valued for their robustness, ability to process hard and bulky materials, and ease of maintenance. The integration of monitoring sensors and automated control systems enables a real-time adjustment of operating parameters, preventing blockages and optimizing production flow [9].

In an industrial landscape where energy efficiency and sustainability have become imperative, research into the operation and maintenance of jaw crushers contributes to the development of cleaner and more efficient processes. Adapting these machines to the demands of digitalization and automation is vital for maintaining competitiveness.

Double-toggle jaw crushers are distinguished by their robustness and, as previously mentioned, are primarily used for the grinding of hard and abrasive materials. Research dedicated to these machines has focused on improving operational performance, energy efficiency, and component durability, addressing the following directions:

• Kinematic and dynamic analysis: Modeling the motion of the jaws and the double-toggle mechanism has enabled a deeper understanding of force distribution and particle trajectories during the crushing process. Mathematical methods and finite element simulations (FEM) have been employed to optimize geometry and reduce mechanical stresses [1,10,11,12,13,14,15,16,17,18,19,20,21].
• Optimization of operating parameters: Experimental studies have highlighted the influence of the nip angle, stroke of the movable jaw, and rotational speed on crushing efficiency, demonstrating that adjusting these parameters can lead to increased throughput and reduced energy consumption [13,18,22,23,24,25,26,27].
• Component wear and advanced materials: Research has focused on the use of manganese steels, hard alloys, and composite materials to extend the service life of active components [28,29].
• CFD and DEM simulations: These methods have been applied to analyze particle behavior within the crushing chamber, particularly under conditions of uneven feed or when processing moist materials [7,30,31,32,33,34,35].
• Automation and intelligent monitoring: The integration of vibration, temperature, and pressure sensors has enabled the development of real-time monitoring systems, contributing to fault prevention and the optimization of predictive maintenance strategies [36].
• Comparison with single-toggle crushers: Comparative studies have highlighted the advantages of the double-toggle design in terms of crushing force, mechanical stability, and energy efficiency, especially in demanding applications [37,38,39,40].
• Energy efficiency and sustainability: Recent research has proposed solutions for reducing the carbon footprint by optimizing the duty cycle and implementing high-performance electric drives [36,41,42,43].

The aim of this study is to identify the motions performed by the components driving a double-toggle jaw crusher. As previously discussed, such investigations are well represented in the specialized literature. What distinguishes the present study is the approach used for the kinematic analysis, which led to the development of complex mathematical models that incorporate all components of the analyzed mechanism. These mathematical models are intended to support a more efficient design of such equipment. The resulting equations are general in nature and can be applied to any type of double-toggle jaw crusher, provided that the laws of motion are respected.

The parameters used in the derived equations were replaced with values found in the scientific literature in order to verify their correctness. Additionally, a series of specialized software tools were employed to validate the results.

2. Working Methodology

The methodology employed in this study aims to develop, validate, and implement a general mathematical model for conducting the kinematic analysis of a double-toggle jaw crusher. This approach enables an accurate evaluation of the motion of the mechanism’s components and facilitates the optimization of the equipment’s performance under industrial operating conditions.

To this end, the following working stages presented in Figure 1 were carried out:

-

The mechanism under investigation was presented, with the following identified:

○

The fixed and moving elements, corresponding to the fixed and movable kinematic pairs of the analyzed mechanism;

○

Dimensional values were assigned to the elements that establish the connections between the kinematic pairs.

-

Based on this mechanism, a set of mathematical relationships was developed, derived from the principles of planar kinematics, with the aim of describing the motion generated by the system.

-

A series of technical specifications corresponding to the structural components of a double-toggle jaw crusher were identified from the specialized literature. From these, a reference configuration was selected to enable subsequent numerical comparisons.

-

For the numerical computation, a software tool capable of handling calculations for multiple input values was required; therefore, Mathcad 15 was selected for this purpose.

-

To validate the mathematical relationships used, an analysis was also performed using three distinct software applications developed by different manufacturers.

-

The values obtained through mathematical computation were compared with the data generated by the three simulation tools.

As previously mentioned, to simulate the motions executed by the actuation system of the double-toggle jaw crusher, the following simulation software tools were employed: (i) Linkage v. 3.16.42 [44] is a free software application for Windows, specifically developed for modeling and simulating two-dimensional planar mechanisms. Created by David Rector, it is widely used for prototyping articulated mechanisms typically found in mechanical engineering and robotics; (ii) Roberts Animator v. 2.1.0 [45] is a component of the WATT Mechanism Suite, developed by Heron Technologies. It is designed for the analysis, visualization, and animation of planar mechanisms, supporting both the extension and refinement of mechanical system models; (iii) GIM v. 2025.4 (Graphical Interactive Mechanisms) [46,47] is an educational software tool developed by the COMPMECH Research Group at the University of the Basque Country (UPV/EHU). It is designed for the analysis and synthesis of planar mechanisms, offering an interactive graphical environment suitable for both academic and research applications.

This methodology was adopted because it provides a rigorous, flexible, and scalable approach for the kinematic analysis of double-toggle jaw crushers.

3. Theoretical Considerations

To determine the trajectories followed by the joints of such a mechanism, the specialized literature recommends decomposing the system into a series of structural groups (simple geometric forms used for geometric calculations) [48]. Specifically, the mechanism can be divided as follows [7,12,13,16,17,25]:

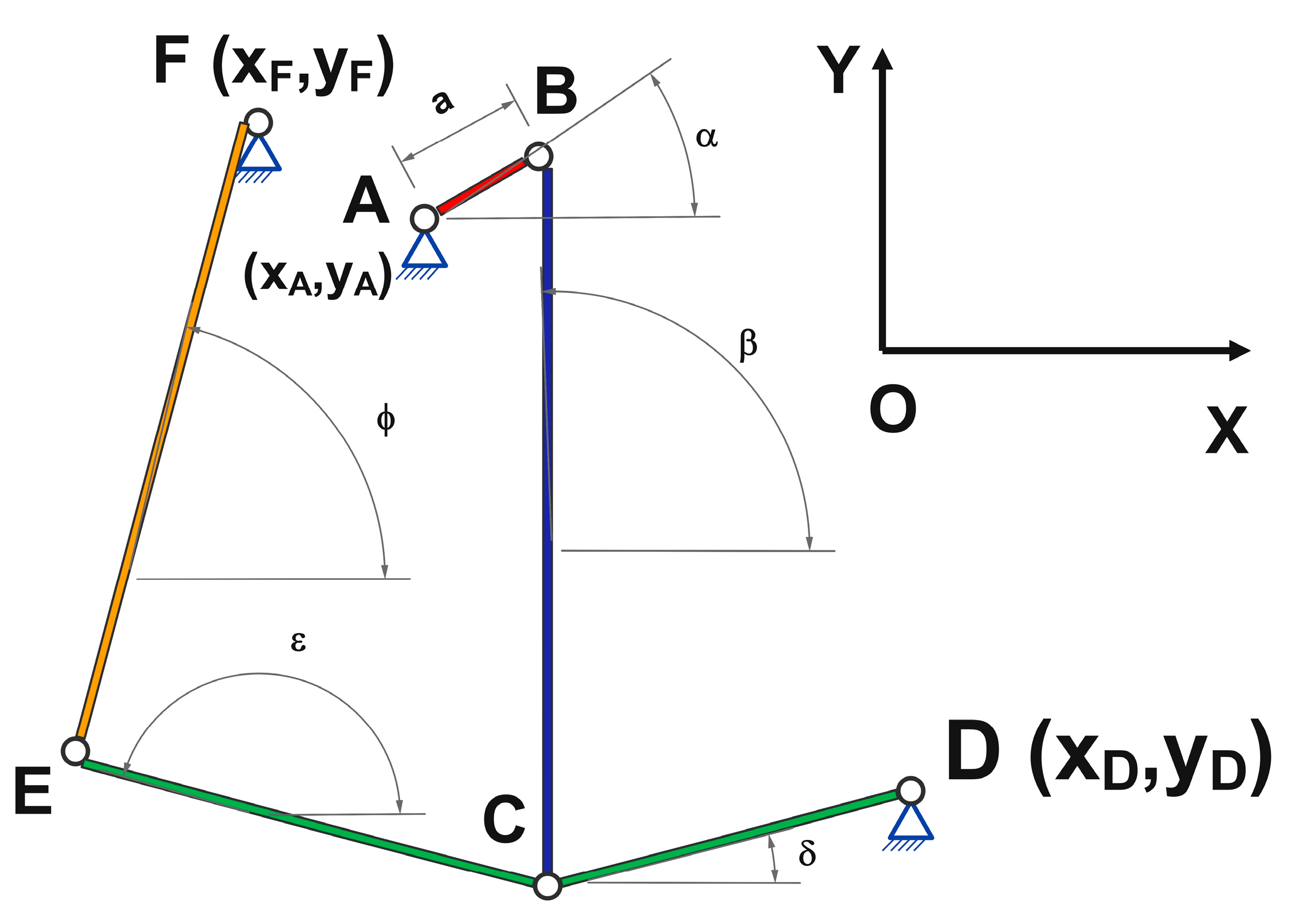
• Group 1 consists of the driving element AB, i.e., the crank. Within this group, the coordinates of joint B can be determined;
• Group 2 may consist of elements AB and BC or, alternatively, of elements DC and BC. Regardless of the chosen configuration, this group allows for the determination of the coordinates of joint C;
• Group 3 can also be formed in two ways: the first variant includes elements BC and CE, while the second includes elements FE and EC. In both cases, the objective is to determine the coordinates of joint E.

The purpose of this type of kinematic analysis is to identify the coordinates of the moving joints of the mechanism under study (joints B, C, and E). Based on these coordinates, various parameters such as velocity and acceleration can be calculated.

This paper proposes an alternative method for analyzing the kinematic structure of the mechanism, which involves performing a global kinematic analysis of the entire structure without decomposing it into structural groups.

For this purpose, the following notations are introduced in Figure 2:

• Each element of the mechanism is assigned a dimensional value;
• The rotating element is identified, and its motion is represented by the rotation angle of the crank, denoted as α.

Since the mechanism under study includes three fixed joints (joints A, D, and F), their coordinates were denoted as follows:

• Joint A—x_A and y_A;
• Joint D—x_D and y_D;
• Joint F—x_F and y_F.

Based on these notations, the following calculation relationships are presented for determining the positions of the moving joints of the mechanism:

• The equations corresponding to joint B are given by the following expressions:

  $$x_B=x_A+a·\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha \right)$$

  (1)

  $$y_B=y_A+a·\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha \right)$$

  (2)
• The calculation relationships corresponding to joint C can be determined using the following equations:

  $$x_C=x_D+{\displaystyle \frac{({-b}^2+c^2+d_0^2)(a·\mathit{cos}\left(\alpha \right)+x_A-x_D)}{2d_0^2}}+{\displaystyle \frac{d_1·(-a·\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha \right)-y_A+y_D)}{2d_0^2}}$$

  (3)

  $$y_C=y_D+{\displaystyle \frac{d_1·(a·\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha \right)+x_A-x_D)}{2d_0^2}}+{\displaystyle \frac{(-b^2+c^2+d_0^2)(a·\mathit{sin}\left(\alpha \right)+y_A-y_D)}{2d_0^2}}$$

  (4)
• The calculation relationships required to determine the coordinates of joint E are

  $$x_E=x_F+{\displaystyle \frac{(-d^2+e^2+d_2^2)(x_C-x_F)}{2d_2^2}}-{\displaystyle \frac{d_3·(-y_C+y_F)}{2d_2^2}}$$

  (5)

  $$y_E=y_F-{\displaystyle \frac{d_3·(x_C-x_F)}{2d_2^2}}+{\displaystyle \frac{(-d^2+e^2+d_2^2)(y_C-y_F)}{2d_2^2}}$$

  (6)

As can be observed, in Equations (3)–(6), a series of notations were introduced due to the considerable length of the resulting expressions. The corresponding definitions for these notations are given by the following calculation relationships:

$$d_0=\sqrt{{(-a·\mathit{cos}\left(\alpha \right)-x_A+x_D)}^2+{(-a·\mathit{sin}\left(\alpha \right)-y_A+y_D)}^2}$$

(7)

$$d_1=\sqrt{b+c-d_0}·\sqrt{b-c+d_0}·\sqrt{-b+c+d_0}·\sqrt{b+c+d_0}$$

(8)

$$d_2=\sqrt{{(-x_C+x_F)}^2+{(-y_C+y_F)}^2}$$

(9)

$$d_3=\sqrt{d+e-d_2}\sqrt{d-e+d_2}\sqrt{-d+e+d_2}\sqrt{d+e+d_2}$$

(10)

In addition to the coordinates of the moving joints, a series of calculation relationships were also established for the angles formed by the moving elements with respect to the horizontal axis OX (Figure 3):

-

Angle β represents the angle formed by element BC with respect to the horizontal axis;

-

Angle δ represents the angle formed by element CD with respect to the horizontal axis;

-

Angle ε represents the angle formed by element CE with respect to the horizontal axis;

-

Angle ϕ represents the angle formed by element EF with respect to the horizontal axis.

The following are the calculation relationships corresponding to these angles:

• For angle β:

  $$\beta =180-a\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left[{\displaystyle \frac{y_A-y_C+a·sin\left(\alpha \right)}{{-x}_A+y_C-a·cos\left(\alpha \right)}}\right]$$

  (11)
• For angle δ:

  $$\delta =-\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left[{\displaystyle \frac{y_C-y_D}{-x_C+x_D}}\right]$$

  (12)
• For angle ε:

  $$\epsilon =180-arctan\left[{\displaystyle \frac{y_C-\left[y_F-\frac{d_3\left({-x}_F{+x}_C\right)}{2d_2^2}+\frac{({-d}^2+e^2+d_2^2)({-y}_F+y_C)}{2d_2^2}\right]}{x_F-x_C+\frac{\left(-d^2+e^2+d_2^2\right)\left({-x}_F{+x}_C\right)}{2d_2^2}-\frac{d_3(y_F-y_C)}{2d_2^2}}}\right]$$

  (13)
• For angle ϕ:

  $$\varnothing =-\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}\left[{\displaystyle \frac{\frac{{-d}_3(x_C-x_F)}{2d_2^2}+\frac{(-d^2+e^2+d_2^2)(y_C-y_F)}{2d_2^2}}{x_F-\left[x_F+\frac{(-d^2+e^2+d_2^2)(x_C-x_F)}{2d_2^2}-\frac{d_3(-y_C+y_F)}{2d_2^2}\right]}}\right]$$

  (14)

By analyzing the previously presented calculation relationships, the following observations can be made:

-

Regardless of which component is being analyzed (calculation relationships for the coordinates of couples B, C, or E, or angles β, δ, ε, and ϕ), their values are closely related to the variation in angle α;

-

Regarding the calculation relationships corresponding to the studied joints,

○

The motion of joint C depends on the positions of the fixed joints A and D, the dimensional values of elements AB, BC, and CD, and the angle formed by the crank AB with respect to the horizontal axis;

○

The motion of joint E depends on the position of the fixed joint F, the position of the moving joint C, and the dimensional values of elements EF and EC;

○

As a result of this analysis, it can be stated that, in order to determine the coordinates of joints C and E, the mechanism can be divided into two subsystems:

▪

For joint C, it is necessary to know the characteristics of the four-bar linkage formed by elements AB, BC, and CD;

▪

For joint E, it is necessary to know the characteristics of the mechanism formed by elements EF and EC.

-

Regarding the calculation relationships corresponding to the analyzed angles,

○

Angle β depends on the coordinates of the fixed joint A, the coordinates of the moving joint C, the dimensional value of the crank, and the angle it forms with the horizontal axis;

○

Angle δ depends only on the coordinates of the fixed joint D and the moving joint C;

○

Both angles ε and ϕ depend on the coordinates of the fixed joint F, the coordinates of the moving joint C, and the dimensional values of elements EF and EC.

4. Results

To verify the previously presented calculation relationships, dimensional values corresponding to a double-toggle jaw crusher were used, as found in the specialized literature (SMD-117 crusher) [48]. The dimensional characteristics used for verification are presented below:

-

Dimensions of the elements in the crusher’s actuation system:

○

Element AB = 42 mm.

○

Element BC = 2165 mm.

○

Element DC = 1099 mm.

○

Element CD = 1839 mm.

○

Element FE = 2885 mm.

-

Coordinates of the fixed joints:

○

Fixed joint A has the coordinates x_A = 0 mm, y_A = 0 mm;

○

Fixed joint D has the coordinates x_D = 1190 mm, y_D = −1800 mm;

○

Fixed joint F has the coordinates x_F = −1625 mm, y_F = 1011 mm.

It should be noted that the calculations were performed using Mathcad 15 software.

To verify the accuracy of the values obtained through the calculation relationships presented in the previous section (Equations (11)–(14) and Equations (7)–(10)), a comparison was made between these results and the values found in the specialized literature, corresponding to the SMD-117 jaw crusher [48]. In the reference article [48], the variations in the angles generated by the elements of the crusher’s actuation system with respect to the horizontal axis were identified. For this reason, Figure 4 presents a comparative view of the two sets of values.

Based on the analysis of the graphical representations in Figure 3, the following observations can be made:

-

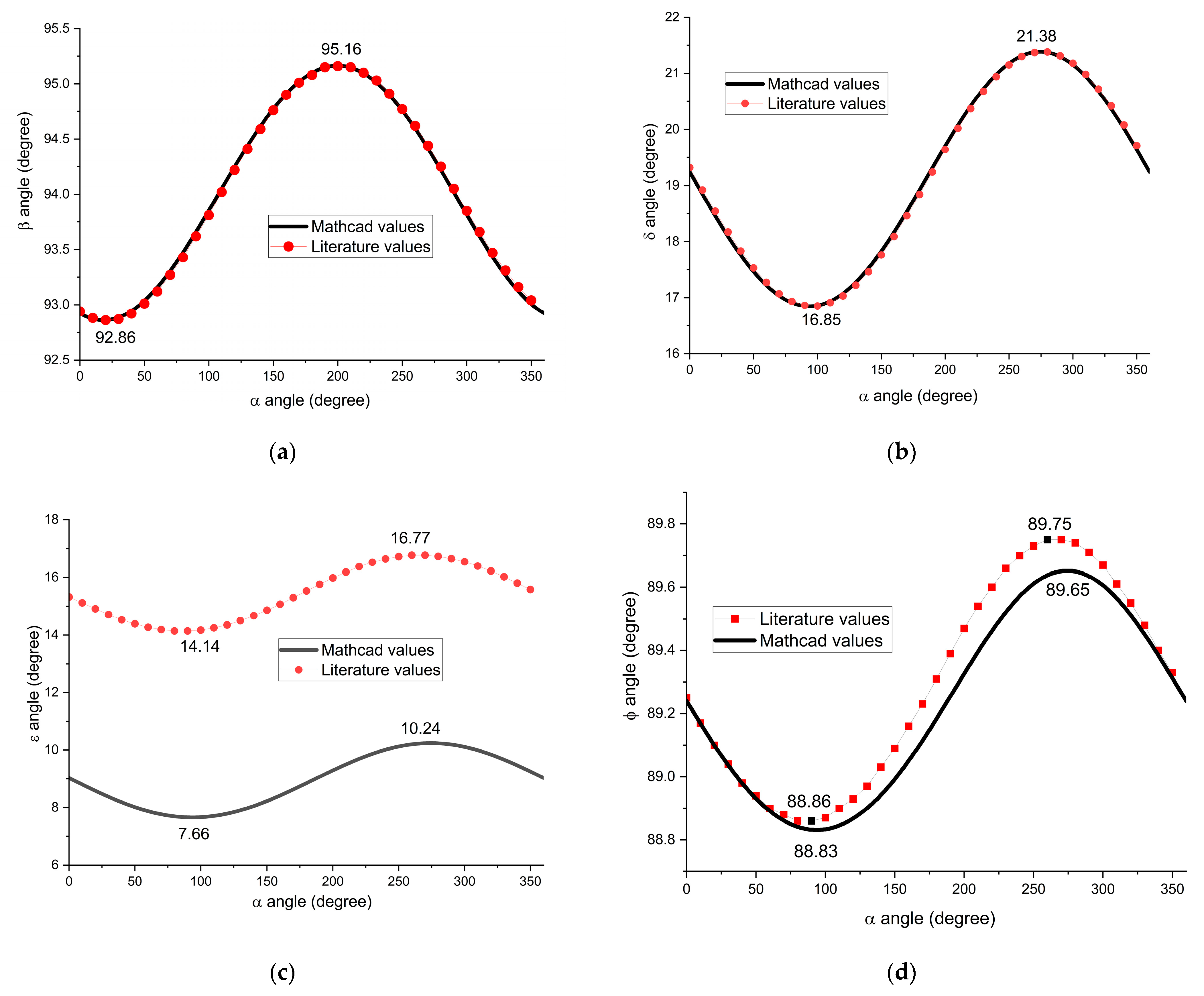
Regarding the variation in angles β and δ, which correspond to the angles formed by elements BC and CD with respect to the horizontal axis, it can be stated that they match the values found in the specialized literature both in terms of magnitude and variation pattern (a sinusoidal trend is observed). Numerically, angle β varies between approximately 92.86° and 95.16°, indicating a relatively small but kinematically significant oscillation. As for angle δ, it varies between 16.85° and 21.38°.

-

Regarding the variation in angle ε, it is observed that its values differ from those found in the specialized literature by approximately 6°. These differences may be caused by errors in measuring the angular value or even in the construction of the mechanism (failure to observe the position of point E may lead to this difference—the reference article [48] does not specify the exact position of coupling E). However, the variation pattern of angle ε with respect to the crank angle α remains consistent. The variation range of angle ε, as obtained using Mathcad, is between a minimum of 7.66° and a maximum of 10.24°.

-

Concerning the variation in angle ϕ, it is noted that for the crank angle intervals 0–55° and 325–360°, there are no differences between the mathematically obtained values and those reported in the literature. Outside these intervals, a maximum deviation of 0.14° is observed between the two data sets. Additionally, angle ϕ varies within a very narrow range, from 88.8° to 89.65°, indicating a limited oscillation, which is a result of the constrained motion within the mechanism.

Additionally, the results obtained through the mathematical relationships presented in this study were also compared with those obtained using simulation software.

Figure 5 presents the trajectories generated both by mathematical relationships and by the three simulation programs used. The trajectories under analysis are those traced by joints C and E. A graphical representation of the motion of joint B was not included, as it performs a rotational motion, being the free end of the crank.

Based on the analysis of the trajectories of the free kinematic pairs, as illustrated in Figure 5, the following conclusions can be drawn:

-

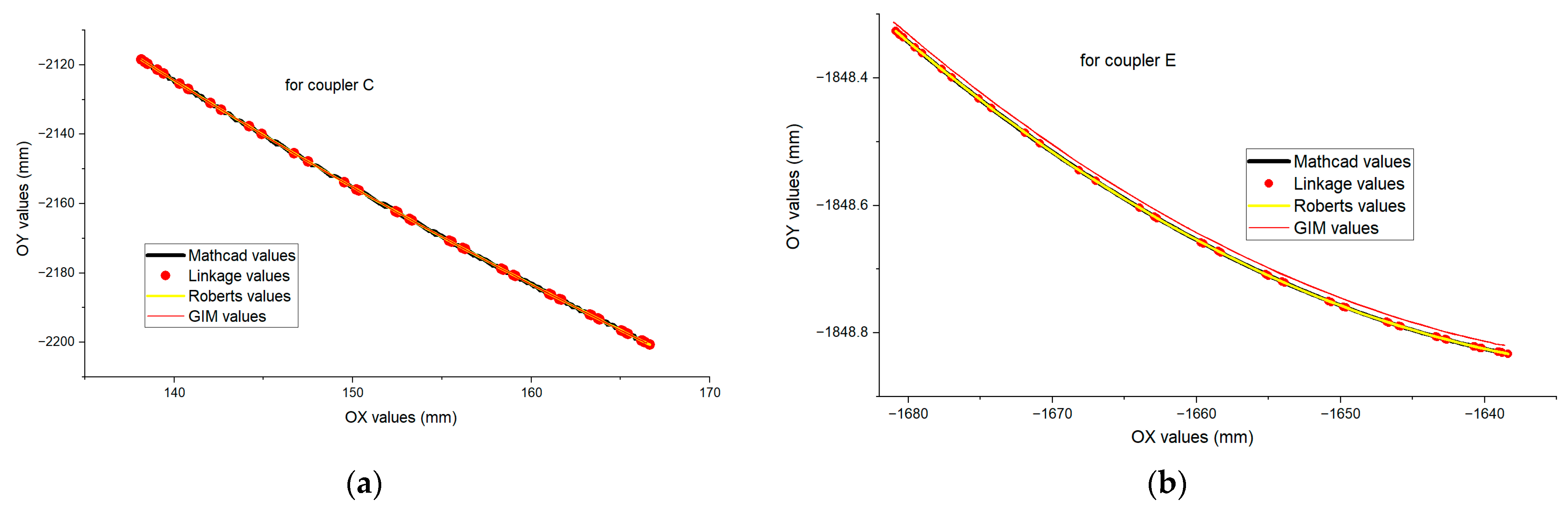
Regarding the trajectory of the C pair, the graph demonstrates a high degree of consistency among the results obtained from the four different motion analysis sources. This coherence validates the identified mathematical model used for analyzing the motion of point C.

-

Regarding the trajectory of the E pair, it is observed that all four curves follow a similar path, indicating good agreement between the applied methods. A minor discrepancy of 0.013 mm is noted between the values obtained using Mathcad, Linkage, and Roberts Animator, compared to those obtained via GIM software. This variation may be attributed to the interpolation algorithms employed by the respective programs.

Using the same comparative method, the variation in the linear velocity generated by the two analyzed kinematic pairs was also examined. For the mathematical determination, calculation relations 1–10 were employed. This parameter, linear velocity, was calculated using the classical finite difference method. These variations are illustrated in Figure 6.

Upon analyzing the graphs in Figure 6, the following observations can be made:

-

Regarding the variation in the linear velocity corresponding to the C pair, the range of variation is between 0.95 and 274 mm/s;

-

For the linear velocity variation in the E pair, it follows a similar pattern to that of the C pair but with a smaller range between 0.4 and 135 mm/s;

-

Regardless of the pair under analysis, the linear velocity variation exhibits a sinusoidal profile;

-

Both pairs show fluctuations in linear velocity, with the parameter reaching a minimum after an interval of 0.5 s, indicating that the mechanism under study performs a cyclic motion;

-

The fact that all applied methods, the mathematical calculation method presented in this paper and the motion simulation methods using the three software tools, yield similar results, validates the proposed model.

5. Conclusions

Jaw crushers are critical machines in the process industry, widely employed for the initial reduction in size for hard and large-sized materials. The present study focuses on an advanced variant of this equipment, namely the double-toggle jaw crusher, providing a detailed analysis of its kinematic behavior with the aim of optimizing operational performance and reducing component wear.

Based on the analysis conducted in this study, the following conclusions can be drawn:

1. This study proposes an alternative method for the kinematic analysis of the crusher mechanism without decomposing it into structural groups, as traditionally performed. Through this approach, the coordinates of the moving kinematic pairs (B, C, and E), as well as the angles formed by the mechanism’s links relative to the horizontal OX axis, are determined. The developed mathematical models are general in nature and can be applied to any double-toggle jaw crusher, provided the laws of motion are respected. This unified approach allows the analysis to be extended to a wide range of structural configurations, which is not always possible with traditional methods, which require specific adaptations for each model. The proposed method also reduces algorithmic complexity and allows for a more direct implementation in computing environments. This computational simplicity translates into increased efficiency in the modeling and simulation process, facilitating rapid integration into engineering design workflows compared to classical methods that involve additional geometric reconstruction steps.

2. The equations presented in this study allow for the calculation of both the positions and velocities of the moving pairs, thus providing a solid foundation for equipment design and optimization. These mathematical models have been validated through comparison with data from the scientific literature and simulations performed using specialized software such as Linkage, Roberts Animator, and GIM.

3. To verify the accuracy of the proposed mathematical models, a set of real dimensional values (sourced from the literature) corresponding to a double-toggle jaw crusher (model SMD-117) was used. The values obtained through the mathematical relations were also compared with the results from the three simulation programs. The results showed excellent agreement between the calculated and simulated trajectories, particularly for the C pair. For the E pair, a minor discrepancy of 0.013 mm was observed between the values obtained using GIM and the other methods, attributed to differences in interpolation algorithms.

4. Another important aspect of the study is the analysis of the variation in the angles formed by the mechanism’s links during operation. It was found that angles β and γ (corresponding to links BC and CD) exhibit sinusoidal variation and match the values reported in the literature. Angle δ (link CE) shows a deviation of approximately 6° from the reference values [48] but maintains the same variation pattern. Angle ε (link EF) varies within a very narrow range (88.8–89.65°), indicating limited oscillation, characteristic of the constrained motion of this link.

5. The article also includes an analysis of the linear velocity variation corresponding to the C and E kinematic pairs. Both velocity profiles exhibit sinusoidal variation, with peak values of approximately 274 mm/s for pair C and 135 mm/s for pair E. The velocity reaches a minimum every 0.5 s, confirming the cyclic nature of the mechanism’s motion.

This study provides a valuable contribution to the understanding and optimization of double-toggle jaw crusher operation. By combining rigorous mathematical analysis with advanced simulation techniques and integrating principles of sustainability and automation, the research opens new avenues for the development of more efficient, durable, and intelligent industrial equipment.

The validation of the proposed mathematical models through a comparison with experimental data and simulation results obtained using specialized software adds robustness to the conclusions and offers a solid framework for practical applications in the design and operation of modern jaw crushers.