A Systematic Review and Meta-Analysis of Model Predictive Control in Microgrids: Moving Beyond Traditional Methods
Abstract
1. Introduction
- Provides a comprehensive classification of MPC techniques applied in MGs based on objectives, algorithms, and application domains;
- Analyses the use of multi-objective optimization and highlights its role in enhancing operational trade-offs in MGs;
- Explores the integration of MPC with hybrid and hierarchical control strategies for complex, real-world implementations;
- Offers a bibliometric meta-analysis to uncover research trends and publication patterns over the past decade.
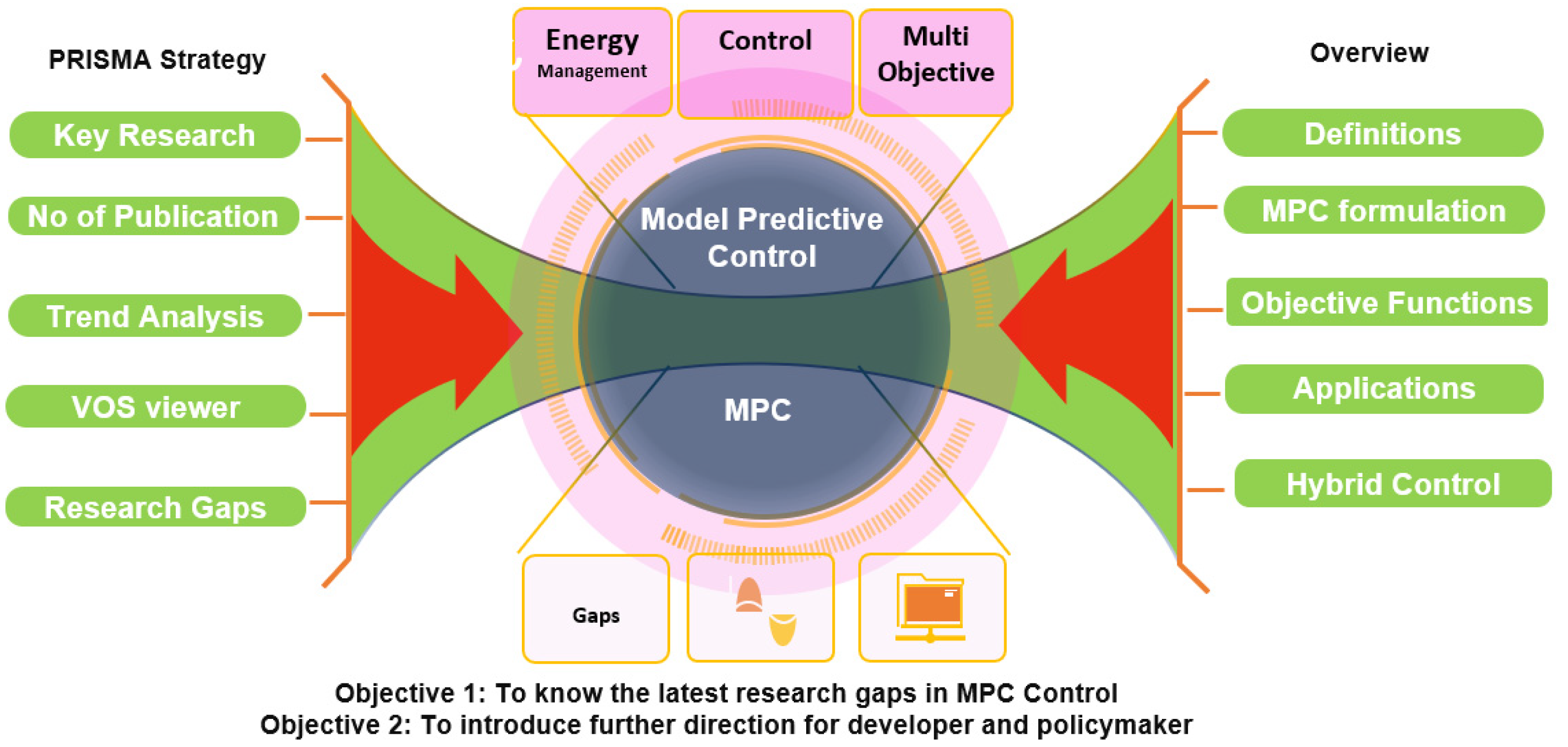
2. Background and Review Methodology
2.1. MPC Fundamentals and Microgrid Applications
2.2. Research Gap and Review Positioning
2.3. Review Methodology and Bibliometric Analysis Approach
- What are the dominant MPC strategies used in microgrid control?
- How do these strategies vary by application (energy management and frequency control)?
- What control objectives and optimization techniques are employed?
- What research gaps exist in terms of hybrid, hierarchical, and multi-objective implementations?
- Data Collection and Source Selection:
3. Overview of MPC Approaches in Microgrid
3.1. System Dynamics in MPC
- In continuous system dynamics, time is conceptualized as a continuous variable, facilitating seamless and uninterrupted changes in the system’s state [61,88]. Characterized by continuous-time differential equations, these equations elucidate the rate of change in the system’s state variables over time [89,90]:
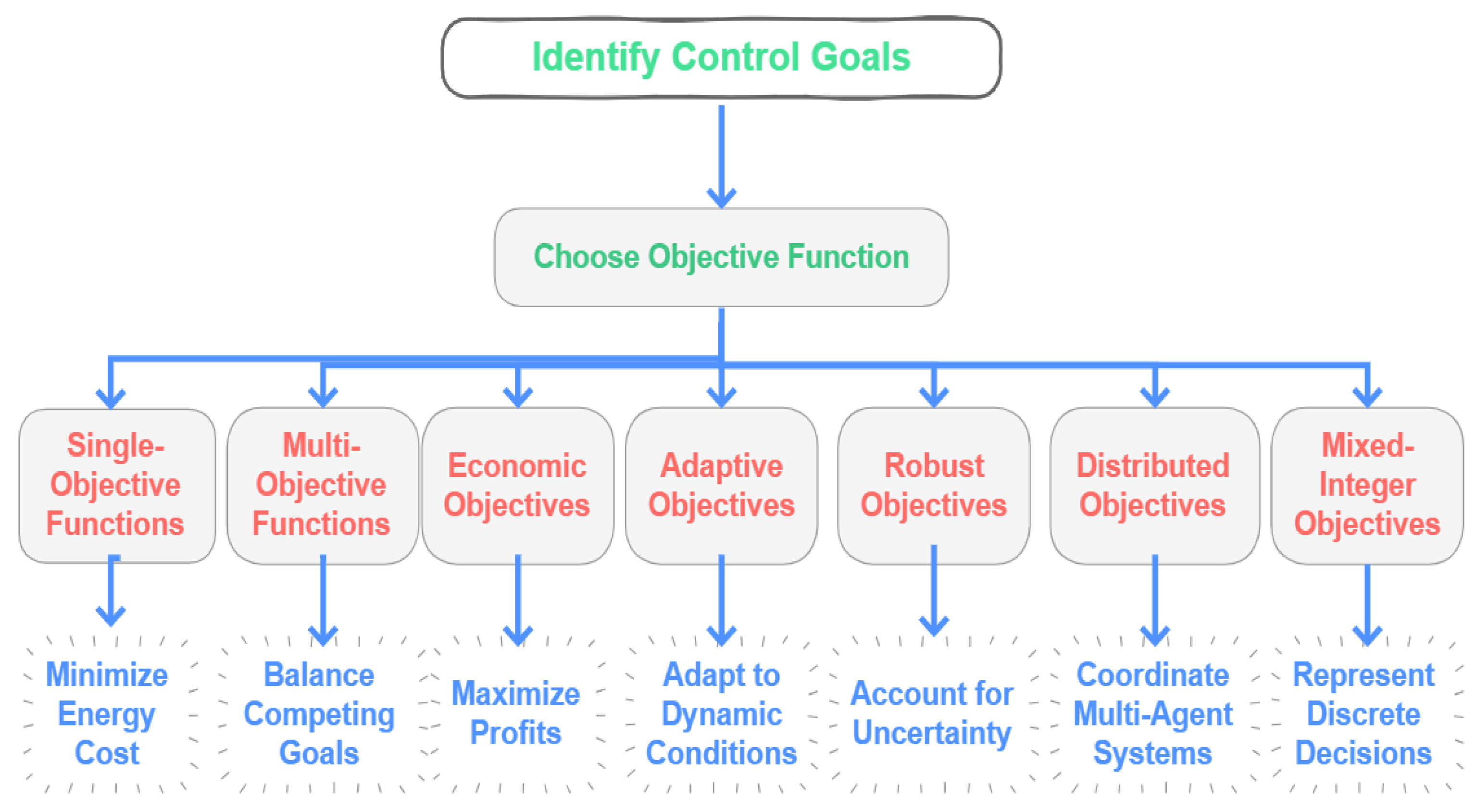
3.2. Types of Objective Functions in MPC
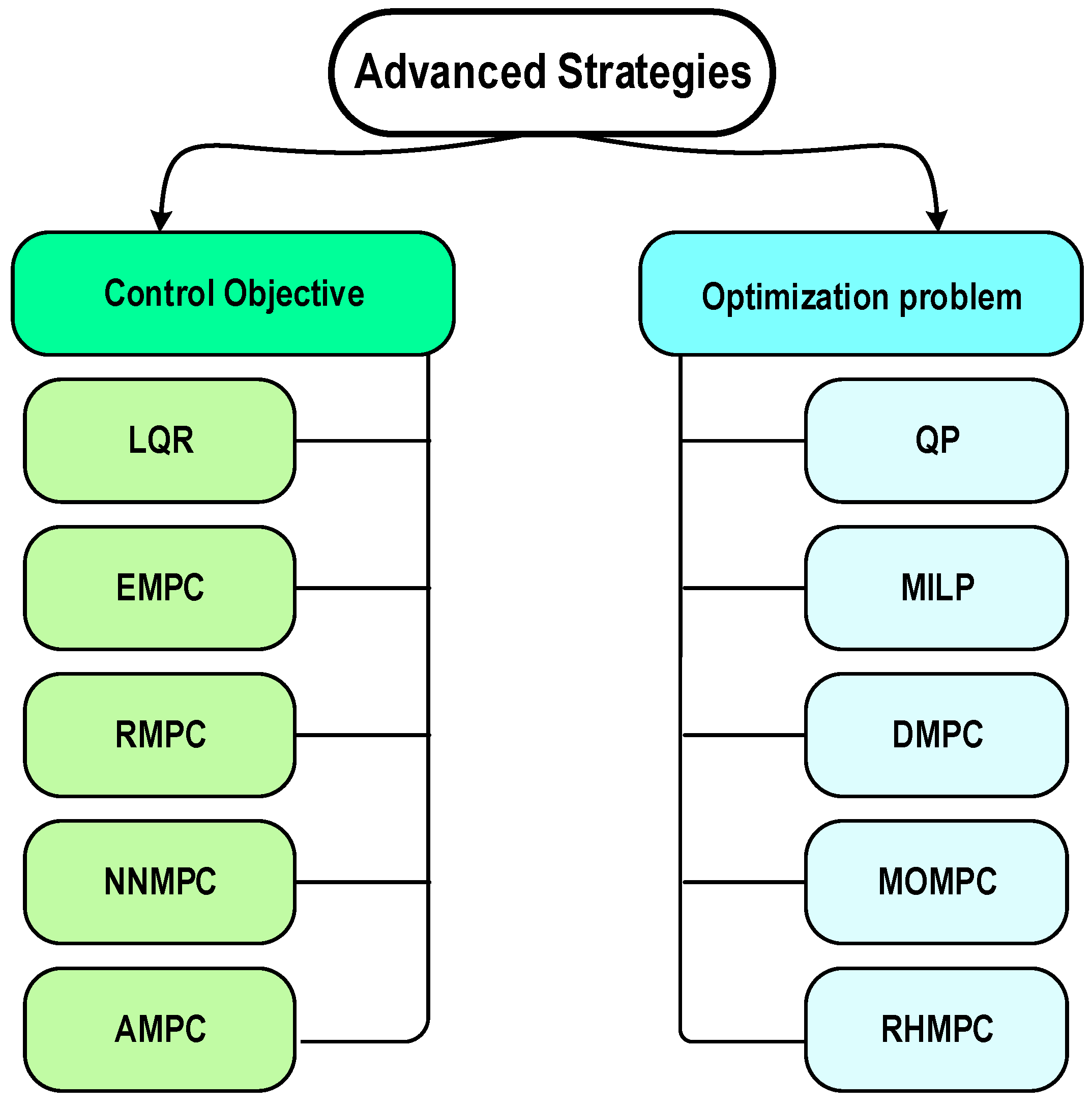
3.3. MPC Algorithm Types (Formulation-Based)
- (1)
- Control-Oriented Classification of MPCs
- Linear Quadratic Regulator (LQR): LQR is a preferred choice in MPC applications due to its simplicity and computational efficiency [128,129]. However, its simplicity comes at a cost, as it is primarily suited for linear systems with quadratic cost functions. To address these limitations, researchers have proposed various approaches, including a novel LQR controller that tackles V-f control in isolated PV–battery MGs [130]. This controller eliminates state estimators, relies on local data, and handles diverse uncertainties, achieving robust performance verified by extensive HIL tests. Building on this success, Reference [131] introduces an even more robust combo of resonant and lead–lag controllers. This approach tackles voltage tracking and stability in isolated MGs, outperforming LQR, MPC, and NI controllers by handling diverse uncertainties and offering excellent tracking, enhanced stability, and flexibility across single- and three-phase systems.
- (2)
- Optimization Problem-Based MPC
- Mixed-Integer Linear Programming (MILP): MILP finds application in MPC scenarios with discrete decision variables, addressing tasks like switching between energy sources or adjusting power setpoints [140,141]. While computationally more demanding than QP, MILP excels in optimizing intricate discrete control strategies [142,143].
| Algorithm | System Dynamics | Objective Function | Optimization Problem | Computational Complexity | Applications |
|---|---|---|---|---|---|
| RHMPC [81,82] | Continuous | Single | QP | Moderate | General control |
| MOMPC [151] | Continuous | Multiple | Multi-objective QP | High | Multi-objective control |
| AMPC [83] | Continuous | Adaptive | Adaptive QP | High | Adaptive control |
| NNMPC [84] | Continuous | Learned | Neural network | High | Nonlinear control |
| DMPC [52] | Distributed | Distributed | Distributed QP | High | Large-scale systems |
| RMPC [85,86] | Continuous | Robust | Robust QP | High | Robust control |
| EMPC [152] | Continuous | Economic | MILP | High | Economic optimization |
| MILP [87] | Discrete/ Continuous | Mixed-integer | MILP | High | Discrete/continuous systems |
| QP [153,154,155,156] | Continuous | Quadratic | QP | Moderate | General control |
| LQR [157] | Continuous | Quadratic | Riccati equation | Moderate | Linear systems |
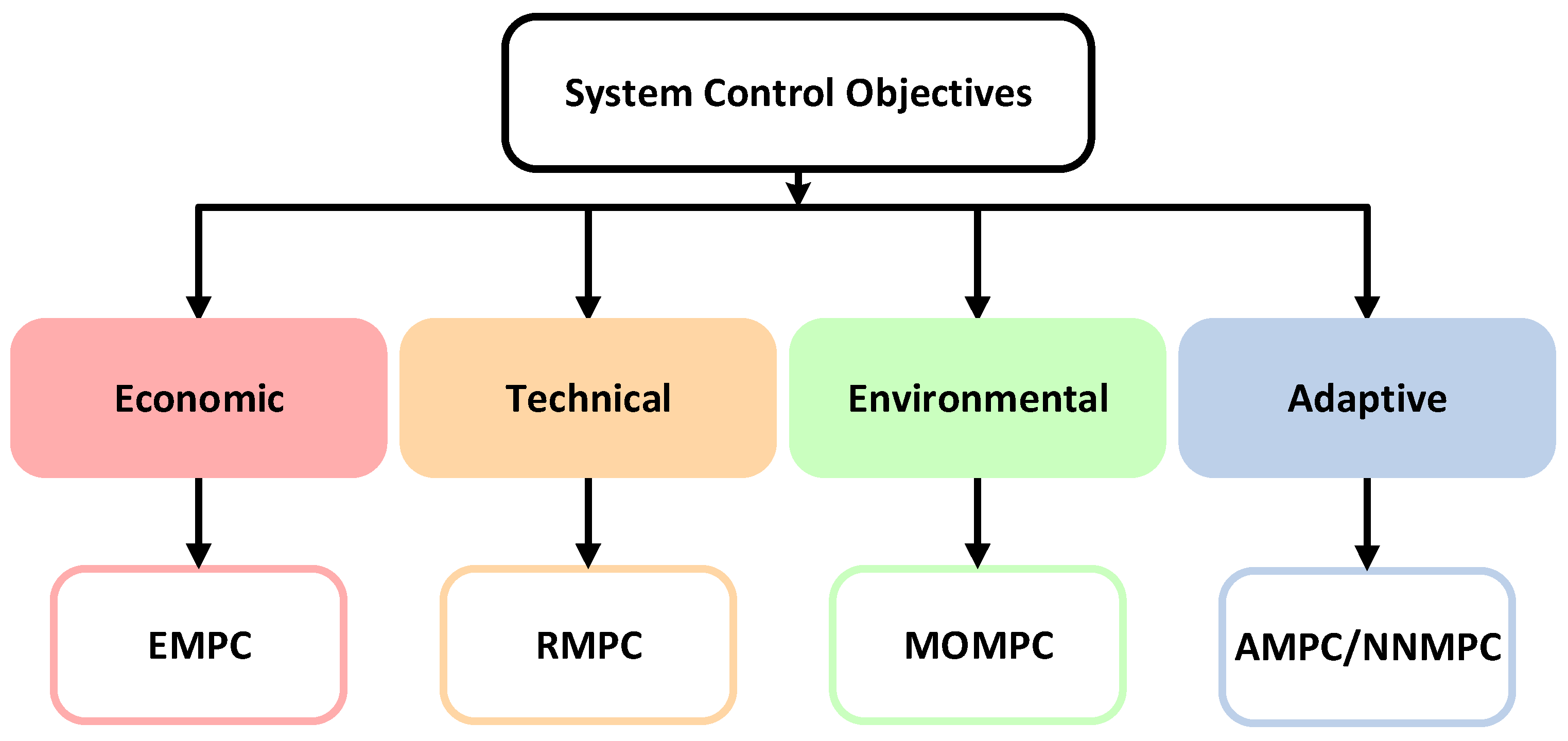
| MPC Technique | Application Area | Performance Indicator | Identified Research Gaps |
|---|---|---|---|
| EMPC [95,158] | Cost optimization in MGs | Operational cost reduction | Limited real-time implementation |
| DMPC [159,160,161] | Multi-agent distributed MGs | Scalability, flexibility | Communication overhead, convergence delays |
| MOMPC [146,162] | Multi-objective energy management | Pareto efficiency | Computational complexity |
| RHMPC [160,163,164] | Islanding transition and fault recovery | Fast frequency/voltage control | Requirement of high-frequency data, instability risks |
| AMPC [83,165] | Dynamic and uncertain loads | Robust response to system changes | Adaptive model-tuning complexity |
| NNMPC [166,167] | Nonlinear system control | Tracking accuracy, generalization | Training data dependency, real time interface challenges |
| RMPC [85,86,168] | Uncertainty resilient control | Robustness against disturbances | Conservative performance, complex constraint handling |
| MILP [169,170] | Scheduling and resource optimization | Global optimality | Scalability and combinatorial explosion |
| QP [171,172] | Fast linear MPC formulations | Computation time, feasibility | Inflexibility in nonlinear/complex system |
| LQR [173,174] | Linear quadric control in stable MGs | Control effort, response speed | Limited adaptability, assumption of linear dynamics |
3.4. MPC Strategies (Deployment/Architecture-Based)
4. Exploring Multi-Objective Optimization Using MPC
4.1. Concept and Benefits
- Reduced risk of suboptimal solutions: Single-objective optimization approaches can sometimes get stuck in local optima, which are solutions that are better than any of their neighbors but not as good as the global optimum [203,204,205]. MOO is less likely to get stuck in local optima because it considers multiple objectives [205,206].
4.2. Challenges in MOO with MPC
5. Hierarchical Control Strategies with MOO and MPC in MGs
5.1. Overview of Hierarchical Structures
5.2. Technical vs. Economic Objectives in MGs
6. Integration of MPC Within Hybrid Control Strategies
- MPC-PID hybrid control: This strategy combines MPC with PID controllers, utilizing MPC for overall optimization and PID controllers for faster response to disturbances [258]. In Reference [259], a novel path-tracking controller is proposed for autonomous vehicles, combining kinematic MPC, PID feedback control, and a vehicle sideslip angle compensator. The controller significantly improves tracking performance at both low and high speeds, effectively handling disturbances and uncertainties. Reference [40] analyzes interlinking converter control in hybrid AC/DC microgrids, summarizing the current state of research and development in control structures, strategies, and techniques. It highlights the strengths and limitations of existing approaches and outlines future directions. In Reference [260], a novel cooperative PSO-based method is proposed for tuning quadrotor trajectory-tracking MPC parameters, enhancing tracking performance and robustness compared to other tuning approaches. The hybrid control strategy combines MPC for position control and PID controllers for attitude control.
- Hierarchical control: This approach employs a hierarchical structure, with MPC at a higher level, handling long-term optimization, and other control techniques at lower levels, managing specific subsystems or fast-changing dynamics [258]. A hybrid control strategy is proposed for a hybrid AC/DC MG, combining low-level, intermediate-level, and high-level control to achieve bus voltage stabilization, ancillary service provision, and power-sharing and frequency-stability improvement. The adaptive virtual inertia outperforms traditional linear controllers in terms of frequency stability [261]. Hierarchical control is a crucial methodology for managing MG complexity, enabling reliable, efficient, and stable operation under various conditions. This layered control structure optimizes MG performance, coordination, and adaptability in both normal and islanding modes [262]. The proposed enhanced MG power flow (EMPF) algorithm accurately incorporates hierarchical control effects, improving power flow analysis and monitoring, especially for complex urban MGs [263].
- Switching control: This strategy dynamically switches between different control techniques based on system conditions. For instance, MPC may be used during normal operation, while PID controllers take over during transient disturbances [258]. An enhanced switching control strategy utilizing droop control and disturbance observer effectively mitigates transient disturbances and ensures seamless and stable operation of AC/DC hybrid MGs during grid-connected and island-mode transitions [264]. In Reference [265], a hybrid smart MG employing intelligent fuzzy control, PID/PI controls, and switching control effectively manages PHEV charging, optimizes renewable energy utilization, and ensures system stability for V2G and G2V operations.
7. Discussion
Practical Barriers and Scalability Challenges
8. Future Research Direction
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wazirali, R.; Yaghoubi, E.; Abujazar, M.S.S.; Ahmad, R.; Vakili, A.H. State-of-the-art review on energy and load forecasting in microgrids using artificial neural networks, machine learning, deep learning techniques. Electr. Power Syst. Res. 2023, 225, 109792. [Google Scholar]
- Jamal, S.; Tan, N.M.; Pasupuleti, J. A review of energy management and power management systems for microgrid and nanogrid applications. Sustainability 2021, 13, 10331. [Google Scholar] [CrossRef]
- Sang, J.; Sun, H.; Kou, L. Deep reinforcement learning microgrid optimization strategy considering priority flexible demand side. Sensors 2022, 22, 2256. [Google Scholar] [CrossRef]
- Hamidieh, M.; Ghassemi, M. Microgrids and resilience: A review. IEEE Access 2022, 10, 106059–106080. [Google Scholar]
- Ma, J.; Ma, X. A review of forecasting algorithms and energy management strategies for microgrids. Syst. Sci. Control Eng. 2018, 6, 237–248. [Google Scholar]
- Wang, Z.; Chen, Y.; Mei, S.; Huang, S.; Xu, Y. Optimal expansion planning of isolated microgrid with renewable energy resources and controllable loads. IET Renew. Power Gener. 2017, 11, 931–940. [Google Scholar]
- Zheng, H.; Ma, H.; Ma, K.; Bo, Z. Modeling and analysis of the AC/DC hybrid micro-grid with bidirectional power flow controller. In Proceeding of the 2017 China International Electrical and Energy Conference (CIEEC), Beijin, China, 25–27 October 2017; pp. 280–284. [Google Scholar]
- Yoldaş, Y.; Önen, A.; Muyeen, S.; Vasilakos, A.V.; Alan, I. Enhancing smart grid with microgrids: Challenges and opportunities. Renew. Sustain. Energy Rev. 2017, 72, 205–214. [Google Scholar]
- Hossain, M.A.; Pota, H.R.; Hossain, M.J.; Blaabjerg, F. Evolution of microgrids with converter-interfaced generations: Challenges and opportunities. Int. J. Electr. Power Energy Syst. 2019, 109, 160–186. [Google Scholar]
- Yusupov, Z.; Yaghoubi, E.; Yaghoubi, E. Controlling and tracking the maximum active power point in a photovoltaic sys-tem connected to the grid using the fuzzy neural controller. In Proceedings of the 2023 14th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkiye, 30 November–2 December 2023. [Google Scholar]
- Rigaut, T.; Nassiopoulos, A.; Bourquin, F.; Giroux, P.; Pény, A. Model predictive control for energy and climate management of a subway station thermo-electrical microgrid. Transp. Res. Procedia 2016, 14, 926–935. [Google Scholar]
- Serale, G.; Fiorentini, M.; Capozzoli, A.; Bernardini, D.; Bemporad, A. Model predictive control (MPC) for enhancing building and HVAC system energy efficiency: Problem formulation, applications and opportunities. Energies 2018, 11, 631. [Google Scholar] [CrossRef]
- Kranda, E.; Gokdag, M.; Gulbudak, O.; Prabaharan, N. Enhancement of Steady-State Performance of PFC Boost Rectifier using Modulated Model Predictive Control. In Proceedings of the 2023 5th Global Power, Energy and Communication Conference (GPECOM), Nevsehir, Turkiye, 14–16 June 2023; pp. 50–55. [Google Scholar]
- Gulbudak, O.; Santi, E. A predictive control scheme for a dual output indirect matrix converter. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition (APEC), Charlotte, NC, USA, 15–19 March 2015; pp. 2828–2834. [Google Scholar]
- Gulbudak, O.; Gokdag, M. FPGA-Based Model Predictive Control for Power Converters. In Proceedings of the 2020 2nd Global Power, Energy and Communication Conference (GPECOM), Izmir, Turkey, 20–23 October 2020; pp. 30–35. [Google Scholar]
- Khokhar, B.; Parmar, K.S. Utilizing diverse mix of energy storage for LFC performance enhancement of a microgrid: A novel MPC approach. Appl. Energy 2023, 333, 120639. [Google Scholar]
- Liu, X.; Suo, Y.; Zhang, Z.; Song, X.; Zhou, J. A New Model Predictive Current Control Strategy for Hybrid Energy Storage System Considering the SOC of the Supercapacitor. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 11, 325–338. [Google Scholar]
- Gulbudak, O.; Gokdag, M.; Akbaba, M. Finite Control Set Model Predictive Control of Six-Phase Induction Motor; Research Square: Durham, NC, USA, 2022. [Google Scholar]
- Yaghoubi, E.; Yaghoubi, E.; Yusupov, Z.; Rahebi, J. Real-time techno-economical operation of preserving microgrids via optimal NLMPC considering uncertainties. Eng. Sci. Technol. Int. J. 2024, 57, 101823. [Google Scholar]
- Miah, M.S.; Lipu, M.S.H.; Meraj, S.T.; Hasan, K.; Ansari, S.; Jamal, T.; Masrur, H.; Elavarasan, R.M.; Hussain, A. Optimized energy management schemes for electric vehicle applications: A bibliometric analysis towards future trends. Sustainability 2021, 13, 12800. [Google Scholar] [CrossRef]
- Gavilema, Á.O.T.; Álvarez, J.D.; Moreno, J.L.T.; García, M.P. Towards optimal management in microgrids: An overview. Energies 2021, 14, 5202. [Google Scholar] [CrossRef]
- Yusupov, Z.; Almagrahi, N.; Yaghoubi, E.; Yaghoubi, E.; Habbal, A.; Kodirov, D. Modeling and Control of Decentralized Microgrid Based on Renewable Energy and Electric Vehicle Charging Station. In World Conference Intelligent System for Industrial Automation; Springer: Cham, Switzerland, 2022; pp. 96–102. [Google Scholar]
- Silveira, J.P.C.; Neto, P.J.D.S.; Barros, T.A.D.S.; Filho, E.R. Power management of energy storage system with modified interlinking converters topology in hybrid AC/DC microgrid. Int. J. Electr. Power Energy Syst. 2021, 130, 106880. [Google Scholar]
- Aljafari, B.; Vasantharaj, S.; Indragandhi, V.; Vaibhav, R. Optimization of DC, AC, and Hybrid AC/DC Microgrid-Based IoT Systems: A Review. Energies 2022, 15, 6813. [Google Scholar]
- Saha, S.; Gholami, S.; Prince, M.K.K. Sensor fault-resilient control of electronically coupled distributed energy resources in islanded microgrids. IEEE Trans. Ind. Appl. 2021, 58, 914–929. [Google Scholar]
- D’silva, S.; Shadmand, M.B.; Abu-Rub, H. Microgrid control strategies for seamless transition between grid-connected and islanded modes. In Proceedings of the 2020 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 6–7 February 2020; pp. 1–6. [Google Scholar]
- Li, Z.; Cheng, Z.; Xu, Y.; Wang, Y.; Liang, J.; Gao, J. Hierarchical control of parallel voltage source inverters in AC microgrids. J. Eng. 2019, 2019, 1149–1152. [Google Scholar]
- Skiparev, V.; Machlev, R.; Chowdhury, N.R.; Levron, Y.; Petlenkov, E.; Belikov, J. Virtual inertia control methods in islanded microgrids. Energies 2021, 14, 1562. [Google Scholar] [CrossRef]
- Abhishek, A.; Ranjan, A.; Devassy, S.; Verma, B.K.; Ram, S.K.; Dhakar, A.K. Review of hierarchical control strategies for DC microgrid. IET Renew. Power Gener. 2020, 14, 1631–1640. [Google Scholar]
- Hesaroor, K.; Das, D. Optimal sizing of energy storage system in islanded microgrid using incremental cost approach. J. Energy Storage 2019, 24, 100768. [Google Scholar]
- Saleh, A.; Hasanien, H.M.; Turky, R.A.; Turdybek, B.; Alharbi, M.; Jurado, F.; Omran, W.A. Optimal Model Predictive Control for Virtual Inertia Control of Autonomous Microgrids. Sustainability 2023, 15, 5009. [Google Scholar] [CrossRef]
- Duan, J.; Yi, Z.; Shi, D.; Lin, C.; Lu, X.; Wang, Z. Reinforcement-learning-based optimal control of hybrid energy storage systems in hybrid AC–DC microgrids. IEEE Trans. Ind. Inform. 2019, 15, 5355–5364. [Google Scholar]
- Jin, X.; Shen, Y.; Zhou, Q. A systematic review of robust control strategies in DC microgrids. Electr. J. 2022, 35, 107125. [Google Scholar]
- Kumar, R.; Bhende, C.N. Active Damping Stabilization Techniques for Cascaded Systems in DC Microgrids: A Comprehensive Review. Energies 2023, 16, 1339. [Google Scholar] [CrossRef]
- Çimen, H.; Bazmohammadi, N.; Lashab, A.; Terriche, Y.; Vasquez, J.C.; Guerrero, J.M. An online energy management system for AC/DC residential microgrids supported by non-intrusive load monitoring. Appl. Energy 2022, 307, 118136. [Google Scholar]
- Tumeran, N.L.; Yusoff, S.H.; Gunawan, T.S.; Hanifah, M.S.A.; Zabidi, S.A.; Pranggono, B.; Yunus, M.S.F.M.; Sapihie, S.N.M.; Halbouni, A.H. Model Predictive Control Based Energy Management System Literature Assessment for RES Integration. Energies 2023, 16, 3362. [Google Scholar] [CrossRef]
- Heidary, J.; Gheisarnejad, M.; Khooban, M.H. Stability Enhancement and Energy Management of AC-DC Microgrid based on Active Disturbance Rejection Control. Electr. Power Syst. Res. 2023, 217, 109105. [Google Scholar]
- Ye, F.; Cheng, Z.; Cao, X.; Chow, M.-Y. A random-weight privacy-preserving algorithm with error compensation for microgrid distributed energy management. IEEE Trans. Inf. Forensics Secur. 2021, 16, 4352–4362. [Google Scholar]
- Samavati, E.; Mohammadi, H. Simultaneous voltage and current harmonics compensation in islanded/grid-connected microgrids using virtual impedance concept. Sustain. Energy Grids Netw. 2019, 20, 100258. [Google Scholar]
- Najafzadeh, M.; Ahmadiahangar, R.; Husev, O.; Roasto, I.; Jalakas, T.; Blinov, A. Recent contributions, future prospects and limitations of interlinking converter control in hybrid AC/DC microgrids. IEEE Access 2021, 9, 7960–7984. [Google Scholar]
- Heidari, S.; Hatami, A.; Eskandari, M. An intelligent capacity management system for interface converter in AC-DC hybrid microgrids. Appl. Energy 2022, 316, 119112. [Google Scholar]
- Kumar, V.; Sharma, V.; Naresh, R. Model predictive controller-based voltage and frequency regulation in renewable energy integrated power system coordinated with virtual inertia and redox flow battery. Iran. J. Sci. Technol. Trans. Electr. Eng. 2023, 47, 159–176. [Google Scholar]
- Jayaram, J.; Srinivasan, M.; Prabaharan, N.; Senjyu, T. Design of decentralized hybrid microgrid integrating multiple renewable energy sources with power quality improvement. Sustainability 2022, 14, 7777. [Google Scholar] [CrossRef]
- Jithin, S.; Rajeev, T. A novel stability index-based virtual synchronous machine droop scheme for performance improvement of hybrid AC/DC microgrid under volatile loading conditions. Electr. Power Syst. Res. 2023, 214, 108901. [Google Scholar]
- Mahdavi, M.S.; Karimzadeh, M.S.; Rahimi, T.; Gharehpetian, G.B. A Fault-Tolerant Bidirectional Converter for Battery Energy Storage Systems in DC Microgrids. Electronics 2023, 12, 679. [Google Scholar] [CrossRef]
- Jain, D.; Saxena, D. Comprehensive review on control schemes and stability investigation of hybrid AC-DC microgrid. Electr. Power Syst. Res. 2023, 218, 109182. [Google Scholar]
- Yan, L.; Zhao, Y.; Xue, T.; Ma, N.; Li, Z.; Yan, Z. Two-Layer Optimal Operation of AC–DC Hybrid Microgrid Considering Carbon Emissions Trading in Multiple Scenarios. Sustainability 2022, 14, 10524. [Google Scholar]
- Rezaei, N.; Pezhmani, Y.; Khazali, A. Economic-environmental risk-averse optimal heat and power energy management of a grid-connected multi microgrid system considering demand response and bidding strategy. Energy 2022, 240, 122844. [Google Scholar]
- Khani, A.; Khakzand, M.; Faizi, M. Multi-objective optimization for energy consumption, visual and thermal comfort performance of educational building (case study: Qeshm Island, Iran). Sustain. Energy Technol. Assess. 2022, 54, 102872. [Google Scholar]
- Kamal, F.; Chowdhury, B. Model predictive control and optimization of networked microgrids. Int. J. Electr. Power Energy Syst. 2022, 138, 107804. [Google Scholar]
- Sen, S.; Kumar, V. Distributed adaptive-MPC type optimal PMS for PV-battery based isolated microgrid. IEEE Syst. J. 2022, 17, 546–557. [Google Scholar]
- Baldivieso-Monasterios, P.R. Distributed Model Predictive Control for Reconfigurable Large-Scale Systems. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2018. [Google Scholar]
- Hu, J.; Shan, Y.; Yang, Y.; Parisio, A.; Li, Y.; Amjady, N.; Islam, S.; Cheng, K.W.; Guerrero, J.M.; Rodríguez, J. Economic Model Predictive Control for Microgrid Optimization: A Review. IEEE Trans. Smart Grid 2023, 15, 472–484. [Google Scholar]
- Xavier, J.; Patnaik, S.; Panda, R.C. Economic optimization and predictive control for nonlinear systems using Lyapunov based nonlinear cost function design. Chem. Eng. Sci. 2023, 270, 118530. [Google Scholar]
- Zhang, X.; Wang, B.; Gamage, D.; Ukil, A. Model predictive and iterative learning control based hybrid control method for hybrid energy storage system. IEEE Trans. Sustain. Energy 2021, 12, 2146–2158. [Google Scholar]
- Ghosh, D.; Moreira, J.; Mhaskar, P. Model predictive control embedding a parallel hybrid modeling strategy. Ind. Eng. Chem. Res. 2021, 60, 2547–2562. [Google Scholar]
- Aghdam, M.M.; Li, L.; Zhu, J. Comprehensive study of finite control set model predictive control algorithms for power converter control in microgrids. IET Smart Grid 2020, 3, 1–10. [Google Scholar]
- Hu, J.; Shan, Y.; Guerrero, J.M.; Ioinovici, A.; Chan, K.W.; Rodriguez, J. Model predictive control of microgrids–An overview. Renew. Sustain. Energy Rev. 2021, 136, 110422. [Google Scholar]
- Razmi, D.; Babayomi, O.; Davari, A.; Rahimi, T.; Miao, Y.; Zhang, Z. Review of model predictive control of distributed energy resources in microgrids. Symmetry 2022, 14, 1735. [Google Scholar] [CrossRef]
- Fontenot, H.; Dong, B. Modeling and control of building-integrated microgrids for optimal energy management—A review. Appl. Energy 2019, 254, 113689. [Google Scholar]
- Moreno-Castro, J.; Guevara, V.S.O.; Viltre, L.T.L.; Landera, Y.G.; Zevallos, O.C.; Aybar-Mejía, M. Microgrid Management Strategies for Economic Dispatch of Electricity Using Model Predictive Control Techniques: A Review. Energies 2023, 16, 5935. [Google Scholar] [CrossRef]
- Marimuthu, R. Review on advanced control techniques for microgrids. Energy Rep. 2023, 10, 3054–3072. [Google Scholar]
- Pamulapati, T.; Cavus, M.; Odigwe, I.; Allahham, A.; Walker, S.; Giaouris, D. A Review of Microgrid Energy Management Strategies from the Energy Trilemma Perspective. Energies 2022, 16, 289. [Google Scholar] [CrossRef]
- Prema, V.; Rao, K.U. Predictive models for power management of a hybrid microgrid—A review. In Proceedings of the 2014 International Conference on Advances in Energy Conversion Technologies (ICAECT), Manipal, India, 23–25 January 2014; pp. 7–12. [Google Scholar]
- Lashab, A.; Sera, D.; Guerrero, J.M.; Mathe, L.; Bouzid, A. Discrete model-predictive-control-based maximum power point tracking for PV systems: Overview and evaluation. IEEE Trans. Power Electron. 2017, 33, 7273–7287. [Google Scholar]
- Gulbudak, O.; Gokdag, M. FPGA Implementation of Model Predictive Control for Driving Multi-Induction Motors. In Proceedings of the 2023 5th Global Power, Energy and Communication Conference (GPECOM), Nevsehir, Turkiye, 14–16 June 2023; pp. 21–26. [Google Scholar]
- Tejeda-Iglesias, M.; Lappas, N.H.; Gounaris, C.E.; Ricardez-Sandoval, L. Explicit model predictive controller under uncertainty: An adjustable robust optimization approach. J. Process Control 2019, 84, 115–132. [Google Scholar]
- Ruan, S.; Ma, Y.; Yang, N.; Xiang, C.; Li, X. Real-time energy-saving control for HEVs in car-following scenario with a double explicit MPC approach. Energy 2022, 247, 123265. [Google Scholar]
- Chen, S.; Saulnier, K.; Atanasov, N.; Lee, D.D.; Kumar, V.; Pappas, G.J.; Morari, M. Approximating explicit model predictive control using constrained neural networks. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 1520–1527. [Google Scholar]
- Garcia, C.E.; Prett, D.M.; Morari, M. Model predictive control: Theory and practice—A survey. Automatica 1989, 25, 335–348. [Google Scholar]
- Abughalieh, K.M.; Alawneh, S.G. A survey of parallel implementations for model predictive control. IEEE Access 2019, 7, 34348–34360. [Google Scholar]
- Ramli, M.A.; Bouchekara, H.; Alghamdi, A.S. Optimal sizing of PV/wind/diesel hybrid microgrid system using multi-objective self-adaptive differential evolution algorithm. Renew. Energy 2018, 121, 400–411. [Google Scholar]
- Leonori, S.; Paschero, M.; Mascioli, F.M.F.; Rizzi, A. Optimization strategies for Microgrid energy management systems by Genetic Algorithms. Appl. Soft Comput. 2020, 86, 105903. [Google Scholar]
- Drgoňa, J.; Picard, D.; Kvasnica, M.; Helsen, L. Approximate model predictive building control via machine learning. Appl. Energy 2018, 218, 199–216. [Google Scholar]
- Drgoňa, J.; Arroyo, J.; Figueroa, I.C.; Blum, D.; Arendt, K.; Kim, D.; Ollé, E.P.; Oravec, J.; Wetter, M.; Vrabie, D.L. All you need to know about model predictive control for buildings. Annu. Rev. Control 2020, 50, 190–232. [Google Scholar]
- Lannelongue, L.; Grealey, J.; Inouye, M. Green algorithms: Quantifying the carbon footprint of computation. Adv. Sci. 2021, 8, 2100707. [Google Scholar]
- Iranmanesh, A.; Naji, H.R. DCHG-TS: A deadline-constrained and cost-effective hybrid genetic algorithm for scientific workflow scheduling in cloud computing. Clust. Comput. 2021, 24, 667–681. [Google Scholar]
- Abed, S.E.; Jaffal, R.; Mohd, B.J.; Al-Shayeji, M. An analysis and evaluation of lightweight hash functions for blockchain-based IoT devices. Clust. Comput. 2021, 24, 3065–3084. [Google Scholar]
- Linaro, D.; Bizzarri, F.; Del Giudice, D.; Pisani, C.; Giannuzzi, G.M.; Grillo, S.; Brambilla, A.M. Continuous estimation of power system inertia using convolutional neural networks. Nat. Commun. 2023, 14, 4440. [Google Scholar]
- Sterman, J. System dynamics at sixty: The path forward. Syst. Dyn. Rev. 2018, 34, 5–47. [Google Scholar]
- Kvasnica, M.; Jones, C.N.; Pejcic, I.; Holaza, J.; Korda, M.; Bakaráč, P. Real-time implementation of explicit model predictive control. In Handbook of Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2019; pp. 387–412. [Google Scholar]
- Ingole, D.; Kvasnica, M. FPGA implementation of explicit model predictive control for closed loop control of depth of anesthesia. IFAC-Pap. 2015, 48, 483–488. [Google Scholar]
- Zhou, F.; Xiao, F.; Chang, C.; Shao, Y.; Song, C. Adaptive model predictive control-based energy management for semi-active hybrid energy storage systems on electric vehicles. Energies 2017, 10, 1063. [Google Scholar]
- Benrabah, M.; Kara, K.; AitSahed, O.; Hadjili, M.L. Constrained nonlinear predictive control using neural networks and teaching–learning-based optimization. J. Control Autom. Electr. Syst. 2021, 32, 1228–1243. [Google Scholar]
- Pandala, A.; Fawcett, R.T.; Rosolia, U.; Ames, A.D.; Hamed, K.A. Robust predictive control for quadrupedal locomotion: Learning to close the gap between reduced-and full-order models. IEEE Robot. Autom. Lett. 2022, 7, 6622–6629. [Google Scholar]
- Zhou, F.; Peng, H.; Qin, Y.; Zeng, X.; Tian, X.; Xu, W. A RBF-ARX model-based robust MPC for tracking control without steady state knowledge. J. Process Control 2017, 51, 42–54. [Google Scholar]
- Cestaro, J.; Conklin, D.; Ziman, D.; Pan, E.; Anhorn, G.; Cunningham, M.; Schulte, N.; Dadgostari, F.; Beling, P. Optimization of Production and Packaging Schedules in a Mixed Discrete/Continuous Manufacturing Environment. In Proceedings of the 2019 Systems and Information Engineering Design Symposium (SIEDS), Charlottesville, VA, USA, 26–26 April 2019; pp. 1–6. [Google Scholar]
- Ilic, M.; Jaddivada, R.; Miao, X.; Popli, N. Toward multi-layered mpc for complex electric energy systems. In Handbook of Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2019; pp. 625–663. [Google Scholar]
- Patino, D.; Riedinger, P.; Iung, C. Practical optimal state feedback control law for continuous-time switched affine systems with cyclic steady state. Int. J. Control 2009, 82, 1357–1376. [Google Scholar]
- Sharp, R.; Peng, H. Vehicle dynamics applications of optimal control theory. Veh. Syst. Dyn. 2011, 49, 1073–1111. [Google Scholar]
- Wang, L. Discrete-time MPC Using Laguerre Functions. In Model Predictive Control System Design and Implementation Using MATLAB®; Springer: Berlin/Heidelberg, Germany, 2009; pp. 85–148. [Google Scholar]
- Wang, L. Model Predictive Control System Design and Implementation Using MATLAB; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Ma, A.; Liu, K.; Zhang, Q.; Xia, Y. Distributed MPC for linear discrete-time systems with disturbances and coupled states. Syst. Control Lett. 2020, 135, 104578. [Google Scholar]
- Alsterda, J.P.; Gerdes, J.C. Contingency model predictive control for linear time-varying systems. arXiv 2021, arXiv:2102.12045. [Google Scholar]
- Joshal, K.S.; Gupta, N. Microgrids with model predictive control: A critical review. Energies 2023, 16, 4851. [Google Scholar] [CrossRef]
- Du, Y.; Zhou, Z.; Zhao, J. Multi-regional building energy efficiency intelligent regulation strategy based on multi-objective optimization and model predictive control. J. Clean. Prod. 2022, 349, 131264. [Google Scholar]
- Yang, S.; Wan, M.P.; Chen, W.; Ng, B.F.; Dubey, S. Model predictive control with adaptive machine-learning-based model for building energy efficiency and comfort optimization. Appl. Energy 2020, 271, 115147. [Google Scholar]
- Chegari, B.; Tabaa, M.; Simeu, E.; Moutaouakkil, F.; Medromi, H. Multi-objective optimization of building energy performance and indoor thermal comfort by combining artificial neural networks and metaheuristic algorithms. Energy Build. 2021, 239, 110839. [Google Scholar]
- He, D.; Zhang, Y.; Yu, S. Prioritized multi-objective model predictive control without terminal constraints and its applications to nonlinear processes. Optim. Control Appl. Methods 2021, 42, 1030–1044. [Google Scholar]
- Lesort, T.; Lomonaco, V.; Stoian, A.; Maltoni, D.; Filliat, D.; Díaz-Rodríguez, N. Continual learning for robotics: Definition, framework, learning strategies, opportunities and challenges. Inf. Fusion 2020, 58, 52–68. [Google Scholar]
- Ma, N.; Aviv, D.; Guo, H.; Braham, W.W. Measuring the right factors: A review of variables and models for thermal comfort and indoor air quality. Renew. Sustain. Energy Rev. 2021, 135, 110436. [Google Scholar]
- Li, G.; Chen, L.; Liu, J.; Fang, X. Comparative study on deep transfer learning strategies for cross-system and cross-operation-condition building energy systems fault diagnosis. Energy 2023, 263, 125943. [Google Scholar]
- Fan, J. A big data and neural networks driven approach to design students management system. Soft Comput. 2024, 28, 1255–1276. [Google Scholar]
- Wang, Y.; Chen, N.; Fan, G.; Yang, D.; Rao, L.; Cheng, S.; Song, X. DLPformer: A hybrid mathematical model for state of charge prediction in electric vehicles using machine learning approaches. Mathematics 2023, 11, 4635. [Google Scholar] [CrossRef]
- Zhao, J.; Han, X.; Ouyang, M.; Burke, A.F. Specialized deep neural networks for battery health prognostics: Opportunities and challenges. J. Energy Chem. 2023, 87, 416–438. [Google Scholar]
- Tehrani, A.A.; Veisi, O.; Fakhr, B.V.; Du, D. Predicting solar radiation in the urban area: A data-driven analysis for sustainable city planning using artificial neural networking. Sustain. Cities Soc. 2024, 100, 105042. [Google Scholar]
- Rădulescu, R.; Mannion, P.; Roijers, D.M.; Nowé, A. Multi-objective multi-agent decision making: A utility-based analysis and survey. Auton. Agents Multi-Agent Syst. 2020, 34, 10. [Google Scholar]
- Herrera, M.; Pérez-Hernández, M.; Parlikad, A.K.; Izquierdo, J. Multi-agent systems and complex networks: Review and applications in systems engineering. Processes 2020, 8, 312. [Google Scholar] [CrossRef]
- Wu, X.; Xu, K.; Lei, M.; He, X. Disturbance-compensation-based continuous sliding mode control for overhead cranes with disturbances. IEEE Trans. Autom. Sci. Eng. 2020, 17, 2182–2189. [Google Scholar]
- Hasani, A.; Mokhtari, H.; Fattahi, M. A multi-objective optimization approach for green and resilient supply chain network design: A real-life case study. J. Clean. Prod. 2021, 278, 123199. [Google Scholar]
- Yeganeh, F.T.; Zegordi, S.H. A multi-objective optimization approach to project scheduling with resiliency criteria under uncertain activity duration. Ann. Oper. Res. 2020, 285, 161–196. [Google Scholar]
- Lotfi, R.; Sheikhi, Z.; Amra, M.; AliBakhshi, M.; Weber, G.-W. Robust optimization of risk-aware, resilient and sustainable closed-loop supply chain network design with Lagrange relaxation and fix-and-optimize. Int. J. Logist. Res. Appl. 2021, 27, 705–745. [Google Scholar]
- Karimi, H.; Jadid, S.; Hasanzadeh, S. Optimal-sustainable multi-energy management of microgrid systems considering integration of renewable energy resources: A multi-layer four-objective optimization. Sustain. Prod. Consum. 2023, 36, 126–138. [Google Scholar]
- Jaber, A. Hybrid Algorithm for Multi-objective Mixed-integer Non-convex Mechanical Design Optimization Problems. Ph.D. Thesis, Université de Technologie de Troyes, Université Libanaise, Beirut, Lebanon, 2021. [Google Scholar]
- Salo, A.; Andelmin, J.; Oliveira, F. Decision programming for mixed-integer multi-stage optimization under uncertainty. Eur. J. Oper. Res. 2022, 299, 550–565. [Google Scholar]
- Shir, O.M.; Emmerich, M. Multi-Objective Mixed-Integer Quadratic Models: A Study on Mathematical Programming and Evolutionary Computation. IEEE Trans. Evol. Comput. 2024, 29, 661–675. [Google Scholar]
- Zhang, C.; Xu, W. Intelligent Vehicle Path Based on Discretized Sampling Points and Improved Cost Function-A Quadratic Programming approach. IEEE Access 2024, 12, 24500–24515. [Google Scholar]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Farag, M.; Mirjalili, S.; Elhosseini, M.A. Quadratic interpolation and a new local search approach to improve particle swarm optimization: Solar photovoltaic parameter estimation. Expert Syst. Appl. 2024, 236, 121417. [Google Scholar]
- Thabtah, F.; Hammoud, S.; Kamalov, F.; Gonsalves, A. Data imbalance in classification: Experimental evaluation. Inf. Sci. 2020, 513, 429–441. [Google Scholar]
- Pantsar, M. Cognitive and computational complexity: Considerations from mathematical problem solving. Erkenntnis 2021, 86, 961–997. [Google Scholar]
- Gao, S.; Xiang, C.; Yu, M.; Tan, K.T.; Lee, T.H. Online optimal power scheduling of a microgrid via imitation learning. IEEE Trans. Smart Grid 2021, 13, 861–876. [Google Scholar]
- Epanchin-Niell, R.S. Economics of invasive species policy and management. Biol. Invasions 2017, 19, 3333–3354. [Google Scholar]
- Pena-Bello, A.; Burer, M.; Patel, M.K.; Parra, D. Optimizing PV and grid charging in combined applications to improve the profitability of residential batteries. J. Energy Storage 2017, 13, 58–72. [Google Scholar]
- Çetin, M.; Bahtiyar, B.; Beyhan, S. Adaptive uncertainty compensation-based nonlinear model predictive control with real-time applications. Neural Comput. Appl. 2019, 31, 1029–1043. [Google Scholar]
- Meng, J.; Xiao, H.; Jiang, L.; Hu, Z.; Jiang, L.; Jiang, N. Adaptive Model Predictive Control for Mobile Robots with Localization Fluctuation Estimation. Sensors 2023, 23, 2501. [Google Scholar] [CrossRef]
- Askari, M.R.; Hajizadeh, I.; Rashid, M.; Hobbs, N.; Zavala, V.M.; Cinar, A. Adaptive-learning model predictive control for complex physiological systems: Automated insulin delivery in diabetes. Annu. Rev. Control 2020, 50, 1–12. [Google Scholar]
- Eddy, Y.F.; Gooi, H.B.; Chen, S.X. Multi-agent system for distributed management of microgrids. IEEE Trans. Power Syst. 2014, 30, 24–34. [Google Scholar]
- Taherian, S.; Halder, K.; Dixit, S.; Fallah, S. Autonomous collision avoidance using MPC with LQR-based weight transformation. Sensors 2021, 21, 4296. [Google Scholar] [CrossRef]
- Rodriguez-Guevara, D.; Favela-Contreras, A.; Beltran-Carbajal, F.; Sotelo, D.; Sotelo, C. Active suspension control using an MPC-LQR-LPV controller with attraction sets and quadratic stability conditions. Mathematics 2021, 9, 2533. [Google Scholar]
- Sen, S.; Kumar, V. Decentralized output-feedback-based robust LQR Vf controller for PV-battery microgrid including generation uncertainties. IEEE Syst. J. 2020, 14, 4418–4429. [Google Scholar]
- Haque, M.Y.-Y.U.; Islam, M.R.; Ahmed, T.; Sheikh, M.R.I. Improved voltage tracking of autonomous microgrid technology using a combined resonant controller with lead-lag compensator adopting negative imaginary theorem. Prot. Control Mod. Power Syst. 2022, 7, 10. [Google Scholar]
- Yang, L.; Lu, J.; Xu, Y.; Li, D.; Xi, Y. Constrained robust model predictive control embedded with a new data-driven technique. IET Control Theory Appl. 2020, 14, 2395–2405. [Google Scholar]
- Dong, X.; Zhang, C.; Sun, B. Optimization strategy based on robust model predictive control for RES-CCHP system under multiple uncertainties. Appl. Energy 2022, 325, 119707. [Google Scholar]
- Cho, Y.; Hwang, G.; Gbadago, D.Q.; Hwang, S. Artificial neural network-based model predictive control for optimal operating conditions in proton exchange membrane fuel cells. J. Clean. Prod. 2022, 380, 135049. [Google Scholar]
- Aouaichia, A.; Kara, K.; Benrabah, M.; Hadjili, M.L. Constrained Neural Network Model Predictive Controller Based on Archimedes Optimization Algorithm with Application to Robot Manipulators. J. Control Autom. Electr. Syst. 2023, 34, 1159–1178. [Google Scholar]
- Albira, M.E.; Zohdy, M.A. Adaptive model predictive control for DC-DC power converters with parameters’ uncertainties. IEEE Access 2021, 9, 135121–135131. [Google Scholar]
- Zhang, H.; Li, Y.; Xie, R.; Song, J.; Liang, B.; Huangfu, Y. Adaptive Model Predictive Control of an Interleaved Boost Converter Using Real-Time Updated Model. IEEE Trans. Power Electron. 2022, 38, 1720–1731. [Google Scholar]
- Johansen, T.A.; Fossen, T.I.; Berge, S.P. Constrained nonlinear control allocation with singularity avoidance using sequential quadratic programming. IEEE Trans. Control Syst. Technol. 2004, 12, 211–216. [Google Scholar]
- Collet, D.; Alamir, M.; Di Domenico, D.; Sabiron, G. Non quadratic smooth model of fatigue for optimal fatigue-oriented individual pitch control. J. Phys. Conf. Ser. 2020, 1618, 022004. [Google Scholar]
- Rawlings, J.B.; Patel, N.R.; Risbeck, M.J.; Maravelias, C.T.; Wenzel, M.J.; Turney, R.D. Economic MPC and real-time decision making with application to large-scale HVAC energy systems. Comput. Chem. Eng. 2018, 114, 89–98. [Google Scholar]
- Mork, M.; Materzok, N.; Xhonneux, A.; Müller, D. Nonlinear Hybrid Model Predictive Control for building energy systems. Energy Build. 2022, 270, 112298. [Google Scholar]
- Alsofyani, I.M.; Lee, K.-B. A unidirectional voltage vector preselection strategy for optimizing model predictive torque control with discrete space vector modulation of IPMSM. IEEE Trans. Ind. Electron. 2021, 69, 12305–12315. [Google Scholar]
- Sorourifar, F.; Choksi, N.; Paulson, J.A. Computationally efficient integrated design and predictive control of flexible energy systems using multi-fidelity simulation-based Bayesian optimization. Optim. Control Appl. Methods 2023, 44, 549–576. [Google Scholar]
- Mercangöz, M.; Doyle, F.J., III. Distributed model predictive control of an experimental four-tank system. J. Process Control 2007, 17, 297–308. [Google Scholar]
- Alonso, C.A.; Li, J.S.; Anderson, J.; Matni, N. Distributed and localized model predictive control. Part I: Synthesis and implementation. IEEE Trans. Control. Netw. Syst. 2022, 10, 1058–1068. [Google Scholar]
- Lin, N.M.; Tian, X.; Rutten, M.; Abraham, E.; Maestre, J.M.; van De Giesen, N. Multi-objective model predictive control for real-time operation of a multi-reservoir system. Water 2020, 12, 1898. [Google Scholar]
- He, D.; Li, H.; Du, H. Lexicographic multi-objective MPC for constrained nonlinear systems with changing objective prioritization. Automatica 2021, 125, 109433. [Google Scholar]
- Etim, N.-B.B.; Giaouris, D.; Papadopoulos, A.I.; Patsios, H.; Papadopoulou, S.; Voutetakis, S.; Seferlis, P.; Walker, S.; Taylor, P.; Gadoue, S. Adaptive power pinch analysis for energy management of hybrid energy storage systems. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar]
- Farraj, M.A.; Kaluthanthrige, R.; Rajapakse, A. Evaluating a Microgrid Control System Using Controller Hardware in the Loop Simulations. In Proceedings of the 2021 IEEE Electrical Power and Energy Conference (EPEC), Toronto, ON, Canada, 22–31 October 2021; pp. 316–321. [Google Scholar]
- Li, H.; Wang, S. Comparative assessment of alternative MPC strategies using real meteorological data and their enhancement for optimal utilization of flexibility-resources in buildings. Energy 2022, 244, 122693. [Google Scholar]
- He, D.; Shi, Y.; Song, X. Weight-free multi-objective predictive cruise control of autonomous vehicles in integrated perturbation analysis and sequential quadratic programming optimization framework. J. Dyn. Syst. Meas. Control 2019, 141, 091015. [Google Scholar]
- Huang, C.; Zong, Y.; You, S.; Træholt, C. Economic model predictive control for multi-energy system considering hydrogen-thermal-electric dynamics and waste heat recovery of MW-level alkaline electrolyzer. Energy Convers. Manag. 2022, 265, 115697. [Google Scholar]
- Gill, P.E.; Jay, L.O.; Leonard, M.W.; Petzold, L.R.; Sharma, V. An SQP method for the optimal control of large-scale dynamical systems. J. Comput. Appl. Math. 2000, 2, 197–213. [Google Scholar]
- Garg, K.; Panagou, D. Control-lyapunov and control-barrier functions based quadratic program for spatio-temporal specifications. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 1422–1429. [Google Scholar]
- Kouzoupis, D.; Frison, G.; Zanelli, A.; Diehl, M. Recent advances in quadratic programming algorithms for nonlinear model predictive control. Vietnam J. Math. 2018, 46, 863–882. [Google Scholar]
- Arnström, D.; Axehill, D. A unifying complexity certification framework for active-set methods for convex quadratic programming. IEEE Trans. Autom. Control 2021, 67, 2758–2770. [Google Scholar]
- Gao, S.; Caines, P.E. Optimal and approximate solutions to linear quadratic regulation of a class of graphon dynamical systems. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 8359–8365. [Google Scholar]
- Cavus, M.; Allahham, A. Enhanced microgrid control through genetic predictive control: Integrating genetic algorithms with model predictive control for improved non-linearity and non-convexity handling. Energies 2024, 17, 4458. [Google Scholar]
- Tazi, K.; Abbou, F.M.; Abdi, F. Multi-agent system for microgrids: Design, optimization and performance. Artif. Intell. Rev. 2020, 53, 1233–1292. [Google Scholar]
- Mohammadikia, R.; Nikoofard, A.; Tavakoli-Kakhki, M. Application of MPC for an automatic voltage regulator and load frequency control of interconnected power system. In Proceedings of the 2020 28th Iranian Conference on Electrical Engineering (ICEE), Tabriz, Iran, 4–6 August 2020; pp. 1–5. [Google Scholar]
- Zheng, Y.; Wang, Y.; Meng, X.; Li, S.; Chen, H. Distributed economic MPC for synergetic regulation of the voltage of an Island DC Micro-Grid. IEEE/CAA J. Autom. Sin. 2024, 11, 734–745. [Google Scholar]
- Su, W.; Yu, S.S.; Li, H.; Iu, H.H.-C.; Fernando, T. An MPC-based dual-solver optimization method for DC microgrids with simultaneous consideration of operation cost and power loss. IEEE Trans. Power Syst. 2020, 36, 936–947. [Google Scholar]
- Long, B.; Liao, Y.; Chong, K.T.; Rodríguez, J.; Guerrero, J.M. MPC-controlled virtual synchronous generator to enhance frequency and voltage dynamic performance in islanded microgrids. IEEE Trans. Smart Grid 2020, 12, 953–964. [Google Scholar]
- Karamanakos, P.; Liegmann, E.; Geyer, T.; Kennel, R. Model predictive control of power electronic systems: Methods, results, challenges. IEEE Open J. Ind. Appl. 2020, 1, 95–114. [Google Scholar]
- Lu, X.; Cannon, M. Adaptive Robust MPC: Combining Robustness with Online Performance Enhancement. In Proceedings of the 2018 UKACC 12th International Conference on Control (CONTROL), Sheffield, UK, 5–7 September 2018; p. 19. [Google Scholar]
- Khather, S.I.; Ibrahim, M.A.; Abdullah, A.I. Review and Performance Analysis of Nonlinear Model Predictive Control--Current Prospects, Challenges and Future Directions. J. Eur. Des Systèmes Autom. 2023, 56, 593–603. [Google Scholar]
- Ławryńczuk, M. Computationally efficient model predictive control algorithms. In A Neural Network Approach, Studies in Systems, Decision and Control; Springer: Berlin/Heidelberg, Germany, 2014; Volume 3. [Google Scholar]
- Kamruzzaman, M.; Saha, S.; Rana, M.S. Eliminating frequency deviation and restoring terminal voltage of an electric power generating unit using MPC. In Proceeding of the 2019 International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’sBazar, Bangladesh, 7–9 February 2019; pp. 1–6. [Google Scholar]
- Bragin, M.A.; Surrogate, E.L.T. “Level-Based” Lagrangian Relaxation for mixed-integer linear programming. Sci. Rep. 2022, 12, 22417. [Google Scholar]
- Khusainov, B.; Kerrigan, E.C.; Constantinides, G.A. Automatic software and computing hardware codesign for predictive control. IEEE Trans. Control Syst. Technol. 2018, 27, 2295–2304. [Google Scholar]
- Gros, S.; Zanon, M.; Quirynen, R.; Bemporad, A.; Diehl, M. From linear to nonlinear MPC: Bridging the gap via the real-time iteration. Int. J. Control 2020, 93, 62–80. [Google Scholar]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Rodriguez, J.; Young, H.A.; Marquez, A.; Zanchetta, P. Model predictive control: A review of its applications in power electronics. IEEE Ind. Electron. Mag. 2014, 8, 16–31. [Google Scholar]
- Ramana, N.V.; Sastry, V. A Novel speed control strategy for five phases permanent magnet synchronous motor with linear quadratic regulator. Int. J. Comput. Electr. Eng. 2015, 7, 408. [Google Scholar]
- Garg, R.; Mittal, A.; Syed, K.; Asim, M.; Chakravorty, A.; Goyal, S. Linear Quadratic Regulator (LQR)-Based Load Frequency Control in Power Systems. In Proceedings of the 2024 2nd World Conference on Communication & Computing (WCONF), Raipur, India, 12–14 July 2024; pp. 1–6. [Google Scholar]
- Gonzales-Zurita, Ó.; Clairand, J.-M.; Peñalvo-López, E.; Escrivá-Escrivá, G. Review on multi-objective control strategies for distributed generation on inverter-based microgrids. Energies 2020, 13, 3483. [Google Scholar]
- Brahmia, I.; Wang, J.; de Oliveira, L.; Xu, H. Hierarchical smart energy management strategy based on cooperative distributed economic model predictive control for multi-microgrids systems. Int. Trans. Electr. Energy Syst. 2021, 31, e12732. [Google Scholar]
- Morstyn, T.; Hredzak, B.; Aguilera, R.P.; Agelidis, V.G. Model predictive control for distributed microgrid battery energy storage systems. IEEE Trans. Control Syst. Technol. 2017, 26, 1107–1114. [Google Scholar]
- Andalibi, M.; Hajihosseini, M.; Teymoori, S.; Kargar, M.; Gheisarnejad, M. A time-varying deep reinforcement model predictive control for dc power converter systems. In Proceedings of the 2021 IEEE 12th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Chicago, IL, USA, 28 June–1 July 2021; pp. 1–6. [Google Scholar]
- Gbadega, P.A. Adaptive model predictive control of renewable energy-based micro-grid. Ph.D. Thesis, University of KwaZulu-Natal, Durban, South Africa, 2021. [Google Scholar]
- Maślak, G.; Orłowski, P. Microgrid operation optimization using hybrid system modeling and switched model predictive control. Energies 2022, 15, 833. [Google Scholar] [CrossRef]
- Duan, Y.; Zhao, Y.; Hu, J. An initialization-free distributed algorithm for dynamic economic dispatch problems in microgrid: Modeling, optimization and analysis. Sustain. Energy Grids Netw. 2023, 34, 101004. [Google Scholar]
- Cominesi, S.R.; Farina, M.; Giulioni, L.; Picasso, B.; Scattolini, R. A two-layer stochastic model predictive control scheme for microgrids. IEEE Trans. Control Syst. Technol. 2017, 26, 1–13. [Google Scholar]
- Li, H.; Li, X.; Xiong, W.; Yan, Y.; Zhang, Y.; Kou, P. Cooperative Voltage and Frequency Regulation with Wind Farm: A Model-Based Offline Optimal Control Approach. Energies 2023, 16, 6307. [Google Scholar] [CrossRef]
- Antony, A.S.M.; Sumithra, J.; Rayudu, K.; Dhanalakshmi, G.; Saravanan, R.A.; Kavitha, A.; Ravindra, G.; Malini, K. Dynamic and Model Predictive Controllers for Frequency Regulation of an Isolated Micro—Grid with Electrical Vehicles and the ESS Integration. Electr. Power Compon. Syst. 2023, 52, 426–444. [Google Scholar]
- Zhao, Z.; Guo, J.; Luo, X.; Lai, C.S.; Yang, P.; Lai, L.L.; Li, P.; Guerrero, J.M.; Shahidehpour, M. Distributed robust model predictive control-based energy management strategy for islanded multi-microgrids considering uncertainty. IEEE Trans. Smart Grid 2022, 13, 2107–2120. [Google Scholar]
- Clarke, W.C.; Brear, M.J.; Manzie, C. Control of an isolated microgrid using hierarchical economic model predictive control. Appl. Energy 2020, 280, 115960. [Google Scholar]
- Ndwali, P.K.; Njiri, J.G.; Wanjiru, E.M. Economic model predictive control of microgrid connected photovoltaic-diesel generator backup energy system considering demand side management. J. Electr. Eng. Technol. 2021, 16, 2297–2312. [Google Scholar]
- Shan, Y.; Hu, J.; Liu, H. A holistic power management strategy of microgrids based on model predictive control and particle swarm optimization. IEEE Trans. Ind. Inform. 2021, 18, 5115–5126. [Google Scholar]
- Bordons, C.; Garcia-Torres, F.; Ridao, M.A.; Bordons, C.; Garcia-Torres, F.; Ridao, M.A. Model predictive control fundamentals. In Model Predictive Control of Microgrids; Springer: Berlin/Heidelberg, Germany, 2020; pp. 25–44. [Google Scholar]
- Wu, S.; Zhang, N.; Luo, X.; Lu, W.-Z. Multi-objective optimization in floor tile planning: Coupling BIM and parametric design. Autom. Constr. 2022, 140, 104384. [Google Scholar]
- Altekin, F.T.; Bukchin, Y. A multi-objective optimization approach for exploring the cost and makespan trade-off in additive manufacturing. Eur. J. Oper. Res. 2022, 301, 235–253. [Google Scholar]
- Wang, Z.; Tan, W.G.Y.; Rangaiah, G.P.; Wu, Z. Machine learning aided model predictive control with multi-objective optimization and multi-criteria decision making. Comput. Chem. Eng. 2023, 179, 108414. [Google Scholar]
- Kim, R.; Lima, F.V. Nonlinear multiobjective and dynamic real-time predictive optimization for optimal operation of baseload power plants under variable renewable energy. Optim. Control Appl. Methods 2023, 44, 798–829. [Google Scholar]
- Schmitt, T.; Hoffmann, M.; Rodemann, T.; Adamy, J. Incorporating Human Preferences in Decision Making for Dynamic Multi-Objective Optimization in Model Predictive Control. Inventions 2022, 7, 46. [Google Scholar] [CrossRef]
- Adefarati, T.; Bansal, R.C. Reliability, economic and environmental analysis of a microgrid system in the presence of renewable energy resources. Appl. Energy 2019, 236, 1089–1114. [Google Scholar]
- Hannan, M.; Tan, S.Y.; Al-Shetwi, A.Q.; Jern, K.P.; Begum, R. Optimized controller for renewable energy sources integration into microgrid: Functions, constraints and suggestions. J. Clean. Prod. 2020, 256, 120419. [Google Scholar]
- Barakat, S.; Ibrahim, H.; Elbaset, A.A. Multi-objective optimization of grid-connected PV-wind hybrid system considering reliability, cost, environmental aspects. Sustain. Cities Soc. 2020, 60, 102178. [Google Scholar]
- Shayesteh, E.; Yu, J.; Hilber, P. Maintenance optimization of power systems with renewable energy sources integrated. Energy 2018, 149, 577–586. [Google Scholar]
- Tezer, T.; Yaman, R.; Yaman, G. Evaluation of approaches used for optimization of stand-alone hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2017, 73, 840–853. [Google Scholar]
- Mostavi, E.; Asadi, S.; Boussaa, D. Development of a new methodology to optimize building life cycle cost, environmental impacts, occupant satisfaction. Energy 2017, 121, 606–615. [Google Scholar]
- Kesireddy, A.; Carrillo, L.R.G.; Baca, J. Multi-criteria decision making-pareto front optimization strategy for solving multi-objective problems. In Proceedings of the 2020 IEEE 16th International Conference on Control & Automation (ICCA), Singapore, 9–11 October 2020; pp. 53–58. [Google Scholar]
- Rao, R.; Lakshmi, R. Ranking of Pareto-optimal solutions and selecting the best solution in multi-and many-objective optimization problems using R-method. Soft Comput. Lett. 2021, 3, 100015. [Google Scholar]
- Ma, X.; Huang, Z.; Li, X.; Qi, Y.; Wang, L.; Zhu, Z. Multiobjectivization of single-objective optimization in evolutionary computation: A survey. IEEE Trans. Cybern. 2021, 53, 3702–3715. [Google Scholar]
- Stewart, R.H.; Palmer, T.S.; DuPont, B. A survey of multi-objective optimization methods and their applications for nuclear scientists and engineers. Prog. Nucl. Energy 2021, 138, 103830. [Google Scholar]
- Castonguay, A.C.; Polasky, S.; Holden, M.H.; Herrero, M.; Chang, J.; Mason-D’Croz, D.; Godde, C.; Lee, K.; Bryan, B.A.; Gerber, J. MOO-GAPS: A multi-objective optimization model for global animal production and sustainability. J. Clean. Prod. 2023, 396, 136440. [Google Scholar]
- Cho, J.-H.; Wang, Y.; Chen, R.; Chan, K.S.; Swami, A. A survey on modeling and optimizing multi-objective systems. IEEE Commun. Surv. Tutor. 2017, 19, 1867–1901. [Google Scholar]
- Williams, P.J.; Kendall, W.L.; Hooten, M.B. Selecting ecological models using multi-objective optimization. Ecol. Model. 2019, 404, 21–26. [Google Scholar]
- Tomczyk, M.K.; Kadziński, M. Interactive co-evolutionary multiple objective optimization algorithms for finding consensus solutions for a group of Decision Makers. Inf. Sci. 2022, 616, 157–181. [Google Scholar]
- Yao, G.; Li, R.; Yang, Y. An Improved Multi-Objective Optimization and Decision-Making Method on Construction Sites Layout of Prefabricated Buildings. Sustainability 2023, 15, 6279. [Google Scholar]
- Ionescu, C.M.; Caruntu, C.F.; Cajo, R.; Ghita, M.; Crevecoeur, G.; Copot, C. Multi-objective predictive control optimization with varying term objectives: A wind farm case study. Processes 2019, 7, 778. [Google Scholar] [CrossRef]
- Rauf, H.T.; Gao, J.; Almadhor, A.; Haider, A.; Zhang, Y.-D.; Al-Turjman, F. Multi population-based chaotic differential evolution for multi-modal and multi-objective optimization problems. Appl. Soft Comput. 2023, 132, 109909. [Google Scholar]
- Ionescu, C.; Diaz, R.A.C.; Zhao, S.; Ghita, M.; Ghita, M.; Copot, D. A low computational cost, prioritized, multi-objective optimization procedure for predictive control towards cyber physical systems. IEEE Access 2020, 8, 128152–128166. [Google Scholar]
- Tamashiro, K.; Omine, E.; Krishnan, N.; Mikhaylov, A.; Hemeida, A.M.; Senjyu, T. Optimal components capacity based multi-objective optimization and optimal scheduling based MPC-optimization algorithm in smart apartment buildings. Energy Build. 2023, 278, 112616. [Google Scholar]
- Yang, D.; Liu, T.; Song, D.; Zhang, X.; Zeng, X. A real time multi-objective optimization Guided-MPC strategy for power-split hybrid electric bus based on velocity prediction. Energy 2023, 276, 127583. [Google Scholar]
- Huang, J.; Liu, Y.; Liu, M.; Cao, M.; Yan, Q. Multi-objective optimization control of distributed electric drive vehicles based on optimal torque distribution. IEEE Access 2019, 7, 16377–16394. [Google Scholar]
- Mallik, S.; Zhao, Z. Multi-objective optimized fuzzy clustering for detecting cell clusters from single-cell expression profiles. Genes 2019, 10, 611. [Google Scholar] [PubMed]
- Tian, Z.; Si, B.; Wu, Y.; Zhou, X.; Shi, X. Multi-objective optimization model predictive dispatch precooling and ceiling fans in office buildings under different summer weather conditions. In Building Simulator; Tsinghua University Press: Beijing, China, 2019; pp. 999–1012. [Google Scholar]
- Martinez-Rico, J.; Zulueta, E.; de Argandoña, I.R.; Fernandez-Gamiz, U.; Armendia, M. Multi-objective optimization of production scheduling using particle swarm optimization algorithm for hybrid renewable power plants with battery energy storage system. J. Mod. Power Syst. Clean Energy 2020, 9, 285–294. [Google Scholar]
- Thakur, S.; Gohil, G.; Balsara, P.T. Multi-objective optimization of triple port converter for photovoltaic and energy storage integration. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 4438–4445. [Google Scholar]
- Gharib, A.; Stenger, D.; Ritschel, R.; Voßwinkel, R. Multi-objective optimization of a path-following MPC for vehicle guidance: A Bayesian optimization approach. In Proceedings of the 2021 European Control Conference (ECC), Delft, The Netherlands, 29 June–2 July 2021; pp. 2197–2204. [Google Scholar]
- Huang, L.; Feng, L.; Wang, H.; Hou, Y.; Liu, K.; Chen, C. A preliminary study of improving evolutionary multi-objective optimization via knowledge transfer from single-objective problems. In Proceedings of the 2020 IEEE International Conference on Systems, Man, Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; pp. 1552–1559. [Google Scholar]
- Cao, P.; Fan, Z.; Gao, R.; Tang, J. A manufacturing oriented single point search hyper-heuristic scheme for multi-objective optimization. In Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Volume 2B: 43rd Design Automation Conference, Cleveland, OH, USA, 6–9 August 2017; p. V02BT03A031. [Google Scholar]
- Singh, G.G.; Cisneros-Montemayor, A.M.; Swartz, W.; Cheung, W.; Guy, J.A.; Kenny, T.-A.; McOwen, C.J.; Asch, R.; Geffert, J.L.; Wabnitz, C.C. A rapid assessment of co-benefits and trade-offs among Sustainable Development Goals. Mar. Policy 2018, 93, 223–231. [Google Scholar]
- Nerini, F.F.; Tomei, J.; To, L.S.; Bisaga, I.; Parikh, P.; Black, M.; Borrion, A.; Spataru, C.; Broto, V.C.; Anandarajah, G. Mapping synergies and trade-offs between energy and the Sustainable Development Goals. Nat. Energy 2018, 3, 10–15. [Google Scholar]
- Li, W.; Zhang, G.; Zhang, T.; Huang, S. Knee Point-Guided Multiobjective Optimization Algorithm for Microgrid Dynamic Energy Management. Complexity 2020, 2020, 8877008. [Google Scholar]
- Anilkumar, M.; Padhiyar, N.; Moudgalya, K. Multi-objective prioritized control of a semi-batch process with multiple feed and multiple products using economic MPC. In Proceedings of the 2018 Indian Control Conference (ICC), Kanpur, India, 4–6 January 2018; pp. 264–269. [Google Scholar]
- Anilkumar, M.; Padhiyar, N.; Moudgalya, K. Multi-objective control of a fed-batch bioreactor using shrinking horizon MPC: A case study. In Proceeding of the 2017 6th International Symposium on Advanced Control of Industrial Processes (AdCONIP), Taipei, Taiwan, 28–31 May 2017; pp. 25–30. [Google Scholar]
- Ravi, A.; Kaisare, N. Integrated multi-objective predictive control for multi-unit system. In Proceeding of the 2019 Sixth Indian Control Conference (ICC), Hyderabad, India, 18–20 December 2019; pp. 212–217. [Google Scholar]
- Das, R.; Wang, Y.; Busawon, K.; Putrus, G.; Neaimeh, M. Real-time multi-objective optimisation for electric vehicle charging management. J. Clean. Prod. 2021, 292, 126066. [Google Scholar]
- Nabin, K. Stochastic MPC for optimal operation of hydropower plant. University of South-Eastern Norway. Master’s Thesis, University of South-Eastern Norway, Notodden, Norway, 2022. [Google Scholar]
- Khare, V.; Chaturvedi, P. Design, control, reliability, economic and energy management of microgrid: A review. E-Prime-Adv. Electr. Eng. Electron. Energy 2023, 5, 100239. [Google Scholar]
- Aziz, A.; Oo, A.T.; Stojcevski, A. Frequency regulation capabilities in wind power plant. Sustain. Energy Technol. Assess. 2018, 26, 47–76. [Google Scholar]
- Liu, H.; Fan, A.; Li, Y.; Bucknall, R.; Chen, L. Hierarchical distributed MPC method for hybrid energy management: A case study of ship with variable operating conditions. Renew. Sustain. Energy Rev. 2024, 189, 113894. [Google Scholar]
- Ferreira, W.M.; Meneghini, I.R.; Brandao, D.I.; Guimarães, F.G. Preference cone based multi-objective evolutionary algorithm applied to optimal management of distributed energy resources in microgrids. Appl. Energy 2020, 274, 115326. [Google Scholar]
- Elmouatamid, A.; Ouladsine, R.; Bakhouya, M.; El Kamoun, N.; Khaidar, M.; Zine-Dine, K. Review of control and energy management approaches in micro-grid systems. Energies 2020, 14, 168. [Google Scholar] [CrossRef]
- Rashidi, R.; Hatami, A.; Abedini, M. Multi-microgrid energy management through tertiary-level control: Structure and case study. Sustain. Energy Technol. Assess. 2021, 47, 101395. [Google Scholar]
- Finke, J.; Bertsch, V. Implementing a highly adaptable method for the multi-objective optimisation of energy systems. Appl. Energy 2023, 332, 120521. [Google Scholar]
- Liu, Z.-F.; Li, L.-L.; Liu, Y.-W.; Liu, J.-Q.; Li, H.-Y.; Shen, Q. Dynamic economic emission dispatch considering renewable energy generation: A novel multi-objective optimization approach. Energy 2021, 235, 121407. [Google Scholar]
- Yazdani, H.; Baneshi, M.; Yaghoubi, M. Techno-economic and environmental design of hybrid energy systems using multi-objective optimization and multi-criteria decision making methods. Energy Convers. Manag. 2023, 282, 116873. [Google Scholar]
- Liu, Y.; Li, T.; Duan, J.; Wu, X.; Wang, H.; Fan, Q.; Lin, J.; Hu, Y. On a hierarchical adaptive and robust inverse dynamic control strategy with experiment for robot manipulators under uncertainties. Control Eng. Pract. 2023, 138, 105604. [Google Scholar]
- López-Rodríguez, R.; Aguilera-González, A.; Vechiu, I.; Bacha, S. Day-ahead mpc energy management system for an island wind/storage hybrid power plant. Energies 2021, 14, 1066. [Google Scholar]
- Gbadega, P.A.; Sun, Y. A hybrid constrained Particle Swarm Optimization-Model Predictive Control (CPSO-MPC) algorithm for storage energy management optimization problem in micro-grid. Energy Rep. 2022, 8, 692–708. [Google Scholar]
- Fabrice, K.; Damour, C.; Grondin, D.; Hilairet, M.; Benne, M. Multistage power and energy management strategy for hybrid microgrid with photovoltaic production and hydrogen storage. Appl. Energy 2022, 323, 119549. [Google Scholar]
- Ali, S.U.; Aamir, M.; Jafri, A.R.; Subramaniam, U.; Haroon, F.; Waqar, A.; Yaseen, M. Model predictive control—Based distributed control algorithm for bidirectional interlinking converter in hybrid microgrids. Int. Trans. Electr. Energy Syst. 2021, 31, e12817. [Google Scholar]
- Guo, T.; Zhu, Y.; Liu, Y.; Gu, C.; Liu, J. Two-stage optimal MPC for hybrid energy storage operation to enable smooth wind power integration. IET Renew. Power Gener. 2020, 14, 2477–2486. [Google Scholar]
- Silva, D.P.E.; Salles, J.L.F.; Fardin, J.F.; Pereira, M.M.R. Management of an island and grid-connected microgrid using hybrid economic model predictive control with weather data. Appl. Energy 2020, 278, 115581. [Google Scholar]
- Huang, C.; Zong, Y.; You, S.; Træholt, C.; Zheng, Y.; Wang, J.; Zheng, Z.; Xiao, X. Economic and resilient operation of hydrogen-based microgrids: An improved MPC-based optimal scheduling scheme considering security constraints of hydrogen facilities. Appl. Energy 2023, 335, 120762. [Google Scholar]
- Subramanian, V.; Vairavasundaram, I.; Aljafari, B. Analysis of Optimal Load Management Using a Stand-Alone Hybrid AC/DC Microgrid System. Int. Trans. Electr. Energy Syst. 2023, 2023, 7519436. [Google Scholar]
- Chen, S.; Yang, Q.; Zhou, J.; Chen, X. A model predictive control method for hybrid energy storage systems. CSEE J. Power Energy Syst. 2020, 7, 329–338. [Google Scholar]
- Li, Y.; Tong, Z. Model predictive control strategy using encoder-decoder recurrent neural networks for smart control of thermal environment. J. Build. Eng. 2021, 42, 103017. [Google Scholar]
- Zhang, Z.; Xie, L.; Lu, S.; Rossiter, J.A.; Su, H. A low-cost pole-placement MPC algorithm for controlling complex dynamic systems. J. Process Control 2022, 111, 106–116. [Google Scholar]
- Faedo, N.; Olaya, S.; Ringwood, J.V. Optimal control, MPC and MPC-like algorithms for wave energy systems: An overview. IFAC J. Syst. Control 2017, 1, 37–56. [Google Scholar]
- Borase, R.P.; Maghade, D.; Sondkar, S.; Pawar, S. A review of PID control, tuning methods and applications. Int. J. Dyn. Control 2021, 9, 818–827. [Google Scholar]
- Asgharnia, A.; Shahnazi, R.; Jamali, A. Performance and robustness of optimal fractional fuzzy PID controllers for pitch control of a wind turbine using chaotic optimization algorithms. ISA Trans. 2018, 79, 27–44. [Google Scholar] [PubMed]
- Podder, A.K.; Chakraborty, O.; Islam, S.; Kumar, N.M.; Alhelou, H.H. Control strategies of different hybrid energy storage systems for electric vehicles applications. IEEE Access 2021, 9, 51865–51895. [Google Scholar]
- Yao, Y.; Shekhar, D.K. State of the art review on model predictive control (MPC) in Heating Ventilation and Air-conditioning (HVAC) field. Build. Environ. 2021, 200, 107952. [Google Scholar]
- Raziei, S.A.; Jiang, Z. Model predictive control for complex dynamic systems. In Proceedings of the 2016 IEEE National Aerospace and Electronics Conference (NAECON) and Ohio Innovation Summit (OIS), Dayton, OH, USA, 25–29 July 2016; pp. 193–200. [Google Scholar]
- Chong, L.W.; Wong, Y.W.; Rajkumar, R.K.; Rajkumar, R.K.; Isa, D. Hybrid energy storage systems and control strategies for stand-alone renewable energy power systems. Renew. Sustain. Energy Rev. 2016, 66, 174–189. [Google Scholar]
- Tang, L.; Yan, F.; Zou, B.; Wang, K.; Lv, C. An improved kinematic model predictive control for high-speed path tracking of autonomous vehicles. IEEE Access 2020, 8, 51400–51413. [Google Scholar]
- Kapnopoulos, A.; Alexandridis, A. A cooperative particle swarm optimization approach for tuning an MPC-based quadrotor trajectory tracking scheme. Aerosp. Sci. Technol. 2022, 127, 107725. [Google Scholar]
- Perez, F. Control of ac/dc microgrids with renewables in the context of smart grids: Including ancillary services and electric mobility. Ph.D. Thesis, Université Paris-Saclay, Universidade federal de Itajuba, Itajubá, Brazil, 2020. [Google Scholar]
- Kabalci, E. Hierarchical control in microgrid. In Microgrid Architectures, Control and Protection Methods; Springer: Berlin/Heidelberg, Germany, 2020; pp. 381–401. [Google Scholar]
- Feng, F.; Zhang, P. Enhanced microgrid power flow incorporating hierarchical control. IEEE Trans. Power Syst. 2020, 35, 2463–2466. [Google Scholar]
- Wang, G.; Wang, X.; Gao, X. Improved seamless switching control strategy for AC/DC hybrid microgrid. IEEE Access 2021, 9, 55790–55801. [Google Scholar]
- Kamal, T.; Karabacak, M.; Hassan, S.Z.; Fernández-Ramírez, L.M.; Riaz, M.H.; Riaz, M.T.; Khan, M.A.; Khan, L. Energy management and switching control of PHEV charging stations in a hybrid smart micro-grid system. Electronics 2018, 7, 156. [Google Scholar] [CrossRef]
- Li, G.; Du, Y. Performance investigation and economic benefits of new control strategies for heat pump-gas fired water heater hybrid system. Appl. Energy 2018, 232, 101–118. [Google Scholar]
- Rana, K.; Dasagi, V.; Haviland, J.; Talbot, B.; Milford, M.; Sünderhauf, N. Bayesian controller fusion: Leveraging control priors in deep reinforcement learning for robotics. Int. J. Robot. Res. 2023, 42, 123–146. [Google Scholar]
- Li, Y.; Wang, C.; Li, G.; Wang, J.; Zhao, D.; Chen, C. Improving operational flexibility of integrated energy system with uncertain renewable generations considering thermal inertia of buildings. Energy Convers. Manag. 2020, 207, 112526. [Google Scholar]
- Zhang, W.; Wang, J.; Xu, Z.; Shen, Y.; Gao, G. A generalized energy management framework for hybrid construction vehicles via model-based reinforcement learning. Energy 2022, 260, 124849. [Google Scholar]
- Shezan, S.A.; Kamwa, I.; Ishraque, M.F.; Muyeen, S.; Hasan, K.N.; Saidur, R.; Rizvi, S.M.; Shafiullah, M.; Al-Sulaiman, F.A. Evaluation of different optimization techniques and control strategies of hybrid microgrid: A review. Energies 2023, 16, 1792. [Google Scholar] [CrossRef]
- Nair, U.R.; Costa-Castelló, R. A model predictive control-based energy management scheme for hybrid storage system in islanded microgrids. IEEE Access 2020, 8, 97809–97822. [Google Scholar]
- Jashfar, S.; Esmaeili, S.; Jahromi, M.Z.; Rahmanian, M. Classification of power quality disturbances using S-transform and TT-transform based on the artificial neural network. Turk. J. Electr. Eng. Comput. Sci. 2013, 21, 1528–1538. [Google Scholar]
- Shahzad, S.; Abbasi, M.A.; Chaudhry, M.A.; Hussain, M.M. Model Predictive Control Strategies in Microgrids: A Concise Revisit. IEEE Access 2022, 10, 122211–122225. [Google Scholar]
- Zafra-Cabeza, A.; Velarde, P.; Maestre, J.M. Multicriteria optimal operation of a microgrid considering risk analysis, renewable resources, model predictive control. Optim. Control Appl. Methods 2020, 41, 94–106. [Google Scholar]
- Topa, A.; Gil, J.; Álvarez, J.; Torres, J. A hybrid-MPC based energy management system with time series constraints for a bioclimatic building. Energy 2023, 287, 129652. [Google Scholar]
- Mohanty, S.; Bhanja, A.; Gautam, S.P.; Chittathuru, D.; Dash, S.K.; Mangaraj, M.; Chinthaginjala, R.; Alamri, A.M. Review of a Comprehensive Analysis of Planning, Functionality, Control, Protection for Direct Current Microgrids. Sustainability 2023, 15, 15405. [Google Scholar] [CrossRef]
- Zhang, Z.; Babayomi, O.; Dragicevic, T.; Heydari, R.; Garcia, C.; Rodriguez, J.; Kennel, R. Advances and opportunities in the model predictive control of microgrids: Part I–primary layer. Int. J. Electr. Power Energy Syst. 2022, 134, 107411. [Google Scholar]
- Habibi, M.R.; Baghaee, H.R.; Blaabjerg, F.; Dragičević, T. Secure MPC/ANN-based false data injection cyber-attack detection and mitigation in DC microgrids. IEEE Syst. J. 2021, 16, 1487–1498. [Google Scholar]
- Trigkas, D.; Gravanis, G.; Diamantaras, K.; Voutetakis, S.; Papadopoulou, S. Energy Management in Microgrids Using Model Predictive Control Empowered with Artificial Intelligence. Chem. Eng. Trans. 2022, 94, 961–966. [Google Scholar]
- Nurkanović, A.; Mešanović, A.; Zanelli, A.; Frison, G.; Frey, J.; Albrecht, S.; Diehl, M. Real-time nonlinear model predictive control for microgrid operation. In Proceeding of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 4989–4995. [Google Scholar]
- Li, Q.; Zou, X.; Pu, Y.; Chen, W. Real-time Energy Management Method for Electric-hydrogen Hybrid Energy Storage Microgrids Based on DP-MPC. CSEE J. Power Energy Syst. 2020, 10, 324–336. [Google Scholar]
- Torres, F.G.; Hornero, J.E.J.; García, V.G.; Jiménez, F.J.; González, J.R.; Raya, F.R.L. Distributed Stochastic Model Predictive Control for Scheduling Deterministic Peer-to-Peer Energy Transactions among Networked Microgrids with Hybrid Energy Storage Systems. IEEE Access 2024, 12, 44539–44552. [Google Scholar]


| Ref. | Scope of Review | MPC in MGs | MOO in MPC | Hybrid Control | Hierarchical Strategy in MGs | Real world Insights | Gap Address in This Study |
|---|---|---|---|---|---|---|---|
| [53] | Thematic; general | ✓ | ✓ | ✕ | ✓ | ✕ | Lacks hybrid/control diversity |
| [57] | Focuses on MG control | ✓ | ✓ | ✕ | ✓ | ✕ | Limited structure and hierarchy |
| [58] | Structured but narrow | ✓ | ✓ | ✕ | ✓ | ✕ | Lacks hybrid control and real-world focus |
| [59,60] | Algorithm centric | ✓ | ✕ | ✕ | ✕ | ✕ | Lacks application perspective |
| [61,62,63] | Practical but partial focus | ✓ | ✕ | ✕ | ✕ | ✕ | No hybrid or hierarchical view |
| [64] | Predictive power management in hybrid RES | ✓ | ✕ | ✓ | ✕ | ✕ | Lacks control taxonomy, real-world cases, and MOO |
| [65] | Evaluation of MPC-based MPPT for PV systems | ✓ | ✕ | ✕ | ✕ | ✓ | Lacks MOO and hybrid/hierarchical control |
| This study | Comprehensive (taxonomy + application) | ✓ | ✓ | ✓ | ✓ | ✓ | Unified taxonomy, hybrid control, MOO, and real-world integration |
| Criteria | Inclusion | Exclusion |
|---|---|---|
| Time range | 2021–2025 | Publications before 2021 or after 2025 |
| Language | English only | Non-English publications |
| Document type | Research articles, review papers | Conference abstracts, editorials, etc. |
| Subject area | Electrical engineering | Other fields of engineering or unrelated fields |
| Search logic | Applied AND, OR for specific filtering | - |
| Source database | WOS | Other databases (e.g., IEEE Xplore) |
| Publishers | All publishers indexed in WOS | - |
| Category | Description | Key Formula | Ref. |
|---|---|---|---|
| Single objective | A single goal (such as the reduction of errors or energy consumption) is optimized. This optimization involves only a single variable. | [96,97] | |
| Multi-objective | Several objectives are considered together, and these objectives can be prioritized by using weights. | (With weights ) | [98,99] |
| Adaptive objective | The function dynamically changes according to system conditions. It adjusts based on past data and current inputs. | [100,101,102] | |
| Learned objective | This function uses neural networks (NNs) to automatically simulate the goal. It is useful for modeling complex, nonlinear relationships. | (NN trained to model the objective) | [103,104,105,106] |
| Distributed objective | In multi-agent systems, each agent accomplishes its specific goal, ultimately resulting in a global goal. | (N is the number of agents) | [107,108] |
| Robust objective | This function is designed to manage uncertainties or disturbances in the system. It optimizes under the largest possible disturbances. | (d is the disturbance parameter) | [109,110,111,112] |
| Economic objective | This function maximizes economic aspects such as cost or profit, emphasizing the economic contribution of system decisions. | ( is the revenue and is cost) | [48,113] |
| Mixed-integer objective | This function includes continuous and discrete (integer or binary) variables. It introduces additional complexity. | ( are continuous variables and are discrete variables) | [114,115] |
| Quadratic objective | This function is expressed as a quadratic form of state and control variables, and convex optimization is used for optimization. | [116,117,118] |
| Ref. | Desired Control Objectives | Advantages | Limitations | Algorithm | Results |
|---|---|---|---|---|---|
| [150] | Enhance the efficient use of flexible resources (such as PV panels and battery storage systems) in buildings to reduce operational energy costs. | (1) SMPC is more likely to realize daily cost savings compared to CMPC and SHMPC strategies. (2) SHMPC can achieve higher cost savings in actual operation by aligning the optimization horizon’s commencement with the onset of the off-peak period. | (1) SMPC still has higher daily costs than the real-time optimal control strategy for most of the winter season due to low forecast accuracy. (2) There is no one control strategy that is definitely superior to the other strategies under all operating conditions. | CMPC SHMPC SMPC RTC | Hybrid control strategies using RTC in winter and SMPC in other seasons effectively optimize building energy flexibility in subtropical regions. |
| [177] | Optimizing the management of power flow among battery ESS involves considering factors such as line losses, voltage constraints, and converter current constraints. Achieving real-time implementation necessitates a significant reduction in computation time. | (1) Fast solution via convex optimization and robust solvers. (2) Handles line losses, voltage, and current constraints. (3) Applicability for real-time MPC in MGs. | (1) The simplified battery model may not fully capture all system dynamics. (2) Assumptions about battery charge and discharge efficiencies may not be universally applicable across all operational scenarios. (3) Approximations inherent to the variable efficiency battery SoC model. | Convex vs. non-convex problems and robust solvers | The convex MPC approach rivals non-convex methods in real-time microgrid simulations, notably cutting computation time while maintaining competitive power loss at 12.638 kW versus 11.596 kW. |
| [178] | Address the instability problems caused by constant power load (CPL) in DC MGs. Develop a robust and fast-responding controller for DC/DC converters feeding CPLs. | (1) AMPC based on DRL provides robustness and fast response to system dynamics. (2) Deep Q-Network (DQN) strategy adaptively designs the controlling signal coefficient for each variable operation point. | (1) The complexity of the AMPC algorithm (2) The requirement for training data for the DQN model | AMPC with DQN | The AMPC controller successfully resolves instability issues in DC MGs caused by CPL, demonstrating robustness and rapid dynamic response. |
| [179] | Optimize energy management in MG Balance power generation and demand through ESS Minimize operating costs. Improve MG efficiency. Reduce environmental impacts. | (1) AMPC addresses issues associated with MG. (2) AMPC optimizes power-sharing among DERs while considering physical and operational constraints. (3) AMPC minimizes operating costs and improves MG efficiency. | (1) AMPC requires accurate prediction of disturbances, which can be challenging (2) AMPC is more complex to implement than traditional control algorithms | AMPC based receding horizon control | AMPC proves to be an effective tool for optimizing energy management in MG, reducing operating costs, enhancing efficiency, and minimizing environmental impact. |
| [180] | Minimize energy costs and maximize renewable energy utilization in MGs. Develop a control scheme that works effectively in both grid-connected and islanded mode. | (1) SHMPC scheme effectively reduces energy costs by 6% compared to non-switched HMPC. (2) SHMPC effectively utilizes renewable energy and storage capabilities under changing grid connection conditions. | (1) No energy demand or production forecasting. (2) Conceptual character, further research needed to implement advanced functionalities. | SHMPC | SHMPC effectively reduces energy costs and maximizes renewable energy utilization in MGs SHMPC is applicable to any standard MG. |
| [121] | Minimize the operating cost of a MG. Handle the intermittency of RESs and the high stochasticity in market prices and loads. | (1) Imitation learning cuts training time by 17 times compared to a Q-learning (2) Proposed approach achieves an operating cost close to the theoretical minimum value under various uncertainties. | (1) Requires a MILP solver to generate an expert policy. (2) May not be applicable to MGs with complex constraints. | Data-driven online approach based on imitation learning | Proposed data-driven approach efficiently optimizes MG operation costs under uncertainties in both simulated and real-world scenarios. |
| [181] | Optimize the overall cost of generation in a hybrid MG, taking into account constraints associated with supply–demand balance, capacity, and ramp-rate. | (1) The proposed decentralized algorithm is independent of the initialization stage. (2) Proposed algorithm can handle convex objective functions. (3) The convergence of the presented algorithm is proven via convex analysis and the utilization of the Lyapunov function technique | Algorithm may not be applicable to non-convex optimization problems. | Fully distributed algorithm | Proposed distributed algorithm minimizes MG generation cost while satisfying constraints, with proven convergence. |
| [182] | The primary goals of control in this context encompass optimizing economic performance metrics through forecasts of PV generation and load demands, minimizing disparities between planned and actual energy transactions, and ensuring compliance with probabilistic constraints. | (1) Efficient energy management across diverse timeframes. (2) Adaptability to stochastic disruptions and correction of predictive inaccuracies. (3) Improved system-wide efficiency via updates to the overarching plan. | (1) Dependency on precise forecast data for optimal functionality. (2) Complexity in deployment and computational demands (3) Sensitivity to the precision of models and tuning of parameters. | Two-layer | The dual-layer algorithm enhances MG energy management by combining economic and stochastic MPC, with recurrent updates improving system performance. |
| [183] | Attain concurrent control of frequency and voltage in an HVDC transmission system during converter blocking. | (1) Cooperative control effectively regulates frequency and voltage during HVDC blocking. (2) EMPC diminishes peak and steady-state deviations in frequency and voltage. (3) EMPC outperforms droop control, LQR, and the original system. | (1) Complexity of the EMPC (2) Requirement for accurate models of the HVDC transmission system and wind farm. | EMPC | Proposed EMPC-based cooperative control effectively regulates frequency and voltage during HVDC blocking, outperforming traditional methods. |
| Ref. | Scenario | Type of MPC | Hardware/Platform Used | Key Outcomes |
|---|---|---|---|---|
| [184] | Frequency regulation using DRL in PV–diesel MG | DRL-MPC | STM32-based embedded system | Improved frequency stability under load changes |
| [185] | Economic dispatch in grid-connected MG | EMPC | Lab-scale OPAL-RT + MATLAB | 52.1% cost reduction and smooth DER transitions |
| [186] | Power sharing across MMGs | DRMPC | Simulink-HIL + TCP/IP network | Enhanced economy and improved data privacy |
| [187] | CO2 reduction in islanded MG with PV and battery | Dual-layer EMPC | Raspberry Pi + SCADA interface | 10% CO2 reduction and optimized generator usage |
| Ref. | [209] | [210] | [99] | [96] | [211] | [212] | [213] | [214] | [215] | [216] | [217] | [218] | [219] | [220] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Improved system performance | ✕ | ✕ | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ | ✕ | ✓ | ✕ | ✓ | ✕ |
| Reduced risk of suboptimal solutions | ✓ | ✕ | ✓ | ✕ | ✕ | ✓ | ✕ | ✕ | ✕ | ✓ | ✕ | ✕ | ✕ | ✕ |
| Increased flexibility | ✕ | ✓ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✕ | ✓ | ✕ | ✓ |
| Ref. | Increased Computational Complexity | Difficulty in Defining Objectives | Trade-Offs Between Objectives |
|---|---|---|---|
| [12] | ✕ | ✓ | ✕ |
| [192] | ✓ | ✕ | ✕ |
| [213] | ✕ | ✕ | ✓ |
| [226] | ✕ | ✕ | ✓ |
| [227] | ✕ | ✓ | ✕ |
| [228] | ✕ | ✕ | ✓ |
| [229] | ✕ | ✕ | ✓ |
| [230] | ✕ | ✕ | ✓ |
| Ref. | Type of MG | Economical Index | Technical Index | Result | Hierarchical Control | Priority | Multi-MGs |
|---|---|---|---|---|---|---|---|
| [180] | Not mentioned | (1) The energy cost of the MG (2) The diesel generator fuel cost (3) The energy price from the main grid | (1) power balance equation (2) SoC (3) The voltage levels of the distribution network (4) The operation of the diesel generator | The results show that the proposed SMPC algorithm can achieve significant cost savings while ensuring the reliable operation of the MG. | ✓ | Economic operation and technical operation | ✕ |
| [241] | AC hybrid | (1) The cost of energy production (2) The cost of battery degradation | (1) SoC (2) Power limits of the ESS (3) Limitation power of wind turbine (4) Limitation of grid connection power (5) Limitation on power transfer between the ESS and grid | The proposed MPC minimizes energy costs and improves power quality by stabilizing the output of wind turbines. It is suitable for the control of wind/ESS hybrid plants, especially in isolated grids. | ✕ | Economic operation | ✕ |
| [242] | Not mentioned | (1) The cost of energy purchased from the main grid (2) The cost of energy consumed by the loads (3) The cost of energy stored and discharged by the ESSs | (1) Battery SoC (2) Battery capacity (3) Using RES (4) Grid power import (5) Grid power export (6) Power balance (7) Power quality (8) Voltage level (9) Switching frequency | This paper used a hybrid constrained CPSO-MPC algorithm. The findings show that the proposed MPC system can reduce the energy-generation cost and improve power quality by decreasing the power-output oscillations in wind farms. | ✕ | Economic operation and technical operation | ✓ |
| [243] | AC/DC hybrid | (1) Cost of energy not served (2) Net present value (3) Levelized cost of energy (4) Payback period (5) Benefit-to-cost ratio | (1) Energy balance error (2) Hydrogen balance error (3) Voltage deviation (4) Frequency deviation (5) SoC | The results revealed that the proposed multistage energy and power management policy for a hybrid MG with photovoltaic and hydrogen storage was efficient in energy management, economic reduction, and environmental sustainability. The proposed policy includes three stages: day-ahead, real-time, and emergency. | ✕ | Economic operation | ✕ |
| [244] | AC/DC hybrid | (1) The cost of energy purchased from the main grid (2) The price of energy sold to the main grid (3) The cost of operating the converters | (1) Power flow (2) Voltage magnitude | Simulation results indicated that the suggested algorithm enhanced the overall system performance with its faster response, improved power sharing, and stable bus voltages in comparison to traditional control techniques. | ✕ | Technical operation | ✓ |
| [245] | Not mentioned | The cost of electricity | (1) Power flow (2) SoC | The paper presents an optimal MPC in two stages for hybrid ESSs that smooths wind fluctuations and load-demand variations, enhancing stability and reliability. | ✕ | Economic operation and technical operation | ✕ |
| [246] | Not mentioned | (1) Fuel consumption (2) Power purchase from the main grid (3) Renewable energy curtailment | (1) Balance between active and reactive power (2) Voltage magnitude (3) Current magnitude (4) SOC of ESSs (5) Ramp rate limits for PV and diesel generators | This study proposes a HEMPC strategy for MG in islanded and grid-connected modes, considering economic factors and weather prediction. Simulations confirm minimized cost and enhanced utilization of RESs. | ✕ | Economic operation | ✕ |
| [247] | Not mentioned | (1) Operation cost (2) Investment cost (3) Income from selling excess power | (1) Hydrogen storage level (2) Load demand (3) Security of hydrogen | This paper discussed an improved MPC-based scheduling approach for cost-effective and robust hydrogen-based MGs, considering hydrogen facility security constraints. Results confirm the effectiveness of the scheme in offering cost-effective and reliable MG operation. | ✕ | Economic operation | ✓ |
| [248] | AC/DC hybrid | (1) Diesel fuel cost (2) Battery replacement cost (3) Diesel generator maintenance cost (4) RESs cost (5) Power purchased/sold cost (6) MG total cost | (1) Frequency (2) Voltage deviation (3) Load balancing (4) Load factor (5) THD (6) RESs Factor (7) SOC (8) Total system losses | This study proposes an optimal load management approach based on finite control set MPC for a wind–solar islanded hybrid AC/DC MG to achieve minimum operating cost with a guarantee of power supply to the critical loads. The results demonstrate that the method successfully decreases cost and provides a reliable power supply. | ✕ | Economic operation | ✕ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yaghoubi, E.; Yaghoubi, E.; Maghami, M.R.; Rahebi, J.; Zareian Jahromi, M.; Ghadami, R.; Yusupov, Z. A Systematic Review and Meta-Analysis of Model Predictive Control in Microgrids: Moving Beyond Traditional Methods. Processes 2025, 13, 2197. https://doi.org/10.3390/pr13072197
Yaghoubi E, Yaghoubi E, Maghami MR, Rahebi J, Zareian Jahromi M, Ghadami R, Yusupov Z. A Systematic Review and Meta-Analysis of Model Predictive Control in Microgrids: Moving Beyond Traditional Methods. Processes. 2025; 13(7):2197. https://doi.org/10.3390/pr13072197
Chicago/Turabian StyleYaghoubi, Elnaz, Elaheh Yaghoubi, Mohammad Reza Maghami, Javad Rahebi, Mehdi Zareian Jahromi, Raheleh Ghadami (Melisa Rahebi), and Ziyodulla Yusupov. 2025. "A Systematic Review and Meta-Analysis of Model Predictive Control in Microgrids: Moving Beyond Traditional Methods" Processes 13, no. 7: 2197. https://doi.org/10.3390/pr13072197
APA StyleYaghoubi, E., Yaghoubi, E., Maghami, M. R., Rahebi, J., Zareian Jahromi, M., Ghadami, R., & Yusupov, Z. (2025). A Systematic Review and Meta-Analysis of Model Predictive Control in Microgrids: Moving Beyond Traditional Methods. Processes, 13(7), 2197. https://doi.org/10.3390/pr13072197











