Next Article in Journal
Technologies for the Remediation of Nitrogen Pollution and Advances in the Application of Metal–Phenolic Networks
Previous Article in Journal
Dynamics of Bacterial Communities and Identification of Microbial Indicators in a Cylindrospermopsis-Bloom Reservoir in Western Guangdong Province, China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Processes
Volume 13
Issue 7
10.3390/pr13072130
processes-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Predicting the Compressive Strength of Concrete Incorporating Olivine Aggregate at Varied Cement Dosages Using Artificial Intelligence

by
Yusuf Tahir Altuncı
Vocational School of Technical Sciences, Isparta University of Applied Sciences, Isparta 32200, Turkey
Processes 2025, 13(7), 2130; https://doi.org/10.3390/pr13072130
Submission received: 25 April 2025 / Revised: 20 June 2025 / Accepted: 3 July 2025 / Published: 4 July 2025
(This article belongs to the Section AI-Enabled Process Engineering)
Browse Figures
Versions Notes

Abstract

This study aimed to identify the most reliable prediction model for estimating the compressive strength of concrete by conducting a comparative analysis of Particle Swarm Optimization (PSO) and Artificial Neural Network (ANN) methodologies. The modeling process utilized 92 experimental data points for training purposes and allocated 28 data points for testing validation. PSO was employed to optimize coefficients within mathematical equations used for concrete compressive strength prediction, facilitating the development of appropriate models based on various error metrics. Specifically, PSO models optimized to minimize Weighted Root Mean Square Error (WRMSE), Root Mean Square Error (RMSE), and Mean Absolute Error (MAE) criteria were evaluated against the highest-performing model developed using ANN. Model A, optimized using a constant term and the WRMSE loss function within a PSO-ANN framework, achieved the highest performance, with a correlation coefficient exceeding 0.99 and low error values on the training dataset. The same model also demonstrated strong predictive accuracy and low error on the test dataset, indicating excellent generalization capability. In contrast, the standalone ANN model exhibited near-perfect accuracy on the training data (R2 = 0.9994) but suffered a significant drop in performance on the test data (correlation ≈ 0.60). This highlights the impact of overfitting and underscores the importance of regularization techniques for improving generalizability. Through comprehensive statistical and visual assessments using Taylor diagram analysis, PSO-based models demonstrated significantly superior accuracy compared to the ANN model. Furthermore, the constant-term WRMSE model exhibited optimal generalization performance and provided the most reliable predictions among all tested models. It has been observed that highly accurate predictions can be made even for values outside the range of the data used. The results obtained in this study indicate that reliable predictive models for concrete production can be developed using both the available data and information from the literature. In cases where data are lacking, it is also possible to establish these models by conducting a sufficient number of experiments.

1. Introduction

Concrete consumption has exhibited a consistent upward trajectory correlating with population growth [1]. As the most widely adopted composite building material, concrete’s popularity continues to rise [2]. It is well-documented that approximately 8% of anthropogenic carbon dioxide (CO2) emissions in the atmosphere are attributed to cement production [3]. Consequently, the judicious utilization of concrete components has become increasingly critical in addressing environmental challenges such as climate change and global warming [4]. Particular attention must be directed toward understanding aggregates, which constitute approximately 60% of concrete’s composition [5]. Aggregates may be directly sourced from various rock formations including andesite, barite, basalt, dolomite, granite, and limestone, or indirectly obtained through alternative methodologies [6,7,8]. Beyond these conventional aggregate resources, olivine rock—which exists in abundance globally—represents a significant material for CO2 sequestration when incorporated as an aggregate in concrete or mortar [9,10,11]. Numerous substantial investigations have been conducted with the objective of enhancing concrete strength and durability performance through the utilization of diverse aggregate types [12,13].
Upon thorough examination of the literature, it was determined that the utilization of diverse aggregate types in concrete production represents a contemporary research focus. Previous investigations [14,15,16] have consistently emphasized the significance of identifying novel aggregate types that enhance concrete performance as a valuable contribution to both industry applications and the scholarly literature. The strategic incorporation of aggregates with varying chemical compositions for specific purposes in concrete is of paramount importance. The chemical composition of aggregates provides critical insights regarding their potential applications [17,18,19]. Olivine aggregate, derived from dunite rock, possesses considerable potential to positively influence the strength and durability performance of concrete due to its high iron (Fe) content and magnesium oxide (MgO) concentration. Additionally, this material offers substantial environmental benefits when utilized as a concrete aggregate [10,11]. Consequently, this study aimed to determine the compressive strength of concrete incorporating various proportions of olivine aggregate through artificial intelligence (AI)-based methodologies.
Testing individual concrete mixtures presents significant challenges regarding both temporal and financial resources. It is therefore of considerable importance to accurately estimate the mixture ratio effects on concrete compressive strength. Numerous methodological approaches have been employed to develop concrete strength prediction models, including Multiple Regression (MR) [20,21,22,23,24,25], Particle Swarm Optimization (PSO) [26,27,28,29,30,31,32,33,34,35], Response Surface Methodology (RSM) [36,37,38,39], and Adaptive Neuro-Fuzzy Inference System (ANFIS) [20,27,40,41,42,43,44,45,46,47,48]. Additional methodologies encompass Fuzzy Logic (FL) [49,50,51,52,53,54,55,56,57,58], Artificial Neural Network (ANN) [23,26,37,38,47,48,52,54,55,56,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77], Support Vector Machine (SVM) [29,61,64,78,79,80,81,82,83,84], and Gaussian Process Regression (GPR) [42,60,61,85,86,87,88,89].
In order to identify significant studies concerning concrete compressive strength and artificial intelligence applications, a systematic literature review was conducted using the Web of Science (WoS) search engine. The search criteria included manuscripts containing ‘Concrete’ in the abstract, ‘Compressive strength’ in the title, and at least one of the following terms within the entire manuscript: artificial intelligence, Machine Learning, Multiple Regression, Particle Swarm Optimization, Response Surface Methodology, Adaptive Neuro-Fuzzy Inference System, Fuzzy Logic, Artificial Neural Network, Support Vector Machine, and Gaussian Process Regression. The literature search was executed by implementing the following formula in the advanced search tab of the WoS platform: (AB = (Concrete) AND TI = (Compressive strength)) AND (AB = (artificial intelligence) OR AB = (Machine Learning) OR AB = (Multiple Regression) OR AB = (Particle Swarm Optimization) OR AB = (Response Surface Methodology) OR AB = (Adaptive Neuro-Fuzzy Inference System) OR AB = (Fuzzy Logic) OR AB = (Artificial Neural Network) OR AB = (Support Vector Machine) OR AB = (Gaussian Process Regression)). The search results were subsequently filtered to include only SCIE and SSCI articles published in English after 2015 or with early access status. The initial search yielded 518 articles, which were comprehensively examined individually. Additionally, 43 articles investigating the mechanical properties of concrete utilizing different aggregate types were incorporated into the analysis. The research gaps identified through this systematic review, which constitute the primary motivation for the present study, are enumerated in Table 1 below.
Researchers have conducted significant investigations regarding the utilization of diverse aggregates in concrete and the determination of their mechanical properties through artificial intelligence methodologies. Notably, recycled aggregates [101,106,111,112,113,118,119,126] and the impact of various aggregate types on concrete performance [97,104,120,124,131] have been examined extensively by numerous researchers. Additionally, machine learning and AI models have been frequently employed to predict concrete performance metrics [90,91,93,95,96,98,99,100,101,102,103,105,112,114,115,116,121,125,128]. Similarly, researchers have undertaken valuable studies concerning the prediction of concrete’s mechanical properties [37,92,94,107,108,110,122,131,132]. Complementing these investigations, researchers have contributed significant studies on comparative analyses and modeling approaches to the literature [123,130]. Upon comprehensive examination of the relevant literature, it becomes evident that researchers consistently emphasize the identification of alternative materials suitable for aggregate applications to enhance concrete’s mechanical properties as an ongoing research priority. Notably, no previous study has investigated the substitution of olivine material as an aggregate in concrete compositions. The present study, which investigates the compressive strength of concrete incorporating olivine aggregate at various dosages, aims to develop artificial intelligence-based prediction models to facilitate future research endeavors and enhance concrete applications. A comprehensive overview of studies using AI to examine the utility of different rock types in concrete production is presented in Table 2.
Based on the analysis presented in the table above, it has been determined that the ANN methodology is frequently employed alongside the RMSE, WRMSE, and MAE metrics described in the existing literature. Additionally, a comprehensive review of the literature on artificial intelligence has revealed that the PSO methodology demonstrates superior performance compared to alternative methods in model training processes [27,28,29,30,31,32,33]. In the present study, models were systematically trained using both PSO and ANN methodologies. Subsequently, models developed via PSO were optimized through the minimization of the WRMSE, RMSE, and MAE metrics. Following this optimization process, the values obtained through the PSO and ANN methodologies were comparatively evaluated using Taylor diagram analysis to identify the most appropriate and reliable results.

2. Significance of This Study

In this study, concrete specimens with variable compressive strengths were fabricated utilizing CEM II 42.5 R cement within a dosage range of 180–325 kg/m3 and incorporating olivine aggregate in the 0–25 mm fraction. For the modeling procedure, 92 experimental data points were allocated for training purposes, while 28 data points were designated for testing validation. A comprehensive analysis of the literature reveals that the PSO methodology is extensively preferred, particularly due to its optimization capabilities, and consistently demonstrates high prediction accuracy [28,29,30,133,134,135,136]. However, research comparing the predictive accuracy of the ANN methodology with PSO and determining which error metric produces superior results remains limited [26,35]. Consequently, in this study, equations developed using the PSO method were analyzed with MATLAB R2023a to predict the compressive strength of concrete. PSO served as an optimization tool to determine the most appropriate coefficient values within these equations. These coefficients, optimized to minimize the Weighted Root Mean Square Error (WRMSE), Root Mean Square Error (RMSE), and Mean Absolute Error (MAE) metrics, were systematically compared with the highest-performing ANN models to evaluate PSO’s effectiveness in identifying optimal solutions. Two models were employed for each of the three different error metrics to identify the optimization results that demonstrate the best performance across various criteria. This approach maximized both the modeling capability and prediction accuracy. Accordingly, this research aimed to compare the predictive accuracy of PSO and ANN methodologies, conduct comprehensive error analysis throughout the modeling process, and determine the most reliable prediction method through rigorous statistical and visual evaluations using Taylor diagram analysis.
The application of olivine aggregate within the construction industry has historically been confined to ceramic glazes, refractory materials, surface coatings, stabilization, and drainage applications [137,138,139]. This investigation, however, aims to expand the implementation of olivine aggregate by demonstrating its beneficial effects on concrete performance. The natural composition of olivine facilitates atmospheric CO2 absorption [11], a characteristic that enables carbon footprint reduction when incorporated into concrete production processes. Compared with conventional aggregates, olivine demonstrates the potential to enhance concrete performance through its superior engineering properties, including exceptional thermal [140] and abrasion resistance [141]. This research therefore contributes to the broader utilization of olivine within the construction sector by elucidating both the engineering and environmental advantages of olivine-based concrete production. Furthermore, the artificial intelligence-supported prediction models employed in this study offer significant advantages regarding concrete production cost reduction and expedited strength determination capabilities. Future research directions could include examining olivine aggregate’s impact on concrete production utilizing CEM III or low-carbon cement varieties, alongside comprehensive investigations into the mechanical and strength properties of concrete incorporating diverse aggregate compositions.

3. Methodology

The literature review reveals that using various aggregate types in concrete production remains a relevant research area, with significant efforts focused on enhancing concrete strength and durability through different aggregate materials [12,44,142,143,144,145,146]. The chemical composition of aggregates substantially influences their application domains, making the selection of optimal aggregates crucial in concrete production [17,18,19]. Several researchers have demonstrated that iron-rich olivine aggregate positively impacts concrete strength and durability performance [9,10,11,147]. Additionally, olivine aggregate has been shown to significantly enhance CO2 absorption in concrete and mortar applications [9,10,11]. For these reasons, olivine aggregate was selected for concrete production in this study. The image of the olivine aggregate used in the study is presented in Figure 1.
This research investigated the influence of olivine volume and grain diameter on concrete compressive strength through the experimental testing of various concrete mixtures. These mixtures contained different proportions of CEM II 42.5 R cement, olivine aggregate, superplasticizer additive, and water. Table 3 presents the chemical composition data for the dry mixtures of cement and olivine aggregate.
Based on the data presented in the table above, calcium oxide (CaO) appears as the predominant compound in cement, while MgO is the most abundant compound in olivine aggregate. The MgO compound chemically reacts with CO2 to form magnesium carbonate (MgCO3). Studies focusing on olivine have demonstrated that MgCO3 reduces the carbon footprint by enhancing CO2 absorption in natural environments [9,10,11]. The volumes of the sample contents were converted for the production of 1 m3 of concrete and are provided in Table 4 below.
The materials were combined in the laboratory under predetermined proportions to produce cube-shaped concrete specimens with dimensions of 15 × 15 × 15 cm. During the specimen preparation process, predetermined amounts of olivine aggregate and cement were first placed into the concrete mixer. These two components were mixed until a homogeneous dry mixture was obtained. Subsequently, the calculated amount of water along with a superplasticizer admixture was added to the dry mix. After the addition of these components, the mixer was operated again for 3 min to ensure a uniform blend and to allow all the constituents to interact effectively. The freshly prepared concrete mixture was carefully poured into 15 × 15 × 15 cm cube molds that had been prepared in advance. Special attention was paid to ensuring the complete filling of the molds and preventing the formation of voids within the concrete. After casting, the specimens were kept under ambient conditions for 24 h to allow for initial setting. At the end of this period, the samples were demolded and subsequently placed in a curing pool for the curing process.
Throughout the curing period, the strength development of the specimens was monitored. Compressive strength tests were conducted on the samples after 7, 28, 56, and 90 days of curing. These tests provided comprehensive data on the mechanical properties of the concrete as they evolved over time. The image of the samples in the curing pool is presented in Figure 2, while the image of the samples subjected to compressive strength testing is shown in Figure 3.
The compressive strength values on days 7, 28, 56, and 90 of specimens produced with cement dosages of 180, 185, 195, 200, 205, 215, 220, 225, 235, 240, 245, 255, 260, 265, 275, 280, 285, 295, 300, 305, 315, 320, and 325 kg/m3 were used as training data, whereas the corresponding strength values of specimens produced with cement dosages of 190, 210, 230, 250, 270, 290, and 310 kg/m3 were utilized as test data. Table 5 presents the statistical analysis of the training parameters implemented in the model, while Table 6 provides the statistical analysis of the test parameters.
Based on the comparison of the average values presented in Table 5 and Table 6, the mean compressive strength is 30.4 MPa in the training dataset and 34.44 MPa in the test dataset, indicating that the model slightly overestimates the strength in the test data. The average amount of plasticizer is also comparable between the datasets: 485.17 kg in training and 472.23 kg in testing. Similarly, the mean values of the aggregate and other components are quite close; for instance, the 5–15 mm aggregate content is 1203.36 kg in training and 1171.27 kg in testing. In terms of the standard deviation, the compressive strength shows values of 9.1 MPa for training and 11.03 MPa for testing, suggesting a slightly wider distribution in the test data. No significant skewness or kurtosis was observed in the distribution metrics; for example, the skewness of the compressive strength was 0.4 in training and −0.47 in testing. When comparing the minimum and maximum values, it becomes evident that the test data generally fall within the range of the training data (e.g., compressive strength: 14.1–52.5 MPa in training vs. 15.75–58.5 MPa in testing). This indicates that the model demonstrates strong generalization performance with minimal tendency toward overfitting.
Analysis of the AI methods in Table 2 indicates that the most frequently used techniques for estimating the compressive strength of concrete with various rock types are ANN [37,38,90,95,98,99,100,102,103,104,105,106,111,116,122,123,124,126,127,128,130], RMSE—WRMSE [37,92,93,106,114,120,121], and MAE [92,93,114,120]. Based on this review, ANN and PSO methods were selected for model development, with the RMSE, WRMSE, and MAE metrics selected for evaluation. All resulting models were subsequently compared to identify which produced the most accurate output [148,149]. Taylor diagrams were also employed to provide both visual and statistical comparisons between the models [150,151,152].

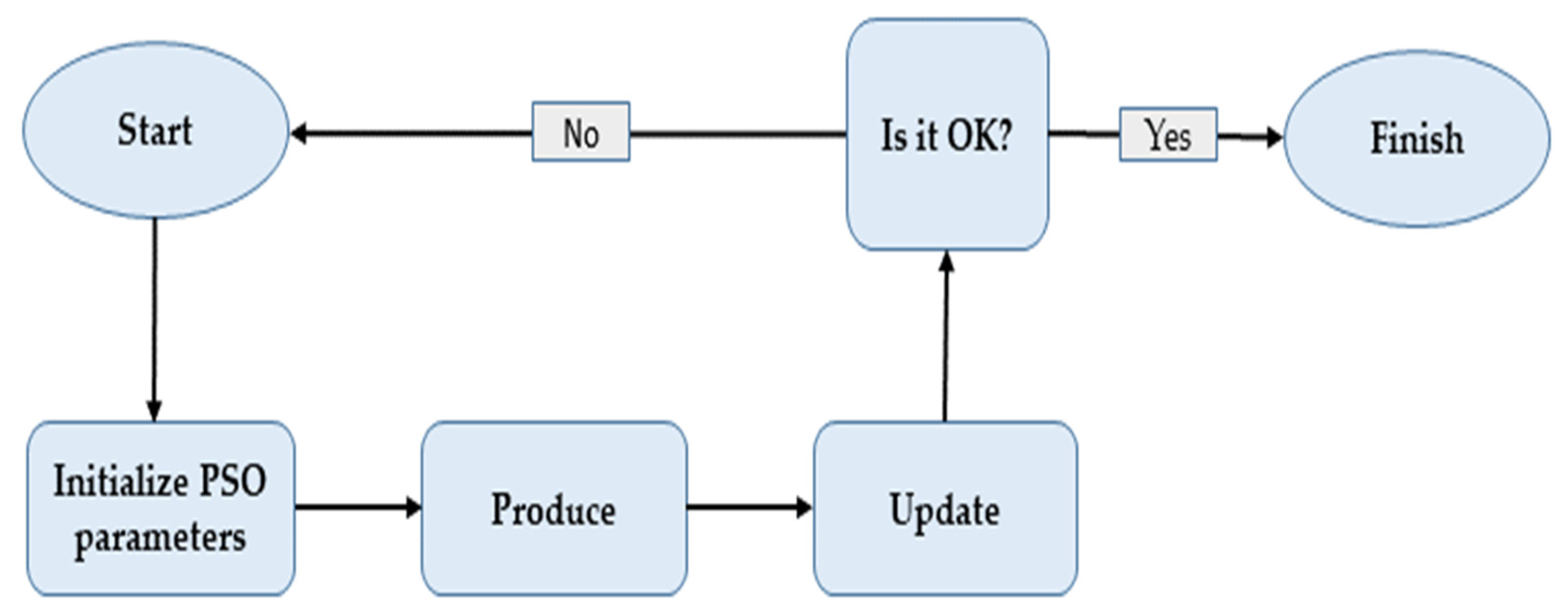
3.1. Particle Swarm Optimization (PSO)

The PSO model is an optimization technique inspired by the optimal navigation behaviors of animals such as fish, birds, and ants [153]. The basic PSO algorithm is illustrated in Figure 4.
In PSO, particle fitness is calculated based on whether particles fall within the defined limit values. The optimization algorithm proceeds by combining these fitness values with the position of the previous particle [33,136]. The standard PSO equations governing velocity and particle position are presented in Equations (1) and (2).
V i d = W ∗ V i d + C 1 x   r a n d ∗ p b e s t i d − X i d + C 2 ∗ r a n d ∗ ( g b e s t i d − X i d )
X i d = X i d ∗ V i d
Various notations are used throughout this study to represent key parameters and variables within the optimization algorithm. Specifically, ‘ V i d ’ denotes velocity, ‘W’ represents the inertia weight, ‘ C 1 ve C 2 ’ indicate scaling factors, ‘rand’ signifies randomly generated numbers, ‘ p b e s t i d ’ represents the local best from the current generation for each particle, ‘ g b e s t i d ’ denotes the best among the local bests in the current generation, and ‘ X i d ’ indicates position.

3.2. Artificial Neural Network (ANN)

An ANN is an artificial intelligence model comprising three layers: an input layer, hidden layers, and an output layer. In an ANN, the core processing occurs within the processors located in the hidden layer. The computational process begins with the assignment of values between successive layer cells during its external operation. This is followed by feedback mechanisms designed to minimize output prediction errors through iterative updates [154,155].
Through training on numerous examples, ANNs develop the ability to make predictions, particularly in areas such as classification, prediction, and regression. Figure 5 illustrates the traditional ANN structure.

3.3. Evaluation Criteria

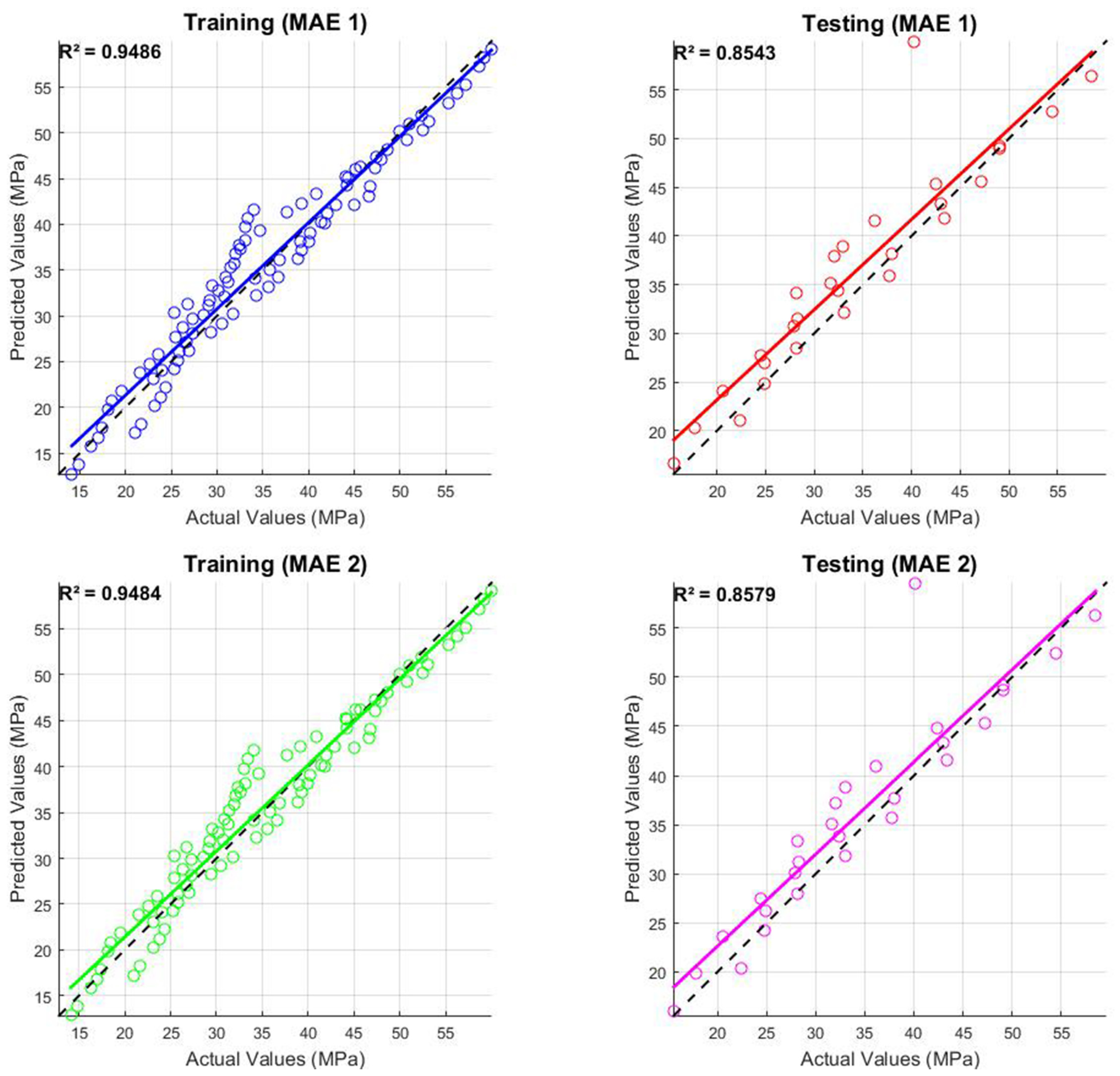
3.3.1. Mean Absolute Error (MAE)

In statistical analysis, the MAE is defined as the absolute difference between the predicted value and the actual value. A lower MAE value indicates that the predicted result closely approximates the actual value, while a higher MAE value suggests a greater deviation from the actual value. The MAE serves as one of the cost functions selected for the PSO models in this study, with the lowest value identifying the model that produces the most accurate results. The MAE equation is presented in Equation (3).
M A E = 1 n ∑ i = 1 n | t − g |
In this equation, ‘MAE’ represents the Mean Absolute Error, and ‘n’ denotes the total number of data points, while ‘t’ and ‘g’ represent the predicted value and true value, respectively.

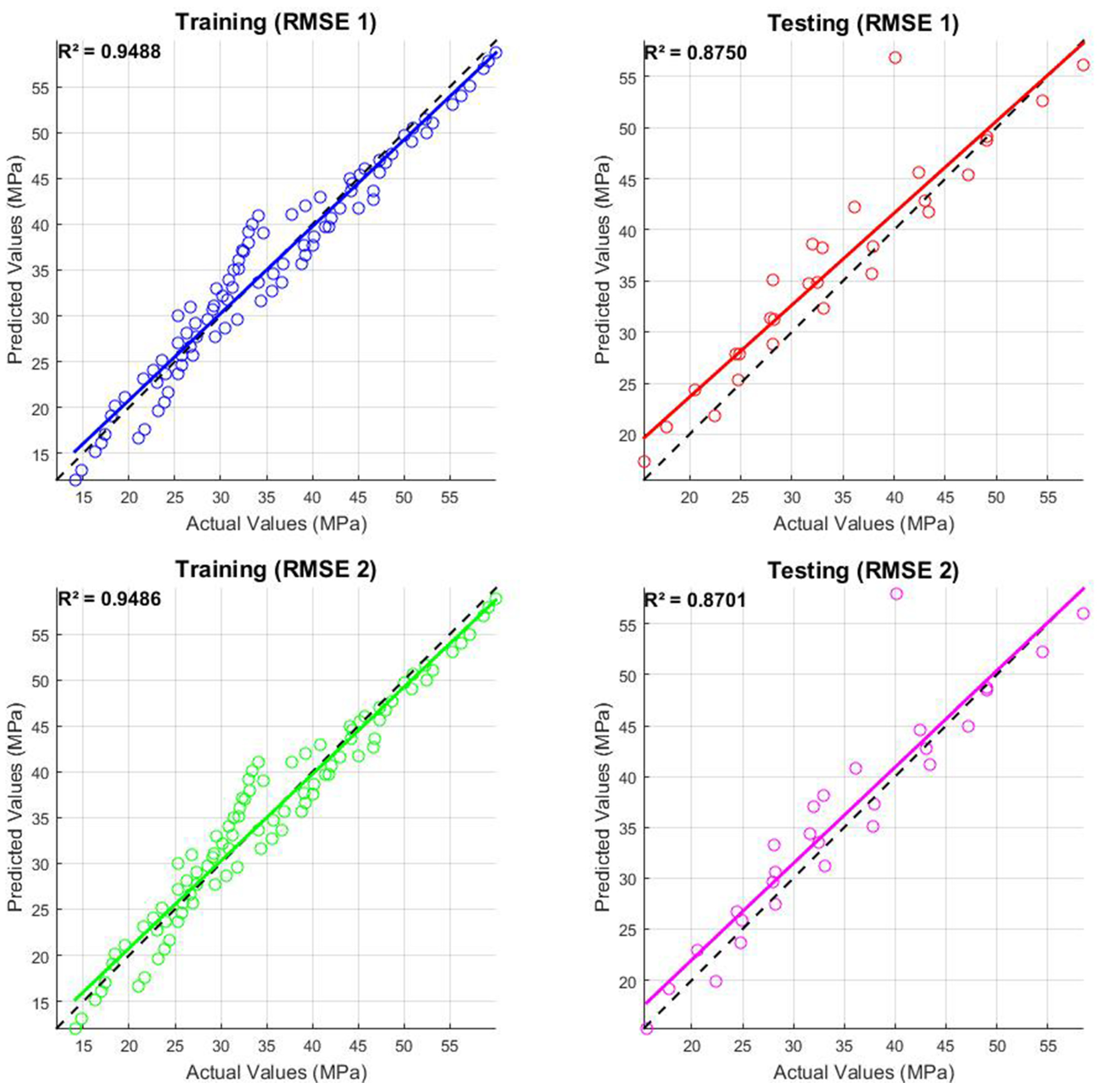
3.3.2. Root Mean Square Error (RMSE)

The RMSE is a statistical evaluation metric used to quantify the agreement between regression or prediction models and the actual values. A small RMSE value confirms that the prediction model closely approximates the actual values. The RMSE functions as the second cost function utilized for PSO in this study. As with the MAE, the model yielding the lowest minimum cost function value represents the optimal solution. The mathematical formulation of the RMSE is presented in Equation (4).
R M S E = 1 n ∑ i = 1 n ( a i − b i ) 2
In the equation above, ‘n’ corresponds to the number of observations, while ‘ai’ and ‘bi’ denote the actual value and predicted value, respectively [156,157].

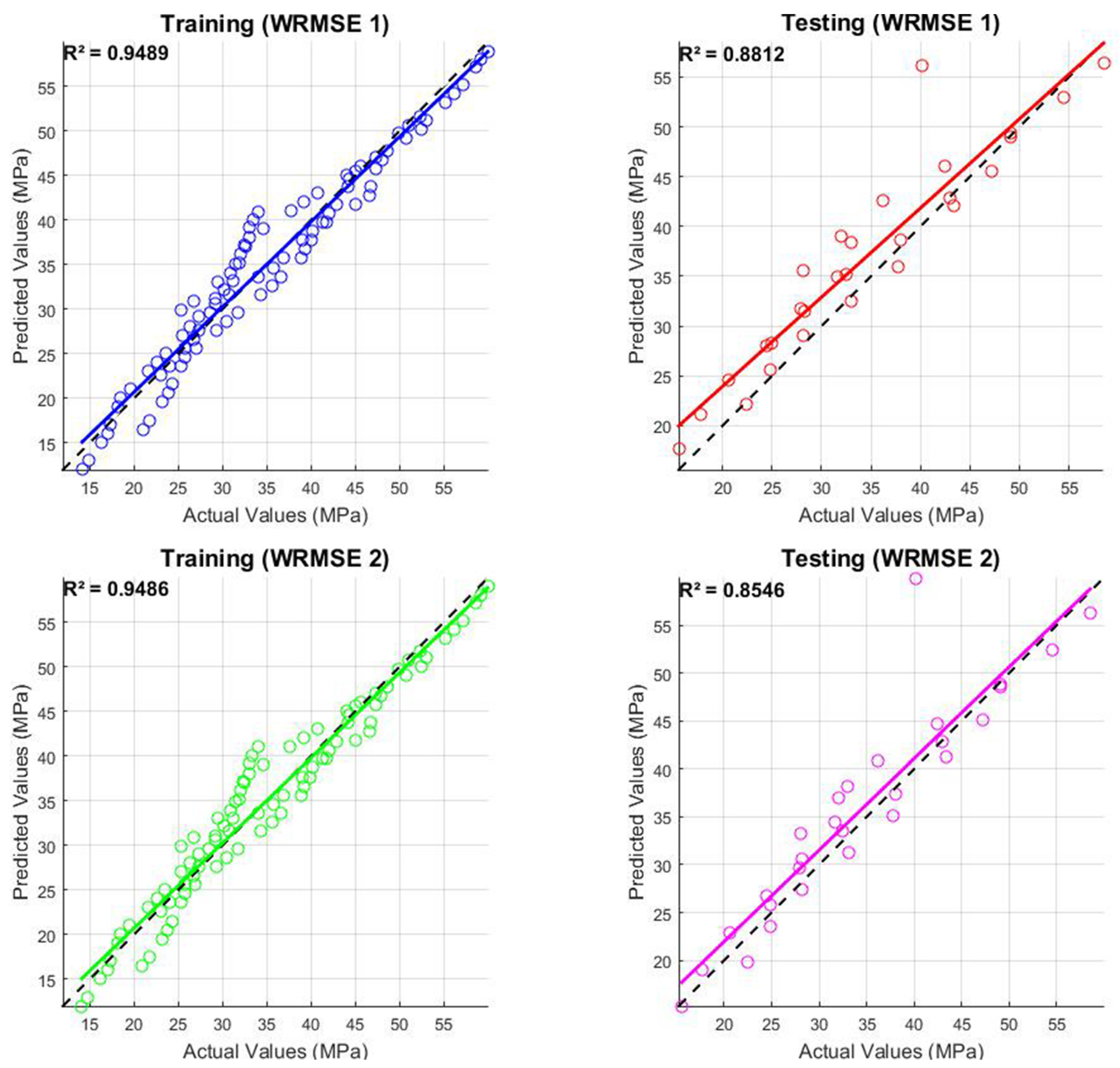
3.3.3. Weighted Root Mean Square Error (WRMSE)

Unlike the traditional RMSE, the WRMSE incorporates weighted factors for each observation, accounting for the relative importance of individual data points when determining model performance. The WRMSE equation is presented in Equation (5) below.
W R M S E = 1 n ∑ i = 1 n w i ( a i − b i ) 2
In this equation, ‘n’ represents the number of observations, ‘ai’ denotes the actual value, ‘bi’ indicates the predicted value, and ‘wi’ represents the weighted factor. The WRMSE is implemented as a cost function in this study, with the lowest minimum cost function value identifying the model that delivers optimal results.

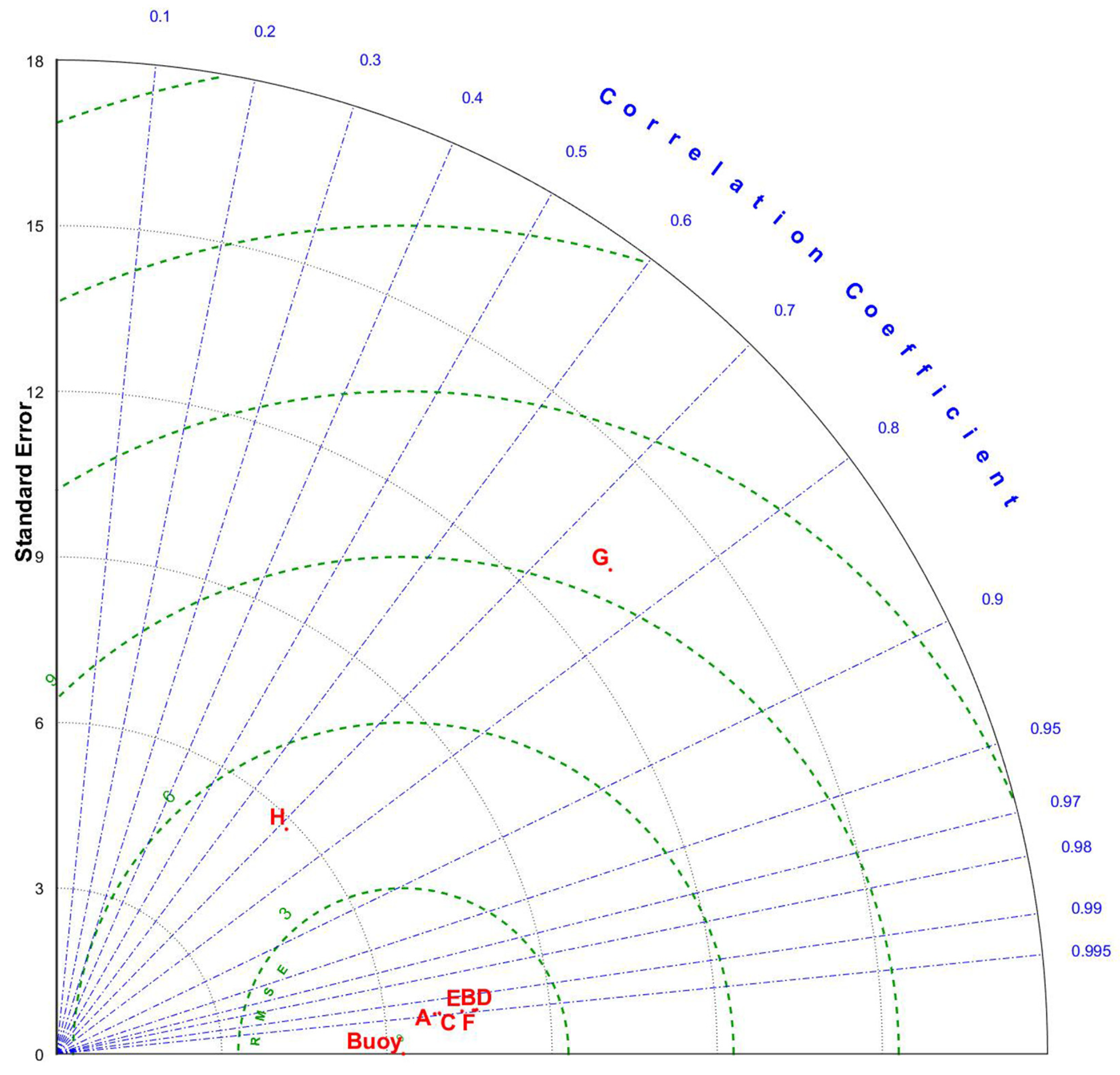
3.3.4. Taylor Diagram

The Taylor diagram is a visualization tool commonly used in engineering and physics to analyze system or process performance [158]. This diagram illustrates how one variable changes in relation to another variable [159,160,161]. Specifically, it examines the values of derivatives of a function relative to another function, mathematically expressing the derivatives of a function at a specific point [162]. The Taylor series of a function is expressed through Equation (6) below.
f x = f a + f ′ a x − a + f ″ a x − a 2 2 ! + f ‴ a x − a 3 3 !
In this equation, ‘f(a)’ represents the value of the function, ‘f′(a)’ denotes the first-order derivative of the function, ‘f″(a)’ symbolizes the second-order derivative of the function, and ‘f‴(a)’ signifies the third-order derivative of the function.

4. Findings and Discussion

In this study, a total of 120 concrete samples were produced, comprising 4 specimens from each of the 30 concrete mixtures with different dosages. After 24 h, the samples were removed from the molds and transferred to the curing pool. Subsequently, the compressive strength of each sample was tested after curing periods of 7, 28, 56, and 90 days. Data collected from these 30 concrete mixture types were used to train both the PSO and ANN models. During PSO model development, cost functions including the WRMSE, RMSE, and MAE were employed to minimize errors. Each model assumes that the input parameters contribute linearly to the output result. Additionally, models were developed both with and without coefficients. For the WRMSE, the two different models utilized are presented in Equations (7) and (8).
C S _ 1 = 0.217 T + 0.167 D + 0.792 A 1 + 0.519 A 2 − 0.839 A 3 − 0.869 P + 50
C S _ 2 = 0.217 T + 0.210 D − 2.617 A 1 − 0.092 A 2 − 4.26 A 3 + 3.027 P
Models developed using the RMSE as the optimization criterion are presented in Equations (9) and (10) as follows.
C S _ 3 = 0.215 T + 0.175 D − 0.114 A 1 + 2.252 A 2 − 5.763 A 3 − 1.858 P + 40.526
C S _ 4 = 0.215 T + 0.190 D − 0.022 A 1 − 0.505 A 2 − 4.084 A 3 + 3.935 P
Additionally, models using the MAE as the optimization criterion were developed. These models are represented by Equations (11) and (12).
C S _ 5 = 0.211 T + 0.204 D − 2.732 A 1 + 0.543 A 2 − 3.561 A 3 + 0.959 P + 14.771
C S _ 6 = 0.209 T + 0.201 D − 1.607 A 1 − 1.07 A 2 − 0.102 A 3 + 2.676 P
In these formulas, ‘CS’ denotes the compressive strength, ‘T’ represents the duration in days, ‘D’ indicates the dosage, and ‘P’ refers to the amount of superplasticizer. Furthermore, A1, A2, and A3 represent the amounts of olivine aggregate in the size ranges of 0–5 mm, 5–15 mm, and 15–25 mm, respectively.
This study also developed ANN models alongside PSO-based models, with the evaluations presented in Table 7. Among these models, the best-performing ANN model (ANN 9) was selected for comparison with the PSO models, while the worst-performing model (ANN 5) was also included in the analysis (Figure 6). The inclusion of a poor-performing example serves to clearly demonstrate that ANNs may be susceptible to overfitting, with the training process relying on memorization rather than learning, potentially resulting in diminished performance during the testing phase. Although the ANN 9 model achieved nearly perfect accuracy on the training data, it performed poorly during testing, indicating its inability to generalize effectively. This finding underscores that while ANN can achieve high accuracy by memorizing training data, it may not perform reliably on new data. Consequently, PSO models have demonstrated superior reliability in terms of generalization capacity.
Figure 6, Figure 7, Figure 8 and Figure 9 compare the prediction performances of the ANN and PSO-ANN hybrid models, each optimized according to different error criteria (MAE, RMSE, WRMSE), on both the training and test datasets. Each figure consists of two parts: part a presents the prediction accuracy distribution for the training data, while part b displays the corresponding results for the test data. In the graphs, the horizontal axis represents the experimental (actual) compressive strength (MPa), whereas the vertical axis shows the predicted values generated by the models. The circular data points indicate model outputs; the black dashed line represents the ideal 1:1 prediction line; and the solid line corresponds to the regression line derived from the model predictions.
Figure 6 presents a comparison between two ANN models (ANN 9 and ANN 5), highlighting the impact of structural differences on the prediction accuracy. Figure 7, Figure 8 and Figure 9, on the other hand, illustrate the performance of PSO-ANN hybrid models trained under different optimization objectives—namely the MAE, RMSE, and WRMSE. These error metrics were used as fitness functions within the Particle Swarm Optimization (PSO) algorithm, meaning that each model aimed to minimize the corresponding error criterion to determine the optimal network weights. Therefore, the terms MAE, RMSE, and WRMSE in the figure captions indicate both the optimization targets and the primary performance metrics used for model comparison.
When examining the coefficient of determination (R2), the ANN models exhibited relatively high accuracy on the training data but poor generalization on the test data (Figure 6), with R2 values of 0.5606 and 0.5046, respectively. In contrast, the PSO-ANN models achieved more balanced and higher predictive performance across both datasets. Notably, the PSO-ANN model optimized using the WRMSE criterion (Figure 9) yielded the highest generalization performance on the test data, with an R2 value of 0.8812. Consequently, the PSO-ANN model based on WRMSE-1 optimization stands out as the most successful model in this study.
Analysis of Figure 7, Figure 8 and Figure 9 and Table 7 clearly shows that PSO-based models deliver the most reliable results across both the training and testing phases. The WRMSE 1 and RMSE 1 models particularly stand out, demonstrating exceptional performance on the test data. All the PSO models achieved impressively high correlation coefficients during training (R2 ≈ 0.9486–0.9489), while in the testing phase, the WRMSE 1 and RMSE 1 models maintained strong performance with R2 values of 0.8812 and 0.8750, respectively, confirming their effective generalization capabilities. In order to evaluate the predictive performance and reliability of the models, as well as to identify potential overfitting issues, the percentage differences between the training and testing datasets were calculated. For Model A, the R2 value decreased by 7.13%, while the WRMSE, RMSE, and MAE increased by 156.62%, 60.21%, and 48.51%, respectively. For Model B, the R2 value decreased by 9.91%, the WRMSE increased by 64.72%, the RMSE showed no change (0%), and the MAE increased by 20.80%. In Model C, changes were observed as –7.78% in R2, 145.73% in the WRMSE, 56.76% in the RMSE, and 42.45% in the MAE. Model D showed an 8.28% decrease in R2, and increases of 86.83%, 26.68%, and 18.69% in the WRMSE, RMSE, and MAE, respectively. Model E experienced changes of –9.94% in R2, 144.46% in the WRMSE, 56.36% in the RMSE, and 37.81% in the MAE. Similarly, Model F exhibited changes of –9.54% in R2, 116.47% in the WRMSE, 47.12% in the RMSE, and 28.54% in the MAE. These results indicate that Models A through F experienced only moderate performance degradation on the test dataset, suggesting that these models possess relatively stable and reliable predictive capabilities. On the other hand, Model G showed drastic changes: a 43.91% decrease in R2 and extreme increases of 179,189.74%, 4125.54%, and 4595.20% in the WRMSE, RMSE, and MAE, respectively. Model H exhibited a similar pattern, with R2 decreasing by 48.83% and the WRMSE, RMSE, and MAE increasing by 5010.11%, 614.81%, and 818.90%, respectively. Although Models G and H achieved near-perfect performance on the training data, they suffered significant performance losses on the test data, clearly indicating severe overfitting. In conclusion, considering overall accuracy and generalization capability, Models A, B, C, and D can be regarded as highly reliable models in the literature. In contrast, ANN-based models (G and H) tend to overfit the training data unless carefully regularized, thus failing to generalize effectively to unseen data.
When using an ANN, there are numerous combinations, and the model that provides the closest result to the correct one may be overlooked by the user. However, with PSO, the entire solution space can be explored through an algorithmic approach based on particles and iterations (provided that it does not become stuck in a local minimum).
Unlike their ANN counterparts, which demonstrated significant overfitting tendencies, PSO models optimized with the WRMSE and RMSE functions produced consistent results throughout both the training and testing phases. Models without fixed numerical constraints showed marginally lower R2 values and higher error rates, making them slightly less effective for generalization purposes.
In summary, PSO-based models clearly outperformed ANN models for this particular problem. While ANN models tend to memorize training data due to their high parameter flexibility, PSO-based models achieved stable and reliable predictions through a more balanced optimization process. The WRMSE 1 and RMSE 1 models, in particular, exhibited superior testing performance, maximizing generalization success. Given the relatively close performance metrics between these models, further evaluation using the Taylor diagrams presented in Figure 10 and Figure 11 is warranted.
Figure 10 and Figure 11 present the Taylor diagrams created to evaluate the prediction performance of the ANN and PSO-ANN models, respectively, on the training and test datasets in a multidimensional manner. These diagrams visually compare each model’s correlation coefficient, standard error, and normalized standard deviation against the reference dataset (Buoy), providing a clear means for analyzing the models’ accuracy and consistency. Figure 10 highlights the learning success of the models on the training data and their adaptation during the optimization process, while Figure 11 assesses the generalization capability of the models on previously unseen independent test data. The letter codes (A–H) in the Taylor diagrams represent the configuration of each model, and these definitions are detailed in Table 7.
During the training phase, the PSO-ANN models with a fixed number of particles (especially A, C, and E) achieved successful results with high correlation coefficients (>0.99) and low error levels. In contrast, the ANN-based G and H models experienced a significant performance drop on the test data (correlation ~0.6) and produced high error values. Models optimized with PSO demonstrated noticeably higher generalization performance in the test phase. Particularly, the models based on the WRMSE (A), RMSE (C), and MAE (E) with a fixed number of particles provided more stable and generalizable results compared to their flexible particle counterparts (B, D, F). Furthermore, considering the impact of the error function, models optimized with the WRMSE (A and B) exhibited better correlation and lower error values than those optimized with the RMSE (C, D) and MAE (E, F). Overall, Model A, optimized with fixed particles and the WRMSE, emerged as the most successful model, while the ANN-based Model G exhibited the weakest performance. In conclusion, it is evident that the models optimized with PSO demonstrated superior performance in both the learning and generalization phases. Based on these findings, the models optimized using the WRMSE function outperformed those using the other error functions by yielding lower error rates and higher correlation coefficients. This highlights the critical role of appropriate parameter selection and optimization strategies in determining model performance. Model A, identified as the most successful configuration, exhibited high performance on the test dataset, ensuring consistency across both the training and generalization stages. In contrast, the standalone ANN models suffered significant performance degradation on the test data, emphasizing the role of PSO in enhancing model robustness. These results indicate that PSO-based optimization, particularly when supported by fixed parameters, is a powerful and reliable approach for future similar studies.

5. Conclusions

In the field of concrete compressive strength estimation, researchers have conducted studies to address the time and cost challenges associated with traditional testing methods. Similarly, testing the compressive strength of concrete across various mixing ratios at different time intervals is both challenging and time-intensive. This study therefore investigated how olivine aggregate affects concrete performance and developed predictive models for the compressive strength of concrete containing olivine aggregate. For this research, 120 samples were produced and tested at 7, 28, 56, and 90 days, with 30 samples at various dosage levels. Using this dataset of 120 measurements, models were developed using both PSO and ANN methods to determine the compressive strength of olivine aggregate concrete at different dosages. In the ANN model’s development, the number of neurons was varied, while in the PSO models, different cost functions were explored. The cost functions implemented in this study aimed to minimize the WRMSE, RMSE, and MAE. For each constraint function, two models were developed—one with fixed coefficients and one without. The performance of these models was evaluated by comparing their R2 values relative to the WRMSE, RMSE, and MAE metrics. Additionally, the models were compared using Taylor diagrams to provide a comprehensive performance assessment.
In order to provide a robust and flexible modeling framework, the PSO algorithm was used to optimize the weight and bias parameters of the ANN models through iterative, population-based search processes. By incorporating various error-based objective functions (WRMSE, RMSE, and MAE), the PSO-enhanced models were able to explore multiple solution landscapes, balancing prediction accuracy and generalization performance. This optimization strategy allowed the study to rigorously evaluate how different learning constraints and control parameters affect the overall model stability and predictive strength.
Analysis of the results reveals that the WRMSE 1 model (with a fixed term) delivered the strongest performance, achieving the highest R2 value (approximately 0.88) during the testing phase and demonstrating superior generalization capabilities. While the RMSE- and MAE-based models also performed well, those incorporating fixed terms consistently outperformed their non-fixed counterparts in terms of generalization ability. In contrast, the ANN models showed nearly perfect fit during training (R2 ≈ 0.99) but suffered dramatic performance declines during testing (R2 ≈ 0.50–0.56), exhibiting classic overfitting behavior and failing to adapt to new data. The ANN 5 model performed particularly poorly in testing, ranking it as the least effective model overall. Ultimately, PSO-based models substantially outperformed ANN approaches across key metrics, with the fixed-term WRMSE model providing the most reliable predictions and the best generalization performance.
This study contributes to the expanding body of research on alternative aggregate use in concrete by demonstrating the technical feasibility and sustainability potential of olivine as a substitute material. The developed AI model enables efficient estimation of compressive strength based on cement dosage and olivine aggregate particle size, addressing the challenges associated with time-consuming and labor-intensive experimental procedures.
The integration of PSO with ANN models resulted in hybrid frameworks that improved the prediction accuracy and generalization performance, particularly when guided by different error metrics such as the WRMSE, RMSE, and MAE. The PSO-enhanced models consistently outperformed standalone ANN models in terms of both interpretability and reliability.
While this study reveals that ANN models alone exhibited reduced performance when exposed to unseen test data, it does not intend to generalize this outcome. Previous studies have reported successful applications of ANN models under varying datasets, network configurations, and training conditions [60,61,62]. Therefore, the findings are specific to the scope and dataset of this research.
In addition to its modeling contributions, this study reinforces the potential of olivine aggregate as a technically viable material, supported by the existing literature on its high temperature resistance and CO2 sequestration capacity via MgO content [9,10,11,140,141]. Overall, this research lays the groundwork for future investigations into olivine-based concrete and highlights the effectiveness of hybrid AI methodologies in advancing sustainable construction materials.

Funding

This research received no external funding.

Data Availability Statement

All the data, models, and code used during the study are available in the submitted manuscript.

Conflicts of Interest

The author declares that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Barbhuiya, S.; Kanavaris, F.; Das, B.B.; Idrees, M. Decarbonising cement and concrete production: Strategies, challenges and pathways for sustainable development. J. Build. Eng. 2024, 86, 108861. [Google Scholar] [CrossRef]
  2. Nehdi, M.L.; Marani, A.; Zhang, L. Is net-zero feasible: Systematic review of cement and concrete decarbonization technologies. Renew. Sustain. Energy Rev. 2024, 191, 114169. [Google Scholar] [CrossRef]
  3. Winnefeld, F.; Leemann, A.; German, A.; Lothenbach, B. CO2 storage in cement and concrete by mineral carbonation. Curr. Opin. Green Sustain. Chem. 2022, 38, 100672. [Google Scholar] [CrossRef]
  4. Oruc, S.; Dikbas, H.A.; Gumus, B.; Yucel, I. The Impact of Climate Change on Construction Activity Performance. Buildings 2024, 14, 372. [Google Scholar] [CrossRef]
  5. Thomas, C.; Setién, J.; Polanco, J.A. Structural recycled aggregate concrete made with precast wastes. Constr. Build. Mater. 2016, 114, 536–546. [Google Scholar] [CrossRef]
  6. Atmiş, E.; Yıldız, D.; Erdönmez, C. A different dimension in deforestation and forest degradation: Non-forestry uses of forests in Turkey. Land Use Policy 2024, 139, 107086. [Google Scholar] [CrossRef]
  7. Solís-Carcaño, R.; Moreno, E.I. Evaluation of concrete made with crushed limestone aggregate based on ultrasonic pulse velocity. Constr. Build. Mater. 2008, 22, 1225–1231. [Google Scholar] [CrossRef]
  8. Ren, P.; Ling, T.C.; Mo, K.H. Recent advances in artificial aggregate production. J. Clean. Prod. 2021, 291, 125215. [Google Scholar] [CrossRef]
  9. Westgate, P.; Ball, R.J.; Paine, K. Olivine as a reactive aggregate in lime mortars. Constr. Build. Mater. 2019, 195, 115–126. [Google Scholar] [CrossRef]
  10. Scott, A.; Oze, C.; Shah, V.; Yang, N.; Shanks, B.; Cheeseman, C.; Marshall, A.; Watson, M. Transformation of abundant magnesium silicate minerals for enhanced CO2 sequestration. Commun. Earth Environ. 2021, 2, 25. [Google Scholar] [CrossRef]
  11. Saridhe, S.P.; Hareesh, M.; Priya, T.S.; Selvaraj, T. Role of olivine aggregate in lime and cement mortars for the sequestration of atmospheric CO2. Mater. Tehnol. 2023, 57, 135–140. [Google Scholar] [CrossRef]
  12. Hamada, H.M.; Al-Attar, A.; Abed, F.; Beddu, S.; Humada, A.M.; Majdi, A.; Yousif, S.T.; Thomas, B.S. Enhancing sustainability in concrete construction: A comprehensive review of plastic waste as an aggregate material. Sustain. Mater. Technol. 2024, 40, e00877. [Google Scholar] [CrossRef]
  13. Gönen, T.; Cemalgil, S. Using the Taguchi Method to Optimize the Compressive Strength of Concrete in Different Aggregates Typology. El-Cezeri J. Sci. Eng. 2023, 10, 90–98. [Google Scholar] [CrossRef]
  14. Xing, W.; Tam, V.W.; Le, K.N.; Hao, J.L.; Wang, J. Life cycle assessment of recycled aggregate concrete on its environmental impacts: A critical review. Constr. Build. Mater. 2022, 317, 125950. [Google Scholar] [CrossRef]
  15. Wang, B.; Yan, L.; Fu, Q.; Kasal, B. A Comprehensive Review on Recycled Aggregate and Recycled Aggregate Concrete. Resour. Conserv. Recycl. 2021, 171, 105565. [Google Scholar] [CrossRef]
  16. Kirthika, S.K.; Singh, S.K.; Chourasia, A. Alternative fine aggregates in production of sustainable concrete—A review. J. Clean. Prod. 2020, 268, 122089. [Google Scholar] [CrossRef]
  17. Fan, Z.; Lin, J.; Chen, Z.; Liu, P.; Wang, D.; Oeser, M. Multiscale understanding of interfacial behavior between bitumen and aggregate: From the aggregate mineralogical genome aspect. Constr. Build. Mater. 2021, 271, 121607. [Google Scholar] [CrossRef]
  18. Özel, C.; Nadi Kaplan, A. Kendiliğinden Yerleşen Beton Özellikleri Üzerinde Agrega Özelliklerinin Etkisi. Int. J. Sustain. Eng. Technol. 2017, 1, 1–6. [Google Scholar]
  19. Solak, A. Classification of rocks in Manisa-Gürle village region and investigation of their usability as concrete aggregate. Niğde Ömer Halisdemir Üniversitesi Mühendislik Bilim. Derg. 2022, 11, 974–981. [Google Scholar] [CrossRef]
  20. Emiroǧlu, M.; Beycioǧlu, A.; Yildiz, S. ANFIS and statistical based approach to prediction the peak pressure load of concrete pipes including glass fiber. Expert Syst. Appl. 2012, 39, 2877–2883. [Google Scholar] [CrossRef]
  21. Jiang, G.; Keller, J.; Bond, P.L.; Yuan, Z. Predicting concrete corrosion of sewers using artificial neural network. Water Res. 2016, 92, 52–60. [Google Scholar] [CrossRef] [PubMed]
  22. Wen, Z.; Zhou, R.; Su, H. MR and stacked GRUs neural network combined model and its application for deformation prediction of concrete dam. Expert Syst. Appl. 2022, 201, 117272. [Google Scholar] [CrossRef]
  23. Yilmaz, I.; Kaynar, O. Multiple regression, ANN (RBF, MLP) and ANFIS models for prediction of swell potential of clayey soils. Expert Syst. Appl. 2011, 38, 5958–5966. [Google Scholar] [CrossRef]
  24. Obianyo, I.I.; Anosike-Francis, E.N.; Ihekweme, G.O.; Geng, Y.; Jin, R.; Onwualu, A.P.; Soboyejo, A.B.O. Multivariate regression models for predicting the compressive strength of bone ash stabilized lateritic soil for sustainable building. Constr. Build. Mater. 2020, 263, 120677. [Google Scholar] [CrossRef]
  25. Chithra, S.; Kumar, S.R.R.S.; Chinnaraju, K.; Alfin Ashmita, F. A comparative study on the compressive strength prediction models for High Performance Concrete containing nano silica and copper slag using regression analysis and Artificial Neural Networks. Constr. Build. Mater. 2016, 114, 528–535. [Google Scholar] [CrossRef]
  26. Chakali, Y.; Sadok, A.H.; Tahlaiti, M.; Nacer, T. A PSO-ANN Intelligent Hybrid Model to Predict the Compressive Strength of Limestone Fillers Roller Compacted Concrete (RCC) to Build Dams. KSCE J. Civ. Eng. 2021, 25, 3008–3018. [Google Scholar] [CrossRef]
  27. Li, J.; Yan, G.; Abbud, L.H.; Alkhalifah, T.; Alturise, F.; Khadimallah, M.A.; Marzouki, R. Predicting the shear strength of concrete beam through ANFIS-GA–PSO hybrid modeling. Adv. Eng. Softw. 2023, 181, 103475. [Google Scholar] [CrossRef]
  28. Kaplanvural, İ. Volumetric water content estimation of concrete by particle swarm optimization of GPR data. Constr. Build. Mater. 2023, 375, 130995. [Google Scholar] [CrossRef]
  29. Jiang, W.; Xie, Y.; Li, W.; Wu, J.; Long, G. Prediction of the splitting tensile strength of the bonding interface by combining the support vector machine with the particle swarm optimization algorithm. Eng. Struct. 2021, 230, 111696. [Google Scholar] [CrossRef]
  30. Qi, C.; Fourie, A.; Chen, Q. Neural network and particle swarm optimization for predicting the unconfined compressive strength of cemented paste backfill. Constr. Build. Mater. 2018, 159, 473–478. [Google Scholar] [CrossRef]
  31. Hanoon, A.N.; Jaafar, M.S.; Hejazi, F.; Aziz, F.N.A.A. Strut-and-tie model for externally bonded CFRP-strengthened reinforced concrete deep beams based on particle swarm optimization algorithm: CFRP debonding and rupture. Constr. Build. Mater. 2017, 147, 428–447. [Google Scholar] [CrossRef]
  32. Nazari, A.; Sanjayan, J.G. Modelling of compressive strength of geopolymer paste, mortar and concrete by optimized support vector machine. Ceram. Int. 2015, 41, 12164–12177. [Google Scholar] [CrossRef]
  33. Uzundurukan, S.; Saplıoğlu, K. Konsol İstinat Duvarlarında Yükseklik Maliyet İlişkisinin Parçacık Sürü Algoritması İle İncelenmesi. Düzce Üniversitesi Bilim. Teknol. Derg. 2020, 8, 2544–2554. [Google Scholar]
  34. Safarzadegan Gilan, S.; Bahrami Jovein, H.; Ramezanianpour, A.A. Hybrid support vector regression–Particle swarm optimization for prediction of compressive strength and RCPT of concretes containing metakaolin. Constr. Build. Mater. 2012, 34, 321–329. [Google Scholar] [CrossRef]
  35. Mashhadban, H.; Kutanaei, S.S.; Sayarinejad, M.A. Prediction and modeling of mechanical properties in fiber reinforced self-compacting concrete using particle swarm optimization algorithm and artificial neural network. Constr. Build. Mater. 2016, 119, 277–287. [Google Scholar] [CrossRef]
  36. Altunci, Y.T.; Özkan, Ş. Design Optimization and Statistical Modeling of Compressive Strtength of Cement Mortars Containing Recycled Waste Brick Dust Using Response Surface Methodology. Int. J. Sustain. Eng. Technol. 2023, 2, 88–97. [Google Scholar]
  37. Hammoudi, A.; Moussaceb, K.; Belebchouche, C.; Dahmoune, F. Comparison of artificial neural network (ANN) and response surface methodology (RSM) prediction in compressive strength of recycled concrete aggregates. Constr. Build. Mater. 2019, 209, 425–436. [Google Scholar] [CrossRef]
  38. Ray, S.; Haque, M.; Ahmed, T.; Nahin, T.T. Comparison of artificial neural network (ANN) and response surface methodology (RSM) in predicting the compressive and splitting tensile strength of concrete prepared with glass waste and tin (Sn) can fiber. J. King Saud Univ.-Eng. Sci. 2023, 35, 185–199. [Google Scholar] [CrossRef]
  39. Kursuncu, B.; Gencel, O.; Bayraktar, O.Y.; Shi, J.; Nematzadeh, M.; Kaplan, G. Optimization of foam concrete characteristics using response surface methodology and artificial neural networks. Constr. Build. Mater. 2022, 337, 127575. [Google Scholar] [CrossRef]
  40. Golafshani, E.M.; Behnood, A.; Arashpour, M. Predicting the compressive strength of normal and High-Performance Concretes using ANN and ANFIS hybridized with Grey Wolf Optimizer. Constr. Build. Mater. 2020, 232, 117266. [Google Scholar] [CrossRef]
  41. Ahmadi-Nedushan, B. Prediction of elastic modulus of normal and high strength concrete using ANFIS and optimal nonlinear regression models. Constr. Build. Mater. 2012, 36, 665–673. [Google Scholar] [CrossRef]
  42. Kumar, A.; Arora, H.C.; Kumar, K.; Garg, H. Performance prognosis of FRCM-to-concrete bond strength using ANFIS-based fuzzy algorithm. Expert Syst. Appl. 2023, 216, 119497. [Google Scholar] [CrossRef]
  43. Madandoust, R.; Bungey, J.H.; Ghavidel, R. Prediction of the concrete compressive strength by means of core testing using GMDH-type neural network and ANFIS models. Comput. Mater. Sci. 2012, 51, 261–272. [Google Scholar] [CrossRef]
  44. Sobhani, J.; Najimi, M.; Pourkhorshidi, A.R.; Parhizkar, T. Prediction of the compressive strength of no-slump concrete: A comparative study of regression, neural network and ANFIS models. Constr. Build. Mater. 2010, 24, 709–718. [Google Scholar] [CrossRef]
  45. Vakhshouri, B.; Nejadi, S. Prediction of compressive strength of self-compacting concrete by ANFIS models. Neurocomputing 2018, 280, 13–22. [Google Scholar] [CrossRef]
  46. Pei, Z.; Wei, Y. Prediction of the bond strength of FRP-to-concrete under direct tension by ACO-based ANFIS approach. Compos. Struct. 2022, 282, 115070. [Google Scholar] [CrossRef]
  47. Yuan, Z.; Wang, L.N.; Ji, X. Prediction of concrete compressive strength: Research on hybrid models genetic based algorithms and ANFIS. Adv. Eng. Softw. 2014, 67, 156–163. [Google Scholar] [CrossRef]
  48. Sadrmomtazi, A.; Sobhani, J.; Mirgozar, M.A. Modeling compressive strength of EPS lightweight concrete using regression, neural network and ANFIS. Constr. Build. Mater. 2013, 42, 205–216. [Google Scholar] [CrossRef]
  49. Akkurt, I.; Başyigit, C.; Kilincarslan, S.; Beycioglu, A. Prediction of photon attenuation coefficients of heavy concrete by fuzzy logic. J. Frankl. Inst. 2010, 347, 1589–1597. [Google Scholar] [CrossRef]
  50. Cao, Y.; Zandi, Y.; Rahimi, A.; Petković, D.; Denić, N.; Stojanović, J.; Spasić, B.; Vujović, V.; Amine Khadimallah, M.; Assilzadeh, H. Evaluation and monitoring of impact resistance of fiber reinforced concrete by adaptive neuro fuzzy algorithm. Structures 2021, 34, 3750–3756. [Google Scholar] [CrossRef]
  51. Güler, K.; Demir, F.; Pakdamar, F. Stress–strain modelling of high strength concrete by fuzzy logic approach. Constr. Build. Mater. 2012, 37, 680–684. [Google Scholar] [CrossRef]
  52. Golafshani, E.M.; Rahai, A.; Sebt, M.H.; Akbarpour, H. Prediction of bond strength of spliced steel bars in concrete using artificial neural network and fuzzy logic. Constr. Build. Mater. 2012, 36, 411–418. [Google Scholar] [CrossRef]
  53. Moon, J.; Kim, J.J.; Lee, T.H.; Lee, H.E. Prediction of axial load capacity of stub circular concrete-filled steel tube using fuzzy logic. J. Constr. Steel Res. 2014, 101, 184–191. [Google Scholar] [CrossRef]
  54. Saridemir, M.; Topçu, I.B.; Özcan, F.; Severcan, M.H. Prediction of long-term effects of GGBFS on compressive strength of concrete by artificial neural networks and fuzzy logic. Constr. Build. Mater. 2009, 23, 1279–1286. [Google Scholar] [CrossRef]
  55. Topçu, I.B.; Saridemir, M. Prediction of compressive strength of concrete containing fly ash using artificial neural networks and fuzzy logic. Comput. Mater. Sci. 2008, 41, 305–311. [Google Scholar] [CrossRef]
  56. Topçu, I.B.; Saridemir, M. Prediction of rubberized concrete properties using artificial neural network and fuzzy logic. Constr. Build. Mater. 2008, 22, 532–540. [Google Scholar] [CrossRef]
  57. Tanyildizi, H. Fuzzy logic model for prediction of mechanical properties of lightweight concrete exposed to high temperature. Mater. Des. 2009, 30, 2205–2210. [Google Scholar] [CrossRef]
  58. Özcan, F.; Atiş, C.D.; Karahan, O.; Uncuoǧlu, E.; Tanyildizi, H. Comparison of artificial neural network and fuzzy logic models for prediction of long-term compressive strength of silica fume concrete. Adv. Eng. Softw. 2009, 40, 856–863. [Google Scholar] [CrossRef]
  59. Jong, B.; Kim, I.; Kim, D.K. Application of neural networks for estimation of concrete strength. KSCE J. Civ. Eng. 2002, 6, 429–438. [Google Scholar]
  60. Asteris, P.G.; Skentou, A.D.; Bardhan, A.; Samui, P.; Pilakoutas, K. Predicting concrete compressive strength using hybrid ensembling of surrogate machine learning models. Cem. Concr. Res. 2021, 145, 106449. [Google Scholar] [CrossRef]
  61. Basaran, B.; Kalkan, I.; Bergil, E.; Erdal, E. Estimation of the FRP-concrete bond strength with code formulations and machine learning algorithms. Compos. Struct. 2021, 268, 113972. [Google Scholar] [CrossRef]
  62. Congro, M.; de Alencar Monteiro, V.M.; Brandão, A.L.T.; Santos, B.F.D.; Roehl, D.; Silva, F. de A. Prediction of the residual flexural strength of fiber reinforced concrete using artificial neural networks. Constr. Build. Mater. 2021, 303, 124502. [Google Scholar] [CrossRef]
  63. Felix, E.F.; Carrazedo, R.; Possan, E. Carbonation model for fly ash concrete based on artificial neural network: Development and parametric analysis. Constr. Build. Mater. 2021, 266, 121050. [Google Scholar] [CrossRef]
  64. Ling, H.; Qian, C.; Kang, W.; Liang, C.; Chen, H. Combination of Support Vector Machine and K-Fold cross validation to predict compressive strength of concrete in marine environment. Constr. Build. Mater. 2019, 206, 355–363. [Google Scholar] [CrossRef]
  65. Liu, Q.; Iqbal, M.F.; Yang, J.; Lu, X.; Zhang, P.; Rauf, M. Prediction of chloride diffusivity in concrete using artificial neural network: Modelling and performance evaluation. Constr. Build. Mater. 2021, 268, 121082. [Google Scholar] [CrossRef]
  66. Moradi, M.J.; Daneshvar, K.; Ghazi-nader, D.; Hajiloo, H. The prediction of fire performance of concrete-filled steel tubes (CFST) using artificial neural network. Thin-Walled Struct. 2021, 161, 107499. [Google Scholar] [CrossRef]
  67. Ramkumar, K.B.; Kannan Rajkumar, P.R.; Noor Ahmmad, S.; Jegan, M. A Review on Performance of Self-Compacting Concrete–Use of Mineral Admixtures and Steel Fibres with Artificial Neural Network Application. Constr. Build. Mater. 2020, 261, 120215. [Google Scholar] [CrossRef]
  68. Shahmansouri, A.A.; Yazdani, M.; Ghanbari, S.; Akbarzadeh Bengar, H.; Jafari, A.; Farrokh Ghatte, H. Artificial neural network model to predict the compressive strength of eco-friendly geopolymer concrete incorporating silica fume and natural zeolite. J. Clean. Prod. 2021, 279, 123697. [Google Scholar] [CrossRef]
  69. Xi, X.; Yin, Z.; Yang, S.; Li, C.Q. Using artificial neural network to predict the fracture properties of the interfacial transition zone of concrete at the meso-scale. Eng. Fract. Mech. 2021, 242, 107488. [Google Scholar] [CrossRef]
  70. Xu, J.; Chen, Y.; Xie, T.; Zhao, X.; Xiong, B.; Chen, Z. Prediction of triaxial behavior of recycled aggregate concrete using multivariable regression and artificial neural network techniques. Constr. Build. Mater. 2019, 226, 534–554. [Google Scholar] [CrossRef]
  71. Xu, J.; Zhao, X.; Yu, Y.; Xie, T.; Yang, G.; Xue, J. Parametric sensitivity analysis and modelling of mechanical properties of normal- and high-strength recycled aggregate concrete using grey theory, multiple nonlinear regression and artificial neural networks. Constr. Build. Mater. 2019, 211, 479–491. [Google Scholar] [CrossRef]
  72. Zhao, Y.; Hu, H.; Song, C.; Wang, Z. Predicting compressive strength of manufactured-sand concrete using conventional and metaheuristic-tuned artificial neural network. Measurement 2022, 194, 110993. [Google Scholar] [CrossRef]
  73. Nazımı, N.; Saplioglu, K. Monthly Streamflow Prediction Using ANN, KNN and ANFIS models: Example of Gediz River Basin. Tek. Bilim. Derg. 2023, 13, 42–49. [Google Scholar] [CrossRef]
  74. Acar, R.; Saplıoğlu, K. Etkili Girdi Parametrelerinin Çoklu Regresyon ile Belirlendiği Su Sertliğinin ANFIS Yöntemi ile Tahmin Edilmesi. Afyon Kocatepe Üniversitesi Fen Mühendis. Bilim. Derg. 2022, 22, 1413–1424. [Google Scholar] [CrossRef]
  75. Getahun, M.A.; Shitote, S.M.; Abiero Gariy, Z.C. Artificial neural network based modelling approach for strength prediction of concrete incorporating agricultural and construction wastes. Constr. Build. Mater. 2018, 190, 517–525. [Google Scholar] [CrossRef]
  76. Dantas, A.T.A.; Batista Leite, M.; De Jesus Nagahama, K. Prediction of compressive strength of concrete containing construction and demolition waste using artificial neural networks. Constr. Build. Mater. 2013, 38, 717–722. [Google Scholar] [CrossRef]
  77. Tam, V.W.Y.; Butera, A.; Le, K.N.; Silva, L.C.F.D.; Evangelista, A.C.J. A prediction model for compressive strength of CO2 concrete using regression analysis and artificial neural networks. Constr. Build. Mater. 2022, 324, 126689. [Google Scholar] [CrossRef]
  78. Le, B.A.; Vu, V.H.; Seo, S.Y.; Tran, B.V.; Nguyen-Sy, T.; Le, M.C.; Vu, T.S. Predicting the Compressive Strength and the Effective Porosity of Pervious Concrete Using Machine Learning Methods. KSCE J. Civ. Eng. 2022, 26, 4664–4679. [Google Scholar] [CrossRef]
  79. Aiyer, B.G.; Kim, D.; Karingattikkal, N.; Samui, P.; Rao, P.R. Prediction of compressive strength of self-compacting concrete using least square support vector machine and relevance vector machine. KSCE J. Civ. Eng. 2014, 18, 1753–1758. [Google Scholar] [CrossRef]
  80. Fan, Z.; Chiong, R.; Hu, Z.; Lin, Y. A fuzzy weighted relative error support vector machine for reverse prediction of concrete components. Comput. Struct. 2020, 230, 106171. [Google Scholar] [CrossRef]
  81. Jueyendah, S.; Lezgy-Nazargah, M.; Eskandari-Naddaf, H.; Emamian, S.A. Predicting the mechanical properties of cement mortar using the support vector machine approach. Constr. Build. Mater. 2021, 291, 123396. [Google Scholar] [CrossRef]
  82. Luo, H.; Paal, S.G. Metaheuristic least squares support vector machine-based lateral strength modelling of reinforced concrete columns subjected to earthquake loads. Structures 2021, 33, 748–758. [Google Scholar] [CrossRef]
  83. Wen, L.; Li, Y.; Zhao, W.; Cao, W.; Zhang, H. Predicting the deformation behaviour of concrete face rockfill dams by combining support vector machine and AdaBoost ensemble algorithm. Comput. Geotech. 2023, 161, 105611. [Google Scholar] [CrossRef]
  84. Zhou, Y.; Zhang, Y.; Pang, R.; Xu, B. Seismic fragility analysis of high concrete faced rockfill dams based on plastic failure with support vector machine. Soil Dyn. Earthq. Eng. 2021, 144, 106587. [Google Scholar] [CrossRef]
  85. Kaloop, M.R.; Kumar, D.; Samui, P.; Hu, J.W.; Kim, D. Compressive strength prediction of high-performance concrete using gradient tree boosting machine. Constr. Build. Mater. 2020, 264, 120198. [Google Scholar] [CrossRef]
  86. Fu, W.; Sun, B.; Wan, H.P.; Luo, Y.; Zhao, W. A Gaussian processes-based approach for damage detection of concrete structure using temperature-induced strain. Eng. Struct. 2022, 268, 114740. [Google Scholar] [CrossRef]
  87. Pereira Dias, P.; Bhagya Jayasinghe, L.; Waldmann, D. Machine learning in mix design of Miscanthus lightweight concrete. Constr. Build. Mater. 2021, 302, 124191. [Google Scholar] [CrossRef]
  88. Saleh, E.; Tarawneh, A.; Naser, M.Z.; Abedi, M.; Almasabha, G. You only design once (YODO): Gaussian Process-Batch Bayesian optimization framework for mixture design of ultra high performance concrete. Constr. Build. Mater. 2022, 330, 127270. [Google Scholar] [CrossRef]
  89. Ziyad Sami, B.H.; Ziyad Sami, B.F.; Kumar, P.; Ahmed, A.N.; Amieghemen, G.E.; Sherif, M.M.; El-Shafie, A. Feasibility analysis for predicting the compressive and tensile strength of concrete using machine learning algorithms. Case Stud. Constr. Mater. 2023, 18, e01893. [Google Scholar] [CrossRef]
  90. Ghanbari, S.; Shahmansouri, A.A.; Akbarzadeh Bengar, H.; Jafari, A. Compressive strength prediction of high-strength oil palm shell lightweight aggregate concrete using machine learning methods. Environ. Sci. Pollut. Res. 2023, 30, 1096–1115. [Google Scholar] [CrossRef]
  91. Xi, B.; Li, E.; Fissha, Y.; Zhou, J.; Segarra, P. LGBM-based modeling scenarios to compressive strength of recycled aggregate concrete with SHAP analysis. Mech. Adv. Mater. Struct. 2023, 31, 5999–6014. [Google Scholar] [CrossRef]
  92. Al-Taai, S.R.; Azize, N.M.; Thoeny, Z.A.; Imran, H.; Bernardo, L.F.A.; Al-Khafaji, Z. XGBoost Prediction Model Optimized with Bayesian for the Compressive Strength of Eco-Friendly Concrete Containing Ground Granulated Blast Furnace Slag and Recycled Coarse Aggregate. Appl. Sci. 2023, 13, 8889. [Google Scholar] [CrossRef]
  93. Van Dao, D.; Trinh, S.H.; Ly, H.B.; Pham, B.T. Prediction of compressive strength of geopolymer concrete using entirely steel slag aggregates: Novel hybrid artificial intelligence approaches. Appl. Sci. 2019, 9, 1113. [Google Scholar] [CrossRef]
  94. Migallón, V.; Navarro-González, F.; Penadés, J.; Villacampa, Y. Parallel approach of a Galerkin-based methodology for predicting the compressive strength of the lightweight aggregate concrete. Constr. Build. Mater. 2019, 219, 56–68. [Google Scholar] [CrossRef]
  95. Salimbahrami, S.R.; Shakeri, R. Experimental investigation and comparative machine-learning prediction of compressive strength of recycled aggregate concrete. Soft Comput. 2021, 25, 919–932. [Google Scholar] [CrossRef]
  96. Lin, C.; Sun, Y.; Jiao, W.; Zheng, J.; Li, Z.; Zhang, S. Prediction of Compressive Strength and Elastic Modulus for Recycled Aggregate Concrete Based on AutoGluon. Sustainability 2023, 15, 12345. [Google Scholar] [CrossRef]
  97. Zhu, W.; Huang, L.; Mao, L.; Esmaeili-Falak, M. Predicting the uniaxial compressive strength of oil palm shell lightweight aggregate concrete using artificial intelligence-based algorithms. Struct. Concr. 2022, 23, 3631–3650. [Google Scholar] [CrossRef]
  98. García, J.A.; Varón, F.A.P. Neural network-based model to predict compressive strength of concrete incorporating supplementary cementitious materials and recycled aggregates. Rev. Mater. 2022, 27, e13218. [Google Scholar] [CrossRef]
  99. Suescum-Morales, D.; Salas-Morera, L.; Jiménez, J.R.; García-Hernández, L. A novel artificial neural network to predict compressive strength of recycled aggregate concrete. Appl. Sci. 2021, 11, 11077. [Google Scholar] [CrossRef]
  100. Kandiri, A.; Sartipi, F.; Kioumarsi, M. Predicting compressive strength of concrete containing recycled aggregate using modified ann with different optimization algorithms. Appl. Sci. 2021, 11, 485. [Google Scholar] [CrossRef]
  101. Phoeuk, M.; Kwon, M. Accuracy Prediction of Compressive Strength of Concrete Incorporating Recycled Aggregate Using Ensemble Learning Algorithms: Multinational Dataset. Adv. Civ. Eng. 2023, 2023, 5076429. [Google Scholar] [CrossRef]
  102. Duan, J.; Asteris, P.G.; Nguyen, H.; Bui, X.N.; Moayedi, H. A novel artificial intelligence technique to predict compressive strength of recycled aggregate concrete using ICA-XGBoost model. Eng. Comput. 2021, 37, 3329–3346. [Google Scholar] [CrossRef]
  103. Bu, L.; Du, G.; Hou, Q. Prediction of the compressive strength of recycled aggregate concrete based on artificial neural network. Materials 2021, 14, 3921. [Google Scholar] [CrossRef]
  104. Shakr Piro, N.; Mohammed, A.; Hamad, S.M.; Kurda, R. Electrical resistivity-Compressive strength predictions for normal strength concrete with waste steel slag as a coarse aggregate replacement using various analytical models. Constr. Build. Mater. 2022, 327, 127008. [Google Scholar] [CrossRef]
  105. Afshoon, I.; Miri, M.; Mousavi, S.R. Using the Response Surface Method and Artificial Neural Network to Estimate the Compressive Strength of Environmentally Friendly Concretes Containing Fine Copper Slag Aggregates. Iran. J. Sci. Technol.-Trans. Civ. Eng. 2023, 47, 3415–3429. [Google Scholar] [CrossRef]
  106. Faraj, R.H.; Mohammed, A.A.; Omer, K.M.; Ahmed, H.U. Soft computing techniques to predict the compressive strength of green self-compacting concrete incorporating recycled plastic aggregates and industrial waste ashes. Clean Technol. Environ. Policy 2022, 24, 2253–2281. [Google Scholar] [CrossRef]
  107. Zhang, T.; Zhang, Y.; Wang, Q.; Aganyira, A.K.; Fang, Y. Experimental study and machine learning prediction on compressive strength of spontaneous-combustion coal gangue aggregate concrete. J. Build. Eng. 2023, 71, 106518. [Google Scholar] [CrossRef]
  108. de-Prado-Gil, J.; Palencia, C.; Jagadesh, P.; Martínez-García, R. A Study on the Prediction of Compressive Strength of Self-Compacting Recycled Aggregate Concrete Utilizing Novel Computational Approaches. Materials 2022, 15, 5232. [Google Scholar] [CrossRef]
  109. Mohammadi Golafshani, E.; Behnood, A.; Hosseinikebria, S.S.; Arashpour, M. Novel metaheuristic-based type-2 fuzzy inference system for predicting the compressive strength of recycled aggregate concrete. J. Clean. Prod. 2021, 320, 128771. [Google Scholar] [CrossRef]
  110. Liu, X.; Jing, H.; Yan, P. Statistical analysis and unified model for predicting the compressive strength of coarse recycled aggregate OPC concrete. J. Clean. Prod. 2023, 400, 136660. [Google Scholar] [CrossRef]
  111. Debbarma, S.; Ransinchung, G.D. Using artificial neural networks to predict the 28-day compressive strength of roller-compacted concrete pavements containing RAP aggregates. Road Mater. Pavement Des. 2022, 23, 149–167. [Google Scholar] [CrossRef]
  112. Falah, M.W.; Hussein, S.H.; Saad, M.A.; Ali, Z.H.; Tran, T.H.; Ghoniem, R.M.; Ewees, A.A. Compressive Strength Prediction Using Coupled Deep Learning Model with Extreme Gradient Boosting Algorithm: Environmentally Friendly Concrete Incorporating Recycled Aggregate. Complexity 2022, 2022, 5433474. [Google Scholar] [CrossRef]
  113. Wang, C.; Wang, J.; Liu, X.; Cai, Y.F.; Zhang, Y.C. Orthogonal experimental design for compressive strength of recycled coarse aggregate concrete with silica fume-slag-fly ash hybrid micro-powders. Constr. Build. Mater. 2023, 408, 133669. [Google Scholar] [CrossRef]
  114. Gao, Y.; Li, Z.; Li, Y.; Zhu, Z.; Zhu, J. Development of chemistry-informed interpretable model for predicting compressive strength of recycled aggregate concrete containing supplementary cementitious materials. J. Clean. Prod. 2023, 425, 138733. [Google Scholar] [CrossRef]
  115. Tipu, R.K.; Batra, V.; Suman; Pandya, K.S.; Panchal, V.R. Efficient compressive strength prediction of concrete incorporating recycled coarse aggregate using Newton’s boosted backpropagation neural network (NB-BPNN). Structures 2023, 58, 105559. [Google Scholar] [CrossRef]
  116. Huang, P.; Dai, K.; Yu, X. Machine learning approach for investigating compressive strength of self-compacting concrete containing supplementary cementitious materials and recycled aggregate. J. Build. Eng. 2023, 79, 107904. [Google Scholar] [CrossRef]
  117. Mai, H.V.T.; Nguyen, M.H.; Trinh, S.H.; Ly, H.B. Toward improved prediction of recycled brick aggregate concrete compressive strength by designing ensemble machine learning models. Constr. Build. Mater. 2023, 369, 130613. [Google Scholar] [CrossRef]
  118. Moghaddas, S.A.; Nekoei, M.; Golafshani, E.M.; Behnood, A.; Arashpour, M. Application of artificial bee colony programming techniques for predicting the compressive strength of recycled aggregate concrete. Appl. Soft Comput. 2022, 130, 109641. [Google Scholar] [CrossRef]
  119. Sun, Z.; Li, Y.; Li, Y.; Su, L.; He, W. Investigation on compressive strength of coral aggregate concrete: Hybrid machine learning models and experimental validation. J. Build. Eng. 2024, 82, 108220. [Google Scholar] [CrossRef]
  120. Huang, Y.; Lei, Y.; Luo, X.; Fu, C. Prediction of compressive strength of rice husk ash concrete: A comparison of different metaheuristic algorithms for optimizing support vector regression. Case Stud. Constr. Mater. 2023, 18, e02201. [Google Scholar] [CrossRef]
  121. Zhang, X.; Dai, C.; Li, W.; Chen, Y. Prediction of compressive strength of recycled aggregate concrete using machine learning and Bayesian optimization methods. Front. Earth Sci. 2023, 11, 1112105. [Google Scholar] [CrossRef]
  122. Munir, M.J.; Kazmi, S.M.S.; Wu, Y.F.; Lin, X.; Ahmad, M.R. Development of a novel compressive strength design equation for natural and recycled aggregate concrete through advanced computational modeling. J. Build. Eng. 2022, 55, 104690. [Google Scholar] [CrossRef]
  123. Sheetal Thapa, R.P.; Halder, S. and L. Developing SonReb models to predict the compressive strength of concrete using different percentage of recycled brick aggregate. Can. J. Civ. Eng. 2022, 49, 346–356. [Google Scholar] [CrossRef]
  124. Lam, N.T.M.; Nguyen, D.L.; Le, D.H. Predicting compressive strength of roller-compacted concrete pavement containing steel slag aggregate and fly ash. Int. J. Pavement Eng. 2022, 23, 731–744. [Google Scholar] [CrossRef]
  125. Jagadesh, P.; de Prado-Gil, J.; Silva-Monteiro, N.; Martínez-García, R. Assessing the compressive strength of self-compacting concrete with recycled aggregates from mix ratio using machine learning approach. J. Mater. Res. Technol. 2023, 24, 1483–1498. [Google Scholar] [CrossRef]
  126. Migallón, V.; Penadés, H.; Penadés, J.; Tenza-Abril, A.J. A Machine Learning Approach to Prediction of the Compressive Strength of Segregated Lightweight Aggregate Concretes Using Ultrasonic Pulse Velocity. Appl. Sci. 2023, 13, 1953. [Google Scholar] [CrossRef]
  127. Babu, B.R.; Thenmozhi, R. Prediction of Compressive Strength of Sintered Fly Ash Aggregate Concrete Using Artificial Neural Networking. Rev. Romana Mater. Rom. J. Mater. 2022, 52, 311–317. [Google Scholar]
  128. Alyaseen, A.; Poddar, A.; Kumar, N.; Sihag, P.; Lee, D.; Kumar, R.; Singh, T. Assessing the compressive and splitting tensile strength of self-compacting recycled coarse aggregate concrete using machine learning and statistical techniques. Mater. Today Commun. 2024, 38, 107970. [Google Scholar] [CrossRef]
  129. Qureshi, H.J.; Alyami, M.; Nawaz, R.; Hakeem, I.Y.; Aslam, F.; Iftikhar, B.; Gamil, Y. Prediction of compressive strength of two-stage (preplaced aggregate) concrete using gene expression programming and random forest. Case Stud. Constr. Mater. 2023, 19, e02581. [Google Scholar] [CrossRef]
  130. de-Prado-Gil, J.; Palencia, C.; Silva-Monteiro, N.; Martínez-García, R. To predict the compressive strength of self compacting concrete with recycled aggregates utilizing ensemble machine learning models. Case Stud. Constr. Mater. 2022, 16, e01046. [Google Scholar] [CrossRef]
  131. Khan, K.; Ahmad, W.; Amin, M.N.; Aslam, F.; Ahmad, A.; Al-Faiad, M.A. Comparison of Prediction Models Based on Machine Learning for the Compressive Strength Estimation of Recycled Aggregate Concrete. Materials 2022, 15, 3430. [Google Scholar] [CrossRef] [PubMed]
  132. Chen, M.; Liu, B.; Li, L.; Cao, L.; Huang, Y.; Wang, S.; Zhao, P.; Lu, L.; Cheng, X. Rheological parameters, thixotropy and creep of 3D-printed calcium sulfoaluminate cement composites modified by bentonite. Compos. Part B Eng. 2020, 186, 107821. [Google Scholar] [CrossRef]
  133. Altuncı, Y.T.; Saplıoğlu, K. Development of Prediction Models for Compressive Strength in Cement Mortar with Development of Prediction Models for Compressive Strength in Cement Mortar with Bentonite using Machine Learning Techniques. Int. J. 3D Print. Technol. Digit. Ind. 2024, 8, 214–224. [Google Scholar] [CrossRef]
  134. Kumar, R.; Kumar, S.; Rai, B.; Samui, P. Development of hybrid gradient boosting models for predicting the compressive strength of high-volume fly ash self-compacting concrete with silica fume. Structures 2024, 66, 106850. [Google Scholar] [CrossRef]
  135. Shakya, D.; Deshpande, V.; Safari, M.J.S.; Agarwal, M. Performance evaluation of machine learning algorithms for the prediction of particle Froude number (Frn) using hyper-parameter optimizations techniques. Expert Syst. Appl. 2024, 256, 124960. [Google Scholar] [CrossRef]
  136. Acar, R.; Saplioglu, K. Using the Particle Swarm Optimization (PSO) Algorithm for Baseflow Separation and Determining the Trends for the Yesilirmak River (North Turkey). Russ. Meteorol. Hydrol. 2024, 49, 40–51. [Google Scholar] [CrossRef]
  137. Kleiv, R.A.; Thornhill, M. Predicting the neutralisation of acid mine drainage in anoxic olivine drains. Miner. Eng. 2008, 21, 279–287. [Google Scholar] [CrossRef]
  138. Canpolat, M.; Beycioğlu, A.; Morova, N.; Çetin, S.; Çetin, H.M.; Gündoğan, H. Atık Olivin Mineralinin Asfalt Betonunda Filler Olarak Kullanımı. Düzce Üniversitesi Bilim Ve Teknol. Derg. 2022, 10, 555–566. [Google Scholar] [CrossRef]
  139. Acar, İ. Sintering properties of olivine and its utilization potential as a refractory raw material: Mineralogical and microstructural investigations. Ceram. Int. 2020, 46, 28025–28034. [Google Scholar] [CrossRef]
  140. Güçlüer, K.; Yaldız, M.R.; Günaydın, O. An investigation of the high-temperature behavior of basalt, olivine, and pyrophyllite additive mortars. Iran. J. Sci. Technol.-Trans. Civ. Eng. 2023, 47, 1467–1484. [Google Scholar] [CrossRef]
  141. Atlı, I.; Ipek, M. Investigation of the Mechanical Behaviors of Sustainable Green Reactive Powder Concrete Produced Using Ferrochrome Slag and Waste Fiber. Sustainability 2024, 16, 4714. [Google Scholar] [CrossRef]
  142. Moon, K.; Park, S.; Kim, S. Compressive Strength of Concrete due to Moisture Conditions of Recycled Coarse Aggregates and Curing Conditions. KSCE J. Civ. Environ. Eng. Res. 2019, 39, 485–492. [Google Scholar]
  143. Park, J.; Park, C.; Kim, S.J.; Jae, Y. Characterization of Compressive Strength and Elastic Modulus of Recycled Aggregate Concrete with Respect to Replacement Ratios. J. Korean Soc. Civ. Eng. 2006, 26, 213–218. [Google Scholar]
  144. Sharba, A.A. The Efficiency of Steel Slag and Recycled Concrete Aggregate on the Strength Properties of Concrete. KSCE J. Civ. Eng. 2019, 23, 4846–4851. [Google Scholar] [CrossRef]
  145. Ge, P.; Huang, W.; Zhang, H.; Quan, W.; Guo, Y. Study on Calculation Model for Compressive Strength of Water Saturated Recycled Aggregate Concrete. KSCE J. Civ. Eng. 2022, 26, 273–285. [Google Scholar] [CrossRef]
  146. Alyamaç, K.E.; Aydin, A.B. Concrete properties containing fine aggregate marble powder. KSCE J. Civ. Eng. 2015, 19, 2208–2216. [Google Scholar] [CrossRef]
  147. Tanyildizi, H.; Şengür, A.; Akbulut, Y.; Şahin, M. Deep learning model for estimating the mechanical properties of concrete containing silica fume exposed to high temperatures. Front. Struct. Civ. Eng. 2020, 14, 1316–1330. [Google Scholar] [CrossRef]
  148. Shariati, M.; Mafipour, M.S.; Mehrabi, P.; Bahadori, A.; Zandi, Y.; Salih, M.N.A.; Nguyen, H.; Dou, J.; Song, X.; Poi-Ngian, S. Application of a Hybrid Artificial Neural Model in Behavior Prediction of Channel Shear Connectors Embedded in Normal and High-Strength Concrete. Appl. Sci. 2019, 9, 5534. [Google Scholar] [CrossRef]
  149. Huang, X.Y.; Wu, K.Y.; Wang, S.; Lu, T.; Lu, Y.F.; Deng, W.C.; Li, H.M. Compressive Strength Prediction of Rubber Concrete Based on Artificial Neural Network Model with Hybrid Particle Swarm Optimization Algorithm. Materials 2022, 15, 3934. [Google Scholar] [CrossRef]
  150. Sammen, S.S.; Ghorbani, M.A.; Malik, A.; Tikhamarine, Y.; AmirRahmani, M.; Al-Ansari, N.; Chau, K.W. Enhanced artificial neural network with Harris hawks optimization for predicting scour depth downstream of ski-jump spillway. Appl. Sci. 2020, 10, 5160. [Google Scholar] [CrossRef]
  151. Ecer, F.; Ardabili, S.; Band, S.S.; Mosavi, A. Training multilayer perceptron with genetic algorithms and particle swarm optimization for modeling stock price index prediction. Entropy 2020, 22, 1239. [Google Scholar] [CrossRef] [PubMed]
  152. Ibrahim, M.A.; Çamur, H.; Savaş, M.A.; Sabo, A.K.; Mustapha, M.; Abba, S.I. Hybrid Artificial Intelligence Models with Multi Objective Optimization for Prediction of Tribological Behavior of Polytetrafluoroethylene Matrix Composites. Appl. Sci. 2022, 12, 8671. [Google Scholar] [CrossRef]
  153. Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
  154. Acar, R.; Saplıoğlu, K. Akarsulardaki Sediment Taşiniminin YapaSinir Ağlari Ve AnfisYöntemleri KullanilaraTespiti. Ömer Halisdemir Üniversitesi Mühendis. Bilim. Derg. 2020, 9, 437–450. [Google Scholar] [CrossRef]
  155. Saplıoğlu, K.; Acar, R. K-Means Kümeleme Algoritması Kullanılarak Oluşturulan Yapay Zekâ Modelleri ile Sediment Taşınımının Tespiti. Bitlis Eren Üniversitesi Fen Bilim. Derg. 2020, 9, 306–322. [Google Scholar] [CrossRef]
  156. Gaidhane, V.H.; Kumar, N.; Mittal, R.K.; Rajevenceltha, J. An efficient approach for cement strength prediction. Int. J. Comput. Appl. 2023, 45, 8–18. [Google Scholar] [CrossRef]
  157. Nafees, A.; Amin, M.N.; Khan, K.; Nazir, K.; Ali, M.; Javed, M.F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Modeling of mechanical properties of silica fume-based green concrete using machine learning techniques. Polymers 2022, 14, 30. [Google Scholar] [CrossRef]
  158. Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
  159. Shiru, M.S.; Shahid, S.; Chae, S.T.; Chung, E.S. Replicability of Annual and Seasonal Precipitation by CMIP5 and CMIP6 GCMs over East Asia. KSCE J. Civ. Eng. 2022, 26, 1978–1989. [Google Scholar] [CrossRef]
  160. Ekwueme, B.N.; Ibeje, A.O. Comparison of Monte Carlo Schemes in the Modeling of Extreme Flood in Tropical Rain Forest Basins. KSCE J. Civ. Eng. 2023, 27, 5175–5189. [Google Scholar] [CrossRef]
  161. Bian, J.; Huo, R.; Zhong, Y.; Guo, Z. XGB-Northern Goshawk Optimization: Predicting the Compressive Strength of Self-Compacting Concrete. KSCE J. Civ. Eng. 2024, 28, 1423–1439. [Google Scholar] [CrossRef]
  162. Jumarie, G. Table of some basic fractional calculus formulae derived from a modified Riemann–Liouville derivative for non-differentiable functions. Appl. Math. Lett. 2009, 22, 378–385. [Google Scholar] [CrossRef]
Processes 13 02130 g001
Figure 1. The image of the olivine aggregate used in the study.
Figure 1. The image of the olivine aggregate used in the study.
Processes 13 02130 g001
Processes 13 02130 g002
Figure 2. The view of the samples placed in the curing pool.
Figure 2. The view of the samples placed in the curing pool.
Processes 13 02130 g002
Processes 13 02130 g003
Figure 3. Specimen under compressive load.
Figure 3. Specimen under compressive load.
Processes 13 02130 g003
Processes 13 02130 g004
Figure 4. Basic PSO algorithm.
Figure 4. Basic PSO algorithm.
Processes 13 02130 g004
Processes 13 02130 g005
Figure 5. Traditional ANN structure.
Figure 5. Traditional ANN structure.
Processes 13 02130 g005
Processes 13 02130 g006
Figure 6. Comparison of predicted and experimental values (ANN).
Figure 6. Comparison of predicted and experimental values (ANN).
Processes 13 02130 g006
Processes 13 02130 g007
Figure 7. Comparison of predicted and experimental values for PSO-ANN model optimized with MAE.
Figure 7. Comparison of predicted and experimental values for PSO-ANN model optimized with MAE.
Processes 13 02130 g007
Processes 13 02130 g008
Figure 8. Comparison of predicted and experimental values for PSO-ANN model optimized with RMSE.
Figure 8. Comparison of predicted and experimental values for PSO-ANN model optimized with RMSE.
Processes 13 02130 g008
Processes 13 02130 g009
Figure 9. Comparison of predicted and experimental values for PSO-ANN model optimized with WRMSE.
Figure 9. Comparison of predicted and experimental values for PSO-ANN model optimized with WRMSE.
Processes 13 02130 g009
Processes 13 02130 g010
Figure 10. Taylor diagram (training).
Figure 10. Taylor diagram (training).
Processes 13 02130 g010
Processes 13 02130 g011
Figure 11. Taylor diagram (testing).
Figure 11. Taylor diagram (testing).
Processes 13 02130 g011
Table 1. Detecting research gaps in the literature.
Table 1. Detecting research gaps in the literature.
Research Gaps in the LiteratureResearch
1, 2, 3[37,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125]
2, 3[126,127,128,129,130,131]
1—A lack of research on the use of different rock types instead of traditional aggregates in concrete production; 2—the absence of compressive strength determination for concrete containing different dosages of olivine aggregate; 3—insufficient focus on reducing the carbon footprint through concrete production.
Table 2. Frequency of use of AI methods on a study basis.
Table 2. Frequency of use of AI methods on a study basis.
MethodNumber of Studies Using the MethodUsage Frequency (%)
Ada Boost (AB)32.0
Mean Absolute Error (MAE)85.2
Adaptive Neuro-Fuzzy Inference System (ANFIS)32.0
Artificial Neural Network (ANN)2113.7
Bagging Regressor (BR)53.3
Cat Boost (CB)32.0
Coefficient of Determination (R2)127.8
Decision Tree (DT)42.6
(Deep Learning Neural Network) DLNN10.7
Extreme Learning Machine (ELM)10.7
Firefly Algorithm (FA)10.7
Fuzzy Logic (FL)95.9
Gene Expression Programming (GEP)42.6
Gradient Boost (GB)74.6
Gray Wolf Optimization (GWO) 10.7
K-Nearest Neighbor (KNN)74.6
Light Gradient-Boosting Machine Regressor (LGBM)32.0
Multivariate Adaptive Regression Spline (MARS)10.7
Machine Learning (ML)21.3
Multiple Linear Regression (MLR) 53.3
M5P Tree (M5PT)32.0
Random Forest (RF)85.2
Root Mean Square Error (RMSE) 95.9
Support Vector Regression (SVR)42.6
Support Vector Machine (SVM) 42.6
Weighted Root Mean Square Error (WRMSE)149.2
XG Boost (XGB)63.9
Particle Swarm Optimization (PSO)42.6
Table 3. Chemical properties of dry mixtures of cement and olivine aggregate.
Table 3. Chemical properties of dry mixtures of cement and olivine aggregate.
ComponentsCEM II 42.5 ROlivine
SiO2 (S)25.2230.19
Al2O3 (A)8.05-
Fe2O3 (F)3.7814.71
CaO52.136.90
MgO1.5444.15
SO33.350.02
Na2O1.020.41
K2O0.89-
Cl−0.071-
Loss of ignition2.993.53
Table 4. Mixture information for olivine aggregate concrete samples (for 1 m3).
Table 4. Mixture information for olivine aggregate concrete samples (for 1 m3).
DosageCEM II
42.5 R (kg)		Aggregate
0–5 mm (kg)		Aggregate
5–15 mm (kg)		Aggregate
15–25 mm (kg)		Water
(kg)		Plasticizer
(kg)
1801801241.46334.35500.531201.26
1851851238.83333.65499.471201.30
1901901236.32332.94498.421201.33
1951951233.59332.23497.361201.37
2002001230.96331.53496.301201.40
2052051228.34330.82495.241201.44
2102101225.72330.11494.191201.47
2152151223.09329.41493.131201.51
2202201220.47328.70492.071201.54
2252251217.85327.99491.011201.58
2302301215.22327.29489.961201.61
2352351212.60326.58488.901201.65
2402401209.98325.88487.841201.68
2452451207.36325.17486.781201.72
2502501204.73324.46485.731201.75
2552551202.11323.76484.671201.79
2602601199.49323.05483.611201.82
2652651196.86322.34482.551201.86
2702701194.24321.64481.501201.89
2752751191.62320.93480.441201.93
2802801188.99320.22479.381201.96
2852851186.37319.52478.321202.00
2902901183.75318.81477.261202.03
2952951181.12318.10476.211202.07
3003001178.50317.40475.151202.10
3053051175.88316.69474.091202.14
3103101173.30316.00473.051202.17
3153151170.73315.30472.021202.21
3203201170.58315.27471.961202.24
3253251170.53315.25471.941202.28
Table 5. Statistical analysis of the training parameters employed in the model.
Table 5. Statistical analysis of the training parameters employed in the model.
DayDosage (kg)Aggregate
0–5 mm (kg)		Aggregate
5–15 mm (kg)		Aggregate
15–25 mm (kg)		Plasticizer (kg)Compressive Strength (MPa)
Average45.25253.261.771203.36324.09485.1730.4
Standard error3.264.630.032.380.640.961.1
Median42.00255.001.791202.11323.76484.6729.3
Standard deviation31.3144.440.3122.806.149.199.1
Sample variance980.341974.960.10519.6737.6984.4783.0
Kurtosis−1.35−1.21−1.21−1.26−1.26−1.26-0.4
Skewness0.25−0.01−0.010.070.070.070.4
Range83.00145.001.0270.9219.1028.5938.3
Minimum7.00180.001.261170.53315.25471.9414.1
Maximum90.00325.002.281241.46334.35500.5352.5
Confidence level (95.0%)9292929292922.3
Table 6. Statistical analysis of the test parameters employed in the model.
Table 6. Statistical analysis of the test parameters employed in the model.
DayDosage (kg)Aggregate
0–5 mm (kg)		Aggregate
5–15 mm (kg)		Aggregate
15–25 mm (kg)		Plasticizer (kg)Compressive Strength (MPa)
Average45.25253.571.751171.27315.45472.2334.44
Standard error5.999.090.050.080.020.032.08
Median42.00250.001.751171.27315.45472.2332.72
Standard deviation31.7148.090.290.400.110.1611.03
Sample variance1005.62312.700.080.160.010.03121.65
Kurtosis−1.360.73−1.26−1.26−1.26−1.25−0.47
Skewness0.260.720.000.000.000.000.38
Range83.00200.000.841.180.320.4842.94
Minimum7.00190.001.331170.68315.29472.0015.57
Maximum90.00390.002.171171.86315.61472.4758.50
Confidence level (95.0%)28282828282828
Table 7. Statistical comparison of training and testing data.
Table 7. Statistical comparison of training and testing data.
Training DataTesting Data
ModelModel NoR2WRMSERMSEMAER2WRMSERMSEMAE
WRMSE 1A0.94890.36700.85676.80730.88120.94181.372510.1092
WRMSE 2B0.94860.36730.85716.81010.85460.6050.85718.2265
RMSE 1C0.94880.35910.84756.78520.87500.88241.32859.6654
RMSE 2D0.94860.36070.84946.79560.87010.67391.16108.0657
MAE 1E0.94860.37290.86366.66910.85430.91161.35039.1910
MAE 2F0.94840.37330.86416.67270.85790.80811.27138.5771
ANN 9G0.99940.00390.08850.57090.56066.99233.739626.8049
ANN 5H0.98610.13550.52063.63530.50466.92423.721333.4046
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Altuncı, Y.T. Predicting the Compressive Strength of Concrete Incorporating Olivine Aggregate at Varied Cement Dosages Using Artificial Intelligence. Processes 2025, 13, 2130. https://doi.org/10.3390/pr13072130

AMA Style

Altuncı YT. Predicting the Compressive Strength of Concrete Incorporating Olivine Aggregate at Varied Cement Dosages Using Artificial Intelligence. Processes. 2025; 13(7):2130. https://doi.org/10.3390/pr13072130

Chicago/Turabian Style

Altuncı, Yusuf Tahir. 2025. "Predicting the Compressive Strength of Concrete Incorporating Olivine Aggregate at Varied Cement Dosages Using Artificial Intelligence" Processes 13, no. 7: 2130. https://doi.org/10.3390/pr13072130

APA Style

Altuncı, Y. T. (2025). Predicting the Compressive Strength of Concrete Incorporating Olivine Aggregate at Varied Cement Dosages Using Artificial Intelligence. Processes, 13(7), 2130. https://doi.org/10.3390/pr13072130

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop