A Numerical Model for Inelastic Buckling in Cold Upset Forging: Stress Analysis and Optimal Billet Geometry
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
2.2. CAD Model Design
2.3. Choice of Simulation Software
2.4. Modelling Approach
2.4.1. Defining Geometry Behaviour
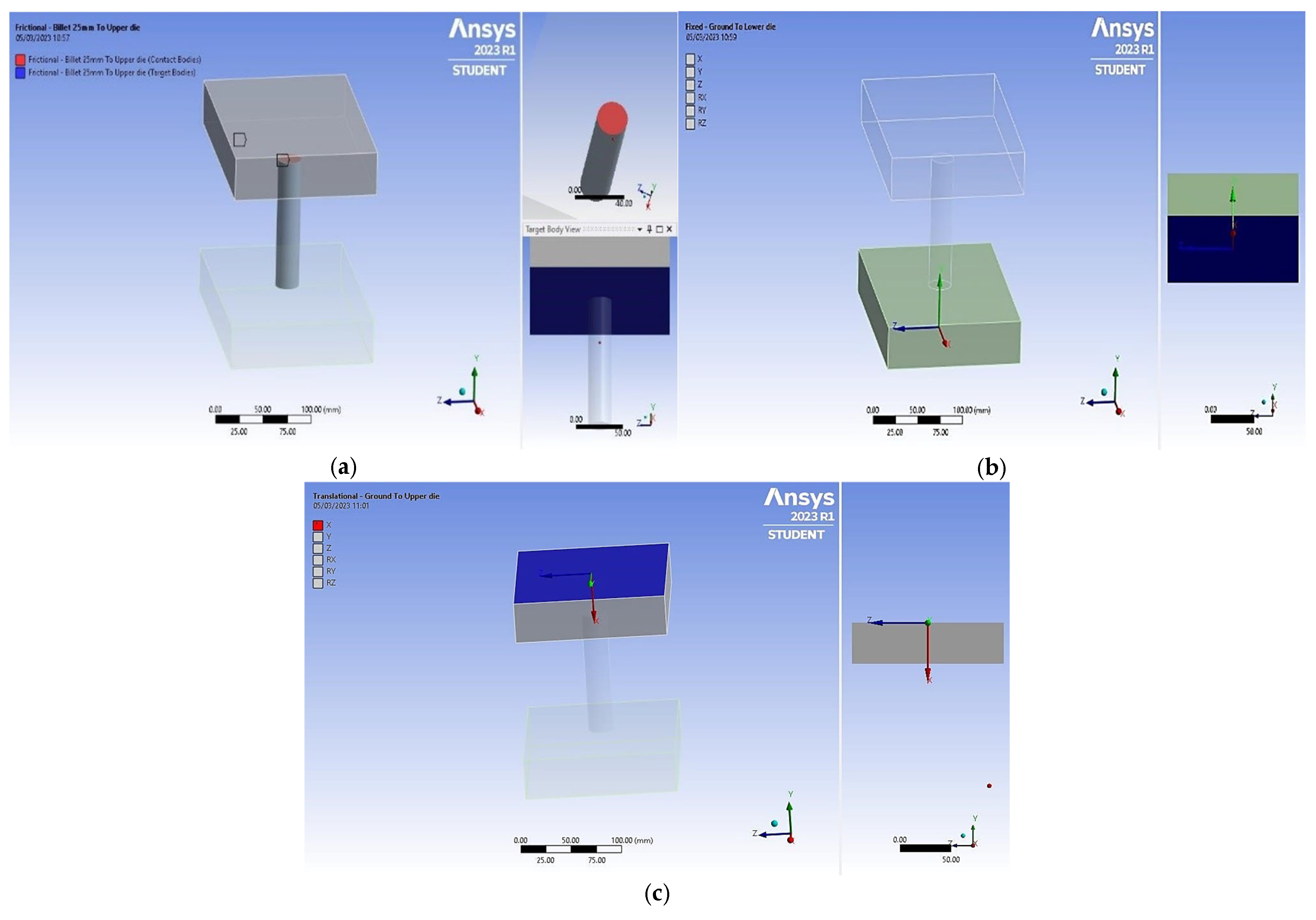
2.4.2. Connection Types
2.4.3. Mesh Generation
2.5. Solution Setup
2.6. Data Analysis
3. Results and Discussions
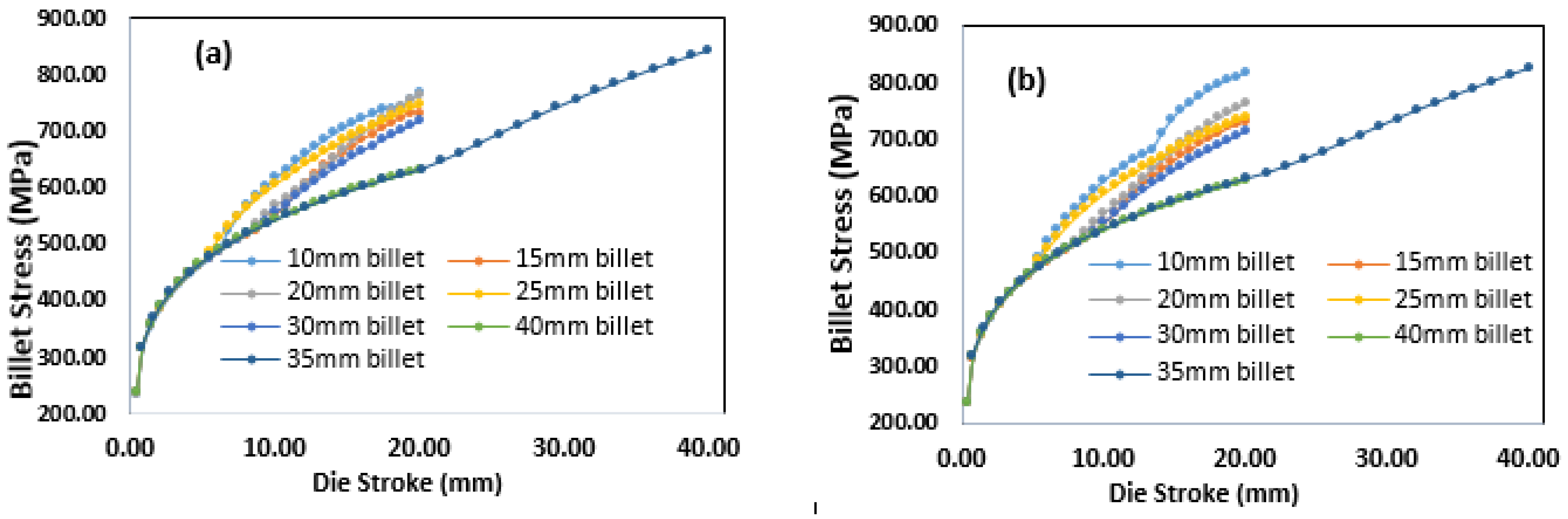
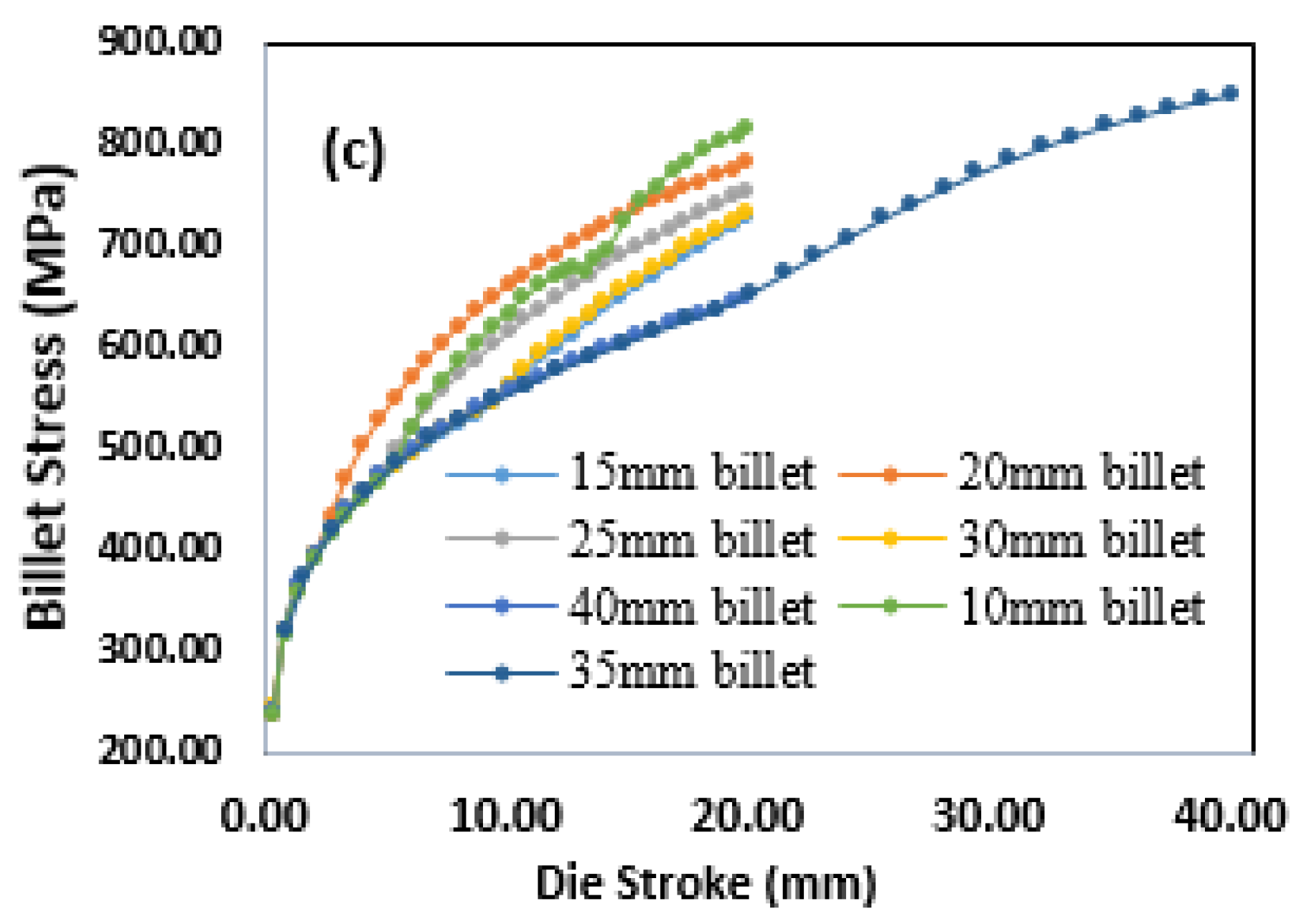
3.1. Stress vs. Die–Stroke
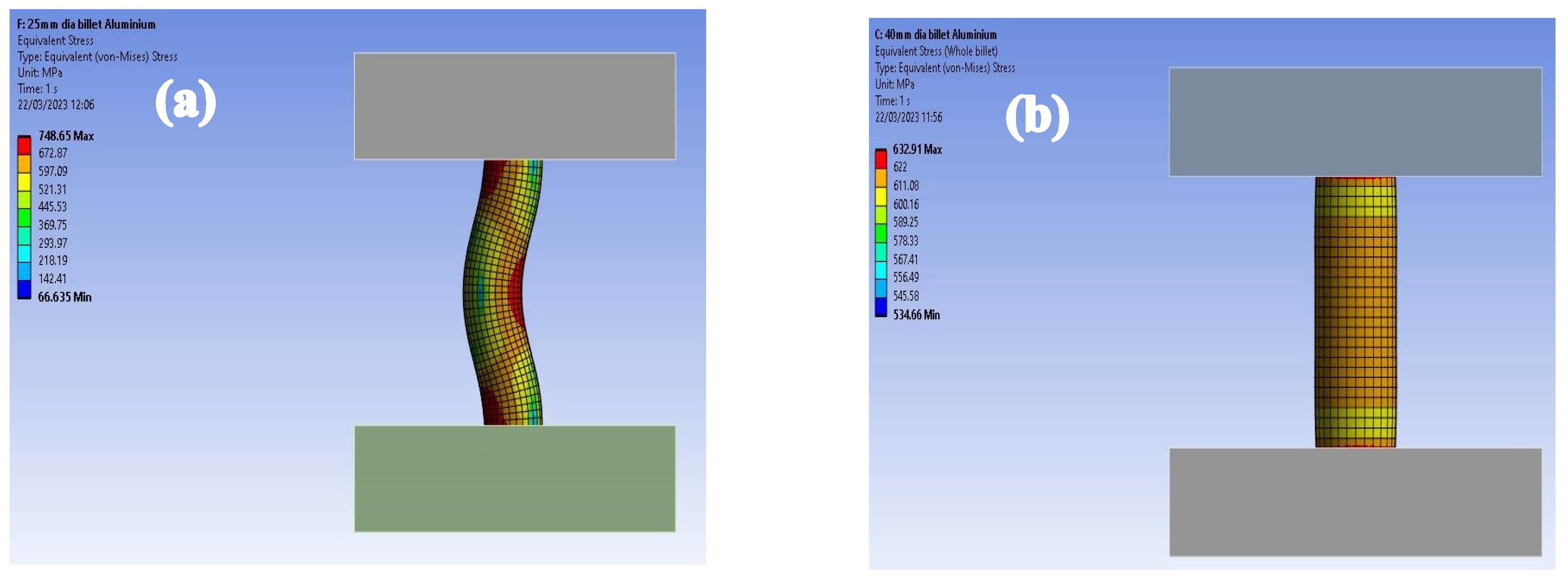
3.2. Effect of Strain Hardening Exponent on Billet Buckling
3.3. Numerical Model for Predicting Billet Stress
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abesin Kodippili, T. Forging Preform Design Optimization for Structural Magnesium Components; University of Waterloo: Waterloo, ON, Canada, 2023. [Google Scholar]
- Dash, J.P. Nizam’s Mint to A People’s Museum: A Pride of Deccan Heritage and Technology; Notion Press: Chennai, India, 2023. [Google Scholar]
- Fan, Q.; Duan, H.; Xing, X. A review of composite materials for enhancing support, flexibility and strength in exercise. Alex. Eng. J. 2024, 94, 90–103. [Google Scholar] [CrossRef]
- Babaei, H.; Kiani, Y.; Reza Eslami, M. Buckling and post-buckling analysis of geometrically imperfect FGM pin-ended tubes surrounded by nonlinear elastic medium under compressive and thermal loads. Int. J. Struct. Stab. Dyn. 2019, 19, 1950089. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, J. Group-theoretic method for efficient buckling analysis of prestressed space structures. Acta Mech. 2015, 226, 957–973. [Google Scholar] [CrossRef]
- Development and Research of the Billet Forging Technology in the Newly Designed Step-Wedge Dies|Request PDF. Available online: https://www.researchgate.net/publication/331348650_Development_and_Research_of_the_Billet_Forging_Technology_in_the_Newly_Designed_Step-Wedge_Dies (accessed on 27 February 2025).
- Dokšanović, T.; Markulak, D.; Džeba, I. State of the art review of the stability and welding of aluminium alloy elements. Građevinar 2014, 66, 115–125. [Google Scholar]
- Kelechava, B. Nondestructive Testing (NDT) in ASTM E1316-25—ANSI Blog. The ANSI Blog. Available online: https://blog.ansi.org/nondestructive-testing-ndt-astm-e1316/ (accessed on 11 April 2022).
- Donmez, A.; Fox, J.; Kim, F.; Lane, B.; Praniewicz, M.; Tondare, V.; Weaver, J.; Witherell, P. In-Process Monitoring and Non-Destructive Evaluation for Metal Additive Manufacturing Processes; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2024.
- Rollston, C.A. Forging history: From antiquity to the modern period. In Archaeologies of Text: Archaeology, Technology, and Ethics; Eisenbrauns: Winona Lake, IN, USA, 2014; pp. 176–197. [Google Scholar]
- Valiulis, A.V. A History of Materials and Technologies Development; Lambert Academic Publishing: Saarbrücken, Germany, 2014. [Google Scholar]
- History of Forging: From Humble Beginnings to a Modern Marvel—Weldaloy Specialty Forgings. Available online: https://weldaloy.com/press-release/history-of-forging/ (accessed on 1 February 2025).
- Fouda, N.; El-Midany, T.; Sadoun, A.M. Bending, buckling and vibration of a functionally graded porous beam using finite elements. J. Appl. Comput. Mech. 2017, 3, 274–282. [Google Scholar]
- Magnucki, K.; Stasiewicz, P. Elastic buckling of a porous beam. J. Theor. Appl. Mech. 2004, 42, 859–868. [Google Scholar]
- The History of Forging Process|Steel Forging. Available online: https://www.steelforging.org/the-history-of-forging-process/ (accessed on 1 February 2025).
- Forge, A.V. Forging Ahead; Angus & Robertson: Sydney, Australia, 2009. [Google Scholar]
- Meyer, D.R. Networked Machinists: High-Technology Industries in Antebellum America; JHU Press: Baltimore, MD, USA, 2006. [Google Scholar]
- Williams, P.H. How Britain Shaped the Manufacturing World, 1851–1951; Pen and Sword History: Barnsley, UK, 2022. [Google Scholar]
- Jianjun, L.; Xinyun, W. Die for Forging and Stamping. In The ECPH Encyclopedia of Mining and Metallurgy; Kuangdi, X., Ed.; Springer Nature: Singapore, 2024; pp. 477–479. ISBN 978-981-9920-85-3. [Google Scholar]
- Bassan, F. Optimization of Industrial Processes for Forging of Carbon and Stainless Steels; Éditions Universitaires Européennes: Saarbrücken, Germany, 2015. [Google Scholar]
- Ha, S.; Cho, D.; Park, J.; Kim, S. A Study on the Design of Bending Process According to the Shape of Initial Billets for Bi-Metal Elbow. Metals 2022, 12, 1474. [Google Scholar] [CrossRef]
- Dokšanović, T.; Džeba, I.; Markulak, D. Variability of structural aluminium alloys mechanical properties. Struct. Saf. 2017, 67, 11–26. [Google Scholar] [CrossRef]
- Zhao, Q.; Sun, Q.; Xin, S.; Chen, Y.; Wu, C.; Wang, H.; Xu, J.; Wan, M.; Zeng, W.; Zhao, Y. High-strength titanium alloys for aerospace engineering applications: A review on melting-forging process. Mater. Sci. Eng. A 2022, 845, 143260. [Google Scholar] [CrossRef]
- Gong, H.; Sun, X.; Zhang, T.; Tang, H. Effects of cold expansion on residual stress of 7050 aluminium alloy frame forging. Metals 2023, 13, 732. [Google Scholar] [CrossRef]
- Bharti, S. Advancement in forging process: A review. Int. J. Sci. Res. 2017, 6, 465–468. [Google Scholar]
- Choi, Y.-J.; Lee, S.-K.; Lee, I.-K.; Hwang, S.K.; Yoon, J.C.; Choi, C.Y.; Lee, Y.S.; Jeong, M.-S. Hot forging process design of sprocket wheel and environmental effect analysis. J. Mech. Sci. Technol. 2018, 32, 2219–2225. [Google Scholar] [CrossRef]
- Malayappan, S.; Narayanasamy, R. An experimental analysis of upset forging of aluminium cylindrical billets considering the dissimilar frictional conditions at flat die surfaces. Int. J. Adv. Manuf. Technol. 2004, 23, 636–643. [Google Scholar] [CrossRef]
- Mohammadi, M.; Khedmati, M.R.; Bahmyari, E. Elastic local buckling strength analysis of stiffened aluminium plates with an emphasis on the initial deflections and welding residual stresses. Ships Offshore Struct. 2019, 14, 125–140. [Google Scholar] [CrossRef]
- Błachut, J. Experimental perspective on the buckling of pressure vessel components. Appl. Mech. Rev. 2014, 66, 010803. [Google Scholar] [CrossRef]
- Adil, H. Characterisation of a New Nanostructured Aluminium Alloy and Piston Design for Internal Combustion Engines. Ph.D. Thesis, Oxford Brookes University, Oxford, UK, 2023. [Google Scholar]
- Muchhala, D.; Yadav, B.N.; Pandey, A.; Chilla, V.; Shafeeq, M.M.; Gupta, G.; Sathaiah, S.; Mondal, D.P. Influences of relative density and strain rate on the mechanical properties of Al-cenosphere-SWNTs hybrid foams. Int. J. Mech. Sci. 2021, 198, 106388. [Google Scholar] [CrossRef]
- Xu, Z.; Tong, G.; Zhang, L.; Guo, Y. Experimental and numerical study of 7A04-T6 extruded aluminium alloy lipped angle columns in axial compression. Thin-Walled Struct. 2022, 179, 109573. [Google Scholar] [CrossRef]
- Li, W.; Jing, Y.; Zhou, T.; Xing, G. A new ductile fracture model for structural metals considering effects of stress state, strain hardening and micro-void shape. Thin-Walled Struct. 2022, 176, 109280. [Google Scholar] [CrossRef]

| Elastic Properties | Plastic Properties | ||
|---|---|---|---|
| Young’s modulus, MPa | Poisson’s ratio | Compressive yield strength, MPa | Strain hardening exponent, n |
| 71,000 | 0.33 | 280 | 0.2 |
| Item | Contact Side | Target Side |
|---|---|---|
| Mesh | Fine | Coarse |
| Geometry | Convex | Flat or concave |
| Material | Soft | Stiff |
| Billet Diameter (Length = 120 mm) | Mesh Size (mm) | Skewness Rating |
|---|---|---|
| 10 mm | 2.0 | 0.02865 |
| 15 mm | 2.2 | 0.040697 |
| 20 mm | 3.0 | 0.063374 |
| 25 mm | 3.0 | 0.068657 |
| 30 mm | 3.5 | 0.096876 |
| 35 mm | 4.0 | 0.083125 |
| 40 mm | 4.0 | 0.10409 |
| Coefficient of Friction | K1 | K2 | |||||
|---|---|---|---|---|---|---|---|
| 10 | 15 | 20 | 25 | 30 | 40 | ||
| µ = 0.16 | 0.7 | 0.8 | 1.000 | 1.135 | 1.25 | 1.25 | 1.34 |
| µ = 0.12 | 0.7 | 0.9 | 1.000 | 1.25 | 1.44 | 1.44 | 1.52 |
| µ = 0.35 | 0.7 | 0.7 | 0.7 | 0.85 | 0.85 | 0.85 | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lagat, D.; Munawar, H.; Alugongo, A.; Rutto, H. A Numerical Model for Inelastic Buckling in Cold Upset Forging: Stress Analysis and Optimal Billet Geometry. Processes 2025, 13, 2078. https://doi.org/10.3390/pr13072078
Lagat D, Munawar H, Alugongo A, Rutto H. A Numerical Model for Inelastic Buckling in Cold Upset Forging: Stress Analysis and Optimal Billet Geometry. Processes. 2025; 13(7):2078. https://doi.org/10.3390/pr13072078
Chicago/Turabian StyleLagat, Dan, Huzeifa Munawar, Alfayo Alugongo, and Hilary Rutto. 2025. "A Numerical Model for Inelastic Buckling in Cold Upset Forging: Stress Analysis and Optimal Billet Geometry" Processes 13, no. 7: 2078. https://doi.org/10.3390/pr13072078
APA StyleLagat, D., Munawar, H., Alugongo, A., & Rutto, H. (2025). A Numerical Model for Inelastic Buckling in Cold Upset Forging: Stress Analysis and Optimal Billet Geometry. Processes, 13(7), 2078. https://doi.org/10.3390/pr13072078






