Holistically Green and Sustainable Pathway Prioritisation for Chemical Process Plant Systems via a FAHP–TOPSIS Framework

Abstract

Multi-criteria Decision Making (MCDM) presents a novel approach towards truly holistic green sustainability, particularly within the context of chemical process plants (CPPs). ASPEN Plus v12.0 was utilised for two representative CPP cases: isopropanol (IPA) production via isopropyl acetate, and green ammonia (NH₃) production. An integrated Fuzzy Analytic Hierarchy Process (FAHP) and Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) was modelled in MATLAB v24.1 to prioritise the holistically green and sustainable pathways. Life cycle assessments (LCAs) were employed to select the pathways, and the most suitable sub-criteria per the four criteria are as follows: social, economic, environmental, and technical. In descending order of optimality, the pathways were ranked as follows for green NH₃ and IPA, respectively: Hydropower (HPEA) > Wind Turbine (WGEA) > Biomass Gasification (BGEA)/Solar Photovoltaic (PVEA) > Nuclear High Temperature (NTEA), and Propylene Indirect Hydration (IAH) > Direct Propylene Hydration (PH) > Acetone Hydrogenation (AH). Sensitivity analysis evaluated the FAHP–TOPSIS framework to be overall robust. However, there are potential uncertainties within and/or among sub-criteria, particularly in the social dimension, due to software and data limitations. Future research would seek to integrate FAHP with VIKOR and the Preference Ranking Organization Method for Enrichment Evaluation (PROMETHEE-II).

1. Introduction

Multi-criteria Decision Making/Analysis (MCDM/A) is an instrumental research branch within decision-making theory [1]. MCDM/A can be divided into two categories: Multi-Objective Decision Making (MODM) and Multi-Attribute Decision Making (MADM). MODM involves obtaining a set of continuous, competing alternatives—from two or more criteria—that require simultaneous optimisation, with respect to constraints via multi-objective programming; examples include genetic algorithm (GA) and Particle Swarm Optimisation (PSO) [1,2,3].

In comparison, MADM addresses problems that have a limited number of discrete, predetermined alternatives; examples include Complex Proportional Assessment (COPRAS) and its progenitor method, Simple Additive Weighting (SAW) [2,3]. Due to their versality and multi-dimensional applications, MCDM methods have been implemented across various disciplines, from (municipal solid) waste management to the production of raw materials [4,5,6]. MCDM/A can be utilised individually or as part of an integrated model, such as the Fuzzy Analytic Hierarchy Process (FAHP) or the FAHP-Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS). Resultantly, different MCDM methods can provide varying ranking results based on their methodologies and the preference of the decision-makers [7]. Decision-makers can then classify and prioritise alternative solutions, based on criteria rankings, and choose which one is the overall “best” [8,9,10,11]. A simple example of an MCDM process is provided in Figure 1, which was used as the basis for the FAHP–TOPSIS framework of this study.

Figure 1. A simplified top-to-bottom MCDM process model, which was used to develop the FAHP–TOPSIS framework [12].

In more recent years, MCDM/A methods have enabled decision-makers to approach green sustainability and sustainable development from more holistic perspectives; socially, economically, environmentally, etc. This has become progressively more important in recent years, as human society and the natural environment may suffer from severe and irreversible consequences, if there is no timely intervention [9,10,11,13]. Sustainability has existed as a concept for centuries, but it is only in the past century that humanity started to grow aware of the consequences in various dimensions: socially, economically, and/or environmentally [14,15,16,17]. Integrated MCDM/A frameworks could be the key towards achieving green sustainability in chemical process plants (CPPs), especially through a holistic approach that has not been fully explored in the existing literature [18,19,20,21,22]. Therefore, this study proposes a novel MCDM approach to implementing truly holistic (green) sustainability for CPPs, which does not neglect/significantly favour any sustainability-related dimension(s). An integrated MCDM framework (FAHP–TOPSIS) was developed and implemented to prioritise holistically green and/or sustainable pathways for two representative CPP case studies: isopropanol (IPA) synthesis via isopropyl acetate and green NH₃ production. IPA synthesis and green NH₃ production are incredibly prevalent in sustainability-related topics, particularly the latter as a staple of chemical engineering, with the potential of being/becoming key drivers towards global decarbonisation and green sustainability targets [23,24,25,26,27].

2. Materials and Methods

2.1. MCDM Framework

FAHP was used to derive the criteria weights for MCDM evaluation based on both quantitative and qualitative criteria and sub-criteria, with more accuracy and reliability than the standard AHP methodology. FAHP enabled the use of linguistic “fuzzy” variables for non-numerical (i.e., qualitative) data in MCDM, with Saaty’s relatively straightforward 1–9 pairwise comparison scoring system [20], provided that they were converted into corresponding and/or reciprocal triangular fuzzy numbers (TFNs). This was achieved via a linguistic-based fuzzy comparison matrix (Appendix A). Appendix A illustrates that each linguistic-based judgement shares a corresponding fuzzy TFN [19], which can then be processed for straightforward application(s) in TOPSIS/additional MCDM ranking methods. TOPSIS was selected for its high computational efficiency, decision-making capabilities with minimal input, and straightforward outputs based on the positive-ideal and negative-ideal solutions [5,23,25,28]. Section 3.2.1 outlines the TOPSIS methodology in a step-by-step process [5,23,29].

Flexibility is one of the key attributes of AHP, in addition to its simplicity, ease of use, and its ability—by itself—to produce consistent judgements [18,20,22]. However, a certain level of complexity is still required to establish the context of the problem [22], albeit it also cannot compromise the flexibility of the AHP framework [12,21]. Due to its high flexibility, an increasing number of studies have adopted hybrid AHP frameworks with fuzzy logic [6,23]. This study has adopted this integrated MCDM approach to mitigate/remove the limitations of individual methods [23,25] and optimise the overall decision-making process [6,18,24].

In comparison, TOPSIS was first developed and presented by Hwang & Yoon in 1981 [5,23,26,27]. Alternatives are evaluated and chosen based on their respective distances from the positive-ideal solution (i.e., maximisation of positive criteria and minimisation of negative criteria) and the negative-ideal solution (i.e., maximisation of negative criteria and minimisation of positive criteria) [5,23,25]. The key advantages of TOPSIS are that decision-makers do not need to implement numerous inputs, high computational efficiency, and the outputs are relatively straightforward to read and understand [23,25,28]. TOPSIS also utilises criteria information to its fullest while not requiring the criteria to be independent; however, this is only possible when all information is available and accurate [25,28]. Moreover, while there are advantages, TOPSIS does have two notable weaknesses: the requirement of vector normalisation for multi-dimensional problems [23,28] and the fact that the relative importance of the distances to the ideal solutions is not properly considered [25,27]. Additionally, a potential weakness/limitation of TOPSIS is the use of crisp data values. Real-life scenarios are often fraught with uncertainty and relativity [26,28,29], which is why fuzzy logic has been incorporated into the FAHP–TOPSIS framework of this study.

A consistency level of ≤10% (CR ≤ 0.1) was deemed acceptable [30,31]. To minimise potential information loss during weight aggregation, the combined coefficient u = 0.5 was assigned. It should also be noted that there is no single ideal method for deriving criterion (and sub-criterion) weights; the literature has varying methodologies that can be equally valid [20,31,32], and thus depends on the surrounding circumstances. Fuzzy pairwise judgement matrices were established for the first-layer index (Appendix B) and the sub-criteria of each criterion (Appendix C and Appendix D). These matrices were derived from expert input (experienced in chemical process engineering, sustainability analysis, and MCDM) and from secondary data in high-quality, peer-reviewed literature (see References). Because CR ≤ 0.1 for all matrices, the consistency levels were deemed acceptable. To derive the objective weights, data first had to be normalised in TOPSIS via vector normalisation, due to the differences in scales and/or units of measurement. Positive indicators and negative indicators were calculated via Equation (10) and Equation (11), respectively. Entropy weighting was utilised to calculate the objective (sub-criteria) weights, W_o. Section 3.2.2 elaborates on the calculations of objective weights (W_o), comprehensive weights (subjective) (W_c), and combination weights (W_i) in Equations (12)–(17).

2.2. Case Studies

An IPA plant at Sinopec Zhenhai Refining & Chemical Co., Ltd., in the Zhenhai District of Ningbo, China, was simulated via ASPEN v12. The main raw material was propylene, one of the by-products of a related ethylene company project. An annual plant capacity of 80,000 tons of ultra-pure, electronic-grade IPA was specified, produced (along with 51,000 tons of anhydrous ethanol annually) via esterification with acetic acid, subsequent hydrogenation and double-effect distillation. The resulting IPA has a purity of ~99.99%, while the anhydrous ethanol has a >99.5% purity. The technologies behind the processes were upgraded in accordance with “Made in China 2025 (MIC2025)” green development targets [33,34]. Due to its location on one of the company’s reserved development sites, the IPA plant simulation benefits from the following: favourable geography, support from local policies, a plentiful supply of raw materials, and well-developed infrastructure (e.g., transportation network). Figure 2 illustrates the process flow diagram, with the entire process simulation in Figure 3 and the plant layout in Figure 4.

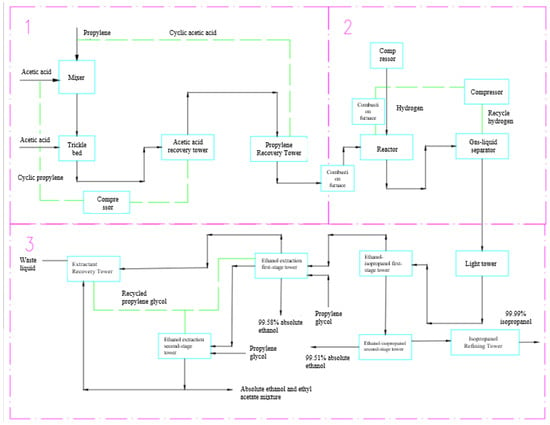
Figure 2. Process flow diagram for IPA synthesis via isopropyl acetate, steps 1–4: (a = 1) isopropyl acetate synthesis, (b = 2) isopropanol synthesis, (c = 3) isopropanol and alcohol refining.

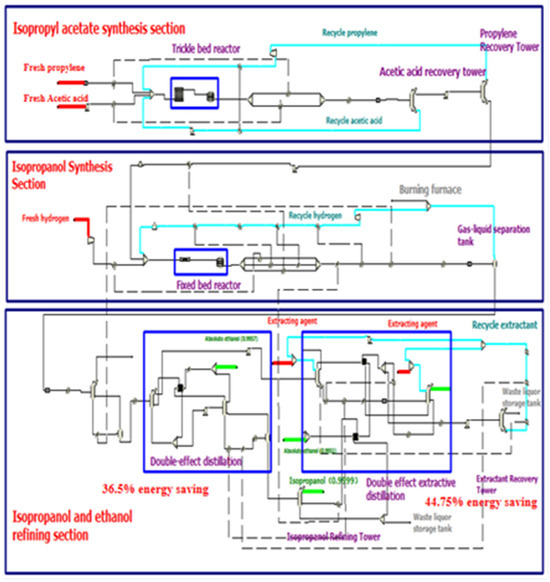
Figure 3. Complete top-to-bottom process simulation per section, modelled in ASPEN v12, highlighting the energy savings and extraction processes per section.

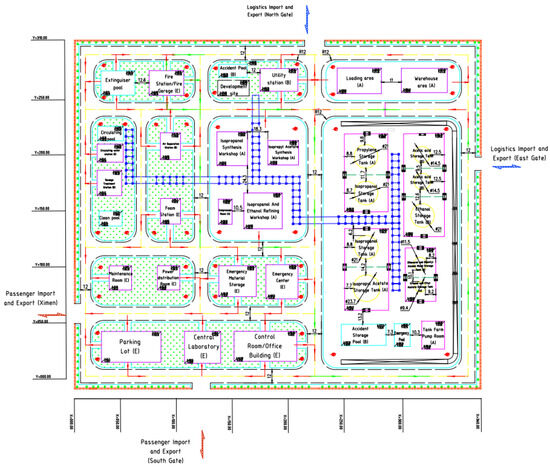
Figure 4. Layout of the simulated IPA synthesis plant, which details the logistics and passenger impots and exports, as well as safety nodes, such as available fire stations.

A small-scale, modular green NH₃ production case study was simulated via the Peng–Robinson (PENG–ROB) in ASPEN Plus v12.0. PENG-ROB is one of the most popular property methods for NH₃ production, primarily due to its high reliability and applicability to various system types. This includes (relatively) non-ideal systems, in contrast to the Soave–Redlich–Kwong equation [35]. The standard 3:1 ratio between H₂ and N₂ was decided for reaction, R-1, to synthesise liquid ammonia. The flowsheet model for clean, modular NH₃ production (Figure 5) via hydrolysis can be divided into three ‘modules’, all developed by [36]: gaseous hydrogen generation via the desalinisation of seawater coupled with Polymer Electrolyte Membrane (PEM) electrolysis (blue), gaseous nitrogen production via air separation unit (ASU) that utilises a cryogenic distillation process (red), and NH₃ synthesis (green).

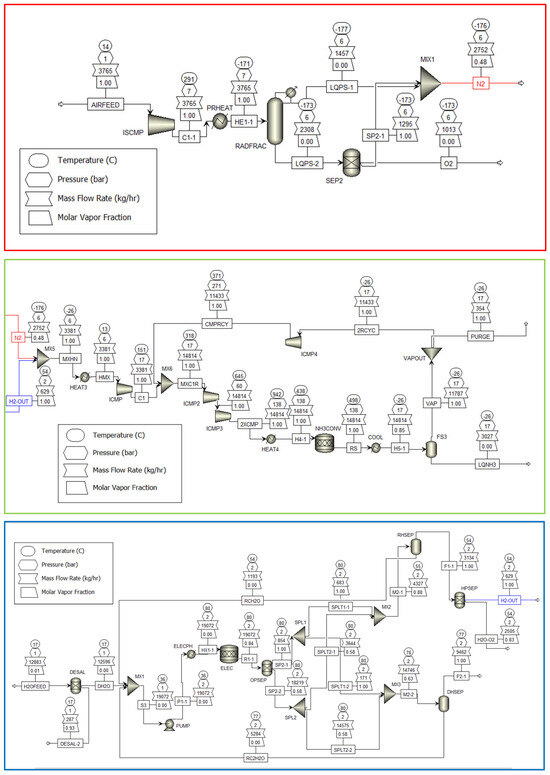
Figure 5. Clean NH₃ production flowsheet model. Three modules: hydrogen generation (blue), nitrogen generation (red), NH₃ synthesis (green). The ‘H2-OUT’ (blue) and ‘N2’ (red) streams are input streams for the NH₃ synthesis module.

Table 1 shows the potential pathways that were identified via LCA for each case study. The integrated FAHP–TOPSIS framework covers four criteria regarding IPA and green NH₃ production: technical, economic, environmental, and social. Each criterion has three sub-criteria that were specific to each case study (Table 2 and Table 3), which were derived based on their prevalence and prominence in the relatively recent literature [9,37,38]. Three sub-criteria per criterion were chosen as the appropriate number; too few would be unusable in the MATLAB model, while too many would increase the likelihood of data distortion, such as rank reversal. The literature review highlights an apparent lack of the in-depth literature that explores the social dimension of holistic green sustainability over the past few decades, and even quite recently, despite the increasing awareness and necessity of holistic green sustainability. Therefore, the social (and by extension, political) criteria for each case study have been expanded with a greater number of CPP-specific social sub-criteria for MCDM. This is based upon literature findings from [8,9,37,38].

Table 1. Potential green and/or sustainable pathways for IPA synthesis and green NH₃ production.

Case Study	Potential Pathways
IPA via isopropyl acetate	Direct propylene hydration (PH) Propylene indirect hydration (IAH) Acetone hydrogenation (AH)
Green NH3	Wind turbine electrolysis (WGEA) Solar photovoltaic electrolysis (PVEA) Hydropower electrolysis (HPEA) Biomass gasification electrolysis (BGEA) Nuclear high temperature electrolysis (NTEA)

Table 2. Criteria and sub-criteria for IPA: technical (tech), economic (econ), environmental (env), and social (soc).

Tech (A)	Econ (B)	Env (C)	Soc (D)
A1: Conversion rate	B1: Total operational costs	C1: Human toxicity	D1: Intrinsic safety
A2: IPA selectivity	B2: Process complexity	C2: CO2 emissions	D2: Policy relevance
A3: Tech maturity	B3: Total annual costs	C3: Pollution	D3: Public perception

Table 3. Criteria and sub-criteria for green ammonia production: environmental (env), economic (econ), social (soc), and technical (tech).

Env (A)	Econ (B)	Soc (C)	Tech (D)
A1: Biodiversity loss	B1: Total operational costs	C1: Employer safety	D1: Exergy efficiency
A2: GHG emissions	B2: Sales prices	C2: Policy applicability	D2: Energy efficiency
A3: Global warming potential	B3: Net present value potential	C3: Public perception	D3: Green performance

3. Results

3.1. FAHP–TOPSIS

TOPSIS was applied to rank the IPA and green NH₃ production pathways. Because the pathway data has already been normalised and transformed into P_ij (Appendix E), further manual data processing was not required for the calculations in this section. Only the following sub-criteria weights were used in the ranking calculations: W_o, W_c, and W_i. W_o, W_c, and W_i encompass a holistically green and/or sustainable ‘perspective’ for each pathway by creating an in-depth profile of how objectivity, (comprehensive) subjectivity, and/or the combination of both can affect the criteria/sub-criteria. W_c was selected over W_s to consider the product subjectivity of the criteria and sub-criteria. Table 4 and Table 5 contain the results of the weight aggregation, which were derived from the results in Appendix F.

Table 4. All weight results by sub-criteria for the IPA synthesis pathways: A = Tech, B = Econ, C = Env, and D = Soc.

Criteria	Sub-Criteria	Ws	Wc	CR	Wo	Wi
A	A1	0.372	0.0455	0.0873	0.0735	0.0607
	A2	0.221	0.0270		0.0769	0.0479
	A3	0.407	0.0499		0.0675	0.0609
B	B1	0.418	0.168	0.0566	0.0732	0.116
	B2	0.249	0.100		0.0675	0.0863
	B3	0.333	0.134		0.0914	0.116
C	C1	0.489	0.142	0.0455	0.0727	0.107
	C2	0.296	0.0859		0.0734	0.0834
	C3	0.216	0.0626		0.0675	0.0683
D	D1	0.454	0.0839	0.0349	0.0769	0.0843
	D2	0.325	0.0601		0.183	0.110
	D3	0.221	0.0408		0.0769	0.0588

Table 5. All weight results by sub-criteria for the green NH₃ production pathways: A = Env, B = Econ, C = Soc, and D = Tech.

Criteria	Sub-Criteria	Ws	Wc	CR	Wo	Wi
A	A1	0.372	0.0455	0.0873	0.0735	0.0607
	A2	0.221	0.0270		0.0769	0.0479
	A3	0.407	0.0499		0.0675	0.0609
B	B1	0.418	0.168	0.0566	0.0732	0.116
	B2	0.249	0.100		0.0675	0.0863
	B3	0.333	0.134		0.0914	0.116
C	C1	0.489	0.142	0.0455	0.0727	0.107
	C2	0.296	0.0859		0.0734	0.0834
	C3	0.216	0.0626		0.0675	0.0683
D	D1	0.454	0.0839	0.0349	0.0769	0.0843
	D2	0.325	0.0601		0.183	0.110
	D3	0.221	0.0408		0.0769	0.0588

D_i⁺ and D_i⁻ represent the distances from the positive Equation (11) and negative Equation (12) ideal solutions, respectively, with u = 0.5. Lower D_i⁺ values denote smaller deviations from the positive-ideal solutions; thereby, aligning closest with positive sub-criteria/farthest from negative criteria [32]. This denotes the most optimal pathways. Therefore, IAH and HPEA are the most optimal pathways for their respective case studies. Moreover, the use of individual and combined weights helped validate the pathway rankings obtained via TOPSIS and suggests relatively high ranking stability, albeit this assumption does not consider the impacts of sensitivity analysis (Figure 6 and Figure 7). Table 6 illustrates the distances for the IPA and green NH₃ pathways [2].

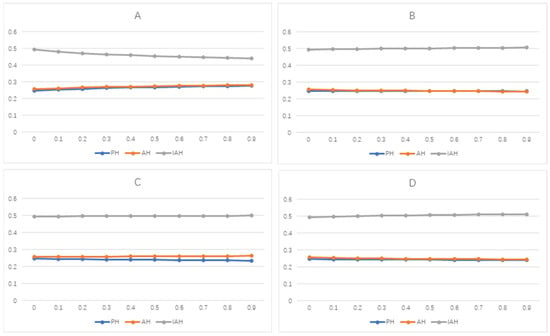
Figure 6. C_i⁺ results relative to changes in technical (A; top-left), economic (B; top-right), environmental (C; bottom-left), and social (D; bottom-right) criterion weights for IPA pathways.

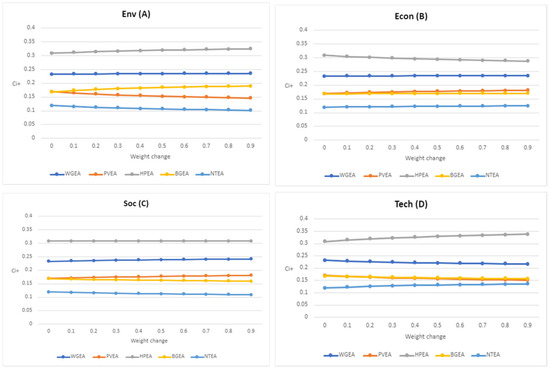
Figure 7. C_i⁺ results relative to changes in environmental (A; top-left), economic (B; top-right), social (C; bottom-left), and technical (D; bottom-right) criterion weights for green NH3 pathways.

Table 6. Distances from the positive and negative ideal solutions for each IPA (top) and green NH₃ (bottom) pathway, using combination, objective, and (comprehensive) subjective sub-criteria weights only.

	Wi		Wo		Wc
	Di+	Di−	Di+	Di−	Di+	Di−
PH	0.532	0.298	0.573	0.307	0.504	0.286
AH	0.551	0.326	0.588	0.335	0.529	0.315
IAH	0.250	0.632	0.292	0.648	0.206	0.625
	Wi		Wo		Wc
	Di+	Di−	Di+	Di−	Di+	Di−
WGEA	0.244	0.267	0.247	0.280	0.235	0.259
PVEA	0.366	0.225	0.392	0.207	0.344	0.233
HPEA	0.180	0.404	0.161	0.431	0.192	0.375
BGEA	0.365	0.222	0.386	0.219	0.341	0.228
NTEA	0.388	0.142	0.411	0.128	0.364	0.156

Goodness-of-fit is the degree of fitness of each potential pathway to the D_i⁻ and D_i⁺ values, in accordance with Equation (13). No significant deviations were apparent in the results for each weight type, which suggests relatively high stability. Moreover, the goodness-of-fit for D_i⁺ (C_i⁺) appears to be in line with the pathway rankings for each case study, and therefore enhances the reliability and accuracy of the rankings for decision-making. Table 7 shows the goodness-of-fit, C_i⁻ and C_i⁺, for each potential pathway in IPA and green NH₃ production. The criterion weights (A–D) were altered in +0.1 increments from +0 to +0.9, with a total of 40 variations with respect to the calculated C_i⁺ values. Figure 6 and Figure 7 show that each pathway maintains relative stability across both case studies, with negligible change(s) in C_i⁺ for W_i in response to criterion weight change.

Table 7. Goodness-of-fit for each IPA (top) and green NH₃ (bottom) pathway, using combination, objective, and comprehensive subjective sub-criteria weights only.

	Wi		Wo		Wc
	Ci−	Ci+	Ci−	Ci+	Ci−	Ci+
PH	0.359	0.248	0.349	0.249	0.362	0.244
AH	0.371	0.257	0.363	0.259	0.373	0.251
IAH	0.716	0.495	0.689	0.492	0.752	0.506
	Wi		Wo		Wc
	Ci−	Ci+	Ci−	Ci+	Ci−	Ci+
WGEA	0.522	0.233	0.531	0.241	0.525	0.229
PVEA	0.381	0.170	0.345	0.157	0.404	0.176
HPEA	0.692	0.309	0.728	0.330	0.662	0.289
BGEA	0.378	0.169	0.362	0.164	0.401	0.175
NTEA	0.268	0.120	0.238	0.108	0.299	0.131

3.2. Formatting of Mathematical Components

3.2.1. TOPSIS

TOPSIS has high computational efficiency, and decision-making capabilities that require minimal input [23,25,28]. The outputs are based upon the positive-ideal and negative-ideal solutions [5,23,25,28]. This section provides a set-by-step summary of the TOPSIS methodology, in the form of the following equations:

$$A={\left(a_{ij}\right)}_{mn},$$

(1)

where the decision matrix, A, was calculated from m = alternatives, with respect to n criteria; a_ij = intersection of each criterion and alternative (Equation (1)).

$$r_{ij}={\displaystyle \frac{a_{ij}}{\surd \sum _{k=1}^m{a_{kj}}^2}}.$$

(2)

Equation (2) derives the normalised decision matrix, R, with the equation for r_ij._, typically via vector normalisation (i = 1, 2, 3…, m; j = 1, 2, 3…, n).

$$T={{(t}_{ij})}_{mn}$$

(3)

and

$$t_{ij}=r_{ij}\times w_j.$$

(4)

Equation (3) calculates the weighted normalised matrix T via Equation (4). i = 1, 2, 3…, m; j = 1, 2, 3…, n. w_j = j criteria weighting.

$$S^{+}=\{{{\tilde{t}}_1}^{+},{{\tilde{t}}_2}^{+},{{\tilde{t}}_n}^{+}\}$$

(5)

and

$$S^{-}=\{{{\tilde{t}}_1}^{-},{{\tilde{t}}_2}^{-},{{\tilde{t}}_n}^{-}\}.$$

(6)

The positive-ideal and negative-ideal solutions were derived via Equation (5) and Equation (6), respectively. [29] applies fuzzy logic, while the classical method applies crisp numbers.

$${D_i}^{+}=\surd \sum _{j=1}^n{(t_{ij}-{t_j}^{+})}^2$$

(7)

and

$${D_i}^{-}=\surd \sum _{j=1}^n{(t_{ij}-{t_j}^{-})}^2$$

(8)

Equations (7) and (8) calculated the distances of each alternative from the positive-ideal and negative-ideal solutions, D_i⁺ and D_i⁻, respectively.

$$C_i={\displaystyle \frac{{D_i}^{-}}{({D_i}^{+}+{D_i}^{-})}}.$$

(9)

Equation (9) was used to derive the relative closeness, C_i; ‘1’ = positive-ideal and ‘0’ = negative-ideal. Preference ranking order was created on C_i, in which max C_i represents the optimum alternative.

3.2.2. Weight Calculations

$$f_{ij}(+)={\displaystyle \frac{f_{ij}^{\prime }-\mathit{min}\left(f_{ij}^{\prime }\right)}{\left(\mathit{max}{f}_{ij}^{\prime }-\mathit{min}{f}_{ij}^{\prime }\right)}}$$

(10)

and

$$f_{ij}(-)={\displaystyle \frac{\mathit{max}\left(f_{ij}^{\prime }\right)-f_{ij}^{\prime }}{\left(\mathit{max}{f}_{ij}^{\prime }-\mathit{min}{f}_{ij}^{\prime }\right)}},$$

(11)

where f_ij represents normalised data, and f’_ij represents the original data for IPA and green NH₃ (Appendix G). To ensure non-zero results for later logarithmic calculations that would lead to calculation errors but also avoid data distortion, a negligible constant C of 0.0001 was added to the normalised data (Appendix H).

$$P_{ij}={\displaystyle \frac{f_{ij}}{{\Sigma }_{i-1}^n{f}_{ij}}},$$

(12)

$$e_j=-{\displaystyle \frac{1}{\mathit{ln}n}}{\Sigma }_{i=1}^n\left(P_{ij}\mathit{ln}{P}_{ij}\right),$$

(13)

$$g_j=1-e_j,$$

(14)

and

$$W_o={\displaystyle \frac{g_j}{{\Sigma }_{j-1}^m{g}_j}}.$$

(15)

Characteristic proportions, P_ij, were calculated via Equation (12). The entropy value, e_j, and the coefficient of difference, g_j, for the i-th object with respect to each j-th (sub-)criterion were then derived via Equation (13) and Equation (14), respectively. Here, n is the number of pathways/routes: n = 3 for IPA and n = 5 for green NH₃. Equation (15) was applied to calculate W_o, where m is the total number of g_j values.

$$w_c=w_r{w}_s$$

(16)

and

$$w_i={\displaystyle \frac{{\left(w_c\right)}^u{\left(w_o\right)}^{1-u}}{{\Sigma }_{i=1}^n{\left(w_c\right)}^u{\left(w_o\right)}^{1-u}}}$$

(17)

Comprehensive subjective weights (W_c) must also be calculated to determine the combination weights (W_i) that can be applied in TOPSIS. Equations (16) and (17) are used to derive each set of weights, respectively, where u = 0.5.

4. Discussion

The FAHP–TOPSIS framework optimises the decision-making process regarding IPA and green NH₃ production via pathway prioritisation based on quantitive and qualitative case-specific criteria and/or sub-criteria, from a holistically green and/or sustainable perspective. FAHP enables the use of qualitative data via TFNs for criteria and sub-criteria weighting. TOPSIS is a straightforward and easy-to-understand methodology with high computational efficiency that relies on minimal input to rank potential pathways [5,23,25,28]. The calculation of positive-ideal solution and negative-ideal solutions is based on decision-making from quantitative and qualitative positive and negative criteria, which leads to more accurate and reliable rankings [5,23,25]. In this paper, the “decision-makers” are regarded as a more homogeneous identity, primarily for the sake of ease and to focus on the MCDM framework. In real-life, the composition of decision-makers would be more explicitly diverse, from industry professionals to more business-orientated stakeholders [5].

IAH (0.250) and HPEA (0.180) were prioritised as the most optimal pathways because they had the smallest D_i⁺ values in W_i for their respective case studies. Likewise, the least optimal pathways were identified as AH (0.551) and NTEA (0.388). Therefore, the most to least optimal pathways for IPA were IAH > PH > AH. However, there may be slight contention between the prioritisation of PH and AH due to the closeness in D_i⁺ values. The green NH₃ pathways were prioritised as follows: HPEA > WGEA > BGEA/PVEA > NTEA, in which the close D_i⁺ values may also cause contentious ranking between BGEA and PVEA, particularly dependent on criteria and/or sub-criteria weighting. This may be attributable to the more subjective sub-criteria weights within the economic and technical dimensions; for example, the varied decision-maker perceptions of PV installation and maintenance costs. Nonetheless, the overall C_i⁺ values for W_i aligns with this order of pathway prioritisation in terms of balance and stability. And as it was highly recommended in the literature, sensitivity analysis (Figure 6 and Figure 7) was thus carried out to evaluate the overall robustness of the FAHP–TOPSIS framework. The sensitivity analysis demonstrates that there are negligible changes in C_i⁺ relative to weight change (Figure 6 and Figure 7); thus, a robust and relatively stable MCDM framework that can generate relatively reliable and accurate pathway rankings.

That said, there are uncertainties among sub-criteria by themselves and in relation to each other, especially in terms of potential changes over time. This can make it difficult to ascertain the extent to which each sustainability dimension (social, economic, etc.) can affect pathway rankings, and specifically, which pathways are most optimal per dimension. The degree of uncertainty may be attributed to a lack of access to reliable and accurate software tools, such as those used for techno-economic analysis. Sub-criteria like NPV, policy applicability, and equipment costs can be greatly influenced by the contingent of various spatial–temporal and often multi-dimensional drivers; this includes seasonal variations in feedstock supply, local/regional/national socio-political factors, and transportation logistics [36,38,39,40,41,42,43]. Model development is contingent on a relatively case-to-case basis, especially if it is designed to be optimised towards truly holistic green sustainability in any CPP. Nevertheless, the proposed FAHP–TOPSIS framework could prove valuable as an adaptable decision-support tool that can ideally balance quantitative process modelling with qualitative sustainability assessments. Criteria and sub-criteria weights could be studied to identify potential weighting issues, for individuals to large-scale organisations (in and outside the context of sustainability). However, how an organisation/individual(s) would act on this information may greatly depend on various factors, e.g., stakeholders = heavy skewness towards the economic dimension, and thus more risk aversion toward anything that could affect profitability.

Future work should seek to develop and implement a more robust and reliable framework for further overall optimisation; specifically, an integrated FAHP–VIKOR with PROMETHEE-II framework with a more explicit integration of process systems engineering (PSE) tools, such as LCAs, LCCA, and social-LCAs. VIKOR, while similar to TOPSIS, has normalised values that are independent of the criterion’s evaluation unit via linear normalisation instead of TOPSIS’ vector normalisation [22,30]. Furthermore, VIKOR can provide a more reliable representation of decision-maker viewpoints via compromise solutions without data distortion [30], especially as closeness to the ideal solution may not equate to the most ideal solution(s) [22]. PROMETHEE-II is a popular MCDM method in green sustainable research fields because it allows for a complete ranking of alternatives [22,37,40]. Additionally, it has a relatively high level of stability and reliability while also providing decisive results with/without grey data and without requiring pre-requisite data normalisation [23,39]. FAHP would provide appropriate criteria and sub-criteria weightings via decision-makers while also mitigating one of PROMETHEE’s key potential weaknesses: questionably reliable criteria/sub-criteria weighting [25,31].

5. Conclusions

The FAHP–TOPSIS framework serves to validate the implementation of an integrated MCDM framework for prioritising holistically green IPA and NH₃ production pathways. However, data must be clearly processed to maximise the understanding and effectiveness of the FAHP–TOPSIS framework. According to the D_i⁺ and C_i⁺ values (Table 6 and Table 7), the most to least optimal pathway for IPA is IAH > PH > AH, albeit there may be slight contention in the prioritisation between PH and AH, as well as between BGEA and PVEA. Meanwhile, the most to least optimal pathway for green NH₃ is as follows: HPEA > WGEA > BGEA/PVEA > NTEA. These prioritisations are further validated via sensitivity analyses for each criterion, which show negligible changes in C_i⁺ relative to weight changes (Figure 6 and Figure 7) and thus a robust MCDM framework. Moreover, the C_i⁺ values for W_i align with this order of pathway prioritisation, from a more balanced and stable perspective. However, while the MCDM results provide an overall perspective with respect to each criterion, there are uncertainties among sub-criteria by themselves and in relation to each other, especially in terms of potential changes over time, exact equipment costs, NPV, and the specific social perceptions regarding the case studies.

Nevertheless, the FAHP–TOPSIS framework demonstrates that MCDM can implement greater optimisation within chemical process plants (CPPs) via pathway prioritisation based on holistically green and/or sustainable, case-specific criteria and/or sub-criteria. At a minimum, FAHP–TOPSIS could provide real-world applications as an adaptable, decision-support tool for quantitative and qualitative early-stage design. Future research should seek to develop a more comprehensive sustainability governance platform. This would involve the systematic integration of process systems engineering (PSE) tools—(life-cycle assessments (LCAs), social-LCAs, and life-cycle cost analysis (LCCA)—via Sima Pro with an integrated MCDM framework (FAHP–VIKOR with PROMETHEE-II). The improved methodology framework will further validate the employment of integrated MCDM frameworks across various CPPs. VIKOR provides a more reliable representation of decision-maker viewpoints with minimal data distortion and possible compromise solutions. PROMETHEE-II is commonly applied in green sustainable research fields, as it allows for a complete ranking of alternatives with a relatively high level of stability and reliability. Furthermore, decisive results can be derived with/without grey data, and without the requirement of data normalisation, unlike TOPSIS.