Deep-Learning-Enhanced Hybrid WOA-FMO Algorithm for Accurate PV Parameter Estimation in Single-, Double-, and Triple-Diode Models
Abstract
1. Introduction
1.1. Literature Review
1.2. Contribution
1.3. Organization
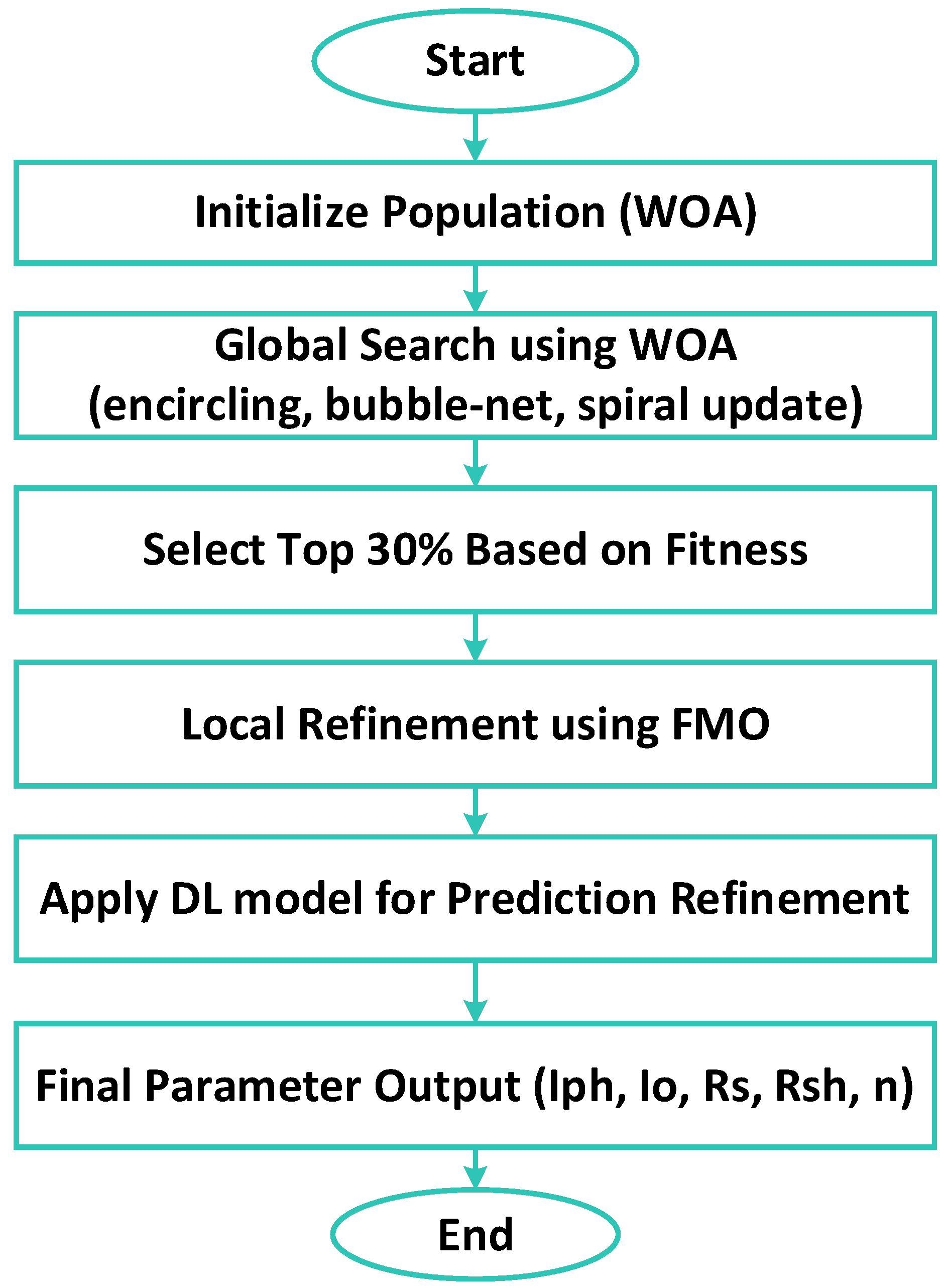
2. Proposed Framework
| Algorithm 1: Hybrid WOA-FMO enhanced with DL Integration |
| Start 1. Initial configuration
def fitness_ function(solution):
3. Position Update Function for WOA (Encircling Prey) def update_ position_ WOA (X_ best, X_ current, A, C): D = np. abs (C * X_ best − X_ current) new_ position = X_ best − A * D return new_ position 4. Position update function for FMO def update _ position_ FMO (X_ i, X _best, X _j, X _k, beta1, beta2): randn1 = np. random. randn () rand1 = np. random. rand () rand2 = np. random. rand () new_ position = X _i + beta1 * randn1 * (X _best − X _i) + beta2 * rand1 * (X _j − X _k) return new _position 5. Population initialization function def initialize_ population (P, dim): return np. random. uniform (−10, 10, (P, dim)) 6. Hybrid WOA-FMO algorithm def WOA_FMO (P, G, dim, max_ iter): 1)Initialize population population = initialize _ population (P, dim) fitness = np. array ([fitness _function(pop) for pop in population]) best_solution = population [np. argmin (fitness)] best_ fitness = np. min(fitness) 2)Generations loop for g in range(G): Update a and C
for i in range(P):
sorted_ indices = np. argsort (fitness) top_30_percent = population [sorted_ indices [:int (0.3 * P)]] 5)Local exploitation with FMO for i in range (int (0.3 * P)):
population [sorted_ indices [:int (0.3 * P))] = top_30_percent 7)Fitness evaluation fitness = np. array ([fitness_ function(pop) for pop in population]) Update best solution
7. Final algorithm for improving prediction def deep_ learning_ prediction (I_ sim, I_DL_ pred, lambda _dl): I_ final = lambda _dl * I_ sim + (1 − lambda _dl) * I_DL_ pred return I_ final 8. Calling the WOA-FMO algorithm
|
3. Problem Formulation
3.1. Objective Function
- : Is the number of data points
- : Is the measured current or power at voltage
- : Is the corresponding simulated value using model parameters
- : is the vector of unknown parameters to be optimized
3.2. Parameter Sets by Model
- Single-Diode Model (SDM):
- Double-Diode Model (DDM):
- Triple-Diode Model (TDM):
3.3. Physical Constraints
3.4. Mathematical Models of PV
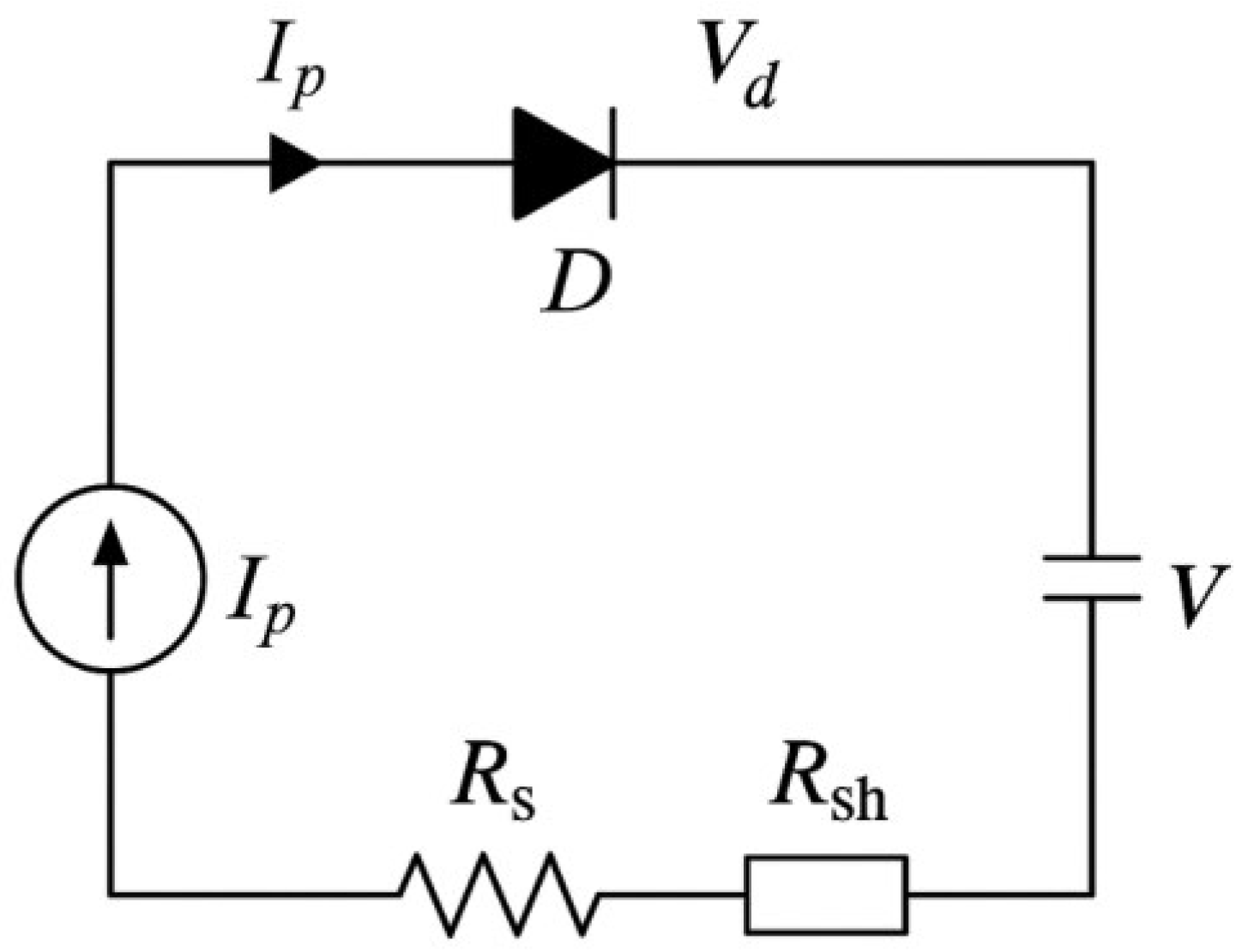
3.4.1. Single-Diode Model (SDM)
- : photo-generated current
- : diode reverse saturation current Rs (series resistance)
- : series and shunt resistance
- : ideality factor of the diode
- : elementary charge
- : cell temperature in Kelvin
- : Boltzmann constant
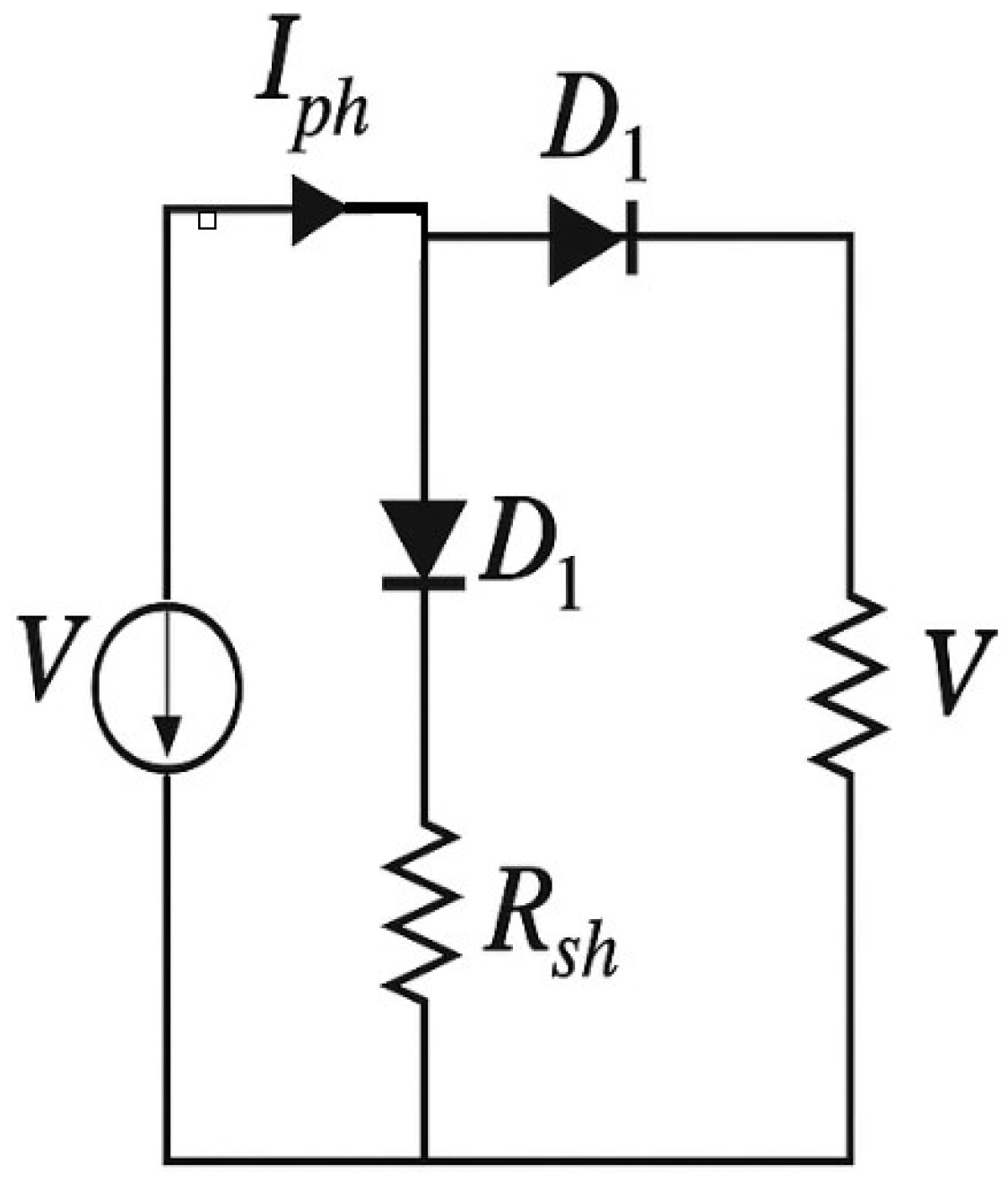
3.4.2. Double-Diode Model (DDM)
- : Saturation currents of two diodes.
- : ideality factor of the diodes
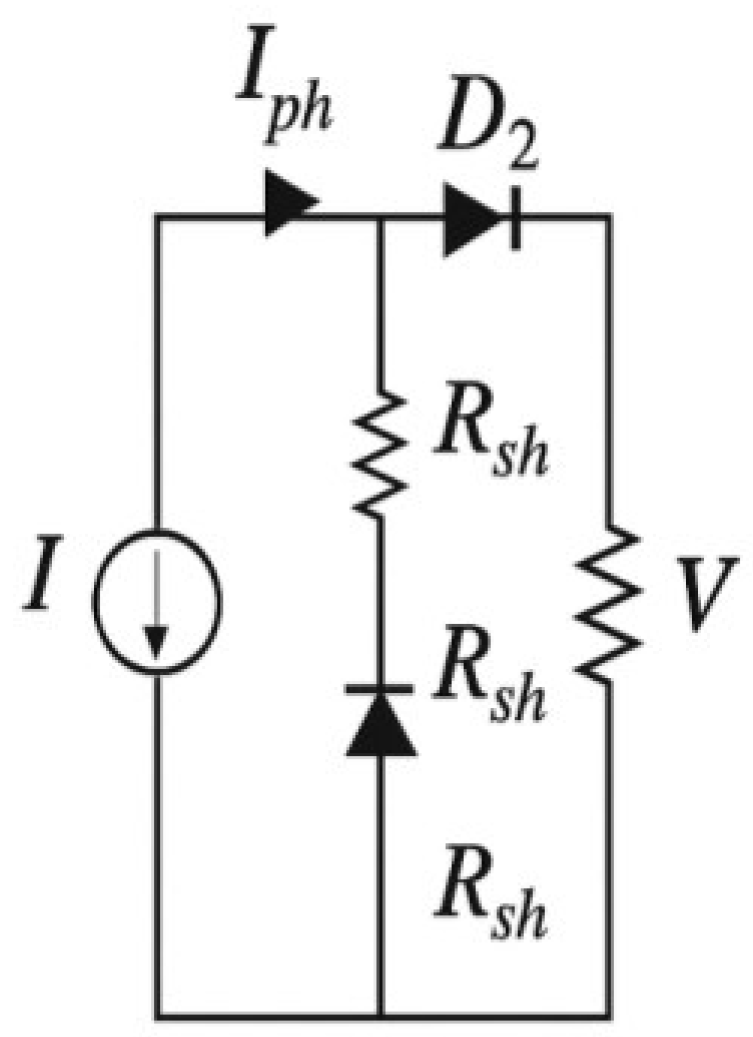
3.4.3. Triple-Diode Model (TDM)
- : Saturation current of the i-th diode
- : Ideality factor of the i-th diode
4. Materials and Methods
5. Results
5.1. Characteristics of the Solar Cell Utilized
5.2. Optimization Results for Single-Diode Model
5.3. Improvement Outcomes for Double-Diode Model
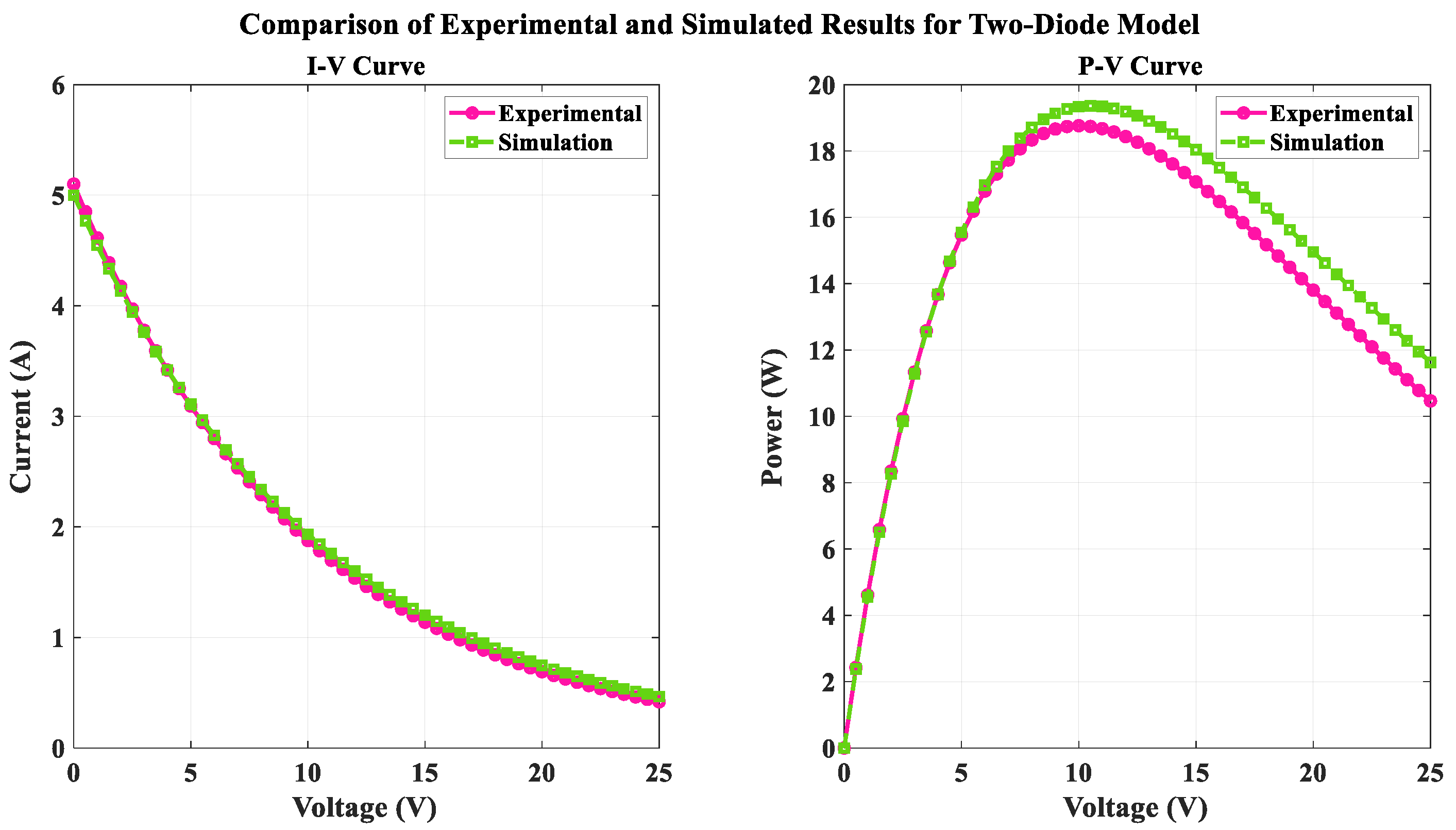
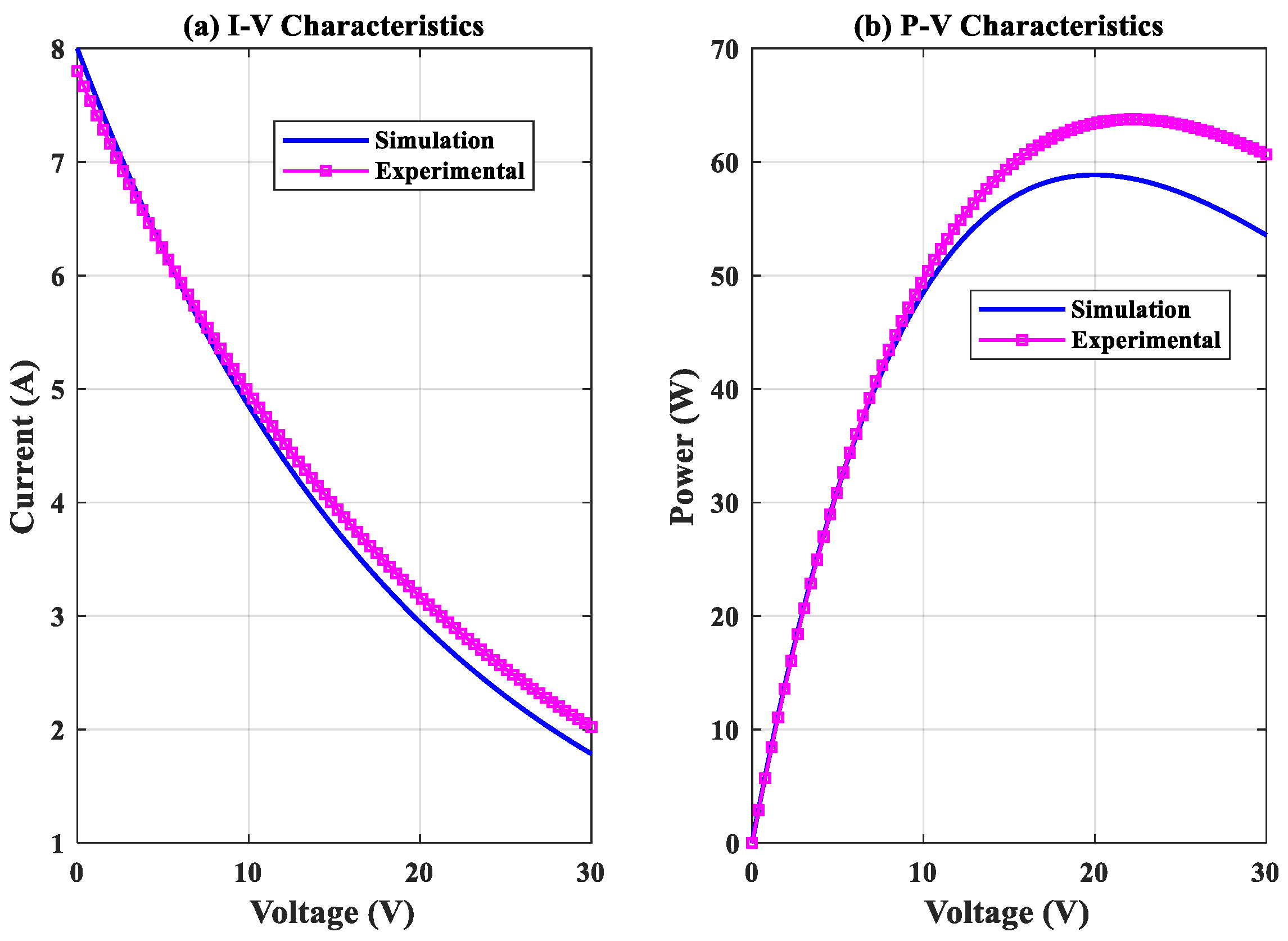
- Current-voltage (I-V) curve
- Power-voltage (P-V) curve
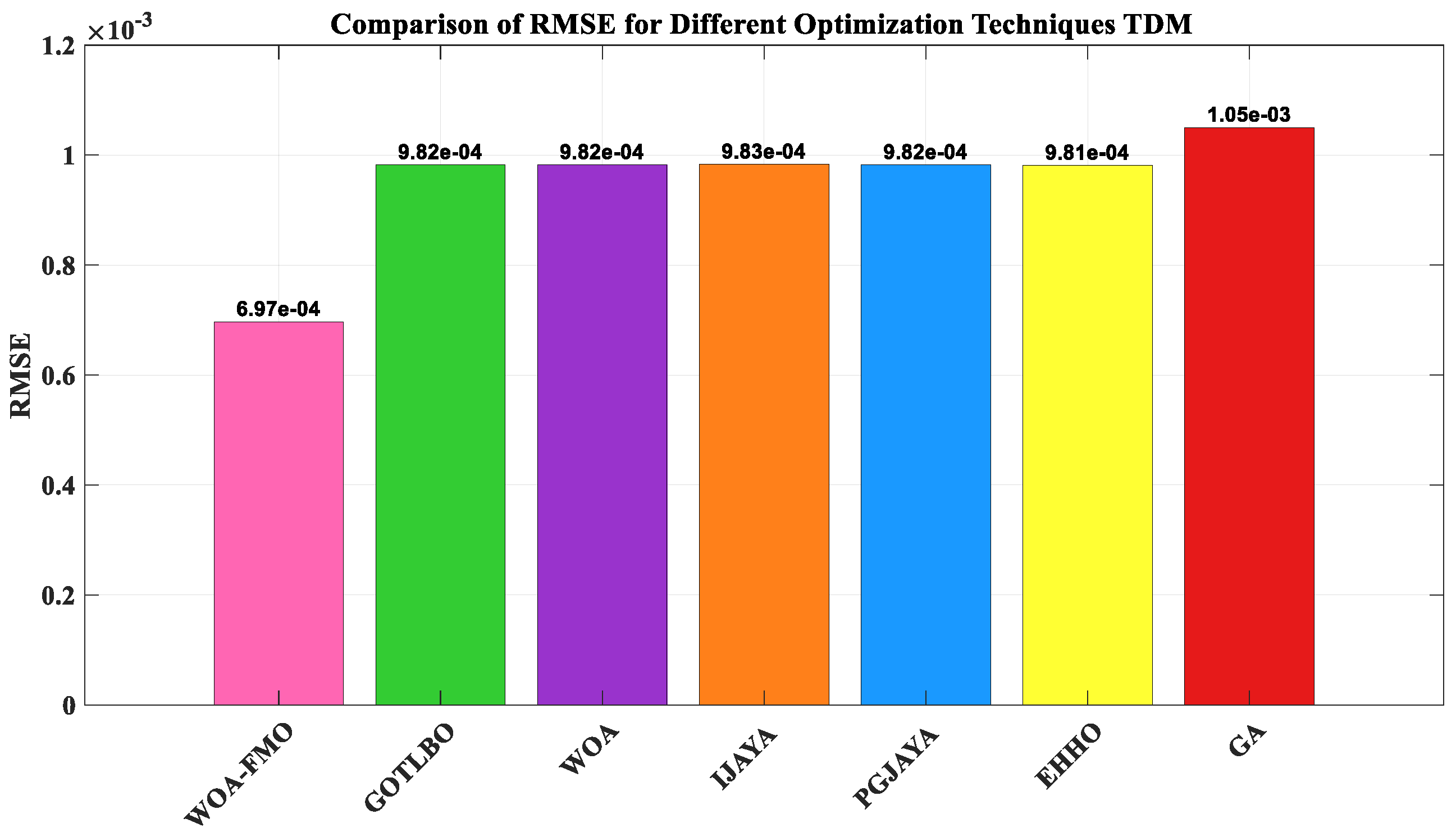
5.4. Outcomes of Optimization of the TDM
- I-V (current-voltage) characteristics
- P-V Characteristics
6. Conclusions
7. Limitations and Future Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| WOA | Whale Optimization Algorithm |
| FMO | Fishier Mantis Optimization |
| SDM | Single-Diode Model |
| DDM | Double-Diode Model |
| TDM | Three-Diode Model |
| RMSE | Root Mean Square Error |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| CNN | Convolutional Neural Network |
| DL | Deep Learning |
| Iph | Photocurrent |
| Io | Saturation Current |
| Rs | Series Resistance |
| Rsh | Shunt Resistance |
| n | Ideality Factor |
References
- Tawalbeh, M.; Al-Othman, A.; Kafiah, F.; Abdelsalam, E.; Almomani, F.; Alkasrawi, M. Environmental impacts of solar photovoltaic systems: A critical review of recent progress and future outlook. Sci. Total Environ. 2021, 759, 143528. [Google Scholar] [CrossRef] [PubMed]
- Izam, N.S.M.N.; Itam, Z.; Sing, W.L.; Syamsir, A. Sustainable development perspectives of solar energy technologies with focus on solar Photovoltaic—A review. Energies 2022, 15, 2790. [Google Scholar] [CrossRef]
- Tripathi, A.K.; Aruna, M.; Elumalai, P.V.; Karthik, K.; Khan, S.A.; Asif, M.; Rao, K.S. Advancing solar PV panel power prediction: A comparative machine learning approach in fluctuating environmental conditions. Case Stud. Therm. Eng. 2024, 59, 104459. [Google Scholar] [CrossRef]
- Gu, Z.; Xiong, G.; Fu, X. Parameter extraction of solar photovoltaic cell and module models with metaheuristic algorithms: A review. Sustainability 2023, 15, 3312. [Google Scholar] [CrossRef]
- Rahman, M.W.; Bathina, C.; Karthikeyan, V.; Prasanth, R. Comparative analysis of developed incremental conductance (IC) and perturb & observe (P&O) MPPT algorithm for photovoltaic applications. In Proceedings of the 2016 10th International Conference on Intelligent Systems and Control (ISCO), Coimbatore, India, 7–8 January 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Martins, F.R.; Pereira, E.B.; Abreu, S.L. Satellite-derived solar resource maps for Brazil under SWERA project. Sol. Energy 2007, 81, 517–528. [Google Scholar] [CrossRef]
- Nunes, H.G.G.; Silva, P.N.C.; Pombo, J.A.N.; Mariano, S.; Calado, M.R.A. Multiswarm spiral leader particle swarm optimisation algorithm for PV parameter identification. Energy Convers. Manag. 2020, 225, 113388. [Google Scholar] [CrossRef]
- Dev, A.; Kumar, V.; Pathak, D.; Tummala, A.S.L.V.; Sharma, S.; Kuppan, V. Improved Extraction of Parameters of Solar PV Cell Diode Model using Marine Walrus Inspired Optimization Algorithm. IEEE Access 2024, 12, 181217–181231. [Google Scholar] [CrossRef]
- Tzanetos, A.; Dounias, G. Nature inspired optimization algorithms or simply variations of metaheuristics? Artif. Intell. Rev. 2021, 54, 1841–1862. [Google Scholar] [CrossRef]
- Ye, M.; Wang, X.; Xu, Y. Parameter extraction of solar cells using particle swarm optimization. J. Appl. Phys. 2009, 105, 094502. [Google Scholar] [CrossRef]
- Singla, M.K.; Gupta, J.; Nijhawan, P.; Singh, P.; Giri, N.C.; Hendawi, E.; Abu El-Sebah, M.I. Parameter estimation techniques for photovoltaic system modeling. Energies 2023, 16, 6280. [Google Scholar] [CrossRef]
- Jeridi, A. Optimizing Photovoltaic Solar Model Parameters. Res. Sq. 2024. [Google Scholar] [CrossRef]
- Bensidhoum, T.; Lekouaghet, B.; Touil, S.-A. Photovoltaic model parameters estimation via the fully informed search algorithm. Int. J. Robot. Control Syst. 2024, 4, 929–940. [Google Scholar] [CrossRef]
- Ghetas, M.; Elshourbagy, M. Parameters extraction of photovoltaic models using enhanced generalized normal distribution optimization with neighborhood search. Neural Comput. Appl. 2024, 36, 14035–14052. [Google Scholar] [CrossRef]
- Ishaque, K.; Salam, Z.; Taheri, H.; Shamsudin, A. A critical evaluation of EA computational methods for Photovoltaic cell parameter extraction based on two diode model. Sol. Energy 2011, 85, 1768–1779. [Google Scholar] [CrossRef]
- Rao, R.V.; Patel, V. An elitist teaching-learning-based optimization algorithm for solving complex constrained optimization problems. Int. J. Ind. Eng. Comput. 2012, 3, 535–560. [Google Scholar] [CrossRef]
- Easwarakhanthan, T.; Bottin, J.; Bouhouch, I.; Boutrit, C. Nonlinear minimization algorithm for determining the solar cell parameters with microcomputers. Int. J. Sol. Energy 1986, 4, 1–12. [Google Scholar] [CrossRef]
- Spampinato, C.; La Magna, P.; Valastro, S.; Smecca, E.; Arena, V.; Bongiorno, C.; Mannino, G.; Fazio, E.; Corsaro, C.; Neri, F. Infiltration of CsPbI3: EuI2 Perovskites into TiO2 Spongy Layers Deposited by gig-lox Sputtering Processes. Solar 2023, 3, 347–361. [Google Scholar] [CrossRef]
- Orioli, A.; Di Gangi, A. A procedure to calculate the five-parameter model of crystalline silicon photovoltaic modules on the basis of the tabular performance data. Appl. Energy 2013, 102, 1160–1177. [Google Scholar] [CrossRef]
- Sandrolini, L.; Artioli, M.; Reggiani, U. Numerical method for the extraction of photovoltaic module double-diode model parameters through cluster analysis. Appl. Energy 2010, 87, 442–451. [Google Scholar] [CrossRef]
- Bonanno, F.; Capizzi, G.; Graditi, G.; Napoli, C.; Tina, G.M. A radial basis function neural network based approach for the electrical characteristics estimation of a photovoltaic module. Appl. Energy 2012, 97, 956–961. [Google Scholar] [CrossRef]
- Amrouche, B.; Guessoum, A.; Belhamel, M. A simple behavioural model for solar module electric characteristics based on the first order system step response for MPPT study and comparison. Appl. Energy 2012, 91, 395–404. [Google Scholar] [CrossRef]
- Wang, J.; Yang, B.; Li, D.; Zeng, C.; Chen, Y.; Guo, Z.; Zhang, X.; Tan, T.; Shu, H.; Yu, T. Photovoltaic cell parameter estimation based on improved equilibrium optimizer algorithm. Energy Convers. Manag. 2021, 236, 114051. [Google Scholar] [CrossRef]
- Garip, Z. Parameters estimation of three-diode photovoltaic model using fractional-order Harris Hawks optimization algorithm. Optik 2023, 272, 170391. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, X.; Wang, W.; Zhang, J.; Du, R.; Li, B.; Liu, W. Uncertainty analysis of photovoltaic cells to determine probability of functional failure. Appl. Energy 2023, 332, 120495. [Google Scholar] [CrossRef]
- Yusupov, Z.; Yaghoubi, E.; Yaghoubi, E. Controlling and tracking the maximum active power point in a photovoltaic system connected to the grid using the fuzzy neural controller. In Proceedings of the 2023 14th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkiye, 30 November–2 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar]
- Ocaya, R.O.; Yakuphanoglu, F. A new symmetry-based extraction method of Schottky diode parameters from resistance-compensated IV characteristics. arXiv 2021, arXiv:2106.12324. [Google Scholar]
- Macabebe, E.Q.B.; Sheppard, C.J.; Van Dyk, E.E. Parameter extraction from I–V characteristics of PV devices. Sol. Energy 2011, 85, 12–18. [Google Scholar] [CrossRef]
- Tay, S.; Lim, I.; Ye, Z.; Yang, D.; Garrigós, A. PV parameter identification using reduced IV data. In Proceedings of the IECON 2017-43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2653–2657. [Google Scholar]
- Jahromi, M.Z.; Yaghoubi, E.; Yaghoubi, E. Optimal generation and distribution planning in smart microgrids under conditions of multi-microgrid disconnection using a hierarchical control strategy. Electr. Eng. 2025, 1–20. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- AlHajri, M.F.; El-Naggar, K.M.; AlRashidi, M.R.; Al-Othman, A.K. Optimal extraction of solar cell parameters using pattern search. Renew. Energy 2012, 44, 238–245. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, P.; Heidari, A.A.; Chen, H.; Mafarja, M. Random reselection particle swarm optimization for optimal design of solar photovoltaic modules. Energy 2022, 239, 121865. [Google Scholar] [CrossRef]
- Naeijian, M.; Rahimnejad, A.; Ebrahimi, S.M.; Pourmousa, N.; Gadsden, S.A. Parameter estimation of PV solar cells and modules using Whippy Harris Hawks Optimization Algorithm. Energy Rep. 2021, 7, 4047–4063. [Google Scholar] [CrossRef]

| Parameter | Mean | Std. Dev | Mean ± Std |
|---|---|---|---|
| Iph (A) | 0.76079 | 0.0000007 | 0.76079 ± 0.0000007 |
| Io (µA) | 0.31052 | 0.00012 | 0.31052 ± 0.00012 |
| Rsh (Ω) | 52.87 | 0.02 | 52.87 ± 0.02 |
| Rs (Ω) | 0.03655 | 0.000002 | 0.03655 ± 0.000002 |
| Ns | 1.4772 | 0.00004 | 1.4772 ± 0.00004 |
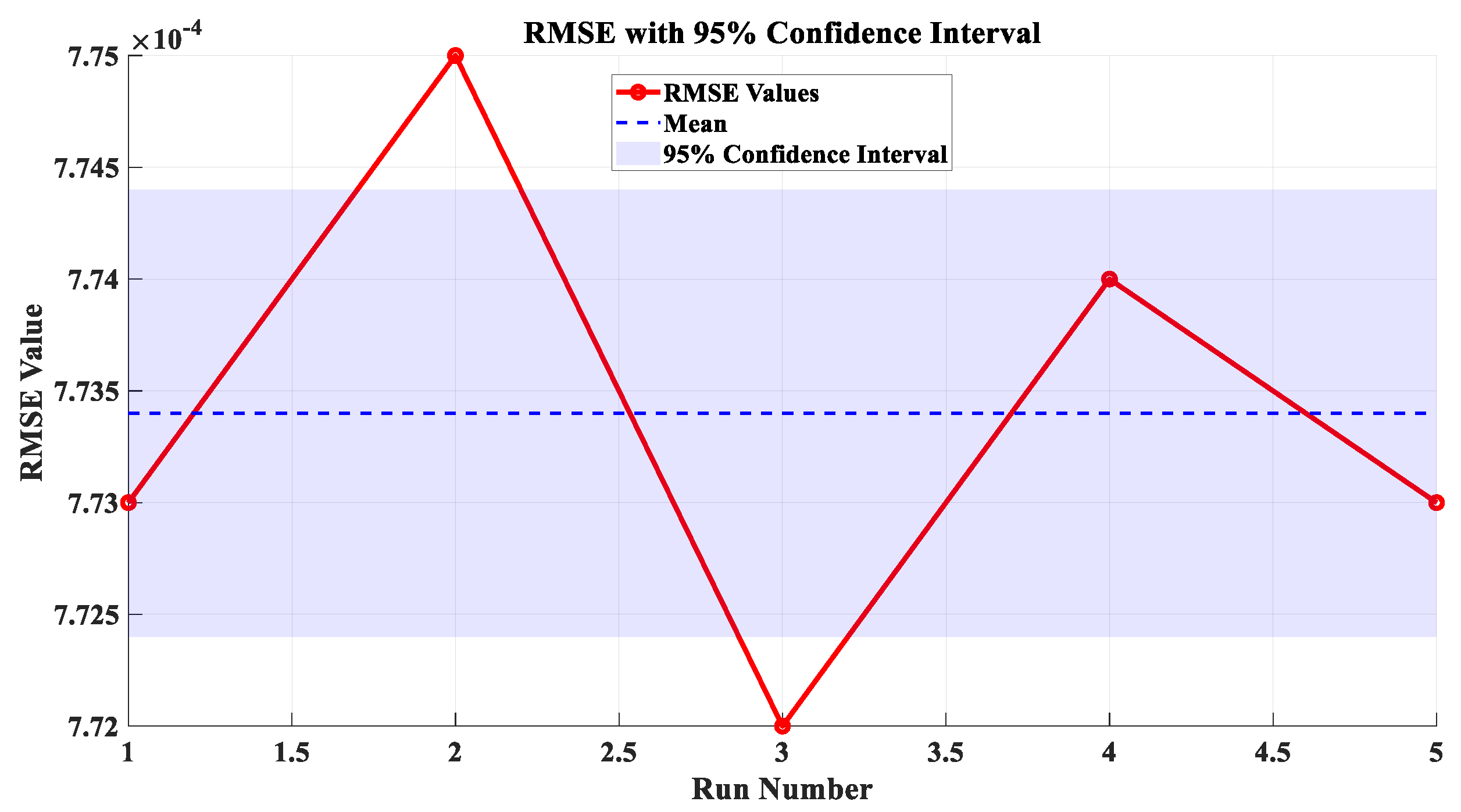
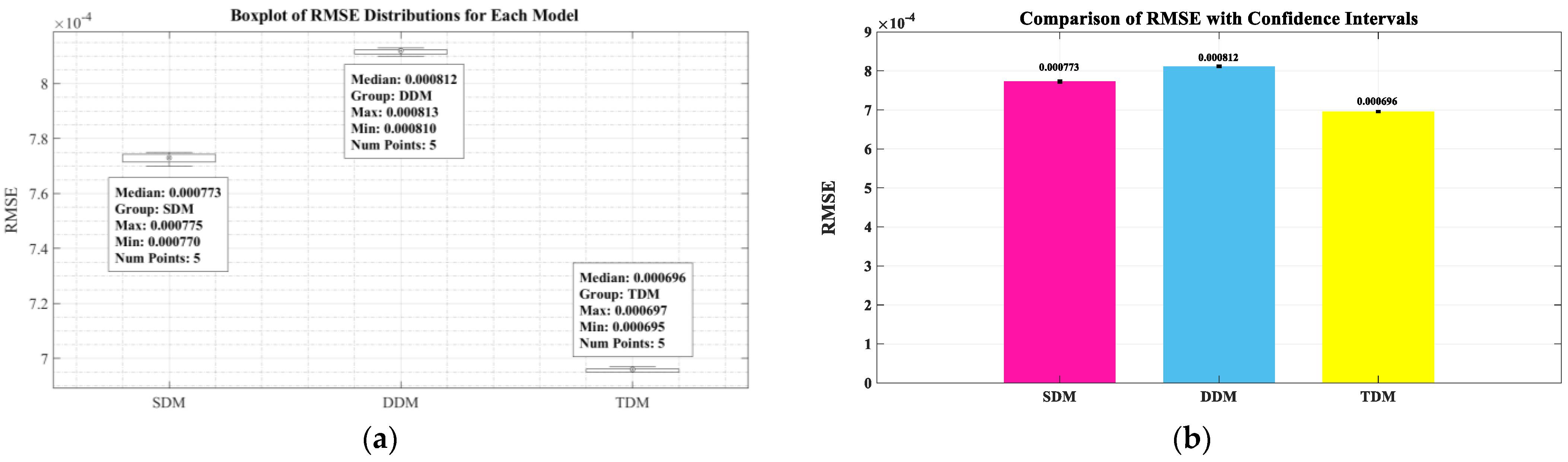
| RMSE | 7.73 × 10−4 | 0.00 | (7.73 ± 0) × 10−4 |
| Parameter | WOA = 15 | WOA = 25 | WOA = 45 | WOA = 65 | WOA = 85 | WOA = 100 |
|---|---|---|---|---|---|---|
| 0.7608 | 0.7608 | 0.7608 | 0.7608 | 0.7608 | 0.7608 | |
| 0.3106 | 0.3105 | 0.3106 | 0.3107 | 0.3107 | 0.3104 | |
| 52.8804 | 52.8905 | 52.8867 | 52.9163 | 52.9084 | 52.8917 | |
| 0.036547 | 0.036547 | 0.036549 | 0.036547 | 0.03655 | 0.036547 | |
| 1.4772 | 1.4773 | 1.4773 | 1.4773 | 1.4773 | 1.4773 | |
| RMSE | 7.73 × 10−4 | 7.73 × 10−4 | 7.73 × 10−4 | 7.73 × 10−4 | 7.73 × 10−4 | 7.73 × 10−4 |
| Parameter | WOA-FMO | WOA | WHHO | EHHO | PGJAYA | IJAYA | GOTLBO | GA | CS |
|---|---|---|---|---|---|---|---|---|---|
| 0.7608 | 0.76054 | 0.760776 | 0.760775 | 0.7608 | 0.7608 | 0.7608 | 0.7619 | 0.7604 | |
| 0.3103 | 0.41228 | 0.323 | 0.323 | 0.323 | 0.3228 | 0.3297 | 0.8087 | 0.34421 | |
| 0.0365 | 0.035409 | 0.036377 | 0.036375 | 0.0364 | 0.0364 | 0.0363 | 0.0299 | 0.03632 | |
| 52.8729 | 62.253 | 53.71867 | 53.74282 | 53.7185 | 53.7595 | 53.3664 | 42.3729 | 57.238 | |
| 1.4772 | 1.5062 | 1.481108 | 1.481238 | 1.4812 | 1.4811 | 1.4833 | 1.5751 | 1.4877 | |
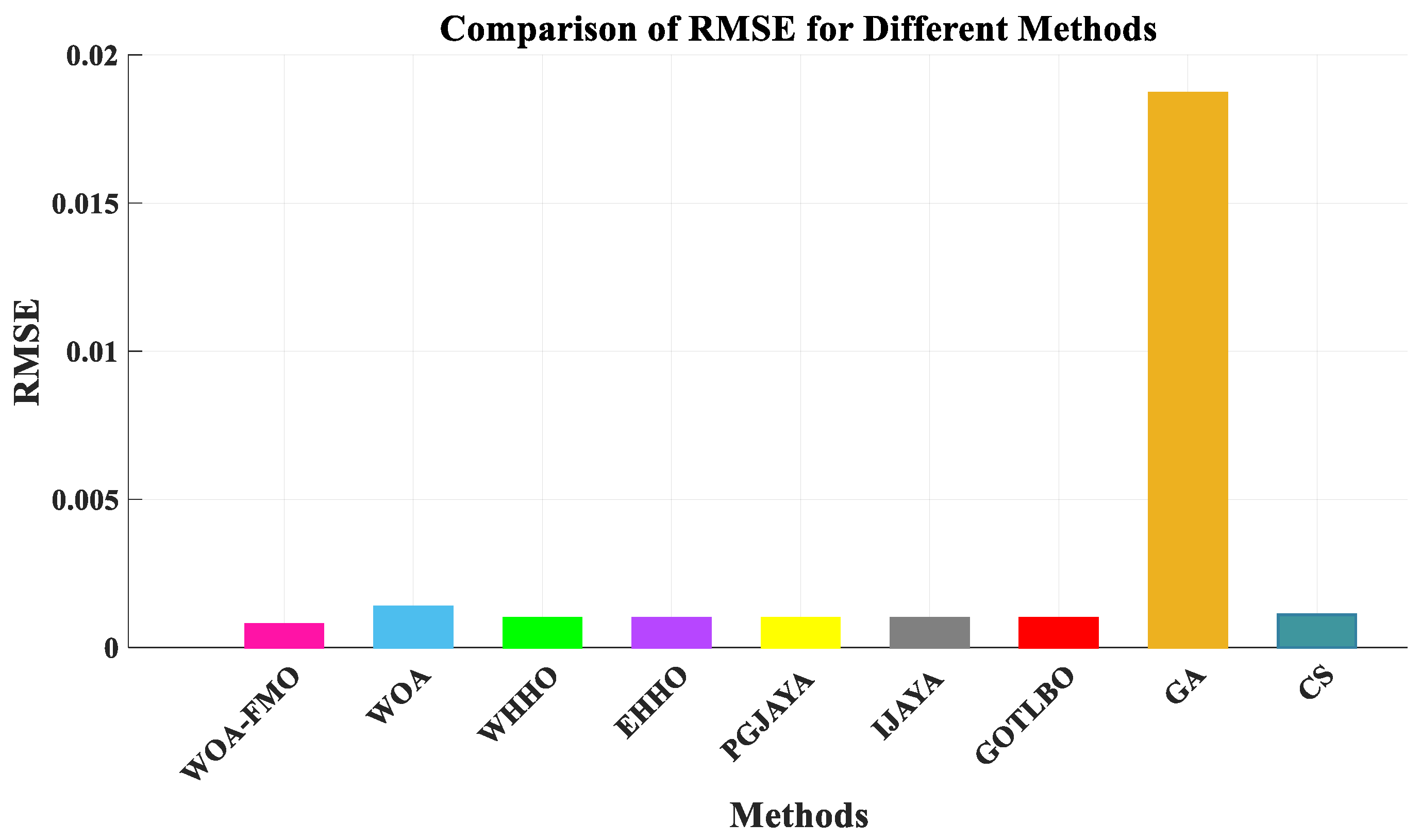
| RMSE | 7.7299 × 10−4 | 1.38 × 10−3 | 9.8602 × 10−4 | 9.8602 × 10−4 | 9.8602 × 10−4 | 9.8603 × 10−4 | 9.8856 × 10−4 | 1.8704 × 10−2 | 1.1085 × 10−3 |
| Results | RMSE | |||||
|---|---|---|---|---|---|---|
| Test 1 | 0.760787963 | 0.310683889 | 52.890785 | 0.036546862 | 1.477269366 | 0.000773 |
| Test 2 | 0.760788056 | 0.310684044 | 52.8356559 | 0.036546867 | 1.477269425 | 0.000773 |
| Test 3 | 0.760788537 | 0.310465454 | 52.88204 | 0.03654989 | 1.477198922 | 0.000773 |
| Test 4 | 0.760788613 | 0.310364064 | 52.86275092 | 0.036551305 | 1.477166178 | 0.000773 |
| Test 5 | 0.760789725 | 0.310403324 | 52.88706223 | 0.036550386 | 1.477179173 | 0.000773 |
| Parameter | WOA = 15 | WOA = 35 | WOA = 55 | WOA = 75 | WOA = 85 | WOA = 100 |
|---|---|---|---|---|---|---|
| 0.7608 | 0.7608 | 0.7607 | 0.7607 | 0.7607 | 0.7607 | |
| 0.4566 | 0.2146 | 0.3251 | 0.255 | 0.415 | 1 | |
| 0.139915 | 0.49909929 | 0.0725265 | 0.24165077 | 0.15177847 | 0.27480144 | |
| 59.9944492 | 61.1184783 | 70.5001609 | 66.7753488 | 64.0562578 | 67.9573234 | |
| 0.03588538 | 0.03564428 | 0.03538192 | 0.03516833 | 0.0353812 | 0.03544677 | |
| 1.53071682 | 1.54206245 | 1.55322132 | 1.55123331 | 1.61204539 | 1.57876809 |
| Results | RMSE | |||||||
|---|---|---|---|---|---|---|---|---|
| Test 1 | 0.7608 | 0.2688 | 0.1982 | 57.4363 | 0.0357 | 1.615 | 1.4607 | 0.00069661 |
| Test 2 | 0.7608 | 0.1639 | 0.3293 | 56.887 | 0.0359 | 1.4459 | 1.6268 | 0.0014 |
| Test 3 | 0.7606 | 0.3386 | 0.1222 | 61.0618 | 0.0357 | 1.576 | 1.4414 | 0.00091667 |
| Test 4 | 0.76 | 0.1883 | 0.2537 | 77.759 | 0.0352 | 1.5268 | 1.5044 | 0.00075928 |
| Test 5 | 0.7611 | 0.2598 | 0.1464 | 48.0595 | 0.0372 | 1.649 | 1.4238 | 0.0012 |
| Results | WOA-FMO | WHHO | PGJAYA | IJAYA | EHHO | WOA | GOTLBO | GA |
|---|---|---|---|---|---|---|---|---|
| (Ω) | 0.0359 | 0.03673 | 0.0368 | 0.0376 | 0.03659 | 0.03651 | 0.0365 | 0.0364 |
| (Ω) | 57.2398 | 55.4264 | 55.8135 | 77.8519 | 55.6394 | 53.173 | 53.4058 | 53.7185 |
| (A) | 0.7608 | 0.760781 | 0.7608 | 0.7601 | 0.76077 | 0.7608 | 0.7608 | 0.7608 |
| (µA) | 0.2038 | 0.228574 | 0.21031 | 0.00504 | 0.586184 | 0.3029 | 0.13894 | 0.0001 |
| (µA) | 0.3059 | 0.727182 | 0.88534 | 0.75094 | 0.240965 | 0.088734 | 0.26209 | 0.0001 |
| 1.5564 | 1.451895 | 1.445 | 1.2186 | 1.9684 | 1.4753 | 1.7254 | 1.3355 | |
| 1.5173 | 2 | 2 | 1.6247 | 1.4569 | 2 | 1.4658 | 1.481 | |
| RMSE | 7.28 × 10−4 | 9.82487 × 10−4 | 9.8263 × 10−4 | 9.8293 × 10−4 | 9.83606 × 10−4 | 9.8638 × 10−4 | 9.8742 × 10−4 | 3.60 × 10−1 |
| Parameter | RMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| WOA = 15 | 0.76067994 | 0.29732343 | 0.25315449 | 0.35916518 | 67.5878082 | 0.0351182 | 1.58703278 | 1.61233489 | 1.6154362 | 6.97 × 10−4 |
| WOA = 25 | 0.76067081 | 0.1172962 | 0.28067481 | 0.18535791 | 67.0470884 | 0.03523617 | 1.60067551 | 1.62439154 | 1.60392549 | 6.97 × 10−4 |
| WOA = 45 | 0.76070543 | 0.35188447 | 0.35327324 | 0.10722626 | 66.2948403 | 0.03517512 | 1.61033108 | 1.64670298 | 1.60628455 | 6.97 × 10−4 |
| WOA = 65 | 0.76063619 | 0.18544709 | 0.12346359 | 0.15841067 | 66.8388473 | 0.03524358 | 1.61503314 | 1.65873179 | 1.6306997 | 6.97 × 10−4 |
| WOA = 85 | 0.76063087 | 0.1072768 | 0.00115486 | 0.24459347 | 66.0096412 | 0.03535478 | 1.60129432 | 1.65916161 | 1.61369572 | 6.97 × 10−4 |
| WOA = 100 | 0.76060902 | 0.12005112 | 0.16124126 | 0.57679939 | 66.3427172 | 0.03544614 | 1.60702834 | 1.66693464 | 1.60935072 | 6.97 × 10−4 |
| Results | RMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Test 1 | 0.7608 | 0.1995 | 0.2591 | 0.925667 | 56.28508 | 0.03805775 | 1.4422 | 1.9967 | 2 | 0.00069663 |
| Test 2 | 0.7608 | 0.1237 | 0.187 | 0.1518088 | 55.0707 | 0.03542337 | 1.4246 | 1.6517 | 1.5804 | 0.00068758 |
| Test 3 | 0.7605 | 0.1489 | 0.1326 | 0.23468076 | 60.7648 | 0.0352843 | 1.5716 | 1.4325 | 1.6812 | 0.00071209 |
| Test 4 | 0.7614 | 0.3307 | 0.0848 | 0.3378643 | 48.1124 | 0.03541798 | 1.709 | 1.3872 | 1.7119 | 0.00071958 |
| Test 5 | 0.7603 | 0.1855 | 0.338 | 0.3347597 | 81.3038 | 0.03632962 | 1.7264 | 1.7208 | 1.7027 | 0.00070875 |
| Techniques | RMSE | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
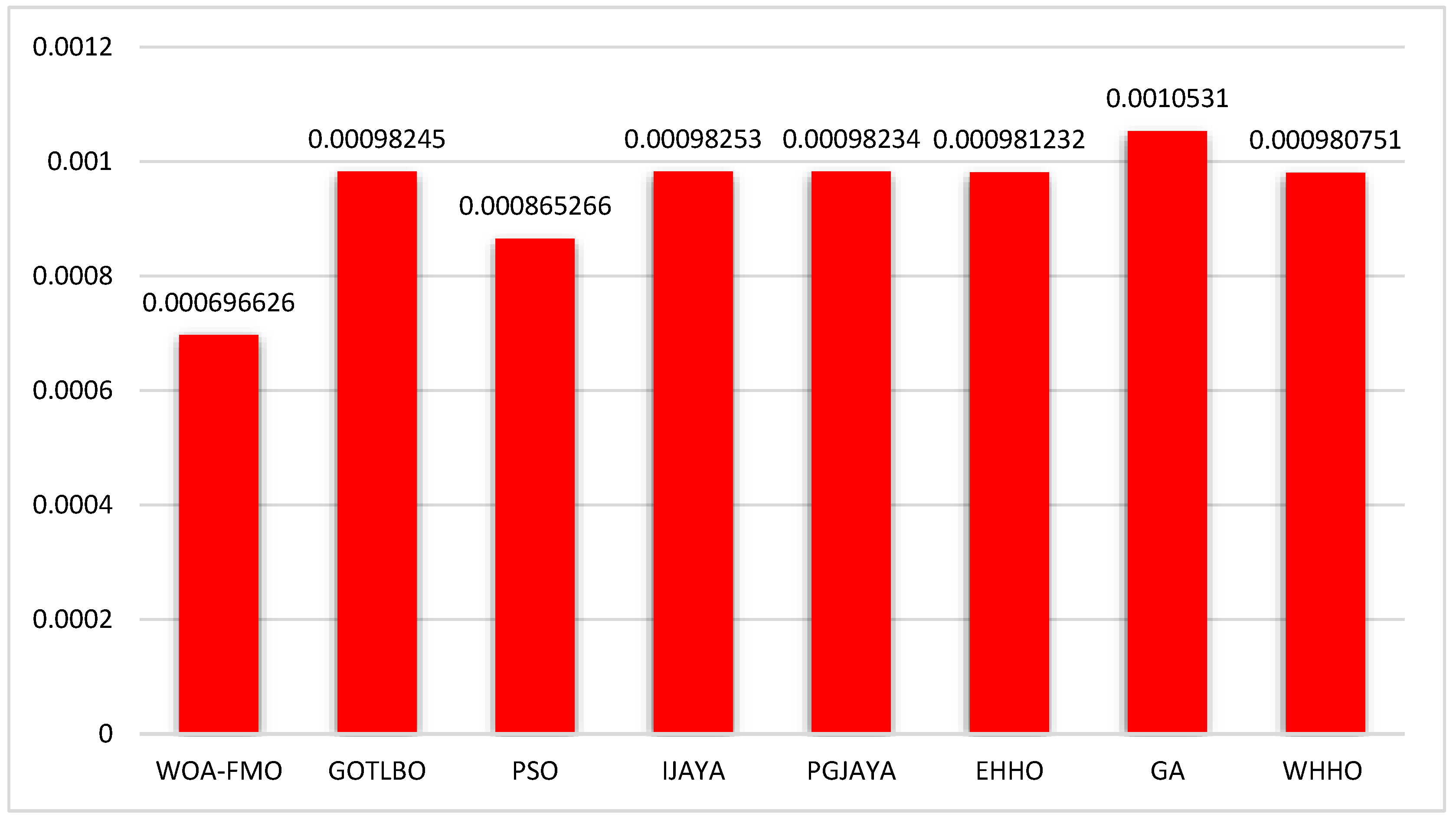
| WOA-FMO | 0.760718 | 0.746098 | 0.281989 | 0.0097088 | 0.035933 | 63.390778 | 1.641042 | 1.606881 | 1.654604 | 6.966263 × 10−4 |
| GOTLBO | 0.7607 | 0.2238 | 0.7583 | 0.0184 | 0.0367 | 55.4743 | 1.4501 | 2 | 2.3191 | 9.82 × 10−4 |
| WOA | 0.7607 | 0.2259 | 0.7491 | 0.0023 | 0.0367 | 55.47571 | 1.4509 | 2 | 2.3156 | 9.82 × 10−4 |
| IJAYA | 0.7608 | 0.2349 | 0.2297 | 0.2297 | 0.0367 | 55.2641 | 1.4541 | 1.8695 | 2 | 9.83 × 10−4 |
| PGJAYA | 0.7607 | 0.2144 | 0.8059 | 0.1178 | 0.0368 | 55.75 | 1.4464 | 2 | 2.2982 | 9.82 × 10−4 |
| EHHO | 0.76078197 | 0.22854289 | 0.57999742 | 0.5861 | 0.03676206 | 55.7706403 | 1.45029359 | 2 | 2.39655345 | 9.81 × 10−4 |
| GA | 0.7605 | 0.3251 | 0.3608 | 0 | 0.0357 | 58.6086 | 1.4843 | 1.9975 | 2.2099 | 1.05 × 10−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Embaresh, H.A.F.; Avci, S.A.; Rahebi, J.; Ghadami, R. Deep-Learning-Enhanced Hybrid WOA-FMO Algorithm for Accurate PV Parameter Estimation in Single-, Double-, and Triple-Diode Models. Processes 2025, 13, 2023. https://doi.org/10.3390/pr13072023
Embaresh HAF, Avci SA, Rahebi J, Ghadami R. Deep-Learning-Enhanced Hybrid WOA-FMO Algorithm for Accurate PV Parameter Estimation in Single-, Double-, and Triple-Diode Models. Processes. 2025; 13(7):2023. https://doi.org/10.3390/pr13072023
Chicago/Turabian StyleEmbaresh, Hatem A. Farag, Selçuk Alparslan Avci, Javad Rahebi, and Raheleh Ghadami. 2025. "Deep-Learning-Enhanced Hybrid WOA-FMO Algorithm for Accurate PV Parameter Estimation in Single-, Double-, and Triple-Diode Models" Processes 13, no. 7: 2023. https://doi.org/10.3390/pr13072023
APA StyleEmbaresh, H. A. F., Avci, S. A., Rahebi, J., & Ghadami, R. (2025). Deep-Learning-Enhanced Hybrid WOA-FMO Algorithm for Accurate PV Parameter Estimation in Single-, Double-, and Triple-Diode Models. Processes, 13(7), 2023. https://doi.org/10.3390/pr13072023







