Optimal Energy Management and Trading Strategy for Multi-Distribution Networks with Shared Energy Storage Based on Nash Bargaining Game
Abstract
1. Introduction
2. Description of Multi-Stakeholder Cooperation Model
3. Optimization and Scheduling Model of Active Distribution Network with Shared Energy Storage
3.1. Optimal Scheduling Model for Active Distribution Network
3.2. Optimal Scheduling Model for Shared Energy Storage Operators
4. Multi-Distribution Grid and Shared Energy Storage Collaborative Optimization Operation Model and Solution Strategy Based on Nash Negotiation
4.1. Collaborative Optimization Mathematical Model
4.2. Solution of Minimizing Alliance Cooperation Costs Based on ADMM Algorithm
4.3. Solution of Transaction Negotiation Problems Among Alliance Parties Based on ADMM Algorithm
5. Case Study
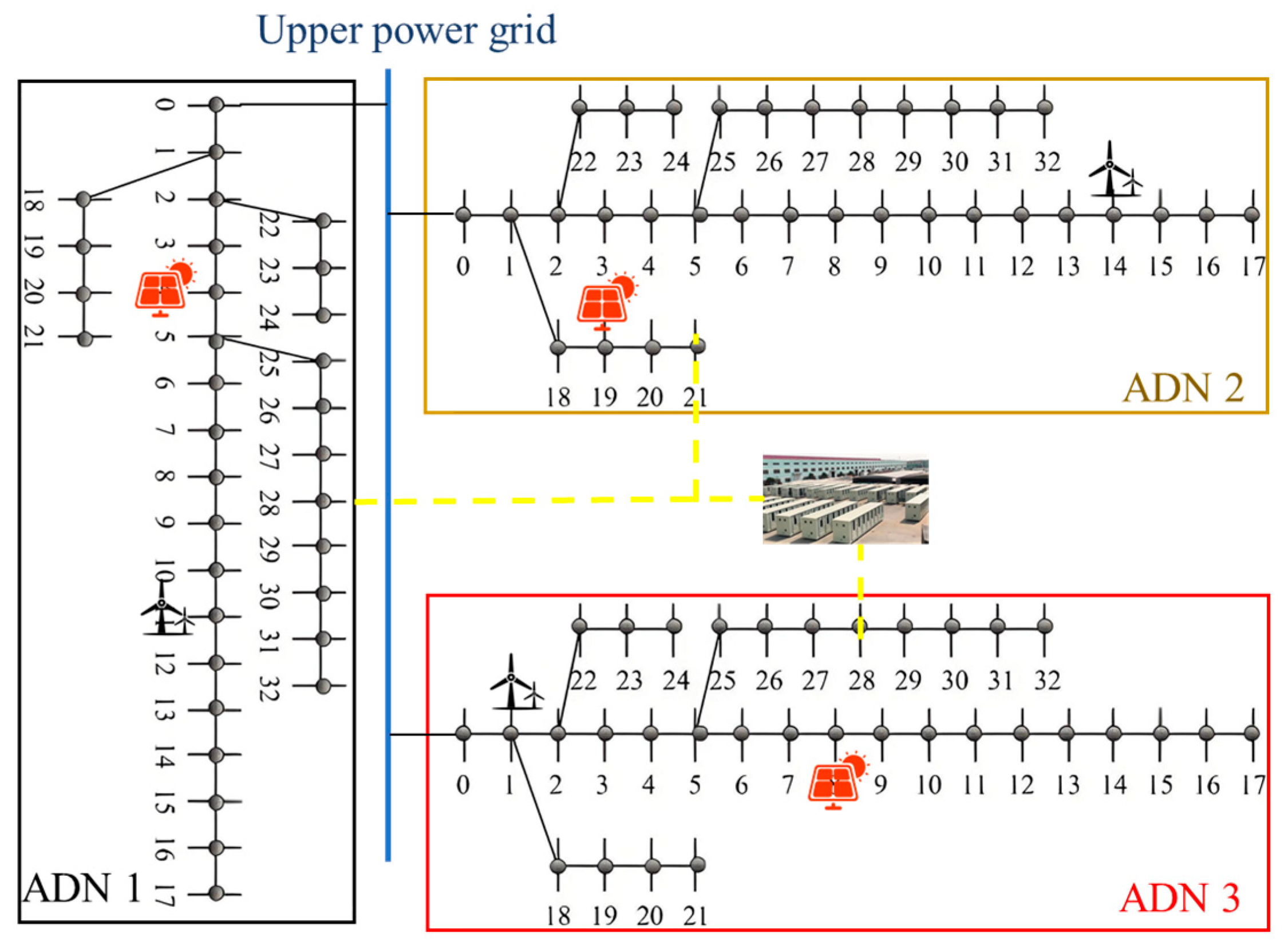
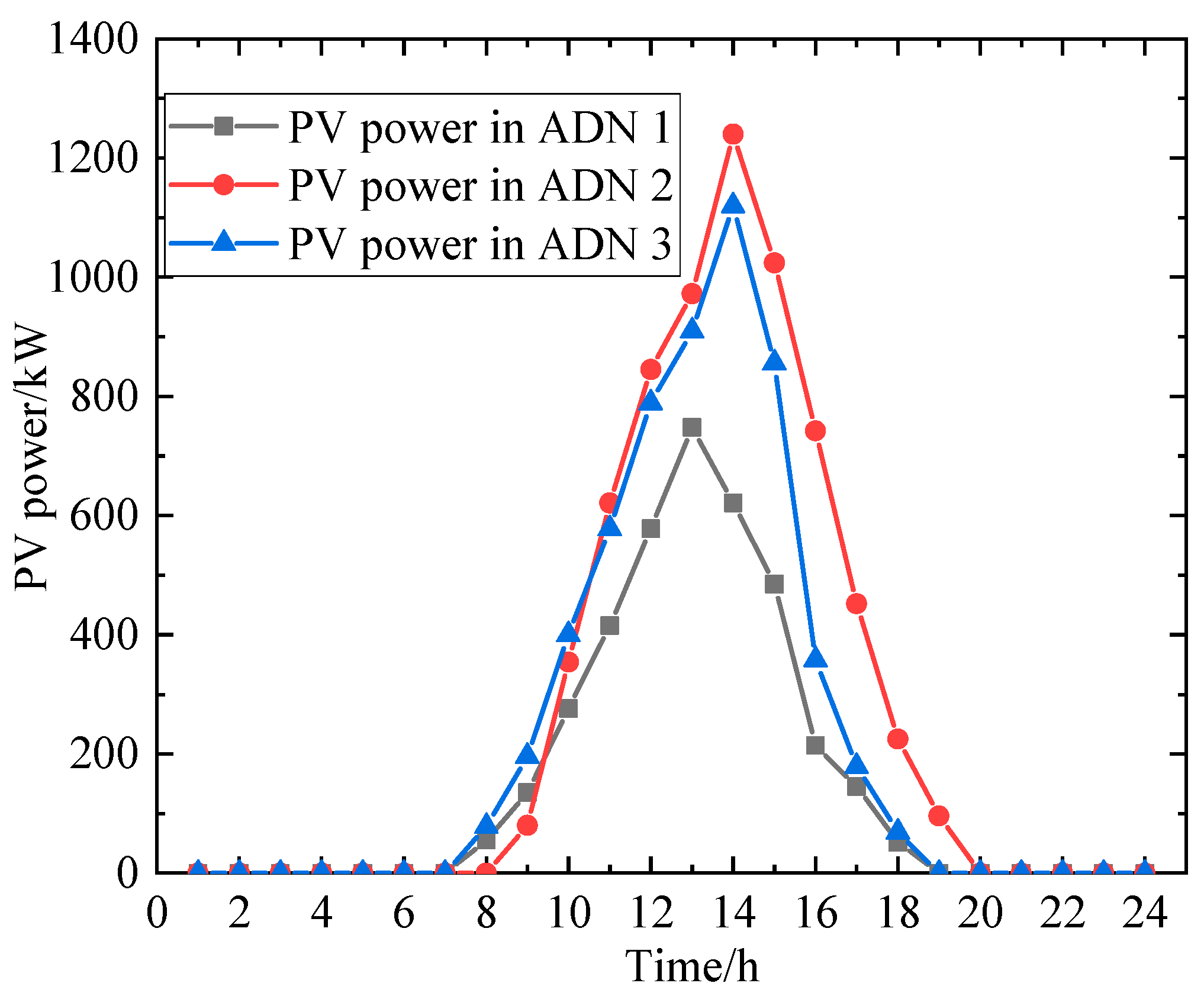
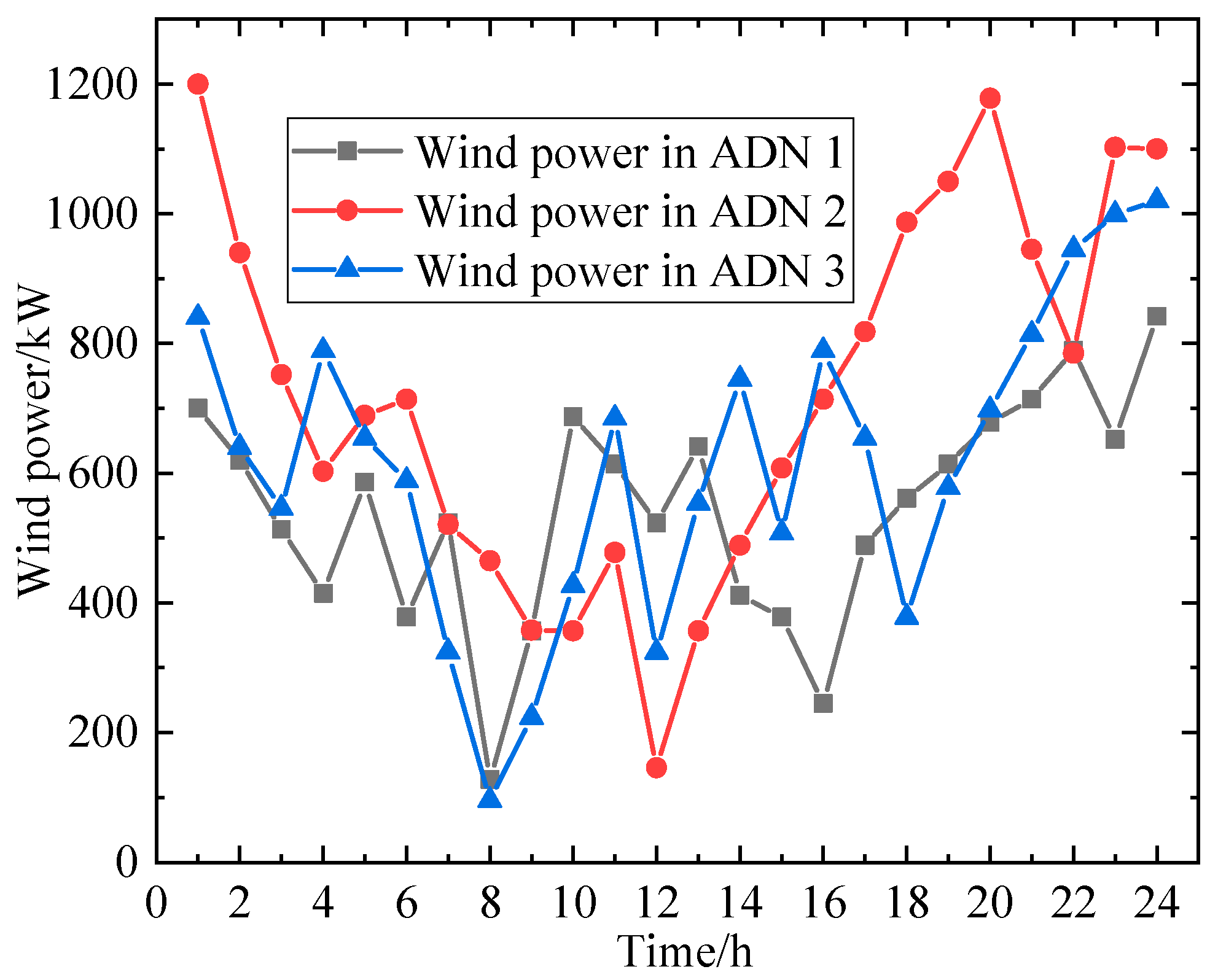
5.1. Introduction to the Test System
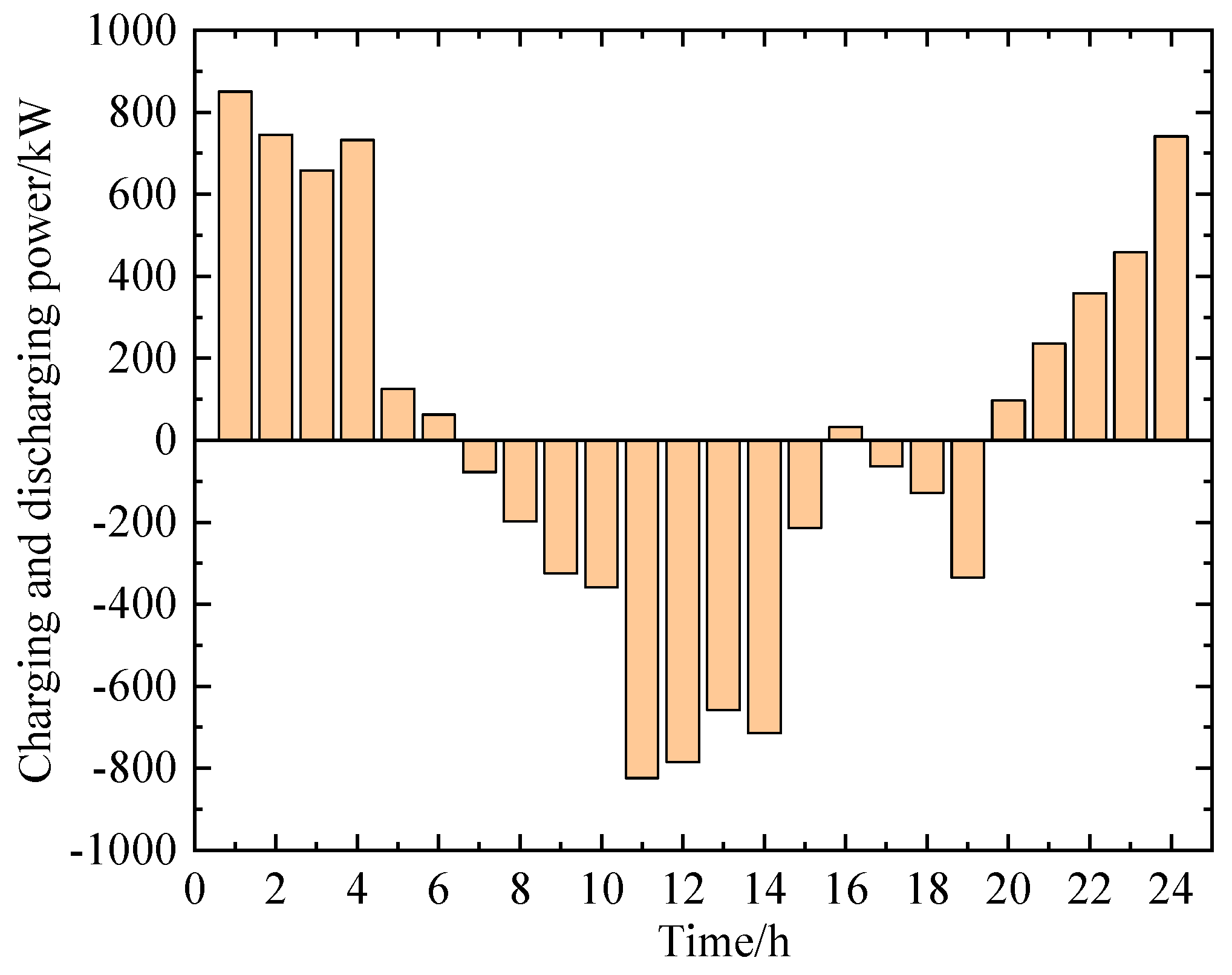
5.2. Effectiveness Validation of the Proposed Method
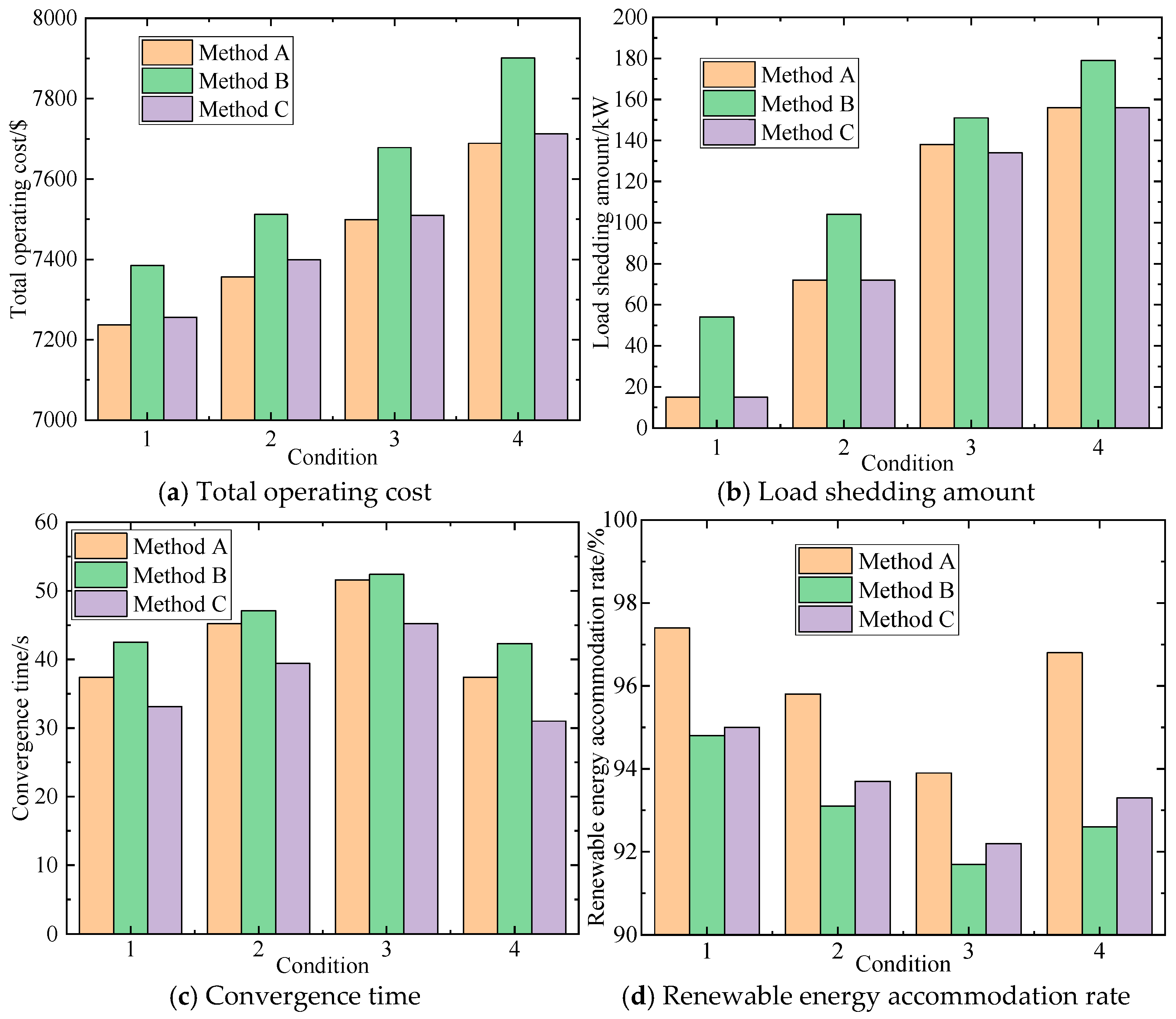
5.3. Comparison with Other Methods
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Fang, Z.; Wang, Q.; Zhang, M.; Li, Y.; Zhang, W. Optimal Operation with Dynamic Partitioning Strategy for Centralized Shared Energy Storage Station with Integration of Large-scale Renewable Energy. J. Mod. Power Syst. Clean Energy 2024, 12, 359–370. [Google Scholar] [CrossRef]
- Deng, L.; Zhang, X.; Yang, T.; Sun, H.; Fu, Y.; Guo, Q.; Oren, S.S. Energy Management of Price-Maker Community Energy Storage by Stochastic Dynamic Programming. CSEE J. Power Energy Syst. 2024, 10, 492–503. [Google Scholar]
- Tanis, Z.; Durusu, A. Cooperative Behaviors and Multienergy Coupling Through Distributed Energy Storage in the Peer-to-Peer Market Mechanism. IEEE Access 2025, 13, 12081–12102. [Google Scholar] [CrossRef]
- Hossain, M.B.; Islam, M.R.; Muttaqi, K.M.; Sutanto, D.; Agalgaonkar, A.P. Component Sizing and Energy Management for a Supercapacitor and Hydrogen Storage Based Hybrid Energy Storage System to Improve Power Dispatch Scheduling of a Wind Energy System. IEEE Trans. Ind. Appl. 2025, 61, 872–883. [Google Scholar] [CrossRef]
- Abdelghany, M.B.; Al-Durra, A.; Gao, F. A Coordinated Optimal Operation of a Grid-Connected Wind-Solar Microgrid Incorporating Hybrid Energy Storage Management Systems. IEEE Trans. Sustain. Energy 2024, 15, 39–51. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, F.; Wu, M.; Wei, L. Research on Optimization and Scheduling Strategies for Generalized Power Sources in Active Distribution Networks. Control Eng. 2019, 26, 1291–1297. [Google Scholar]
- Kong, S.; Hu, Z.; Xie, S.; Yang, L.; Lin, W. Dual layer collaborative planning of active distribution network considering wind and solar energy storage and charging stations. Electr. Meas. Instrum. 2019, 56, 60–68. [Google Scholar]
- Xu, Y.; Yan, X.; Li, R.; Li, T.; Zeng, H. Active/Reactive Joint Optimization of Active Distribution Networks with “Source Grid Load Storage” Interaction in the Electricity Market Environment. Grid Technol. 2019, 43, 3778–3789. [Google Scholar]
- Yan, X.; Xu, Y.; Li, R.; Jin, Y.; Li, T. Multi time scale reactive power dynamic optimization of distribution networks with participation of renewable distributed power sources based on model predictive control. J. Electr. Eng. 2019, 34, 2022–2037. [Google Scholar]
- Ning, Y.; Hu, Z.; Lin, W.; Xie, W.; Kong, S.; Chen, K. ADN hierarchical planning based on game theory for the coordination and interaction of interests among multiple stakeholders in “source grid load”. J. Electr. Power Sci. Technol. 2021, 36, 63–72. [Google Scholar]
- Qiu, W.; Wang, M.; Lin, Z.; Yang, L.; Wang, L.; Sun, J. Conducted a comprehensive evaluation of shared energy storage for new energy consumption scenarios under the “dual carbon” goal. Power Autom. Equip. 2021, 41, 244–255. [Google Scholar]
- Sun, S.; Chen, L.; Qiu, X.; Zheng, T.; Mei, S. A planning model for shared energy storage on the generation side based on cooperative game theory. Glob. Energy Internet 2019, 2, 360–366. [Google Scholar]
- Yang, J.; Huang, J.; Qin, Z.; Xu, H. Research on the Shared Business Model of Battery Energy Storage Stations on the Grid Side. Public Electr. 2020, 35, 20–22. [Google Scholar]
- Zhang, F.; Pei, X.; Wang, B. Active distribution network and transmission network coordinated scheduling and congestion management. Electr. Meas. Instrum. 2020, 57, 46–53. [Google Scholar]
- Li, L.; Xu, Q.; Wang, X.; Lin, J.; Sun, H. Industrial users have recently optimized economic dispatch based on shared energy storage power stations. Electr. Power Constr. 2020, 41, 100–107. [Google Scholar]
- Wang, S.; Ping, C.; Xue, G. Research on Collaborative Optimization of Community Integrated Energy System Considering Shared Energy Storage. China Electr. Power 2018, 51, 77–84. [Google Scholar]
- Han, J.; Fang, Y.; Li, Y.; Du, E.; Zhang, N. Optimal Planning of Multi-Microgrid System With Shared Energy Storage Based on Capacity Leasing and Energy Sharing. IEEE Trans. Smart Grid 2025, 16, 16–31. [Google Scholar] [CrossRef]
- Paternost, R.F.P.; Diab, I.; Mouli, G.R.C.; Ricco, M.; Bauer, P.; Grandi, G. Stationary Energy Storage Solutions and Power Management for Bus Fleet Electrification in Congested Grid Areas. IEEE Access 2024, 12, 140211–140222. [Google Scholar] [CrossRef]
- Kalathil, D.; Wu, C.; Poolla, K.; Varaiya, P. The Sharing Economy for the Electricity Storage. IEEE Trans. Smart Grid 2019, 10, 556–567. [Google Scholar] [CrossRef]
- Zhang, J.; Zhong, K.; Zhang, Y.; Qin, S.; Qin, Y.; Deng, W. Multi regional electricity storage sharing operation model and economic benefits analysis based on mixed game theory. Power Syst. Autom. 2024, 48, 31–41. [Google Scholar]
- Zhu, Z.; Wang, X.; Wu, X.; He, J.; Xin, C.; Huang, R. Investment and Operation Analysis of Shared Energy Storage Considering Multi scenario Planning. Power Syst. Autom. 2023, 47, 23–31. [Google Scholar]
- Li, J.; Cui, Y.; Ma, S.; Wu, Y.; Jiang, Y.; Xin, D. Optimization of Demand Side Shared Energy Storage Operation Mode and Economic Benefit Analysis. Grid Technol. 2022, 46, 4954–4969. [Google Scholar]
- Liu, J.; Chen, X.; Xiang, Y. Energy Storage Optimization Configuration and Investment Benefit Analysis of Sales Companies under Market Mechanism Considering Sharing Mode. Grid Technol. 2020, 44, 1740–1750. [Google Scholar]
- Liu, Y.; Dai, H.; Liu, Z.; Liu, R. Distributed Shared Energy Storage Configuration and Investment Benefit Analysis for Multiple Types of Industrial Users. Electr. Power Autom. Equip. 2021, 41, 256–264. [Google Scholar]
- Wang, H. Dual functional shared energy storage configuration for multi-stage planning of industrial parks. Electr. Power Saf. Technol. 2021, 23, 40–47. [Google Scholar]
- Doostmohammadian, M. Distributed Energy Resource Management: All-Time Resource-Demand Feasibility, Delay-Tolerance, Nonlinearity, and Beyond. IEEE Control Syst. Lett. 2023, 7, 3423–3428. [Google Scholar] [CrossRef]
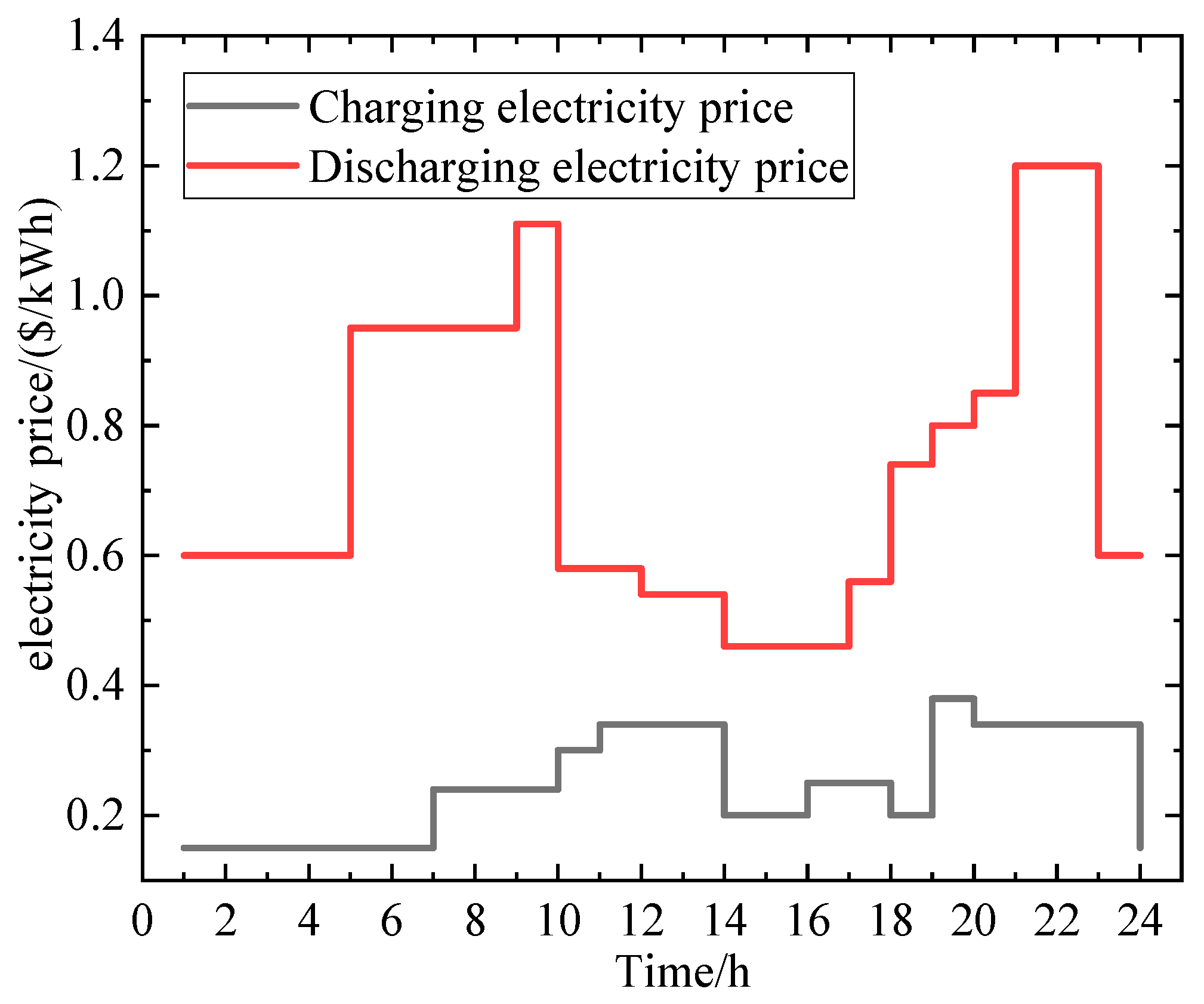
| Parameters and Units | Value |
|---|---|
| Rated capacity/kWh | 7500 |
| Maximum charging and discharging power/kW | 2000 |
| Charge/discharge efficiency | 0.92 |
| State of Charge Interval | [0.1, 0.9] |
| Time | Electricity Sell Price/($/kWh) | Electricity Purchase Price/($/kWh) |
|---|---|---|
| 00:00–05:00, 22:00–24:00, | 0.42 | 0.15 |
| 05:00–08:00, 13:00–17:00, | 0.85 | 0.35 |
| 08:00–13:00, 17:00–22:00, | 1.20 | 0.45 |
| Index | Scenario 1 | Scenario 2 | Scenario 3 |
|---|---|---|---|
| Peak valley load difference/kW | 1742 | 1268 | 458 |
| New energy consumption rate/% | 87.4 | 91.2 | 97.4 |
| Total operating cost/$ | 8452.7 | 7456.4 | 7137.2 |
| Calculation time/s | 35.6 | 45.8 | 61.7 |
| The Test System Scale | The Number of Distribution Networks | Total Number of Nodes | Number of Time Periods | Total Number of Variables |
|---|---|---|---|---|
| Small-scale | 4 | 132 | 24 | 3168 |
| Medium-scale | 10 | 330 | 24 | 7920 |
| Large-scale | 50 | 1650 | 24 | 39,600 |
| Scales | The Number of Iterations | Time Consumption Per Iteration/s | Total Computation Time/s | The Converged Value of the Objective Function/$ |
|---|---|---|---|---|
| 4-distribution network system | 46 | 1.47 | 67.6 | 7437.2 |
| 10-distribution network system | 58 | 3.21 | 186.2 | 23,891.5 |
| 50-distribution network system | 76 | 8.95 | 680.2 | 118,744.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Wu, Z.; Ding, Y.; Yuan, K.; Zhao, F.; Shi, T. Optimal Energy Management and Trading Strategy for Multi-Distribution Networks with Shared Energy Storage Based on Nash Bargaining Game. Processes 2025, 13, 2022. https://doi.org/10.3390/pr13072022
Hu Y, Wu Z, Ding Y, Yuan K, Zhao F, Shi T. Optimal Energy Management and Trading Strategy for Multi-Distribution Networks with Shared Energy Storage Based on Nash Bargaining Game. Processes. 2025; 13(7):2022. https://doi.org/10.3390/pr13072022
Chicago/Turabian StyleHu, Yuan, Zhijun Wu, Yudi Ding, Kai Yuan, Feng Zhao, and Tiancheng Shi. 2025. "Optimal Energy Management and Trading Strategy for Multi-Distribution Networks with Shared Energy Storage Based on Nash Bargaining Game" Processes 13, no. 7: 2022. https://doi.org/10.3390/pr13072022
APA StyleHu, Y., Wu, Z., Ding, Y., Yuan, K., Zhao, F., & Shi, T. (2025). Optimal Energy Management and Trading Strategy for Multi-Distribution Networks with Shared Energy Storage Based on Nash Bargaining Game. Processes, 13(7), 2022. https://doi.org/10.3390/pr13072022





