Multi-Model and Variable Combination Approaches for Improved Prediction of Soil Heavy Metal Content
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodology
2.1.1. Spatial Autocorrelation Methods
2.1.2. Construction of Spatial Regionalization Variables (SRs)
2.1.3. Hierarchical Testing of Variable Combinations
2.1.4. Model-Agnostic Spatial Enhancement
2.2. Experimental Setup
2.2.1. Study Area and Data Collection
2.2.2. Environmental Variables
2.2.3. Spatial Variable Construction
- (1)
- Spatial Autocorrelation Variables (SAs)
- (2)
- Spatial Regionalization Variables (SRs)
2.2.4. Model Implementation
2.2.5. Evaluation Protocol
3. Results
3.1. Comparative Performance of Predictive Models
3.2. Impact of Spatial Regionalization Variables
3.3. Robustness to Training Data Reduction
3.4. Variable Importance Analysis
3.5. Cross-Region Validation
3.6. Extrapolation Testing Protocol
4. Discussion
4.1. Limitations and Robustness of Variable Combinations and Models
4.2. Practical Applications in Environmental Monitoring and Policy
4.3. Future Directions: Dynamic Data Integration and Model Interpretability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiang, M.; Li, Y.; Yang, J.; Lei, K.; Li, Y.; Li, F.; Zheng, D.; Fang, X.; Cao, Y. Heavy Metal Contamination Risk Assessment and Correlation Analysis of Heavy Metal Contents in Soil and Crops. Environ. Pollut. 2021, 278, 116911. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zhang, H.; Wong, C.U.I.; Li, F.; Xie, S. Assessment of Heavy Metal Contamination and Ecological Risk in Soil within the Zheng–Bian–Luo Urban Agglomeration. Processes 2024, 12, 996. [Google Scholar] [CrossRef]
- Suruliandi, A.; Mariammal, G.; Raja, S. Crop Prediction Based on Soil and Environmental Characteristics Using Feature Selection Techniques. Math. Comput. Model. Dyn. Syst. 2021, 27, 117–140. [Google Scholar] [CrossRef]
- Xie, Z.M.; Huang, C.Y. Control of Arsenic Toxicity in Rice Plants Grown on an Arsenic-Polluted Paddy Soil. Commun. Soil Sci. Plant Anal. 1998, 29, 2471–2477. [Google Scholar] [CrossRef]
- Jia, X.; Cao, Y.; O’Connor, D.; Zhu, J.; Tsang, D.C.; Zou, B.; Hou, D. Mapping Soil Pollution by Using Drone Image Recognition and Machine Learning at an Arsenic-Contaminated Agricultural Field. Environ. Pollut. 2021, 270, 116281. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Qin, S.; Lin, L.; Wang, X.; Cornelis, W. Evaluating Ensemble Learning in Developing Pedotransfer Functions to Predict Soil Hydraulic Properties. J. Hydrol. 2024, 640, 131658. [Google Scholar] [CrossRef]
- Lombard, N.; Prestat, E.; van Elsas, J.D.; Simonet, P. Soil-Specific Limitations for Access and Analysis of Soil Microbial Communities by Metagenomics. FEMS Microbiol. Ecol. 2011, 78, 31–49. [Google Scholar] [CrossRef]
- Palansooriya, K.N.; Li, J.; Dissanayake, P.D.; Suvarna, M.; Li, L.; Yuan, X.; Sarkar, B.; Tsang, D.C.; Rinklebe, J.; Wang, X.; et al. Prediction of Soil Heavy Metal Immobilization by Biochar Using Machine Learning. Environ. Sci. Technol. 2022, 56, 4187–4198. [Google Scholar] [CrossRef]
- Jingzhe, W.; Jianing, Z.; Weifang, H.; Songchao, C.; Ivan, L.; Mojtaba, Z.; Xiaodong, Y. Remote Sensing of Soil Degradation: Progress and Perspective. Int. Soil Water Conserv. Res. 2023, 11, 429–454. [Google Scholar]
- Liu, Z.; Lu, Y.; Peng, Y.; Zhao, L.; Wang, G.; Hu, Y. Estimation of Soil Heavy Metal Content Using Hyperspectral Data. Remote Sens. 2019, 11, 1464. [Google Scholar] [CrossRef]
- Chen, X.; Cui, F.; Wong, C.; Zhang, H.; Wang, F. An Investigation into the Response of the Soil Ecological Environment to Tourist Disturbance in Baligou. PeerJ 2023, 9, E15780. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhao, M.; Huang, X.; Song, X.; Cai, B.; Tang, R.; Sun, J.; Han, Z.; Yang, J.; Liu, Y.; et al. Improving Prediction of Soil Heavy Metal (Loid) Concentration by Developing a Combined Co-Kriging and Geographically and Temporally Weighted Regression (GTWR) Model. J. Hazard. Mater. 2024, 468, 133745. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.; Yee, L.; ChangLin, M.; Tung, F. Backfitting Estimation for Geographically Weighted Regression Models with Spatial Autocorrelation in the Response. Geogr. Anal. 2021, 54, 357–381. [Google Scholar]
- Zheng, Y.; Zhang, G.; Tan, S.; Feng, L. Research on Progress of Forest Fire Monitoring with Satellite Remote Sensing. Agric. Rural. Stud. 2023, 1, 0008. [Google Scholar] [CrossRef]
- Anthony, T. Assessment of Heavy Metal Contamination in Wetlands Soils Around an Industrial Area Using Combined GIS-Based Pollution Indices and Remote Sensing Techniques. Air Soil Water Res. 2023, 16, 11786221231214062. [Google Scholar] [CrossRef]
- Li, X. Influence of Variation of Soil Spatial Heterogeneity on Vegetation Restoration. Sci. China Ser. D Earth Sci. 2005, 48, 2020–2031. [Google Scholar] [CrossRef]
- Song, I.; Kim, D. Three Common Machine Learning Algorithms Neither Enhance Prediction Accuracy Nor Reduce Spatial Autocorrelation in Residuals: An Analysis of Twenty-Five Socioeconomic Data Sets. Geogr. Anal. 2023, 55, 585–620. [Google Scholar] [CrossRef]
- Li, Y.; Rahardjo, H.; Satyanaga, A.; Rangarajan, S.; Lee, D.T.T. Soil Database Development with the Application of Machine Learning Methods in Soil Properties Prediction. Eng. Geol. 2022, 306, 106769. [Google Scholar] [CrossRef]
- Song, X.; Sun, Y.; Wang, H.; Huang, X.; Han, Z.; Shu, Y.; Wu, J.; Zhang, Z.; Zhong, Q.; Li, R.; et al. Uncovering Soil Heavy Metal Pollution Hotspots and Influencing Mechanisms through Machine Learning and Spatial Analysis. Environ. Pollut. 2025, 370, 125901. [Google Scholar] [CrossRef]
- Yang, H.; Huang, K.; Zhang, K.; Weng, Q.; Zhang, H.; Wang, F. Predicting Heavy Metal Adsorption on Soil with Machine Learning and Mapping Global Distribution of Soil Adsorption Capacities. Environ. Sci. Technol. 2021, 55, 14316–14328. [Google Scholar] [CrossRef]
- Hu, H.; Zhou, W.; Liu, X.; Guo, G.; He, Y.; Zhu, L.; Chen, D.; Miao, R. Machine Learning Combined with Geodetector to Predict the Spatial Distribution of Soil Heavy Metals in Mining Areas. Sci. Total Environ. 2025, 959, 178281. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Chen, S.; Chen, L.; Wang, L.; Chao, Y.; Shi, Z.; Lin, D.; Yang, K. Drivers Distinguishing of PAHs Heterogeneity in Surface Soil of China Using Deep Learning Coupled with Geo-Statistical Approach. J. Hazard. Mater. 2024, 468, 133840. [Google Scholar] [CrossRef] [PubMed]
- Hua, W.; Junfeng, Z.; Fubao, Z.; Weiwei, Z. Analysis of Spatial Pattern of Aerosol Optical Depth and Affecting Factors Using Spatial Autocorrelation and Spatial Autoregressive Model. Environ. Earth Sci. 2016, 75, 822. [Google Scholar] [CrossRef]
- Kuang, Y.; Chen, X. Spatial Heterogeneity of Forest Carbon Stocks in the Xiangjiang River Basin Urban Agglomeration: Analysis and Assessment Based on the Multiscale Geographically Weighted Regression (MGWR) Model. Front. Environ. Sci. 2025, 13, 1573438. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. Spatial Interpolation Methods Applied in the Environmental Sciences: A Review. Environ. Model. Softw. 2014, 53, 173–189. [Google Scholar] [CrossRef]
- Lv, J. Multivariate Receptor Models and Robust Geostatistics to Estimate Source Apportionment of Heavy Metals in Soils. Environ. Pollut. 2019, 244, 72–83. [Google Scholar] [CrossRef]
- Pauchard, A.; Alaback, P.B.; Edlund, E.G. Plant Invasions in Protected Areas at Multiple Scales: Linaria Vulgaris (Scrophulariaceae) in the West Yellowstone Area. West. N. Am. Nat. 2003, 63, 416–428. [Google Scholar]
- Sreenivas, K.; Sujatha, G.; Sudhir, K.; Kiran, D.V.; Fyzee, M.; Ravisankar, T.; Dadhwal, V. Spatial Assessment of Soil Organic Carbon Density through Random Forests Based Imputation. J. Indian Soc. Remote Sens. 2014, 42, 577–587. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, H.; Wong, C.U.I. Spatial Distribution Characteristics and Pollution Evaluation of Soil Heavy Metals in Wulongdong National Forest Park. Sci. Rep. 2024, 14, 8880. [Google Scholar] [CrossRef]
- Gadepalle, V.P.; Ouki, S.K.; Herwijnen, R.V.; Hutchings, T. Immobilization of Heavy Metals in Soil Using Natural and Waste Materials for Vegetation Establishment on Contaminated Sites. Soil Sediment Contam. 2007, 16, 233–251. [Google Scholar] [CrossRef]
- Shu, X.; Gao, L.; Yang, J.; Xia, J.; Song, H.; Zhu, L.; Zhang, K.; Wu, L.; Pang, Z. Spatial Distribution Characteristics and Influencing Factors of Soil Organic Carbon Based on the Geographically Weighted Regression Model. Environ. Monit. Assess. 2024, 196, 1083. [Google Scholar] [CrossRef] [PubMed]
- Tilahun, Y.; Xiao, Q.; Ashango, A.A.; Han, X.; Negewo, M. Prediction of Spatial Soil-California Bearing Ratio of Subgrade Soil Using Particle Swarm Optimization—Artificial Intelligence Method. Transp. Infrastruct. Geotechnol. 2025, 12, 80. [Google Scholar] [CrossRef]
- Dai, X.; Wang, Z.; Liu, S.; Yao, Y.; Zhao, R.; Xiang, T.; Fu, T.; Feng, H.; Xiao, L.; Yang, X.; et al. Hyperspectral Imagery Reveals Large Spatial Variations of Heavy Metal Content in Agricultural Soil-A Case Study of Remote-Sensing Inversion Based on Orbita Hyperspectral Satellites (OHS) Imagery. J. Clean. Prod. 2022, 380, 134878. [Google Scholar] [CrossRef]
- Galelli, S.; Humphrey, G.B.; Maier, H.R.; Castelletti, A.; Dandy, G.C.; Gibbs, M.S. An Evaluation Framework for Input Variable Selection Algorithms for Environmental Data-Driven Models. Environ. Model. Softw. 2014, 62, 33–51. [Google Scholar] [CrossRef]
- Zhang, Y.; Lei, M.; Li, K.; Ju, T. Spatial Prediction of Soil Contamination Based on Machine Learning: A Review. Front. Environ. Sci. Eng. 2023, 17, 93. [Google Scholar] [CrossRef]
- Wang, D.; Wang, M.; Qiao, X. Support Vector Machines Regression and Modeling of Greenhouse Environment. Comput. Electron. Agric. 2008, 66, 46–52. [Google Scholar] [CrossRef]
- Zhao, M.; Wang, H.; Sun, J.; Tang, R.; Cai, B.; Song, X.; Huang, X.; Huang, J.; Fan, Z. Spatio-Temporal Characteristics of Soil Cd Pollution and Its Influencing Factors: A Geographically and Temporally Weighted Regression (GTWR) Method. J. Hazard. Mater. 2023, 446, 130613. [Google Scholar] [CrossRef]
- Kuang, Y.; Chen, X.; Zhu, C. Characteristics of Soil Heavy Metal Pollution and Health Risks in Chenzhou City. Processes 2024, 12, 623. [Google Scholar] [CrossRef]
- Chen, S.; Li, B.; Cao, J.; Mao, B. Research on Agricultural Environment Prediction Based on Deep Learning. Procedia Comput. Sci. 2018, 139, 33–40. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, S.; Jiang, H.; Qin, B.; Li, D.; Jia, K.; Wang, C. Towards Interpretable Machine Learning for Observational Quantification of Soil Heavy Metal Concentrations under Environmental Constraints. Sci. Total Environ. 2024, 926, 171931. [Google Scholar] [CrossRef]
- Zhai, L.; Liao, X.; Chen, T.; Yan, X.; Xie, H.; Wu, B.; Wang, L. Regional Assessment of Cadmium Pollution in Agricultural Lands and the Potential Health Risk Related to Intensive Mining Activities: A Case Study in Chenzhou City, China. J. Environ. Sci. 2008, 20, 696–703. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Gao, J.; Zha, Y. Hyperspectral Sensing of Heavy Metals in Soil and Vegetation: Feasibility and Challenges. ISPRS J. Photogramm. Remote Sens. 2018, 136, 73–84. [Google Scholar] [CrossRef]
- Wei, S.; Dai, Y.; Liu, B.; Zhu, A.; Duan, Q.; Wu, L.; Ji, D.; Ye, A.; Yuan, H.; Zhang, Q.; et al. A China Data Set of Soil Properties for Land Surface Modeling. J. Adv. Model. Earth Syst. 2013, 5, 212–224. [Google Scholar]
- Sun, Q.; Miao, C.; Duan, Q.; Kong, D.; Ye, A.; Di, Z.; Gong, W. Would the ‘Real’ Observed Dataset Stand up? A Critical Examination of Eight Observed Gridded Climate Datasets for China. Environ. Res. Lett. 2014, 9, 015001. [Google Scholar] [CrossRef]
- Miao, S.; Ni, G.; Kong, G.; Yuan, X.; Liu, C.; Shen, X.; Gao, W. A Spatial Interpolation Method Based on 3D-CNN for Soil Petroleum Hydrocarbon Pollution. PLoS ONE 2025, 20, e0316940. [Google Scholar] [CrossRef]
- Justyna, K.; Janusz, P. Temporal and Spatial Variations of Selected Biomarker Activities in Flounder (Platichthys Flesus) Collected in the Baltic Proper. Ecotoxicol. Environ. Saf. 2008, 70, 379–391. [Google Scholar]
- Sergeev, A.P.; Buevich, A.G.; Baglaeva, E.M.; Shichkin, A.V. Combining Spatial Autocorrelation with Machine Learning Increases Prediction Accuracy of Soil Heavy Metals. Catena 2019, 174, 425–435. [Google Scholar] [CrossRef]
- Veronesi, F.; Schillaci, C. Comparison between Geostatistical and Machine Learning Models as Predictors of Topsoil Organic Carbon with a Focus on Local Uncertainty Estimation. Ecol. Indic. 2019, 101, 1032–1044. [Google Scholar] [CrossRef]
- Tian, Y.; Su, D.; Lauria, S.; Liu, X. Recent Advances on Loss Functions in Deep Learning for Computer Vision. Neurocomputing 2022, 497, 129–158. [Google Scholar] [CrossRef]
- Babu, G.R.; Gokuldhev, M.; Brahmanandam, P.S. Integrating IoT for Soil Monitoring and Hybrid Machine Learning in Predicting Tomato Crop Disease in a Typical South India Station. Sensors 2024, 24, 6177. [Google Scholar] [CrossRef]
- Amato, F.; Guignard, F.; Robert, S.; Kanevski, M. A Novel Framework for Spatio-Temporal Prediction of Environmental Data Using Deep Learning. Sci. Rep. 2020, 10, 22243. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Fan, G.; Liu, C.; Zhou, D. Predicting Soil Available Cadmium by Machine Learning Based on Soil Properties. J. Hazard. Mater. 2023, 460, 132327. [Google Scholar] [CrossRef] [PubMed]
- Eisenberg, J.N.; Bennett, D.H.; McKone, T.E. Chemical Dynamics of Persistent Organic Pollutants: A Sensitivity Analysis Relating Soil Concentration Levels to Atmospheric Emissions. Environ. Sci. Technol. 1998, 32, 115–123. [Google Scholar] [CrossRef]
- Laura, U.; Moustapha, S.M.; MarcAndré, G.; Philipp, H.; Martin, S. Quantification of Conceptual Model Uncertainty in the Modeling of Wet Deposited Atmospheric Pollutants. Risk Anal. Off. Publ. Soc. Risk Anal. 2021, 42, 757–769. [Google Scholar]
- Murakami, D.; Kajita, M.; Kajita, S. Spatial Process-Based Transfer Learning for Prediction Problems. J. Geogr. Syst. 2025, 27, 147–166. [Google Scholar] [CrossRef]
- Wang, F.; Huo, L.; Li, Y.; Wu, L.; Zhang, Y.; Shi, G.; An, Y. A Hybrid Framework for Delineating the Migration Route of Soil Heavy Metal Pollution by Heavy Metal Similarity Calculation and Machine Learning Method. Sci. Total Environ. 2023, 858, 160065. [Google Scholar] [CrossRef]
- Li, P.; Hao, H.; Mao, X.; Xu, J.; Lv, Y.; Chen, W.; Ge, D.; Zhang, Z. Convolutional Neural Network-Based Applied Research on the Enrichment of Heavy Metals in the Soil–Rice System in China. Environ. Sci. Pollut. Res. 2022, 29, 53642–53655. [Google Scholar] [CrossRef]
- Zha, Y.; Yang, Y. Innovative Graph Neural Network Approach for Predicting Soil Heavy Metal Pollution in the Pearl River Basin, China. Sci. Rep. 2024, 14, 16505. [Google Scholar] [CrossRef]

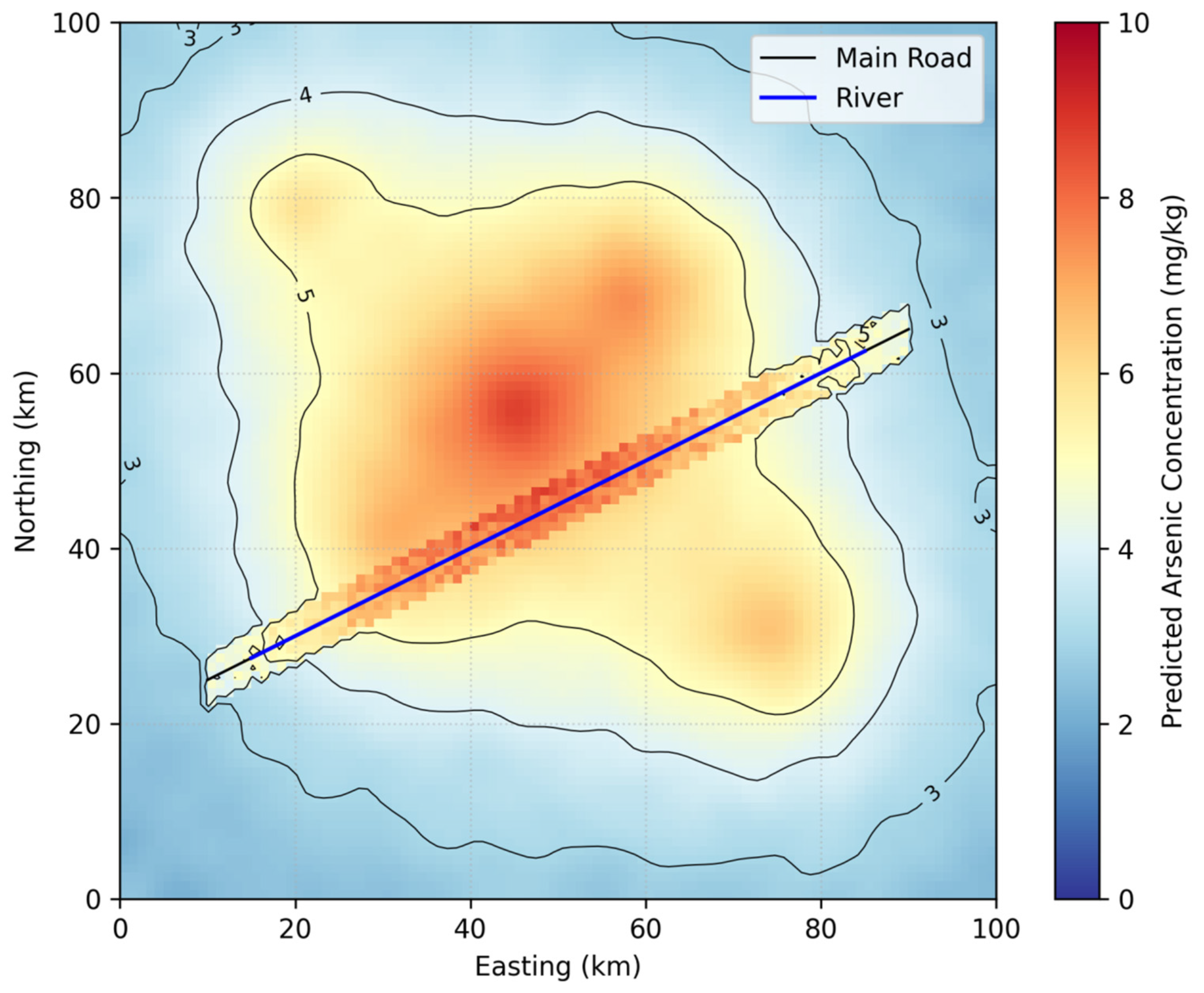
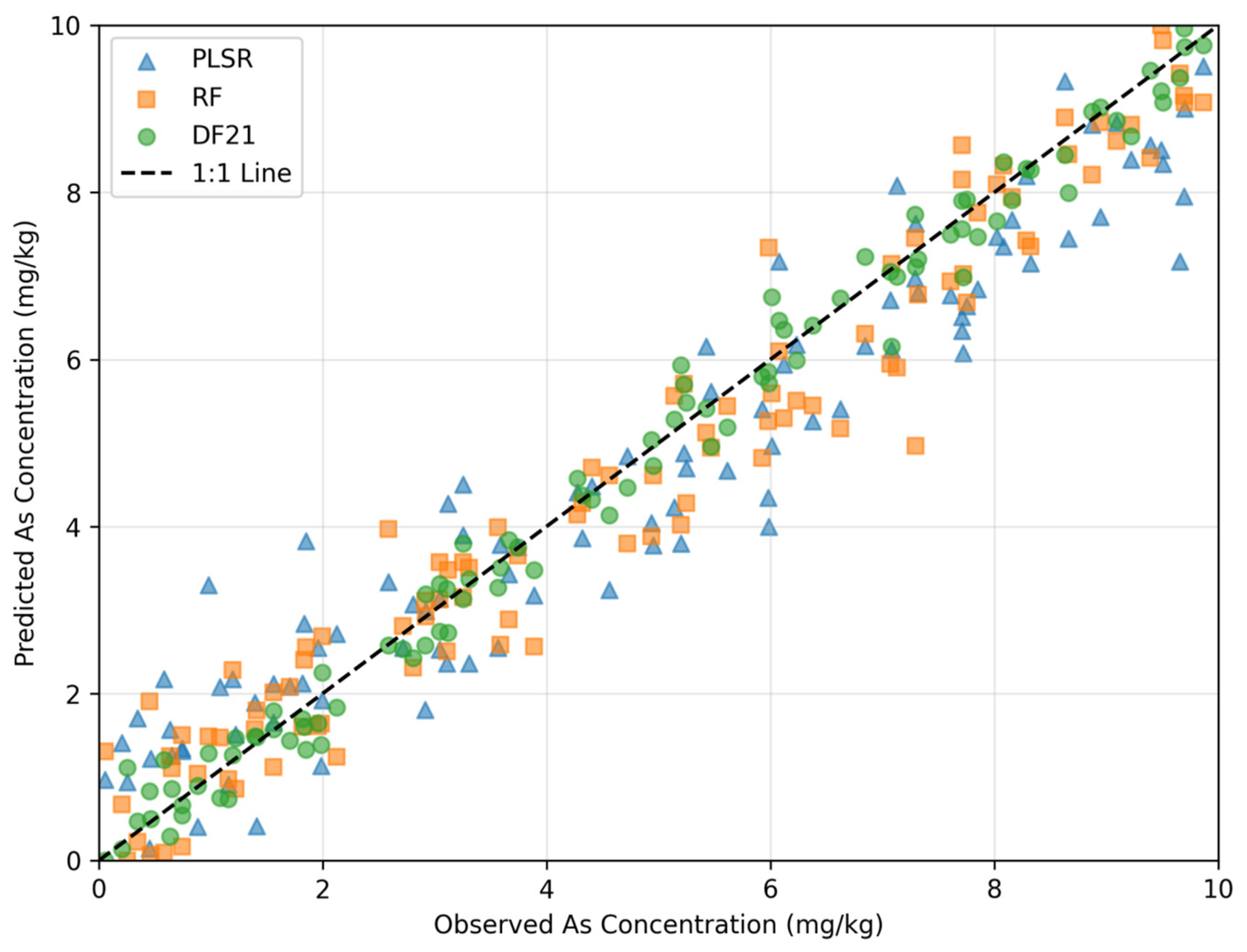
| Variable Category | Variable | Unit | Mean | Std. Dev. | Min | Median | Max | Skewness |
|---|---|---|---|---|---|---|---|---|
| Soil Properties | pH | - | 6.24 | 0.82 | 4.53 | 6.31 | 7.92 | −0.32 |
| Organic Carbon | % | 2.12 | 0.87 | 0.72 | 2.05 | 4.53 | 0.68 | |
| Clay Content | % | 28.4 | 12.1 | 5.3 | 27.8 | 52.7 | 0.21 | |
| Remote Sensing Indices | NDVI | - | 0.65 | 0.12 | 0.32 | 0.67 | 0.88 | −0.82 |
| SAVI | - | 0.58 | 0.15 | 0.25 | 0.61 | 0.82 | −0.53 | |
| NDWI | - | 0.42 | 0.18 | 0.11 | 0.44 | 0.79 | 0.31 | |
| Topography | Elevation | m | 243.5 | 87.2 | 125.3 | 231.8 | 487.6 | 0.89 |
| Slope | ° | 5.2 | 3.1 | 0.5 | 4.7 | 15.3 | 1.12 | |
| TWI | - | 8.7 | 2.5 | 3.2 | 8.9 | 14.1 | −0.15 | |
| Climate | Annual Precipitation | mm | 1452 | 210 | 1120 | 1465 | 1830 | −0.42 |
| Mean Temperature | °C | 17.8 | 1.2 | 15.3 | 17.9 | 20.1 | −0.08 | |
| Anthropogenic | Distance to Roads | m | 685 | 423 | 25 | 620 | 1850 | 0.95 |
| Distance to Rivers | m | 320 | 280 | 10 | 250 | 1250 | 1.32 | |
| Population Density | persons/km2 | 215 | 185 | 15 | 165 | 850 | 1.78 |
| Variable Set | PLSR (R2) | RF (R2) | DF21 (R2) | PLSR (RMSE) | RF (RMSE) | DF21 (RMSE) |
|---|---|---|---|---|---|---|
| S-1 (ECs only) | 0.62 | 0.68 | 0.72 | 1.25 | 1.12 | 1.05 |
| S-2 (ECs + SAs) | 0.71 | 0.75 | 0.79 | 1.08 | 0.99 | 0.92 |
| S-3 (ECs + SAs + SRs) | 0.76 | 0.81 | 0.85 | 0.95 | 0.87 | 0.78 |
| Training Proportion | R2 | RMSE (mg/kg) |
|---|---|---|
| 90% | 0.84 | 0.80 |
| 70% | 0.82 | 0.85 |
| 50% | 0.80 | 0.89 |
| 30% | 0.78 | 0.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Zhang, H.; Wong, C.U.I.; Song, Z. Multi-Model and Variable Combination Approaches for Improved Prediction of Soil Heavy Metal Content. Processes 2025, 13, 2008. https://doi.org/10.3390/pr13072008
Chen X, Zhang H, Wong CUI, Song Z. Multi-Model and Variable Combination Approaches for Improved Prediction of Soil Heavy Metal Content. Processes. 2025; 13(7):2008. https://doi.org/10.3390/pr13072008
Chicago/Turabian StyleChen, Xiaolong, Hongfeng Zhang, Cora Un In Wong, and Zhengchun Song. 2025. "Multi-Model and Variable Combination Approaches for Improved Prediction of Soil Heavy Metal Content" Processes 13, no. 7: 2008. https://doi.org/10.3390/pr13072008
APA StyleChen, X., Zhang, H., Wong, C. U. I., & Song, Z. (2025). Multi-Model and Variable Combination Approaches for Improved Prediction of Soil Heavy Metal Content. Processes, 13(7), 2008. https://doi.org/10.3390/pr13072008






