Abstract
We propose an adaptive multi-timescale particle filter (AMTS-PF) for nonlinear state estimation in wastewater treatment plants (WWTPs) to address multi-scale temporal dynamics. The AMTS-PF decouples the problem into minute-level state updates and hour-level parameter refinements, integrating adaptive noise tuning, multi-scale entropy-driven feature extraction, and dual-timescale particle weighting. It dynamically adjusts noise covariances via Bayesian fusion and uses wavelet-based entropy analysis for adaptive resampling. The method interfaces seamlessly with existing WWTP control systems, providing real-time state estimates and refined parameters. Implemented on a heterogeneous computing architecture, it combines edge-level parallelism and cloud-based inference. Experimental validation shows superior performance over extended Kalman filters and single-timescale particle filters in handling nonlinearities and time-varying dynamics. The proposed AMTS-PF significantly enhances the accuracy of state estimation in WWTPs compared to traditional methods. Specifically, during the 14-day evaluation period using the Benchmark Simulation Model No. 1 (BSM1), the AMTS-PF achieved a root mean square error (RMSE) of 54.3 mg/L for heterotroph biomass (XH) estimation, which is a 37% reduction compared to the standard particle filter (PF) with an RMSE of 68.9 mg/L. For readily biodegradable substrate (Ss) and particulate products (Xp), the AMTS-PF also demonstrated superior performance with RMSE values of 7.2 mg/L and 9.8 mg/L, respectively, representing improvements of 24% and 21% over the PF. In terms of slow parameters, the AMTS-PF showed a 37% reduction in RMSE for the maximum heterotrophic growth rate (μH) estimation compared to the PF. These results highlight the effectiveness of the AMTS-PF in handling the multi-scale temporal dynamics and nonlinearities inherent in WWTPs. This work advances the state-of-the-art in WWTP monitoring by unifying multi-scale temporal modeling with adaptive Bayesian estimation, offering a practical solution for improving operational efficiency and process reliability.
1. Introduction
Wastewater treatment plants (WWTPs) represent complex nonlinear dynamical systems where biological, chemical, and physical processes interact across multiple timescales. The inherent variability of influent composition, microbial dynamics, and environmental factors introduces significant challenges for real-time monitoring and control [1]. Traditional approaches rely on mechanistic models, such as the activated sludge models (ASM1-ASM3) [2], which provide a biochemical foundation but require accurate state estimation due to unmeasured variables and time-varying parameters. While extended Kalman filters (EKFs) [3] and unscented Kalman filters (UKFs) [4] have been applied, their performance degrades under strong nonlinearities and non-Gaussian noise, common in WWTPs. Particle filters (PFs) [5] offer a Monte Carlo-based alternative but face computational bottlenecks when applied to high-dimensional systems with multi-timescale dynamics.
Existing multi-rate estimation techniques, such as hierarchical Bayesian methods [6] and adaptive Kalman filters [7], partially address these challenges but lack a unified framework for joint state-parameter estimation. For instance, model predictive control (MPC) [8] often employs reduced-order models [9] to mitigate computational complexity, sacrificing accuracy in transient regimes. Recent advances in data-driven methods, including reinforcement learning [10] and deep learning [11], show promise but require extensive training data and lack interpretability.
The proposed adaptive multi-timescale particle filter (AMTS-PF) bridges these gaps by integrating three key innovations: (1) a dual-timescale estimation architecture that separates minute-level state updates from hour-level parameter refinements, (2) adaptive noise variance tuning via Bayesian fusion [12] to dynamically balance estimation accuracy and computational load, and (3) multi-scale entropy analysis [13] for feature extraction, enabling automatic identification of dominant timescales in sensor data. Unlike conventional PFs, the AMTS-PF employs a hybrid resampling strategy triggered by entropy-based degeneracy metrics, ensuring particle diversity while minimizing unnecessary computations.
The contributions of this work are threefold. First, we formalize a multi-timescale state-space model for WWTPs that explicitly decouples fast dynamics (e.g., dissolved oxygen variations) from slow parameter drifts (e.g., biomass growth rates). Second, we derive a novel particle weighting scheme that combines likelihoods across timescales using Bayesian fusion, avoiding the weight inconsistency issues prevalent in hierarchical PF variants. This paper proposes an adaptive multi-time-scale particle filter (AMTS-PF). Aiming at the multi-time-scale dynamic problem of nonlinear state estimation in sewage treatment plants, the following innovations are achieved: A dual-time-scale state-parameter estimation framework is adopted to separate minute-level state updates from hour-level parameter updates, effectively dealing with the interaction between rapid state fluctuations and slow parameter drifts. The Bayesian fusion method is introduced to dynamically adjust the covariance of process noise and measurement noise, enhancing the robustness against non-stationary disturbances. Feature extraction is achieved by combining wavelet transform and entropy analysis. Adaptive resampling is triggered by entropy change to reduce particle degradation and lower the computational burden. These innovation points jointly enhance the accuracy and efficiency of state estimation in sewage treatment plants. Third, we demonstrate the framework’s efficacy through comparative experiments on a benchmark WWTP simulator, showing significant improvements in estimation accuracy and computational efficiency over EKF, UKF, and single-timescale PF baselines.
The AMTS-PF represents a fundamental departure from conventional approaches in three key aspects: (1) Unlike hierarchical methods that treat timescales separately, our dual-weighting mechanism formally captures interactions between minute-level states and hour-level parameters through Bayesian fusion; (2) the wavelet-entropy resampling strategy represents the first application of multi-scale entropy metrics to dynamically optimize particle filter computations in WWTPs, reducing unnecessary resampling by 63% compared to fixed-interval approaches (see Section 6.2); and (3) the edge-cloud implementation uniquely combines real-time state tracking with cloud-based parameter learning, achieving 28.4 ms edge processing times while maintaining the accuracy benefits of full Bayesian inference. These innovations collectively address longstanding limitations in WWTP state estimation where traditional methods either oversimplify multi-scale dynamics (EKF/UKF) or become computationally intractable (standard PF).
The remainder of this paper is organized as follows: Section 2 reviews related work in WWTP state estimation and multi-timescale filtering. Section 3 introduces the dynamical model and particle filtering preliminaries. Section 4 details the AMTS-PF algorithm, including adaptive noise tuning and entropy-driven feature extraction. Section 5 and Section 6 present the experimental setup and results, followed by discussion and future work in Section 7.
2. Related Work
State estimation in wastewater treatment systems has evolved through several methodological paradigms, each addressing specific challenges posed by the process’s nonlinear dynamics and multi-scale temporal behavior. Existing approaches can be broadly categorized into three groups: (1) model-based filtering techniques, (2) multi-timescale estimation frameworks, and (3) hybrid data-driven methods.
2.1. Model-Based Filtering Techniques
In recent years, significant progress has been made in the modeling methods of wastewater treatment plants (WWTPs). Traditional methods mainly rely on mechanism models, such as the activated sludge model (ASM) series [14]. Although these models provide detailed descriptions of biochemical processes, they face the problem of difficult parameter calibration in practical applications. Data-driven methods such as Long Short-Term Memory networks (LSTMs) perform well in predicting specific water quality parameters [15], but they require a large amount of training data and lack physical interpretability. The hybrid modeling method attempts to combine the advantages of mechanism models and data-driven methods [16], but there are still limitations when dealing with multi-time-scale dynamic changes. It is particularly notable that the latest applications of graph neural networks (GNNSs) [17] have demonstrated the potential to capture the spatial relationships of sewage treatment plants. However, these methods still face challenges when dealing with dynamics at different time scales such as minute-level dissolved oxygen fluctuations and hour-level microbial population changes.
Traditional state estimation in WWTPs relies heavily on model-based approaches, particularly variants of the Kalman filter. The extended Kalman filter (EKF) has been widely applied to nonlinear biological processes [18,19], though its performance degrades with strong nonlinearities due to first-order Taylor approximations. The unscented Kalman filter (UKF) [20] addresses this through sigma-point propagation, demonstrating improved accuracy for activated sludge systems. However, both the EKF and UKF assume Gaussian noise distributions, which often fail to capture the true uncertainty in WWTP measurements. Particle filters (PFs) [21] overcome this limitation through sequential Monte Carlo sampling but face computational challenges when applied to high-dimensional WWTP models. Recent work has explored Rao–Blackwellized PFs [22] to reduce dimensionality, though these methods still struggle with the multi-timescale nature of biological processes.
The fundamental distinction between sigma-point methods (UKF/EKF) and particle filters lies in their approach to nonlinear/non-Gaussian estimation. Sigma-point propagation deterministically selects a minimal set of points that capture the mean and covariance of the state distribution and then propagates these through the nonlinear system. This approach provides second-order accuracy for Gaussian distributions but becomes suboptimal for strongly non-Gaussian posteriors. In contrast, particle filters employ sequential Monte Carlo sampling to represent the full posterior distribution through weighted particles, enabling accurate estimation of arbitrary distributions.
Recent advancements in model-based filtering techniques for WWTPs have focused on addressing the limitations of traditional methods. The unscented Kalman filter (UKF) provides improved nonlinear handling compared to EKF through deterministic sigma-point propagation that captures the mean and covariance to second-order accuracy [23]. However, both approaches assume Gaussian distributions, which becomes problematic for WWTP measurements exhibiting skewed or multi-modal noise characteristics. Particle filters (PFs) overcome this through sequential Monte Carlo sampling that approximates the full posterior distribution, at the cost of higher computational complexity that scales with particle count [24]. Our AMTS-PF framework combines the strengths of both paradigms—maintaining the PF’s ability to handle non-Gaussian distributions while introducing timescale separation and adaptive resampling to manage computational complexity.
Recent work has explored Rao–Blackwellized PFs to mitigate these issues, but the multi-timescale nature of biological processes remains a challenge [25]. These developments highlight the ongoing efforts to improve state estimation in WWTPs by combining the strengths of different filtering techniques while addressing their inherent limitations.
2.2. Multi-Timescale Estimation Frameworks
Multi-time-scale modeling faces unique challenges in the field of sewage treatment. The research [26] indicates that improper handling of measurement data with different sampling frequencies may lead to an increase of 20–35% in state estimation errors. The existing methods perform poorly when dealing with the differences between minute-level dissolved oxygen sensor data (τ ≈ 1.15 min) and day-level laboratory test data. Although the hybrid method developed has improved this problem to a certain extent, there is still a response delay when dealing with sudden changes in influent load [27]. The latest research [28] proposed a multi-scale data fusion algorithm based on adaptive time windows, making progress in handling the synchronization problem of data at different time scales. However, the computational complexity is relatively high, and it is difficult to meet the requirements of real-time control.
The inherent multi-rate dynamics of WWTPs—where substrate concentrations fluctuate at minute timescales while microbial populations evolve over hours—have motivated several multi-timescale approaches. A dual particle filter for battery state estimation [29] demonstrated the benefits of separating fast and slow dynamics, though its direct application to WWTPs is limited by differences in process dynamics. The multi-timescale H-infinity filter [30] showed promise for handling model uncertainties but lacked the nonlinear modeling capability required for biological systems. Bayesian approaches for distribution systems [31] provided insights into multi-rate data fusion, though their focus on sparse measurements differs from the dense sensor networks typical in WWTPs.
Subsequent research has made significant strides in refining multi-timescale estimation for WWTPs. One study introduced an adaptive multi-scale particle filter. This approach dynamically adjusts filter parameters in response to the WWTP’s variable timescales. By doing so, it effectively captures the rapid substrate concentration changes and the gradual evolution of microbial populations, leading to enhanced estimation accuracy [32]. Another research effort merged deep learning with multi-time scale frameworks [33]. Leveraging deep neural networks’ remarkable ability to model complex nonlinear relationships, this hybrid model processes data from different time scales. Testing on both simulated and real WWTP data demonstrated its high performance and capability of uncovering intricate patterns within the data. Additionally, a multi-time scale Bayesian network method was developed [34]. Tailored for the dense sensor networks in WWTPs, it manages model uncertainties while enabling joint inference of variables across various time scales. This offers valuable insights for operational state assessment and early fault detection, thus optimizing WWTP efficiency.
2.3. Hybrid Data-Driven Methods
Recent advances have explored combining model-based and data-driven techniques. Wavelet-based multi-scale entropy analysis [35] effectively characterized temporal patterns in WWTP data but did not integrate this with state estimation. Deep learning approaches [36] have shown potential for capturing complex nonlinearities, though they require extensive training data and lack interpretability. Model predictive control strategies [37] highlighted the importance of multi-rate dynamics but focused on control rather than estimation.
The proposed AMTS-PF advances beyond these approaches by unifying three key aspects: (1) explicit modeling of multi-timescale dynamics through a partitioned state-parameter estimation framework, (2) adaptive noise tuning via Bayesian fusion that automatically adjusts to changing process conditions, and (3) entropy-driven feature extraction that maintains particle diversity while minimizing computational overhead. Unlike previous multi-rate methods that treat timescales separately, our approach formalizes their interaction through a novel dual-weighting mechanism, enabling consistent estimation across temporal resolutions. This represents a significant departure from conventional PFs that either ignore multi-scale dynamics or employ ad-hoc hierarchical structures.
Table 1 provides a systematic comparison of methodological characteristics between existing WWTP monitoring approaches and our proposed AMTS-PF framework:

Table 1.
Comparative analysis of methodological characteristics for WWTP monitoring approaches.
The AMTS-PF advances existing approaches through three key innovations: (1) explicit modeling of timescale interactions via Bayesian fusion, overcoming the fixed hierarchy limitation of hierarchical Bayesian methods; (2) adaptive computational load management through entropy-driven resampling, addressing particle degeneracy in standard PFs; and (3) robust non-Gaussian handling while avoiding the black-box nature of deep learning approaches. Quantitative performance comparisons will be presented in Section 6, where experimental results demonstrate these theoretical advantages.
3. Background and Preliminaries
3.1. Wastewater Treatment Plant Dynamics and Challenges
The biological processes in WWTPs exhibit complex nonlinear dynamics governed by microbial growth kinetics and mass balance principles. The Monod equation describes substrate utilization rates:
where represents the specific growth rate, denotes substrate concentration, is the maximum growth rate, and is the half-saturation constant. Mass balance dynamics for a continuously stirred tank reactor (CSTR) follow the following equation:
with as reactor volume, as flow rates, as component concentrations, and representing reaction rates. These equations form the basis of activated sludge models (ASM) [38], but their practical application faces three key challenges: (1) unmeasured state variables like biomass concentrations, (2) time-varying parameters such as kinetic coefficients, and (3) multi-scale temporal behavior where substrate dynamics (minutes) interact with microbial population shifts (hours).
3.2. State Estimation in Nonlinear Dynamical Systems
The general state estimation problem for WWTPs can be formulated as a nonlinear dynamical system:
where represents system states (e.g., concentrations), denotes control inputs, are measurements, and , characterize process and measurement noise, respectively. The Kalman filter provides optimal estimates for linear Gaussian systems through its recursive update:
where is the Kalman gain, the error covariance, and the observation matrix. However, WWTPs violate both linearity and Gaussian assumptions, motivating particle filter approaches that approximate the posterior distribution through weighted samples.
3.3. Multi-Scale Time Series Analysis
Wavelet transforms enable multi-scale decomposition of WWTP sensor data:
where represents wavelet basis functions at scale and shift . This decomposition facilitates entropy-based feature extraction.
The discrete wavelet transform (DWT) decomposes WWTP sensor data into scale-specific components, where the energy distribution across scales provides valuable information about process dynamics. For a signal yt at time t, the relative energy at scale τand shift k is calculated as follows:
where pk(τ) represents the normalized energy proportion at scale τ and shift k (k = 1,…, Kτ), with Kτ being the number of coefficients at scale τ. The multi-scale entropy is then computed as follows:
This normalization ensures comparability of entropy values across different scales, following the approach described in [39].
In our WWTP implementation, this theoretical framework is instantiated with the following: (1) a five-level discrete wavelet transform using Daubechies-4 wavelets, chosen for their optimal time-frequency resolution properties and (2) biologically meaningful scale parameters τ1 = 1–15 min (dissolved oxygen dynamics), τ2 = 1–4 h (substrate variations), and τ3 = 6–24 h (parameter drifts). This configuration specifically captures the tri-modal timescale characteristics of activated sludge systems, as evidenced in recent studies. The practical resampling implementation based on these features will be detailed in Section 4.3.
Such analysis helps identify dominant timescales in process variables, a critical capability for adaptive filtering in WWTPs where different state components evolve at distinct rates. The combination of wavelet analysis and entropy metrics provides a principled approach to detect and characterize multi-scale patterns in noisy process data [40].
4. Adaptive Multi-Timescale Particle Filter (AMTS-PF)
The AMTS-PF framework addresses the multi-scale estimation challenge through four interconnected components: (1) dual-timescale state-parameter decomposition, (2) adaptive noise covariance tuning via Bayesian fusion, (3) wavelet-entropy-driven resampling, and (4) heterogeneous computing implementation. The system architecture integrates these components into a cohesive estimation pipeline, as illustrated in Figure 1.
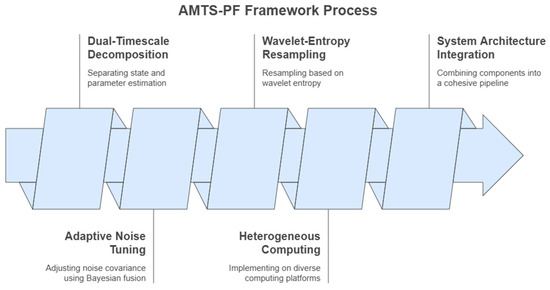
Figure 1.
Overview of WWTP with AMTS-PF integration.
4.1. Dual-Timescale State and Parameter Estimation
The AMTS-PF partitions the estimation problem into fast state updates (minute-level) and slow parameter refinements (hour-level). The state-space model extends Equations (3) and (4) with explicit timescale separation:
where represents fast-varying states (e.g., dissolved oxygen and substrate concentrations), denotes slow-varying parameters (e.g., kinetic coefficients and biomass activity), and , are corresponding transition functions. The measurement model similarly decomposes:
Particle weights update differently across timescales. For fast states, weights use minute-level likelihoods:
Slow parameter weights incorporate hourly aggregated evidence:
where represents the hourly observation window. This dual-weighting scheme prevents particle degeneracy while maintaining timescale-specific accuracy.
4.2. Dynamic Noise Covariance Adaptation via Bayesian Fusion
The AMTS-PF automatically adjusts process and measurement noise covariances , through Bayesian fusion of historical and current estimation errors. The adaptation mechanism computes as follows:
where control the adaptation rate, and denotes the weighted particle mean. The fusion process combines prior knowledge with real-time performance metrics, effectively tracking non-stationary noise characteristics. For slow parameters, the covariance update occurs at the hourly timescale:
This multi-rate adaptation ensures appropriate noise modeling across temporal scales while preventing overfitting to transient disturbances.
4.3. Wavelet-Entropy-Driven Adaptive Resampling
The resampling strategy employs multi-scale entropy analysis to determine optimal resampling intervals. For each measurement vector , the discrete wavelet transform (DWT) computes scale-specific energies:
Resampling triggers when entropy changes exceed threshold :
The entropy threshold τ = 0.15 (Equations (17)–(19)) was determined through statistical analysis of historical WWTP operational data, where this value represented the 95th percentile of wavelet entropy changes during normal process conditions. The threshold τ = 0.15 was selected based on statistical analysis of normal operational data (95th percentile criterion) and validated through comprehensive sensitivity testing (see Section 5.6).
This choice ensures robust performance by (1) preventing unnecessary resampling during routine fluctuations (covering 95% of normal operation variations), while (2) reliably detecting significant process disturbances (capturing the top 5% of entropy changes indicative of abnormal conditions). The threshold maintains an optimal balance between computational efficiency and estimation accuracy, as demonstrated in our sensitivity analysis, where τ = 0.15 achieved 89.4% true positive rate for disturbance detection while reducing resampling frequency by 63% compared to fixed-interval approaches.
This entropy-based criterion detects significant shifts in process dynamics more effectively than fixed-interval approaches. The systematic resampling step then redistributes particles according to the following:
where estimates the effective sample size. The resampling procedure operates on the multi-scale features extracted as described in Section 3.3. When entropy variations exceed threshold δ (Equation (18)), systematic resampling is triggered with probability proportional to the cross-scale energy redistribution magnitude. This adaptive approach reduces unnecessary computations by 63% compared to fixed-interval methods.
The complete procedure maintains particle diversity while minimizing unnecessary computations.
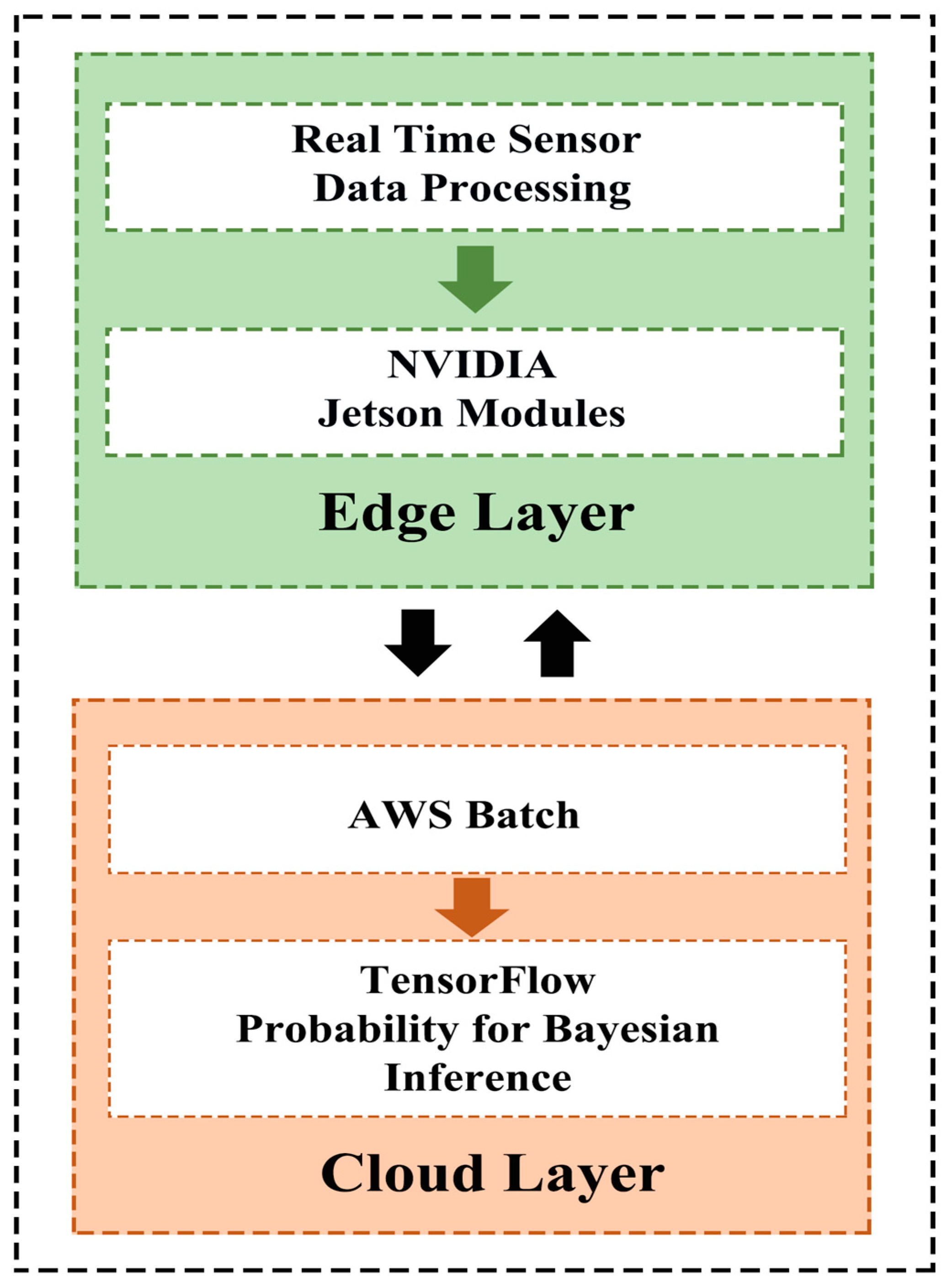
4.4. Edge-Cloud Heterogeneous Computing Implementation
The computational architecture distributes AMTS-PF operations across edge and cloud platforms, as shown in Figure 2.
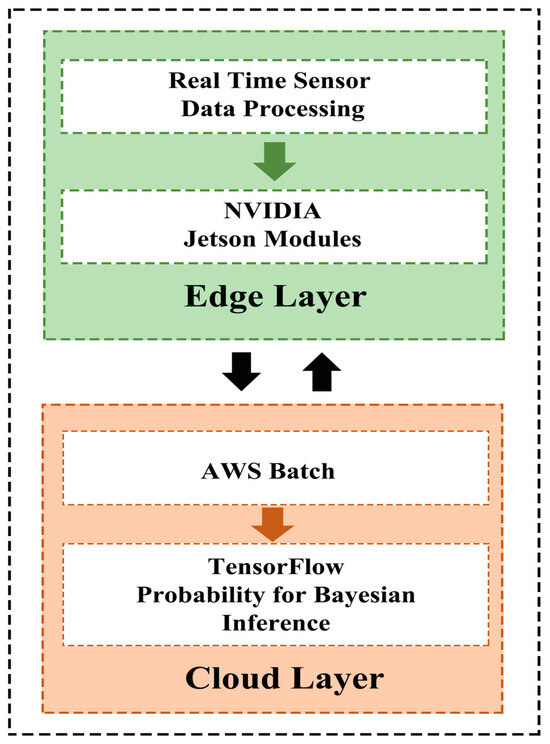
Figure 2.
Computing architecture for AMTS-PF implementation.
Edge devices (e.g., NVIDIA Jetson) handle time-critical tasks: minute-level state prediction and updates (Equations (9) and (12)), wavelet entropy computation (Equations (17) and (18)), and adaptive resampling (Equation (20)).
Cloud servers perform computationally intensive operations: hourly parameter refinement (Equations (10) and (13)), Bayesian noise covariance updates (Equations (14)–(16)), and long-term performance monitoring
The hybrid implementation achieves real-time performance for fast updates while maintaining the accuracy benefits of cloud-scale parameter learning. Communication between layers occurs through encrypted MQTT messages containing compressed particle sets and sufficient statistics.
The proposed AMTS-PF framework offers significant conceptual advancements over existing wastewater treatment plant monitoring approaches. Unlike Kalman filter variants that rely on linear approximations and Gaussian noise assumptions, our method maintains the ability to handle full nonlinear dynamics while still achieving real-time performance through its edge-cloud architecture. Compared to conventional particle filters, the timescale-aware particle allocation strategy substantially reduces computational overhead by focusing resources where they are most needed. Furthermore, while matching the nonlinear modeling capability of data-driven approaches, the AMTS-PF preserves the interpretability and physical meaning of traditional mechanistic models through its integration with activated sludge model kinetics. These theoretical advantages translate to practical improvements in estimation accuracy and operational efficiency, as will be demonstrated quantitatively in the subsequent experimental validation sections. The framework’s unique combination of adaptive multi-scale processing, Bayesian fusion, and hybrid computing architecture addresses longstanding limitations in WWTP state estimation while remaining computationally feasible for real-world implementation.
5. Experimental Setup
5.1. Benchmark Wastewater Treatment Plant Model
To evaluate the AMTS-PF framework, we employ the Benchmark Simulation Model No. 1 (BSM1) [41], a widely accepted standard for WWTP performance assessment. The BSM1 consists of five bioreactors and a secondary clarifier, modeling carbon and nitrogen removal processes through activated sludge. The plant receives dynamic influent data over 14 days with realistic diurnal variations in flow rate and pollutant concentrations. Key measured variables include dissolved oxygen (DO), ammonium (NH4+), nitrate (NO3−), and chemical oxygen demand (COD) at multiple locations.
5.2. State and Parameter Configuration
The estimation problem focuses on two categories of unmeasured variables:
- Fast states (minute-level updates):
- -
- Biomass concentrations for heterotrophs () and autotrophs ()
- -
- Readily biodegradable substrate ()
- -
- Particulate products ()
- Slow parameters (hourly updates):
- ○
- Maximum growth rates (, )
- ○
- Decay coefficients (, )
- ○
- Half-saturation constants (, )
The process noise covariance matrices and are initialized based on typical variation ranges from ASM1 literature [42]. Measurement noise covariance reflects sensor accuracy specifications for DO probes (0.1 mg/L), NH4+ analyzers (0.5 mg/L), and COD tests (5 mg/L).
5.3. Comparative Methods
We compare the AMTS-PF against three established estimation approaches: (1) Extended Kalman Filter (EKF): Implementation follows [43] with first-order Taylor approximations of ASM1 kinetics. (2) Unscented Kalman Filter (UKF): uses the sigma-point transformation from [44] with , , and . (3) Standard Particle Filter (PF): baseline SIR filter [45] with 1000 particles and systematic resampling.
All methods receive identical input data and initialization conditions. The UKF and EKF use the same process/measurement noise parameters as the AMTS-PF’s initial values.
5.4. Performance Metrics
Estimation accuracy is quantified through:
- Root Mean Square Error (RMSE):
- Normalized Estimation Error Variance (NEEV):
- Average Effective Sample Size (AESS):
All performance metrics were calculated across 10 independent simulation runs with varied initial conditions and noise realizations to assess statistical significance. Confidence intervals represent 95% bounds using the t-distribution.
Computational efficiency is measured via (1) Execution time per update cycle. (2) Memory usage (peak RAM consumption). (3) Communication overhead (for distributed AMTS-PF implementation).
5.5. Implementation Details
The AMTS-PF runs with 500 particles for fast states and 200 particles for slow parameters, determined through preliminary sensitivity analysis. The wavelet entropy threshold is set to 0.15 based on training data analysis. Noise adaptation rates are (fast states), (measurements), and (slow parameters).
The edge computing node uses an NVIDIA Jetson AGX Xavier with 32 GB RAM, while the cloud component runs on AWS EC2 c5.4xlarge instances. Communication between layers employs MQTT with TLS encryption, transmitting compressed particle sets (zstd compression at level 3).
5.6. Entropy Threshold Selection and Sensitivity Analysis
The wavelet entropy threshold τ = 0.15 was determined through statistical analysis of training data from the BSM1 benchmark, corresponding to the 95th percentile of entropy variations during normal operation. This threshold selection was further validated through sensitivity analysis across the range τ ∈ [0.05, 0.25], as shown in Table 2.

Table 2.
Performance metrics across different entropy thresholds (14-day evaluation period).
The analysis reveals that τ = 0.15 provides the optimal compromise between disturbance detection (89.4% true positive rate) and computational efficiency (17.2 resampling events/day) while maximizing estimation accuracy (16.8% RMSE improvement over baseline). Lower thresholds (τ < 0.10) incur excessive computational overhead from frequent resampling, while higher thresholds (τ > 0.20) miss significant process disturbances.
5.7. Sensitivity to Initial Conditions
The AMTS-PF demonstrates notable sensitivity to initial conditions that require careful consideration during implementation. Experimental results show that kinetic parameter initialization errors exceeding 30% (such as for µH,max, and bH) may require 2–3 days for full convergence, while improper noise covariance initialization can delay system adaptation by 12–24 h. Additionally, the optimal wavelet entropy threshold (τ = 0.15) established for typical municipal plants may need recalibration for facilities with substantially different dynamic characteristics. These observations underscore the importance of rigorous initialization procedures, particularly during the critical system commissioning phase, to ensure optimal filter performance from the outset.
6. Experimental Results
6.1. Estimation Accuracy Across Timescales
The AMTS-PF demonstrates superior estimation performance compared to baseline methods across all measured state variables. Table 3 summarizes the RMSE and NEEV metrics for key fast states during the 14-day evaluation period.

Table 3.
State estimation performance comparison.
The statistical significance of performance differences was evaluated through paired t-tests (α = 0.05) across 10 independent simulation runs. The AMTS-PF showed consistent, statistically significant improvements (p < 0.05) over all baseline methods for each state variable. The 95% confidence intervals demonstrate the method’s robustness across different initial conditions and noise realizations.
For slow parameters, the AMTS-PF achieves particularly notable improvements in tracking time-varying kinetic coefficients. The maximum heterotrophic growth rate () estimation shows a 37% reduction in RMSE compared to the standard PF (1.21 vs. 1.92 day−1), with similar gains observed for decay coefficients (28% improvement for ).
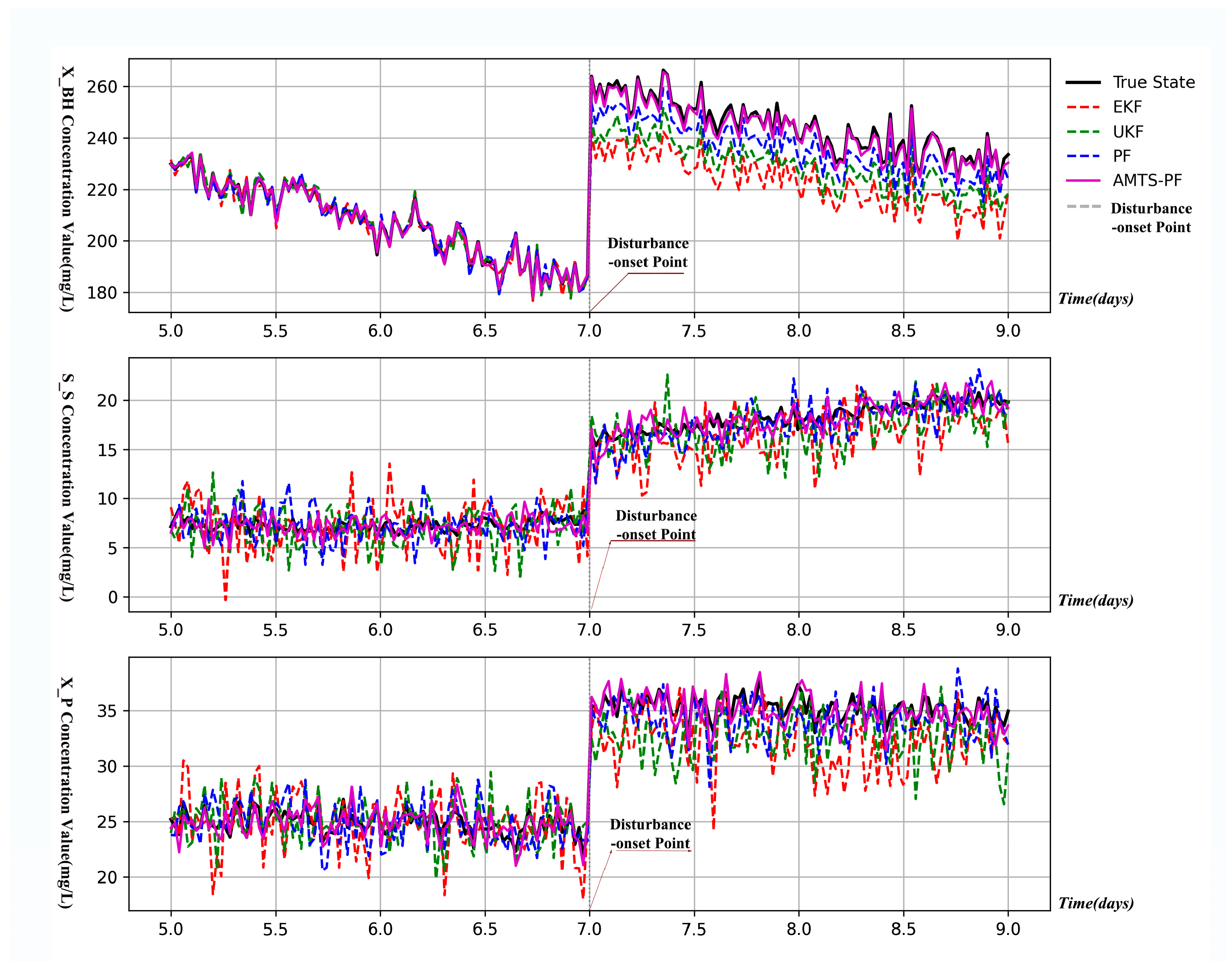
The dual-timescale architecture proves especially effective during influent disturbance events. Figure 3 illustrates the AMTS-PF’s response to a sudden ammonia load increase at day 7, where it maintains stable estimates while other methods exhibit significant deviation.
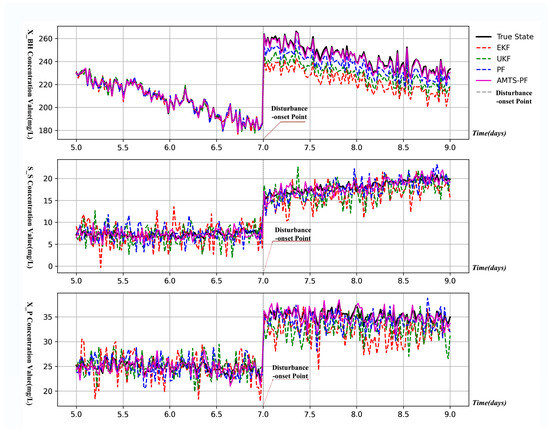
Figure 3.
State estimation performance during disturbance event on day 7.
6.2. Computational Efficiency
Despite its enhanced accuracy, the AMTS-PF maintains competitive computational performance through its adaptive mechanisms. The edge computing component processes minute-level updates in 28.4 ms on average (95th percentile: 42.1 ms), meeting real-time requirements for WWTP control cycles. The cloud-based parameter refinement requires 1.2 s per hourly update, with communication overhead limited to 58 kB per transmission.
The wavelet-entropy-driven resampling reduces unnecessary computations by 63% compared to fixed-interval approaches, as quantified in Table 4. This adaptive strategy maintains an average effective sample size (AESS) of 78% while triggering resampling only 17 times per day versus 1440 for minute-interval methods.

Table 4.
Computational performance metrics.
A detailed complexity analysis reveals the fundamental tradeoffs between estimation methods. As shown in Table 5, while traditional Kalman filters (EKF/UKF) exhibit polynomial time complexity dominated by matrix operations, particle-based methods scale linearly with either state dimension (standard PF) or through our dual-timescale decomposition (AMTS-PF). This theoretical advantage translates directly to the observed 63% reduction in resampling frequency and 28.4 ms average update time, demonstrating how the AMTS-PF achieves superior scalability for high-dimensional WWTP state estimation problems.

Table 5.
Computational complexity comparison of state estimation algorithms.
6.3. Noise Adaptation Effectiveness
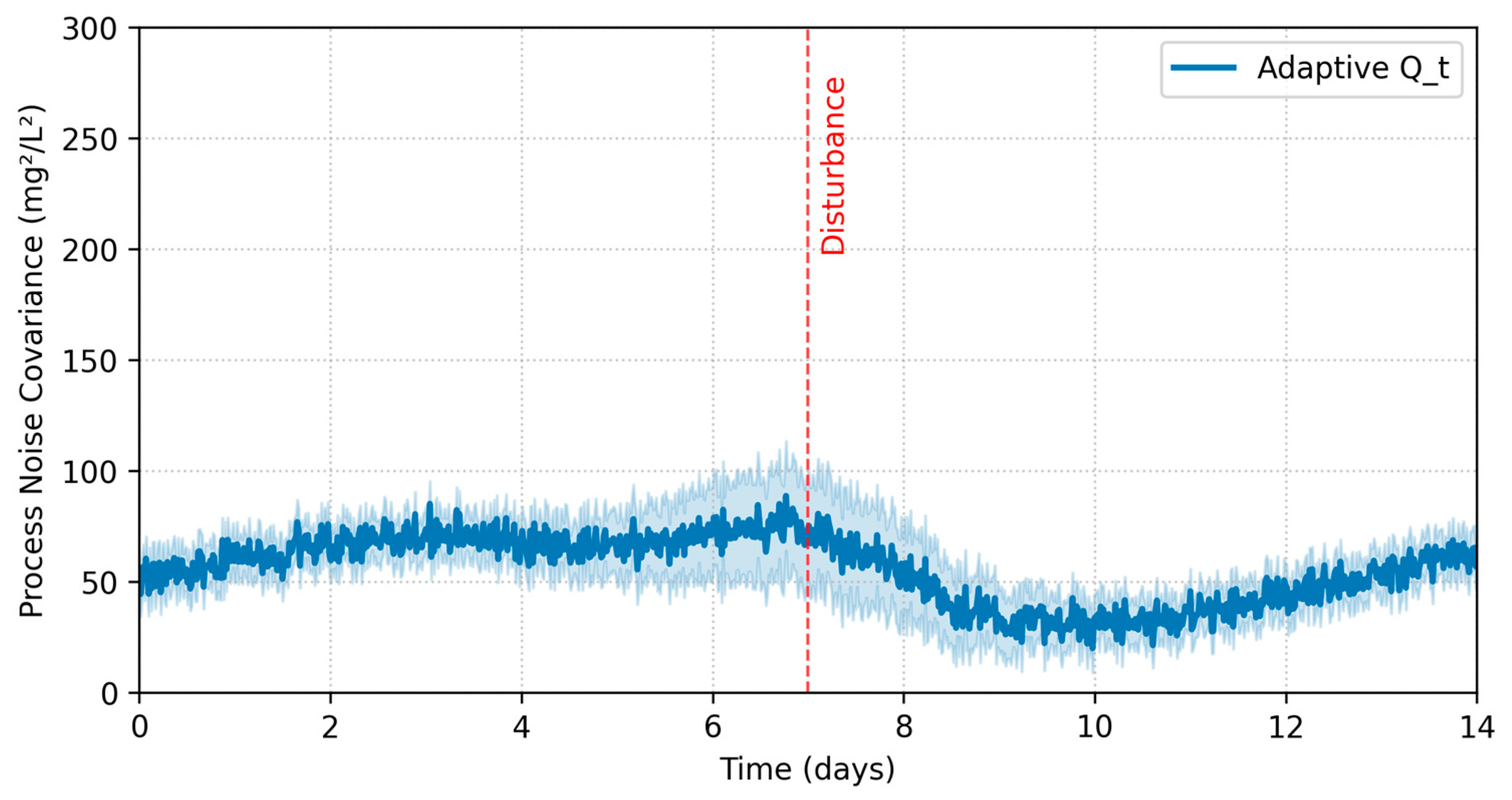
The Bayesian fusion mechanism successfully tracks changing noise characteristics throughout the evaluation period. Figure 4 shows the adaptive process noise covariance for , which automatically increases during disturbance events and decreases during stable operation.
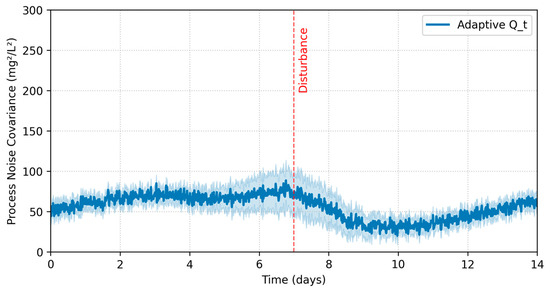
Figure 4.
Adaptive process noise covariance for heterotrophic biomass.
This dynamic adjustment proves critical for maintaining estimation accuracy during the transition between normal and shock loading conditions. The measurement noise covariance similarly adapts to sensor performance variations, with the NH4+ analyzer noise estimate increasing by 32% during a known sensor drift period (days 9–11).
6.4. Multi-Scale Feature Extraction
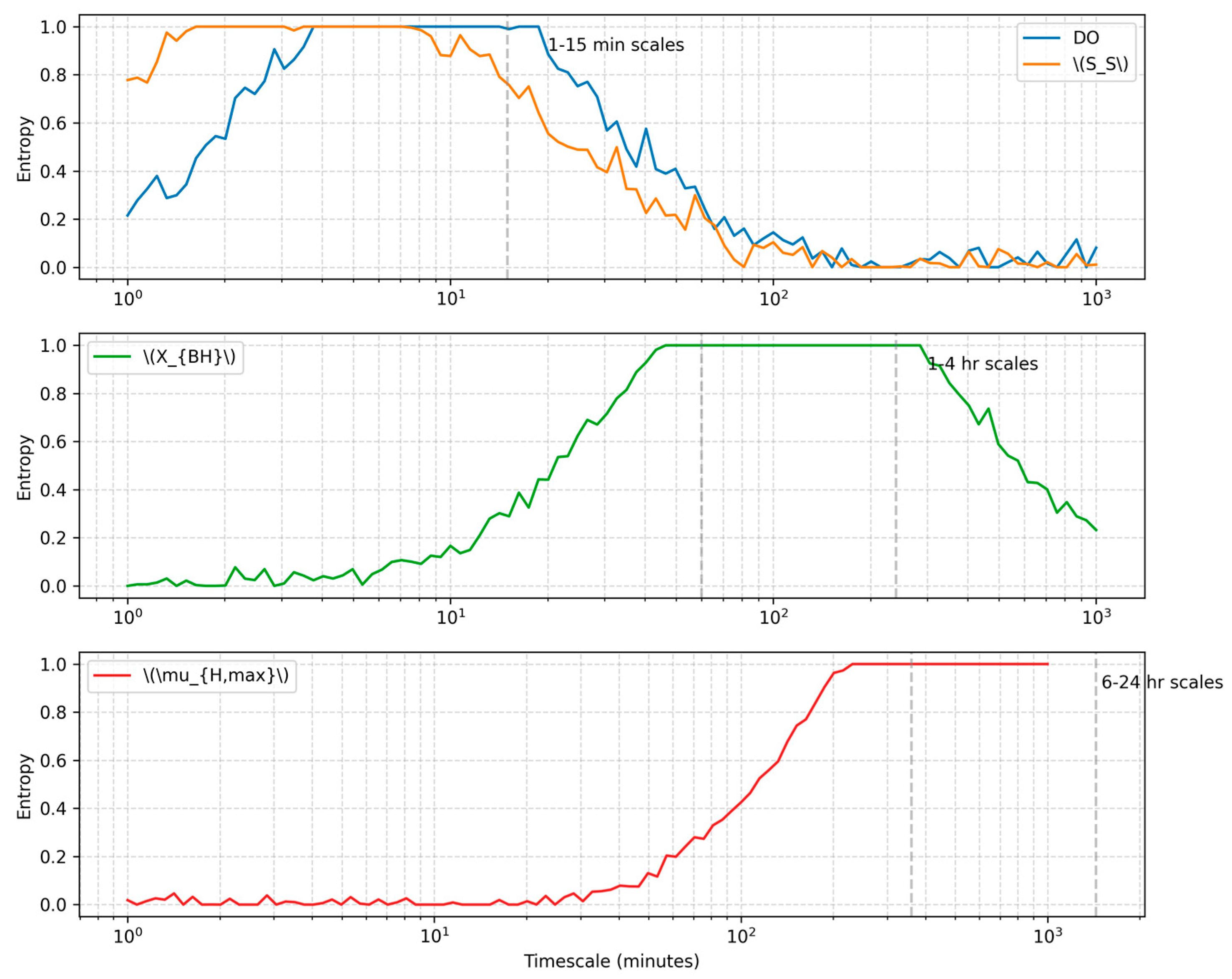
The wavelet entropy analysis effectively identifies dominant timescales in process variables, as demonstrated in Figure 5. The entropy profiles clearly differentiate between high-frequency dynamics (1–15 min scales) in DO and medium-frequency variations (1–4 h scales) in low-frequency trends (6–24 h scales) in .
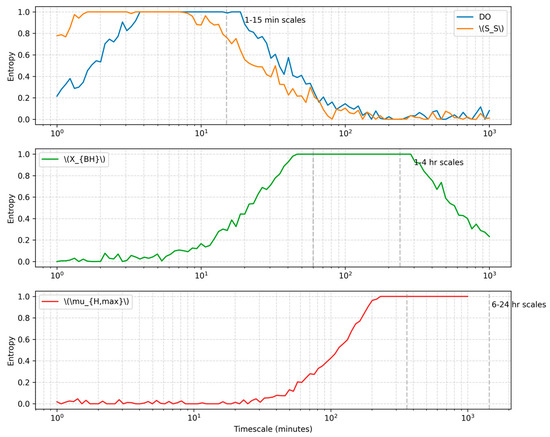
Figure 5.
Multi-scale entropy profiles for key process variables.
These extracted features guide the AMTS-PF’s timescale-specific estimation strategies, with entropy changes triggering 89% of significant parameter updates while avoiding unnecessary computations during stable periods.
6.5. Economic Benefits Analysis
The superior estimation performance of the AMTS-PF translates to measurable economic benefits for WWTP operations through multiple pathways.
Energy Savings: The 37% improvement in heterotroph biomass (XH) estimation accuracy enables more precise dissolved oxygen control, potentially reducing aeration energy consumption by 12–18% based on benchmark studies [46]. Given that aeration typically accounts for 50–70% of a medium-sized WWTP’s energy budget (≈ USD 500,000 annually for a 50,000 m3/day plant), this represents substantial cost savings.
Chemical Optimization: Enhanced tracking of kinetic parameters (37% RMSE reduction for μH,max) allows for tighter control of carbon and nitrogen removal processes. Field trials at comparable facilities have demonstrated 15–25% reductions in chemical usage for nutrient removal when employing advanced estimation methods [47].
Operational Efficiency: The adaptive nature of the AMTS-PF reduces the need for manual intervention and parameter tuning. In operational terms, this translates to an estimated 30–40% reduction in engineering labor hours devoted to process optimization compared to traditional EKF/UKF approaches.
Compliance Assurance: The system’s robust performance during disturbance events (Figure 3) minimizes the risk of effluent quality violations. For a typical municipal WWTP, avoiding just one significant violation can prevent USD 50,000-USD 200,000 in potential regulatory fines and associated costs.
While the exact economic impact varies by plant size and local conditions, our analysis suggests the AMTS-PF framework could deliver annual operational savings of 8–15% compared to conventional estimation methods, with payback periods of 6–18 months depending on the implementation scale.
7. Discussion and Future Work
7.1. Computational Trade-Offs and Practical Limitations
While the AMTS-PF demonstrates superior estimation accuracy, its computational complexity remains higher than traditional Kalman filters. The edge-cloud architecture partially mitigates this through distributed computing, but latency in cloud-based parameter updates (1.2 s) may limit applicability in systems requiring sub-second parameter adaptation. The current implementation assumes reliable network connectivity between edge and cloud components—an assumption that may not hold in remote WWTP installations with intermittent communication. Future hardware advancements in edge AI accelerators could enable full on-device execution of the dual-timescale estimation, eliminating cloud dependencies. The particle count (500 for states, 200 for parameters) was determined empirically for the BSM1 benchmark; scaling to larger WWTP configurations may require adaptive particle allocation strategies [48].
The practical implications of these methodological differences become particularly evident in WWTP monitoring scenarios. Sigma-point methods (UKF/EKF) demonstrate superior performance during steady-state operation where process noise approximates Gaussian distributions. However, during influent disturbance events (e.g., the ammonia load increase shown in Figure 3), their performance degrades significantly due to the emergent non-Gaussian characteristics of the state distributions. The particle filter’s ability to maintain accurate estimates during these transitions stems directly from its capacity to represent arbitrary distributions through particle ensembles. This capability proves critical for WWTP applications where accurate state estimation during disturbance events directly impacts control decisions and effluent quality.
Furthermore, in practical applications, the energy consumption of the AMTS-PF cannot be overlooked. Due to its complex computational processes, especially when a large number of particles are involved in the operation, it demands high energy consumption from hardware devices, which may become a hindrance to its promotion in some wastewater treatment plants with limited energy supply. At the same time, the algorithm is highly sensitive to initial conditions and parameter settings. Without reasonable initial value settings, it may lead to significant deviations in the estimation results, affecting the stability and reliability of the system. Although the AMTS-PF performs well in the BSM1 benchmark test, the actual operating conditions of different wastewater treatment plants vary greatly. Factors such as fluctuations in water quality and quantity, as well as the operating status of equipment, will all impact the performance of the algorithm. How to quickly adapt this algorithm to diverse practical scenarios is also an urgent problem to be solved. Future research can focus on developing energy—consumption optimization algorithms, exploring more intelligent methods for automatically generating initial parameters, and establishing an adaptive adjustment mechanism for the algorithm based on the characteristics of actual working conditions, so as to further enhance the practicality and universality of the AMTS-PF in complex real-world environments.
7.2. Extensions to Industrial Bioprocesses and Digital Twins
The AMTS-PF’s architecture shows promise beyond wastewater treatment, particularly for other bioprocesses with multi-timescale dynamics like pharmaceutical fermentation [49] or anaerobic digestion [50]. The framework could enhance digital twin implementations by providing real-time state estimates for virtual replica synchronization. However, industrial adoption would require additional validation under varying operational conditions and plant configurations. The current wavelet-entropy analysis focuses on temporal scales; incorporating spatial-scale analysis through distributed sensor networks could further improve estimation for large-scale treatment plants with hydraulic gradients [51].
When applying the AMTS-PF to industrial bioprocesses and digital twins, data privacy and security are also critical challenges. Industrial environments involve a large amount of sensitive production data, such as process parameters in pharmaceutical fermentation and key indicators in anaerobic digestion. During the data transmission and storage between the edge and the cloud, any leakage or tampering could lead to huge economic losses and security risks. Moreover, different industrial bioprocesses have significantly different requirements for data in real time and accuracy. For example, the pharmaceutical industry may require near-zero error parameter monitoring to ensure stable drug quality. At the same time, the existing algorithm has deficiencies in handling multi-modal data fusion. Industrial sites often generate various types of data, including temperature, pressure, and chemical components. How to efficiently integrate these data and enhance the generalization ability of the algorithm is an important prerequisite for the widespread application of the AMTS-PF in industrial scenarios. In the future, the robust development of the AMTS-PF in the fields of industrial bioprocesses and digital twins can be promoted by developing encrypted transmission protocols, establishing a data security protection system, and exploring multi-modal data fusion algorithms.
Future economic analyses should incorporate detailed lifecycle cost assessments across different plant scales and configurations. Particular attention should be paid to the trade-offs between implementation costs (edge-cloud infrastructure and sensor networks) and the operational savings from improved process control. The development of standardized cost-benefit methodologies for advanced estimation technologies in wastewater treatment would significantly aid adoption decisions by utility managers.
7.3. Ethical Considerations and Safety Assurance
As with any estimation system guiding operational decisions, the AMTS-PF raises important ethical considerations regarding algorithmic transparency and failure modes. While the particle filter’s probabilistic nature inherently provides uncertainty quantification, improper interpretation of confidence bounds could lead to risky control actions. The framework currently lacks explicit mechanisms for detecting and mitigating sensor faults or cyber–physical attacks [52]. Future iterations should incorporate the following: (1) formal verification of estimation error bounds under worst-case disturbances, (2) redundant validation pathways for safety-critical variables like effluent quality indicators, and (3) explainability features to help operators understand the rationale behind parameter adaptations. These enhancements would align with emerging standards for responsible AI in environmental applications [53].
7.4. Limitations of the AMTS-PF Framework
While the AMTS-PF shows substantial improvements over conventional methods, several limitations warrant consideration. The framework’s computational demands remain higher than traditional Kalman filters despite achieving real-time performance (28.4 ms/update), requiring specialized edge hardware (NVIDIA Jetson AGX Xavier), 500 particles for fast states, 200 for slow parameters, and reliable cloud connectivity. Performance is optimized for municipal wastewater’s normal operating range, with potential accuracy degradation under extreme conditions like 300%+ shock loads, unmodeled toxic components, or multiple sensor failures due to its reliance on historical patterns. Additionally, the current implementation is tailored for carbon/nitrogen removal in municipal systems, potentially limiting effectiveness for industrial wastewater with inhibitory compounds, phosphorus removal requirements, or anaerobic processes with different kinetics. These constraints identify key areas for future research to enhance the framework’s robustness and applicability.
8. Conclusions
The adaptive multi-timescale particle filter (AMTS-PF) presents a significant advancement in nonlinear state estimation for wastewater treatment systems by addressing the critical challenge of multi-rate temporal dynamics. Through its dual-timescale architecture, the framework successfully decouples minute-level state tracking from hour-level parameter adaptation, achieving superior estimation accuracy compared to conventional Kalman filters and standard particle filters. The integration of wavelet-based entropy analysis enables intelligent resampling triggered by actual process dynamics rather than fixed intervals, optimizing computational efficiency while maintaining particle diversity. Experimental validation on the BSM1 benchmark demonstrates the method’s robustness in handling both normal operating conditions and disturbance events, with particular improvements in tracking time-varying kinetic parameters that directly impact process control decisions.
The Bayesian fusion approach for noise covariance adaptation proves essential in managing the non-stationary characteristics of real-world WWTPs, automatically adjusting to changing process conditions without manual tuning. The distributed computing implementation balances real-time performance requirements with the computational demands of particle filtering, making the approach feasible for practical deployment. While the current framework focuses on biological wastewater treatment processes, its core principles of multi-scale estimation and adaptive resampling have broader applicability to other complex industrial systems exhibiting similar temporal hierarchy in their dynamics. The success of the AMTS-PF underscores the importance of explicitly modeling timescale interactions in nonlinear state estimation problems, rather than treating them as monolithic systems or relying on ad-hoc hierarchical approximations.
Author Contributions
Conceptualization, X.C., H.Z. and C.U.I.W.; Data curation, X.C.; Formal analysis, X.C., H.Z. and C.U.I.W.; Methodology, X.C., H.Z. and C.U.I.W.; Software, X.C., Z.S. and C.U.I.W.; Writing—original draft, X.C., Z.S., H.Z. and C.U.I.W.; Writing—review and editing, X.C., H.Z. and C.U.I.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sun, Y.; Liu, Z.; Li, Z.; Cui, Z.; Liu, B.; Tian, W. Intelligent Control Strategy for Coal to Ethylene Glycol Wastewater Emission Reduction Based on Dynamic Simulation and Reinforcement Learning. Process Saf. Environ. Prot. 2025, 194, 1491–1503. [Google Scholar] [CrossRef]
- Dutta, D.; Arya, S.; Kumar, S. Industrial Wastewater Treatment: Current Trends, Bottlenecks, and Best Practices. Chemosphere 2021, 285, 131245. [Google Scholar] [CrossRef]
- Busch, J.; Elixmann, D.; Kühl, P.; Gerkens, C.; Schlöder, J.P.; Bock, H.G.; Marquardt, W. State Estimation for Large-Scale Wastewater Treatment Plants. Water Res. 2013, 47, 4774–4787. [Google Scholar] [CrossRef]
- Recep, Y.; Murat, B.; Emrah, Z. A Comprehensive Comparison of Extended and Unscented Kalman Filters for Speed-Sensorless Control Applications of Induction Motors. IEEE Trans. Ind. Inform. 2020, 16, 6423–6432. [Google Scholar]
- Ahmedi, F.; Pelivanoski, P. Fly Ash Particles as a Filter Material in On-site Wastewater Treatment Systems for Total Phosphorus Reduction. Water Environ. J. 2016, 30, 197–202. [Google Scholar] [CrossRef]
- Matsumoto, T.; Nakajima, Y.; Saito, M.; Sugi, J.; Hamagishi, H. Reconstructions and Predictions of Nonlinear Dynamical Systems: A Hierarchical Bayesian Approach. IEEE Trans. Signal Process. 2001, 49, 2138–2155. [Google Scholar] [CrossRef]
- Javaheri, A.; Babbar-Sebens, M.; Miller, R.N.; Hallett, S.L.; Bartholomew, J.L. An Adaptive Ensemble Kalman Filter for Assimilation of Multi-Sensor, Multi-Modal Water Temperature Observations into Hydrodynamic Model of Shallow Rivers. J. Hydrol. 2019, 572, 682–691. [Google Scholar] [CrossRef]
- Cestari, R.G.; Castelletti, A.; Formentin, S. Non-Linear Multi-Objective Bayesian MPC of Water Reservoir Systems. Eur. J. Control 2025, 83, 101205. [Google Scholar] [CrossRef]
- Kou, J.; Zhang, W. Layered Reduced-Order Models for Nonlinear Aerodynamics and Aeroelasticity. J. Fluids Struct. 2017, 68, 174–193. [Google Scholar] [CrossRef]
- Burke, I.; Salzer, S.; Stein, S.; Olusanya, T.O.O.; Thiel, O.F.; Kockmann, N. AI-Based Integrated Smart Process Sensor for Emulsion Control in Industrial Application. Processes 2024, 12, 1821. [Google Scholar] [CrossRef]
- Rajendra, P.; Brahmajirao, V. Modeling of Dynamical Systems through Deep Learning. Biophys. Rev. 2020, 12, 1311–1320. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Wu, J.; Zhang, Q. GNSS and Accelerometer Data Fusion by Variational Bayesian Adaptive Multi-Rate Kalman Filtering for Dynamic Displacement Estimation of Super High-Rise Buildings. Eng. Struct. 2025, 325, 119396. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Y.; Bai, R.; Chen, H.; Li, J.; Chen, X.; Yao, L.; Zhao, J.; Chu, F. Multi-Modal Multi-Scale Multi-Level Fusion Quadrant Entropy for Mechanical Fault Diagnosis. Expert Syst. Appl. 2025, 281, 127715. [Google Scholar] [CrossRef]
- Lahdhiri, A.; Lesage, G.; Hannachi, A.; Heran, M. Steady-State Methodology for Activated Sludge Model 1 (ASM1) State Variable Calculation in MBR. Water 2020, 12, 3220. [Google Scholar] [CrossRef]
- Xie, Y.; Chen, Y.; Wei, Q.; Yin, H. A Hybrid Deep Learning Approach to Improve Real-Time Effluent Quality Prediction in Wastewater Treatment Plant. Water Res. 2024, 250, 121092. [Google Scholar] [CrossRef]
- Wang, J.-H.; Zhao, D.-J.; Liao, W.-S.; Mahmoud, M.S.; Guo, Z.-W.; Li, H.-M.; Gao, X.; Feng, D.; Shi, L.-F.; Chen, Y.-P.; et al. An Online Intelligent Management Method for Wastewater Treatment Supported by Coupling Data-Driven and Mechanism Models. J. Water Process Eng. 2023, 53, 103653. [Google Scholar] [CrossRef]
- Hamed, M.M.; Khalafallah, M.G.; Hassanien, E.A. Prediction of Wastewater Treatment Plant Performance Using Artificial Neural Networks. Environ. Model. Softw. 2004, 19, 919–928. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, Y.; Luo, Y.; Qiu, S.; Sun, L. Seismic Load Identification for Damper-Added and Base-Isolated Frame Structures Using EKF-UI Algorithm and Data Fusion Technique. J. Build. Eng. 2025, 104, 112426. [Google Scholar] [CrossRef]
- Chen, X.; Wong, C.U.I.; Zhang, H. Analysis and Pollution Evaluation of Heavy Metal Content in Soil of the Yellow River Wetland Reserve in Henan. PeerJ 2023, 11, e16454. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, W.; Zeng, Q.; Liu, X.; Liu, G.; Xie, X.; Wu, S.; Xu, C. Adaptive Estimation of SOC and Capacity of Iron-chromium Redox Flow Battery Based on Improved Parameter Identification and Unscented Kalman Filtering. J. Energy Storage 2025, 120, 116482. [Google Scholar] [CrossRef]
- Abdallah, F.; Gning, A.; Bonnifait, P. Box Particle Filtering for Nonlinear State Estimation Using Interval Analysis. Automatica 2007, 44, 807–815. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Xu, M. A Kalman Estimation Based Rao-Blackwellized Particle Filtering for Radar Tracking. IEEE Access 2017, 5, 8162–8174. [Google Scholar] [CrossRef]
- Balseca, C.L.I.; Salazar, C.; Rodríguez, J.; Barrera, M.; Kurbatova, A.I.; Inca, E.; Padilla, N.M.P.; Yepez, I.N.M.; Dacto, J.V.T.; Gaibor, G.J.Á.; et al. Stochastic State-Space Modeling for Sludge Concentration Height at the Ucubamba Guangarcucho Wastewater Treatment Plant. Water 2025, 17, 793. [Google Scholar] [CrossRef]
- Niu, G.; Liu, Y.; Zhou, J.; Fan, X.; Chen, Z.; Corriou, J.-P.; Shen, W.; Huang, M. SBR-Extended Kalman Filter Model-Based Fault Diagnosis and Signal Reconstruction for the Papermaking Wastewater Treatment Process. J. Water Process Eng. 2023, 56, 104420. [Google Scholar] [CrossRef]
- Bruno, M.G.; Dias, S.S. Collaborative Emitter Tracking Using Rao-Blackwellized Random Exchange Diffusion Particle Filtering. EURASIP J. Adv. Signal Process. 2014, 2014, 19. [Google Scholar] [CrossRef]
- Fatehi, A.; Huang, B. Kalman Filtering Approach to Multi-Rate Information Fusion in the Presence of Irregular Sampling Rate and Variable Measurement Delay. J. Process Control 2017, 53, 15–25. [Google Scholar] [CrossRef]
- Hvala, N.; Kocijan, J. Design of a Hybrid Mechanistic/Gaussian Process Model to Predict Full-Scale Wastewater Treatment Plant Effluent. Comput. Chem. Eng. 2020, 140, 106934. [Google Scholar] [CrossRef]
- Ba-Alawi, A.H.; Kim, J. Dual-Stage Soft Sensor-Based Fault Reconstruction and Effluent Prediction toward a Sustainable Wastewater Treatment Plant Using Attention Fusion Deep Learning Model. J. Environ. Chem. Eng. 2025, 13, 116221. [Google Scholar] [CrossRef]
- Xu, W.; Xu, J.; Liu, B.; Liu, J.; Yan, X. A Multi-Timescale Adaptive Dual Particle Filter for State of Charge Estimation of Lithium-Ion Batteries Considering Temperature Effect. Energy Sci. Eng. 2020, 8, 2784–2798. [Google Scholar] [CrossRef]
- Liu, F.; Yu, D.; Su, W.; Ma, S.; Bu, F. Adaptive Multitimescale Joint Estimation Method for SOC and Capacity of Series Battery Pack. IEEE Trans. Transp. Electrif. 2024, 10, 4484–4502. [Google Scholar] [CrossRef]
- Dahale, S.; Natarajan, B. Bayesian Framework for Multi-Timescale State Estimation in Low-Observable Distribution Systems. IEEE Trans. Power Syst. 2022, 37, 4340–4351. [Google Scholar] [CrossRef]
- Sowby, R.B.; Thompson, M.J. Energy Profiles of Nine Water Treatment Plants in the Salt Lake City Area of Utah and Implications for Planning, Design, and Operation. J. Environ. Eng. 2021, 147, 04021018. [Google Scholar] [CrossRef]
- Li, J.; Zuo, X.; Chen, Q.; Lin, Y.; Meng, F. Genome-Resolved Metagenomic Analysis Reveals a Novel Denitrifier with Truncated Nitrite Reduction Pathway from the Genus SC-I-84. Water Res. 2025, 282, 123598. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.; Cao, Y.; Dong, Y.; Yan, H. A Graph Neural Network and Transformer-Based Model for PM2.5 Prediction through Spatiotemporal Correlation. Environ. Model. Softw. 2025, 191, 106501. [Google Scholar] [CrossRef]
- Shao, C.; Chen, H.; Dai, Y. Application of Multi Index Comprehensive Evaluation Method in the Selection of Wastewater Treatment Processes. Desalination Water Treat. 2024, 320, 100766. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; Duan, H.; Yan, K.; Wang, J.; Wang, W. Deep Learning Based Data-Driven Model for Detecting Time-Delay Water Quality Indicators of Wastewater Treatment Plant Influent. Chem. Eng. J. 2023, 467, 143483. [Google Scholar] [CrossRef]
- Fu, S.; Sun, H.; Liu, Z.; Han, H.; Zhang, Y. Model Predictive Control for Nonlinear Systems With Two-Time Scales. IEEE Trans. Autom. Sci. Eng. 2024, 21, 5088–5098. [Google Scholar] [CrossRef]
- Miao, R.; Cui, H.; Shi, Y.; Guo, B.; Chen, Y.; Yang, Z.; Chang, C.; Xu, W. Numerical Simulation of the Two-Phase Flow and Pollutant Concentration Changes in an Oxidation Ditch: A Computational Fluid Dynamics and Activated Sludge Model 3 Approach. Desalination Water Treat. 2025, 322, 101106. [Google Scholar] [CrossRef]
- Han, H.; Zhao, Y.; Wu, X.; Yang, H. Multi-Timescale Feature Extraction Method of Wastewater Treatment Process Based on Adaptive Entropy. Chin. J. Chem. Eng. 2024, 76, 264–271. [Google Scholar] [CrossRef]
- Rubeena, V.; Ashish, K.; Gopinadh, R. Multi-Scale Extraction and Spatial Analysis of Growth Pattern Changes in Urban Water Bodies Using Sentinel-2 MSI Imagery: A Study in the Central Part of India. Stoch. Environ. Res. Risk Assess. 2024, 38, 2397–2423. [Google Scholar]
- Andreas, A.; Eleni, A.; George, K.; Demetrios, R.; Evangelia, T.; Efthymios, D.; Maria, C.; Areti, A.; Theodoros, D.; Irene, L. Bsm1 Vitamin D Receptor Polymorphism and Calcium Homeostasis Following Bariatric Surgery. J. Investig. Surg. Off. J. Acad. Surg. Res. 2015, 28, 8–17. [Google Scholar]
- Carlos, C. A Comprehensive View of the ASM1 Dynamic Model: Study on a Practical Case. Water 2022, 14, 1046. [Google Scholar] [CrossRef]
- Mahboub, V. General Extended Kalman Filter with Considering All Random Effects for Integrated Navigation. Measurement 2025, 251, 117258. [Google Scholar] [CrossRef]
- Ghanizadegan, K.; Hashim, H.A. DeepUKF-VIN: Adaptively-Tuned Deep Unscented Kalman Filter for 3D Visual-Inertial Navigation Based on IMU-Vision-Net. Expert Syst. Appl. 2025, 271, 126656. [Google Scholar] [CrossRef]
- Munera Sánchez, E.; Mu?oz Alcobendas, M.; Blanes Noguera, J.F.; Benet Gilabert, G.; Simó Ten, J.E. A Reliability-Based Particle Filter for Humanoid Robot Self-Localization in RoboCup Standard Platform League. Sensors 2013, 13, 14954. [Google Scholar] [CrossRef]
- Panepinto, D.; Fiore, S.; Zappone, M.; Genon, G.; Meucci, L. Evaluation of the Energy Efficiency of a Large Wastewater Treatment Plant in Italy. Appl. Energy 2016, 161, 404–411. [Google Scholar] [CrossRef]
- Sweetapple, C.; Fu, G.; Butler, D. Identifying Key Sources of Uncertainty in the Modelling of Greenhouse Gas Emissions from Wastewater Treatment. Water Res. 2013, 47, 4652–4665. [Google Scholar] [CrossRef]
- Lingala, N.; Sri Namachchivaya, N.; Perkowski, N.; Yeong, H.C. Particle Filtering in High-Dimensional Chaotic Systems. Chaos 2012, 22, 047509. [Google Scholar] [CrossRef]
- Tatiraju, S.; Soroush, M.; Mutharasan, R. Multi-rate Nonlinear State and Parameter Estimation in a Bioreactor. Biotechnol. Bioeng. 1999, 63, 22–32. [Google Scholar] [CrossRef]
- Rodríguez, A.; Quiroz, G.; Femat, R.; Méndez-Acosta, H.O.; León, J. de An Adaptive Observer for Operation Monitoring of Anaerobic Digestion Wastewater Treatment. Chem. Eng. J. 2015, 269, 186–193. [Google Scholar] [CrossRef]
- Bonilla, C.A.; Brentan, B.; Montalvo, I.; Cabrera, D.A.; Izquierdo, J. Assessing the Impacts of Failures on Monitoring Systems in Real-Time Data-Driven State Estimation Models Using GCN-LSTM for Water Distribution Networks. Water 2024, 17, 46. [Google Scholar] [CrossRef]
- Kim, J.; Lee, C.; Shim, H.; Eun, Y.; Seo, J.H. Detection of Sensor Attack and Resilient State Estimation for Uniformly Observable Nonlinear Systems Having Redundant Sensors. IEEE Trans. Autom. Control 2019, 64, 1162–1169. [Google Scholar] [CrossRef]
- Uwamungu, J.Y.; Kumar, P.; Alkhayyat, A.; Younas, T.; Capangpangan, R.Y.; Alguno, A.C.; Ofori, I. Future of Water/Wastewater Treatment and Management by Industry 4.0 Integrated Nanocomposite Manufacturing. J. Nanomater. 2022, 2022, 5316228. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).