Critical Threshold for Fluid Flow Transition from Linear to Nonlinear in Self-Affine Rough-Surfaced Rock Fractures: Effects of Shear and Confinement
Abstract
1. Introduction
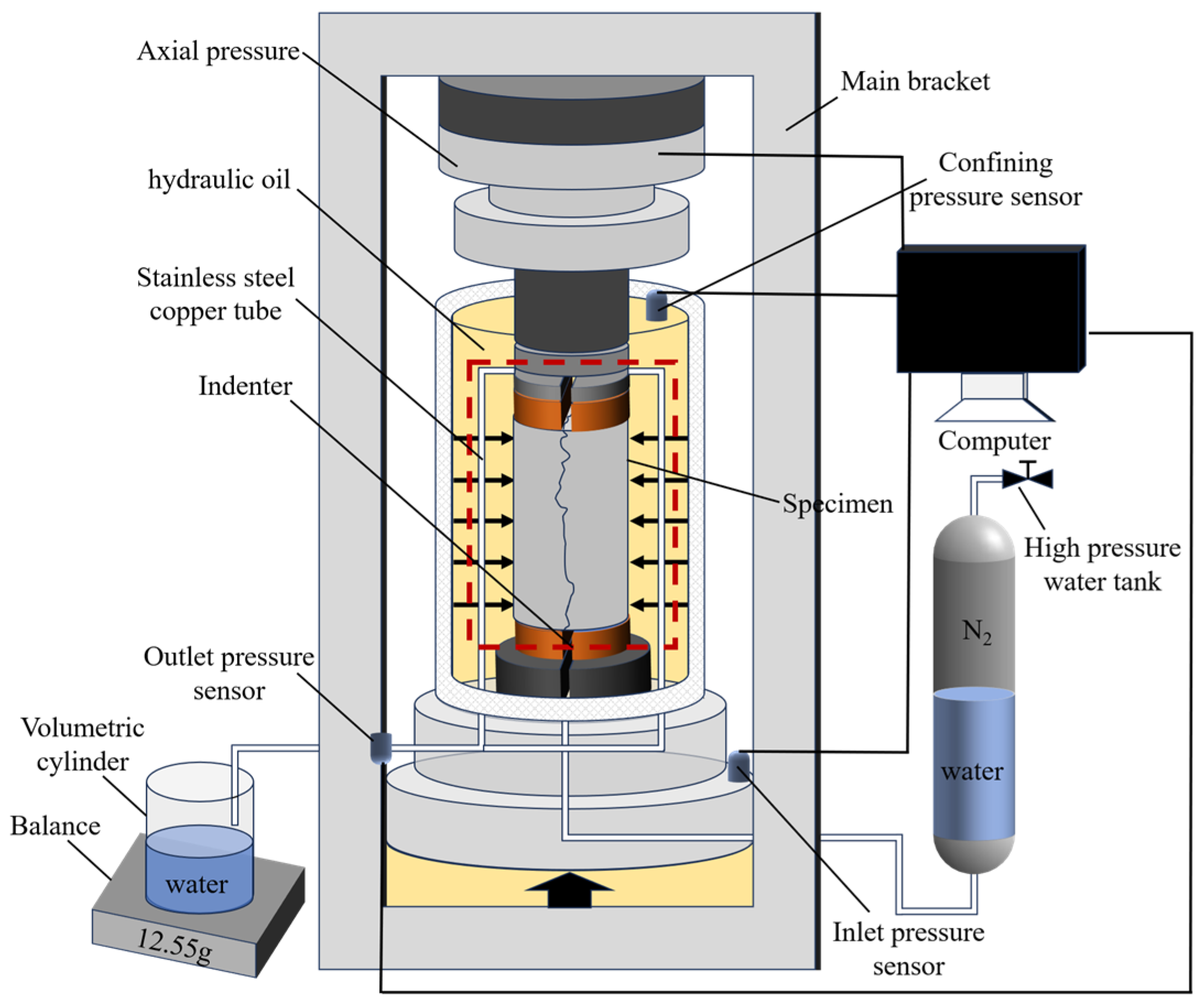
2. Specimen Preparation and Test Method Design
2.1. Rock Fractured Specimen Preparation
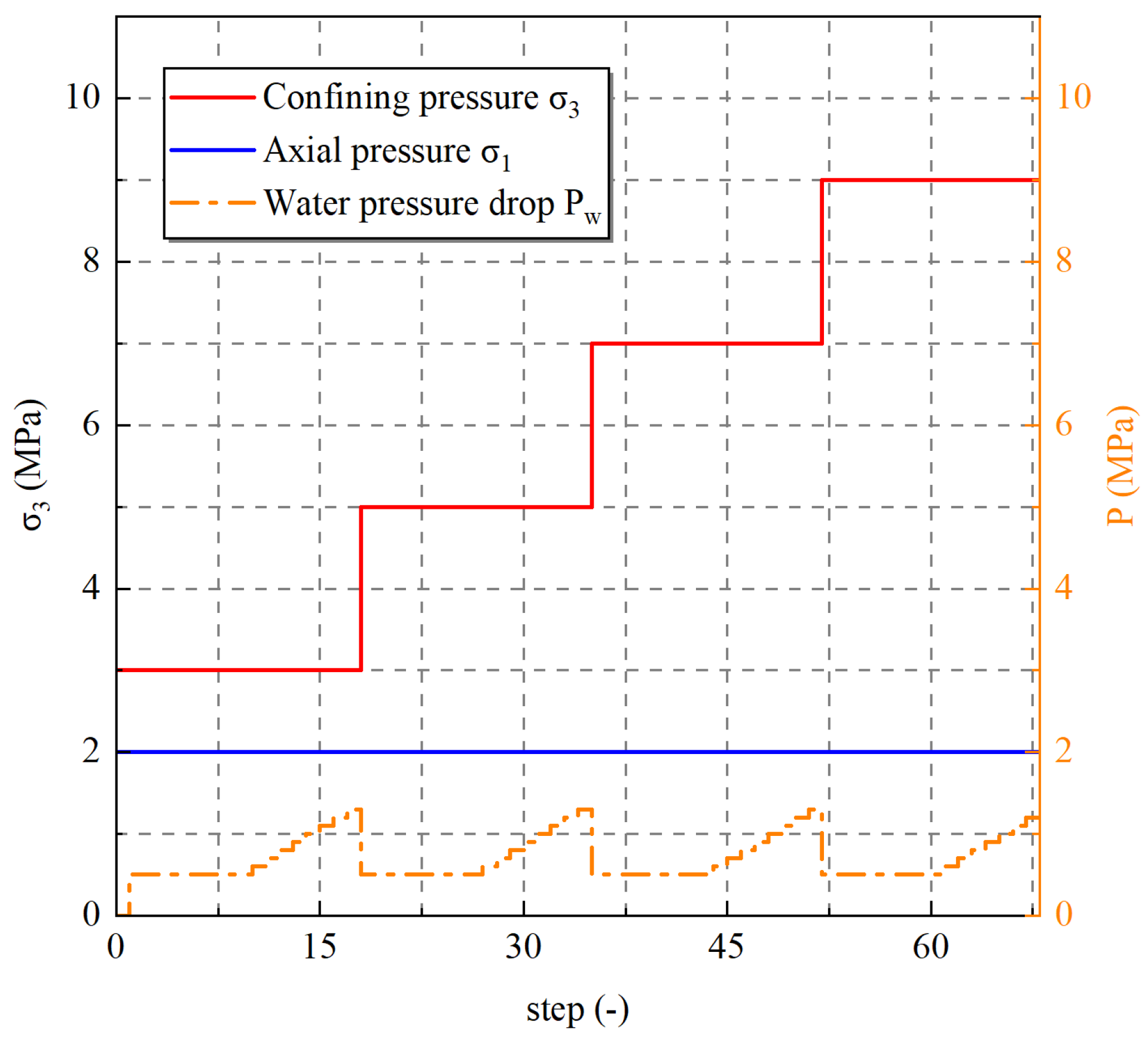
2.2. Seepage Experiment Design
3. Theoretical Background
3.1. Governing Equations for Fluid Flow Through Rock Fracture
3.2. Fracture Surface Roughness Characterization
4. Fluid Flow Behavior in Rock Fracture
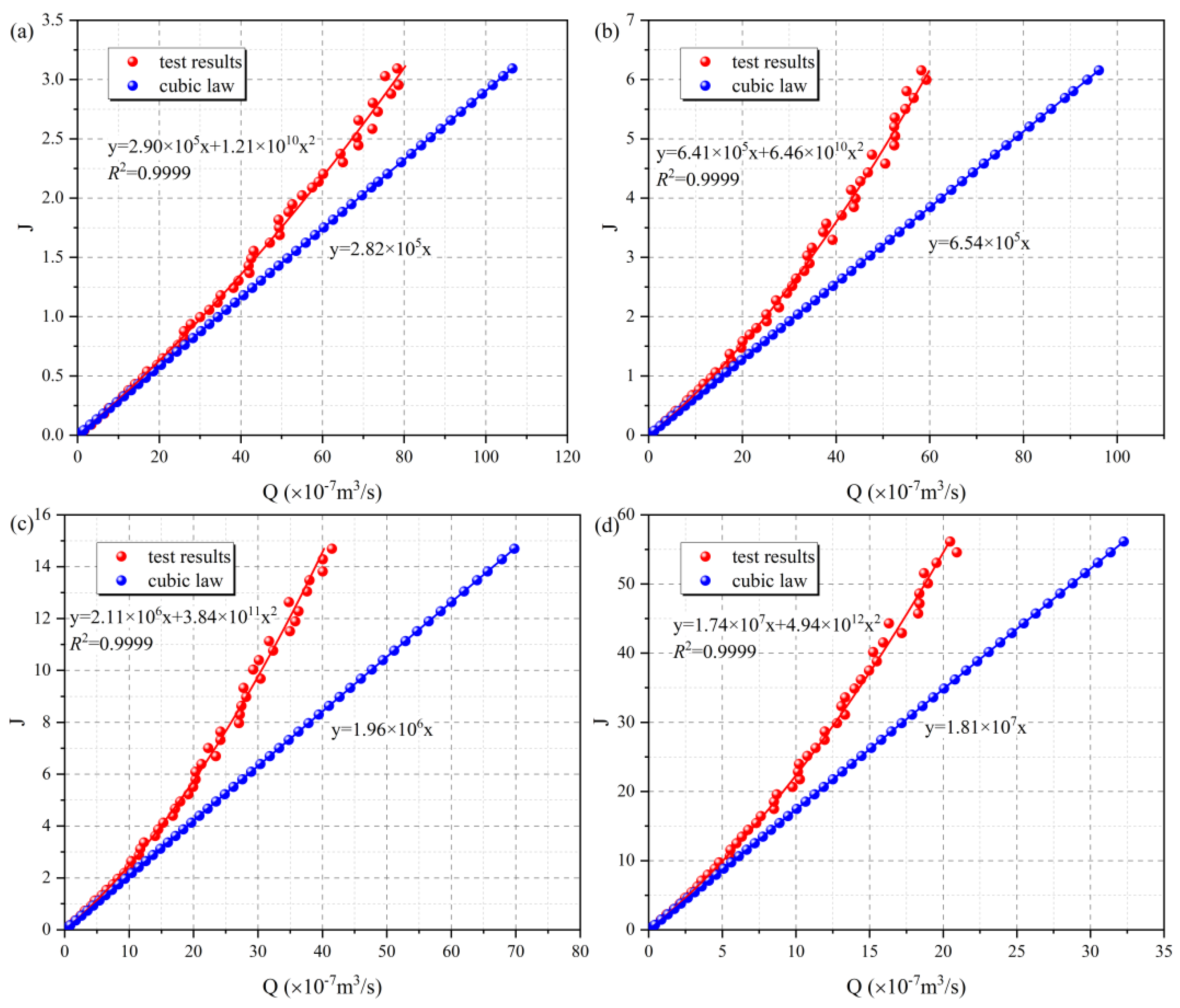
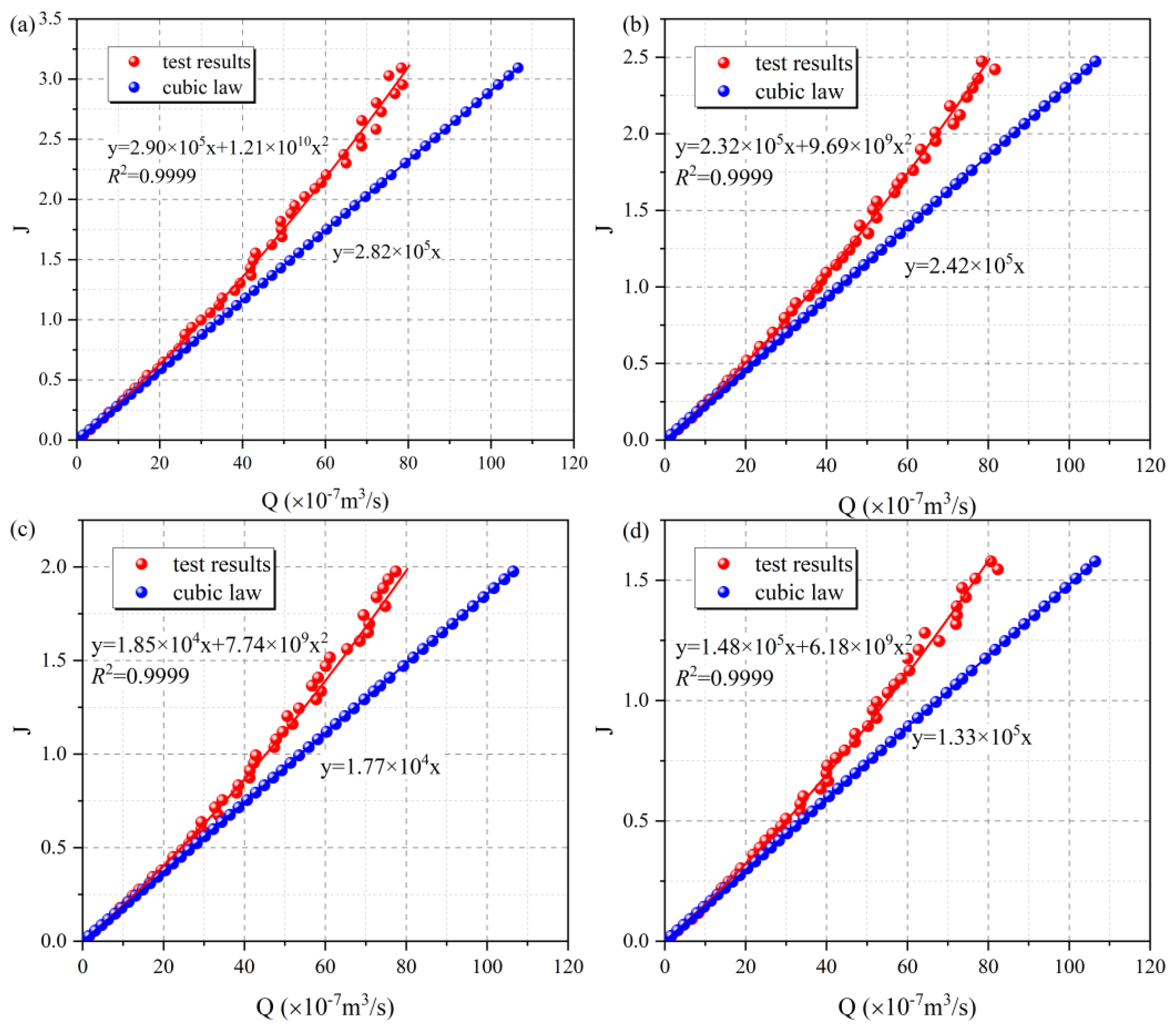
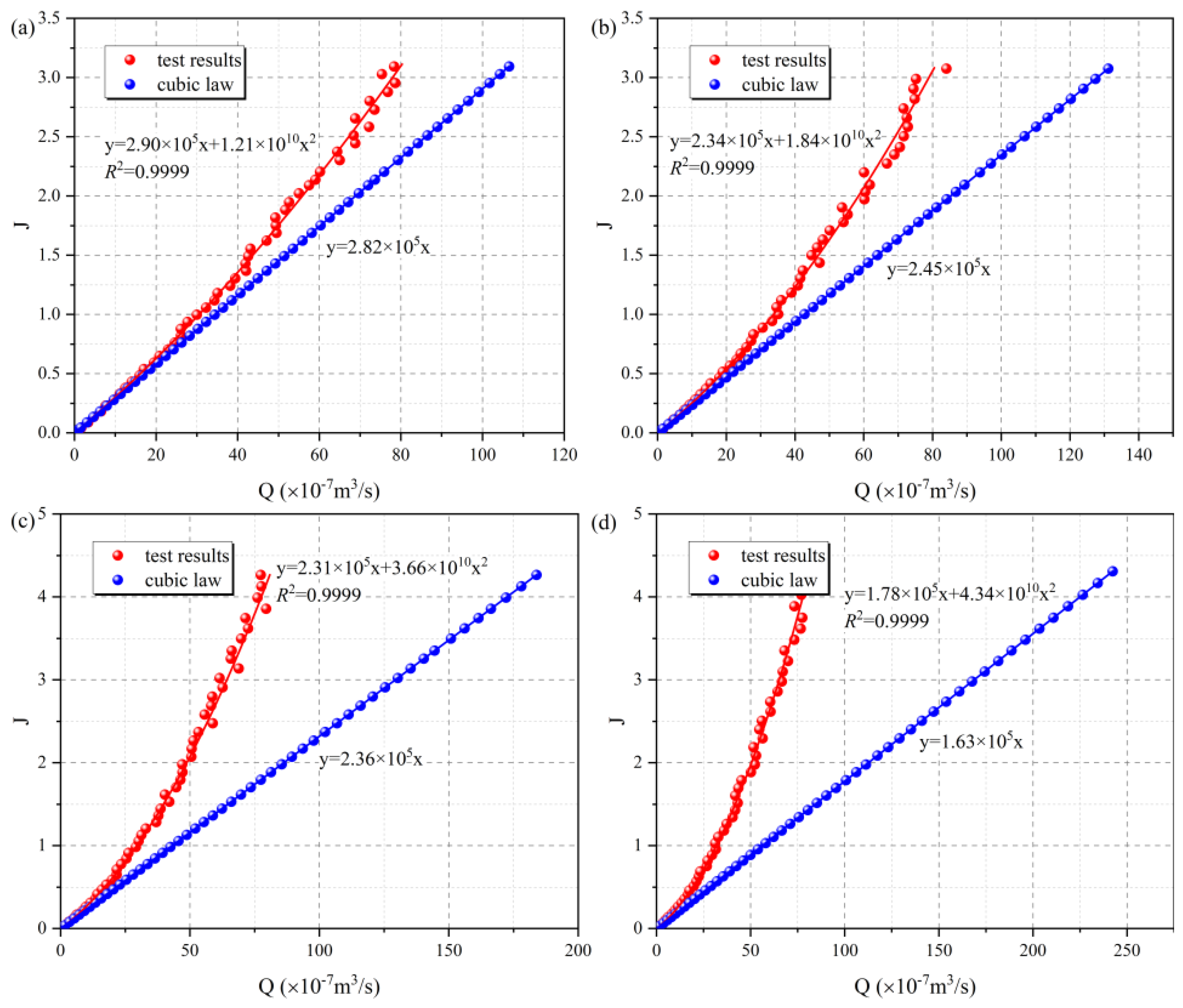
4.1. The Relationship Between the Hydraulic Gradient and Flow Flux
4.1.1. Effect of Confining Pressure
4.1.2. Effect of Shear Displacement
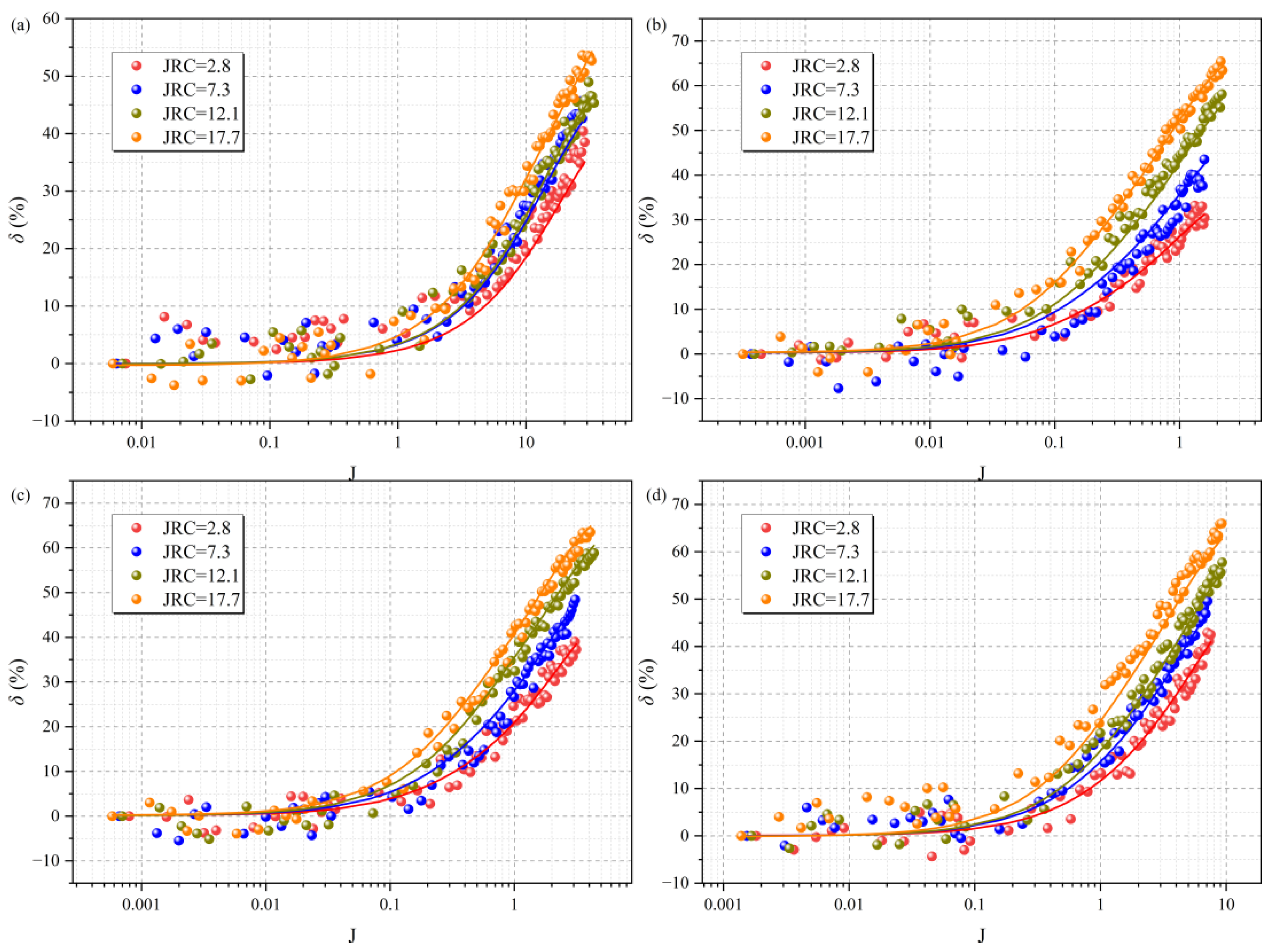
4.1.3. Effect of Surface Roughness
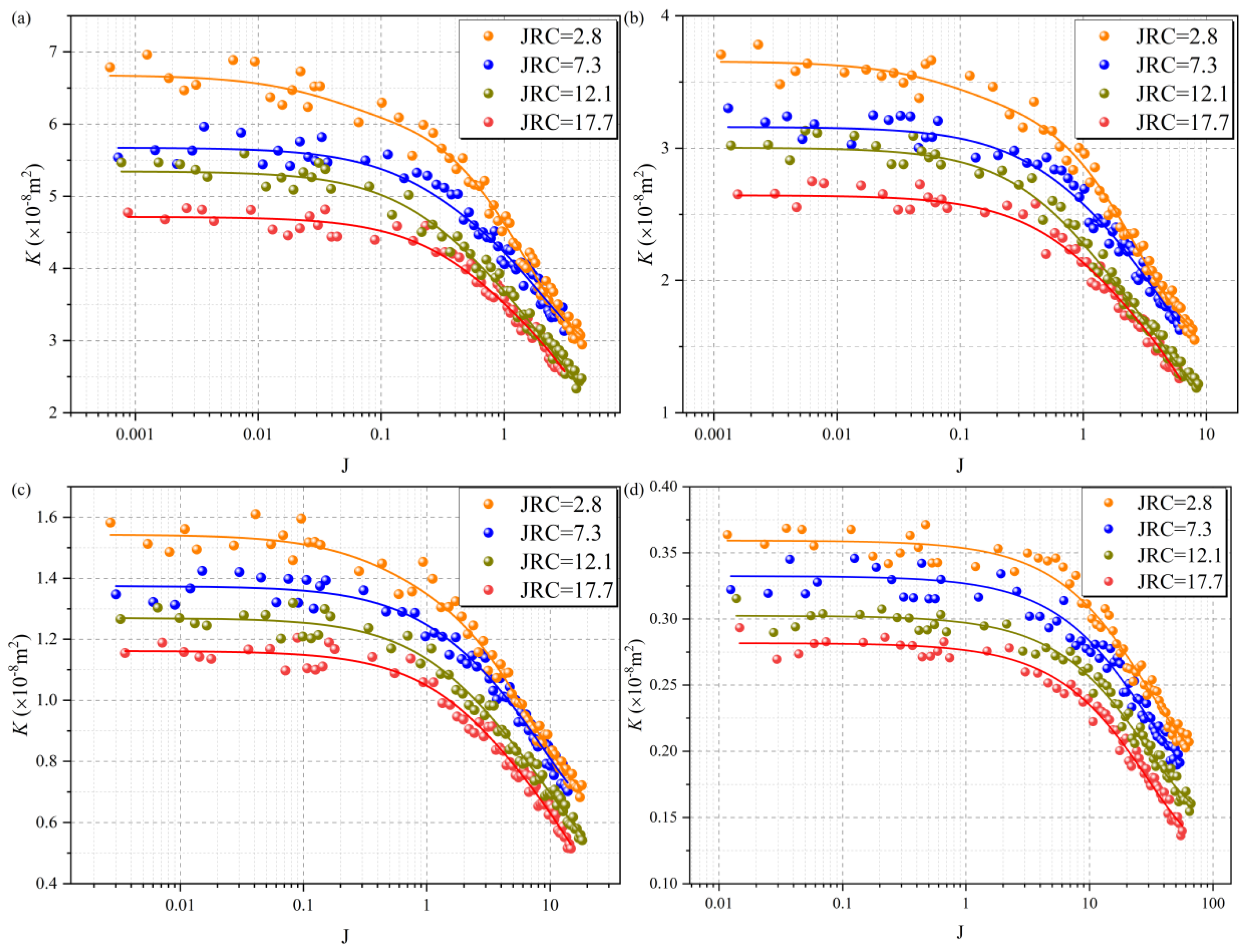
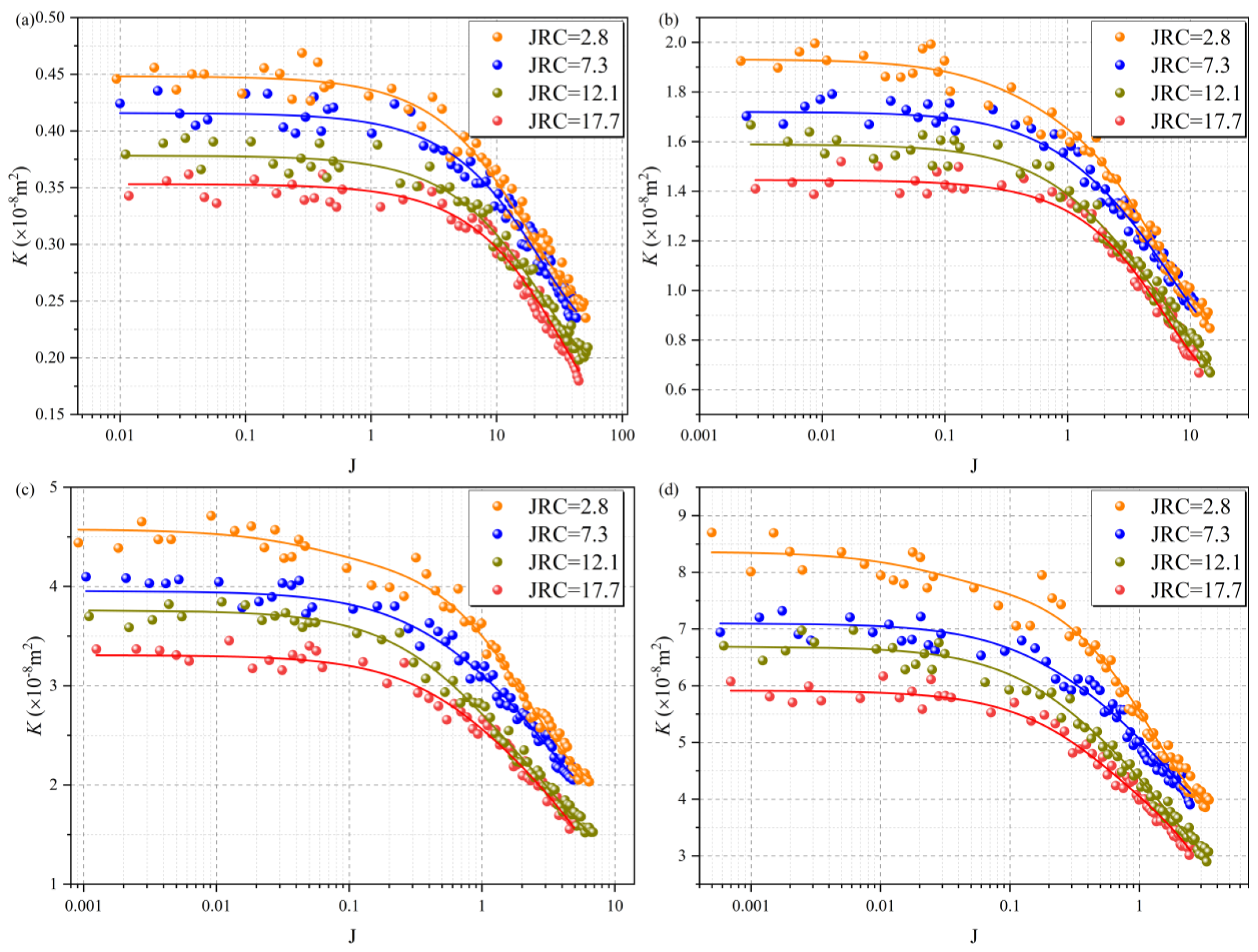
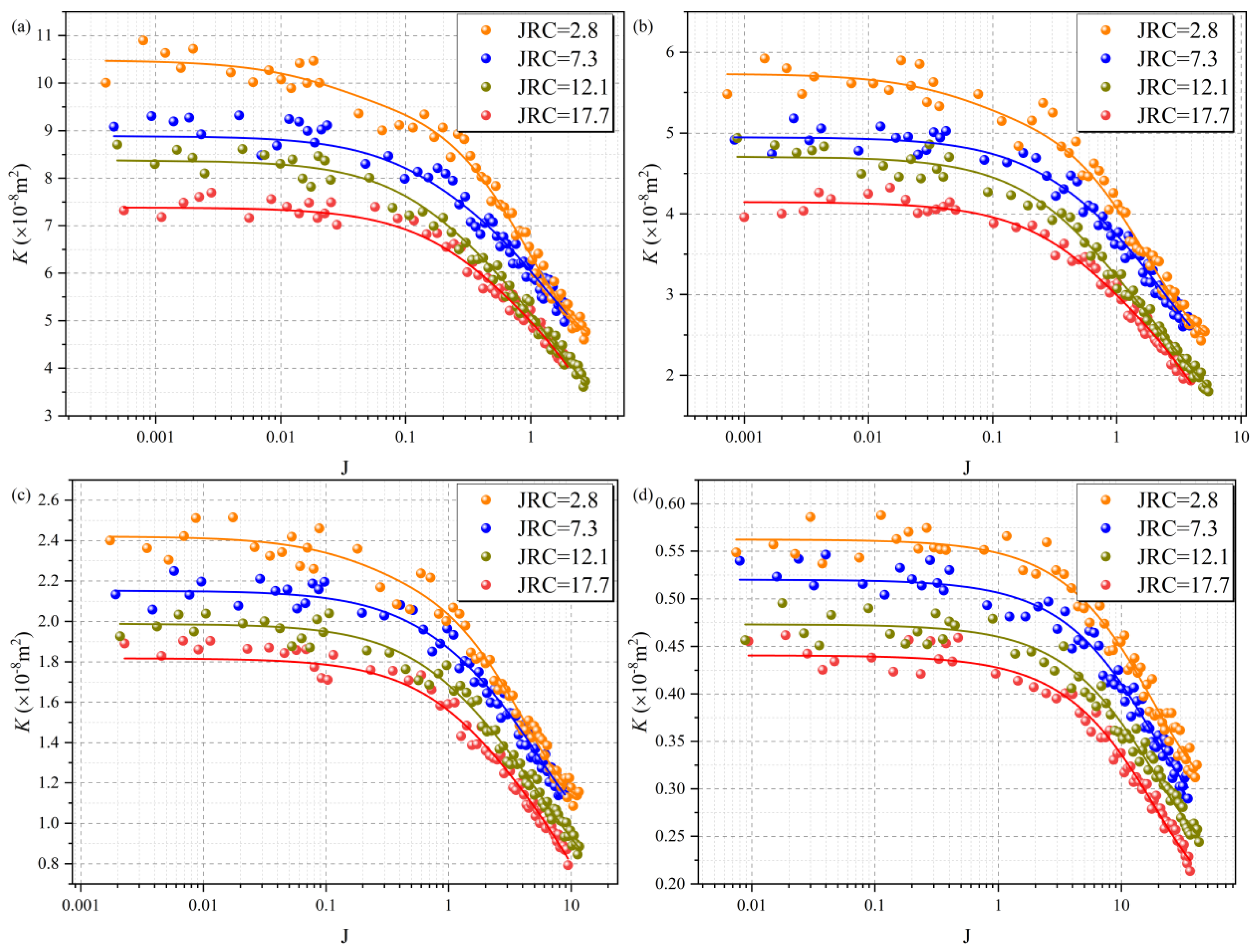
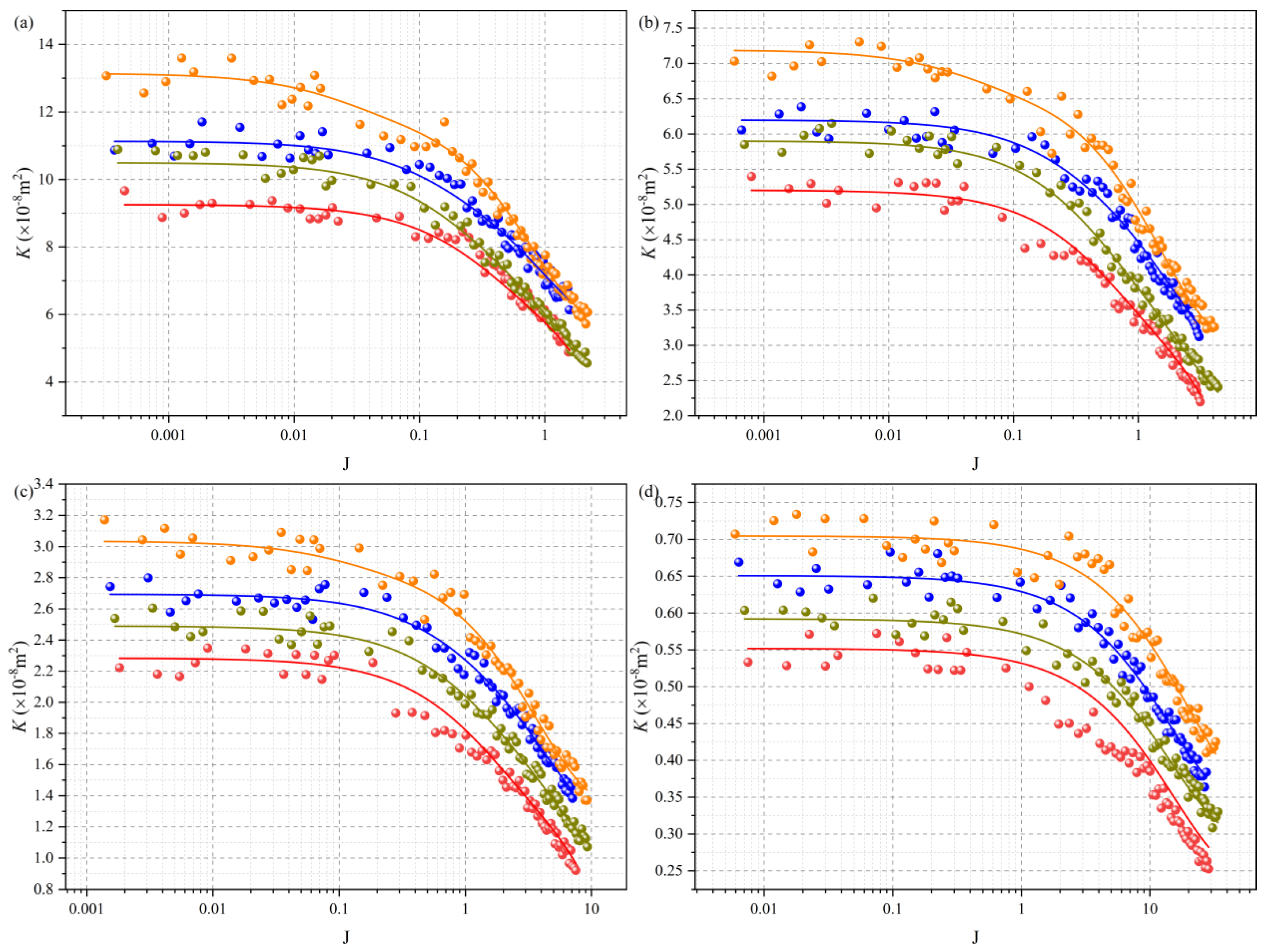
4.2. Permeability Evolution
4.2.1. Permeability Evolution Under Multivariate Conditions
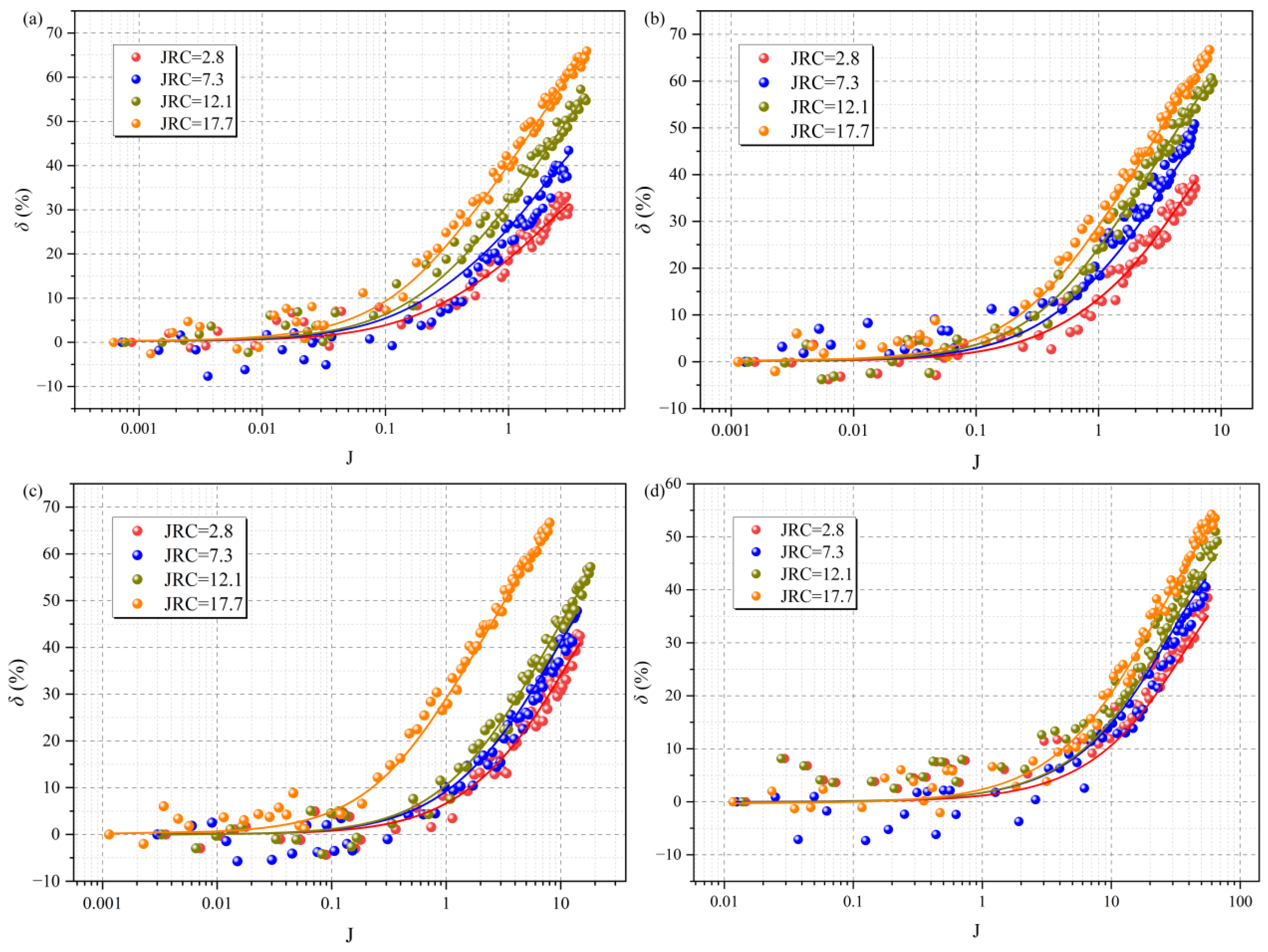
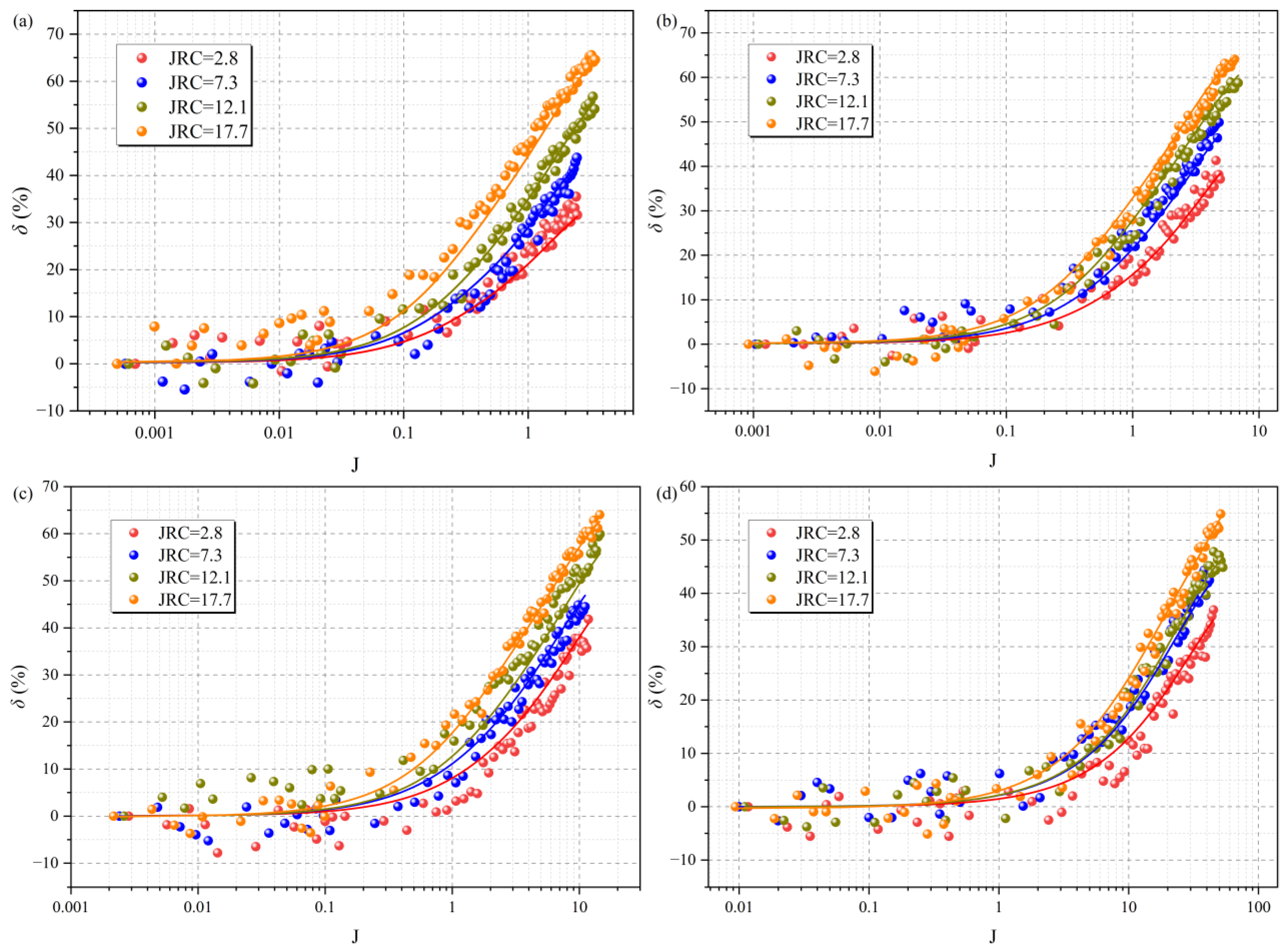
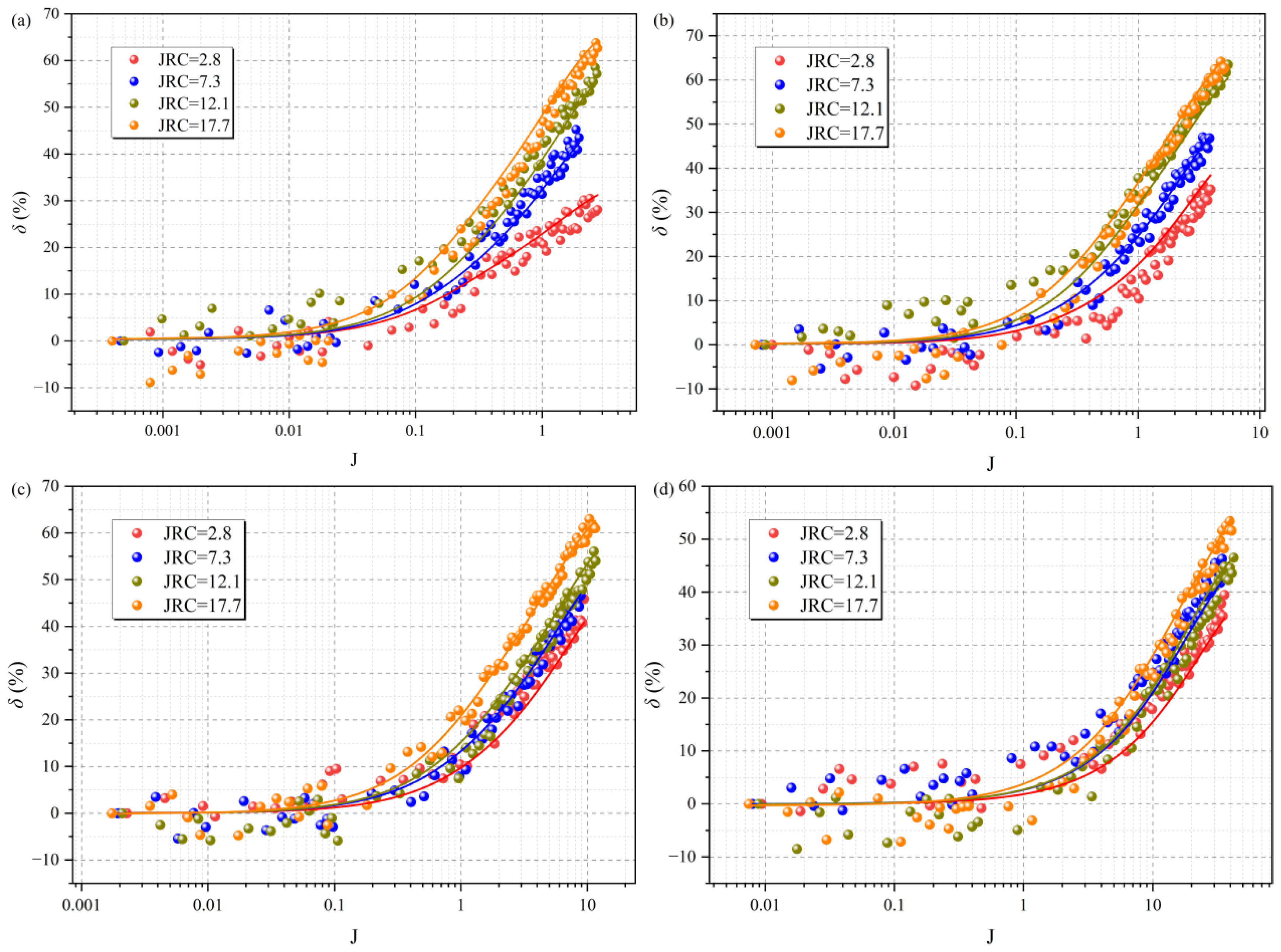
4.2.2. Quantitative Evolution of the Permeability Reduction
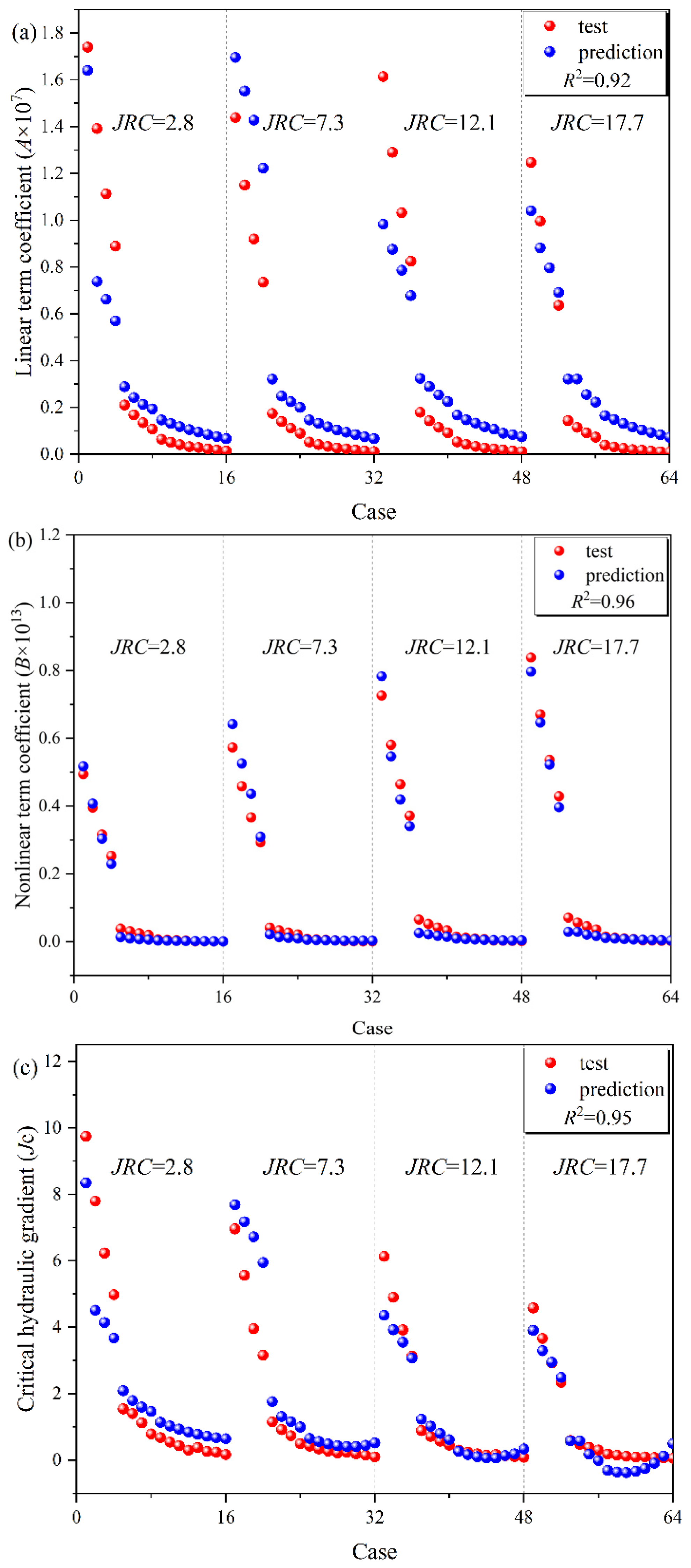
4.3. Prediction Model for Critical Hydraulic Gradient Jc and Forchheimer’s Coefficients A and B
| No | Shear (mm) | Pressure (MPa) | em (mm) | JRC | A(T) | B(T) | Jc(T) | A(P) | B(P) | Jc(P) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.0 | 9 | 0.16 | 2.8 | 1.74 × 107 | 4.94 × 1012 | 9.75 | 1.64 × 107 | 7.17 × 1012 | 8.35 |
| 2 | 0.5 | 9 | 0.27 | 2.8 | 1.39 × 107 | 3.95 × 1012 | 7.79 | 7.39 × 106 | 1.07 × 1012 | 4.51 |
| 3 | 1.0 | 9 | 0.29 | 2.8 | 1.11 × 107 | 3.16 × 1012 | 6.23 | 6.62 × 106 | 8.36 × 1011 | 4.14 |
| 4 | 1.5 | 9 | 0.32 | 2.8 | 8.90 × 106 | 2.53 × 1012 | 4.98 | 5.70 × 106 | 5.93 × 1011 | 3.67 |
| 5 | 0.0 | 7 | 0.5 | 2.8 | 2.11 × 106 | 3.84 × 1011 | 1.54 | 2.89 × 106 | 1.35 × 1011 | 2.09 |
| 6 | 0.5 | 7 | 0.56 | 2.8 | 1.68 × 106 | 3.07 × 1011 | 1.40 | 2.43 × 106 | 9.47 × 1010 | 1.80 |
| 7 | 1.0 | 7 | 0.61 | 2.8 | 1.35 × 106 | 2.46 × 1011 | 1.12 | 2.13 × 106 | 7.30 × 1010 | 1.60 |
| 8 | 1.5 | 7 | 0.65 | 2.8 | 1.08 × 106 | 1.96 × 1011 | 0.79 | 1.94 × 106 | 6.04 × 1010 | 1.47 |
| 9 | 0.0 | 5 | 0.78 | 2.8 | 6.41 × 105 | 6.46 × 1010 | 0.68 | 1.47 × 106 | 3.57 × 1010 | 1.14 |
| 10 | 0.5 | 5 | 0.84 | 2.8 | 5.12 × 105 | 5.17 × 1010 | 0.54 | 1.31 × 106 | 2.90 × 1010 | 1.03 |
| 11 | 1.0 | 5 | 0.9 | 2.8 | 4.09 × 105 | 4.13 × 1010 | 0.43 | 1.18 × 106 | 2.41 × 1010 | 0.93 |
| 12 | 1.5 | 5 | 0.97 | 2.8 | 3.27 × 105 | 3.30 × 1010 | 0.30 | 1.05 × 106 | 1.97 × 1010 | 0.85 |
| 13 | 0.0 | 3 | 1.04 | 2.8 | 2.90 × 105 | 1.21 × 1010 | 0.38 | 9.47 × 105 | 1.64 × 1010 | 0.78 |
| 14 | 0.5 | 3 | 1.12 | 2.8 | 2.32 × 105 | 9.69 × 109 | 0.26 | 8.46 × 105 | 1.36 × 1010 | 0.72 |
| 15 | 1.0 | 3 | 1.21 | 2.8 | 1.86 × 105 | 7.74 × 109 | 0.24 | 7.52 × 105 | 1.12 × 1010 | 0.68 |
| 16 | 1.5 | 3 | 1.31 | 2.8 | 1.48 × 105 | 6.18 × 109 | 0.17 | 6.67 × 105 | 9.20 × 109 | 0.65 |
| 17 | 0.0 | 9 | 0.17 | 7.3 | 1.44 × 107 | 5.73 × 1012 | 6.96 | 1.70 × 107 | 6.42 × 1012 | 7.69 |
| 18 | 0.5 | 9 | 0.18 | 7.3 | 1.15 × 107 | 4.58 × 1012 | 5.57 | 1.55 × 107 | 5.26 × 1012 | 7.18 |
| 19 | 1.0 | 9 | 0.19 | 7.3 | 9.20 × 106 | 3.67 × 1012 | 3.96 | 1.43 × 107 | 4.36 × 1012 | 6.72 |
| 20 | 1.5 | 9 | 0.21 | 7.3 | 7.35 × 106 | 2.93 × 1012 | 3.16 | 1.22 × 107 | 3.09 × 1012 | 5.95 |
| 21 | 0.0 | 7 | 0.5 | 7.3 | 1.75 × 106 | 4.15 × 1011 | 1.15 | 3.21 × 106 | 2.13 × 1011 | 1.76 |
| 22 | 0.5 | 7 | 0.59 | 7.3 | 1.40 × 106 | 3.32 × 1011 | 0.92 | 2.49 × 106 | 1.37 × 1011 | 1.31 |
| 23 | 1.0 | 7 | 0.63 | 7.3 | 1.12 × 106 | 2.66 × 1011 | 0.74 | 2.25 × 106 | 1.15 × 1011 | 1.16 |
| 24 | 1.5 | 7 | 0.68 | 7.3 | 8.92 × 105 | 2.12 × 1011 | 0.50 | 2.00 × 106 | 9.51 × 1010 | 0.99 |
| 25 | 0.0 | 5 | 0.83 | 7.3 | 5.22 × 105 | 7.86 × 1010 | 0.42 | 1.47 × 106 | 5.83 × 1010 | 0.65 |
| 26 | 0.5 | 5 | 0.89 | 7.3 | 4.17 × 105 | 6.28 × 1010 | 0.34 | 1.32 × 106 | 4.94 × 1010 | 0.56 |
| 27 | 1.0 | 5 | 0.96 | 7.3 | 3.33 × 105 | 5.03 × 1010 | 0.27 | 1.18 × 106 | 4.14 × 1010 | 0.49 |
| 28 | 1.5 | 5 | 1.04 | 7.3 | 2.66 × 105 | 4.02 × 1010 | 0.22 | 1.04 × 106 | 3.44 × 1010 | 0.43 |
| 29 | 0.0 | 3 | 1.11 | 7.3 | 2.35 × 105 | 1.84 × 1010 | 0.24 | 9.40 × 105 | 2.97 × 1010 | 0.41 |
| 30 | 0.5 | 3 | 1.19 | 7.3 | 1.88 × 105 | 1.47 × 1010 | 0.19 | 8.45 × 105 | 2.54 × 1010 | 0.41 |
| 31 | 1.0 | 3 | 1.29 | 7.3 | 1.50 × 105 | 1.18 × 1010 | 0.15 | 7.46 × 105 | 3.36 × 1010 | 0.45 |
| 32 | 1.5 | 3 | 1.39 | 7.3 | 1.20 × 105 | 9.41 × 109 | 0.10 | 6.65 × 105 | 2.87 × 1010 | 0.52 |
| 33 | 0.0 | 9 | 0.26 | 12.1 | 1.61 × 107 | 7.26 × 1012 | 6.13 | 9.83 × 106 | 1.83 × 1012 | 4.36 |
| 34 | 0.5 | 9 | 0.28 | 12.1 | 1.29 × 107 | 5.81 × 1012 | 4.90 | 8.76 × 106 | 1.46 × 1012 | 3.93 |
| 35 | 1.0 | 9 | 0.3 | 12.1 | 1.03 × 107 | 4.64 × 1012 | 3.92 | 7.87 × 106 | 1.19 × 1012 | 3.55 |
| 36 | 1.5 | 9 | 0.33 | 12.1 | 8.25 × 106 | 3.71 × 1012 | 3.13 | 6.78 × 106 | 9.07 × 1011 | 3.07 |
| 37 | 0.0 | 7 | 0.53 | 12.1 | 1.79 × 106 | 6.52 × 1011 | 0.89 | 3.24 × 106 | 2.56 × 1011 | 1.23 |
| 38 | 0.5 | 7 | 0.57 | 12.1 | 1.43 × 106 | 5.22 × 1011 | 0.71 | 2.90 × 106 | 2.14 × 1011 | 1.02 |
| 39 | 1.0 | 7 | 0.62 | 12.1 | 1.15 × 106 | 4.18 × 1011 | 0.57 | 2.54 × 106 | 1.75 × 1011 | 0.80 |
| 40 | 1.5 | 7 | 0.67 | 12.1 | 9.15 × 105 | 3.34 × 1011 | 0.45 | 2.25 × 106 | 1.45 × 1011 | 0.62 |
| 41 | 0.0 | 5 | 0.81 | 12.1 | 5.26 × 105 | 1.45 × 1011 | 0.30 | 1.68 × 106 | 9.35 × 1010 | 0.27 |
| 42 | 0.5 | 5 | 0.88 | 12.1 | 4.20 × 105 | 1.16 × 1011 | 0.24 | 1.47 × 106 | 7.75 × 1010 | 0.16 |
| 43 | 1.0 | 5 | 0.94 | 12.1 | 3.35 × 105 | 9.25 × 1010 | 0.19 | 1.33 × 106 | 6.69 × 1010 | 0.10 |
| 44 | 1.5 | 5 | 1.02 | 12.1 | 2.68 × 105 | 7.40 × 1010 | 0.15 | 1.17 × 106 | 5.59 × 1010 | 0.07 |
| 45 | 0.0 | 3 | 1.08 | 12.1 | 2.32 × 105 | 3.66 × 1010 | 0.17 | 1.07 × 106 | 4.93 × 1010 | 0.07 |
| 46 | 0.5 | 3 | 1.21 | 12.1 | 1.85 × 105 | 2.93 × 1010 | 0.13 | 9.00 × 105 | 3.86 × 1010 | 0.14 |
| 47 | 1.0 | 3 | 1.26 | 12.1 | 1.48 × 105 | 2.34 × 1010 | 0.11 | 8.45 × 105 | 3.54 × 1010 | 0.19 |
| 48 | 1.5 | 3 | 1.36 | 12.1 | 1.18 × 105 | 1.87 × 1010 | 0.09 | 7.50 × 105 | 4.31 × 1010 | 0.34 |
| 49 | 0.0 | 9 | 0.27 | 17.7 | 1.25 × 107 | 8.38 × 1012 | 4.58 | 1.04 × 107 | 1.97 × 1012 | 3.91 |
| 50 | 0.5 | 9 | 0.3 | 17.7 | 9.97 × 106 | 6.71 × 1012 | 3.66 | 8.82 × 106 | 1.47 × 1012 | 3.29 |
| 51 | 1.0 | 9 | 0.32 | 17.7 | 7.97 × 106 | 5.36 × 1012 | 2.93 | 7.96 × 106 | 1.23 × 1012 | 2.94 |
| 52 | 1.5 | 9 | 0.35 | 17.7 | 6.36 × 106 | 4.29 × 1012 | 2.34 | 6.92 × 106 | 9.67 × 1011 | 2.49 |
| 53 | 0.0 | 7 | 0.57 | 17.7 | 1.44 × 106 | 7.08 × 1011 | 0.59 | 3.21 × 106 | 2.89 × 1011 | 0.58 |
| 54 | 0.5 | 7 | 0.57 | 17.7 | 1.15 × 106 | 5.66 × 1011 | 0.47 | 3.21 × 106 | 2.89 × 1011 | 0.58 |
| 55 | 1.0 | 7 | 0.66 | 17.7 | 9.16 × 105 | 4.53 × 1011 | 0.38 | 2.55 × 106 | 2.06 × 1011 | 0.18 |
| 56 | 1.5 | 7 | 0.72 | 17.7 | 7.31 × 105 | 3.63 × 1011 | 0.30 | 2.23 × 106 | 1.69 × 1011 | −0.01 |
| 57 | 0.0 | 5 | 0.87 | 17.7 | 3.98 × 105 | 1.48 × 1011 | 0.18 | 1.66 × 106 | 1.12 × 1011 | −0.31 |
| 58 | 0.5 | 5 | 0.93 | 17.7 | 3.18 × 105 | 1.19 × 1011 | 0.15 | 1.49 × 106 | 9.65 × 1010 | −0.36 |
| 59 | 1.0 | 5 | 1.01 | 17.7 | 2.53 × 105 | 9.50 × 1010 | 0.12 | 1.31 × 106 | 8.08 × 1010 | −0.38 |
| 60 | 1.5 | 5 | 1.09 | 17.7 | 2.02 × 105 | 7.60 × 1010 | 0.09 | 1.16 × 106 | 6.87 × 1010 | −0.34 |
| 61 | 0.0 | 3 | 1.17 | 17.7 | 1.78 × 105 | 4.34 × 1010 | 0.10 | 1.04 × 106 | 5.91 × 1010 | −0.25 |
| 62 | 0.5 | 3 | 1.26 | 17.7 | 1.42 × 105 | 3.47 × 1010 | 0.08 | 9.28 × 105 | 5.06 × 1010 | −0.09 |
| 63 | 1.0 | 3 | 1.35 | 17.7 | 1.13 × 105 | 2.78 × 1010 | 0.06 | 8.33 × 105 | 4.38 × 1010 | 0.12 |
| 64 | 1.5 | 3 | 1.47 | 17.7 | 9.02 × 104 | 2.23 × 1010 | 0.05 | 7.29 × 105 | 3.66 × 1010 | 0.50 |
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, X.; Yeh, T.C.J.; Yan, E.C.; Wang, W.; Cai, J.; Liang, Y.; Ge, J.; Qi, Y.; Hao, Y. Fusion of hydraulic tomography and displacement back analysis for underground cavern stability investigation. Water Resour. Res. 2018, 54, 8632–8652. [Google Scholar] [CrossRef]
- Zhu, L.; Yang, Q.; Luo, L.; Cui, S. Pore-water pressure model for carbonate fault materials based on cyclic triaxial tests. Front. Earth Sci. 2022, 10, 842765. [Google Scholar] [CrossRef]
- Yang, Y.; Feng, H.; Zhang, Y.; Wang, Y.; Ma, M.; Zhu, P. Mechanical properties and brittleness characterization method of low-rank coal and its char particles under a uniaxial compression test. Energy Fuels 2023, 37, 7696–7706. [Google Scholar] [CrossRef]
- Nie, Z.; Chen, J.; Zhang, W.; Tan, C.; Ma, Z.; Wang, F.; Zhang, Y.; Que, J. A new method for three-dimensional fracture network modelling for trace data collected in a large sampling window. Rock Mech. Rock Eng. 2020, 53, 1145–1161. [Google Scholar] [CrossRef]
- Huang, N.; Jiang, Y.; Li, B.; Liu, R. A numerical method for simulating fluid flow through 3-D fracture networks. J. Nat. Gas Sci. Eng. 2016, 33, 1271–1281. [Google Scholar] [CrossRef]
- Kim, S.Y.; Koo, J.-M.; Kuznetsov, A.V. Effect of anisotropy in permeability and effective thermal conductivity on thermal performance of an aluminum foam heat sink. Numer. Heat Transfer. 2001, 40, 21–36. [Google Scholar] [CrossRef]
- Tang, H.; Lin, B.; Wang, D. Granular collapse in fluids: Dynamics and flow regime identification. Particuology 2024, 92, 30–41. [Google Scholar] [CrossRef]
- Xiong, F.; Jiang, Q.; Ye, Z.; Zhang, X. Nonlinear flow behavior through rough-walled rock fractures: The effect of contact area. Comput. Geotech. 2018, 102, 179–195. [Google Scholar] [CrossRef]
- Wang, M.; Chen, Y.-F.; Ma, G.-W.; Zhou, J.-Q.; Zhou, C.-B. Influence of surface roughness on nonlinear flow behaviors in 3D self-affine rough fractures: Lattice Boltzmann simulations. Adv. Water Resour. 2016, 96, 373–388. [Google Scholar] [CrossRef]
- Gong, J.; Rossen, W.R. Modeling flow in naturally fractured reservoirs: Effect of fracture aperture distribution on dominant sub-network for flow. Pet. Sci. 2017, 14, 138–154. [Google Scholar] [CrossRef]
- Sudarja; Haq, A.; Deendarlianto; Indarto; Widyaparaga, A. Experimental study on the flow pattern and pressure gradient of air-water two-phase flow in a horizontal circular mini-channel. J. Hydrodyn. 2019, 31, 102–116. [Google Scholar] [CrossRef]
- Pu, H.; Xue, K.; Wu, Y.; Zhang, S.; Liu, D.; Xu, J. Estimating the permeability of fractal rough rock fractures with variable apertures under normal and shear stresses. Phys. Fluids 2025, 37, 036635. [Google Scholar] [CrossRef]
- Zhao, Z.; Jing, L.; Neretnieks, I.; Moreno, L. Analytical solution of coupled stress-flow-transport processes in a single rock fracture. Comput. Geosci. 2011, 37, 1437–1449. [Google Scholar] [CrossRef]
- Wu, X.; Gao, Z.; Meng, H.; Wang, Y.; Cheng, C. Experimental study on the uniform distribution of gas-liquid two-phase flow in a variable-aperture deflector in a parallel flow heat exchanger. Int. J. Heat Mass Transf. 2020, 150, 119353. [Google Scholar] [CrossRef]
- Wang, C.; Jiang, Y.; Gao, R.; Wang, X. On the evolution of relative permeability of two-phase flow in rock fractures: The effect of aperture distribution. IOP Conf. Ser. Earth Environ. Sci. 2021, 861, 042112. [Google Scholar] [CrossRef]
- Rong, G.; Yang, J.; Cheng, L.; Zhou, C. Laboratory investigation of nonlinear flow characteristics in rough fractures during shear process. J. Hydrol. 2016, 541, 1385–1394. [Google Scholar] [CrossRef]
- Zhou, J.-Q.; Wang, M.; Wang, L.; Chen, Y.-F.; Zhou, C.-B. Emergence of nonlinear laminar flow in fractures during shear. Rock Mech. Rock Eng. 2018, 51, 3635–3643. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Z.; Qiao, L.; Li, W.; Liu, J. Effects of roughness and aperture on mesoscopic and macroscopic flow characteristics in rock fractures. Environ. Earth Sci. 2023, 82, 594.1–594.16. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, C.; Dowd, P. A Modified Cubic Law for single-phase saturated laminar flow in rough rock fractures. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2018, 103, 107–115. [Google Scholar] [CrossRef]
- Javadi, M.; Sharifzadeh, M.; Shahriar, K.; Mitani, Y. Critical Reynolds number for nonlinear flow through rough-walled fractures: The role of shear processes. Water Resour. Res. 2014, 50, 1789–1804. [Google Scholar] [CrossRef]
- Xue, K.; Pu, H.; Li, M.; Luo, P.; Liu, D.; Yi, Q. Fractal-based analysis of stress-induced dynamic evolution in geometry and permeability of porous media. Phys. Fluids 2025, 37, 036630. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, K.; Yeo, I.W. Assessment of the validity of Stokes and Reynolds equations for fluid flow through a rough-walled fracture with flow imaging. Geophys. Res. Lett. 2014, 41, 4578–4585. [Google Scholar] [CrossRef]
- Huang, N.; Jiang, Y.; Liu, R.; Li, B.; Sugimoto, S. A novel three-dimensional discrete fracture network model for investigating the role of aperture heterogeneity on fluid flow through fractured rock masses. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2019, 116, 25–37. [Google Scholar] [CrossRef]
- Ishibashi, T.; Watanabe, N.; Hirano, N.; Okamoto, A.; Tsuchiya, N. Beyond-laboratory-scale prediction for channeling flows through subsurface rock fractures with heterogeneous aperture distributions revealed by laboratory evaluation. J. Geophys. Res. Solid Earth 2015, 120, 106–124. [Google Scholar] [CrossRef]
- Lee, H.S.; Cho, T.F. Hydraulic characteristics of rough fractures in linear flow under normal and shear load. Rock Mech. Rock Eng. 2002, 35, 299–318. [Google Scholar] [CrossRef]
- Zhang, Y.; Chai, J. Effect of surface morphology on fluid flow in rough fractures: A review. J. Nat. Gas Sci. Eng. 2020, 79, 103343. [Google Scholar] [CrossRef]
- Zou, L.; Jing, L.; Cvetkovic, V. Roughness decomposition and nonlinear fluid flow in a single rock fracture. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2015, 75, 102–118. [Google Scholar] [CrossRef]
- Hansen, C.; Yang, X.I.A.; Abkar, M. Data-driven dynamical system models of roughness-induced secondary flows in thermally stratified turbulent boundary layers. J. Fluids Eng. 2023, 145, 061102. [Google Scholar] [CrossRef]
- Vilarrasa, V.; Koyama, T.; Neretnieks, I.; Jing, L. Shear-induced flow channels in a single rock fracture and their effect on solute transport. Transp. Porous Media 2011, 87, 503–523. [Google Scholar] [CrossRef]
- Zareidarmiyan, A.; Parisio, F.; Makhnenko, R.Y.; Salarirad, H.; Vilarrasa, V. How equivalent are equivalent porous media? Geophys. Res. Lett. 2011, 38, L24401. [Google Scholar] [CrossRef]
- Xiong, F.; Jiang, Q.; Xu, C.; Zhang, X.; Zhang, Q. Influences of connectivity and conductivity on nonlinear flow behaviours through three-dimension discrete fracture networks. Comput. Geotech. 2019, 107, 128–141. [Google Scholar] [CrossRef]
- Hu, B.; Wang, J.G.; Sun, R.; Zhao, Z. A permeability model for the fractal tree-like fracture network with self-affine surface roughness in shale gas reservoirs. Géoméch. Geophys. Geo-Energy Geo-Resour. 2024, 10, 24. [Google Scholar] [CrossRef]
- Xue, K.; Zhang, Z.; Hao, S.; Luo, P.; Wang, Y. On the onset of nonlinear fluid flow transition in rock fracture network: Theoretical and computational fluid dynamic investigation. Phys. Fluids 2022, 34, 125114. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Liu, X.; Xue, K. Relative permeability of two-phase fluid flow through rough fractures: The roles of fracture roughness and confining pressure. Adv. Water Resour. 2023, 175, 104426. [Google Scholar] [CrossRef]
- Liu, X.; Xue, K.; Luo, Y.; Long, K.; Liu, Y.; Liang, Z. The Effect of Pore Pressure on the Mechanical Behavior of Coal with Burst Tendency at a Constant Effective Stress. Sustainability 2022, 14, 14568. [Google Scholar] [CrossRef]
- de Dreuzy, J.; Méheust, Y.; Pichot, G. Influence of fracture scale heterogeneity on the flow properties of three-dimensional discrete fracture networks (DFN). J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, Z.; Zhang, L.; Xue, K.; Long, K. Influence of fracture roughness and void space morphology on nonlinear fluid flow through rock fractures Concept Discrete Fracture Network Model Simulator. Eur. Phys. J. Plus. 2022, 137. [Google Scholar] [CrossRef]
- Ju, Y.; Dong, J.; Gao, F.; Wang, J. Evaluation of water permeability of rough fractures based on a self-affine fractal model and optimized segmentation algorithm. Adv. Water Resour. 2019, 129, 99–111. [Google Scholar] [CrossRef]
- Ji, S.; Lee, H.; Yeo, I.W.; Lee, K. Effect of nonlinear flow on DNAPL migration in a rough-walled fracture. Water Resour. Res. 2008, 44, 636–639. [Google Scholar] [CrossRef]
- Zhou, J.-Q.; Hu, S.-H.; Fang, S.; Chen, Y.-F.; Zhou, C.-B. Nonlinear flow behavior at low Reynolds numbers through rough-walled fractures subjected to normal compressive loading. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2015, 80, 202–218. [Google Scholar] [CrossRef]
- Javadi, M.; Sharifzadeh, M.; Shahriar, K. A new geometrical model for non-linear fluid flow through rough fractures. J. Hydrol. 2010, 389, 18–30. [Google Scholar] [CrossRef]
- Chen, Z.; Qian, J.; Qin, H. Experimental study of the non-Darcy flow and solute transport in a channeled single fracture. J. Hydrodyn. 2011, 23, 745–751. [Google Scholar] [CrossRef]
- Qian, J.; Chen, Z.; Zhan, H.; Guan, H. Experimental study of the effect of roughness and Reynolds number on fluid flow in rough-walled single fractures: A check of local cubic law. Hydrol. Process. 2011, 25, 614–622. [Google Scholar] [CrossRef]
- Zou, L.; Jing, J.; Cvetkovic, V. Shear-enhanced nonlinear flow in rough-walled rock fractures. Int. J. Rock Mech. Min. Sci. 2017, 97, 33–45. [Google Scholar] [CrossRef]
- Barton, N.; Choubey, V. The shear strength of rock joints in theory and practice. Rock Mech. Rock Eng. 1977, 10, 1–54. [Google Scholar] [CrossRef]
- Tse, R.; Cruden, D. Estimating joint roughness coefficients. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1979, 16, 303–307. [Google Scholar] [CrossRef]
- Kabir, H.; Wu, J.; Dahal, S.; Joo, T.; Garg, N. Automated estimation of cementitious sorptivity via computer vision. Nat. Commun. 2024, 15, 9935. [Google Scholar] [CrossRef]
- Song, Z.; Zou, S.; Zhou, W.; Huang, Y.; Shao, L.; Yuan, J.; Gou, X.; Jin, W.; Wang, Z.; Chen, X.; et al. Clinically applicable histopathological diagnosis system for gastric cancer detection using deep learning. Nat. Commun. 2020, 11, 4294. [Google Scholar] [CrossRef]
- Aguirre, L.A.; Barbosa, B.H.; Braga, A.P. Prediction and simulation errors in parameter estimation for nonlinear systems. Mech. Syst. Signal Process. 2010, 24, 2855–2867. [Google Scholar] [CrossRef]
- Oberkampf, W.L. Simulation Accuracy, Uncertainty, and Predictive Capability: A Physical Sciences Perspective. In Computer Simulation Validation: Fundamental Concepts, Methodological Frameworks, and Philosophical Perspectives; Beisbart, C., Saam, N.J., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 69–97. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, H.; Chen, Y.; Xue, K.; Zhang, S.; Han, X.; Xu, J. Critical Threshold for Fluid Flow Transition from Linear to Nonlinear in Self-Affine Rough-Surfaced Rock Fractures: Effects of Shear and Confinement. Processes 2025, 13, 1991. https://doi.org/10.3390/pr13071991
Pu H, Chen Y, Xue K, Zhang S, Han X, Xu J. Critical Threshold for Fluid Flow Transition from Linear to Nonlinear in Self-Affine Rough-Surfaced Rock Fractures: Effects of Shear and Confinement. Processes. 2025; 13(7):1991. https://doi.org/10.3390/pr13071991
Chicago/Turabian StylePu, Hai, Yanlong Chen, Kangsheng Xue, Shaojie Zhang, Xuefeng Han, and Junce Xu. 2025. "Critical Threshold for Fluid Flow Transition from Linear to Nonlinear in Self-Affine Rough-Surfaced Rock Fractures: Effects of Shear and Confinement" Processes 13, no. 7: 1991. https://doi.org/10.3390/pr13071991
APA StylePu, H., Chen, Y., Xue, K., Zhang, S., Han, X., & Xu, J. (2025). Critical Threshold for Fluid Flow Transition from Linear to Nonlinear in Self-Affine Rough-Surfaced Rock Fractures: Effects of Shear and Confinement. Processes, 13(7), 1991. https://doi.org/10.3390/pr13071991








