Design and Experiment of a Multi-Row Spiral Quantitative Fertilizer Distributor
Abstract
1. Introduction
2. Materials and Methods
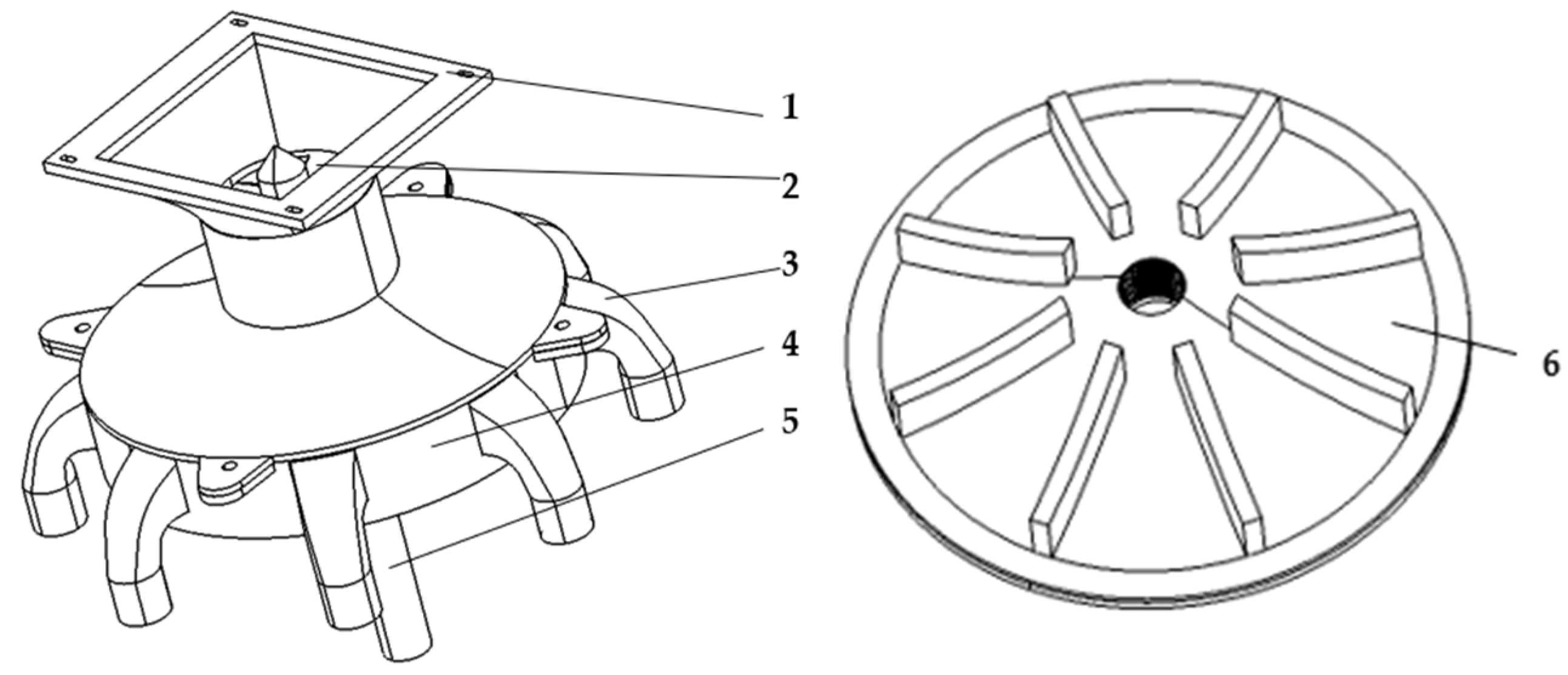
2.1. Fertilizer Distributor Structure and Working Principle
2.2. Fertilizer Distributor Key Parameters Design and Analysis
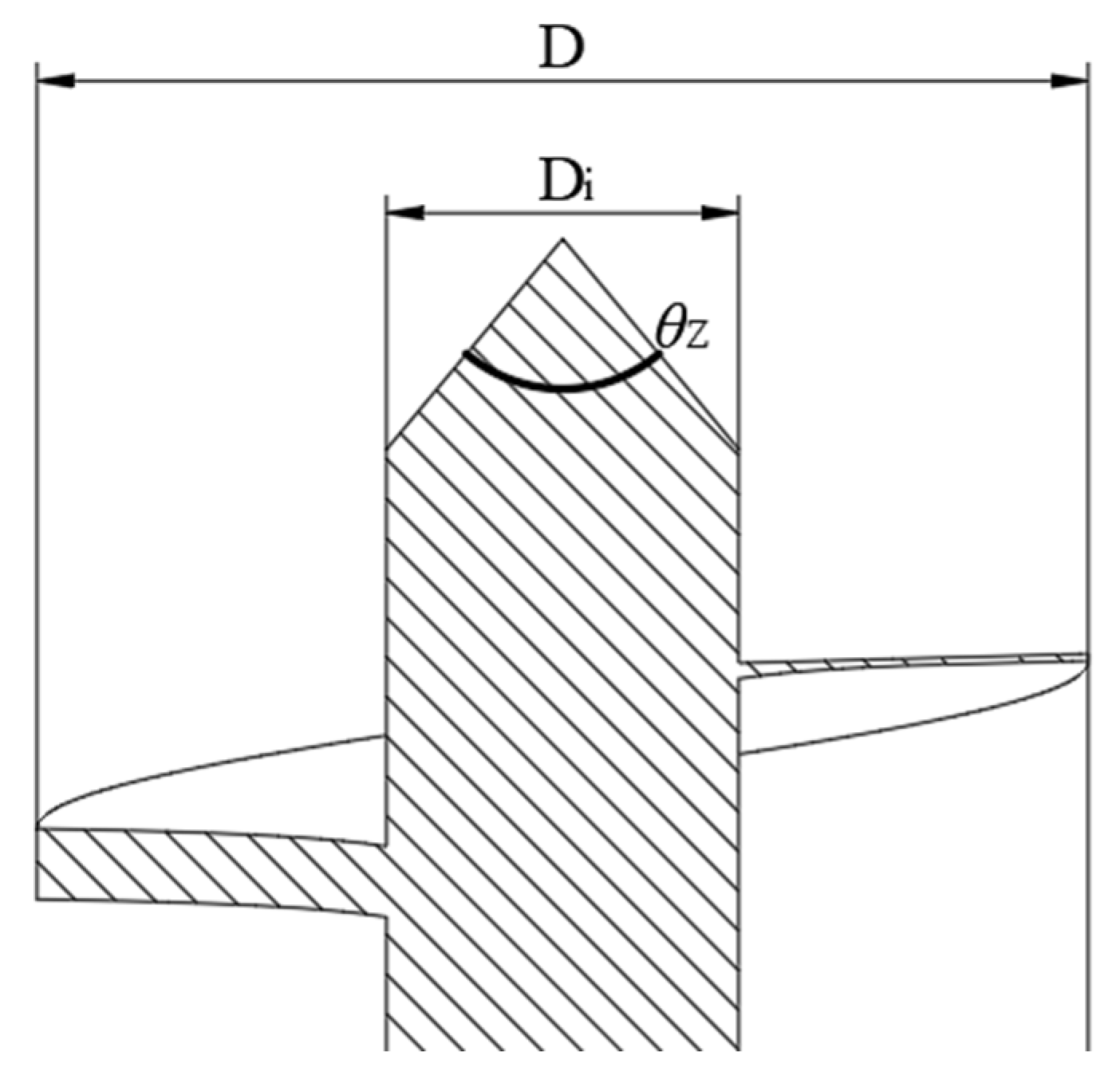
2.2.1. Parameter Design of the Fertilizer Dosing Mechanism
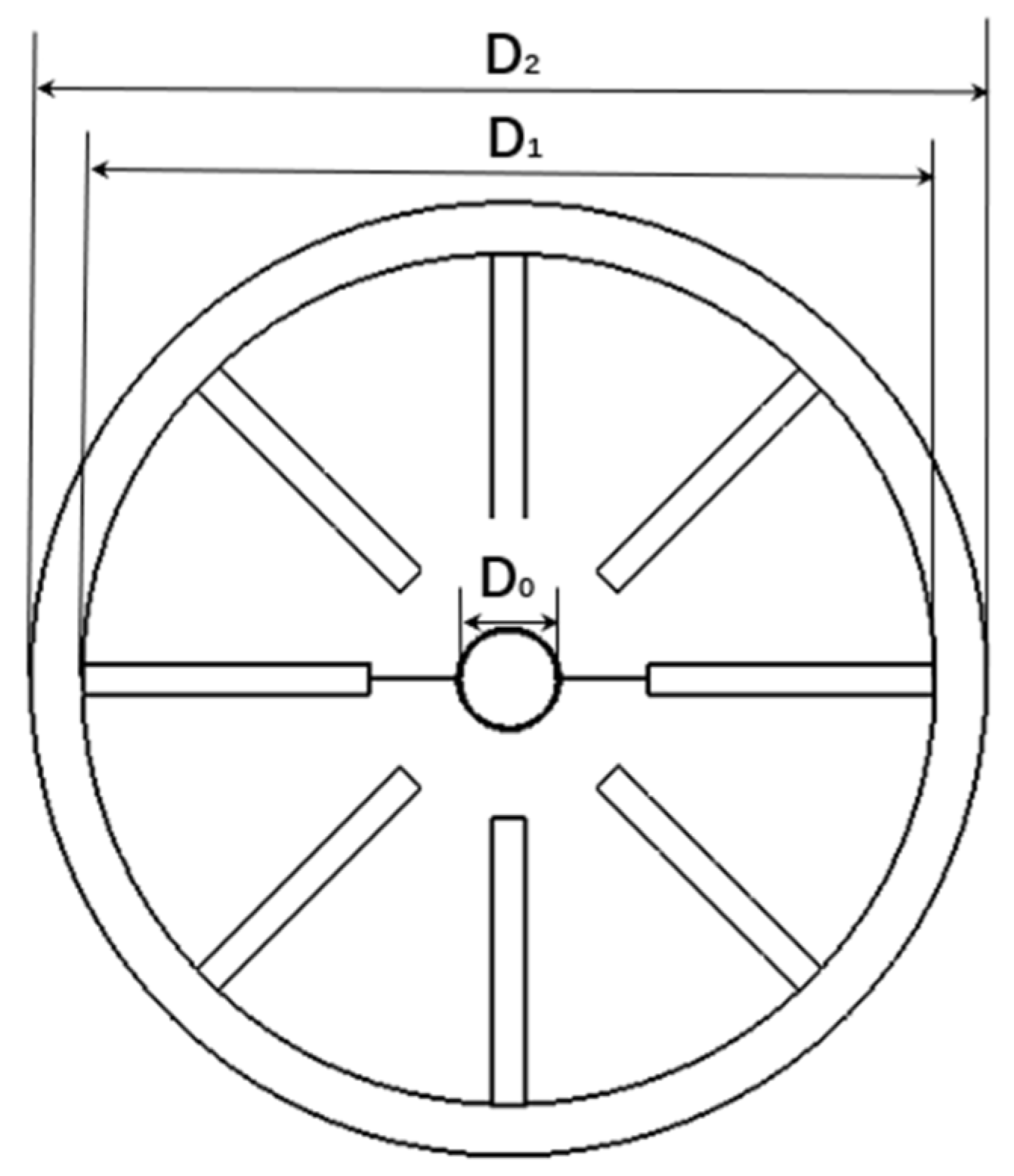
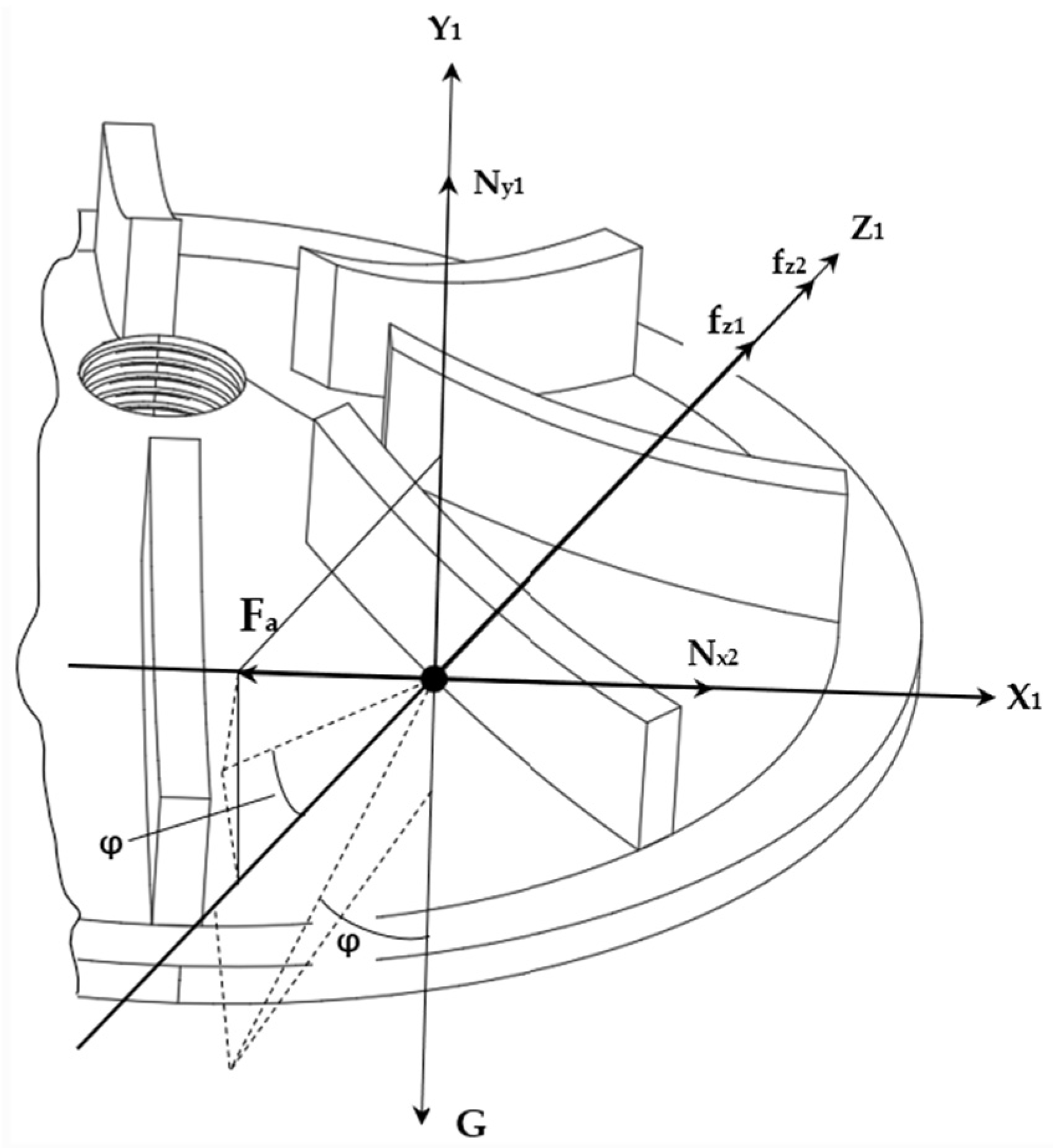
2.2.2. Centrifugal Cone Disc Parameter Design
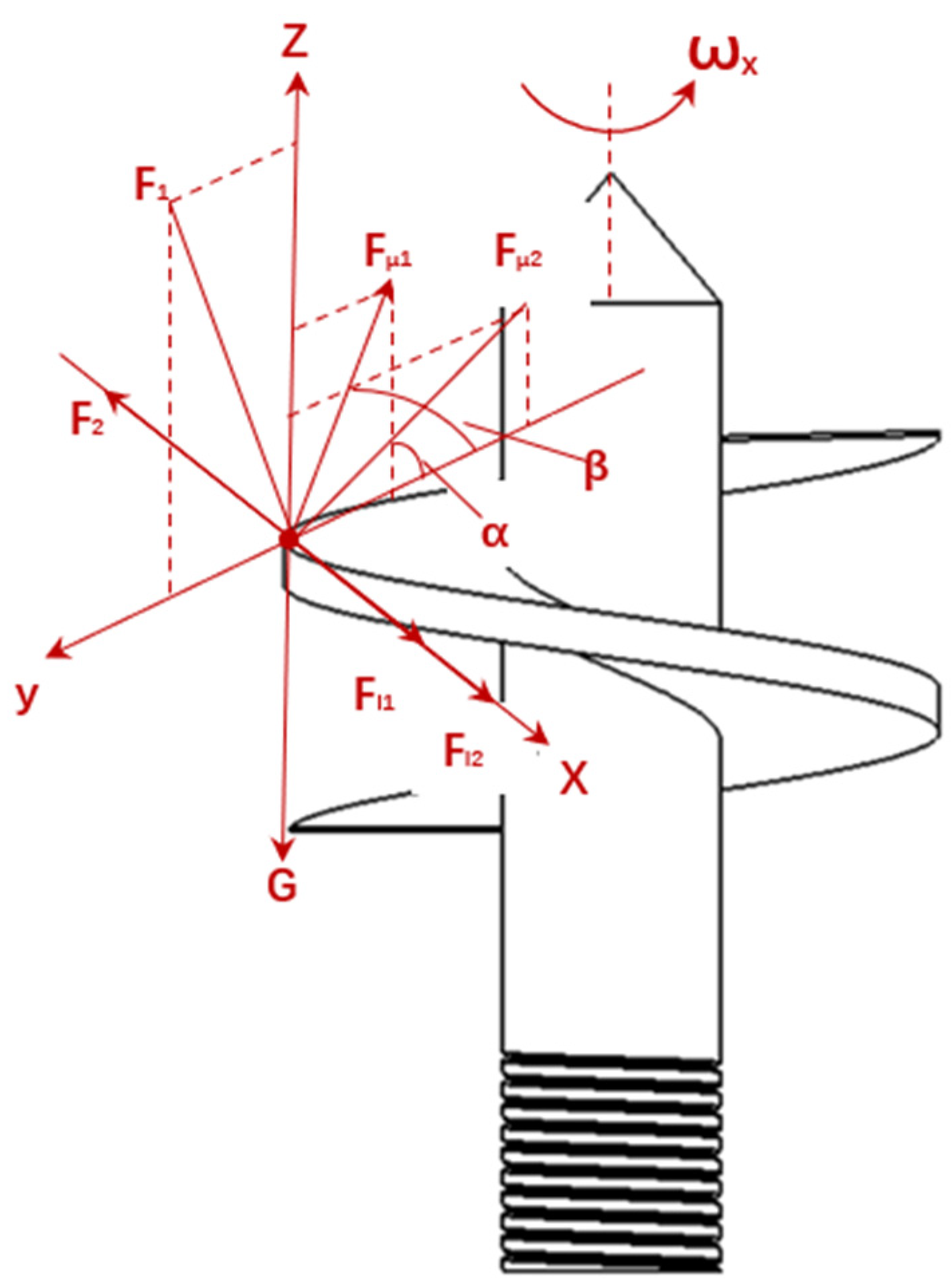
2.2.3. Motion Analysis of Fertilizer Supply Processes
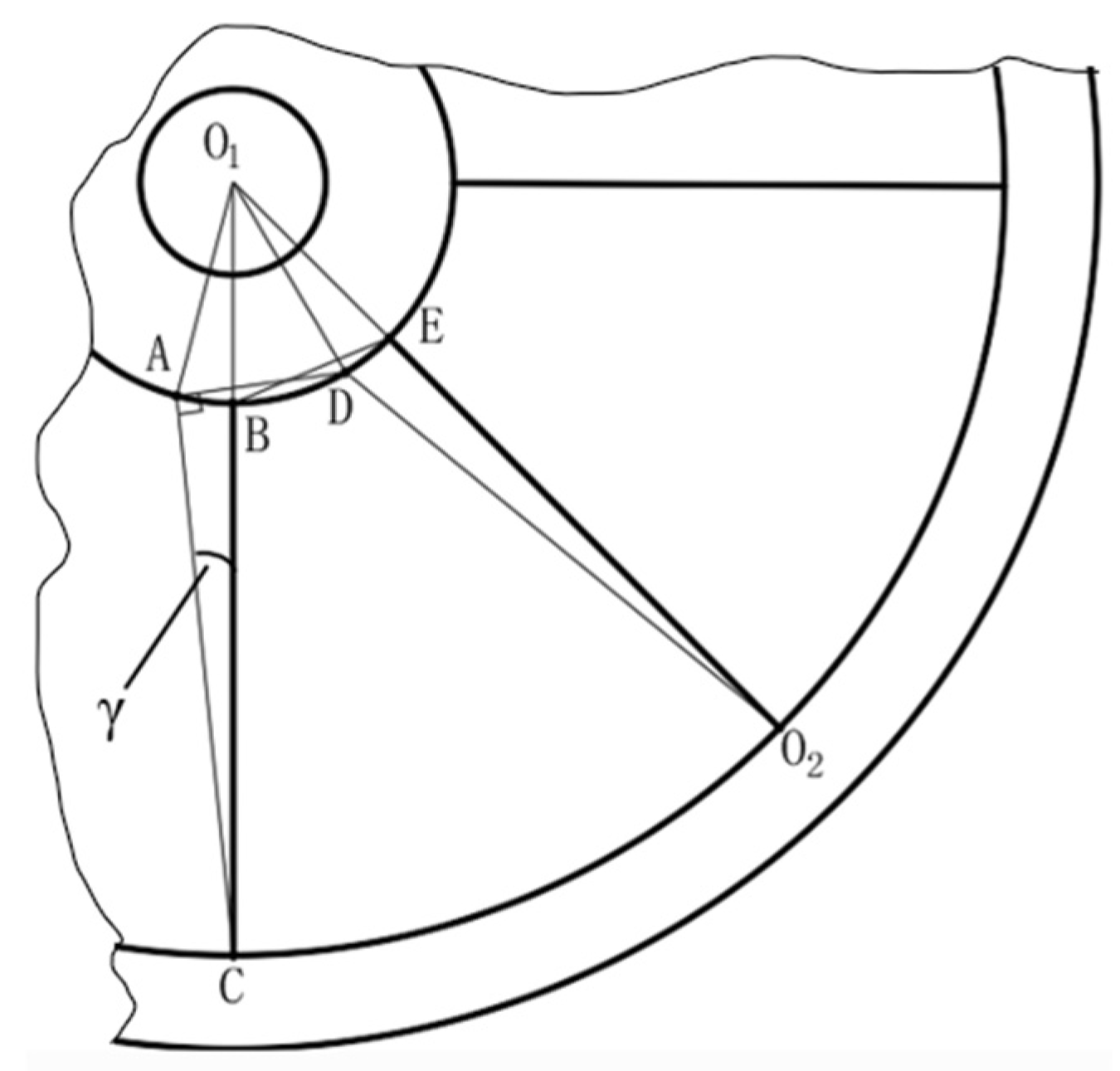
2.2.4. Analysis of the Movement During the Fertilizer Application Process
2.3. EDEM-Based Simulation Performance Test
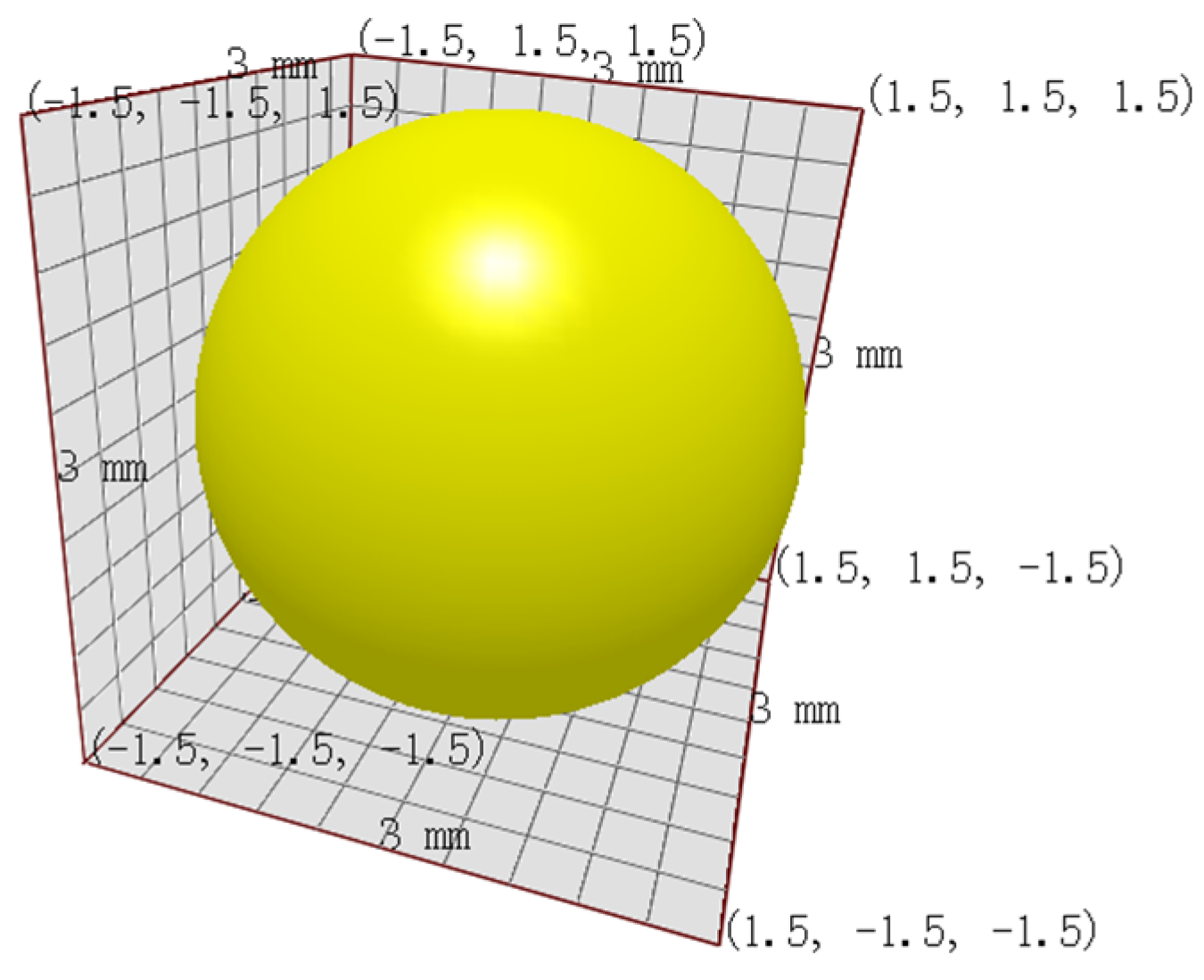
2.3.1. Establishment of Fertilizer Particle Model
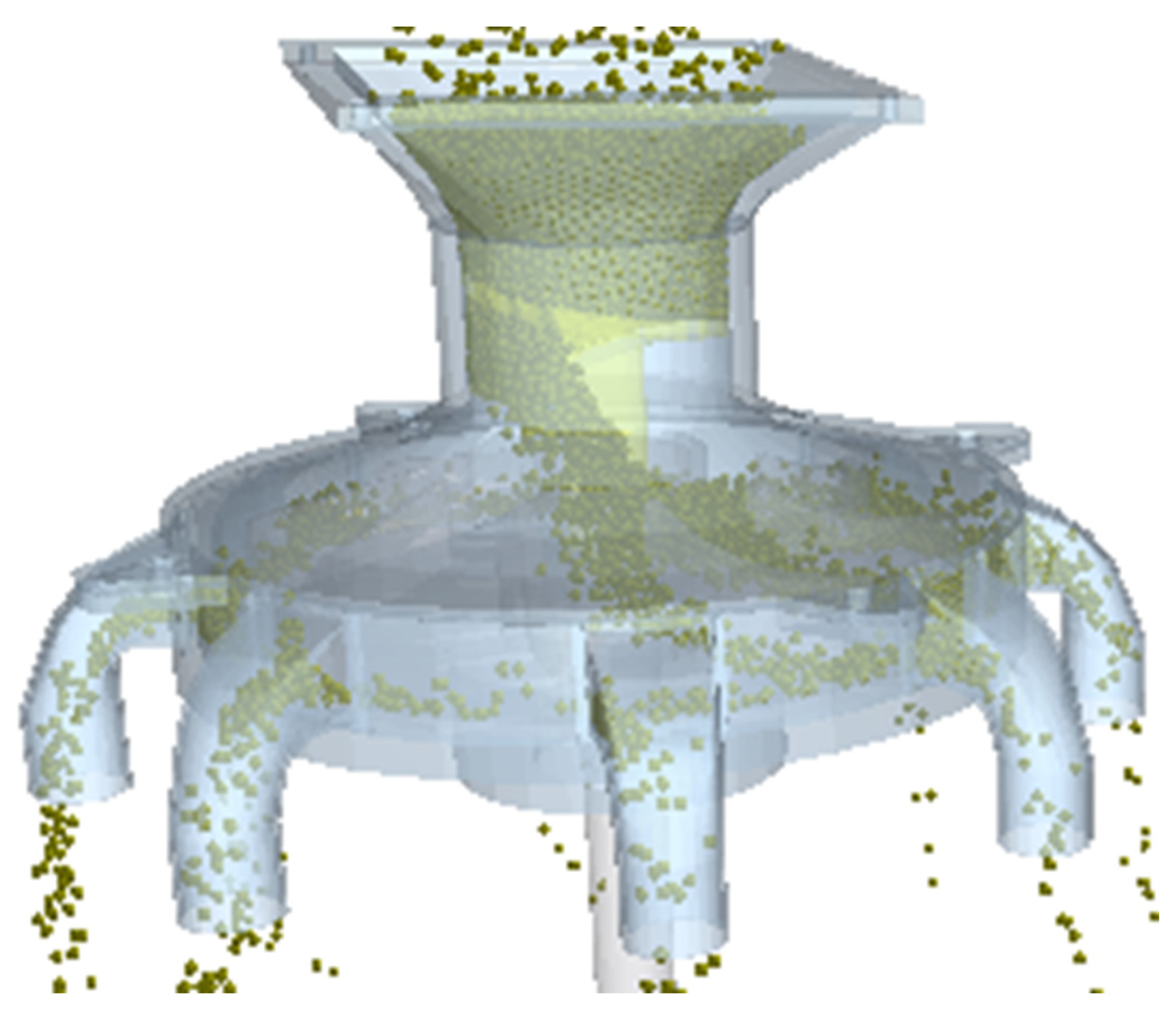
2.3.2. Simulation Model Construction
2.3.3. Experimental Design
2.4. Bench Test
3. Test Results
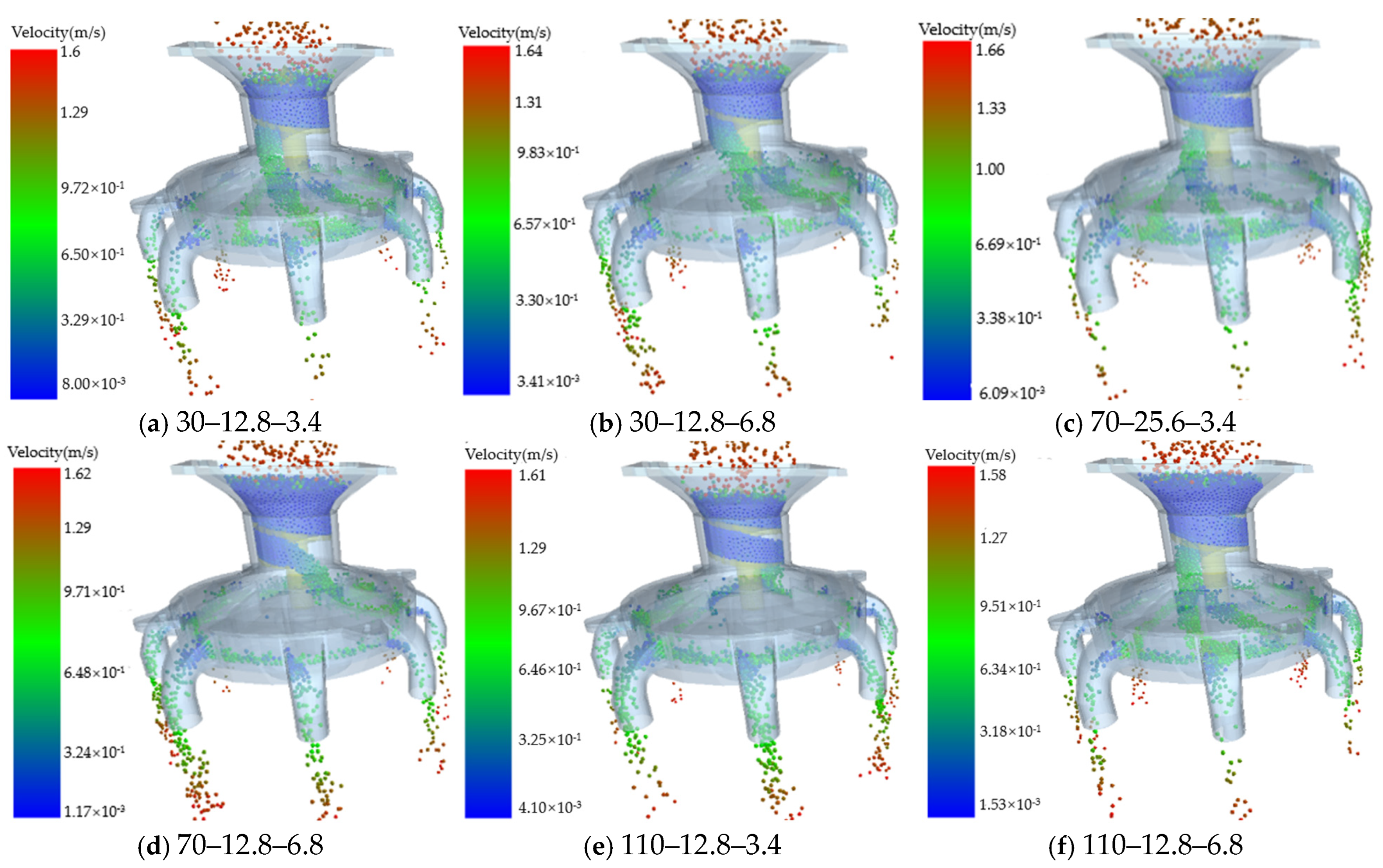
3.1. Simulation Test
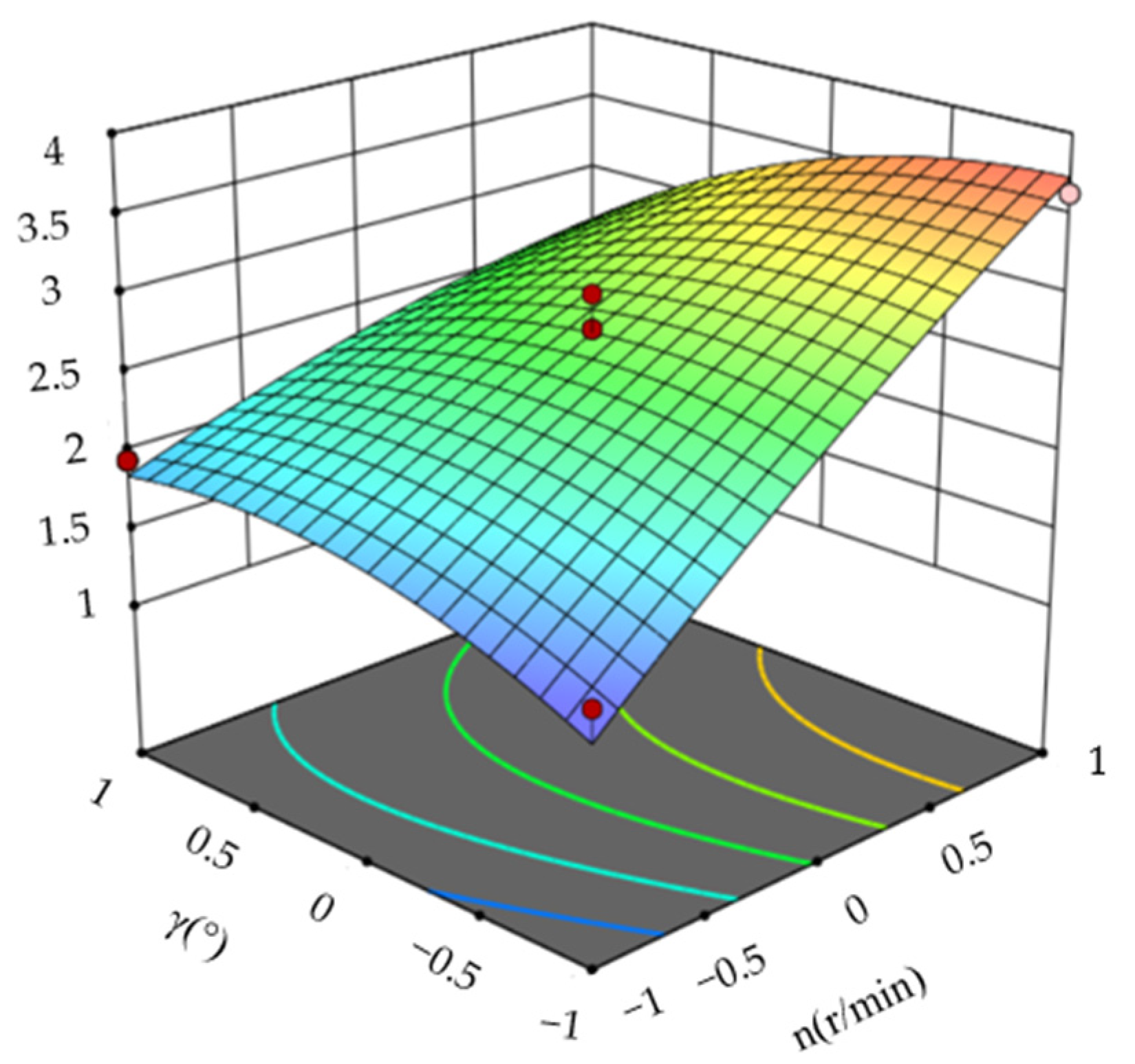
3.1.1. Coefficient of Variation for the Consistency of Fertilizer Application Amount Among Rows Yv1 Significance Level Analysis
3.1.2. Coefficient of Variation for the Consistency of Fertilizer Application Amount Within the Same Row Yv2 Significance Analysis
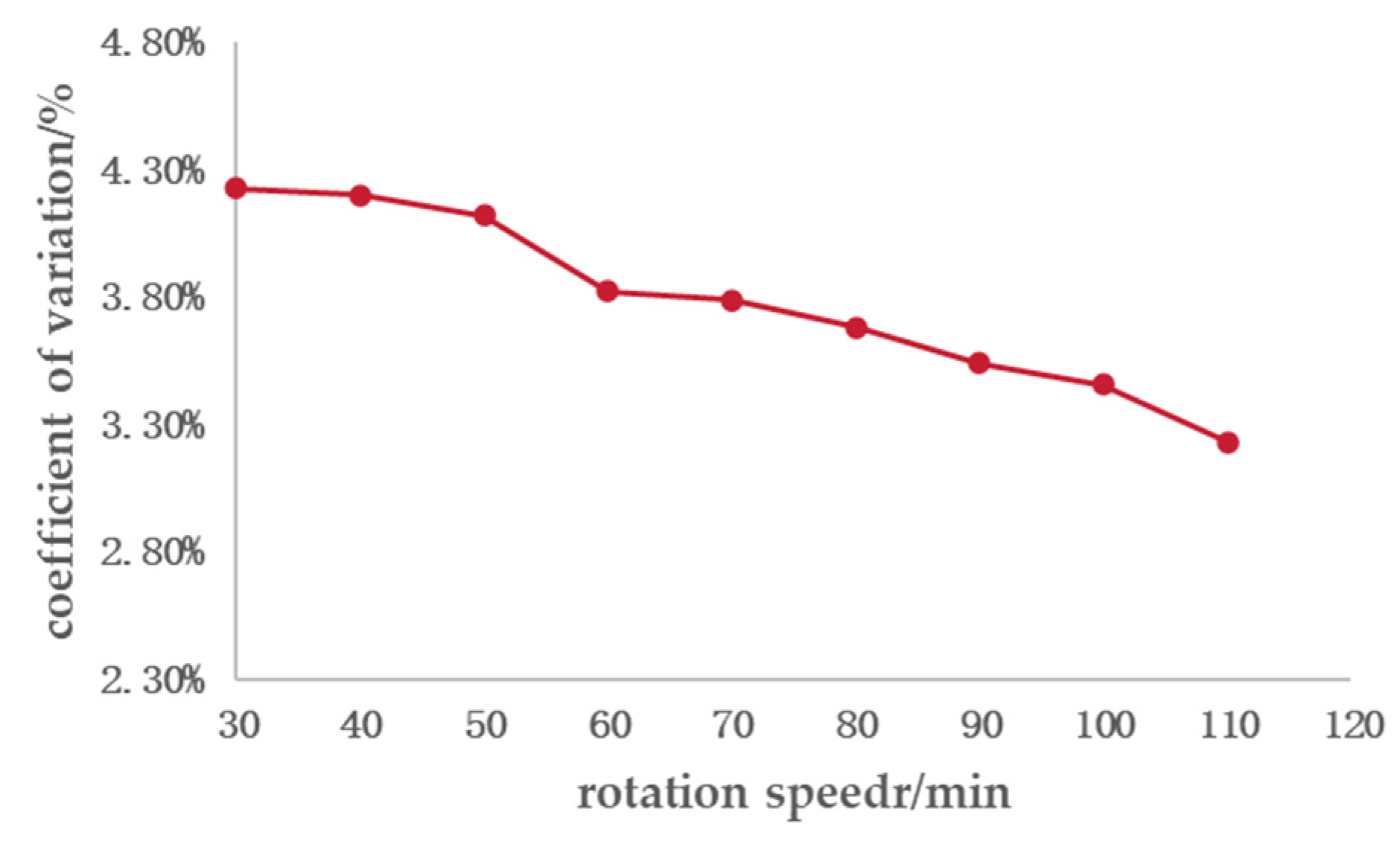
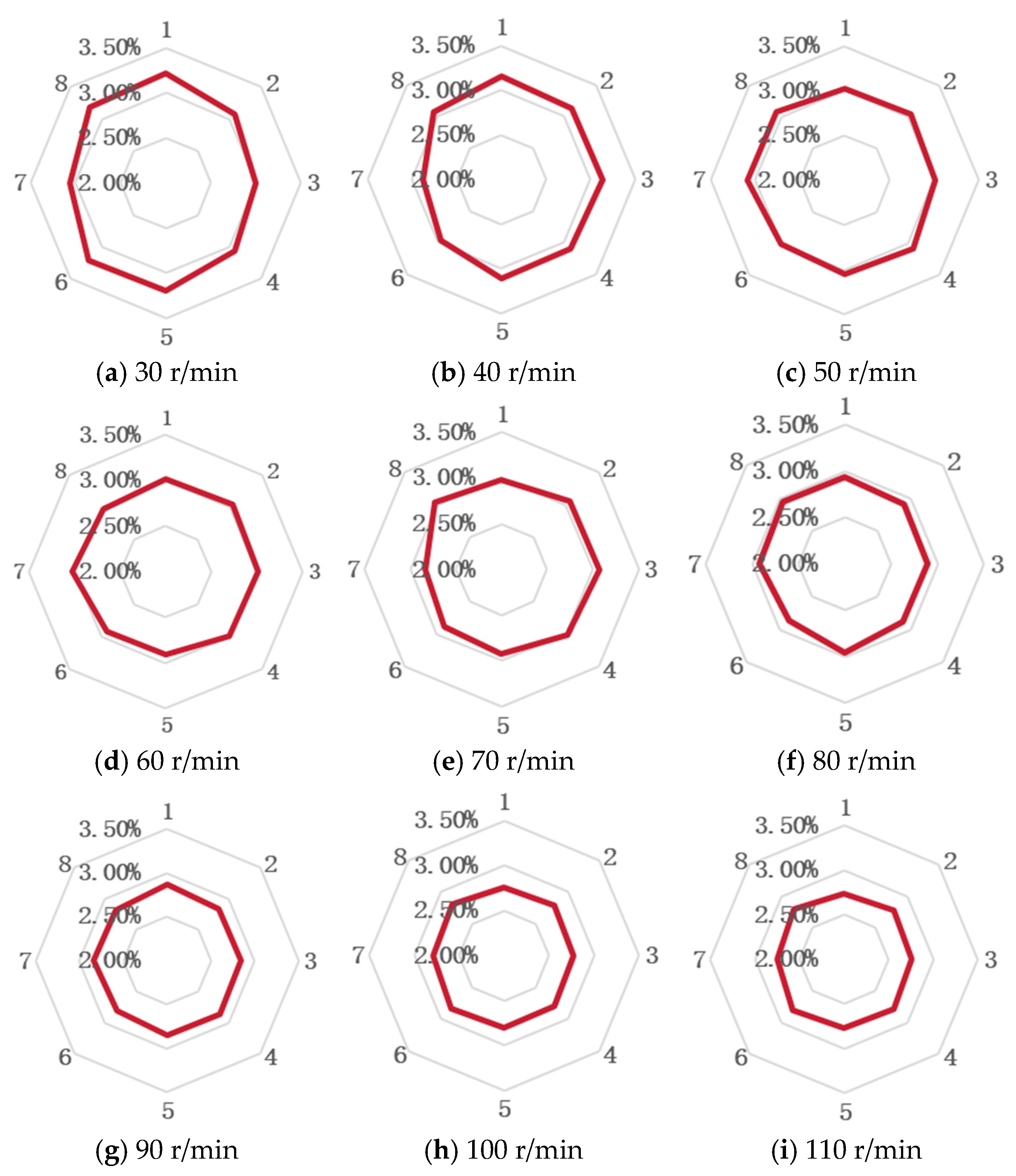
3.2. Bench Test
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, H.; Wang, J.; Xu, C.; Zhou, W.; Wang, J.; Wang, X. Research progress analysis on key technology of chemical fertilizer reduction and efficiency increase. Trans. Chin. Soc. Agric. Mach. 2019, 4, 1–19. [Google Scholar]
- Song, L.; Zhang, R. Research on change trend and risk of China’s food production. J. Agric. Sci. Technol. China 2023, 2, 1–9. [Google Scholar]
- Chen, Y.; Sun, Y. Study on the production increasing potential and guarantee capacity of grain in China in the next 30 years. J. Sichuan Agric. Univ. 2022, 33, 312–318. [Google Scholar]
- Yang, S.; Yan, X. Research on the risk assessment of farmland non-point source pollution at regional scale from the perspective of crop fertilizer application amount. J. China Agric. Univ. 2023, 22, 147–159. [Google Scholar]
- Gao, L.; Zhang, Q.; Chen, H.; Wang, H.; Liu, W.; Zhang, S.; Xu, G.; Shen, Y. Pollution status and control measures of agricultural non-point source pollution in China. Phosphate Compd. Fertil. 2018, 88, 37–38, 45. [Google Scholar]
- Feng, S. Research on the impact of agricultural mechanization on agricultural development. South Agric. Mach. 2025, 8, 171–173+180. [Google Scholar]
- Ou, M.; Wang, G.; Lu, Y.; Zhang, Z.; Pan, H.; Jia, W.; Dong, X. Structure Optimization and Performance Simulation of a Double-Disc Fertilizer Spreader Based on EDEM-CFD. Agronomy 2025, 5, 1025. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, K.; Yang, S.; Han, X.; Wei, X.; Zhu, Q.; Chen, L. Design and Experiment of an Unmanned Variable-Rate Fertilization Control System with Self-Calibration of Fertilizer Discharging Shaft Speed. Agronomy 2024, 10, 2336. [Google Scholar] [CrossRef]
- Guo, Q.; Quan, B.; Sun, H.; Ji, X.; Yu, Z.; Wang, H.; Wu, X.; Wei, Y.; Zhang, C.; Shang, G.; et al. Design Optimization and Experimentation of Triple-Head Gradually Reducing Spiral Precision Fertilizer Apparatus. Processes 2024, 9, 1988. [Google Scholar]
- Peng, M.; Zhang, Z.; Zhang, W.; Huang, H.; Zhang, G.; Liu, W.; Wu, X.; Zhang, J. Design and Optimization of Sugarcane Spiral Fertilizer Applicator Based on Response Surface Methodology and Artificial Neural Networks. Processes 2023, 10, 2881. [Google Scholar] [CrossRef]
- Li, H. Design and Test of the Screw Auger Fertilizer—Discharging Device for Oil—Tea Camellia Forests. Master’s Thesis, Jiangxi Agricultural University, Nanchang, China, 2024. [Google Scholar]
- Dun, G.; Liu, W.; Wu, X.; Mao, N.; Ji, W.; Ma, H. Simulation optimization and experiment of screw extrusion precision fertilizer ejector. J. Jilin Univ. (Eng. Technol. Ed.) 2023, 10, 3026–3037. [Google Scholar]
- Sui, X. Development of a Tou-Row Equal Application Vehicle for Granular Organic Fertilizers in Blueberry Plantations and Study of Consistency of Application and Sowing. Master’s Thesis, Qingdao University of Technology, Qingdao, China, 2024. [Google Scholar]
- Xu, W.; Yuan, Q.; Zeng, J.; Lü, X. Design and Experiment of Four-head Inclined Spiral Precision Fertilizer Dischargers in Orchard. Trans. Chin. Soc. Agric. Mach. 2024, Z2, 30–40. [Google Scholar]
- Zhang, X.; Wu, Y.; Li, J.; Wang, L.; Tong, Z.; Chen, X. Design and experiment of tobacco pellet fertilizer mixture applicator. J. Henan Agric. Univ. 2020, 5, 829–835. [Google Scholar]
- Xu, C.; Dong, W.; Li, H.; Yu, Q.; Zhang, C.; Ding, Y. Design and experiment of a centrifugal cavity disc extrusion type high-speed precision fertilizer apparatus for rapeseed. Trans. Chin. Soc. Agric. Eng. 2024, 20, 22–34. [Google Scholar]
- Shi, J. Optimized Design of Fertilizer Distributor for Substrate-Covered No-Till Planter and Its Impact on Maize Growth. Master’s Thesis, Heilongjiang Bayi Agricultural University, Daqing, China, 2024. [Google Scholar]
- Shi, Y.; Chen, M.; Wang, X.; Morice, O.O.; Ding, W. Numerical simulation of spreading performance and distribution pattern of centrifugal variable-rate fertilizer applicator based on DEM software. Comput. Electron. Agric. 2018, 144, 249–259. [Google Scholar]
- Song, S. Optimal Design and Experimental Research on the Layered Fertilizer Apparatus of the Specific row-Following Layered Fertilize. Master’s Thesis, Shihezi University, Xinjiang, China, 2021. [Google Scholar]
- Wang, X.; Shi, J.; Li, X.; Jiang, Q.; Zhan, C.; Song, Z. Analysis of Research Status and Development Trends of Organic Fertilizer Applicators at Home and Abroad. Agric. Dev. Equip. 2025, 4, 100–103. [Google Scholar]
- Xue, Z.; Zhao, L.; Wang, F.; Wang, S.; Song, G.; Wang, G. Study on the Performance of Spiral Fertilizer Distributor Based on EDEM. J. Agric. Mech. Res. 2020, 6, 87–95. [Google Scholar]
- Zhu, Q. Study on Inclined Fluted Roller Fertilizer Distributor. Master’s Thesis, College of Engineering, South China Agricultural University, Guangzhou, China, 2017. [Google Scholar]
- China Academy of Agricultural Machinery Sciences (CAAMS). Agricultural Machinery Design Handbook; China Academy of Agricultural Machinery Sciences (CAAMS): Beijing, China, 2007. [Google Scholar]
- Wang, Y. Research on Key Parameters and Fertilization Performance of Outer Groove-Wheel Fertilizer Apparatus Based on EDEM. Master’s Thesis, Tarim University, Xinjiang, China, 2024. [Google Scholar]
- Qi, J.; Deng, Y.; Zhang, J.; Meng, H.; Li, Y. Design and Experiment of Manure and Granular Fertilizer Mixed Fertilizer Discharging Device Based on EDEM. J. Chin. Agric. Mech. 2025, 4, 1–9. [Google Scholar]
- GB/T 22923-2008; Determination of Nitrogen Phosphorus Potassium for Fertilizers by Auto Analyzer. Standardization Administration of the People’s Republic of China: Beijng, China, 2008.
- Liu, X.; Hu, R.; Wang, D.; Lu, B.; Wang, W.; Ding, Y. Optimization and Experiment of Fertilizer Discharger Based on Granular Fertilizer Motion Model. Trans. Chin. Soc. Agric. Mach. 2021, 12, 85–95. [Google Scholar]
- Liu, X. Design and Experiment on Precise Discharge-Apply Fertilizer System of Rapeseed Planter. Ph.D. Thesis, Huazhong Agricultural University, Wuhan, China, 2022. [Google Scholar]
- NY/T 1143-2006; Technical Specifications of Quality Evaluation for Drills. Ministry of Agriculture of the People’s Republic of China: Beijng, China, 2006.
- Liao, Q.; Shen, W.; Wang, L.; Huo, J.; Luo, Z.; Liao, Y. Design and Experiment of High-speed Mechanical Centrifugal Collecting and Discharging Device for Rapeseed. Trans. Chin. Soc. Agric. Mach. 2024, 7, 154–167. [Google Scholar]
- Liu, X.; Lü, Q.; Li, G.; Wang, J.; Yan, D.; Yang, L.; Liu, E. Design Optimization and Experimental Verification of Spiral Cone Centrifugal Fertilizer Apparatus Based on the Discrete Element Method. Processes 2023, 11, 199. [Google Scholar] [CrossRef]


| Item | Parameter | Value |
|---|---|---|
| Fertilizer granules | Poisson’s ratio | 0.25 |
| Shear modulus/pa | 1.1 × 108 | |
| Density/kg·m−3 | 845.61 | |
| Fertilizer distributor | Poisson’s ratio | 0.394 |
| Shear modulus/pa | 8.9 × 108 | |
| Density/kg·m−3 | 1060 | |
| Fertilizer granules–Fertilizer granules | Coefficient of recovery | 0.3 |
| Coefficient of static friction | 0.34 | |
| Coefficient of rolling friction | 0.16 | |
| Fertilizer granules–Fertilizer distributor | Coefficient of recovery | 0.2 |
| Coefficient of static friction | 0.18 | |
| Coefficient of rolling friction | 0.01 |
| Level | Factor | ||
|---|---|---|---|
| Cone Disc Speed N (r/min) | Cone Disc Cone Angle φ (°) | Cone Disc Blade Inclination Angle γ (°) | |
| −1 | 30 | 0 | 0 |
| 0 | 70 | 12.8 | 3.4 |
| 1 | 110 | 25.6 | 6.8 |
| Experimentation Control | Factor | Coefficient of Variation for the Consistency of Fertilizer Application Amount Among Rows Yv1 (%) | Coefficient of Variation for the Consistency of Fertilizer Application Amount Within the Same Row Yv2 (%) | ||
|---|---|---|---|---|---|
| Cone Disc Speed X1 | Cone Disc Cone Angle X2 | Cone Disc Blade Inclination Angle X3 | |||
| 1 | 0 | −1 | 1 | 6.24 | 2.41 |
| 2 | 0 | 1 | 1 | 5.46 | 1.96 |
| 3 | 0 | 0 | 0 | 6.52 | 2.57 |
| 4 | 1 | −1 | 0 | 2.65 | 3.81 |
| 5 | −1 | 0 | −1 | 2.32 | 1.57 |
| 6 | 0 | −1 | −1 | 5.65 | 2.56 |
| 7 | 0 | 1 | −1 | 5.24 | 2.19 |
| 8 | 1 | 0 | 1 | 2.02 | 2.45 |
| 9 | 1 | 1 | 0 | 2.56 | 2.95 |
| 10 | 0 | 0 | 0 | 5.57 | 3.01 |
| 11 | 1 | 0 | −1 | 1.12 | 3.63 |
| 12 | −1 | −1 | 0 | 5.43 | 1.49 |
| 13 | 0 | 0 | 0 | 6.49 | 2.79 |
| 14 | −1 | 0 | 1 | 2.56 | 1.95 |
| 15 | 0 | 0 | 0 | 5.37 | 2.79 |
| 16 | 0 | 0 | 0 | 5.97 | 2.67 |
| 17 | −1 | 1 | 0 | 3.28 | 1.49 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|
| Model | 51.67 | 9 | 5.74 | 24.65 | 0.0002 | ** |
| X1 | 3.43 | 1 | 3.43 | 14.73 | 0.0064 | ** |
| X2 | 1.47 | 1 | 1.47 | 6.31 | 0.0402 | * |
| X3 | 0.4753 | 1 | 0.4753 | 2.04 | 0.1962 | |
| X1X2 | 1.06 | 1 | 1.06 | 4.55 | 0.0702 | |
| X1X3 | 0.1089 | 1 | 0.1089 | 0.4675 | 0.5161 | |
| X2X3 | 0.0342 | 1 | 0.0342 | 0.1465 | 0.7129 | |
| X12 | 39.77 | 1 | 39.77 | 170.73 | <0.0001 | ** |
| X22 | 1.36 | 1 | 1.36 | 5.86 | 0.0461 | * |
| X32 | 3.45 | 7 | 3.45 | 14.83 | 0.0063 | ** |
| Residual | 1.63 | 7 | 0.2329 | |||
| Lack of Fit | 0.5386 | 3 | 0.1795 | 0.6577 | 0.6194 | |
| Pure Error | 1.09 | 4 | 0.2730 | |||
| Cor Total | 53.31 | 16 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Significance |
|---|---|---|---|---|---|---|
| Model | 6.95 | 9 | 0.7720 | 17.07 | 0.0006 | ** |
| X1 | 5.02 | 1 | 5.02 | 111.08 | <0.0001 | ** |
| X2 | 0.3528 | 1 | 0.3528 | 7.80 | 0.0268 | ** |
| X3 | 0.1741 | 1 | 0.1741 | 3.85 | 0.0906 | |
| X1X2 | 0.1849 | 1 | 0.1849 | 4.09 | 0.0829 | |
| X1X3 | 0.6084 | 1 | 0.6084 | 13.45 | 0.0080 | ** |
| X2X3 | 0.0016 | 1 | 0.0016 | 0.03554 | 0.8562 | |
| X12 | 0.0469 | 1 | 0.0469 | 1.04 | 0.3426 | |
| X22 | 0.2141 | 1 | 0.2141 | 4.73 | 0.0661 | |
| X32 | 0.2857 | 7 | 0.2857 | 6.32 | 0.0402 | ** |
| Residual | 0.3166 | 7 | 0.0452 | |||
| Lack of Fit | 0.2083 | 3 | 0.0694 | 2.56 | ||
| Pure Error | 0.1083 | 4 | 0.0271 | |||
| Cor Total | 7.26 | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Huang, J.; Wan, E.; Ma, F.; Chu, M.; Yang, L.; Zhang, H.; Du, H. Design and Experiment of a Multi-Row Spiral Quantitative Fertilizer Distributor. Processes 2025, 13, 1992. https://doi.org/10.3390/pr13071992
Liu X, Huang J, Wan E, Ma F, Chu M, Yang L, Zhang H, Du H. Design and Experiment of a Multi-Row Spiral Quantitative Fertilizer Distributor. Processes. 2025; 13(7):1992. https://doi.org/10.3390/pr13071992
Chicago/Turabian StyleLiu, Xiaodong, Junya Huang, Enchao Wan, Fangbo Ma, Mingle Chu, Liquan Yang, He Zhang, and Hongyi Du. 2025. "Design and Experiment of a Multi-Row Spiral Quantitative Fertilizer Distributor" Processes 13, no. 7: 1992. https://doi.org/10.3390/pr13071992
APA StyleLiu, X., Huang, J., Wan, E., Ma, F., Chu, M., Yang, L., Zhang, H., & Du, H. (2025). Design and Experiment of a Multi-Row Spiral Quantitative Fertilizer Distributor. Processes, 13(7), 1992. https://doi.org/10.3390/pr13071992






