Unraveling the Degradation Kinetics of Genipin-Cross-Linked Chitosan Hydrogels via Symbolic Regression
Abstract
1. Introduction
1.1. Nomenclature
1.2. Novelty Statement and Organization
2. Genipin-Cross-Linked Chitosan Gels
Material, Sample Preparation, and Degradation Monitoring
3. Fundamentals of Symbolic Regression
- Selection: Models that exhibit better performance are more likely to be selected for reproduction.
- Crossover (recombination): Pairs of models exchange subtrees to generate offspring, encouraging the combination of beneficial traits.
- Mutation: Random modifications are introduced to the expression trees, maintaining diversity and facilitating the exploration of new regions in the solution space.
Methodological Analysis of SR
- 1.
- Model representation: Each candidate model is represented as an expression tree, where internal nodes represent mathematical operations (e.g., ) and leaves represent variables or constants.
- 2.
- Initial population: A diverse initial population of symbolic expressions is generated using a predefined function and terminal set. Constants are randomly initialized and later optimized.
- 3.
- Fitness evaluation: The fitness of each model is computed using a regularized objective function:where is a loss function (e.g., RMSE or AARD), penalizes the model size , and is a penalty constant commonly referred to as the parsimony coefficient.
- 4.
- Selection: Models are selected for reproduction based on their fitness scores, using methods such as tournament selection or roulette wheel sampling.
- 5.
- Crossover and Mutation: (i) Crossover: Two parent trees exchange randomly selected subtrees to produce offspring. (ii) Mutation: A node or subtree is randomly altered, which may include replacing operators, variables, or constants.
- 6.
- Parameter optimization (optional): Once a symbolic structure is identified, its numerical parameters can be refined using local optimization techniques. This corresponds to solving the parameter estimation problem (4).
- 7.
- Termination: The algorithm iterates over generations until a termination criterion is met, such as a fixed number of generations or convergence in fitness.
- 8.
- Model selection: The best-performing model is selected as the solution to the SR problem.
- PySR [54], which combines mutation-heavy evolutionary search, Pareto front-based model selection, and deterministic expression simplification.
- gplearn [55], a tree-based genetic programming library implementing fitness-based SR and classification.
- DEAP [56], a general-purpose evolutionary computation framework that supports GP.
- TPOT [57], which applies GA to automate machine learning pipelines, including SR components.
4. Algorithm for Constructing Kinetic Degradation Models
- 1.
- Preprocessing of experimental data, including scaling and noise reduction;
- 2.
- Construction of symbolic regression models from the processed data;
- 3.
- Symbolic manipulation and simplification of the resulting expressions;
- 4.
- Comparison of the derived symbolic forms with standard kinetic models associated with known degradation mechanisms, leading to the identification of the most probable mechanism underlying the observed behavior.
4.1. Pre-Processing of Experimental Data
- To smooth the raw degradation data while preserving key local features of the degradation profile;
- To estimate local degradation rates, denoted as , through numerical differentiation of the smoothed retention curve:where is the retained mass fraction, is the continuous time variable over which smoothing is performed, and t refers to discrete time points of interest.
4.2. Symbolic Regression for Kinetic Rate Modeling
4.3. Parsing and Simplifying the SR Output
4.4. Kinetic Law Identification
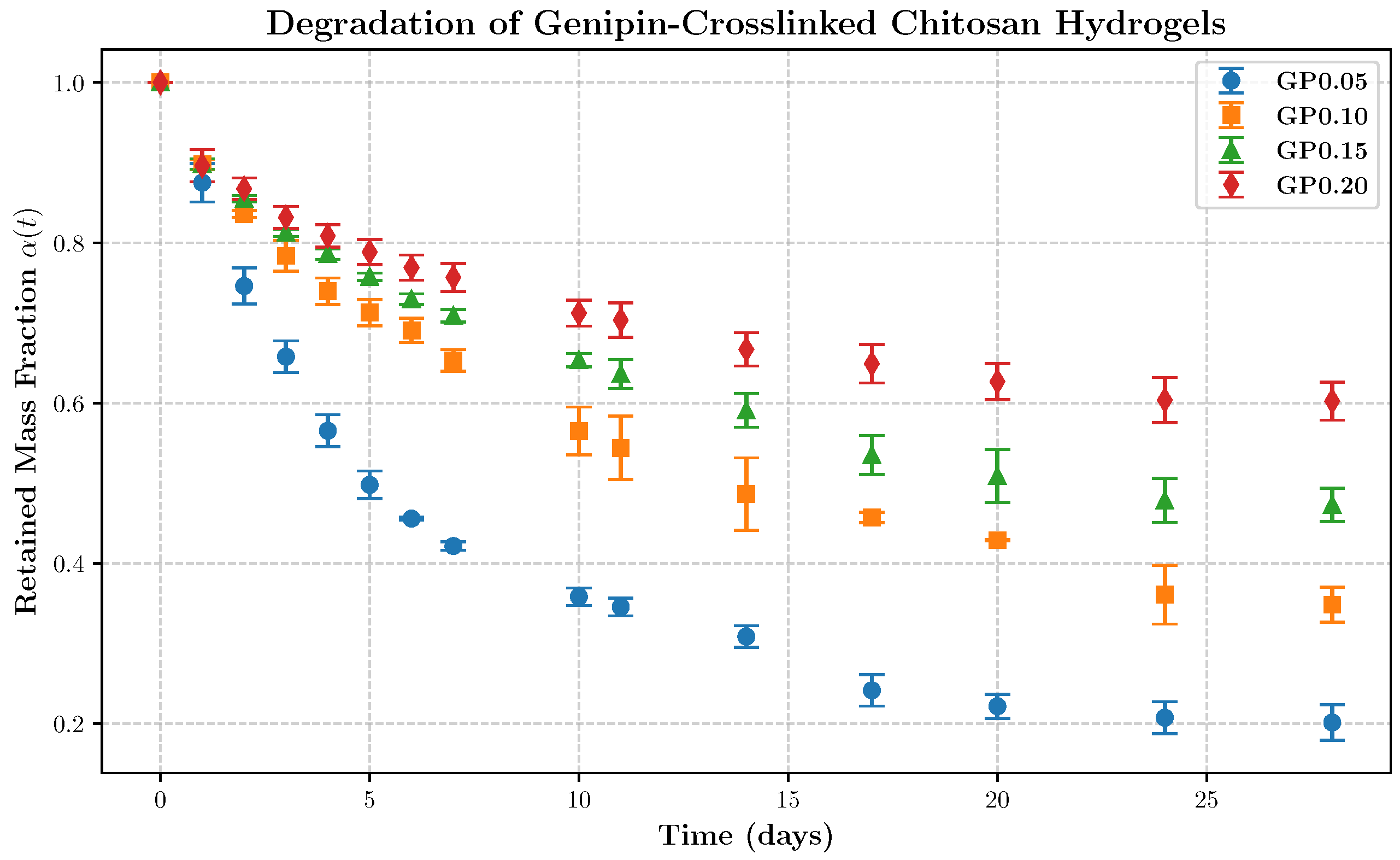
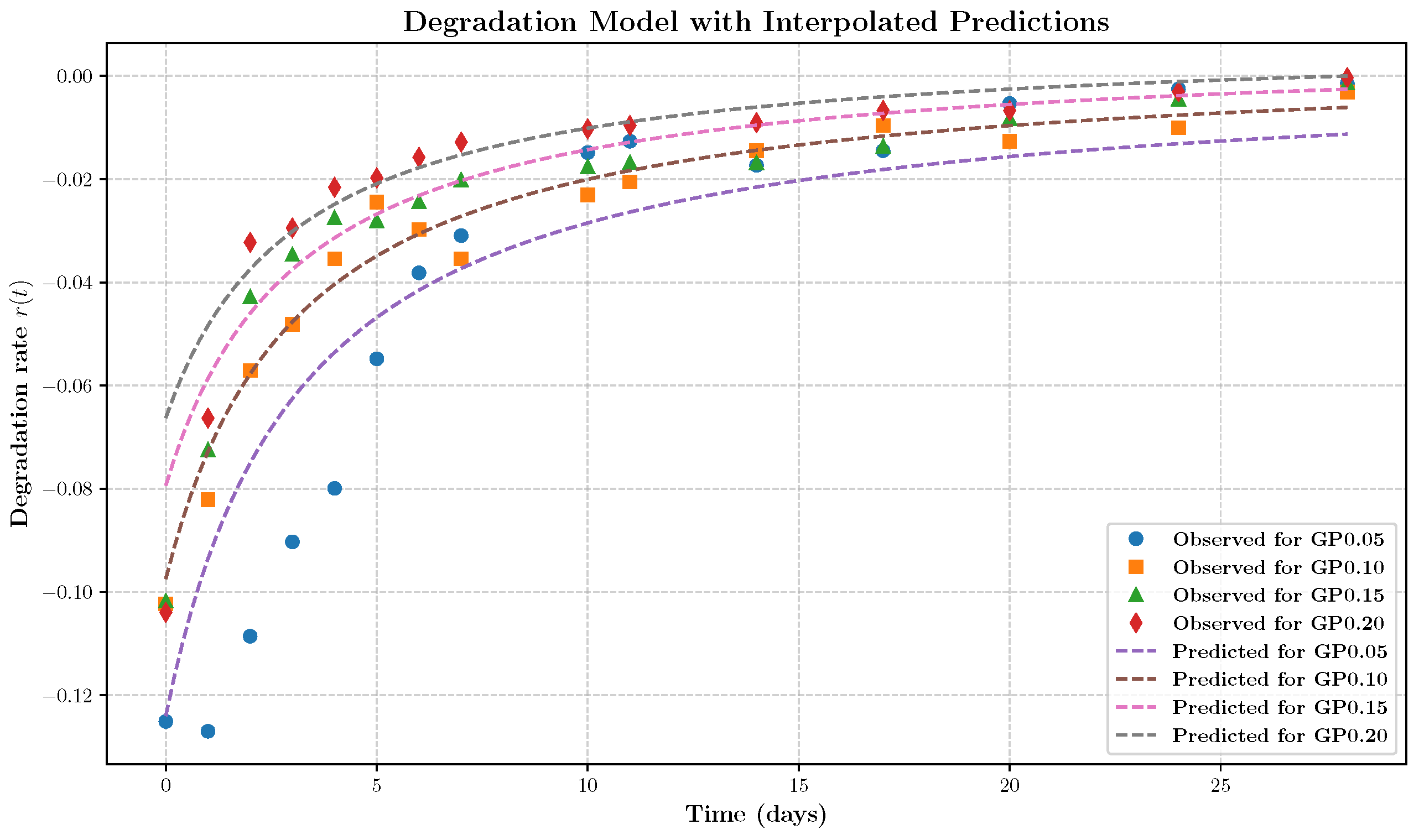
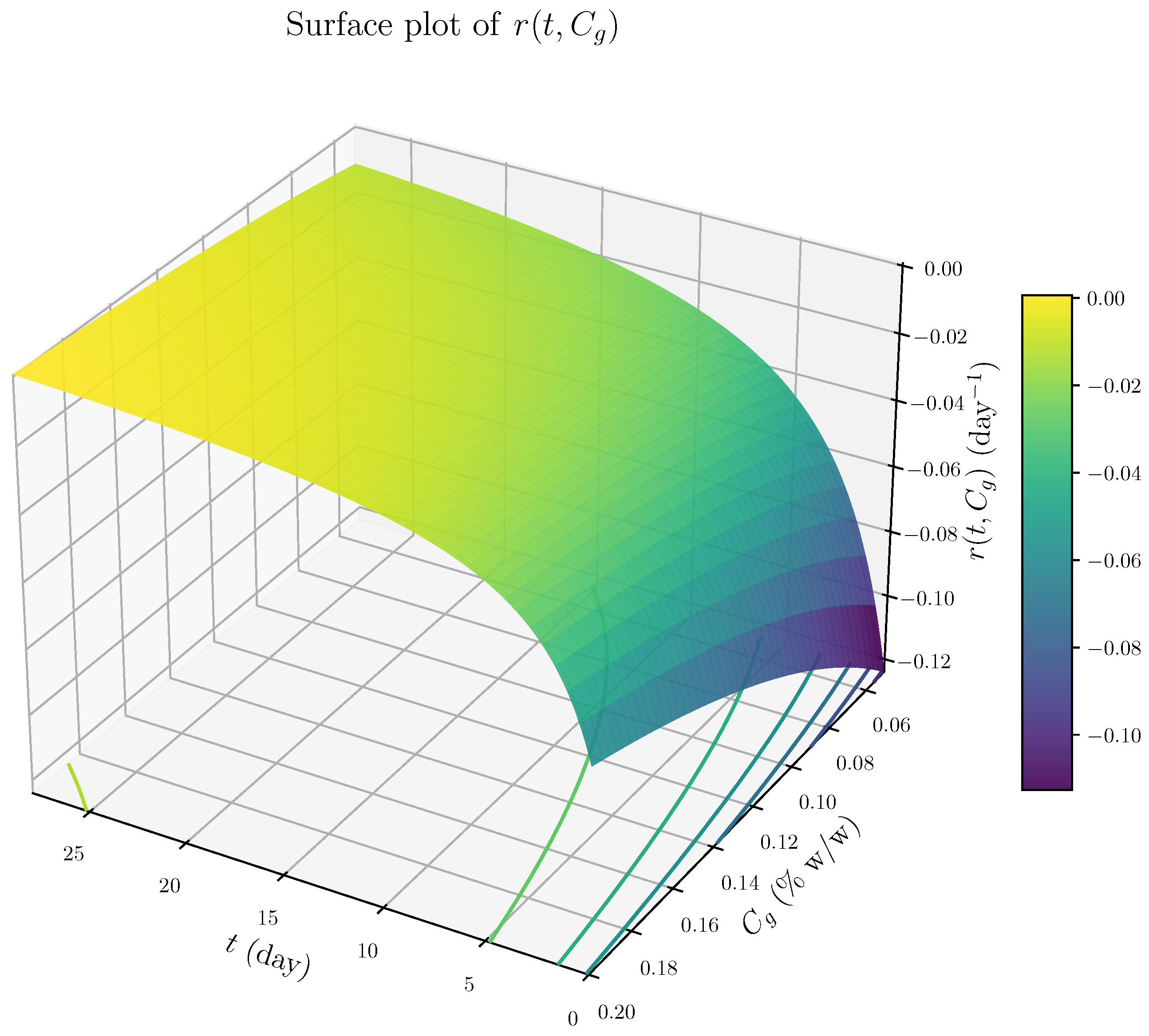
5. Application to the Degradation Kinetics of Genipin-Cross-Linked Chitosan Hydrogels
- 1.
- The rate expression is independent of the retained mass fraction , indicating that degradation proceeds at a rate largely unaffected by the remaining material. This behavior is characteristic of surface-limited, zero-order kinetics rather than mass-dependent bulk degradation.
- 2.
- The term proportional to dominates at early times, resulting in a high initial degradation rate and rapid loss of loosely bound material. As time progresses, the influence of this term diminishes, leading to a decelerating degradation rate. This behavior likely reflects the depletion of accessible reactive surface sites or time-dependent structural changes that hinder further erosion.
- 3.
- At later times, the degradation rate stabilizes to a constant value dependent on the cross-linker concentration . This indicates a buffering or inhibitory effect of cross-linking, consistent with increased network stability or steric hindrance at higher genipin concentrations.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Islam, S.; Bhuiyan, M.R.; Islam, M. Chitin and chitosan: Structure, properties and applications in biomedical engineering. J. Polym. Environ. 2017, 25, 854–866. [Google Scholar] [CrossRef]
- Singh, G.; Chanda, A. Mechanical properties of whole-body soft human tissues: A review. Biomed. Mater. 2021, 16, 062004. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.; Shitiz, K.; Singh, A. Chitin and chitosan: Biopolymers for wound management. Int. Wound J. 2017, 14, 1276–1289. [Google Scholar] [CrossRef] [PubMed]
- Prabaharan, M.; Mano, J. Chitosan-based particles as controlled drug delivery systems. Drug Deliv. 2004, 12, 41–57. [Google Scholar] [CrossRef]
- Kim, I.Y.; Seo, S.J.; Moon, H.S.; Yoo, M.K.; Park, I.Y.; Kim, B.C.; Cho, C.S. Chitosan and its derivatives for tissue engineering applications. Biotechnol. Adv. 2008, 26, 1–21. [Google Scholar] [CrossRef]
- Lin, X.; Zhao, X.; Xu, C.; Wang, L.; Xia, Y. Progress in the mechanical enhancement of hydrogels: Fabrication strategies and underlying mechanisms. J. Polym. Sci. 2022, 60, 2525–2542. [Google Scholar] [CrossRef]
- Yammine, P.; El Safadi, A.; Kassab, R.; El-Nakat, H.; Obeid, P.J.; Nasr, Z.; Tannous, T.; Sari-Chmayssem, N.; Mansour, A.; Chmayssem, A. Types of crosslinkers and their applications in biomaterials and biomembranes. Chemistry 2025, 7, 61. [Google Scholar] [CrossRef]
- Esparza-Flores, E.E.; Siquiera, L.B.; Cardoso, F.D.; Costa, T.H.; Benvenutti, E.V.; Medina-Ramírez, I.E.; Perullini, M.; Santagapita, P.R.; Rodrigues, R.C.; Hertz, P.F. Chitosan with modified porosity and crosslinked with genipin: A dynamic system structurally characterized. Food Hydrocoll. 2023, 144, 109034. [Google Scholar] [CrossRef]
- Zielińska, A.; Karczewski, J.; Eder, P.; Kolanowski, T.; Szalata, M.; Wielgus, K.; Szalata, M.; Kim, D.; Shin, S.R.; Słomski, R.; et al. Scaffolds for drug delivery and tissue engineering: The role of genetics. J. Control. Release 2023, 359, 207–223. [Google Scholar] [CrossRef]
- Ding, R.; Zhu, Y.; Jing, L.; Chen, S.; Lu, J.; Zhang, X. Sulfhydryl functionalized chitosan-covalent organic framework composites for highly efficient and selective recovery of gold from complex liquids. Int. J. Biol. Macromol. 2024, 282, 137037. [Google Scholar] [CrossRef]
- Dang, Q.F.; Yan, J.Q.; Li, J.J.; Cheng, X.J.; Liu, C.S.; Chen, X.G. Controlled gelation temperature, pore diameter and degradation of a highly porous chitosan-based hydrogel. Carbohydr. Polym. 2011, 83, 171–178. [Google Scholar] [CrossRef]
- Jennings, J. 7—Controlling chitosan degradation properties in vitro and in vivo. In Chitosan Based Biomaterials Volume 1; Jennings, J.A., Bumgardner, J.D., Eds.; Woodhead Publishing: Cambridge, UK, 2017; pp. 159–182. [Google Scholar] [CrossRef]
- Ganji, F.; Abdekhodaie, M.; Ramazani, S.A.A. Gelation time and degradation rate of chitosan-based injectable hydrogel. J. Sol-Gel Sci. Technol. 2007, 42, 47–53. [Google Scholar] [CrossRef]
- Eivazzadeh-Keihan, R.; Noruzi, E.B.; Mehrban, S.F.; Aliabadi, H.A.M.; Karimi, M.; Mohammadi, A.; Maleki, A.; Mahdavi, M.; Larijani, B.; Shalan, A.E. The latest advances in biomedical applications of chitosan hydrogel as a powerful natural structure with eye-catching biological properties. J. Mater. Sci. 2022, 57, 3855–3891. [Google Scholar] [CrossRef]
- Xu, C.; Sun, N.; Li, H.; Han, X.; Zhang, A.; Sun, P. Stimuli-responsive vesicles and hydrogels formed by a single-tailed dynamic covalent surfactant in aqueous solutions. Molecules 2024, 29, 4984. [Google Scholar] [CrossRef]
- Berger, J.; Reist, M.; Mayer, J.M.; Felt, O.; Gurny, R. Structure and interactions in chitosan hydrogels formed by complexation or aggregation for biomedical applications. Eur. J. Pharm. Biopharm. 2004, 57, 35–52. [Google Scholar] [CrossRef]
- Dash, M.; Chiellini, F.; Ottenbrite, R.; Chiellini, E. Chitosan—A versatile semi-synthetic polymer in biomedical applications. Prog. Polym. Sci. 2011, 36, 981–1014. [Google Scholar] [CrossRef]
- Tanioka, S.; Matsui, Y.; Irie, T.; Tanigawa, T.; Tanaka, Y.; Shibata, H.; Sawa, Y.; Kono, Y. Oxidative depolymerization of chitosan by hydroxyl radical. Biosci. Biotechnol. Biochem. 1996, 60, 2001–2004. [Google Scholar] [CrossRef]
- Samani, S.; Bonakdar, S.; Farzin, A.; Hadjati, J.; Azami, M. A facile way to synthesize a photocrosslinkable methacrylated chitosan hydrogel for biomedical applications. Int. J. Polym. Mater. Polym. Biomater. 2021, 70, 730–741. [Google Scholar] [CrossRef]
- Kocak, F.Z.; Yar, M.; Rehman, I.U. In vitro degradation, swelling, and bioactivity performances of in situ forming injectable chitosan-matrixed hydrogels for bone regeneration and drug delivery. Biotechnol. Bioeng. 2024, 121, 2767–2779. [Google Scholar] [CrossRef]
- Li, J.; Liu, P. One-pot fabrication of pH/reduction dual-stimuli responsive chitosan-based supramolecular nanogels for leakage-free tumor-specific DOX delivery with enhanced anti-cancer efficacy. Carbohydr. Polym. 2018, 201, 583–590. [Google Scholar] [CrossRef]
- Xia, M.; Pan, N.; Zhang, C.; Zhang, C.; Fan, W.; Xia, Y.; Wang, Z.; Sui, K. Self-powered multifunction ionic skins based on gradient polyelectrolyte hydrogels. ACS Nano 2022, 16, 4714–4725. [Google Scholar] [CrossRef] [PubMed]
- Lu, P.; Ruan, D.; Huang, M.; Tian, M.; Zhu, K.; Gan, Z.; Xiao, Z. Harnessing the potential of hydrogels for advanced therapeutic applications: Current achievements and future directions. Signal Transduct. Target. Ther. 2024, 9, 166. [Google Scholar] [CrossRef] [PubMed]
- Duarte, A.R.C.; Correlo, V.M.; Oliveira, J.M.; Reis, R.L. Recent Developments on Chitosan Applications in Regenerative Medicine. In Biomaterials from Nature for Advanced Devices and Therapies; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016; Chapter 14; pp. 221–243. [Google Scholar] [CrossRef]
- Kean, T.; Thanou, M. Biodegradation, biodistribution and toxicity of chitosan. Adv. Drug Deliv. Rev. 2010, 62, 3–11. [Google Scholar] [CrossRef] [PubMed]
- Koza, J.R. Genetic programming as a means for programming computers by natural selection. Stat. Comput. 1994, 4, 87–112. [Google Scholar] [CrossRef]
- Banzhaf, W.; Nordin, P.; Keller, R.E.; Francone, F.D. Genetic programming: An Introduction: On the Automatic Evolution of Computer Programs and Its Applications; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1998. [Google Scholar]
- Schmidt, M.; Lipson, H. Distilling free-form natural laws from experimental data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef]
- Narayanan, H.; Cruz Bournazou, M.N.; Guillén-Gosálbez, G.; Butté, A. Functional-Hybrid modeling through automated adaptive symbolic regression for interpretable mathematical expressions. Chem. Eng. J. 2022, 430, 133032. [Google Scholar] [CrossRef]
- Forster, T.; Vázquez, D.; Müller, C.; Guillén-Gosálbez, G. Machine learning uncovers analytical kinetic models of bioprocesses. Chem. Eng. Sci. 2024, 300, 120606. [Google Scholar] [CrossRef]
- Rogers, A.W.; Lane, A.; Mendoza, C.; Watson, S.; Kowalski, A.; Martin, P.; Zhang, D. Integrating knowledge-guided symbolic regression and model-based design of experiments to automate process flow diagram development. Chem. Eng. Sci. 2024, 300, 120580. [Google Scholar] [CrossRef]
- Papastamatiou, K.; Sofos, F.; Karakasidis, T.E. Machine learning symbolic equations for diffusion with physics-based descriptions. Aip Adv. 2022, 12, 025004. [Google Scholar] [CrossRef]
- Servia, M.A.D.; del Rio Chanona, E.A. Interpretable Machine Learning for Kinetic Rate Model Discovery. In Machine Learning and Hybrid Modelling for Reaction Engineering: Theory and Applications; Royal Society of Chemistry: London, UK, 2023; pp. 133–158. [Google Scholar] [CrossRef]
- Bragone, F.; Morozovska, K.; Laneryd, T.; Shukla, K.; Markidis, S. Discovering partially known ordinary differential equations: A case study on the chemical kinetics of cellulose degradation. arXiv 2025, arXiv:2504.03484. [Google Scholar] [CrossRef]
- Ravi Kumar, M.; Muzzarelli, R.; Muzzarelli, C.; Sashiwa, H.; Domb, A. Chitosan chemistry and pharmaceutical perspectives. Chem. Rev. 2004, 104, 6017–6084. [Google Scholar] [CrossRef] [PubMed]
- Alexeev, V.; Evmenenko, G. Salt-free chitosan solutions: Thermodynamics, structure and intramolecular force balance. Polym. Sci. Ser. A 1999, 41, 966–974. [Google Scholar]
- Singha, I.; Basu, A. Chitosan based injectable hydrogels for smart drug delivery applications. Sens. Int. 2022, 3, 100168. [Google Scholar] [CrossRef]
- Kildeeva, N.; Chalykh, A.; Belokon, M.; Petrova, T.; Matveev, V.; Svidchenko, E.; Surin, N.; Sazhnev, N. Influence of genipin crosslinking on the properties of chitosan-based films. Polymers 2020, 12, 1086. [Google Scholar] [CrossRef]
- Yu, Y.; Xu, S.; Li, S.; Pan, H. Genipin-cross-linked hydrogels based on biomaterials for drug delivery: A review. Biomater. Sci. 2021, 9, 1583–1597. [Google Scholar] [CrossRef]
- Chenite, A.; Buschmann, M.; Wang, D.; Chaput, C.; Kandani, N. Rheological characterisation of thermogelling chitosan/glycerol-phosphate solutions. Carbohydr. Polym. 2001, 46, 39–47. [Google Scholar] [CrossRef]
- Moura, M.J.; Figueiredo, M.M.; Gil, M.H. Rheological study of genipin cross-linked chitosan hydrogels. Biomacromolecules 2007, 8, 3823–3829. [Google Scholar] [CrossRef]
- Han, H.; Nam, D.; Seo, D.; Kim, T.; Shin, B.; Choi, H. Preparation and biodegradation of thermosensitive chitosan hydrogel as a function of pH and temperature. Macromol. Res. 2004, 12, 507–511. [Google Scholar] [CrossRef]
- Balakrishnan, B.; Jayakrishnan, A. Self-cross-linking biopolymers as injectable in situ forming biodegradable scaffolds. Biomaterials 2005, 26, 3941–3951. [Google Scholar] [CrossRef]
- Brouwer, J.; van Leeuwen-Herberts, T.; Otting-van de Ruit, M. Determination of lysozyme in serum, urine, cerebrospinal fluid and feces by enzyme immunoassay. Clin. Chim. Acta 1984, 142, 21–30. [Google Scholar] [CrossRef]
- Kronberger, G.; Burlacu, B.; Kommenda, M.; Winkler, S.M.; Affenzeller, M. Symbolic Regression; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar]
- Shmuel, A.; Glickman, O.; Lazebnik, T. Symbolic regression as a feature engineering method for machine and deep learning regression tasks. Mach. Learn. Sci. Technol. 2024, 5, 025065. [Google Scholar] [CrossRef]
- Zhong, J.; Feng, L.; Cai, W.; Ong, Y.S. Multifactorial genetic programming for symbolic regression problems. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 4492–4505. [Google Scholar] [CrossRef]
- Virgolin, M.; Alderliesten, T.; Witteveen, C.; Bosman, P.A. Improving model-based genetic programming for symbolic regression of small expressions. Evol. Comput. 2021, 29, 211–237. [Google Scholar] [CrossRef] [PubMed]
- Murdoch, W.J.; Singh, C.; Kumbier, K.; Abbasi-Asl, R.; Yu, B. Definitions, methods, and applications in interpretable machine learning. Proc. Natl. Acad. Sci. USA 2019, 116, 22071–22080. [Google Scholar] [CrossRef]
- Makke, N.; Chawla, S. Interpretable scientific discovery with symbolic regression: A review. Artif. Intell. Rev. 2024, 57, 2. [Google Scholar] [CrossRef]
- Keren, L.S.; Liberzon, A.; Lazebnik, T. A computational framework for physics-informed symbolic regression with straightforward integration of domain knowledge. Sci. Rep. 2023, 13, 1249. [Google Scholar] [CrossRef]
- La Cava, W.; Orzechowski, P.; Burlacu, B.; de França, F.O.; Virgolin, M.; Jin, Y.; Kommenda, M.; Moore, J.H. Contemporary symbolic regression methods and their relative performance. arXiv 2021, arXiv:2107.14351. [Google Scholar] [CrossRef]
- Radwan, Y.A.; Kronberger, G.; Winkler, S. A comparison of recent algorithms for symbolic regression to genetic programming. arXiv 2024, arXiv:2406.03585. [Google Scholar] [CrossRef]
- Cranmer, M. Interpretable machine learning for science with PySR and SymbolicRegression.jl. arXiv 2023, arXiv:2305.01582. [Google Scholar] [CrossRef]
- Stephens, T. gplearn: Genetic Programming in Python, with a Scikit-Learn Inspired API. 2022. Available online: https://github.com/trevorstephens/gplearn (accessed on 26 March 2025).
- Fortin, F.A.; De Rainville, F.M.; Gardner, M.A.; Parizeau, M.; Gagné, C. DEAP: Evolutionary algorithms made easy. J. Mach. Learn. Res. 2012, 13, 2171–2175. [Google Scholar]
- Olson, R.S.; Bartley, N.; Urbanowicz, R.J.; Moore, J.H. Evaluation of a Tree-based Pipeline Optimization Tool for Automating Data Science. In Proceedings of the Genetic and Evolutionary Computation Conference 2016, GECCO’16, New York, NY, USA, 20–24 July 2016; pp. 485–492. [Google Scholar] [CrossRef]
- Meurer, A.; Smith, C.P.; Paprocki, M.; Čertík, O.; Kirpichev, S.B.; Rocklin, M.; Kumar, A.; Ivanov, S.; Moore, J.K.; Singh, S.; et al. SymPy: Symbolic computing in Python. PeerJ Comput. Sci. 2017, 3, e103. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Neumann, P.; Cao, L.; Russo, D.; Vassiliadis, V.S.; Lapkin, A.A. A new formulation for symbolic regression to identify physico-chemical laws from experimental data. Chem. Eng. J. 2020, 387, 123412. [Google Scholar] [CrossRef]
- Abooali, D.; Khamehchi, E. New predictive method for estimation of natural gas hydrate formation temperature using genetic programming. Neural Comput. Appl. 2019, 31, 2485–2494. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, M.; Xue, B. Feature selection to improve generalization of genetic programming for high-dimensional symbolic regression. IEEE Trans. Evol. Comput. 2017, 21, 792–806. [Google Scholar] [CrossRef]
- Sikorski, D.; Gzyra-Jagieła, K.; Draczyński, Z. The kinetics of chitosan degradation in organic acid solutions. Mar. Drugs 2021, 19, 236. [Google Scholar] [CrossRef]
- Chang, K.L.B.; Tai, M.C.; Cheng, F.H. Kinetics and products of the degradation of chitosan by hydrogen peroxide. J. Agric. Food Chem. 2001, 49, 4845–4851. [Google Scholar] [CrossRef]

| Function/Operator | Notation | Arity |
|---|---|---|
| Addition | 2 | |
| Subtraction | 2 | |
| Multiplication | 2 | |
| Division | 2 | |
| Exponential | 1 | |
| Logarithm | 1 | |
| Power | or | 2 |
| Square root | 1 | |
| Negation | 1 | |
| Reciprocal (inverse) | or | 1 |
| Degradation Type | Rate Law | Description |
|---|---|---|
| Surface degradation (zero-order) | Degradation occurs primarily at the surface at a constant rate, independent of the remaining mass. | |
| Surface degradation (first-order) | Surface-mediated degradation where the rate is proportional to the remaining mass fraction [63]. | |
| Bulk degradation (first-order) | Homogeneous degradation throughout the hydrogel, described by first-order kinetics [63]. | |
| Bulk degradation (power-law) | Non-linear degradation characterized by a power-law relationship with respect to the remaining mass [64]. | |
| Gradient-dependent degradation | Diffusion-limited degradation where the rate decreases as the remaining mass approaches a saturation threshold. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duarte, B.P.M.; Moura, M.J. Unraveling the Degradation Kinetics of Genipin-Cross-Linked Chitosan Hydrogels via Symbolic Regression. Processes 2025, 13, 1981. https://doi.org/10.3390/pr13071981
Duarte BPM, Moura MJ. Unraveling the Degradation Kinetics of Genipin-Cross-Linked Chitosan Hydrogels via Symbolic Regression. Processes. 2025; 13(7):1981. https://doi.org/10.3390/pr13071981
Chicago/Turabian StyleDuarte, Belmiro P. M., and Maria J. Moura. 2025. "Unraveling the Degradation Kinetics of Genipin-Cross-Linked Chitosan Hydrogels via Symbolic Regression" Processes 13, no. 7: 1981. https://doi.org/10.3390/pr13071981
APA StyleDuarte, B. P. M., & Moura, M. J. (2025). Unraveling the Degradation Kinetics of Genipin-Cross-Linked Chitosan Hydrogels via Symbolic Regression. Processes, 13(7), 1981. https://doi.org/10.3390/pr13071981






