Research on Dynamic Calculation Methods for Deflection Tools in Deepwater Shallow Soft Formation Directional Wells
Abstract
1. Introduction
2. Three-Dimensional Finite Element Dynamic Calculation of the Hole-Deflecting Drilling Tool with a Screw Motor
2.1. The Finite Element Method Based on the Euler–Bernoulli Beam Element of the Spatial Rigid Frame
2.2. Calculation of the Coordinate Transformation Matrix Based on the Borehole Trajectory
2.3. Calculation of the Rayleigh Damping Matrix
2.4. Transient Boundary Conditions at the Bottom and Top Ends of the Drill String
3. Calculation of the Reaction Force of the Soft Seabed Formation on the Drilling Tool
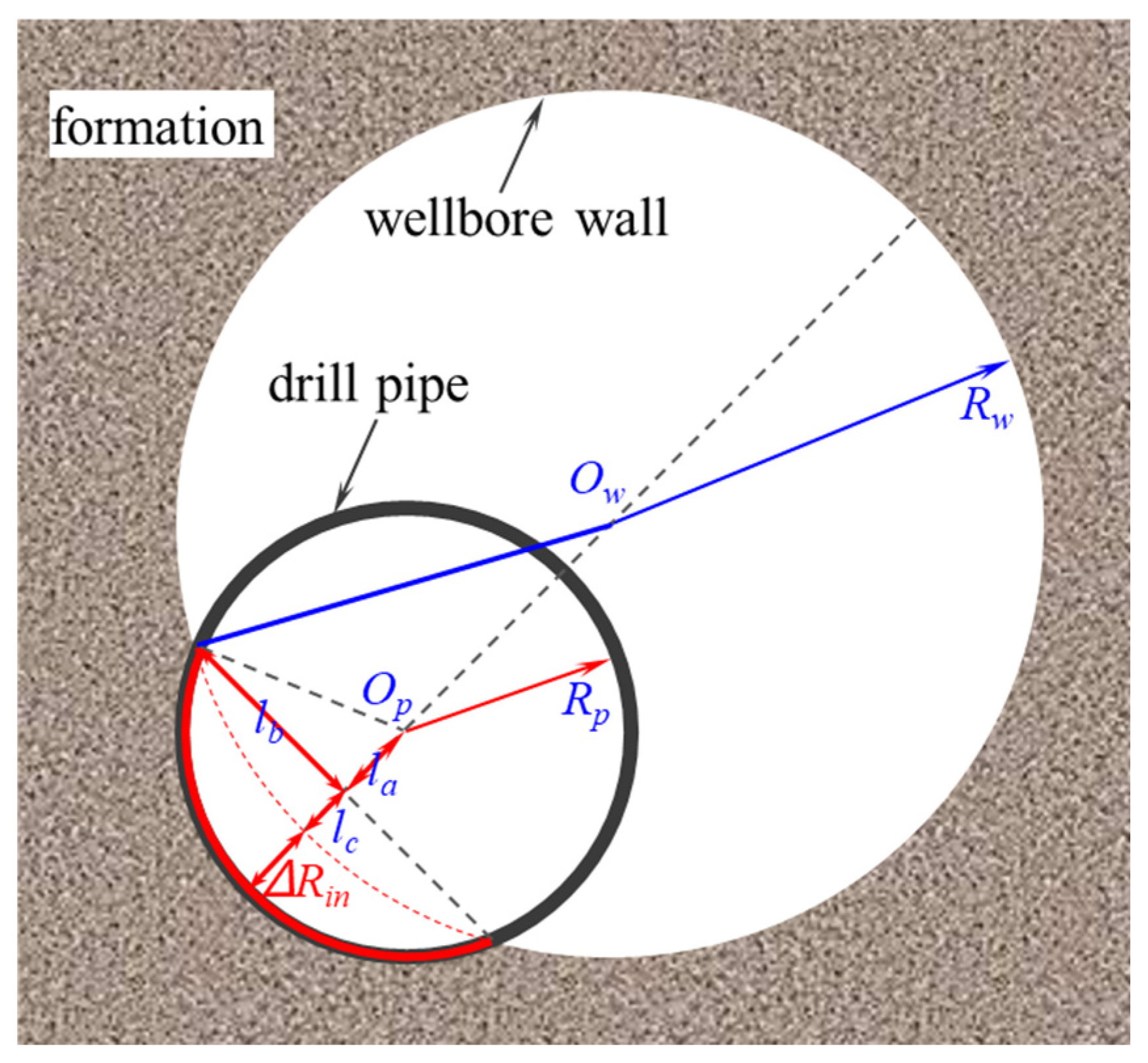
3.1. Calculation Method of Contact, Friction, and Collision Between the Drill String and the Borehole Wall
3.2. Calculation of the Contact Force Between the Drill String and the Plastic Soil Mass Based on the p-y Curve Method
4. Discrete Solution Algorithm for the System of Dynamic Finite Element Equations in the Time Domain
4.1. Optimization of the Transient Dynamics Solution Algorithm
4.2. Optimization of the Solution Algorithm for Large Sparse Systems of Equations
5. Case Calculation and Variable Parameter Analysis
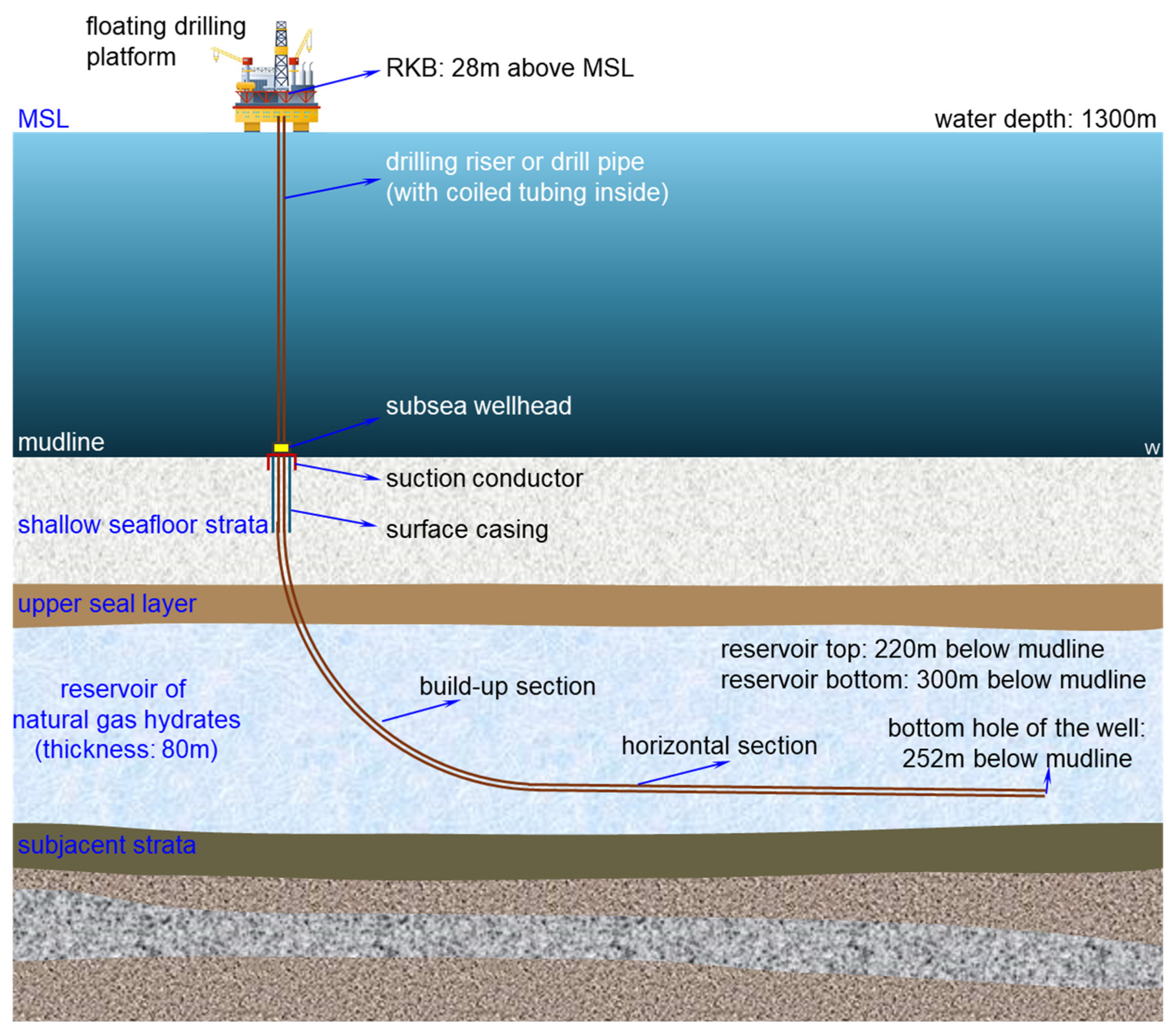
5.1. Case Calculation and Verification
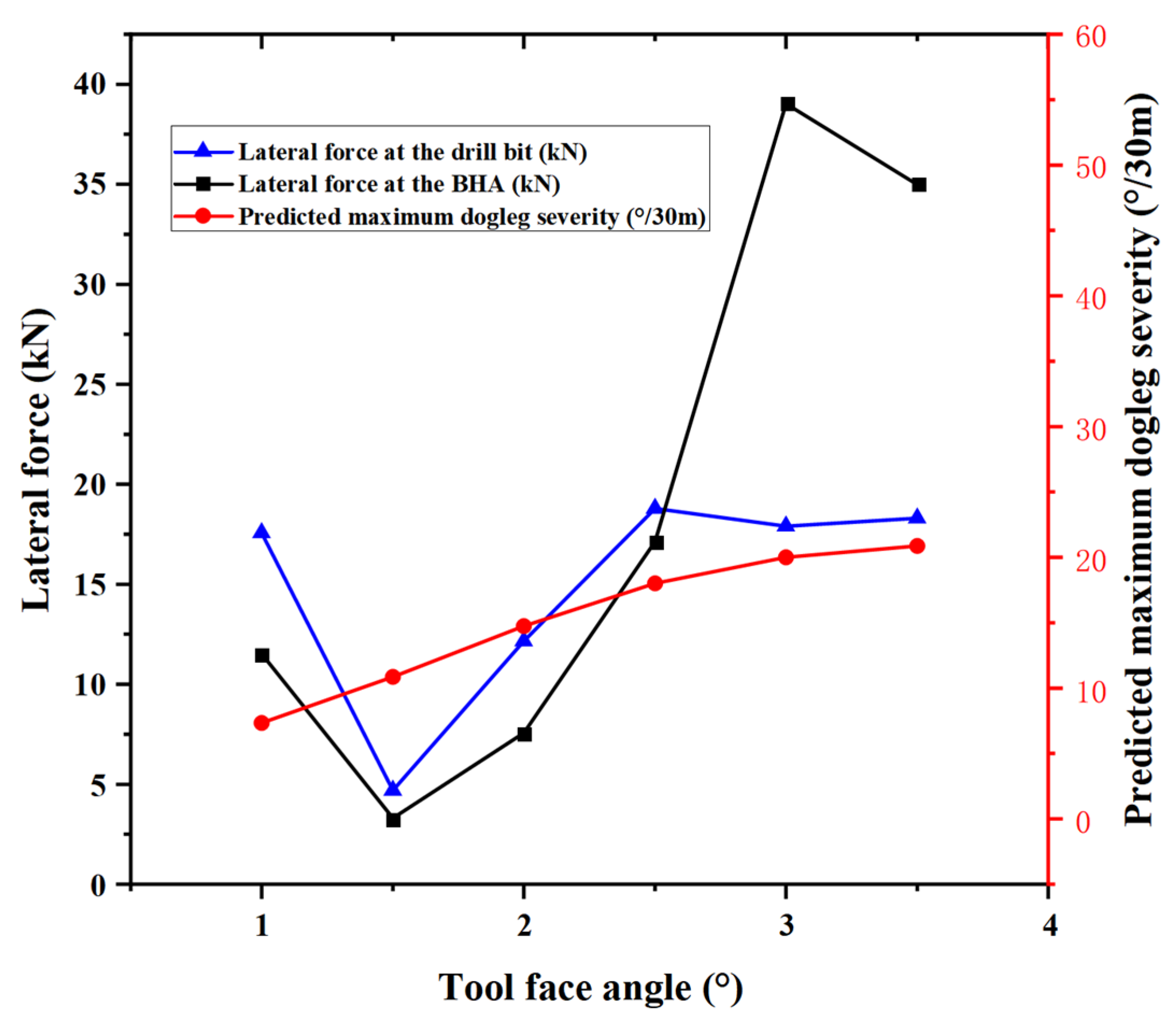
5.2. Influence of the Tool Face Rotation Angle of the Hole-Deflecting Drilling Tool
5.3. Influence of the Properties of the Shallow Seabed Soil Mass
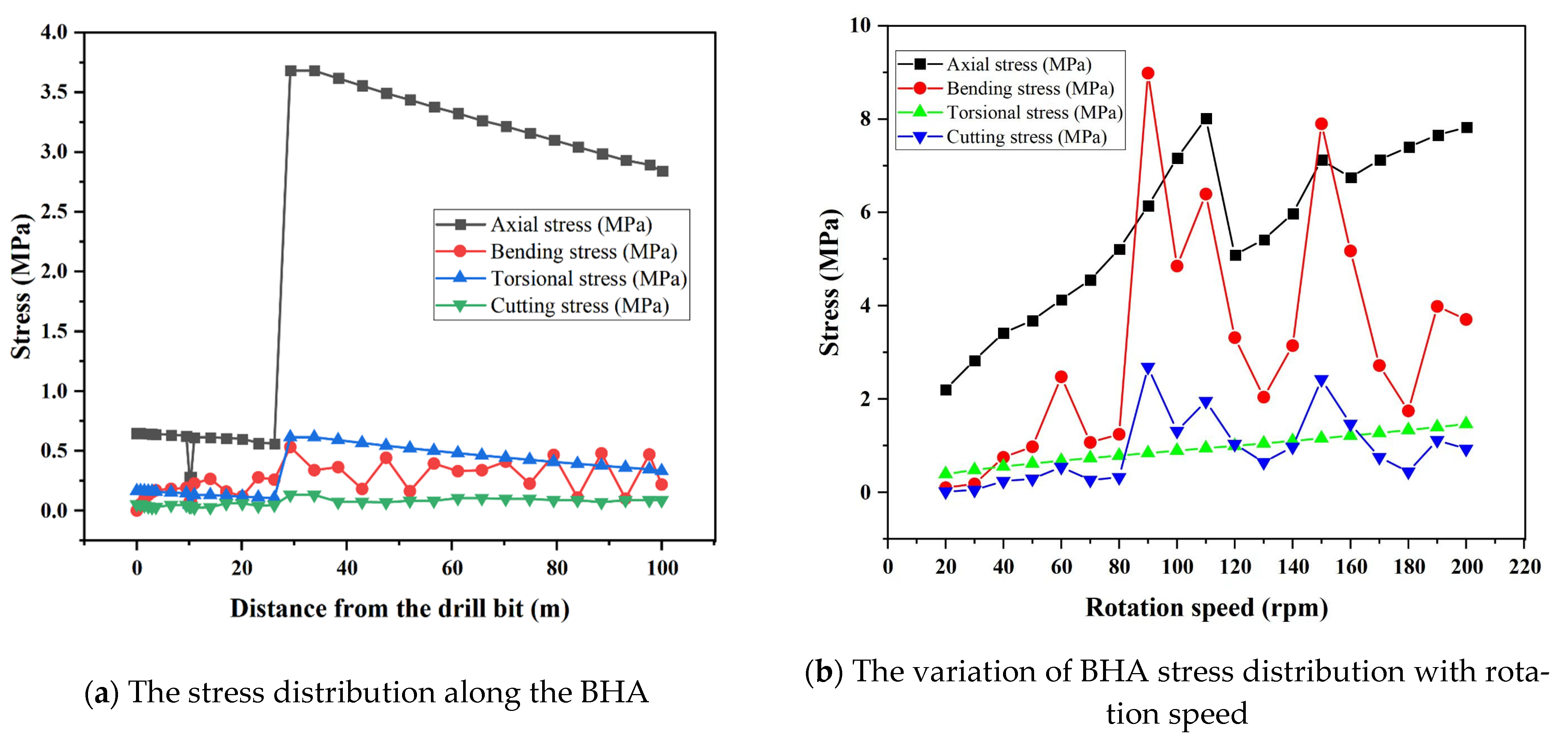
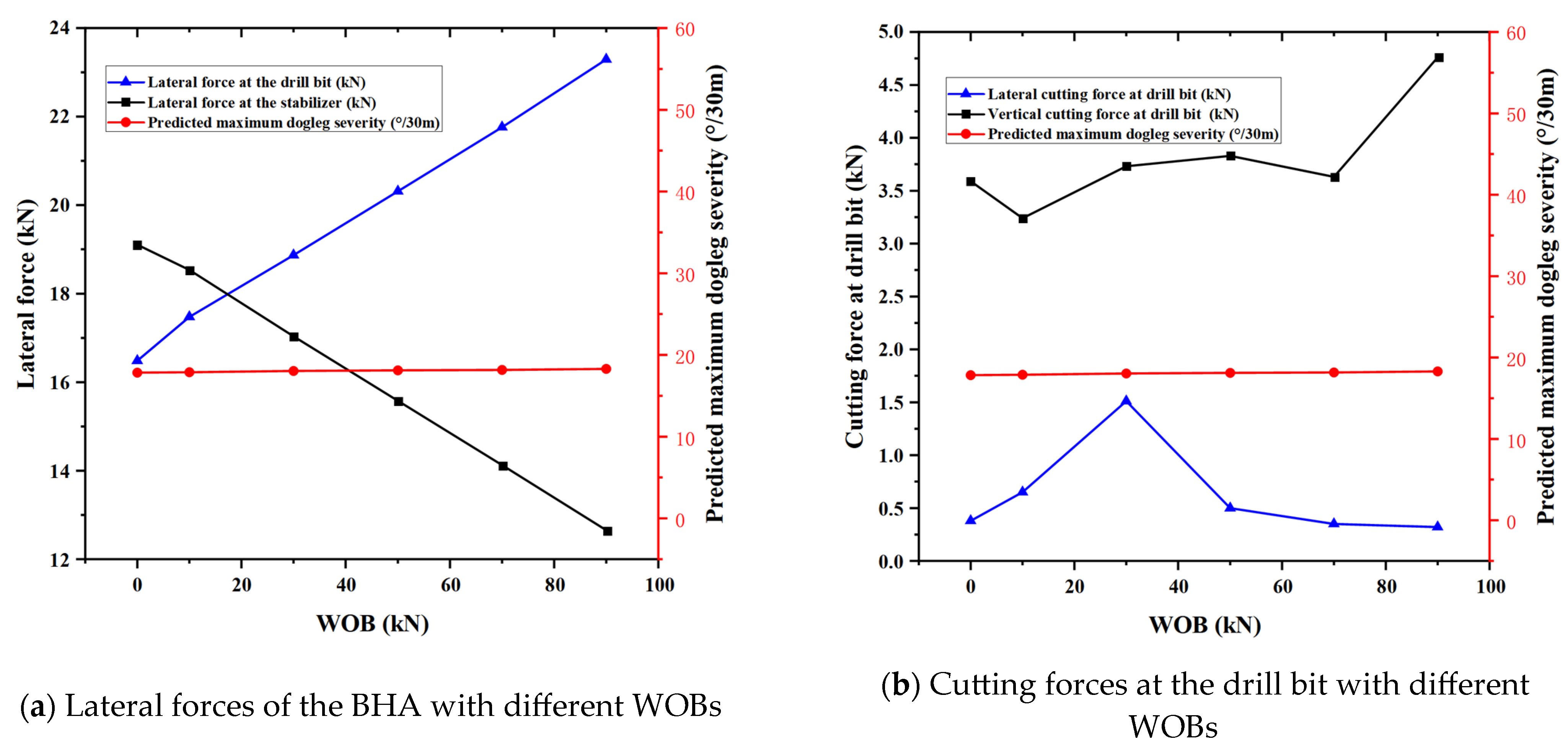
5.4. Analysis of the Effects of WOB and Pump Displacement on the Drilling Tool Assemblies
5.5. Analysis of Model Algorithm Advancements and Limitations
- (1).
- Transient dynamics modeling: This study establishes a transient dynamic computational model for deflection tools driven by positive displacement motors (PDMs). The model employs a spatial frame finite element formulation based on Euler–Bernoulli beam theory, simultaneously characterizing deformation and motion across six degrees of freedom (axial, transverse [x,y], and torsional) at each drill string node.
- (2).
- Trajectory-adaptive computation: The methodology meticulously accounts for directional well trajectory effects through three-dimensional coordinate transformations that quantify tool deviation from the wellbore centerline.
- (3).
- Advanced pipe–soil interactions: Incorporating axial/tangential friction, normal contact forces, and collision reactions between the drill string and unconsolidated formation, the model integrates pipe–soil dynamics with a p-y curve methodology. This establishes a geometric correlation between the penetration depth and contact area, significantly enhancing contact force calculation accuracy in soft formations.
- (4).
- Computational optimization: The algorithm implements a temporally discrete dynamic scheme, solving large-scale sparse equation systems via the GMRES method with iLU preconditioning, thereby improving computational efficiency compared to conventional solvers.
- (1).
- Bit motion simplification: The transient displacement of the bit in all directions was modeled solely as a combination of harmonic and random components. Future work should couple the bit’s equations of motion with the BHA dynamics to capture interaction effects.
- (2).
- Formation heterogeneity: Shallow subsea strata typically comprise interbedded sandy and muddy lithologies, exhibiting increasing strength with depth. For improved accuracy, layer-specific p-y curve analyses should be implemented for distinct geological horizons along the burial depth profile.
- (3).
- Sand liquefaction potential: Continuous vibrations during drilling in water-saturated sandy formations may induce soil liquefaction, significantly reducing lateral support for steerable assemblies. This mechanism warrants dedicated experimental and numerical investigations.
- (4).
- Wellbore irregularities: The effects of borehole wall collapse (“cavings”), washouts, shale creep-induced narrowing, and cuttings beds in horizontal sections were not considered. Subsequent research should quantify the tool–wall contact area and indentation depth in irregular wellbores and develop advanced models for contact force prediction under realistic geometric constraints.
6. Conclusions and Suggestions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| API | American petroleum institute |
| BHA | bottom hole assembly |
| CFD | computational fluid dynamics |
| DOAJ | directory of open access journals |
| DLS | dogleg severity |
| FEM | finite element method |
| GMRES | generalized minimal residual method |
| LD | linear dichroism |
| MDPI | multidisciplinary digital publishing institute |
| MSL | mean sea level |
| ROP | rate of penetration |
| RMS | root-mean-square |
| TLA | three letter acronym |
| WOB | weight on bit |
References
- Sampaio, J.H., Jr. Designing three-dimensional directional well trajectories using Bézier curves. J. Energy Resour. Technol. 2017, 139, 032901. [Google Scholar] [CrossRef]
- Di, Q.F.; Peng, G.R. The study of the influence of well trajectory parameters on side force acting on bit. J. Xi’an Pet. Inst. (Nat. Sci. Ed.) 2000, 15, 20–23. [Google Scholar] [CrossRef]
- Di, Q.F.; Zhu, W.P.; Yao, J.L.; Zou, H. Dynamic model of bottom hole assembly used in pre-bending dynamic vertical and fast drilling technology. Acta Pet. Sin. 2007, 28, 118–121. [Google Scholar] [CrossRef]
- Abbassian, F.; Dunayevsky, V. Application of stability approach to torsional and lateral bit dynamics. SPE Drill. Complet. 1998, 13, 99–107. [Google Scholar] [CrossRef]
- Greenwood, J.A. Directional control and rathole elimination while underreaming depleted formations with a rotary-steerable system. SPE Drill. Complet. 2018, 33, 252–258. [Google Scholar] [CrossRef]
- Epikhin, A.; Zhironkin, V.; Cehlar, M. Prospects for the use of technology of rotary steerable systems for the directional drilling. In Proceedings of the E3S Web of Conferences, Constanta, Romania, 26–27 June 2020; EDP Sciences: Les Ulis, France, 2020; Volume 174, p. 01022. [Google Scholar] [CrossRef]
- Liu, H.S.; Ma, T.S.; Chen, P.; Wang, X.D.; Wang, X.M. Mechanical behaviors of bottom hole assembly with bent-housing positive displacement motor under rotary drilling. Arab. J. Sci. Eng. 2018, 44, 6029–6043. [Google Scholar] [CrossRef]
- Chen, R.; Huang, W.J.; Gao, D.L. Prediction model of build-up rate for bottom-hole assembly in rotary drilling. Geoenergy Sci. Eng. 2025, 246, 213610. [Google Scholar] [CrossRef]
- Yu, T.; Li, X.Y.; Zhang, H.B.; Duan, C.C.; Zeng, H.; Agila, W. Nonlinear analysis of axial-torsional vibration of drill string based on a 3 DOF model. Adv. Mech. Eng. 2022, 14, 1–17. [Google Scholar] [CrossRef]
- Yang, C.X.; Wang, R.H.; Han, L.J.; Xue, Q.L. Dynamic analysis of the longitudinal vibration on bottom drilling tools. J. Vibroeng. 2020, 22, 252–266. [Google Scholar] [CrossRef]
- Mohammad, M.J.; Shiri, H.; Martins, C.A. Numerical investigation of the nonlinear drill string dynamics under stick–slip vibration. Vibration 2024, 7, 1086–1110. [Google Scholar] [CrossRef]
- Guo, Y.C.; Pang, X.Q.; Li, Z.X.; Guo, F.T.; Song, L.C. The critical buoyancy threshold for tight sandstone gas entrapment: Physical simulation, interpretation, and implications to the Upper Paleozoic Ordos Basin. J. Pet. Sci. Eng. 2017, 149, 88–97. [Google Scholar] [CrossRef]
- Li, W.; Huang, G.L.; Ni, H.J.; Yu, F.; Huang, B.; Jiang, W. Experimental study and mechanism analysis of the motion states of bottom hole assembly during rotary drilling. J. Pet. Sci. Eng. 2020, 195, 107859. [Google Scholar] [CrossRef]
- Zhu, X.H.; Li, K.; Li, W.Z. Drill string mechanical behaviors of large-size borehole in the upper section of a 10000 m deep well. Nat. Gas Ind. 2024, 44, 49–57. [Google Scholar] [CrossRef]
- Akgun, F. A finite element model for analyzing horizontal well BHA behavior. J. Pet. Sci. Eng. 2004, 42, 121–132. [Google Scholar] [CrossRef]
- Li, H.; Zhang, P.; Ma, C.; Zhao, J.; Shi, Y.; Jiang, X.B.; Yu, J.S. Optimization of lateral force balance of PDC bits based on ant colony particle swarm hybrid algorithm. Drill. Prod. Technol. 2009, 32, 58–60. [Google Scholar] [CrossRef]
- Wang, Z.B.; Yang, H.Y.; Wang, W.C.; Chen, F.; Di, Q.F. Prediction method of combined guiding force of pre-bent BHA bit based on PSO-SVR algorithm. J. Shanghai Univ. (Nat. Sci. Ed.) 2024, 30, 968–979. [Google Scholar] [CrossRef]
- Oueslati, H.; Jain, R.; Reckmann, H.; Ledgerwood, L.I.; Pessier, R.; Chandrasekaran, S. New insights into drilling dynamics through high-frequency vibration measurement and modeling. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 30 September–2 October 2013; SPE: Richardson, TX, USA, 2013; p. D031S042R001. [Google Scholar] [CrossRef]
- Wang, P.; Tang, B.; Ji, J.Y.; Feng, D. A new method for mechanical calculation of bottom hole assembly in rotary steerable system. Chin. Q. Mech. 2022, 43, 670–680. [Google Scholar] [CrossRef]
- Hai, W.G.; Xue, Q.L.; Wang, M.C.; He, Y.M. Parameter optimization based on deepwater drilling system simulation: A pre-salt exploration well in Brazil. Geoenergy Sci. Eng. 2024, 241, 213120. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, Y.H.; Chen, L.T.; Wang, X.R.; Liu, K.; Sun, B.J. Experimental investigation of the behavior of methane gas hydrates during depressurization-assisted CO2 replacement. J. Nat. Gas Sci. Eng. 2019, 61, 284–292. [Google Scholar] [CrossRef]
- Fang, P.; Yang, K.; Li, G.; Feng, Q.F.; Ding, S.J. Vibration-collision mechanism of dual-stabilizer bottom hole assembly system in vertical wellbore trajectory. J. Vibroeng. 2023, 25, 226–246. [Google Scholar] [CrossRef]
- Gao, D.L.; Wang, Y.B. Some research progress in deepwater drilling mechanics and control technology. Acta Pet. Sin. 2019, 40, 102. [Google Scholar] [CrossRef]
- Chen, W.; Shen, Y.L.; Chen, R.B.; Zhang, Z.X.; Rawlins, S. Simulating drill-string post-buckling state and weight transfer with advanced transient dynamics model. In Proceedings of the IADC/SPE International Drilling Conference and Exhibition, Galveston, TX, USA, 3–5 March 2020. SPE-199557-MS. [Google Scholar] [CrossRef]
- American Petroleum Institute. Planning, Designing, and Constructing Fixed Offshore Platforms-Working Stress Design, 22nd Edition. API. 2020, API RP 2A-WSD-2014(2020). Available online: https://www.intertekinform.com/en-au/standards/api-rp-2a-wsd-2014-r2020--98372_saig_api_api_2925841/?srsltid=AfmBOor1dn_YM_Y41tASmJ837JcNAD22Uz4xOwp3Psa1TT2Xz-G4oejo (accessed on 16 June 2025).
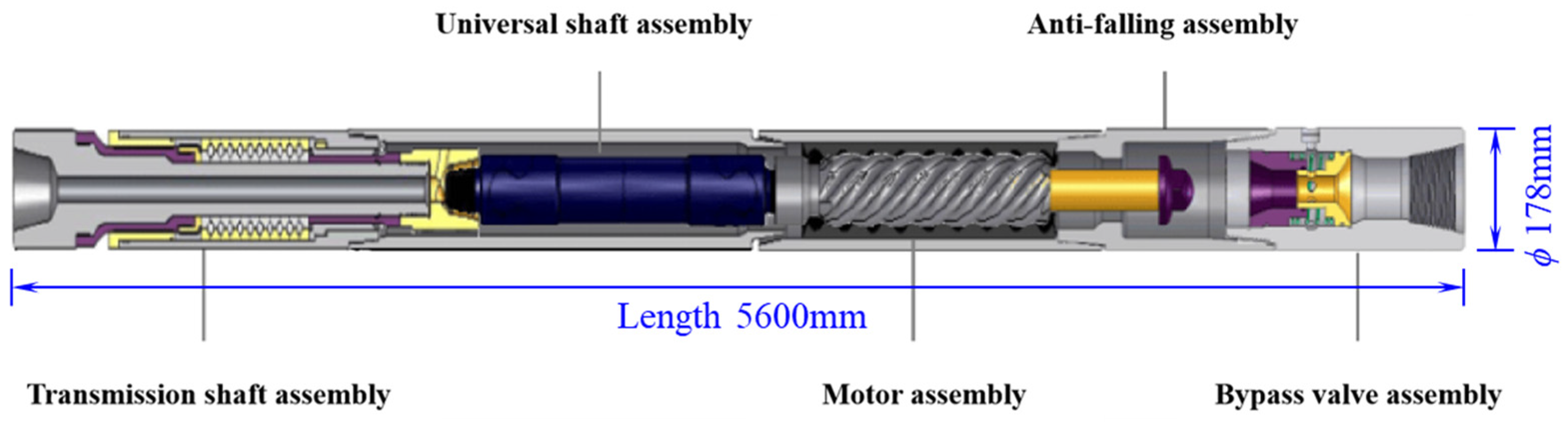
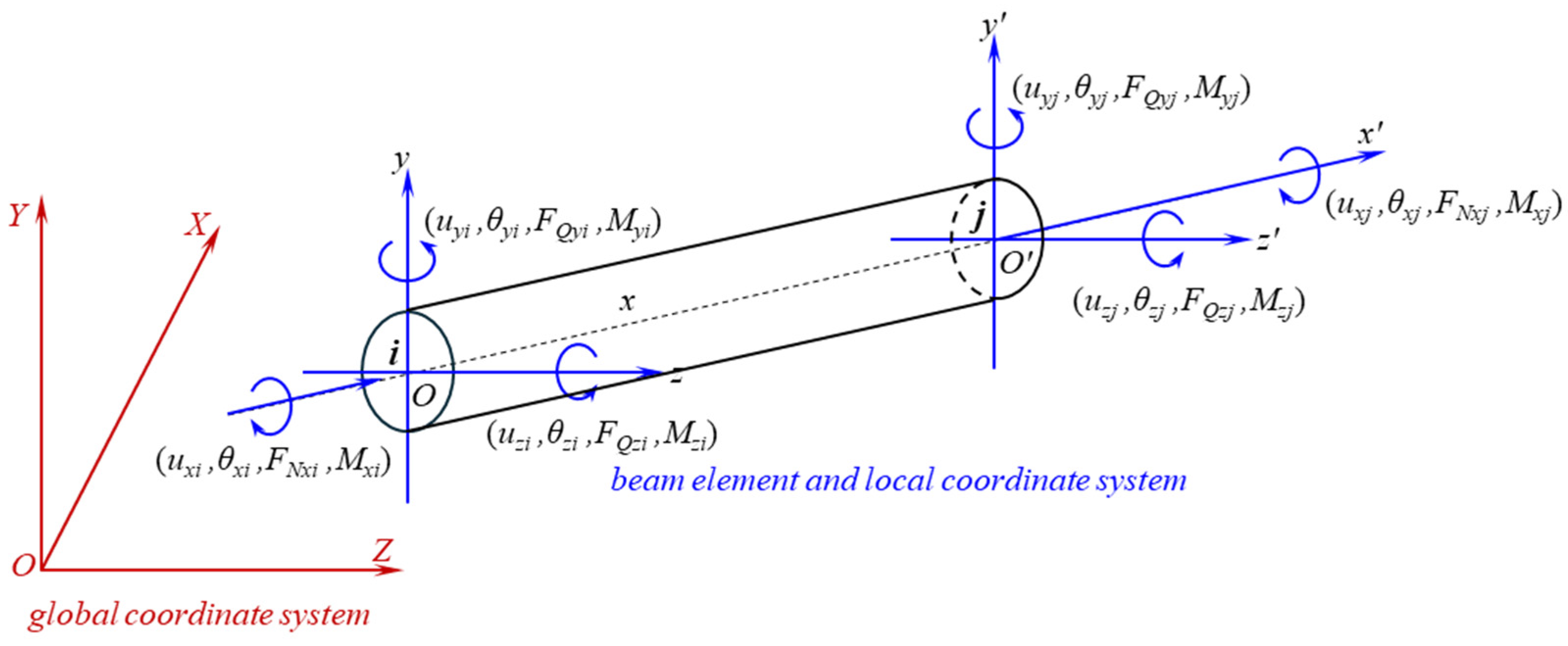
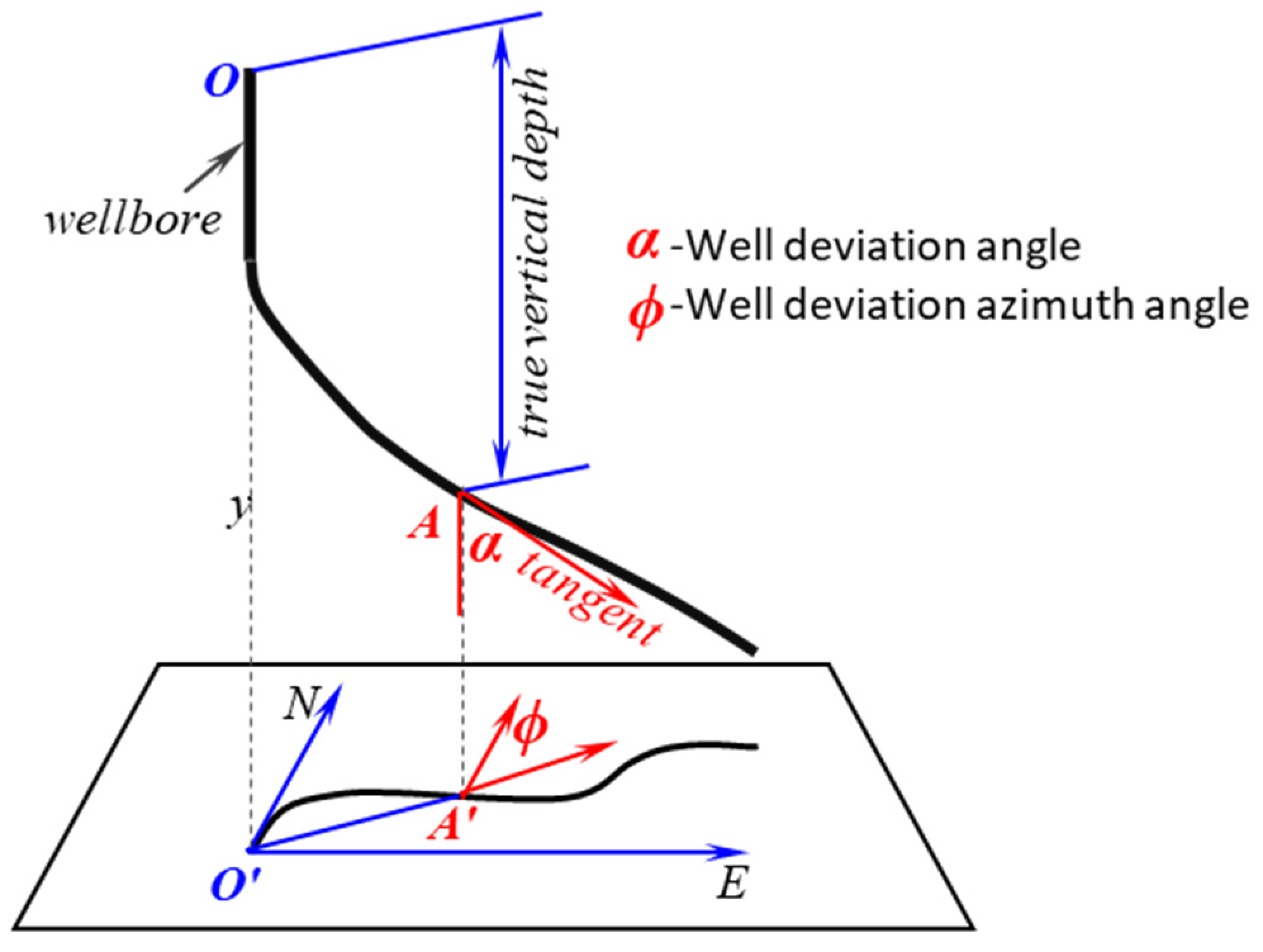
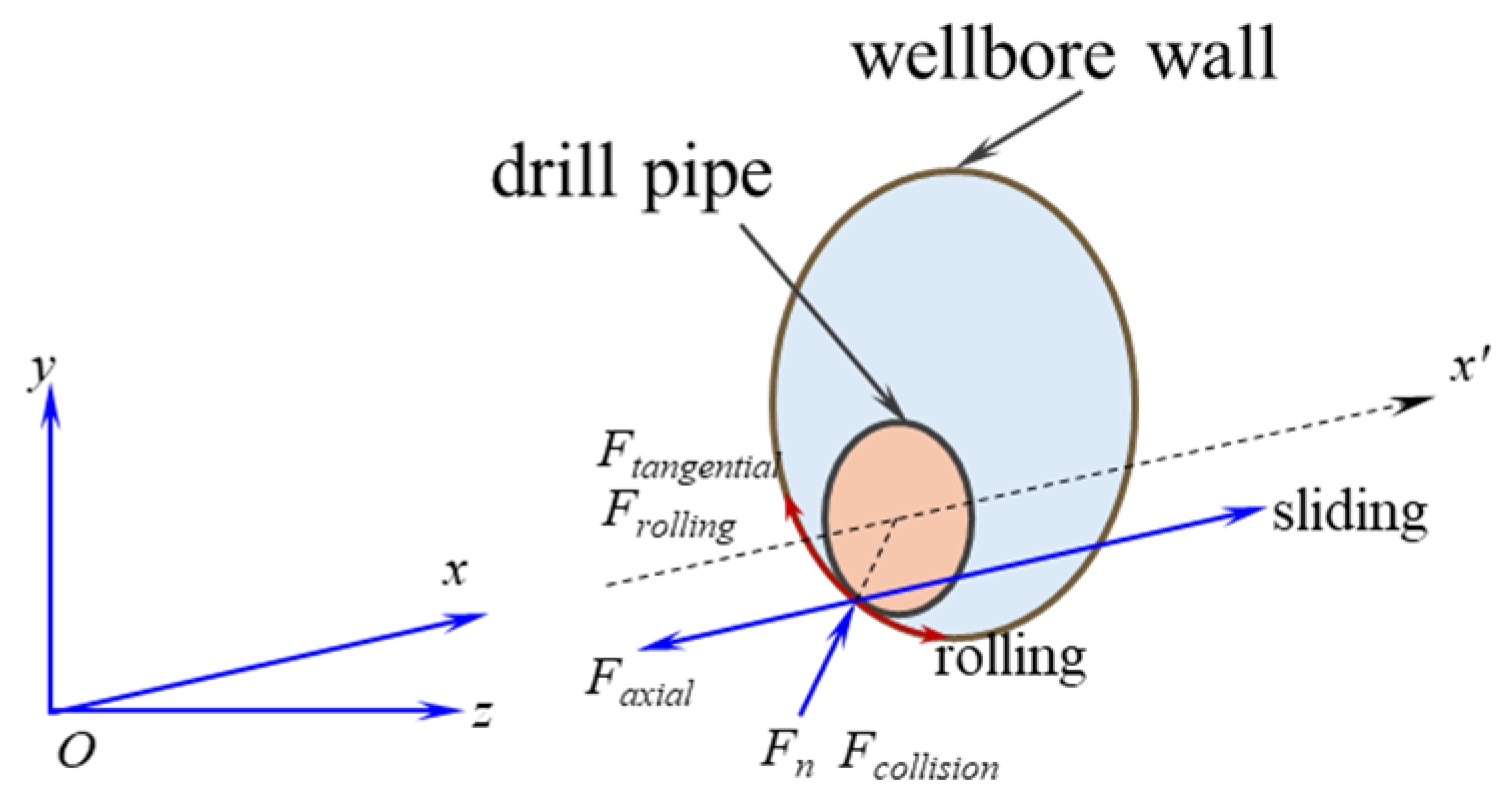


| Authors, Year | Models and Algorithms | Model Advantages | Model Limitations and Constraints |
|---|---|---|---|
| Di, Q.F.; Zhu, W.P.; Yao, J.L.; 2007 [3] | Pre-bent BHA dynamic model | Proposed a “dynamic centralization” mechanism to reduce well deviation by optimizing tool bending, suitable for vertical drilling trajectory control. | Did not consider the impact of high temperature on tool material properties, limiting the model’s applicable temperature range. |
| Greenwood, J.A.; 2018 [5] | Rotary steerable system (RSS) directional control model | Integrated RSS and underreaming technology to improve trajectory control accuracy and dynamic response in depleted formations. | Relied on specific formation mechanical parameters, prone to trajectory loss in water-sensitive mudstone/shale formations due to wellbore shrinkage. |
| Chen, R.; Huang, W.J.; Gao, D.L.; 2025 [8] | Multi-source data fusion BUR prediction model | Coupled formation anisotropy with whirling effects, reducing build-up rate prediction error from 15% to within 5%. | Ignored the strong coupling between hydraulic parameters and vibration, leading to accuracy degradation under high pump pressure. |
| Wang, Z.B.; Yang, H.Y.; Wang, W.C.; 2024 [17] | PSO-SVR algorithm for bit guiding force prediction | Achieved rapid guiding force prediction via machine learning, reducing manual intervention. | Relied on extensive drilling data training, with prediction errors exceeding 10% in new exploration areas. |
| Oueslati, H;, Jain, R.; Reckmann, H.; 2013 [18] | CFD-FEM coupled fluid-Structure interaction model | Revealed the influence of drilling fluid flow velocity on BHA vibration. | Did not consider the induction mechanism of flow field turbulence on vortex-induced vibration, with critical velocity prediction deviations of ±20%. |
| Wang, P.; Tang, B.; Ji, J.Y.; 2022 [19] | Mechanical solution method based on tubular element combination | Improved computational reliability in complex wellbores by optimizing contact variable handling. | Did not validate the interference of large slenderness ratio drill string flexible deformation on contact location identification, potentially leading to boundary condition misjudgment. |
| Fang, P.; Yang, K.; Li, G., 2023 [22] | Vibration–collision coupling model for dual-stabilizer BHA in soft formations | Quantified the influence of contact force amplitude and collision frequency on well deviation, providing theoretical support for lateral vibration analysis. | Did not quantify the impact of drilling fluid density on collision energy transfer. |
| Gao, D.L.; Wang, Y.B.; 2019 [23] | “3D dynamic beam-formation contact” model | Introduced formation reaction force matrix to improve prediction accuracy of drill string–formation contact behavior in extended-reach wells. | Did not distinguish contact stiffness differences between soft formations, with significant reaction force calculation deviations in high-porosity formations. |
| Chen, W.; Shen, Y.L.; Chen, R.B.; 2020 [24] | Transient dynamics model for drill string buckling and post-buckling | Considered large deformation contact friction nonlinearity, suitable for weight transfer analysis in shallow soft formations. | Did not modify contact parameters for shear strength differences in various soft formations, lacking model universality. |
| Measured Depth (m) | Well Inclination Angle (°) | Well Inclination Azimuth (°) | True Vertical Depth (m) | Visual Translation (m) |
|---|---|---|---|---|
| 1400 | 0 | 0 | 1400 | 0 |
| 1402.08 | 0.74 | 0 | 1402.08 | 0.01 |
| 1432.56 | 11.66 | 0 | 1432.34 | 3.3 |
| 1463.04 | 22.57 | 0 | 1461.42 | 12.26 |
| 1493.52 | 33.49 | 0 | 1488.29 | 26.56 |
| 1524 | 44.4 | 0 | 1511.95 | 45.69 |
| 1554.48 | 55.32 | 0 | 1531.57 | 68.96 |
| 1584.96 | 66.23 | 0 | 1546.43 | 95.52 |
| 1615.44 | 77.15 | 0 | 1555.99 | 124.41 |
| 1645.92 | 88.06 | 0 | 1559.91 | 154.59 |
| 1651.327 | 90 | 0 | 1560 | 160 |
| No. | Single Name | Quantity | Single Length (m) | Single Wire Weight (kg/m) | Body Outer Diameter (m) | Body Inner Diameter (m) |
|---|---|---|---|---|---|---|
| 1 | 5-1/2″DP | -- | 9.144 | 35.37 | 0.1397 | 0.1213 |
| 2 | 5-1/2″HWDP | 14 | 9.144 | 39.18 | 0.1397 | 0.1186 |
| 3 | 8″NMDC | 1 | 9.144 | 227.33 | 0.2032 | 0.0714 |
| 4 | 8″MWD | 1 | 9.144 | 212.55 | 0.2032 | 0.08255 |
| 5 | 11-1/2″Armature | 1 | 1.524 | 212.56 | 0.28575 | 0.08255 |
| 6 | 8″Screw Motor Drill Tool | 1 | 9.144 | 212.56 | 0.2032 | 0.08255 |
| 7 | 12-1/4″Drill Bit | 1 | 0.305 | 397.34 | 0.31115 | eq0.01905 |
| No. | Soil or Rock Types | Modulus of Elasticity (MPa) | Poisson’s Ratio |
|---|---|---|---|
| 1 | Saturated Soft Clay | 2~5 | 0.50 |
| 2 | Hard Clay | 7~18 | 0.35 |
| 3 | Sandy Clay | 30~40 | 0.20~0.25 |
| 4 | Loose Sand | 10~25 | 0.20~0.25 |
| 5 | Compact Sand | 50~100 | 0.15~0.25 |
| 6 | Pink Sandy Mudstone | (5~15) × 103 | 0.25~0.35 |
| 7 | Rocky Sandstone | (10~30) × 103 | 0.20~0.30 |
| 8 | Fine Sandstone | (2.79~4.76) × 104 | 0.15~0.52 |
| 9 | Coarse Sandstone | (1.66~4.03) × 104 | 0.10~0.45 |
| 10 | Shale | (1.25~4.12) × 104 | 0.09~0.35 |
| Tool Face Angle (°) | 1 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
|---|---|---|---|---|---|---|
| Maximum stress (bending stress) (MPa) | 1.64 | 1.64 | 1.64 | 1.64 | 1.64 | 1.64 |
| Lateral cutting force at the drill bit (kN) | 1.57 | 1.57 | 1.57 | 1.57 | 1.57 | 1.57 |
| Vertical cutting force at the drill bit (kN) | 3.45 | 3.45 | 3.75 | 3.75 | 3.75 | 3.75 |
| Lateral force at the drill bit (kN) | 17.576 | 4.693 | 12.152 | 18.788 | 17.905 | 18.306 |
| Lateral force at the BHA (kN) | 11.522 | 3.301 | 7.573 | 17.128 | 39.029 | 34.981 |
| Predicted maximum degree of dogleg (°/30 m) | 7.343 | 10.863 | 14.749 | 18.024 | 19.997 | 20.863 |
| Soil Property Parameters | Modulus of Elasticity (MPa) | 10 | 100 | 1000 | 5000 | 10,000 | 50,000 |
|---|---|---|---|---|---|---|---|
| Poisson’s Ratio | 0.50 | 0.30 | 0.30 | 0.30 | 0.30 | 0.30 | |
| Maximum stress (bending stress) (MPa) | 1.64 | 1.64 | 1.64 | 1.64 | 1.64 | 1.64 | |
| Lateral maximum cutting force (kN) | 2.04 | 2.04 | 2.04 | 2.04 | 2.04 | 2.04 | |
| Vertical maximum cutting force (kN) | 4.17 | 4.17 | 4.17 | 4.17 | 4.17 | 4.17 | |
| Lateral force at the drill bit (kN) | 18.788 | 18.788 | 18.788 | 18.788 | 18.788 | 18.788 | |
| Lateral force at the stabilizer (kN) | 17.128 | 17.128 | 17.128 | 17.128 | 17.128 | 17.128 | |
| Predicted maximum dogleg (°/30 m) | 18.024 | 18.024 | 18.024 | 18.024 | 18.024 | 18.024 | |
| WOB (kN) | 0 | 10 | 30 | 50 | 70 | 90 |
|---|---|---|---|---|---|---|
| Maximum stress (bending stress) (MPa) | 1.09 | 2.16 | 1.76 | 1.00 | 2.05 | 1.44 |
| Lateral cutting force at drill bit (kN) | 0.38 | 0.65 | 1.51 | 0.50 | 0.35 | 0.32 |
| Vertical cutting force at drill bit (kN) | 3.59 | 3.24 | 3.73 | 3.83 | 3.63 | 4.76 |
| Lateral force at drill bit (kN) | 16.485 | 17.474 | 18.869 | 20.312 | 21.760 | 23.291 |
| Lateral force at the stabilizer (kN) | 19.108 | 18.537 | 17.034 | 15.578 | 14.127 | 12.656 |
| Predicted maximum degree of dogleg (°/30 m) | 17.824 | 17.873 | 18.035 | 18.104 | 18.164 | 18.292 |
| Pump Displacement (m3/min) | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 | 4.2 |
|---|---|---|---|---|---|---|
| Maximum stress (bending stress) (MPa) | 1.98 | 2.05 | 1.64 | 1.76 | 1.69 | 1.47 |
| Lateral cutting force at drill bit (kN) | 1.38 | 1.49 | 1.57 | 1.51 | 1.23 | 0.86 |
| Vertical cutting force at drill bit (kN) | 3.66 | 3.67 | 3.75 | 3.73 | 3.74 | 3.76 |
| Lateral force at drill bit (kN) | 18.640 | 18.712 | 18.788 | 18.869 | 18.953 | 19.052 |
| Lateral force at the stabilizer (kN) | 17.302 | 17.218 | 17.128 | 17.034 | 16.934 | 16.843 |
| Predicted maximum degree of dogleg (°/30 m) | 18.004 | 18.014 | 18.024 | 18.035 | 18.048 | 18.077 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Chen, Y.; Hao, X.; Deng, S.; Li, C. Research on Dynamic Calculation Methods for Deflection Tools in Deepwater Shallow Soft Formation Directional Wells. Processes 2025, 13, 1947. https://doi.org/10.3390/pr13061947
He Y, Chen Y, Hao X, Deng S, Li C. Research on Dynamic Calculation Methods for Deflection Tools in Deepwater Shallow Soft Formation Directional Wells. Processes. 2025; 13(6):1947. https://doi.org/10.3390/pr13061947
Chicago/Turabian StyleHe, Yufa, Yu Chen, Xining Hao, Song Deng, and Chaowei Li. 2025. "Research on Dynamic Calculation Methods for Deflection Tools in Deepwater Shallow Soft Formation Directional Wells" Processes 13, no. 6: 1947. https://doi.org/10.3390/pr13061947
APA StyleHe, Y., Chen, Y., Hao, X., Deng, S., & Li, C. (2025). Research on Dynamic Calculation Methods for Deflection Tools in Deepwater Shallow Soft Formation Directional Wells. Processes, 13(6), 1947. https://doi.org/10.3390/pr13061947







