Multifractal Characterization of Full-Scale Pore Structure in Middle-High-Rank Coal Reservoirs: Implications for Permeability Modeling in Western Guizhou–Eastern Yunnan Basin
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Collection and Preparation
2.2. Full-Scale Pore Structure Characterization
2.3. Multifractal Parameter Calculations
2.3.1. Single-Fractal Analysis Based on MIP
2.3.2. Multifractal Analysis
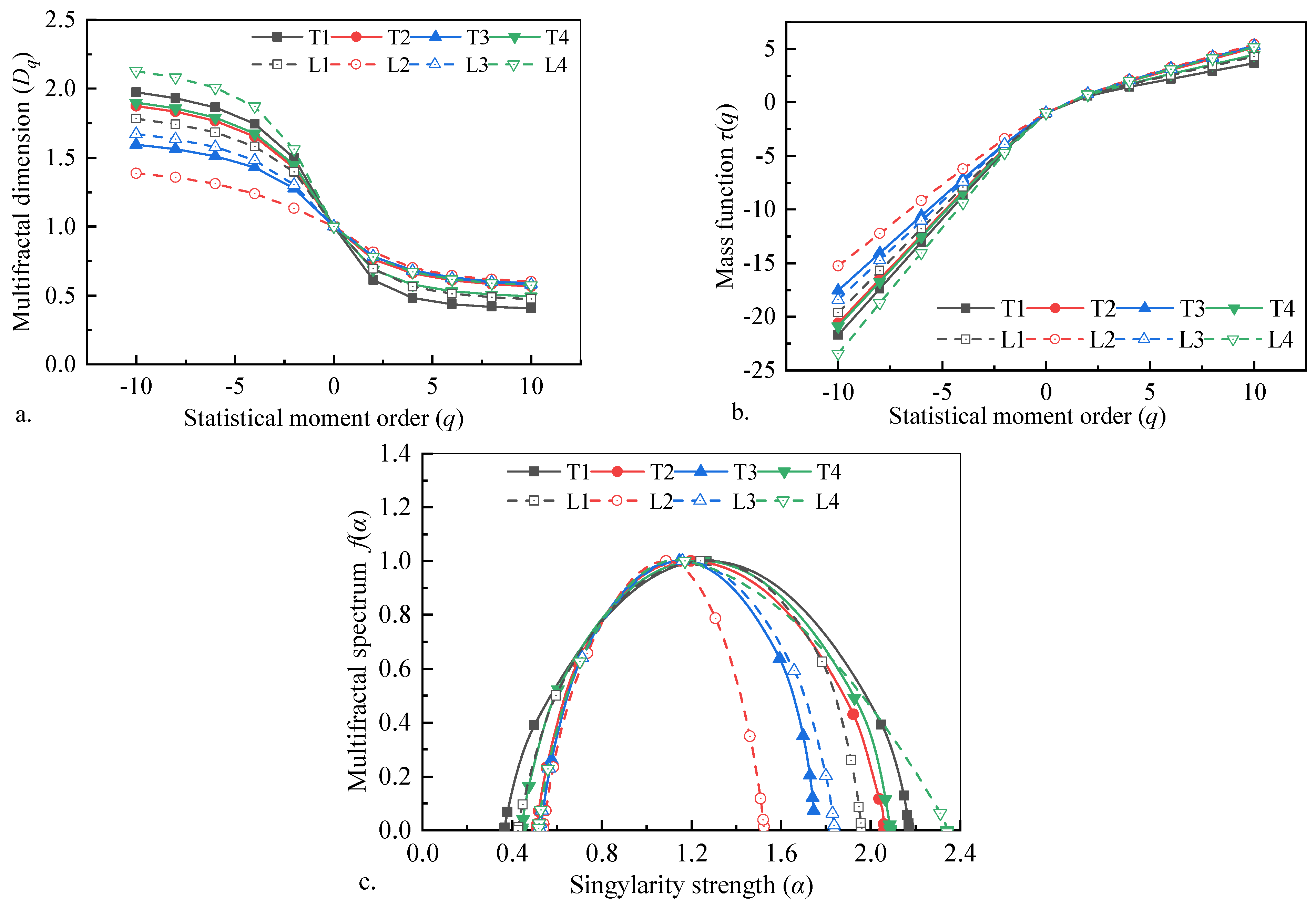
3. Results and Discussion
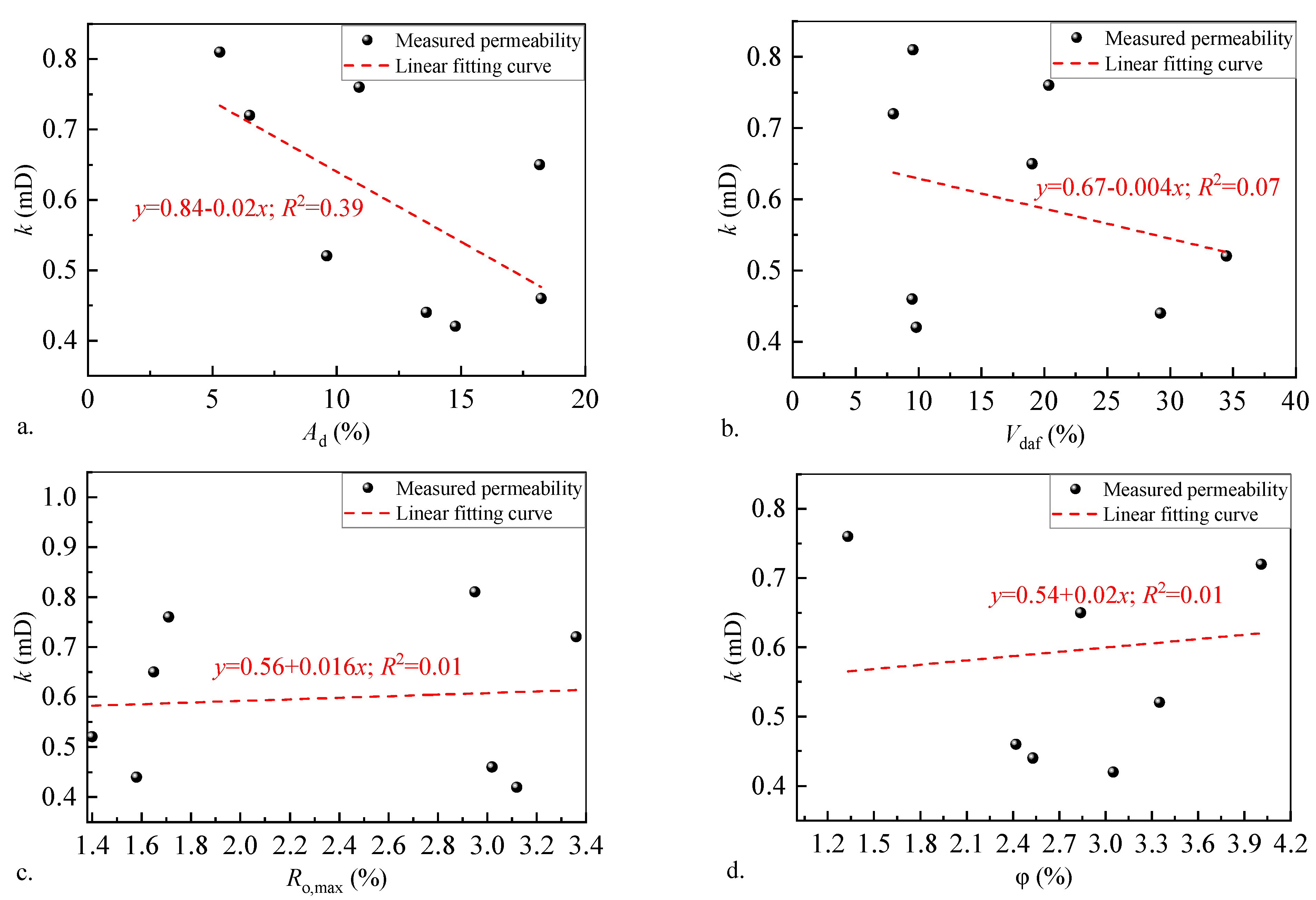
3.1. Conventional Petrophysical Properties and Permeability of Reservoirs
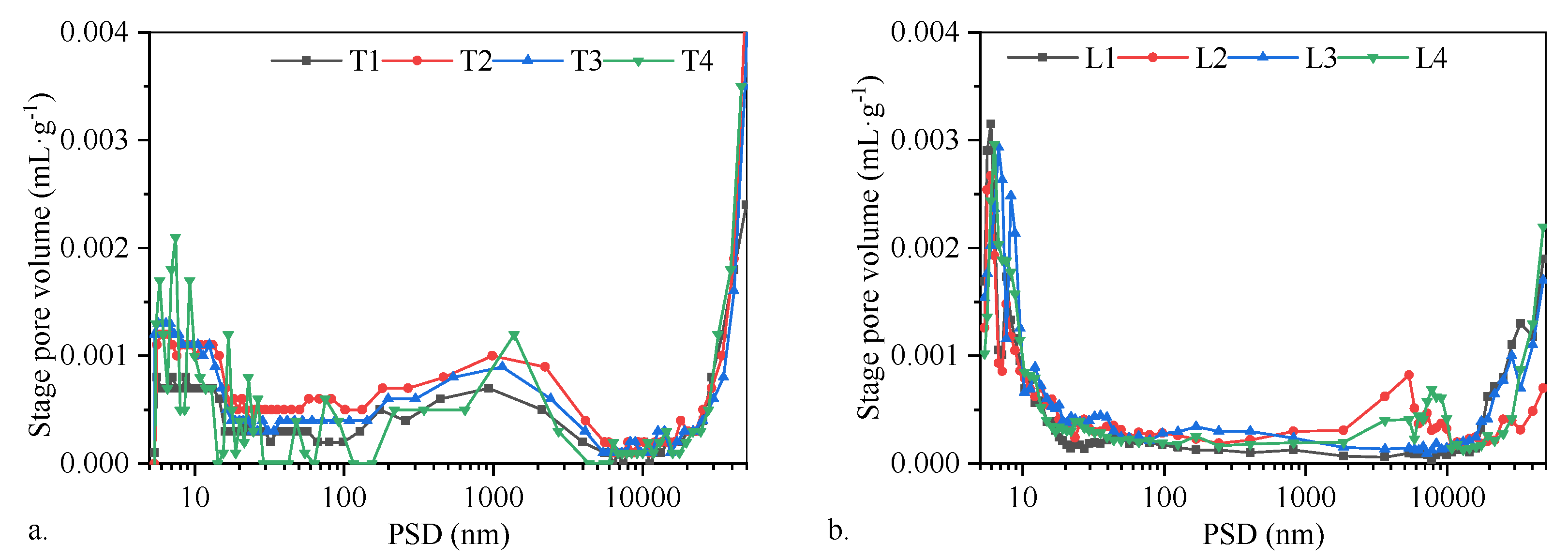
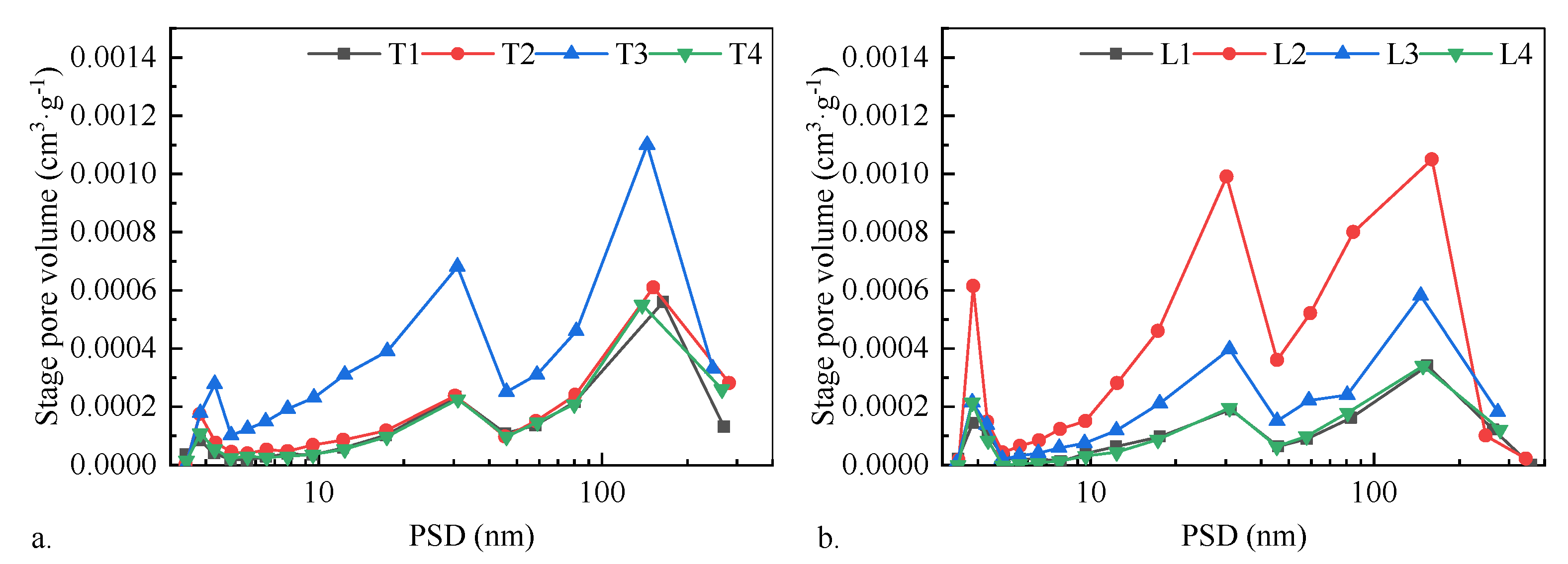
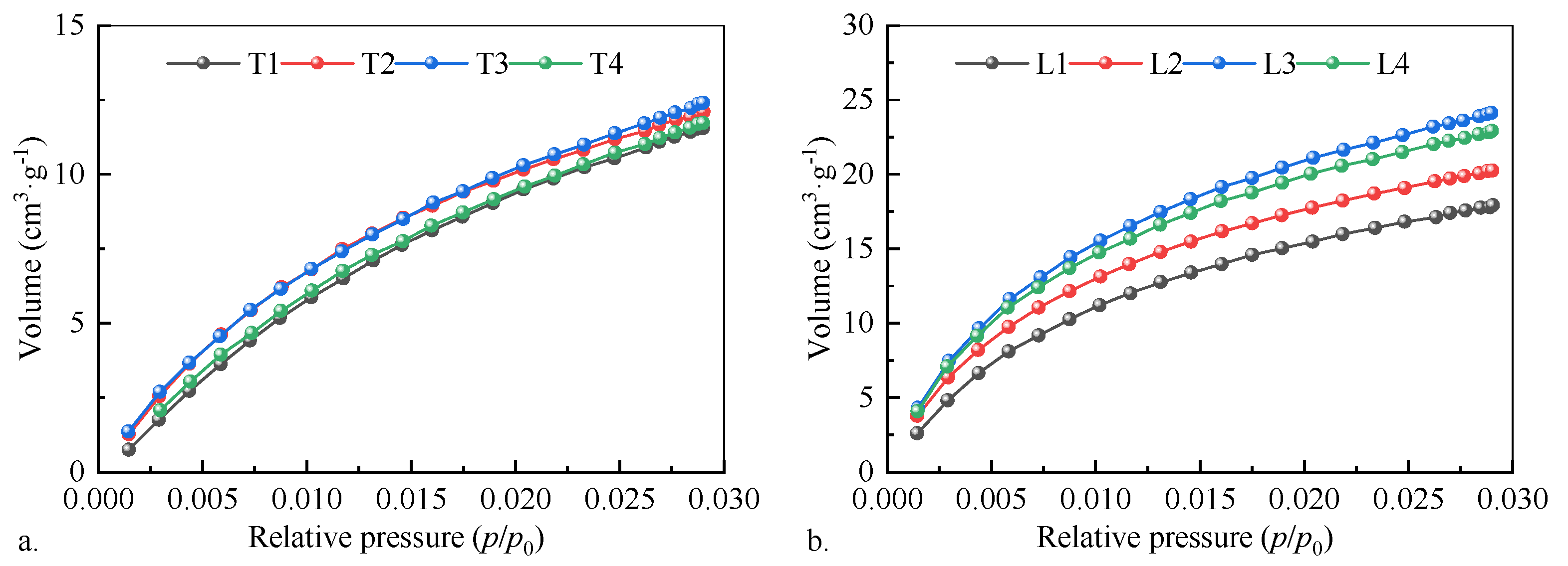
3.2. Characteristics of Pore Distribution
3.3. Full-Scale Pore Size Distribution and Fractal Spectrum Characteristics
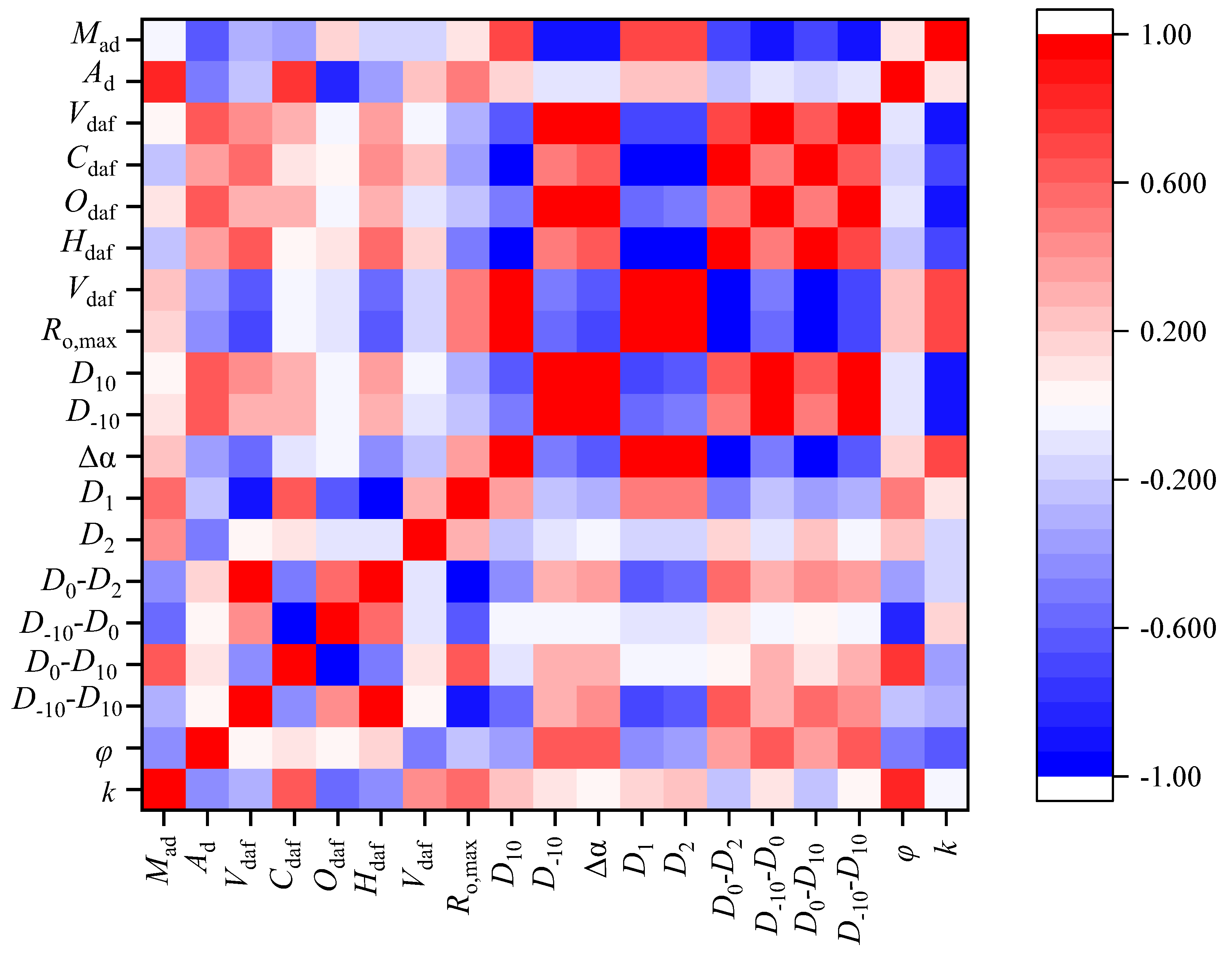
3.4. Development of Permeability Prediction Model
4. Conclusions
- (1)
- Weak correlations (R2 < 0.39) between ash yield, volatile matter, porosity, and permeability confirm that conventional parameters fail to capture flow dynamics in heterogeneous coals in study area. Counterintuitive permeability–porosity relationships underscore the necessity of pore-scale characterization.
- (2)
- Laochang’s high-rank coals (Ro,max = 2.95–3.36%) exhibit microporous dominance (0.45–0.55 nm; CO2 adsorption = 17.90–24.11 cm3·g−1) and ink-bottle pore reduction (H3-type hysteresis), favoring adsorption but limiting seepage. Tucheng’s mid-rank coals (Ro,max = 1.40–1.71%) feature tri-modal pore distributions with robust seepage networks (100–5000 nm; 0.00385 cm3·g−1 stage volumes), enhancing permeability despite lower maturity.
- (3)
- Multifractal spectra (Δα = 0.98−1.82) quantify structural complexity, with Laochang’s uniform pores (D1 = 0.863) contrasting Tucheng’s heterogeneous networks (D1 = 0.821). The singularity width Δα emerged as the prime permeability regulator (R = −0.93), where increased heterogeneity elevates flow tortuosity by 34–68% in high-Δα samples.
- (4)
- The multifractal-derived permeability model (R2 = 0.91) reconciles pore throat geometry (D10) and structural disorder (Δα), demonstrating the following: Permeability declines 0.82 mD per unit Δα increase due to flow-path occlusion. Throat size enlargement (D10 > 0.58) enhances permeability by 0.68 mD/unit, offsetting heterogeneity effects.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Q.; Zhao, D.; Yin, J.; Zhou, X.; Li, Y.; Chi, P.; Han, Y.; Ansari, U.; Cheng, Y. Sediment instability caused by gas production from hydrate-bearing sediment in Northern South China Sea by horizontal wellbore: Evolution and mechanism. Nat. Resour. Res. 2023, 32, 1595–1620. [Google Scholar] [CrossRef]
- Ma, Z.; Tao, S.; Gao, L.; Cui, Y.; Jing, Q.; Chen, S.; He, W.; Guo, J.; Hai, L. Detailed characterization of microscopic pore structure in low-rank coal: A case study of zhalainuoer coalfield. Nat. Resour. Res. 2024, 33, 2261–2277. [Google Scholar] [CrossRef]
- Quan, F.; Wei, C.; Li, R.; Hao, S.; Zhang, J.; Song, Y.; Yan, G. Reservoir Damage in Coalbed Methane Commingled Drainage Wells and its Fatal Impact on Well Recovery. Nat. Resour. Res. 2023, 32, 295–319. [Google Scholar] [CrossRef]
- Li, G.; Qin, Y.; Wang, B.; Zhang, M.; Lin, Y.; Song, X.; Mi, W. Fluid seepage mechanism and permeability prediction model of multi-seam interbed coal measures. Fuel 2024, 356, 129556. [Google Scholar] [CrossRef]
- Li, Z.; Yu, H.; Bai, Y.; Wang, Y.; Hu, H.; Gao, Y.; Yan, F. Analysis of reservoir permeability evolution and influencing factors during CO2-Enhanced coalbed methane recovery. Energy 2024, 304, 132045. [Google Scholar] [CrossRef]
- Tao, S.; Chen, S.; Pan, Z. Current status, challenges, and policy suggestions for coalbed methane industry development in China: A review. Energy Sci. Eng. 2019, 7, 1059–1074. [Google Scholar] [CrossRef]
- Kang, J.; Fu, X.; Elsworth, D.; Liang, S. Vertical Heterogeneity of Permeability and Gas Content of Ultra-High-Thickness Coalbed Methane Reservoirs in the Southern Margin of the Junggar Basin and its Influence on Gas Production. J. Nat. Gas Sci. Eng. 2020, 81, 103455. [Google Scholar] [CrossRef]
- Zhang, Z.; Gong, F.; Zou, G.; Zhu, G.; Liu, W.; Chen, H. Prediction of anisotropic coalbed methane reservoir brittleness index based on rock physics modelling. Geophys. Prospect. 2025, 73, 1488–1509. [Google Scholar] [CrossRef]
- Liu, G.; Tang, R.; Mu, C.; Liu, X.; Zhang, J. Physical Properties of High-Rank Coal Reservoirs and the Impact on Coalbed Methane Production. Processes 2024, 12, 1754. [Google Scholar] [CrossRef]
- Yao, P.; Zhang, J.; Lv, D.; Vandeginste, V.; Chang, X.; Zhang, X.; Wang, D.; Han, S.; Liu, Y. Effect of water occurrence in coal reservoirs on the production capacity of coalbed methane by using NMR simulation technology and production capacity simulation. Geoenergy Sci. Eng. 2024, 243, 213353. [Google Scholar] [CrossRef]
- Guo, C.; Li, R.; Qin, Y.; Lu, L.; Yi, T.; Chen, Z.; Yuan, H.; Gao, W.; Cheng, X. Evolution path of water produced from coalbed methane wells and its significance in judging productivity: A case study of Zhijin block in western Guizhou Province. Acta Pet. Sin. 2024, 45, 517. [Google Scholar]
- Zhang, B.; Wang, G.; Li, W.; Jiao, X. Characteristics and Sources of CBM Well-Produced Water in the Shouyang Block, China. Appl. Sci. 2024, 14, 4218. [Google Scholar] [CrossRef]
- Chen, S.; Tao, S.; Tang, D. In situ coal permeability and favorable development methods for coalbed methane (CBM) extraction in China: From real data. Int. J. Coal Geol. 2024, 284, 104472. [Google Scholar] [CrossRef]
- Zhou, X.; Hu, B.; He, Q.; Huang, X.; Hou, H. Physical Characteristics of Coal Reservoirs and CBM Favorable Area Prediction in the Huaibei Coalfield, Northern China. ACS Omega 2024, 9, 12158–12174. [Google Scholar] [CrossRef]
- Zhao, F.; Han, S.; Sang, S.; Zhou, P.; Mondal, D.; Guo, Z.; Xu, A. Modified Method for Calculating Saturation Gas Content in Deep Coal and the Pore Size Effect of Methane Adsorption on Guizhou Middle- and High-Rank Coals. Nat. Resour. Res. 2023, 32, 1215–1233. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, Y.; You, Z.; Yang, Z. Distribution Characteristics of In Situ Stress Field and Vertical Development Unit Division of CBM in Western Guizhou, China. Nat. Resour. Res. 2021, 30, 3659–3671. [Google Scholar] [CrossRef]
- Sun, W.; Zuo, Y.; Wu, Z.; Liu, H.; Xi, S.; Shui, Y.; Wang, J.; Liu, R.; Lin, J. Fractal analysis of pores and the pore structure of the Lower Cambrian Niutitang shale in northern Guizhou province: Investigations using NMR, SEM and image analyses. Mar. Petrol. Geol. 2019, 99, 416–428. [Google Scholar] [CrossRef]
- Chen, S.; Tang, D.; Tao, S.; Ji, X.; Xu, H. Fractal analysis of the dynamic variation in pore-fracture systems under the action of stress using a low-field NMR relaxation method: An experimental study of coals from western Guizhou in China. J. Petrol. Sci. Eng. 2019, 173, 617–629. [Google Scholar] [CrossRef]
- Li, R.; Hou, X.; Chen, L.; Fang, H.; Zheng, C. Multifractal investigation on multi-scale pore structure heterogeneity of high rank coal reservoirs. Nat. Resour. Res. 2022, 31, 1665–1685. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, C.; Chu, X.; Vandeginste, V.; Ju, W. Multifractal analysis in characterizing adsorption pore heterogeneity of middle-and high-rank coal reservoirs. ACS Omega 2020, 5, 19385–19401. [Google Scholar] [CrossRef]
- Sun, Y.; Zhai, C.; Zhao, Y.; Xu, J.; Cong, Y.; Zheng, Y.; Tang, W. Multifractal analysis and neural network prediction of pore structures in coal reservoirs based on NMR T2 spectra. Energ. Fuel 2021, 35, 11306–11318. [Google Scholar] [CrossRef]
- Zhang, N.; Guo, S.; Wang, S.; Tong, Y.; Li, Z.; Wu, J. Fractal and Multifractal Characteristics on Pore Structure of Coal-Based Sedimentary Rocks Using Nuclear Magnetic Resonance. SPE J. 2024, 29, 2624–2637. [Google Scholar] [CrossRef]
- Zhang, J.; Quan, F.; Zhang, H.; Shao, Y.; Han, Y.; Yang, Y.; Chang, X.; Zhang, X. Multi-method characterization of sandstone pore size distribution heterogeneity and its influence on porosity and permeability variation. Front. Earth Sci. 2024, 18, 814–830. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, C.; Ju, W.; Yan, G.; Lu, G.; Hou, X.; Kai, Z. Stress sensitivity characterization and heterogeneous variation of the pore-fracture system in middle-high rank coals reservoir based on NMR experiments. Fuel 2019, 238, 331–344. [Google Scholar] [CrossRef]
- Qin, L.; Lv, S.; Li, S.; Wang, H.; Liu, P.; Mu, M.; Li, J. Freeze–Thaw Response of Permeability and Absorption Channel Structure and Moisture Distribution in Different Coal Ranks. Nat. Resour. Res. 2025, 34, 1103–1122. [Google Scholar] [CrossRef]
- Zhong, B.; Zhu, Y.; Feng, G.; Xiang, J.; Wang, Y. Matrix Compression and Pore Heterogeneity in the Coal-Measure Shale Reservoirs of the Qinshui Basin: A Multifractal Analysis. Fractal Fract. 2024, 8, 580. [Google Scholar] [CrossRef]
- Pan, J.; Du, X.; Wang, X.; Hou, Q.; Wang, Z.; Yi, J.; Li, M. Pore and permeability changes in coal induced by true triaxial supercritical carbon dioxide fracturing based on low-field nuclear magnetic resonance. Energy 2024, 286, 129492. [Google Scholar] [CrossRef]
- Duan, C.; Fu, X.; Deng, Z.; Kang, J.; Zhang, B.; Lu, J.; Hong, X.; Dai, R.; Li, X. Pore Structure Multifractal Characteristics of Coal Reservoirs in the Central and Eastern Qinshui Basin and Influencing Factors. Processes 2023, 11, 286. [Google Scholar] [CrossRef]
- Ni, X.; Liu, Z.; Wei, J. Quantitative Evaluation of the Impacts of Drilling Mud on the Damage Degree to the Permeability of Fractures at Different Scales in Coal Reservoirs. Fuel 2019, 236, 382–393. [Google Scholar] [CrossRef]
- Jones, S.C. A technique for faster pulse-decay permeability measurements in tight rocks. SPE Form. Eval. 1997, 12, 19–25. [Google Scholar] [CrossRef]
- Washburn, E.W. The dynamics of capillary flow. Phys. Rev. 1921, 17, 273. [Google Scholar] [CrossRef]
- Groen, J.C.; Pérez-Ramírez, J. Critical appraisal of mesopore characterization by adsorption analysis. Appl. Catal. A Gen. 2004, 268, 121–125. [Google Scholar] [CrossRef]
- Bardestani, R.; Patience, G.S.; Kaliaguine, S. Experimental methods in chemical engineering: Specific surface area and pore size distribution measurements—BET, BJH, and DFT. Can. J. Chem. Eng. 2019, 97, 2781–2791. [Google Scholar] [CrossRef]
- Geerlings, P.; De Proft, F.; Langenaeker, W. Conceptual density functional theory. Chem. Rev. 2003, 103, 1793–1874. [Google Scholar] [CrossRef]
- Balzer, C.; Cimino, R.T.; Gor, G.Y.; Neimark, A.V.; Reichenauer, G. Deformation of microporous carbons during N2, Ar, and CO2 adsorption: Insight from the density functional theory. Langmuir 2016, 32, 8265–8274. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH freeman: New York, NY, USA, 1982; Volume 1. [Google Scholar]
- Lu, G.; Wang, J.; Wei, C.; Song, Y.; Yan, G.; Zhang, J.; Chen, G. Pore fractal model applicability and fractal characteristics of seepage and adsorption pores in middle rank tectonic deformed coals from the Huaibei coal field. J. Petrol. Sci. Eng. 2018, 171, 808–817. [Google Scholar] [CrossRef]
- Song, W.; Wang, D.; Yao, J.; Li, Y.; Sun, H.; Yang, Y.; Zhang, L. Multiscale image-based fractal characteristic of shale pore structure with implication to accurate prediction of gas permeability. Fuel 2019, 241, 522–532. [Google Scholar] [CrossRef]
- Martínez, F.S.J.; Martín, M.A.; Caniego, F.J.; Tuller, M.; Guber, A.; Pachepsky, Y.; García-Gutiérrez, C. Multifractal analysis of discretized X-ray CT images for the characterization of soil macropore structures. Geoderma 2010, 156, 32–42. [Google Scholar] [CrossRef]
- Tian, T.; Zhang, D.; Shi, Y.; Quan, F.; Qin, Z. Pore-Fracture System Distribution Heterogeneity by Using the T2 Spectral Curve under a Centrifugal State. Processes 2024, 12, 1812. [Google Scholar] [CrossRef]








| Sample ID | Proximate | Elemental Analysis | Coal Petrology | Porosity | Permeability | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mad | Ad | Vdaf | Cdaf | Odaf | Hdaf | Ndaf | Ro,max | V | I | E | |||
| T1 | 1.14 | 13.62 | 29.24 | 85.64 | 7.86 | 4.73 | 1.58 | 1.58 | 72.18 | 27.82 | 0 | 2.53 | 0.44 |
| T2 | 1.14 | 18.17 | 19.05 | 88.27 | 4.89 | 4.55 | 0.99 | 1.65 | 69.48 | 30.52 | 0 | 2.84 | 0.65 |
| T3 | 1.00 | 10.91 | 20.36 | 73.38 | 18.06 | 4.61 | 1.54 | 1.71 | 69.17 | 30.83 | 0 | 1.33 | 0.76 |
| T4 | 1.56 | 9.61 | 34.47 | 86.60 | 6.11 | 5.28 | 1.84 | 1.40 | 51.00 | 39.73 | 9.27 | 3.35 | 0.52 |
| L1 | 1.27 | 18.23 | 9.52 | 91.07 | 3.26 | 3.62 | 1.68 | 3.02 | 73.21 | 27.79 | 0 | 2.42 | 0.46 |
| L2 | 1.32 | 5.3 | 9.57 | 87.95 | 0.87 | 3.37 | 1.67 | 2.95 | 71.32 | 28.68 | 0 | 3.65 | 0.81 |
| L3 | 1.93 | 6.51 | 8.02 | 92.07 | 2.42 | 3.39 | 1.65 | 3.36 | 66.08 | 33.92 | 0 | 4.01 | 0.72 |
| L4 | 1.58 | 14.79 | 9.83 | 91.15 | 3.29 | 3.52 | 1.62 | 3.12 | 67.76 | 32.24 | 0 | 3.05 | 0.42 |
| Sample ID | D10 | D−10 | D0 | Δα | D1 | D2 | D0–D2 | D−10–D0 | D0–D10 | D−10–D10 |
|---|---|---|---|---|---|---|---|---|---|---|
| T1 | 0.41 | 1.97 | 1.00 | 1.81 | 0.76 | 0.61 | 0.39 | 0.97 | 0.59 | 1.57 |
| T2 | 0.57 | 1.87 | 1.00 | 1.55 | 0.85 | 0.76 | 0.24 | 0.87 | 0.43 | 1.31 |
| T3 | 0.59 | 1.59 | 1.00 | 1.22 | 0.87 | 0.78 | 0.22 | 0.59 | 0.41 | 1.01 |
| T4 | 0.49 | 1.90 | 1.00 | 1.65 | 0.80 | 0.69 | 0.31 | 0.90 | 0.51 | 1.41 |
| L1 | 0.47 | 1.78 | 1.00 | 1.53 | 0.81 | 0.69 | 0.31 | 0.78 | 0.53 | 1.31 |
| L2 | 0.60 | 1.39 | 1.00 | 0.98 | 0.90 | 0.82 | 0.19 | 0.39 | 0.40 | 0.79 |
| L3 | 0.58 | 1.67 | 1.00 | 1.32 | 0.87 | 0.79 | 0.22 | 0.67 | 0.42 | 1.09 |
| L4 | 0.58 | 2.13 | 1.00 | 1.82 | 0.87 | 0.78 | 0.22 | 1.13 | 0.43 | 1.55 |
| Parameter | Mad | Ad | Vdaf | Cdaf | Odaf | Hdaf | Ndaf | Ro,max | D10 | D−10 | Δα | D1 | D2 | D0–D2 | D−10–D0 | D0–D10 | D−10–D10 | Porosity | Permeability |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mad | 1.00 | −0.44 | −0.31 | 0.65 | −0.58 | −0.41 | 0.44 | 0.58 | 0.22 | 0.12 | 0.06 | 0.18 | 0.23 | −0.23 | 0.12 | −0.22 | 0.04 | 0.80 | −0.05 |
| Ad | −0.44 | 1.00 | 0.05 | 0.12 | 0.07 | 0.18 | −0.52 | −0.20 | −0.39 | 0.62 | 0.63 | −0.41 | −0.39 | 0.39 | 0.62 | 0.39 | 0.63 | −0.49 | −0.63 |
| Vdaf | −0.31 | 0.05 | 1.00 | −0.43 | 0.46 | 0.96 | 0.05 | −0.92 | −0.57 | 0.33 | 0.41 | −0.69 | −0.66 | 0.66 | 0.33 | 0.57 | 0.42 | −0.26 | −0.27 |
| Cdaf | 0.65 | 0.12 | −0.43 | 1.00 | −0.95 | −0.53 | 0.07 | 0.60 | −0.09 | 0.29 | 0.28 | −0.04 | −0.03 | 0.03 | 0.29 | 0.09 | 0.27 | 0.77 | −0.36 |
| Odaf | −0.58 | 0.07 | 0.46 | −0.95 | 1.00 | 0.58 | −0.10 | −0.61 | −0.03 | −0.06 | −0.05 | −0.12 | −0.11 | 0.11 | −0.06 | 0.03 | −0.04 | −0.84 | 0.16 |
| Hdaf | −0.41 | 0.18 | 0.96 | −0.53 | 0.58 | 1.00 | −0.13 | −0.97 | −0.46 | 0.30 | 0.36 | −0.60 | −0.55 | 0.55 | 0.30 | 0.46 | 0.38 | −0.40 | −0.19 |
| Ndaf | 0.44 | −0.52 | 0.05 | 0.07 | −0.10 | −0.13 | 1.00 | 0.28 | −0.22 | −0.11 | −0.05 | −0.17 | −0.18 | 0.18 | −0.11 | 0.22 | −0.04 | 0.22 | −0.19 |
| Ro,max | 0.58 | −0.20 | −0.92 | 0.60 | −0.61 | −0.97 | 0.28 | 1.00 | 0.40 | −0.21 | −0.27 | 0.51 | 0.49 | −0.49 | −0.21 | −0.40 | −0.28 | 0.47 | 0.08 |
| D10 | 0.22 | −0.39 | −0.57 | −0.09 | −0.03 | −0.46 | −0.22 | 0.40 | 1.00 | −0.47 | −0.63 | 0.97 | 0.99 | −0.99 | −0.47 | −1.00 | −0.66 | 0.20 | 0.72 |
| D−10 | 0.12 | 0.62 | 0.33 | 0.29 | −0.06 | 0.30 | −0.11 | −0.21 | −0.47 | 1.00 | 0.98 | −0.55 | −0.51 | 0.51 | 1.00 | 0.47 | 0.97 | −0.07 | −0.88 |
| Δα | 0.06 | 0.63 | 0.41 | 0.28 | −0.05 | 0.36 | −0.05 | −0.27 | −0.63 | 0.98 | 1.00 | −0.69 | −0.66 | 0.66 | 0.98 | 0.63 | 1.00 | −0.10 | −0.93 |
| D1 | 0.18 | −0.41 | −0.69 | −0.04 | −0.12 | −0.60 | −0.17 | 0.51 | 0.97 | −0.55 | −0.69 | 1.00 | 0.99 | −0.99 | −0.55 | −0.97 | −0.71 | 0.21 | 0.72 |
| D2 | 0.23 | −0.39 | −0.66 | −0.03 | −0.11 | −0.55 | −0.18 | 0.49 | 0.99 | −0.51 | −0.66 | 0.99 | 1.00 | −1.00 | −0.51 | −0.99 | −0.69 | 0.22 | 0.71 |
| D0–D2 | −0.23 | 0.39 | 0.66 | 0.03 | 0.11 | 0.55 | 0.18 | −0.49 | −0.99 | 0.51 | 0.66 | −0.99 | −1.00 | 1.00 | 0.51 | 0.99 | 0.69 | −0.22 | −0.71 |
| D−10–D0 | 0.12 | 0.62 | 0.33 | 0.29 | −0.06 | 0.30 | −0.11 | −0.21 | −0.47 | 1.00 | 0.98 | −0.55 | −0.51 | 0.51 | 1.00 | 0.47 | 0.97 | −0.07 | −0.88 |
| D0–D10 | −0.22 | 0.39 | 0.57 | 0.09 | 0.03 | 0.46 | 0.22 | −0.40 | −1.00 | 0.47 | 0.63 | −0.97 | −0.99 | 0.99 | 0.47 | 1.00 | 0.66 | −0.20 | −0.72 |
| D−10–D10 | 0.04 | 0.63 | 0.42 | 0.27 | −0.04 | 0.38 | −0.04 | −0.28 | −0.66 | 0.97 | 1.00 | −0.71 | −0.69 | 0.69 | 0.97 | 0.66 | 1.00 | −0.11 | −0.93 |
| Porosity | 0.80 | −0.49 | −0.26 | 0.77 | −0.84 | −0.40 | 0.22 | 0.47 | 0.20 | −0.07 | −0.10 | 0.21 | 0.22 | −0.22 | −0.07 | −0.20 | −0.11 | 1.00 | 0.11 |
| Permeability | −0.05 | −0.63 | −0.27 | −0.36 | 0.16 | −0.19 | −0.19 | 0.08 | 0.72 | −0.88 | −0.93 | 0.72 | 0.71 | −0.71 | −0.88 | −0.72 | −0.93 | 0.11 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quan, F.; Zhang, Y.; Lu, W.; Wei, C.; Dai, X.; Qin, Z. Multifractal Characterization of Full-Scale Pore Structure in Middle-High-Rank Coal Reservoirs: Implications for Permeability Modeling in Western Guizhou–Eastern Yunnan Basin. Processes 2025, 13, 1927. https://doi.org/10.3390/pr13061927
Quan F, Zhang Y, Lu W, Wei C, Dai X, Qin Z. Multifractal Characterization of Full-Scale Pore Structure in Middle-High-Rank Coal Reservoirs: Implications for Permeability Modeling in Western Guizhou–Eastern Yunnan Basin. Processes. 2025; 13(6):1927. https://doi.org/10.3390/pr13061927
Chicago/Turabian StyleQuan, Fangkai, Yanhui Zhang, Wei Lu, Chongtao Wei, Xuguang Dai, and Zhengyuan Qin. 2025. "Multifractal Characterization of Full-Scale Pore Structure in Middle-High-Rank Coal Reservoirs: Implications for Permeability Modeling in Western Guizhou–Eastern Yunnan Basin" Processes 13, no. 6: 1927. https://doi.org/10.3390/pr13061927
APA StyleQuan, F., Zhang, Y., Lu, W., Wei, C., Dai, X., & Qin, Z. (2025). Multifractal Characterization of Full-Scale Pore Structure in Middle-High-Rank Coal Reservoirs: Implications for Permeability Modeling in Western Guizhou–Eastern Yunnan Basin. Processes, 13(6), 1927. https://doi.org/10.3390/pr13061927







