Stress Sensitivity of Tight Sandstone Reservoirs Under the Effect of Pore Structure Heterogeneity
Abstract
1. Introduction
2. Geological Setting and Experimental Methods
2.1. Geological Settings
2.2. Experimental Methods
3. Results and Discussion
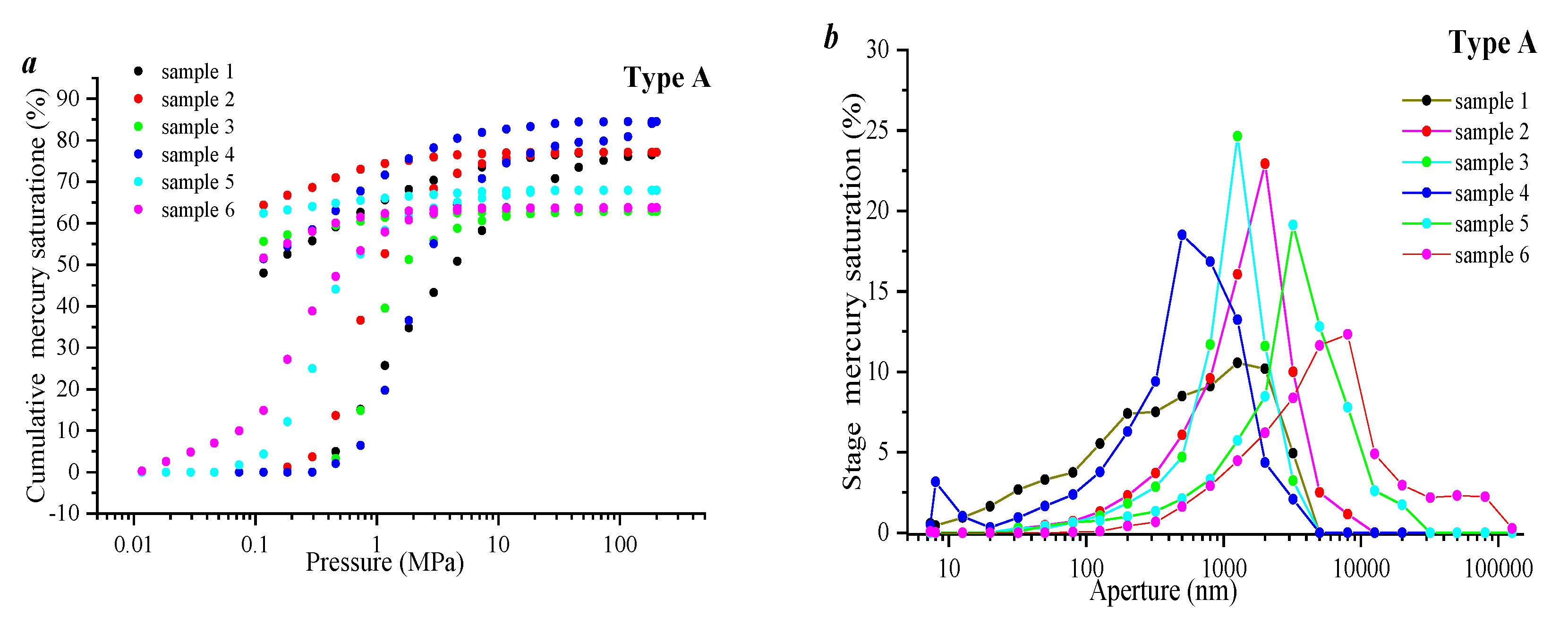
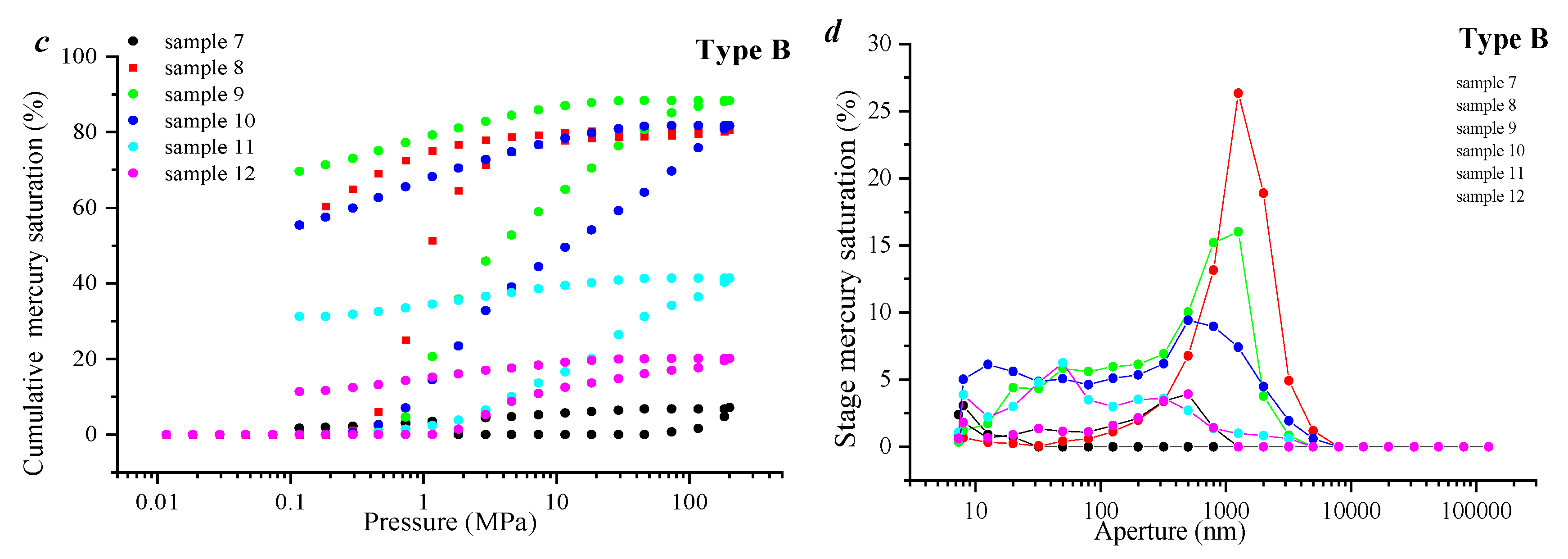
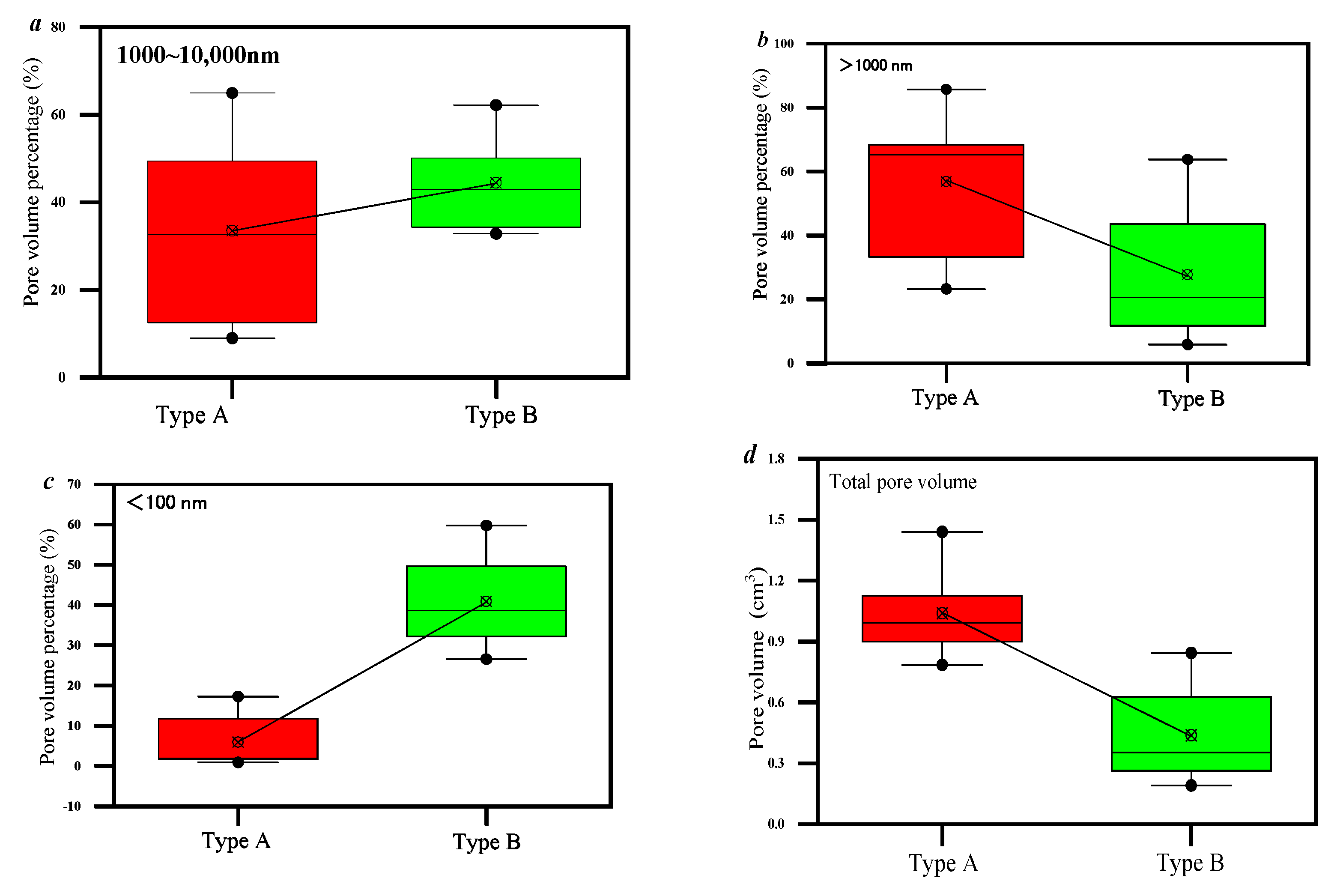
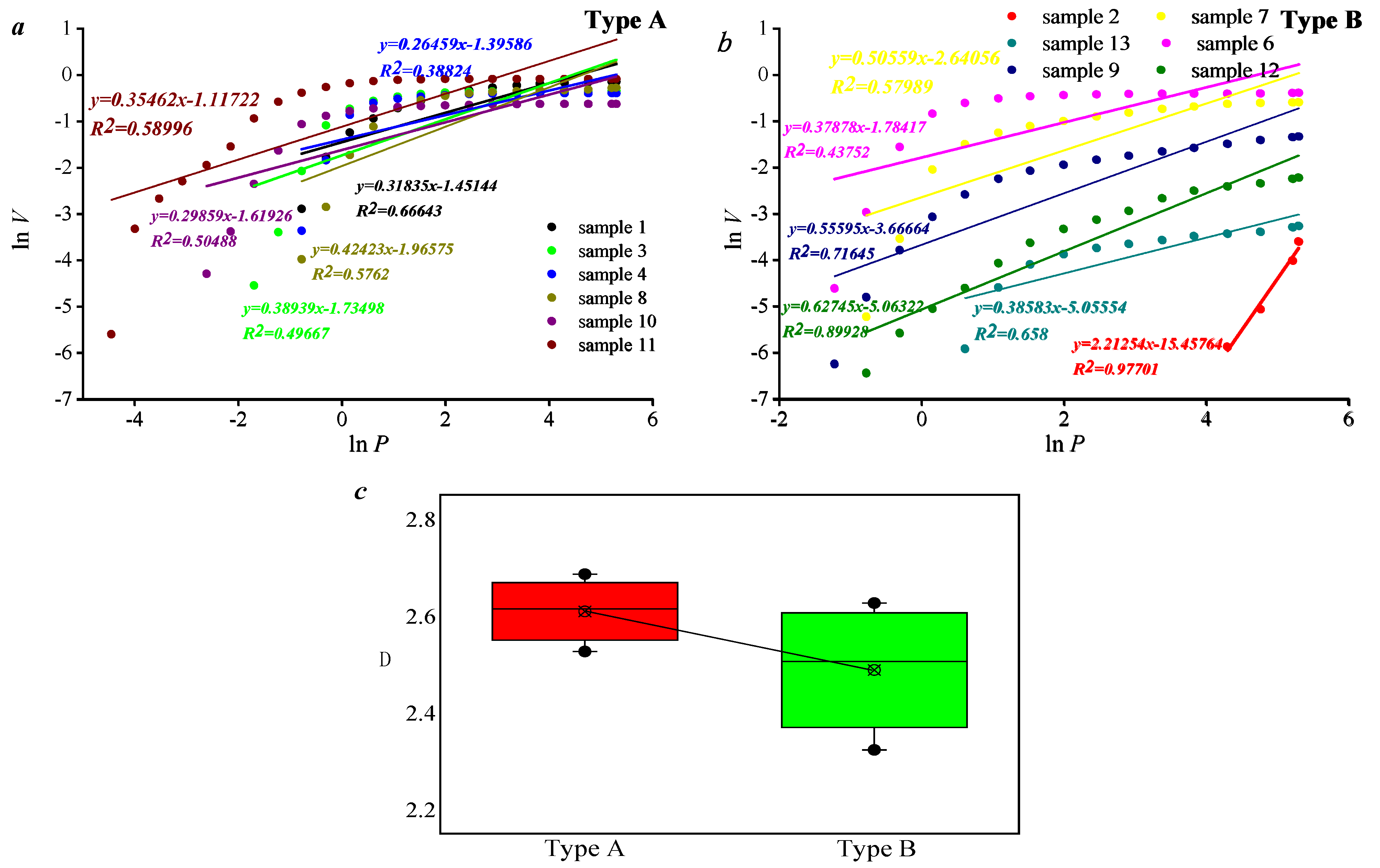
3.1. Pore Volume Distribution of Tight Sandstone Reservoirs Based on High-Pressure Mercury Injection
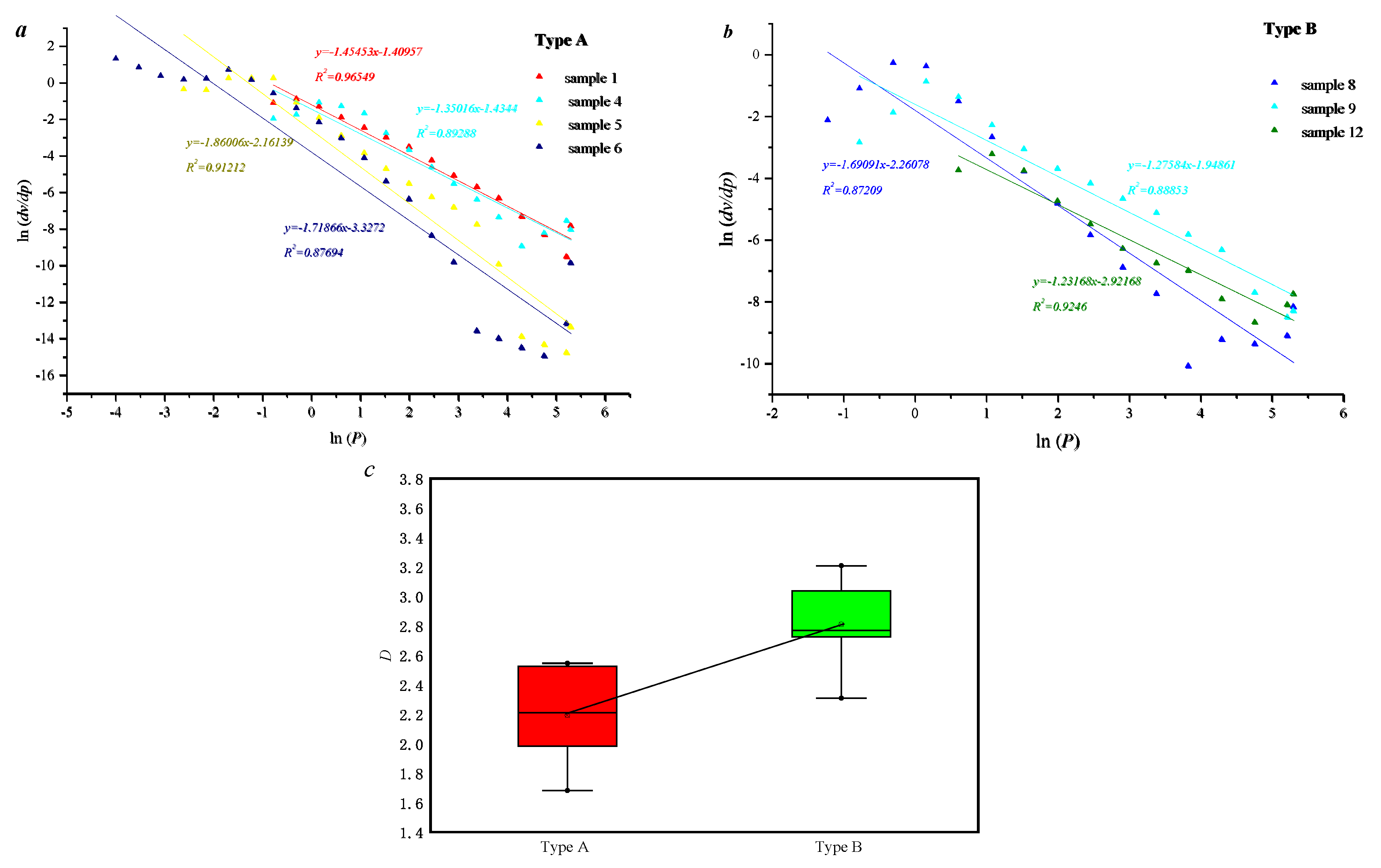
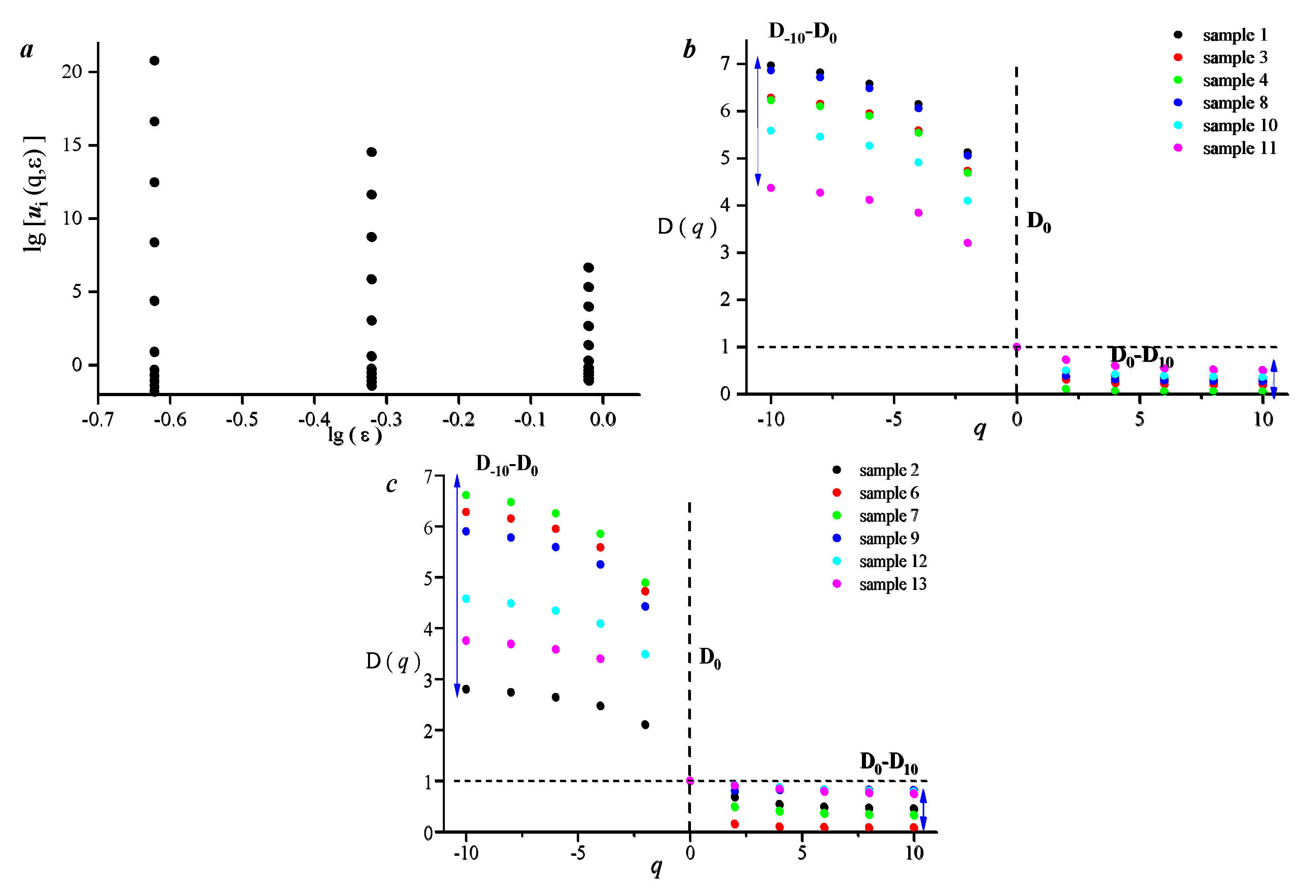
3.2. Applicability of Different Fractal Models in Characterizing Pore–Fracture Structures
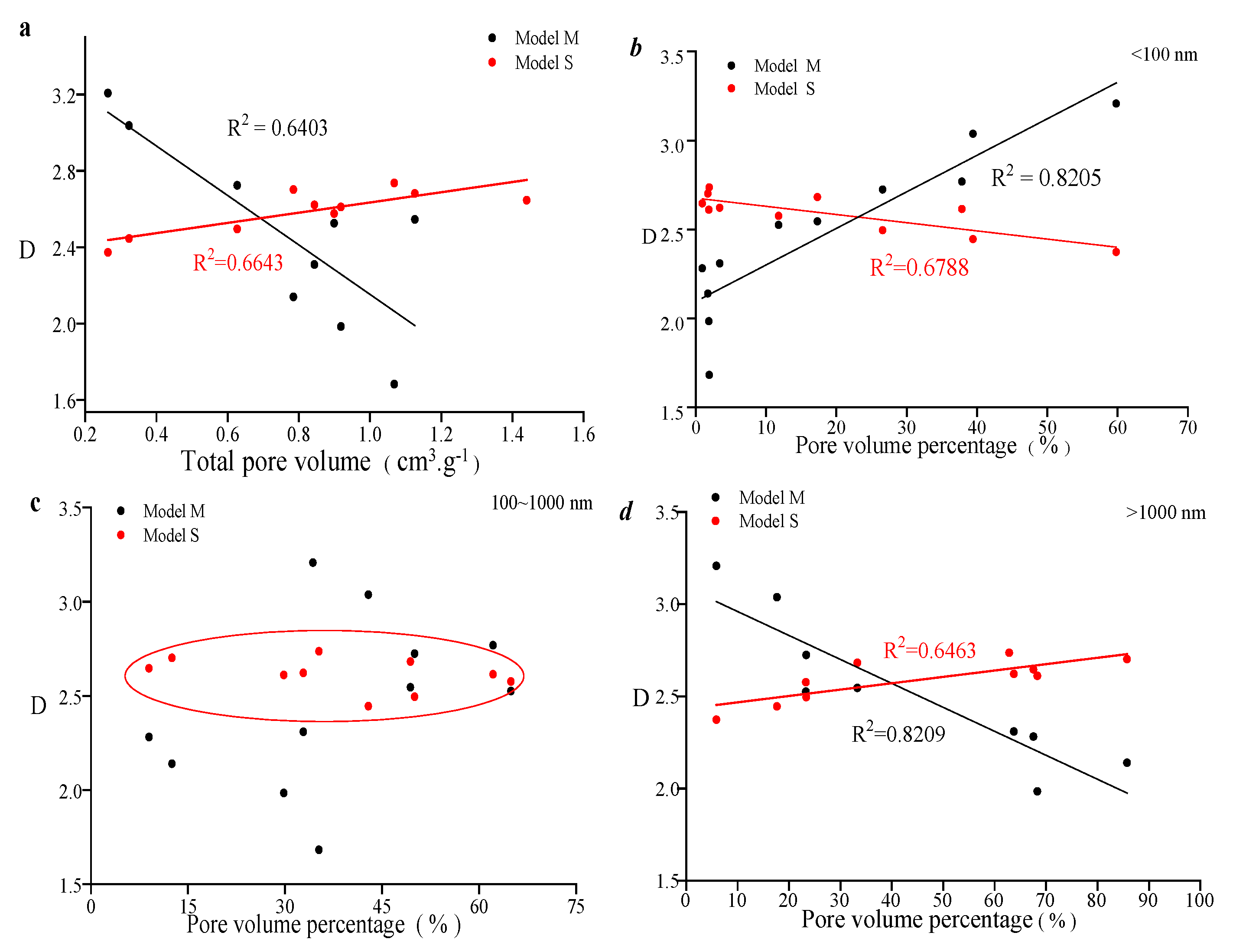
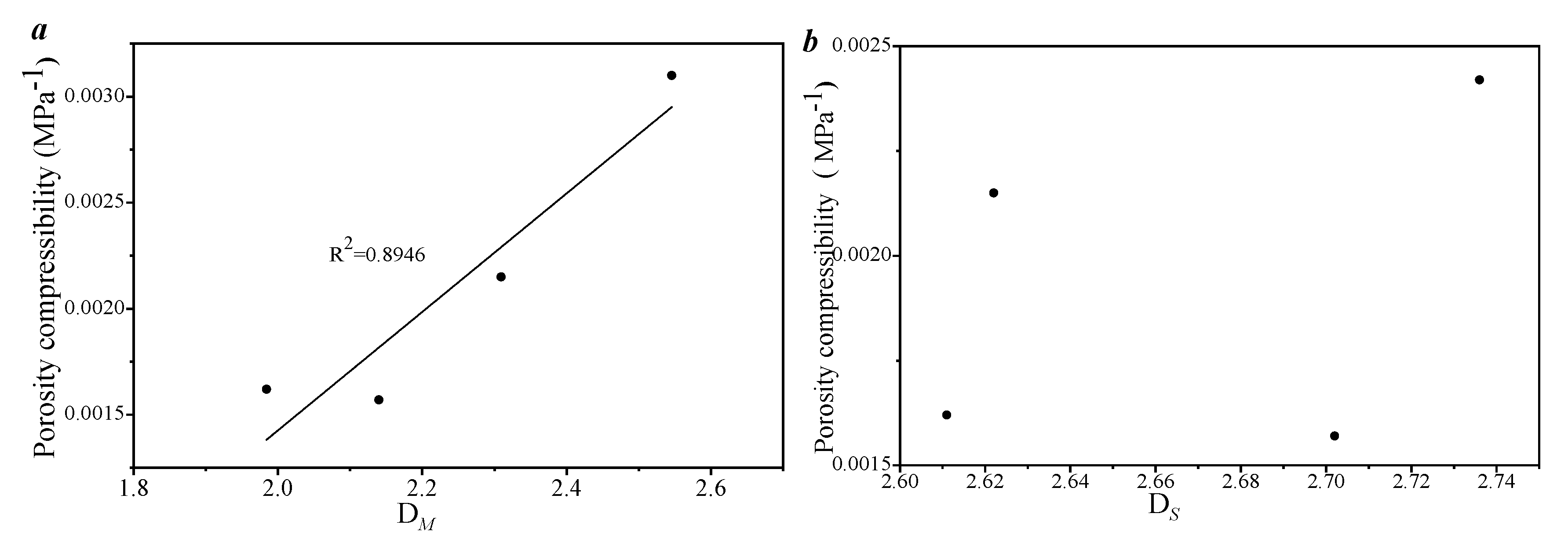
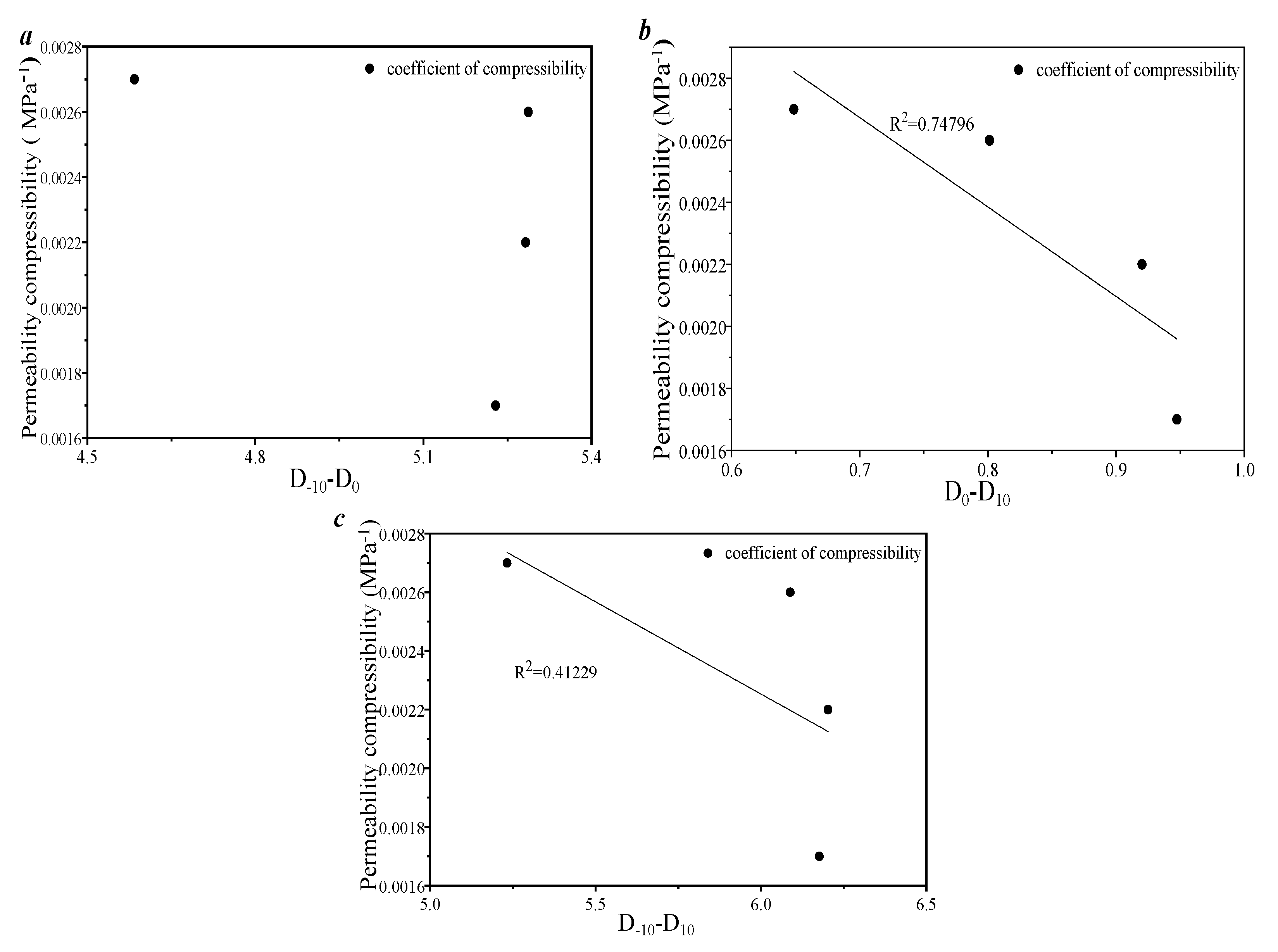
3.3. Porosity–Permeability and Compressibility Under the Effect of Pore–Fracture Structure Heterogeneity
4. Conclusions
- (1)
- Based on the mercury-in and mercury-out curves, the samples can be divided into two categories, A and B. There is a significant hysteresis loop in the mercury inlet and outlet curves of type A, and the efficiency of the mercury inlet and outlet in pores is relatively high. Then, the pore volume is 0.785 to1.44 cm3/g, the average value is 1.039 cm3/g and the mercury removal rate is 32%~43%. The mercury removal curve of type B is almost parallel, and its mercury removal efficiency is relatively low. The pore volume of this type of sample is 0.191~0.844 cm3/g, the average value is 0.439 cm3/g, and the mercury removal rate is 31%~39%.
- (2)
- This type of tight sandstone reservoir has strong heterogeneity characteristics. The applicability of singlet fractals in characterizing the heterogeneity of dense pores is higher than that of multifractals. This is because the single fractal characteristics of the two types of samples mentioned above have significant differences, while the differences in the multifractals are relatively weak.
- (3)
- The compressibility of this type of sample was calculated based on the overburden pore permeability test, with porosity compressibility of 0.00157~0.0031 and the average value is 0.002172, with permeability compressibility of 0.0017~0.0154 and the average value is 0.00492. The pores of 100–1000 nm provide the main compression space for this type of sample. The results of the factor correlation analysis indicate that the heterogeneity of the pore distribution between 100 and 1000 nm affects the compression effect and stress sensitivity of this type of sample. Therefore, in the process of studying the production capacity of tight sandstone in the research area, it is necessary to focus on strengthening the research and influence on this part of the space.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Q.; Zhao, D.; Yin, J.; Zhou, X.; Li, Y.; Chi, P.; Han, Y.; Ansari, U.; Cheng, Y. Sediment Instability Caused by Gas Production from Hydrate-bearing Sediment in Northern South China Sea by Horizontal Wellbore: Evolution and Mechanism. Nat. Resour. Res. 2023, 32, 1595–1620. [Google Scholar] [CrossRef]
- Yao, P.; Zhang, J.; Lv, D.; Vandeginste, V.; Chang, X.; Zhang, X.; Wang, D.; Han, S.; Liu, Y. Effect of water occurrence in coal reservoirs on the production capacity of coalbed methane by using NMR simulation technology and production capacity simulation. Geoenergy Sci. Eng. 2024, 243, 213353. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, C.; Yang, Y.; Ansari, U.; Han, Y.; Li, X.; Cheng, Y. Preliminary experimental investigation on long-term fracture conductivity for evaluating the feasibility and efficiency of fracturing operation in offshore hydrate-bearing sediments. Ocean Eng. 2023, 281, 114949. [Google Scholar] [CrossRef]
- Zou, C.N.; Tao, S.Z.; Han, W.X.; Zhao, Z.Y.; Ma, W.J.; Li, C.W.; Bai, B.; Gao, X.H. Geological and Geochemical Characteristics and Exploration Prospect of Coal-Derived Tight Sandstone Gas in China: Case Study of the Ordos, Sichuan, and Tarim Basins. Acta Geol. Sin. Engl. Ed. 2018, 92, 1609–1626. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Q.Y.; Wu, S.T.; Lin, S.H.; Liu, X.S. Evidence of the Near-Source Accumulation of the Tight Sandstone Gas in Northern Ordos Basin, North-Central China. Acta Geol. Sin. Engl. Ed. 2017, 91, 1820–1835. [Google Scholar] [CrossRef]
- Yuan, K.; Li, Y.; Shi, T.; Huang, H.; Li, Y.; He, M.; Liu, D. Conventional Mercury Penetration and Constant Velocity Mercury Penetration Experiments Are Used to Quantitatively Characterize the Difference in Micropore Structure in Low Permeability Reservoirs and Its Influence on Movable Fluid Saturation. Geofluids 2023, 2023, 1–15. [Google Scholar] [CrossRef]
- Zhao, D.; Hou, J.; Sarma, H.; Guo, W.; Liu, Y.; Xie, P.; Dou, L.; Chen, R.; Zhang, Z. Pore throat heterogeneity of different lithofacies and diagenetic effects in gravelly braided river deposits: Implications for understanding the formation process of high-quality reservoirs. Geoenergy Sci. Eng. 2023, 221, 111309. [Google Scholar] [CrossRef]
- Tang, Y.; Lei, J.C.; Dong, H.R.; Tan, S.A.; Ma, D.Y.; Zhang, N.; Wang, M.X. Study on Pore Structure and the Microscopic Mechanism of the Difference in Petrophysical Properties of Tight Sandstone: A Case Study of the Chang 3 Member of Weibei Oilfield, Ordos Basin. Front. Earth Sci. 2022, 10, 870332. [Google Scholar] [CrossRef]
- Deng, J.; Zeng, H.; Wu, P.; Du, J.; Gao, J.; Zhao, F.; Jiang, Z.; Davarpanah, A. Pore Structure Differentiation between Deltaic and Epicontinental Tight Sandstones of the Upper Paleozoic in the Eastern Linxing Area, Ordos Basin, China. Geofluids 2021, 2021, 1–17. [Google Scholar] [CrossRef]
- Lu, S.; Li, J.; Zhang, P.; Xue, H.; Wang, G.; Zhang, J.; Liu, H.; Li, Z. Classification of microscopic pore-throats and the grading evaluation on shale oil reservoirs. Pet. Explor. Dev. 2018, 45, 452–460. [Google Scholar] [CrossRef]
- Jiang, F.; Zhang, C.; Wang, K.; Zhao, Z.; Zhong, K. Characteristics of micropores, pore throats, and movable fluids in the tight sandstone oil reservoirs of the Yanchang Formation in the southwestern Ordos Basin, China. Aapg. Bull. 2019, 103, 2835–2859. [Google Scholar] [CrossRef]
- Hu, Y. Differential Evolution Mechanism of Pores in Tight Sandstone Reservoirs of Jinci Formation in the Central and Eastern Ordos Basin. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2022. [Google Scholar]
- Zhang, J.; Hu, Q.; Chang, X.; Qin, Z.; Zhang, X.; Marsh, S.; Grebby, S.; Agarwal, V. Water Saturation and Distribution Variation in Coal Reservoirs: Intrusion and Drainage Experiments Using One- and Two-Dimensional NMR Techniques. Energy Fuels 2022, 36, 6130–6143. [Google Scholar] [CrossRef]
- Meng, Y.; Li, Z. Experimental study on porosity and permeability of coal under overburden pressure and its stress sensitivity. Coal J. 2015, 40, 154–159. [Google Scholar]
- GB/T 19222-2003; Sampling of Coal Petrology. China National Coal Association: Beijing, China, 2003.
- GB/T18023-2000; Classification of Macrolithotype for Bituminouscoal. China National Coal Association: Beijing, China, 2003.
- GB/T 6948-2008; Method of Determining Microscopically the Reflectance of Vitrinite in Coal. China National Coal Association: Beijing, China, 2003.
- GB/T 212-2008; Proximate Analysis of Coal. China National Coal Association: Beijing, China, 2003.
- Yao, Y.; Liu, D.; Tang, D.; Tang, S.; Huang, W.; Liu, Z.; Che, Y. Fractal characterization of seepage-pores of coals from China: An investigation on permeability of coals. Comput. Geosci. 2009, 35, 1159–1166. [Google Scholar] [CrossRef]
- Li, Z. Evolution of Coal Reservoir Pores and Fractures and Their Influence on Micro Flow of Coalbed Methane; China University of Geosciences (Beijing): Beijing, China, 2018. [Google Scholar]
- He, C.; Liu, W. Research on fractal model and fractal characteristics of coal particle pores. Coal Sci. Technol. 2017, 45, 150–155. [Google Scholar]
- Shao, P.; Wang, X.; Song, Y.; Li, Y. Study on the characteristics of matrix compressibility and its influence factors for different rank coals. J. Nat. Gas Sci. Eng. 2018, 56, 93–106. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, X.; Huang, X.; Wu, S. Morphological characterization of super fine pulverized coal particle. Part 2. AFM investigation of single coal particle. Fuel 2010, 89, 3884–3891. [Google Scholar] [CrossRef]
- Liang, L.X.; Xiong, J.; Liu, X. An investigation of the fractal characteristics of the Upper Ordovician Wufeng Formation shale using nitrogen adsorption analysis. J. Nat. Gas Sci. Eng. 2015, 27, 402–409. [Google Scholar] [CrossRef]
- Lai, J.; Wang, G. Fractal analysis of tight gas sandstones using high-pressure mercury intrusion techniques. J. Nat. Gas Sci. Eng. 2015, 24, 185–196. [Google Scholar] [CrossRef]
- Hu, J.; Tang, S.; Zhang, S. Investigation of pore structure and fractal characteristics of the lower silurian longmaxi shales in western Hunan and Hubei Provinces in China. J. Nat. Gas Sci. Eng. 2016, 28, 522–535. [Google Scholar] [CrossRef]
- Friesen, W.I.; Mikula, R.J. Fractal dimensions of coal particles. J. Colloid Interface Sci. 1987, 120, 263–271. [Google Scholar] [CrossRef]

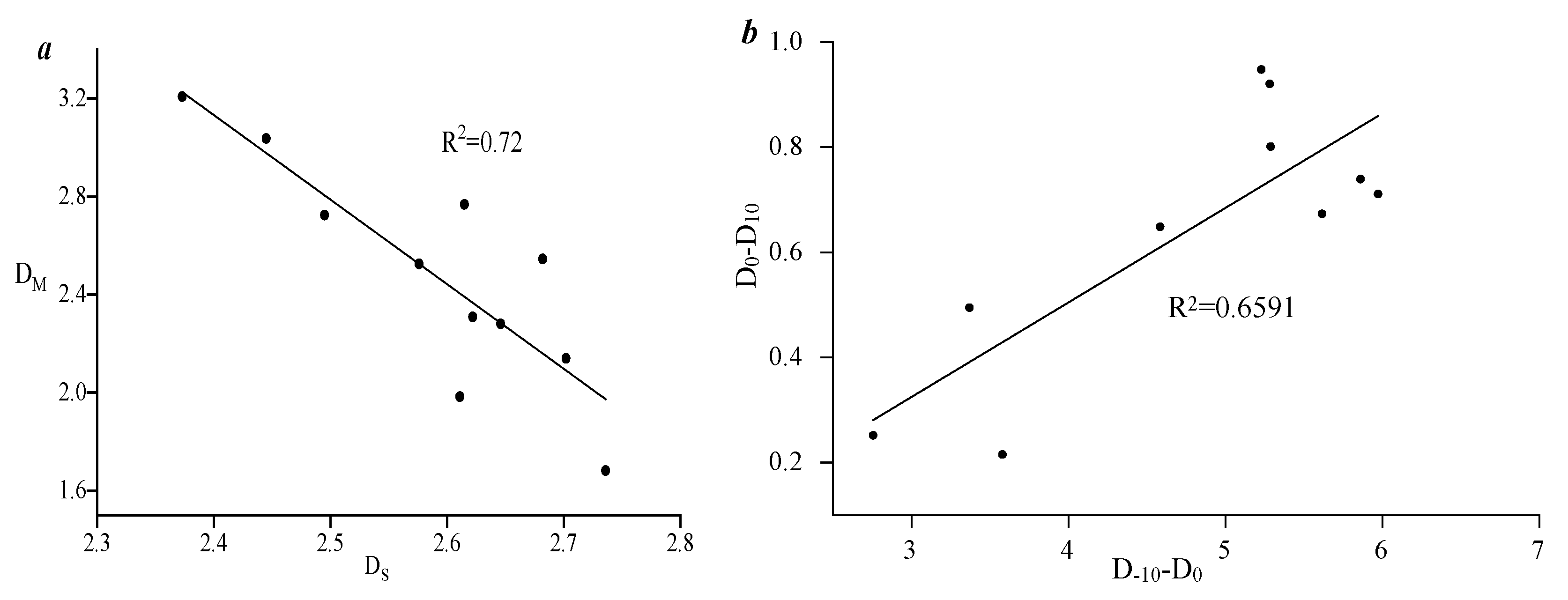



| Sample Number | Pore Volume (cm3·g−1) | Porosity (%) | Permeability (mD) | Mercury Withdrawal Efficiency (%) | Mineral Content (%) | ||
|---|---|---|---|---|---|---|---|
| Quartz | Calcite | Clay Mineral | |||||
| 1 | 0.191 | 8.8 | 0.627 | 37.74 | 2 | ||
| 2 | 0.469 | 8.2 | 0.7615 | 16.47 | 90 | 7 | |
| 3 | 0.253 | 11.6 | 0.406 | 11.46 | 98 | 1 | |
| 4 | 0.323 | 7.3 | 0.1545 | 39.0533 | 94 | 5 | |
| 5 | 0.391 | 9 | 1.805 | 82.3529 | |||
| 6 | 0.542 | 12 | 5.56 | 18.9953 | |||
| 7 | 0.202 | 3.1 | 0.001 | 76.06 | 2 | ||
| 8 | 0.844 | 6.8 | 0.9228 | 31.18 | 94 | 4 | 2 |
| 9 | 1.126 | 4.9 | 0.2891 | 21.15 | 83 | 10 | |
| 10 | 1.02 | 2.6 | 0.2737 | 32.2738 | 73 | 2 | 20 |
| 11 | 0.899 | 3.5 | 3.13 | 24.4552 | 61 | 31 | |
| 12 | 0.974 | 4.6 | 0.0315 | 43.2836 | 72 | 2 | 26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, H.; Du, Y.; Zuo, Q.; Xie, Z.; Zhou, Y.; Xu, A.; Zhang, J.; Guo, Y. Stress Sensitivity of Tight Sandstone Reservoirs Under the Effect of Pore Structure Heterogeneity. Processes 2025, 13, 1960. https://doi.org/10.3390/pr13071960
Pan H, Du Y, Zuo Q, Xie Z, Zhou Y, Xu A, Zhang J, Guo Y. Stress Sensitivity of Tight Sandstone Reservoirs Under the Effect of Pore Structure Heterogeneity. Processes. 2025; 13(7):1960. https://doi.org/10.3390/pr13071960
Chicago/Turabian StylePan, Haiyang, Yun Du, Qingling Zuo, Zhiqing Xie, Yao Zhou, Anan Xu, Junjian Zhang, and Yuqiang Guo. 2025. "Stress Sensitivity of Tight Sandstone Reservoirs Under the Effect of Pore Structure Heterogeneity" Processes 13, no. 7: 1960. https://doi.org/10.3390/pr13071960
APA StylePan, H., Du, Y., Zuo, Q., Xie, Z., Zhou, Y., Xu, A., Zhang, J., & Guo, Y. (2025). Stress Sensitivity of Tight Sandstone Reservoirs Under the Effect of Pore Structure Heterogeneity. Processes, 13(7), 1960. https://doi.org/10.3390/pr13071960







