Dimension-Adaptive Machine Learning for Efficient Uncertainty Quantification in Geological Carbon Storage Models
Abstract
1. Introduction
2. Background and Related Work
2.1. Carbon Storage Modeling Approaches Across Dimensional Scales
2.2. Sources of Uncertainty in 2D Versus 3D Carbon Storage Models
2.3. Machine Learning for Cross-Dimensional Surrogate Modeling
2.4. Uncertainty Quantification Techniques for Dimensional Transfer
3. Materials and Methods
3.1. Mathematical Formulation of Carbon Storage Models
3.1.1. 2D Carbon Storage Model
3.1.2. 3D Carbon Storage Model
3.2. Dataset Generation
3.2.1. Parameter Space Sampling
3.2.2. Simulation Setup
3.2.3. Data Preprocessing
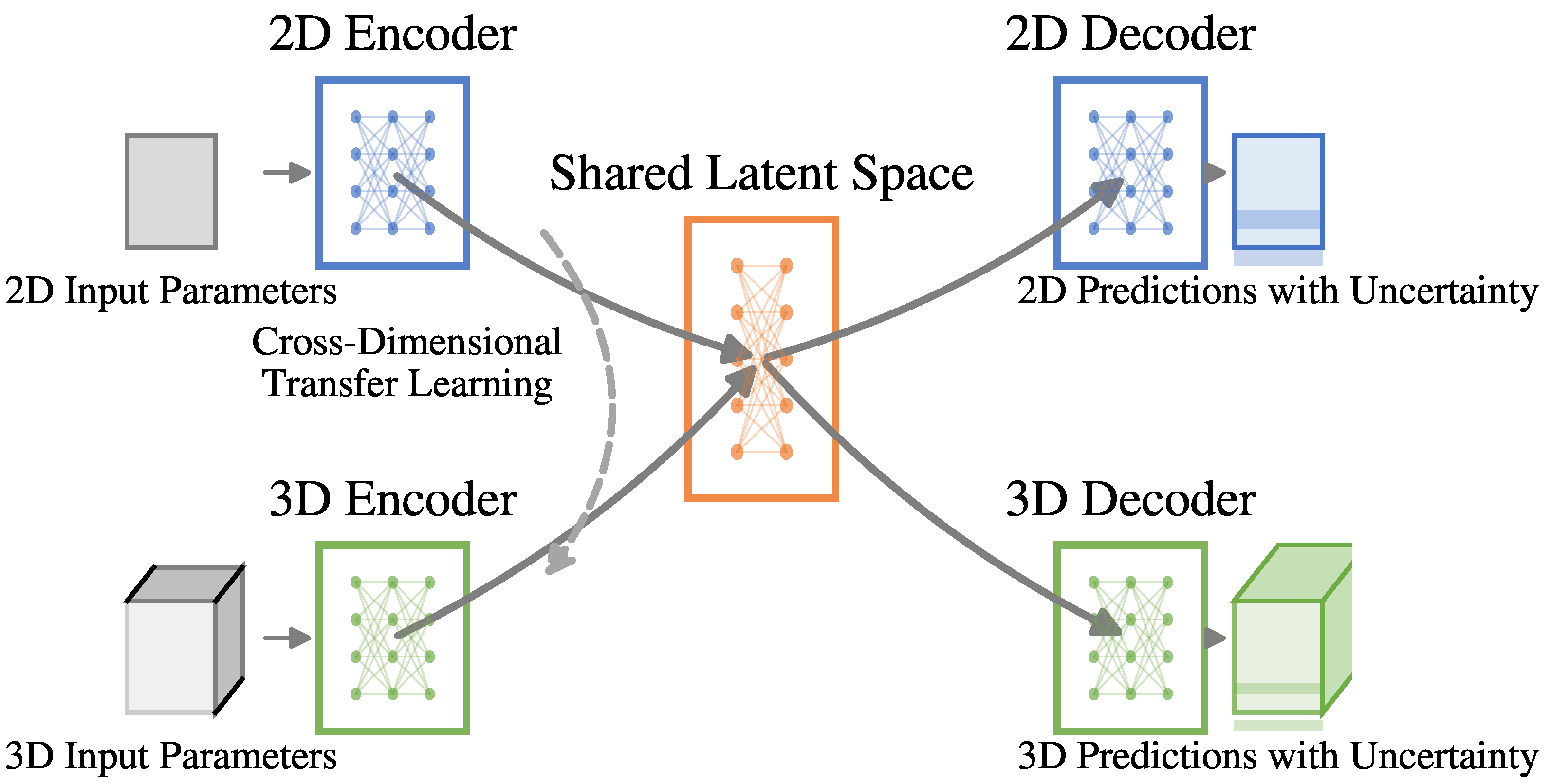
3.3. Dimension-Adaptive Machine Learning Architecture
3.3.1. Overall Framework
3.3.2. Dimension-Adaptive Neural Network
3.3.3. Bayesian Formulation for Uncertainty Quantification
3.3.4. Cross-Dimensional Transfer Learning
3.3.5. Network Architecture Details
3.3.6. Training Procedure and Loss Function
3.4. Evaluation Metrics
4. Results
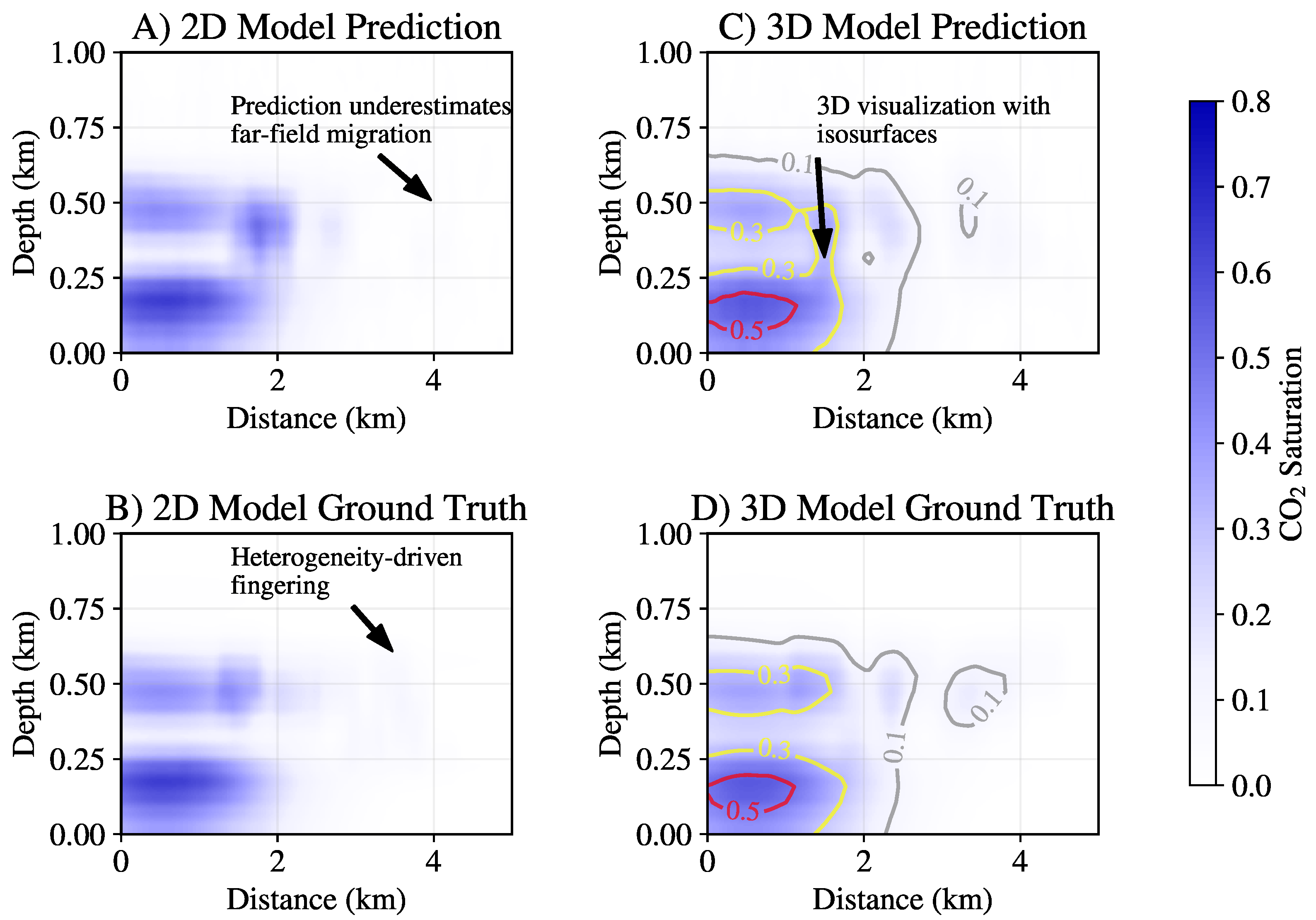
4.1. Prediction Accuracy Across Dimensional Scales
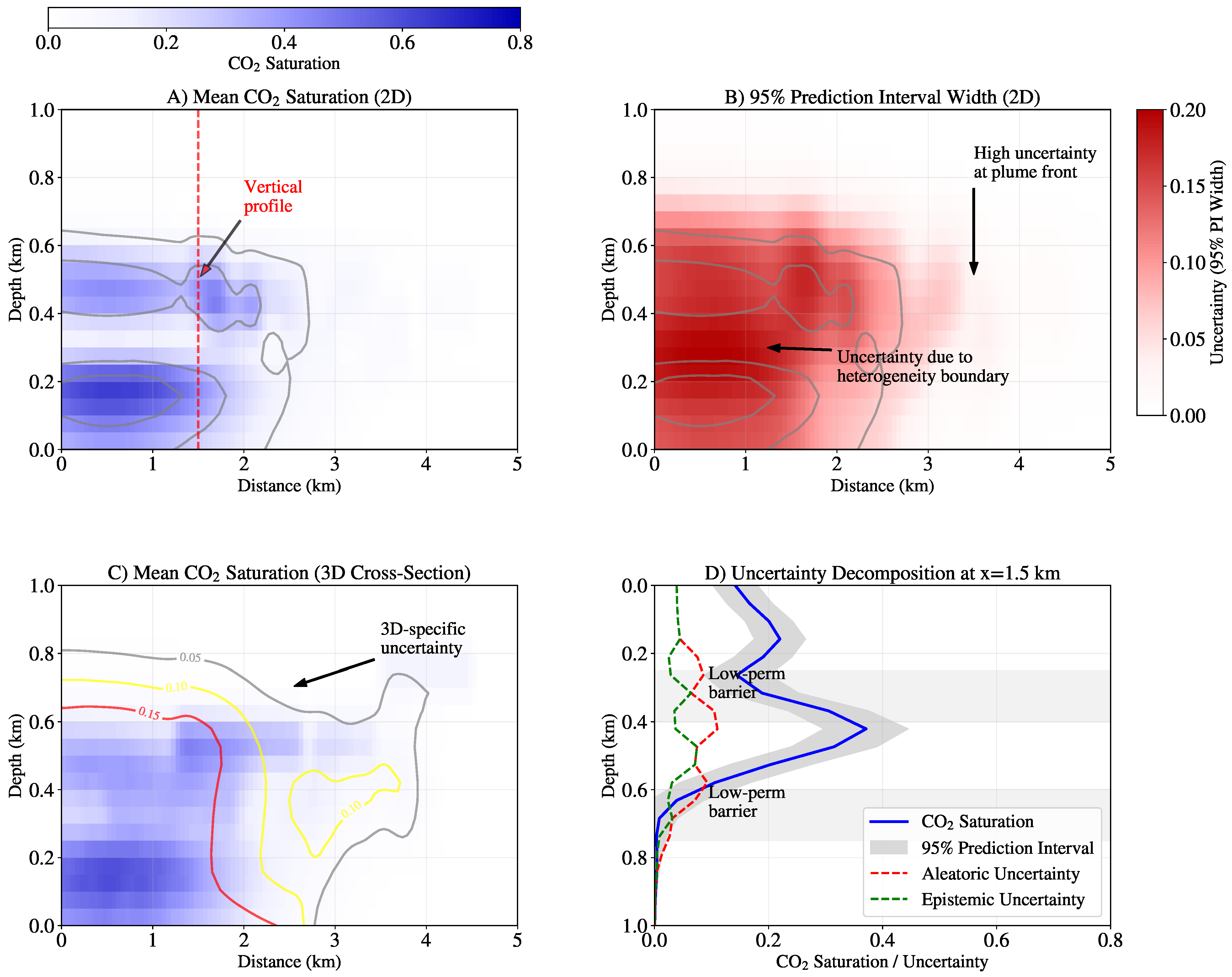
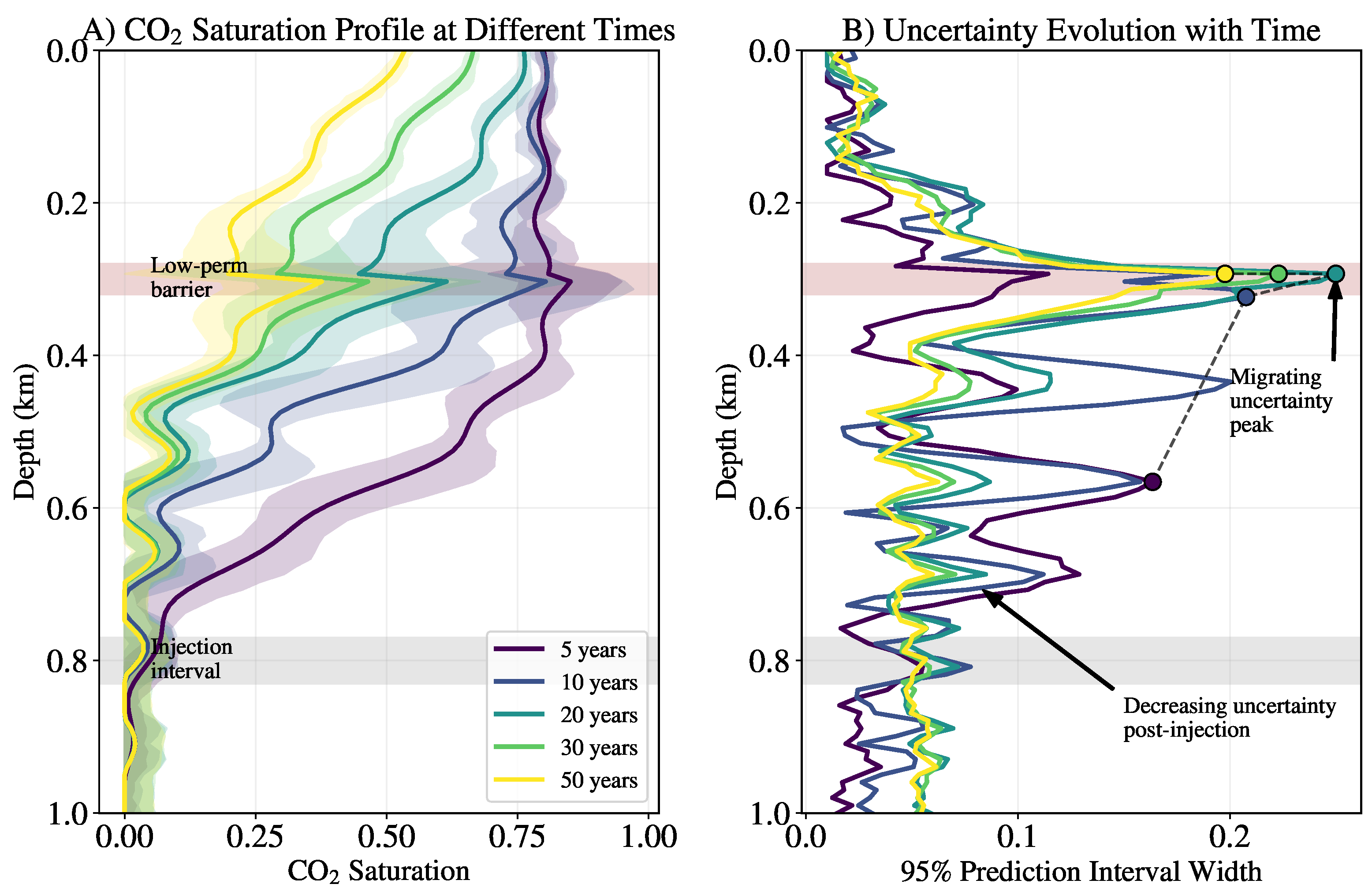
4.2. Uncertainty Quantification Performance
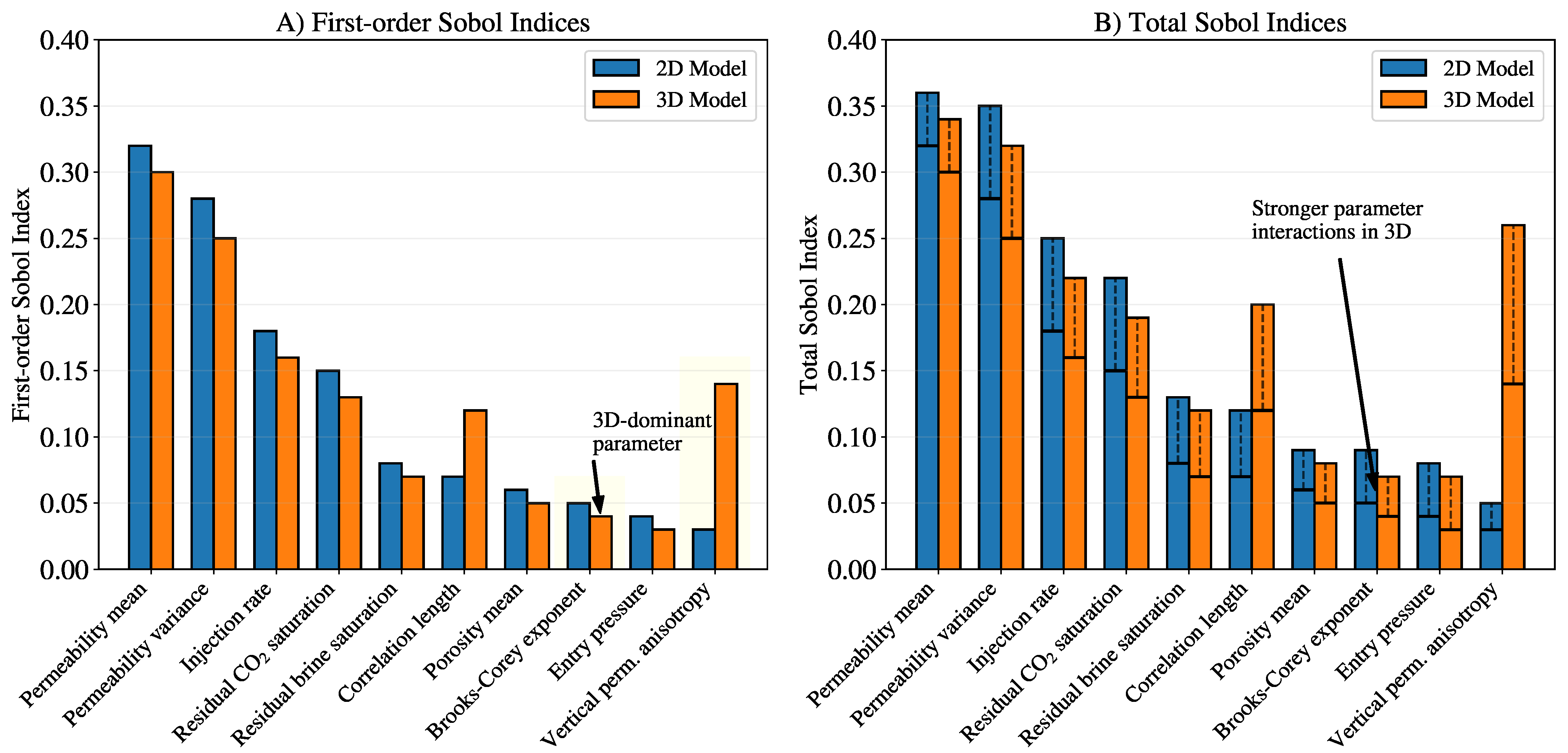
4.3. Parameter Interdependencies and Dimensional Uncertainty Gap
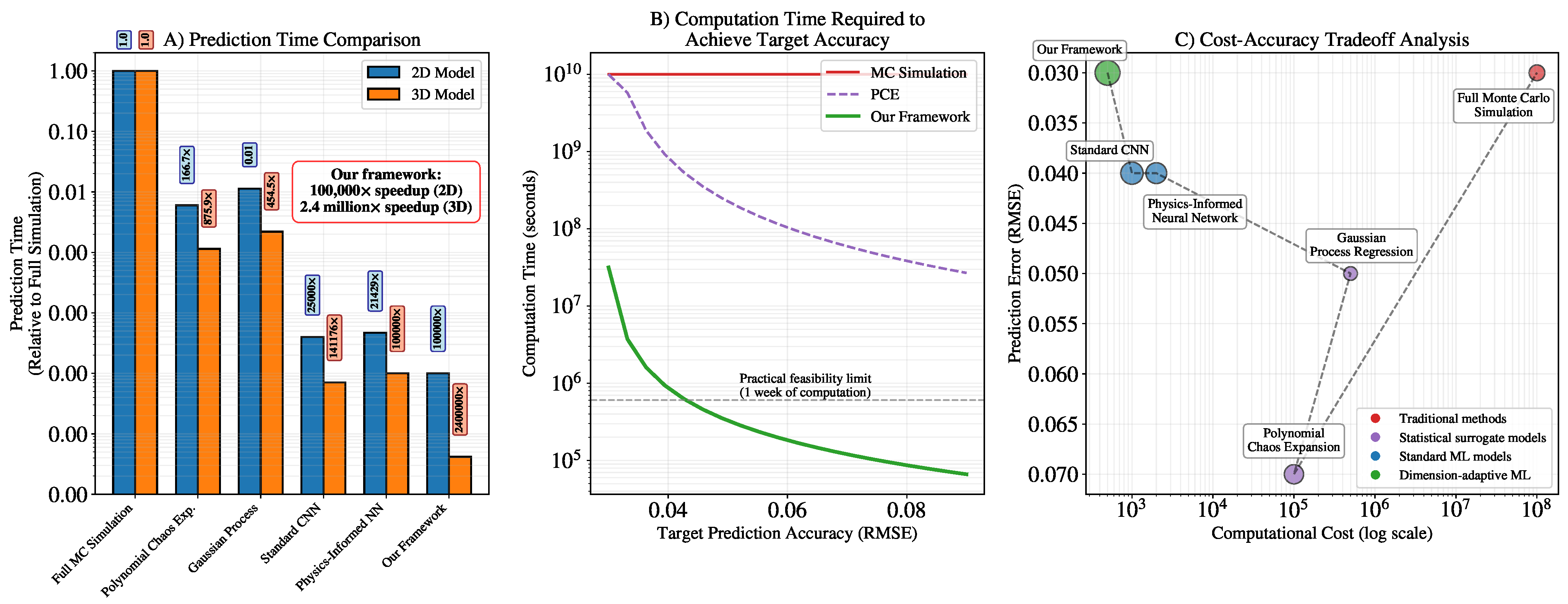
4.4. Computational Efficiency
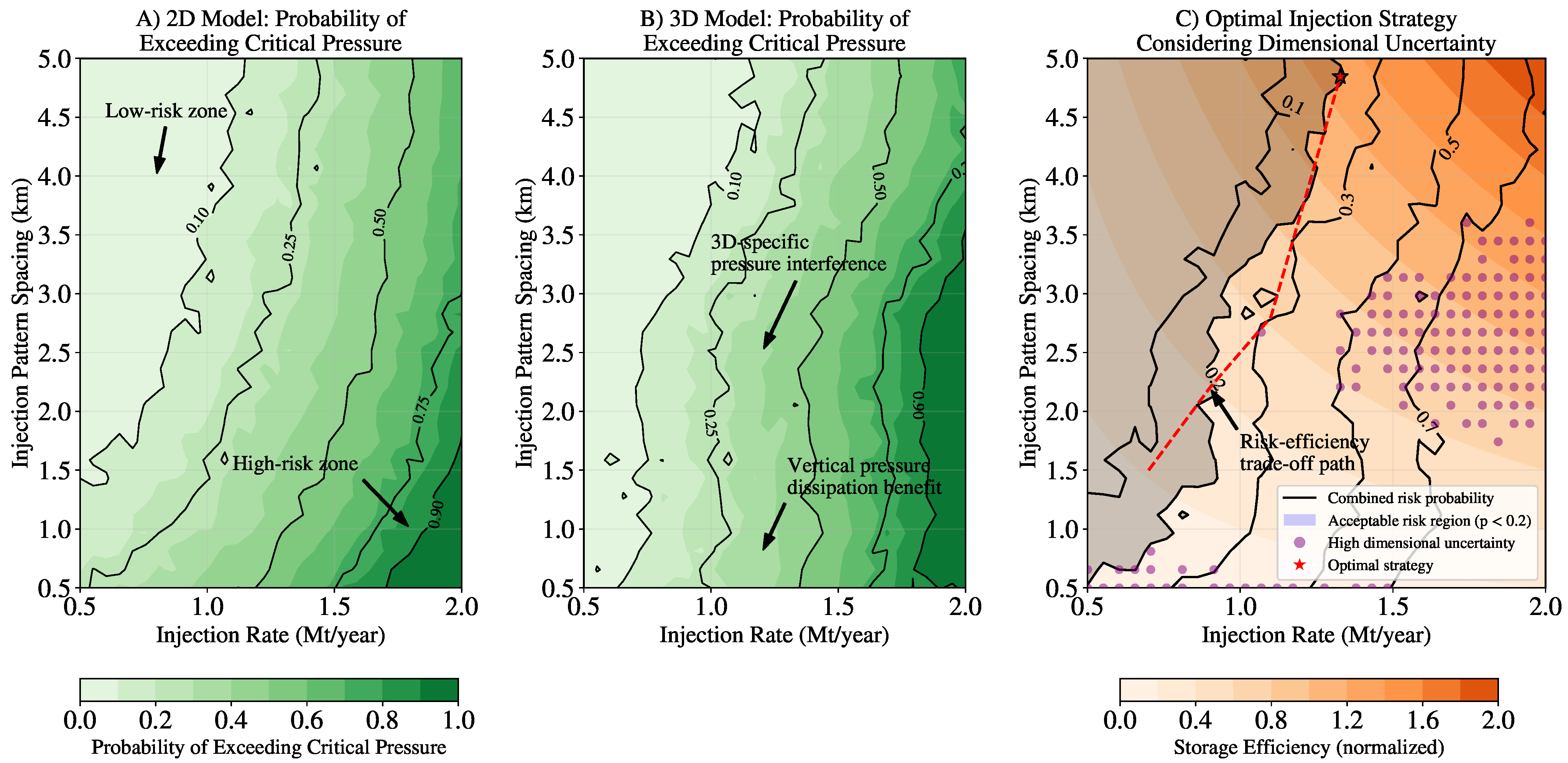
4.5. Application to Risk Assessment
4.6. Generalizability to Different Geological Settings
5. Discussion
5.1. Implications for Carbon Storage Modeling
5.2. Advantages and Limitations of the Machine Learning Approach
5.3. Computational Considerations and Scalability
5.4. Implementation Challenges and Regulatory Considerations
5.5. Real-World Field Data Integration and Preprocessing
5.6. Dimensional Uncertainty Gap and Monitoring Implications
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BNN | Bayesian Neural Network |
| CCS | Carbon Capture and Storage |
| CNN | Convolutional Neural Network |
| DA-BNN | Dimension-Adaptive Bayesian Neural Network |
| DoE | Design of Experiments |
| GPU | Graphics Processing Unit |
| IPCC | Intergovernmental Panel on Climate Change |
| LHS | Latin Hypercube Sampling |
| MC | Monte Carlo |
| ML | Machine Learning |
| MPIW | Mean Prediction Interval Width |
| PCE | Polynomial Chaos Expansion |
| PICP | Prediction Interval Coverage Probability |
| PVT | Pressure-Volume-Temperature |
| RMSE | Root Mean Square Error |
| SI | Système International (International System of Units) |
| SSIM | Structural Similarity Index Measure |
| TL | Transfer Learning |
| TPU | Tensor Processing Unit |
| UQ | Uncertainty Quantification |
References
- Lee, H.; Calvin, K.; Dasgupta, D.; Krinner, G.; Mukherji, A.; Thorne, P.; Trisos, C.; Romero, J.; Aldunce, P.; Barret, K.; et al. IPCC, 2023: Climate Change 2023: Synthesis Report, Summary for Policymakers, Proceedings of the Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, Geneva, Switzerland, 26 June 2023; Core Writing Team, Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023. [Google Scholar]
- Haque, F.; Santos, R.M.; Chiang, Y.W. Urban farming with enhanced rock weathering as a prospective climate stabilization wedge. Environ. Sci. Technol. 2021, 55, 13575–13578. [Google Scholar] [CrossRef] [PubMed]
- Chronopoulos, T.; Fernandez-Diez, Y.; Maroto-Valer, M.M.; Ocone, R.; Reay, D.A. CO2 desorption via microwave heating for post-combustion carbon capture. Microporous Mesoporous Mater. 2014, 197, 288–290. [Google Scholar] [CrossRef]
- Fentaw, J.W.; Emadi, H.; Hussain, A.; Fernandez, D.M.; Thiyagarajan, S.R. Geochemistry in Geological CO2 Sequestration: A Comprehensive Review. Energies 2024, 17, 5000. [Google Scholar] [CrossRef]
- Dai, S.; Liao, T.; Wu, Y. Progress of CO2 geological storage research, policy development and suggestions in China. Carbon Manag. 2025, 16, 2485104. [Google Scholar] [CrossRef]
- Zuberi, M.J.S.; Shehabi, A.; Rao, P. Cross-sectoral assessment of CO2 capture from US industrial flue gases for fuels and chemicals manufacture. Int. J. Greenh. Gas Control 2024, 135, 104137. [Google Scholar] [CrossRef]
- Flemisch, B.; Nordbotten, J.M.; Fernø, M.; Juanes, R.; Both, J.W.; Class, H.; Delshad, M.; Doster, F.; Ennis-King, J.; Franc, J.; et al. The FluidFlower validation benchmark study for the storage of CO2. Transp. Porous Media 2024, 151, 865–912. [Google Scholar] [CrossRef]
- Wen, G.; Li, Z.; Long, Q.; Azizzadenesheli, K.; Anandkumar, A.; Benson, S.M. Real-time high-resolution CO2 geological storage prediction using nested Fourier neural operators. Energy Environ. Sci. 2023, 16, 1732–1741. [Google Scholar] [CrossRef]
- Enyi, Y.; Yuan, D.; Hui, W.; Xiaopeng, C.; Qingfu, Z.; Chuanbao, Z. Numerical simulation on risk analysis of CO2 geological storage under multi-field coupling: A review. Chin. J. Theor. Appl. Mech. 2023, 55, 2075–2090. [Google Scholar]
- Mahjour, S.K.; Faroughi, S.A. Risks and uncertainties in carbon capture, transport, and storage projects: A comprehensive review. Gas Sci. Eng. 2023, 119, 205117. [Google Scholar] [CrossRef]
- Saad, B.M.; Alexanderian, A.; Prudhomme, S.; Knio, O.M. Probabilistic modeling and global sensitivity analysis for CO2 storage in geological formations: A spectral approach. Appl. Math. Model. 2018, 53, 584–601. [Google Scholar] [CrossRef]
- Brown, C.F.; Lackey, G.; Mitchell, N.; Baek, S.; Schwartz, B.; Dean, M.; Dilmore, R.; Blanke, H.; O’Brien, S.; Rowe, C. Integrating risk assessment methods for carbon storage: A case study for the quest carbon capture and storage facility. Int. J. Greenh. Gas Control 2023, 129, 103972. [Google Scholar] [CrossRef]
- Köppel, M.; Franzelin, F.; Kröker, I.; Oladyshkin, S.; Santin, G.; Wittwar, D.; Barth, A.; Haasdonk, B.; Nowak, W.; Pflüger, D.; et al. Comparison of data-driven uncertainty quantification methods for a carbon dioxide storage benchmark scenario. Comput. Geosci. 2019, 23, 339–354. [Google Scholar] [CrossRef]
- Mahjour, S.K.; Santos, A.A.S.; Santos, S.M.d.G.; Schiozer, D.J. Selection of representative scenarios using multiple simulation outputs for robust well placement optimization in greenfields. In Proceedings of the SPE Annual Technical Conference and Exhibition? Dubai, United Arab Emirates, 21–23 September 2021; p. D011S020R003. [Google Scholar]
- Jenkins, C.; Pestman, P.; Carragher, P.; Constable, R. Long-term risk assessment of subsurface carbon storage: Analogues, workflows and quantification. Geoenergy 2024, 2, geoenergy2024-014. [Google Scholar] [CrossRef]
- Alqahtani, A.; He, X.; Yan, B.; Hoteit, H. Uncertainty analysis of CO2 storage in deep saline aquifers using machine learning and Bayesian optimization. Energies 2023, 16, 1684. [Google Scholar] [CrossRef]
- Abdellatif, A.; Elsheikh, A.H.; Busby, D.; Berthet, P. Generation of non-stationary stochastic fields using Generative Adversarial Networks with limited training data. arXiv 2022, arXiv:2205.05469. [Google Scholar]
- Chandrasekaran, S.; Gorman, C.; Mhaskar, H.N. Minimum Sobolev norm interpolation of scattered derivative data. J. Comput. Phys. 2018, 365, 149–172. [Google Scholar] [CrossRef]
- Liu, N.; Jia, W.; Qin, S. A smooth gradient approximation neural network for general constrained nonsmooth nonconvex optimization problems. Neural Netw. 2025, 184, 107121. [Google Scholar] [CrossRef]
- Tangestani, E.; Ghanbarzadeh, S.; Garcia, J.F. Prediction of catalytic hydrogen generation by water–gas shift reaction using a neural network approach. Catal. Lett. 2023, 153, 863–875. [Google Scholar] [CrossRef]
- Mura, M.; Sharma, M.M. Mechanisms of Degradation of Cement in CO2 Injection Wells: Maintaining the Integrity of CO2 Seals. In Proceedings of the SPE International Conference and Exhibition on Formation Damage Control, Dubai, United Arab Emirates, 21–23 September 2021; p. D011S006R004. [Google Scholar]
- Wang, Q.Y. High order difference schemes for nonlinear Riesz space variable-order fractional diffusion equations. Comput. Math. Appl. 2025, 188, 221–243. [Google Scholar] [CrossRef]
- Hermans, T.; Goderniaux, P.; Jougnot, D.; Fleckenstein, J.H.; Brunner, P.; Nguyen, F.; Linde, N.; Huisman, J.A.; Bour, O.; Lopez Alvis, J.; et al. Advancing measurements and representations of subsurface heterogeneity and dynamic processes: Towards 4D hydrogeology. Hydrol. Earth Syst. Sci. 2023, 27, 255–287. [Google Scholar] [CrossRef]
- Kutsienyo, E.J.; Appold, M.S.; White, M.D.; Ampomah, W. Numerical modeling of CO2 sequestration within a five-spot well pattern in the morrow B sandstone of the farnsworth hydrocarbon field: Comparison of the toughreact, stomp-eor, and gem simulators. Energies 2021, 14, 5337. [Google Scholar] [CrossRef]
- Kim, K.Y.; Oh, J.; Han, W.S.; Park, K.G.; Shinn, Y.J.; Park, E. Two-phase flow visualization under reservoir conditions for highly heterogeneous conglomerate rock: A core-scale study for geologic carbon storage. Sci. Rep. 2018, 8, 4869. [Google Scholar] [CrossRef] [PubMed]
- Alamara, H.; Blondeau, C.; Thibeau, S.; Bogdanov, I. Vertical Equilibrium Simulation for Industrial-Scale CO2 Storage in Heterogeneous Aquifers. Sci. Rep. 2025, 15, 17115. [Google Scholar] [CrossRef]
- Templeton, D.C.; Schoenball, M.; Layland-Bachmann, C.; Foxall, W.; Guglielmi, Y.; Kroll, K.; Burghardt, J.; Dilmore, R.; White, J. Recommended Practices for Managing Induced Seismicity Risk Associated with Geologic Carbon Storage; Technical Report; Lawrence Livermore National Laboratory (LLNL): Livermore, CA, USA, 2021. [Google Scholar]
- Juanes, R.; MacMinn, C.W.; Szulczewski, M.L. The footprint of the CO2 plume during carbon dioxide storage in saline aquifers: Storage efficiency for capillary trapping at the basin scale. Transp. Porous Media 2010, 82, 19–30. [Google Scholar] [CrossRef]
- Khan, S.; Han, H.; Ansari, S.; Khosravi, N. An integrated geomechanics workflow for Caprock-integrity analysis of a potential carbon storage. In Proceedings of the SPE International Conference on CO2 Capture, Storage, and Utilization, New Orleans, LA, USA, 10–12 November 2010; p. SPE-139477. [Google Scholar]
- Postma, T.; Bandilla, K.; Peters, C.; Celia, M. Field-Scale Modeling of CO2 Mineral Trapping in Reactive Rocks: A Vertically Integrated Approach. Water Resour. Res. 2022, 58, e2021WR030626. [Google Scholar] [CrossRef]
- Ahmadinia, M.; Shariatipour, S.M.; Andersen, O.; Sadri, M. Benchmarking of vertically integrated models for the study of the impact of caprock morphology on CO2 migration. Int. J. Greenh. Gas Control 2019, 90, 102802. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Y.; Zhang, Q.; Wang, Q.; Song, H.; Sun, H.; Zhang, L.; Zhong, J.; Zhang, K.; Yao, J. Pore scale modeling of wettability impact on CO2 capillary and dissolution trapping in natural porous media. Adv. Water Resour. 2025, 201, 104982. [Google Scholar] [CrossRef]
- Bachu, S. Review of CO2 storage efficiency in deep saline aquifers. Int. J. Greenh. Gas Control 2015, 40, 188–202. [Google Scholar] [CrossRef]
- Zhang, Q.; Hirsch, R.M. River water-quality concentration and flux estimation can be improved by accounting for serial correlation through an autoregressive model. Water Resour. Res. 2019, 55, 9705–9723. [Google Scholar] [CrossRef]
- Joel, A.S.; Wang, M.; Ramshaw, C.; Oko, E. Process analysis of intensified absorber for post-combustion CO2 capture through modelling and simulation. Int. J. Greenh. Gas Control 2014, 21, 91–100. [Google Scholar] [CrossRef]
- Li, B.; Li, Y.E. Neural network-based co2 interpretation from 4d sleipner seismic images. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022524. [Google Scholar] [CrossRef]
- Wang, H.; Kou, Z.; Ji, Z.; Wang, S.; Li, Y.; Jiao, Z.; Johnson, M.; McLaughlin, J.F. Investigation of enhanced CO2 storage in deep saline aquifers by WAG and brine extraction in the Minnelusa sandstone, Wyoming. Energy 2023, 265, 126379. [Google Scholar] [CrossRef]
- Hamed, M.; Shirif, E. Sustainable CO2 Storage Assessment in Saline Aquifers Using a Hybrid ANN and Numerical Simulation Model Across Different Trapping Mechanisms. Sustainability 2025, 17, 2904. [Google Scholar] [CrossRef]
- Kim, S.; Hosseini, S.A. Above-zone pressure monitoring and geomechanical analyses for a field-scale CO2 injection project in Cranfield, MS. Greenh. Gases: Sci. Technol. 2014, 4, 81–98. [Google Scholar] [CrossRef]
- James, O.; Alokla, K.; Voulanas, D.; Okoroafor, R. Exploring Sparsity-Promoting Dynamic Mode Decomposition for Data-Driven Reduced Order Modeling of Geological CO2 Storage. In Proceedings of the SPE Annual Technical Conference and Exhibition? New Orleans, LA, USA, 23–25 November 2024; p. D021S028R006. [Google Scholar]
- Zhou, Z.; Zabaras, N.; Tartakovsky, D.M. Deep learning for simultaneous inference of hydraulic and transport properties. Water Resour. Res. 2022, 58, e2021WR031438. [Google Scholar] [CrossRef]
- Panda, N.; Osthus, D.; Srinivasan, G.; O’Malley, D.; Chau, V.; Wen, D.; Godinez, H. Mesoscale informed parameter estimation through machine learning: A case-study in fracture modeling. J. Comput. Phys. 2020, 420, 109719. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Zhang, N. Advancing practical geological CO2 sequestration simulations through transfer learning integration and physics-informed networks. Gas Sci. Eng. 2025, 134, 205523. [Google Scholar] [CrossRef]
- Kazemi, A.; Esmaeili, M. Reservoir Surrogate Modeling Using U-Net with Vision Transformer and Time Embedding. Processes 2025, 13, 958. [Google Scholar] [CrossRef]
- Hillier, M.; Wellmann, F.; Brodaric, B.; de Kemp, E.; Schetselaar, E. Three-dimensional structural geological modeling using graph neural networks. Math. Geosci. 2021, 53, 1725–1749. [Google Scholar] [CrossRef]
- Wang, Y.; Chu, H.; Lyu, X. Deep learning in CO2 geological utilization and storage: Recent advances and perspectives. Adv. Geo-Energy Res. 2024, 13, 161–165. [Google Scholar] [CrossRef]
- Kamil, H.; Soulaïmani, A.; Beljadid, A. A transfer learning physics-informed deep learning framework for modeling multiple solute dynamics in unsaturated soils. Comput. Methods Appl. Mech. Eng. 2024, 431, 117276. [Google Scholar] [CrossRef]
- Le, V.H.; Caumon, M.C.; Tarantola, A. FRAnCIs calculation program with universal Raman calibration data for the determination of PVX properties of CO2-CH4-N2 and CH4-H2O-NaCl systems and their uncertainties. Comput. Geosci. 2021, 156, 104896. [Google Scholar] [CrossRef]
- Amrouche, F.; Xu, D.; Short, M.; Iglauer, S.; Vinogradov, J.; Blunt, M.J. Experimental study of electrical heating to enhance oil production from oil-wet carbonate reservoirs. Fuel 2022, 324, 124559. [Google Scholar] [CrossRef]
- Sun, L.; Gao, H.; Pan, S.; Wang, J.X. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data. Comput. Methods Appl. Mech. Eng. 2020, 361, 112732. [Google Scholar] [CrossRef]
- Zhu, L.; Lu, W.; Luo, C. A high-precision and interpretability-enhanced direct inversion framework for groundwater contaminant source identification using multiple machine learning techniques. J. Hydrol. 2025, 659, 133237. [Google Scholar] [CrossRef]
- Kovshov, V.; Lukyanova, M.; Zalilova, Z.; Frolova, O.; Galin, Z. International regional competitiveness of rural territories as a factor of their socio-economic development: Methodological aspects. Heliyon 2024, 10, e23795. [Google Scholar] [CrossRef] [PubMed]
- Faghani, S.; Gamble, C.; Erickson, B.J. Uncover this tech term: Uncertainty quantification for deep learning. Korean J. Radiol. 2024, 25, 395. [Google Scholar] [CrossRef]
- Mahjour, S.K.; Badhan, J.H.; Faroughi, S.A. Uncertainty Quantification in CO2 Trapping Mechanisms: A Case Study of PUNQ-S3 Reservoir Model Using Representative Geological Realizations and Unsupervised Machine Learning. Energies 2024, 17, 1180. [Google Scholar] [CrossRef]
- Faghani, S.; Moassefi, M.; Rouzrokh, P.; Khosravi, B.; Baffour, F.I.; Ringler, M.D.; Erickson, B.J. Quantifying uncertainty in deep learning of radiologic images. Radiology 2023, 308, e222217. [Google Scholar] [CrossRef]
- Mahjour, S.K.; Santos, A.A.S.; Correia, M.G.; Schiozer, D.J. Scenario reduction methodologies under uncertainties for reservoir development purposes: Distance-based clustering and metaheuristic algorithm. J. Pet. Explor. Prod. Technol. 2021, 11, 3079–3102. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Marrero, C.O.; Perdikaris, P.; Tartakovsky, G.D.; Barajas-Solano, D. Physics-informed deep neural networks for learning parameters and constitutive relationships in subsurface flow problems. Water Resour. Res. 2020, 56, e2019WR026731. [Google Scholar] [CrossRef]
- Moortgat, J.; Amooie, M.A.; Soltanian, M.R. Implicit finite volume and discontinuous Galerkin methods for multicomponent flow in unstructured 3D fractured porous media. Adv. Water Resour. 2016, 96, 389–404. [Google Scholar] [CrossRef]
- Berends, K.D.; Ji, U.; Penning, W.E.; Warmink, J.J.; Kang, J.; Hulscher, S.J. Stream-scale flow experiment reveals large influence of understory growth on vegetation roughness. Adv. Water Resour. 2020, 143, 103675. [Google Scholar] [CrossRef]
- Xiao, W.; Shen, Y.; Zhao, J.; Lv, L.; Chen, J.; Zhao, W. An Adaptive Multi-Fidelity Surrogate Model for Uncertainty Propagation Analysis. Appl. Sci. 2025, 15, 3359. [Google Scholar] [CrossRef]
- Mahjour, S.K.; da Silva, L.O.M.; Meira, L.A.A.; Coelho, G.P.; dos Santos, A.A.d.S.; Schiozer, D.J. Evaluation of unsupervised machine learning frameworks to select representative geological realizations for uncertainty quantification. J. Pet. Sci. Eng. 2022, 209, 109822. [Google Scholar] [CrossRef]
- Fernández-Godino, M.G. Review of multi-fidelity models. arXiv 2016, arXiv:1609.07196. [Google Scholar]
- Nole, M.; Bartrand, J.; Naim, F.; Hammond, G. Modeling commercial-scale CO 2 storage in the gas hydrate stability zone with PFLOTRAN v6. 0. Geosci. Model Dev. 2025, 18, 1413–1425. [Google Scholar] [CrossRef]
- Alzahrani, M.K.; Shapoval, A.; Chen, Z.; Rahman, S.S. MicroGraphNets: Automated characterization of the micro-scale wettability of porous media using graph neural networks. Capillarity 2024, 12, 57–71. [Google Scholar] [CrossRef]
- Fang, X.; Lv, Y.; Yuan, C.; Zhu, X.; Guo, J.; Liu, W.; Li, H. Effects of reservoir heterogeneity on CO2 dissolution efficiency in randomly multilayered formations. Energies 2023, 16, 5219. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, Y.; Pang, H.; Lin, B. Upscaling for Full-Physics Models of CO2 Injection Into Saline Aquifers. SPE J. 2025, 30, 3065–3082. [Google Scholar] [CrossRef]
- Shah, S.Y.A.; Du, J.; Iqbal, S.M.; Du, L.; Khan, U.; Zhang, B.; Tan, J. Integrated Three-Dimensional Structural and Petrophysical Modeling for Assessment of CO2 Storage Potential in Gas Reservoir. Lithosphere 2024, 2024, lithosphere_2024_222. [Google Scholar] [CrossRef]
- Vo Thanh, H.; Sugai, Y.; Sasaki, K. Impact of a new geological modelling method on the enhancement of the CO2 storage assessment of E sequence of Nam Vang field, offshore Vietnam. Energy Sources, Part A: Recover. Util. Environ. Eff. 2020, 42, 1499–1512. [Google Scholar] [CrossRef]
- Rathmaier, D.; Naim, F.; William, A.C.; Chakraborty, D.; Conwell, C.; Imhof, M.; Holmes, G.M.; Zerpa, L.E. A reservoir modeling study for the evaluation of CO2 storage upscaling at the decatur site in the Eastern Illinois Basin. Energies 2024, 17, 1212. [Google Scholar] [CrossRef]
- Petríková, D.; Cimrák, I. Survey of recent deep neural networks with strong annotated supervision in histopathology. Computation 2023, 11, 81. [Google Scholar] [CrossRef]
- Duchanoy, C.A.; Calvo, H.; Moreno-Armendáriz, M.A. ASAMS: An adaptive sequential sampling and automatic model selection for artificial intelligence surrogate modeling. Sensors 2020, 20, 5332. [Google Scholar] [CrossRef]
- Giljarhus, K.E.T.; Munkejord, S.T.; Skaugen, G. Solution of the Span–Wagner equation of state using a density–energy state function for fluid-dynamic simulation of carbon dioxide. Ind. Eng. Chem. Res. 2012, 51, 1006–1014. [Google Scholar] [CrossRef]
- Dilmore, R.M.; Allen, D.E.; Jones, J.R.M.; Hedges, S.W.; Soong, Y. Sequestration of dissolved CO2 in the Oriskany formation. Environ. Sci. Technol. 2008, 42, 2760–2766. [Google Scholar] [CrossRef]
- Liu, N.; Deng, W.; Li, F.; Wang, Z.; Wu, H.; Gao, J. Recent advances on deep residual learning based seismic data reconstruction: An overview. J. Geophys. Eng. 2025, 22, 854–876. [Google Scholar] [CrossRef]
- Mao, S.; Carbonero, A.; Mehana, M. Deep learning for subsurface flow: A comparative study of U-net, Fourier neural operators, and transformers in underground hydrogen storage. J. Geophys. Res. Mach. Learn. Comput. 2025, 2, e2024JH000401. [Google Scholar] [CrossRef]
- Bera, P.; Bhanja, S. Quantification of Uncertainties in Probabilistic Deep Neural Network by Implementing Boosting of Variational Inference. arXiv 2025, arXiv:2503.13909. [Google Scholar]
- Kummaraka, U.; Srisuradetchai, P. Monte Carlo Dropout Neural Networks for Forecasting Sinusoidal Time Series: Performance Evaluation and Uncertainty Quantification. Appl. Sci. 2025, 15, 4363. [Google Scholar] [CrossRef]
- Li, Z.; Hu, X.; Qian, J.; Zhao, T.; Xu, D.; Wang, Y. Self-Supervised Feature Contrastive Learning for Small Weak Object Detection in Remote Sensing. Remote Sens. 2025, 17, 1438. [Google Scholar] [CrossRef]
- Guo, Y.; Fu, Z.; Min, J.; Lin, S.; Liu, X.; Rashed, Y.F.; Zhuang, X. Long-term simulation of physical and mechanical behaviors using curriculum-transfer-learning based physics-informed neural networks. arXiv 2025, arXiv:2502.07325. [Google Scholar]
- Chen, Y.; Wan, Z.; Zhuang, Y.; Liu, N.; Lo, D.; Yang, X. Understanding the OSS Communities of Deep Learning Frameworks: A Comparative Case Study of PyTorch and TensorFlow. ACM Trans. Softw. Eng. Methodol. 2025, 34, 1–30. [Google Scholar]
- Yang, J.; Long, Q. A modification of adaptive moment estimation (adam) for machine learning. J. Ind. Manag. Optim. 2024, 20, 2516–2540. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Garain, B.C.; Pinheiro, M., Jr.; Bispo, M.O.; Barbatti, M. Enhancing Uncertainty Quantification in Molecular Machine Learning: A Comparative Study of Deep Evidential Regression and Ensembles with Posthoc Calibration. ChemRxiv 2025. [Google Scholar] [CrossRef]
- Pollak, M.F.; Wilson, E.J. Regulating geologic sequestration in the United States: Early rules take divergent approaches. Environ. Sci. Technol. 2009, 43, 3035–3041. [Google Scholar] [CrossRef]
- Shogenova, A.; Piessens, K.; Holloway, S.; Bentham, M.; Martínez, R.; Flornes, K.M.; Poulsen, N.E.; Wójcicki, A.; Sliaupa, S.; Kucharič, L.; et al. Implementation of the EU CCS Directive in Europe: Results and development in 2013. Energy Procedia 2014, 63, 6662–6670. [Google Scholar] [CrossRef]







| Feature | This Work | Zhu & Zabaras [18] | 3D CNNs [45] | Dropout-Based UQ [51] |
|---|---|---|---|---|
| Dimensional capability | 2D and 3D with cross-dimensional transfer | Single dimension (2D) | Single dimension (3D) | Single dimension (2D) |
| UQ approach | Bayesian neural networks with aleatoric and epistemic uncertainty separation | Bayesian deep convolutional encoder-decoder | Deterministic with ensemble-based UQ | Monte Carlo dropout |
| Physical constraints | Explicit physics-informed constraints | Implicit through data | None | None |
| Parameter interdependencies | Explicitly modeled | Not addressed | Not addressed | Not addressed |
| Computational efficiency | 104–105 × vs. Monte Carlo | 103 × vs. Monte Carlo | 103 × vs. Monte Carlo | 102 × vs. Monte Carlo |
| Real-world applicability | Tested on multiple geological scenarios | Limited to synthetic cases | Single reservoir type | Single reservoir type |
| Parameter | Minimum | Maximum | Units |
|---|---|---|---|
| Log-permeability mean (aquifer) | −14 | −12 | log (m2) |
| Log-permeability mean (aquitard) | −17 | −15 | log (m2) |
| Log-permeability variance | 0.5 | 2.0 | log (m2)2 |
| Porosity mean (aquifer) | 0.1 | 0.3 | - |
| Porosity mean (aquitard) | 0.05 | 0.15 | - |
| Porosity variance | 0.001 | 0.01 | - |
| Residual CO2 saturation | 0.05 | 0.3 | - |
| Residual brine saturation | 0.1 | 0.4 | - |
| Brooks–Corey exponent (CO2) | 1.5 | 4.0 | - |
| Brooks–Corey exponent (brine) | 1.5 | 4.0 | - |
| Entry pressure | Pa | ||
| Pore size distribution index | 0.3 | 0.7 | - |
| Anisotropy ratio (/) | 0.01 | 0.5 | - |
| Horizontal correlation length | 500 | 5000 | m |
| Vertical correlation length | 5 | 50 | m |
| Injection rate | 0.5 | 2.0 | Mt/year |
| Injection duration | 10 | 30 | years |
| Regional pressure gradient | 0 | 500 | Pa/m |
| Model | CO2 Saturation RMSE | Pressure RMSE (MPa) | ||
|---|---|---|---|---|
| 2D | 3D | 2D | 3D | |
| Dimension-specific | 0.035 | 0.058 | 0.17 | 0.31 |
| Dimension-adaptive (ours) | 0.031 | 0.042 | 0.15 | 0.22 |
| Improvement | 11.4% | 27.6% | 11.8% | 29.0% |
| Method | PICP (%) ± std | MPIW ± std | ||
|---|---|---|---|---|
| 2D | 3D | 2D | 3D | |
| Monte Carlo Dropout | 89.5 ± 2.1 | 86.2 ± 2.8 | 0.16 ± 0.02 | 0.21 ± 0.03 |
| Deep Ensembles | 92.3 ± 1.8 | 90.5 ± 2.2 | 0.19 ± 0.02 | 0.26 ± 0.03 |
| Gaussian Process | 94.2 ± 1.5 | N/A | 0.22 ± 0.03 | N/A |
| Our Framework | 93.8 ± 1.3 | 92.1 ± 1.9 | 0.18 ± 0.02 | 0.24 ± 0.02 |
| Method | Computation Time | Speedup Factor | Memory (MB) |
|---|---|---|---|
| Full Physics Simulation (2D) | 20 min | 1 × | N/A |
| Full Physics Simulation (3D) | 8 h | 1 × | N/A |
| Monte Carlo UQ (1000 samples, 2D) | 14 days | 1 × | N/A |
| Monte Carlo UQ (1000 samples, 3D) | 333 days | 1 × | N/A |
| Polynomial Chaos Expansion | 2–6 h | 102–103 | 50–100 |
| Sparse Grid Interpolation | 1–4 h | 102–103 | 100–200 |
| Our Framework (2D prediction) | 0.2 s | 6 × 103 | 125 |
| Our Framework (3D prediction) | 1.5 s | 1.9 × 104 | 400 |
| Our Framework (UQ, 2D) | 15 s | 8 × 104 | 125 |
| Our Framework (UQ, 3D) | 2 min | 2.4 × 105 | 400 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahjour, S.K.; Saleh, A.; Mahjour, S.S. Dimension-Adaptive Machine Learning for Efficient Uncertainty Quantification in Geological Carbon Storage Models. Processes 2025, 13, 1834. https://doi.org/10.3390/pr13061834
Mahjour SK, Saleh A, Mahjour SS. Dimension-Adaptive Machine Learning for Efficient Uncertainty Quantification in Geological Carbon Storage Models. Processes. 2025; 13(6):1834. https://doi.org/10.3390/pr13061834
Chicago/Turabian StyleMahjour, Seyed Kourosh, Ali Saleh, and Seyed Saman Mahjour. 2025. "Dimension-Adaptive Machine Learning for Efficient Uncertainty Quantification in Geological Carbon Storage Models" Processes 13, no. 6: 1834. https://doi.org/10.3390/pr13061834
APA StyleMahjour, S. K., Saleh, A., & Mahjour, S. S. (2025). Dimension-Adaptive Machine Learning for Efficient Uncertainty Quantification in Geological Carbon Storage Models. Processes, 13(6), 1834. https://doi.org/10.3390/pr13061834






