Mechanistic Insights into Ammonium Chloride Particle Deposition in Hydrogenation Air Coolers: Experimental and CFD-DEM Analysis
Abstract
1. Introduction
2. Simulation Methods
2.1. Governing Equations for Particle Models (DEM)
2.1.1. Particle Motion
2.1.2. Contact Force Models
- (1)
- Normal force
- (2)
- Tangential force
2.2. Governing Equations for Fluid Models (CFD)
2.3. Forces on Particles in a Flow Field
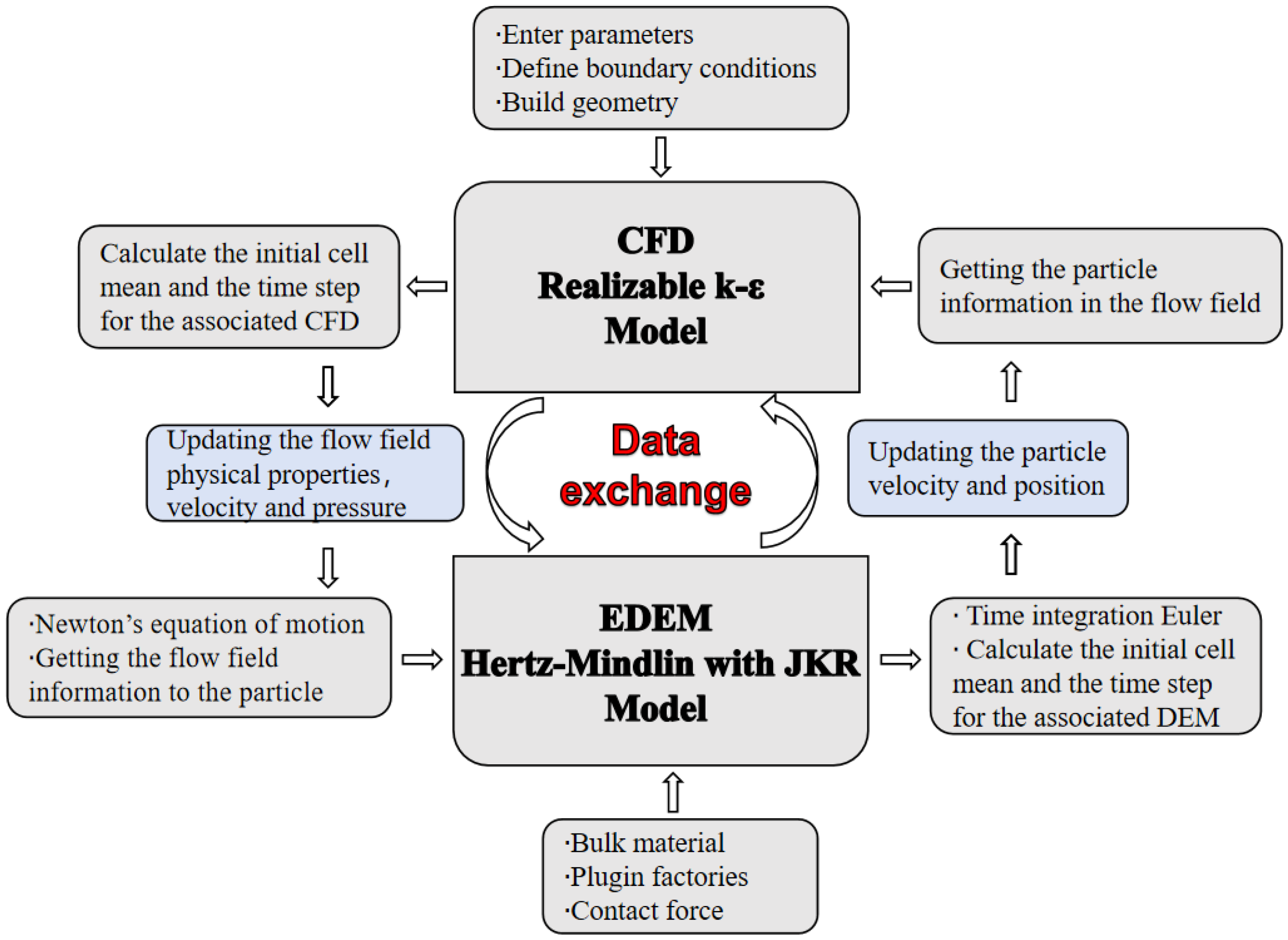
2.4. Coupling Process of the Fluid and Particles
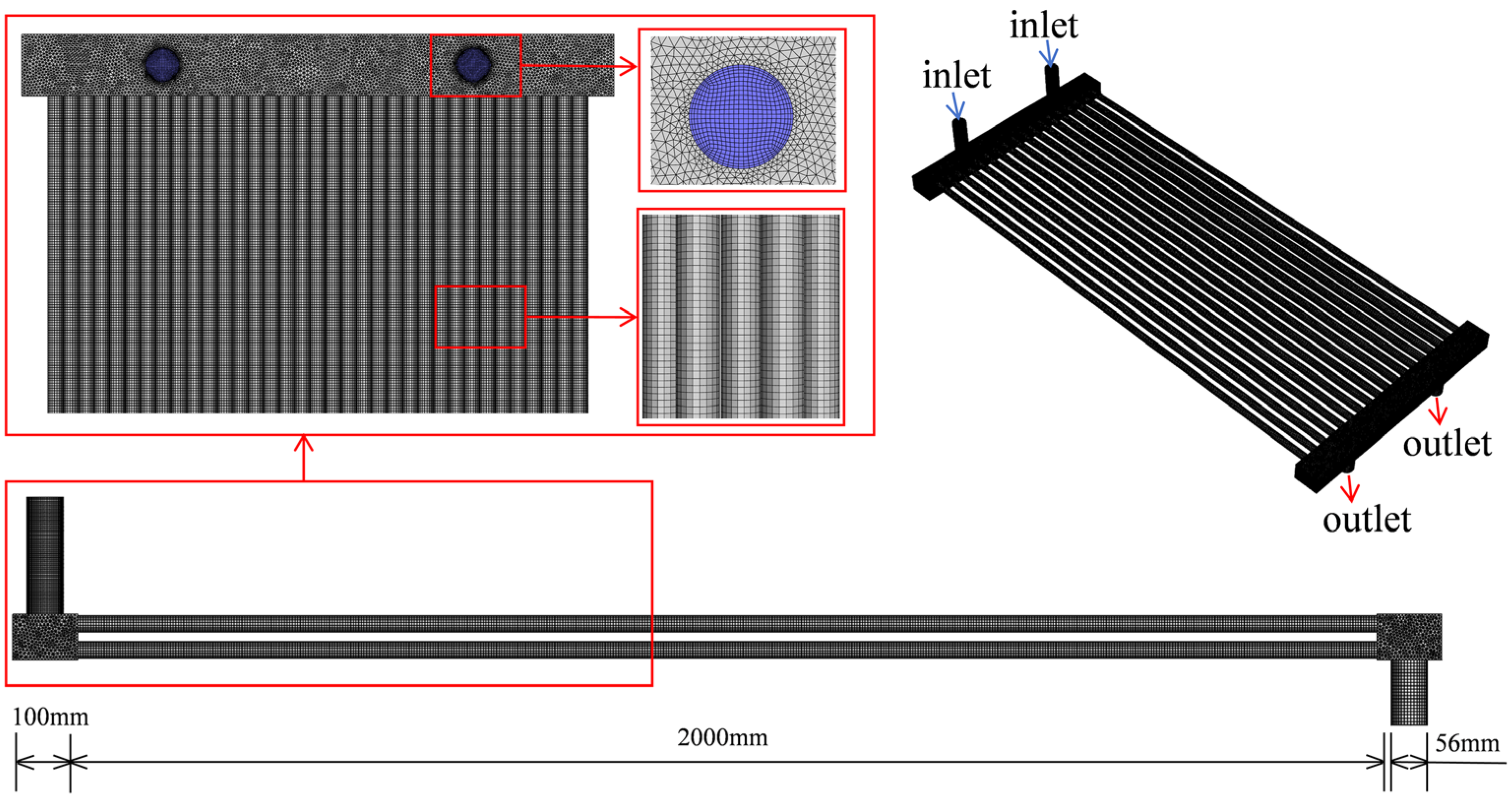
2.5. Geometric Modeling and Meshing
3. Experimental Method
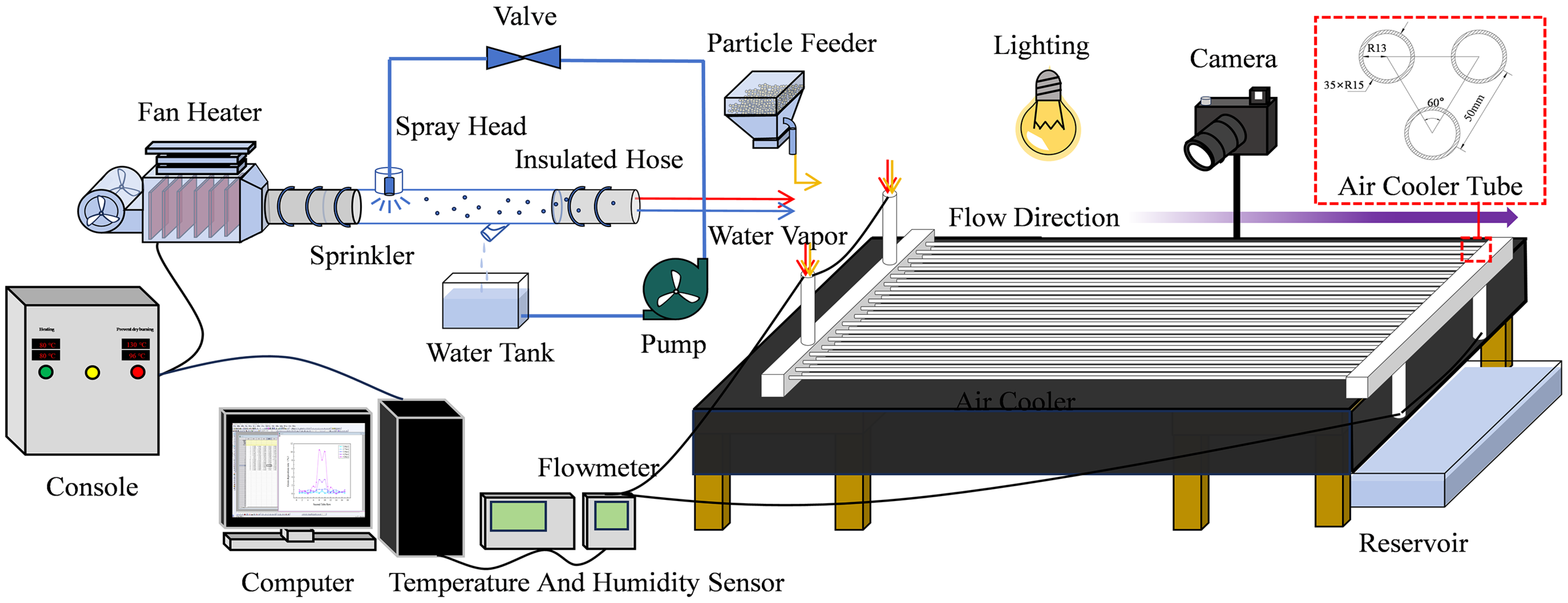
3.1. Experimental Setup
3.2. Experimental Operation
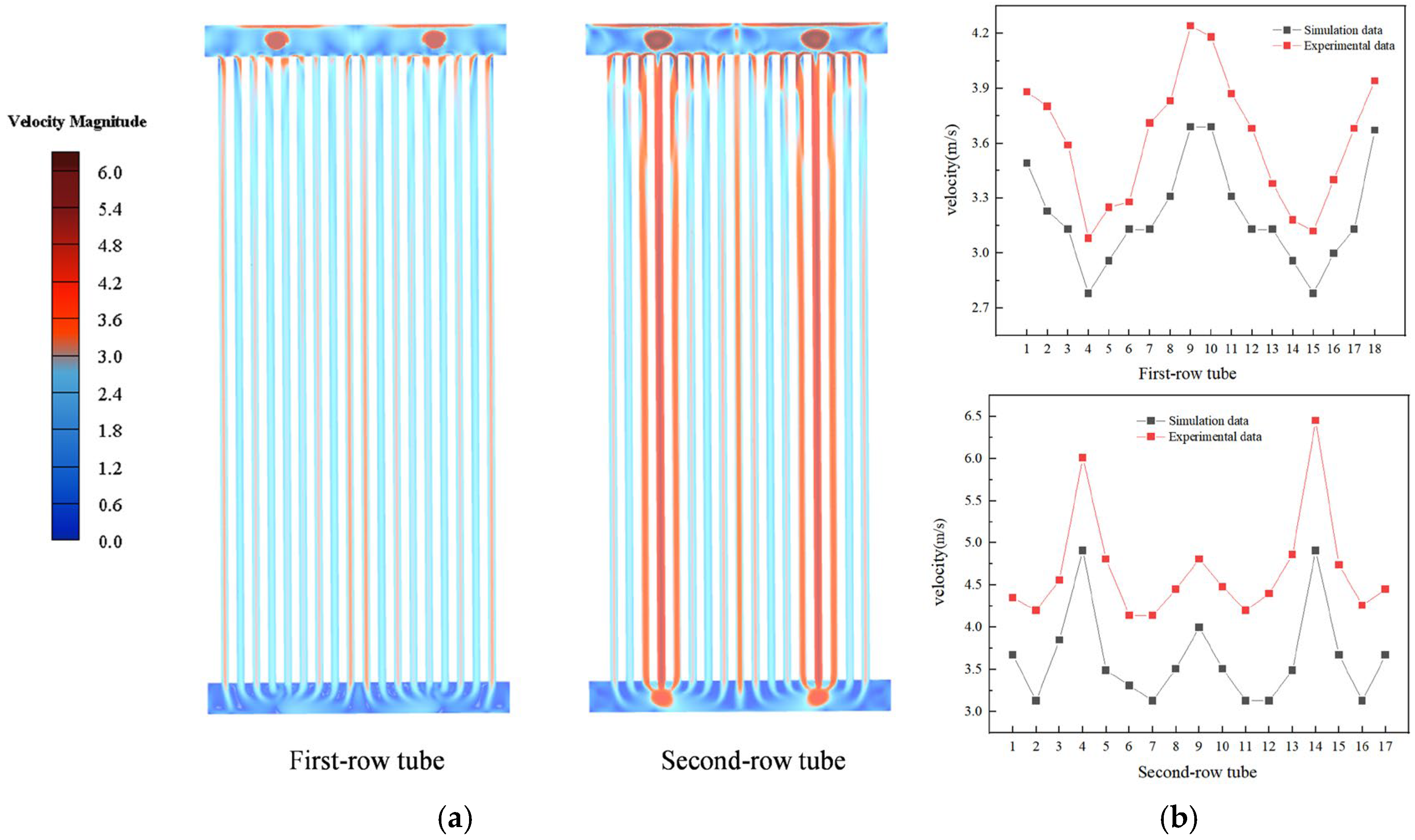
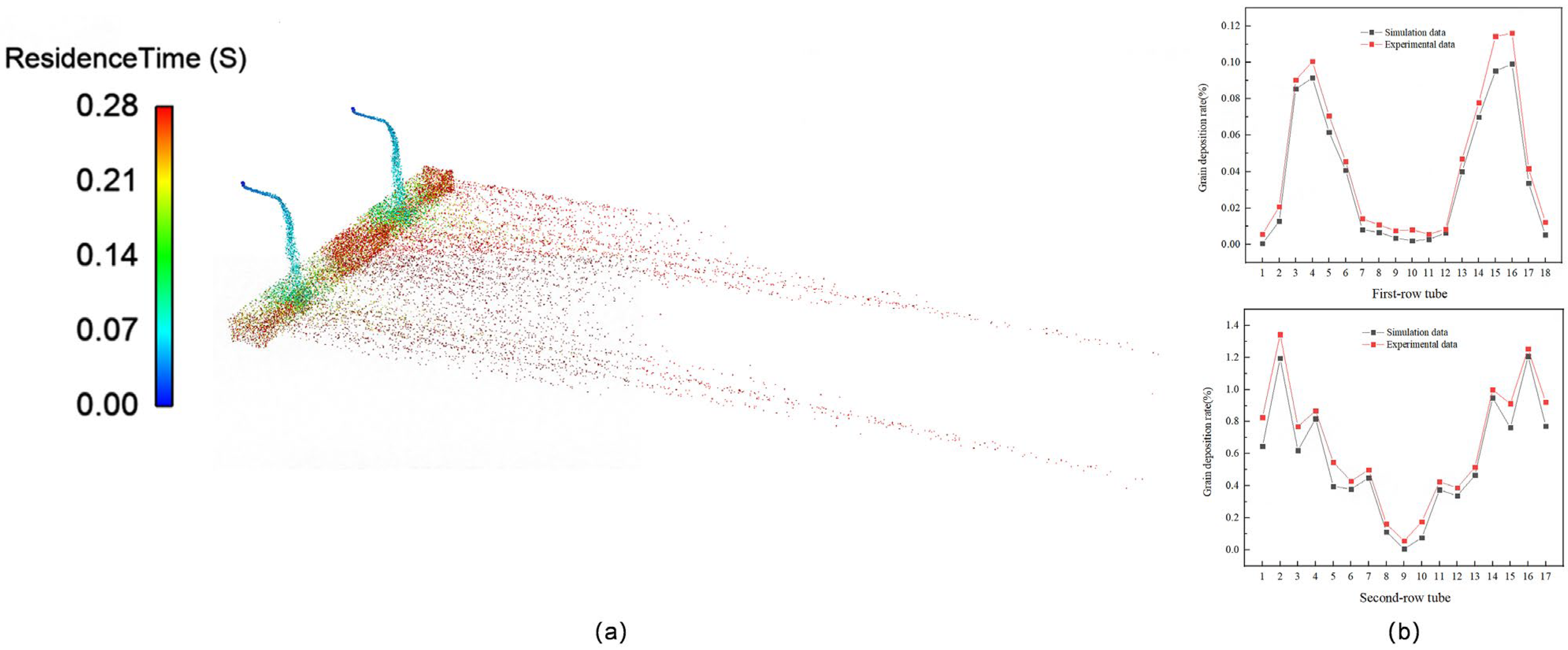
3.3. Validation of the Numerical Simulation Method
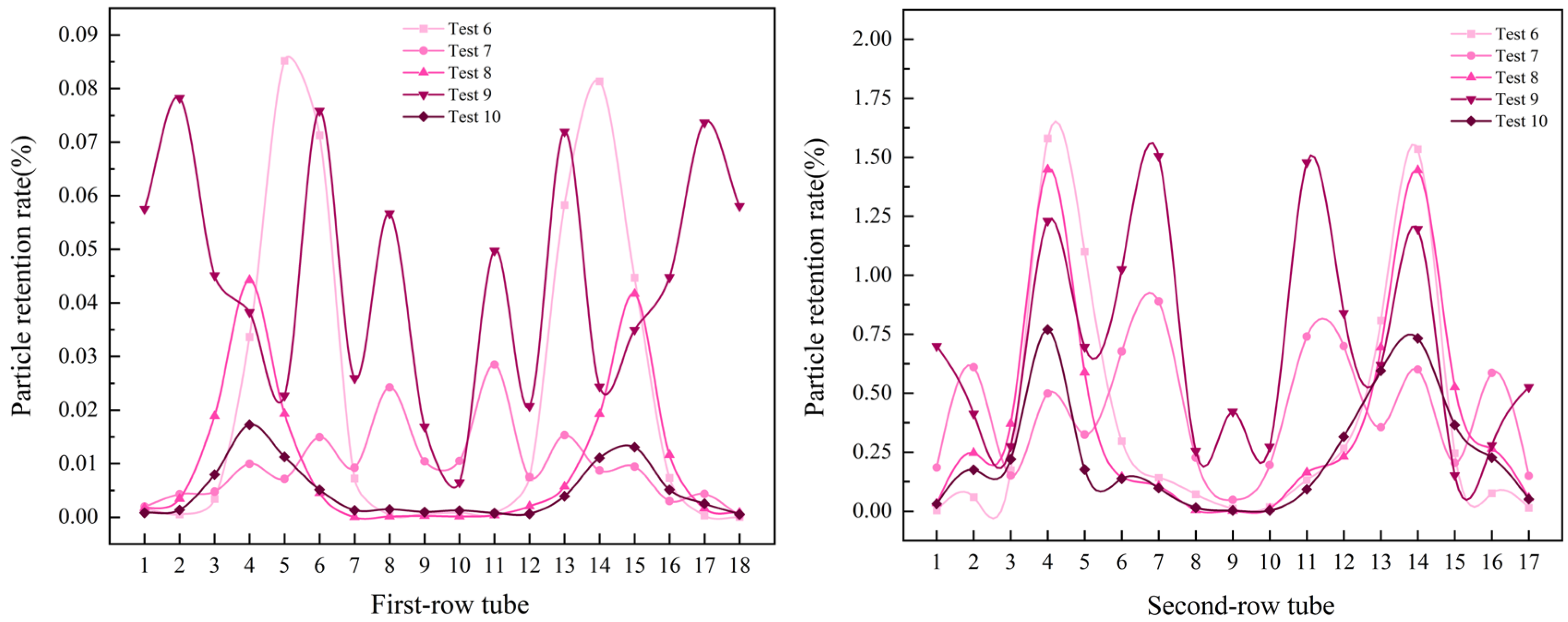
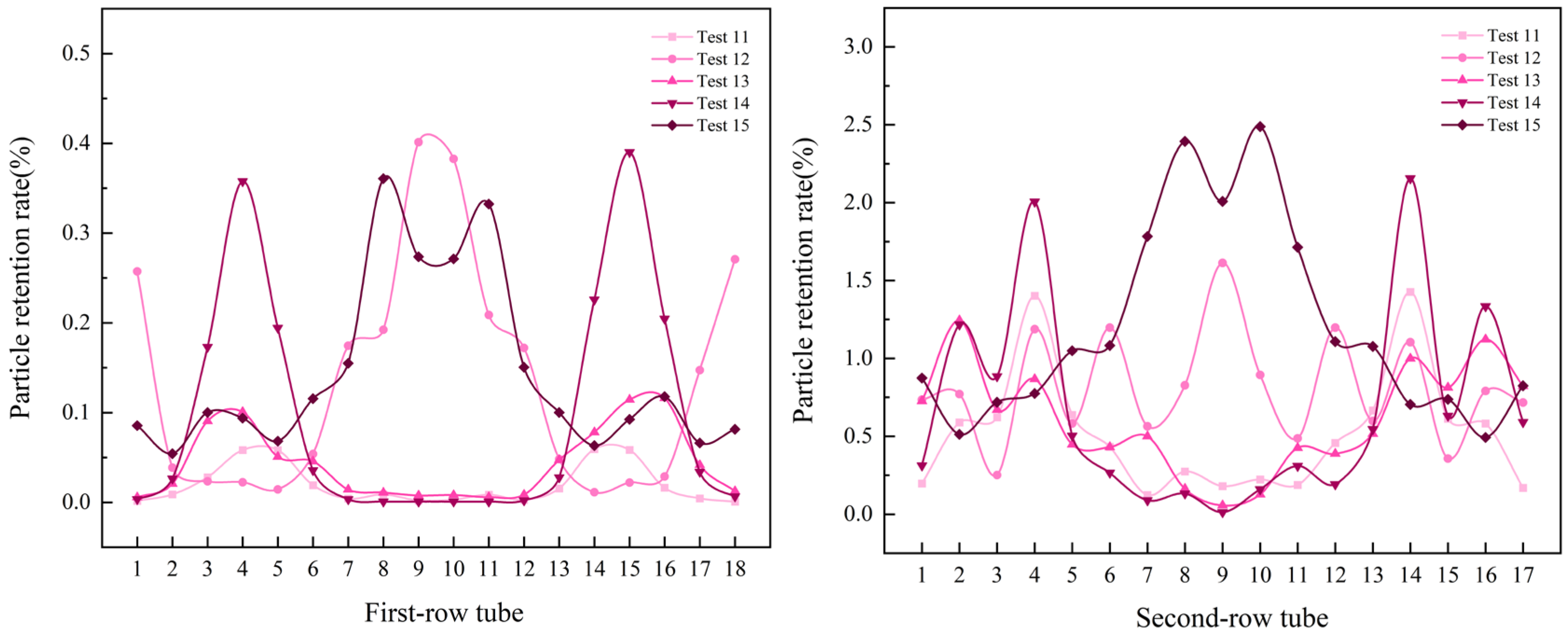
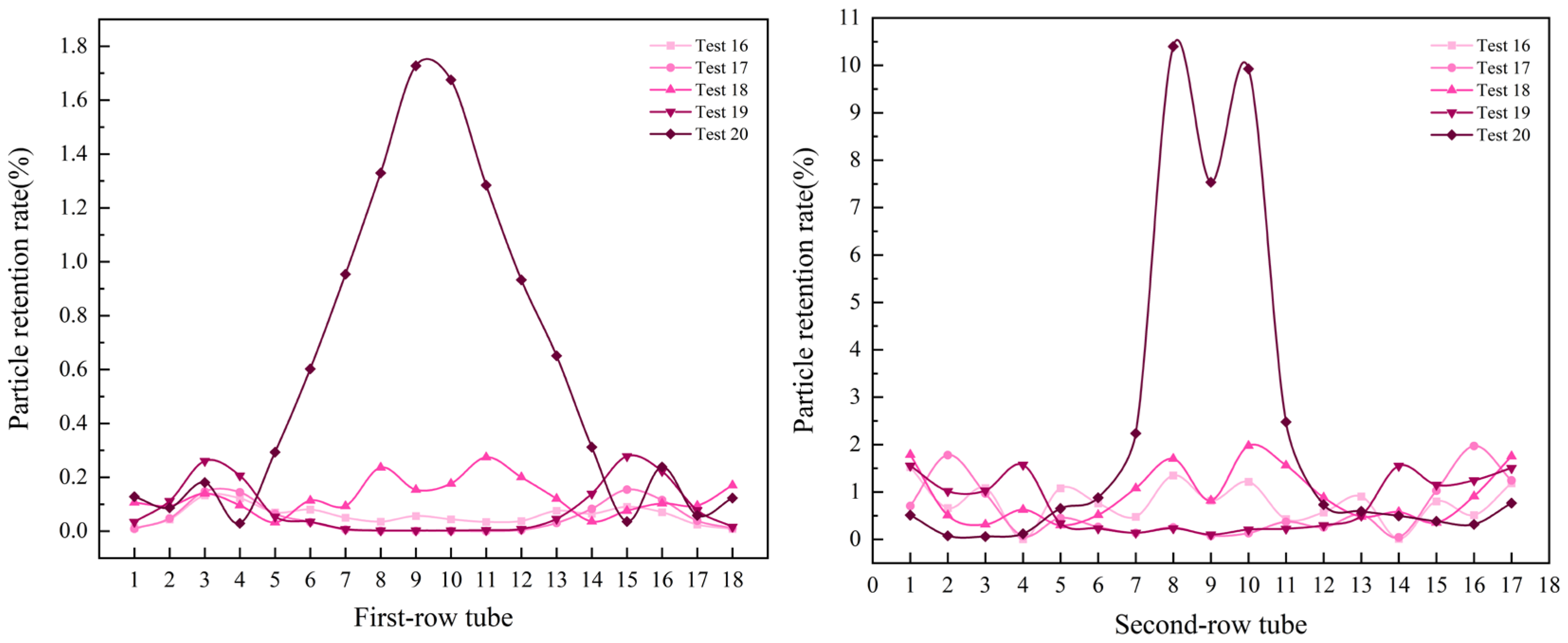
3.4. Effects of Multi-Factor Interactions
- (1)
- Effects of temperature and particle size at a flow velocity of 2 m/s
- (2)
- Effects of temperature and particle size at a flow velocity of 2.75 m/s
- (3)
- Effects of temperature and particle size at a flow velocity of 3.5 m/s
- (4)
- Effects of temperature and particle size at a flow velocity of 4.25 m/s
- (5)
- Effects of temperature and particle size at a flow velocity of 5 m/s
4. Results and Discussion
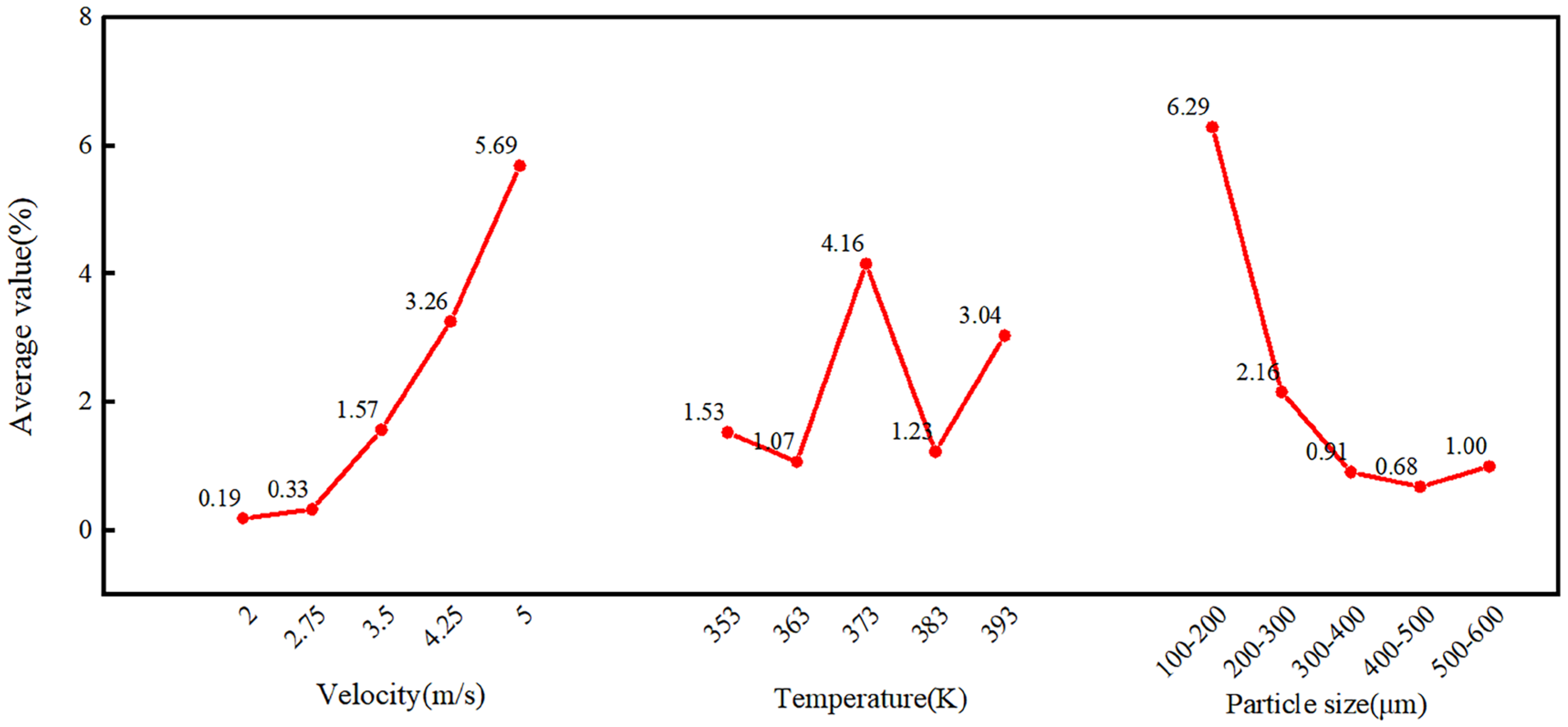
4.1. Range Analysis
4.2. Fitting with Equations
5. Conclusions
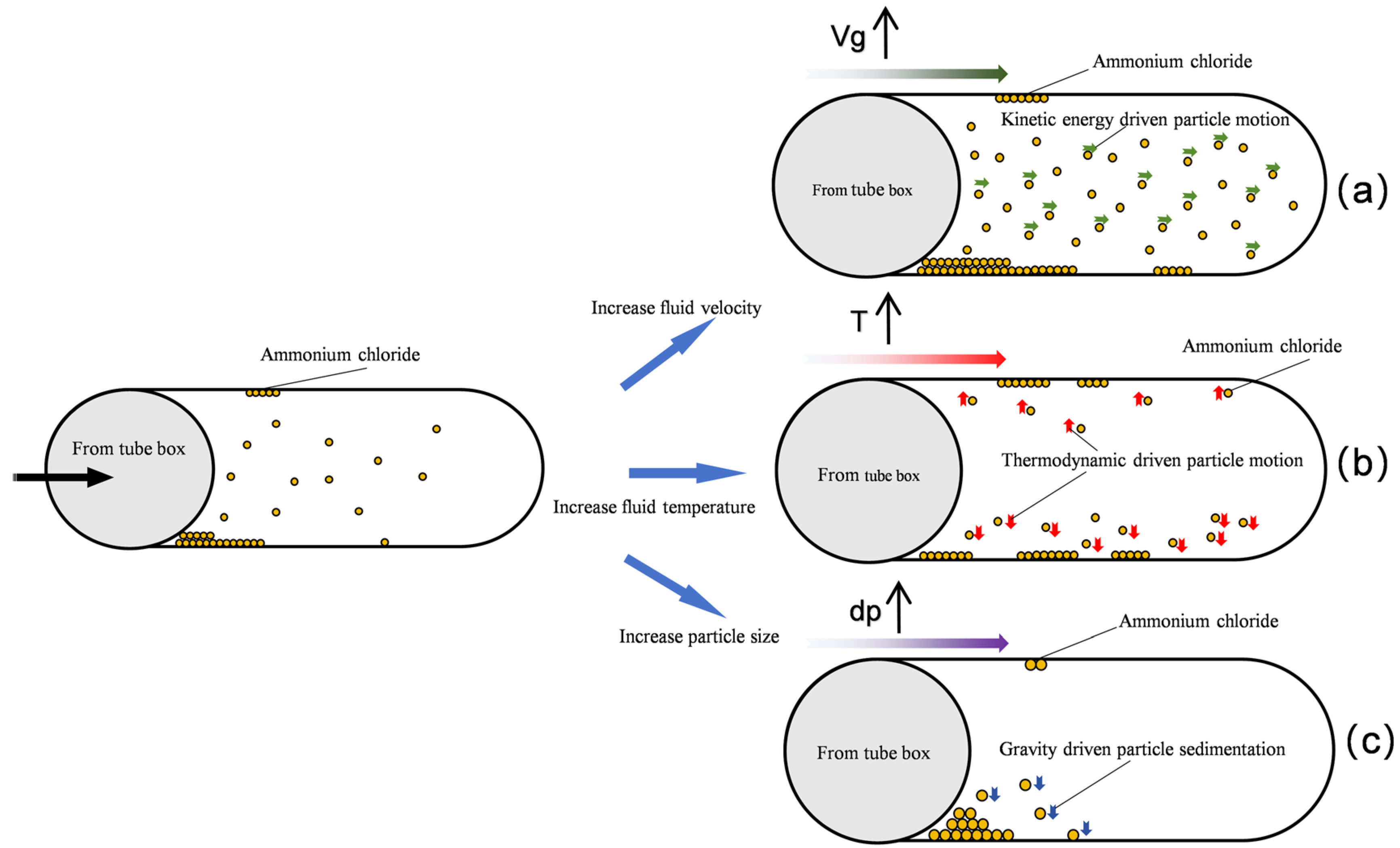
- The fluid resistance governs the distribution of NH4Cl particles deposited within the air-cooler tube bundle. However, the particle size modulates the dominance of the fluid resistance, with larger particles indirectly diminishing its influence through inertial effects. Under the conditions of a fluid velocity of 2 m/s, particle size of 400–500 μm, and temperature of 393 K, the minimum deposition rate of particles (4.43385%) in the tube bundle was observed, which is attributable to the synergistic effects of larger particle sizes at lower flow velocities, which promoted preferential deposition in the tube box. In contrast, a significantly higher particle deposition rate of 63.91887% was recorded at an elevated fluid velocity (5 m/s), smaller particle sizes (100–200 μm), and a temperature of 373 K. The increased particle deposition is due to the finer particles being more effectively entrained by the high-velocity fluid, resulting in intensified particle transport and accumulation within the tube bundle.
- The numerical simulation provided the following key results: for double-tube-row structures, the particle residence rate in the second tube row is significantly higher than that in the first tube row, and the spatial distribution of particles is highly sensitive to operational parameters. Furthermore, as the flow velocity and inlet temperature increase, particles tend to accumulate in the central region of the tube rows. Notably, the key parameters that influence the particle deposition behavior in the two tube rows differ significantly. For the first tube row, the order of the factor importance is particle size > flow velocity > inlet temperature, whereas that for the second tube row has a distinct sequence of flow velocity > particle size > inlet temperature. This finding conclusively indicates that in complex multiphase flow systems, hydrodynamic factors exert a more dominant influence on the particle deposition behavior than temperature fields and particle properties, particularly in the second-row tube region.
- The orthogonal experimental results were fitted with second-order polynomial and power-law equations. Between the two, the power-law equation provides superior accuracy in predicting the particle deposition rates. The power-law exponents revealed that for deposition rates in both the upper and lower tube rows, the gas velocity and temperature exhibit positive correlations, while the particle size shows a negative exponential relationship.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| CFD–DEM | Computational Fluid Dynamics–Discrete Element Method |
| DEM | Discrete Element Method |
| JKR | Johnson–Kendall–Roberts (contact model) |
| NH4Cl | Ammonium Chloride |
| PID | Proportional–Integral–Derivative |
| PMMA | Polymethyl Methacrylate |
| R2 | Coefficient of Determination |
| RMSE | Root-Mean-Square Error |
References
- Mao, Q.; Wang, Z.; Hu, Z.; Yang, Z.; Li, H.; Yao, Y.; Yong, Z.; Ma, T. Facial detection of formaldehyde by using acidichromic carbon dots and the reaction between formaldehyde and ammonium chloride. Chin. Chem. Lett. 2024, 35, 110499. [Google Scholar] [CrossRef]
- Chai, X.; Chen, L.; Xue, B.; Liu, E. Granulation of ammonium chloride fertilizer and agglomeration mechanism. Powder Technol. 2017, 319, 148–153. [Google Scholar] [CrossRef]
- Zhang, S.-S.; Fang, F.; Wang, P.; Zhao, L.-J.; Guo, Y.-Y.; Wang, R.-D.; Zhang, Z.; Du, L.; Zhao, Q.-H. High proton conductivity enhancement of post-modified 2D cadmium metal–organic frameworks with ammonium chloride. Inorg. Chem. Commun. 2024, 168, 112848. [Google Scholar] [CrossRef]
- Pereira Nicacio, J.A.; Castro Oliveira, F.; Rosa Dumont, M. Failure analysis and electrochemical testing of ammonium chloride corrosion in a heat exchanger in a diesel hydrotreating unit of a petroleum refinery. Eng. Fail. Anal. 2024, 156, 107758. [Google Scholar] [CrossRef]
- Akpanyung, K.V.; Loto, R.T.; Fajobi, M.A. An overview of ammonium chloride (NH4Cl) corrosion in the refining unit. J. Phys. Conf. Ser. 2019, 1378, 022089. [Google Scholar] [CrossRef]
- Ali, M.; Ul-Hamid, A.; Alhems, L.M.; Saeed, A. Review of common failures in heat exchangers—Part I: Mechanical and elevated temperature failures. Eng. Fail. Anal. 2020, 109, 104396. [Google Scholar] [CrossRef]
- Liu, D.; Hu, J.; Yuan, X.; Zhou, L.; Zhong, X. Failure analysis and experimental verification on the hydrogen-driven pitting corrosion of heat exchanger tube material. Eng. Fail. Anal. 2022, 137, 106283. [Google Scholar] [CrossRef]
- Zhu, H.; Jin, H.; Zhang, S.; Liu, X.; Wang, C. Numerical simulation and experimental studies on the ammonia absorption process by water injection in reaction effluent air cooler system. Chem. Eng. Sci. 2023, 269, 118455. [Google Scholar] [CrossRef]
- Li, R.; Wang, X.; Chen, J.; Wang, Y. Understanding of ammonium salts under-deposit corrosion: Electrochemical and AIMD investigations. Corros. Sci. 2024, 229, 111887. [Google Scholar] [CrossRef]
- Jin, H.; Yin, H.; Xu, S.; Chen, W.; Liu, X.; Jiang, Y. Experimental study on the deposition characteristics of ammonium chloride particles in a hydrogenation air cooler. Powder Technol. 2025, 452, 120533. [Google Scholar] [CrossRef]
- Vainio, E.; Yrjas, P.; Hupa, L.; Hupa, M. Cold-end corrosion caused by hygroscopic ammonium chloride in thermal conversion of biomass and waste. Fuel 2023, 346, 128061. [Google Scholar] [CrossRef]
- Liu, X.; Li, R.; Yao, H.; Jin, H.; Wang, C. Research on the corrosion mechanism of Q345R steel under water-oil two-phase flow with the HCl and NH4Cl corrosive medium in low-temperature system of petrochemical plants. Colloids Surf. A Physicochem. Eng. Aspects 2024, 703, 135360. [Google Scholar] [CrossRef]
- Xing, H.; Jin, H.; Liu, X.; Li, R.; Wang, M.; Xiang, H.; Wang, C. Effect of NH4Cl fouling on heat transfer process of heat exchange tube under forced convection condition. Int. J. Heat Mass Transf. 2023, 217, 124826. [Google Scholar] [CrossRef]
- Pudasaini, S.P. A fully analytical model for virtual mass force in mixture flows. Int. J. Multiph. Flow 2019, 113, 142–152. [Google Scholar] [CrossRef]
- Feng, Y.H.; Zhang, Z.; Qiu, L.; Zhang, X.X. Heat recovery process modelling of semi-molten blast furnace slag in a moving bed using XDEM. Energy 2019, 186, 115876. [Google Scholar] [CrossRef]
- Zbib, H.; Ebrahimi, M.; Ein-Mozaffari, F.; Lohi, A. Comprehensive analysis of fluid-particle and particle-particle interactions in a liquid-solid fluidized bed via CFD-DEM coupling and tomography. Powder Technol. 2018, 340, 116–130. [Google Scholar] [CrossRef]
- Fang, J.C.; Jiao, B.L.; Zhao, G.; He, L.; Wu, Y.N.; Dai, C.L. Study on the channel flow control regulation of particle agents in fractured-vuggy carbonate reservoirs via CFD-DEM coupling method. J. Petrol. Sci. Eng. 2019, 180, 495–503. [Google Scholar] [CrossRef]
- Wang, C.; Liu, M.; Yan, J. Flow irreversibility versus wear of elbow-reducer connection with gas-solid two-phase flow: A numerical study via CFD-DEM coupling method. Powder Technol. 2023, 428, 118835. [Google Scholar] [CrossRef]
- Gou, D.; Shen, Y. GPU-accelerated CFD-DEM modeling of gas-solid flow with complex geometry and an application to raceway dynamics in industry-scale blast furnaces. Chem. Eng. Sci. 2024, 294, 120101. [Google Scholar] [CrossRef]
- Metzger, J.P.; Mehring, C. Particle removal from solid surfaces via an impinging gas jet pulse: Comparison between experimental and CFD-DEM modeling results. J. Aerosol. Sci. 2024, 179, 106364. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Kosinski, P.; Hoffmann, A.C. An extension of the hard-sphere particle-particle collision model to study agglomeration. Chem. Eng. Sci. 2010, 65, 3231–3239. [Google Scholar] [CrossRef]
- Breuer, M.; Almohammed, N. Modeling and simulation of particle agglomeration in turbulent flows using a hard-sphere model with deterministic collision detection and enhanced structure models. Int. J. Multiph. Flow 2015, 73, 171–206. [Google Scholar] [CrossRef]
- Zhu, H.P.; Zhou, Z.Y.; Yang, R.Y.; Yu, A.B. Discrete particle simulation of particulate systems: Theoretical developments. Chem. Eng. Sci. 2007, 62, 3378–3396. [Google Scholar] [CrossRef]
- Wang, G.; Yang, S.; Zhang, X.; Wang, H. Investigation of complex gas-particle flow characteristics in fluidizing process of non-spherical particles by CFD-DEM. Powder Technol. 2024, 445, 120068. [Google Scholar] [CrossRef]
- Zhang, G.; Mao, Y.H.; Liu, Z.X.; Chen, D.S.; Wu, F.; Lin, Z. Study on particle deposition in pipeline groove from gas–particle two-phase flow. Powder Technol. 2024, 438, 119630. [Google Scholar] [CrossRef]
- Wang, D.; You, Z.; Wang, M.; Li, Q.; Wu, L. Numerical investigation of proppant transport at hydraulic-natural fracture intersection. Powder Technol. 2022, 398, 117123. [Google Scholar] [CrossRef]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A 1971, 324, 301–313. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Deresiewicz, H. Elastic spheres in contact under varying oblique forces. J. Appl. Mech. 1953, 20, 327–344. [Google Scholar] [CrossRef]
- Pasha, M.; Dogbe, S.; Hare, C.; Hassanpour, A.; Ghadiri, M. A linear model of elasto-plastic and adhesive contact deformation. Matter 2014, 16, 151–162. [Google Scholar] [CrossRef]


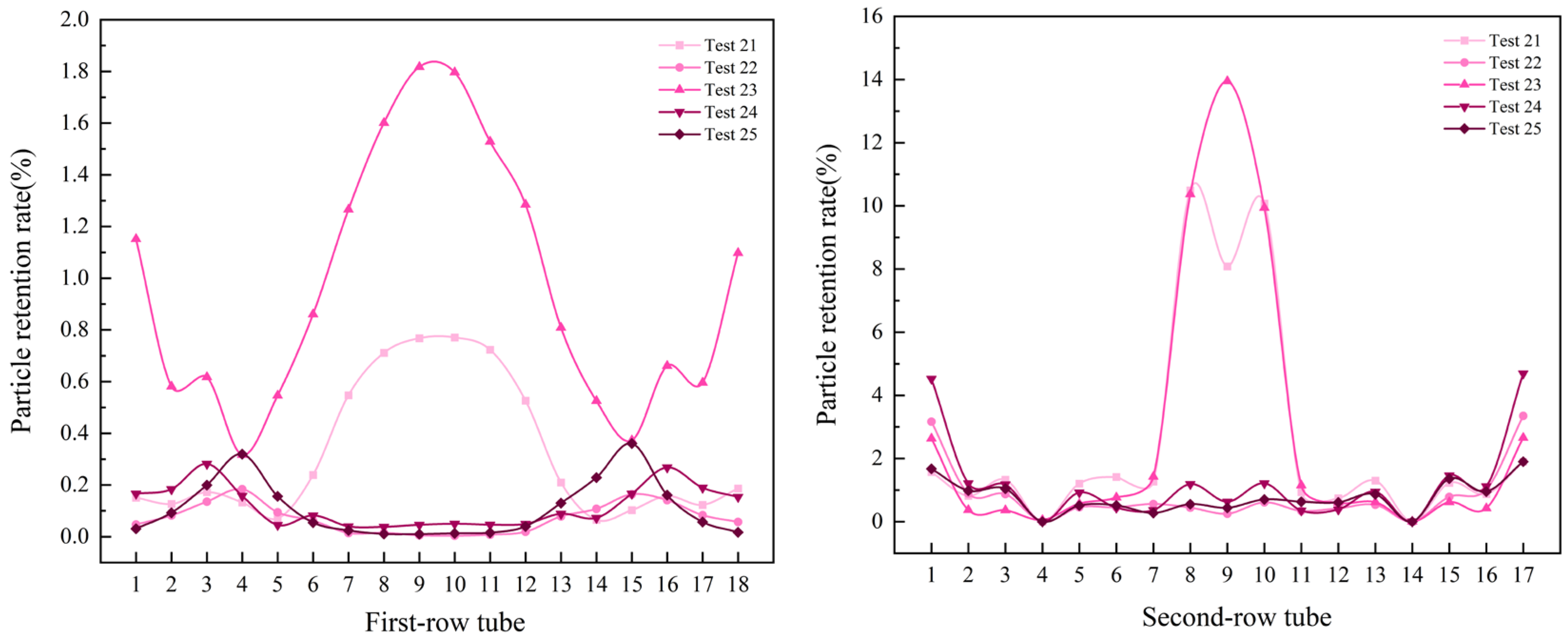

| Test Plan | Vg (m/s) | T (K) | dp (μm) | DI | DII |
|---|---|---|---|---|---|
| 1 | 2.00 | 353 | 100–200 | 0.2023 | 5.0911 |
| 2 | 2.00 | 363 | 300–400 | 0.5242 | 4.7938 |
| 3 | 2.00 | 373 | 500–600 | 0.0945 | 5.4510 |
| 4 | 2.00 | 383 | 200–300 | 0.0536 | 4.3880 |
| 5 | 2.00 | 393 | 400–500 | 0.0858 | 4.3480 |
| 6 | 2.75 | 353 | 500–600 | 0.4049 | 6.5315 |
| 7 | 2.75 | 363 | 200–300 | 0.1746 | 7.1435 |
| 8 | 2.75 | 353 | 500–600 | 0.4049 | 6.5315 |
| 9 | 2.75 | 383 | 100–200 | 0.8020 | 11.8854 |
| 10 | 2.75 | 393 | 300–400 | 0.0865 | 4.4086 |
| 11 | 3.50 | 353 | 400–500 | 0.3380 | 6.1459 |
| 12 | 3.50 | 363 | 100–200 | 2.4692 | 13.8758 |
| 13 | 3.50 | 373 | 300–400 | 0.7774 | 10.3134 |
| 14 | 3.50 | 383 | 500–600 | 1.6875 | 11.3452 |
| 15 | 3.50 | 393 | 200–300 | 2.5813 | 20.3427 |
| 16 | 4.25 | 353 | 300–400 | 1.0465 | 13.3730 |
| 17 | 4.25 | 363 | 500–600 | 0.8894 | 10.2492 |
| 18 | 4.25 | 373 | 200–300 | 2.3122 | 16.1314 |
| 19 | 4.25 | 383 | 400–500 | 1.5061 | 12.8981 |
| 20 | 4.25 | 393 | 100–200 | 10.5426 | 38.1582 |
| 21 | 5.00 | 353 | 200–300 | 5.6782 | 41.8306 |
| 22 | 5.00 | 363 | 400–500 | 1.2969 | 14.1524 |
| 23 | 5.00 | 373 | 100–200 | 17.4240 | 46.4879 |
| 24 | 5.00 | 383 | 300–400 | 2.1224 | 20.6385 |
| 25 | 5.00 | 393 | 500–600 | 1.9189 | 13.0158 |
| Term | Level | Vg (m/s) | T0 (K) | dp (μm) |
|---|---|---|---|---|
| K-value | 1 | 0.96 | 7.67 | 31.44 |
| 2 | 1.64 | 5.35 | 10.80 | |
| 3 | 7.85 | 20.78 | 4.56 | |
| 4 | 16.30 | 6.17 | 3.40 | |
| 5 | 28.44 | 15.22 | 5.00 | |
| K-avg-value | 1 | 0.19 | 1.53 | 6.29 |
| 2 | 0.33 | 1.07 | 2.16 | |
| 3 | 1.57 | 4.16 | 0.91 | |
| 4 | 3.26 | 1.23 | 0.68 | |
| 5 | 5.69 | 3.04 | 1.00 | |
| The best level | 5 | 3 | 1 | |
| R | 5.50 | 3.09 | 5.61 | |
| Level quantity | 5 | 5 | 5 | |
| Number of replicates per level, r | 5.0 | 5.0 | 5.0 | |
| Term | Level | Vg (m/s) | T0 (K) | dp (μm) |
|---|---|---|---|---|
| K-value | 1 | 24.03 | 72.97 | 115.50 |
| 2 | 35.90 | 50.21 | 89.80 | |
| 3 | 62.02 | 84.71 | 53.13 | |
| 4 | 90.81 | 61.12 | 43.87 | |
| 5 | 136.13 | 79.87 | 46.59 | |
| K-avg-value | 1 | 4.81 | 14.59 | 23.10 |
| 2 | 7.18 | 10.04 | 17.96 | |
| 3 | 12.40 | 16.94 | 10.63 | |
| 4 | 18.16 | 12.22 | 8.77 | |
| 5 | 27.23 | 15.97 | 9.32 | |
| The best level | 5 | 3 | 1 | |
| R | 22.42 | 6.90 | 14.32 | |
| Level quantity | 5 | 5 | 5 | |
| Number of replicates per level, r | 5.0 | 5.0 | 5.0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, H.; Jin, H.; Liu, X.; Wang, C.; Chen, W.; Chen, F.; Xu, S.; Li, S. Mechanistic Insights into Ammonium Chloride Particle Deposition in Hydrogenation Air Coolers: Experimental and CFD-DEM Analysis. Processes 2025, 13, 1816. https://doi.org/10.3390/pr13061816
Yin H, Jin H, Liu X, Wang C, Chen W, Chen F, Xu S, Li S. Mechanistic Insights into Ammonium Chloride Particle Deposition in Hydrogenation Air Coolers: Experimental and CFD-DEM Analysis. Processes. 2025; 13(6):1816. https://doi.org/10.3390/pr13061816
Chicago/Turabian StyleYin, Haoyu, Haozhe Jin, Xiaofei Liu, Chao Wang, Wei Chen, Fengguan Chen, Shuangqing Xu, and Shuangquan Li. 2025. "Mechanistic Insights into Ammonium Chloride Particle Deposition in Hydrogenation Air Coolers: Experimental and CFD-DEM Analysis" Processes 13, no. 6: 1816. https://doi.org/10.3390/pr13061816
APA StyleYin, H., Jin, H., Liu, X., Wang, C., Chen, W., Chen, F., Xu, S., & Li, S. (2025). Mechanistic Insights into Ammonium Chloride Particle Deposition in Hydrogenation Air Coolers: Experimental and CFD-DEM Analysis. Processes, 13(6), 1816. https://doi.org/10.3390/pr13061816






