Drill Sticking Prediction Based on Modal Decomposition and Physical Constraint Model of Near-Bit Data
Abstract
1. Introduction
2. Algorithm Principles
2.1. Empirical Mode Decomposition
2.2. Variational Mode Decomposition
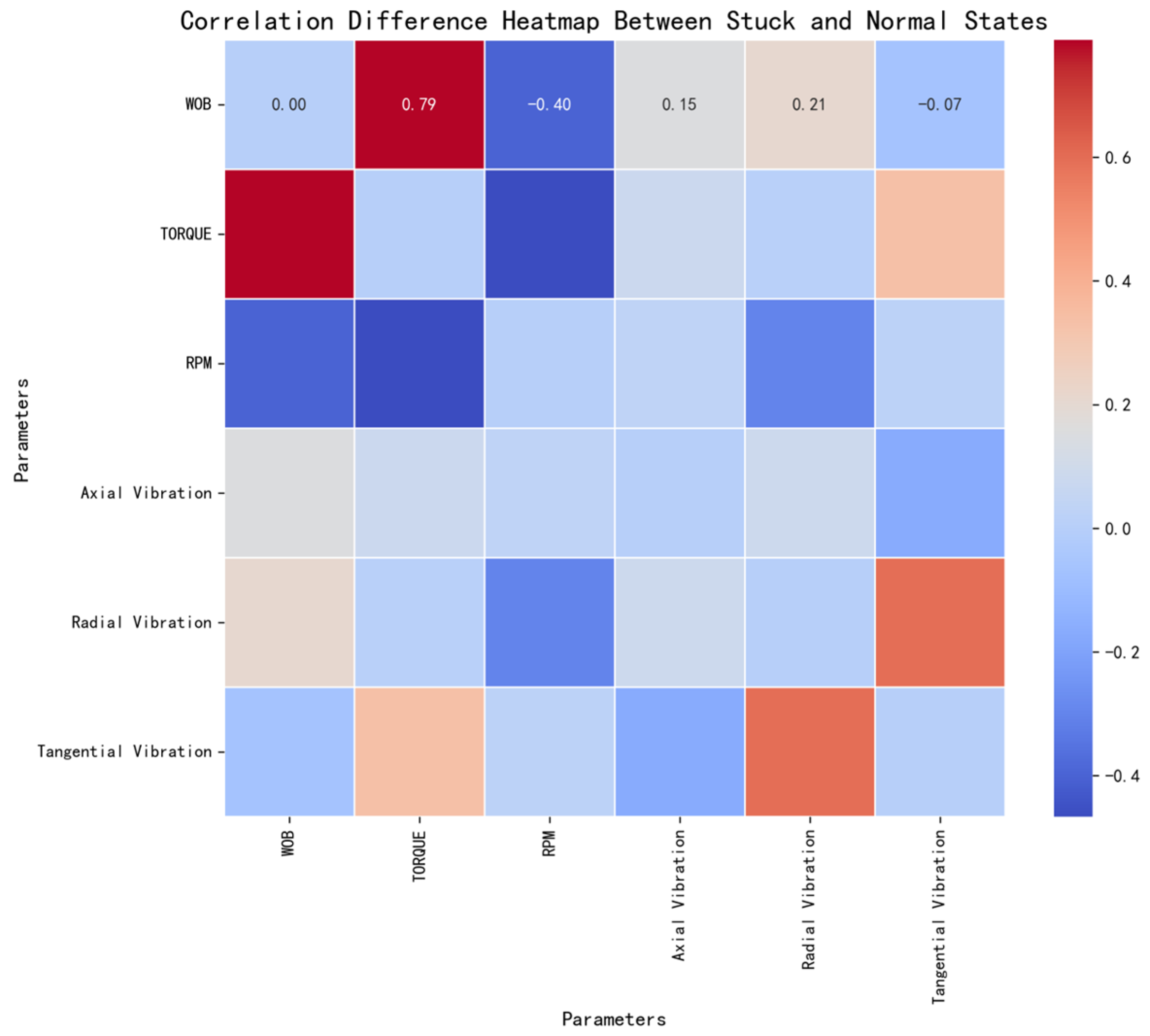
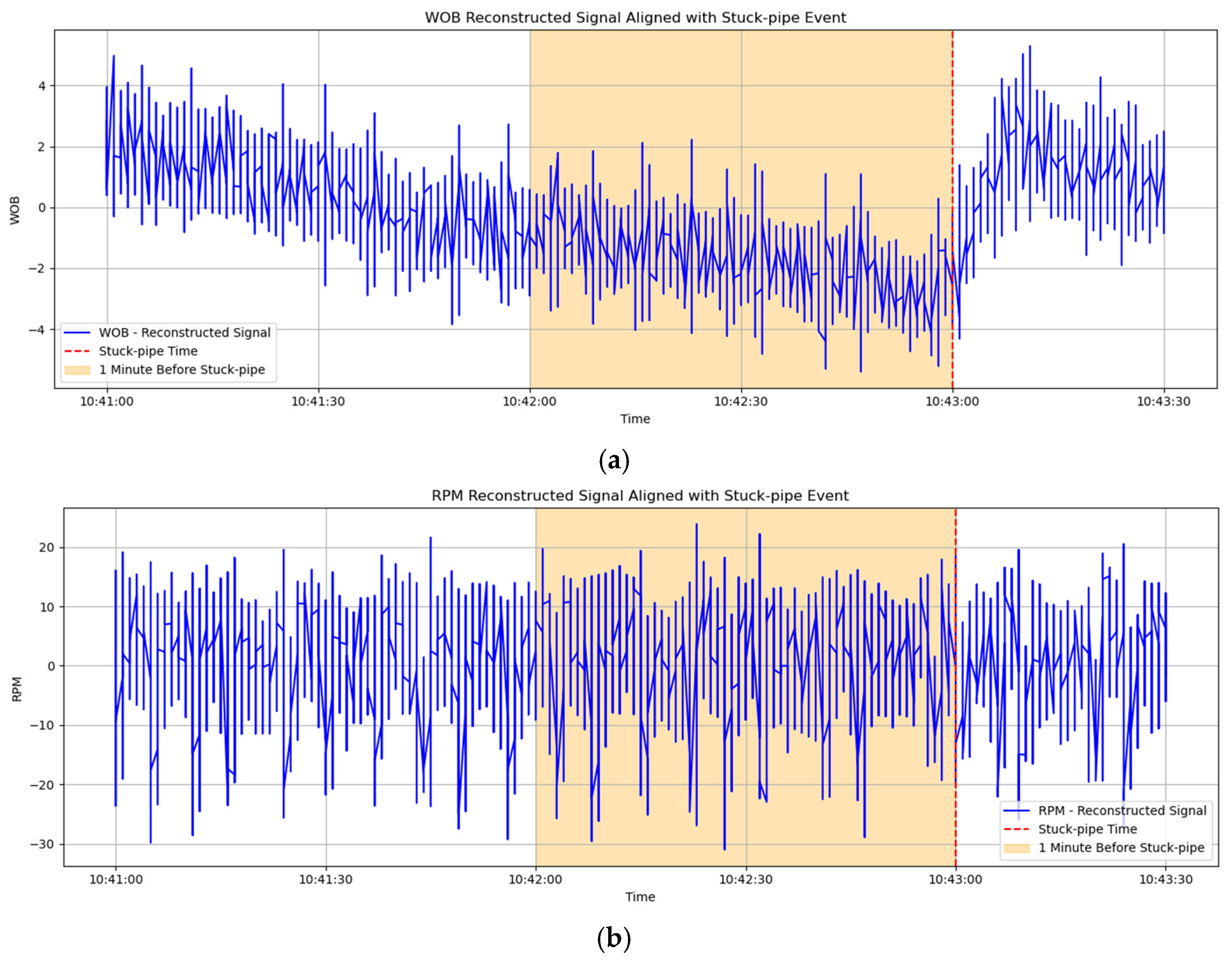
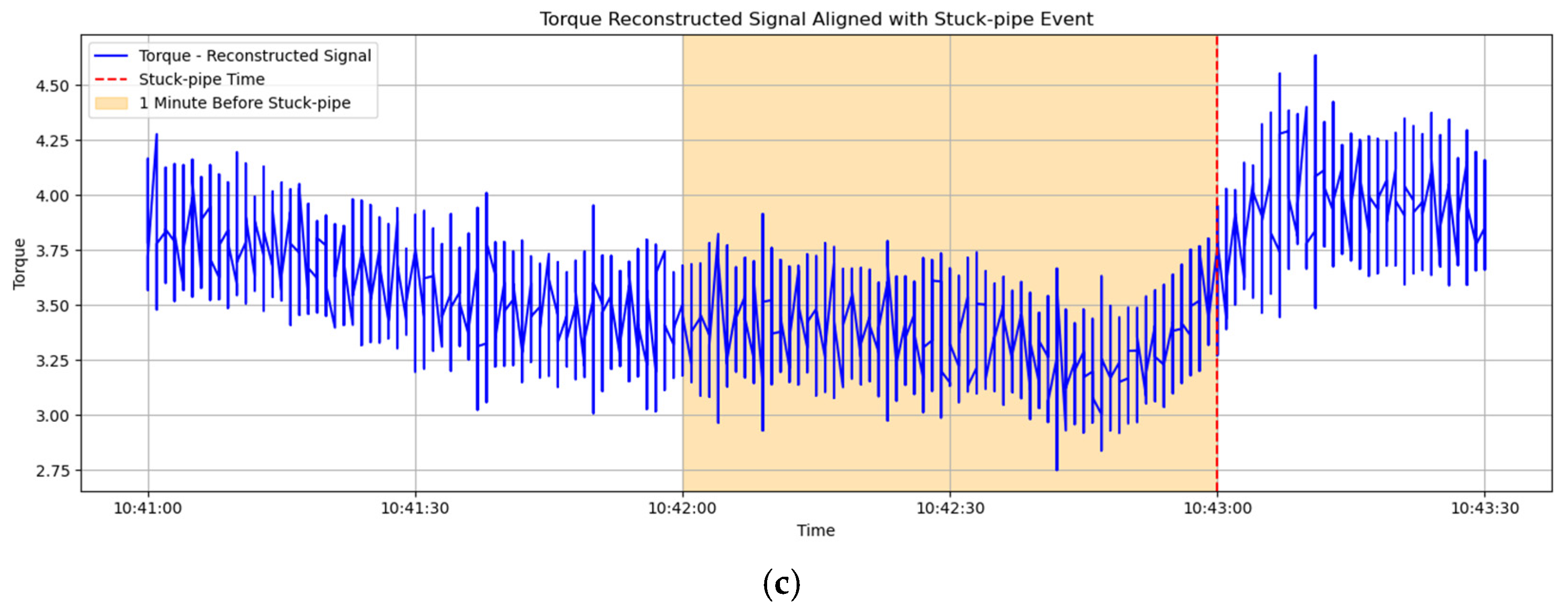
3. The Characteristics Analysis of Sticking
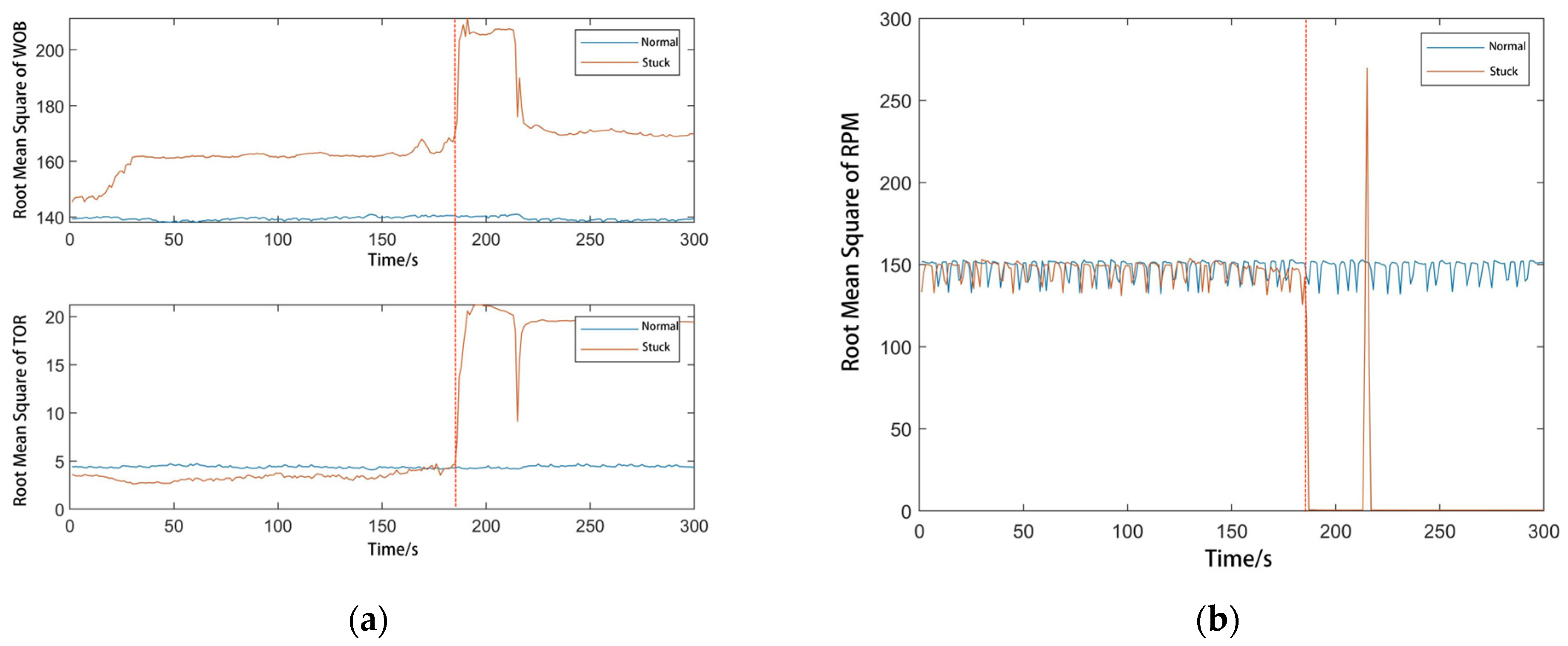
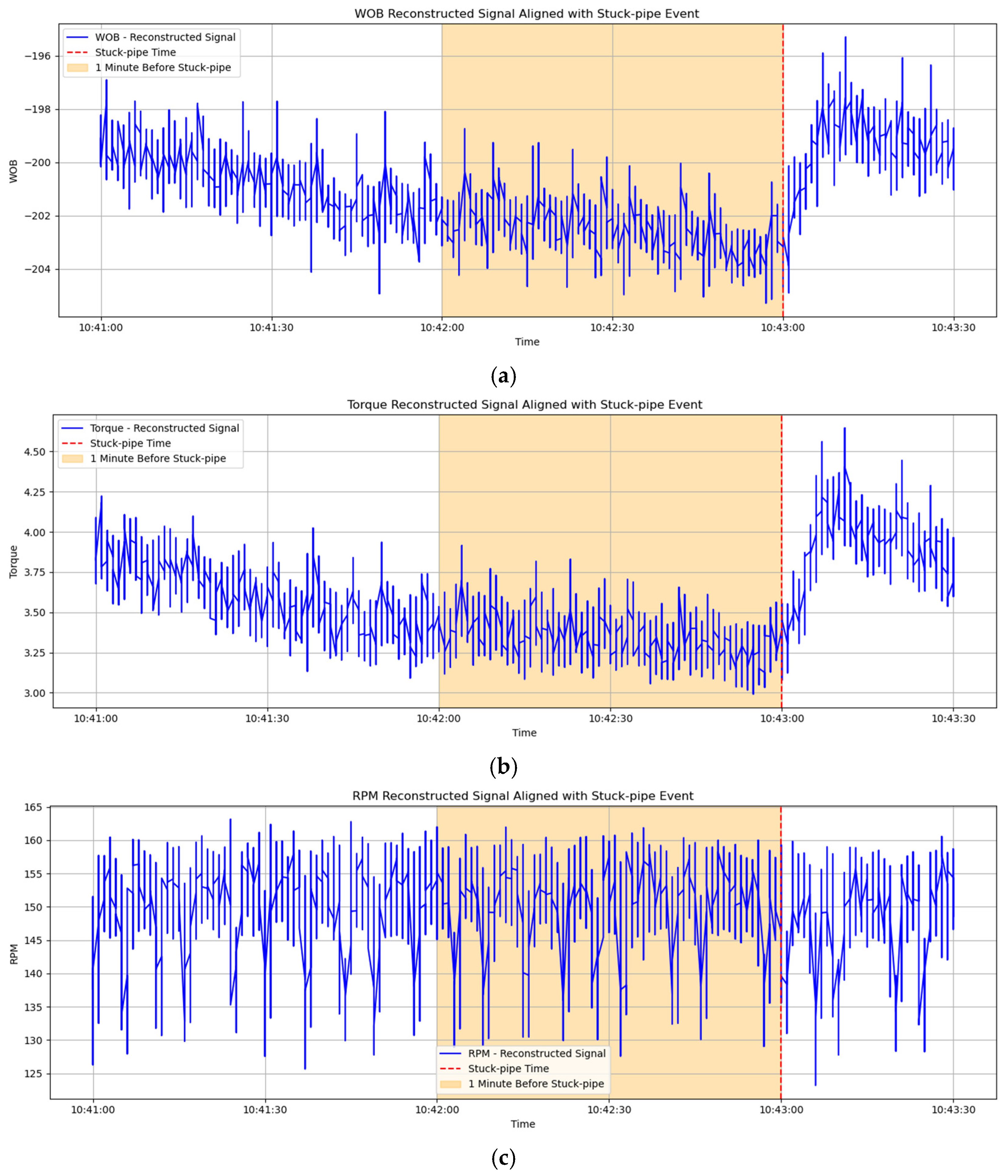
3.1. Time Domain Analysis
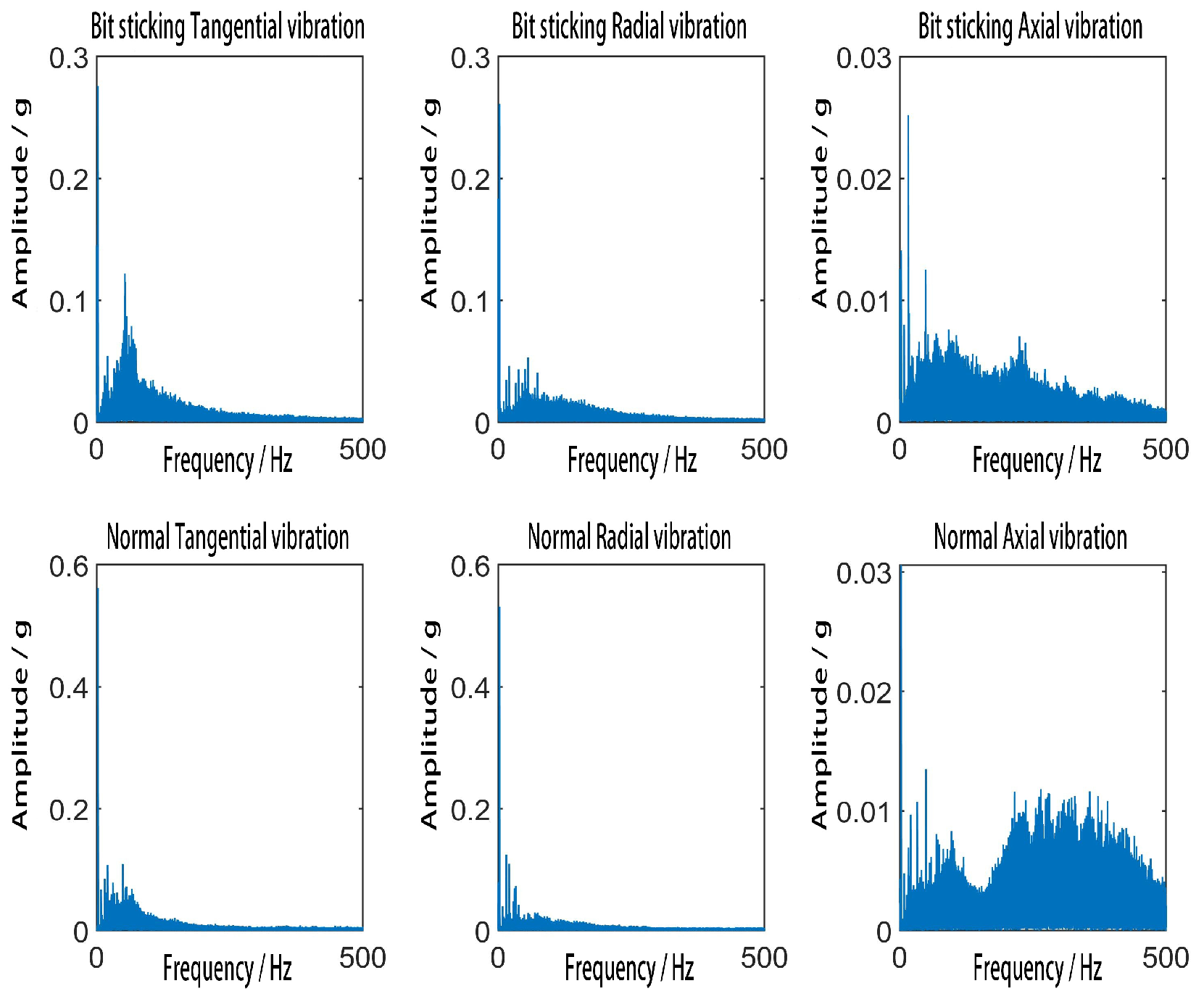
3.2. Frequency Domain Analysis
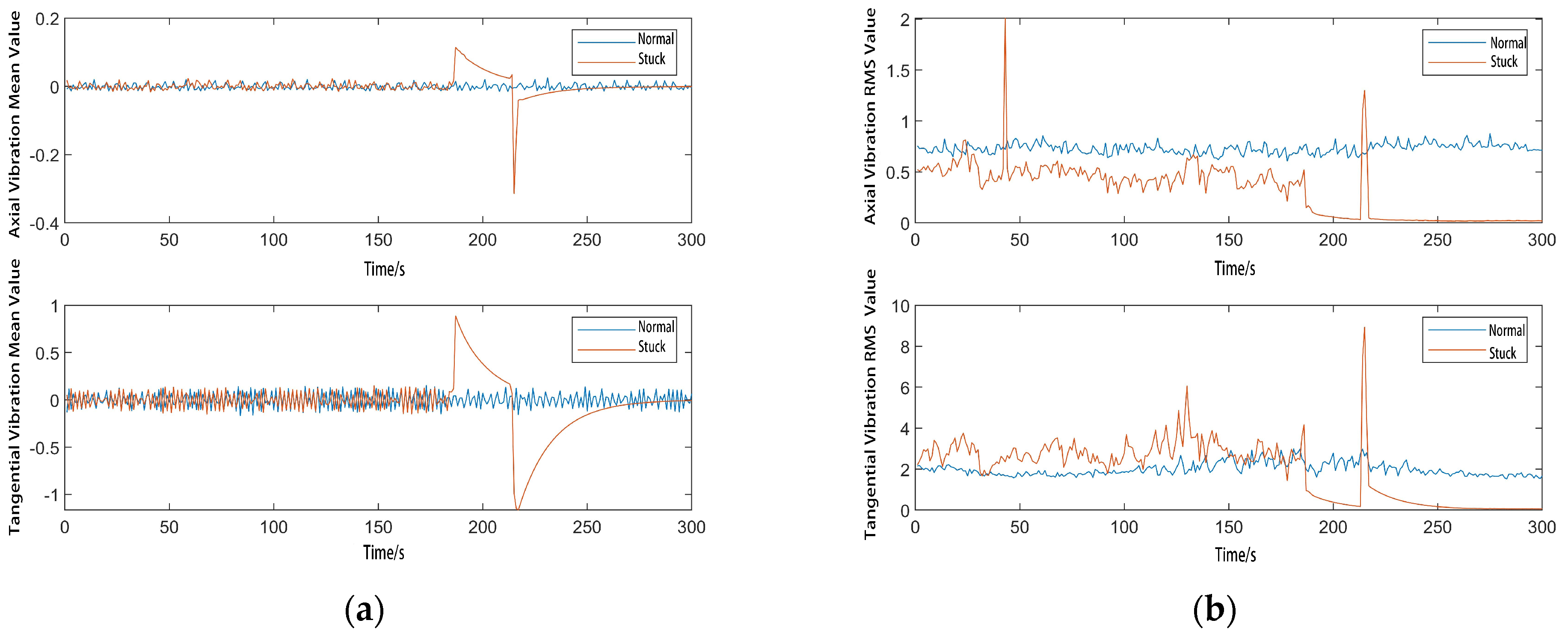
3.3. Vibration Analysis
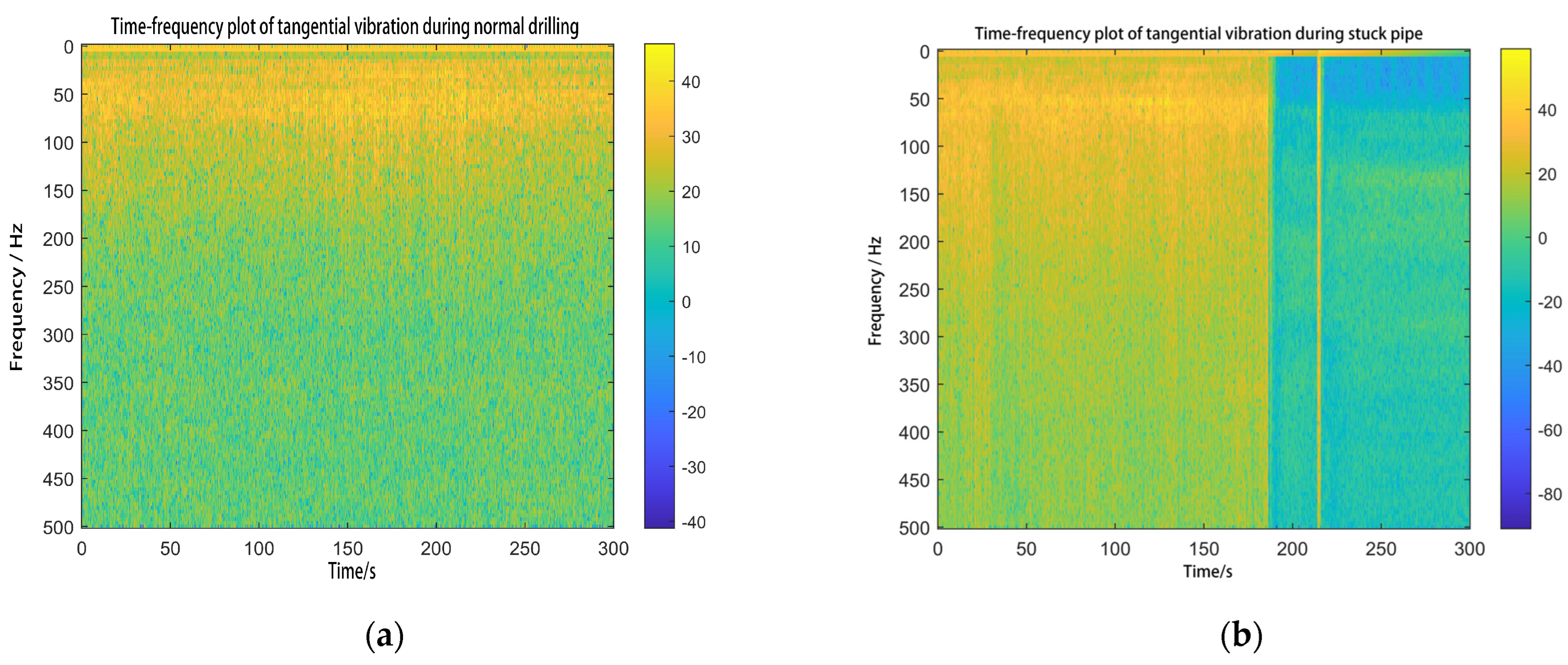
3.4. Time-Frequency Domain Analysis
4. Experimentation and Analysis
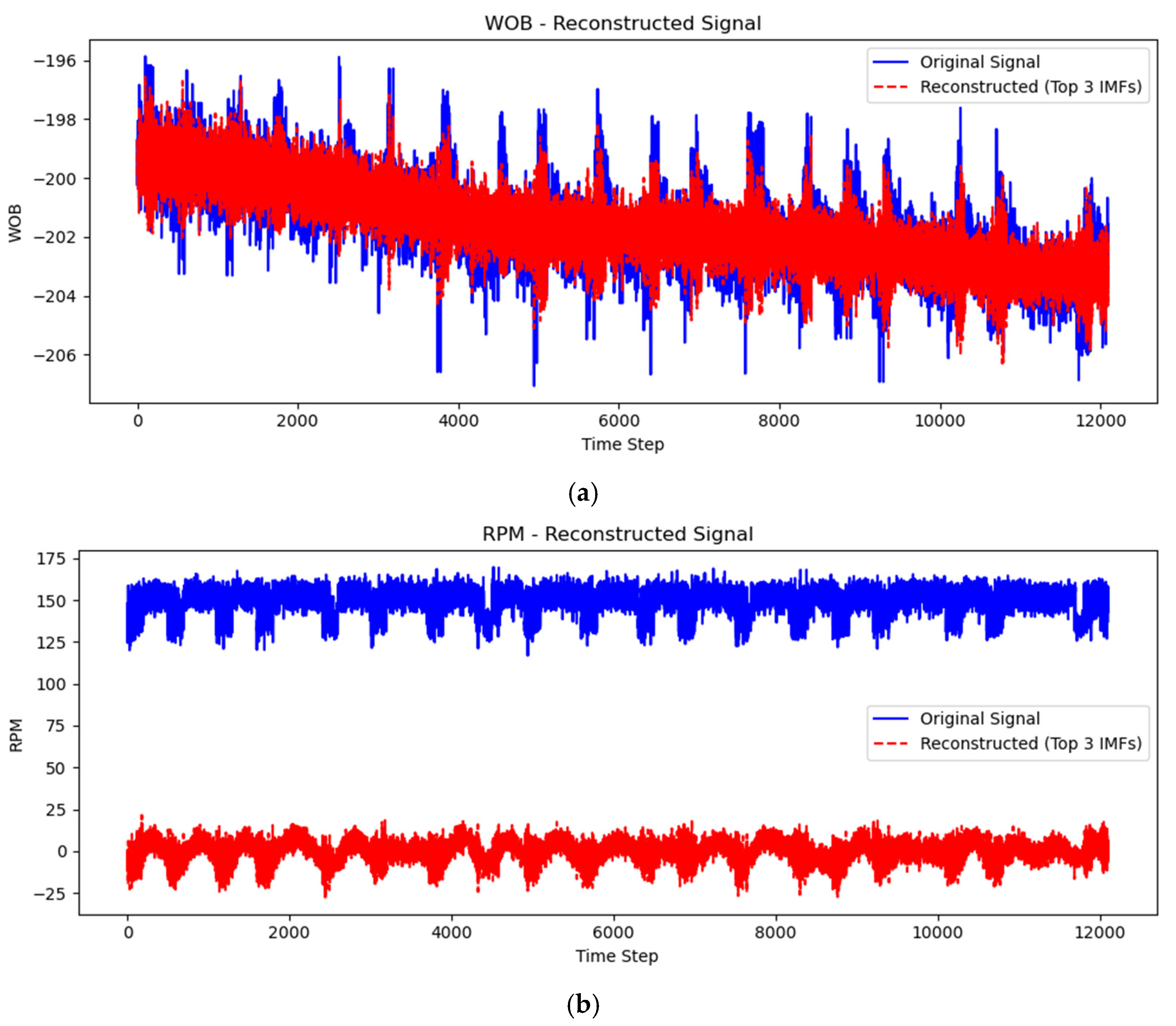
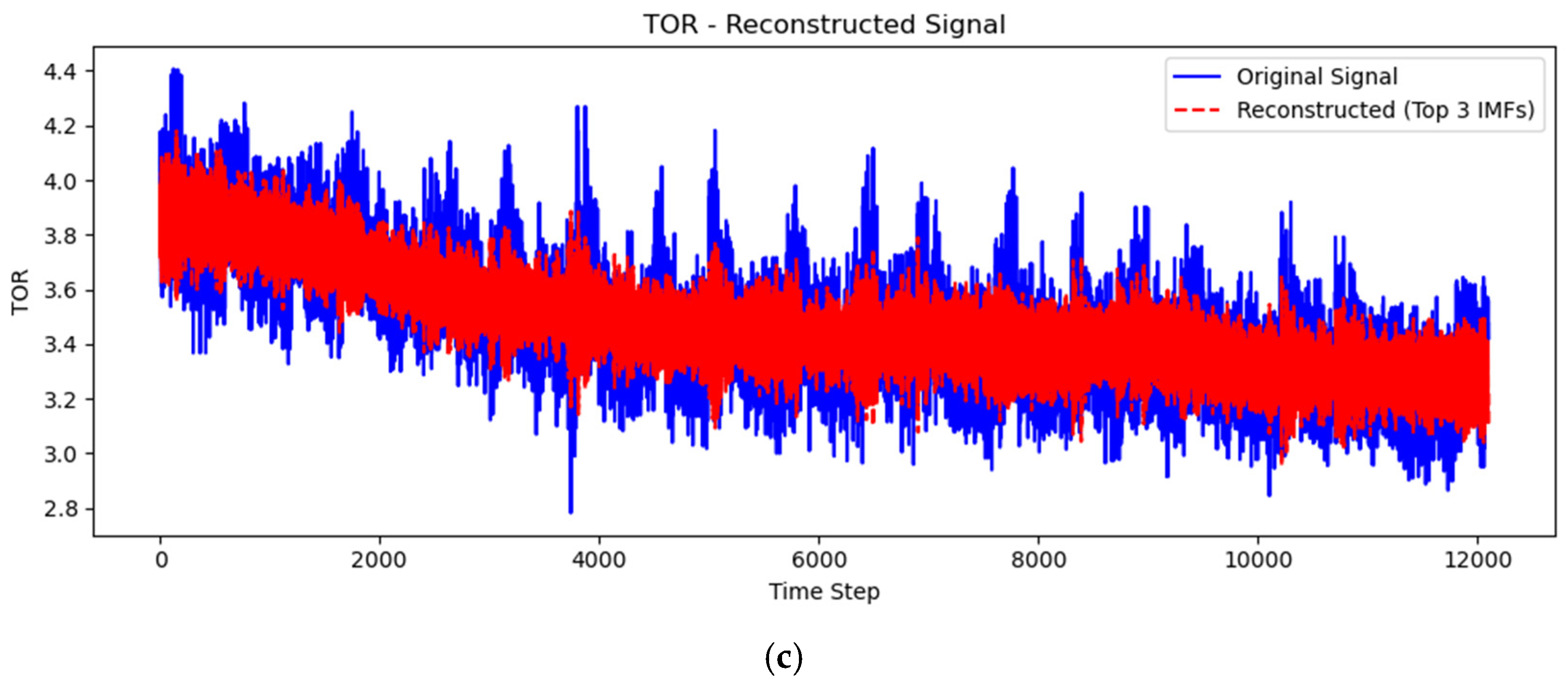
4.1. Data Preprocessing
4.1.1. Parameter Selection
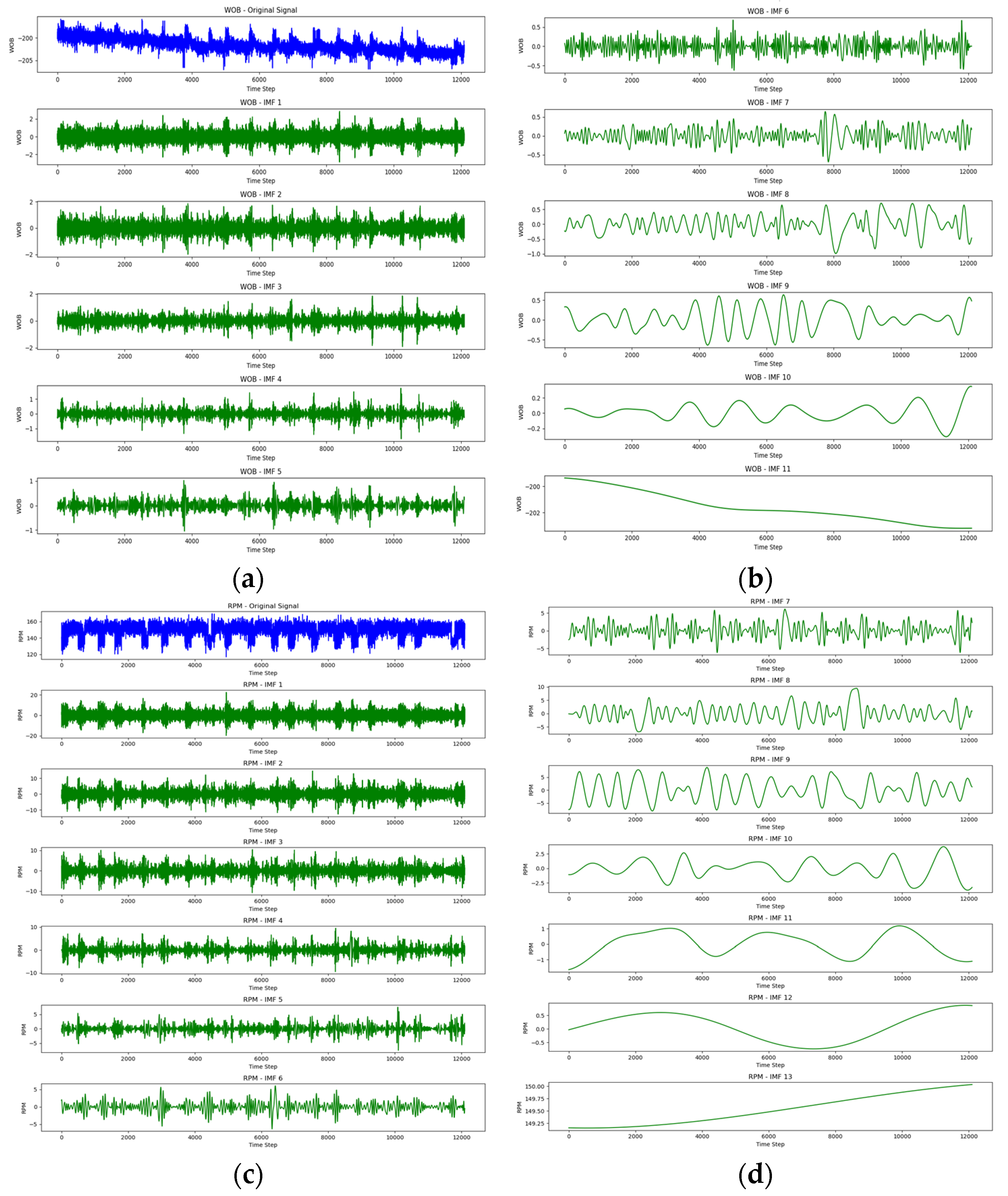
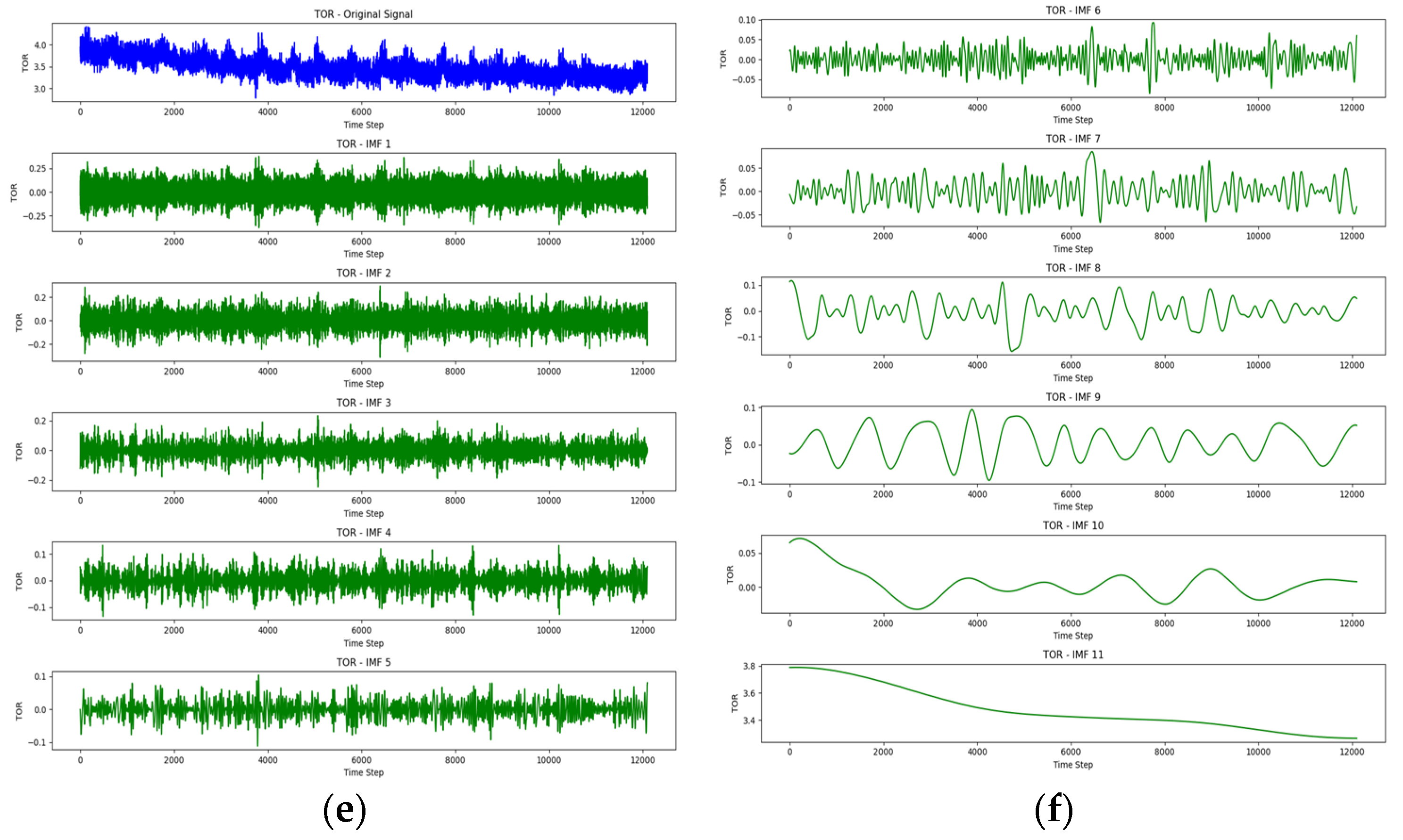
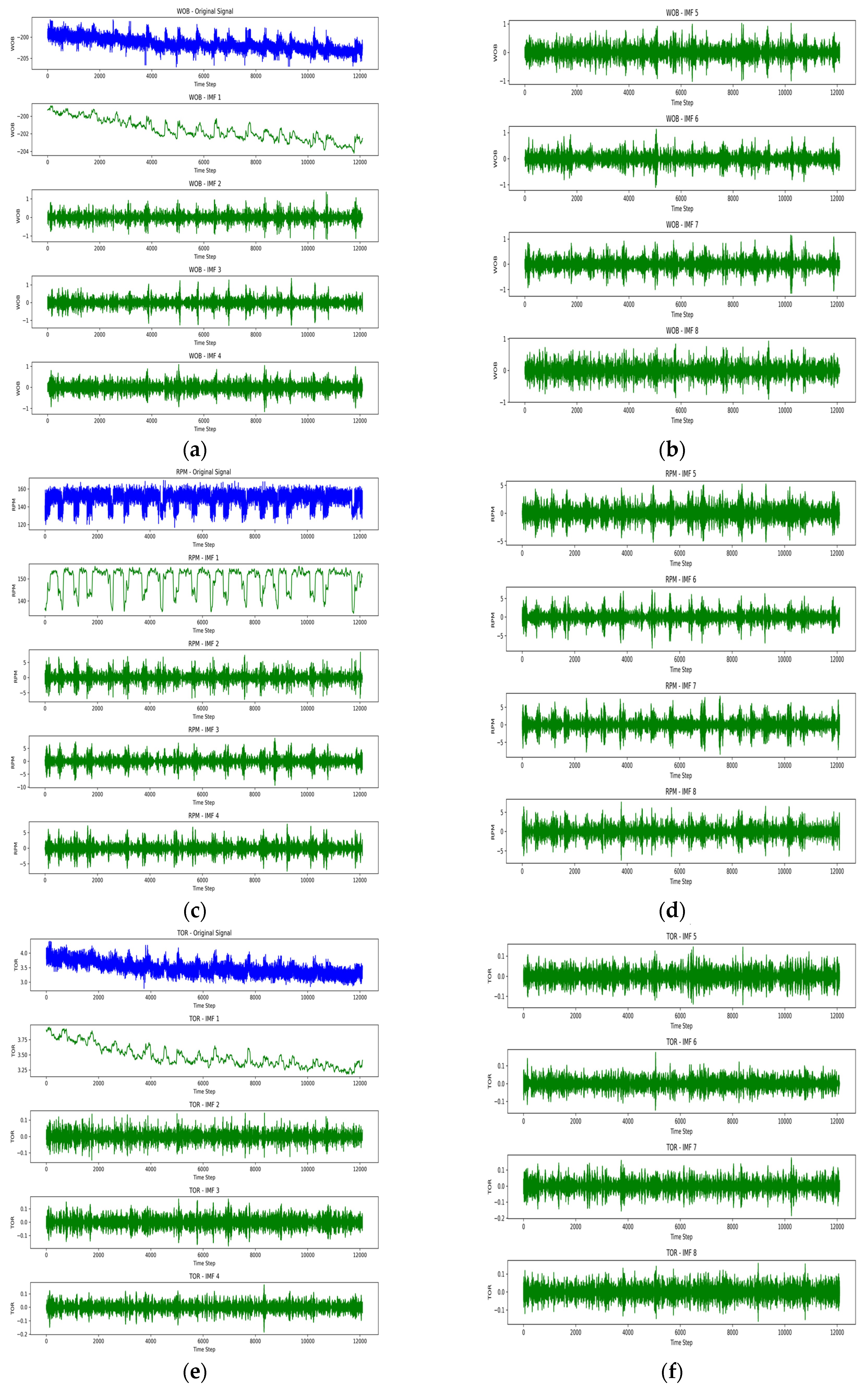
4.1.2. Mode Decomposition Techniques
- Empirical Mode Decomposition (EMD)
- 2.
- Variational Mode Decomposition (VMD)
4.2. Model Construction
4.2.1. Rationale for a Data-Physics Dual-Driven Approach
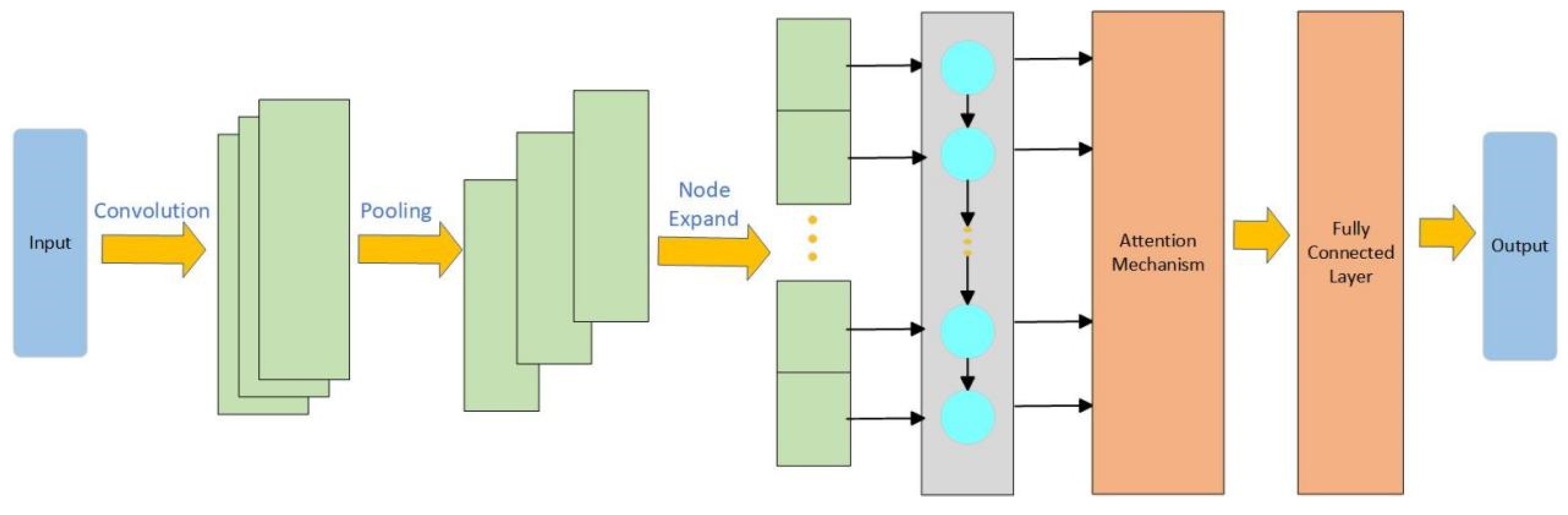
4.2.2. CNN-LSTM-Attention Architecture
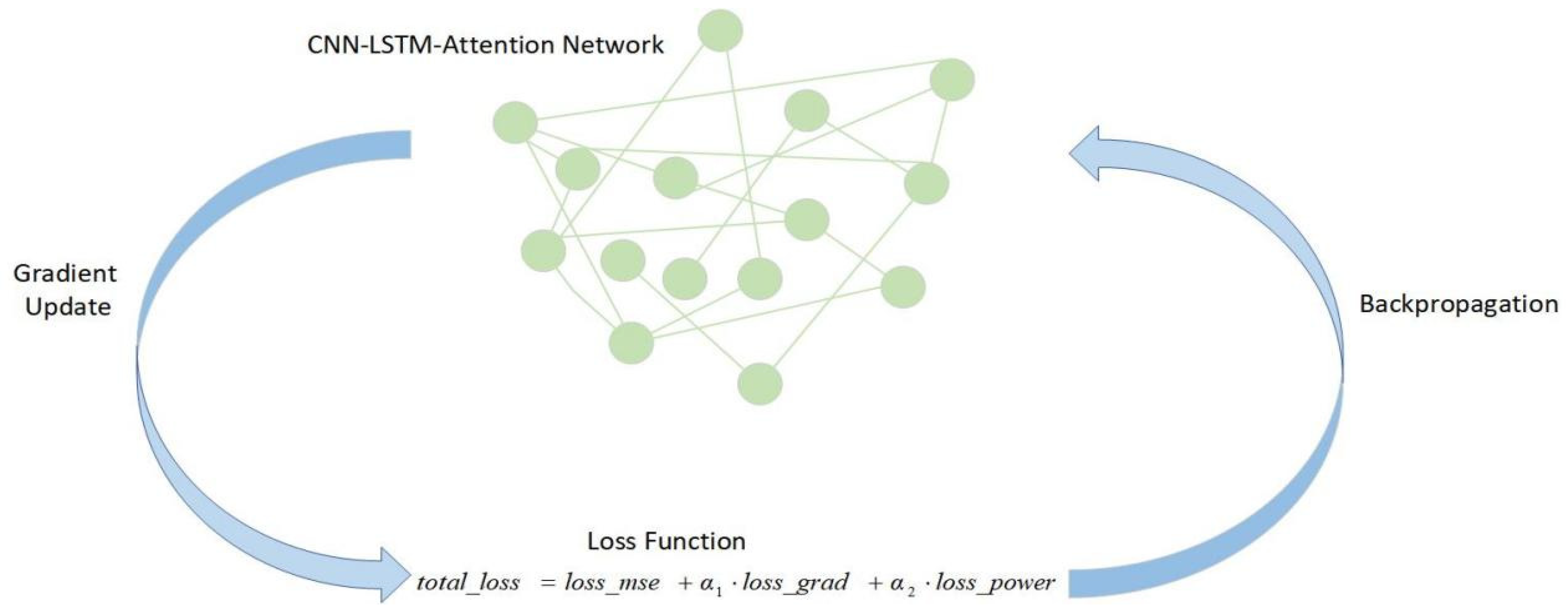
4.2.3. Design of Adaptive Physics-Constrained Loss Function
- Gradient Constraint
- 2.
- Power Constraint
- 3.
- Design of Adaptive Weights
- 4.
- Design of the Final Loss Function
4.3. Model Construction
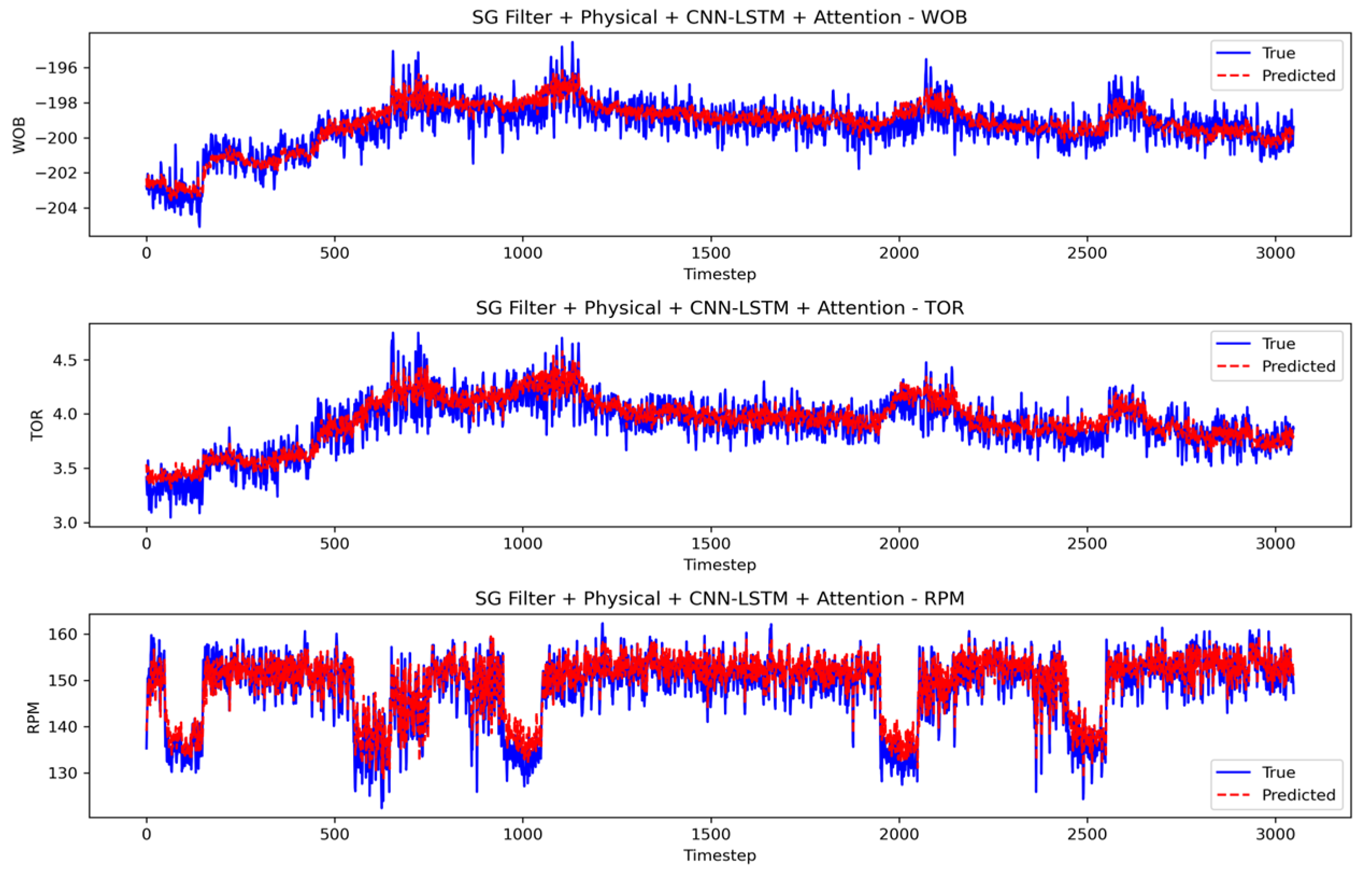
4.3.1. The Role of Physical Constraints in the Model
4.3.2. The Impact of EMD and VMD on the Model
4.3.3. Comprehensive Comparison
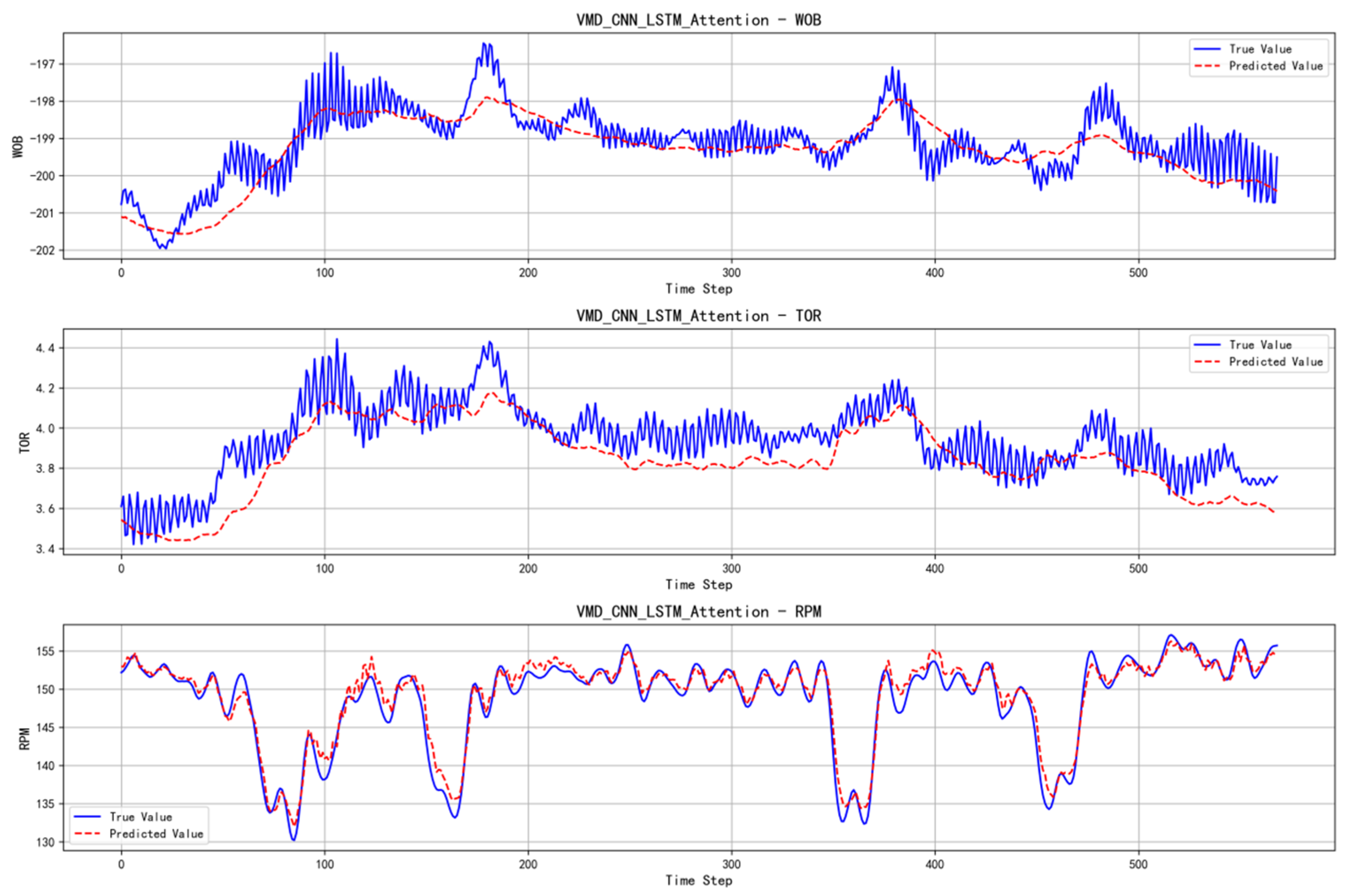
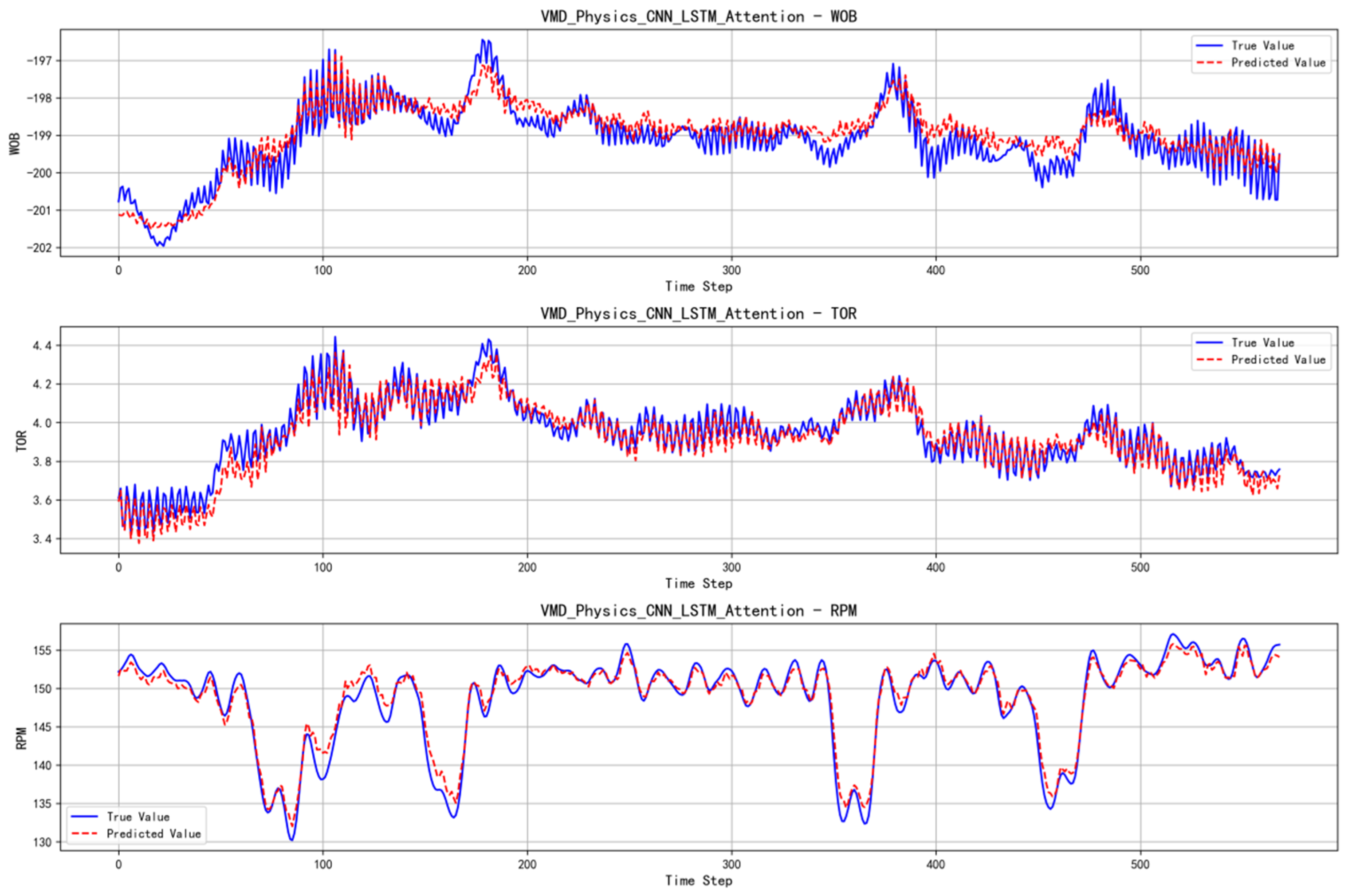
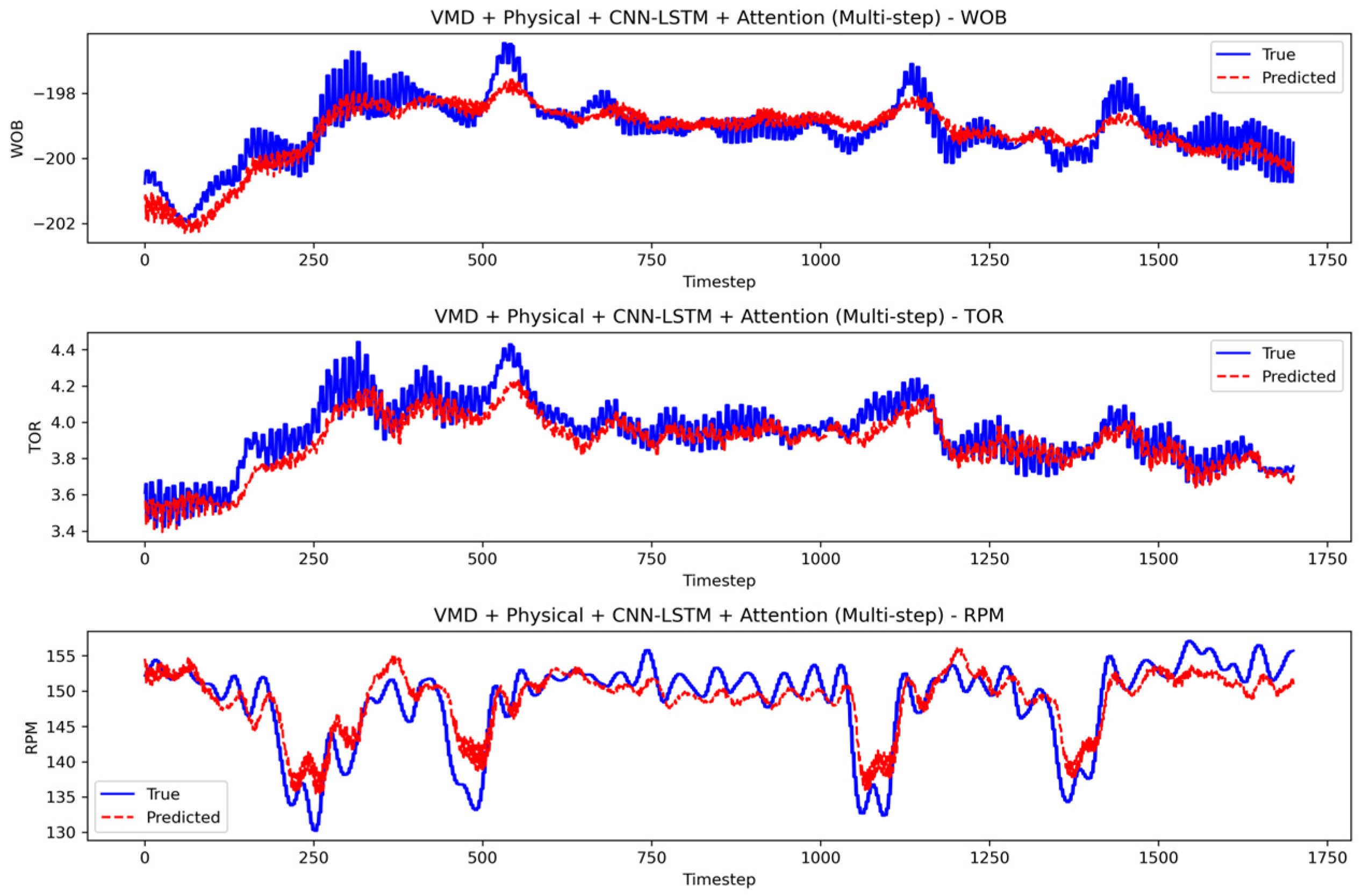
- Performance of the VMD + CNN-LSTM-Attention + Physical Model
- 2.
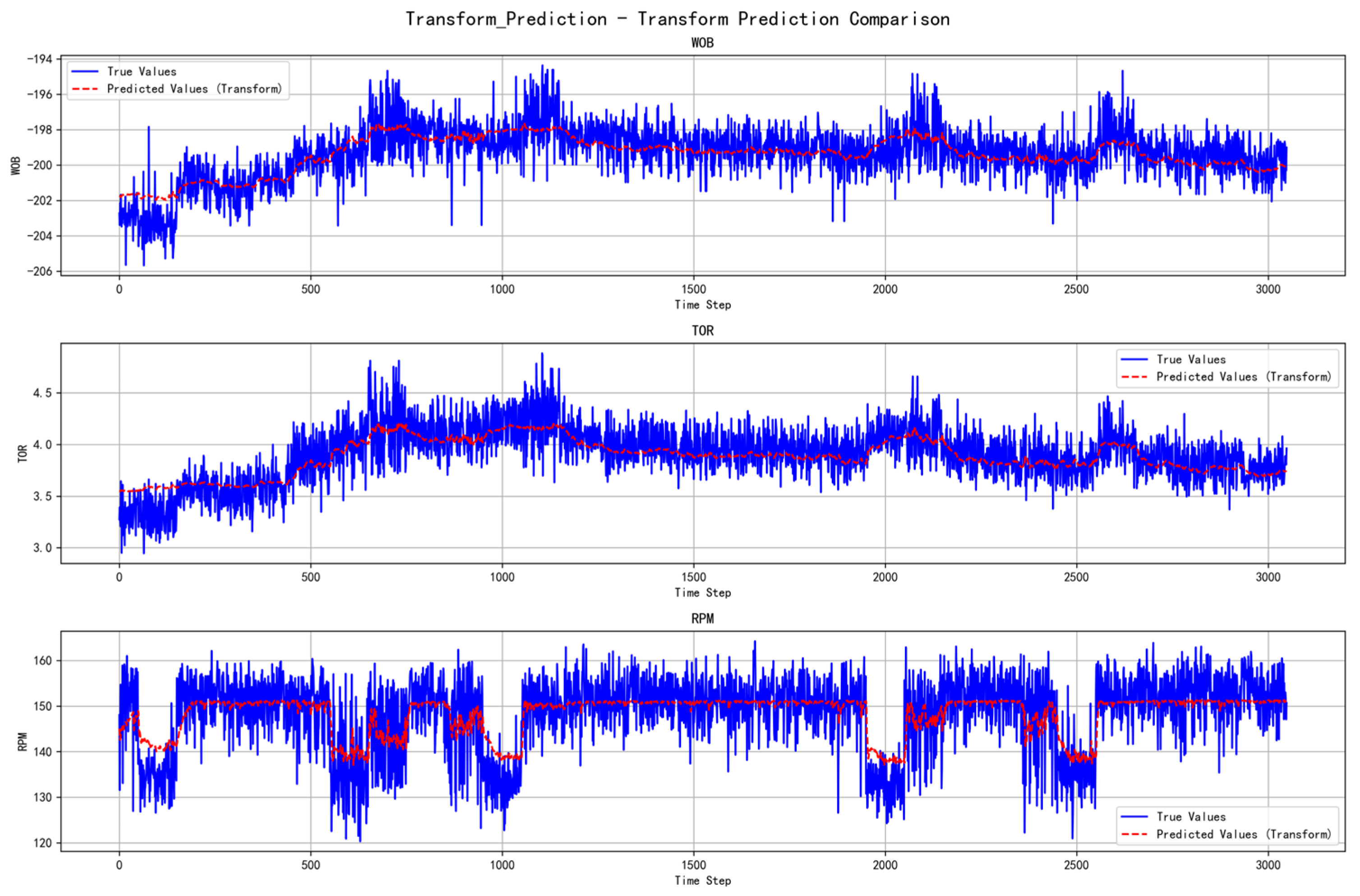
- Performance of the Transform Model
- 3.
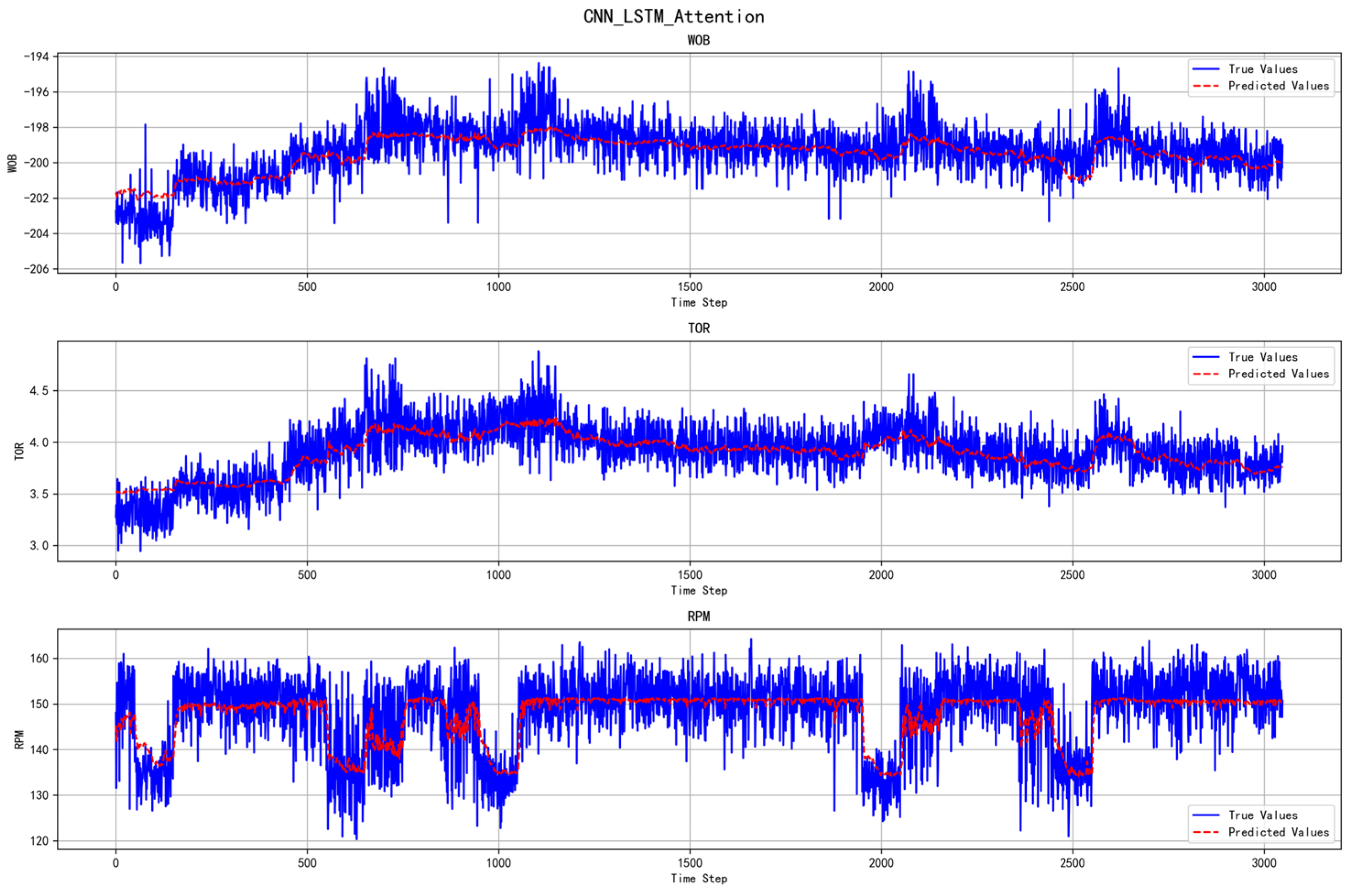
- Performance of the CNN-LSTM-Attention Model
- 4.
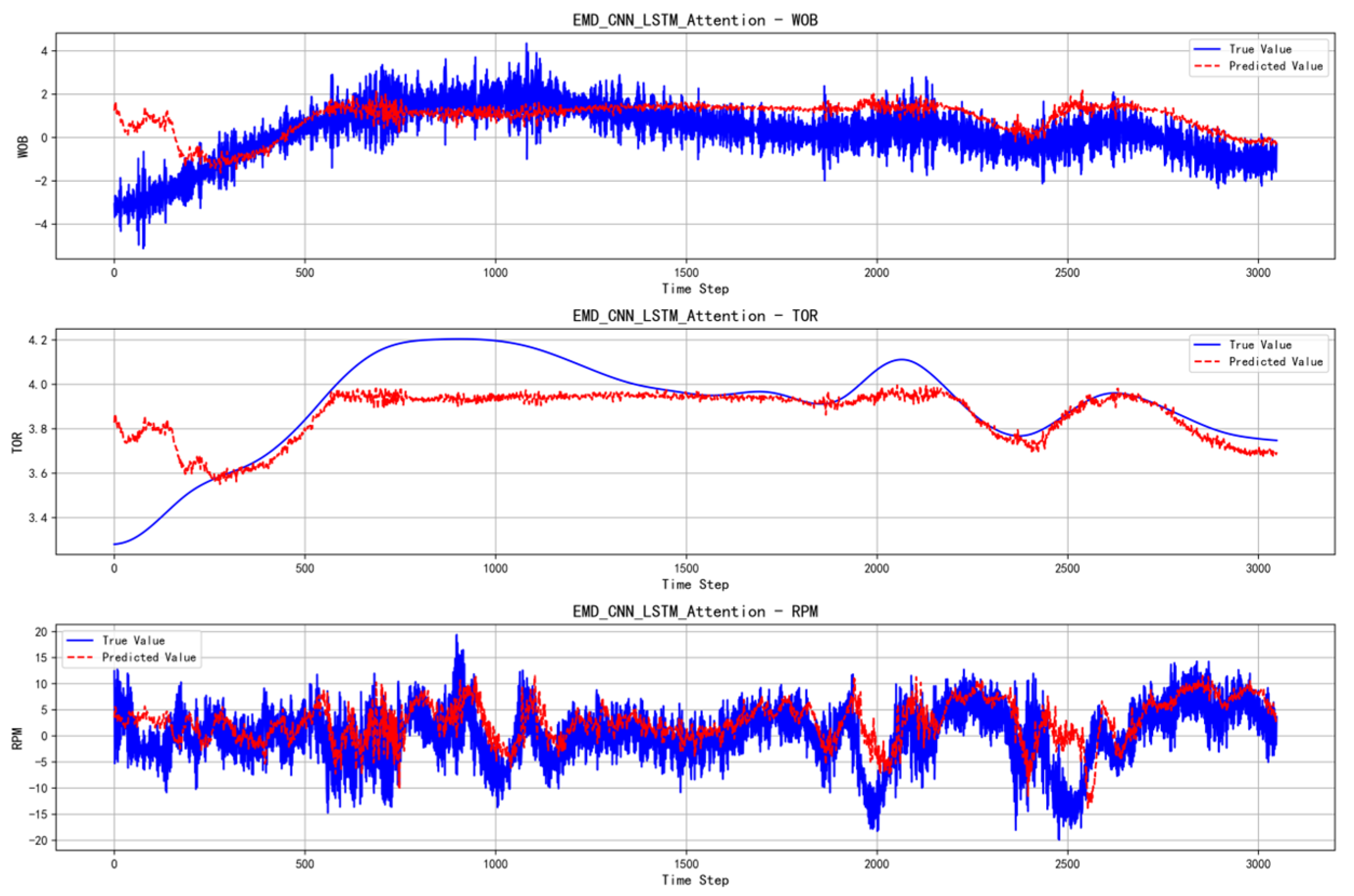
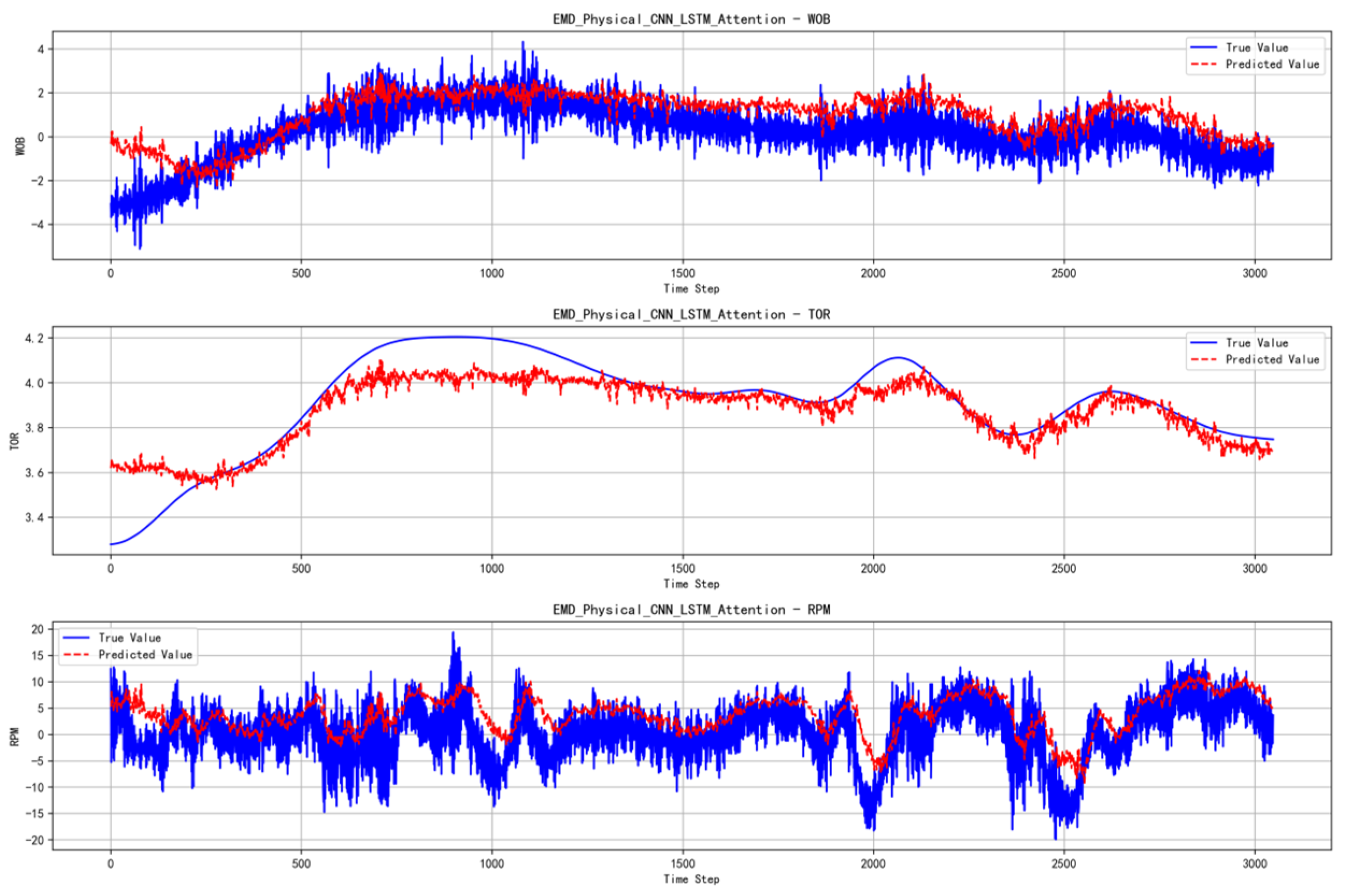
- Disadvantages of the EMD Model
- 5.
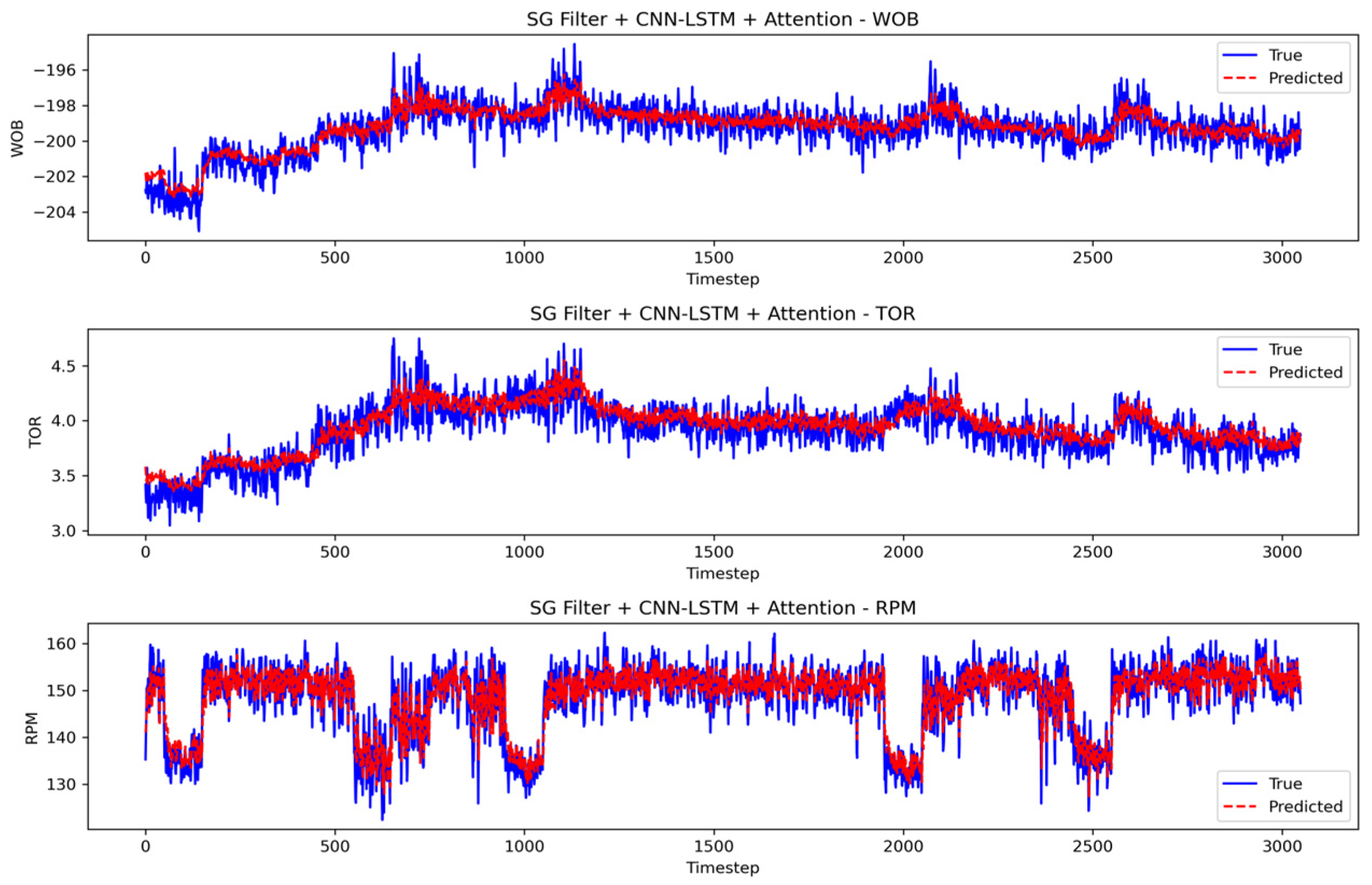
- The superiority of deep learning over traditional filtering methods in data preprocessing
- 6.
- Multi-step Prediction and Practical Significance
5. Conclusions
- (1)
- Through time domain, frequency domain, time-frequency domain, and vibration analysis of near-bit downhole data, no significant characteristics were found before and after a stuck pipe event. Modal decomposition methods were employed to extract features, which were then used as inputs for the model.
- (2)
- In response to the limitations of the three common approaches in previous stuck pipe prediction studies—simple rule-based, physics-based, and data-driven methods—a more efficient model based on modal decomposition of near-bit data with physical constraints was proposed.
- (3)
- By comparing the six models and evaluating their performance metrics, it was found that the VMD + CNN-LSTM-Attention + Physical model achieved the best prediction results, with an R2 value reaching approximately 0.9, significantly outperforming other algorithms.
- (4)
- When applied to actual drilling operations, the model can effectively detect early signals of stuck pipe events and prevent stuck pipe accidents. It facilitates the implementation of timely and effective corrective measures, thereby reducing the occurrence of downhole incidents.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Q.; Li, Q.; Han, Y. A numerical investigation on kick control with the displacement kill method during a well test in a deep-water gas reservoir: A case study. Processes 2024, 12, 2090. [Google Scholar] [CrossRef]
- Li, Q.; Li, Q.; Wu, J.; Li, X.; Li, H.; Cheng, Y. Wellhead stability during development process of hydrate reservoir in the Northern South China Sea: Evolution and mechanism. Processes 2024, 13, 40. [Google Scholar] [CrossRef]
- Kaneko, T.; Inoue, T.; Nakagawa, Y.; Wada, R.; Abe, S.; Yasutake, G.; Fujita, K. Hybrid Approach Using Physical Insights and Data Science for Stuck-Pipe Prediction. SPE J. 2024, 29, 641–650. [Google Scholar] [CrossRef]
- Fernandez, B.M. Estimation of the Free Rotating Hook Load for WOB Estimation. Master’s Thesis, UIS, Springfield, IL, USA, 2022. Available online: https://hdl.handle.net/11250/3018193 (accessed on 20 November 2024).
- Esmael, B.; Arnaout, A.; Fruhwirth, R.; Thonhauser, G. A statistical feature-based approach for operations recognition in drilling time series. Int. J. Comput. Inf. Syst. Ind. Manag. Appl. 2012, 4, 100–108. [Google Scholar]
- Agrawal, R.; Malik, A.; Samuel, R.; Saxena, A. Real-time prediction of Litho-facies from drilling data using an Artificial Neural Network: A comparative field data study with optimizing algorithms. J. Energy Resour. Technol. 2022, 144, 043003. [Google Scholar] [CrossRef]
- Montes, A.C.; Pradeepkumar, A.; Eric, V.O. Review of Stuck Pipe Prediction Methods and Future Directions. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 6–8 October 2024. [Google Scholar] [CrossRef]
- Zhu, S.; Song, X.; Zhu, Z.; Yao, X.; Liu, M. Intelligent prediction of stuck pipe using combined data-driven and knowledge-driven model. Appl. Sci. 2022, 12, 5282. [Google Scholar] [CrossRef]
- Oyedere, M.O. Improved Torque and Drag Modeling Using Traditional and Machine Learning Methods. Diss. 2020. Available online: https://hdl.handle.net/2152/115839 (accessed on 20 November 2024).
- Zhou, Y. Data-Driven Drilling Optimization and Field Development in Unconventionals. Diss. 2019. Available online: https://hdl.handle.net/2152/88680 (accessed on 20 November 2024).
- Zhang, F.; Islam, A.; Zeng, H.; Chen, Z.; Zeng, Y.; Wang, X.; Li, S. Real time stuck pipe prediction by using a combination of physics-based model and data analytics approach. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 11–14 November 2019. [Google Scholar] [CrossRef]
- Agwu, O.E.; Akpabio, J.U.; Alabi, S.B.; Dosunmu, A. Artificial intelligence techniques and their applications in drilling fluid engineering: A review. J. Pet. Sci. Eng. 2018, 167, 300–315. [Google Scholar] [CrossRef]
- Hussain, B.; Du, Q.; Ren, P. Semi-supervised learning based big data-driven anomaly detection in mobile wireless networks. J. China Commun. 2018, 15, 41–57. [Google Scholar] [CrossRef]
- Wang, T.; Qiao, M.; Zhang, M.; Yang, Y.; Snoussi, H. Data-driven prognostic method based on self-supervised learning approaches for fault detection. J. Intell. Manuf. 2020, 31, 1611–1619. [Google Scholar] [CrossRef]
- Xu, H.; Sun, Z.; Cao, Y.; Bilal, H. A data-driven approach for intrusion and anomaly detection using automated machine learning for the Internet of Things. J. Soft Comput. 2023, 27, 14469–14481. [Google Scholar] [CrossRef]
- Taqvi, S.A.A.; Zabiri, H.; Tufa, L.D.; Uddin, F.; Fatima, S.A.; Maulud, A.S. A review on data-driven learning approaches for fault detection and diagnosis in chemical processes. ChemBioEng Rev. 2021, 8, 239–259. [Google Scholar] [CrossRef]
- Woldaregay, A.Z.; Årsand, E.; Botsis, T.; Albers, D.; Mamykina, L.; Hartvigsen, G. Data-driven blood glucose pattern classification and anomalies detection: Machine-learning applications in type 1 diabetes. J. Med. Internet Res. 2019, 21, e11030. Available online: https://preprints.jmir.org/preprint/11030 (accessed on 25 November 2024). [CrossRef] [PubMed]
- Daubechies, I.; Lu, J.; Wu, H.T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool. Appl. Comput. Harmon. Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Gilles, J. Empirical wavelet Transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. London Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Sharpley, R.C. Analysis of the intrinsic mode functions. Constr. Approx. 2006, 24, 17–47. [Google Scholar] [CrossRef]
- Wang, Y.-Q.; Gao, Y.-S.; Liu, J.-M.; Liu, C. Explicit formula for the Liutex vector and physical meaning of vorticity based on the Liutex-Shear decomposition. J. Hydrodyn. 2019, 31, 464–474. [Google Scholar] [CrossRef]
- Ben Ali, J.; Fnaiech, N.; Saidi, L.; Chebel-Morello, B.; Fnaiech, F. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals. Appl. Acoust. 2015, 89, 16–27. [Google Scholar] [CrossRef]
- Andrade, A.O.; Kyberd, P.; Nasuto, S.J. The application of the Hilbert spectrum to the analysis of electromyographic signals. Inf. Sci. 2008, 178, 2176–2193. [Google Scholar] [CrossRef]
- Chen, H.; Wu, H.; Kan, T.; Zhang, J.; Li, H. Low-carbon economic dispatch of integrated energy system containing electric hydrogen production based on VMD-GRU short-term wind power prediction. Int. J. Electr. Power Energy Syst. 2023, 154, 109420. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar] [CrossRef]
- Ma, J.; Huo, M.; Han, J.; Liu, Y.; Lu, S.; Yu, X. Integrated CNN-LSTM for Photovoltaic Power Prediction based on Spatio-Temporal Feature Fusion. Eng. Rep. 2025, 7, e13088. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. J. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- de Moura, J.; Xiao, Y.; Yang, J.; Butt, S.D. An empirical model for the drilling performance prediction for roller-cone drill bits. J. Pet. Sci. Eng. 2021, 204, 108791. [Google Scholar] [CrossRef]
- Gomes, D.; Jaritz, T.; Robinson, T.S.; and Revheim, O.E. Enhancing Stuck Pipe Risk Detection in Exploration Wells Using Machine Learning Based Tools: A Gulf of Mexico Case Study. In Proceedings of the IADC/SPE International Drilling Conference and Exhibition, Galveston, TX, USA, 5–7 March 2024. [Google Scholar] [CrossRef]
- Zhu, X.; Cheng, D.; Zhang, Z.; Lin, S.; Dai, J. An empirical study of spatial attention mechanisms in deep networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Lian, J.; Liu, Z.; Wang, H.; Dong, X. Adaptive variational mode decomposition method for signal processing based on mode characteristic. J. Mech. Syst. Signal Process. 2018, 107, 53–77. [Google Scholar] [CrossRef]
- Ullah, W.; Ullah, A.; Haq, I.U.; Muhammad, K.; Sajjad, M.; Baik, S.W. CNN features with bi-directional LSTM for real-time anomaly detection in surveillance networks. Multimed. Tools Appl. 2021, 80, 16979–16995. [Google Scholar] [CrossRef]
- Lai, G.; Chang, W.C.; Yang, Y.; Liu, H. Modeling long-and short-term temporal patterns with deep neural networks. In Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 95–104. [Google Scholar] [CrossRef]



| a. Initialize . |
| b. Extract the i-th Intrinsic Mode Function (IMF): 1. Initialization; . 2. Extract the local maxima and minima of . 3. Fit the upper and lower envelopes of the data sequence using cubic spline functions, respectively. 4. Calculate the mean of the upper and lower envelopes, denoted as . 5. Subtract the mean from the original data sequence to obtain a new sequence . If is an Intrinsic Mode Function (IMF), then . Otherwise, , and proceed to step 2 to repeat steps 2 to 5. |
| c. Calculate . |
| d. If has no fewer than two extreme points, then , and proceed to step 2. Otherwise, the decomposition is completed, and is the residual component. |
| WOB IMF Correlations (Sorted) | TOR IMF Correlations (Sorted) | RPM IMF Correlations (Sorted) |
|---|---|---|
| IMF 11: Correlation = 0.7276 | IMF 11: Correlation = 0.7077 | IMF 1: Correlation = 0.5562 |
| IMF 1: Correlation = 0.4265 | IMF 1: Correlation = 0.4611 | IMF 9: Correlation = 0.4347 |
| IMF 2: Correlation = 0.2688 | IMF 10: Correlation = 0.3782 | IMF 2: Correlation = 0.3298 |
| IMF 3: Correlation = 0.2039 | IMF 2: Correlation = 0.2986 | IMF 3: Correlation = 0.2731 |
| IMF 4: Correlation = 0.1835 | IMF 3: Correlation = 0.2070 | IMF 8: Correlation = 0.2640 |
| IMF 8: Correlation = 0.1447 | IMF 8: Correlation = 0.1870 | IMF 7: Correlation = 0.2262 |
| IMF 5: Correlation = 0.1210 | IMF 4: Correlation = 0.1415 | IMF 4: Correlation = 0.2117 |
| IMF 9: Correlation = 0.1146 | IMF 9: Correlation = 0.1362 | IMF 5: Correlation = 0.1552 |
| IMF 10: Correlation = 0.1100 | IMF 5: Correlation = 0.1142 | IMF 10: Correlation = 0.1530 |
| IMF 7: Correlation = 0.1091 | IMF 6: Correlation = 0.1107 | IMF 6: Correlation = 0.1518 |
| IMF 6: Correlation = 0.0936 | IMF 7: Correlation = 0.0984 | IMF 11: Correlation = 0.0634 |
| IMF 12: Correlation = 0.0202 | ||
| IMF 13: Correlation = 0.0157 |
| WOB IMF Correlations (Sorted) | TOR IMF Correlations (Sorted) | RPM IMF Correlations (Sorted) |
|---|---|---|
| IMF 1: Correlation = 0.8003 | IMF 1: Correlation = 0.7827 | IMF 1: Correlation = 0.6729 |
| IMF 2: Correlation = 0.2596 | IMF 3: Correlation = 0.2631 | IMF 2: Correlation = 0.3352 |
| IMF 3: Correlation = 0.2450 | IMF 7: Correlation = 0.2558 | IMF 7: Correlation = 0.3105 |
| IMF 7: Correlation = 0.2447 | IMF 8: Correlation = 0.2544 | IMF 3: Correlation = 0.3057 |
| IMF 5: Correlation = 0.2421 | IMF 2: Correlation = 0.2514 | IMF 8: Correlation = 0.2994 |
| IMF 4: Correlation = 0.2419 | IMF 6: Correlation = 0.2416 | IMF 4: Correlation = 0.2882 |
| IMF 6: Correlation = 0.2384 | IMF 4: Correlation = 0.2397 | IMF 6: Correlation = 0.2739 |
| IMF 8: Correlation = 0.2183 | IMF 5: Correlation = 0.2391 | IMF 5: Correlation = 0.2611 |
| Mode | Running Time | Drilling Parameters | MSE | MAE | R2 |
|---|---|---|---|---|---|
| VMD + CNN-LSTM-Attention | 9 s | WOB | 0.3963 | 0.5306 | 0.5715 |
| TOR | 0.0138 | 0.0944 | 0.5926 | ||
| RPM | 5.1653 | 1.8672 | 0.8581 | ||
| VMD + CNN-LSTM-Attention + Physical | 10 s | WOB | 0.1700 | 0.3319 | 0.8636 |
| TOR | 0.0034 | 0.0477 | 0.9128 | ||
| RPM | 1.0040 | 0.7626 | 0.9801 |
| Mode | Running Time | Drilling Parameters | MSE | MAE | R2 |
|---|---|---|---|---|---|
| EMD + CNN-LSTM-Attention | 18 s | WOB | 1.0888 | 0.8331 | 0.4131 |
| TOR | 0.0089 | 0.0705 | 0.8058 | ||
| RPM | 33.7098 | 4.5010 | 0.0782 | ||
| EMD + CNN-LSTM-Attention + Physical | 37 s | WOB | 0.8935 | 0.7496 | 0.5183 |
| TOR | 0.0074 | 0.0659 | 0.8382 | ||
| RPM | 25.5727 | 4.0667 | 0.3007 |
| Mode | Drilling Parameters | MSE | MAE | R2 |
|---|---|---|---|---|
| EMD + CNN-LSTM-Attention | WOB | 1.0888 | 0.8331 | 0.4131 |
| TOR | 0.0089 | 0.0705 | 0.8058 | |
| RPM | 33.7098 | 4.5010 | 0.0782 | |
| VMD + CNN-LSTM-Attention | WOB | 0.3963 | 0.5306 | 0.5715 |
| TOR | 0.0138 | 0.0944 | 0.5926 | |
| RPM | 5.1653 | 1.8672 | 0.8581 |
| Mode | Drilling Parameters | MSE | MAE | R2 |
|---|---|---|---|---|
| EMD + CNN-LSTM-Attention + Physical | WOB | 0.8935 | 0.7496 | 0.5183 |
| TOR | 0.0074 | 0.0659 | 0.8382 | |
| RPM | 25.5727 | 4.0667 | 0.3007 | |
| VMD + CNN-LSTM-Attention + Physical | WOB | 0.1700 | 0.3319 | 0.8636 |
| TOR | 0.0034 | 0.0477 | 0.9128 | |
| RPM | 1.0040 | 0.7626 | 0.9801 |
| Mode | Drilling Parameters | MSE | MAE | R2 |
|---|---|---|---|---|
| SG + CNN-LSTM-Attention | WOB | 0.4545 | 0.5301 | 0.6673 |
| TOR | 0.2143 | 0.0942 | 0.6587 | |
| RPM | 11.4169 | 2.4854 | 0.7128 | |
| SG + CNN-LSTM-Attention + Physical | WOB | 0.4426 | 0.4241 | 0.7738 |
| TOR | 0.0117 | 0.0847 | 0.8109 | |
| RPM | 11.3061 | 2.6220 | 0.7968 |
| Mode | Drilling Parameters | MSE | MAE | R2 |
|---|---|---|---|---|
| VMD + Physical + CNN-LSTM + Attention (multi-step) | WOB | 0.2321 | 0.2307 | 0.7983 |
| TOR | 0.0074 | 0.0668 | 0.8602 | |
| RPM | 8.2553 | 2.3528 | 0.8409 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Xue, Y.; Meng, Z.; Sader, M.; Zhang, W.; Li, J. Drill Sticking Prediction Based on Modal Decomposition and Physical Constraint Model of Near-Bit Data. Processes 2025, 13, 1802. https://doi.org/10.3390/pr13061802
Zhang T, Xue Y, Meng Z, Sader M, Zhang W, Li J. Drill Sticking Prediction Based on Modal Decomposition and Physical Constraint Model of Near-Bit Data. Processes. 2025; 13(6):1802. https://doi.org/10.3390/pr13061802
Chicago/Turabian StyleZhang, Tao, Yixiao Xue, Zhuoran Meng, Malika Sader, Wenjie Zhang, and Jun Li. 2025. "Drill Sticking Prediction Based on Modal Decomposition and Physical Constraint Model of Near-Bit Data" Processes 13, no. 6: 1802. https://doi.org/10.3390/pr13061802
APA StyleZhang, T., Xue, Y., Meng, Z., Sader, M., Zhang, W., & Li, J. (2025). Drill Sticking Prediction Based on Modal Decomposition and Physical Constraint Model of Near-Bit Data. Processes, 13(6), 1802. https://doi.org/10.3390/pr13061802






